Generalizing Quantile Regression for Counting Processes with Applications to Recurrent Events

Abstract

In survival analysis, quantile regression has become a useful approach to account for covariate effects on the distribution of an event time of interest. In this paper, we discuss how quantile regression can be extended to model counting processes, and thus lead to a broader regression framework for survival data. We specifically investigate the proposed modeling of counting processes for recurrent events data. We show that the new recurrent events model retains the desirable features of quantile regression such as easy interpretation and good model flexibility, while accommodating various observation schemes encountered in observational studies. We develop a general theoretical and inferential framework for the new counting process model, which unifies with an existing method for censored quantile regression. As another useful contribution of this work, we propose a sample-based covariance estimation procedure, which provides a useful complement to the prevailing bootstrapping approach. We demonstrate the utility of our proposals via simulation studies and an application to a dataset from the US Cystic Fibrosis Foundation Patient Registry (CFFPR).

1. INTRODUCTION

Quantile regression (Koenker and Bassett 1978) has gained increasing popularity in survival analysis for its easy interpretation and flexibility in exploring the dynamic relationship between a time-to-event outcome and covariates (Powell 1984; Ying, Jung, and Wei 1995; Yang 1999; Portnoy 2003; Neocleous, Vanden Branden, and Portnoy 2006; Peng and Huang 2008; Portnoy and Lin 2010; Huang 2010, among others). For a time-to-event response T , a quantile regression model may assume that

$$Q_T(\tau \mid \mathit{Z})=\exp \left\{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)\right\},\tau \in (0,1),$$ (1)

where Q_T (τ|Z) inf{t : Pr(T ≤ t|Z) ≥ τ denotes the τ-th quantile of T given the p × 1 covariate vector Z, X = (1, Z^T)^T, and ${\beta }_0^{nr}\left(\tau \right)$ is a (p + 1) × 1 vector of regression coefficients. By formulating covariate effects on different quantiles of T , model (1) enables a comprehensive examination of covariates’ impact on the distribution of a time-to-event outcome. Unless otherwise specified, this article is confined to regression settings with only time-independent covariates.

In this paper, we consider extending quantile regression to model counting processes, a more general notion for describing outcomes observed in survival studies as compared to the time-to-event formulation adopted by model (1). In the traditional setting concerning only one event time, the survival information can be characterized by a counting process with a single jump at the observed event time. In recurrent events settings, where the event of interest (e.g. infection, hospitalization) can occur repeatedly, a single event time usually fails to fully capture the event history information of interest. In contrast, the counting process of recurrent events, which allows for multiple jumps, can well depict the trajectory of event occurrence and thus capture event history in full.

Many traditional survival models have been studied for their extensions for counting processes. Examples include the Cox's regression model to counting processes by Andersen and Gill (1982), the accelerated failure time model for counting processes by Lin, Wei, and Ying (1998), and more recently, transformation models for counting processes by Zeng and Lin (2006). As quantile regression has emerged as a valuable regression tool for survival data, studying its generalization for counting processes constitutes a sensible effort that can lead to two-fold benefits. First, the new counting process model is expected to handle additional types of survival data that cannot be straightforwardly covered by quantile regression model (1), such as recurrent events data. Second, as will be explained below, counting process based modeling generally facilitates the accommodation of various incomplete follow-up scenarios, a task that can be more difficult when a time-to-event formulation is adopted, as in quantile regression model (1).

Overall, this work bears a general goal of developing new counting process models extended from quantile regression modeling of a time-to-event response. We shall expound the main ideas in a recurrent events setting that arises from our motivating study. The presented strategies for estimation and inference are readily adaptable to other survival settings where data can be meaningfully captured by counting processes.

2. THE PROPOSED COUNTING PROCESS MODEL

We begin with a review of Andersen and Gill (1982)'s counting process formulation of the Cox proportional hazards model (Cox 1972). Let T and C denote time to an event of interest and time to censoring, respectively. With T subject to right censoring by C, observables include $\tilde{T}\equiv T\wedge C$ and δ ≡ I(T ≤ C), where ∧ is the minimum operator. When there are only time-independent covariates, the counting process formulation of the Cox model can be given by

$$E\{d{N}^{nr}\left(t\right)\mid Y^{nr}\left(t\right),\mathit{Z}\}=Y^{nr}\left(t\right){\lambda }_0\left(t\right)e^{{\mathit{Z}}^{\mathsf{T}}\mathit{b}}dt,t>0,$$ (2)

where N^nr(t) = I(T̃ ≤ t, δ = 1), and Y^nr(t) = I(T̃ ≥ t), representing the observed counting process and the at-risk process for the event of interest, respectively. Here λ₀(s) stands for the baseline hazard function, Z denotes a p × 1 covariate vector, and b denotes the vector of regression coefficients. Model (2) formulates proportional covariate effects on E{dN^nr(t)|Y ^nr(t), Z}, which corresponds to the intensity process for the counting process N^nr(t) given Z. As shown by Andersen and Gill (1982), the counting process formulation of the Cox model not only facilitates a rigorous development of asymptotic theory, but also renders a broadened regression framework that can well accommodate recurrent events data.

Through a re-examination of the work by Peng and Huang (2008), we can derive a counting process formulation of censored quantile regression model (1). That is, when T is subject to random censoring by C, which is independent of T given Z, it holds under model (1) that

$$E\{N^{nr}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}}\left(\tau \right)\right)\mid \mathit{Z}\}=E\left\{{\int }_0^{\tau }{Y}^{nr}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(s\right)}\right)\frac{1}{1-s}ds\mid \mathit{Z}\right\},\tau \in (0,1).$$ (3)

In terms of the intensity process, (3) can be rewritten as

$$E\{d{N}^{nr}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)}\right)\mid Y^{nr}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)}\right)\mathit{Z}\}=Y^{nr}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)}\right)\frac{1}{1-\tau }d\tau .$$ (4)

By (4), the intensity for N^nr(t) equals $\frac{Y^{nr}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)}\right)}{(1-\tau )e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)}\left\{{\mathit{X}}^{\mathsf{T}}{\stackrel{.}{\beta }}_0^{nr}\left(\tau \right)\right\}}$ at time $t=e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0^{nr}\left(\tau \right)}$, where ${\stackrel{.}{\beta }}_0^{nr}\left(\tau \right)$ denotes the derivative of ${\beta }_0^{nr}\left(\tau \right)$ with regard to τ. This shows that censored quantile regression does not imply a simple relationship between event intensity process and covariates, unlike the Cox model (2). Nevertheless, there exists an analogy between (2) and (4) in the sense that both models incorporate covariate effects via specifying the link between the counting process N^nr(·) and the at-risk process Y ^nr(·). Such a view implicates a general strategy for modeling a counting process, which is not limited to formulating covariate effects on its intensity process.

Following this general modeling strategy, we propose a new counting process model that takes the form,

$$E\{N\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(u\right)}\right)\mid \mathit{Z}\}=E\left\{{\int }_0^{u}Y\left(e^{{\mathit{X}}^{\mathsf{T}{\beta }_0}\left(s\right)}\right)g\left(s\right)ds\mid \mathit{Z}\right\},u\in (0,U],$$ (5)

where N(·) is a counting process of interest, Y (·) is an at-risk process appropriately specified according to N(·), g(·) is a known positive and continuous function, β₀(·) is a (p + 1) × 1 vector of unknown regression coefficient functions, and U is a positive constant. Note that the at-risk process Y (·) is only required to be left continuous, and thus it can be well defined in many incomplete follow-up scenarios (e.g. window observations of recurrent events). This indicates the flexibility of model (5) to accommodate realistic data observation schemes in survival studies.

The proposed model (5) is motivated by the counting process model (3) implied by the quantile regression model (1). In the standard survival setting with N(·) = N^nr(·), Y (·) = Y ^nr(·), and g(u) = 1/(1 − u), model (5) becomes model (3). Proposition A1 of the Supplementary Materials shows that model (3) is equivalent to a weaker version of model (1) with τ ∈ (0, 1) replaced by τ ∈ (0, τ_U], where τ_U is a positive constant less than 1. This result reflects the connection between censored quantile regression and the proposed counting process model.

In model (5), a general function g(u) is adopted in place of the function 1/(1 − u) in (3). The specification of g(·) determines the scale in which covariate effects are formulated. For example, in the standard random censoring case concerning a single event time T , specifying g(u) ≡ 1, rather than 1/(1 − u), would yield a model that formulates covariate effects on the inverse cumulative hazard function, namely inf{t : Λ_T (t|Z) ≥u}, rather than the conditional quantile function, where Λ_T (t|Z) denotes the cumulative hazard function of T given Z. At the same time, we can show that allowing g(·) to take a general form in the proposed model generally does not incur extra complications in inference and computation.

3. THE APPLICATION TO RECURRENT EVENTS DATA

We shall illustrate the major methodological ideas by applying the proposed counting process model to recurrent events data.

Recurrent events data is an important type of survival data, which is frequently encountered in clinical and epidemiological studies. There has been a vast literature on recurrent events data analysis. For example, well-known methods include modeling the intensity process of recurrent events (Prentice, Williams, and Peterson 1981; Andersen and Gill 1982; Chang and Wang 1999, among others) and modeling the marginal hazard of each recurrent event (Wei, Lin, and Weissfeld 1989; Cai and Prentice 1995, 1997; Spiekerman and Lin 1998, among others) or the gap time between recurrent events (Huang and Chen 2003; Schaubel and Cai 2004; Sun, Park, and Sun 2006, among others). In addition, Hougaard (2000) provided a detailed account of how recurrent events problems can be fit into the paradigm of multi-state models, for which transition probability or transition intensity between states can be estimated to characterize event progression. Shared frailty models were also proposed to explicitly model intra-subject correlations (Liang, Self, Nanndeen-Roche, and Zeger 1995; Wei and Glidden 1997; Hougaard 2000, among others). Adopting frailty models can provide additional information on the dependency among the event time components of recurrent events data.

Another popular approach for recurrent events data is to specify covariate effects on mean or rate functions of recurrent events (Pepe and Cai 1993; Lawless and Nadeau 1995; Lin, Wei, Yang, and Ying 2000; Schaubel, Zeng, and Cai 2006; Huang and Peng 2009; Sun and Guo 2011, among others). This type of approach is attractive because mean or rate functions are more intuitive to interpret than intensity or hazard functions. Modeling these quantities can avoid assumptions about the dependency of recurrent events, which are difficult to verify but are required by intensity models, multi-state models or shared frailty models.

3.1 The proposed recurrent events model

We consider a general data situation, where the observation of recurrent events is subject to an observation window specified as a time interval (L, R] (Nelson 2003). As a result, the counting process for the observed recurrent events is given by $N^{re}\left(t\right)={\sum }_{j=1}^{\infty }I(L\le T_j^{\left(i\right)}\le t\wedge R)$, where T^(j) denotes the jth recurrent event time (j = 1, 2, . . .), and the at-risk process is given by Y^re (t) = I (L < t ≤ R). The observed recurrent events data include n i.i.d. replicates of N^re(·), Z, L, and R, denoted by ${\{N_i^{re}(\cdot ),{\mathit{Z}}_i,L_i,R_i\}}_{i=1}^n$.

Take the U.S. Cystic Fibrosis (CF) Foundation Patient Registry (CFFPR) data for example. Pseudomonas aeruginosa (PA) is a common and major pathogen in cystic fibrosis (CF) lungs, often resulting in chronic infections. Since no record of PA infections is available before registry entry, the observation window for PA infections is from the age at the first registry visit (L) to the age at the last follow-up before data collection cut-off date (R).

It is worth mentioning that nonzero lower bounds of observation windows have traditionally been paid less attention in recurrent events data analyses as compared to upper bounds. However, they are commonly encountered in observational studies. In CFFPR, a large proportion of subjects did not enter the registry right after birth due to delayed CF diagnosis or other reasons, resulting in many nonzero L_i's. As implied by our numerical studies, naively treating them as zeros can considerably bias the inference regarding PA infection recurrence times.

The proposed counting process model (5) offers a natural way to model recurrent events subject to window observation. With N(·) and Y (·) specified as N^re(·) and Y ^re(·) respectively, model (5) gives rise to a new recurrent events model,

$$E\{N^{re}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(u\right)}\right)\mid \mathit{Z}\}=E\{{\int }_0^u{Y}^{re}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(s\right)}\right)g\left(s\right)ds\mid \mathit{Z}\},u\in (0,U].$$ (6)

Assume (L, R) is independent of Ñ(·) given Z. Proposition A2 of the Supplementary Materials shows that (6) is equivalent to

$${\mu }_{\mathit{Z}}\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(u\right)}\right)=G\left(u\right)\equiv {\int }_0^{u}g\left(s\right)ds,u\in (0,U],$$

where μ_Z(t) is the so-called mean function of recurrent events, defined as μ_Z(t) = E{Ñ(t)|Z with $\tilde{N}\left(t\right)={\sum }_{j=1}^{\infty }I(T^{\left(j\right)}\le t)$. The mean function (or expected frequency) of recurrent events reflects the cumulative rate of counting process N^re(t), in contrast to the intensity function, which characterizes the instantaneous rate of events conditional on past history (Lin et al. 2000).

Therefore, an alternative representation of model (6) is given by

$${\tau }_{\mathit{Z}}\left(G\left(u\right)\right)=\exp \left\{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(u\right)\right\},u\in (0,U],$$ (7)

where τ_Z(u) = inf{t ≥ 0 : μ_Z(t) ≥ u}. The quantity τ_Z(u) was termed time to expected frequency u by Huang and Peng (2009). When the event of interest can occur only once and thus frequency u is restricted to the range of [0, 1], τ_Z(u) becomes the conditional quantile of T ⁽¹⁾ given Z. By model representation (7), the non-intercept coefficients in β₀(u) capture the covariate effects on time to expected frequency at G(u).

When g(u) = 1 (and thus G(u) = u), model (7) becomes the accelerated recurrence time (ART) model (Huang and Peng 2009), which is known to include the accelerated failure time model for recurrent events (Lin et al. 1998) as a special case. On the other hand, equation (6) provides information on how the observed counting process and the at-risk process are related under the ART model. One may choose g(u) as a positive continuous function other than g(u) = 1. The essential difference of the resulting model from the ART model would be the coefficient function rescaled from β₀(·) to β₀(G⁻¹(·)), the result of formulating covariate effects on τ_Z(G(u)) instead of τ_Z(u). Given that (7) implies (6), we shall refer to model (6) as the generalized accelerated recurrence time (GART) model.

The proposed recurrent events model has considerable practical appeal. It models time to expected frequency, τ_Z(u), which may be viewed as the inverse of the mean function of recurrent events. Consequently, like means/rates based recurrent events models, the proposed model is intuitive to interpret and does not require specification of dependency through event history. While current means/rates based models mostly target the frequency scale of the mean function, the proposed model formulates covariate effects on the time scale of the mean function, and thus permits “direct physical interpretations” (Reid 1994). Such a feature may be preferred by many practitioners.

Furthermore, as elaborated in Sections 3.2–3.4, we uncover a general theoretical and inferential framework that can unify the studies of the GART model with recurrent events data and the quantile regression model (1) with randomly censored nonrecurrent event data. Thus, it is highly feasible that current software for censored quantile regression may be extended to carry out the proposed method for recurrent events data.

As another useful contribution of this work, based on our theoretical studies, we present in Section 3.4 a sample-based procedure to estimate the asymptotic covariance of the proposed estimator. According to our simulations, the new covariance estimation procedure can save two-to-three fold computation time as compared to the prevailing bootstrapping-based inference. This feature is particularly attractive for analyzing large datasets, such as the registry data from CFFPR.

3.2 The proposed estimation procedure

In the special case where L_i = 0 (i = 1, . . . , n) and G(u) = u, Huang and Peng (2009) proposed an estimator of β₀(u) as the minimizer of the following objective function:

$$\Psi (\beta ;u)=n^{-1}\sum _{i=1}^n\left\{\sum _{j=1}^{\infty }I(T_i^{\left(j\right)}<R_i){({\mathit{X}}_i^{\mathsf{T}}\beta \wedge \log R_i-\log T_i^{\left(j\right)})}^{+}-({\mathit{X}}_i^{\mathsf{T}}\beta \wedge \log R_i)u\right\}.$$

This estimator is a generalization of Powell (1984, 1986)'s estimator for censored quantile regression when the censoring time is always known. It is easy to see that the objective function, Ψ(β; u), is not convex. Huang and Peng (2009) developed an algorithm which is guaranteed to find a local strict minimizer that is asymptotically equivalent to the global minimizer of the proposed objective function.

While it is rather intuitive to modify Powell (1984, 1986)'s estimator to handle double censoring to an event time (Fitzenberger 1997) based on the equivariance property of quantiles (Koenker 2005), it is quite challenging to apply the same strategy to extend Huang and Peng (2009)'s method to window observed recurrent events data with nonzero L_i's. This is because the presence of nonzero L_i's can greatly increase the amount of missing information on the underlying counting process of recurrent events,Ñ_i(t). When L_i = 0, $T_i^{\left(j\right)}$ is observed if $T_i^{\left(j\right)}\le R_i$; otherwise $T_i^{\left(j\right)}$ is known to be greater than or equal to R_i. This meansÑ_i(t) is partially observable. However, with L_i > 0, some recurrent events may have occurred before time L_i, but when such events have occurred, and how many are generally unknown. Therefore, one always lacks definitive information on $T_i^{\left(1\right)}$, and a similar ambiguity exists for any T^(j) with j ≥ 2. As a result, Ñ_i(t) is never observable when L_i > 0. Such a significant information loss onÑ_i(t) given L_i > 0 is the main factor that prevents a straightforward adaptation of Huang and Peng (2009)'s method to handle window-observed recurrent events data.

Our estimating equation for β₀(u) is directly motivated by the counting process based model representation (6). Specifically, by (6), we can readily identify an observable stochastic process, $M\left(u\right)\equiv N\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(u\right)}\right)-{\int }_0^{u}Y\left(e^{{\mathit{X}}^{\mathsf{T}}{\beta }_0\left(s\right)}\right)g\left(s\right)ds$, such that E{M(u)|X} = 0 for u > 0. Here and hereafter, N(·) and Y (·) stand for the counting process and the at-risk process adopted in our recurrent events setting, namely N^re(·) and Y ^re(·) respectively. Note that M(u) is not a martingale in general but possesses the same utility as a martingale to construct an estimating equation for β₀(·).

More specifically, we propose to estimate β₀(u) based on the estimating equation:

$$n^{1∕2}{\mathit{S}}_n(\beta ,u)=0,$$ (8)

where

$${\mathit{S}}_n(\beta ,u)=n^{-1}\sum _{i=1}^n{\mathit{X}}_i\left\{N_i\left(\exp \left\{{\mathit{X}}_i^{\mathsf{T}}\beta \left(u\right)\right\}\right)-{\int }_0^u{Y}_i\left(\exp \left\{{\mathit{X}}_i^{\mathsf{T}}\beta \left(s\right)\right\}\right)g\left(s\right)ds\right\}.$$

In the traditional nonrecurrent event setting with N_i(·) and Y_i(·) replaced by $N_i^{nr}(\cdot )$ and $Y_i^{nr}(\cdot )$ respectively, equation (8) boils down to the estimating equation proposed in Peng and Huang (2008) for censored quantile regression. This connection shows that equation (8) unifies the existing estimation for censored quantile regression and the proposed estimation for the new recurrent events model (6).

We can adopt a grid-based algorithm for estimating β₀(·) based on equation (8). More specifically, define a grid, S_L(n) = {0 = u₀ < u₁ < . . . < u_L(n) = U}. The size of S_L(n) is denoted by ∥S_L(n)∥ ≡ max_j=1,...,L | u_j − u_j−1|. Our proposed estimator, $\widehat{\beta }(\cdot )$, is a right-continuous piecewise-constant function that jumps only at the grid S_L(n). Given that τ_Z(0) = exp{X^T β₀(0)} = 0, we set $\exp \left\{{\mathit{X}}_i^{\mathsf{T}}\widehat{\beta }\left(0\right)\right\}=0$ for all i. We propose to obtain $\widehat{\beta }\left(u_k\right)$, k - 1, 2, ..., L(n), by sequentially solving the estimating equation,

$$n^{-1∕2}\sum _{i=1}^n{\mathit{X}}_i\left\{{\tilde{N}}_i\left(\exp \left\{{\mathit{X}}_i^T\beta \left(u_k\right)\right\}\right)-\sum _{m=0}^{k-1}{Y}_i\left(\exp \left\{{\mathit{X}}_i^T\widehat{\beta }\left(u_m\right)\right\}\right){\int }_{u_m}^{u_{m+1}}g\left(s\right)ds\right\}=0,$$ (9)

for β(u_k).

Note that equation (9) is not continuous; thus an exact solution that makes (9) strictly hold may not exist. Therefore, $\widehat{\beta }\left(u_k\right)$ is defined as a generalized solution to equation (9) (Fygenson and Ritov 1994). Because equation (9) is monotone, the set of generalized solutions is convex of diameter O(n⁻¹) (Fygenson and Ritov 1994). To find a generalized solution to equation (9), an equivalent alternative approach is to locate the minimizer of the L₁-type convex function,

$$l_k\left(\mathit{h}\right)=\sum _{i=1}^n\sum _{j=1}^{\infty }I(L_i\le T_i^{\left(j\right)}\le R_i)\mid \log T_i^{\left(j\right)}-{\mathit{X}}_i^{\mathsf{T}}\mathit{h}\mid +\mid R^{\ast }-\left\{\sum _{i=1}^n\sum _{j=1}^{\infty }I(L_i\le T_i^{\left(j\right)}\le R_i){(-{\mathit{X}}_i)}^{\mathsf{T}}\mathit{h}\right\}\mid +\mid R^{\ast }-\delta \left\{\sum _{i=1}^{n}2{\mathit{X}}_i^{\mathsf{T}}\mathit{h}\sum _{m=0}^{k-1}{Y}_i\left(\exp \left\{{\mathit{X}}_i^{\mathsf{T}}\widehat{\beta }\left(u_m\right)\right\}\right){\int }_{u_m}^{u_{m+1}}g\left(s\right)ds\right\}\mid ,$$

where R* is a very large number and j = 1, . . . , L(n). Following arguments similar to those in the Appendix of Peng and Fine (2009), we can show that ∂l_k(β(u_k))/∂β (u_k) equals 2 times the estimating function in (9) when R* is chosen large enough to bound $\mid \left\{{\sum }_{i=1}^n{\sum }_{j=1}^{\infty }I(L_i\le T_i^{\left(j\right)}\le R_i){(-{\mathit{X}}_i)}^{\mathsf{T}}\mathit{h}\right\}\mid$ and $\mid \left\{{\sum }_{i=1}^{n}2{\mathit{X}}_i^{\mathsf{T}}\mathit{h}{\sum }_{m=0}^{k-1}{Y}_i\left(\exp \left\{{\mathit{X}}_i^{\mathsf{T}}\widehat{\beta }\left(u_m\right)\right\}\right){\int }_{u_m}^{u_{m+1}}g\left(s\right)ds\right\}\mid$. This to equation then justifies the use of the minimizer of l_k(h) as a generalized solution(9).

One can solve the minimization of l_k(h) by using standard statistical software–for example, the l1fit() function in S-PLUS or the rq() function in R package quantreg. As shown in our theoretical studies, a grid size of order o(n^−1/2) would be su cient for our grid-based estimator to have desirable asymptotic properties, including uniform consistency and weak convergence to a Gaussian process. In our numerical studies, our choice of ∥S_L(n)∥ is of order O(n⁻¹), by which we achieve good empirical results on both estimation accuracy and computational feasibility. A grid-free algorithm may be developed by adapting the strategy of Huang (2010).

3.3 Asymptotic properties

We establish the uniform consistency and weak convergence of the proposed estimator $\widehat{\beta }(\cdot )$. Define A(b) = E{XN(exp(X^Tb))}, B(b) = dA(b)/db^T, à b) = E{XY (exp(X^Tb))}, J(b) = dà (b)/db^T, ${\tilde{\mu }}_Z\left(x\right)=E\{N\left(x\right)\mid \mathit{Z}\}$, $g_{\mathit{Z}}\left(x\right)=d{\tilde{\mu }}_{\mathit{Z}}\left(x\right)∕dx$, and ${\stackrel{.}{\mu }}_{\mathit{Z}}\left(x\right)=d{\mu }_{\mathit{Z}}\left(x\right)∕dx$. For a vector v, define ${\mathit{v}}^{\otimes 2}=\mathit{v}{\mathit{v}}^{\mathsf{T}}$. We let $f_{\mathit{Z}}^L\left(x\right)$ and $f_{\mathit{Z}}^R\left(x\right)$ denote the conditional density functions of L and R given Z respectively. Simple algebra can show that $\mathit{B}\left(\mathit{b}\right)=E\left\{{\mathit{X}}^{\otimes 2}{e}^{{\mathit{X}}^{\mathsf{T}}b}{g}_{\mathit{Z}}\left(e^{{\mathit{X}}^{\mathsf{T}}b}\right)\right\}$ and $\mathit{J}\left(\mathit{b}\right)=E{\mathit{X}}^{\otimes 2}{e}^{{\mathit{X}}^{\mathsf{T}}b}\{f_{\mathit{Z}}^L\left(e^{{\mathit{X}}^{\mathsf{T}}b}\right)-f_{\mathit{Z}}^R\left(e^{{\mathit{X}}^{\mathsf{T}}b}\right)\}]$.

We assume the following regularity conditions:

• C1: Z and N(R) are bounded.

• C2: Each component of A(β₀(u)) is a Lipschitz function of u.

• C3: (a) g_Z(exp(X^Tb)) > 0 for any $\mathit{b}\in \mathcal{B}\left(d_0\right)$ and $\mathit{Z}\in \mathcal{Z}$, (b) $E\left({\mathit{Z}}^{\otimes 2}\right)$ is positive definite, and (c) each component of J(b)B(b)⁻¹ is uniformly bounded in $\mathbf{b}\in \mathcal{B}\left(d_0\right)$, where $\mathcal{B}\left(d_0\right)$ is a neighborhood containing $\{{\beta }_0\left(u\right),u\in (0,U]\}$, defined in Supplement B of the Supplementary Materials.

• C4: inf_u∈[v,U] eigminB(β₀(u)) > 0 for any v 2 (0, U], where eigmin(·) denotes the minimum eigenvalue of a matrix.

Condition C1 assumes bounded covariates and a bounded total number of events observed during follow-up, and condition C2 implies the smoothness of β₀(u). Condition C3 asserts additional mild assumptions, such as positive rate function of Ñ(t) and positive definite $E\left({\mathit{Z}}^{\otimes 2}\right)$. Condition C4 is a key technical assumption which ensures the consistency of the proposed estimator. By the definition of B(b), condition C4 implies g_z (exp{X^T ₀(u)}) > 0 for 0 < u < U. This means the recurrent event should have a positive rate of being observed throughout the time interval (0, τ_Z(U)) under the random window observation scheme. This would generally require that the lower bound of the support of $f_{\mathit{Z}}^L(\cdot )$ equals 0 and the upper bound of the support of $f_{\mathit{Z}}^R(\cdot )$ exceeds τ_Z(U).

We can establish the following theorems:

Theorem 1. Under conditions C1-C4, if lim_n→∞ ∥S_L(n)∥ = 0, then ${\sup }_{u\in [v,U]}\Vert \widehat{\beta }\left(u\right)-{\beta }_0\left(u\right)\Vert {\to }_{p}0$, where 0 < v < U.

Theorem 2. Under conditions C1-C4, if lim_n→∞ n^1/2∥S_L(n)∥ = 0, then $n^{1∕2}\{\widehat{\beta }\left(u\right)-{\beta }_0\left(u\right)\}$ converges weakly to a Gaussian process for u ∈ [v, U], where 0 < v < U.

The proofs of Theorems 1–2 follow the same set of lines that Peng and Huang (2008) adopted for censored quantile regression. This is because of the uniformity in the estimation framework demonstrated in Section 3.2; both estimation methods are closely tied to a Volterra integral equation, which, in this work, takes the form,

$$\mathit{A}\left(\beta \left(u\right)\right)-{\int }_0^u\tilde{\mathit{A}}\left(\beta \left(s\right)\right)g\left(s\right)ds=0.$$

The proposed sequential estimation procedure is essentially the first-order Euler scheme to the numerical solution to the above equation. The proofs are relegated to Supplement B of the Supplementary Materials.

3.4 Inference

To make inference on β₀(u), bootstrapping procedures can be used. For example, one may adopt a resampling procedure along the lines of Jin, Ying, and Wei (2001) by considering a perturbed estimating equation,

$$n^{-1∕2}\sum _{i=1}^n{v}_i{\mathit{X}}_i\left\{N_i\left(e^{{\mathit{X}}_i^T\beta \left(u\right)}\right)-{\int }_0^u{Y}_i\left(e^{{\mathit{X}}_i^T\beta \left(s\right)}\right)g\left(s\right)ds\right\}=0,$$

where ${\left\{v_i\right\}}_{i=1}^n$ are i.i.d. variates from a nonnegative distribution of unit mean and unit variance, such as an exponential distribution of unit rate. The above stochastic integral equation can be solved via a procedure similar to that proposed for equation (8). Denote the resulting solution by ${\widehat{\beta }}^{\ast }(\cdot )$. It can be shown that the distribution of $n^{1∕2}\{{\widehat{\beta }}^{\ast }\left(u\right)-\widehat{\beta }\left(u\right)\}$ conditionally on the observed data and the unconditional distribution of $n^{1∕2}\{\widehat{\beta }\left(u\right)-{\beta }_0\left(u\right)\}$ have the same limiting distribution. By repeatedly generating ${\left\{v_i\right\}}_{i=1}^n$, one may obtain a large number of realizations of $n^{1∕2}\{{\widehat{\beta }}^{\ast }\left(u\right)-\widehat{\beta }\left(u\right)\}$, the empirical distribution of which can be used to give a covariance estimate for $\widehat{\beta }\left(u\right)$ or a confidence interval for β₀(u).

We develop a sample-based approach for covariance estimation that does not involve bootstrapping and thus can save considerable computation time. The key idea is to find consistent estimates for B(β₀(τ)) and J(β₀(τ)) and then plug them into the closed form derived for the asymptotic covariance matrix of $n^{1∕2}\{\widehat{\beta }\left(u\right)-{\beta }_0\left(u\right)\}$; see equation (B.6) in Supplement B of the Supplementary Materials. However, directly evaluating B(β₀(τ)) and J(β₀(τ)) based on their definitions would involve density estimation, which may not be stable nor efficient with small to moderate sample sizes.

To avoid density estimation, we propose a novel adaptation of the technique of Huang (2002) and Peng and Fine (2009). Note that neither Huang (2002) nor Peng and Fine (2009) handles stochastic integral estimating equations that are involved in our estimation setting. For the proposed estimator, we need to properly design working estimating equations so that they can be theoretically justified and stably solved.

Define ${\mathit{L}}_n\left(\mathit{b}\right)=n^{-1∕2}{\sum }_{i=1}^n{\mathit{X}}_i{N}_i\left(e^{{\mathit{X}}_i^{\mathsf{T}}b}\right)$, ${\tilde{\mathit{L}}}_n\left(\mathit{b}\right)=n^{-1∕2}{\sum }_{i=1}^n{\mathit{X}}_i{Y}_i\left(e^{{\mathit{X}}_i^{\mathsf{T}}b}\right)$, ${\iota }_j\left(u\right)={\mathit{X}}_j{N}_j\left(e^{{\mathit{X}}_j^{\mathsf{T}}\widehat{\beta }\left(u\right)}\right)$, and ${\Omega }_n\left(u\right)=n^{-1}{\sum }_{j=1}^n{\left\{{\iota }_j\left(u\right)\right\}}^{\otimes 2}$. The procedure for estimating B(β₀(u)) and J(β₀(u)) follows.

1. Find a symmetric and nonsingular (p+1)×(p+1) matrix E_n(u) {e_n,1(u), . . . , e_n,p+1(u)} such that Ω_n(u) = {E_n(u)}².

2. Solve the equation,

   $${\mathit{L}}_n\left(\mathit{b}\right)={\mathit{L}}_n\left(\widehat{\beta }\left(u\right)\right)+e_{n,j}\left(u\right),$$ (10)

   for b, and denote the solution by b_n,j(u) (j = 1, . . . , p + 1).

3. Calculate ${\mathit{D}}_n\left(u\right)\equiv ({\mathit{b}}_{n,1}\left(u\right)-\widehat{\beta }\left(u\right),\dots ,{\mathit{b}}_{n,p+1}\left(u\right)-\widehat{\beta }\left(u\right))$, and ${\tilde{\mathit{E}}}_n\left(u\right)\equiv ({\tilde{\mathit{L}}}_n\left({\mathit{b}}_{n,1}\left(u\right)\right)-{\tilde{\mathit{L}}}_n\left(\widehat{\beta }\left(u\right)\right),\dots ,{\tilde{\mathit{L}}}_n\left({\mathit{b}}_{n,p+1}\left(u\right)\right)-{\tilde{\mathit{L}}}_n\left(\widehat{\beta }\left(u\right)\right))$.

4. Compute n^−1/2E_n(u)D_n (u)⁻¹ and n^−1/2 Ê_n(u)Dn(u)⁻¹, which provide consistent estimates for B(β₀(u)) and J(β₀(u)), respectively.

In Step 2, we adopt a working estimating equation, ${\mathit{L}}_n\left(\mathit{b}\right)={\mathit{L}}_n\left(\widehat{\beta }\left(u\right)\right)+{\mathit{e}}_{n,j}\left(u\right)$, which is monotone and can be solved via L₁–minimization. The key motivation for considering this estimating equation is the asymptotic linearity associated with L_n(b) in the neighborhood of β₀(u), which can give ${\mathit{L}}_n\left({\mathit{b}}_{n,j}\left(u\right)\right)-{\mathit{L}}_n\left(\widehat{\beta }\left(u\right)\right)\approx \mathit{B}\left({\beta }_0\left(u\right)\right)n^{1∕2}\{{\mathit{b}}_{n,j}\left(u\right)-\widehat{\beta }\left(u\right)\}$, where ≈ denotes asymptotic equivalence uniformly in u ∈ [v, U]. Likewise, we have ${\tilde{\mathit{L}}}_n\left({\mathit{b}}_{n,j}\left(u\right)\right)-{\tilde{\mathit{L}}}_n\left(\widehat{\beta }\left(u\right)\right)\approx \mathit{J}\left({\beta }_0\left(u\right)\right)n^{1∕2}\{{\mathit{b}}_{n,j}\left(u\right)-\widehat{\beta }\left(u\right)\}$. These results are key for justifying the proposed estimation of B(β₀(u)) and J(β₀(u)). More detailed justifications are given in Supplement C of the Supplementary Materials.

Remark 1. The proposed procedure for obtaining e_n,j(u) ensures that e_n,j(u) (j = 1, . . . , p + 1) have the desired asymptotic order. The working estimating equation (10) would remain valid when one replaces e_n,j(u) by γ_c · e_n,j(u), where γ_c is a constant. This fact adds flexibility to the implementation of the proposed covariance estimation procedure.

Denote the estimators of B(β₀(u)) and J(β₀(u)) by B̂(u) and Ĵ(u) respectively. A consistent sample-based covariance estimator may be given by

$$n^{-1}\sum _{i=1}^n{\widehat{\zeta }}_i\left(s\right){\widehat{\zeta }}_i\left(t\right),$$

where ${\widehat{\zeta }}_i\left(t\right)=\widehat{\mathit{B}}{\left(t\right)}^{-1}\widehat{\varphi }\left({\widehat{\xi }}_i\right),\widehat{\varphi }(\cdot )$ is the plug-in estimate for the operator ϕ(·) defined in Supplement B of the Supplementary Materials, and

$${\widehat{\xi }}_i\left(u\right)={\mathit{X}}_i\{N_i\left(e^{{\mathit{X}}_i^{\mathsf{T}}\widehat{\beta }\left(u\right)}\right)-{\int }_0^u{Y}_i\left(e^{{\mathit{X}}_i^{\mathsf{T}}\widehat{\beta }\left(s\right)}\right)g\left(s\right)ds\},i=1,\dots ,n.$$

Our simulation studies suggest that the proposed sample-based covariance estimator works quite well with small to moderate sample sizes.

3.5 Second-stage inference

One practical benefit of using the GART model to analyze recurrent events data is that it allows for accommodating and exploring varying covariate effects. Second-stage inference can be employed to serve this need. Given $\widehat{\beta }\left(\tau \right)$ for a range of τ's, it is often of interest to summarize the information provided by these estimators to help understand the underlying effect mechanism, and to determine whether some covariates have constant effects, so that a simpler model may be considered.

A summary of covariate effects can be generally formulated as some functional of β₀(·), denoted by (Ψ₀). A natural estimator of (Ψ₀) is $\Psi \left(\widehat{\beta }\right)$. This estimator may be justified by using the functional delta method provided that Ψ(·) is compactly differentiable at β₀ (Andersen, Borgan, Gill, and Keiding 1998). The detailed inference on Ψ(β₀) can follow the discussions in Section 2.4 of Peng and Fine (2009).

To test the constancy of a covariate effect, it is equivalent to consider the null hypothesis that takes the form, $H_{0,j}:{\beta }_0^{\left(j\right)}\left(u\right)={\rho }_0,u\in [u_L,u_U]$, where the superscript ^(j) indicates the jth component of a vector, and ρ₀ is an unspecified constant (j = 2, . . . , or p + 1). Appropriate test statistics for H_0,j can be developed along similar lines of Peng and Huang (2008) and Peng and Fine (2009). Accepting H_0,j for all j ∈ {2, . . . , p + 1} may indicate the adequacy of a constant effect model. Therefore, such a procedure may be used to test the goodness-of-fit of an accelerated failure time model for recurrent events.

4. SIMULATION STUDIES

We conducted Monte Carlo simulations to assess the finite-sample performance of the proposed method. Like in Huang and Peng (2009), a Gamma frailty on a standard homogeneous Poisson process was applied to generate recurrent event times. Two covariates, Z₁ and Z₂, were considered, following the distributions, Bernoulli(0.5) and Unif(−0.5, 0.5), respectively. The recurrent event time sequence was generated by

$$T^{\left(j\right)}=\exp \left\{\min \left(1,\frac{T^{\ast \left(j\right)}}{1.5\gamma }\right)Z_1+Z_2\right\}{T}^{\ast \left(j\right)}∕\gamma ,j=1,2,\dots ,$$

where {T * ^(j), j = 1, 2, . . .} was a recurrent event sequence from a standard homogeneous Poisson process and the frailty γ followed a Gamma distribution. The variance of γ, denoted by σ², determines the level of intra-individual correlation, and was chosen to be 0 or 0.5. It can be shown that, under our simulation setup,

$${\tau }_{\mathit{Z}}\left(u\right)=\exp \{\log \left(u\right)+\min (1,u∕1.5)Z_1+Z_2\}.$$

Covariate Z₂ has a constant effect on τ_Z(u), while the effect of Z₁ increases with expected frequency. We generated L from ω · Unif(0, 1) and R from Unif(L, 12), where ω was a Bernoulli(0.8) variate. Under these simulation set-ups, the average number of observed recurrent events per subject was about 4.0. With each selection of σ², we generated 500 datasets of sample size n = 100. For bootstrapping-based inference, the resampling size of 100 was chosen. We set g(u) = 1 and adopted an equally spaced grid on u ∈ (0, 3] with step size, 0.02.

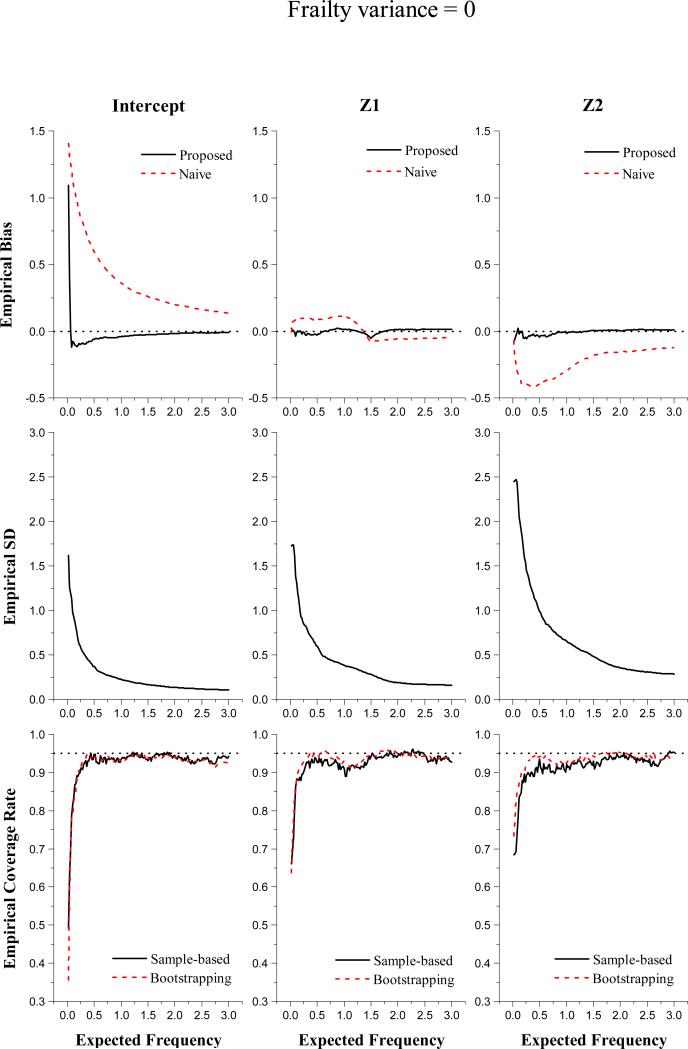
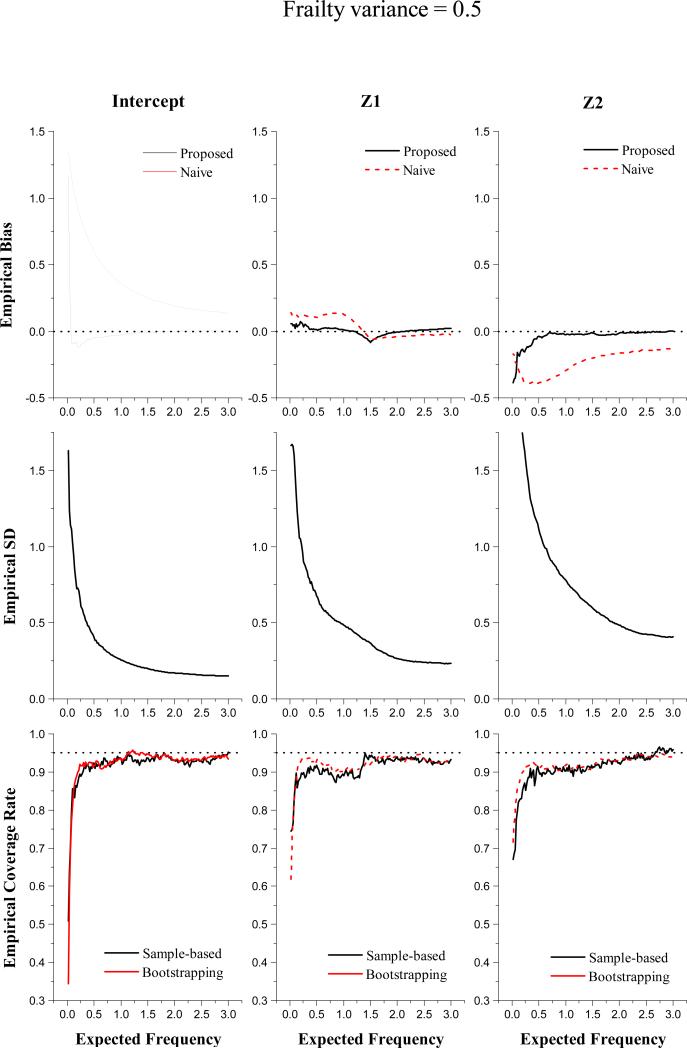
In Figures 1 and 2, we present the simulation results from the set-up with σ² = 0 and the set-up with σ² = 0.5, respectively. In the first row, we plot the empirical bias of the proposed estimator $\widehat{\beta }\left(u\right)$ (solid lines) and the empirical bias of Huang and Peng (2009)'s estimator (dashed lines), which naively assumes L = 0, versus expected frequency u. It is shown that our estimates have small bias except for those corresponding to small u's. Treating all L's as 0 clearly produces very biased coefficient estimation. The plots in the second row depict the empirical mean squared errors (MSE) versus expected frequency u. The empirical MSEs indicate reasonable efficiency of the proposed estimator with n = 100. In addition, the empirical MSE follows a similar pattern to the empirical bias. The observation of large bias and MSE at small u's is consistent with our theoretical results, which suggest substantial variability in estimating β₀(u) as u is close to zero.

Figure 1.

Simulation results with sample size n = 100 for the set-up with Gamma frailty of variance 0

Figure 2.

Simulation results with sample size n = 100 for the set-up with Gamma frailty of 0.5

The last row of Figures 1 and 2 presents the coverage probabilities of 95% confidence intervals (CI) obtained from the proposed sample-based covariate estimates (solid lines) and those from bootstrapping (dashed lines). It shows that the bootstrapping-based procedure and the sample-based procedure have quite comparable performance. The resulting 95% CIs are slightly under-covered and yet have coverage probabilities fairly close to the nominal value. We examined the simulation results with a larger sample size, n = 200 (not reported here). We observe that the empirical bias and MSE decrease as the sample size increases. The coverage probabilities from either bootstrapping or sample-based procedure are much closer to the nominal value as compared to those with n = 100. We also evaluated the computation time taken to construct confidence intervals in each simulation setup. The computation time ratio of the sample-based approach to the bootstrapping procedure ranges from 0.16 to 0.47 with mean=0.24 and median=0.24, suggesting a significant saving in computation time by using the proposed sample-based procedure.

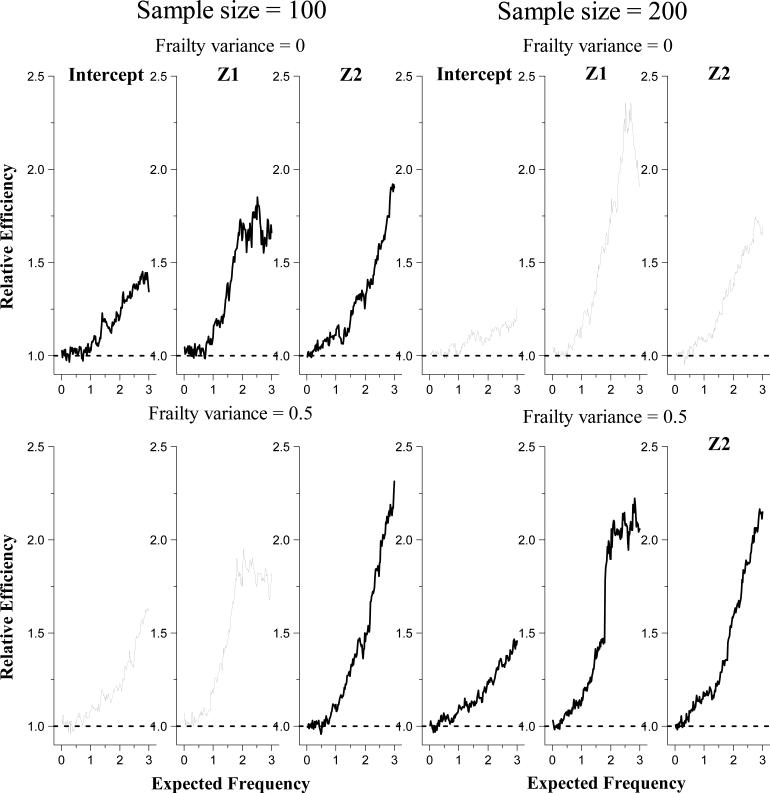
We also compared the estimation efficiency between the proposed estimator and Huang and Peng (2009)'s estimator when observation windows always start from 0. In these simulations, we set L = 0 while keeping (T^(j), R, Z) generated the same way. In Figure 3, we plot the relative efficiency of $\widehat{\beta }\left(u\right)$ to Huang and Peng (2009)'s estimator. It is shown that our estimator for the ART model is always more efficient than the method of Huang and Peng (2009). The efficiency gain seems to increase with the expected frequency and can be over 100% at some large u's. Such results may be explained by the fact that Huang and Peng (2009)'s estimator only employs the accelerated recurrence time assumption, (7), at a single u. Therefore, though Huang and Peng (2009)'s estimator is more robust than the proposed estimator, it does not make a full use of the global accelerated recurrence time assumption as the proposed estimator does, and thus is less efficient. The results in Figure 3 are consistent with Koenker (2008)'s findings from comparing the efficiency between Peng and Huang (2008)'s and Powell (1984, 1986)'s methods on censored quantile regression.

Figure 3.

Simulation results on the efficiency of the proposed estimator relative to Huang and Peng (2009)'s estimator.

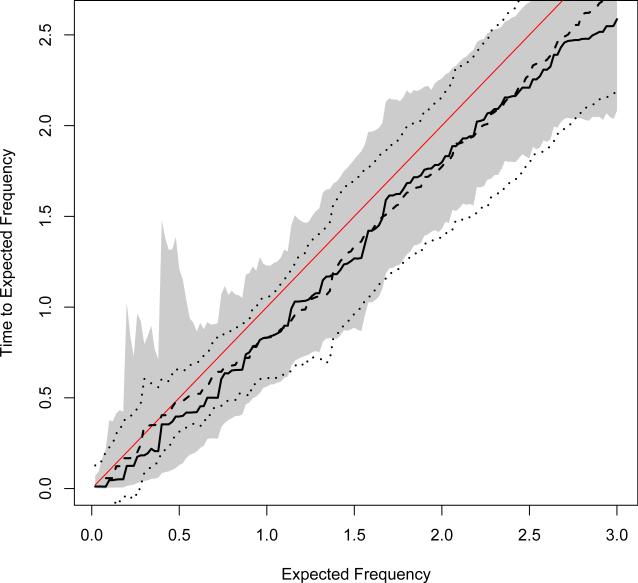
We also investigated a special case in which both the Cox regression model (Andersen and Gill 1982) and the GART model hold. Specifically, we generated a recurrent events dataset based on an GART model by letting T^(j) = exp(Z₁ + Z₂)T*^(j). Here T* ^(j) , (Z₁, Z₂), and (L, R) are defined in the same way as those for the other simulations. In this case, the true intensity process is given by exp(−Z₁−Z₂), and the time to expected frequency u equals exp(Z₁ + Z₂)u. Figure 4 compares the estimates for τ_Z(u) with Z = (0, 0) based on the Cox regression model with those based on the GART model with g(u) = 1. The 95% pointwise confidence intervals are also presented. It is shown by Figure 4 that the estimates for time to expected frequency based on both models are quite similar; both curves are close to the true line of τ_Z(u). The confidence intervals derived based on the Cox regression model are generally tighter Ψ(β₀) than those based on the GART model. The difference in confidence interval width is evident at small u's but gradually diminishes as u increases.

Figure 4.

Estimated τ_Z(u) curves with Z = (0, 0) based on Cox regression model (bolded dashed lines) and GART model (bolded solid lines) along with 95% pointwise confidence intervals based on Cox regression model (bolded dotted lines) and GART model (shaded area) when both Cox regression model and GART model hold. The true curve is presented in unbolded solid line.

The observations from Figure 4 well match our expectation given the following facts: (a) the Cox regression model imposes the constancy assumption for each coefficient function, and thus its estimation can make good use of all observations; (b) the GART model allows for varying covariate effects, and the proposed estimation of β₀(u) essentially utilizes only observations from time 0 to τ_Z(u). The stronger modeling assumption of Cox regression may contribute to the tighter confidence intervals. Since τ_Z(u) is increasing with u, the proposed estimates for τ_Z(u) under the GART model can use fuller data information at larger u's and then become more comparable to those obtained from the Cox regression model. This may explain the observed smaller differences in estimation accuracy at larger u's.

5. AN APPLICATION TO A CYSTIC FIBROSIS DATASET

Cystic Fibrosis (CF) is a life-limiting genetic disorder with an incidence of 1:3400 in Caucasians (Boat and Acton 2007). Pseudomonas aeruginosa (PA) is the most important pathogen that shortens the survival of CF patients. According to Cystic Fibrosis Foundation (CFF) 2011 annual report, it infects more than half of CF patients and often leads to chronic conditions. Characterizing the timing of PA infections and assessing how it is influenced by potential risk factors can help improve treatment decisions and are thus of scientific interest. To address these questions, we utilized the data from 2875 children documented in 1986-2008 CFF Patient Registry (CFFPR), who were born in or after 1998, had at least one F508del mutation, and had 5 or more years of follow-up in the registry.

We applied the proposed method to this CFFPR dataset, with the recurrent event time T^(j) being the age of a CF child when he or she had the jth PA infection. While some CF children entered the registry right after birth given the availability of early diagnosis by newborn screening, others had delayed CFFPR entries due to later diagnosis of CF or other reasons. Observation of PA infections started from the first CFFPR visit, and thus the time from birth to registry entry constitutes the L in our method framework. In this dataset, age at the first CFFPR visit ranges from 0 to 5.7 years with mean=0.7 years and median=0.4 years. The number of positive PA cultures at CFFPR visits ranges from 0 to 50; the mean and median number of PA infections are 3.9 and 2.0, respectively. We considered risk factors including sex, patient's CFTR genotype (I=F508del homozygous, II=F508del heterozygous), meconium ileus (MI)status , and pancreatic su ciency status (defined as never on pancreatic enzymes). The covariates for a subject are coded as Female, 1 if the subject was female and 0 otherwise; F 508/Other, 1 if the subject was F508del heterozygous and 0 otherwise; MI, 1 if the subject was diagnosed by MI and 0 otherwise; and Pancreat, 1 if the subject was pancreatic sufficient and 0 otherwise.

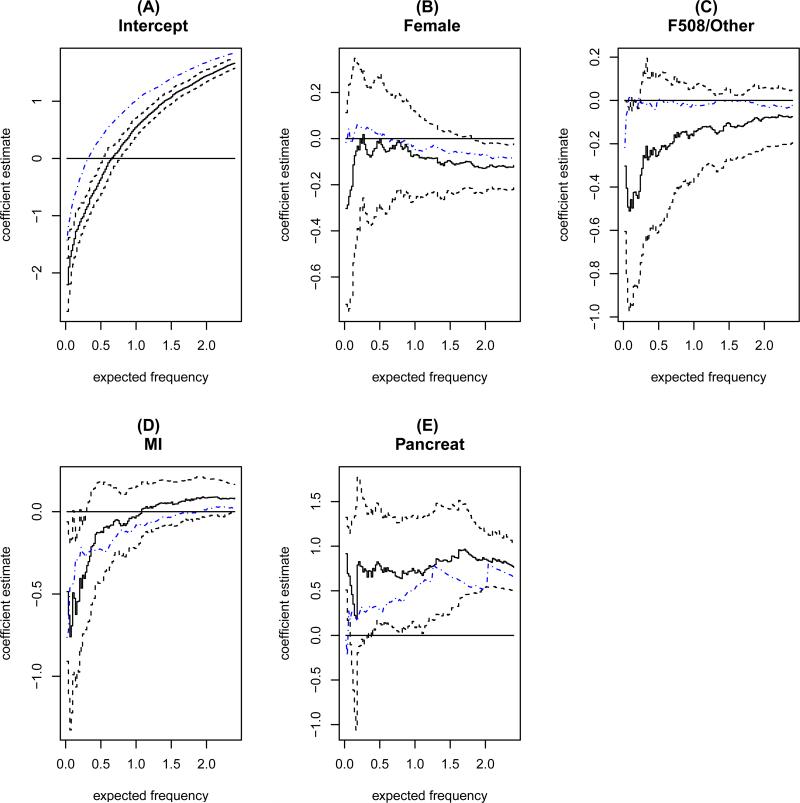
We fit the proposed model to the CFFPR dataset with the covariates described above, setting g(u) = 1. In Figure 5, we plot the estimated coefficients along with the 95% point-wise confidence intervals. The intercept coefficient estimates (panel A of Figure 5) represent the estimated log time to expected frequency of PA infection for the reference group, which consisted of CF boys with homozygous F508del mutations who had no MI and were pancreatic insufficient. For example, the time from birth to expected PA infection frequency of 1.0 is approximately 1.7 years. An alternative interpretation of this result is that, at age of 1.7 years old, CF patients in the reference group are expected to have acquired one PA infection on average. Figure 5 (panel A) also suggests that the time to expected PA infection frequencies of 2.0 in the reference group is about 4.3 years.

Figure 5.

CFFPR data example: coefficient estimates (solid lines) and 95% pointwise confidence intervals (dashed lines) from the proposed method and the coefficient estimates from Huang and Peng (2009)'s method (dash dotted lines).

The non-intercept coefficient estimates in Figure 5 (panels B–E) depict the estimated effects of covariates, which are allowed to be frequency-varying. Negative coefficient estimates indicate more rapid progression to recurrence of PA infections. To better summarize the varying covariate effect estimates, we present in Table 1 the average covariate effects in the frequency intervals (0.4, 1.4], (1.4, 2.4], and (0.4, 2.4] respectively, along with estimated standard errors and p values. The results in Table 1 suggest a strong disadvantage to CF children with pancreatic insu ciency, who tend to experience recurrent PA infections at earlier ages. Girls with CF appear to have marginal increased risk of recurrent PA infections only in the frequency interval (1.4, 2.4], which indicates later recurrence of PA infections. The average effect estimates for MI demonstrate a cross-over pattern, changing from −0.37 to 0.74, though not reaching statistical significance in either frequency interval. From Table 1, we find little difference in time to expected frequency between the F508del homozygous group and the F508del heterozygous group. This is consistent with literature that reported relatively weak associations between genotype and pulmonary phenotype in CF patients. We also conducted constancy tests for each covariate effect. The results given in Table 1 indicate that MI had a frequency-dependent effect on the timing of PA recurrence, while other covariates displayed fairly constant effects over the frequency of PA infections.

Table 1.

The CFFPR example: average covariate effect estimates along with standard errors (SE) and the corresponding p values, and the p values from constancy tests.

Average Covariate Effect Estimates
Frequency Interval		Sex	F508/Other	MI	Pancreat
(0.4,1.4]	Estimate	–0.06	–0.17	–0.04	0.74
	SE	0.10	0.12	0.09	0.29
	P value	0.55	0.15	0.69	0.01
(1.4, 2.4]	Estimate	–0.11	–0.10	0.07	0.86
	SE	0.06	0.07	0.06	0.21
	P value	0.05	0.19	0.21	< 0.001
(0.4, 2.4]	Estimate	–0.09	–0.13	0.02	0.80
	SE	0.08	0.09	0.08	0.24
	P value	0.28	0.16	0.81	< 0. 001
Constancy Tests
Constancy tests	P value	0.32	0.26	0.06	0.50

In Figure 5, we also plot the coefficient estimates obtained from applying Huang and Peng (2009)'s method (dash dotted lines). Huang and Peng (2009)'s estimator, which assumes that the PA observation window always starts from zero, may suggest a smaller difference caused by pancreatic insufficiency in time to expected frequency less than 1.0. Such a discrepancy may be expected because, when the lower bound of PA observation window is ignored, the frequency of PA infection before registry entry is naively taken as 0, though it may be positive. Intuitively, this would result in a frequency-lag in the estimated effect as a function of frequency. We also note that the intercepts estimated by Huang and Peng (2009)'s method are significantly larger than those from the proposed method. This observation conforms to the intuition that naively treating PA infection frequency before registry entry as 0 would lead to over-optimistic estimates for time to expected frequency.

6. REMARKS

In this work, we propose a new approach to model counting processes that are naturally embedded in event history data. The new counting process model can be transformed to a quantile regression model in the traditional survival setting with random censoring or a generalized accelerated recurrence time (GART) model in the recurrent events setting with random observation windows. We are able to generalize the current methodological framework for censored quantile regression (Peng and Huang 2008) to serve the broader class of survival regression models implied by the proposed counting process model. We expect that the existing software for censored quantile regression can be extended to implement proposed regression methods for recurrent events data.

Our proposals for the GART model offer a useful and flexible alternative to current approaches for analyzing recurrent events data. The new method is easy to interpret and implement. It is also straightforward to adapt the proposed recurrent events method to accommodate the realistic on-and-off observation scheme of recurrent events, corresponding to observation windows that take the form as a union of multiple disjoint time intervals, say ${\cup }_{j=1}^K(L_j,R_j]$. In this case, the at-risk process needs to be specified as $Y\left(t\right)={\sum }_{j=1}^{K}I(L_j<t\le R_j)$.

As mentioned in Section 2, the specification of g(·) is tied to the scale in which the covariate effects are formulated. In practice, we anticipate that the preferable forms of g(·) would be the ones that make model (5) easily interpretable. For example, with the standard set-up for randomly censored data, popular choices of g(·) may include g(u) = 1/(1 − u) and g(u) = 1, which lead to quantile regression modeling and modeling of the inverse cumulative hazard function, respectively. In the recurrent events setting, the most compelling choice of g(·) for model (6) may be g(u) = 1. Given the common stochastic structure implied by censored quantile regression model (1) and the proposed counting process model (5), we anticipate that model diagnostics for model (5) with a specified g(·) can be developed along the lines of Peng and Huang (2008).

The proposed method for window observed recurrent events implies an alterative quantile regression approach for doubly censored data that include n i.i.d. replicates of η ≡ I(L < T ≤ R), W ≡ Tη , L and R, denoted by ${\{{\eta }_i,W_i,L_i,R_i\}}_{i=1}^n$. In this data setting, both left and right censoring variables, L and R, are always observed, and T is the event time of interest assumed to follow quantile regression model (1). To estimate model (1), one may use the proposed estimating equation (8) with N_i(t) and Y_i(t) replaced by I(W_i ≤ t, η_i = 1) and I(L_i < t ≤ R_i), respectively. Inference procedures may be carried out by adapting the lines in Section 3.