Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 May 20.
Published in final edited form as: Nat Genet. 2015 Sep 7;47(10):1107–1113. doi: 10.1038/ng.3395

Class II HLA interactions modulate genetic risk for multiple sclerosis

Loukas Moutsianas 1,#, Luke Jostins 1,#, Ashley H Beecham 2,#, Alexander T Dilthey 1, Dionysia K Xifara 1, Maria Ban 3, Tejas S Shah 4, Nikolaos A Patsopoulos 5,6,7,8, Lars Alfredsson 9, Carl A Anderson 4, Katherine E Attfield 10, Sergio E Baranzini 11, Jeffrey Barrett 4, Thomas M C Binder 12, David Booth 13, Dorothea Buck 14, Elisabeth G Celius 15, Chris Cotsapas 8,16,17, Sandra D’Alfonso 18, Calliope A Dendrou 19, Peter Donnelly 1, Bénédicte Dubois 20, Bertrand Fontaine 21, Lars Fugger 10,19, An Goris 20, Pierre-Antoine Gourraud 11, Christiane Graetz 22, Bernhard Hemmer 14,23,24, Jan Hillert 25; International IBD Genetics Consortium (IIBDGC)26, Ingrid Kockum 25, Stephen Leslie 27,28, Christina M Lill 22,29, Filippo Martinelli-Boneschi 30,31, Jorge R Oksenberg 11, Tomas Olsson 25, Annette Oturai 32, Janna Saarela 33, Helle Bach Søndergaard 32, Anne Spurkland 34, Bruce Taylor 35, Juliane Winkelmann 14,23,36,37,38, Frauke Zipp 22, Jonathan L Haines 39, Margaret A Pericak-Vance 2, Chris C A Spencer 1, Graeme Stewart 13, David A Hafler 8,16,40, Adrian J Ivinson 41, Hanne F Harbo 15,42, Stephen L Hauser 11, Philip L De Jager 5,6,7,8, Alastair Compston 3, Jacob L McCauley 2, Stephen Sawcer 3,44, Gil McVean 1,44, for the International Multiple Sclerosis Genetics Consortium
PMCID: PMC4874245  NIHMSID: NIHMS782000  PMID: 26343388

Abstract

Association studies have greatly refined the understanding of how variation within the human leukocyte antigen (HLA) genes influences risk of multiple sclerosis. However, the extent to which major effects are modulated by interactions is poorly characterized. We analyzed high-density SNP data on 17,465 cases and 30,385 controls from 11 cohorts of European ancestry, in combination with imputation of classical HLA alleles, to build a high-resolution map of HLA genetic risk and assess the evidence for interactions involving classical HLA alleles. Among new and previously identified class II risk alleles (HLA-DRB1*15:01, HLA-DRB1*13:03, HLA-DRB1*03:01, HLA-DRB1*08:01 and HLA-DQB1*03:02) and class I protective alleles (HLA-A*02:01, HLA-B*44:02, HLA-B*38:01 and HLA-B*55:01), we find evidence for two interactions involving pairs of class II alleles: HLA-DQA1*01:01–HLA-DRB1*15:01 and HLA-DQB1*03:01–HLA-DQB1*03:02. We find no evidence for interactions between classical HLA alleles and non-HLA risk-associated variants and estimate a minimal effect of polygenic epistasis in modulating major risk alleles.

Since the earliest reports of association between multiple sclerosis and genetic variation in the HLA genes1, linkage screens2,3 and association studies4–11, together with imputation of classical HLA alleles from linked SNP data9,12–14, have established the key factors driving patterns of association. In populations of northern European origin, risk is dominated by the HLA-DRB1*15:01 allele, with additional effects from class II risk alleles (HLA-DRB1*03:01 (refs. 15,16) and HLA-DRB1*13:03 (refs. 4,9)) and class I protective alleles, including HLA-A*02:01 (ref. 9), HLA-B*44:02 (ref. 7) and HLA-B*38:01 (ref. 14). In addition, deviation from an additive model has been reported for some variants, with evidence that HLA-DRB1*15:01 exerts a dominant effect and HLA-DRB1*03:01 exerts a recessive effect17. However, the extent to which the effects of classical HLA alleles are modulated by interactions with alleles from other loci within or outside the HLA region remains to be established. Several studies have suggested the presence of such interactions17–21, although these did not achieve genome-wide significance or take account of linkage disequilibrium (LD) between alleles, population stratification and departures from additivity, any of which could either obscure or create false signals suggesting biological interaction. Furthermore, mouse models have indicated the presence of functional interactions between class II alleles22, although whether equivalent epistasis also occurs in humans is unknown. Interactions between classical HLA alleles and non-HLA risk-associated loci have been described previously for coding variation in the antigen-processing ERAP1 gene and the class I HLA-B*27 allele in ankylosing spondylitis23, HLA-C*06 in psoriasis24 and HLA-B*51 in Behçet’s disease25, findings that provide insights into the putative mechanisms of these diseases. However, thus far, no such interactions have been reported for multiple sclerosis.

RESULTS

To assess the evidence for interactions involving classical HLA alleles influencing genetic risk for multiple sclerosis and quantifiable features of the disease, we analyzed patterns of HLA association in 17,465 multiple sclerosis cases and 30,385 controls from across 11 independent cohorts genotyped as part of the Immunochip study (Supplementary Table 1). Classical HLA alleles were imputed at HLA-A, HLA-B, HLA-C, HLA-DQA1, HLA-DQB1, HLA-DRB1, HLA-DRB3, HLA-DRB4, HLA-DRB5 and HLA-DPB1 from linked SNP data using previously published methods12,13,26. Using cross-validation, we estimate the accuracy at four-digit resolution to be between 0.95 and 0.99 across loci for a posterior probability threshold of 0.7 and call rates of between 0.90 and 1.00 across loci (Supplementary Table 2), except for HLA-DPB1, for which limited training data were available, leading to a low call rate of 0.85 although the accuracy was 0.98. Uncertainty in HLA imputation, which is well calibrated13, was accounted for in our model analysis (Online Methods and Supplementary Fig. 1). Validation accuracy for all alleles reported here is shown in Supplementary Table 3. Population stratification within each cohort was controlled for by including the first five principal components of ancestry as covariates.

Our analysis had four goals: (i) to define the key components of genetic risk for multiple sclerosis arising from classical HLA alleles; (ii) to test for interactions among classical HLA alleles; (iii) to test for interactions between classical HLA alleles and non-HLA loci associated with multiple sclerosis; and (iv) to estimate the contribution of polygenic epistasis as a modulator of risk conferred by classical HLA alleles. We first used three stepwise approaches to construct a general logistic model of HLA risk for multiple sclerosis (Online Methods): analysis of the UK data set, guided initially by prior knowledge, followed by validation of known and new effects through fixed-effect meta-analysis across cohorts; an automated model search involving mega-analysis of all alleles at four-digit resolution; and an augmented automated model search involving additional groupings of alleles at serological (two-digit) resolution and sharing of amino acid residues at variable positions, similar to an approach used in earlier work14. Our goal was to identify strong and repeatable signals of association most likely driven by classical HLA alleles and all other effects within the HLA region of comparable importance that cannot easily be attributed to classical HLA alleles. Only alleles with a fixed-effect meta-analysis P value of <1 × 10−9 are reported, a conservative threshold chosen to identify factors with compelling evidence for association (approximately equivalent to P = 0.001 after correcting for genome-wide multiple testing). Deviations from additivity were considered in both the manually guided and automated approaches. The results from the three approaches identified a consistent set of factors, although there was some variation in the ranking and identity of the focal variants in cases where the LD between alleles was strong (Supplementary Fig. 2). A consensus approach was used to summarize the findings.

A high-resolution map of HLA risk for multiple sclerosis

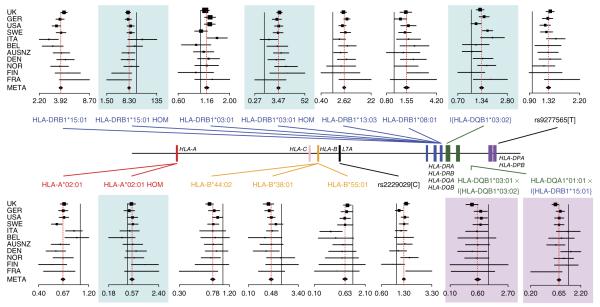
Across multiple cohorts of European ancestry, we found that the architecture of genetic risk for multiple sclerosis was dominated by a series of class II risk alleles (consistent with most risk signals being driven by alleles at HLA-DRB1) and a series of protective signals driven by class I alleles (Fig. 1 and Table 1). Risk was dominated by the well-characterized HLA-DRB1*15:01 allele (odds ratio (OR) = 3.92; fixed-effect meta-analysis under a model including all reported effects, P = 2 × 10−686), which was partially dominant (homozygous OR = 8.30, P = 8.5 × 10−22 for the homozygote correction term, a measure of the deviation from additivity of the homozygous odds ratio). We also found largely recessive risk for HLA-DRB1*03:01 (heterozygous OR = 1.16, P = 3.5 × 10−8; homozygous OR = 3.47, P = 1.3 × 10−30), additive risk effects from HLA-DRB1*13:03 (OR = 2.62, P = 6.2 × 10−55) and HLA-DRB1*08:01 (OR = 1.55, P = 1 × 10−23), and a dominant risk effect from HLA-DQB1*03:02 (heterozygous/homozygous OR = 1.30, P = 1.8 × 10−22). Protective alleles included HLA-A*02:01 (OR = 0.67, P = 7.8 × 10−70), along with HLA-B*44:02 (OR = 0.78, P = 4.7 × 10−17), HLA-B*38:01 (OR = 0.48, P = 8.0 × 10−23) and HLA-B*55:01 (OR = 0.63, P = 6.9 × 10−11), which, except for HLA-B*55:01, have been reported previously as being associated7,9,14,17, although HLA-B*38:01 was not reported at genome-wide significance. We found departure, albeit weak, from additivity at HLA-A*02:01 (homozygous OR = 0.56, homozygous correction P = 3.3 × 10−5; the protective effect was weakly dominant), which is important to include for analyses of interactions.

Figure 1.

Figure 1

Open in a new tab

Overview of genetic effects in the HLA region influencing risk for multiple sclerosis. The relative locations of the classical HLA loci are shown (central bar) along with forest plots for each of the major effects identified. Each forest plot shows the estimated odds ratio from the cohort-specific logistic model and the 95% confidence interval, with point size proportional to sample size and the cohorts ordered by size (Supplementary Table 1). The bottom point for each locus and the corresponding red dashed line show the result from fixed-effect meta-analysis (META). Plot background indicates the nature of the effect: none, main effect; blue, departure from additivity; pink, interaction. The lead allele for each signal is indicated. The solid black line represents OR = 1 for additive effects and the expected homozygote effect for departures from additivity. Curly brackets represent an indicator function that combines heterozygotes and homozygotes into a single category. HOM, homozygote.

Table 1.

HLALA alleles and SNSNPs found to be significantly associated with multiple sclerosis in this study

HLA allele or SNP Parameter Frequency in
UK/all controls		 FEM P valuea FEM ORb
(95% CI)c 		HLA alleles in LD
(UK controls)d 		SNPs in LD
(UK controls)e
HLA-DRB1*15:01 Additive effect
Homozygote correction		 0.143/0.134 <1 × 10−600
8.5 × 10−22 		3.92 (3.74–4.12)
0.54 (0.47–0.61)		 HLA-DQB1*06:02,
HLA-DRB5*01, HLA-DRB5
negative (r2 > 0.9),
HLA-DQA1*01:02 (r2 > 0.8)		 rs3135391, rs3135388,
rs3129889, rs9271366
(r2 > 0.95)
HLA-A*02:01 Additive effect
Homozygote correction		 0.276/0.285 7.8 × 10−70
3.3 × 10−5 		0.67 (0.64–0.70)
1.26 (1.13–1.41)		 None rs4713274, rs9295825,
rs2517840, rs2523822
(r2 > 0.9)
HLA-DRB1*03:01 Additive effect
Homozygote correction		 0.143/0.124 3.5 × 10−8
1.3 × 10−30 		1.16 (1.10–1.22)
2.58 (2.19–3.03)		 HLA-DQA1*05:01,
HLA-DQB1*02:01
(r2 > 0.95), HLA-DRB3*01,
HLA-B*08:01 (r2 > 0.5)		 rs2854275 and five more
SNPs with r2 > 0.95
HLA-DRB1*13:03 Additive effect 0.009/0.010 6.2 × 10−55 2.62 (2.32–2.96) None None
HLA-DRB1*08:01 Additive effect 0.020/0.027 1.0 × 10−23 1.55 (1.42–1.69) HLA-DQA1*04:01 (r2 > 0.95),
HLA-DQB1*04:02 (r2 > 0.9)		 rs7775055, rs4713586
(r2 > 0.9)
rs9277565[T] Additive effect 0.206/0.204 2.1 × 10−52 1.32 (1.27–1.36) HLA-DPB1*03:01 (r2 > 0.5) rs9277561, rs9277567
(r2 > 0.95)
HLA-B*44:02 Additive effect 0.114/0.093 4.7 × 10−17 0.78 (0.74–0.83) HLA-C*05:01 (r2 > 0.5) rs9266773 (r2 > 0.95)
HLA-B*38:01 Additive effect 0.011/0.018 8.0 × 10−23 0.48 (0.42–0.56) None None
HLA-B*55:01 Additive effect 0.018/0.016 6.9 × 10−11 0.63 (0.55–0.73) None rs3819284, rs3093547
(r2 > 0.5)
HLA-DQA1*01:01 Additive effect in
the presence of
HLA-DRB1*15:01		 0.144/0.147 1.3 × 10−17 0.65 (0.59–0.72) HLA-DQB1*05:01,
HLA-DRB1*01:01
(r2 > 0.5)		 rs13193645 (r2 > 0.95)
rs2229092[C] Additive effect 0.060/0.063 1.7 × 10−22 1.33 (1.26–1.41) None None
HLA-DQB1*03:02 Dominant effect 0.105/0.105 1.8 × 10−22 1.30 (1.23–1.37) HLA-DQA1*03:01 (r2 > 0.5) rs3957146, rs3998159
(r2 > 0.95)
HLA-DQB1*03:01 Allelic interaction with
HLA-DQB1*03:02		 0.187/0.194 7.1 × 10−12 0.60 (0.52–0.69) None rs2858312 (r2 > 0.5)
Open in a new tab
a

Fixed-effect meta-analysis (FEM) P value from the full model. The order of reporting follows a manually curated approach.

b

Estimated odds ratio (OR) from fixed-effect meta-analysis.

c

95% confidence interval (CI) from fixed-effect meta-analysis.

d

All HLA alleles with r2 >0.5 in the UK cohort are shown, classified with r2 thresholds of 0.95, 0.9, 0.8 and 0.5.

e

Only the most strongly associated SNPs in the UK cohort are shown, classified with r2 thresholds of 0.95, 0.9, 0.8 and 0.5.

For several alleles, there were a number of SNPs and classical alleles at other loci in strong LD (Table 1), and these cannot be excluded as potential determinants of the signal. In addition, we found evidence for risk variants in the vicinity of HLA-DPB1 that correlated with HLA-DPB1*03:01 (OR = 1.33, P = 5 × 10−36) but, as previously reported9,14,27, were strongest at rs9277565 (OR = 1.32, P = 2.1 × 10−52; r2 = 0.50). We also identified a missense variant in LTA, the gene encoding lymphotoxin α (rs2229092: C-allele OR = 1.33, P = 1.7 × 10−22), which is in LD (r2 ~0.50) with multiple other SNP variants in the samples of European ancestry from the 1000 Genomes Project and weak association (r2 = 0.29) with the previously reported haplotype in MICB-LST1 (ref. 14).

After accounting for these effects, no other classical HLA allele was associated in the UK (P < 1 × 10−5), replicated in the meta-analysis (P < 1 × 10−9) and identified by the automated model searches. The analysis of alleles grouped by serological activity or sharing of encoded amino acid residues led to similar conclusions as the analysis based on four-digit alleles; however, it identified a protective effect for HLA-B alleles that shared a cysteine residue at position 326 (OR = 0.84, P = 1.2 × 10−24), and these alleles somewhat reduced the inferred protective effect of HLA-B*44:02 (although the latter remained genome-wide significant in a fixed-effect meta-analysis that included both). The grouping approach identified one shared amino acid residue (a serine at position 57 in HLA-DRβ1) that captured the risk associated with HLA-DRB1*08:01 and HLA-DRB1*13:03, although a model with separate effects for the two loci is preferred. The grouping approach also identified a homozygous protective effect for HLA-DQB1 alleles encoding a glycine residue at position 70, although this signal was better explained by an interaction.

Interactions among classical HLA alleles

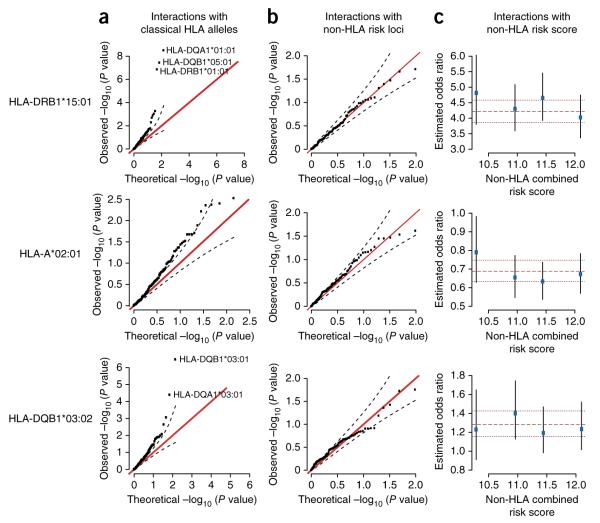
Having defined the major loci affecting multiple sclerosis risk and their marginal mode of action, we next investigated evidence for interactions between the classical HLA alleles identified above and all other classical HLA alleles, within the UK cohort (Fig. 2a and Supplementary Fig. 3). We found evidence for a strong protective effect of HLA-DQA1*01:01 only in the presence of HLA-DRB1*15:01 (Fig. 2a), which replicated in meta-analysis (OR = 0.65, P = 1.3 × 10−17; Fig. 1). The strongest signal was seen at HLA-DQA1*01:01; however, this allele was in LD with HLA-DRB1*01:01 (r2 = 0.6 in the UK), which also showed strong association (OR = 0.66, P = 5 × 10−12). The interaction can also be explained as occurring between HLA-DRB1*15:01 and the presence of two copies of HLA-DQB1 alleles encoding a glycine residue at position 70 (OR = 0.60, P = 8 × 10−33), with the evidence for the involvement of HLA-DQA1*01:01 being stronger in the UK but weaker in the combined analysis (Supplementary Table 4). A second allelic interaction involving HLA-DQB1*03:02 and HLA-DQB1*03:01 was also identified (Figs. 1 and 2a), such that the latter abolished the risk associated with the former (OR in the presence of HLA-DQB1*03:02 = 0.60, P = 7.1 × 10−12). No other pairs of alleles showed strong evidence for interaction within the UK cohort (P < 1 × 10−5) and/or replicated in meta-analysis.

Figure 2.

Figure 2

Open in a new tab

Evidence for interactions with associated HLA alleles. Results are shown here for HLA-DRB1*15:01 (top row), HLA-A*02:01 (middle row) and HLA-DQB1*03:02 (bottom row). Results for the other associated HLA alleles are shown in Supplementary Figures 3–5. (a) Quantile-quantile plot showing the distribution of P values for the interaction terms between the indicated multiple sclerosis–associated allele and all 152 other classical HLA alleles analyzed. (b) Quantile-quantile plot showing the distribution of P values for the interaction terms with the 98 previously identified non-HLA multiple sclerosis–associated alleles11. In each plot in a and b, the red line represents the expected relationship, and dashed lines represent the 95% confidence interval. (c) The effect of the indicated allele among individuals stratified in quartiles by a combined non-HLA risk score. The point estimate and 95% confidence interval for effect size are estimated independently for each quartile of non-HLA genetic risk. For each plot, the dashed and dotted lines represent the combined point estimate and 95% confidence interval, respectively. All analyses are for the UK cohort only. Interaction analyses included all non-epistatic effects within the model of Figure 1, including non-additive effects of the indicated allele.

Interactions with non-HLA risk loci

We then tested for association between classical HLA alleles and 98 independent and previously identified non-HLA variants that influence risk for multiple sclerosis11. We found no evidence for interactions outside the HLA region involving any of the identified classical HLA alleles (Fig. 2b and Supplementary Fig. 4). Similarly, we found no evidence for interactions between classical HLA alleles and the effects of all non-HLA variants combined in a single risk score (Fig. 2c and Supplementary Fig. 5). We note that, initially, no departure from additivity was included for HLA-A*02:01, which led to inflation of the interaction terms with non-HLA associated alleles. This inflation disappeared when the partially dominant effect of HLA-A*02:01 was included in the model, illustrating how failing to include departures from additivity can generate false evidence of interaction (Supplementary Fig. 6). Similar patterns were observed if the non-additive term for HLA-DRB1*15:01 was not included (Supplementary Fig. 6).

Testing for polygenic epistasis

Despite the lack of evidence for specific interactions, it is nevertheless possible that the effects of individual classical alleles are modulated by many weak effects at many loci across the genome. Such polygenic epistasis could be manifest by an elevated contribution of background relatedness to variation in disease risk in individuals who carry a specific risk allele. In theory, it would be possible to estimate separate random-effects components for additive and interacting components of background risk. However, in practice, such components are highly correlated, which makes efficient estimation for very large kinship matrices impractical. However, an alternative approach is to estimate the difference between cases and controls in the effect of background relatedness on predicting the allele of interest (Supplementary Note). In effect, this approach builds upon the intuition that genetic interactions generate LD that is manifest only in cases. Moreover, effects can be estimated using existing linear mixed-model methodology28, and simulations demonstrated that a study of this size is well powered to detect substantial epistasis if present (Supplementary Note). We applied the approach independently to the key associated classical HLA alleles and combined the results across cohorts through meta-analysis (Fig. 3). We found that, although the point estimate of the contribution of polygenic epistasis was substantial for some loci, the P value for a nonzero polygenic epistatic component was never less than 0.05, and, for the two most significant alleles (HLA-DRB1*15:01 and HLA-A*02:01), the point estimate was close to zero. Moreover, HLA-B*38:01, which showed the strongest effect, in being a rare allele might have greater population stratification than common alleles29, and a related estimator put the epistatic component for this allele at 0 (Supplementary Note). Overall, we conclude that there is no strong evidence for major polygenic epistasis modulating influence on classical HLA allele risk for multiple sclerosis.

Figure 3.

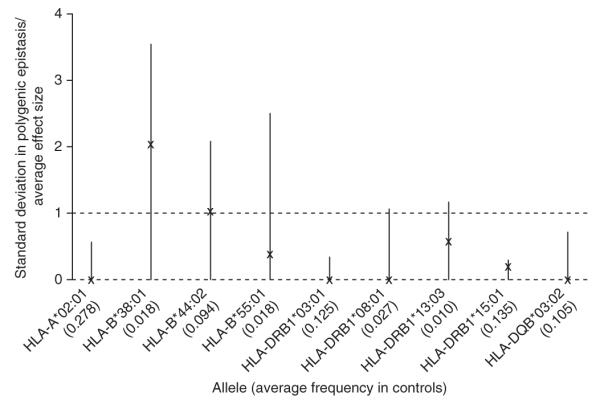
Figure 3

Open in a new tab

Estimates of polygenic epistasis influencing the effects of major HLA loci on multiple sclerosis. Point estimates (X’s) and 95% confidence intervals (lines; floored to zero) are shown for the ratio of the standard deviation in effect induced by genome-wide polygenic epistasis to the absolute magnitude of the average effect size for classical HLA alleles influencing risk of multiple sclerosis. Results are shown from fixed-effect meta-analysis across cohorts. Under a simple model (Supplementary Note), this factor can be estimated by comparing the difference in apparent heritability for major alleles between cases and controls. The dashed lines at 0 and 1 indicate, respectively, the case with no epistasis and the case where the standard deviation in the epistatically induced effect equals the average main effect.

Genetic influences on disease features

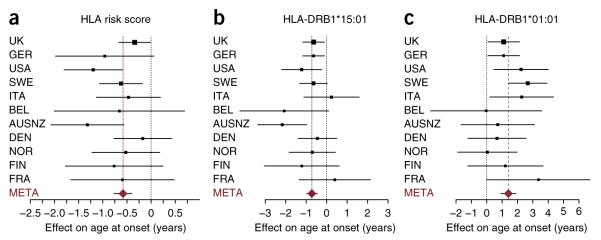
Finally, we considered whether HLA factors influence phenotypic features, including age at onset (n = 11,019), disease severity (MS severity score; n = 8,065) and clinical course (comparing primary progressive with relapsing onset disease; n = 12,450) (n is the number of cases for which data were available); Supplementary Table 5). First, we tested for association with an HLA-specific risk score obtained by multiplying the odds ratios of each individual’s geno-types across loci. We found evidence for association between the HLA risk score and age at onset (P = 6.6 × 10−10; Fig. 4a), which was driven by the HLA-DQB*06:02–HLA-DRB1*15:01 haplotype (with each allele of HLA-DQB1*06:02 reducing age at onset by 0.72 years, P = 2 × 10−8; comparable to previous estimates9,30) (Fig. 4b) and the HLA-DQA*01:01–HLA-DRB1*01:01 haplotype (with each copy of HLA-DRB1*01:01 increasing age at onset by ~1.4 years, P = 2 × 10−8) (Fig. 4c). Data for other alleles on these haplotypes are shown in Supplementary Figure 7. The preferred model for age at onset within the UK cohort included additive and independent effects for HLA-DQB1*06:02 and HLA-DRB1*01:01, although these alleles are in strong positive LD with HLA-DRB1*15:01 and HLA-DQA1*01:01, respectively (r = 0.97 and 0.76), and there was only a small difference in likelihood in comparison to a model involving these alleles (Supplementary Table 4). When the entire cohort was considered, the age-at-onset effect was better explained by a recessive effect for HLA-DQB1 alleles encoding a glycine at position 70 (Supplementary Table 4), again without evidence for an interaction. Consistent with earlier observations, we found no strong or consistent associations with other disease features9 nor did we find evidence for interactions. In summary, genetic factors within the HLA region have only a weak effect on any aspect of disease subphenotype, and, where they do have an effect, it is in a manner broadly consistent with overall risk for multiple sclerosis, although without evidence for the interactions identified for disease risk.

Figure 4.

Figure 4

Open in a new tab

HLA effects on age at onset. The point estimate and 95% confidence interval are shown for each cohort (with the area of each square proportional to sample size) along with the meta-analysis estimate (META; brown dashed line). (a) Forest plots showing fixed-effect meta-analysis of the effect of combined HLA risk score (Online Methods) on age at onset of multiple sclerosis. (b,c) Meta-analysis of the effects of the HLA-DRB1*15:01 (b) and HLA-DRB1*01:01 (c) alleles on age at onset (results for HLA-DQB1*06:02 and HLA-DQA1*01:01 are shown in Supplementary Fig. 7).

DISCUSSION

Our results establish important features of the architecture of genetic risk for multiple sclerosis. In particular, a picture of relative simplicity emerges, with a series of class II risk alleles (consistent with most being driven by HLA-DRB1) alongside a series of protective class I alleles and with no strong contribution to disease severity or clinical course. Such findings are in direct contrast to the complexity found in inflammatory bowel diseases (IBD)31. Rather, we find a landscape largely absent of statistical interactions involving classical HLA alleles at the loci studied, although there are occasional substantial modulating effects for particular allelic combinations. These findings raise questions about disease mechanisms that require analysis in functional studies. For example, the finding that the protective effect of the HLA-DQA1*01:01–bearing haplotype is restricted to HLA-DRB1*15:01 carriers suggests the possibility of a process mediated by T cell receptor cross-reactivity (as proposed for HLA-DRB1*15:01–HLA-DRB5 interactions32). In contrast, the lack of interactions between class I and class II alleles suggests that the respective risk and protective effects of alleles within these two systems may act through very different mechanisms. The presence of multiple protective alleles, including rare alleles with strong effects (HLA-B*38:01, frequency ~1.1% in UK controls; HLA-B*55:01, frequency ~1.8% in UK controls), raises the question of whether carriers of these different alleles share related immunological properties that can potentially be manipulated through therapeutic intervention. More generally, although more might be learned from the use of even larger sample sizes, our finding of a modest contribution of interactions to variation in genetic risk suggests that epistasis involving classical HLA alleles does not contribute substantially to missing heritability33 in multiple sclerosis.

ONLINE METHODS

Data

The data consist of 11 country-level cohorts of European ancestry from Australia and New Zealand (AUSNZ), Belgium (BEL), Denmark (DEN), Finland (FIN), France (FRA), Germany (GER), Italy (ITA), Norway (NOR), Sweden (SWE), the UK (UK) and the United States (USA). In total, there were 47,850 individuals, and the per-population breakdown of the sample sizes, after quality control and exclusions, can be found in Supplementary Table 1. Full details of the quality control that was performed can be found in the supplementary materials of the first multiple sclerosis Immunochip analysis11. Briefly, sample-level quality checks included sex checks (samples excluded if the reported sex was inconsistent with the one observed on the basis of sex chromosome markers), call rate (samples were excluded if the call rate was <98%), autosomal heterozygosity (samples were excluded if more than 3 s.d. from the mean), ambiguity or inconsistency in the Sequenom fingerprint ID and an excess of identity-by-descent (IBD) sharing (PI_HAT > 0.25). Contrary to the previous analysis11, here we have included individuals who overlapped with those included in the 2011 GWAS9.

SNP-level quality control was carried out for each population separately, using individuals who passed sample quality control. The quality control consisted of checking (in the following order) whether the SNPs had a call rate of <98%, had a Hardy-Weinberg equilibrium P value of <1 × 10−5, exhibited differential missingness between cases and controls with a P value <1 × 10−3 or were monomorphic. Only SNPs that passed quality control in all populations were kept. Principal components were also calculated separately for each population, using the samples and an LD-pruned set of SNPs that passed quality control. An 1,330 additional samples were removed as being outliers from the principal-component analysis (PCA). Further details on the choice of SNPs for the PCA calculations can be found in ref. 11. Full sample and SNP exclusion lists by cohort can be found in Supplementary Tables 10 and 11 of ref. 11, respectively. In total, in this study, we considered 6,218 SNPs from within the extended MHC region34, from 29.9 Mb to 33.6 Mb (hg19/GRC37) on chromosome 6.

Imputation of HLA alleles

Classical HLA types were imputed using the program HLA*IMP:02 (ref. 13). Briefly, HLA*IMP:02 uses a graphical representation of the haplotype structure (‘haplotype graph’) in the extended MHC region to statistically infer a sample’s classical HLA alleles. For this study, we created a haplotype graph from a pan-European reference panel (GS&HLARES_EU from ref. 26) combining sample data from the CEU34, CEU+ (ref. 34), 1958 British Birth Cohort and HLARES13,26 data sets.

GS&HLARES_EU comprises 6,056 SNPs across the extended MHC (as defined in ref. 26) and a varying number of individuals with classical HLA type data available (1,864 individuals with at least one 4-digit allele defined for HLA-A; 2,630 for HLA-B; 1,502 for HLA-C; 366 for HLA-DQA1; 2,031 for HLA-DQB1; 2,414 for HLA-DRB1; 74 for HLA-DPB1; and 282 individuals with at least one 2-digit allele available for HLA-DRB3; 282 for HLA-DRB4; 282 for HLA-DRB5).

In the process of standard HLA*IMP:02 preimputation quality control, all SNPs with more than 20% ‘missing data’ in the multiple sclerosis data set were removed, and, for complementary SNPs, strandedness was aligned to HapMap. These steps were carried out with the standard HLA*IMP front end and are described in detail in the supplementary information of the 2011 GWAS9.

HLA alleles were imputed at a four-digit resolution for the loci HLA-A, HLA-C, HLA-B, HLA-DRB1, HLA-DQA1, HLA-DQB1 and HLA-DPB1 and at a two-digit resolution for the loci HLA-DRB3, HLA-DRB4 and HLA-DRB5 as no four-digit resolution data were available as reference for the latter.

Validation of classical allele imputation for reported alleles

We assessed imputation accuracy by conducting a 2/3 (training) – 1/3 (validation) cross-validation experiment on samples of known HLA types, used as a reference panel for the imputation. We employed the same statistical model and the identical set of informative SNPs as were employed in the analysis. At four-digit resolution, without imposing a threshold for calling on the posterior probabilities (call rate = 100%), the accuracy ranged from 0.9 to 0.99 (Supplementary Table 2).

We also investigated the sensitivity, specificity and positive predictive value (PPV) of all alleles found to be associated with multiple sclerosis or secondary phenotypes (Supplementary Table 3). Specificity was extremely high across all putatively associated alleles. Sensitivity and PPV were above 90% for all alleles found to be associated, apart from HLA-B*38:01 (PPV = 0.89), HLA-DRB1*08:01 (PPV = 0.84) and HLA-DRB1*01:01 (sensitivity = 0.82, PPV = 0.90). No systematic pattern in misimputation was found for HLA-B*38:01, whereas the majority of misimputations for HLA-DRB1*01:01 and HLA-DRB1*08:01 were with other alleles of the same two-digit type (for example, HLA-DRB1*01:03 and HLA-DRB1*08:02, respectively).

Building a model of HLA risk for multiple sclerosis

Our aim was to identify the key classical HLA drivers of genetic risk for multiple sclerosis and other effects within the region that are of comparable significance but are not explained through LD to specific HLA alleles. We used three different approaches to build such a model, taking a consensus strategy to summarize the findings.

Approach 1: manually curated search with UK focus

Approach 1 focused initial discovery on the UK cohort, which is the largest of all and most closely matched to the imputation training data, and then combined evidence across all cohorts using fixed-effect meta-analysis to confirm (validate and replicate) the association, estimate effect size (odds ratios) and test for potential heterogeneity between cohorts. We recognize that if HLA allele imputation were perfect and population stratification were completely controlled, this approach would lose power relative to a simple joint analysis. Our approach, therefore, is conservative but robust to particular failures in imputation or control of population stratification.

We started by incorporating in our model the four HLA alleles that were found to be significantly associated with multiple sclerosis in the 2011 GWAS9, namely HLA-DRB1*15:01, HLA-DRB1*13:03, HLA-DRB1*03:01 and HLA-A*02:01. As anticipated, these all replicated in the fixed-effect meta-analysis. Given that our training data only allowed two-digit resolution of HLA-DRB5 alleles, it was not possible for us to fully resolve the relative contributions of the tightly correlated HLA-DRB5*01:01 and HLA-DRB1*15:01 alleles. On the basis of the known LD of virtually 100% between HLA-DRB1*15:01 and HLA-DRB5*01:01 in populations with European ancestry, the relative contribution of either allele to multiple sclerosis cannot be addressed in this study.

We then employed a stepwise logistic regression approach where additional parameters (both HLA alleles and SNPs in the MHC region) were considered for addition to the model if the strength of association in the relevant conditional analysis within the UK cohort had P < 1 × 10−5. We only report effects that had combined P < 1 × 10−9 in the fixed-effect meta-analysis of the model containing all other alleles identified through this iterative process (the ‘full’ model). Five principal components were included as covariates in all models (these principal components were calculated from SNPs across the genome, not including any from the extended MHC region, as described in the 2013 multiple sclerosis Immunochip study11). Sex was not included as a covariate. Where appropriate, we employed likelihood-ratio tests (LRTs) to choose among competing models where they were nested and the Bayesian information criterion35 (BIC) otherwise. The Supplementary Note provides details of the models considered and the steps taken at each stage of the selection procedure. A summary of the factors identified at each step is shown in Supplementary Figure 2.

To check consistency, we also rebuilt the model without any prior inclusion. All the alleles and effects reported were included, although in a slightly different order. In particular, the risk effect of HLA-DRB1*03:01 appears later (although it is still included).

Approach 2: automated model search at four-digit HLA alleles with cross-cohort mega-analysis

To approach the construction of a general model for HLA allele risk for multiple sclerosis in a manner that was not guided by prior knowledge, we used an automated model search strategy in which all cohorts were considered jointly (referred to as a mega-analysis). Before analyses, we took the following steps: (i) we set the threshold for imputation to be 0, that is, taking the allele call with the highest posterior probability in each case and treating it as fixed. This step is needed to enable appropriate model comparison between loci. By way of comparison, setting a threshold of 0.5 would remove 2.2% of the imputed genotypes across loci. (ii) We removed alleles with a combined frequency after imputation across cohorts of 0.5%. This step removed 55 alleles of 232 across the loci considered. (iii) We removed alleles imputed to be in perfect association (r2 = 1) with each other. This step removed 8 of 177 alleles. (iv) We removed individuals for whom the imputed allele was not present in the IMGT database. This step removed 530 of 47,849 individuals.

Starting with a baseline model including effects for each cohort (as a factor) and principal components, at each stage, we performed logistic regression on disease risk for every classical HLA allele in turn, considering a general geno-type model (separate coefficients for each genotype). Consequently, the allele that led to the highest increase in likelihood was identified, and, in a separate step, the Bayesian information criterion (BIC) was used to decide whether the effect was best described as additive, recessive, dominant or general. A range of strategies for backward elimination were considered, although in practice no allele was ever removed. The model selection process was run until the BIC no longer increased. However, only effects that also achieved P < 1 × 10−9 in the fixed-effect meta-analysis are reported. A summary of the factors identified at each step and how these relate to the factors identified by the other approaches is shown in Supplementary Figure 2.

We note that we also considered an automated search including SNP variants. However, because most classical HLA alleles are well tagged by at least one (and often many) SNP within the region, we commonly observed that effects that are typically interpreted as being driven by classical HLA alleles were assigned to SNPs (potentially owing to errors in imputation and/or chance fluctuations in association). We therefore only considered classical HLA alleles in the automated approach, although we compared results to the manually curated selection process to check consistency.

Approach 3: automated model search augmented with allele groupings at the two-digit level and by sharing of amino acids at variable residues

Previous research has demonstrated that some association between groups of classical HLA alleles and genetic risk for disease can be explained by the sharing of particular amino acid residues at variable sites within the mature protein14. We therefore considered a separate automated model search strategy on the combined cohorts in which we augmented the set of HLA alleles by genotypes at allele groups defined by both two-digit resolution and the sharing of specific amino acid residues at variable sites. Group membership was inferred from the imputed allele at four-digit resolution. Aligned amino acid sequences for the imputed alleles were obtained from IMGT on 4 March 2015. In a few instances, full amino acid sequences were not available for all alleles imputed.

We took the following steps: (i) we set the threshold for imputation to be 0, that is, taking the allele call with the highest posterior probability in each case and treating it as fixed. (ii) We removed alleles or allele groups with a combined frequency after imputation across cohorts of 0.5%. This step removed 108 alleles and allele groups of 454 across the loci considered. (iii) We removed alleles or allele groups imputed to be in perfect association (r2 = 1) with each other. This step removed 22 of 346 alleles and allele groups. (iv) We removed individuals for whom the imputed allele was not present in the IMGT database. This step removed 530 of 47,849 individuals.

We considered a general genotype model for each allele or allele group at each step, starting from a baseline model with coefficients for each cohort and principal components. At each stage, the allele or allele group leading to the greatest increase in likelihood was identified, and BIC was used to assign additive, dominant, recessive or general models. The procedure was run until BIC no longer increased, although only effects that achieved P < 1 × 10−9 in the fixed-effect meta-analysis are reported. A summary of the effects identified at each stage is shown in Supplementary Figure 2.

Consensus strategy and comparison

The three model selection strategies identified a series of related although non-identical effects (Supplementary Fig. 2). Moreover, in two cases, the effects identified by the automated approaches were better described as interactions. For example, the homozygous protective effect identified as associated with HLA-DQB1 alleles with a glycine at residue 70 in step (vii) of the augmented model selection process was better explained (the data were 400 times more likely) through an interaction with HLA-DRB1*15:01.

Integrating uncertainty in classical allele imputations

To ensure that the identified associations were not affected by imputation quality, additional analyses where conducted where the uncertainty associated with imputation (quantified by the posterior probability of each call) was incorporated into the logistic regression framework, with numerical optimization used to find maximum-likelihood estimates. Specifically, for every classical allele, we fitted logistic models with additive and non-additive effects for HLA-DRB1*15:01 and HLA-A*02:01, the top five principal components and the allele in question (with the disease model inferred from the initial analysis), with no uncertainty (alleles treated as perfectly measured) and with uncertainty (integrating out uncertainty in the genotype). Correspondence in the effect sizes and statistical significance are shown in Supplementary Figure 1.

Secondary phenotypes

Secondary phenotypes, including clinical course (primary progressive versus relapsing remitting multiple sclerosis), severity (calculated by the multiple sclerosis severity score, MSSS, which reflects the rate at which patients affected with the disease accumulate disability36) and age at onset were available for a proportion of the samples studied (Supplementary Table 5). We used a combination of manually curated and automated searches to explore genetic associations to secondary phenotypes. Details are provided in the Supplementary Note.

Interactions among classical HLA alleles

To investigate potential interactions between the HLA alleles included in our model and other HLA alleles, we first ran models with (i) two parameters (one additive and one homozygote correction term) to model the effects of HLA-DRB1*15:01 and HLA-A*02:01; (ii) parameters for each of the top five principal components; (iii) a single parameter included for each other SNP or HLA allele identified as associated with multiple sclerosis in this analysis (additive on the log-odds scale for all alleles apart from HLA-DRB1*03:01 and HLA-DQB1*03:02, where a recessive and a dominant effect, respectively, were assumed); (iv) a single parameter (additive on the log-odds scale) for each other HLA allele in turn; and (v) an interaction term, which models the effect of each other HLA allele in the presence of the allele under consideration. Quantile-quantile plots of the interaction term for these analyses are shown in Figure 2 and Supplementary Figure 3 for the UK cohort.

Interactions between classical HLA alleles and non-HLA associated loci

We assessed evidence of interaction between HLA risk alleles and non-HLA risk loci associated with multiple sclerosis identified in the recent Immunochip study11, by fitting models with (i) risk parameters for the classical HLA allele as identified above (Table 1); (ii) parameters for the top five principal components; (iii) a parameter for the non-HLA variant (additive on the log-odds scale); and (iv) an interaction parameter for the effect of the non-HLA SNP in the presence of the classical HLA allele in question. Quantile-quantile plots of the interaction term for these analyses are shown in Figure 2 and Supplementary Figure 4 for the UK cohort.

For HLA-A*02:01, initial evidence for deviation from the expected uniform distribution of P values led to the identification of a weak non-additive effect of the allele, correction for which removed any evidence for HLA–non-HLA interactions (Supplementary Fig. 6).

We also asked whether the effect of HLA alleles on multiple sclerosis risk was stratified by the cumulative risk from the non-HLA effects. To do this, we divided the samples (combined cases and controls within the UK cohort) into quartiles of non-HLA risk score (RS), defined by combining information across the L loci found associated in ref. 11. Specifically, the RS for an individual j was calculated as

RSj=exp(∑i=1LGijbi)

where Gij ∈{0,1,2} is the genotype for non-HLA SNP i and bi is the corresponding inferred log-odds risk ratio. Results are shown in Figure 2 and Supplementary Figure 5.

Estimating the contribution of polygenic epistasis to HLA allele risk

To assess whether many weak effects spread across the genome modulate the genetic risk for multiple sclerosis arising from classical HLA alleles, we developed and validated a new statistical approach that exploits the idea that interactions generate case-only LD among interacting alleles. Full details of the method are provided in the Supplementary Note.

Supplementary Material

Supplementary Information

ACKNOWLEDGMENTS

We thank the individuals, nurses and referring physicians who participated in this study. This project was supported by the US National Institutes of Health (NS049477, NS26799, R01NS032830, RC2NS070340, R01NS067305 and RC2GM093080), the Wellcome Trust (085475/B/08/Z, 085475/Z/08/Z, 084702/Z/08/Z and 098051), the UK MS Society (857/07, 861/07, 862/07, 894/08, 898/08 and 955/11), the UK Medical Research Council (G0700061), Naomi Branson, the Sainsbury Foundation, NMSS (RG 4198-A-1 and 4680-A-1, FG 1938-A-1, JF2138A1, JF-2137A4 and South Florida chapter), the Cambridge National Institute for Health Research (NIHR) British Research Council (BRC), DeNDRon, the Bibbi and Niels Jensens Foundation, the Swedish Brain Foundation, the Swedish Research and County Council, the Knut and Alice Wallenberg Foundation, the Swedish Heart-Lung Foundation, the AFA Foundation, the Foundation for Strategic Research, the Stockholm County Council (592229), the Strategic Cardiovascular and Diabetes Programmes of Karolinska Institutet, the Swedish Council for Working Life and Social Research, INSERM, ARSEP, AFM, GIS-IBISA, BMBF, KKNMS (01GI0917), Deutsche Forschungsgemeinschaft (530/1-1), Munich Biotec Cluster M4, the Fidelity Biosciences Research Initiative, FWO-Vlaanderen, Research Fund KU Leuven (OT/11/087), the Belgian Neurological Society, the Belgian Charcot Foundation, Gemeinnützige Hertie Stiftung, CRPPMS University Zurich, the Danish MS Society, the Danish Council for Strategic Research, the Center of Excellence for Disease Genetics of the Academy of Finland, the Sigrid Juselius Foundation, the Helsinki University Central Hospital Research Foundation, FISM (2011/R/14), Fondazione Cariplo (2010-0728), MIUR (PRIN08), CRT Foundation Turin, the Italian Ministry of Health (502/92), the Italian Foundation for Multiple Sclerosis, INSPE, the Multiple Sclerosis Association of Oslo, the Norwegian Research Council (143153 and 143410), the South-Eastern Norwegian Health Authorities (51852/ILM) and the Australian National Health and Medical Research Council (633275 and 1053756).

We acknowledge the use of samples from the British 1958 Birth Cohort DNA collection (UK Medical Research Council, G0000934 and Wellcome Trust, 068545/Z/02), the UK National Blood Service controls, the Vanderbilt University Medical Center’s BioVU DNA Resources Core (US National Institutes of Health, 1UL1RR024975-01), CRB-REFGENSEP, Norwegian Bone Marrow Registry controls, the Norwegian Multiple Sclerosis Registry and Biobank, NARCOMS Registry (CMSC), the Brigham and Women’s Hospital PhenoGenetic Project and Academy of Finland DILGOM (136895, 263836 and 118065).

The GWAS made use of external control data from the popgen biobank, Swedish Breast Cancer study, HYPERGENES, CHOP, the Swedish CAD study, BRC-REFGENSEP, Pitié-Salpêtrière CIC, Généthon, the Wellcome Trust Sanger Institute, the University of Miami John P. Hussman Institute, ICM, the Norwegian Multiple Sclerosis Registry and Biobank, the SNP Technology Platform in Uppsala, Sweden, and the University of California, San Francisco. Full acknowledgments are included in the Supplementary Note.

Footnotes

Note: Any Supplementary Information and Source Data files are available in the online version of the paper.

AUTHOR CONTRIBUTIONS

A.C., A.O., A.S., B.D., B.F., B.H., B.T., C.G., C.M.L., D.A.H., D. Booth, D. Buck, E.G.C., F.M.-B., F.Z., G.S., H.F.H., I.K., IIBDGC, J.H., J.L.H., J.L.M., J.R.O., J.S., L.A., P.L.D.J., S.D’A., S.L.H., S.S., T.M.C.B. and T.O. were involved with case ascertainment and phenotyping. A.G., A.O., B.F., D. Booth, D. Buck, F.M.-B., H.B.S., H.F.H., I.K., J.L.M., J.R.O., M.B., P.L.D.J., S.D’A. and S.S. processed the DNA. A.O., B.F., D.A.H., H.B.S., IIBDGC, J.L.M., M.B., P.L.D.J. and S.S. conducted and supervised the genotyping of samples. A.H.B., A.T.D., C.A.A., C.C.A.S., C.C., D.K.X., G.M., J.L.H., J.L.M., L.F., L.J., L.M., M.B., N.A.P., P.D., P.L.D.J., P.-A.G., S.E.B., S.L., S.S. and T.S.S. performed the analysis. A.G., A.H.B., A.J.I., A.O., A.T.D., B.D., B.F., B.H., C.A.A., C.C.A.S., C.C., C.G., C.M.L., D. Booth, D. Buck, D.K.X., E.G.C., F.M.-B., F.Z., G.M., H.B.S., H.F.H., I.K., J.B., J.L.H., J.L.M., J.S., J.W., L.J., L.M., M.B., N.A.P., P.D., P.L.D.J., S.D’A., S.L., S.S., T.M.C.B. and T.S.S. collected and managed the project data. A.C., A.H.B., A.J.I., A.S., B.H., C.A.A., C.A.D., C.C.A.S., C.C., C.G., C.M.L., D.A.H., E.G.C., F.M.-B., F.Z., G.M., G.S., H.F.H., J.B., J.H., J.L.H., J.L.M., J.R.O., J.S., J.W., K.E.A., L.A., L.J., M.A.P.-V., M.B., N.A.P., P.D., P.L.D.J., S.D’A., S.L., S.L.H., S.S., T.M.C.B., T.O. and T.S.S. contributed to the study concept and design. All authors reviewed and approved the final manuscript.

COMPETING FINANCIAL INTERESTS

The authors declare competing financial interests: details are available in the online version of the paper.

Accession codes. SNP genotypes are available upon request from the International Multiple Sclerosis Genetics Consortium via Jonathan Haines (jonathan.haines@case.edu).

References

  • 1.Jersild C, Svejgaard A, Fog T. HL-A antigens and multiple sclerosis. Lancet. 1972;1:1240–1241. doi: 10.1016/s0140-6736(72)90962-2. [DOI] [PubMed] [Google Scholar]
  • 2.Ligers A, et al. Evidence of linkage with HLA-DR in DRB1*15-negative families with multiple sclerosis. Am. J. Hum. Genet. 2001;69:900–903. doi: 10.1086/323480. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.International Multiple Sclerosis Genetics Consortium A high-density screen for linkage in multiple sclerosis. Am. J. Hum. Genet. 2005;77:454–467. doi: 10.1086/444547. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Kwon OJ, et al. HLA class II susceptibility to multiple sclerosis among Ashkenazi and non-Ashkenazi Jews. Arch. Neurol. 1999;56:555–560. doi: 10.1001/archneur.56.5.555. [DOI] [PubMed] [Google Scholar]
  • 5.International Multiple Sclerosis Genetics Consortium Risk alleles for multiple sclerosis identified by a genomewide study. N. Engl. J. Med. 2007;357:851–862. doi: 10.1056/NEJMoa073493. [DOI] [PubMed] [Google Scholar]
  • 6.Baranzini SE, et al. Genome-wide association analysis of susceptibility and clinical phenotype in multiple sclerosis. Hum. Mol. Genet. 2009;18:767–778. doi: 10.1093/hmg/ddn388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.De Jager PL, et al. Meta-analysis of genome scans and replication identify CD6, IRF8 and TNFRSF1A as new multiple sclerosis susceptibility loci. Nat. Genet. 2009;41:776–782. doi: 10.1038/ng.401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Australia and New Zealand Multiple Sclerosis Genetics Consortium (ANZgene) Genome-wide association study identifies new multiple sclerosis susceptibility loci on chromosomes 12 and 20. Nat. Genet. 2009;41:824–828. doi: 10.1038/ng.396. [DOI] [PubMed] [Google Scholar]
  • 9.International Multiple Sclerosis Genetics Consortium. Wellcome Trust Case Control Consortium 2 Genetic risk and a primary role for cell-mediated immune mechanisms in multiple sclerosis. Nature. 2011;476:214–219. doi: 10.1038/nature10251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Patsopoulos NA, et al. Genome-wide meta-analysis identifies novel multiple sclerosis susceptibility loci. Ann. Neurol. 2011;70:897–912. doi: 10.1002/ana.22609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.International Multiple Sclerosis Genetics Consortium Analysis of immune-related loci identifies 48 new susceptibility variants for multiple sclerosis. Nat. Genet. 2013;45:1353–1360. doi: 10.1038/ng.2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Leslie S, Donnelly P, McVean G. A statistical method for predicting classical HLA alleles from SNP data. Am. J. Hum. Genet. 2008;82:48–56. doi: 10.1016/j.ajhg.2007.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Dilthey A, et al. Multi-population classical HLA type imputation. PLOS Comput. Biol. 2013;9:e1002877. doi: 10.1371/journal.pcbi.1002877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Patsopoulos NA, et al. Fine-mapping the genetic association of the major histocompatibility complex in multiple sclerosis: HLA and non-HLA effects. PLoS Genet. 2013;9:e1003926. doi: 10.1371/journal.pgen.1003926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Marrosu MG, et al. Dissection of the HLA association with multiple sclerosis in the founder isolated population of Sardinia. Hum. Mol. Genet. 2001;10:2907–2916. doi: 10.1093/hmg/10.25.2907. [DOI] [PubMed] [Google Scholar]
  • 16.Sanna S, et al. Variants within the immunoregulatory CBLB gene are associated with multiple sclerosis. Nat. Genet. 2010;42:495–497. doi: 10.1038/ng.584. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Barcellos LF, et al. Heterogeneity at the HLA-DRB1 locus and risk for multiple sclerosis. Hum. Mol. Genet. 2006;15:2813–2824. doi: 10.1093/hmg/ddl223. [DOI] [PubMed] [Google Scholar]
  • 18.Dyment DA, et al. Complex interactions among MHC haplotypes in multiple sclerosis: susceptibility and resistance. Hum. Mol. Genet. 2005;14:2019–2026. doi: 10.1093/hmg/ddi206. [DOI] [PubMed] [Google Scholar]
  • 19.Marrosu MG, et al. Interaction of loci within the HLA region influences multiple sclerosis course in the Sardinian population. J. Neurol. 2006;253:208–213. doi: 10.1007/s00415-005-0957-y. [DOI] [PubMed] [Google Scholar]
  • 20.Lincoln MR, et al. Epistasis among HLA-DRB1, HLA-DQA1, and HLA-DQB1 loci determines multiple sclerosis susceptibility. Proc. Natl. Acad. Sci. USA. 2009;106:7542–7547. doi: 10.1073/pnas.0812664106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Hedström AK, et al. Smoking and two human leukocyte antigen genes interact to increase the risk for multiple sclerosis. Brain. 2011;134:653–664. doi: 10.1093/brain/awq371. [DOI] [PubMed] [Google Scholar]
  • 22.Gregersen JW, et al. Functional epistasis on a common MHC haplotype associated with multiple sclerosis. Nature. 2006;443:574–577. doi: 10.1038/nature05133. [DOI] [PubMed] [Google Scholar]
  • 23.Evans DM, et al. Interaction between ERAP1 and HLA-B27 in ankylosing spondylitis implicates peptide handling in the mechanism for HLA-B27 in disease susceptibility. Nat. Genet. 2011;43:761–767. doi: 10.1038/ng.873. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Strange A, et al. A genome-wide association study identifies new psoriasis susceptibility loci and an interaction between HLA-C and ERAP1. Nat. Genet. 2010;42:985–990. doi: 10.1038/ng.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Kirino Y, et al. Genome-wide association analysis identifies new susceptibility loci for Behcet’s disease and epistasis between HLA-B*51 and ERAP1. Nat. Genet. 2013;45:202–207. doi: 10.1038/ng.2520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dilthey AT, Moutsianas L, Leslie S, McVean G. HLA*IMP—an integrated framework for imputing classical HLA alleles from SNP genotypes. Bioinformatics. 2011;27:968–972. doi: 10.1093/bioinformatics/btr061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Field J, et al. A polymorphism in the HLA-DPB1 gene is associated with susceptibility to multiple sclerosis. PLoS ONE. 2010;5:e13454. doi: 10.1371/journal.pone.0013454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Mathieson I, McVean G. Differential confounding of rare and common variants in spatially structured populations. Nat. Genet. 2012;44:243–246. doi: 10.1038/ng.1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Masterman T, et al. HLA-DR15 is associated with lower age at onset in multiple sclerosis. Ann. Neurol. 2000;48:211–219. [PubMed] [Google Scholar]
  • 31.Goyette P, et al. High-density mapping of the MHC identifies a shared role for HLA-DRB1*01:03 in inflammatory bowel diseases and heterozygous advantage in ulcerative colitis. Nat. Genet. 2015;47:172–179. doi: 10.1038/ng.3176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Lang HL, et al. A functional and structural basis for TCR cross-reactivity in multiple sclerosis. Nat. Immunol. 2002;3:940–943. doi: 10.1038/ni835. [DOI] [PubMed] [Google Scholar]
  • 33.Manolio TA, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.de Bakker PI, et al. A high-resolution HLA and SNP haplotype map for disease association studies in the extended human MHC. Nat. Genet. 2006;38:1166–1172. doi: 10.1038/ng1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Schwarz GE. Estimating the dimension of a model. Ann. Stat. 1978;6:461–464. [Google Scholar]
  • 36.Roxburgh RH, et al. Multiple Sclerosis Severity Score: using disability and disease duration to rate disease severity. Neurology. 2005;64:1144–1151. doi: 10.1212/01.WNL.0000156155.19270.F8. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
NIHMS782000-supplement-Supplementary_Information.pdf (4.6MB, pdf)

RESOURCES