Continuum descriptions of membranes and their interaction with proteins: towards chemically accurate models

Abstract

Biological membranes deform in response to resident proteins leading to a coupling between membrane shape and protein localization. Additionally, the membrane influences the function of membrane proteins. Here we review contributions to this field from continuum elastic membrane models focusing on the class of models that couple the protein to the membrane. While it has been argued that continuum models cannot reproduce the distortions observed in fully-atomistic molecular dynamics simulations, we suggest that this failure can be overcome by using chemically accurate representations of the protein. We outline our recent advances along these lines with our hybrid continuum-atomistic model, and we show the model is in excellent agreement with fully-atomistic simulations of the nhTMEM16 lipid scramblase. We believe that the speed and accuracy of continuum-atomistic methodologies will make it possible to simulate large scale, slow biological processes, such as membrane morphological changes, that are currently beyond the scope of other computational approaches.

Graphical Abstract

1. Introduction

Biological membranes are crowded with transmembrane proteins and peripherally associated proteins that carry out a host of tasks ranging from ion and small molecule transport to cell motility. The distribution of proteins is highly variable and heterogeneous leading to specialized compartments with dedicated chemistries, polarized cells with distinct apical and basal membranes, and membrane structures with intricate morphologies. In this review, we are interested in the role that membrane proteins play in sculpting membrane shape as well as how local membrane properties influence protein function. The distinct shapes of many intracellular membrane structures are often the result of specific membrane proteins as is the case for the spherical vesicles that shuttle between the endoplasmic reticulum (ER) and Golgi that have a defined protein coat composed of COPI or COPII complexes [1], the convoluted folds of the inner mitochondrial membrane whose cristea are created by rows of transmembrane F-ATPase dimers [2], and ER tubular networks created by the homotypic fusion of embedded proteins on opposing membranes [3]. Additionally, membranes can adopt exotic configurations such as the cubic phases, or ‘plumber’s nightmares’, and the equilibrium between flat L_α phase and other membrane phases can be biased by the presence of membrane proteins [4, 5], which forms the basis of membrane protein crystallization from the lipidic cubic phase (LCP) [4, 6]. Meanwhile, the mechanical properties of the membrane can affect the biophysical properties of the protein. For instance, the thickness of the membrane drives dimerization of gramicidin channels, antibiotics that kill bacteria through the dissipation of ion concentration gradients [7], in-plane tension and the hydrophobic thickness of the membrane bias the opening and closing of mechanosensitive channels in response to touch and osmotic stress [8, 9], and tension can induce redistribution of Slm1 proteins that subsequently lead to downstream signalling [10]. Additionally, the shape or curvature of the membrane is thought to influence the probability of alamethicin conductance states [11] and to allosterically regulate the ion channel function of α–hemolysin [12], while also influencing the mobility of proteins in the membrane [13].

There are several mechanisms by which membrane proteins are thought to influence the shape of membranes, and here we present several top candidates loosely following the work of Kozlov and coworkers [14, 15]. We have grouped the shaping mechanisms into two main categories:

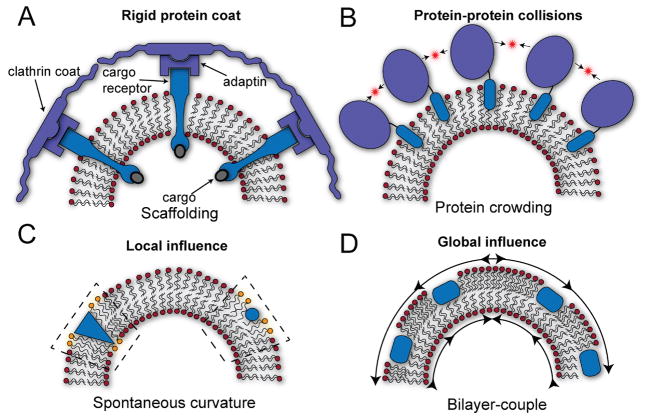
• First, proteins can induce membrane deformations by forming a coat around the membrane in which hydrophilic protein domains insert into the bilayer while adjacent soluble domains impart forces on the membrane surface. Two examples are the scaffolding mechanism and protein crowding effect. The scaffolding machinery involves the creation of a rigid protein coat composed of a protein template, such as clathrin in the case of endocytosis, that molds the membrane underneath (Fig. 1A). COPI and COPII complexes, discussed above, fall into this category since the array of proteins cover the membrane causing bending and curvature to produce a final shape. Additionally, the protein crowding effect gives rise to membrane bending through protein-protein forces resulting from membrane bound proteins [16, 17]. As the density of bound proteins increases, the rate of thermally driven protein-protein collisions of the soluble domains also increases causing lateral steric pressure parallel to the membrane surface that can drive bending (Fig. 1B).

• Second, membrane shaping can occur through changes induced by the insertion of hydrophobic protein domains into the lipid bilayer. Within this category two non-mutually exclusive mechanisms have been proposed: local spontaneous curvature and the bilayer-couple mechanism [14, 18]. In the local spontaneous curvature mechanism, the embedded protein interacts with the surrounding lipid molecules to alter the membrane’s local properties such as the propensity to curve, which is known as the spontaneous curvature (Fig. 1C). For instance, a shallow inserting amphipathic helix (circle) or conically shaped transmembrane protein (wedge) may differentially distort the packing of the lipid head-groups compared to the hydrocarbon chains resulting in a local change of the spontaneous curvature. However, besides spontaneous curvature changes, the locally induced packing distortions by inserted proteins can potentially change the value of other bilayer parameters such as the Gaussian/mean bending moduli, or compression modulus. In this manner, a few proteins in a region may make the local membrane more accommodating toward tubulating or budding into a vesicle. Proteins that contain BAR (Bin-Amphiphysin-Rvs) domains, which are banana-shaped proteins that have their own intrinsic curvature [19, 20], deform membranes potentially through a local spontaneous curvature mechanism; however, scaffolding may also be important [21–23]. Finally, the bilayer-couple mechanism involves an area expansion of one leaflet of the membrane with respect to the other (Fig. 1D). This can occur if a large number of proteins partially insert into one leaflet causing a differential area expansion. The area mismatch will cause in-plane compression on the protein side and tension in the opposing leaflet, and the relief of this strain can cause large scale bending into cylindrical, spherical and curved surfaces. Because the strain is spread over the entire surface, this mechanism works as a global phenomenon rather than a local one.

Figure 1.

How can proteins bend membranes? A. Scaffold mechanism. A rigid array of proteins (blue) assemble over the much more compliant membrane deforming the entire system into a new shape. B. Protein crowding mechanism. Thermally driven protein-protein collisions of bound proteins to the membrane surface can create significant lateral pressure and drive bending. C. Spontaneous curvature mechanism. The proteins act locally to distort the surrounding lipid molecules and alter their elastic properties, such as the local spontaneous curvature. These local changes can give rise to new stable morphological structures such as tubules or vesicle budding events. Orange lipids inside the dashed boxes represent the region over which the protein insertion induces local distortions. D. Bilayer-couple mechanism. The asymmetric insertion of many proteins on one side of the membrane generates an area mismatch between the upper and lower leaflets resulting in stress that spreads globally over the entire surface. The generation of curvature relieves the in-plane components of the stress in both leaflets.

Different shaping mechanisms may be involved in the formation of specific geometries as recently suggested for endophilin A1 [23], where vesiculation and tubulation were found to be a function of the protein depth of insertion. But given the membrane shaping mechanisms are not mutually exclusive, it is possible that these mechanism work in concert to generate various types of membrane curvature.

Membrane proteins adopt different conformations, and forces from the lipids can bias these conformations. Thus, just as membrane proteins can influence the shape of the surrounding membrane, the local structure of the membrane can act back on the protein. There are several ways that this can occur, such as hydrophobic mismatch. In-plane tension can thin membranes causing a decrease in the hydrophobic thickness, which causes tilting of hydrophobic stretches of transmembrane proteins so that the greasy portions of the protein remain buried in the membrane core. Mechanosensitive channels, such as MscS and MscL, are thought to gate in this manner, whereby membrane thinning causes helix tilting and outward radial expansion that opens a water filled pathway through the center of the channel [8]. A second view of this gating mechanism is that the in-plane tension acts to expand the area of the channel through line tension at the membrane-protein interface. Single channel studies have also demonstrated that the membrane curvature can influence the conduction state of ion channels, as is the case for hemolysins that lyse red blood cells [12]. It is unclear how the physical forces and torques from the membrane are imparted to the protein in this later case, but it is likely to occur through a mechanism similar to the previous example in which the local ordering of the lipids causes a reconfiguration in the protein to minimize hydrophobic and electrostatic energy. In addition to influencing protein function, membranes may guide the localization, diffusional properties, and protein-protein interactions of membrane and membrane associated proteins.

While there is emerging evidence that the interaction of the membrane with resident membrane proteins is important to many biological phenomena, it is difficult to elucidate these interactions both experimentally and computationally. From an experimental perspective, this is a difficult problem because the length scales are small and the lipid environment is dynamic making it difficult to probe via standard high resolution techniques such as X-ray crystallography, NMR and cryo-electron-microscopy. From a computational stand point, the study of protein interactions with the membrane presents its own challenges. Fully atomistic molecular dynamics (MD) simulations can elucidate with very high spatial and temporal resolution the interactions that the membrane has with the membrane protein. One particularly illuminating example is the studies of N-BAR proteins interacting with a membrane in which it is shown that the membrane can adopt a curvature similar to the intrinsic curvature of the BAR domain [24, 25]. However, typical simulations last for hundreds of nanoseconds to microseconds, and even long multi-microsecond simulations have highlighted the difficulty in capturing the local relaxation of the membrane to penetration by small amphipathic helices [26]. The other difficulty is the size of relevant systems. Even small highly curved vesicles contain thousands of lipids and millions of atoms [27]. Propagating these large systems forward in time is computationally taxing resulting in even shorter simulation timescales. Coarse-grained MD simulations are becoming more popular, and they make it possible to simulate larger systems by reducing the number of atoms at the expense of some loss of chemical detail [28–32]. However, many of the same problems inherent to fully atomistic MD are still present in CG simulations. That is, timescales are often too short to observe major reorganization events that involve long wavelength, low energy conformational changes in the membrane [33, 34].

An alternative to atomistic simulations is the use of continuum methods to model the membrane and the surrounding aqueous environment. Instead of explicitly representing every atom in the system, or groups of atoms, the biophysical properties and shape of the membrane are represented mathematically. Such a description dramatically reduces the computational load allowing for the determination of equilibrium configurations over very long length scales. However, chemical accuracy is lost and the mathematical equation can be very difficult to solve. There is a long history of describing the shapes and equilibrium fluctuations of membrane systems using elasticity theory starting with the work of Helfrich [35] and Canham [36] in the early 1970s. The propensity to bend and adopt different shapes is dictated by the material properties (elastic moduli) of the membrane, which must be determined from experiment or atomistic simulation. However, once these values are known, a set of partial differential equations (PDEs) can be derived that satisfy the minimum energy configurations of the membrane, and their shapes can be computed. Several theoretical approaches have been developed to incorporate the influence of membrane proteins into this framework. Initial studies focused on the membrane deformation energies of single particles embedded in membranes with finite thickness, known as mattress models [37–39]. Later in the 1990s, researchers became interested in the interplay between embedded particles and whether membrane-mediated interactions could give rise to attraction or repulsion [40–42]. A common theme among all of these early studies is that the protein is represented as a simple point particle or rigid cylinder, and its influence on the surrounding membrane is included through a boundary condition imposing height, angle, and/or curvature constraints at the membrane where it meets the protein. Unfortunately, these models lack all of the complex geometric and chemical features present in real proteins. Later, the Honig lab began to explore the energetics of alpha helices associating with model lipid bilayers using an energy model with terms for continuum electrostatics [43], hydrophobic interactions, lipid perturbation effects, and other terms following the work of Jacobs and White [44]. While membrane deformations were not explicitly considered, the protein was treated with atomic detail. This allowed for a description of the system with increased chemical accuracy for the protein, while still using fast continuum calculations to account for electrostatic and other energetic terms.

In this review, we will focus on recent advances that have merged continuum models of the membrane with atomistic representations of the embedded proteins. In Section 2, we will briefly outline the mathematical and geometrical tools required to model thin sheets. Next, in Section 3 we will present the Helfrich Hamiltonian and other commonly used continuum models to describe the energetic state of pure membranes. We then survey in Section 4 ways in which the protein is coupled to the membrane, and we outline the evolution of protein representations from simple point particles to realistic high resolution structures. In Section 5, we highlight the recent advances from several groups that have made progress in bridging continuum membrane mechanics with atomistic representations of the protein, while Section 6 provides a detailed view of the hybrid model and associated machinery developed in our lab to carry out these calculations. In Sections 7, we present an application of our hybrid atomistic-continuum model showing that the predicted membrane deformations are in good agreement with fully-atomistic MD simulations making it possible to explore the biological function of membrane proteins and suggest testable hypotheses. Concluding remarks concerning future directions and challenges are discussed in Section 8.

2. Membrane geometry

Lipid bilayers are fascinating soft-matter systems which self-assemble from single molecules into very thin fluid films that can extend over macroscopic lateral scales. Therefore, the natural limit when the lateral dimensions greatly exceed the thickness is to describe the membrane as a two dimensional curved surface (single sheet) embedded in a three dimensional space. We start by reviewing some of the important geometric elements and definitions required to describe membranes in a continuum fashion including differences between a two-sheet model that describes the upper and lower leaflets independently versus a one-sheet model that represents the bilayer by a single surface. For a more complete description of the differential geometry tools necessary to model soft materials and membranes, we refer the readers to work by Kamien [45] and Deserno [46]; here, we simplify the discussion to the most essential elements needed to describe membrane deformations in the small angle deflection limit.

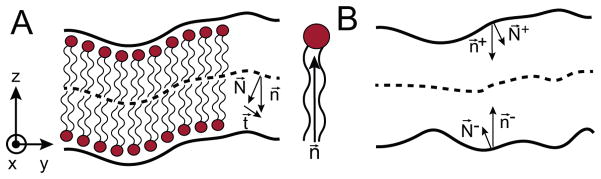
The two-leaflet model is composed of two very thin surfaces (monolayers) that are stacked upon each other at an equilibrium distance L₀ = 2h₀ (Fig. 2). From here on, we denote variables associated with the upper and lower leaflets by + and − superscripts, respectively, unless otherwise noted. We use a Monge Gauge parametrization of the surfaces, such that each leaflet shape is described by a height function (h^±(x, y)) [47]. Working within the linearized, small deflections limit, the normal vector to each surface N⃗^± is [45]:

$${\overrightarrow{N}}^{+}=\left\{\frac{\partial h^{+}}{\partial x},\frac{\partial h^{+}}{\partial y},-1\right\}=\left(\overrightarrow{\nabla }{h}^{+},-1\right),{\overrightarrow{N}}^{-}=-\left\{\frac{\partial h^{-}}{\partial x},\frac{\partial h^{-}}{\partial y},-1\right\}=-\left(\overrightarrow{\nabla }{h}^{-},-1\right),$$ (1)

where the geometries are depicted in Fig. 2. The thickness variables (u^±(x₁, x₂)) represent compression or expansion perpendicular to the plane of the membrane relative to the undeformed height ±h₀:

$$u^{\pm }(x_1,x_2)=h^{\pm }(x_1,x_2)\mp h_0.$$ (2)

Figure 2.

Mathematical representation of the membrane. A. A cartoon model representing the upper and lower leaflets and the corresponding lipid molecules. N⃗ is the normal vector of the bilayer midplane (dashed line), n⃗ is the head-to-tail vector of the lipids, and t⃗ is the difference of these two vectors. B. The upper and lower surfaces representing the head-group interfaces with the water from panel A (solid lines) and the bilayer midplane (dashed line). The lipids have been removed in this purely mathematical representation, but the vectorial descriptions N⃗^± and n⃗^± remain.

It is also important to distinguish the true monolayer surface in three dimensional space (Γ^±) from the two dimensional projection of the surface used in calculations (Ω^±) [48]:

$$d{\mathrm{\Gamma }}^{\pm }=\left[\sqrt{1+{(\nabla u^{\pm })}^2}\right]d{\mathrm{\Omega }}^{\pm }\approx \left[1+\frac{{(\nabla u^{\pm })}^2}{2}\right]d{\mathrm{\Omega }}^{\pm },$$ (3)

where the dΩ^± is the differential dx dy in the projected plane. Often the bilayer geometry and energetics are represented by the dilation (d) and bilayer midplane (h) as shown in Fig. 2:

$$d=\frac{u^{+}-u^{-}}{2},h=\frac{h^{+}+h^{-}}{2}.$$ (4)

For those cases where the in-plane compression is ignored, the bilayer can be represented by a single midplane surface (h) and the normal vector and projected surface area are defined analogously to Eqs. (1) and (3).

3. Continuum elastic energy models of the membrane

Many theoretical models have been developed starting from different view points [35, 36, 48–51], and they all reach similar a conclusion – the crucial soft-mode is the membrane curvature deformation [46]. The separation of length scales between the thickness and lateral dimension of lipid membranes makes it possible to construct a large-scale membrane Hamiltonian that primarily depends on the curvature of the surface, and then additional energetic terms concerning local lipid physics enter through a small set of parameters that couple to the curvature [46]. The seminal work in this field comes from Canham [36] and Helfrich [35] where they derived a Hamiltonian, which is only a function of membrane geometry (Fig. 2):

$$E_{\mathit{Helfrich}-\mathit{Canham}}={\int }_{\mathrm{\Gamma }}\left(\sigma +\frac{K_c}{2}{(2H-J_0)}^2+K_{G}K\right)d\mathrm{\Gamma },$$ (5)

where σ penalizes the creation of new surface area Γ, 2H is the mean curvature, K is the Gaussian curvature, J₀ is the preferred curvature of the membrane in the absence of external forces and torques, and K_C and K_G are the bilayer bending modulus and Gaussian modulus, respectively. The integral of σ corresponds to the total surface tension energy (E_S), while the second term is the mean curvature bending energy (E_B), and the last term is the Gaussian curvature energy (E_G). The mean and Gaussian curvatures are defined in the small angle limit as:

$$2H=\overrightarrow{\nabla }·\overrightarrow{N}\approx {\nabla }^{2}h\&K\approx \frac{{\partial }^{2}h}{\partial x^2}·\frac{{\partial }^{2}h}{\partial y^2}-{\left(\frac{{\partial }^{2}h}{\partial y\partial x}\right)}^2,$$ (6)

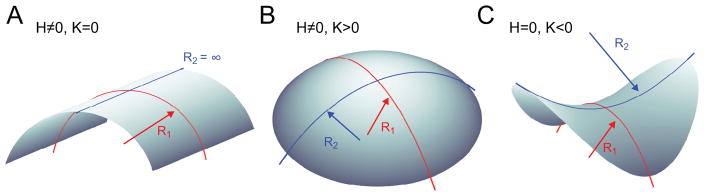
and they correspond to shapes shown in Fig. 3. For the chosen normal vector N⃗ in Fig. 2, positive curvature H > 0 corresponds to a concave up bilayer. Similarly, for the two-leaflet model, positive curvature at the upper leaflet is a concave up shape, while positive curvature at the lower leaflet is concave down.

Figure 3.

Examples of curved surfaces. A. cylinder, B. spherical cap, and C. saddle. The geometry of each surface can be defined as a function of the two principal radii of curvature R₁ and R₂. When R₁ and R₂ change in a bilayer there is a curvature energetic penalty in the Helfrich Hamiltonian (Eq. (5)). The mean curvature is equal to the sum of the principal curvatures (inverse of the radius of curvature) $H=\frac{1}{R_1}+\frac{1}{R_2}$ and the Gaussian Curvature is the product $K=\frac{1}{R_1}·\frac{1}{R_2}$.

Rewriting Eq. (5) in the small angle deflection limit we arrive at:

$$E_{\mathit{Helfrich}-\mathit{Canham}}={\int }_{\mathrm{\Omega }}\left(\sigma +\alpha \frac{{(\nabla h)}^2}{2}+\frac{K_c}{2}{({\nabla }^{2}h-J_0)}^2+K_{G}K\right)dxdy,$$ (7)

where the effective surface tension contribution is given by $2\alpha =2\sigma +K_c{J}_0^2$. Since σ is constant, it does not contribute to the equilibrium solution, and it is commonly dropped (see Ref. [52] for instance). However, the physical interpretation of α(σ) is complicated, and it has generated significant controversy [46]. For a more in depth description of membrane surface tension, we refer the reader to the work of Schmid [53], Diamant [54] and Watson et al. [52]. Here we interpret σ as the conjugate variable that opposes the addition of new area Γ, in which case σ plays the role of a chemical potential with the area per lipid constant.

The Gauss-Bonnet theorem shows that the total Gaussian bending energy integrated over a closed surface, such as a vesicle with no defects or inclusions, is a constant [55]. Thus, the Gaussian term is often neglected. However, vesicles undergoing shape transitions with co-existing fluid phases [56] or vesicles with open patches that contain embedded protein inclusions, as we consider here, require more care [57, 58]. For this reason, we retain the Gaussian term. Next, we consider two extensions to the basic Helfrich model that we believe are important when considering interactions with membrane proteins: compression of the membrane and orientation of the lipid.

3.1. Compression of the membrane

Going beyond the Helfrich Hamiltonian framework, which depends solely on curvature variations, additional microscopic details can be added, and a logical first step is to include the finite thickness of the membrane [48]. Assuming incompressibility of individual lipids, changes in thickness can be related to the change in area (ΔA) per lipid molecule [47, 48] allowing for a description of the membrane in terms of curvature and area changes. In contrast to idealized single sheet descriptions where the midplane is used to describe the membrane, when a single surface also accounts for thickness variations, the choice of surface representation becomes important [48]. To better illustrate how this choice influences the mathematics, consider the downward bending of a thin film: stretching occurs at the upper surface and compression at the lower surface. Thus, a representation of the membrane at the upper surface will result in a different description than a representation at the lower surface. We are free to choose any surface, but it is often useful to construct the so called neutral plane [48]. Due to the geometry at a mathematical surface and how the geometry relates to the local curvature and thickness values, the energy description may involve cross terms between these two values, and the neutral plane is constructed to explicitly remove these cross terms. Therefore, in the small deflection limit, the Helfrich Hamiltonian (Eq. (7)) is modified by the addition of a single quadratic energy term related to area changes [59]:

$$E_{\mathit{compression}}=\frac{K_a}{2}{\int }_{\mathrm{\Gamma }}{\left(\frac{A-A_0}{A_0}\right)}^{2}d\mathrm{\Gamma }\approx \frac{K_a}{2}{\int }_{\mathrm{\Omega }}\left(\frac{u^2}{h_0^2}\right)dxdy,$$ (8)

where we have assumed V = Ah = A₀h₀, u = h − h₀, and K_a is the bilayer compression modulus [46, 60].

3.2. Lipid tilt

The discussion up to this point has assumed that the lipids are oriented along the bilayer normal vector (N⃗); however, this is generally not the case. Experiments on DPPC bilayers in the gel-phase revealed that lipids tilt at an angle of approximately π/6 with respect to the surface normal [61]. At low temperatures, lipids exhibit internal structures with long range ordering, which are independent of local curvature and can only be described through the inclusion of an additional degree of freedom corresponding to the local orientation of the lipids [50, 62, 63]. A tilt degree of freedom has also been used in the literature to discuss a number of different phenomena including orientational lipid order in vesicles [63], inverted amphiphilic mesophases [64], and membrane fusion events [65]. Even for membranes in the liquid state at room temperature, order can be imposed on the tilt of the hydrocarbon chain due to geometrical constraints and imposed boundary conditions at the contact sites with rigid proteins [50, 66], and it has been suggested that tilt should be included in continuum models based on results from simulation [67, 68]. Recently, the first experimental support for lipid tilt in the fluid lamellar phase was provided based on X-ray scattering [69].

While originally introduced by Helfrich [35], a rigorous theoretical framework for studying lipid tilt in liquid state membranes was put forward by Hamm and Kozlov [50] in which they assumed that the core of a monolayer could be treated with standard elastic continuum theory (as in Refs. [47, 70]). The key element is the definition of a variable t⃗, which characterizes the difference between the direction of the monolayer surface normals N⃗ and the average local head-to-tail vector of the lipids n⃗ (Fig. 2). For small deformations, we have [50, 64]:

$$\overrightarrow{n}\approx \overrightarrow{N}+\overrightarrow{t}\&\overrightarrow{\nabla }·\overrightarrow{n}={\nabla }^{2}h+\overrightarrow{\nabla }·\overrightarrow{t}.$$ (9)

Incorporation of tilt into the Helfrich model requires some care. First, the gradient of the tilt and surface bending curvature are additive, and both terms are penalized by the same macroscopic elastic moduli, which can be determined from experiment and/or simulation. Thus, in a model with tilt, the curvature (∇²h) in Eq. (7) is replaced by ∇⃗ · n⃗ yielding an analogous term to the mean-curvature deformation cost often referred to in the lipid tilt literature as the lipid splay penalty [50, 71]:

$$E_{\mathit{tilt}-\mathit{splay}}=\frac{K_c}{2}{\int }_{\mathrm{\Omega }}{\left({\nabla }^{2}h+\nabla ·\overrightarrow{t}\right)}^{2}dxdy.$$ (10)

Second, there is an energy contribution due to the twist of the lipid molecules [50]:

$$E_{\mathit{tilt}-\mathit{twist}}=\frac{K_{tw}}{2}{\int }_{\mathrm{\Omega }}{\left(\overrightarrow{\nabla }\times \overrightarrow{n}\right)}^{2}dxdy\approx \frac{K_{tw}}{2}{\int }_{\mathrm{\Omega }}{\left(\overrightarrow{\nabla }\times \overrightarrow{t}\right)}^{2}dxdy,$$ (11)

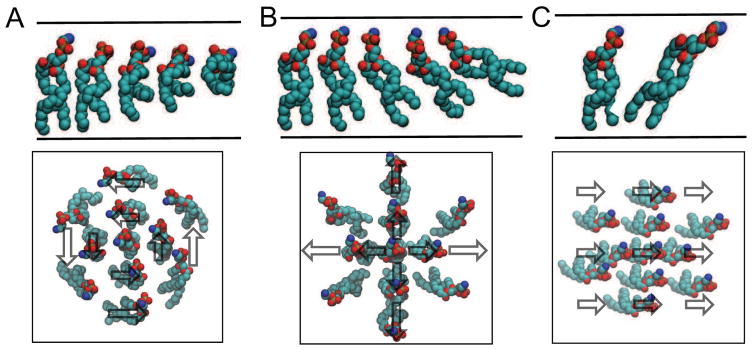
where × is the cross product (∇⃗ × n⃗ = ε_{i jk}n_jk), K_tw is the lipid twist modulus, and the last equality comes from applying the small deformation relation (Eq. (9)) together with the fact that the curl of the divergence is zero (∇⃗ × ∇⃗h = 0). The lipid twist energy arises from the same physical origin as described above for Eq. (10) – spatial changes in the direction of the vector n⃗ [72]; however, (∇ · n⃗)² does not always properly penalize all possible distortions, such as divergence free patterns. This is most easily understood by considering a flat bilayer with a divergence free director field n⃗, which adopts vortices as depicted in Fig. 4A. The difference between twist penalty (Eq. (11)) and splay penalty (Eq. (10)) becomes evident when comparing Fig. 4A with Fig. 4B. In Fig. 4A there is no splay since the divergence of n⃗ is zero, but the curl term properly penalizes the directional spiraling change of the lipid tails. On the other hand Fig. 4B shows pure splay of the lipids away from the center, which is penalized by the divergence.

Figure 4.

Lipid tilt degrees of freedom. A. A patch of membrane exhibiting pure twist. In all panels, the top image is a side view of the upper leaflet, and the bottom panel is a top down view of a patch of lipids. Vectors demonstrate the head-to-tail orientation of individual lipids. B. A patch of membrane exhibiting pure splay. C. A patch of membrane exhibiting pure tilt. The lipid density was intentionally decreased for clarity.

Third, the use of n⃗ instead of N⃗ to penalize changes in orientation yields an analogous term to the Gaussian curvature penalty appearing in Eq. (7) [45, 73]:

$$E_{\mathit{saddle}-\mathit{splay}}={\int }_{\mathrm{\Omega }}(K_{G}K)dxdy,\text{where}K=\overrightarrow{\nabla }·\left[\left(\overrightarrow{\nabla }\overrightarrow{n}\right)\overrightarrow{n}-\left(\overrightarrow{\nabla }·\overrightarrow{n}\right)\overrightarrow{n}\right].$$ (12)

Although having the same functional form as the Gaussian curvature term in Helfrich’s theory, the lipid tilt literature refers to the term above as the lipid saddle-splay penalty [50, 71].

Finally, when the tilt vector does not align with the monolayer surface normal, the lipids become stretched, which is penalized by an independent tilt elastic modulus K_t [50]:

$$E_{\mathit{tilt}-\mathit{stretch}}=\frac{K_t}{2}{\int }_{\mathrm{\Omega }}\left(\overrightarrow{t}·\overrightarrow{t}\right)dxdy.$$ (13)

The physical origin of the tilt-stretching penalty can be understood by considering a single hydrocarbon chain, which adopts a resting cross sectional area A₀. The lipid volume can be approximated by the area times the equilibrium height h₀: V = h₀A₀. Assuming incompressibility, if external forces cause the lipid vector t⃗ to deviate from the surface normal N⃗ with no change in the vertical height of the monolayer, then the lipid chain must stretch [50] as shown in Fig. 4C. The full lipid tilt energy is then:

$$E_{\mathit{lipid}}=E_{\mathit{tilt}-\mathit{splay}}+E_{\mathit{saddle}-\mathit{splay}}+E_{\mathit{tilt}-\mathit{twist}}+E_{\mathit{tilt}-\mathit{stretch}},$$ (14)

where E_tilt-twist is often assumed to be small, and E_saddle-splay is also often ignored since it is a Gaussian term.

3.3. Other approaches to membrane energetics

We end this section with a brief survey of additional techniques that have been developed to study membrane deformations. One of the most influential models has come from a liquid crystal description of the elastic energy of orientable molecules by Frank [72], and this methodology has been applied to the study of membranes and other soft materials [45, 55, 73]. Another approach popularized by May and Ben-Shaul [49, 71], has been to build up a lipid bilayer total free energy F by starting from the average free energy per molecule f = F/N, where N is the total number of lipid molecules. The basic premise is that f can be expressed as the sum of three terms (f = f_h + f_i + f_c): where f_h is repulsive and arises from electrostatic and/or steric interactions between polar heads [74]; f_i is attractive and reflects the surface energy associated with the hydrocarbon-water interface [74]; and f_c is the chain conformational energy accounting for lipid-lipid interactions. Yet another more recent development is to use dimensional reduction to obtain membrane energetics [75]. The membrane is treated as a fluid surface of finite thickness with internal structure yielding an effective energy that depends on area changes and misalignment between the surface normal and lipid orientation. The equations naturally recover a large-scale Hamiltonian that depends on curvature with the addition of new terms that account for local-microscopic physics. Finally, while we have focused on single-lipid or single-component membranes, there are a number of continuum studies addressing multicomponent, fluid membranes that have varying lipid composition and inhomogeneous spontaneous curvature [76–78].

3.4. High order bending terms

The Helfrich Hamiltonian in Eq. (5) is a phenomenological expansion up to quadratic order in the curvature, and common concerns are whether higher order terms are needed to faithfully describe membrane mechanics and when does this description break down. There are biological situations in which it has been argued that higher order terms are required. For instance, elasticity equations with higher order terms produce stable tubular solutions [79], and they have been used to study the periodic, egg carton shaped membranes observed in L-form bacteria, which lack a cell wall [80]. Moreover, high order equations have proven useful in the analysis of inverted cubic phases [81]. On the other hand, experiments of membrane tether formation suggest that Eq. (5) is sufficient and that higher order terms are not needed to accurately describe the high curvature regime [82–84]. Similarly, coarse-grained simulations also support the validity of the Helfrich framework for large deflections, with only minor errors [85–88]. In support of these later two observations, it has been argued that the higher order quartic curvature terms will only compete with the quadratic term when the radius of curvature is of the order of a lipid tail, which is half the bilayer thickness [46]. This theoretical argument is consistent with a study from the Cui lab showing that deviations between coarse-grained and continuum models of fusion pore formation only become notable when the radius of curvature is close to the monolayer thickness [88]. Another concern is whether a particular situation may fail because geometries exceed the small angle deflection limit in Eq. (7).

Next, we will explore how the membrane deformations discussed in this section relate to embedded or associated membrane proteins.

4. Coupling between the membrane and embedded proteins

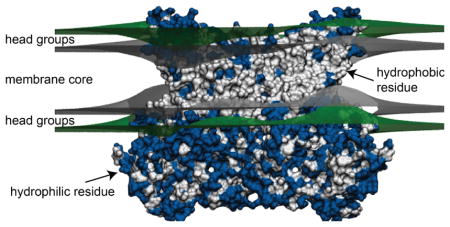
Membrane proteins are surrounded by a shell of lipid molecules often referred to as a lipid annulus. As the bilayer deforms, the lipids in this annulus will impart forces to the protein potentially influencing its conformation and function. Likewise, the chemistry and geometry of the protein will act back on the membrane causing it to deform. How does one merge the continuum elastic treatment of the membrane already discussed with the presence of a protein inclusion? Generally, researchers have treated the proteins as hard constraints on the local membrane geometry, and formally, the proteins enter as boundary conditions imposed on the partial differential equations describing the surface. These constraints are based on the assumption that proteins are much more rigid than the membrane so that it is more energetically favorable for the membrane to adjust to the protein than vice versa. However, several research groups have considered the gating or transition of proteins from one conformation to another and explored the role that the membrane plays in biasing those discrete protein conformations [89–92]. The protein is thought to influence the neighboring lipid membrane through its geometry and its surface chemistry. First, membrane proteins are characterized by a belt of hydrophobic amino acids that insert into the hydrophobic core of the membrane (Fig. 5). If the lipids pull away from this protein-membrane interface, then water becomes exposed to the region at a very high energetic penalty due to the hydrophobic effect. Meanwhile, there are typically a ring of residues on the membrane protein surface, such as tryptophans, at both the upper and the lower head-group regions that favor the amphipathic interfacial region. This ring provides favorable electrostatic contacts with the polar and charged moieties on the lipid molecules. These considerations impose geometric constraints on the adjacent membrane through a mechanism termed hydrophobic mismatch [93]. The tight hydrophobic seal between the protein and membrane then imposes geometric constraints on the membrane due to the specific chemistry and shape of the protein. For instance, wedge shaped proteins, such as the KcsA potassium channel (Fig. 5), can only smoothly mesh with lipids if the membrane approaches the interface at a prescribed angle called the contact angle. This later consideration can also impose tilt constraints on the adjacent lipids. As we will discuss, the contact angle and hydrophobic mismatch enter the equations through the boundary conditions, and they couple to the curvature, compression, and lipid tilt ultimately influencing the membrane deformation energy. Because these protein-induced membrane deformations can extend for long distances [40], a significant amount of research has been dedicated to the role of membrane mediated interactions between embedded proteins, which we will review. In what follows, we constrain our survey to approaches that retain a geometrical description of the protein shape, but we acknowledge that a number of studies treat the proteins as a mean density field that couples to the membrane curvature [76, 94–97].

Figure 5.

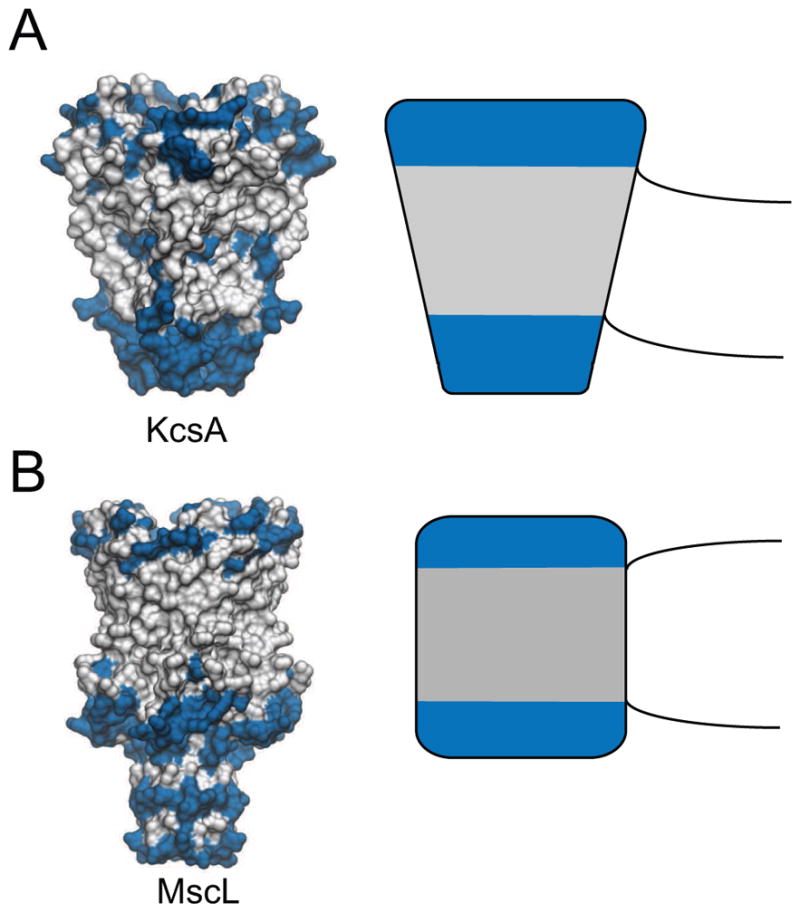
Cartoon models of membrane protein interactions. A. The potassium channel KcsA adopts a conical shape in the closed state (left). The hydrophilic residues are blue and the hydrophobic residues are white, and the hydrophobic residues localize to a belt around the protein that creates the energetic ‘seal’ with the membrane. This seal would impose a negative contact angle on the membrane (black lines) potentially causing bending in the simplified geometry on the right. B. The mechanosensitive channel MscL is cylindrical with a more well defined hydrophobic belt (left). This shape would not impose a contact angle on the protein, but if the hydrophobic height of the protein differed from the equilibrium width of the membrane it may impose a hydrophobic mismatch that causes compression or expansion of the adjacent membrane (right).

4.1. Coupling through hydrophobic mismatch

One of the most important sources of coupling between the protein and the membrane comes from hydrophobic mismatch [93]. This phenomenon arises when the length of the protein’s hydrophobic transmembrane domain (d_p) is different from the hydrophobic thickness of the bilayer (d₀). Whenever d_p ≠ d₀ the protein and bilayer will adapt to each other either by local changes in lipid bilayer thickness and/or changes in the orientation or tilt of the protein in the membrane [93]. If the mismatch is positive (d₀ < d_p), there is an energetic penalty for exposing hydrophobic residues to water, which will cause the membrane thickness to increase through stretching. On the other hand if the mismatch is negative (d₀ > d_p), then the bilayer will compress (pinch down) to prevent exposure of hydrophilic residues to the hydrophobic core. Early experiments investigated the aggregation propensity of bacteriorhodopsin in phophatidylcholine (PC) bilayers of varying thickness, which induced different degrees of hydrophobic mismatch [98]. The authors determined that the protein remains mono-dispersed in bilayers with thickness values close to the protein’s value, but that aggregation occurs at extreme positive and negative mismatch values.

The antibiotic ion channel forming peptide, gramicidin A (gA), has also been a model system used to study the role of hydrophobic mismatch in controlling protein function [99]. Gramicidin is a short peptide that forms functional ion channels when two monomers (one from each leaflet) come together to create a dimer. Each monomer alone cannot span the width of the membrane, and hence, dimer formation and channel activity are tightly coupled to the hydrophobic thickness of the host membrane through a hydrophobic mismatch mechanism. The changes in the average channel lifetimes are related to the bilayer energetics [99, 100] giving rise to a direct experimental readout of the underlying microscopic interactions between the membrane and the protein. Moreover, Harroun et al. [101] used small angle X-ray scattering to provide experimental evidence for the theorized membrane thinning adjacent to channels.

4.1.1. Proteins influence bilayer thickness

The first two theoretical models that addressed hydrophobic mismatch were carried out using simplified protein geometries and accounted for only two modes of deformation: interfacial tension (change in total surface area) and change in bilayer thickness [102, 103]. Marcelja’s model employed microscopic statistical mechanics in which the protein was treated as a simple hexagonal shape that occupied a certain number of lipid chain sites [102]. Meanwhile, Owicki and McConnell used a phenomenological, Landau-type model, where the protein was assumed to be radially symmetric [103]. Both models assume that the membrane adopts a fixed width at the protein surface due to the hydrophobic mismatch constraint. The models predicted that the bilayer thickness relaxes exponentially from the value imposed at the site of contact with the protein to the bulk value. Additionally, both models predicted that the membrane-induced deformations create a short range, attractive force between proteins that decays monotonically with distance. A few years later, Mouritsen and Bloom took a slightly different approach and introduced the well known mattress model, where both the protein and the membrane (mattress) are represented as one-dimensional springs [37].

4.1.2. Proteins influence membrane curvature

Following initial work that focused on thickness changes [37, 102, 103], Huang then adapted the free energy description used in smectic liquid crystal theory and introduced membrane curvature as a third mode of deformation, while retaining both compression and tension [38]. For analytic tractability, Huang also assumed a simple cylindrical protein and imposed constraints on the membrane thickness where it contacted the protein. This study was among the first to show that curvature in fact dominated the bilayer deformation energy, not compression, and that the energy density was confined to the vicinity near the protein [38]. Thus, retaining thickness distortions and introducing curvature in the elastic membrane model yields a theoretical framework that describes both long range (curvature mediated) and short range (compression) deformations². The resulting model is quite similar to the Helfrich model in Eq. (7), but rather than expressing the membrane shape as a single sheet representing the bilayer, the compression is incorporated by describing the upper and lower leaflets by two independent surfaces with similar forms:

$$\begin{array}{l}{G}^{(me)}=\frac{1}{2}{\int }_{\mathrm{\Omega }}\underset{\mathit{Mean}\mathit{Curvature}-\mathit{Bending}}{\underbrace{\frac{K_c}{2}\left({\left[{\nabla }^2{u}^{+}-J_0^{+}\right]}^2-{\left[{\nabla }^2{u}^{-}-J_0^{-}\right]}^2\right)}}dxdy\\ +\frac{1}{2}{\int }_{\mathrm{\Omega }}\underset{\mathit{Surface}\mathit{tension}}{\underbrace{\frac{\alpha }{2}\left({\left(\overrightarrow{\nabla }{u}^{+}\right)}^2+{\left(\overrightarrow{\nabla }{u}^{-}\right)}^2\right)}}dxdy\\ +\frac{1}{2}{\int }_{\mathrm{\Omega }}\underset{\mathit{Compression}}{\underbrace{\frac{K_a}{2L_0^2}\left[{(u^{+}-u^{-})}^2\right]}}dxdy\\ +{\int }_{\mathrm{\Omega }}\underset{\mathit{Gaussian}\mathit{Curvature}}{\underbrace{\frac{K_G}{2}[K^{-}+K^{+}]}}dxdy,\end{array}$$ (15)

where all symbols retain their meaning as in Eq. (5), we have used the u^± definitions in Eq. (2), and factors of 2 are present due to a monolayer versus bilayer description.

The equilibrium shape of the membrane is then determined by taking the functional derivative of Eq. (15) to arrive at:

$${\nabla }^4{u}^{+}-{\nabla }^2{J}_0^{+}-\gamma {\nabla }^2{u}^{+}+\beta (u^{+}-u^{-})=0,\text{in}\mathrm{\Omega }$$ (16)

$${\nabla }^4{u}^{-}+{\nabla }^2{J}_0^{-}-\gamma {\nabla }^2{u}^{-}+\beta (u^{-}-u^{+})=0,\text{in}\mathrm{\Omega }$$ (17)

$$\gamma =\frac{\alpha }{K_c},\beta =\frac{2K_a}{L_0^2{K}_c},{\beta }^{\pm }=\frac{2K_a^{\pm }}{L_0^2{K}_c},u^{\pm }=\left(h^{\pm }\mp \frac{L_0}{2}\right),L_0=2h_0.$$ (18)

The equations presented above are quite similar to the ones obtained by minimizing the linearized version of the Helfrich-Canham Hamiltonian (Eq. (7)), except the lateral compression of the membrane becomes an important degree of freedom necessitating the need for another independent variable. Additionally, membrane proteins exert their influence on the membrane surface through the boundary conditions, which can sometimes make the equations incredibly hard to solve, but does not change their form.

The method discussed here for incorporating the influence of membrane proteins into continuum models of the membrane is not unique. Rather than incorporating membrane compression through the use of relative height differences between two monolayers, others have followed the work of Safran and described the membrane thickness changes by a dilatation variable as well as surface curvature [59]. Nonetheless, the influence of proteins on the membrane energetics and shape are also incorporated through boundary conditions motivated by ideas of hydrophobic mismatch and shape constraints [51, 58, 59, 104, 105].

4.1.3. Proteins influence lipid tilt

As discussed in Section 3, the membrane exhibits internal lipid orientation degrees of freedom that are independent of the curvatures and compression, and many studies have described how to couple membrane proteins to the lipid tilt [71, 106–111]. Fournier proposed one of the earliest phenomenological models based on symmetry expansions of a Helfrich-type Hamiltonian in two structural variables for each monolayer: one for lipid orientation and one for shape [106]. The protein inclusion was treated as an idealized, radially symmetric, piecewise conical shape with two distinct angles pertaining to each monolayer. The conical shape asymmetry could consequently lead to independent deformations of the upper and lower leaflets by imposing two different contact angles [106]. This model was found to always produce repulsive forces between inclusions, but the lipid tilt relaxes membrane curvature more quickly at short distances reducing interprotein repulsion [106].

The hydrocarbon chains making up the core of the bilayer can rapidly change their conformations often resulting in tilt, which elastically stretches the molecules [50, 106]. The large number of conformational states also indicates that lipids have a considerable amount of entropy. Near the membrane-protein interface, tail movement is restricted reducing the number of available conformations that can be adopted [107, 108]. Thus, the entropic free energy (E_entropic) of the lipids can be written as an explicit function of the distance from the protein. May constructed a simple 1D model for the entropic energy that depended on the lipid orientation n⃗ [107]. It was assumed that at each point in the membrane a spontaneous director field (n⃗₀) existed that defined the maximum entropy orientation of the lipids, and a model for n⃗₀ was developed based on the assumption that the inclusion is an infinitely hard wall. The value of n⃗₀ reflects the preferred lipid orientation in the presence of an inclusion ignoring other elastic terms; and therefore, the value of n⃗ that maximizes the entropy need not be the value that minimizes the total bending and tilt energies. In the absence of a rigid inclusion, n⃗₀ = 0 vanishes, the average lipid orientation will align perpendicular to the surface normal, and there is no loss of conformational entropy. In the small deviation limit, expanding the entropic energy to quadratic order [108] results in:

$$E_{\mathit{entropic}}=\frac{1}{2}{\int }_{\mathrm{\Omega }}{K}_e(x,y){(\overrightarrow{n},{\overrightarrow{n}}_0)}^{2}dxdy,$$ (19)

where symmetric deformations about the horizontal mid-plane are assumed and K_e(x, y) is the space dependent tilt-entropic modulus. Note that the tilt modulus K_t in Eq. (13) has a different physical origin from K_e, and hence they are not the same. Both K_e and n⃗₀ have been estimated with molecular-level mean field theories [107, 108, 112] and simpler continuum chain models [107, 108], where both methods produce similar results. Unlike other membrane parameters, they have spatial dependence since they vary with the distance from the inclusion having larger values at the protein interface.

4.1.4. Additional energetic terms

Several studies have included additional refinements to the protein-coupled membrane models presented already such as the relaxation of the constant lipid volume constraint [58], higher order coupling terms between changes in area per lipid molecule and curvature [51], and additional degrees of freedom that account for lipid protrusion in the short wavelength regime [105, 113]. Meanwhile, models for certain proteins such as mechanosensitive ion channels have added membrane tension as an external parameter that contributes to the total deformation free energy [89, 91, 114–117], rather than the intrinsic surface tension term in Eqs. (7) and (15).

4.2. Protein shape impacts membrane deformations

The interaction between the lipids and the protein surface impose height and angle constraints on the membrane, but the shape of the membrane protein itself and the placement and chemistry of residues at the interface are also crucial. For instance, a cylindrical protein with a well defined hydrophobic belt of uniform height will produce a different pattern of distortion than an elliptical protein whose hydrophobic belt changes height along the outer edge. Most theoretical studies have considered proteins as highly idealized shapes such as point particles, two dimensional flat disks and ellipses, or conical shapes - all lacking chemical detail [40, 41, 118]. As already discussed, the height of the hydrophobic domain of the protein, or conversely the membrane width, influence the compression and curvature energies of proteins that exhibit hydrophobic mismatch, but most studies assume simple cylindrically symmetric inclusions [38, 39, 93, 119, 120]. Similarly, Goulian and co-workers considered circular, conically shaped inclusions that imposed a fixed contact angle on the membrane all along the membrane-protein contact curve [40]. Minimizing the membrane elastic energy using a field-theoretic approach, the authors showed that proteins experience a membrane-mediated repulsion, and follow up corrections to these initial calculations also revealed purely repulsive interactions [121]. Adding membrane fluctuations to this framework, however, produces attractions between proteins [40]. Interestingly, several years later, experiments with symmetric colloidal particles embedded in giant unilamellar vesicles produced colloid clustering, revealing that the source of the attraction was likely curvature mediated not fluctuations [122].

In an attempt to determine if the membrane could provide attractive forces between inclusions, Fournier and colleagues considered the interaction of point-like inclusions that imposed anisotropic curvatures on the membrane [123, 124]. With this change in protein geometry, the inclusions now exhibit long-range attractive interactions strong enough to induce aggregation; however, the results still failed to explain why symmetric particles aggregated [125]. Around the same time, Oster and co-workers employed a mechanical approach involving the solution of a PDE originating from the Helfrich Hamiltonian for the membrane with fixed height and contact angles corresponding to rigid, flat, circular, inclusions [41]. They showed that the solution is not additive, but rather the inclusions interact via an N-body potential that can exhibit stable clusters of particles. They emphasized that high order aggregates may exist even if the pair-wise forces are repulsive, and later work by Deserno highlighted this finding that the boundary conditions give rise to non-additive solutions even though the underlying equations are linear [122, 126]. In a follow up study, Oster’s lab extended the analysis to consider elliptical discs, and they concluded that the change in the shape of the inclusion greatly affects the character of the multi-body interactions [42]. An even more sophisticated treatment of the membrane shape employed a Fourier representation of the membrane-protein contact boundary to explore the membrane deformation energies of MscL mechanosensitive channels [116, 117]. Nonetheless, the vast majority of continuum membrane models have treated membrane proteins as highly idealized shapes that lack the complex geometric and chemical detail that real membrane proteins have, yet several studies have shown that shape is important [42, 116, 117, 123, 124].

In Section 5, we will outline recent advances that have made strides in treating the complex nature of real membrane proteins.

5. Towards a more realistic geometric and chemical representation of the protein

In the last section, we suggested that a more detailed description of the protein is required to better understand how proteins interact with the membrane, how the membrane acts back on proteins, and how the membrane mediates protein-protein interactions. An outstanding question is then, “Can continuum elastic models really capture the salient features of membrane-protein interactions?” One of the best ways to quantitatively address this question is by comparing the membrane distortions generated by embedded proteins produced by fully-atomistic MD simulations with those from continuum theory. Lee and colleagues recently did this, and they showed that the lipid behavior in the annulus surrounding a gramicidin channel was quite complex, with specific tryptophan residues playing a key role in sculpting the membrane [119, 127]. When they compared their MD results with continuum calculations using a smectic-liquid crystal description of the membrane, they realized that the model failed to produce the same deformations [119, 127]. Are we then stuck with atomistic MD simulations, or are there additional advances that can be made with continuum models? While fully atomistic MD simulations are powerful and provide a high level of chemical and spatial resolution, in certain cases, they are not able to match the timescale of biological phenomena, especially membrane relaxation, which can be very slow [26]. We believe that a new wave of hybrid continuum-atomistic models will be helpful in bridging the speed of continuum methods with the accuracy of MD simulations. To do this, the specific chemistry of the protein must be taken into account, as pointed out by Lee and colleagues [127], and we must move beyond idealized geometries.

In recent years, several research groups have worked on coupling continuum elastic models of the membrane with richer chemical and geometric descriptions of the protein to better understand membrane protein insertion and stability [33, 90, 128–132]. In many of these studies, the starting point for the protein is an atomic structure, often determined by X-ray crystallography or NMR, following the seminal work by the Honig lab in which they considered the interaction of a helix with a flat, rigid membrane [43]. This approach of bringing atomistic detail to the continuum membrane models makes it possible to carry out continuum electrostatics calculations, non-polar solvation energy calculations, and other protein mechanics considerations that are quite standard in molecular biophysics. A first order approximation to the total system energy is then:

$$G^T=G^{(e)}+G^{(np)}+G^{(me)},$$ (20)

where G^(e) is the electrostatic energy, G^(np) is the non-polar energy, is G^(me) is the membrane bending energy. Thus, Eq. (20) might serve as a good alternative to fully atomistic approaches, while retaining the speed, and other positive attributes, of continuum membrane models. Moving beyond a flat, passive description of the bilayer, our group allowed the membrane to move in response to the presence of the protein [128] by adopting the continuum membrane deformation model put forth by Huang [38]. The presence of the membrane creates a complex dielectric environment around the protein that significantly impacts the electrostatic (G^(e)) and non-polar energies (G^(np)) of the system. We first solve for a given membrane deformation and then feed the shape of the solution into a continuum Poisson-Boltzmann electrostatic solver [133] by ‘painting’ the new dielectric environment around the protein [128]. Electrostatic considerations are crucial due to the low-dielectric environment of the membrane core, which poses a barrier to charged moieties on the protein, and computationally the protein, membrane, and aqueous solution are all given distinct dielectric values and solved easily with the numeric software APBS or APBSmem [134–136]. One of the most important driving forces for protein association with the membrane is the hydrophobic effect or non-polar solvation energy. Upon entering the greasy, water free region of the membrane, water is liberated from the surface of the protein, which gives rise to an increase in the entropy of the water. This consideration, which is also an important determinant of protein folding, can be estimated from the shape of the protein and how the membrane forms around it. The simplest hydrophobic model assumes that the energy change is proportional to the surface area of the protein buried in the membrane with parameter values obtained from the Sitkoff and colleagues based on small molecule partitioning [137].

The membrane distortions around proteins are then determined by identifying the membrane boundaries that minimize the total energy in Eq. (20). We identify the contact curve where the membrane touches the protein and then move the curve by hand [128] or through a search algorithm [33, 129] and calculate G^T for each configuration (Fig. 6) We also use a Fourier expansion to describe the contact curve [33, 128, 129], similar to Haselwandter and Phillips [116, 117]. We can identify stable equilibria that show a mechanical balance between bending energies, electrostatic solvation of buried polar groups, and exposure of transmembrane domains to water [128]. With this approach, our lab has been able to quantitatively reproduce results from fully-atomistic MD simulations regarding the insertion energy of a helix harboring a charged residue [128], and we have qualitatively matched the energetics and deformations produced by the insertion of K⁺ channel voltage sensor segments (S4 segments) from coarse-grained and fully-atomistic simulations [129, 138]. Moreover, this hybrid atomistic-continuum approach also explains why charged residue insertion into membranes is non-additive – charged residues bend the membrane as they insert, and once the first residue has paid the elastic cost of bending the membrane, the second residue is water exposed at very little additional cost [129]. In Latorraca et al. [33] the work was extended to explore the energetics of ion and small peptide penetration into membranes, where thickness and membrane mechanical properties played a crucial role. Most importantly, the hybrid model probes questions related to membrane distortion at a tiny fraction of the computational cost required by fully atomistic approaches. Lastly, we believe that our approach can overcome the failure of simpler continuum models employed by Lee and colleagues [127] through the incorporation of protein side chain chemistry and relaxing the assumption that the protein is cylindrically symmetric.

Figure 6.

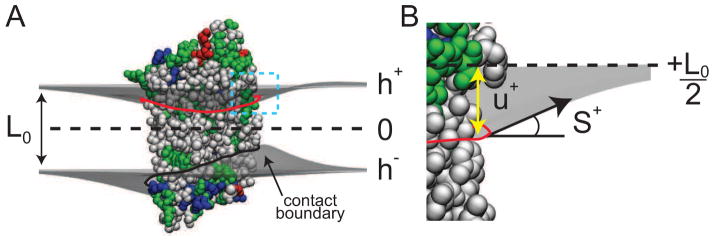
The geometry of the membrane near an atomistic protein. A. Side view of a membrane protein illustrating the membrane distortions around the protein by h⁺ (upper gray surface) and h⁻ (lower gray surface). B. Close up view of the contact curve, showing the displacement (u⁺) and slope (S⁺) boundary conditions at one point of the upper leaflet contact curve.

The Feig group has extended this mechanical deformation model to include a more dynamic view of small molecules, peptides, and proteins [130]. They coupled the membrane elastic energy with a dynamic heterogeneous generalized Born (DHDBG) formalism for fast dynamics simulations in the presence of an implicit membrane. The authors found that when using the dynamic version that allows for membrane bending, instead of a static implicit model of the membrane, the insertion of charged and polar molecules (amino acid side chain analogs, the WALP23 peptide, gramicidin channels and arginine-containing helices) is much more in-line with results from fully-atomistic simulations [130]. Another important advance has been to more realistically treat the membrane-protein boundary. TheWeinstein group runs fully atomistic simulations of a membrane protein of interest and then extract the membrane height directly from the simulations for use in continuum elastic energy calculations [132, 139]. They developed a Cartesian grid-based finite difference method to solve the underlying elasticity equations allowing them to calculate the energetic cost of the membrane deformations arising from hydrophobic mismatch and curvature. The contact angle boundary conditions were not obtained from the simulations, but rather by an iterative minimization procedure performed over the membrane curvature (H) at the boundary. This multiscale modeling approach proved to be a useful tool in quantifying the hydrophobic mismatch-driven remodeling of membranes by G-Protein Coupled Receptors (GPCRs) [132] and was later used to understand how the coupling to the membrane influences the conformational state of the bacterial leucine transporter (LeuT) [139].

Other researchers have employed sophisticated numerics, such as finite-element methods and mean-field approaches, to treat membrane mechanics, while also retaining some level of chemical detail in the protein [90, 131, 140, 141]. Powerful numeric schemes, such as these, have the potential to accurately handle large membrane deformations where the small angle limit breaks down [142] and/or non-linear elasticity may play a role. For instance, Zhou and co-workers developed a finite-element model of a membrane with non-linear elasticity in close apposition to a curvature inducing BAR domain [131]. The protein was treated atomistically, and its electrostatic influence on the nearby membrane caused it to curve. Similarly, Khelashvili et al. [141] studied BAR-domain induced remodeling of a heterogeneous membrane making use of a self-consistent mean-field model that combined a BAR domain in atomistic detail with a free energy density functional based on the continuum Helfrich model and on Poisson-Boltzmann (PB) electrostatics. Another related area for improvement is the description of lipid order around the protein and how this can give rise to spatially dependent moduli [143].

Finally, while we have focused in this section on hybrid approaches that predict deformation profiles around a protein by solving a PDE. However, some authors have used MD simulations to determine the membrane shape, similar to the Weinstein group, but then analyze the energies, forces, and torques with a continuum model without formulating and solving a PDE [92, 144–146].

In Section 6, we will briefly outline the energetic terms of our hybrid continuum-atomistic model, discuss our recent advances in treating complex membrane shapes, and then show how our method compares to fully atomistic MD simulations for complex membrane proteins in Section 7.

6. A detailed look at our hybrid continuum-atomistic model

Here we describe the energetic terms in Eq. (20) and the machinery needed for identifying the membrane-protein contact curve, and optimizing the curve to determine deformations that minimize the total energy. As discussed in the last section, many other researchers are approaching this problem from a number of different interesting and unique perspectives - ours is just one of these approaches.

6.1. Electrostatic energy

We calculate the electrostatic component of the energetic cost for the protein to be in the membrane using Poisson-Boltzmann (PB) theory:

$$-\nabla ·[\epsilon (\overrightarrow{r})\nabla \varphi (\overrightarrow{r})]+{\kappa }^2(\overrightarrow{r})sinh[\varphi (\overrightarrow{r})]=\frac{e}{k_{B}T}4\pi \rho (\overrightarrow{r}),\varphi (\overrightarrow{r})=\frac{\mathrm{\Phi }(\overrightarrow{r})}{k_{B}T},$$ (21)

where ϕ(r⃗) is the reduced electrostatic potential at position r⃗, k_B is the Boltzmann constant, T is the absolute temperature, κ is the Debye-Hückel screening coefficient, ε is the spatially-dependent dielectric constant, ρ is the space-dependent charge density, and e is the fundamental charge unit. The influence of the membrane enters through the spatial dependence of ε, κ, and ρ in cases where we explicitly include charged groups to represent anionic lipids at discrete locations in the head group interface [147]. The solution to the continuum membrane equations (Eqs. (16) – (17)) determine the boundaries delineating these spatial regions, and the APBS software provides a flexible platform for modifying these three parameters [34] and solving the PB equation [134]. Once ϕ(r⃗) is calculated, G^(e) is readily computed:

$$G^{(e)}=\frac{1}{2}{\int }_{\mathit{all}\mathit{space}}\mathrm{\Phi }(\overrightarrow{r})\rho (\overrightarrow{r})d\mathrm{\Omega },$$ (22)

where G^(e) is the linearized form, but in practice we report values computed with the full non-linear energy. The electrostatic energy is formally divergent when calculated as in Eq. (22), and we always determine values with respect to the protein in solution far from the membrane [128], which removes the singularities.

6.2. Non-polar energy

The non-polar energy arises, in part, from the solvent reorganization that happens when large molecules are sequestered away from water. This phenomenon is responsible for the clustering of hydrophobic proteins and peptides and the stabilization of molecules in the membrane. A fast and simple theory for estimating the strength of this interaction within the continuum framework is to assume that the stabilization energy of the molecule in the hydrophobic environment is proportional to the solvent accessible surface area (SASA) [137, 148]. The physical motivation is that the number of conformationally restricted water molecules that are released upon removal from solution is related to the amount of surface area; however, more sophisticated theories have been applied to this problem [149–151]. We model the non-polar energy contribution to the protein in the membrane as [128]:

$$G^{(np)}=a·(A_{\mathit{mem}}-A_{\mathit{sol}})+b,$$ (23)

where A_mem is protein’s SASA in the membrane and A_sol is value in solution. The phenomenological constant a (a = 0.028 kcal/mol·Å²) is taken from earlier work exploring the transfer of small solutes between polar and non-polar solvents [137]; however, we set b to zero given that the meaning of this offset is difficult to interpret for partial insertion into a hydrophobic environment and its magnitude is small compared to all other energetic terms in Eq. (20). Finally, we use the MSMS program to quickly compute the protein surface area [152]. As described elsewhere [33], we use the solution for the upper and lower membrane leaflet surfaces to determine which portions of the protein are solvent accessible when computing A_mem.

6.3. Membrane elastic energy

Any of the membrane models proposed in the literature and discussed in Section 4 could be used to compute the membrane energy G^(me), but the models that are most compatible with our energetic treatment of the protein are ones that explicitly account for the membrane width. Thus, our work has utilized a dual monolayer leaflet description [33, 128, 129] as proposed by Huang [38], which treats the upper and lower leaflets independently and depends on changes in curvature (mean and Gaussian), thickness and tension. We assume that the total bilayer elastic energy is given by the sum of the contributions from each monolayer, we employ a Monge gauge representation, and we ignore spontaneous curvature. Near the protein, where there is not always a one-to-one correspondence between a patch in the upper leaflet with a patch in the lower leaflet, it becomes difficult to define the compression, and we have recently developed a method for handling these complex boundaries (currently in preparation [153]). In the past, we used a finite difference approach to solve the underlying PDEs in Cartesian or radial coordinates, but more recently we have developed a finite volume approach [154] that is more appropriate for solving biharmonic equations on complex boundaries by using a level set function to describe the membrane-protein boundary curves ([153]). In Section 7, we will employ this membrane model as shown in Eq. (15) with the standard parameters given in Table 1; however, our algorithm is flexible and any single energy term, including G^(me), can readily be exchanged with a different theory.

Table 1.

Parameter values used in continuum model calculations in Fig. 7. All membrane values correspond to POPC bilayers, respectively. Additional parameters used in the electrostatic calculations are identical to values reported in Ref. [33].

Parameter	Value	Reference
Membrane thickness (L0)	27.95 Å, 28.5 Å	[156, 157]
Surface tension (α)	3.00 × 10−13 N/Å	[33]
Bending modulus (Kc)	8.5 × 10−10 NÅ	[158]
Gaussian modulus (KG)	~ −0.9 × Kc	[159, 160]
Compression modulus (Ka)	2.13 × 10−11 N/Å	[156, 161]
Protein dielectric (εp)	2.0	[148]
Membrane core dielectric (εhc)	2.0	[162]
Head group dielectric (εhg)	80.0	[162]
Water dielectric (εw)	80.0	[148]
SASA prefactor for non-polar energy (a)	0.028 kcal/mol·Å2	[137]

6.4. Identifying and optimizing the contact curve

Within the dual monolayer framework, there are two contact curves – one for the upper leaflet and one for the lower leaflet (Fig. 6). These curves represent the lipid excluded surface, which is the surface of closest contact between a spherical lipid probe and the protein atoms [155]. We first erect a flat, Cartesian grid for the upper and lower leaflets, and then use level set theory to move grid points near the membrane-protein surface onto the boundary curve representing the lipid excluded surface [154]. Next, we represent the initial displacement of the membrane on the protein (the hydrophobic mismatch) by a Fourier expansion with an arbitrary number of terms. Such a representation gives rise to smooth boundary curves, which are generally seen in simulation, that are not characterized by prohibitively large curvature energies. Once the boundary is set up with particular values of the Fourier coefficients, we solve for the total membrane shape to determine G^(me), then the monolayer surfaces from the solution are used to determine G^(e) and G^(np), as described above. Finally, we optimize using simulated annealing followed by Powell’s method to determine the membrane-protein contact curves and the total energy of the system as in Eq. (20). Convergence of the search is highly dependent on the protein, but generally it requires 500 to 1500 iterations and about 2 to 7 hours on a desktop computer. For a more detailed description of the energetic model or its solution, we refer the reader to our previous studies [33, 128, 129, 147].

7. Continuum membrane models can match atomistic simulation

While membrane elastic models are incredibly fast, compared to coarse-grained and fully-atomistic simulations, and make it possible to quantify membrane bending energies, there is an open question as to whether they can accurately reproduce the true membrane deformations induced by membrane proteins. Unfortunately, experimental methods cannot be used to benchmark the quality of continuum models since they lack the spatial resolution required to determine how lipids are configured around proteins, thus, atomistic simulations remain the best means of comparison. Only a few studies have directly compared continuum results with coarse-grained [33] and fully-atomistic [127, 145, 146] simulations, and the main conclusion from Lee and co-workers is that continuum models have major deficiencies [127]. Here we highlight some of the recent developments in our continuum model discussed in Section 6 by showing that we can quantitatively match deformation profiles observed in MD simulations for the lipid scramblase nhTMEM16. The MD simulations and our model predict extensive membrane remodeling.

7.1. The nhTMEM16 lipid scramblase produces large deformations

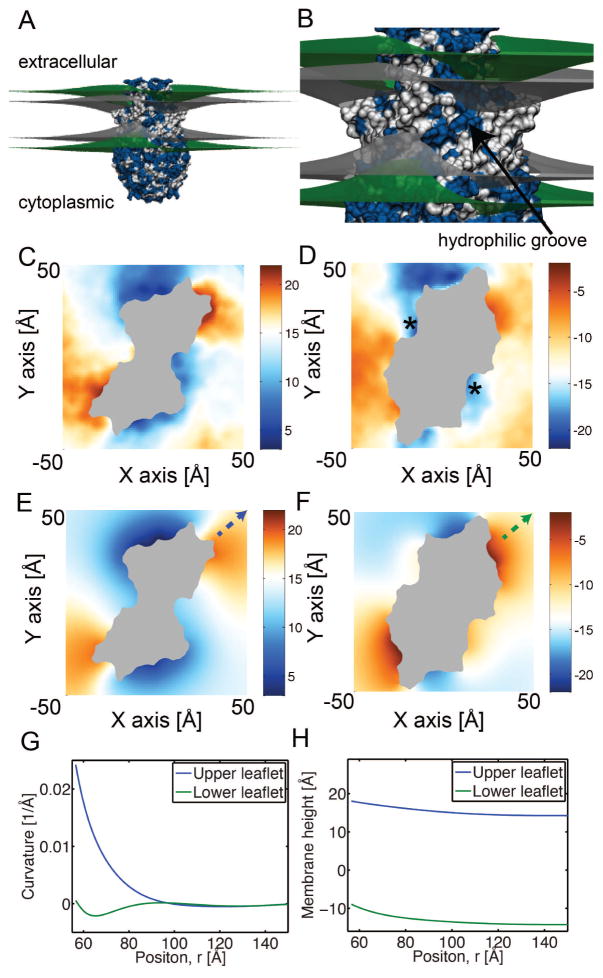
The compositional asymmetry of lipids between the leaflets at the plasma membrane influences signaling properties of cells. Scramblases are a class of proteins that disrupt membrane asymmetry by facilitating the transfer of phospholipids from one leaflet to the other in an energy independent manner. These transmembrane proteins play a role in events such as coagulation of the blood and cellular apoptosis by transporting phosphotidylserine (PS) from the inner leaflet to the outer leaflet of the plasma membrane [163]. In particular, TMEM16 family members have gained recent attention for their role in phospholipid scrambling in platelets and fungi [164, 165]. Additional insight has come from the high-resolution structure of a family member from Nectria hematococcus (nh) (nhTMEM16), which has revealed a possible mechanism for phospholipid conduction across the membrane. The molecule forms a dimer, and each subunit has a hydrophilic cavity that faces the core of the membrane. It is believed that head groups are conducted from one leaflet to the other through this groove, and this hypothesis is supported by chimera studies carried out on family members that have lost the ability to flip lipids [166].

No lipids were resolved in the 3.3 Å resolution structure, which is not surprising, so a molecular level view of how nhTMEM16 interacts with the membrane was not clear. Using their software, MemProtMD, the Sansom group embedded the protein in a DPPC lipid membrane and ran a microsecond coarse-grained simulation of nhTMEM16, and in this short time frame they observed deviations from a planar bilayer and 15 lipids traversed the lipid-facing cavity [167]. We turned to all-atom simulations to determine if the distortions around nhTMEM16 compared favorably with results from our continuum method. We centered the dimer in the membrane with far-field boundaries taken from OPM [168], and then used our algorithm to identify the membrane-protein boundary followed by optimization to minimize the total energy (Eq. (20)). Our model shows that nhTMEM16 drives significant membrane bending in what appears to be a pinching mode from the upper and lower leaflets (green surfaces in Fig. 7A) indicative of hydrophobic mismatch. The induced curvature is largest at the hydrophilic groove, but it is also present at the periphery of the groove (Fig. 7B). Surface views of the upper (panel C) and lower (panel D) leaflets reveal a pseudo-two fold pattern consistent with nhTMEM16 being a dimer, and they also reveal that the leaflets bend down by as much as 10 Å from the upper leaflet and up by nearly as much from the bottom leaflet. Additionally, there is little compression as suggested from the comparison of the upper leaflet displacement (panels C and E) with the lower leaflet displacement (panels D and F), but rather the upper and lower leaflets move in concert (panel H).

Figure 7.

Membrane bending around nhTMEM16 determined from fully-atomistic MD and continuum elasticity. A. Membrane distortions caused by nhTMEM16 predicted from continuum elasticity. The protein is represented at the atomistic level, with the upper and lower head group-water interfaces in green and the surfaces delineating the hydrocarbon core gray. All hydrophobic amino acids are white and polar residues are blue. B. Enlarged view from panel A with the hydrophilic groove indicated. C, D. Upper and lower membrane surfaces averaged from fully-atomistic MD simulations. E, F. Upper and lower membrane surfaces determined from continuum elasticity. The protein is gray. White values correspond to the undeformed height of the membrane far from the protein, blue are downward deflections, and red are upward deflections. All color bars are in ångströms. Color scheme is the same throughout. The stars in panel D indicate points of discrepancy between simulations (panel D) and continuum solution (panel F). G, H. Curvatures (G) and membrane heights (H) for upper and lower leaflets along the x equal y axis in panels E and F. The starting point and direction is specified by the dashed arrows in panels E and F.

Next, we ran four MD simulations for 50 ns (full simulation details in Table 2) for an aggregate simulation time of 200 ns and plotted the average height of the upper and lower leaflets (Fig. 7E, F). The pattern of the deformations predicted from the all-atom simulations is strikingly similar to the results from our continuum calculations. The two fold symmetry is again present, and the pattern of downward deflection (blue) and upward deflection (red) at the upper leaflet is nearly identical (panels C and E). Moreover, our continuum model is also in quantitative agreement with MD in predicting the absolute magnitude of the deflections from −10 to +5 Å. The agreement at the lower leaflet is also quite good both qualitatively and quantitatively (panels D and F), with the biggest discrepancy (of about 5 Å) occurring at the inlets indicated by stars panel (Fig. 7D). We believe that our results provide insight into the function of nhTMEM16, and that the pattern of membrane distortion across the hydrophilic groove is likely essential for its ability to move lipids from one leaflet to the other efficiently, and this hypothesis can be tested through the design of future experiments. Lastly, the continuum calculations are very fast. The molecular dynamics simulations took 32 GPU days to produce the full 200 ns trajectory, while the continuum calculation took 8 hours to complete on a single CPU (100 times faster without considering the cost differences between GPUs and CPUs). We note that in our continuum methods rather than using the averaged structure from our MD, we have performed the calculations using the crystal structure of nhTMEM16 [169]. Often the protein conformation will change during the simulation, which can confound comparisons between simulation and continuum calculations on static snapshots. To quantify the structural differences and degree of nhTMEM16 drift we calculated the root mean squared deviation (RMSD) of the entire protein (4.3 Å) and the transmembrane domain (1.1 Å) alone. Since the latter region is responsible for inducing membrane deformations, and has a small RMSD value, we beleive that our continuum results on a single structure are relevant as evidenced by our close match to MD (Fig. 7). In cases where the protein drifts significantly, it may be more appropriate to use the averaged structure obtained from molecular simulations or carry out many continuum calculations on many different configurations.

Table 2.

Parameter values used in atomistic molecular dynamics simulations of nhTMEM16.

Parameter	nhTMEM16
MD engine	Amber
PDB ID	4WIS
Lipid type	POPC
Forcefield	CHARMM36
Ensemble	NPT
Barostat	Berendsen
Pressure coupling	0.5 ps
Pressure tensor	Semi-isotropic
Thermostat	Langevin
Temperature	303.15 K
Friction coefficient	1 ps−1
Time step	2 fs
Shake	yes
Electrostatics	PME
Non-bonded cutoff	8 Å
Switching distance	N/A
Atom count	335,204
Aggregate time	200 ns

8. Conclusions

In this review, we have briefly outlined the evolution of continuum elastic models of the membrane and how these models have been coupled to the presence of embedded integral membrane proteins. The original studies by Helfrich and Canham were concerned with the curvature energies of a membrane represented as a two dimensional sheet [35, 36]. Early attempts to include membrane proteins in this framework treated the proteins as simple geometric objects such as point particles, hard discs, or ellipses. Additional degrees of freedom such as bilayer thickness [38, 48, 106] and the tilt of the lipid molecules [50, 106, 108] have become essential considerations for adequately studying different aspects of protein-membrane interactions. With these advances in membrane complexity, the height of embedded proteins could be explicitly accounted for, introducing the concept of hydrophobic mismatch as a means to couple membrane compression and curvature to the protein.

Here we have argued that the next generation of continuum models must adopt a more realistic representation of the protein both in terms of its chemical composition and its geometric shape [122, 127, 128, 131, 132, 170]. These steps require moving away from treating proteins as simple geometric shapes and employing modern molecular modeling methods together with high resolution structures to represent the protein. In Section 6, we presented our approach for merging protein biophysics with continuum elasticity theory to better understand membrane protein interactions. By employing continuum electrostatics and fast non-polar estimates of the energy, the calculations remain extremely fast compared to CG and atomistic MD, but retain amino acid level detail. Thus, our model can be used to make in silico point mutations that can be tested experimentally, as we successfully did for the RegIIIα toxin [147].

In Sections 6 and 7, we highlighted our most recent advances to our continuum elasticity solver, in which we have developed new methods for defining the protein-membrane boundary and applying boundary conditions [153]. The model does a very good job at quantitatively predicting membrane deformations around proteins when benchmarked against fully-atomistic MD simulations, but at a tiny fraction of the computational cost. This close connection allows us to generate sound hypotheses regarding the function of membrane proteins. For instance, both MD and our hybrid atomistic-continuum model reveal extreme bending of the membrane around the hydrophilic groove in nhTMEM16. Since the continuum calculations are faster, they can be used to scan through various mutants and protein chimeras to determine which residues are responsible for the large-scale membrane rearrangements. These select residues could then be further examined with molecular dynamics simulations, followed by experimental tests on a much reduced subset of candidates. Thus, continuum and molecular dynamics approaches can be used in a pipeline to accelerate experimental predictions. Nonetheless, continuum elasticity approaches have unique advantages over simulation. First, it is difficult to determine the membrane bending energy from atomistic simulations, but this information is readily available from the solution of the PDEs or from integrating surfaces determined from simulation (see Refs. [2, 132]). Second, membrane relaxation around transmembrane peptides and proteins can be very slow [26], and simulations may not be at equilibrium. Continuum methods do not suffer from this limitation; however, identifying and optimizing membrane contact boundary curves can be difficult [129].

While we believe that the field is making good progress towards accurate continuum models of the membrane around proteins, there is much to be done. For instance, the comparison of continuum calculations with all-atom simulation from the Andersen and Im groups revealed a failure of the continuum models to show the correct behavior near the protein [119]. Likewise, there are regions around nhTMEM16 in which the direction of membrane deflection predicted from the continuum calculation gives the opposite sign from the MD simulations. It will always be difficult to describe specific lipid interactions with the protein using a continuum or field theory, but we spent a good portion of our review highlighting extensions that treat the orientation of the lipids and their entropy, because we believe that adding these degrees of freedom may significantly improve continuum models. Kim and co-workers identified that continuum models failed to reproduce shell hardening or stiffening near the protein boundary [119], and we believe a more in-depth description of the lipid degrees of freedom may capture this feature. We have focused almost exclusively on the subset of continuum membrane models that have been formulated in the small angle deflection limit and represented in the Monge gauge. In order to address large-scale conformational changes that occur during SNARE-mediated fusion [171] or M2 channel mediated fission [172], more sophisticated mathematical approaches must be employed. Moreover, as with many numeric schemes, the fidelity of the solution to the elasticity equations is highly dependent on how well refined the mesh is around the protein surface where the boundary conditions are applied. Extending dense grids far from the protein creates large sets of equations that are prohibitively difficult to solve, limiting solutions to small membrane patches. If adaptive mesh refinement were employed [173], then large membrane patches containing many inclusions could be examined, and membrane mediated interactions between proteins could be probed. This advancement would open up the possibility of studying multi-protein processes that involve long-timescale membrane rearrangements at large length scales while also requiring an accurate view of the protein-membrane interaction at short length scales.

Highlights.

• The evolution of continuum elastic models of the membrane is briefly outlined.

• Membrane elastic models need to incorporate protein’s chemistry and geometry.

• A fast and accurate hybrid continuum-atomistic model is proposed.

• Hybrid model reveals extreme bending of the membrane in the presence of nhTMEM16.