Using quantile regression to create baseline norms for neuropsychological tests

Abstract

Introduction

The Uniform Data Set (UDS) contains neuropsychological test scores and demographic information for participants at Alzheimer's disease centers across the United States funded by the National Institute on Aging. Mean regression analysis of neuropsychological tests has been proposed to detect cognitive decline, but the approach requires stringent assumptions.

Methods

We propose using quantile regression to directly model conditional percentiles of neuropsychological test scores. An online application allows users to easily implement the proposed method.

Results

Scores from 13 different neuropsychological tests were analyzed for 5413 cognitively normal participants in the UDS. Quantile and mean regression models were fit using age, gender, and years of education. Differences between the mean and quantile regression estimates were found on the individual measures.

Discussion

Quantile regression provides more robust estimates of baseline percentiles for cognitively normal adults. This can then serve as standards against which to detect individual cognitive decline.

1. Introduction

The Uniform Data Set (UDS) is a central database containing information on participants at contributing Alzheimer's disease centers and Alzheimer's disease research centers funded by the National Institute on Aging. The participants in UDS are self-selecting and may not be representative of the entire population. Using the UDS, Weintraub et al. [1] provided an exploratory analysis of the relationship between neuropsychological test scores and age, years of education and gender. They found that, in almost all cases, age, education, and gender should be taken into account when modeling the expected score of a test. Shirk et al. [2] proposed using these models to estimate percentiles for a given patient by calculating a z-score conditional on the patient's individual characteristics. The z-score was then referenced to the standard normal distribution to estimate the percentile for the subject's performance on a given test.

Natural cognitive decline due to age can be accounted for by adopting a statistical model that incorporates age. This results in an estimate of the percentiles that are dependent on the age of the patient. The statistical models can be made more precise by also including years of education and gender. Ideally, participants can take the test while healthy and create a baseline percentile for the subject in comparison with the peer group that share the same age, education, and gender. Any future substantial decline from the baseline percentiles would provide a warning sign to take more sophisticated tests to detect cognitive decline. For example, suppose we have a patient who initially scored at the 95th percentile for a given test, meaning 95% of the cognitively healthy population with the same age, gender, and years of education performed worse than the patients on the test. If after 1 or 2 years when taking the test again, their test score dropped to the 80th percentile as calibrated by the same statistical model, this would flag the subject for further medical attention. Even though the patient is still performing relatively well, we would expect them to stay around the same high percentile because the statistical model accounts for decline due to age.

In the literature, mean regression analysis is often used to model the percentiles, which relies on strong modeling assumptions. The popular z-score approach by Shirk et al. [2] adopts mean regression and assumes that the random errors are normally distributed and the variance is constant. The model assumes that the variance of test scores is the same for different genders, years of education, and age. These assumptions are also crucial for the mean regression method to calculate confidence intervals and P values for coefficient estimates. For sufficiently large samples sizes, the confidence intervals and P values are approximately valid even if the normality assumption is violated. If the constant variance assumption is not satisfied, then the P values and confidence intervals will not be correct, although the estimates of the coefficients are not systematically biased. When modeling percentiles, deviations from these underlying assumptions become more problematic. A deviation from either assumption could result in biased percentile estimates that cannot be corrected even if the data set is huge.

We propose a new approach to create baseline norms for neuropsychological tests using quantile regression and provide a web-based application to implement the procedure. Quantile regression was proposed in a seminal article of Koenker and Bassett [3] and aims to directly model the conditional percentiles. We refer to Koenker [4] for a thorough review of quantile regression. In the present article, we applied both quantile regression and mean regression to analyze a cognitively normal subset of the UDS neuropsychological data to create the baseline norms and compared the results.

2. Methods

2.1. Subject selection

To create baseline percentiles for patients without signs of cognitive decline, analysis was limited to cognitively normal adults with complete information on age, gender, and years of education. Specifically, we limit the analysis to participants in the UDS that met the following criteria: (1) a global clinical dementia rating score of 0; (2) a total functional assessment questionnaire score of 0; (3) a normal score from the neuropsychiatric inventory questionnaire (NPI-Q); (4) no missing data for age, gender, or education; and (5) visit dates from January 2005 to February 2013. In addition, we only use data from a subject's first visit. These criteria are similar to those used by Weintraub et al. [1], with the difference that analysis was limited to participants with first visits from September 2005 to August 2007. In our study, there were 5413 participants who met the aforementioned requirements.

Of the 5413 participants, 78% were white, 16% black, 3% multiracial, 2% Asian, and 1% other. Hispanic was not included as a category for race. The age range was 13% younger than 60, 30% between 60 and 69, 37% between 70 and 79, 18% between 80 and 89, and 2% older than 90 at the time of first visit. Females were over-represented (69% of the participants). The breakdown by total years of education was 18% with <12 years, 20% between 13 and 15 years, 24% with 16 years, and 38% with ≥17 years of education.

2.2. Neuropsychological tests

We analyzed results from the following UDS neuropsychological tests: mini-mental state examination (MMSE) [5], Wechsler memory scale-revised subtests logical memory A (first story, immediate and delayed recall) [6], digit span forward and backward [6], semantic fluency (animals and vegetables) [7], Boston naming test (BNT; 30 item—odd numbered) [8], Wechsler adult intelligence scale-revised (WAIS-R) digit symbol coding subtest [9], and trail making test (TMT) parts A and B [10]. A review of these tests and how they have been used for the UDS was provided in Weintraub et al. [1]. For delayed recall of logical memory A, participants were asked to remember parts of a story after a delay. In version 1.1 of the UDS, the delay was 30 minutes and for version 1.2 and 2.0, the delay was 20 minutes, but not all participants were delayed at the recommended time. The precise delay time had been recorded for each subject, and this information was used when modeling the performance for the logical memory A delayed recall test [1].

2.3. Data analysis

Both quantile and mean regression models were fit for the aforementioned neuropsychological tests. For the predictors, we considered age, years of education, and gender as single variable models, and also a full model that includes all three variables. To test the assumptions of normality and homoscedasticity, we used a Kolmogorov-Smirnov test for normality [11] and a Breusch-Pagan [12] test for homoscedasticity. Quantile regression does not rely on the assumptions of normality or homoscedastic errors to model the conditional percentiles. All analyses were carried out using R 3.1.1. The quantreg package [13] was used for quantile regression, and the lmtest package [14] was used for the Breusch-Pagan test; otherwise, calculations were implemented using the base software.

3. Results

3.1. Marginal test scores

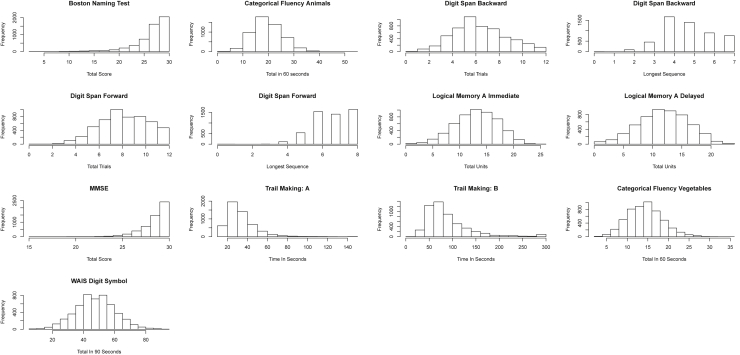
Fig. 1 contains histograms similar to those presented in Weintraub et al. [1] but updated for our data selection method. The test scores of the BNT, MMSE, and TMT A and B all have skewed distributions. Not all participants had values for all the tests. Sample sizes ranged from 5117 for the WAIS-R digit symbol coding test to 5315 subjects who took the MMSE. The scores for the TMT A and B are the number of seconds to complete the test, with maximum times of 150 and 300 seconds, respectively. Censoring can result in biased estimators when using standard mean regression, but the problem of censoring was fairly light for our targeted sample, namely, less than 1% for test TMT A (7 of 5270), and 1.6% for TMT B (86 of 5238). The skewness for the BNT scores is caused by a large number of participants scoring very high on the examination. Almost 18% (925 of 5250) received the maximum score of 30. For MMSE total scores, this was more extreme with almost 45% (2406 of 5315 participants) getting the maximum score of 30. We will later demonstrate with the BNT that quantile regression does a better job than mean regression at modeling response values for skewed data. Another potential problem is that the digit span test has integer-valued scores in a small range, 0–12 for digit span backward and forward, 0–8 for digit span backward: Length and 0–7 for digit span forward: Length. To limit the complexity of our models, we will not be incorporating the discrete nature of the results for the digit span tests in our models, but using a generalized linear model may be a better approach. The scores for WAIS digit symbol, logical memory A immediate and delayed are approximately symmetric and bell shaped.

Fig. 1.

Histogram of sample test scores. Abbreviations: MMSE, mini-mental state examination; WAIS, Wechsler adult intelligence scale.

3.2. Conditional analysis

Shirk et al. [2] proposed to calculate the z-score to estimate a person's test score percentile. The z-score was obtained by dividing the difference of the observed score and the model predicted score by the standard deviation estimate from the model. The test score percentile is then estimated by finding the corresponding percentile from a standard normal distribution. In their article, they recognize their approach requires the assumptions that the error terms follow a normal distribution and have constant variances [2]. The normality and constant variance assumption are common in mean regression models, but are mostly used to derive P values for the estimates of the coefficients. The regression coefficients are valid under milder conditions and for large sample sizes the P values are robust to the assumption of normality. Estimation of the conditional percentiles, however, is sensitive to these assumptions, and deviations from the assumptions are likely to result in biased estimates.

For each test, except logical memory A delayed, four different regressions are fit. One each for the three predictors: years of education, age, and gender, and a model that includes all three predictors. The models for logical memory A delayed also included length of the time delay as an additional predictor in all four models. Log transformations are used for TMT A and (B) These models were fit to replicate the results of Weintraub et al. [1], but they will not be exactly the same because of the different criteria used for data selection. For each model, we performed a Kolmogorov-Smirnov test for normality [11] and a Breusch-Pagan test for homoscedasticity [12]. In both cases, very low P values indicate violations of the regression assumptions. Table 1 reports the P values for these tests when using all predictors. The results demonstrate that these assumptions do not hold for the vast majority of the models. Tests of normality are very sensitive for large samples sizes, and the Breusch-Pagan test relies on the assumption that the errors are normally distributed. We also analyzed QQ plots and residuals versus fitted plots that confirm the assumptions of constant variance and normality do not hold for many of these models. As these two underlying assumptions are crucial for the mean regression, we propose quantile regression as an alternative approach that does not require the error terms to have a normal distribution or constant variance.

Table 1.

P values for the K-S test for normality and B-P test for homoscedasticity

Neuropsychological test	K-S test for normality	B-P tests for homoscedasticity
Boston naming test	<.01	<.01
Category fluency: Animals	<.01	.18
Category fluency: Vegetables	.01	<.01
Digit span backward	<.01	<.01
Digit span backward: longest sequence	<.01	.01
Digit span forward	<.01	.21
Digit span forward: longest sequence	<.01	.12
Logical memory A delayed	.31	<.01
Logical memory A immediate	.34	<.01
MMSE	<.01	<.01
Trail making: A	<.01	<.01
Trail making: B	<.01	<.01
WAIS digit symbol	.09	<.01

Abbreviations: K-S, Kolmogorov-Smirnov; B-P, Breusch-Pagan; MMSE, mini-mental state examination; WAIS, Wechsler adult intelligence scale.

NOTE. Small P values indicate evidence against normality or constant variances assumptions.

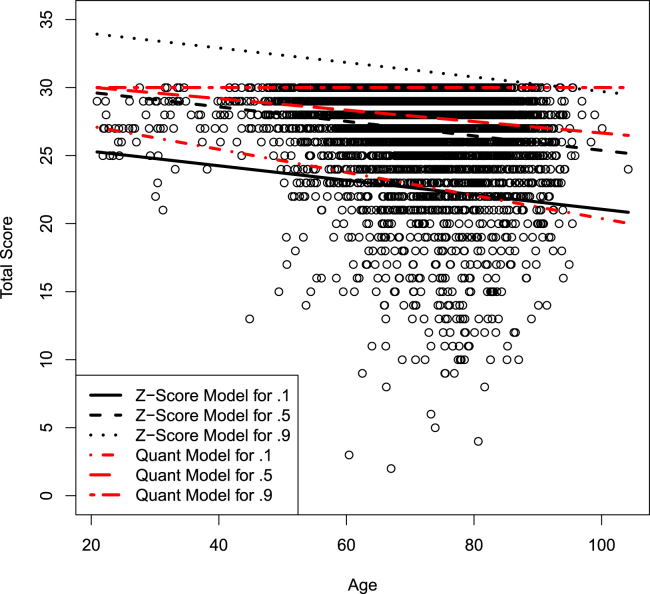
We use the BNT to demonstrate the differences between quantile regression and mean regression. Fig. 2 depicts quantile regression and z-score method [2] fits for the 10th, 50th, and 90th percentiles. In these models, BNT score is the response and age is the sole predictor. In mean regression, a line is fit to the data to model the conditional mean. The conditional mean is interpreted as the average score on the BNT for a given age. The conditional 90th percentile is the score that 90% of the population scores below for a given age. The mean regression method shifts the line to model the conditional percentiles, but the slope remains the same. In quantile regression, the lines for each percentile are fit separately and the slopes for the lines can change with the percentile. In Fig. 2, the middle black line is the least squares fit. Using the mean regression method to find a line for the 90th percentile is problematic because for the majority of the range of age the line is above the maximum score of 30 for the test. Directly modeling the conditional 90th percentile results in horizontal line at 30 indicating that regardless of age the 90th percentile score is the maximum of 30. For the 10th percentile, the quantile regression estimator has larger estimates for early ages, but it has a steeper slope. Indicating that for subjects at the 10th percentile, we can expect a steeper decline due to age.

Fig. 2.

Models of conditional percentile using approach of Shirk et al. [2] are labeled as z-score. Quantile regression fits are labeled as quant model.

To create a more precise model, we also include the variables age, years of education, and gender. For gender, we use males as the baseline, and the coefficient represents the models estimated difference between females and males. Results for the mean, median, and 10th and 90th percentiles are presented in Table 2. Estimates for the conditional mean and median are similar with education being the only variable that does not have an overlapping confidence interval. For the 90th percentile fit, none of the variables have a slope. The reason for this is across age, years of education, and gender, there are a large number of participants who got the maximum score of 30. For the 10th percentile, the slopes are all different from those of the median. Of particular interest is that the slope for age has a steeper decline than the fit for median behavior. This implies that for patients that performed poorly on the BNT, we would expect their performance to decline quicker than the rest of the population. This information is helpful in differentiating between potential cognitive decline and decline that is expected due to age.

Table 2.

Mean and quantile regression models for Boston naming test score

Model	Coefficient	Estimate	95% confidence interval	P value
Mean	Age	−0.045	(−0.053 to −0.037)	<.01
Education	0.33	(0.30 to 0.36)	<.01
Female	−0.69	(−0.88 to −0.54)	<.01
Median	Age	−0.036	(−0.043 to −0.029)	<.01
Education	0.23	(0.20 to 0.26)	<.01
Female	−0.46	(−0.61 to −0.31)	<.01
10th percentile	Age	−0.07	(−0.085 to −0.052)	<.01
Education	0.60	(0.51 to 0.69)	<.01
Female	−1.18	(−1.73 to −0.64)	<.01
90th percentile	Age	0	(−0.0036 to 0.0036)	1
Education	0	(−0.03 to 0.03)	1
Female	0	(−0.05 to 0.05)	1

Motivated by the work of Shirk et al. [2], we used quantile regression and the z-score method to estimate the percentile for an 80-year-old male with 12 years of education. The scores and estimated percentiles from that method are given in Table 3. To get the estimates using the quantile regression method, 99 quantile regression models were fit for each test, from the 1st percentile to the 99th. The 99 models provide 99 predicted values for each percentile. The estimated conditional percentile is the number of the predicted values smaller than the observed score, except for the TMT A and B tests. Those two tests measure time to completion for a task, and a lower score indicates higher performance so the estimated conditional percentile is the number of predicted values larger than the observed score.

Table 3.

Percentile estimates for an 80-year-old male with 12 years of education

Test	Score	Z all	Q all	Z gender	Q gender	Z education	Q education	Z age	Q age
Boston naming test	25	41	27	23	10	33	21	43	29
Category fluency: Animals	9	7	4	2	1	4	2	5	2
Category fluency: Vegetables	7	14	9	7	3	4	2	5	2
Digit span backward	4	19	17	10	4	12	5	16	12
Digit span backward: longest sequence	3	11	7	6	1	8	1	10	2
Digit span forward	6	16	17	9	5	12	7	16	14
Digit span forward: longest sequence	5	9	3	5	2	6	2	9	3
Digit span forward	6	16	17	9	5	12	7	16	14
Digit span forward: longest sequence	5	9	3	5	2	6	2	9	3
Logical memory A delayed	7	13	15	6	5	6	6	8	7
Logical memory A immediate	6	20	23	12	15	10	12	13	14
MMSE	27	22	23	11	8	10	10	14	14
Trail making: A	3.37	82	79	58	52	74	72	71	68
Trail making: B	4.43	73	69	43	38	60	56	62	58
WAIS digit symbol	52	92	90	67	65	79	81	76	75

Abbreviations: MMSE, mini-mental state examination; WAIS, Wechsler adult intelligence scale.

NOTE. Mean regression with z-score method and quantile regression are indicated by Z and Q. All, gender, education, and age represent models with all three variables, gender only, education only, or age only as the predictors.

Table 3 demonstrates that the z-score and quantile regression methods give different estimates for the percentiles. Most noticeable are the differences for the BNT estimates with all three variables as predictors. For this model, the z-score approach has the subject in the 41st percentile, whereas the quantile regression approach having the subject at the 27th percentile. The estimates also depend on which predictors are included in the model. The quantile regression estimates for the WAIS score method range from the 60th percentile to the 90th depending on which model is used.

3.3. Differential analysis

To compare the quantile and mean-based approaches, we used the baseline models for the BNT to provide percentile predictions for subjects who did follow-up tests. For the follow-up data, we limit our analysis to (1) subjects included in the baseline model, (2) visits between January 2005 and February 2013, and (3) a normal score from the NPI-Q or the first non-normal score. We then have a total of 9283 follow-up visits from 3869 patients and 1642 visits that included a non-normal score NPI-Q. The baseline models include age, gender, and years of education. We fit quantile regression models for the 0.01, 0.02, up to 0.99 percentiles. To perform the differential analysis, we first estimate the conditional percentile using the subjects' age, gender, years of education, and test score at the follow-up visit. Then, we calculate the change in percentile from their initial visit. Negative changes may be indicative of a decline in cognitive ability beyond what is expected due to aging. In Table 4, we report the sensitivity and specificity for different thresholds, where sensitivity measures the percentage of non-normal cognitive abilities correctly classified. At a given threshold, negative changes that are larger in magnitude than the threshold are classified as potential cognitive decline. If a subject's original score was at the 0.60 percentile and had a follow-up score at the 0.54 percentile, then they would be classified as non-normal at a threshold of 0.05 but not 0.10. The results in Table 4 show that using the quantile regression approach provides better specificity than the mean regression–based approach. Note that sensitivity is potentially the more important criterion as the goal is to identify cognitive decline as early as possible.

Table 4.

Differential analysis for BNT, where a subject with a negative change in percentile larger than the given threshold is classified as having cognitive decline.

Threshold	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50
Mean regression sensitivity	0.30	0.22	0.15	0.12	0.07	0.06	0.04	0.03	0.02	0.02
Quantile regression sensitivity	0.29	0.25	0.21	0.15	0.12	0.10	0.07	0.05	0.03	0.02
Mean regression specificity	0.75	0.84	0.90	0.92	0.96	0.97	0.98	0.99	0.99	1.00
Quantile regression specificity	0.76	0.79	0.83	0.88	0.91	0.93	0.95	0.97	0.97	0.98

3.4. Website application

We have developed a website, https://bsherwood.shinyapps.io/quantEst/, that allows users to implement our method without any programming. Users can upload data, specify a model, and specify the grid size of the percentiles. Then, they can download the estimated percentiles. In addition, the web produces a plot that shows how the slopes vary by percentiles. The Supplemental Material includes a tutorial on how to use the website.

4. Discussion

There exists a wide range of tests for early signs of cognitive impairment, but the results of these tests depend on several factors. To compare a patient's scores to their peers, we recommend including age, years of education, and gender in the model. Controlling for age recognizes that even if patients are not suffering from cognitive impairment, we expect their scores to decrease as a natural result of aging.

In our modeling, we controlled for age, gender, and years of education. Dikmen et al. [15] observed practice/retest effects for several neuropsychological tests including the BNT. Our models could be further improved by also accounting for the practice effects, which is expected to produce a more accurate and useful model. Crawford and Howell [16] suggested that one approach is to include an individual's initial score as a predictor. This can be incorporated into our quantile regression model. Furthermore, we believe the time between repeated tests could be another useful predictor if such information is available. In Shirk et al. [2], they did not account for retesting, although their model could also handle these adjustments. The goal of this article was to demonstrate the differences between the mean regression approach presented in Shirk et al. [2] and using quantile regression. For this reason, we choose not to incorporate practice/retest effect in the models proposed in this article.

Baseline percentiles can be used to create standards for patients that take into account demographic factors. Declines from these baselines can be used to identify early stages of cognitive decline. It has already been suggested to use z-scores with mean regression models to estimate conditional percentiles, but this approach is likely to yield biased estimates if there is nonconstant variance or the error terms do not follow a normal distribution. We propose a new quantile regression approach to directly estimating the conditional percentiles, an approach that will not be biased by non-normal distributions or nonconstant variances. To make the proposed approach more accessible, we have developed a website that allows users to implement the method through a graphical user interface.

Research in context.

• 1.Systematic review: Statistical methods have been proposed in the literature for estimating conditional percentiles of neuropsychological tests scores, but they often rely on stringent assumptions. We introduce quantile regression to directly estimate the conditional percentiles. Previous related work in Alzheimer's literature and foundational articles for quantile regression are cited.
• 2.Interpretation: Using quantile regression provides different estimates for conditional percentiles than methods based on mean regression. In addition, we find that the assumptions required to apply mean regression to estimate conditional percentiles often do not hold for the neuropsychological tests of interest. The quantile regression method is more robust and does not require such strict assumptions.
• 3.Future directions: The article proposes an alternative method for estimating conditional percentiles of a neuropsychological test score. These scores can be used to monitor cognitive decline while accounting for natural decline due to age. Determining how large a change in percentile should be a flag for cognitive decline merits further investigation.