Abstract
By following single fluorescent molecules in a microscope, single-particle tracking (SPT) can measure diffusion and binding on the nanometer and millisecond scales. Still, although SPT can at its limits characterize the fastest biomolecules as they interact with subcellular environments, this measurement may require advanced illumination techniques such as stroboscopic illumination. Here, we address the challenge of measuring fast subcellular motion by instead analyzing single-molecule data with spatiotemporal image correlation spectroscopy (STICS) with a focus on measurements of confined motion. Our SPT and STICS analysis of simulations of the fast diffusion of confined molecules shows that image blur affects both STICS and SPT, and we find biased diffusion rate measurements for STICS analysis in the limits of fast diffusion and tight confinement due to fitting STICS correlation functions to a Gaussian approximation. However, we determine that with STICS, it is possible to correctly interpret the motion that blurs single-molecule images without advanced illumination techniques or fast cameras. In particular, we present a method to overcome the bias due to image blur by properly estimating the width of the correlation function by directly calculating the correlation function variance instead of using the typical Gaussian fitting procedure. Our simulation results are validated by applying the STICS method to experimental measurements of fast, confined motion: we measure the diffusion of cytosolic mMaple3 in living Escherichia coli cells at 25 frames/s under continuous illumination to illustrate the utility of STICS in an experimental parameter regime for which in-frame motion prevents SPT and tight confinement of fast diffusion precludes stroboscopic illumination. Overall, our application of STICS to freely diffusing cytosolic protein in small cells extends the utility of single-molecule experiments to the regime of fast confined diffusion without requiring advanced microscopy techniques.
Introduction
Microscopy has long been a staple technique in biological research. In particular, based on the development of techniques for selectively labeling specific cellular components, fluorescence microscopy has enormous value for elucidating intracellular biology (1). More recently, the ability to visualize a single molecule at a time has improved the localization precision below the standard diffraction limit of light (2, 3, 4). In live cells, the function of a protein in a biological process can be inferred from its rate of diffusion under different chemical or genetic conditions (5, 6, 7, 8, 9). Traditionally, optical measurements of subcellular diffusion have been done using fluorescence recovery after photobleaching (FRAP) (10, 11, 12), but single-molecule imaging techniques like single-particle tracking (SPT) are being increasingly used to precisely evaluate the motion of a diffusing biomolecule (13, 14, 15).
SPT is achieved by connecting a series of single-molecule positions over time. In an optimal SPT experiment, the camera integration time is fast enough that within one frame, the target diffusing molecule does not produce blur by moving far compared to the diffraction limit of light. Acquiring long trajectories improves the statistical significance, but unfortunately, there is a tradeoff due to the finite fluorescence yield of a single-molecule probe: increasing the illumination intensity to enable single-molecule detection in a shorter imaging frame time will shorten the trajectory lengths. This is a particular problem for the most common fluorescent labels in live-cell intracellular imaging, fluorescent proteins (1, 16). These two conflicting requirements of fast imaging and long tracks limit the total range of measurable diffusion rates; this range limit is an important issue when heterogeneities yield a range of diffusion coefficients that are measured simultaneously. If a pulsed illumination source is available, stroboscopic illumination can be applied to decrease the amount of blur without increasing the frame rate or decreasing the trajectory lengths (17). However, confining diffusion to a small volume—for instance, within a cell or organelle—introduces a further constraint: the data acquisition rate must be faster than the time it takes for the diffusing molecule to explore the entire confinement volume. Stroboscopic illumination does not increase the data acquisition rate, and so the maximum measureable diffusion coefficient for a molecule in a confined volume is still limited by the maximum camera frame rate. Additionally, in all cases, because SPT relies on a tracking algorithm to construct trajectories for single diffusing molecules, these trajectories should not overlap. Overall, SPT is best suited for characterizing a collection of sparse and homogeneously diffusing molecules in unconfined environments.
Alternatives that can overcome some limitations of the localization-based SPT analysis include spatiotemporal image correlation spectroscopy (STICS) (18, 19, 20, 21), which has previously been used both in vitro (21) and in live cells (22), and the related methods of k-space image correlation spectroscopy (23, 24) and superresolution optical fluctuation imaging (25). All of these methods compute the correlation function of an entire fluorescence imaging movie instead of relying on localization and tracking, and like fluorescence correlation spectroscopy, these powerful image correlation approaches can be extended to measure 2D maps of heterogeneous diffusion (18, 26) and very fast diffusion (27). Particle image correlation spectroscopy measures diffusion dynamics by computing a similar correlation function from data that have already been processed with the Gaussian localization used in SPT and other methods (28). In STICS, the spatial cross-correlation at some time lag, τ, is the average of the spatial cross-correlations of all pairs of images separated by this τ and has a width (termed the image-mean-squared displacement (iMSD)) that increases with τ. The iMSD-versus-τ function can be fit to calculate the diffusive characteristics of a collection of fluorescent molecules.
In this article, we use STICS to resolve fast, confined motion in a widefield imaging microscope. If a confocal microscope is available, extremely fast diffusion (>100 μm2/s) can be measured with raster image correlation spectroscopy, which uses a scanning mirror to eliminate image blur (27, 29). Here, we instead focus on developing STICS to extend the capabilities of a single-molecule imaging microscope beyond the limits of SPT (maximum measurable diffusion coefficient, ∼10 μm2/s (30)) to an order-of-magnitude-faster motion. Unlike SPT, STICS does not require accurate position determinations for delocalized, fast-moving molecules. Rather, we show here that STICS analysis can explicitly account for in-frame motion blur based on a modification to the mathematical formulation. Conventionally, STICS assumes that molecular diffusion is described by a Gaussian distribution of step sizes, but both in-frame motion and tight confinement will alter the shape of this distribution. In-frame motion corrupts the distribution because the time lag between two frames becomes poorly defined when the integration time or the diffusion rate is large. Tight confinement further distorts the distribution, because this boundary condition excludes the largest step sizes. The artifacts introduced by confinement and in-frame motion were not encountered in previous applications of image correlation spectroscopy, because those experiments focused on slow motion (26, 31, 32, 33, 34), or else minimized pixel dwell time, as in raster image correlation spectroscopy (29). On the other hand, here in the regime of fast, confined motion, the two independent effects of blur and confinement manifest themselves as two independent diffusion-coefficient measurement biases.
Here, we use STICS to measure the rapid subcellular dynamics of a freely diffusing protein in the highly confined interior of a bacterial cell for the first time, to our knowledge. We describe the measurement biases that arise from confinement and fast motion by simulating unconfined diffusion and diffusion confined to bacteria-sized cylinders, both with and without in-frame blur. We develop a method to correct these diffusion-coefficient measurement biases when molecules diffusing up to 15 μm2·s−1 are confined inside bacterial cells as small as 1 μm in length. We find that in-frame motion adds a positive bias to the diffusion-coefficient estimation and that confinement adds an independent, nonmonotonically varying bias. We show how both biases can be removed by directly computing the variances of the STICS correlation function. Finally, we apply STICS to experimental fluorescence microscopy movies of freely diffusing mMaple3 fluorescent protein in the Escherichia coli cytoplasm, and we find a diffusion coefficient, D = 9.6 ± 1.0 μm2 × s−1, for these molecules. This value agrees well with previous fluorescence recovery after photobleaching measurements of fluorescent protein mobility in the E. coli cytoplasm (D = 6.1–14.1 μm2 × s−1 (14)), as well as with SPT measurements with very short camera integration times (0.75–4 ms, D = 7.3 μm2 × s−1 (30)). In this last case, a shortened camera integration time minimized the data loss due to in-frame motion (30). In this work, we instead analyze data taken with typical camera imaging rates (25–100 frames/s) by modifying the STICS protocol to explicitly account for confinement and in-frame motion. Overall, this relaxation of the experimental constraints enables direct, single-molecule-based diffusion measurements in a conventional wide-field single-molecule imaging setup (35) of samples that necessarily contain densely packed fluorophores, systems that contain multiple interacting diffusive populations, and systems that exhibit fast confined diffusion in cellular and subcellular compartments and nanomaterials (36).
Materials and Methods
Simulations
Three-dimensional diffusion was simulated by generating step sizes from a zero-mean normal distribution with variance of 200 nm2 in each of the three dimensions independently. This variance produces a root mean-square (RMS) displacement that is <10% of the waist of the smallest microscope point-spread function () considered, enabling us to simulate smooth motion blurring. For simulations of diffusion confined to a cylinder, candidate steps that fell outside of the cylinder boundary were elastically reflected. The cell boundary is expected to act as an impermeable wall that does not interact with cytoplasmic proteins like the mMaple3 fluorescent protein used here. These 3D trajectories were projected onto the xy plane to simulate two-dimensional (2D) imaging.
The pixel brightness value in each subframe was calculated using a symmetric Gaussian function centered at the position of the diffusing molecule. For one-dimensional (1D) motion, the step-size distribution variance is , where D is the diffusion coefficient and the camera integration time is tframe. Motion with any desired D was therefore simulated by combining the appropriate number of simulation subframes; i.e., any D and tframe can be calculated by taking the average of subframes. The pixel width was set to 49 nm for all simulations for consistency with experiments. The 2D probability distribution of step sizes from one frame to the next is a normal distribution with zero mean and a variance of 4Dtframe:
| (1) |
The squared step sizes and correlation functions were calculated for the SPT and STICS methods, respectively, as described below. For the bias estimation simulations (see Figs. 2 and 3), incremental iterations were used to more precisely compute the STICS correlation function (see STICS analysis, below, for details). Once ∼50,000 total image frames were simulated, D was estimated with STICS and we computed the bias on this value, , from the ratio of the estimated value, θ, to the true value, θ0. For the error estimation simulations (see Fig. 4), both STICS and SPT were performed on identical simulated raw data to which zero-mean white noise had been added with the Matlab built-in function randn to achieve a signal/noise ratio (SNR) of 6 for immobile molecules. The effective SNR, however, is reduced by motion blur and will be <6. The simulated data set used in this study consisted of 1200 frames of contiguous motion.
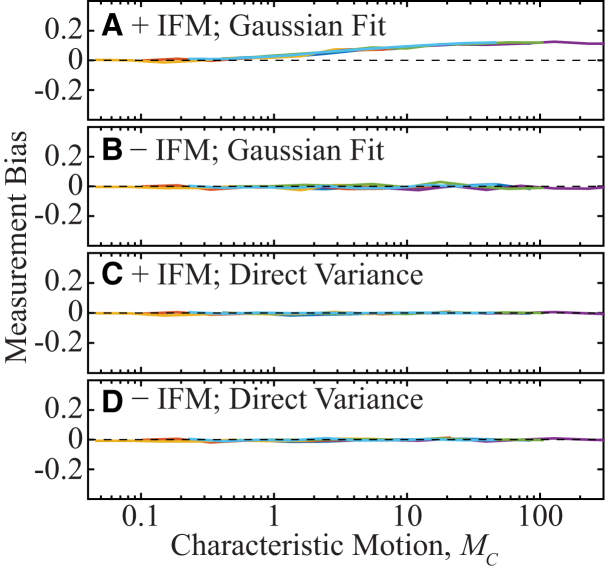
Figure 2.
Diffusion coefficient measurement bias estimated from simulations of unconfined diffusion of a fluorescent molecule with no noise. Colors indicate the set of parameters (tframe, σPSF) (Table S1), and MC is defined according to Eq. 3A. (A) STICS analysis by Gaussian fitting of simulations that contain in-frame motion (IFM). Significant bias is measured for MC > 1. (B) STICS analysis by Gaussian fitting of simulated movies that exclude in-frame motion. (C and D) The results of analyzing the same data as in (A) and (B), but determining the step-size distribution variance in the STICS protocol by directly calculating the variance rather than by fitting the correlations to Gaussian functions. Both the removal of in-frame motion in (B) and the direct calculation of variance in (C) and (D) eliminate the measurement bias. To see this figure in color, go online.
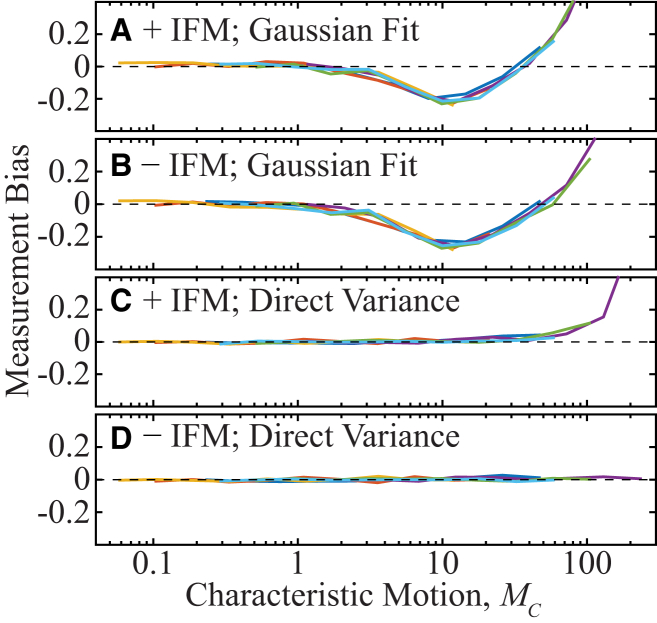
Figure 3.
Diffusion coefficient measurement bias estimated from simulations without noise of a fluorescent molecule confined to a cylinder. Colors indicate the set of parameters (tframe, σPSF) (Table S1), and MC is defined according to Eq. 3B. (A) STICS analysis by Gaussian fitting of simulations that contain in-frame motion (IFM). Significant, nonmonotonically varying bias occurs for fast characteristic motion, MC > 1. (B) STICS analysis by Gaussian fitting of simulated movies that exclude in-frame motion. The nonmonotonically varying bias from (A) is still present at all values of MC considered, although the bias due to in-frame motion is removed. (C and D) The results of analyzing the same data as in (A) and (B), but determining the step size distribution variance in the STICS protocol by directly calculating the variance rather than by fitting the correlations to Gaussian functions. The combination of direct variance calculation and removal of in-frame motion in (D) removes the bias completely. To see this figure in color, go online.
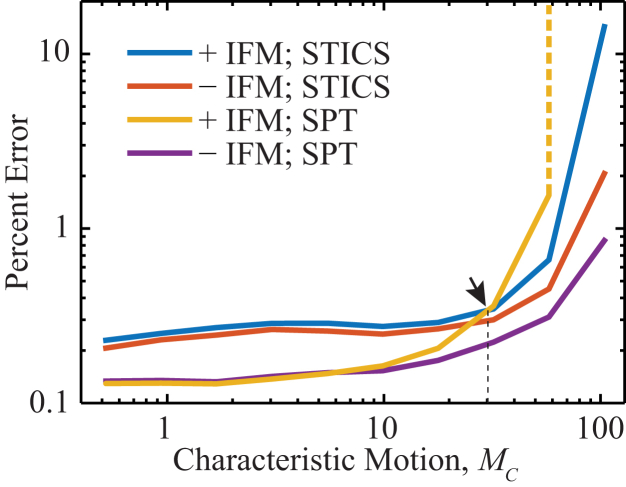
Figure 4.
Simulated movies (see text for parameters) of confined diffusion with and without in-frame motion were analyzed with the SPT and STICS methods to compare the precision of the two methods. The diffusion coefficient determination by STICS was done by direct calculation of the variance. SPT has higher precision at slow speeds, but becomes less precise for fast characteristic motion. The inclusion of in-frame motion causes the precision of SPT to become worse than that of STICS at MC ∼ 30 (arrow), which, for this parameter set, corresponds to a diffusion coefficient of 5.76 μm2 × s−1. The tenth data point of the yellow curve (SPT with in-frame motion) was infinite due to the data loss described in Fig. 1A; this singularity is indicated by a dashed vertical line beginning at the ninth data point. To see this figure in color, go online.
SPT analysis
Candidate molecular locations were found in simulated single-molecule movies by following a band-pass filter in the Fourier domain with a watershed algorithm. These positions were refined to the local center of mass within a 15 pixel × 15 pixel window. The refined locations were then used as the initial guess for a least-squares fit of the raw image of the molecule by a seven-parameter generalized bivariate Gaussian function using Matlab’s built-in function lsqcurvefit. The center of this fit was taken to be the position of the diffusing molecule. Because only a single molecule was present in our simulations at any time, the time series of localizations was used as the single-particle trajectory, with no need for a more advanced tracking algorithm. Infrequently, the analysis of a single-molecule image incorrectly indicated more than one molecule, in which case all putative molecules from that image were ignored. The MSDs for the first 15 possible time lags, τ, were then computed and these results were fit to a model for 1D confined diffusion inside an infinite square well (13):
| (2A) |
Here, L is the confinement length and B is a constant offset equal to the measurement variance of the position of an immobile molecule. Only the MSD curve computed in the direction of the cylinder long axis was considered, because with the diffusion coefficients considered here, the diffusing molecule may explore the entire short axis of the cell in a single frame. 1D motion was recovered from 2D position data by projection onto the long axis of the cell.
STICS analysis
For both simulated and experimental data, the full time-space correlation functions were computed using the Fourier transform method for convolutions, as described previously (17, 33). The width of the correlation function increases with time lag, and Gaussian fitting can estimate these widths. The time lag series of widths is called the iMSD, which for our model of square-confined diffusion (13) has the functional form
| (2B) |
Here, C is a constant offset proportional to the diameter of the image of the diffusing molecule. The sum was truncated after the change in the function value dropped below 10−10, a condition which was always satisfied with fewer than 10 terms. Only the iMSD curve computed from the cell long axis was considered, because for the fast diffusion coefficients considered here, the diffusing molecule explores the entire short axis of the cell in a single image frame. For the experimental bacterial cell data analysis, one iMSD curve was calculated for each of 87 movies, which had ∼4000 imaging frames each. The function iMSD(τ) was fit to Eq. 2B for the first 15 values of τ (with the Matlab function lsqcurvefit) to estimate the diffusion coefficient, D.
Each frame of the simulated movies was symmetrically padded to double the original width with a padding value of zero because the data were generated with zero intensity offset. For the experimental data, the phase contrast image of the bacterial cell was used to automatically compute, with a valley filter, a selection mask that describes the position of each bacterium. Pixels that fell outside of this mask were replaced with the mean intensity value inside the selection mask. Because the absolute offset of the real bacterial cell image is ill-defined or weakly measureable, the experimental bacterial cell data were padded with the average intensity value inside the cell.
Bacterial strains and growth conditions
DH5α E. coli cells containing a pBAD plasmid encoding the fluorescent protein mMaple3 under the arabinose promoter (37) were struck out from a freezer stock on a 1.5% Luria Bertani (LB)/agar plate containing 50 μg × mL−1 ampicillin and incubated overnight at 37°C. A single colony from the plate was used to inoculate 2 mL LB containing 50 μg × mL−1 ampicillin. This culture was incubated overnight (∼16 h) at 37°C with shaking. Following incubation, the culture was diluted 1:50 into M9 minimal medium containing 0.4% glycerol as the carbon source. The culture was incubated at 37°C with shaking to an optical density at 595 nm of ∼0.35, at which time mMaple3 expression was induced by adding arabinose to a final concentration of 0.01%. After induction, the culture was incubated at 37°C with shaking for an additional 2 h. Cells were pipetted onto a 2% agarose/M9/arabinose pad and inverted onto a plasma-etched coverslip for imaging, as previously described (38).
Alternatively, longer cells were grown by using cephalexin, a β-lactam antibiotic that blocks cell division but allows cell growth (39). Here, the overnight culture was diluted 1:100 into LB and incubated at 37°C with shaking to an optical density at 595 nm of ∼0.5. The culture was then centrifuged for 5 min at 5000 × g, the supernatant was decanted, and the cell pellet was resuspended in an equal volume of M9 medium containing 0.4% glycerol and 0.01% arabinose. Cephalexin was added to a final concentration of 60 μg × mL−1. The culture was then incubated at 37°C with shaking for an additional 30 min. Cells were pipetted onto a 2% agarose/M9/arabinose pad (which also contained 60 μg × mL−1 cephalexin) and inverted onto a plasma-etched coverslip for imaging.
Imaging conditions
Bacterial samples were imaged at room temperature using wide-field epifluorescence microscopy in an Olympus IX71 inverted microscope with a 100×, 1.40 NA oil immersion objective (in Immersol 518F immersion oil, Carl Zeiss, Oberkochen, Germany) and appropriate excitation, emission, and dichroic filters (LL01-561, BLP01-561, and Di01-R561, respectively, Semrock, Rochester, NY). After a 3× beam expander, a Photometrics (Tucson, AZ) Evolve EMCCD camera with >90% quantum efficiency captured the images at 25–100 frames/s. Each camera pixel corresponds to a 49 nm × 49 nm area of the sample. Fluorescence of mMaple3 in the cells was photoswitched from green to red photon emission using a 406 nm laser (Cube 406-100, Coherent, Santa Clara, CA), co-aligned with the 561 nm fluorescence excitation laser (Sapphire 560-50, Coherent). The samples were illuminated with low laser power densities (0.07 μW × μm−2 and 0.01 mW × μm−2 for the 406 nm illumination and the 561 nm illumination, respectively). Both laser beams were circularly polarized with a quarter waveplate (AO15Z 1/4 556 and AO15Z 1/4 408, respectively, Tower Optical, Boynton Beach, FL). During imaging, the cells were given a 1- to 10-ms dose of 406 nm light every ∼30 s. Movie acquisitions lasted 2–5 min each.
Due to the small (∼1 μm) cell thickness, a low background noise is maintained even when single-molecule imaging in bacteria cells is done with a wide-field microscopy configuration (40). Thus, this work describes the analysis of wide-field microscopy, though these methods could be readily applied to total internal fluorescence microscopy.
Theory
Characteristic motion, MC: a unit-free parameter describing the amount of in-frame motion and the extent of confinement
Because of the high dimensionality of the simulation parameter space, which includes, e.g., camera integration time, pixel size, and magnification, it is desirable to have an invariant description of the degree of in-frame motion. To this end, we renormalize the diffusion rate, D, to produce a unit-free characteristic motion parameter, MC. This MC simplifies the presentation of the simulation results and can highlight consistencies among parameter sets. MC is proportional to the squared distance, traveled in each captured image and inversely proportional to the variance of the point-spread function of the diffusing molecule (). For consistency among dimensionalities, the factor 2/d is applied, where d = 2 for 2D image data:
| (3A) |
For confined diffusion, doubling the confinement length, L, is equivalent to halving the RMS in-frame displacement value. In the case of confined diffusion, the unconfined characteristic motion, MC,unconfined, is therefore modified by a scaling factor that describes the degree of confinement, the unit-free factor :
| (3B) |
where L0 is a reference confinement length chosen here to be the average cell length, 3 μm.
In Figs. 2, 3, and 6, we rescale D based on the simulation parameters (Table S1 in the Supporting Material) according to these definitions of MC. The overlap seen in these figures demonstrates the validity of Eqs. 3A and 3B.
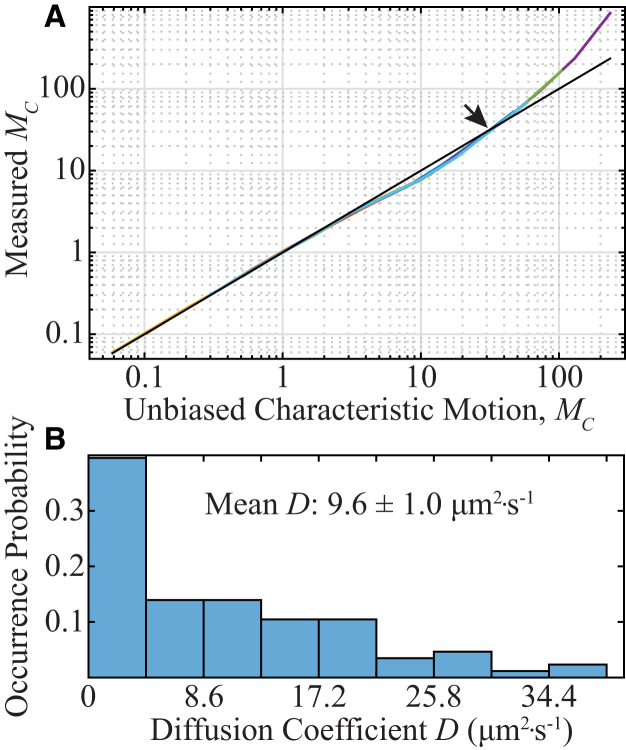
Figure 6.
Analysis of the diffusion coefficients of mMaple3 in 87 E. coli cells measured with STICS. (A) The measured MC may be converted to unbiased MC based on the simulations in Fig. 3A, which are used here to create a lookup table. The overlapping colored lines represent the same experimental parameter sets as in Fig. 3A (Table S1). The black line indicates 1:1 correspondence (no bias). (B) Histogram of the unbiased average mMaple3 diffusion coefficient measured in each of 87 different E. coli cells as estimated by the STICS method. Between 5 and 15 mMaple3 fluorescent proteins are photoswitched one at a time in each cell, and the biased measurements are corrected by cubic interpolation of the curve in (A). To see this figure in color, go online.
The effect of in-frame motion on STICS
In STICS, the correlation function, G, is the convolution of the step-size probability distribution, p, with WPSF, the approximately Gaussian microscope point-spread function (19):
| (4) |
Here, ξ and χ are displacements in x and y, respectively, for each time lag τ. N is the average number of molecules present in each frame and γ is a geometric factor that accounts for an underrepresentation of intensity fluctuations due to the illumination beam shape. The 2D step-size distribution, p, of unconfined Brownian diffusion is traditionally assumed to be normally distributed:
| (5) |
where d is the dimensionality and D is the diffusion coefficient. When Eq. 5 applies, G in Eq. 4 will be a Gaussian distribution, because it is the convolution of two Gaussians. However, when there is significant in-frame motion, the diffusing molecule will have moved a nonnegligible distance during the imaging integration time, . In this case of significant in-frame motion, the step-size distribution, p, is not only a function of the average time lag, ; p also depends on a range of effective time lags, , in the range of . This mixture of step sizes from nonidentical time lags causes p to become the sum of nonidentical normal distributions, and importantly, this p is not a normal distribution. When such in-frame motion is present, the correlation function, Gblur, is the convolution of the point-spread function with a weighted average of Gaussians:
| (6) |
Here, is a zero-mean normal distribution with variance and weighting factor . The point-spread function, WPSF, is an Airy Disk, which we approximate here by a Gaussian function (41).
The effect of confinement on STICS
To simulate confinement, we imposed reflective boundary conditions on the step-size distribution, p. In the limit of fast diffusion and small confinement, p approaches a uniform distribution. In general, if zero-flux boundary conditions are imposed on ξ and χ in the distribution, , which is a symmetric function centered on zero, then the correlation function, G, is modified:
| (7) |
Overall, the effect of Eqs. 6 and 7 is a deviation of the Gaussian function in Eq. 4 to a degree that depends directly on the amount of in-frame motion or confinement.
Estimation of the diffusion coefficient by direct calculation of the variance
According to Eq. 5, D is proportional to the variance of the step-size distribution, p. If p describes ideal free diffusion, then p is Gaussian-shaped. The correlation function, G, computed by STICS for this type of data would then also be Gaussian. However, G is not generally Gaussian due to in-frame motion and confinement, as described above. In its traditional implementation, STICS estimates the correlation-function variance, iMSD, as being the variance parameter of a least-squares fit of G to a Gaussian function. If G is not Gaussian, then fitting G to a Gaussian will not accurately measure the variance. In this case, the inaccuracy can be removed by directly computing the variance according to its definition:
| (8A) |
| (8B) |
Here, we consider in-plane diffusion in each of the two dimensions, x and y, separately. The marginal distributions Gξ and Gχ for displacements in x and y, respectively, are computed from the 2D correlation function, G, by discrete summation:
| (9A) |
| (9B) |
This separation allows diffusion along the long and short axes of bacterial cells to be treated independently. We fixed the orientation of the cylindrical boundary in the simulations to lie parallel to the x axis and directly calculated the variance for the simulated data. This direct variance calculation method was not used to estimate the iMSD of the experimental data, because the measurement precision was too low to be useful for this analysis, especially after the interpolation involved in image rotation.
It should be noted that this method for finding the variance requires the distribution, G, to be normalized at every value of τ. In general, however, the integral of G with respect to and is not unity for each time lag. In principle, this integral can be normalized by dividing it by the discrete integral of G or by dividing it by the known prefactor in Eq. 4. In our simulations, we ensured a priori that G was normalized at every τ by fixing .
Results and Discussion
Effect of in-frame motion on SPT
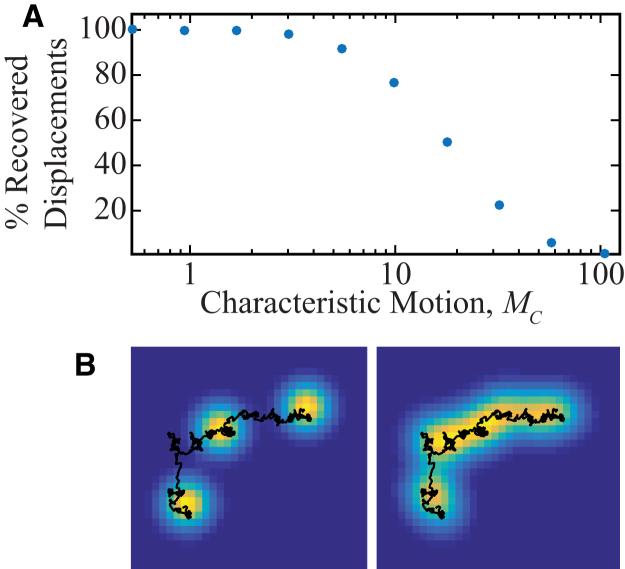
We simulated diffusion with 10 different values of D in 3-μm-long cylinders with reflective boundary conditions. These movies were processed by SPT, and the diffusion coefficient, D, for each trajectory was estimated from the MSDs. Each measured D was scaled to the corresponding unit-free characteristic motion, MC, according to Eq. 3B. Because not all single-molecule images could be fit in our regime of finite SNR, trajectories were truncated. We computed for each MC the percent recovered displacements, , where is the number of measured displacements that have a time lag of one frame and is the total number of frames in the simulated movie. The percent recovered displacements decreases as MC increases, and the number of recovered displacements approaches zero for large MC (Fig. 1).
Figure 1.
Motion blur degrades the single-particle tracking (SPT) signal as characteristic motion, MC, increases. Diffusion confined in a cylinder was simulated and analyzed with SPT. MC is defined according to Eq. 3B. (A) The percent of recovered data decreases with increasing MC. The pixel width is 49 nm, confinement length is L = 3 μm, integration time is tframe = 50 ms, and σPSF = 98 nm. (B) Representative simulated images of a diffusing molecule with three of the subframes (left) or all of the subframes (right) included in the image. The actual trajectory (black curve) is the same in both panels. To see this figure in color, go online.
In general, MC is proportional to D and tframe, and increasing either of these parameters increases the degree of in-frame motion of the diffusing molecule. Accordingly, Fig. 1 A indicates that increasing in-frame motion leads to decreased data recovery. Fig. 1 B compares simulations of the same trajectory (black line) with different amounts of in-frame motion. On the left side, the trajectory is sampled instantaneously at three distinct time points, producing three ideal point-spread functions (punctate yellow spots); the molecular positions at those time points can be determined from a Gaussian fitting algorithm. On the other hand, the right side shows the case when the trajectory is sampled continuously. Such in-frame motion can blur and distort the molecule image. Thus, when in-frame motion is dominant, this distortion prevents a Gaussian fitting algorithm from identifying molecular positions. Because SPT creates a trajectory from a series of single-molecule fits, such a failed fit decreases the percent recovered displacements. SPT, then, is a method that tolerates only subtle in-frame motion. In Fig. 1 A, <50% of the one-frame displacements are recoverable when MC is >20, even though 20 is a reasonable value for subcellular diffusion in a typical single-molecule microscope (40). For instance, MC = 20 could correspond to a molecule diffusing with a rate of 2.88 μm2/s measured with a microscope that has a point-spread function standard deviation of 98 nm, a camera integration time of 50 ms, and a pixel width of 49 nm in the object plane. Experimentally, in-frame motion can be minimized for even extremely fast diffusers with stroboscopic illumination (e.g., pulsed sample illumination with pulse widths that are shorter than tframe; Fig. 1 B, left panel) (17) or very high imaging frame rates (30).
Effect of in-frame motion on STICS
STICS has the potential to estimate the diffusion coefficient in the regime of large MC (i.e., significant image blurring) that precludes SPT analysis. However, a description of the accuracy and precision of this method are required to validate its use in this regime. To investigate the accuracy of STICS in different diffusion regimes, we first simulated unconfined, single-molecule diffusion with 10 diffusion coefficients between 0.1 μm2 × s−1 and 20 μm2 × s−1 (Fig. 2). Each diffusion coefficient was considered for tframe = 10 ms and 50 ms and for point-spread function standard deviations of σPSF = 49 nm, 98 nm, and 147 nm. No noise was included in this set of simulations. Per Eq. 3A, different combinations of these parameters can lead to the same degree of in-frame motion, so each measured diffusion coefficient, D, was converted to the corresponding value of the unit-free parameter MC. Simulated movies were analyzed by STICS, and the diffusion-coefficient measurement bias, , is plotted as a function of MC in Fig. 2 A. According to Fig. 2 A, STICS very accurately estimates D at low MC, but overestimates the diffusion coefficient as MC increases. This positive measurement bias increases monotonically with increasing in-frame motion, with a bias of ∼10% when . The measurement bias for each set of parameters (tframe, σPSF) was assigned a unique color in Fig. 2 A (Table S1). The different color sets overlap and show the same trend, demonstrating that the characteristic motion, MC in Eq. 3A, is indeed the right variable for considering diffusion at different rates under different experimental conditions.
We generated the images of a diffusing fluorescent molecule with in-frame motion analyzed in Fig. 2 A from a series of images of a stationary molecule that diffuses between subframes (Fig. 1 B, right panel). We hypothesized that the measurement bias in Fig. 2 A can be attributed to in-frame motion because this bias disappears when MC is small. To examine the role of in-frame motion, we excluded this motion from the simulation by excluding all subframes but the first in each image (Fig. 1 B, left panel). We repeated STICS analysis on this stroboscopic data set, which is free of in-frame motion (Fig. 2 B), and found that the measurement bias is removed when no in-frame motion is allowed. Thus, the bias in Fig. 2 A is attributed to in-frame motion.
For the conventional STICS analysis in Fig. 2, A and B, the correlation function variance is estimated as the variance parameter of a fit to a Gaussian function (18). Although curve fitting to the correlation function is a powerful method of increasing the diffusion coefficient measurement precision, as described in the Theory section, in the case of in-frame motion, the step sizes will not be normally distributed. Therefore, we hypothesized that the diffusion coefficient measurement bias in Fig. 2 A comes from fitting a non-Gaussian correlation function to a Gaussian fitting function. We therefore calculated the correlation function variances directly instead of by a fit to a Gaussian (Eq. 8). The measurement biases from this method are shown in Fig. 2, C and D, for simulated data with and without in-frame motion, respectively. This direct variance calculation allows for bias-free measurements of the diffusion coefficient even when in-frame motion is included in the simulated movies (compare Fig. 2, A and C). The bias due to in-frame motion in Fig. 2 A is therefore the result of fitting STICS correlation functions to a fit function that incorrectly assumes an absence of in-frame motion, and the discrepancy in shape between the actual correlation function and this assumed Gaussian function increases with increasing in-frame motion.
Effect of confinement on STICS
In addition to the artifacts that arise from fitting fast diffusion to the wrong function in the STICS method (Fig. 2 A), we hypothesized that confinement also gives rise to a diffusion-coefficient measurement bias in the case of fast-diffusing molecules (high MC). We considered the diffusion of a fluorescent molecule in the cytoplasm of a bacterial cell by simulating diffusion of a molecule in cylinders of diameter 1 μm and lengths L = 2, 3, and 4 μm with 10 diffusion coefficients between 0.1 μm2 × s−1 and 20 μm2 × s−1. We considered that tframe = 10 and 50 ms, and σPSF was 98 nm. No noise was included in this set of simulations. In Fig. 3, each set of parameters is scaled to the unit-free parameter MC as described in Eq. 3B.
Conventional STICS analysis of these simulations of confined motion (Fig. 3 A) revealed a large, nonmonotonically varying bias when , with biases as large as 50% for . This effect persists even when in-frame motion is eliminated from the simulations (Fig. 3 B) by excluding all subframes but the first in each image, as described in Fig. 2 B. Comparing Fig. 3, A and B, (see Fig. S1 A) indicates that in-frame motion does contribute slightly to the bias in Fig. 3 A, but the persistence of a significant bias in Fig. 3 B indicates that the effect of in-frame motion is minimal relative to the effect of confinement on the measurement bias.
We hypothesized that this confinement artifact arose from using an incorrect fit function to determine the correlation-function variance. To circumvent this fit function, the correlation-function variances were calculated directly, as for Fig. 2, C and D. Again, the direct variance calculation allows a bias-free measurement of D: directly calculating the variance in this manner removed nearly all of the measurement bias for simulated data even with in-frame motion (Fig. 3 C). The fact that direct variance calculation can remove the large biases in estimation of D indicates that, as was true for in-frame motion (Fig. 2 A), confinement leads to a large discrepancy between the assumed normal step size distribution (Eq. 1) and the actual observed distribution. As confinement (and therefore MC) increases, a Gaussian fitting function no longer correctly describes the STICS correlation function, and the resulting bias increases with increasing MC (Fig. S1 B). There remains in Fig. 3 C a large positive bias at large MC that is caused by in-frame motion and is removed upon excluding in-frame motion (Fig. 3 D).
Comparing the precision of STICS and SPT
Given the protocol established above to remove measurement bias artifacts from STICS analysis through direct calculation of the variance, we next considered the measurement errors incurred in estimating single-molecule diffusion coefficients by either STICS or SPT in the presence of realistic noise and experimental parameters. We examined the ability of STICS to precisely determine D in simulated 1200-frame movies of a fluorescent molecule diffusing inside a cylinder of diameter 1 μm and L = 3 μm, with SNR = 6, σPSF = 98 nm, tframe = 50 ms, and 10 diffusion coefficients between 0.1 μm2 × s−1 and 20 μm2 × s−1. In Fig. 4, the percent error in the determination of the diffusion coefficient is plotted as a function of MC (as defined in Eq. 3B). STICS and SPT analysis are performed on two identical data sets: movies simulated with and without in-frame motion. For minimal in-frame motion and minimal confinement (small MC), the precision of SPT is higher than that of STICS. Yet, when (Fig. 4, arrow), in-frame motion causes SPT (yellow curve) to be significantly less precise than STICS (blue curve). This is consistent with the data loss during tracking (Fig. 1 A). However, in the absence of in-frame motion, SPT outperforms STICS under all experimental conditions considered in this work. The error in determining D for both methods increases with increasing MC, because the effective SNR of each simulated image decreases with increasing MC, as is the case when the number of photons emitted by a molecule is kept constant, but these are spread over more pixels due to image blur.
By directly considering the correlation-function variance rather than assuming a Gaussian functional form for this distribution, the diffusion of even fast-moving, highly confined molecules can be estimated with STICS. Indeed, because of in-frame motion, when , one can no longer track diffusing molecules at all with SPT (Fig. 4, yellow curve), whereas STICS can still determine the diffusion coefficient with <1% error. Overall, Fig. 4 can indicate the appropriate analytical method for a given single-molecule diffusion measurement based on the experimental parameters.
Cytosolic mMaple3 diffusion in E. coli
Although single-molecule imaging has successfully answered a host of questions in cell biology (40, 42, 43, 44), one current challenge is a limited ability to characterize the dynamics of the fastest molecules—especially when confinement precludes stroboscopic illumination—for instance, freely diffusing proteins in the bacterial cytoplasm (5). We imaged E. coli cells expressing the photoswitchable fluorescent protein mMaple3, which is switched from a green state to a red state upon activation with 406-nm light (37). Before activation, the cells were nonfluorescent (Fig. S3 B). We exposed the cells to 406-nm laser pulses to photoswitch one mMaple3 molecule at a time (Fig. S3 C), and we sequentially imaged dozens of mMaple3 molecules in each of 87 different cells. The cells were imaged in the red channel (imaging wavelength, 561 nm) with tframe = 40 ms, σPSF = 98 nm, and pixel width = 49 nm (Fig. S3; Movie S1). We measured the cell lengths, which varied from 1 to 10 μm. Single-molecule photoswitching was evident as the average fluorescence intensity of the cell increased after each photoswitching pulse and decreased a short time later due to photobleaching, but the large degree of in-frame motion due to the fast diffusion prevented single molecules from being visualized as punctate fluorescent spots and localized with Gaussian fitting in the majority of the images. This is consistent with the low data recovery rate for simulations of molecules with high MC in Fig. 1 A.The diffusion of free mMaple3 under these conditions could therefore not be analyzed by SPT. Although the method of direct variance determination removes the systematic error (compare Figs. 2 C and 3 C to Figs. 2 A and 3 A) and explains the source of the bias, this method has extremely low precision (Fig. S2, light blue and green curves). This approach is therefore not used to analyze the experimental results that follow.
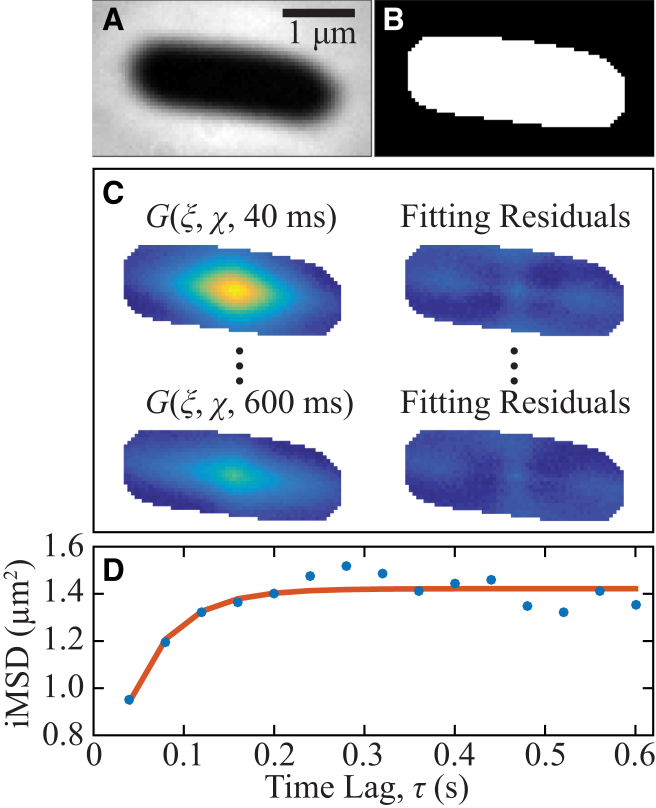
Fig. 5 illustrates our implementation of Gaussian-fitting STICS for one representative cell (L = 3.1 μm). A phase-contrast image of the cell (Fig. 5 A) provided the boundaries for a cell mask (Fig. 5 B), and a single iMSD curve was compiled for each cell’s axial dimension based on Gaussian fits to the correlation function within this mask (Fig. 5 C). Each iMSD was fit to the square-confined diffusion model in Eq. 2B to estimate the coefficient of diffusion of mMaple3 in that cell (Fig. 5 D). Gaussian fitting was used to calculate the iMSD with increased precision in our experimental regime of relatively noisy data. Also, because transverse and longitudinal diffusion must be considered independently, here, due to the different confinement lengths in the two directions, the correlation-function variances cannot be calculated directly without interpolating the raw data onto a rotated pixel array, which would impose additional errors.
Figure 5.
Analysis procedure for estimating by STICS the diffusion coefficient of free cytosolic mMaple3 inside a single E. coli cell. (A) A phase contrast image of the E. coli cell provides (B) a mask of the cell location and orientation. (C) The STICS correlation function is computed and then fit to a Gaussian function, G. The phase mask in (B) includes only the correlation amplitudes that correspond to displacements inside the cell. (D) The long-axis variances of the Gaussian fits to the correlation functions (iMSD) were plotted as a function of time lag, τ (dots), and this iMSD curve was fit to a model for square-confined diffusion (Eq. 2B; red curve) to obtain a single diffusion coefficient measurement for each cell. To see this figure in color, go online.
We analyzed 87 unique bacterial cells and used the small molecule cephalexin to generate cells with L = 1–10 μm. The effect of cephalexin on the diffusion of mMaple3 in the cytoplasm of E. coli is expected to be minimal (12). The simulations described in Fig. 3 A indicate the biases that are expected, and the expected bias from Fig. 3 A can be used to convert biased experimental diffusion measurement made with Gaussian-fitting STICS to the corresponding unbiased value (Fig. 6 A). For instance, in the example of the representative cell in Fig. 5, Gaussian-fitting STICS measured D = 5.20 μm2 × s−1 in a cell with L = 2.41 μm. This measurement was taken with σPSF = 98 nm, tframe = 40 ms, and pixel width = 49 nm, so Eq. 3B gives , for which value Fig. 3 A predicts a bias of −0.01 (Fig. 6 A, arrow). Interestingly, for the representative cell in Fig. 5 (), the measured D (5.20 μm2 × s−1) is converted to an unbiased D of 5.15 μm2 × s−1; i.e., Gaussian-fitting STICS produces a nearly unbiased estimate of D for the amount of in-frame motion and confinement in this regime.
Based on the interpolated curve in Fig. 6 A, all D measurements were converted to unbiased D, and Fig. 6 B shows a histogram of the average diffusion-coefficient estimates for single mMaple3 molecules in each of the 87 different E. coli cells. The unbiased mean diffusion coefficient of 9.6 ± 1.0 μm2 × s−1 agrees with the range of free protein diffusion inside the cytoplasm of E. coli reported elsewhere (30, 45), indicating that Gaussian-fitting STICS is an appropriate analysis method for obtaining the average D of a cytoplasmic fluorescent protein in E. coli. We found no correlation between the measured D and L, indicating that the degree of confinement did not strongly affect our measurements (Fig. S4). Overall, these experiments demonstrate that the diffusion of fluorescent molecules in small volumes with a significant amount of in-frame motion that precludes SPT can be characterized by the STICS method.
Conclusions
In this study, we have extended STICS to the regime of rapidly moving molecules in highly confined environments by considering the motion of freely diffusing fluorescent proteins inside living E. coli bacterial cells. In this regime, such fast, confined motion can still be characterized with negligible bias, although we have also identified regimes where fast, confined motion results in a significant bias in diffusion-coefficient measurement by STICS. Simulations of this bias indicate that it stems from a STICS correlation function that is not well approximated by a Gaussian function (Figs. 2 A and 3 A); this bias increases with increasing diffusion coefficient, D, and increasing confinement, L−2, as described here by the unit-free parameter characteristic motion (MC). Thus, when MC becomes large due to in-frame motion or confinement, Gaussian-fitting STICS is a biased method for estimating the diffusion coefficient. Interestingly, this bias can be removed by directly calculating the variances of the correlation function rather than estimating the variance by Gaussian fitting (Figs. 2 C and 3 C), and we provide an analytical description of this process. Furthermore, because this unbiased direct calculation of the correlation function variances is less precise than Gaussian fitting and therefore not desirable for the treatment of noisy experimental data, the simulations described in this article provide a way to remove the bias when Gaussian-fitting STICS is used. In particular, the plot of measured MC versus unbiased MC in Fig. 6 A, together with the definition of MC in Eq. 3B, provides a look-up table for all experimental parameter sets in future experiments where in-frame motion and confinement causes Gaussian-fitting STICS to measure a biased value of MC. In this way, some of the precision of Gaussian-fitting STICS is preserved while the measurement bias is eliminated. Still, in the future, it would be desirable to solve Eqs. 6 and 7 and replace the Gaussian fit function entirely with a more accurate description of a correlation function computed from a movie of a highly confined diffusing fluorescent molecule that exhibits in-frame motion; that is beyond the scope of this work.
Overall, Fig. 4 illustrates one of the primary strengths of STICS: when , in-frame motion dominates and SPT fails entirely to estimate the diffusion coefficient because of data loss, as shown in Fig. 1 A. Thus, although the experimental data in Figs. 5 and 6 were not analyzable by SPT, diffusion coefficients were still recovered by STICS. Based on this article, independent researchers in single-molecule fields should be able to determine the value of characteristic motion in their experiments and decide which analysis method (STICS or SPT) produces the most precise or least biased estimate of the diffusion coefficient for the relevant experimental regime. This decision can be made based on performance or pragmatism: for instance, the timing and optics of stroboscopic illumination can be difficult to implement, especially in commercial single-molecule instruments, and current EMCCD camera technology requires a very small imaging area for the highest accessible frame rates. The relative precision of STICS compared to SPT at large MC makes STICS a promising and facile method for the estimation of diffusion coefficients in experimental measurements of fast diffusion that is confined within small cells and organelles, within nanomaterials, and in any other highly confined system where the imaging camera frame rate is longer than the time that the molecule takes to explore the confinement volume.
Author Contributions
D.J.R. and J.S.B. designed the research. D.J.R. performed the simulations. H.H.T. performed the experiments. D.J.R. analyzed the data. D.J.R., H.H.T., and J.S.B. discussed all the results. D.J.R. wrote the article, which was edited by all authors. All authors read and approved the final manuscript.
Acknowledgments
Thanks to Xiaowei Zhuang for generously providing the mMaple3 plasmid. Thanks also to Sarah Veatch and Matthew Stone for insightful discussions.
The authors were supported by funding from a Burroughs Wellcome Career Award at the Scientific Interface (to J.S.B.) and by National Science Foundation grant DB-1306434 (to H.H.T.).
Editor: Paul Wiseman.
Footnotes
Four figures, one table, Matlab codes, and one movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30218-1.
Supporting Material
To visualize single molecules, a low-power 406-nm laser (shown in the movie as a flash in the background) was used to photoswitch 0–1 copies of mMaple3 per cell at a time. Two frames from this movie are presented in Fig. S3, B and C. The imaging rate was 25 frames/s, and the movie area is 2.50 μm × 3.14 μm.
References
- 1.Nienhaus K., Nienhaus G.U. Fluorescent proteins for live-cell imaging with super-resolution. Chem. Soc. Rev. 2014;43:1088–1106. doi: 10.1039/c3cs60171d. [DOI] [PubMed] [Google Scholar]
- 2.Rust M.J., Bates M., Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat. Methods. 2006;3:793–795. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Betzig E., Patterson G.H., Hess H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 4.Hess S.T., Girirajan T.P., Mason M.D. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys. J. 2006;91:4258–4272. doi: 10.1529/biophysj.106.091116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Haas B.L., Matson J.S., Biteen J.S. Single-molecule tracking in live Vibrio cholerae reveals that ToxR recruits the membrane-bound virulence regulator TcpP to the toxT promoter. Mol. Microbiol. 2015;96:4–13. doi: 10.1111/mmi.12834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Uphoff S., Reyes-Lamothe R., Kapanidis A.N. Single-molecule DNA repair in live bacteria. Proc. Natl. Acad. Sci. USA. 2013;110:8063–8068. doi: 10.1073/pnas.1301804110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hammar P., Walldén M., Elf J. Direct measurement of transcription factor dissociation excludes a simple operator occupancy model for gene regulation. Nat. Genet. 2014;46:405–408. doi: 10.1038/ng.2905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sanamrad A., Persson F., Elf J. Single-particle tracking reveals that free ribosomal subunits are not excluded from the Escherichia coli nucleoid. Proc. Natl. Acad. Sci. USA. 2014;111:11413–11418. doi: 10.1073/pnas.1411558111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Karunatilaka K.S., Cameron E.A., Biteen J.S. Superresolution imaging captures carbohydrate utilization dynamics in human gut symbionts. mBio. 2014;5:e02172-14. doi: 10.1128/mBio.02172-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Axelrod D., Koppel D.E., Webb W.W. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 1976;16:1055–1069. doi: 10.1016/S0006-3495(76)85755-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sochacki K.A., Shkel I.A., Weisshaar J.C. Protein diffusion in the periplasm of E. coli under osmotic stress. Biophys. J. 2011;100:22–31. doi: 10.1016/j.bpj.2010.11.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Elowitz M.B., Surette M.G., Leibler S. Protein mobility in the cytoplasm of Escherichia coli. J. Bacteriol. 1999;181:197–203. doi: 10.1128/jb.181.1.197-203.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kusumi A., Sako Y., Yamamoto M. Confined lateral diffusion of membrane receptors as studied by single particle tracking (nanovid microscopy). Effects of calcium-induced differentiation in cultured epithelial cells. Biophys. J. 1993;65:2021–2040. doi: 10.1016/S0006-3495(93)81253-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lill Y., Kaserer W.A., Ritchie K. Single-molecule study of molecular mobility in the cytoplasm of Escherichia coli. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;86:021907. doi: 10.1103/PhysRevE.86.021907. [DOI] [PubMed] [Google Scholar]
- 15.Saxton M.J., Jacobson K. Single-particle tracking: applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 1997;26:373–399. doi: 10.1146/annurev.biophys.26.1.373. [DOI] [PubMed] [Google Scholar]
- 16.Donehue J.E., Wertz E., Biteen J.S. Plasmon-enhanced brightness and photostability from single fluorescent proteins coupled to gold nanorods. J. Phys. Chem. C Nanomater. Interfaces. 2014;118:15027–15035. [Google Scholar]
- 17.Elf J., Li G.-W., Xie X.S. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hebert B., Costantino S., Wiseman P.W. Spatiotemporal image correlation spectroscopy (STICS) theory, verification, and application to protein velocity mapping in living CHO cells. Biophys. J. 2005;88:3601–3614. doi: 10.1529/biophysj.104.054874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Di Rienzo C., Gratton E., Cardarelli F. Fast spatiotemporal correlation spectroscopy to determine protein lateral diffusion laws in live cell membranes. Proc. Natl. Acad. Sci. USA. 2013;110:12307–12312. doi: 10.1073/pnas.1222097110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Petersen N.O., Höddelius P.L., Magnusson K.-E. Quantitation of membrane receptor distributions by image correlation spectroscopy: concept and application. Biophys. J. 1993;65:1135–1146. doi: 10.1016/S0006-3495(93)81173-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pozzi D., Marchini C., Caracciolo G. Mechanistic understanding of gene delivery mediated by highly efficient multicomponent envelope-type nanoparticle systems. Mol. Pharm. 2013;10:4654–4665. doi: 10.1021/mp400470p. [DOI] [PubMed] [Google Scholar]
- 22.Brown C.M., Hebert B., Wiseman P.W. Probing the integrin-actin linkage using high-resolution protein velocity mapping. J. Cell Sci. 2006;119:5204–5214. doi: 10.1242/jcs.03321. [DOI] [PubMed] [Google Scholar]
- 23.Kolin D.L., Ronis D., Wiseman P.W. k-Space image correlation spectroscopy: a method for accurate transport measurements independent of fluorophore photophysics. Biophys. J. 2006;91:3061–3075. doi: 10.1529/biophysj.106.082768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Abu-Arish A., Pandzic E., Wiseman P.W. Cholesterol modulates CFTR confinement in the plasma membrane of primary epithelial cells. Biophys. J. 2015;109:85–94. doi: 10.1016/j.bpj.2015.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kisley L., Brunetti R., Landes C.F. Characterization of porous materials by fluorescence correlation spectroscopy super-resolution optical fluctuation imaging. ACS Nano. 2015;9:9158–9166. doi: 10.1021/acsnano.5b03430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hendrix J., Baumgärtel V., Lamb D.C. Live-cell observation of cytosolic HIV-1 assembly onset reveals RNA-interacting Gag oligomers. J. Cell Biol. 2015;210:629–646. doi: 10.1083/jcb.201504006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Digman M.A., Sengupta P., Gratton E. Fluctuation correlation spectroscopy with a laser-scanning microscope: exploiting the hidden time structure. Biophys. J. 2005;88:L33–L36. doi: 10.1529/biophysj.105.061788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Semrau S., Schmidt T. Particle image correlation spectroscopy (PICS): retrieving nanometer-scale correlations from high-density single-molecule position data. Biophys. J. 2007;92:613–621. doi: 10.1529/biophysj.106.092577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Digman M.A., Brown C.M., Gratton E. Measuring fast dynamics in solutions and cells with a laser scanning microscope. Biophys. J. 2005;89:1317–1327. doi: 10.1529/biophysj.105.062836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bakshi S., Bratton B.P., Weisshaar J.C. Subdiffraction-limit study of Kaede diffusion and spatial distribution in live Escherichia coli. Biophys. J. 2011;101:2535–2544. doi: 10.1016/j.bpj.2011.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Deville S., Penjweini R., Ameloot M. Intracellular dynamics and fate of polystyrene nanoparticles in A549 Lung epithelial cells monitored by image (cross-) correlation spectroscopy and single particle tracking. Biochim. Biophys. Acta. 2015;1853:2411–2419. doi: 10.1016/j.bbamcr.2015.07.004. [DOI] [PubMed] [Google Scholar]
- 32.Chiu C.L., Aguilar J.S., Digman M.A. Nanoimaging of focal adhesion dynamics in 3D. PLoS One. 2014;9:e99896. doi: 10.1371/journal.pone.0099896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Storti B., Di Rienzo C., Beltram F. Unveiling TRPV1 spatio-temporal organization in live cell membranes. PLoS One. 2015;10:e0116900. doi: 10.1371/journal.pone.0116900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Meucci S., Travagliati M., Cecchini M. Tubeless biochip for chemical stimulation of cells in closed-bioreactors: anti-cancer activity of the catechin-dextran conjugate. RSC Adv. 2014;4:35017–35026. [Google Scholar]
- 35.Moerner W.E., Fromm D.P. Methods of single-molecule fluorescence spectroscopy and microscopy. Rev. Sci. Instrum. 2003;74:3597–3619. [Google Scholar]
- 36.Liao Y., Yang S.K., Biteen J.S. Heterogeneous single-molecule diffusion in one-, two-, and three-dimensional microporous coordination polymers: directional, trapped, and immobile guests. Nano Lett. 2012;12:3080–3085. doi: 10.1021/nl300971t. [DOI] [PubMed] [Google Scholar]
- 37.Wang S., Moffitt J.R., Zhuang X. Characterization and development of photoactivatable fluorescent proteins for single-molecule-based superresolution imaging. Proc. Natl. Acad. Sci. USA. 2014;111:8452–8457. doi: 10.1073/pnas.1406593111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Haas B.L., Matson J.S., Biteen J.S. Imaging live cells at the nanometer-scale with single-molecule microscopy: obstacles and achievements in experiment optimization for microbiology. Molecules. 2014;19:12116–12149. doi: 10.3390/molecules190812116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Greenwood D., O’Grady F. The comparative performance of β-lactam antibiotics against ampicillin sensitive Escherichia coli in conditions simulating those of the infected urinary bladder. Br. J. Exp. Pathol. 1974;55:245–250. [PMC free article] [PubMed] [Google Scholar]
- 40.Tuson H.H., Biteen J.S. Unveiling the inner workings of live bacteria using super-resolution microscopy. Anal. Chem. 2015;87:42–63. doi: 10.1021/ac5041346. [DOI] [PubMed] [Google Scholar]
- 41.Thompson R.E., Larson D.R., Webb W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Persson F., Barkefors I., Elf J. Single molecule methods with applications in living cells. Curr. Opin. Biotechnol. 2013;24:737–744. doi: 10.1016/j.copbio.2013.03.013. [DOI] [PubMed] [Google Scholar]
- 43.Cattoni D.I., Fiche J.B., Nöllmann M. Single-molecule super-resolution imaging in bacteria. Curr. Opin. Microbiol. 2012;15:758–763. doi: 10.1016/j.mib.2012.10.007. [DOI] [PubMed] [Google Scholar]
- 44.Xia T., Li N., Fang X. Single-molecule fluorescence imaging in living cells. Annu. Rev. Phys. Chem. 2013;64:459–480. doi: 10.1146/annurev-physchem-040412-110127. [DOI] [PubMed] [Google Scholar]
- 45.Lill Y., Kaserer W.A., Ritchie K. Single-molecule study of molecular mobility in the cytoplasm of Escherichia coli. Phys. Rev. E. 2012;86:021907. doi: 10.1103/PhysRevE.86.021907. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
To visualize single molecules, a low-power 406-nm laser (shown in the movie as a flash in the background) was used to photoswitch 0–1 copies of mMaple3 per cell at a time. Two frames from this movie are presented in Fig. S3, B and C. The imaging rate was 25 frames/s, and the movie area is 2.50 μm × 3.14 μm.