Abstract
The fusion of lipid membranes is a key process in biology. It enables cells and organelles to exchange molecules with their surroundings, which otherwise could not cross the membrane barrier. To study such complex processes we use simplified artificial model systems, i.e., an optical fusion assay based on membrane-coated glass spheres. We present a technique to analyze membrane-membrane interactions in a large ensemble of particles. Detailed information on the geometry of the fusion stalk of fully fused membranes is obtained by studying the diffusional lipid dynamics with fluorescence recovery after photobleaching experiments. A small contact zone is a strong obstruction for the particle exchange across the fusion spot. With the aid of computer simulations, fluorescence-recovery-after-photobleaching recovery times of both fused and single-membrane-coated beads allow us to estimate the size of the contact zones between two membrane-coated beads. Minimizing delamination and bending energy leads to minimal angles close to those geometrically allowed.
Introduction
Membrane fusion events triggered by specialized proteins are not only essential for intracellular trafficking, viral infection, and neurotransmitter release, but also play a pivotal role in embryogenesis, i.e., tissue formation and pathogenesis (1, 2). Generally, fusion of two adjacent membranes requires lowering of the free energy barrier by concerted action of proteins in the context of an overall exergonic reaction. While viral fusion through trimer-of-hairpins formation and neurotransmitter release mediated by SNARE proteins is considerably well understood, extracellular cell-cell fusion is much less investigated. Apart from the largely unknown set of molecules participating in cell-cell fusion, the role of the cytoskeleton is of particular interest in many studies. Major dynamic remodeling of the actomyosin cortex is required to accommodate the cell shape changes involved in cell-cell fusion. The actomyosin cortex attaches to the inner leaflet of the plasma membrane and thereby prohibits fusion pore formation by a free energy penalty to delaminate membrane from the cortex. Plasma membranes are generally subjected to a lateral tension largely generated by this membrane-cytoskeleton adhesion. Chen et al. (3) found that formation of fusion pores is accompanied by disassembly of the actin cortex below the pores. Fusion pores usually develop over the entire contact zone and the increase of the pore size provides the most prominent energy barrier. Along these lines, severing the actin cytoskeleton by administration of Latrunculin A accelerates pore formation considerably.
Conversely, the actin-filament-crosslinking reagents jasplakinolide or phalloidin inhibit cell-cell fusion by slowing down pore growth. In other studies employing electroporation, a local accumulation of actin bundles was observed driving syncytium formation by active expansion of fusion pores (4). In contrast to vesicle fusion that is presumably facilitated by release of lateral tension stored in the plasma membrane, fusion pore expansion between cells requires partial removal of the actin cortex. The important question remains what actually drives the pore expansion that obviously requires a persistent energy input. Chernomordik and Kozlov (5) suggest that a negative line tension might lead to an increase in circumference due to relaxation of bending energy once fusion is initiated. It is conceivable that cells actively—by means of energy consumption—control expansion of fusion pore through membrane-bending proteins. To devise a far less complex model system to study fusion pore development, we used silica beads coated with phospholipid bilayers that are doped with fusogenic peptides. The system mimics the situation where the plasma membrane is attached to the cytoskeleton via linkers such as those from the ezrin-radixin-moesin family. In view of the inhibitory role of the actin cytoskeleton on formation of large fusion pores, it is important to understand the energetics of fusion in the context of a support connected to the lipid bilayer.
Previously, we could show that membrane-coated beads are excellently suitable to document fusion events mediated by coiled-coil peptides (6). The use of monodisperse silica beads as a support for lipid bilayers solves problems associated, for instance, with membrane undulations, light scattering, and excessive labeling with fluorophores because the beads can also be detected and identified through their size in bright field microscopy. To fuse the membranes, we used the well-established fusogenic E-peptides (i-E3Cys) and K-peptides (i-K3Cys) coupled to a lipid anchor MCC-DOPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[4-(p-maleimidomethyl)cyclohexane-carboxamide]), which is embedded in the deposited bilayer. These peptides are known to form heterodimeric coiled-coil structures, which foster docking between two lipid bilayers and eventually facilitate membrane fusion (7, 8). We showed that docking, hemifusion, and full fusion of the membrane coats are observable and easily distinguished. We found that, after full fusion, the membrane is continuously covering both beads. This inevitably requires the membrane to partially lift off from the substrate but it is unclear how far this delamination of the bilayer proceeds to enable fusion. Besides delamination of the bilayer from the silica substrate, the bilayer is bent in the contact zone, forming essentially a toroidal-like shape that also costs energy depending on the amount of spontaneous curvature. A higher degree of delamination reduces the bending penalty substantially, and vice versa. These two energy contributions govern the size and geometry of the contact zone between two beads. Eventually, compensation of the required free energy changes to delaminate and bend the membranes is needed. The system needs to gain a considerable amount of free energy from fusion.
In contrast to vesicle fusion assays, the overall driving force for fusion cannot be drawn from release of bending energy; i.e., two vesicles fuse to become one, and thereby release ∼500 kBT of bending energy. The gain in energy originates predominately from van der Waals interactions that increase if the two beads come into closer contact by removing the membrane material from the contact zone. Here, we used fluorescence recovery after photobleaching (FRAP) experiments paired with Monte Carlo simulations of the recovery process to infer the precise geometry of the contact zone of fused membranes covering a bead pair. Fluorescence recovery on fused bead pairs is significantly slowed down compared to the fluorescence recovery on single beads, for purely geometric reasons. The lipids have to cross the contact zone and the smaller this becomes, the slower the recovery. Conversely, this finding offers us a route to estimate the size of the contact zone by measuring the recovery time. We also relate our findings to free energy estimations to obtain a plausible model for membrane fusion of supported bilayers and thereby obtain a robust determination of the possible shape of the membrane in the contact zone after fusion.
Materials and Methods
Materials
All lipids were used as purchased: DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine), DOPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine), and MCC-DOPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[4-(p-maleimidomethyl)cyclohexane-carboxamide]) from Avanti Polar Lipids (Alabaster, AL); Texas Red DPPE (1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, triethylammonium salt) and Oregon Green 488 DPPE (1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine) from Life Technologies (Carlsbad, CA); and cholesterol (3β-hydroxy-5-cholestene) from Sigma-Aldrich (St. Louis, MO). Atto390-DOPE, Atto488-DOPE, and Atto655-DPPE were from ATTO-TEC (Siegen, Germany). Monodispersed silica beads with a diameter of 6.5 μm were purchased from Bang Laboratories (Fisher, IN), and used as received. Glass bottom petri dishes with a dish size of 35 mm and a 14 mm bottom well (glass 0.16–0.19 mm) from In Vitro Scientific (Sunnyvale, CA) were coated with casein from bovine milk (Sigma-Aldrich) to inhibit membrane spreading of the membrane-coated silica beads on the glass surface of the petri dish.
Buffers
Phosphate buffer (50 mM Na2HPO4, pH 6.8) was used to introduce ions into the buffer solution reducing Brownian motion of the silica beads on the glass surface. The buffer was filtered with a 0.2-μm cellulose acetate filter from Sartorius Stedim Biotech (Göttingen, Germany) and degassed. Pure, deionized water was obtained by using a Milli-Q Advantage A10 Ultrapure Water Purification System from Merck Millipore (Darmstadt, Germany).
Lipopeptides
Peptides forming heterodimeric coiled-coil structures were synthesized as described in Pähler et al. (8) and Marsden et al. (9). The amino-acid sequences are: acetyl-(EIAALEK)3-GWGGGC-amide (E3Cys) and acetyl-WG-(KIAALKE)3-GGGGC-amide (K3Cys). These peptides contain a thiol group at the cysteine that reacts with the maleimide group of the lipid headgroup by Michael addition. Covalent binding of the peptide (7 nmol; Eq. 1) was achieved by reacting the peptide with MCC-DOPE (Eq. 1) in n,n-dimethylformamide (7 mL) with a few drops of diisopropylamine (Sigma-Aldrich). The organic solvents were removed in vacuum and the lipopeptides were dissolved in a mixture of chloroform/methanol (2:1) to a final concentration of 10 mg mL−1. The lipopeptides were analyzed by electrospray-ionization mass spectrometry (E3Cys-MCCDOPE: 3882 m z−1 [M+], K3Cys-MCCDOPE: 3827 m z−1 [M+]). Additionally, cholesterol-PEG12-E4 and cholesterol-PEG12-K4 were used to induce membrane fusion between the silica beads (10, 11, 12, 13).
Lipid composition
The lipid compositions of all FRAP experiments were DOPC/DOPE/Chol/TexasRed DPPE/lipopeptide (50:24:24:1:1) mol % for the membrane coating of the silica beads. To distinguish two mixed bead fractions, in some experiments one fraction contained a different fluorescent dye lipid such as Oregon Green 488 DPPE, Atto488-DOPE, or ATTO390DOPE (1 mol %).
Preparation of vesicles
Lipid films were produced by mixing stock solutions of the lipids in chloroform (1–10 mg mL−1) and drying under nitrogen flow. After drying in a vacuum oven overnight, the lipid film was dissolved in deionized water to obtain multilamellar vesicles (1 mg mL−1). The mixture was then sonicated in a vessel resonator (Sonoplus HD 2070; Bandelin, Berlin, Germany) for 30 min (60 W, 0.4 s pulse) to produce small unilamellar vesicles (SUVs, 20–50 nm). The SUVs were stored at 4°C for a maximum of two weeks.
Membrane coating of silica beads
Membrane-coated silica beads were formed according to a protocol previously introduced in Bao et al. (6). Silica beads (10 μL, 10 wt %) were mixed with buffer (250 μL, 10 mM TRIS, 300 mM NaCl, pH 7.4) and SUV solution (250 μL). The mixture was incubated and pulse-vortexed in a centrifuge tube for 30 min. Subsequently, the excess SUVs were removed by rinsing six times with 500 μL of the desired solvent. Rinsing was performed by centrifuging the suspension for 5 s using a model No. MCF-2360 mini-centrifuge (LMS, Heidelberg, Germany) at 6600 rpm, removing the supernatant, and suspending the beads for the next rinsing step. The final volume of the suspension was 200 μL, containing 0.5 wt % of beads.
Fusion of membrane-coated beads
For fusion experiments, two sets of beads (50 μL each) that are either functionalized with E- or K-peptides, respectively, were gently mixed and incubated at room temperature for 90 min to induce membrane fusion between the bead fractions. A 35 mm glass-bottom dish with a 14-mm bottom well was incubated with 600 μL of phosphate buffer containing 1.5 mg mL−1 casein for 30 min and then rinsed a few times with 1 mL of phosphate buffer each. A quantity of 10 μL of the mixed bead fraction was added to 2 mL of phosphate buffer. Eventually, the membrane-coated silica beads sediment onto the passivated glass substrate. In contrast to our previous study in Bao et al. (6), we used buffer solution instead of deionized water for the bead dispersion to increase fusion efficiency through increase of the attractive forces between the beads.
Confocal laser scanning microscopy
Confocal microscopy and FRAP experiments were carried out using a model No. FV1000 inverted confocal laser scanning microscope (Olympus Deutschland, Hamburg, Germany) with a 40 air objective (LUCPLFLN 40× PH; Olympus Deutschland). FRAP experiments on fused pairs of beads were carried out by bleaching Texas Red DPPE with a 561 nm laser on one of the fusion partners for 2 s and recording Texas Red fluorescence for at least 15 min. Images were scanned unidirectionally with a speed of 2 μs per pixel. To gain a full view of the spherical, membrane-coated bead, the pinhole of the microscope was opened.
Particle tracking
ATTO 655-DPPE was used as a lipid dye for particle tracking measurements on single-membrane-coated silica spheres. The lipid composition was DOPC/DOPE/Chol/ATTO 655-DPPE (50:24.997:25:0.003). A small cap of the silica sphere was tracked with a 200-Hz charge-coupled device camera and a laser was used to bleach most of the fluorescent lipid dyes so that some single fluorescent molecules remain to be tracked over time (14).
Results
FRAP experiments
The goal was to investigate lipid molecule diffusion over a small fusion stalk by FRAP. Hence, membrane fusion between two membrane-coated silica spheres had to be initiated. By mixing two fractions of membrane coated silica spheres containing the complementary peptides for the formation of a coiled-coil α-helix, membrane fusion was achieved. In general, membrane fusion occurred mostly between two silica spheres and only a few clusters of spheres could be observed. In contrast to a previous study in Bao et al. (6), the hemifused state, i.e., where only the outer lipid monolayers fuse, could not be observed for a longer period of time, because this state is only metastable. Mixing times and ionic strength of the solution were increased in our study to increase fusion efficiency. In Fig. 1, a scheme of the membrane fusion process is shown, where membrane-coated spheres come into close contact initiating the formation of coiled-coil dimers between the lipopeptides on the opposing beads. Hemifusion of the outer lipids is usually observed before membranes merge entirely. Eventually, a continuous membrane is formed in which both lipid leaflets are fused to one lipid membrane covering both spheres. The used lipid composition ensures a fluid membrane at room temperature. TexasRed-DPPE was used as a lipid-based fluorescent dye for our FRAP measurements. The dye is photostable over a longer period of time but could still be bleached easily within a few seconds employing full laser intensity.
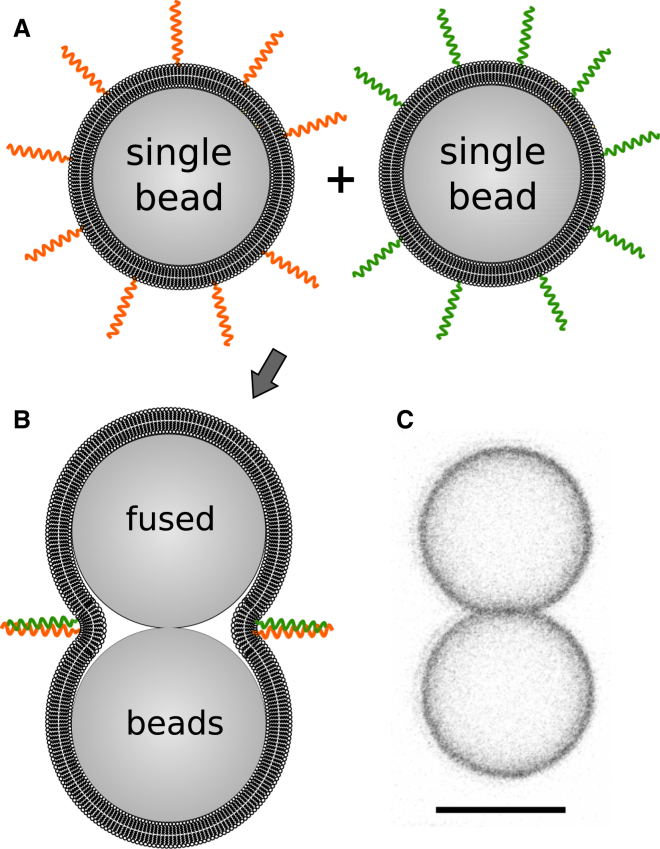
Figure 1.
Schematic depiction of the membrane fusion process. (A) Two species of membrane-coated beads are present in our experiments—one fraction of beads carries E3/E4 fusogenic peptides incorporated into the membrane (orange helices) and the other fraction displays the complementary K3/K4 fusogenic peptides (green helices). (B) Close contact of two complementary beads facilitated by formation of coiled-coil structures leads to membrane fusion, yielding a single continuous membrane covering both spheres. (C) Confocal laser scanning micrograph of membrane-coated beads with a continuous membrane spanning both spheres. Gray scale with inverted colors. Scale bar, 5 μm. To see this figure in color, go online.
FRAP was then used to monitor diffusion of lipid molecules between two silica spheres with a radius of 3.25 μm that were connected to each other by a fusion stalk. Fig. 2 shows a typical reference experiment, in which half of a single sphere was bleached. To obtain a full view of the lipid bilayer on the silica spheres, the pinhole of the confocal microscope was opened. This three- to two-dimensional projection was necessary to observe the entire membrane on both spheres. Initially, a bead pair was selected, where the fluorescent dye distribution was uniform on both spheres. A pair of membrane-coated beads is shown in Fig. 1 C. On one sphere, all lipid dye molecules were bleached for 2 s (Fig. 3, A–C). Because the recovery of fluorescence originates solely from dye molecules located on the other sphere, the process is rather slow (30 min) compared to FRAP measurements with identical spot size on solid supported membranes, e.g., glass surfaces (1 min). Therefore, consecutive images were taken in an appropriate time interval (∼10 s) to reduce photobleaching due to prolonged exposure to the scanning laser.
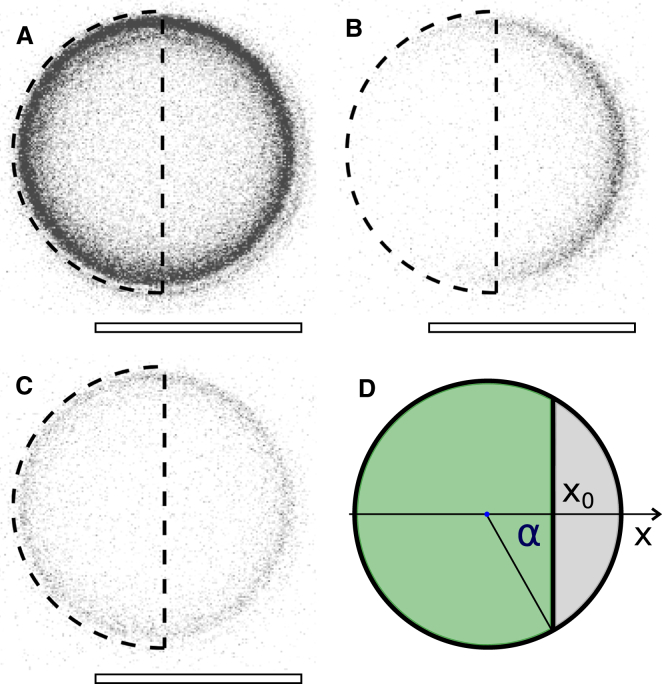
Figure 2.
Illustration of the reference FRAP experiment performed on single spheres. (A) Confocal laser scanning micrograph of single sphere with fluorescently labeled lipid membrane before bleaching. (B) Fluorescence micrograph after bleaching half of the sphere vertically; bleaching area highlighted as black half-circle. (C) Recovery of fluorescence intensity within bleached area. Overall intensity lowered. (D) Schematic representation of the FRAP experiment with x0 as a variable bleaching position. All fluorescence micrographs are in gray scale with inverted colors. Scale bar, 5 μm. To see this figure in color, go online.
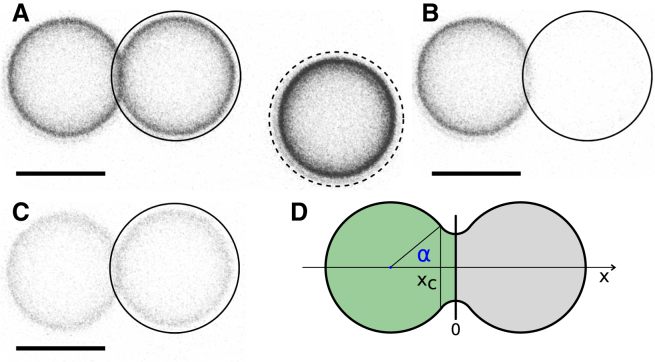
Figure 3.
Illustration of the FRAP experiment performed on fused pairs of membrane-coated silica spheres. Scale bar, 5 μm. (A) Confocal laser scanning micrograph of two silica spheres with fused membranes. A region of interest (black circle) is chosen to cover one of the two spheres. Another region on a distant sphere (black circle, dashed line) is chosen as a reference to account for general photobleaching. (B) Region of interest is bleached with a high-intensity laser pulse. (C) Recovery of fluorescence intensity recorded in bleaching region. Fusion of membranes is clearly visible due to loss in fluorescence intensity of the second, unbleached sphere. Homogeneous fluorescence intensity before and after bleaching indicates full fusion. (D) Sketch of the experiment. One sphere of the fused pair is bleached; the fluorescence recovery is observed within the bleached area. The contact angle α is introduced as the angle between the x axis connecting sphere centers and a line connecting a sphere center and the point of delamination of the membrane from the sphere. All fluorescence micrographs are in gray scale and inverted colors. To see this figure in color, go online.
To compare experimental data with Monte Carlo simulations of dye diffusion, we applied the following analysis procedure. Four distinct regions of interest (ROIs) of equal size were selected within the fluorescence micrographs: 1) one ROI covering the bleached area, 2) one ROI covering the unbleached part, 3) one ROI covering a distant sphere, and 4) one ROI covering the background. Fluorescence intensities within the ROIs were integrated, yielding intensities I1–I4. Background intensity I4 was subtracted from I1–3. Lastly, I1 and I2 were divided by I3 to account for general bleaching. Fluorescence intensities were then normalized according to
| (1) |
where denotes the experimentally obtained time-dependent fluorescence recovery after correction for bleaching, is the fluorescence intensity reached after infinite time, and denotes the fluorescence intensity before bleaching. Normalized fluorescence depletion was integrated, yielding a time constant τ of fluorescence decay:
| (2) |
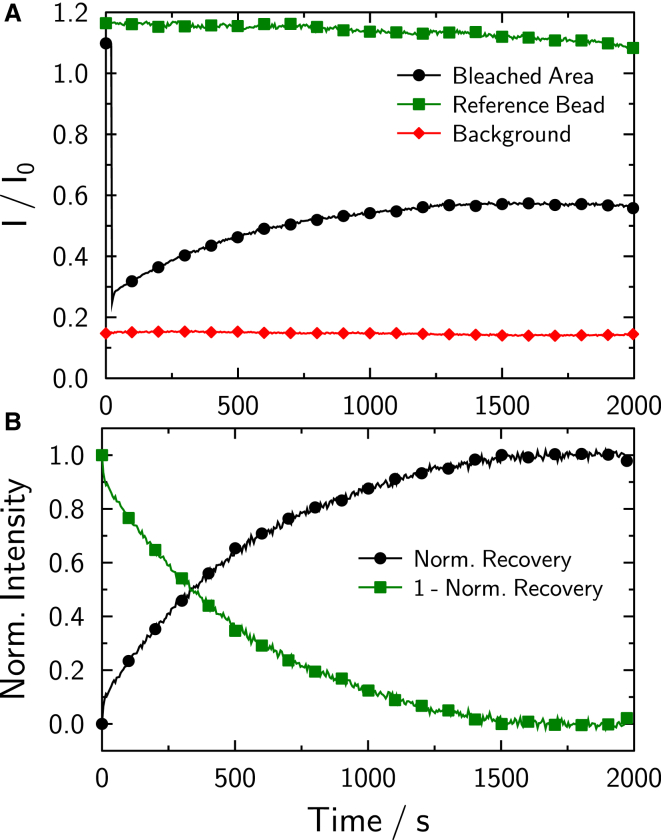
Fig. 4 illustrates the aforementioned procedure. The figure shows the collected raw fluorescence intensities of the four ROIs of one example FRAP measurement and the correspondingly transformed fluorescence depletion (green).
Figure 4.
(A) Example FRAP experiment performed on a pair of fused membrane-coated silica beads. Fluorescence recovery within the bleached area (circles) alongside the intensity of a single reference bead (squares) to correct for general bleaching and the background (diamonds) is shown. (B) Normalized fluorescence recovery (circles), and the fluorescence depletion calculated (squares). To see this figure in color, go online.
Quantities of 20 FRAP measurements on bead pairs that exhibit full fusion of the membrane coats (Fig. 3) and 10 FRAP measurements on single membrane-coated spheres were carried out. In the latter case, half of the bead was bleached (Fig. 2). The results of the processed measurements are compiled in Fig. 5 for single membrane-coated beads and in Fig. 6 for fused membrane-coated beads. Note that a fast fluorescence recovery corresponds to a lower value for τ. All calculated values for τ are in the range of 100–800 s (Fig. 6).
Figure 5.
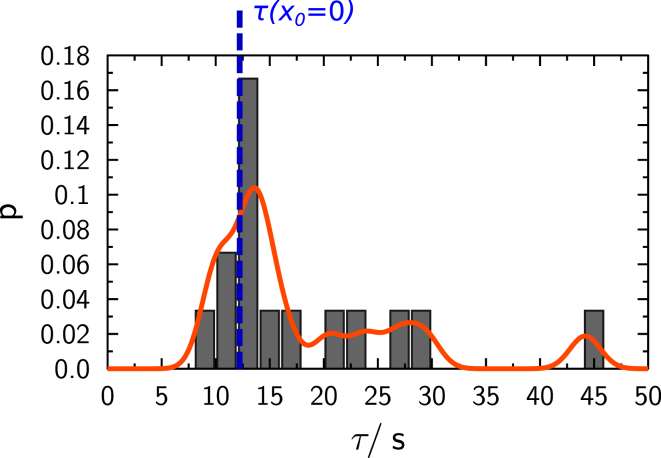
Histogram of experimental values for the time constant τ obtained on single spheres with a Gaussian kernel density estimate (red). Time constant τ obtained from simulations is shown in blue (dashed line). To see this figure in color, go online.
Figure 6.
Histogram of time constants τ found experimentally with fusion pairs of both E3/K3 and E4/K4 pairs combined. The simulated time constant is shown as a green dashed line. To see this figure in color, go online.
As a result, a rather broad distribution of time constants τ for the diffusion of lipids over a small fusion stalk was obtained. The most probable time constant of all FRAP measurements lies in between 250 and 300 s. These values indicate that full recovery is very slow compared to bleaching measurements of geometrically unrestricted lipid diffusion on single spheres. A smaller contact zone reduces the flow of lipid from one sphere to the other, which results in a slower apparent diffusion and fluorescence recovery.
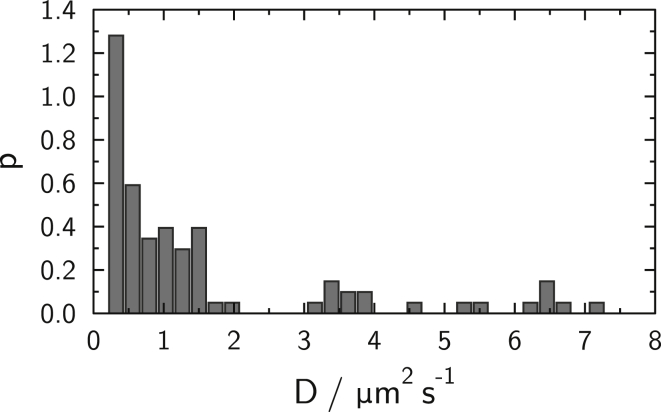
If no reference experiments exist, the precision of the contact size analysis heavily relies on the exact knowledge of the diffusion constant of the lipid composition. Therefore, we carried out particle tracking experiments of single fluorescent lipid dyes to obtain D from the mean-square displacement. In Fig. 7, a histogram of diffusion coefficients is shown that was measured by particle tracking of single fluorescent molecules that were excited with a high power laser. Most of the fluorescent lipid dye molecules were bleached so that a few excited molecules could be tracked over time. From this time-dependent measurement of lipid diffusion, a mean diffusion constant for a membrane on a single-membrane-coated silica sphere of D = (1.32 ± 0.20) μm2 s−1 was calculated, which is comparable to a flat solid supported membrane deposited on a glass surface (15). Note that the distribution of diffusion coefficients obtained from various spheres is rather broad. As the diffusion coefficient and the FRAP time constants are directly proportional, the deviation in time constants reflects the deviation in diffusion coefficients.
Figure 7.
Histogram of diffusion coefficients found experimentally with particle tracking of single fluorescently labeled lipids on single spheres.
Monte Carlo simulation
The objective is now to relate lateral diffusion to the geometry of the contact zone. Because the contact zone is the bottleneck, which is responsible for the slow recovery time of fluorescence on the bleached sphere, we designed Monte Carlo simulations to mirror this situation as closely as possible. Comparison between simulation and experiment allows us to correlate the observed slowdown of fluorescence recovery to the size of the contact zone between two membrane-coated beads.
Geometry
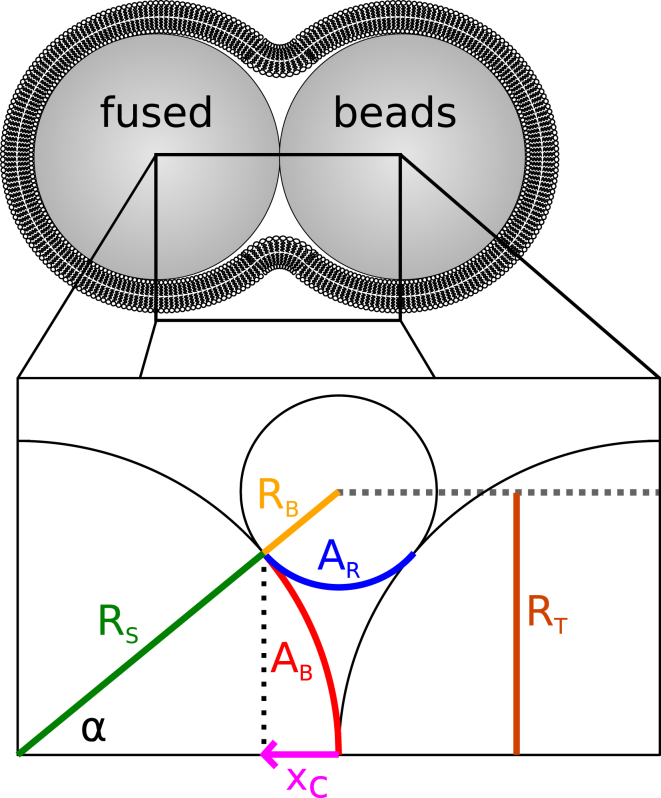
In the following section we describe the envisioned geometry of two membrane-coated beads in close contact. Let two spheres and of equal radius , whose centers are located on the x axis and that touch each other at the origin of the coordinate system, with x ≤ 0 on and x > 0 on , be covered with a bilayer of thickness dm. Bilayer thickness is assumed to be negligible with respect to sphere radius. If fusion takes place, one or both leaflets of the membrane will detach from the surface of the sphere and span the contact zone with a shape function minimizing free energy. In this work, the membrane surface within the contact zone will be modeled by a section of a ring torus , whose parameters are defined by the condition of continuity and differentiability at the transition between sphere and torus at xc (Fig. 8). This geometry is defined by (16)
| (3) |
The values and are the major and minor radii of the ring torus, respectively; and 2xc is the width of the contact zone projected onto the x axis. We define a contact angle α as the angle between the segment connecting the center of the torus and the center of either sphere and the x axis. The parameters defining the ring torus are:
| (4) |
| (5) |
| (6) |
Due to finite thickness of biological membranes, dm, the contact angle α is limited by the condition , that is:
| (7) |
With , the following approximation holds:
| (8) |
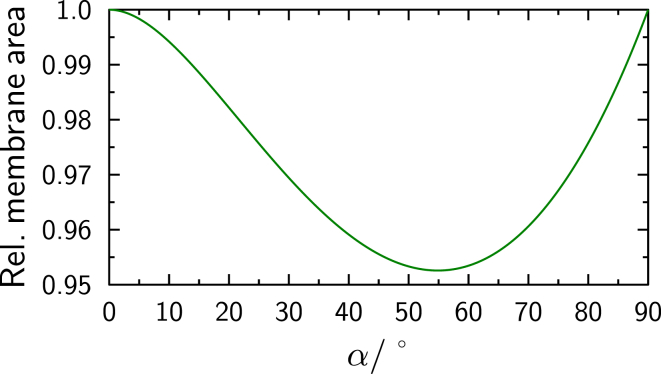
With and , the minimal angle possible with this geometry is . Using the toroidal geometry of the contact zone, the total membrane area is not strictly conserved during fusion. Relative membrane area, defined as the ratio of and in Fig. 8 and shown in Fig. 9, decreases for relatively small contact angles. Compression and stretching of membranes is energetically unfavorable. While rupture occurs at relative stretching larger than a few percent, compression might be avoided by formation of membrane protrusions. As our data analysis suggests contact angles much smaller than 10°, membrane compression is expected to be far below 1% and is therefore negligible in this context.
Figure 8.
Schematic cut through the geometry of the contact zone of two beads in contact. The value denotes the radius of the spheres, and and are the minor and major radii of the ring torus, respectively. The value shows the membrane supported by the spheres before fusion, and shows an approximation of the new geometry of the membrane after fusion, forming a torus in three dimensions. The value α is the contact angle, determined by the transition of the sphere and the torus. The value xc is half the width of the contact zone. To see this figure in color, go online.
Figure 9.
Relative membrane area, defined as the ratio of to in Fig. 8, as a function of the contact angle α. The ratio is independent of the size of the spheres. To see this figure in color, go online.
Surface diffusion
For the analysis of FRAP experiments performed on the geometry of fused beads, it is necessary to simulate diffusion of fluorescently labeled lipids on the surface of the geometry. In this work, surface diffusion is simulated using random walkers performing random steps with Gaussian step length distribution. Moving a random walker under confinement with respect to the curved membrane is performed in two approximate steps: 1) isotropic motion within the local tangent plane and 2) projection back onto the surface. With implicitly defined surfaces, the surface normal is easily given by
| (9) |
The new position of the random walker after a step is given by (17)
| (10) |
where σ is a step length drawn from a χ(2)-distribution with standard deviation chosen according to the diffusion coefficient D. After execution of a diffusion step, random walkers are reprojected onto the surface. This is done using a cutoff series expansion in Φ (17):
| (11) |
The reprojection is stable even for large step lengths compared to the dimensions of the spheres; nevertheless, the distance of reprojected random walkers to the surface is dependent on the local curvature, which leads to a different accuracy of reprojection within the toroid-shaped contact zone compared to the spheres. An adaptive step length approach is used in this work: the step length of random walkers within the contact zone is typically orders-of-magnitude smaller than the step length on the sphere. Fig. 10 shows an example random walk on the surface.
Figure 10.
Random walk of a single particle on the geometry of a pair of fused beads. The time is color-coded in arbitrary units; the geometry of the fused beads is depicted via a mesh of belts around the geometry. To see this figure in color, go online.
Initial configuration
The equilibrium surface concentration of fluorescently labeled lipids is homogeneous. Random walkers are distributed uniformly along the x axis with random rotation angle φ on the surface of revolution. This procedure does not yield a homogeneous area density of random walkers. Therefore, every random walker is attributed a brightness value, and , which is adjusted such that the surface brightness is homogeneous. The brightness of a random walker on the sphere is given by
| (12) |
while on the torus it is
| (13) |
To simulate a FRAP experiment, the brightness factor of random walkers in the bleached area is set to zero.
Simulation results
In the following section, we will present random walker-based Monte Carlo simulations of FRAP experiments. Time constants, defined as the integral of normalized fluorescence depletion, calculated as a function of the size of the contact zone, are compared to experimentally obtained time constants to determine plausible contact zone geometries. We introduce two distinct simulations: firstly, the partial bleaching of a single membrane-coated sphere; and secondly, partial bleaching of a fused pair of membrane-coated beads. The first one can be used as a reference experiment, yielding reference time constants as a normalization for time constants obtained in the second experiment, eliminating the need of determination of the diffusion coefficient of the lipids.
Comparing experiment with simulation
Reference experiment: FRAP on a single bead
As the lipid composition and membrane surface interaction are the same for both the fusion pairs and the single sphere experiments, a reduced, unitless reduction factor can be defined as the ratio of time constants of fluorescence depletion in fused pair simulations and the time constant of bleaching a defined part of a single sphere. Reduction factors are independent of the diffusion coefficient of fluorescently labeled lipids, therefore eliminating the need to determine D with high accuracy. A sketch of the reference experiment on single beads is shown in Fig. 2 D. A spherical cap of the fluorescently labeled sphere is bleached, and the recovery or depletion of fluorescence intensity within the bleached or the nonbleached area, respectively, is recorded as a function of the bleaching position x0.
In our simulations, bleaching is performed instantaneously and completely, i.e., all random walkers’ brightness whose position projected onto the x axis is larger than x0, is set to zero.
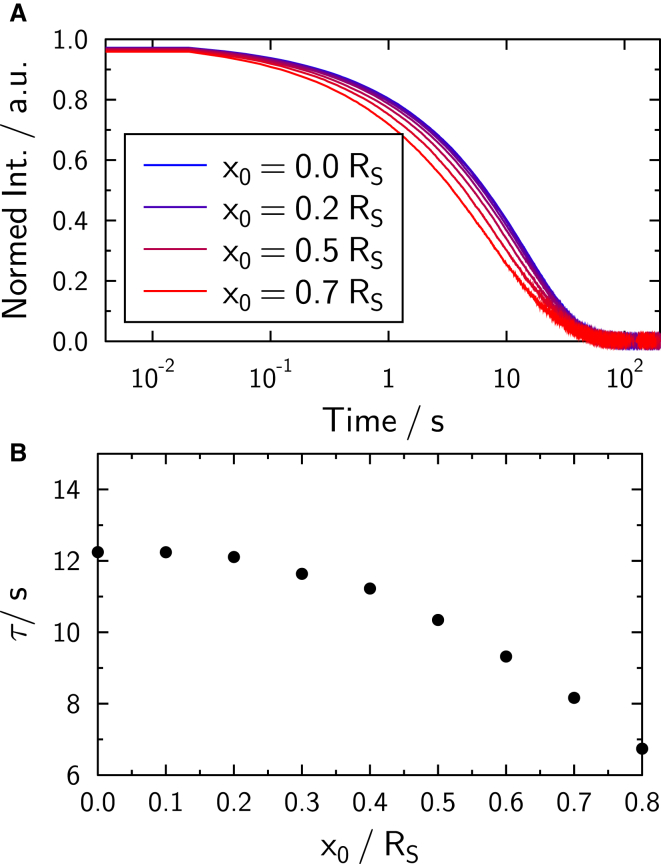
Simulated fluorescence depletion curves for single spheres are shown in Fig. 11 A and calculated time constants are displayed in Fig. 11 B. The simulation parameters are given in Table 1. The time constants in this simulation decrease with increasing x0, as the time constant is roughly proportional to the bleached area, which itself is inversely proportional to x0. For the purpose of a reference experiment, bleaching half a sphere, corresponding to x0 = 0, is favorable, because time constants are least influenced by experimental error in x0, as the slope of τ (x0) is minimal around x0 = 0.
Figure 11.
(A) Fluorescence recovery simulated on a single bead as a function of the bleaching position x0, according to the bleaching scheme in Fig. 2. (B) The time constant of the fluorescence recovery is roughly proportional to the area bleached. To see this figure in color, go online.
Table 1.
Parameters Used in the Simulation of FRAP on a Single Sphere
| Parameter | Value |
|---|---|
| No. of random walkers | 2 × 106 |
| Δt | 4.1 × 10−3 s |
| RS | 3.25 μm |
| D | 1.32 μm2 s−1 |
Comparison of simulated time constants given in Fig. 5 shows good agreement for the most probable value of τ obtained, although some experiments exhibit significantly larger time constants than predicted by the simulations.
FRAP on fused membrane-coated beads
In this section, we present simulations of FRAP experiments on fused membrane-coated beads with varying contact angle α. We calculate the reduction factor of time constants with respect to single bead time constants. The toroidal-like membrane spanning the contact zone in between both spheres presents a geometrical barrier for diffusing lipids, and time constants are significantly increased. Comparison of simulation and experiment offers a way to obtain information about the size of the contact zone.
A sketch of the simulation performed is shown in Fig. 3 D. One sphere of the fusion pair was bleached and the fluorescence depletion subsequently recorded. Note that because the timescales of lipid diffusion on the spheres and across the fusion pore are significantly different (the latter being an order of magnitude slower), an imprecise determination of the bleaching position and thus, bleaching of not exactly half of the geometry, would have only a minor impact on fluorescence depletions. It can therefore be neglected. Simulation parameters are given in Table 2.
Table 2.
Parameters Used in the Simulation of FRAP on a Fusion Pair of Two Beads
| Parameter | Value |
|---|---|
| No. of random walkers | 5 × 105 |
| Δt on sphere | 3.7 × 10−4 s |
| Δt within contact zone | 3.4 × 10−8 s |
| RS | 3.25 μm |
| D | 1.32 μm2 s−1 |
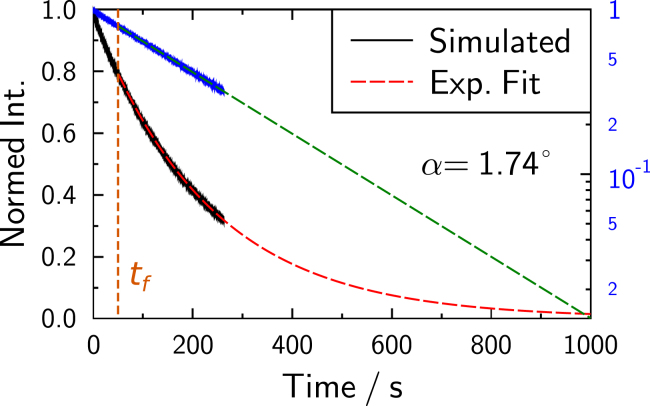
At the smallest contact angle, the simulations are not able to reach the long-term equilibrium state. However, the fluorescence depletion curves can be described as sums of exponential decays (Fig. 12). Semilogarithmic scaling confirms linearity for long times, justifying an extrapolation to infinity. Time constants were then computed as the sum of the integral over the simulated data and the integral over extrapolated long time behavior. An example of this extrapolation procedure is given in Fig. 12.
Figure 12.
Extrapolation of fluorescence depletion curves exemplified with simulation assuming α = 1.74°. Black and red with linear scaling, and blue and green with semilogarithmic scaling, showing dominance of a single exponential decay for long times. Simulated intensities above were used for the fit. Extrapolation was used for small angles to compute time constants, where explicit simulation would not be computationally feasible and, in fact, unnecessary. To see this figure in color, go online.
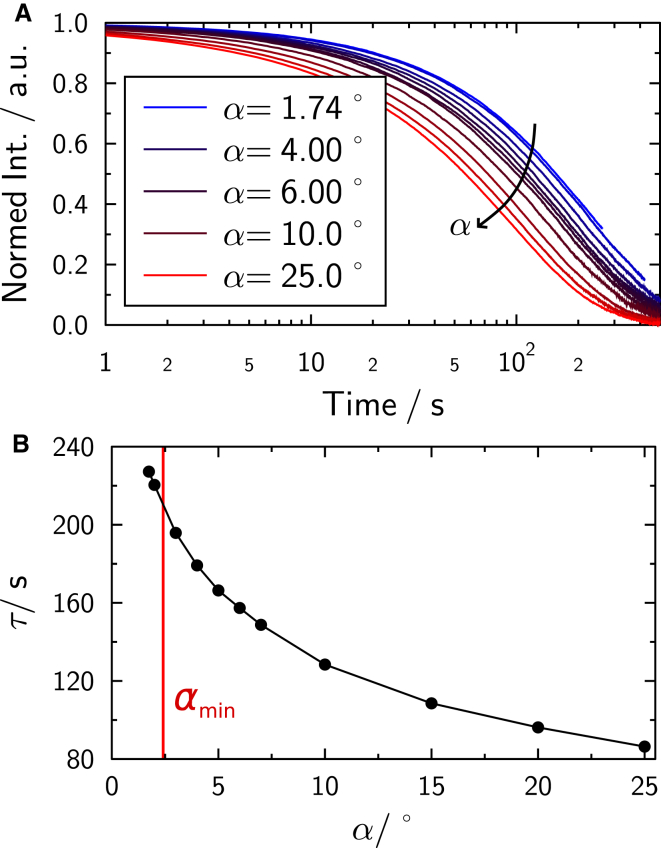
Simulated fluorescence depletion curves as a function of angle α are given in Fig. 13 A, and calculated time constants are shown in Fig. 13 B. The minimal angle possible for a given sphere radius according to Eq. 8 is depicted as αmin. Simulated values of the time constant are compatible with time constants acquired experimentally, shown in Fig. 6. Hence, experimentally observed reduction of fluorescence recovery times ∼17-fold is well reproduced by simulations assuming geometrical obstruction in the toroidal-like geometry. However, in some cases, geometrical obstruction alone is not sufficient to explain the recovery slowdown seen in experiments; in fact, some values are up to a factor-of-four higher than simulated. It is instructive to compare the distribution of time constants obtained from our FRAP measurements with the distribution of diffusion coefficients measured with single fluorophore particle tracking (Fig. 7). Both types of measurements reveal similarly broad distributions. Indeed, the slowest and fastest diffusion constants are approximately a factor-of-four smaller or larger than the mean value used in our simulations. As the time constants are directly proportional to diffusion coefficients, we would expect measurements to deviate by the same factor. Bearing in mind that diffusion coefficients are generally accurate on a logarithmic scale, we think that the observed deviation is not unreasonably large. Moreover, some inherent accuracy is lost due to the presence of a solid support. Any small defect in the solid supported membrane on the spheres would lead to reduced apparent diffusion coefficients, thus increasing time constants.
Figure 13.
(A) Fluorescence recovery simulated on fused beads as a function of the contact angle α, according to the bleaching scheme in Fig. 3. Contact angle is increasing from red to blue. (B) Calculated time constants τ. To see this figure in color, go online.
Because our experimental values essentially show some realizations with significantly larger time constants but only a few with significantly smaller time constants, we are confident to assume that the geometry given here is minimal in respect to the size of the contact zone. The silica spheres will be in close contact due to high van der Waals interactions; tetherlike structures are unlikely, because this would require separation of the beads.
Discussion
In this study, we have performed FRAP experiments on single membrane-coated silica beads as well as pairs of membrane-coated beads, whose membranes have fused in close contact of the spheres mediated by fusogenic model peptides forming coiled-coil dimers consisting of E3/K3 or E4/K4, respectively. Both peptides led to full fusion of membrane-coated beads. The goal was to infer the geometry of the contact zone from diffusion measurements. Due to the limited resolution, direct observation of the contact zone with optical microscopy is not feasible. However, it is clear that the zone is smaller than the resolution of the microscope (250 nm), because contact zone radius for a minimal contact angle is ∼137 nm. Comparison of fluorescence recovery of single spheres and fused pairs revealed a striking slowdown of diffusion upon fusion, mainly caused by strong geometrical restriction of lipids in a confined contact geometry. Monte Carlo simulations of the diffusion of lipids across a toroidal membrane connection, between the two beads sharing one continuous membrane, revealed that indeed minimal geometries within the contact zone reproduce strong diffusion slowdown. Simulations suggest that if fusion occurs, a minimal geometry is necessary to explain experimental observations. What is the driving force of fusion in this experiment, and additionally, what is the force prohibiting wide opening of the fusion pore? To address these questions, we first provide an estimation of energy contributions to the overall fusion free energy. In vesicle fusion, the gain in free energy originates from the release of bending energy in the order of 500 kBT. Notably, bending energy of vesicles is independent of the radius. The main energy release during fusion in our experiment, however, cannot be the release of bending energy, but instead comes from the attractive van der Waals interaction of both silica spheres upon close contact. The interaction energy is given by (18)
| (14) |
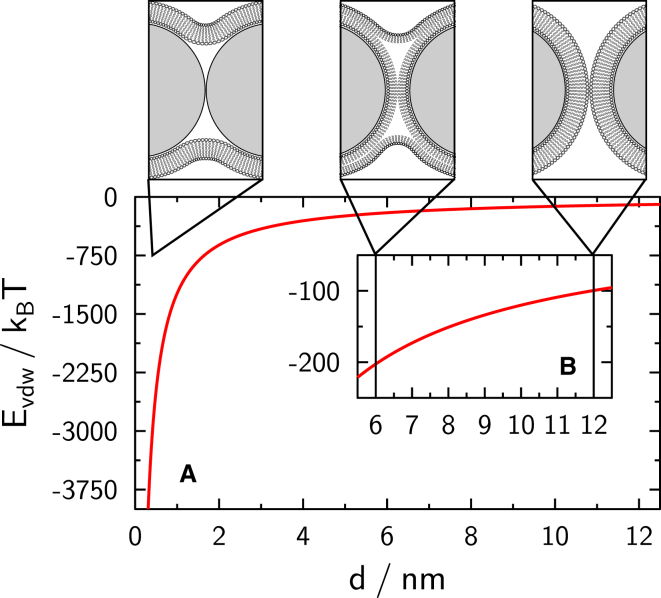
The Hamaker constant for silica spheres in water is found to be (19). For a configuration corresponding to the docking state, where the spheres are separated by roughly 12 nm due to two intact and separated lipid membranes with , an energy contribution of ∼100 kBT is to be expected. A hemifused state with a sphere-sphere separation of 6 nm corresponding to two leaflets of the lipid membranes in contact would suggest an interaction energy of roughly 200 kBT. Thus, the transition from docking to hemifusion would release 100 kBT. For full fusion with close contact of the spheres in the range of d ≈ 2 nm, an energy release of ∼6204 kBT is expected, this being a strong driving force for fusion (Fig. 14). The selective interaction of E/K-peptides upon formation of coiled-coil structures is small compared to the van der Waals interactions, but provides a specific way of bringing the two spheres into close contact, thereby lowering the hydration barrier.
Figure 14.
(A) van der Waals interaction energy as a function of intersphere distance. (B) Enlarged section of the interaction energy, corresponding to shown intermediates. To see this figure in color, go online.
As the fusion pore forms, the membrane in the contact zone has to change its topology at the expense of adhesion energy. While the membrane before fusion is closely interacting with the solid support, upon fusion the bilayer has to be partly delaminated from the spheres to bridge the contact zone. Besides raising free energy for delamination, the membrane enters a state of high curvature in the contact zone. Using the geometry introduced above, one can calculate the membrane area delaminated as a function of contact angle α:
| (15) |
Thus, with a typical surface energy of γ = 0.1 mN m−1, the delamination energy is given by
| (16) |
Delamination energies clearly increase with increasing contact angle α; thus, with increasing fusion pore size, delamination energies should increase strongly with sphere size. As the van der Waals interaction is independent of α, this delamination energy will strongly limit possible contact zone sizes. This is in accordance with findings in cell-cell fusion experiments where the remodeling of cytoskeleton-membrane contacts is the prerequisite for growing of the fusion pore (3). Additionally, we consider the energies involved in bending the membrane into small tori around the contact. We approximate bending contribution by considering the Helfrich bending energy given by
| (17) |
Mean curvature H and Gaussian curvature K for tori and spheres are well known from differential geometry (20). Solving the integral above using the approximation that the minor torus radius is much smaller than the major torus radius and further using a small angle approximation, we estimate the bending energy change upon fusion to be
| (18) |
where is the spontaneous curvature of the membrane, κ is the bending modulus, and is the saddle splay modulus.
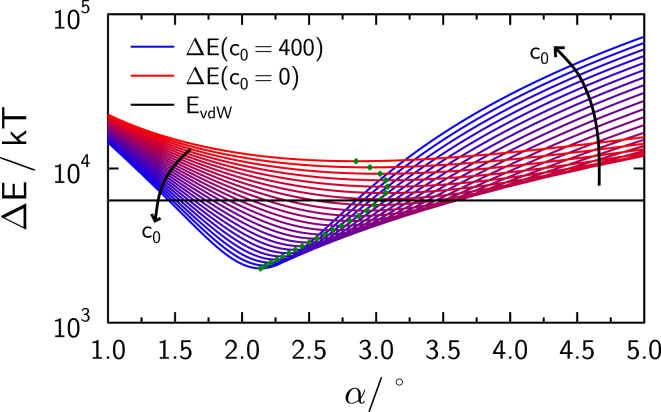
Fig. 15 shows the free energy as a function of contact angle α, comprising contributions from delamination and bending for varying spontaneous curvature assuming κ = 20 kBT (21, 22) and kBT. The black line indicates the possible release of van der Waals energy upon close contact of the two beads. Free energy values below this line correspond to an exergonic fusion reaction.
Figure 15.
Change in energy upon full fusion of the membranes on two membrane-coated silica spheres. The different values of the spontaneous curvature c0 are color-coded. Black lines depict the van der Waals energy released by the interaction of the two spheres, thus total energy change below this line is negative. Green dots indicate the potential minimum, i.e., the contact angle with minimal free energy for given spontaneous curvature [μm−1]. To see this figure in color, go online.
Decreasing bending energy for geometries with larger contact zones competes with increasing delamination penalty, thus leading to a free energy minimum for a given spontaneous curvature. While for a membrane with no net spontaneous curvature the van der Waals interaction energy is not sufficient to overcome the delamination and bending barriers, a membrane that has a negative spontaneous curvature in the order of 100 μm−1, thus favoring considerably bent structures as they occur within the contact zone, render the fusion process energetically favorable. Given the minimal spontaneous curvature needed to release free energy during the fusion process of c0 = 103.6 μm−1, the free energy minimum is found at a contact angle of α = 3.03°. The minimal, geometrical contact angle for this geometry is found to be αmin = 2.46°. Increased spontaneous curvature shifts free energy minima toward smaller angles. A minimum at 2.46° is found for a spontaneous curvature of 261.4 μm−1, releasing ∼3020 kBT, which could explain lower time constants observed experimentally. We can conclude that a lipid membrane composition, containing lipids that can show considerable spontaneous curvatures, is needed to facilitate fusion in this experiment. Note that we used PE/cholesterol in our lipid composition to provide the required spontaneous curvature. Because a symmetrical double membrane should not exhibit net spontaneous curvatures, it is likely that either flip-flop of lipids or lateral phase separation precedes the formation of the fusion pore, leading to a net spontaneous curvature and thus a decrease of bending energy penalties. A typical value for spontaneous curvature of PE is ±0.31 nm−1 (22), where the sign depends on convention. Here, curvatures within the toroid contact zone are positive, while the curvature on the sphere is taken to be negative. This observation is backed up by our experiments, which show essentially no fusion events if PE and cholesterol are omitted. Furthermore, interaction of the K-peptide with the lipid membrane could influence lipid composition and local curvature, facilitating membrane reorganization within the contact zone. Enrichment of cholesterol in the vicinity of K-peptide membrane interaction has been suggested (23, 24).
Thus, energy considerations suggest a minimal geometry, consistent with the finding that a minimal angle is needed to account for large diffusion slowdowns compared to the reference experiment on single spheres. Simulated fluorescence depletion time constants are still smaller than those encountered in some of the experiments. Changes in diffusion coefficient within the contact zone are a possible explanation, e.g., due to interaction of lipids upon close contact with membrane sheets (25).
With increasing contact angle α, dimensions of the contact zone and distance between membrane sheets increases rapidly. Effects decreasing mobility of lipids within the membrane due to close contact should diminish quickly, suggesting that a geometrical obstruction is indeed the main contribution to the diffusion slowdown encountered in experiments.
Conclusions
We have performed FRAP experiments on both single membrane-coated silica spheres and fused pairs of two membrane-coated silica spheres, whose membranes did undergo full fusion. Interaction of the spheres is initiated by formation of coiled-coil structures of fusogenic, SNARE-mimicking peptides, E3/4 and K3/4, respectively. Analysis of FRAP experiments revealed a strong reduction of fluorescence recovery times for fused pairs compared to single spheres.
Comparison of experimental time constants of lipid diffusion across the membrane surfaces with Monte Carlo simulations of lipid diffusion suggests that geometrical restriction due to a minimal contact zone reproduces the diffusion slowdown. Consideration of the energetic contributions to fusion in this geometry proposes that delamination of the membrane from the silica substrate poses the main barrier of fusion pore opening, while release of bending energy favors larger fusion geometries, thus freezing a transition state of membrane fusion.
In contrast to fusion studies involving vesicles, our approach eliminates several complex steps in the fusion process such as shape fluctuations or adaptation of a new final surface to volume. Instead, it preserves the overall geometry and the volume of the two initial spherical bodies during the whole fusion process. It should also be emphasized that our model does not resolve the fast initial steps of membrane fusion in time. Instead, this model yields a frozen state of an early but fully developed fusion pore stabilized by the competition of delamination and bending energies.
The strength of this model is that it allows a sensitive, very predictable, and reproducible fine-tuning of the various energetic contributions to the process of membrane fusion. By varying the size and the surface properties of the spheres or even coating the spheres with an actin cytoskeleton, we expect that this model, in future experiments, will allow us to infer detailed information about the role of fusogenic membrane proteins and membrane compositions in the fusion process.
These findings are important also for native cell fusion experiments where remodeling or even dissolution of the actin cortex is important to reduce the free energy barrier for fusion pore growth. In contrast to driving forces found in cells and vesicles, van der Waals interactions between the two solid beads are the main driving force of fusion in our assay. But as the dispersion energy contribution is not a function of fusion progression after close contact of spheres, i.e., no function of contact angle α, it can be treated as a mere facilitator of fusion generating an offset to the overall free energy. The interplay of delamination and bending, which is present in cellular systems as well, dominates the main findings of our study. Indeed, the energies involved in delamination of membranes from silica spheres and cellular cytoskeletons are quite similar, thus allowing us to infer information about the process of cellular fusion from an artificial model system (26).
Besides reduction of delamination energy by means of active energy-consuming processes, the lipid composition in the contact zone is decisive in reducing bending energy. Here flipases could help to establish the necessary asymmetry to accommodate high curvature in the contact zone between two cells on a reasonably short timescale.
Author Contributions
F.S. carried out Monte Carlo simulations; S.V., C.B., and T.-T.K. performed membrane fusion experiments and FRAP analysis; J.T. performed diffusion measurement; A.K. provided peptides; and F.S., B.G., and A.J. wrote the article.
Acknowledgments
We thank Jörg Enderlein for support and fruitful discussions.
This work was financially supported by SFB grant 803 (B08).
Editor: Tobias Baumgart.
Footnotes
Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30229-6.
Contributor Information
Burkhard Geil, Email: bgeil@gwdg.de.
Andreas Janshoff, Email: ajansho@gwdg.de.
Supporting Citations
References (27, 28) appear in the Supporting Material.
Supporting Material
References
- 1.Chen E.H., Grote E., Vignery A. Cell-cell fusion. FEBS Lett. 2007;581:2181–2193. doi: 10.1016/j.febslet.2007.03.033. [DOI] [PubMed] [Google Scholar]
- 2.Oren-Suissa M., Podbilewicz B. Cell fusion during development. Trends Cell Biol. 2007;17:537–546. doi: 10.1016/j.tcb.2007.09.004. [DOI] [PubMed] [Google Scholar]
- 3.Chen A., Leikina E., Chernomordik L.V. Fusion-pore expansion during syncytium formation is restricted by an actin network. J. Cell Sci. 2008;121:3619–3628. doi: 10.1242/jcs.032169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zheng Q.A., Chang D.C. Reorganization of cytoplasmic structures during cell fusion. J. Cell Sci. 1991;100:431–442. doi: 10.1242/jcs.100.3.431. [DOI] [PubMed] [Google Scholar]
- 5.Chernomordik L.V., Kozlov M.M. Protein-lipid interplay in fusion and fission of biological membranes. Ann. Rev. Biochem. 2003;72:175–207. doi: 10.1146/annurev.biochem.72.121801.161504. [DOI] [PubMed] [Google Scholar]
- 6.Bao C., Pähler G., Janshoff A. Optical fusion assay based on membrane-coated spheres in a 2D assembly. J. Am. Chem. Soc. 2013;135:12176–12179. doi: 10.1021/ja404071z. [DOI] [PubMed] [Google Scholar]
- 7.Robson Marsden H., Elbers N.A., Kros A. A reduced SNARE model for membrane fusion. Angew. Chem. Int. Ed. Engl. 2009;48:2330–2333. doi: 10.1002/anie.200804493. [DOI] [PubMed] [Google Scholar]
- 8.Pähler G., Panse C., Janshoff A. Coiled-coil formation on lipid bilayers--implications for docking and fusion efficiency. Biophys. J. 2012;103:2295–2303. doi: 10.1016/j.bpj.2012.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Marsden H.R., Tomatsu I., Kros A. Model systems for membrane fusion. Chem. Soc. Rev. 2011;40:1572–1585. doi: 10.1039/c0cs00115e. [DOI] [PubMed] [Google Scholar]
- 10.Versluis F., Voskuhl J., Kros A. In situ modification of plain liposomes with lipidated coiled coil forming peptides induces membrane fusion. J. Am. Chem. Soc. 2013;135:8057–8062. doi: 10.1021/ja4031227. [DOI] [PubMed] [Google Scholar]
- 11.Zheng T., Voskuhl J., Kros A. Controlling the rate of coiled coil driven membrane fusion. Chem. Commun. (Camb.) 2013;49:3649–3651. doi: 10.1039/c3cc38926j. [DOI] [PubMed] [Google Scholar]
- 12.Zope H.R., Versluis F., Kros A. In vitro and in vivo supramolecular modification of biomembranes using a lipidated coiled-coil motif. Angew. Chem. Int. Ed. Engl. 2013;52:14247–14251. doi: 10.1002/anie.201306033. [DOI] [PubMed] [Google Scholar]
- 13.Mora N.L., Bahreman A., Kros A. Targeted anion transporter delivery by coiled-coil driven membrane fusion. Chem. Sci. (Camb.) 2016;7:1768–1772. doi: 10.1039/c5sc04282h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sbalzarini I.F., Koumoutsakos P. Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 2005;151:182–195. doi: 10.1016/j.jsb.2005.06.002. [DOI] [PubMed] [Google Scholar]
- 15.Benda A., Beneš M., Hof M. How to determine diffusion coefficients in planar phospholipid systems by confocal fluorescence correlation spectroscopy. Langmuir. 2003;19:4120–4126. [Google Scholar]
- 16.Savić F. Springer; Berlin, Germany: 2015. Theorie und Design von FRAP-Experimenten auf Komplexen Geometrien. [Google Scholar]
- 17.Hołyst R., Plewczyński D., Burdzy K. Diffusion on curved, periodic surfaces. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;60:302–307. doi: 10.1103/physreve.60.302. [DOI] [PubMed] [Google Scholar]
- 18.Israelachvili J.N., editor. van der Waals forces between particles and surfaces. 3rd Ed. Chapter 13. Academic Press; San Diego, CA: 2011. pp. 253–289. (Intermolecular and Surface Forces). [Google Scholar]
- 19.Lomboy G., Sundararajan S., Subramaniam S. A test method for determining adhesion forces and Hamaker constants of cementitious materials using atomic force microscopy. Cement Concr. Res. 2011;41:1157–1166. [Google Scholar]
- 20.Deserno M., Gelbart W.M. Adhesion and wrapping in colloid-vesicle complexes. J. Phys. Chem. B. 2002;106:5543–5552. [Google Scholar]
- 21.Chen Z., Rand R.P. The influence of cholesterol on phospholipid membrane curvature and bending elasticity. Biophys. J. 1997;73:267–276. doi: 10.1016/S0006-3495(97)78067-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kamal M.M., Mills D., Howard J. Measurement of the membrane curvature preference of phospholipids reveals only weak coupling between lipid shape and leaflet curvature. Proc. Natl. Acad. Sci. USA. 2009;106:22245–22250. doi: 10.1073/pnas.0907354106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rabe M., Zope H.R., Kros A. Interplay between lipid interaction and homo-coiling of membrane-tethered coiled-coil peptides. Langmuir. 2015;31:9953–9964. doi: 10.1021/acs.langmuir.5b02094. [DOI] [PubMed] [Google Scholar]
- 24.Pluhackova K., Wassenaar T.A., Böckmann R.A. Spontaneous adsorption of coiled-coil model peptides K and E to a mixed lipid bilayer. J. Phys. Chem. B. 2015;119:4396–4408. doi: 10.1021/acs.jpcb.5b00434. [DOI] [PubMed] [Google Scholar]
- 25.Pronk S., Lindahl E., Kasson P.M. Coupled diffusion in lipid bilayers upon close approach. J. Am. Chem. Soc. 2015;137:708–714. doi: 10.1021/ja508803d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pietuch A., Brückner B.R., Janshoff A. Elastic properties of cells in the context of confluent cell monolayers: impact of tension and surface area regulation. Soft Matter. 2013;9:11490–11502. [Google Scholar]
- 27.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 28.Boal D. Cambridge University Press; Cambridge, UK: 2012. Mechanics of the Cell. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.