Identifying Allosteric Hotspots with Dynamics: Application to Inter- and Intra-species Conservation

SUMMARY

The rapidly growing volume of data being produced by next-generation sequencing initiatives is enabling more in-depth analyses of conservation than previously possible. Deep sequencing is uncovering disease loci and regions under selective constraint, despite the fact that intuitive biophysical reasons for such constraint are sometimes absent. Allostery may often provide the missing explanatory link. We use models of protein conformational change to identify allosteric residues by finding essential surface pockets and information-flow bottlenecks, and we develop a software tool that enables users to perform this analysis on their own proteins of interest. Though fundamentally 3D-structural in nature, our analysis is computationally fast, thereby allowing us to run it across the PDB and to evaluate general properties of predicted allosteric residues. We find that these tend to be conserved over diverse evolutionary time scales. Finally, we highlight examples of allosteric residues that help explain poorly understood disease-associated variants.

Graphical Abstract

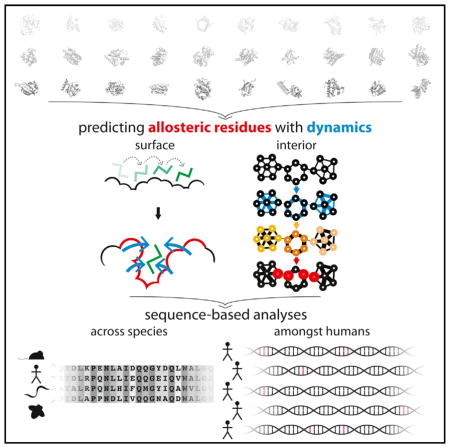
INTRODUCTION

The ability to sequence large numbers of human genomes is providing a much deeper view into protein evolution than previously possible. When trying to understand the evolutionary pressures on a given protein, structural biologists now have at their disposal an unprecedented breadth of data regarding patterns of conservation, both across species and among humans. As such, there are greater opportunities to take an integrated view of the context in which a protein and its residues function. This view necessarily includes structural constraints such as residue packing, protein-protein interactions, and stability. However, deep sequencing is unearthing a class of conserved residues on which no obvious structural constraints appear to be acting. The missing link in understanding these regions may be provided by studying the protein’s dynamic behavior through the lens of the distinct functional and conformational states within an ensemble.

The underlying energetic landscape responsible for the relative distributions of alternative conformations is dynamic in nature: allosteric signals or other external changes may reconfigure and reshape the landscape, thereby shifting the relative populations of states within an ensemble (Tsai et al., 1999). Landscape theory thus provides the conceptual underpinnings necessary to describe how proteins change behavior and shape under changing conditions. A primary driving force behind the evolution of these landscapes is the need to efficiently regulate activity in response to changing cellular contexts, thereby making allostery and conformational change essential components of protein evolution.

Given the importance of allosteric regulation, as well as its role in imparting efficient functionality, several methods have been devised for the identification of likely allosteric residues. Conservation itself has been used, either in the context of conserved residues (Panjkovich and Daura, 2012), networks of co-evolving residues (Halabi et al., 2009; Lee et al., 2008; Lockless et al., 1999; Reynolds et al., 2011; Shulman et al., 2004; Süel et al., 2003), or local conservation in structure (Panjkovich and Daura, 2010). In related studies, both conservation and geometric-based searches for allosteric sites have been successfully applied to several systems (Capra et al., 2009).

The concept of “protein quakes” has been introduced to explain local conformational changes that are essential for global conformation transitions of functional importance (Ansari et al., 1985; Miyashita et al., 2003). These local changes cause strain within the protein that is relieved by subsequent relaxations (which are also termed functionally important motions), which terminate when the protein reaches the second equilibrium state. Such local perturbations often end with large conformational changes at the focal points of allosteric regulation, and these motions may be identified in a number of ways, including modified normal modes analysis (Miyashita et al., 2003) or time-resolved X-ray scattering (Arnlund et al., 2014).

In addition to conservation and geometry, protein dynamics have also been used to predict allosteric residues. Normal modes analysis has been used to examine the extent to which bound ligands interfere with low-frequency motions, thereby identifying potentially important residues at the surface (Ming and Wall, 2005; Mitternacht and Berezovsky, 2011a; Panjkovich and Daura, 2012). Normal modes have also been used by the Bahar group to identify important subunits that act in a coherent manner for specific proteins (Chennubhotla and Bahar, 2006; Yang and Bahar, 2005). Rodgers et al. (2013) have applied normal modes to identify key residues in CRP/FNR transcription factors.

With the objective of identifying allosteric residues within the interior, molecular dynamics (MD) simulations and network analyses have been used to identify residues that may function as internal allosteric bottlenecks (Csermely et al., 2013; Gasper et al., 2012; Rousseau and Schymkowitz, 2005; Sethi et al., 2009; Vanwart et al., 2012). Ghosh and Vishveshwara (2008) have taken a novel approach of combining MD and network principles to characterize allosterically important communication between domains in methionyl tRNA synthetase. In conjunction with nuclear magnetic resonance (NMR), Rivalta et al. (2012) have used MD and network analysis to identify important regions in imidazole glycerol phosphate synthase.

Despite having provided valuable insights, many of these approaches have been limited in terms of scale (the numbers of proteins which may feasibly be investigated), computational demands, or the class of residues to which the method is tailored (surface or interior). Here, we use models of protein conformational change to identify both surface and interior residues that may act as essential allosteric hotspots in a computationally tractable manner, thereby enabling high-throughput analysis. This framework directly incorporates information regarding 3D protein structure and dynamics, and can be applied on a PDB-wide scale to proteins that exhibit conformational change. Throughout the PDB (Berman et al., 2000), the residues identified tend to be conserved both across species and among humans, and they may help to elucidate many of the otherwise poorly understood regions in proteins. In a similar vein, several of our identified sites correspond to human disease loci for which no clear mechanism for pathogenesis had previously been proposed. Finally, we make the software associated with this framework, termed STRESS (STRucturally identified ESSential residues), publicly available through a tool to enable users to submit their own structures for analysis.

RESULTS

Identifying Potential Allosteric Residues

Allosteric residues at the surface generally play a regulatory role that is fundamentally distinct from that of allosteric residues within the protein interior. While surface residues often constitute the sources or sinks of allosteric signals, interior residues act to transmit such signals. We use models of protein conformational change to identify both classes of residues (Figure 1). Throughout, we term these potential allosteric residues at the surface and interior “surface-critical” and “interior-critical” residues, respectively.

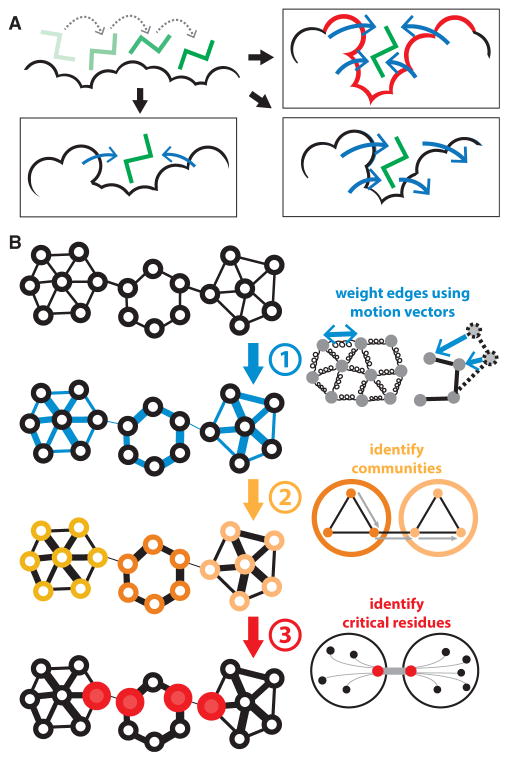
Figure 1. Schematic Overviews of Methods for Finding Surface- and Interior-Critical Residues.

(A) A simulated ligand probes the protein surface in a series of Monte Carlo simulations (top left). The cavities identified may be such that occlusion by the ligand strongly interferes with conformational change (top right; such a site is likely to be identified as surface-critical, in red), or they may have little effect on conformational change, as in the case of shallow pockets (bottom left) or pockets in which large-scale motions do not drastically affect pocket volume (bottom right).

(B) Interior-critical residues are identified by weighting residue-residue contacts (edges) on the basis of correlated motions, and then identifying communities within the weighted network. Residues involved in the highest-betweenness interactions between communities (in red) are selected as interior-critical residues.

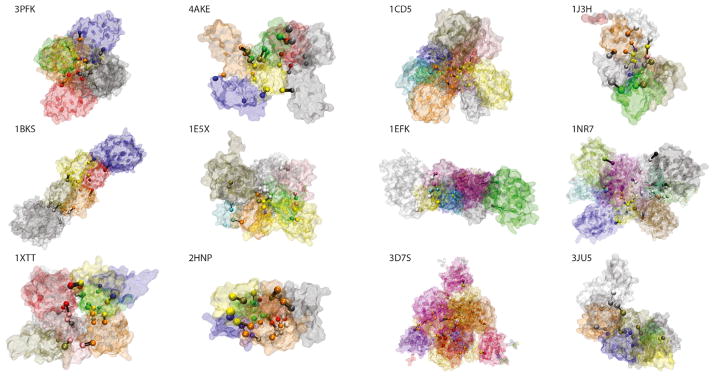
To gauge the effectiveness of our approach, we identified and analyzed critical residues within a set of 12 well-studied canonical systems (see Figure S1, as well as Table S1 for rationale regarding the set selection). We then apply this protocol on a large scale across hundreds of proteins for which crystal structures of alternative conformations are available.

Identifying Surface-Critical Residues

Allosteric ligands often act by binding to surface pockets/ cavities and modulating protein conformational dynamics. The surface-critical residues, some of which may act as latent ligand-binding sites and active sites, are first identified by finding cavities using Monte Carlo (MC) simulations to probe the surface with a flexible ligand (Figure 1A, top left). The degree to which cavity occlusion by the ligand disrupts large-scale conformational change is used to assign a score to each cavity: sites at which ligand occlusion strongly interferes with conformational change earn high scores (Figure 1A, top right), whereas shallow pockets (Figure 1A, bottom left) or sites at which large-scale motions are largely unaffected (Figure 1A, bottom right) earn lower scores. Further details are provided in Supplemental Experimental Procedures section 3.1-a.

This approach is a modified version of the binding leverage framework introduced by Mitternacht and Berezovsky (2011a). The main modifications implemented here include the use of heavy atoms in the protein during the MC search, in addition to an automated means of thresholding the list of ranked scores. These modifications were implemented to provide a more selective set of sites; without them, a very large fraction of the protein surface would be occupied by critical sites (Figure S2A). Within our dataset of proteins exhibiting alternative conformations, we find that this modified approach results in an average of approximately two distinct sites per domain (Figure S2A; see Figure S2B for the distribution for distinct sites within entire complexes).

Within the canonical set of 12 proteins, we positively identify an average of 55.6% of the sites known to be directly involved in ligand or substrate binding (see Table 1, Figure S1; Supplemental Experimental Procedures section 3.1-a-iv). Some of the sites identified do not directly overlap with known binding regions, but we often find that these “false positives” nevertheless exhibit some degree of overlap with binding sites (Table S2). In addition, those surface-critical sites that do not match known binding sites may nevertheless correspond to latent allosteric regions: even if no known biological function is assigned to such regions, their occlusion may nevertheless disrupt hitherto unfound large-scale motions.

Table 1.

Statistics on the Surfaces of apo Structures within the Canonical Set of Proteins

PDB ID	Surf (SC Res)	Surf (LB Res)	SC-LB Overlap	No. of SC Sites	No. of LB Sites	No. of Overlapping Sites	% LB Sites Identified
3pfk	0.51	0.204	0.255 (0.155)	19	3	3	1
4ake	0.454	0.178	0.274 (0.154)	29	2	2	1
1cd5	0.589	0.1	0.153 (0.096)	24	2	1	0.5
1j3h	0.066	0.08	0.25 (0.041)	2	1	1	1
1bks	0.343	0.097	0.079 (0.079)	24	4	1	0.25
1e5x	0.207	0.093	0.139 (0.077)	17	3	2	0.667
1efk	0.055	0.086	0.03 (0.036)	10	10	0	0
1nr7	0.149	0.175	0.187 (0.102)	45	24	6	0.25
1xtt	0.298	0.196	0.295 (0.154)	31	5	5	1
2hnp	0.739	0.133	0.16 (0.134)	25	2	2	1
3d7s	0.267	0.137	0.054 (0.064)	26	9	0	0
3ju5	0.016	0.039	0 (0.013)	1	2	0	0
Mean	0.308	0.127	0.156 (0.092)	21.083	5.583	1.917	0.556

For each apo structure within the canonical set of proteins, statistics relating surface-critical sites to known ligand-binding sites are reported. The surface of a given structure is defined to be the set of all residues that have a relative solvent accessibility of at least 50%, where relative solvent accessibility is evaluated using all heavy atoms in both the main chain and side chain of a given residue. Mean values are given in the bottom row. NACCESS is used to calculate relative solvent accessibility (Hubbard and Thornton, 1993). Column 1: protein name and PDB IDs for each structure. Column 2: among these surface residues, the fraction that constitutes surface-critical residues (SC Res). Column 3: among surface residues, the fraction that constitutes known ligand-binding residues (LB Res) (known ligand-binding residues are taken to be those within 4.5 Å of the ligand in the holo structure; Table S1). Column 4: the Jaccard similarity between the sets of residues represented in columns 2 and 3 (i.e., surface-critical and known ligand-binding residues), where values given in parentheses represent the expected Jaccard similarity, given a null model in which surface-critical and ligand-binding residues are randomly distributed throughout the surface (for each structure, 10,000 simulations are performed to produce random distributions, and the expected values reported here constitute the mean Jaccard similarity among the 10,000 simulations for each structure). Column 5: the number of distinct surface-critical sites identified in each structure. Column 6: the number of known ligand-binding sites in each structure. Column 7: the number of known ligand-binding sites which are positively identified within the set of surface-critical sites, where a positive match occurs if a majority of the residues in a surface-critical site coincide with the known ligand-binding site. Column 8: the fraction of ligand-binding sites captured is simply the ratio of the values in column 7 to those in column 6. See also Figure S1; Tables S1 and S2.

Dynamical Network Analysis to Identify Interior-Critical Residues

The binding leverage framework described above is intended to capture hotspot regions at the protein surface, but the MC search employed is a priori excluded from the protein interior. Allosteric residues often act within the protein interior by functioning as essential information-flow “bottlenecks” within the communication pathways between distant regions.

To identify such bottleneck residues, we first model the protein as a network, wherein residues represent nodes and edges represent contacts between residues (in much the same way that the protein is modeled as a network in constructing anisotropic network models, see below). In this regard, the problem of identifying interior-critical residues is reduced to a problem of identifying nodes that participate in network bottlenecks (see Figure 1B and Supplemental Experimental Procedures section 3.1-b for details). In brief, the network edges are first weighted by the degree of strength in the correlated motions of contacting residues: a strong correlation in the motion between contacting residues implies that knowing how one residue moves better enables one to predict the motion of the other, thereby suggesting a strong information flow between the two residues. The weights are used to assign “effective distances” between connecting nodes, with strong correlations resulting in shorter effective node-node distances.

Using the motion-weighted network, “communities” of nodes are identified using the Girvan-Newman formalism (Girvan et al., 2002). This formalism entails calculating the betweenness of each edge, where the betweenness of a given edge is defined as the number of shortest paths between all pairs of residues that pass through that edge. Each path length is the sum of that path’s effective node-node distances assigned in the weighting scheme above. Each community identified is a group of nodes such that each node within the community is highly inter-connected (in terms of betweenness), but loosely connected to other nodes outside the community. Communities are thus densely inter-connected regions within proteins. The community partitions and the resultant critical residues for the canonical set are given in Figure 2.

Figure 2. Community Partitioning for Canonical Systems.

Different network communities are colored differently, and communities were identified using the dynamical network-based analysis with the GN formalism discussed in the main text and in Supplemental Experimental Procedures section 3.1-b. Residues shown as spheres are interior-critical residues, and are colored based on community membership, and black lines connecting pairs of critical residues represent the highest-betweenness edges between the corresponding communities. See also Table S3.

Those residues that are involved in the highest-betweenness edges between pairs of interacting communities are identified as the interior-critical residues. These residues are essential for information flow between communities, as their removal would result in substantially longer paths between the residues of one community to those of another.

Software Tool: STRESS

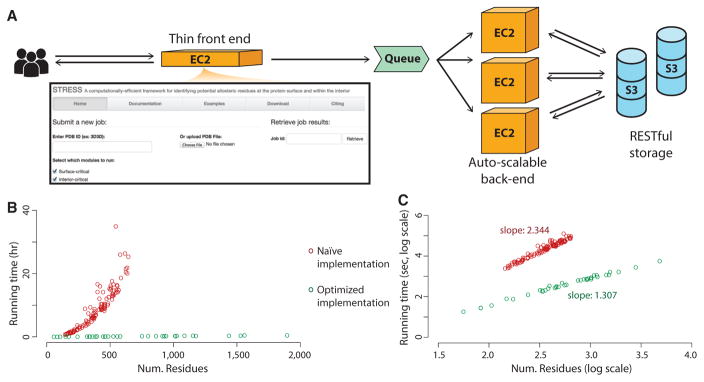
We have made the implementations for finding surface- and interior-critical residues available through a new software tool, STRESS, which may be accessed at stress.molmovdb.org (Figure 3A). Users may submit a PDB file or a PDB ID corresponding to a structure to be analyzed, and the output provided constitutes the set of identified critical residues.

Figure 3. STRESS Web Server Front Page, Running Times, and Server Architecture.

(A) The server enables users to either provide PDB IDs or to upload their own PDB files for proteins of interest. Users may opt to identify surface-critical residues, interior-critical residues, or both. A thin front-end server handles incoming user requests, and more powerful back-end servers perform the heavier algorithmic calculations. The back-end servers are dynamically scalable, making them capable of handling wide fluctuations in user demand. Amazon’s Simple Queue Service is used to coordinate between user requests at the front-end and the back-end compute nodes: when the front-end server receives a request, it adds the job to the queue, and back-end servers pull that job from the queue when ready. Source code is available through Github (https://github.com/gersteinlab/STRESS).

(B) Running times are shown for systems of various sizes. Shown in red are the running times without optimizing for speed, and green shows running times with algorithmic optimization.

(C) The same data represented as a log-log plot. The slopes of these two approaches demonstrate that our algorithm reduces the computational complexity by an order of magnitude. Our speed-optimized algorithm scales at O(n^1.3), where n is the number of residues.

Running times are minimized by using a scalable server architecture that runs on the Amazon cloud (Figure 3). A light front-end server handles incoming user requests, and more powerful back-end servers, which perform the calculations, are automatically and dynamically scalable, thereby ensuring that they can handle varying levels of demand both efficiently and economically. In addition, the algorithmic implementation of our software is highly efficient, thereby obviating long wait times. Relative to a naive global MC search implementation, local searches supported with hashing and additional algorithmic optimizations for computational efficiency reduce running times considerably (Figures 3B and 3C). A typical protein of ~500 residues takes only about 30 min on a 2.6-GHz CPU.

High-Throughput Identification of Alternative Conformations

We use a generalized approach to systematically identify instances of alternative conformations throughout the PDB. We first perform multiple structure alignments (MSAs) across sequence-identical structures that are pre-filtered to ensure structural quality. We then use the resultant pairwise root-mean-square deviation (RMSD) values to infer distinct conformational states (Figure S3; see also Supplemental Experimental Procedures section 3.2).

The distributions of the resultant numbers of conformations for domains and chains are given in Figures S3D and S3E, respectively, and an overview is given in Figure S3F. We note that the alternative conformations identified arise in an extremely diverse set of biological contexts, including conformational transitions that accompany ligand binding, protein-protein or protein-nucleic acid interactions, post-translational modifications, changes in oxidation or oligomerization states, and so forth. The dataset of alternative conformations identified is provided as a resource in Data S1 (see also Figure S3G).

Evaluating Conservation of Critical Residues using Various Metrics and Sources of Data

The large dataset of dynamic proteins culled throughout the PDB, coupled with the high algorithmic efficiency of our critical residue search implementation, provide a means of identifying and evaluating general properties of a large pool of critical residues. In particular, we use a variety of conservation metrics and data sources to measure the inter- and intra-species conservation of the residues within this pool. As discussed below, we find that both surface-critical (Figures 4A–4D) and interior-critical (Figures 4E–4H) residues are consistently more conserved than non-critical residues. We emphasize that the signatures of conservation identified not only provide a means of rationalizing many of the otherwise poorly understood regions of proteins, but also reinforce the functional importance of the residues predicted to be allosteric.

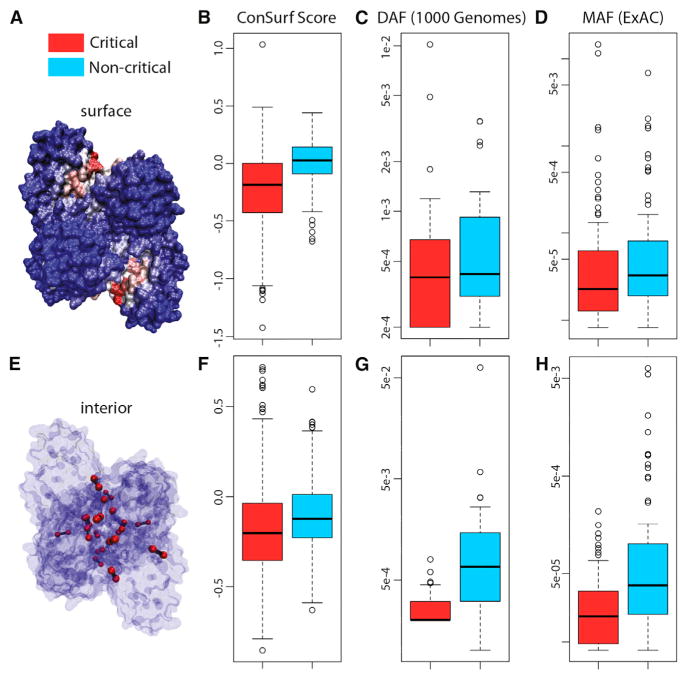
Figure 4. Multiple Metrics and Datasets Reveal that Critical Residues Tend to Be Conserved.

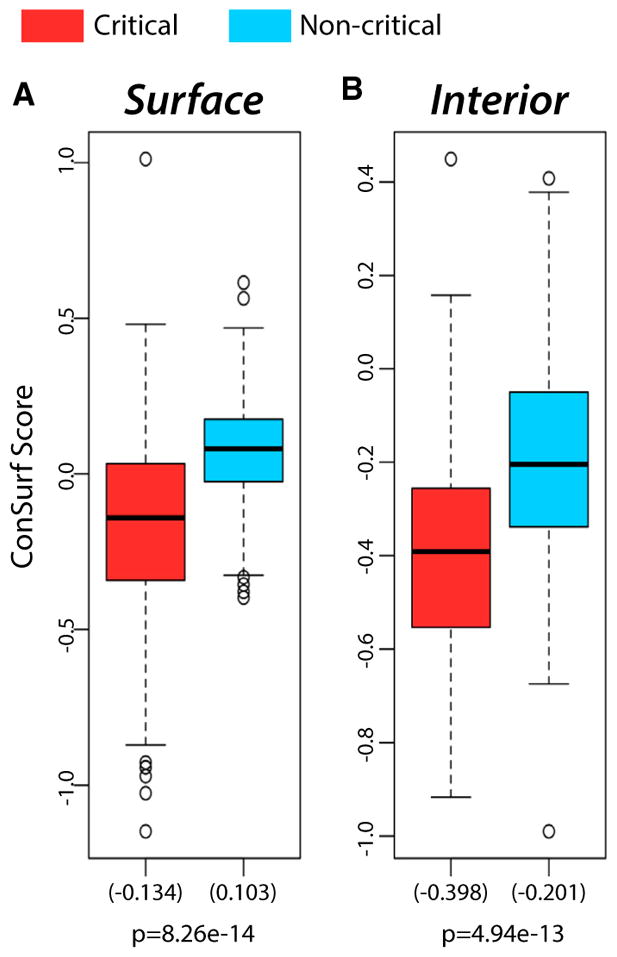
(A–H) Surface- and interior-critical residues (red) in phosphofructokinase (PDB: 3PFK) are given in (A) and (E), respectively. Distributions of cross-species conservation scores, 1,000 Genomes SNV DAF averages, and ExAC SNV MAF averages for surface- and non-critical residue sets are given in (B), (C), and (D), respectively. The same distributions corresponding to interior- and non-critical residue sets are given in (F), (G), and (H), respectively. In (B), mean inter-species conservation scores for surface-critical sets are −0.131, whereas non-critical residue sets with the same degree of burial have a mean score of +0.059 (p < 2.2 × 10⁻¹⁶). In (F), mean inter-species conservation scores for interior-critical sets are −0.179, whereas non-critical residue sets with the same degree of burial have a mean score of −0.102 (p = 3.67 × 10⁻¹¹). In (C), means for surface- and non-critical sets are 9.10 × 10⁻⁴ and 8.34 × 10⁻⁴, respectively (p = 0.309); corresponding means in (D) are 4.09 × 10⁻⁰⁴ and 2.26 × 10⁻⁰⁴, respectively (p = 1.49 × 10⁻³). In (G), means for interior- and non-critical sets are 2.82 × 10⁻⁴ and 3.12 × 10⁻³, respectively (p = 1.80 × 10⁻⁰⁵); corresponding means in (H) are 3.08 × 10⁻⁰⁵ and 3.27 × 10⁻⁰⁴, respectively (p = 7.98 × 10⁻⁰⁹). N = 421, 32, 84, 517, 31, and 90 structures for (B), (C), (D), (F), (G), and (H), respectively. p Values are based on Wilcoxon rank-sum tests. The whiskers extend to the most extreme data point which is no more than 1.5 times the interquartile range from the box. See Supplemental Experimental Procedures for further details. See also Figures S2 and S4.

Conservation across Species

When evaluating conservation across species, we find that both surface- and interior-critical residues tend to be significantly more conserved than non-critical residues with the same degree of burial (Figures 4B and 4F, respectively; note that negative conservation scores designate stronger conservation—see Supplemental Experimental Procedures section 3.3-a).

Leveraging Next-Generation Sequencing to Measure Conservation among Humans

In addition to measuring inter-species conservation, we have also used fully sequenced human genomes and exomes to investigate conservation among human populations, as many constraints may be species specific and active in more recent evolutionary history. Commonly used metrics for quantifying intra-species conservation include minor allele frequency (MAF) and derived allele frequency (DAF). Low MAF or DAF values are interpreted as signatures of deleteriousness, as purifying selection is prone to reduce the frequencies of harmful variants (see Supplemental Experimental Procedures section 3.3-b).

Non-synonymous single-nucleotide variants (SNVs) from the 1,000 Genomes dataset (McVean et al., 2012) that intersect surface-critical residues tend to occur at lower DAF values than do SNVs that intersect non-critical residues (Figure 4C). Although this difference is not observed to be significant, the significance improves when examining the shift in DAF distributions, as evaluated with a KS test (p = 0.159, Figure S4A), and we point out only a limited number of proteins (32) for which these 1,000 Genomes SNVs intersect with surface-critical sites. Furthermore, the long tail extending to lower DAF values for surface-critical residues may suggest that only a subset of the residues in our prioritized binding sites is essential. In contrast to surface-critical residues, however, interior-critical residues intersect 1,000 Genomes SNVs with significantly lower DAF values than do non-critical residues (Figure 4G; see also Figure S4B).

When analyzing human polymorphism data, a variety of statistical measures relating SNVs to selective constraint may be calculated, and the results obtained (along with their associated significance levels) are highly dependent on sample size. 1,000 Genomes datasets are attractive partially because of their status as a well-established “blue-chip” set of variants in human populations. However, given the relatively limited number of proteins that intersect with 1,000 Genomes SNVs, we also analyzed the larger dataset provided by the Exome Aggregation Consortium (ExAC) (Exome Aggregation Consortium et al., 2015). Although this dataset has been released much more recently (and is consequently not yet as well established as 1,000 Genomes), ExAC provides sequence data from more than 60,000 individuals, and samples are sequenced at much higher coverage, thereby ensuring better data quality. This larger dataset enables us to more easily examine trends in the data as they relate to critical and non-critical residues.

Using MAF as a conservation metric, we performed a similar analysis using this data. MAF distributions for surface- and non-critical residues in the same set of proteins are given in Figure 4D. Although the mean value of the MAF distribution for surface-critical residues is slightly higher than that of non-critical residues, the median for surface-critical residues is substantially lower than that for non-critical residues, demonstrating that the majority of proteins are such that MAF values are lower in surface-critical than in non-critical residues. In addition, the overall shifts of these distributions also point to a trend of lower MAF values in surface-critical residues (Figure S4C, KS test p = 9.49 × 10⁻²).

Interior-critical residues exhibit significantly lower MAF values than do non-critical residues in the same set of proteins. MAF distributions for interior- and non-critical residues are given in Figure 4H (see also Figure S4D).

In addition to analyzing overall allele frequency distributions, we also evaluate the fraction of rare alleles as a metric for measuring selective pressure. This fraction is defined as the ratio of the number of rare (i.e., low-DAF or low-MAF) non-synonymous SNVs to the number of all non-synonymous SNVs in a given protein annotation (such as all surface-critical residues of the protein, for example; see Supplemental Experimental Procedures section 3.3-b). A higher fraction is interpreted as a proxy for greater conservation (Khurana et al., 2013; Sethi et al., 2015). Using variable DAF (MAF) cutoffs to define rarity for 1,000 Genomes (ExAC) SNVs, both surface- and interior-critical residues are shown to harbor a higher fraction of rare alleles than do non-critical residues, further suggesting a greater degree of evolutionary constraint on critical residues (Figure 5).

Figure 5. Critical Residues Are Shown to Be More Conserved, as Measured by the Fraction of Rare Alleles.

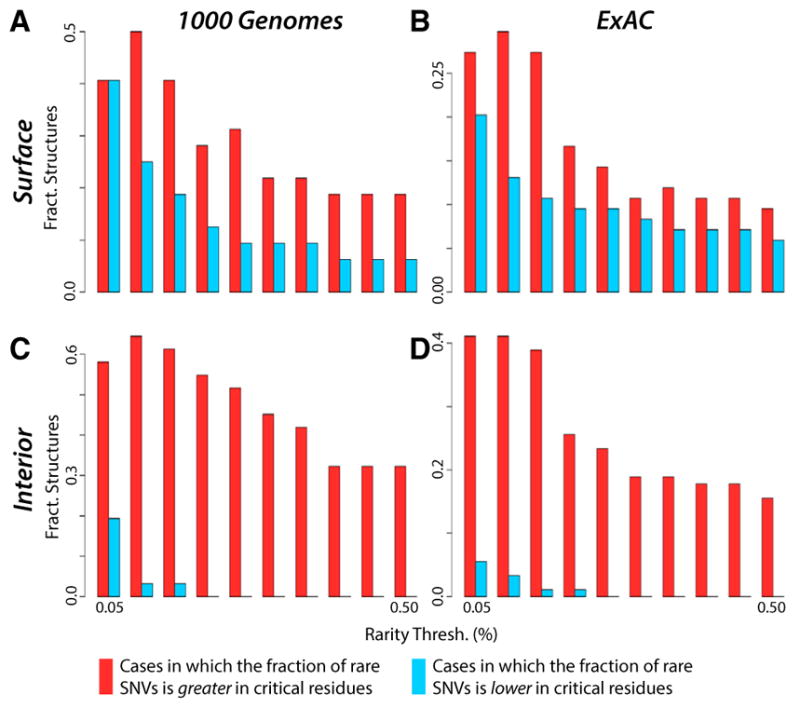
Protein regions with high fractions of rare variants are believed to be more sensitive to sequence variants than other regions, thereby explaining why such variants occur infrequently in the population.

(A and C) Distributions for rare (low-DAF) non-synonymous SNVs (taken from the 1,000 Genomes dataset) in which the critical residues are defined to be the surface-critical (A) and interior-critical (C) residues.

(B and D) Distributions for rare (low MAF) non-synonymous SNVs (taken from the ExAC dataset) in which the critical residues are defined to be the surface-critical (B) and interior-critical (D) residues. For varying thresholds to define rarity, there are more structures in which the fraction of rare variants is higher in critical residues than in non-critical residues. Cases in which the fraction is equal in both categories are not shown. We consider all structures such that at least one critical and at least one non-critical residue intersect a non-synonymous SNV.

(A), (B), (C), and (D) represent data from 31, 90, 32, and 84 structures, respectively.

Comparisons between Different Models of Protein Motions

The identification of surface- and interior-critical residues entails using sets of vectors (on each protein residue) to describe conformational change. Notably, our framework enables one to determine these vectors in multiple ways. Conformational changes may be modeled using vectors connecting residues in crystal structures from alternative conformations. We term this approach ACT, for “absolute conformational transitions” (see Supplemental Experimental Procedures section 3.2-c). The crystal structures of such paired conformations may be obtained using the framework discussed above. The protein motions may also be inferred from anisotropic network models (ANMs) (Atilgan et al., 2001). ANMs entail modeling interacting residues as nodes linked by flexible springs, in a manner similar to elastic network models (Fuglebakk et al., 2015; Tirion, 1996) or normal modes analysis (Figure 1B). ANMs are not only simple and straightforward to apply on a database scale, but unlike using alternative crystal structures, the motion vectors inferred may be generated using a single structure.

We find that modeling conformational change using vectors from either ACTs or ANMs gives the same general trends in terms of the disparities in conservation between critical and non-critical residues. Our framework is thus general with respect to how the motion vectors are obtained (see Figure 6 and Supplemental Experimental Procedures section 3.2-c for further details).

Figure 6. Modeling Protein Conformational Change Through a Direct Use of Crystal Structures from Alternative Conformations using Absolute Conformational Transitions.

(A) Distributions (155 structures) of the mean conservation scores on surface-critical (red) and non-critical residues with the same degree of burial (blue).

(B) Distributions (159 structures) of the mean conservation scores for interior-critical (red) and non-critical residues with the same degree of burial (blue). Mean values are given in parentheses. Results for single-chain proteins are shown, and p values were calculated using a Wilcoxon rank-sum test. See also Figure S3.

The whiskers extend to the most extreme data point which is no more than 1.5 times the interquartile range from the box.

Critical Residues in the Context of Human Disease Variants

Directly related to conservation is confidence with which an SNV is believed to be disease associated. SIFT (Ng and Henikoff, 2001) and PolyPhen (Adzhubei et al., 2010) are two tools for predicting SNV deleteriousness. ExAC SNVs that intersect critical residues exhibit significantly higher PolyPhen scores relative to non-critical residues, suggesting the potentially higher disease susceptibility at critical residues (Figure S5). Significant disparities were not observed in SIFT scores (Figure S6).

Using HGMD (Stenson et al., 2014) and ClinVar (Landrum et al., 2014), we identify proteins with critical residues that coincide with disease-associated SNVs (Data S2). Several critical residues coincide with known disease loci for which the mechanism of pathogenicity is otherwise unclear (Data S3). The fibroblast growth factor receptor (FGFR) is a case in point (Figure 7A). SNVs in FGFR have been linked to craniofacial defects. Dotted lines in Figure 7B highlight poorly understood disease SNVs that coincide with critical residues. In addition, we identify Y328 as a surface-critical residue, which coincides with a disease-associated SNV from HGMD, despite the lack of confident predictions of deleteriousness by several widely used tools for predicting disease-associated SNVs, including PolyPhen (Adzhubei et al., 2010), SIFT (Ng and Henikoff, 2001), and SNPs&GO (Calabrese et al., 2009). Together, these results suggest that the incorporation of surface- and interior-critical residues introduces a valuable layer of annotation to the protein sequence, and may help to explain otherwise poorly understood disease-associated SNVs.

Figure 7. Potential Allosteric Residues Add a Layer of Annotation to Structures in the Context of Disease-Associated SNVs.

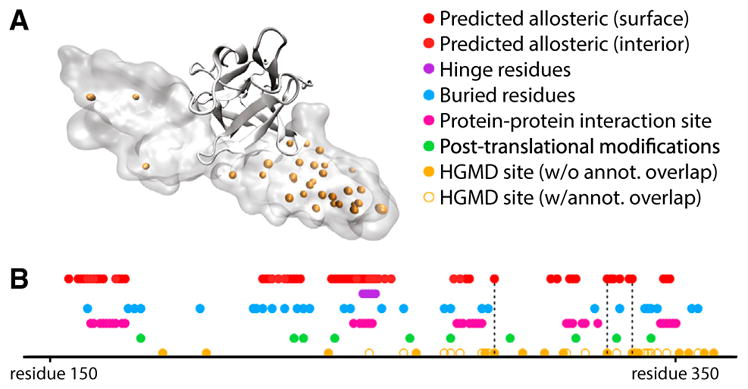
(A) Structure of the fibroblast growth factor receptor (FGFR) in VMD Surf rendering, with HGMD SNVs shown in orange, bound to FGF2, in ribbon rendering (PDB: 1IIL).

(B) Linear representation of structural annotation for FGFR. Dotted lines highlight loci which correspond to HGMD sites that coincide with critical residues, but for which other annotations fail to coincide. Deeply buried residues are defined to be those that exhibit a relative solvent-exposed surface area of 5% or less, and binding-site residues are defined as those for which at least one heavy atom falls within 4.5 Å of any heavy atom in the binding partner (heparin-binding growth factor 2). The loci of post-translational modification sites were taken from UniProt (UniProt: P21802). See also Figures S5 and S6.

DISCUSSION

The same principles of energy landscape theory that dictate protein folding are integral to how proteins explore different conformations once they adopt their fully folded states. These landscapes are shaped not only by the protein sequence itself but also by extrinsic conditions. Such external factors often regulate protein activity by introducing allosteric-induced changes, which ultimately reflect changes in the shapes and population distributions of the energetic landscape. In this regard, allostery provides an ideal platform from which to study protein behavior in the context of their energetic landscapes. For investigation of allosteric regulation, and to simultaneously add an extra layer of annotation to conservation patterns, an integrated framework to identify potential allosteric residues is essential. We introduce a framework to select such residues, using knowledge of conformational change.

When applied to many proteins with distinct conformational changes in the PDB, we investigate the conservation of potential allosteric residues in both inter-species and intra-human genomes contexts, and find that these residues tend to exhibit greater conservation in both cases. In addition, we identify several disease-associated variants for which plausible mechanisms had been unknown, but for which allosteric mechanisms provide a reasonable rationale.

Unlike the characterization of many other structural features, such as secondary structure assignment, residue burial, protein-protein interaction interfaces, disorder, and even stability, allostery inherently manifests through dynamic behavior. It is only by considering protein motions and changes in these motions that a fuller understanding of allosteric regulation can be realized. As such, MD and NMR are some of the most common means of studying allostery and dynamic behavior (Kornev and Taylor, 2015). However, these methods have limitations when studying large and diverse protein datasets. MD is computationally expensive and impractical when studying large numbers of proteins. NMR structure determination is extremely labor intensive and better suited to certain classes of structures or dynamics. In addition, NMR structures constitute a relatively small fraction of structures currently available.

Despite these limitations in MD and NMR, allosteric mechanisms and signaling pathways may be conserved across many different but related proteins within the same family, suggesting that such computationally intensive or labor-intensive approaches for all proteins may not be entirely essential. Flock et al. (2015) have carefully demonstrated that the allosteric mechanisms responsible for regulating G proteins through GPCRs tend to be conserved. Investigations into representative families have also been enlightening in other contexts. In one of the early studies employing network analysis, del Sol et al. (2006) conducted a detailed study of several allosteric protein families (including GPCRs) to demonstrate that residues important for maintaining the integrity of short paths within residue contact networks are essential to enabling signal transmission between distant sites. Another notable result in the same work is that these key residues (which match experimental results) may become redistributed when the protein undergoes conformational change, thereby changing optimal communication routes as a means of conferring different regulatory properties.

There are several notable implications of our dynamics-based analysis across a database of proteins. Relative to sequence data, allostery and dynamic behavior are far more difficult to evaluate on a large scale. The framework described here enables one to evaluate dynamic behavior in a systemized and efficient way across many proteins while simultaneously capturing residues on both the surface and within the interior. That this pipeline can be applied in a high-throughput manner enables the investigation of system-wide phenomena, such as the roles of potential allosteric hotspots in protein-protein interaction networks.

It is only by analyzing a large dataset of proteins that one can investigate general trends in predicted allosteric residues. In addition, the implementation detailed here enables one to match structural features with the high-throughput data generated through deep sequencing initiatives, which are providing an unprecedented window into conservation patterns, many of which may be human specific.

We anticipate that, within the next decade, deep sequencing will enable structural biologists to study evolutionary conservation using sequenced human exomes just as routinely as cross-species alignments. Furthermore, intra-species metrics for conservation provide added value in that the confounding factors of cross-species comparisons are removed: different species evolve in various evolutionary contexts and at different rates, and it can be difficult to decouple these different effects from one another. Cross-species metrics of protein conservation entail comparisons between proteins that may be very different in structure and function. Sequence-variable regions across species may not be conserved, but nevertheless impart essential functionality. Intra-species comparisons, however, can often provide a more direct and sensitive evaluation of constraint.

In particular, selective constraints within human populations are particularly relevant to understanding human disease. Formalisms for analyzing large structural and sequence datasets will become increasingly important in the context of human health. We anticipate that the framework and formalisms detailed here, along with the accompanying web tool we have introduced, will help to further motivate future studies along these directions.

EXPERIMENTAL PROCEDURES

Identifying Potential Allosteric Residues

Identifying Surface-Critical Residues

We employ a modified version of the binding leverage method for identifying likely ligand-binding sites (Figure 1A), as described previously (Mitternacht and Berezovsky, 2011a). Further details are given below, as well as within Supplemental Experimental Procedures section 3.1-a.

Monte Carlo Simulations to Identify Candidate Allosteric Sites on the Surface

Candidate sites on the surface are generated by MC simulations in which a flexible ligand (comprising of four “atoms” linked by bonds of fixed length 3.8 Å, but variable bond and dihedral angles) explores the protein’s surface. The number of MC simulations is set to ten times the number of residues in the structure, and the number of MC steps per simulation in our implementation is set to 10,000 times the size of the simulation box, as measured in angstroms. The size of this box is set to twice the maximum size of the PDB along any of the x, y, or z axes. Heavy atoms are used in the protein when evaluating a ligand’s affinity for each location.

The parameters (for a square well potential function) used to evaluate the energy of the system at each step is as follows (here, D_lig-prot designates the distance between a ligand atom and a protein atom, in angstroms):

Widths	Depths and Heights
∞ > Dlig-prot ≥ 4.5:	energy = 0
4.5 > Dlig-prot ≥ 3.5:	energy = −0.35 (attractive)
3.5 > Dlig-prot ≥ 3.0:	energy = +10 (repulsive)
3.0 > Dlig-prot ≥ 0.0:	energy = +10,000 (strongly repulsive: effectively prohibited)

What form does the MC ensemble take, and how exactly is this MC ensemble turned into a list of candidate sites? Prior to thresholding the list of ranked sites (see Supplemental Experimental Procedures section 3.1-a-iii), we generally follow the same formalism detailed in Mitternacht and Berezovsky (2011a). We first detail the output provided by a single MC simulation. This MC simulation involves a ligand probing the protein surface through a large number of steps in which the ligand explores translational, rotational, and angular degrees of freedom. The potential function usually “pushes” the ligand to favorably occupy a pocket on the protein surface after all steps of the MC simulation are completed. The ligand is thus in contact with a number of residues (typically 10–20) at the end of the simulation. As with the approach taken by Mitternacht and Berezovsky, this list of residues is ordered by local closeness (LC). LC is a geometric quantity that provides a measure of the degree of a residue in the residue-residue contact network; see Mitternacht and Berezovsky (2011b) for further discussion of LC. The ten residues with greatest LC are taken as the final “site” occupied by the ligand at the end of this MC simulation (the remaining residues are not considered to be part of the site). Thus, the output of this single MC simulation is a list of ten residues on the protein surface such that these residues form a geometrically favorable site for the ligand.

Now consider a very large number (typically 5,000–10,000, depending on the protein’s size) of the MC simulations detailed above. These ~10,000 MC simulations result in many sites, where each of these sites is the list of residues in contact with the ligand by the end of the MC simulation. This long list of sites generally contains many sites with a strong degree of overlap. Thus, to remove redundancy, pairs of sites with extremely high overlap are merged. The residues of a given merged site are then listed by their LC, and no more than ten residues for a site are used. This entire process results in a list of sites on which binding leverage calculations can be performed.

Binding Leverage Calculations

When the ten lowest-frequency normal modes are produced for each structure, the binding leverage score for a given site is calculated as

$$\text{Binding}\text{leverage}=\sum _{m=1}^{10}\left(\sum _i\sum _j\mathit{\Delta }{d}_{ij(m)}^2\right).$$

The outer sum is taken over the ten modes, and the pair of inner sums are taken over all pairs of residues (i,j) such that the line connecting the pair lies within 3.0 Å of any atom within the simulated ligand. The value Δd_ij(m) for each residue pair (i,j) represents the change in the distance between residues i and j when this distance is calculated using mode m. Further details are given in Supplemental Experimental Procedures section 3.1-a-ii.

Identifying Interior-Critical Residues

A protein structure is represented as a network of interacting residues, and the edges between residues are weighted using inferred motions. Network modules are then identified, and residues that are important for inter-module communication are identified as being interior-critical. Detailed information is given below and in Supplemental Experimental Procedures section 3.1-b.

Network Formalism and Weighting Scheme

An edge between residues i and j is drawn if any heavy atom within residue i is within 4.5 Å of any heavy atom of residue j, and we exclude the trivial cases of pairs of residues that are adjacent in sequence, which are not considered to be in contact within the network.

An “effective distance” D_ij for an edge between interacting residues i and j is set to D_ij = −log(|C_ij|), where C_ij designates the correlated motions between residue i and j,

$$C_{ij}={\text{Cov}}_{ij}/\sqrt{\left(\langle {\mathbf{r}}_{\mathrm{i}}^2\rangle \langle {\mathbf{r}}_{\mathrm{j}}^2\rangle \right)},$$

where

$${\text{Cov}}_{ij}=\langle {\mathbf{r}}_{\mathrm{i}}•{\mathbf{r}}_{\mathrm{j}}\rangle .$$

Here, r_i and r_j designate the vectors associated with residues i and j (respectively) under a particular normal mode. The brackets in the term 〈r_i·r_j〉 indicate that we are taking the mean value for the dot product r_i·r_j over the ten lowest-frequency non-trivial modes.

Once all connections between interacting pairs of residues are appropriately weighted and the communities are assigned using the Girvan-Newman (GN) algorithm (Girvan et al., 2002) with these effective distances, a residue is deemed to be an interior-critical residue if it is involved in the highest-betweenness edge connecting two distinct communities.

High-Throughput Identification of Alternative Conformations

We start by removing structures with resolution values poorer than 2.8, as well as any PDB files with R_free values poorer than 0.28. STAMP (Russell and Barton, 1992) and MultiSeq (Roberts et al., 2006) were used to generate the MSAs. For each MSA, the final output is a symmetric matrix representing all pairwise RMSD values, which are then used as input to the K-means module (see below).

Using a modified version of the K-means clustering algorithm, termed K-means clustering with the gap statistic (Tibshirani et al., 2001), pairwise RMSD values are used to identify the biologically distinct conformations represented by an ensemble.

As a first step toward clustering the structure ensemble of N structures, we use multidimensional scaling (MDS) to convert an N-by-N matrix of pairwise RMSD values into a set of N distinct points. These matrices are then provided as input for K-means with the gap statistic; we point the reader to the work by Tibshirani et al. (2001) for details. Further details are also provided in Supplemental Experimental Procedures section 3.2.

Models of Conformational Change via Displacement Vectors from Alternative Conformations

Inferring Protein Conformational Change using Displacement Vectors from Alternative Conformations

Given a particular protein, how are these ACT vectors defined to find critical residues? We discuss a hypothetical example consisting of a multiple structure alignment of eight sequence-identical structures. Starting with the protein’s alignment using all eight structures, we determine the optimal number of clusters represented by the alignment (see above). Suppose that these eight structures may be grouped into two distinct clusters. A representative structure is taken from each of these two clusters (structure A and structure B). We use structure A and structure B to infer information about the protein’s global conformational shifts by assigning a displacement vector to each residue, where the displacement vector is simply defined by the two corresponding residues in the different structures within the structure alignment.

When using ACT vectors, the binding leverage score for a given site is simply calculated as

$$\text{Binding}\text{leverage}=\sum _i\sum _j\mathit{\Delta }{d}_{ij}^2.$$

When identifying interior-critical residues, there is only one ACT vector for each residue. Thus, the weight parameters are calculated as

$$C_{ij}={\text{Cov}}_{ij}/\surd \left({\mid {\mathbf{r}}_i\mid }^2\times {\mid {\mathbf{r}}_j\mid }^2\right),$$

where

$${\text{Cov}}_{ij}={\mathbf{r}}_i•{\mathbf{r}}_j.$$

Here, r_i denotes the vector that defines the change in position for residue i when going from one representative conformation to the other.

Evaluating Conservation of Critical Residues using Various Metrics and Sources of Data

Conservation across Species

All cross-species conservation scores represent the ConSurf scores, as downloaded from the ConSurf server (Ashkenazy et al., 2010; Celniker et al., 2013; Glaser et al., 2003; Landau et al., 2005). Low (i.e., negative) ConSurf scores represent a stronger degree of conservation. Cross-species conservation scores were analyzed in those PDBs for which full ConSurf files are available through the ConSurf server.

Each point within the cross-species conservation plots (e.g., Figures 4B, 4F, and 6) represents data from one structure: the value of the point for any given structure represents the mean conservation score for all residues within one of two classes: the set of N critical residues within a protein structure (surface or interior) or a randomly selected set of N non-critical residues (with the same “degree,” see below) within the same structure. The randomly selected noncritical set of residues was chosen in a way such that, for each critical residue with degree k (k being the number of non-adjacent residues with which the critical residue is in contact, see below), a randomly selected non-critical residue with the same degree k was included in the set. The distributions of non-critical residues shown are very much representative of the distributions observed when rebuilding the random set many times.

The degree (i.e., k) of residue j is defined as the number of residues which interact with residue j, where residues adjacent to residue j in sequence are not considered, and an interaction is defined whenever any heavy atom in an interacting residue is within 4.5 Å of any heavy atom in the residue j.

Measures of Conservation among Humans from Next-Generation Sequencing

Only non-synonymous SNVs are analyzed in this study. All 1,000 Genomes SNVs represent data from the phase 3 release of The 1,000 Genomes Project (McVean et al., 2012). ExAC SNVs were downloaded from the Broad Institute in May 2015 from the ExAC Browser (Beta).

When analyzing both 1,000 Genomes and ExAC data, we consider only those structures in which at least one critical and one non-critical residue intersect a non-synonymous SNV. Each individual point within the intra-human conservation plots (e.g., Figures 4C, 4D, 4G, and 4H) represents data from one structure: the value of the point for any given structure represents the mean score (DAF or MAF, for 1,000 Genomes or ExAC SNVs, respectively) for all critical (red bars) or non-critical (blue bars) residues to intersect SNVs.

Highlights.

• Allostery often provides a biophysical rationale for signatures of conservation

• Models of protein conformational change are used to predict key allosteric residues

• These predicted allosteric residues are conserved across species and amongst humans

• A web tool makes this analysis publicly available to the scientific community