Dictionary-driven Ischemia Detection from Cardiac Phase-Resolved Myocardial BOLD MRI at Rest

Abstract

Cardiac Phase-resolved Blood-Oxygen-Level Dependent (CP–BOLD) MRI provides a unique opportunity to image an ongoing ischemia at rest. However, it requires post-processing to evaluate the extent of ischemia. To address this, here we propose an unsupervised ischemia detection (UID) method which relies on the inherent spatio-temporal correlation between oxygenation and wall motion to formalize a joint learning and detection problem based on dictionary decomposition. Considering input data of a single subject, it treats ischemia as an anomaly and iteratively learns dictionaries to represent only normal observations (corresponding to myocardial territories remote to ischemia). Anomaly detection is based on a modified version of One-class Support Vector Machines (OCSVM) to regulate directly the margins by incorporating the dictionary-based representation errors. A measure of ischemic extent (IE) is estimated, reflecting the relative portion of the myocardium affected by ischemia. For visualization purposes an ischemia likelihood map is created by estimating posterior probabilities from the OCSVM outputs, thus obtaining how likely the classification is correct. UID is evaluated on synthetic data and in a 2D CP–BOLD data set from a canine experimental model emulating acute coronary syndromes. Comparing early ischemic territories identified with UID against infarct territories (after several hours of ischemia), we find that IE, as measured by UID, is highly correlated (Pearson’s r = 0.84) w.r.t. infarct size. When advances in automated registration and segmentation of CP–BOLD images and full coverage 3D acquisitions become available, we hope that this method can enable pixel-level assessment of ischemia with this truly non-invasive imaging technique.

I. Introduction

CARDIAC Phase-resolved Blood-Oxygen-Level Dependent (CP–BOLD) Magnetic Resonance Imaging (MRI) is a state-of-the-art technique for directly examining changes in myocardial oxygenation without any contrast media [1], [2]. In a single acquisition it obtains both BOLD contrast and myocardial function that can be seen as a movie (effectively a cine BOLD acquisition). Recently, it was shown that CP–BOLD can be used even at rest [3], without any contraindicated provocative stress (exercise or pharmacological agents) [4], offering a truly non-invasive “needle-free” approach to ischemia evaluation. This approach relies on examining differential myocardial signal intensity variations (when seen as a function of cardiac phase) among territories affected by ischemia and “remote territories” (i.e. not affected by the disease) [3]. However, since signal intensity changes are subtle (≈15%) and need information across cardiac phases, direct visualization is difficult and requires post-processing. Here, we propose a method to detect ischemia by identifying remote and ischemic patterns of oxygenation and wall motion synergistically using a dictionary-based decomposition. Ischemia quantification and visualization are obtained in a completely unsupervised fashion without any prior knowledge on disease status using as sole input the CP-BOLD data of the subject.

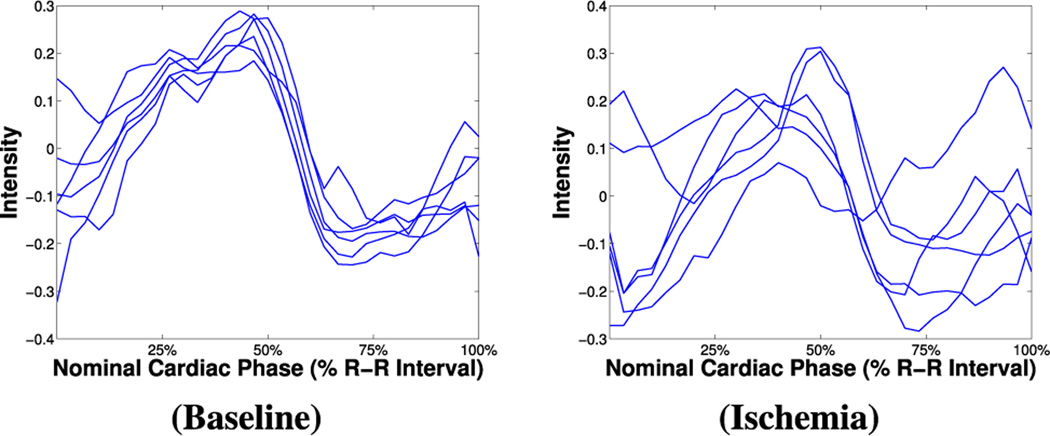
As Fig. 1 illustrates the BOLD signal intensity is maximum in systole and minimum in diastole in healthy conditions, but territories of the myocardium, affected by arterial occlusion, do not exhibit this behavior. Exploiting this phenomenon, Tsaftaris et al. [3] used myocardial radial segments from late systolic and diastolic frames to define S/D: the ratio of average segmental intensity at systole over diastole. It was hypothesized and shown that S/D>1 in baseline scenarios or remote to ischemia, and S/D<1 in affected myocardial territories. However, S/D uses only two images of the cine acquisition and provides a coarse segmental analysis.

Fig. 1.

BOLD signal intensity time series (as segmental averages of six different radial segments across the images, ie., frames, of the cine movie) extracted from rest CP–BOLD MRI data of the same subject, at baseline (left) and under ischemia (right). (CP–BOLD is ECG-triggered and first and last time points correspond to diastole. Time series have been normalized according to the process described in Section II-B for ease of visualization.)

On the other hand, there are significant benefits to obtaining visualization maps and quantification at a finer segmental level (ideally that of a single pixel): enabling differential diagnosis into epicardial or endocardial ischemia and other transmural effects, and improving the spatial characterization of the area at risk [5]. Unfortunately, with the S/D approach when averages are taken in smaller segments, noise increases and more often than not the S/D>1 hypothesis may not hold. To this end, we envision that it would be advantageous to use all images from the CP–BOLD image sequence for a better identification of ischemic regions. Recent experiments on properly generated synthetic data [6] have shown that an independent component analysis (ICA) approach adopted from fMRI [7] outperformed S/D. However, ICA cannot accommodate time shifts present in BOLD time series, which are likely due to physiological differences between different myocardial territories [8]. This shifting in time characteristic CP–BOLD effect, was suspected by Tsaftaris et al. [3] and was statistically shown by Rusu et al. [6], using a circulant dictionary model.

In this paper, we use the temporal features of CP–BOLD to establish an unsupervised method for identifying time series affected by ischemia as anomalous w.r.t. remote, which are considered as normal. Our only underlying assumption is that remote time series are more populous w.r.t. those that could be affected, an assumption reasonable for evaluating acute ischemia in single vessel disease. We propose an unsupervised ischemia detection (UID) algorithm by combining time series of the BOLD signal (i.e., radial segmental intensity) and also myocardial function as radial wall thickness (typically used to assess wall motion anomalies from cine MRI). A general multi-component dictionary-driven anomaly detection (DDAD) algorithm, which combines sparse decomposition and a One-class Support Vector Machines classifier (OCSVM) [9] forms the core of UID. In an iterative fashion it finds a normal pattern (with the dictionaries) and classifies anomalous observations incorporating within the OCSVM optimization problem the errors related to the dictionary-based approximation. To detect ischemia with DDAD, observations as time series of both intensity and function are represented by two separate dictionaries, which are learned to characterize normal time series (i.e., those likely to belong to remote territories), and are linked in the joint classification step with OCSVM. Finally, to aid interpretation we provide visualization maps of ischemia likelihood, computing posterior probabilities by approximating the OCSVM outputs with a sigmoid function. The quantitative outcome of UID is a notion of ischemia extent (IE) [10], which measures the relative portion of the myocardium affected by ischemia. We evaluate UID using synthetic data and in 2D CP–BOLD data from a canine experimental model emulating acute coronary syndromes, and validate IE, as measured by UID, w.r.t. infarct size.

The contributions of this paper are both technical and physiological. DDAD is the first method that combines dictionaries and an unsupervised classifier as OCSVM for anomaly detection. Other sparsity enforcing methods (e.g., [11]) base the decision on regularization parameters contained in the dictionary learning formulation itself, which, in practice, turn into hard thresholds applied on the sparse representation coefficients. Moreover, they assume fixed dictionaries [11], whereas here DDAD learns the dictionary in the presence of outliers, which are progressively detected (with OCSVM) without thresholds and excluded from the learning process. Furthermore, this paper also uses for the first time myocardial function (as additional time series) to jointly identify BOLD and functional effects, taking advantage of complementary information between the two [3]. This paper exploits this directly at the raw data level, elevating further the diagnostic power of CP–BOLD imaging as one of the new “multicriteria” cardiac ischemia testing methods. Interestingly, we find that wall thickness as a function of cardiac phase also shifts –a finding unique in the cardiovascular literature. This work is also the first to obtain visual maps of ischemia likelihood, based on inference methods. Our only input is the CP–BOLD data of a single subject and myocardial delineations. As algorithms for precise registration and segmentation of CP–BOLD images advance, we hope to rapidly accelerate the deployment of this method for the pixel-level assessment of ischemia with this truly non-invasive imaging technique.

This work is inspired by the approach of Rusu and Tsaftaris [12], where a circulant dictionary model is used for ischemia detection. However, in this paper, decisions are based on OCSVM and not on thresholds, functional information is also used, and outcomes are validated with extensive experiments.

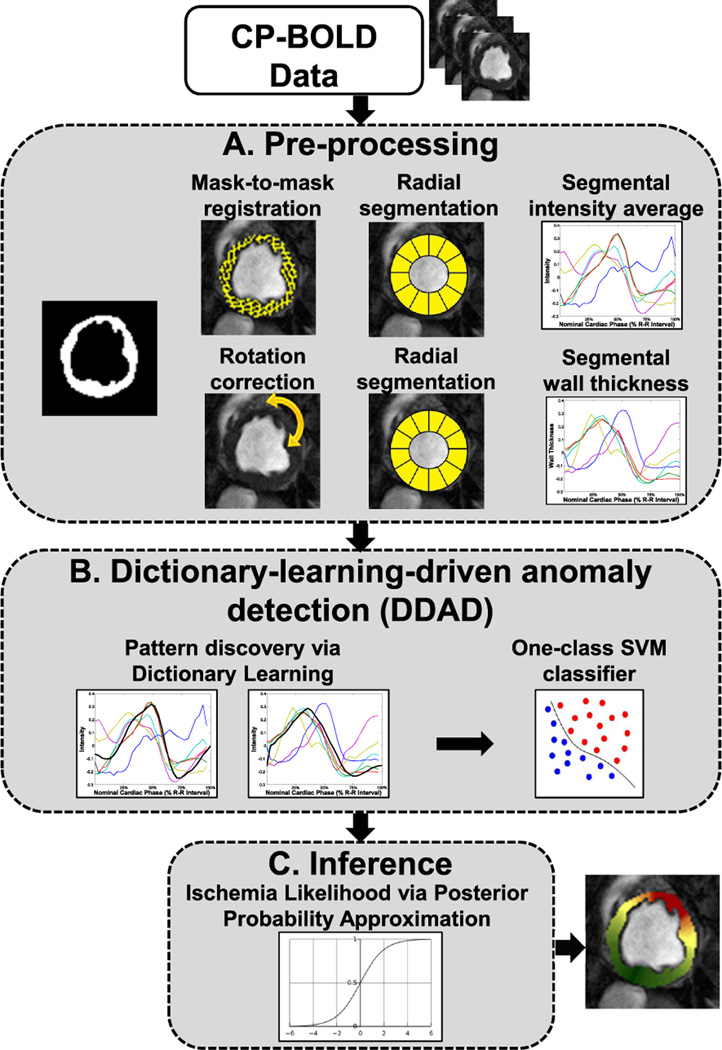
UID’s steps are visually outlined in Fig. 2. After preprocessing (Step A), both intensity and functional time series are extracted from a single image sequence and are given to DDAD for classification (Step B). DDAD identifies anomalous and normal observations, which are used to define an ischemia extent (IE). Finally, Step C performs probabilistic inference, which is used for visualization purposes.

Fig. 2.

Workflow of the proposed unsupervised ischemia detection (UID).

In the following, we present first in Section II data and preprocessing. We present DDAD separately in Section III for clarity, and in Section IV we detail how we apply DDAD to UID (Step B) together with Step C. Before drawing conclusions, Section V presents results on synthetic and real data. Shorthands used in this paper are summarized in Table I.

TABLE I.

Acronyms appearing in the manuscript.

Acronym	Definition	First appearance
CP–BOLD	Cardiac Phase-resolved Blood-Oxygen-Level Dependent	Abstract
DDAD	Dictionary-Driven Anomaly Detection	Sec. I, p. 2
DL	Dictionary Learning	Sec. III, p. 4
DLwT	Dictionary Learning with Theshold	Sec. V, p. 8
FD-OCSVM	Frequency-Domain One-Class Support Vector Machines	Sec. V, p. 8
GT	Ground-Truth	Section V, p. 9
ICA	Independent Component Analyis	Sec. I, p. 2
IE	Ischemic Extent	Abstract
LAD	Left Anterior Descending	Sec. II, p. 3
LGE	Late Gadolinium Enhancement	Sec. II, p. 3
MRI	Magnetic Resonance Imaging	Sec. I, p. 1
NMP	Nonnegative Matching Pursuit	Sec. IV, p. 6
OCSVM	One-Class Support Vector Machines	Abstract
S/D	Systole to Diastole ratio	Sec. I, p. 1
SVM	Support Vector Machines	Sec. IV, p. 6
UID	Unsupervised Ischemia Detection	Abstract
WT	Wall Thickness	Sec. II, p. 3

II. Data and pre-processing

A. Experimental data

We use CP–BOLD MRI data obtained from 11 controlled canine experiments modeling early acute ischemia and reperfusion injury [3], where a controllable hydraulic occluder is affixed to the Left Anterior Descending (LAD) artery and inflated to cause ischemia. While anesthetized and mechanically ventilated, canines were imaged using a clinical 1.5T MRI system twice at rest: before occluder activation (baseline) and during > 90% LAD occlusion.

The protocol, detailed in [3], included breath-held acquisitions at mid-ventricle position with a flow compensated CP–BOLD sequence [2] at baseline and at 20mins post-occlusion. Scan parameters were: field of view, 240×145 mm²; spatial resolution, 1.2×1.2×8 mm³; readout bandwidth, 930 Hz per pixel; flip angle, 70°; TR/echo time (TE), 6.2/3.1 ms; and temporal resolution 37.2 ms). Late Gadolinium Enhancement (LGE) imaging data were also acquired in 8 of the 11 canines after 3 hours of occlusion and during reperfusion (the occluder being released) to identify myocardial regions succumbed to ischemic tissue damage, using a sequence employing a PSIR reconstruction with TurboFLASH readout [13]. Scan parameters were: spatial resolution, 1.3×1.3×8 mm³; TE/TR, 3.9/8.2 ms; TI, 200 to 220 ms; flip angle, 25°; and readout bandwidth, 140 Hz/pixel.

B. Data pre-processing and time series extraction

The goal of UID is to estimate the presence of myocardial ischemia, given as input a single CP–BOLD sequence of images at rest. As mentioned previously, we extract both intensity and “functional time series”, the latter reflecting variations of myocardial wall thickness over time. They are exploited in a common framework.

To accurately isolate the myocardium we rely on expert myocardial delineations and extract time series corresponding to average BOLD signal intensity and myocardial function. Cardiac motion is corrected via registration or via rotation on the basis of a known cardiac landmark. The myocardium is partitioned into K radial segments, and we extract time series of length N across the cardiac cycle (N is the number of images in the sequence), each of it referring to a particular radial segment. This process is repeated for BOLD intensity and function, forming two matrices, Y^I ∈ ℝ^N×K and Y^F ∈ ℝ^N×K, respectively, where time series are arranged column-wise. Each time series is further processed by removing the average value and normalizing it w.r.t. its ℓ²-norm. Y^I and Y^F form the input data to the adapted DDAD.

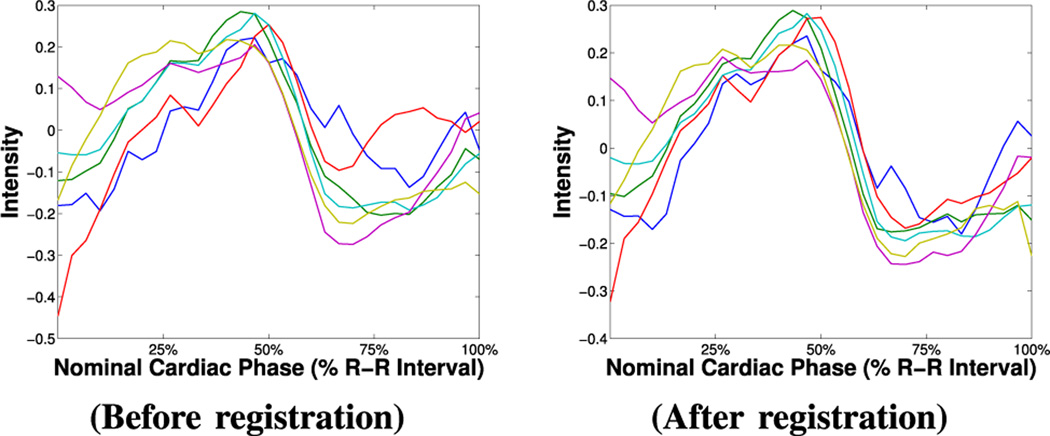
In detail, to obtain intensity time series the segmentation masks are used to elastically register the myocardium relying only on binary shape. (The BOLD effect can introduce errors to intensity driven registration.) More precisely, let ${\{{ℳ}_n\}}_{n=1}^N$ and ${\{{ℐ}_n\}}_{n=1}^N$ be the sets of the segmentation masks and the sequence of images, respectively, and let ℳ₁ be chosen as the reference mask. When processing the n-th image of the sequence, ℐ_n, then, ℳ_n is registered to ℳ₁, and the transformation found T is applied to ℐ_n to obtain the registered image ℐ̂_n = T(ℐ_n). (Note that the transformation fields forming T are zero outside the myocardium, i.e. only the myocardium “moves”.) We use the well-known Demons algorithm [14], with σ = 4, and simple linear interpolation. At the end, we obtain a new sequence of registered images, where the myocardium appears globally registered. Fig. 3 shows that after registration time series follow closer a unique pattern.

Fig. 3.

Effect of registration on intensity time series.

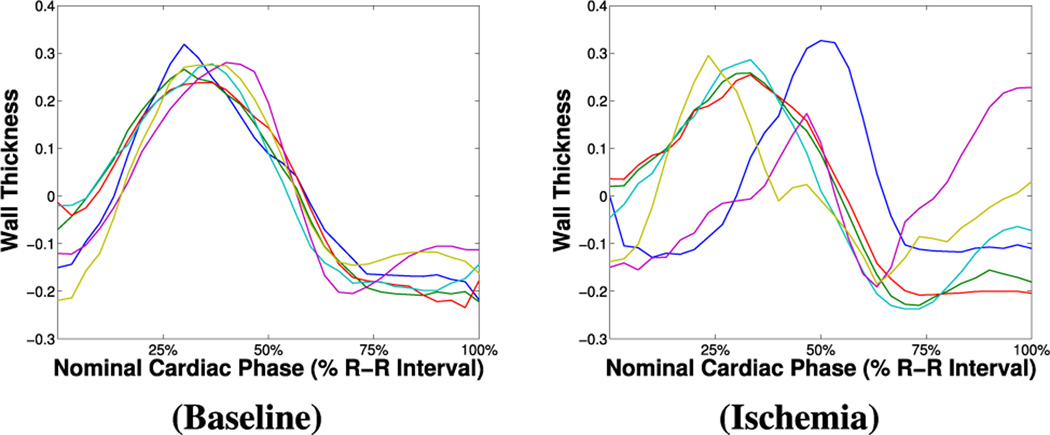
To obtain functional time series per each segment, we need to first correct for cardiac motion to achieve good intra-phase cardiac segment correspondence. Since registration (as the above) will render wall thickness constant across the cardiac phase, a different strategy is adopted here. Rotation correction is performed on the basis of the insertion points of the ventricle (the RV groove), annotated by the expert. Papillary muscles are excluded (via fitting a ellipsoidal model on the convex hull of the endocardial boundary) and the final myocardial mask is then radially partitioned. For each segment and per each image, average wall thickness (WT) is calculated as the average radial distance between the endo- and epicardial boundaries of the related segmentation masks. The collection for all images in the image sequence of the related WT measures forms per-segment functional time series. The examples in Fig. 4 show that under baseline conditions functional time series do follow a common pattern. As expected, the presence of disease differentially affects myocardial function: time series related to segments remote to ischemia appear to follow a “normal” pattern, whereas others considerably deviate from it.

Fig. 4.

Example of “functional time series” from rest CP–BOLD MRI of a subject under baseline (left) and ischemia (right) conditions.

We should note that while here we used myocardial thickness, alternate functional indicators can be used, such as segmental (regional) circumferential strain [15]–[17] and others as reviewed in [18]. Also, strain measures obtained from various definitions of strain tensors are better suited for pixel-level analysis and should be preferred over segmental variants discussed here (see also Section VI).

III. Dictionary-Driven Anomaly Detection (DDAD)

The proposed dictionary-driven anomaly detection (DDAD) algorithm aims at finding anomalies occurring in a multi-signal scenario. We suppose to have available M different yet equally-sized data sets of time series referring to the same test case, ${\{{\mathbf{Y}}^j\}}_{j=1}^M$. Each data set Y^j ∈ ℝ^N×K, corresponds to a type of signal (in the case of UID M = 2, as we have intensity and functional information), N is the length of each signal and K their number. (For simplicity we assume that signals have equal length N, but this is not necessary.) Hence our approach is based on two assumptions. (i) Most of the time series (the “normal” ones) conform with a dictionary-based decomposition model (Y^j ≈ D^jX^j), whereas a fraction of them (the “anomalous” time series) significantly deviates from this model. (ii) Anomalies occur contextually in the different data sets, i.e. if ${\mathbf{y}}_i^j$ is an anomaly in Y^j, ${\mathbf{y}}_i^k$ is an anomaly in Y^k. We can then define a single vector of labels (statuses), l ∈ ℝ^K, which determines if a specific instance is an anomaly (l(i) = −1) or not (l(i) = 1).

DDAD consists of two iterative steps: first, ${\{{\mathbf{Y}}^j\}}_{j=1}^M$ are provided as input to the dictionary learning (DL) algorithm(s), which aim at finding for each Y^j a dictionary-based model to characterize the normal behavior. The same assumption about the presence of a linear model that characterizes the normal time series is used by Adler et al. [11]. Unlike the latter, where the dictionary is assumed known, here we perform DL in the presence of outliers (which are meant to be discovered and excluded progressively), i.e. the models are trained directly on the given data sets. As a second step, a modified OCSVM classifier identifies the anomalies, by jointly considering all signals. We adapt OCSVM to take into account representation errors obtained with the DL step, i.e., deviations from the normal model. The two steps are repeated in an iterative fashion, so that the learning of the dictionary-based models increasingly benefits from a refined classification step, and vice versa. As a consequence, at each iteration, refined normal patterns (i.e. the M dictionaries) are found, and OCSVM, in turn, can rely on an increasingly better characterization of the “normal” class. The complete DDAD procedure can be found in Algorithm 1. The inputs of the algorithm are M data sets ${\{{\mathbf{Y}}^j\}}_{j=1}^M$, each one referring to a different type of signal, and M dictionary models ${\{𝒟{ℳ}^j\}}_{j=1}^M$ to characterize the desired DL problems. Each step is detailed below.

Algorithm 1.

Proposed Dictionary-driven Anomaly Detection (DDAD) algorithm.

1:	procedure DDAD(Y1, …, YM, 𝒟ℳ1, …, 𝒟ℳM)
2:	Label initialization: $$l(i)=1\forall i=1,\dots K$$
3:	Separate dictionary learning problems: $$\text{Learn }[{\mathbf{D}}^1,{\mathbf{X}}^1]\text{ from }{\mathbf{Y}}_{\mathbf{l}\equiv 1}\text{ according to }𝒟{ℳ}^1\dots \text{Learn }[{\mathbf{D}}^M,{\mathbf{X}}^M]\text{ from }{\mathbf{Y}}_{\mathbf{l}\equiv 1}\text{ according to }𝒟{ℳ}^M$$
4:	Jointly consider all different types of time series: $$\mathbf{Z}=[{\mathbf{Y}}^1;\dots ;{\mathbf{Y}}^M]$$ $$\mathbf{Ẑ}=[{\mathbf{D}}^1{\mathbf{X}}^1;\dots ;{\mathbf{D}}^M{\mathbf{X}}^M]$$
5:	Compute distances in the Kernel space: $$d_i=2(C-\varphi {({\mathbf{z}}_i)}^{𝖳}\varphi ({\mathbf{ẑ}}_i))\forall i=1,\dots K$$
6:	Solve the modified OCSVM: $$\underset{\mathit{\omega },\rho }{\text{min }}\frac{{\Vert \mathit{\omega }\Vert }^2}{2}-\rho \mathrm{s}.\mathrm{t}.{\mathit{\omega }}^{𝖳}\varphi ({\mathbf{z}}_i)\ge \rho -\lambda d_i$$
7:	Update the labels: $$l(i)=\text{sgn}({\mathit{\omega }}^{𝖳}\varphi ({\mathbf{z}}_i)-\rho )\forall i=1,\dots K$$
8:	If num. max iterations not reached go to Step 3.
9:	return l     ▷ Output labels
10:	end procedure

A. Pattern discovery via Multi-component Dictionaries

Sparse representations have been shown to be useful for the development of data-driven models to represent 1-D signals and images [19] with several good properties, e.g., capability of handling high-dimensional vectors [20] and robustness to noise [21]. Moreover, sparse representations, when enriched with special constraints on the objects to learn (dictionary atoms or sparse coefficients), can provide useful interpretations of the given data [22]. Dictionaries and sparse representations have been used successfully in medical imaging, and particularly in MRI, for example to reconstruct image data (e.g., [23]), to model brain networks (e.g., [24]), or to obtain higher resolution (e.g., [25]) or different contrast (e.g., [26]).

In a general way, we can see dictionary learning (DL) as a flexible framework to train a multi-component dictionary (i.e., composed by several sub-dictionaries, each one possibly characterized by a special structure), with several additional constraints (soft and hard) to provide further expressiveness:

$$\begin{array}{cc}\underset{\mathbf{D},\{{\mathbf{X}}_i\}}{\text{min }}\hfill & {\Vert \mathbf{Y}-\sum _{i=1}^t{\mathbf{D}}_i{\mathbf{X}}_i\Vert }_F+\sum _{i=1}^t\sum _j{\alpha }_{ij}{\mathrm{\Phi }}_j({\mathbf{X}}_i)\hfill \\ \hfill \text{s.t. }\hfill & g_j({\mathbf{X}}_i)=c_j,i=1,\dots ,t,j=1,\dots ,n_1\hfill \\ \hfill & h_j({\mathbf{X}}_i)\le d_j,i=1,\dots ,t,j=1,\dots ,n_2\hfill \end{array},$$ (1)

where Y is the data matrix, {D₁, …, D_t} are t sub-dictionaries composing the dictionary D ({X₁, …, X_t} being the respective sparse representation matrices). {Φ_i} represents a set of possible “soft” constraints that are summed up to the cost function as a penalization and can be possibly applied to any of the t matrices X_i. As for the “hard” constraints, we can consider both equality constraints (g_j(X_i) = c_j) and inequality constraints (h_j(X_i) ≤ d_j), the latter possibly including conditions on the norm of the sparse vectors.

The formulation in (1) gives a very general framework for dictionary learning. A dictionary model (𝒟ℳ) is given after defining the structure of the dictionary D (type and size of each sub-dictionary D_i), as well as all the possible soft and hard constraints. In the scenario considered for DDAD of multiple signal sources, such that M data sets of time series ${\{{\mathbf{Y}}^j\}}_{j=1}^M$ are available, we generally assume that each dictionary-based model is trained independently. In other words, for the j-th data set, we define a dictionary model 𝒟ℳ^j that leads to a particular expression of (1), to learn the related dictionary D^j.

B. Modified One-class Support Vector Machines (OCSVM)

At each iteration, once all the dictionary-based models for characterizing the normal cases for all M types of time series are trained, a joint classification step is performed. To this end, we propose to use an OCSVM classifier [9], [27], [28]. OCSVM is an SVM-like classifier, which aims at finding the boundaries to separate data points related to a single dominant class from the rest of the data points, considered as outliers. In a multi-signal scenario, we perform the classification jointly, i.e. matrices related to all signal types are vertically concatenated to form a unique data matrix Z = [Y¹; … ; Y^M] (each joint observation is a column of the matrix Z).

In the original formulation of OCSVM [9], the goal is to find the hyperplane achieving the maximal separation between the points and the origin in an appropriate high-dimensional kernel space. The hyperplane is characterized by the vector ω, which is perpendicular to the decision boundary, and ρ, which represents a bias. ω and ρ are found by solving:

$$\underset{\mathit{\omega },\rho ,\mathit{\xi }}{\text{min }}\frac{{\Vert \mathit{\omega }\Vert }^2}{2}-\rho +\frac{1}{\nu N}\sum _{i=1}^N{\mathit{\xi }}_i,$$ (2)

$$\mathrm{s}.\mathrm{t}.{\mathit{\omega }}^{𝖳}\varphi ({\mathbf{z}}_i)\ge \rho -{\mathit{\xi }}_i,{\mathit{\xi }}_i\ge 0$$

where ν is a regularization parameter and {ξ_i} are the so-called slack variables, which play as soft margins in allowing some data points, the outliers, to lie on the other side of the decision boundary (a data point z_i may lie on the side of the origin, i.e., ω^𝖳ϕ(z_i) − ρ < 0, but thanks to an appropriate positive ξ_i it can still respect the constraint in (2)). An interesting property of OCSVM is that it can be used in an unsupervised setting as an anomaly detection algorithm: in fact, once a model for the normal class (i.e., a decision boundary) is learned on a data set, it can be tested on the same data set to detect anomalies by evaluating the sign of the function g(z_i) = ω^𝖳ϕ(z_i) − ρ (the slack variables are in this case neglected).

As others have previously done [29], [30], we propose a new mechanism in how the slack variables are implemented. As the dictionary learning (DL) step is meant to find a model to characterize the normal time series, we want to use this information to “guide” the OCSVM classifier, such that data points with a larger reconstruction error in the DL step are considered to most likely be anomalies. Given a data point z_i (the concatenation of M corresponding time series), its dictionary-based reconstruction is then given by:

$${\mathbf{ẑ}}_i=[{\mathbf{D}}^1{\mathbf{x}}_i^1;\dots ;{\mathbf{D}}^M{\mathbf{x}}_i^M].$$ (3)

The distance between z_i and ẑ_i, evaluated in the high-dimensional kernel space, can then be used as an indicator on how much the data point z_i deviates from the normal pattern. The expression of this distance is derived as follows:

$$d_i={\Vert \varphi ({\mathbf{z}}_i)-\varphi ({\mathbf{ẑ}}_i)\Vert }^2=\varphi {({\mathbf{z}}_i)}^{𝖳}\varphi ({\mathbf{z}}_i)+\varphi {({\mathbf{ẑ}}_i)}^{𝖳}\varphi ({\mathbf{ẑ}}_i)-2\varphi {({\mathbf{z}}_i)}^{𝖳}\varphi ({\mathbf{ẑ}}_i)=2(C-\varphi {({\mathbf{z}}_i)}^{𝖳}\varphi ({\mathbf{ẑ}}_i)).$$ (4)

In the last step in (4), note that the inner product ϕ(z_i)^𝖳ϕ(z_i) equals 𝒦(ϕ(z_i), ϕ(z_i)), which equals a constant C for most of the commonly adopted kernels.

We propose to use distances {d_i} in the OCSVM objective to regulate accordingly the margin of each data point. The original problem (2) is then changed into:

$$\underset{\mathit{\omega },\rho }{\text{min }}\frac{{\Vert \mathit{\omega }\Vert }^2}{2}-\rho \mathrm{s}.\mathrm{t}.{\mathit{\omega }}^{𝖳}\varphi ({\mathbf{z}}_i)\ge \rho -\lambda d_i$$ (5)

where λ is a regularization parameter that weights each distance to provide the actual margin. Eq. (5) can be transferred into its dual formulation and solved with the usual method of Lagrange multipliers. Note that the original OCSVM formulation does not explicitly enforce any structural invariance. Using the proposed distances {d_i} (4) in this modified formulation does have benefits of introducing structural invariance to the classifier. As we will discuss below, in the case of UID, we can use these distances to directly promote shift-invariance.

IV. Unsupervised ischemia detection (UID) with DDAD

UID falls into the category of problems addressed in Section III, since we have M = 2 signals (BOLD and functional information) that provide different (but correlated) time series. Moreover, since we address a single vessel disease (LAD typically supplies <50% of the left ventricle (LV)), we can consider the remote territories larger in number and hence treat ischemia detection as an anomaly identification problem.

The main feature of DDAD is its flexibility in the choice of the dictionary models for the normal classes of each type of signal: any model can be “plugged” into the DDAD framework, since the classification step via OCSVM is independent of the particular model chosen. As we discussed in the Introduction, and it is visible in the examples (cf. Fig. 1 and Fig. 4, left columns), due to the expected characteristic CP-BOLD effect, we decide to adopt a shift-invariant model. We then use the following DL problem to find the pattern:

$$\underset{\mathbf{C},\mathbf{X}}{\text{min }}{\Vert \mathbf{Y}-\mathbf{C}\mathbf{X}\Vert }_F^2\mathrm{s}.\mathrm{t}.{\Vert {\mathbf{x}}_i\Vert }_0=1,{\mathbf{1}}^{𝖳}{\mathbf{x}}_i\ge 0,$$ (6)

where C ∈ ℝ^N×P is a single circulant dictionary (of P atoms, shifts) and a unitary constraint on the ℓ⁰-norm of the sparse coefficient vectors is employed (i.e. each time series is seen as a weighted shifted version of a unique circulant pattern). In addition to the sparsity constraint, we propose to add a nonnegative constraint: this aids the learning of a circulant kernel without sign ambiguity, in order to prevent the case where a time series, although maybe behaving very differently than the underlying remote pattern, can get a negative coefficient, yet large in absolute value. The problem in (6) is solved by modifying the C–DLA algorithm of Rusu et al. [31], to incorporate a non-negativity constraint on the sparse coefficients. While keeping the standard SVD-based initialization of C–DLA, the modified version alternates the construction of the circulant dictionary C (which involves the solution of ⌈N/2⌉ complex least squares problems in the Fourier domain) with the Nonnegative Matching Pursuit (NMP) algorithm [32], a variant of the well-known Orthogonal Matching Pursuit (OMP) algorithm [33], to compute a nonnegative sparse coefficient matrix X. The DL procedure is the same for both intensity and functional time series, and is repeated to learn two independent remote patterns expressed by, respectively, the circulant dictionaries C^I and C^F. Using our modified step, i.e. plugging our distances {d_i} (4) into the OCSVM objective, makes the classifier invariant to shifts: the “normality” of each data point is in fact evaluated with relation to its dictionary-based, shift-corrected, reconstruction.

Let us now discuss this model (a choice which we also elaborate on in the results) w.r.t. previous dictionary-based approaches. Rusu et al. [6] proposed a multi-component DL problem, which, along the lines of Eq. (1), employs a circulant dictionary C and a general dictionary G learned via K–SVD [34]. A similar model was later used by the same authors [12] but also considering a soft spatial constraint Φ(X) with the aim of enforcing similarity between the sparse representations of time series referring to neighboring locations. However, both models were designed under different inputs. Their primary purpose was to learn statistical models of how CP-BOLD intensity varies in the myocardium and extract a common characteristic CP-BOLD pattern with the circulant dictionary, which forms a primary assumption of this work too. However, they did so using information from a population (all the resulting time series are aggregated into a unique data matrix Y). The general dictionary serves to better learn inter-patient variability. In our case, instead, since our input matrices only consist of time series from a single-subject acquisition, we do not need this extra dictionary component. Moreover, since the input data considered here are “mixed” (we have both remote and ischemic time series) and relatively small in number, we want to have a model for the remote time series as compact as possible, in order not to encapsulate within it also patterns related to ischemic areas.

Algorithm 2.

Unsupervised Ischemia Detection (UID) using DDAD.

1:	procedure $\mathrm{U}\mathrm{I}\mathrm{D}({\{{ℐ}_n\}}_{n=1}^N,{\{{ℳ}_n\}}_{n=1}^N,𝒟ℳ)$
2:	Time series extraction with pre-processing: $${\mathbf{Y}}^I,{\mathbf{Y}}^F\leftarrow {\{{ℐ}_n\}}_{n=1}^N,{\{{ℳ}_n\}}_{n=1}^N$$
3:	Perform ischemia detection with DDAD: $$[\mathbf{l},g(·),\mathit{\epsilon }]=\mathrm{D}\mathrm{D}\mathrm{A}\mathrm{D}({\mathbf{Y}}^I,{\mathbf{Y}}^F,𝒟ℳ,𝒟ℳ)$$
4:	Obtain ischemia likelihood values with PPA: $$\mathbf{i}\mathbf{l}\mathbf{v}=\mathrm{P}\mathrm{P}\mathrm{A}(\mathbf{l},g(·),\mathit{\epsilon })$$
5:	return l, ilv
6:	end procedure

Following the formalism of DDAD, (6) represents the dictionary model (𝒟ℳ) for both types of time series (𝒟ℳ^I and 𝒟ℳ^F). Y^I, Y^F, 𝒟ℳ^I and 𝒟ℳ^F are the inputs of a customized DDAD algorithm for ischemia detection. The output of the algorithm is a vector of labels l ∈ {−1, 1}^K, denoting remote and ischemic territories. Given l, the obtained ischemia extent (IE) is defined as the number of ischemic labels (l(i) = −1) over the total number of time series (K):

$$\mathrm{I}\mathrm{E}=\frac{|\{l(i)\equiv -1\}|}{K}$$ (7)

Algorithm 2 summarizes the complete unsupervised ischemia detection procedure, which uses DDAD to perform the proper ischemia detection step (𝒟ℳ is the model defined by (6)) and subsequently computes ischemia likelihood values by first estimating the posterior probability for each time series to belong to the normal class (the method to approximate the posterior probabilities is detailed in Section IV-A). Note that the three steps listed in Algorithm 2 reflect Fig. 2.

A. Inference via posterior probability approximation (PPA)

While the previous steps provide opportunities for a classification of where ischemia occurs and a quantification with IE, for practical purposes it is necessary to provide a measure of confidence for each particular status assignment. To obtain such a confidence, we propose to utilize the well-established method of Platt [35], which maps the output score of a Support Vector Machines (SVM) classifier prior to the sign operation (g(z) = ω^𝖳ϕ(z)−ρ) to a posterior class probability by fitting a sigmoid function:

$$\text{Pr}(l=1|\mathbf{z})={(1+\text{exp}(A+g(\mathbf{z})+B))}^{-1}.$$ (8)

To estimate the parameters A and B, we adopt the implementation proposed by Lin et al. [36]. This approach requires some validation labels and SVM scores as priors, i.e. observations for which the labeling is considered reliable. We propose to select these observations among the joint time series z_i that are represented as the best and the worst according to the dictionary-based decomposition model (i.e. they have the largest and smallest reconstruction error ε(i) = ‖z_i−ẑ_i‖₂), and thus can most likely be considered as anomalies and normal samples, respectively. For each joint time series we can finally obtain an ischemia likelihood value as the complement of the estimated posterior probability, ilv(i) = 1 − Pr(l = 1|z_i).

V. Experimental analysis

We test and validate UID on multiple data sets of both synthetic and real data. As for the latter, our testing data consists of S = 11 canine subjects imaged in controlled rest experiments, as described in Section II-A. For each subject we have available 2 CP–BOLD MRI image sequences: at baseline (prior to occlusion) and under ischemia (with critical LAD stenosis). First, in Section V-A we explore the presence of shifts in intensity and functional time series in baseline cases, and provide insights on the model choice for UID (Section IV). Then, we experimentally evaluate our proposed algorithm both on synthetic data (Section V-B), appropriately generated to simulate CP–BOLD patterns, and on real data (Section V-C). Finally, Section V-D discusses the performance of the algorithm under minor presence of anomalies.

In all experiments conducted, given the small size of the data sets considered, we chose for the OCSVM within DDAD a Gaussian kernel with σ = 1. For the regularization parameter in the OCSVM objective (Eq. (5)), we found via grid search on synthetic data experiments an optimal value of λ = 0.1. The maximum number of DDAD iterations is fixed to 10.

A. Model justification

By observing the BOLD intensity curves of a single subject under an ongoing ischemia (left column of Fig. 1), we can see that certain time series follow a regular pattern, while presenting slight mutual shifts. This is valid also for the so-called functional time series (left column of Fig. 4): as in the case of intensity, there is a supposedly unique “remote-to-ischemia” pattern, whereas time series related to ischemic territories appear much more delayed. We can in fact hypothesize that disease yields notable delays and irregularities in the contraction patterns of the heart.

In Section IV we formulated the dictionary learning model (6), where such time series are decomposed w.r.t. a single circulant dictionary (C^I for intensity time series and C^F for functional time series), with a nonnegative constraint and sparsity strictly set to one.

1) Presence of shifts

The model for intensity and functional time series proposed in Eq. (6) is assumed to be valid both at baseline (for all time series) and under ischemia (in this case only for the so-called remote time series). To evaluate the presence of shifts, and identify a suitable number of circulant atoms (shifts) P, we consider the baseline data sets available and compute for each time series the relative representation error (ε_i = ‖y_i − Cx_i‖²/‖y_i‖²), for different shift values. To learn the circulant dictionaries we adopt again C-DLA [31]. The error values obtained as average on all the baseline time series are reported in Table II.

TABLE II.

Relative representation error (%) with different shifts considered in the dictionary-based representation model.

	No. of Shifts
	1	2	3	4	5
BOLD Intensity	36.4	34.0	33.2	33.1	33.0
Function	21.6	20.3	20.1	20.1	20.1

Table II shows that both types of time series (intensity and function) can be represented by the simple shift-invariant model proposed, and that shifts are present in both of them. In particular, both for intensity and shape time series, it turns out that considering P = 3 shifts of the pattern already leads to the lowest representation error achievable by the model. Thus, hereinafter, in all the experiments conducted we consider P = 3 shifts (and consequently dictionaries of P = 3 atoms).

2) Dictionary composition

The model described in Section IV relies on a single dictionary component (circulant only) because we want to learn well the normal patterns in the data, but not the “anomalous” ones (ischemic). Here we experimentally demonstrate that indeed a multi-component dictionary (e.g., the two-component dictionary used by Rusu et al. [6]), by adding more degrees of freedom (general atoms), leads to learning also the ischemic data.

We identified remote (normal in our definition) and ischemic territories (segments) on the CP–BOLD data (under ischemia) on the basis of visually inspecting infarct location on LGE images. We learned for each data set a two-component dictionary composed by a circulant, with a fixed number of atoms, and a general one, with a number of atoms that varies: 0 (only the circulant part is present), 1 or 2, respectively, and computed the relative dictionary-based representation errors. Results, averaged on multiple subjects, are reported in Table III (for K = 24). The first row reflects the simple model, with only circulant dictionary, adopted in this study.

TABLE III.

Average relative representation error (%) on remote and ischemic (intensity and functional) time series for different numbers of “general atoms” (# atoms).

	Intensity TS			Functional TS
# atoms	Remote	Ischemic	Δ	Remote	Ischemic	Δ
0	56.7	68.1	11.4	30.6	48.7	18.1
1	45.9	40.0	−5.8	24.4	27.0	2.6
2	33.1	30.1	−3.0	13.7	20.8	7.1

Observe the larger difference in representation error between remote and ischemic with the simple model, which shows that the simple model better separates the remote from ischemic case. On the other hand, as we add general atoms, the representation error decreases in both cases (remote and ischemic). However, the rate of decrease for ischemic is higher, and the difference in representation between the two cases becomes less and less evident. For intensity time series, ischemic patterns are actually better represented by this two-component dictionary, which is undesirable.

B. Evaluation on synthetic data

To provide a quantitative evaluation of the proposed method, we first test it with synthetic data because by generating synthetic data we can control composition such as number of available time series and the percentage and location of anomalies (ground truth in other words is available). Data resembling the CP–BOLD time series patterns are appropriately generated according to the sparse generative model described below (for testing purposes we used a fixed time series length N = 28); a comparison with other possible approaches for unsupervised anomaly detection is then carried out, to evaluate the performance of our method in terms of detection accuracy.

1) Generating synthetic data

To simulate the scenario of a CP–BOLD data set in presence of ischemia, we synthetically generate K time series, of which composition is known by design: K_n are considered “normal” (ideally referring to remote territories) and K_a are “anomalous” (i.e., related to ischemia). We can then define a ground truth ischemic extent (IE) as the ratio K_a / K. The normal time series are generated by following the sparse generative model of Rusu et al. [6], using a simple circulant Cⁿ ∈ ℝ^N×P allowing for P shifts of a single kernel (for the sake of generality we consider random variations resembling a CP–BOLD effect), and a unitary ℓ⁰-norm constraint is set for each coefficient vector. We also considered additive Gaussian noise $({\mathbf{n}}_i~𝒩(\mathbf{0},{\sigma }_n^2))$. The parameters of the variables involved are estimated by considering baseline time series, and the ratio between the variances of the signal and the noise reflects the signal-to-noise ratio observed on the real data.

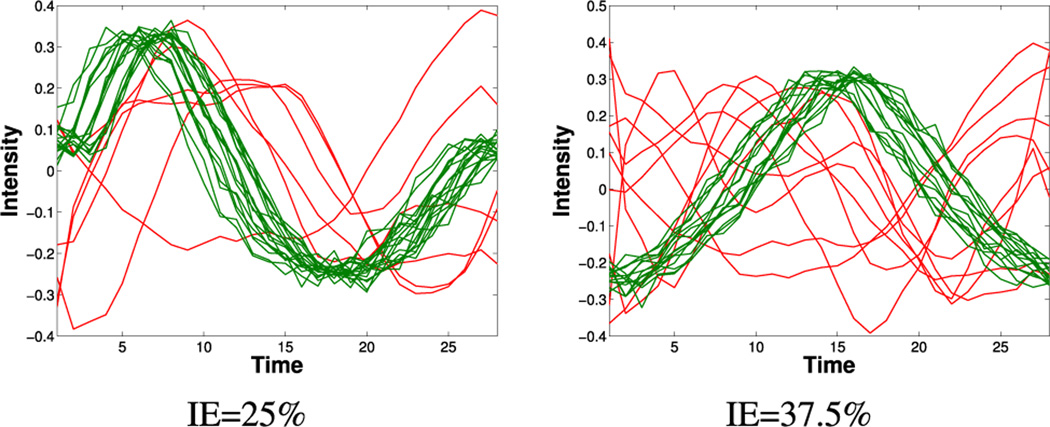
To generate anomalous (i.e. ischemic) time series we rely again on [6], but, instead, a compact dictionary D^a is learned from time series extracted from CP–BOLD image sequences under ischemia, corresponding to segments identified with the aid of LGE images to be well-within the area suspected of ischemia. The dictionary is then used as a basis to sparsely generate anomalies (as parameters, we chose a dictionary size for D^a equal to 5 atoms, and a sparsity s = 3). Fig. 5 shows two examples of synthetic data sets (K = 24) with mixed remote (normal) and ischemic (anomalous) time series, in a percentage reflecting an IE of, 25% and 37.5% respectively.

Fig. 5.

Examples of synthetic data sets with simulated remote (green) and ischemic (red) time series, for two different ischemic extents (IE) considered.

We use the models described to generate data sets for two types of time series (reflecting ‘intensity’ and ‘function’ origins). The sparse models to synthetically generate two corresponding time series of two types are totally independent (shifts, coefficients, and noise vary), but both are generated to belong to the same class (anomaly vs. normal).

2) Performance in detection accuracy

Given the procedure described previously for generating realistic synthetic data of CP–BOLD time series, we can evaluate the performance of the proposed UID detailed in Section IV w.r.t. other approaches. In particular, we consider:

• One-class SVM (OCSVM) [9] performed directly on the original time series Y (we use a fixed parameter ν = 0.3);

• One-class SVM performed in the frequency domain (FD–OCSVM), i.e. on the magnitude of the vectors transformed via the Fourier transform (this should reduce shift effects and lead to a more shift-invariant classifier);

• Dictionary learning (DL) with a threshold directly applied on the sparse coefficients (DLwT) [12] (a circulant dictionary is computed via C–DLA and the decision on a single time series is made by thresholding, with τ = 0.5, the related sparse coefficient); and

• Independent component analysis (ICA) as described in [6] (thresholding the best spatial independent component found via ICA decomposition).

The above-listed methods are compared with the proposed method (with two time series to resemble cases where both intensity and function are used) but also a variant that uses only one time series (intensity).

Table IV reports accuracy, measured as correct assignments w.r.t. the known by design ground-truth composition. Accuracy values are obtained by averaging the outcomes of each method across M = 200 simulations (i.e. 200 different synthetic data sets are generated). The methods have been tested on several values of K and for IE percentages (25% and 37.5%) compatible with ischemia attributed to single vessel disease.

TABLE IV.

Accuracy (mean ± standard deviation) of several algorithms for anomaly detection, including the proposed one, on synthetic data tests emulating variable IE (%).

	K=24		K=48
Methods	IE=25	IE=37.5	IE=25	IE=37.5
OCSVM	79±7	74±7	84±5	77±5
FD-OCSVM	80±8	78±11	82±8	82±10
ICA [6]	88±15	88±12	89±12	88±11
DLwT [12]	84±6	74±7	83±5	73±7
PROPOSED	87±10	84±11	90±10	86±11
PROP. (2 TS types)	91±7	86±10	92±7	90±8
	K=60		K=90
Methods	IE=25	IE=37.5	IE=25	IE=37.5
OCSVM	84±4	77±4	85±4	78±3
FD-OCSVM	83±7	78±11	83±8	79±11
ICA [6]	88±12	88±11	90±14	89±9
DLwT [12]	84±5	74±5	84±4	74±4
PROPOSED	90±9	87±11	91±9	88±11
PROP. (2 TS types)	91±6	89±9	93±6	91±9

One can readily observe that the proposed UID, when both types of time series are used, outperforms all other approaches, including the version of the proposed with only one. It has always the highest average and lower variation w.r.t. other unsupervised techniques. It is important to note that no assumptions are made in UID except that anomalies contextually occur in the two types of time series. Overall we see that using fixed thresholds (DLwT) under-performs, and projecting to a shift-invariant space has benefits (OCSVM performs worse than FD-OCSVM). While in FD-OCSVM a fixed basis is used (Fourier), learning the basis and adapting the anomaly detection process always has benefits, since ICA and UID outperform the other approaches. We should note that for ICA we identify the principal spatial component to threshold by examining the correlation of the time component with the ground-truth, so in that sense ICA numbers are elevated. When we use non-Gaussian measures to do that ICA numbers fall down to ≈ 60%.

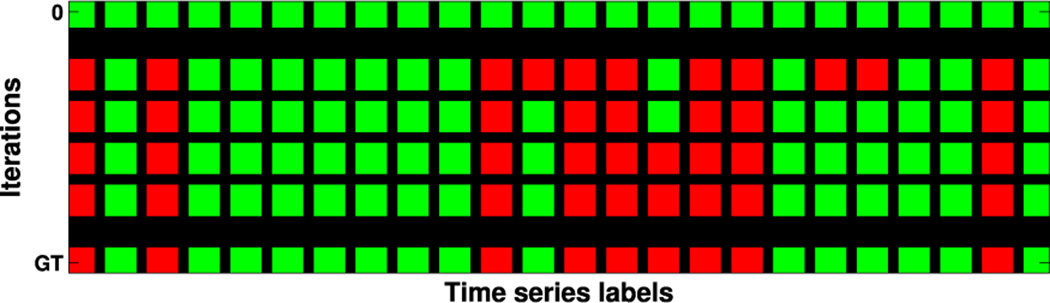
In our tests, DDAD converges after 4.8 iterations (on average). For an intuitive understanding of DDAD’s convergence process, see Fig. 6, which shows how labels change across iterations. Starting with “all-normal” labels (top row), the algorithm stops when the same vector of labels is produced for two consecutive runs, matching here the ground-truth.

Fig. 6.

Visual representation of the evolution of the classification labels at each iteration of DDAD (green for normal, red for anomaly) from an initial state (top row). Bottom row represents ground-truth (GT) assignments.

C. Visual and quantitative assessment on real data

On real data, UID takes as input only the CP–BOLD sequence of images (of N images, with N varying among subjects) of an imaged subject, with no additional information but its segmentation masks. Intensity and shape time series are extracted according to the pre-processing step described in Section II-B, Y^I ∈ ℝ^N×K and Y^F ∈ ℝ^N×K, where K is the number of radial segments. We used K = 36, since it provided the best balance between learning performance (enough data to learn) and accuracy w.r.t. pre-processing errors. Finally, IE (Eq. (7)) and likelihood estimates are obtained.

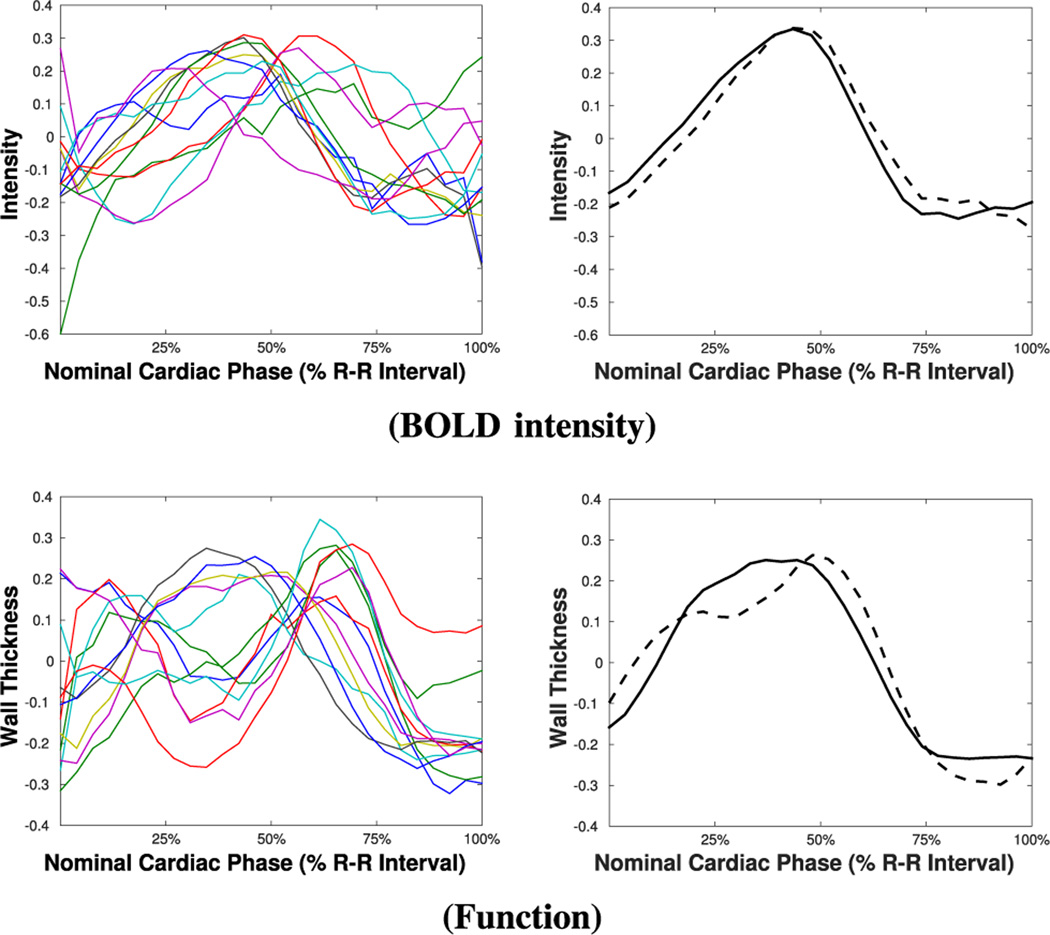
To show the potential of iteratively refining the learned pattern on real data, as an example, Fig. 7 shows intensity and functional time series of a particular subject under ischemia, along with the circulant patterns learned at the first and the last iterations of UID. As we can observe, the patterns change to better represent the remote time series (this is more evident for functional time series in this case), as the anomalies are correctly detected and excluded from the learning process.

Fig. 7.

Examples of intensity and functional time series under ischemia (left) and related circulant patterns (right), learned at the first (dashed line) and last iteration (solid line) of UID.

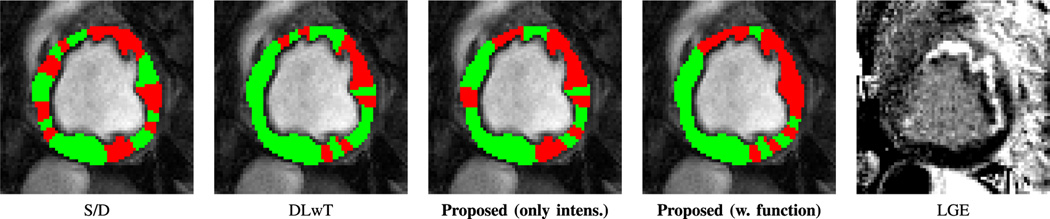
Using this iterative process UID produces a classification to remote (normal) and ischemia (anomalous) as Fig. 8 illustrates. Other approaches for myocardial ischemia detection, namely the S/D method [3] and the DLwT method [12], where we have a dictionary learning (DL) step followed by hard thresholding, along with the corresponding LGE image obtained after 3 hours of occlusion and during reperfusion are also shown. Observe the close correspondence with LGE, of the proposed (UID) when both intensity and function time series are used. S/D shows incoherent findings, whereas DLwT does not capture a large and continuous ischemic territory.

Fig. 8.

Ischemia classification maps related to one subject obtained with several methods (overlaid on an image in diastole from the CP–BOLD image sequence) compared with the corresponding LGE image obtained after 3hrs of ischemia and during reperfusion.

Beyond these visual examples, the superiority of UID is quantified also statistically when testing it across our subject population. For each subject with LGE data available we obtained IE (with UID and all other methods considered), collected IE values and correlated them with infarct size. Infarct size was measured using standard practice [37], considering an infarcted region wherever signal intensity exceeds by 5 times the standard deviation of the mean of a reference region. As summarized in Table V, together with standard p-values and bootstrapped estimates (after 10⁶ permutations), IE measured with the proposed method (UID) shows an exceptional, statistically significant, correlation of 0.84 with infarct size. Even when using only intensity the proposed method outperforms all others. Although its p-value is close to the significance threshold (p-value = 0.05), the bootstrapped estimate is 0.0394 and thus is statistical significant. All other methods under-perform, yielding non-significant correlations. DLwT and ICA, although they did well in some of the synthetic experiments, here having a fixed threshold or not being able to deal with shifts, lead to poorer performance. Our method finds an optimal basis (dictionaries), exploits both function and BOLD signal intensity, and finds a suitable per subject ‘threshold’, all in an unsupervised fashion. S/D as we mentioned in the introduction, shows poorer performance since less averaging within a segment (due to a finer partitioning) leads to more noisy S/D estimates. UID, instead, thanks to sparsity is more resistant to noise [21].

TABLE V.

Pearson correlation coefficients (r) and related p-values, obtained by correlating, for different methods, ischemic extent (IE) with infarct size in our subject population.

Method	r	p-value	Bootstrap. p-value
S/D [3]	−0.0808	0.8491	0.5751
FD-OCSVM	0.2495	0.5512	0.3138
ICA [6]	0.2708	0.5164	0.2634
DLwT [12]	0.3233	0.4347	0.2247
PROPOSED (only intens.)	0.6643	0.0723	0.0394
PROPOSED (w. function)	0.8425	0.0087	0.0040

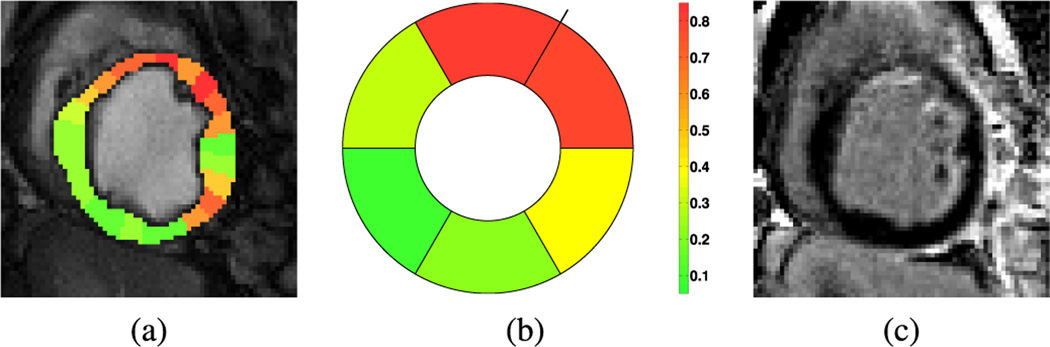
UID can also estimate likelihood values for each time series (which are viewed as a probability of a time series to be originated from an ischemic territory) using the optional inference Step C of UID, as seen in the example of Fig. 9, along with the LGE image for this subject. Observe again the close correspondence between the derived visualization map and the LGE image, capturing a broad ischemic territory (and potential area at risk), which eventually led to the diffuse endocardial infarct. By averaging those likelihoods we can provide a 6-segment bulls-eye representation, following standard clinical practice [38]. With this plot, a clinician can readily ascertain that the culprit artery causing myocardial ischemia is LAD.

Fig. 9.

An ischemia likelihood map as obtained by UID for another subject, color-coded and overlaid on the original CP–BOLD image in diastole (a). Together we also show a six-segment bulls-eye plot of likelihood for the same case (b); the color bar shown refers to both (a) and (b). In (c) the corresponding LGE image is reported.

D. Performance under presence of minor anomalies

Our approach assumes that some anomalies are present. To address clinical scenarios where ischemia is not so apparent in the myocardium, we performed tests both on synthetic and real data. Specifically, for synthetic experiments, we used the same data generation models described in Section V-B, by setting IE = 5%. This value of ischemic extent can either reflect very minor ischemia or account for artifacts (e.g., flow artifacts) that can make normal patterns appear anomalous. As Table VI shows, our method adapts adequately to this case without any modifications, finding an IE consistent with the value set by design. Once again, jointly exploiting two types of time series leads to a significant increase of the performance. Note also that the DLwT method [12] has high accuracy, but tends to under-estimate the anomalies.

TABLE VI.

Accuracy (mean ± standard deviation) and resulting IE obtained with several algorithms, including the proposed one, on synthetic data tests emulating minor ischemia (IE=5%).

	K=60, IE=5%
Methods	Accuracy	IE measured
OCSVM	72±2	33±2
FD-OCSVM	71±2	34±2
ICA [6]	75±11	29±11
DLwT [12]	96±1	1±1
PROPOSED	91±12	10±14
PROP. (2 TS types)	96±9	4±9

Furthermore, we ran our algorithm on a set of real data from 7 baseline canine studies (operated animals, but without occluder activation). After feeding these baseline data sets to our algorithm, we found an average IE of 7%, whereas the second best performing algorithm (i.e. detecting the lowest number of anomalous territories), FD-OCSVM, gave an average IE = 15%. Moreover, visual inspection of the ischemia maps (not shown for brevity) revealed that the identified anomalous segments are spatially diffuse, suggesting that the anomalies are not likely to be attributed to pathological findings.

VI. Conclusion and Discussion

In this paper we presented UID, an algorithm for dictionary-driven anomaly detection, and its application to ischemia detection in CP–BOLD MRI at rest. The outcome of the algorithm, when applied to time series originating from CP–BOLD data of a single subject imaged at rest, is the unsupervised classification of the time series as remote or affected by ischemia, and a measure of ischemic extent, as the ratio of those affected divided by their total number. The method combines both signal intensity and myocardial function in a unifying framework. An optional inference step obtains a confidence as to classification certainty, and provides visualization maps of ischemia likelihood.

Using real data from controlled experiments under baseline conditions we found that a circulant dictionary model can suitably describe not only BOLD signal intensity but also wall thickness. We tested the algorithm and underlying circulant structures in a variety of settings. Using synthetic experiments we showed superior performance when all aspects considered are combined: (a) a shift-invariant model has benefits; (b) anomaly detection (via OCSVM) performed better than using fixed thresholds; and (c) combining two complementary time series (to emulate in our case BOLD intensity and myocardial function) proved beneficial than using only one. Of course, as we increase the number of time series available, accuracy improves, illustrating the potential of pixel-level analysis when segmentation and registration performance improves (please see discussion below). Our experiments on subjects under severe coronary occlusion showed significant visual agreement between infarct size (LGE) and visualization maps of ischemia extent. Quantitatively, ischemic extent (IE) obtained using our method is statistically significantly correlated (p < 0.05) with infarct size as estimated with LGE.

In this paper, we used ischemia detection in CP–BOLD as an application of DDAD. However, this algorithm is general and can be used wherever we need to combine subspace decomposition with anomaly detection via OCSVM. With DDAD, when combing different dictionary learning algorithms with an appropriate choice of sparsity, several complex data manifolds (subspaces) can be considered and can be linked with OCSVM directly via the representation error. Depending on the number of dictionary atoms (in a general context) or union of circulants (in a structural shift-invariant context) multiple “normal” classes and behaviors can be accommodated. Our synthetic experiments showed that is better to rely on OCSVM rather than fixed thresholds, which may have a nonlinear effect on the performance instead of the linear one of a regularization-based approach as ours. Currently, we are also exploring applications of DDAD in shape discrimination and object segmentation in other domains.

This paper relies on segmental analysis and expert myocardial delineation to reduce the bias of any errors introduced by automated segmentation algorithms. Even with standard cine MRI, myocardial segmentation accuracy (measured with Dice Overlap criteria) is reported to be close to 80%, based on recent automated atlas-based state-of-the-art algorithms [39], [40]. With such accuracy, segmentation errors, of 20% e.g., can have undesirable effects to the fidelity of extracted BOLD signals. Since we focus on the detection part here, we opted to use expert delineations. Nonetheless, in clinical settings full automation is desirable and we are investigating segmentation algorithms tailored for CP–BOLD [41], [42] to fill this need. Also, this paper does not use intensity-based registration to elastically register sequential images within the sequence. Again this is done to avoid any registration errors, since it is known that the BOLD effect adversely affects myocardial registration accuracy. As segmentation and registration accuracy for CP–BOLD increases, we hope to obtain ischemia extent maps and quantification at the pixel-level, which will also increase the number of available time series. As our synthetic experiments show, this will in fact benefit the algorithm.

Overall performance is also expected to increase moving from 2D to 3D, when full cardiac coverage cine BOLD sequences using free-breathing approaches [43] become available. We rely on radially-defined myocardial wall thickness to assess myocardial function, which is not translatable to the pixel-level. We will need to adopt either pixel-level definitions of Jacobian or strain measures (including radial and circumferential strain) from their appropriate tensors [15]–[17], [44], to obtain pixel-level time series of myocardial function. Currently, we do not enforce any spatial correlation among time series; however we can readily adopt the spatial constraint in our formulation, as done in [12]. At the single pixel-level, adding such spatial constraints should help produce smoother (and contiguous) ischemia maps. Finally, our validation is limited solely due to inherent difficulties of relating ischemia (from CP–BOLD) with infarct (from LGE). It is well known that the ischemic territory (area at risk) could be larger than the infarcted territory, and that a one-to-one correspondence does not exist, since ischemia is a trigger (hence an early effect), while infarction is a consequence (i.e. occurs after prolonged ischemia). We are in the process of tandem PET-MRI experiments in a dedicated scanner, which ideally should provide co-registered PET perfusion and BOLD MRI data offering additional validation. Our method has been tested in cases where single-vessel disease is present, i.e. unaffected (remote) territories are expected to be more populous. In the case of multi-vessel disease, modifications on the assumptions and the methodology might be necessary; however, current animal models cannot readily emulate such disease scenarios. Thus, we are also in the process of recruiting patient and volunteer populations to test the method on humans with a larger range of ischemia conditions. However, the presentation of both of these outcomes is the subject of a future manuscript.

In conclusion, we showed that the proposed approach can reliably detect ischemic territories with CP–BOLD MRI at rest. It learns and represents normal patterns of signal intensity and myocardial function from remote territories efficiently, taking advantage of a unique structurally sparse decomposition framework combined with anomaly detection performed via OCSVM to iteratively identify normal (remote) and anomalous (ischemic) behaviors. To aid visualization and diagnosis, a probabilistic inference step provides confidence for ischemia likelihood. When combined with advances in myocardial segmentation and registration tailored to the BOLD effect, our approach will help to accelerate the clinical translation of this truly non-invasive and repeatable method for pixel-level and transmural assessment of ischemia.