QMRAcatch: Microbial Quality Simulation of Water Resources including Infection Risk Assessment

Abstract

Given the complex hydrologic dynamics of water catchments and conflicts between nature protection and public water supply, models may help to understand catchment dynamics and evaluate contamination scenarios and may support best environmental practices and water safety management. A catchment model can be an educative tool for investigating water quality and for communication between parties with different interests in the catchment. This article introduces an interactive computational tool, QMRAcatch, that was developed to simulate concentrations in water resources of Escherichia coli, a human-associated Bacteroidetes microbial source tracking (MST) marker, enterovirus, norovirus, Campylobacter, and Cryptosporidium as target microorganisms and viruses (TMVs). The model domain encompasses a main river with wastewater discharges and a floodplain with a floodplain river. Diffuse agricultural sources of TMVs that discharge into the main river are not included in this stage of development. The floodplain river is fed by the main river and may flood the plain. Discharged TMVs in the river are subject to dilution and temperature-dependent degradation. River travel times are calculated using the Manning–Gauckler–Strickler formula. Fecal deposits from wildlife, birds, and visitors in the floodplain are resuspended in flood water, runoff to the floodplain river, or infiltrate groundwater. Fecal indicator and MST marker data facilitate calibration. Infection risks from exposure to the pathogenic TMVs by swimming or drinking water consumption are calculated, and the required pathogen removal by treatment to meet a health-based quality target can be determined. Applicability of QMRAcatch is demonstrated by calibrating the tool for a study site at the River Danube near Vienna, Austria, using field TMV data, including a sensitivity analysis and evaluation of the model outcomes.

The River Danube, with floodplains downstream of Vienna, Austria, is important for public water supply by river bank filtration. The floodplains represent unique ecosystems receiving increasing appreciation as areas of high biodiversity and biomass and are therefore highly protected nature reserves. Unfortunately, due to human activities (e.g., damming, river regulation, etc.), the area has lost its typical appearance as a highly dynamic and patchy environment, and many characteristic habitats are endangered. To increase hydrological interactions with the main river (e.g., flooding, erosion, and sedimentation), major revitalization measures have been undertaken or planned; however, conflicts between conservation and water supply demands may arise if measures decrease water quality at the respective well sites. This conflict of interest between nature protection and public water supply is a common phenomenon because revitalization is considered a major public goal for many European rivers (EU, 2012).

Given the complexity of the hydrologic dynamics of water catchments and the conflicts of interest, catchment models may provide solutions in terms of understanding the system dynamics and may be a basis to evaluate various contamination scenarios. Such models can support the design of appropriate environmental practices and water safety management to achieve required pathogen removal by water treatment. Moreover, a catchment model can be implemented as an educative tool for investigating water quality and for the communication between parties with different interests in the catchment.

Inspired by the Rotorua Declaration (HRWM, 2011) and the European Water Framework Directive (EU, 2012), it was decided to develop a generic catchment model. Catchment microbial contamination modeling is a relatively new and developing field with the potential to greatly enhance our knowledge and understanding of catchment processes and nearshore microbial contamination dynamics. Changing regulatory paradigms, primarily in North America and Europe, require the estimation of microbial health risk to inform integrated catchment management and to protect water quality and human health. Although sanitary profiling and water safety plans have been recommended as tools to meet these new needs, significant knowledge gaps remain, and an additional challenge is to resource their implementation in developing nations and in the developed world. Emerging literature demonstrates that the use of microbial modeling represents an opportunity to enhance these approaches to water quality protection (HRWM, 2011).

The aim of the current study was to develop and introduce a user-friendly interactive computational tool that simulates target microorganism and virus (TMV) concentrations in water resources in a catchment. Target microorganisms and viruses encompass fecal indicators, genetic markers, and waterborne pathogens. Data on indicators and microbial source tracking (MST) markers can be used to calibrate the model for a specific catchment. Recent developments in MST and molecular fecal marker detection increasingly provide useful information on host- or source-associated fecal contamination levels. Microbial infection risks are then assessed from known or assumed concentrations of pathogens from literature in the considered fecal contamination sources under various emission scenarios.

A considerable body of literature has appeared on catchment models, including transport fecal indicator organisms (e.g., Hipsey et al., 2008; Wu et al., 2009) often coupled to SWAT (Soil and Water Assessment Tool) (e.g., Benham et al., 2006; Chin et al., 2009; Coffey et al., 2010; Kim et al., 2010) and pathogens (Ferguson et al., 2007; Åstrom et al., 2009; Schijven et al., 2013).

The tool that is described herein, QMRAcatch, simulates discharges of wastewater carrying TMVs into a main river. Fertilizer application, grazing animals, and urban runoff are diffuse input sources that require accounting for spatial distribution. Such diffuse agricultural sources of TMVs that discharge into the main river are therefore not included in this stage of development. The TMVs are transported in the main river and subjected to dilution and degradation or inactivation. The river in the floodplain is a side-arm of the main river. The floodplain is an area that is regularly flooded by river water. In the floodplain, fecal deposition from animals, birds, and humans takes place. In these deposits, TMVs are released by flooding and rainfall. Through runoff and flooding, the TMVs enter the floodplain river, and a part infiltrates groundwater. Humans may be exposed to the pathogens by consumption of drinking water produced from riverbank-filtrated or abstracted groundwater or by swimming in the river.

QMRAcatch is unique in encompassing a generic domain with a river and floodplain with a combination of functions (nature, recreation, water storage, and drinking water production). It combines inputs of pathogens, indicators, and MST markers from fecal sources, transport and fate of these microorganisms in the domain, treatment of wastewater and of river water for drinking water production, and Quantitative Microbial Risk Assessment (QMRA). As such, QMRAcatch is not limited to estimating the status quo of health risks from human and animal fecal contamination sources for a catchment; rather, it is designed to simulate future health risk scenarios for a constantly changing environment. This allows the evaluation of various mitigation scenarios to deliver sustainable decisions for water quality safety management. Moreover, QMRAcatch is implemented as an easy-to-use interactive tool that can make use of generic hydrologic inputs as well as location-specific hydrologic data.

Applicability of QMRAcatch is demonstrated by calibrating the tool for a study site at the River Danube in Vienna, Austria using field microbial data, including a sensitivity analysis and evaluation of the model outcomes.

Model/Tool Description

General Information

QMRAcatch was developed in Mathematica (version 9.0.1, Wolfram Inc.). It is available in Computable Document Format and can be run with the free CDF Player. QMRAcatch provides a user-friendly interface in which parameters values can be selected from low, medium, or high default values from the literature to support the user or can be set to any value. Default values and literature references are listed in Table 1. Scenarios can be defined from a selection of parameter settings. Spreadsheets in excel format are used for saving and loading parameter settings and for loading location-specific hydrologic and microbiological data. These data can be used for calibrating the model to a specific location. Saving and loading data from and to files requires that QMRAcatch runs with Mathematica or Player Pro. In QMRAcatch, time-dependent variables are arrays of 365 values for each day in 1 yr.

Table 1. Default and calibration parameter values.

	Dimension		Default values			Calibration parameter	Reference
			Low	Medium	High
Concentration of TMVs† in raw wastewater; calibration WWTP‡ 2 and 3
Mean	N/L§	enterovirus	1	102	103	103	WHO (2011)
		norovirus	103	105	106	–	Katayama et al. (2008)
		Campylobacter	102	104	106	–	WHO (2011)
		Cryptosporidium	1	102	104	–
		Escherichia coli	106	108	1010	5.4 × 107
		HF183	108	109	1010	(2.2, 1.4) × 109	this paper
95%	×mean	all TMVs	1	2	5	–
	N/L	enterovirus				2.8 × 103
		E. coli				(9.8, 11) × 107
		HF183				(5.8, 3.5) × 109
Concentration of TMVs in storm water overflow, multiplication factor of TMV concentration in raw wastewater
Mean and 95%	–		0.1	1	10
		2010				1.4
		2011				0.2
		2012				0.2
		2013				0.1
Log removal by wastewater treatment
Mean	Log10	enterovirus	0	1	2	1.2	Lodder and de Roda Husman (2005)
		norovirus	0	1	2	–
		Campylobacter	0	2	4	–	Hoogenboezem et al. (2001)
		Cryptosporidium	0	1	2	–
		E. coli	0	2	4	2.4, 2.2
		HF183	0	2	3	2.8, 2.2	this paper
95%	×mean	all TMVs	0.5	0.75	1	–
	Log10	enterovirus				0.4
		E. coli				1.4, 1.8
		HF183				1.9, 1.4
Characteristics of wastewater treatment plants WWTP1–5
Upstream distance	km		10	50	200	13, 17, 35, 70, 186
Discharge	m3 s-1		0.02	0.1	0.5	0.1, 0.1, 0.1, 0.2, 2.2	Schijven et al. (2005)
Overflow	N yr-1		0	2	5	5
Mixing degree	–	2010	0.2	0.5	1	1.0, 1.0, 1.0, 1.0, 1.0
		2011	0.2	0.5	1	1.0, 1.0, 1.0, 1.0, 1.0
		2012	0.2	0.5	1	1.0, 1.0, 1.0, 1.0, 1.0
		2013	0.2	0.5	1	0.17, 0.21, 0.28, 0.33, 0.49
Fecal droppings of boar/red deer
Mean weight	g	boar	5	10	15	–	Schmidt et al. (2004)
		red deer	5	15	25	–	von Oheimb et al. (2005)
95% of weight	×mean		1	2	5	–
Number	per day per	boar	2	5	10	–	Schmidt et al. (2004)
	animal	red deer	5	15	30	–	von Oheimb et al. (2005)
Mean TMV concentrations	N g-1	Campylobacter	102	104	105	–	Ogden et al. (2009)
		Cryptosporidium	106	107	108	–
		E. coli	106	107	108	–
95%	×mean	All TMV	1	2	5	–
Prevalence	–	Campylobacter	0	0.2	0.3	–	Ogden et al. (2009)
		Cryptosporidium	0	0.01	0.1	–
Fecal droppings of birds
Mean weight	G		0.2	0.5	1	–	Hahn et al. (2007)
95% of weight	×mean		1	2	5	–
Number	per day per bird		20	50	100	–	Hahn et al. (2007)
Mean TMV concentrations	N g-1	Campylobacter	102	104	105	–	Ogden et al. (2009)
		Cryptosporidium	106	107	108	–
		E. coli	106	107	108	–
95%	×mean	all TMV	1	2	5	–
Prevalence	–	Campylobacter	0	0.4	0.7	–	Fallacara et al. (2001)
		Cryptosporidium	0	0.01	0.1	–
Fecal droppings of humans
Weight	g	mean	100	150	200	–	Encyclopedia Brittanica, 2015
	×mean	95%	1	2	5	–
Probability	–		0	0.001	0.01	–
Mean TMV concentrations	N g-1	enterovirus	105	108	109	–	Melnick and Rennick (1980)
		norovirus	105	108	109	–	Atmar et al. (2008)
		Campylobacter	105	106	107	–	WHO (2011)
		Cryptosporidium	105	108	109	–	RIVM/LCI (2012), Gerba, (2000)
		E. coli	106	107	108	–
		HF183	106	107	108	–
95%	×mean	all TMVs	1	2	5	–
Prevalence	–	enterovirus	0	0.01	0.1	–
		norovirus	0	0.01	0.1	–	Glass et al. (2009)
		Campylobacter	0	0.001	0.01	–	Kemmeren et al. (2006)
		Cryptosporidium	0	0.001	0.01	–	RIVM/LCI (2012)
Main river
Discharge, Qmr	m3 s-1	data from spreadsheet or monthly mean values
ARMA(1,1)¶		a	0.5	0.7	0.9	–
		b	0	0.5	1	–
		v	5 × 104	105	2 × 105	–
Width	m		200	250	300	250	Viadonau (1997)
Depth	m		2	4	8	4	Viadonau (1997)
Floodplain river
Discharge from main river	m3 s-1	threshold	1000	2000	3000	–
	–	fraction of Qmr	–	0.01	–	–
Groundwater recharge	m3 s-1		0.1	0.25	1	–
Length	km		5	10	20	–
Width	m		5	10	20	–
Depth	m		1	2	5	–
Main river and floodplain river
Manning coefficient	–	0.05 for sand and 0.1 for gravel				0.024	Manning (1891), MA45 (2014)
River bed slope	m m-1		0.001	0.004	0.01	0.0005	Viadonau (1997)
Water temperature	°C	from 1–22, triangular or data from spreadsheet	data from spreadsheet
Floodplain
Precipitation	mm d-1	data from spreadsheet or generated
Precipitation rate	1 d-1	0.2	0.5	1	–
Precipitation depth	mm	1	2	3	–
Maximum month	month	1	6	12	–
Floodplain angle	degrees	0.5	1	2	–
Floodplain area	km2	20	50	100	–
Release from fecal deposits	1 d-1	0	0.1	1	–
Evaporation	–	0	0.4	0.8	–
Runoff	–	0.1	0.1	0.2	–

^†Target microorganism and virus.

^‡Wastewater treatment plant.

^§Numbers per liter.

^¶Autoregressive moving average.

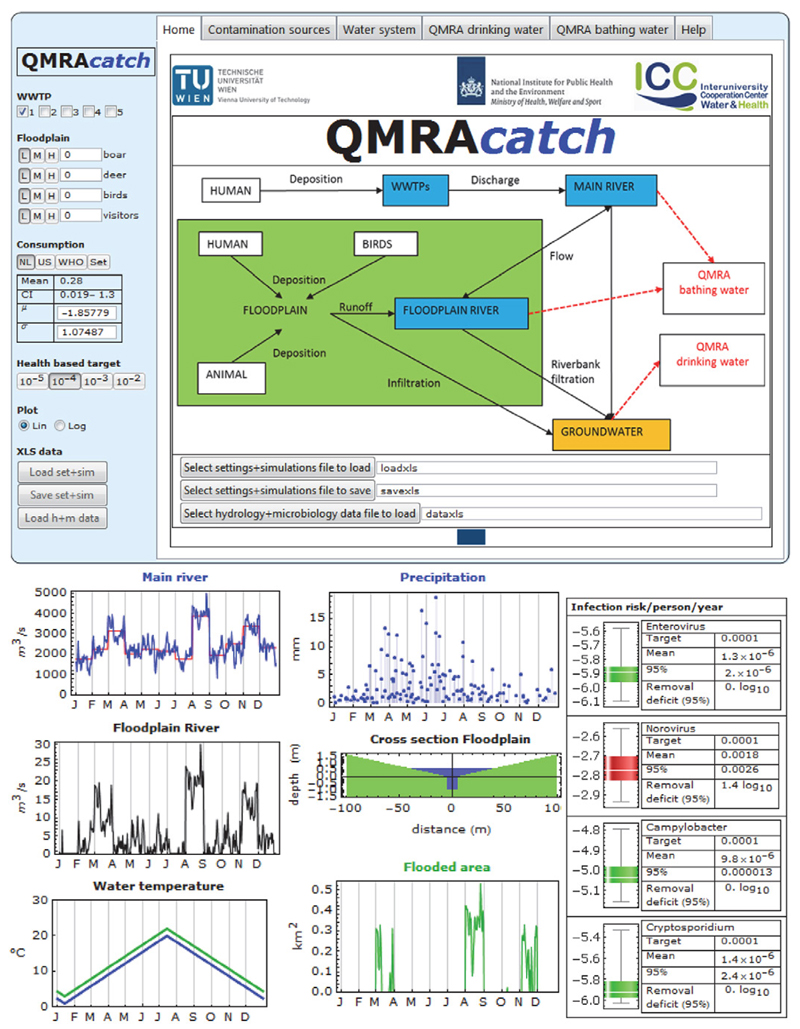
Home Screen and Dashboard

Figure 1 shows the home screen and dashboard. The home screen presents the model domain that contains the following compartments: (i) wastewater treatment plants (WWTPs), predominantly receiving domestic wastewater; (ii) a main river receiving raw and treated wastewater discharges, which dilute and transport TMVs; (iii) a floodplain in which fecal deposition from animal, bird, and human sources takes place (TMVs in the fecal deposits are partly released by rainfall, are resuspended when inundated by water from the floodplain river, and partly infiltrate the underlying aquifer); (iv) a floodplain river within the floodplain (the floodplain river receives water from the main river and collects runoff from the floodplain and occasionally inundates the floodplain); and (v) groundwater collects infiltrating water from the floodplain and river water by riverbank filtration. In the environment, TMVs are inactivated or degraded at a temperature-dependent rate. The model also includes QMRA for drinking water from abstracted groundwater and for swimming in the rivers.

Fig. 1. Screenshot of home screen and dashboard of QMRAcatch (top); discharges and water temperature of main and floodplain river (bottom left); precipitation, cross-section, and flooded area of floodplain (bottom center); and infection risks from consumption of drinking water produced from bank-filtrated water from the main river (bottom right).

The currently included waterborne enteric pathogens are enterovirus, norovirus, Campylobacter, and Cryptosporidium. Escherichia coli was included as a cultivation-based standard fecal indicator parameter, and the HF183 Taqman bacteroidetes quantitative PCR assay was selected to represent a human-associated genetic fecal marker.

The dashboard on the left-hand side is always visible and allows switching on/off up to five WWTPs and setting the number of boar and deer (as representatives of wildlife), birds, and visitors in the floodplain.

The log normal distributed consumption of unboiled drinking water per person per day for The Netherlands (Teunis et al., 1997) and the United States (USEPA, 2006)—a fixed value of 2 L per person per day—or free input of lognormal distribution parameters and a health based target (risk level) can be set. Furthermore, linear and semilog plotting and spreadsheet files can be selected.

Contamination Sources: Wastewater Treatment Plants

The location of a WWTP is given by its upstream distance to the point of interest (PI), which may be water intake for drinking water production or a swimming area. A discharge value can be set as well. The number of raw wastewater overflows due to heavy rainfall can be set and is uniformly distributed over the year.

In this way, combined sewer overflow is simulated. It is also possible to mimic single sewer overflow by using a WWTP in which treatment is set to zero log removal. Mixing of discharged wastewater with river water can be set by a mixing degree between 0 and 1. In the case of 1, the TMV concentrations are the same across the river at the PI (fully mixed). For example, in the case of 0.1, mixing is incomplete, and it is assumed that the concentrations of the TMVs that infiltrate the river bank, or to which swimmers are exposed, are 10 times higher than the concentrations in the fully mixed case. Mixing degrees can be estimated, for example, with hydraulic surface water models or by using rule-of-thumb methods (Kühlers et al., 2010).

Concentrations of TMV in raw wastewater, including storm overflow events, are described by a gamma distribution with shape parameter r and scale parameter λ. In the tool, mean and 95th percentile values can be set. Parameters r and λ are determined from the mean and 95th percentile by moment estimation. Monte Carlo samples from the gamma distributions are drawn to simulate a concentration value for each day in a year.

Target microorganisms and viruses are removed by the treatment of wastewater. Log removal is the logarithmic reduction in concentrations by treatment. The mean (µ) and 95th percentile values (p95) can be set. It is assumed that log removal follows a normal distribution, with mean µ and SD σ = (µ − p95)/1.64485.

Contamination Sources: Fecal Droppings from Boar, Deer, Birds, and Visitors

Fecal droppings from wildlife in the floodplain may be relevant sources of contamination. Boar and deer were chosen as representative of wildlife. In addition, birds may be abundant and may form a relevant source of fecal contamination, especially for Campylobacter and E. coli. The mass (g) of feces of each dropping is assumed to be Normal distributed, and the number of droppings per day per animal or birds is assumed to be Poisson distributed. For the variability of the TMV concentration in feces, a gamma distribution is applied. The prevalence of TMV excretion is assumed to follow a binomial distribution. For humans who visit the floodplain, a binominal-distributed probability of a fecal deposition is assumed, which may be highly geographically dependent.

Fecal deposition only takes place in the nonflooded area of the floodplain. For each day in the year, the total number of pathogens in the fecal droppings is calculated.

River Discharge and Water Temperature

Discharge values and water temperatures are shown in Fig. 1. Discharge values of the main river Q_mr (m³ s⁻¹) for each day in a year can be read from a spreadsheet or simulated by means of an autoregressive moving average [ARMA(1,1)] process (Whittle, 1983):

$$X_t={\epsilon }_t+\alpha X_{t-1}+\beta {\epsilon }_{t-1}$$ [1]

where X_t (m³ s⁻¹) is the change in discharge around the mean discharge Q_mr on time t (d), ε_t (m³ s⁻¹) is the variance, α (–) is an autoregression coefficient, and β (–) is a moving average coefficient. Values of X_t are added to monthly mean values of Q_mr that can be set interactively.

From the main river, discharge, width, Manning coefficient, slope of the river bed, and the flow velocity (v [m s^-1]) of the water is calculated; hence, travel times for microorganism between points of discharge and exposure are calculated (Manning, 1891):

$$v=\frac{1}{n}{\left(\frac{wh}{w+2h}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$ [2]

where n (s m^-1/3) is the Manning coefficient, w (m) is the river bed width, h (m) is the depth of the river, and s (m m^-1) is the slope of the river bed.

When Q_mr exceeds a threshold value, a fraction of the Q_mr discharge enters the floodplain river (Q_mr→fr [m³ s^-1]). The Q_mr→fr data may also be loaded from a spreadsheet. The floodplain river may in addition be recharged continuously by groundwater (Q_gw [m³ s^-1]).

Water temperature of the main river and the floodplain river (T_mr and T_fr [°C]), can be spreadsheet data or interpolations from the values on the coldest and warmest day.

Fate and Transport of Target Microorganisms and Viruses in the Main River and Floodplain River

Dilution of wastewater in river water is the ratio of wastewater and main river water discharges (m³ s^-1) divided by the mixing degree. During transport in the river, TMVs gradually inactivate or degrade at a microorganism- and temperature-dependent first-order rate with rate coefficient (µ_T, [d^-1]) (Bertrand et al., 2012):

$${\mu }_T=-\frac{\ln 10}{{10}^{a_0+a_{1}T}}$$ [3]

where T is the temperature (°C), and a₀ (log₁₀ day) and a₁ (log₁₀ day °C^-1) are inactivation rate parameters. The values for a₀ and a₁ are, respectively, 1.8 and −0.035 for enterovirus (Bertrand et al., 2012), 2.3 and −0.035 for norovirus (Bertrand et al., 2012), 0.53 and −0.017 for Campylobacter (Schijven et al., 2013), and 3.1 and −0.078 for Cryptosporidium (Schijven et al., 2013). The values for E. coli are 1.04 and −0.017 (Franz et al., 2014). The values for the human-associated HF183 genetic fecal marker are 3.5 and −0.1 (Dick et al., 2010; Liang et al., 2012; Jeanneau et al., 2012; Green et al., 2011; Korajkic et al., 2014).

After a travel time of m days to PI, TMV concentrations (C_m,T [m^-3]) are calculated as:

$$C_{\text{m},\text{T}}=C_0\exp \left[-{\displaystyle \sum _{i=1}^m{\mu }_{T_{\text{i}}}}\right]$$ [4]

where C₀ is the initial concentration (m^-3), and T_i is the temperature (°C) on the ith day.

Target microorganisms and viruses in the floodplain river are also subject to temperature-dependent inactivation/degradation:

$$\frac{\text{d}{C}_{\text{fr}}\left(t\right)}{\text{d}t}=\frac{Q_{\text{mr}\to \text{f}r}}{V_{\text{fr}}}{C}_{\text{mr}}-\left(\frac{Q_{\text{mr}\to \text{fr}}+Q_{\text{gw}}}{V_{\text{fr}}}+\mu \left(T_{\text{fr}}\right)\right)C_{\text{fr}}(t)$$ [5]

where C_fr(t) is the TMV concentration (m^-3) in the floodplain river on time t (d), C_mr is the daily mean TMV concentration (m^-3) in the main river, Q_mr→fr is the daily mean discharge of the main river into the floodplain river (m³ d^-1), V_fr the floodplain river compartment volume (*m³), µ(T_fr) is the temperature-dependent inactivation/degradation rate coefficient (d^-1), and T_fr is the daily mean water temperature of the floodplain river (°C).

Assuming steady-state conditions and complete mixing on each day, the analytical solution of Eq. [5] is as follows:

$$C_{\text{fr}}\left(t\right)=\frac{Q_{\text{mr}\to \text{fr}}}{Q_{\text{mr}\to \text{fr}}+Q_{\text{gw}}+\mu (T_{\text{fr}})V_{\text{fr}}}{C}_{\text{mr}}+\left(C_{\text{fr}}(t-1)-\frac{Q_{\text{mr}\to \text{fr}}}{Q_{\text{mr}\to \text{fr}}+Q_{\text{gw}}+\mu (T_{\text{fr}})V_{\text{fr}}}{C}_{\text{mr}}\right)\exp \left(-\frac{Q_{\text{mr}\to \text{fr}}+Q_{\text{gw}}+\mu \left(T_{\text{fr}}\right)V_{\text{fr}}}{V_{\text{fr}}}t\right)$$ [6]

Concentrations of TMVs in the floodplain river are calculated for 1-d time periods for each day in the year, where C_fr(t − 1) is the TMV concentration in the floodplain river of the previous day. For the first day in the year, C_fr(0) is assumed to be zero.

Floodplain

Rainfall in the floodplain releases TMVs from fecal deposits and runs them off to the floodplain river. In QMRAcatch, this rainfall does not cause flooding. Rainfall data can be spreadsheet data or generated by means of a stochastic rainfall model, which was modified from Sivapalan et al. (2005) and Viglione et al. (2012). Rainfall rate (events per day) and depth (mm) are subject to seasonality, which is mimicked by a cosine function:

$$\cos (t)=1+\frac{1}{2}\cos \left\{2\pi /365\left[t-1-30\left(\phi -1\right)\right]\right\}$$ [7]

where ϕ is the first day of the month with maximum rainfall. Both rainfall rate and depth are exponentially distributed. Their mean values are used for the random rainfall generation for each day. The inverse of the rainfall rate per day is used to calculate the arrival times of the rainfall events. Each rainfall event is assumed to last 1 d because the model simulations are based on daily values. Sequential sampling from the exponential distributions generates days without rain and days with one or more rainfall events, from which the amount of rainfall is summed per day (Fig. 1).

The floodplain is flooded when the discharge from the main river into the floodplain river exceeds the discharge capacity of the floodplain river. This discharge capacity is determined by its depth, width, and Manning coefficient. The floodplain is schematized as a plain with the floodplain river in the middle (Fig. 1). Both riverbanks of the floodplain have the same slope with angle ϕ. The excess daily discharge floods an area of the floodplain (A_fl [m²]):

$$A_{\text{fl}}=\left(-w_{\text{fr}}+2\sqrt{\frac{w_{\text{fr}}^2}{4}+\frac{\left(Q_{\text{mr}\to \text{fr}}+Q_{\text{gw}}\right)/v_{\text{fr}}-h_{\text{fr}}{w}_{\text{fr}}}{\tan \phi }}\right)l_{\text{fr}}$$ [8]

where w_fr (m) is the width of the floodplain river, v_fr (m d⁻¹) is the flow velocity of the water in the floodplain river, h_fr (m) is the depth of the floodplain river, and l_fr (m) is the length of the floodplain river.

Target Microorganism and Virus Fate and Transport in the Floodplain

Flooded fecal deposits are assumed to be completely resuspended. Rainfall releases a fraction of TMVs from the fecal deposits in the floodplain. A fraction (f_evapo [–]) of the precipitation (prec [mm]) evaporates, and another fraction runs off, carrying released TMVs. The residual precipitation infiltrates the floodplain aquifers. First, the volume of rainwater in the area with fecal deposits is calculated for each day in the year:

$$V_{\text{rel}}=\left(1-f_{\text{evapo}}\right)\text{prec}\hspace{0.17em}{A}_{\text{dep}}$$ [9]

where V_rel (m³) is the rainwater volume in the area with fecal deposits (A_dep [m²]). It is the water volume in which deposited TMVs are released.

In Eq. [10], N_rel is a 2 × 365 matrix per TMV, with the first row containing the numbers of released TMVs that run off and the second row containing the numbers of resuspended TMV in flood water. On the first day, the numbers of released TMVs (N_rel,1,1) are calculated:

$$N_{\text{rel},1,1}=\{\begin{array}{c}{V}_{\text{rel},1}=0\Rightarrow 0\\ V_{\text{rel},1}>0\Rightarrow f_{\text{rel}}{N}_{\text{dep},1}\end{array}$$ [10]

where f_rel [–] is the fraction of released TMVs. If there is no release volume (V_rel [m³]), then no TMVs are released from the fecal deposits.

The number of TMVs that are not released (N_depres) is calculated as:

$$N_{\text{depres}}=N_{\text{dep},1}-N_{\text{rel},1,1}$$ [11]

Then for each of the following days (d) in the year, the total deposited number of TMVs (N_deptot) is calculated from the newly deposited numbers (N_dep,d) plus those numbers that were not released the previous day (N_depres) in the nonflooded area. If the nonflooded area is at least large as on the previous day then it is this area; otherwise it is a fraction of it:

$$N_{\text{deptot}}=N_{\text{dep},\text{d}}+N_{\text{depres}}\text{Min}(1,A_{\text{dep},\text{d}}/A_{\text{dep},\text{d}-1})$$ [12]

Release from the deposits occurs in the nonflooded area. The next step is to calculate the number of TMVs that are released in the nonflooded area from N_deptot if V_rel,d > 0:

$$N_{\text{rel},\text{d},1}=\{\begin{array}{c}{V}_{\text{rel},\text{d}}=0\Rightarrow 0\\ V_{\text{rel},\text{d}}>0\Rightarrow f_{\text{rel}}{N}_{\text{deptot}}\end{array}$$ [13]

For TMVs in deposits from the previous day that are flooded on the current day, it is assumed that they are completely resuspended in the floodplain river water:

$$N_{\text{rel},\text{d},2}=\{\begin{array}{c}{\text{A}}_{\text{dep,d}}\ge A_{\text{dep},\text{d}-1}\Rightarrow 0\\ A_{\text{dep},\text{d}}<A_{\text{dep},\text{d}-1}\Rightarrow N_{\text{depres}}\left(1-A_{\text{dep},\text{d}}/A_{\text{dep},\text{d}-1}\right)\end{array}$$ [14]

Release occurs from new deposits and residual deposits of the previous day, accounting for inactivation/degradation. The residual number of TMVs that were not released is calculated and is to be used for the next day. The number of released TMVs (N_rel,d,1) is subtracted from the total number of deposited TMVs (N_deptot) and reduced by temperature-dependent inactivation/degradation:

$$N_{\text{depres}}=\left(N_{\text{deptot}}-N_{\text{rel},\text{d},1}\right)\exp \left(-{\mu }_{\text{Ti}}\right)$$ [15]

The numbers of released TMVs from boar, deer, birds, and humans are summed.

Released TMVs infiltrate into the subsurface. The TMV concentrations in rainwater (S_inf) are calculated from N_rel and V_rel, which can be used as source water concentration for calculations with infiltration and subsurface transport as treatment of the water.

The numbers of released TMVs running off to the floodplain river are added to those released from flooded deposits:

$$N_{\text{vro}}=f_{\text{ro}}/\left({\text{f}}_{\inf }+f_{\text{ro}}\right)N_{\text{rel},\text{d},1}+N_{\text{rel},\text{d},2}$$ [16]

where f_ro and f_inf are the fractions of the rainfall that run off and infiltrate, respectively.

Infection Risk Assessment for Groundwater Used as a Drinking Water Resource

Pathogen concentrations in drinking water are calculated from their concentrations in surface water and log removal by bank filtration along the main river and floodplain river. Exposure or dose (D) is calculated from the pathogen concentration in drinking water and drinking water consumption (see Dashboard [Fig. 1]). The infection risk per person per day is calculated by applying the hypergeometric dose–response relation with betadistributed dose response parameters α and β (Teunis and Havelaar, 2000). The formula for calculating the risk of infection for a specific dose is as follows (Teunis and Havelaar, 2000):

$$P_{\text{inf},\text{person},\text{day}}=1{-}_1{F}_1\left(\alpha ,\alpha +\beta ;-D\right)$$ [17]

where ₁F₁ is the confluent hypergeometric function. The implemented values for the dose response parameters α and β are 0.253 and 0.422 for enterovirus (Teunis et al., 1996), 0.04 and 0.055 for norovirus (Teunis et al., 2008), 0.038 and 0.022 for Campylobacter (Teunis et al., 2005), and 0.3 and 1.1 for Cryptosporidium. The latter are equivalent to those used in QMRAspot (Schijven et al., 2011).

The distribution of the risk that a person per year is infected at least once is calculated from Monte Carlo sampling from the daily infection risk (Teunis et al., 1997):

$$P_{\inf ,\text{person},\text{year}}=1-{\displaystyle {\prod }_{i=1}^{365}\left(1-P_{\inf ,\text{person},\text{day,}i}\right)}$$ [18]

In the case that the risk exceeds the health target, a so-called removal deficit is given, which is defined as the logarithm of the ratio of the 95th percentile of the infection risk and the health target. It indicates how much extra log removal would be required to comply with the health target. The tool provides the option of calculating the required log removal of the pathogens for compliance with a health target by adjusting the 95th percentile log removal using the removal deficit.

By default, for each year day, the infection per person per day is calculated for 27 persons, resulting in a total of 365 × 27 = 9855 Monte Carlo samples. This default is chosen to have a very short time for calculation. An option is provided to recalculate infection risk for selected enteric pathogens using a higher number of Monte Carlo samples.

Depending on the location of the well, a mixture of bank-filtrated water from both rivers and from groundwater, which may be contaminated with pathogens that infiltrated from the floodplain, is collected. The composition of the mixture can be set.

Infection risk distributions are presented by box-and-whisker plots that are green when below the health target, yellow when the 95th percentile exceeds the target, and red when the mean risk exceeds the target (Fig. 1).

Infection Risk Assessment from Swimming in the Surface Water

A period for swimming can be defined by setting a minimum swimming water temperature. For this kind of risk assessment, dose (D) is calculated from the pathogen concentration in the river and the gamma-distributed volume (V, [liter]) of swallowed water per person per swimming event for men (r = 0.45 and λ = 60), women (r = 0.51 and λ = 35), and children (r = 0.64 and λ = 58) (Schets et al., 2011). Monte Carlo samples from these distributions using these parameter values are in milliliters but are converted to liters.

Swimming Water Quality Classification

From E. coli concentrations during the swimming period, the swimming water quality class is calculated as described in EU Directive 2006/7/EC (EU, 2006). This directive classifies swimming water quality as “excellent” when the 95th percentile of the E. coli concentration is <500/100 mL, as “good” when the 95th percentile lies between 500 and 100 mL and 1000/100 mL, as “sufficient” when the 90th percentile does not exceed 900/100 mL, and otherwise as “poor.”

Model Calibration and Sensitivity Analysis

Site Description

The model was calibrated for a study site located at the River Danube in Vienna, Austria. The alpine River Danube is one of the largest European rivers, with a mean river discharge of 1900 m³ s⁻¹ near the study site. Five WWTPs (WWTPs 1–5) are situated 13, 17, 35, 70, and 186 km upstream of the Danube Island with PI. The Danube Island and the artificial side arm of the Danube, the New Danube, were designed and built for flood protection for the City of Vienna. The Danube Island is also an important recreational area, with beaches along both sides. The New Danube is a popular swimming area, but the River Danube currently does not meet the water quality criteria for swimming.

Measured Target Microorganism and Virus Concentrations for Calibration

In 2010 to 2013, 10-L samples of main river water at the PI and 1-L samples of wastewater were taken (all single samples). Concentrations of E. coli and HF183 (n = 72) and enteroviruses (n = 18) were determined for raw and treated wastewater (WWTP2 and -3). For the PI, E. coli concentrations were determined in samples from 2010 to 2013 (n = 32), but HF183 (n = 17) and enterovirus (n = 6) concentrations were determined only in samples from 2013. Escherichia coli were enumerated as colony forming units according to ISO 16649-1 (ISO, 2001). HF183 was enumerated as PCR-detectable units after Green et al. (2014) with a modification for sample processing and DNA extraction after Reischer et al. (2008). Isolation of virus particles as plaque forming units in tissue cultures was done as described by Walter and Rüdiger (1981) and enumerated as described by Chang et al. (1958).

Model Calibration

For model calibration, mean and 95th percentile values from the measured concentrations of enterovirus, E. coli, and HF183 in raw wastewater as well as discharge rates were set for all five WWTPs (Table 1). The same settings as in WWTP2 were assumed for WWTP1, -4, and -5 for E. coli and HF183 and for WWTP1, -3, -4, and -5 for enterovirus. Mean and 95th percentiles of the log₁₀ removal by wastewater treatment were set manually such that mean and 95th percentiles and the parameter values of the gamma distributions describing the simulated concentrations in treated wastewater matched those of the measured concentrations. These values are presented next to all graphs with TMV concentrations. The R² value is included. However, although there may be a perfect match based on mean and distribution values, because simulated concentrations are randomized in time, the R² value may be negative. The random simulated concentrations that correspond in time with the measured ones may be quite different. In that case, R² has no added value. For microorganisms like Campylobacter where seasonal variation may be pronounced and when peak events would be matched in time, R² may become a more meaningful calibration measure. It is important to realize this limitation of R².

Five overflow events per year were considered for calibration based on expert guesses. Concentrations of TMVs in raw wastewater were multiplied by constant factors for determining the TMV concentrations in overflow water. These factors and the mixing degrees at all WWTPs were adjusted, increasing with upstream distance, to match the mean and 95th percentiles of simulated and measured HF183 concentrations at PI as well as their respective gamma distribution parameters. With these settings, the concentrations of E. coli and enterovirus at PI were predicted.

A successful prediction of E. coli in the River Danube justifies the assumption that WWTPs are the dominant source. To confirm this assumption, QMRAcatch was calibrated to observed E. coli concentrations in the River Danube for different time periods (2010–2012) than during the calibration (2013). Drinking water QMRA was conducted at PI under the calibrated settings for 2013. For norovirus, Campylobacter, and Cryptosporidium, default medium input concentrations and log removal in the WWTPs were used from the literature (Table 1).

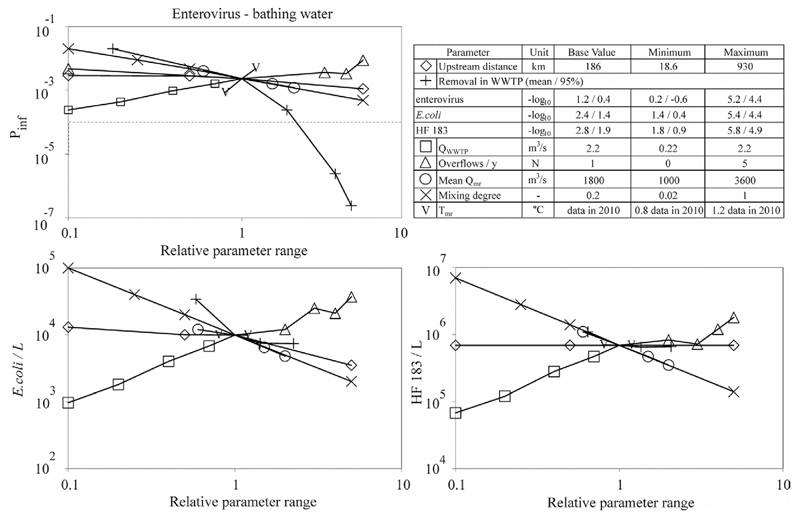
Sensitivity Analysis on Concentrations and Infection Risks for Swimming

Sensitivity analysis was restricted to E. coli, HF183, and enterovirus under the calibrated settings for 2010. First, the WWTP that determines their concentrations at PI the most was identified by switching off one WWTP at a time. Having switched on only the most important WWTP (with 10 times higher TMV concentrations in overflow water than in raw wastewater to simulate pronounced peak concentrations in the surface water), main river discharge, mixing degree, and water temperature were varied to evaluate their effects on the infection risk from exposure to enterovirus by swimming and the concentrations of E. coli and HF183 at PI. In addition, infection risks using main river discharge data from 2010 were compared with infection risks using main river discharge generated by the ARMA(1,1) model (Table 1) to evaluate the ARMA(1,1) model.

Results

Model Calibration

Time series plots of simulated and measured TMV concentration in raw and treated wastewater effluent and in the river at PI show that the variabilities are similar and that the measured values lie within the simulated concentration ranges (Supplemental Material, Fig. 1). The simulated concentrations vary from day to day because of the random sampling from the concentration and treatment distributions. All calibrated parameter values are shown in Table 1. After calibration to HF183, E. coli, and enterovirus concentrations at WWTP2 and -3, the differences between the mean and 95th percentile of observed and simulated concentrations were <0.3 log₁₀. After calibration to HF183 in 2013, these differences were <0.04 log₁₀. Escherichia coli concentrations at PI were slightly underpredicted. The mean and 95th percentiles of the predicted and observed E. coli concentrations at PI deviated by <0.2 log₁₀. For enterovirus concentrations at PI, the predictions and observations deviated by 0.5 log₁₀.

After calibration to E. coli for different time periods (2010– 2012), the mean and 95th percentiles of the observed and simulated E. coli concentrations at PI deviated by <0.5 log₁₀.

The required mean and 95th percentile log₁₀ removals by river bank filtration to meet the infection risk target for drinking water were 6.1 and 5.3 log₁₀ for enterovirus, 7.7 and 7.0 for norovirus, 5.6 and 4.8 for Campylobacter, and 4.9 and 3.7 for Cryptosporidium, respectively.

Sensitivity Analysis

Despite its largest upstream distance from PI, WWTP5 determined TMV concentrations at PI the most because of its largest discharge. Concentrations of TMVs at PI decreased by 0.4 log₁₀ when switching off WWTP5, compared with <0.1 log₁₀ when switching off the other WWTPs.

Figure 2 shows that the TMV concentrations at PI and especially infection risks from swimming at PI are most affected by the log₁₀ removal by wastewater treatment, followed by mixing degree and wastewater discharge. Sensitivity to TMV concentrations in wastewater is the same as to log₁₀ removal by wastewater treatment (not shown). Within increasing river discharge, there is more dilution and, hence, a decrease in TMV concentrations and infection risk. The range over which river discharge varies is limited; therefore, its effect is limited too. For conventional wastewater treatment, commonly not achieving more than 2 log₁₀ removal, mean infection risk from swimming at PI are around 0.3% per person per swimming event, which is high.

Fig. 2. Sensitivity of enterovirus infection risk (swimming) and Escherichia coli and HF183 concentrations at the point of interest to upstream distance of wastewater treatment plant (WWTP) 5, removal by wastewater treatment, wastewater discharge, number of wastewater overflows, river water discharge, mixing degree, and water temperature. P_inf is infection risk, Q_mr, is the main river discharge (m³d⁻¹), and T_mr is the main river water temperature (°C).

Infection risks based on simulated main river discharge data according to the ARMA(1,1) process showed good agreement with infection risks based on actual main river discharge data. For enterovirus with ARMA and actual data, the drinking water risks are 9.8 × 10⁻⁴ and 6.6 × 10⁻⁴ for the mean and 1.6 × 10⁻³ and 1 × 10⁻³ for the 95th percentiles, respectively. The bathing risks are 2.3 × 10⁻³ for both means and 1.1 × 10⁻² for both 95th percentiles.

The number of overflows only affects the concentrations if they fall into the bathing period by chance. This was not the case in the simulation, and therefore an increase in simulated concentrations with increasing wastewater overflows show only random effects. Over the whole year, concentrations decreased with increasing water temperature but only by 0.1 log₁₀, reflecting a minor impact of temperature on the inactivation/degradation of E. coli, HF183, and enteroviruses. The upstream distance of WWTP5 and the water temperature did not affect concentrations of HF183 at PI but did affect E. coli concentrations for distances above the base value of 186 km.

Discussion

The interactive computational tool QMRAcatch was introduced, and its underlying models were explained. QMRAcatch can be run using location-specific hydrological data as well as generated hydrological data from setting sets of parameter values. The user of the tool is supported in making realistic choices by the included default parameter values. In that regard, the tool already fulfils its educational purposes, and various emission and treatment scenarios can be explored easily.

For simulations to be meaningful, calibration of the tool for a specific site is a requirement. So far, as demonstrated, QMRAcatch has been calibrated satisfactorily for a few TMVs for only part of the domain, namely from points of wastewater discharge to a PI in the main river. It allowed determining the contribution of several WWTPs to the TMV concentrations at PI. This strongly suggests that, in the study area, TMV concentrations at PI are primarily determined by wastewater discharges. Sensitivity analysis showed that concentrations at PI were most sensitive to changes in concentrations in wastewater and wastewater treatment. In this regard, QMRAcatch is an excellent tool to explore the balance between treatment of wastewater and treatment of abstracted river water for drinking water production.

The tool has not been evaluated for the flooding, runoff, and infiltration that occur in the floodplain. This will be the focus of a future study. Data on fecal deposition, the prevalence of infections, the concentration of TMVs in feces, and runoff come with high uncertainties and even large data gaps. Simulations with QMRAcatch using the default medium values suggest a high impact on water quality in the floodplain river from even a small number of wildlife overshadowing the fecal load from the main river to the floodplain river (data not shown). At this stage of development, QMRAcatch can be applied to set up appropriate monitoring programs to study the impacts of flooding, runoff, and infiltration in floodplains on the water quality of the floodplain river and the underlying aquifers. Diffuse agricultural runoff to the main river will be part of extending the tool.

The aim of this study was to investigate how well QMRAcatch predicts E. coli and pathogen (enterovirus) concentrations at a PI after having calibrated for MST marker (HF183) concentrations in wastewater and in the river at PI. Successful use of MST markers provides potential for future applications of QMRAcatch. Parameters could be set easily such that TMV concentrations in wastewater matched measured concentrations. Next, mixing degrees were set such that simulated and measured concentrations matched at the PI (e.g., swimming or intake for drinking water production). It appeared that the same mixing degree could be applied for different TMVs, encompassing viruses and bacteria. This suggests that the assumed parameter values describing the dilution and transport, including temperature-dependent inactivation/degradation using literature data, were adequate to describe the transport processes. The mixing degree is effectively a correction factor, not only accounting for mixing of a discharged contamination plume but also covering for other transport processes, such as sedimentation. Sedimentation and resuspension are more important for the larger microorganisms (Kim et al., 2010).

To demonstrate the feasibility of MST without requiring an unreasonably high effort, the implementation into QMRAcatch was limited to one human-associated genetic fecal marker (Green et al., 2014) and to its occurrence in WWTPs. A future extension of MST could easily cover contamination source, such as from ruminants or pigs (Wuertz et al., 2011), to support source-targeted calibration and model verification. This is likely very helpful when the analysis covers wildlife fecal sources from wetlands and from WWTPs (Reischer et al., 2011). However, experimental data on the persistence and mobilization of MST markers in fecal droppings of various animal sources during rain or flood events have to be established to exploit the full potential of QMRAcatch. Also, in this paper, the E. coli data used were based on grab samples, thus representing only a small percentage of the river. Flow-weighted samples for measurement of TMVs during a day would provide a better representation (Stadler et al., 2008; Mayer et al., 2015).

The current version of QMRAcatch covers four pathogens that are often used as reference pathogens in QMRA. A recently performed study on the importance of zoonotic pathogens in Austria indicates the need to extend the TMV collection with Giardia, Yersinia enterocolitica, enterohemorrhagic E. coli, nontubercolous Mycobacteria, Salmonellae, and Toxoplasma gondii (Stalder et al., 2011a, 2011b). This is especially important when the impact of fecal contamination from wetland (zoonotic sources) is to be compared with the impact from wastewater discharge in the main river (human source) in backwater habitats.

Conclusions

The results of this study lead to the following conclusions: (i) A generic, easy-to-use, interactive, computational, and educational tool was developed to simulate concentrations of TMVs at a PI (e.g., recreational water activity and drinking water production) and to assess associated microbial infection risks. It can be used to evaluate various emission and treatment scenarios. (ii) QMRcatch has been calibrated successfully for the pathway from wastewater discharge to a PI and enables us to determine the contribution of several WWTPs to the river water quality. (iii) QMRAcatch still needs to be calibrated for the processes in the floodplain. (iv) QMRAcatch joins the field of microbial fecal contamination analysis by using data from fecal indicator bacteria monitoring, advanced MST, and “multi-target” QMRA.

Supplementary Material

Supplemental material is avaiable online for this article.

Abbreviations

ARMA

autoregressive moving average

MST

microbial sources tracking

PI

point of interest, which may be water intake for drinking water production or a swimming area

QMRA

quantitative microbial risk assessment

TMV

target microorganism and virus

WWTP

wastewater treatment plant