PETSTEP: Generation of synthetic PET lesions for fast evaluation of segmentation methods

Abstract

Purpose

This work describes PETSTEP (PET Simulator of Tracers via Emission Projection): a faster and more accessible alternative to Monte Carlo (MC) simulation generating realistic PET images, for studies assessing image features and segmentation techniques.

Methods

PETSTEP was implemented within Matlab as open source software. It allows generating three-dimensional PET images from PET/CT data or synthetic CT and PET maps, with user-drawn lesions and user-set acquisition and reconstruction parameters. PETSTEP was used to reproduce images of the NEMA body phantom acquired on a GE Discovery 690 PET/CT scanner, and simulated with MC for the GE Discovery LS scanner, and to generate realistic Head and Neck scans. Finally the sensitivity (S) and Positive Predictive Value (PPV) of three automatic segmentation methods were compared when applied to the scanner-acquired and PETSTEP-simulated NEMA images.

Results

PETSTEP produced 3D phantom and clinical images within 4 and 6 min respectively on a single core 2.7 GHz computer. PETSTEP images of the NEMA phantom had mean intensities within 2% of the scanner-acquired image for both background and largest insert, and 16% larger background Full Width at Half Maximum. Similar results were obtained when comparing PETSTEP images to MC simulated data. The S and PPV obtained with simulated phantom images were statistically significantly lower than for the original images, but led to the same conclusions with respect to the evaluated segmentation methods.

Conclusions

PETSTEP allows fast simulation of synthetic images reproducing scanner-acquired PET data and shows great promise for the evaluation of PET segmentation methods.

Introduction

In Positron Emission Tomography (PET) images, the segmentation of tumor from background has a number of important applications in both prognosis [1,2] and therapy [3,4]. However, implementation of automated segmentation into the clinical environment has been slow primarily due to the lack of standardized means with which to evaluate the various methods [5]. This includes the availability of data with a known ground truth. At present, such data are available on a limited scale and for a very large range of image types, making standardization problematic. The American Association of Physicists in Medicine (AAPM) Task Group-211¹ (TG-211), Classification and evaluation strategies of auto-segmentation approaches for PET, is seeking to establish a methodology and a framework for evaluating auto-segmentation methods. In a forthcoming report, the TG-211 will be highlighting the need for standard evaluation data available to all and containing a large number of varied images for the evaluation of PET auto-segmentation tools. In particular, the use of simulated PET images can be beneficial for the evaluation of segmentation methods, as it theoretically allows generating realistic PET images simulated from different lesion uptakes with known ground truth [6]. However, the large variation of observed lesion geometries and uptake distributions requires a large number of test images to provide clinically relevant and robust results. For such applications, there is a need for a fast, flexible, and accessible simulation tool dedicated to the generation of large datasets.

Simulated PET images are useful for a number of applications, ranging from equipment calibration and optimization to testing of novel image processing approaches [7]. The advantages of simulation over both physical phantom and patient data include a greater knowledge, control, and flexibility in defining the tracer uptake distribution. Furthermore, it provides the ability to perform these studies without requiring access to a scanner, which can be limited. When simulating PET images with synthetic lesions, Monte Carlo (MC) simulation of the data followed by reconstruction of the image is most commonly used [6,8–12]. However work presented by Manjeshwar et al. has shown that realistic synthetic lesions can be placed in existing PET images by using arbitrary combinations of ellipsoidal primitives [13] that are added, with noise, to the existing projection data. This work extends Manjeshwar et al. by obviating the need for access to the actual patient projection data and the subsequent required knowledge of and use of the associated imaging system's system matrix. Furthermore, this approach sidesteps the vast computation expense that generally accompanies MC methods [8–11], which can often require hundreds of hours of simulation time to recreate a single bed position from a patient's scan, especially when Graphics Processing Units (GPUs) are not available. This study introduces this forward-projection simulation method to the segmentation community in the form of a fast simulation tool for generating simulated PET lesions and images for use in developing and evaluating segmentation methods.

In this work, we present PETSTEP (PET Simulator of Tracers via Emission Projection), a tool that allows the simulation of synthetic PET lesions with a high degree of flexibility, minimal computational time, and intrinsic data/projector matching, and we describe its implementation. We also compare the images provided by our software to both phantom and clinical data obtained from our scanner as well as to MC simulated phantom data. Finally, we evaluate the impact of using images simulated with our software compared to scanner-acquired images for the evaluation of segmentation methods.

Methods

Description of PETSTEP

Generation of synthetic lesions

PETSTEP allows the generation of synthetic PET images based on inserting a lesion-like sub-image into an image representing the background. The background image may be a reconstructed PET scan of a patient or phantom, or it can be an idealized image² representing the background object prior to its being acted on by the PET system and the subsequent reconstruction. These two cases are described in the following paragraphs.

Inserting synthetic lesions into images of the idealized background

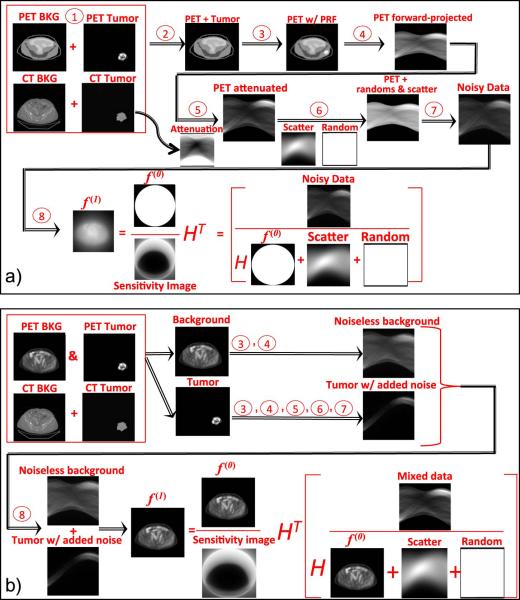
The most straightforward case is to insert an idealized synthetic lesion directly into an idealized background that represents the underlying distribution of tracer uptake. In this case, it is assumed that neither the background image nor the lesion has been operated on by the system's Point Response Function (PRF), and the image is noise free. The simulation process includes the following steps, illustrated on Fig. 1a):

1. The lesion is added to or used to replace the background at its location, as specified by the user.

2. The resulting combined-object, representing the idealized background and lesion is blurred to mimic the effect of a real PET system's PRF. In this study we represent this with a spatially shift invariant PRF, commonly referred to as a Point Spread Function (PSF).

3. The blurred image is then forward-projected via a radon transform to produce noise free projection data.

4. The resulting projection data are attenuated by a forward-projection of the attenuation map derived from the computed tomography (CT) image. The attenuated data are then scaled, so that the sum of the intensities corresponds to the number of true counts being simulated, which are calculated from the user-defined maximum uptake, uptake distribution, scan time and system sensitivity.

5. Random events and scatter are added to the image. The random distribution is generated from a uniform background, whereas the scatter distribution is generated from the forward projection of the blurred image. The random and scatter distributions are scaled to the number of counts corresponding to the user defined scatter (SF) and random (RF) fractions,

   $$SF=\frac{S}{T+S},\text{and}RF=\frac{R}{T+S+R},$$ (1)

   where T is the number of true counts, S is the number of scatter counts, and R is the number of random counts.

6. Noise is added to the data as a Poisson distribution of values with mean value corresponding to the forward projected data with added random and scatter counts.

7. The noisy realizations of the projection data can then be reconstructed using filtered back-projection (FBP) or a maximum-likelihood scheme such as ordered-subset expectation-maximization (OSEM). In this study we use an OSEM scheme that allows for PSF correction (this can be generalized to a spatially variant PRF) [14] given by,

   $$f^{k+1,0}={\sum }_j\frac{f^{k,j-1}}{PS{F}^T\ast H_j^T{\mu }_j}PS{F}^T\ast H_j^T\left(\frac{g_j}{H_j(f^{k,j-1}\ast PSF)+\frac{R{S}_j}{{\mu }_j}}\right)$$ (2)

   where f^k is the k^th iteration of the image, g_j is the j^th subset of the data, μ is the attenuation on each projection, RS are the scatter and randoms, H is the forward-projection, H^T is the back-projection, and ∗ is the convolution operator between the images and the system's PSF. Note that f^0,0 is the initial image for the iterative reconstruction: an image of the unit cylinder. For reconstruction without system response the PSF is the delta function.

8. The resulting images can be post-filtered. In this study we use a Gaussian kernel for the transverse plane and 3-point smoothing in the axial direction.

Figure 1.

Workflows illustrating the simulation process for inserting tumor lesions in both idealized PET objects (above, a) and preexisting PET objects (below, b). The left hand side of the data formation pseudo-equations shows the sinograms used in the image reconstruction. The image reconstruction pseudo-equations show the data with Poisson noise and initializing images for the iterative reconstruction.

Inserting synthetic lesion(s) into preexisting patient or phantom images

When inserting a lesion into a preexisting PET image, the lesion and background PET image must be treated separately, since the preexisting PET image has already been acted on by an imaging system's PRF, while the lesion has not. This is shown on Fig. 1b).

The background and tumor images are blurred independently. Next, both images are forward-projected and attenuated independently. The number of true counts specified by the user is reflected as the sum of both background and lesion images. However, the scatter and random distributions and counts are determined using the number of counts from the lesion only to avoid adding noise from the background image that is already present in the preexisting image. The noise realizations are also generated for the lesion sub-image data only. In addition, when reconstructing the data the initializing image f^0,0 is now the original PET background image. In this way, as each iteration is performed, the only portions of the image that are updated are the lesion and its associated scatter and random noise.

For post-filtering the image, only the inserted lesion and its associated noise are smoothed. This is accomplished by subtracting the preexisting image from the reconstructed one, performing the filtering as described above, and then adding the preexisting image back to the filtered image.

Implementation

The simulation code is written in Matlab using the radon transform and its adjoint for the forward- and back-projectors, respectively. The PETSTEP package was implemented as a plug-in to the open source software CERR [15].

A user interface was written to allow selecting the parameters for the segmentation. The package relies on the availability of some functions in CERR, in particular the contouring tool for drawing lesion outlines on the scans displayed. PETSTEP requires the presence of one CT scan and one PET scan stored in CERR format, with lesion outlines drawn on the PET image. If several outlines are present, the software adds the corresponding binary masks and multiplies the result by the maximum lesion Standardized Uptake Value (SUV) set by the user. This allows modeling several intensity uptake levels and complex geometric distributions.

The following parameters can be set by the user via a graphical user interface:

• The maximum lesion SUV.

• The blurring filter size in millimeters, corresponding to the scanner's intrinsic resolution.

• The scan time in seconds.

• The background activity concentration in kBq/mL.

• The count sensitivity in cps/kBq.

• The scatter and random fractions to be simulated.

• The initial projection data as angular bins and gantry diameter, according to the number of crystals in the scanner and the effective detector diameter.

• The filter size used for PSF correction (the default matches the blurring filter above and is recommended).

• The image size, representing the number of voxels in the transverse plane of the reconstructed image.

• The number of iterations and subsets for the OSEM reconstruction (the subset number should be a divisor of the angular bins, which is verified by the program).

• The size of the blurring filter applied post reconstruction.

• The type of axial filtering required (3-point smoothing: light, heavy, standard filtering or no axial filtering).

• The number of simulation instances required, corresponding to independent noise realizations.

Additionally, options are provided for the user to:

• Use the lesion uptake data either additively or as a replacement for the original uptake values.

• Use an original PET scan as a ¹⁸F-fluorodeoxyglucose (FDG) uptake map as described in the next section.

• Select the type of reconstructions to use.

• Save the PET scans corresponding to the different noise realizations and reconstruction iterations in the current study.

The output of PETSTEP consists of new 3D PET images which are appended to the CERR file from which the simulation was started. These can include:

• The original CT image with inserted lesion density map.

• The original FDG uptake map with inserted lesion, before simulation.

• The simulated PET image for each of the reconstructions selected, and for the number of noise realizations specified.

• The PET scans corresponding to the different noise reconstruction iterations for each reconstruction and noise realization, if specified.

All parameters entered by the user are saved together with each new image generated in CERR. The list of parameters entered can also be saved in a text file in the current folder and retrieved from an existing file.

Evaluation of PETSTEP

The aim of this investigation was to evaluate the ability of PETSTEP to reproduce realistic FDG PET images for segmentation. For this purpose, we calibrated PETSTEP by determining the set of parameters allowing the closest reproduction of the scanner acquisition and reconstruction process. Work was based on the GE Discovery 690 (D690) PET/CT scanner available at both of our centers (Cardiff and New York) and MC simulations performed with the GATE software using a well validated model of the GE Discovery LS (DLS) PET/CT [16].

Comparison to phantom data

First, we aimed at reproducing images of the NEMA IEC body phantom acquired previously with a GE D690 PET/CT scanner at our center. The phantom contains six spherical plastic inserts, which were filled with a FDG activity five times higher than the filled-in background activity, and scanned with one bed position. Template images were derived by extracting the phantom geometry from the CT image, and assigning to background and spheres voxel values corresponding to the filled-in activities of the scanned plastic phantom, to model the desired spheres-to-background activity ratio. The scanner specific parameters, such as gantry diameter were set to values obtained from the manufacturer. The number of radial bins and projection angles was derived from the number and size of detector crystals found in the scanner specifications and the reconstructed Field of View (FOV). The system sensitivity was extracted from NEMA NU2 test results published by Bettinardi et al. [17], where the value of 7.5 true cps/kBq was obtained for a source length of 700 mm and was adapted to the modeled detector FOV length of 157 mm, leading to a value of 33.4 true cps/kBq. The scan time and activity concentration (calculated as an average for the whole phantom) were matched to the experimental values. The bed position overlap was set to 50%, to account for axial sensitivity fluctuations across slices, of the D690 scanner, which has 24 detector rings (47 slices per bed position) and an axial coincidence acceptance of ±23 slices. The blurring filter size was set to 4.9 mm, which is the average of the PSF Full Width at Half Maximum (FWHM) values of the D690 PET/CT scanner obtained at 1 cm and 10 cm of the FOV center using the NEMA NU2 tests obtained at the Cardiff center. The matching PSF correction filter size was set to the same value of 4.9 mm. Scatter and random fractions were also obtained from the NEMA NU2 tests. The OSEM + PSF reconstruction was chosen as the closest to the scanner reconstruction method Vue Point HD algorithm with SharpIR available for the D690 scanner (not including Time-Of-Flight (TOF) correction). The image was reconstructed to a matrix size of 256 × 256 to match the matrix size of images from the scanner, with a 3-point axial smoothing filter of [1 3 1]/5, and post reconstruction filter size of 6.4 mm, matching the filter used for the scanner-acquired image.

The values used for the simulation are summarized in Table 1.

Table 1.

Parameters used for the simulation of the NEMA IEC body phantom PET scan, for both D690 and DLS scanners, using PETSTEP.

Parameter name	D690	DLS
CT maximum contrast (% above background)	12.5	12.5
Maximum SUV	N/A	N/A
Blurring filter size (mm)	4.9	5.1
Activity concentration (kBq/mL)	5.9	4.5
Sensitivity (true cps/kBq)	33.4	42.0
Bed position overlap (%)	50	31.4
Scan time (s)	180	300
Random fraction	0.07	0.0003
Scatter fraction	0.37	0.40
Radial bins at FOV	381 (700 mm)	283 (550 mm)
Projection angles	288	336
Gantry diameter (mm)	810	927
Image matrix size	256	295
Reconstruction type	OSEM + PSF	OSEM
Number of iterations	2	8/4a
Number of subsets	24	12
Post-reconstruction filter size (mm)	6.4	6.0

^a8 iterations for the GATE simulation, 4 iterations for the PETSTEP simulation.

The simulated images (without TOF correction) were compared to the corresponding original scanned PET qualitatively and quantitatively in terms of their intensity spectrum and intensity variations in the background and sphere regions. The total activity in the scan was measured as the sum of all voxel intensities in the three-dimensional (3D) image, multiplied by the voxel volume in mL, as well as the mean intensity value.

The following parameters were estimated for slice No. 14, corresponding to the phantom background only, and for the largest sphere, S6:

• Mean intensity,

• Intensity distribution histogram maximum value,

• Relative (to mean intensity) intensity distribution histogram FWHM.

The background was masked according to its known contour. The values for S6 were calculated within contours generated from the known sphere dimensions and positioned via the high-resolution CT. Histograms were created following the Freedman–Diaconis [18] rule for choosing the bin width and fitted with a Gaussian distribution to estimate the mean value and variation (FWHM) of the image intensity in the background and S6.

Comparison to a GATE Monte Carlo reference simulation

To further validate PETSTEP, the MC software GATE [19] was used together with the previously validated DLS PET camera model [16] to simulate a voxelized representation of the NEMA IEC body phantom, which was simulated with a 5:1 ratio of activity concentration in the hot spheres to background. This was compared to a simulation of the phantom using PETSTEP, with the scanner and reconstruction parameters listed in Table 1, to match the DLS model. The DLS PET camera consists of 18 detector rings of 672 BGO crystals each. Each coincidence from the list-mode data was binned [20] into 1) a sinogram matrix of total prompts and 2) a sinogram matrix corresponding to the coincidence type: true, scattered or random. The size of the sinogram matrices was 283 radial and 336 angular bins.

The system sensitivity parameter and phantom activity concentrations used in PETSTEP were adjusted to reproduce the count statistics obtained with the MC simulation given in Table 2. The prompt coincidences were reconstructed using the software STIR [21] with OSEM (12 subsets, 72 sub-iterations) with normalization, attenuation, scatter and random corrections applied (see Appendices A and B for more details). To account for difference in the reconstruction processes, the simulated PETSTEP image was reconstructed for 1 to 10 iterations (for 12 subsets), and the number of iterations best matching the DLS GATE image, which was reconstructed with 8 iterations, was selected. The images were post-filtered with a 6.0 mm FWHM Gaussian transverse filter and the 3-point smoothing filter [1 2 1]/4 in the axial direction. The resulting image was of size 295 × 295 × 35 with a voxel size of 1.97 × 1.97 × 4.25 mm.

Table 2.

Count statistics obtained for the DLS simulation with GATE and PETSTEP.

Property	Value
Number of trues	4.13 × 107
Number of randoms	1.95 × 104
Number of scatters	2.72 × 107
Total counts	6.85 × 107

The variations in the background and largest hot sphere S6 were analyzed in the same manner as with the clinical phantom scan (background slice No. 10), and compared across simulations.

Simulation of realistic clinical data

PETSTEP, calibrated for the DLS scanner, was used to model realistic head and neck (H&N) data. A PET uptake map was generated using an available clinical PET/CT scan. This image was manually segmented with CT-based thresholding to separate different anatomical structures. All structures delineated with thresholding were visually checked and manually edited when necessary. A 3D gray level image was generated by assigning a gray level value to each anatomical structure segmented corresponding to its mean intensity on the PET image. The choice of the PET scan and the design of the final template were both validated by a radiologist. The template is shown on Fig. 3b. Normal PET images were simulated from the original CT and uptake template without an added lesion.

In addition, a PET image was simulated from an original H&N scan, with the insertion of a synthetic lesion using the methodology described above. The simulation parameters used were the same as presented in Table 1, except for the maximum lesion uptake, which was set to 10 times the background uptake.

Finally, a highly heterogeneous lesion was generated by drawing three different overlapping contours in CERR on the H&N PET uptake map described above, and the simulation was carried out using these contours.

Evaluation of segmentation with PETSTEP

Finally, we investigated the use of images generated with PETSTEP for the evaluation of PET automatic segmentation (PET-AS) methods. Three different PET-AS algorithms described in previous works [22,23] were chosen to represent segmentation approaches found in the recent literature. These included: adaptive iterative thresholding (AT), a gradient-based deformable contouring algorithm (AC) and a fuzzy C-means clustering method for two clusters (FCM2). All PET-AS methods were applied to images of the NEMA phantom acquired with a D690 PET/CT scanner, and to five different noise realizations of simulated images generated in PETSTEP as calibrated to reproduce the D690 scanner (cf. previous section). The segmentation was applied to all six spheres in both images using an initial volume corresponding to a cube centered on the true sphere with 1 cm margin in all directions. Segmentation results on original and simulated data (averaged over noise realizations) were compared in terms of their spatial conformity by calculating the Sensitivity (S) and Positive Predictive Value (PPV), defined as:

$$S=\frac{TP}{TP+FN}$$ (3)

$$PPV=\frac{TP}{TP+FP}$$ (4)

with TP as the true positives (voxels accurately classified), FN as the false negatives (voxels in true contour not included in segmented contour) and FP as the false positives (voxels in segmentation results not included in true contour).

Statistically significant differences between S and PPV values obtained by the different PET-AS were compared between the two different types of images, and were determined for each PET-AS using the Wilcoxon signed rank test available in SPSS 20 (IBM, Chicago, USA).

Results

Evaluation of PETSTEP

Comparison to phantom data

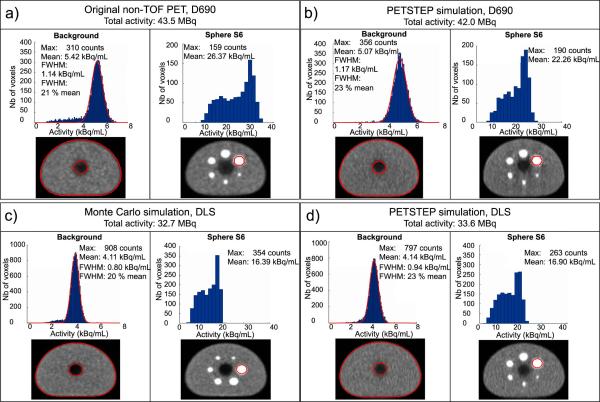
Figure 2a and b provides a comparison of the total activity, background and largest sphere mean intensity and intensity distribution histograms for both D690 original and simulated PET image respectively. The simulated PET image was generated with PESTEP in 1 min 23 s, corresponding to 1.8 s per slice on average on a 2.7 GHz Intel core computer. The number of bins used for background and S6 regions was 135 (bin width 0.06 kBq/mL) and 26 (bin width 1.41 kBq/mL) respectively, using the average from the Freedman–Diaconis rule. The intensity distribution within S6 was not close enough to be fitted to a Gaussian distribution, and FWHM values are therefore not reported. The total activity measured in the simulated image was within 2% of the activity in the original non TOF D690 PET scan. The mean intensity in the simulated image was also within 2% of the original values for both sphere S6 and mean background intensities. The intensity distributions obtained for the background were close, with slightly higher number of counts for the original PET compared to the simulated image (41,045 compared to 32,723 and 187 compared to 164 counts for background and S6 respectively) and larger background FWHM value obtained on the PETSTEP image (20% compared to 17% of the mean intensity for the original PET).

Figure 2.

Comparison of total activity and intensity distribution histograms of the background (slice No. 14 for D690 and No. 10 for DLS) and sphere S6 for (a) the original non-TOF D690 PET image, (b) the simulated D690 PET, (c) the MC GATE simulated DLS PET image with 8 iterations and (d) the DLS simulated in PETSTEP with 4 iterations.

Comparison to a GATE Monte Carlo reference simulation

The number of iterations used in PETSTEP to best match data from the GATE MC simulation (reconstructed with 8 iterations) was 4. The total simulation time was 2750 h divided over 960 AMD Opteron 6238 (Interlagos) 12-core 2.6 GHz processors. The PETSTEP simulated image was generated in 3 min and 8 s on a 2.7 GHz Intel core computer, corresponding to approximately 5.4 s per slice. The same comparison as for the D690 is shown on Fig. 2c and d for the NEMA phantom image acquired with the DLS scanner simulated with MC GATE and with PETSTEP respectively, for the same number of bins as for the GE D690. The total measured activity was 2.5% higher on the simulated PETSTEP image compared to the GATE simulated image. The mean intensity in the simulated image was within 1% and 3% of the original values for the background and sphere S6 respectively. The background FWHMs of the PETSTEP image was slightly larger than for the GATE MC image (23% of the mean value compared to 20%), which corresponds to a slightly noisier image shown on the bottom row of Fig. 3.

Preliminary work (see Appendix C) showed that the scatter distribution as modeled in PETSTEP was closest to the corresponding MC simulated scatter distribution for a 20 cm Gaussian kernel, as determined with a minimum Root Mean Squared Error (RMSE) (see Figs. C1 and C2 in Appendix C).

Simulation of realistic clinical data

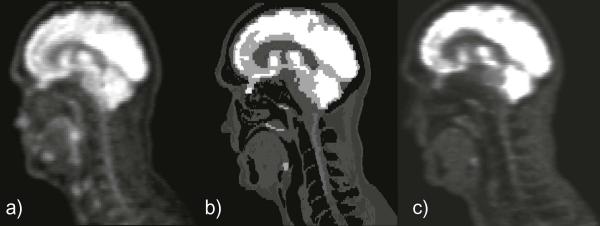
Figure 3 shows a comparison between sagittal slices of the original patient H&N PET image (panel a), the FDG uptake map extracted from the PET/CT dataset (panel b), and the corresponding simulated PET image (panel c). Observable differences between the original and simulated PET images are located in the nose, tongue and larynx area, for which the image intensity obtained is lower than for the original image. The simulated image was visibly closer to the FDG uptake map. The simulation was completed on a 2.7 GHz Intel core computer in 5 min and 47 s, for a 117-slice image, corresponding to the superior–inferior length of the initial uptake map.

Figure 3.

Sagittal slice No. 187 of (a) the original PET image, (b) the FDG uptake map used in the simulation and (c) the simulated PET image.

Figure 4a and b shows a PET image simulated from an existing PET scan, to which a homogeneous synthetic lesion was added, at a target-to-background ratio of 10. The new lesion on Fig. 4b is visible at the location of the contour drawn on the original PET (Fig. 4a). The lesion measured mean and peak intensities were 8.7 and 10.6 times higher than the background mean intensity measured in a Region of Interest of the same geometry positioned in the soft tissue background. Figure 4c shows the FDG uptake map derived automatically by PETSTEP using the initial background uptake map and the three different overlapping contours. The resulting image is shown on Fig. 4d, with the contour corresponding to the outline of the heterogeneous lesion modeled.

Figure 4.

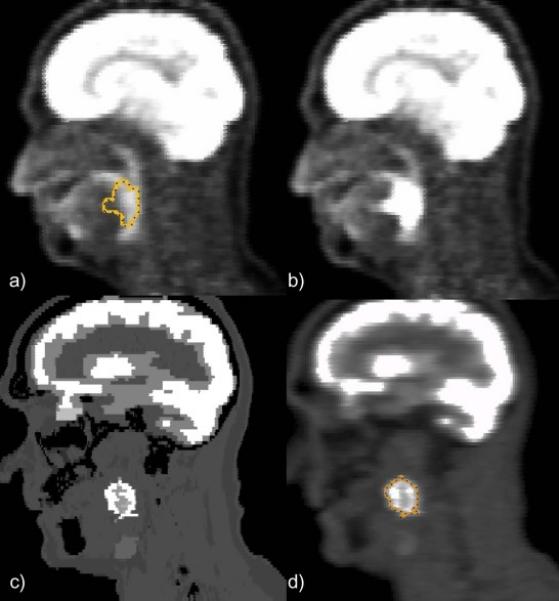
Example of PETSTEP images obtained with showing (a) original PET scan with lesion contour (b) PET image obtained using preexisting PET image and contour, (c) PET uptake map with highly heterogeneous lesion and (d) PET image obtained with lesion contour.

Evaluation of segmentation with PETSTEP

Figure 5 shows S values and PPVs obtained for the segmentation of spheres S1 to S6 on PETSTEP and original images by the three PET-AS methods used. Lower S values and PPVs were obtained for PETSTEP simulated images in 16 and 12 out of 18 cases respectively. Differences in S and PPV were below 24% and 29% of the value corresponding to the original PET in all cases. The largest differences (and cases with higher S for PETSTEP images) were observed for the smallest spheres, for which the standard deviation of values across noise realizations was also the highest (up to 9% of the value for the original image). FCM2 showed lower S values compared to the other methods for both types of images, and PPVs of 1 for all spheres were obtained for both image types. Slightly higher S values were also obtained for AT compared to AC for both image types. Both results obtained with PETSTEP and scanner-acquired images showed higher S value for S1 than S2 and S3 when delineated by FCM2.

Figure 5.

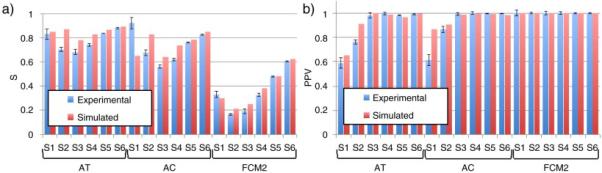
(a) Sensitivity values and (b) Positive Predictive Values of the contours obtained by segmentation on original and PETSTEP simulated images. Values for the simulated case are given as an average on 5 noise realizations, with error bars of one standard deviation of the range of values obtained.

The comparison of S values and PPVs obtained by segmenting the simulated (average across simulated instances) and original images showed a significant difference with the Wilcoxon signed rank test (p < 0.05, Z = −4.386 and p < 0.05, Z = −2.844 respectively).

Discussion

We have developed and implemented PETSTEP, a fast and accessible simulation tool for the generation of synthetic PET images from existing PET as well as from user-defined uptake maps. PETSTEP as implemented as open source uses functionalities already present in CERR and a custom user interface to allow fast simulation of full PET images from complex tracer uptake distributions (FDG in this study), while remaining accessible to users with little or no experience in PET simulation. The addition of synthetic lesions to existing PET images in PETSTEP is similar to work by Manjeshwar et al. (the overlay of freeform shapes versus ellipsoidal primitives) [13]. However, whereas in Manjeshwar et al.'s method tumors are forward-projected and added to the real projection data, PETSTEP forward-projects the existing image to create a synthetic sinogram. To our knowledge, no similar process for PET simulation has been documented in the literature.

PETSTEP involves forward projection with matched projectors,³ using the Matlab two-dimensional (2D) radon and unfiltered inverse (adjoint) radon transforms. Modeling of the scanner system is done with filtering and addition of noise distributions. This approach allows matching the simulated data to scanner-acquired images using known measures such as counts, sampling, iterations, etc. This is more clearly seen in the case of maximum-likelihood PET images where the resolution and noise properties are well known to be locally dependent of the imaged objects [8,9]. As a consequence of using this approach, the MC simulation required 2750 h to generate as many prompts as PETSTEP did in 3 minutes, computing to a factor of ~55,000 less simulation time. Although recent developments using GPUs can lead to acceleration factors of 400–800 for MC simulations [24], the Radon transform and its adjoint can also utilize GPUs for improved performance. This feature will be added to PETSTEP in the near future so that its rapidity compared to MC remains a key advantage. PETSTEP can therefore be extremely useful in the generation of large datasets for quantitative studies and the development of learning methods.

The “inverse crime” model, i.e. the same model is used to generate the data and to reconstruct the images, leads to ignoring normal data inconsistencies due to mismatched acquisition and projectors. However, evidence from Kim et al. [25] shows little effect on image improvement when better system models are used (except for the periphery of the object), which validates the choice of this approach in our work where lesions were at least 3 cm from the object boundaries. Further limitations of PETSTEP include the absence of correlations between slices that exists in real 3D data. This is accounted for by adjusting the number of counts obtained from the 2D projection data to obtain similar Noise Equivalent Counts (NEC) as measured in 3D. This preserves the effective local NEC in the projection space, so that the appropriate ratios of true, scatter, and random counts are seen by each line of response. In addition, the radon and adjoint radon transforms available in Matlab are defined on a uniformly spaced grid in projection space, and therefore do not match the real detector system spacing. As discussed in the paragraph above the affects of this are small and outweighed by the improvement in image generation speed. The scatter distribution in PETSTEP is modeled using a large Gaussian-blurring kernel of 20 cm forward-projected into projection space. Since scatter is known [26] to be a slowly varying count distribution dependent on the real source distribution and the attenuation map, realistic local NEC can be achieved by using this underlying distribution in the reconstruction. This approach is justified by the good agreement observed between our scatter model and the MC simulation (cf. Appendix C). However, because of this, PETSTEP is not appropriate for studies specifically investigating or depending on the image scatter distribution. Finally, the attenuation correction is currently performed under the assumption that the whole object or patient scanned has a density equivalent to water. Although the use of the CT image in both simulation and reconstruction should limit the bias added to the image, work is in process to improve this approximation/correction by using a bilinear approach to calculate the attenuation map from the CT image. It should be noted that PETSTEP avoids extensive system modeling, and is therefore designed for evaluating image processing performance rather than true system response. Nevertheless, more advanced image reconstruction schemes and data models can be added easily and work is in progress to do so.

Comparison with phantom images obtained with the D690 PET/CT scanner have shown that PETSTEP can reproduce the intensity distributions of scanner-acquired non-TOF corrected PET images, with intensity distribution means within 3% (cf. Fig. 2a and b). The slightly higher heterogeneity observed on the simulated images (cf. Fig. 2b) in the background region correlates with a larger FWHM of the intensity distribution histograms. Although the focus of this study was not to reproduce PET images acquired with a specific scanner, such a calibration could be done by applying an additional post-reconstruction filter, such as a de-blurring filter to simulate motion correction.

PETSTEP was further used and calibrated to reproduce an image of the NEMA phantom simulated with a MC GATE model of the DLS PET/CT scanner. For otherwise matched parameters the number of iterations necessary to reproduce the FWHM of the background obtained for the MC simulation was smaller for PETSTEP reconstruction. It is consistent with the fact that idealized PETSTEP model uses data matched to the projectors and is therefore expected to converge with a smaller number of iterations than MC data reconstructed with STIR. This is a known effect when using “inverse crime” models. However, we additionally note that PETSTEP's convergence was similar to the Discovery 690 PET/CT system, which uses a model that is better matched to the data than STIR. This indicates that our “inverse crime” model for the purposes outlined in this paper is acceptably accurate. Furthermore, even though the MC simulation features a reconstruction algorithm implemented in different software (STIR), the results are still close enough for validation of the scatter model implemented in PETSTEP and to compare image properties.

The flexibility of PETSTEP was demonstrated by reproducing a clinical H&N scan acquired on the GE D690 and by simulating PET images with both homogeneous and heterogeneous lesions. The H&N image simulated (cf. Fig. 3c) shows a high degree of similarity with the original PET. Differences in PET intensities in the nose, tongue and vocal cords were due to the fact that the FDG uptake map was designed to represent typical uptake in the resting state. In addition the FDG uptake map was limited to modeling a finite number of tissue structures and of uptake levels in this work. This issue is not observed on Fig. 4b, for which the initial image was an original PET scan. The peak target-to-background ratio measured on the simulated image was within 6% of the targeted ratio, whereas the mean ratio was 14% lower, which was expected because of blurring and partial volume effects at the edges of the lesion caused by the simulation process representing the system response and reconstruction. Furthermore, Fig. 4c and d show the ability of PETSTEP to produce images with highly heterogeneous lesion uptake.

The absolute evaluation of the three PET-AS methods for the segmentation of the six NEMA spheres using S and PPV measures provided statistically significantly different results (with the Wilcoxon signed rank test) for images obtained with PETSTEP and original D690 PET images (cf. Fig. 5a and b). Smaller S and PPV were obtained for the PETSTEP images in 16 and 12 out of 18 cases respectively, which could be due to higher noise (background FWHM) observed on the PETSTEP image (cf. Fig. 2). The largest differences in S values obtained across images, especially for AT and AC, were observed for some of the smallest spheres with higher standard deviation across noise realizations, indicating that these differences may be due to noise fluctuations. AT and AC are indeed based on thresholding and on the image gradient respectively. Both processes are particularly sensitive to noise and intensity fluctuations for small objects. The lower performance (low S and PPV of 1) of FCM2 compared to other methods, observed for the scanner-acquired image, was also clearly visible and quantifiable when using PETSTEP data. The superiority of AT to AC seen on scanner-acquired images was confirmed with PETSTEP images. Other small differences in S and PPV observed were too weak to draw any strong conclusions on the relative accuracy of the methods as they were evaluated on a single image. These results show that images simulated with PETSTEP have the potential to provide similar conclusions to scanner-acquired images when used to assess and compare a range of PET-AS approaches. Although PETSTEP may not be capable, at this stage, of providing absolute segmentation results, it could be a very useful tool for the comparison within a same framework of PET-AS methods on a variety of complex and realistic data, which would help in addressing the lack of reliable inter-comparisons of PET-AS methods on relevant data [27]. This result is important in the light of a growing interest for PET-AS for applications such as RT planning. PETSTEP is currently implemented within the PET-AS set [28] software of the AAPM TG-211 for standardized evaluation of PET auto-segmentation methods.

PETSTEP simulated images also have the potential to be used beyond segmentation evaluation in a number of applications requiring accurate modeling of clinical systems, such as investigations into lesion detection [29,30] or assessment of response to therapy [31,32]. Such studies often focus on image processing performance and accurate tracer uptake modeling, thus requiring a large number of images. In addition, PETSTEP can potentially be applied to any given radiotracer, although in the case of cascade photon emitting isotopes the tool will need to be modified. Further, we think that PETSTEP can be a useful starting point for a number of image-based tasks, such as resident education, tumor segmentation and detection, and other machine learning-based processes (radiomics).

Conclusion

We have developed a fast and flexible PET simulator tool, PETSTEP, for the generation of synthetic PET images representing any user-defined FDG uptake distribution. This tool is open source and designed to be extensible to other isotope and image studies including kinetic modeling. The open source nature of PETSTEP allows user defined uptake distributions that can, in principle, be as complex as desired. We have shown that PETSTEP allows the fast generation of images reproducing scanner-acquired data and can be calibrated to accurately reproduce high quality MC simulated images. We have also shown that PETSTEP provides PET images that can be used for the evaluation of PET segmentation algorithms, providing similar evaluation conclusions to common fillable phantoms. The high flexibility of PETSTEP could further be used for modeling any complex and heterogeneous tracer uptake and for applications such as resident education.

Appendix

A. Scatter correction of Monte Carlo data

The scatter and random corrections were done by including an additive sinogram in the OSEM loop in STIR. The additive sinogram was created by taking the real scattered and random sinograms and applying filtered back-projection and post-filtering with the same filter as described for the comparison to GATE MC simulation. The images were then forward projected back into projection data and scaled according to the real scatter + random count.

B. Normalization in simulated PET image reconstruction

In PET image reconstruction, a normalization correction is used to ensure that the data in each line of response are properly weighted to remove the influence of detector response and geometric view factors. Because detector response is generally uniform in most Monte Carlo simulations (it should be noted that GATE does offer non-uniform detector response, however, it is not used here), only the geometric view factors remain. For these simulations, a large cylindrical source without attenuation was used to generate a normalization projection file. This file was used with STIR to perform normalization correction on all image reconstructions. Figure B1 is provided to show the effect of normalization on the image reconstruction of a 50 cm diameter uniform water cylinder.

The procedure for normalization outlined here was originally implemented in a study by Schmidtlein et al. [16] examining the performance of the GE Discovery ST PET camera, but was here implemented for the GE DLS PET camera. To perform the normalization, a 100 kBq uniform cylindrical source, 59 cm in diameter by 16 cm in height, was simulated in a vacuum using a back-to-back photon source for 100,000 s with decay turned off which resulted in approximately 380 million counts. Several symmetries of the camera were then exploited to amplify the number of effective counts used to create the normalization correction file. These involved the projection angles, the ring differences, and the radial positions. The block structure of the camera repeats itself every 12-projection angles forming a basic symmetry element that was repeated 56 times within each ring difference. If the spacing between the detector blocks in the z-direction is ignored then the geometric response between detectors within each ring difference segment can be assumed to be identical. Furthermore, mirror symmetry in the radial direction between odd and even segments was exploited. Utilizing these symmetries, the number of effective counts increases almost by a factor of 2000, in this case producing 660 billion effective counts.

In addition to exploiting the symmetries, the geometry of the source must also be taken into account. The volume of activity seen by each line of response is a volume given by,

$$V_{LOR}(r,\Delta ring)=\sqrt{C{\left(r\right)}^2+\Delta rin{g}^2}{W}_r{W}_z,$$

where C(r) is the cord length at a particular radial position, Δring is the ring difference spacing, W_r is the distance subtended by the detector in the r-direction, and W_z is the distance subtended by the detector in the z-direction. Each bin of the projection file must be normalized with respect to the activity within its FOV. In this case, the activity is proportional to V_LOR (r, Δring). Figure B2 illustrates these symmetries.

C. Validation of synthetic PET scatter

In order to validate the scatter model as implemented in PETSTEP, the same methodology as used for the GE D690 scanner was applied to the GATE simulated data. The voxelized NEMA IEC phantom (noiseless) used as input to GATE was blurred with six Gaussian kernels of different FWHMs: 50, 100, 200, 300, 400, and 500 mm. The resulting images were then forward-projected in STIR and the resulting sinograms were scaled according to the MC prompt count of the scan and the MC simulated scatter fraction. The RMSE was calculated for the difference between the GATE simulated sinogram and the blurred scatter models to evaluate the optimal model.

The comparison of the real scattered coincidences obtained by the GATE MC scan to the true object, blurred by different Gaussians, is seen in Fig. C1. Visual inspection as well as an optimal (minimal) relative RMSE confirmed that the synthetic scatter based on a 20 cm Gaussian blurring produced the closest fit to the MC data (Figs. C1 and C2).

Figure B1.

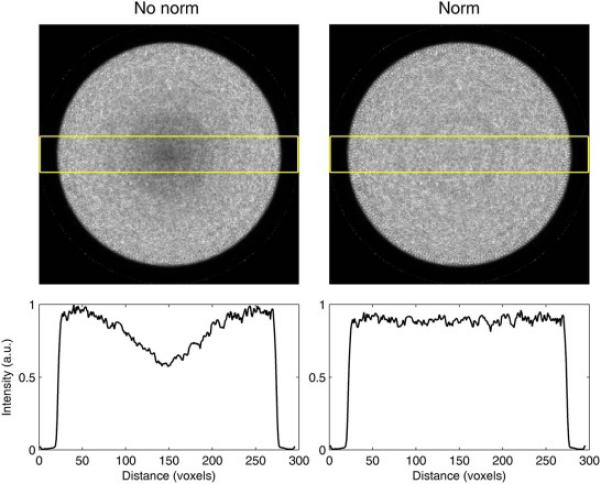
Before and after normalization correction (left to right) for image reconstrucitons of the central slice of a 50 cm diameter phantom and a plot of the slice's profile.

Figure B2.

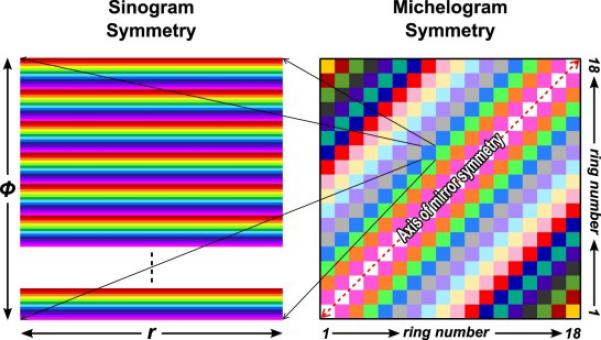
The symmetries in the DLS's detector geometry are depicted by color where similar elements are represented by the same color. Note that the radial symmetry is flipped when crossing the central segment.

Figure C1.

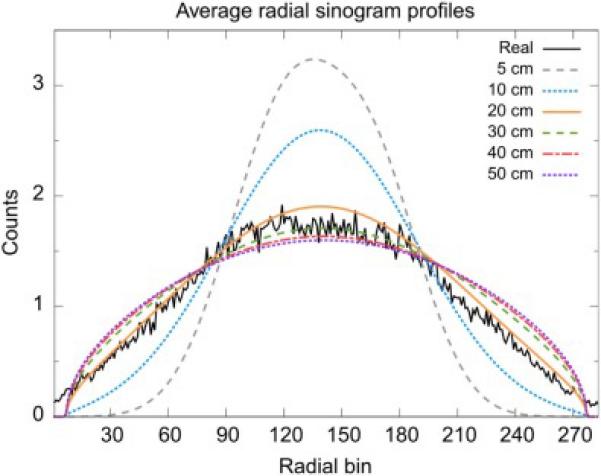
Radial profiles of the direct, central sinograms, averaged over all 336 angular bins. The real profile is obtained from the GATE MC simulation scan and the other 6 from the scatter model with Gaussian kernels of different FWHMs.

Figure C2.

Direct, central sinogram difference (scatter model – real scatters from the GATE simulation), divided by the square root of the model. The scatter model is blurred with a Gaussian of 20 cm FWHM9.