Satellite retrieval of cloud condensation nuclei concentrations by using clouds as CCN chambers

Abstract

Quantifying the aerosol/cloud-mediated radiative effect at a global scale requires simultaneous satellite retrievals of cloud condensation nuclei (CCN) concentrations and cloud base updraft velocities (W_b). Hitherto, the inability to do so has been a major cause of high uncertainty regarding anthropogenic aerosol/cloud-mediated radiative forcing. This can be addressed by the emerging capability of estimating CCN and W_b of boundary layer convective clouds from an operational polar orbiting weather satellite. Our methodology uses such clouds as an effective analog for CCN chambers. The cloud base supersaturation (S) is determined by W_b and the satellite-retrieved cloud base drop concentrations (N_db), which is the same as CCN(S). Validation against ground-based CCN instruments at Oklahoma, at Manaus, and onboard a ship in the northeast Pacific showed a retrieval accuracy of ±25% to ±30% for individual satellite overpasses. The methodology is presently limited to boundary layer not raining convective clouds of at least 1 km depth that are not obscured by upper layer clouds, including semitransparent cirrus. The limitation for small solar backscattering angles of <25° restricts the satellite coverage to ∼25% of the world area in a single day.

The Intergovernmental Panel on Climate Change (IPCC) report (1) states that the uncertainty in aerosol/cloud interactions dominates the uncertainty about the degree of influence that human activities have on climate. Because clouds form in ascending air currents, whereas cloud droplets nucleate on aerosols that serve as cloud condensation nuclei (CCN), we need accurate measurements of both updrafts and CCN supersaturation (S) spectra before we can disentangle aerosol effects on cloud radiative forcing (CRF) from dynamical effects.

Need for Global Measurements of Cloud Base Updrafts and CCN(S)

Tackling the global change problems as identified by the IPCC requires that these quantities be measured on a global scale. However, satellites have not been able to measure updraft speed of the air that forms the clouds or the concentrations of aerosols that are capable of forming cloud drops, which are ingested into the clouds as they grow. Lack of such fundamental quantities has greatly hindered our capability of disentangling the effects of meteorology and anthropogenic aerosol emissions on cloud properties (2). This situation is starting to change with our recently developed methodology to retrieve updrafts at cloud base (3, 4) using the Visible/Infrared Imager Radiometer Suite (VIIRS) instrument onboard the Suomi National Polar-orbiting Partnership (NPP) satellite. This satellite is sun-synchronous, with an overpass time near 13:30 solar time.

Missing such fundamental quantities as CCN(S) and cloud base updraft W_b has been preventing us from disentangling the effects of aerosols from atmospheric dynamics (i.e., meteorology). Their absence also has limited our ability to validate the hypothesized impacts of added aerosols on a large range of phenomena, including (i) maintaining full cloud cover in marine stratocumulus, thus incurring a strong cooling effect on the climate system (5); (ii) suppressing precipitation from shallow clouds (6–8); (iii) invigorating the convection in deep tropical clouds (9); (iv) enhancing cloud electrification (10, 11); (v) intensifying severe convective storms to produce more large hail and tornadoes (12); and (vi) decreasing the intensity of tropical cyclones (13). In addition to their intrinsic importance, these aerosol effects could induce radiative effects that change Earth’s energy budget in a significant way (1).

Previous satellite-based studies related cloud properties mostly to the aerosol optical depth (AOD) and the Ångstrom coefficient (14–18). However, AOD as a proxy for CCN is a rather crude tool that is fraught with problems (19) due to a large number of reasons, including (i) aerosol swelling with high relative humidity (20, 21); (ii) uncertainty in solubility and size distribution (18); (iii) lack of a discernible optical signal from small CCN; (iv) cloud contamination (22); (v) AOD not representing aerosol concentrations near cloud base; (vi) cloud obscuration of the aerosols in the boundary layer; (vii) cloud detrainment of aerosols aloft (23, 24) yielding an increase in AOD for deeper and more extensive clouds without corresponding increase in cloud base aerosol concentrations; and (viii) lack of accurate AOD signal for the pristine boundary layer, where accuracy is most critical because clouds respond to the relative change in CCN concentrations, which can be a very small absolute change at very low absolute concentrations (25). These factors often explain a substantial part of the indicated associations of AOD with cloud top properties (18, 26), which has been erroneously ascribed to aerosol effects. Aerosol optical properties are useful for measuring aerosol type and particle size, which can be identified by active sensor backscatter intensity, color ratio, and polarimetry, or by passive multiangle intensity measurements even without polarimetry. Adding polarimetry to passive, multiangle imaging should improve the precision and range of conditions under which particle size, shape, and refractive indices can be retrieved. However, this still leaves most of the issues unresolved, especially issues iii and v−viii, as listed above. To overcome this conundrum, a complete shift in approach is needed. Instead of addressing the limited information content in the optical signal of the aerosols, we extract CCN(S) by using clouds as an analog for CCN counter (CCNC) chambers.

The structure of this paper is as follows: This section provides the importance and motivation for retrieving CCN(S). Methodology provides a summary of the recent advancements which constitute a critical mass enabling satellite-only retrieval of CCN(S) and applies it while describing the essence of the methodology. An extensive validation effort is described in Validation of the Satellite-Retrieved CCN(S), and its results are given in Results, along with error calculations. The possibilities that open up with the emerging capabilities for coincident satellite retrieval of convective cloud base updrafts and CCN(S) are discussed in Applications of Satellite-Retrieved Updrafts. Finally, the conclusions are given in Conclusions.

Methodology

Using Clouds as CCN Chambers.

The commonly used CCNCs measure the number concentration of aerosol particles in a sample air stream (N_a), which at a given S can be activated into the same number of cloud droplets at its base (N_db) (27). Alternatively, retrieving N_db and S in clouds can provide CCN(S). The peak vapor supersaturation at an adiabatic cloud base, S, is determined by CCN(S) and W_b. Therefore, a good approximation of S can be calculated from the retrieved N_db and W_b according to

$$S=C\left(T_b,P_b\right)W_b^{3/4}{N}_{db}^{-1/2},$$ [1]

where C is a coefficient that depends weakly on cloud base temperature (T_b) and pressure (P_b) (28). This is an analytical expression that was derived based on theoretical considerations. Recently, it has become possible to estimate N_db and W_b from satellite measurements, thus calculating also S. This constitutes the ability to calculate CCN(S) from satellite measurements only. The following subsections describe the methodology of satellite estimation of N_db and W_b.

Estimation of Cloud Base Drop Concentrations.

Retrieving T_b, P_b, W_b, and N_db became possible with the advent of the Suomi NPP satellite, which was launched in October 2011. The VIIRS onboard this satellite has a moderate spatial resolution of 750 m. The VIIRS has an Imager with a subset of five channels with double resolution of 375 m at 0.64 μm, 0.865 μm, 1.61 μm, 3.74 μm, and 11.45 μm. Although VIIRS Imager 375-m data were not designed for retrieving cloud properties, a methodology was developed for using it to retrieve cloud drop effective radius (r_e) and cloud-top temperatures (T). The retrieval of r_e was based on the methodology developed by Rosenfeld and Lensky (29) for the Advanced Very High Resolution Radiometer. It has been applied to VIIRS by Rosenfeld et al. (30). The ability to retrieve cloud properties at a resolution of 375 m is a breakthrough compared with the previous best available resolution of 1 km. This allows microphysical monitoring of cloud properties with unprecedented accuracy and makes it possible to obtain the microstructure of small clouds at the top of the boundary layer (30).

A VIIRS-retrieved T−r_e relationship, which is obtained from a convective cloud ensemble within an area of ∼30 × 30 km (28), serves as the basis for retrieving T_b, P_b, and N_db. This satellite method is based on extensive aircraft measurements of T−r_e relationships. It was demonstrated that r_e varies with altitude nearly as in an adiabatic cloud, and therefore adiabatic cloud drop number concentrations (N_da) can be calculated at different altitudes in the cloud using the calculated adiabatic water content LWC_a and r_e, which is assumed to vary adiabatically with altitude, thus marked as r_ea (31). Then, N_da approximates N_db, because the cloud can be assumed to be adiabatic at its base. The retrieved r_e is assumed to be r_ea based on the assumption that the measured r_e is adiabatic, which is the case for clouds with extreme inhomogeneous mixing and with all cloud drops nucleated at their base. Deviations from the extreme inhomogeneous assumption lead to a reduction of the aircraft-based calculation of N_da by an average factor of 1.3 with respect to the value calculated under this assumption (31). The cloud base drop concentration is approximated by the adiabatic cloud drop concentration as calculated by Eq. 2 (32),

$$N_{da}={\mathrm{\alpha }}^{3}LW{C}_a/r_{ea}^3,$$ [2]

$$\mathrm{\alpha }=62.03r_e/r_v,$$ [3]

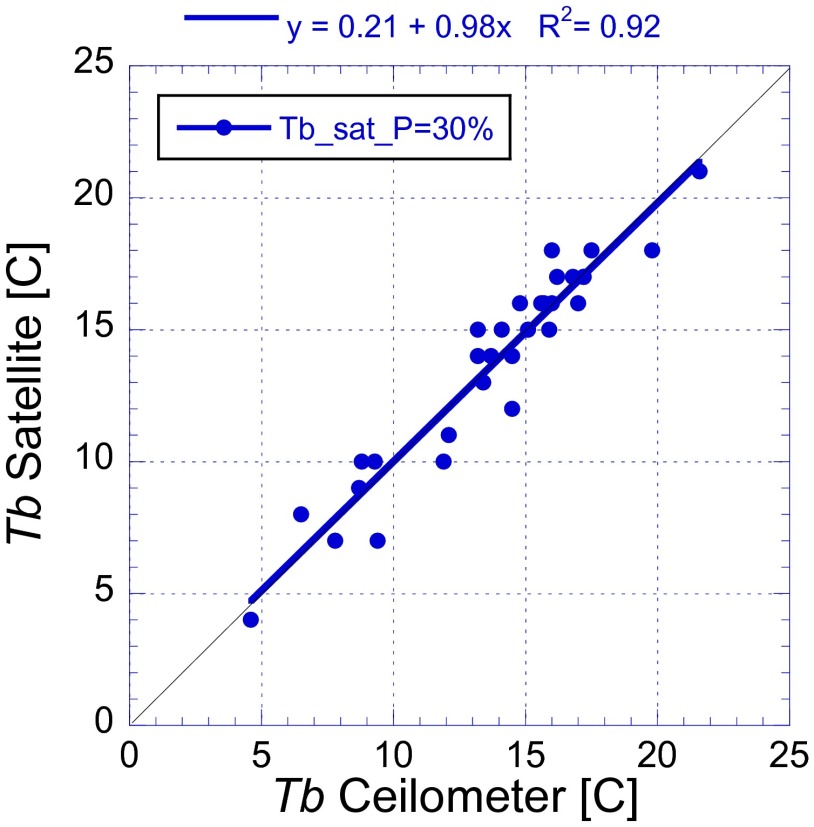
where r_v is the cloud drop mean volume radius, as calculated by equally distributing cloud water content between the cloud droplets. We used the value of r_e = 1.08 r_v (31). The adiabatic water is obtained from the VIIRS-measured T_b, which is simply the warmest cloudy pixel, based on a specially developed cloud mask (33). The LWC_a is calculated based on an adiabatic parcel that rises from cloud base at T_b and P_b to the isotherm T, where multiple pairs of T and r_ea are retrieved for different cloudy pixels of the same cloud cluster at different heights above cloud base. Here, P_b is obtained from the pressure at the isotherm of satellite-retrieved cloud base height (H_b), which was computed from the European Center for Medium-range Weather Forecasting reanalysis data. H_b was calculated as the difference between reanalysis surface air temperature and T_b divided by the dry adiabatic lapse rate. T_b was validated at a root-mean-square (RMS) error of 1.1 K, as shown in Fig. 1 (33). H_b and T_b were calculated for conditions of convective clouds that developed from well-mixed boundary layer at the early afternoon satellite overpass time (33), before the peak of the convective rain and the resultant cooling and moistening of the boundary layer by evaporating precipitation.

Fig. 1.

The relationship between satellite-measured cloud base temperature and validation measurements by a combination of a ceilometer and soundings at the Department of Energy (DOE)/Atmospheric System Research (ASR) sites on the SGP in Oklahoma. Reproduced from ref. 33.

Estimation of Cloud Base Updrafts.

Until now, only lidar and radar measurements of W_b were used. This is expanded here to satellite-retrieved W_b. According to Eq. 1, knowing W_b and N_db at cloud base yields S. Then, N_db is numerically identical to CCN(S). Rosenfeld et al. (32) used this method to retrieve CCN(S) over the Atmospheric Radiation Measurement (ARM) site of the Southern Great Plains (SGP), using N_db retrieved from a satellite and W_b measured by ARM’s vertically pointing K_a-band radar. The W_b was calculated from all full Doppler statistics during a 2-h window centered at the satellite overpass time, where the W_b of each point in time was weighted by W_b itself, thus representing its relative contribution to building the cloud volume. More specifically, equation 5 in Rosenfeld et al. (32) (replicated as Eq. 4 here) shows that the radar or lidar updraft W was constructed from all of the N realizations W_i of single data points within the time window as follows:

$$W={\frac{{\displaystyle \sum N_i{W}_i^2}}{{\displaystyle \sum N_i{W}_i}}|}_{W_i\mathrm{>}0}.$$ [4]

According to Eq. 4, W is the cloud volume-weighted updraft. Good agreement was achieved by Rosenfeld et al. (32) between CCN(S) as constructed by satellite-retrieved N_a and radar-retrieved W_b with the SGP ground base-measured CCN(S), but the number of cases with useful clouds and data were rather small and served mainly to verify the methodology. The need for ground-based measurements of W_b limited severely the occasions where CCN could be retrieved to sites where cloud Doppler lidars or radars measurements are available. The present study is the first one, to our knowledge, to retrieve CCN(S) from satellite estimates of both N_db and W_b, thus becoming potentially very widely applicable, despite some limitations in the retrievals of N_db and W_b.

Retrieval of CCN solely from satellite data requires W_b to be retrieved from satellite. This was done by using satellite-retrieved components of the energy that propels the convection (3). Subsequently, Zheng and Rosenfeld (4) showed that W_b can be simply calculated by

$$W_b=A{H}_b,$$ [5]

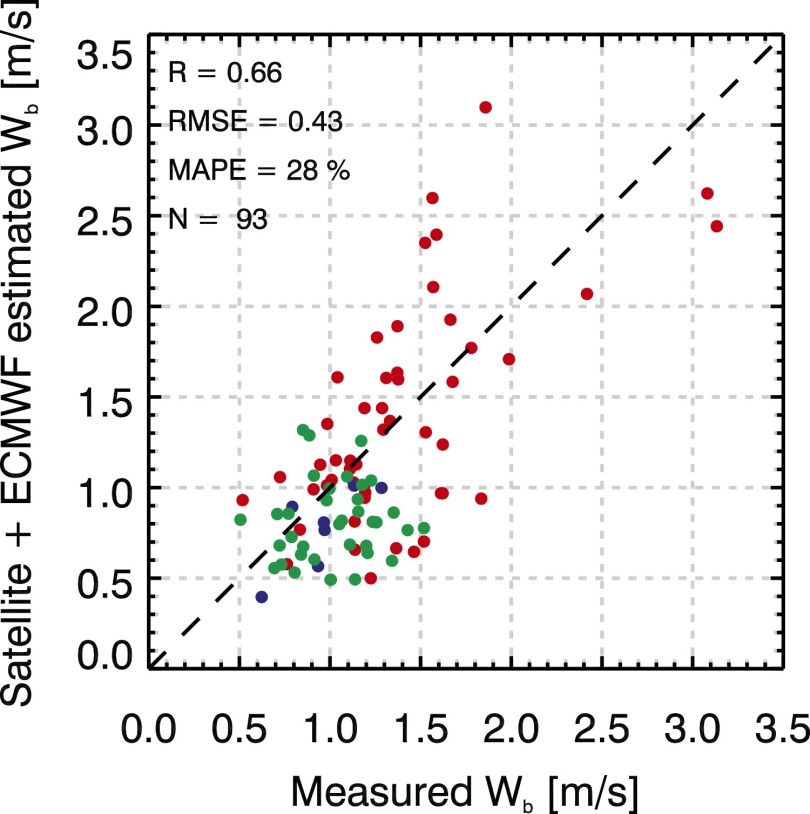
where W_b is cloud base updraft in meters per second, A is a coefficient (0.0009 s⁻¹) obtained in a previous study (4), and H_b is the cloud base height above the ground in meters, which is determined by the difference between the surface air and cloud base temperatures, as explained at the end of Estimation of Cloud Base Drop Concentrations. This relationship was developed based on synchronous satellite and lidar measurements from the ARM SGP site and at the ARM Mobile Facility onboard a ship on a line between Los Angeles and Honolulu [Marine ARM GPCI Investigations of Clouds (MAGIC)]. The satellite-retrieved W_b was validated against the Doppler measurements, resulting in an RMS error of 0.41 m⋅s⁻¹ and a mean absolute percentage error (MAPE) of 24% and 21% by Zheng et al. (3) and Zheng and Rosenfeld (4), respectively. When forcing the relationships through zero (Eq. 5 and Fig. 2), the error becomes 27%. These results are consistent with the physical considerations of Williams and Stanfill (10). This means that the methodology is very likely to be universally applicable to boundary layer convective clouds.

Fig. 2.

Relationship between satellite-estimated W_b =0.0009H_b and directly measured W_b by Doppler lidars at the SGP (red dots), Green Ocean Amazon (GOAmazon) (green), and MAGIC (blue). After Zheng and Rosenfeld (4). The satellite-retrieved T_b was converted to height using the European Centre for Medium-Range Weather Forecasts reanalysis data. RMSE is the estimation root mean square error.

Table 1 summarizes the methodology. It shows the satellite measurements, their combination with reanalysis data, and their propagation into the eventual W_b and CCN(S), and the associated errors.

Table 1.

Propagation of the calculations from the satellite retrievals to the resultant CCN(S)

Symbol	Parameter and unit	Source of calculation	Error
re	cloud drop effective radius, μm	satellite retrieval	8%
T	cloud surface temperature, °C	satellite retrieval	0.2 °C
Tb	cloud base temperature, °C	satellite retrieval	1.1 °C
Pb	cloud base pressure, hPa	Tb + reanalysis	15 hPa
rv	drop mean volume radius, μm	re (Eq. 3)	8%
LWCa	cloud adiabatic water, g⋅kg−1	T + Tb + Pb (parcel)	15%
Nd	cloud base drop concentrations, cm−3	rv(T) + LWCa(T) (Eq. 2)	30%
Hb	cloud base height above surface, m	Tb + reanalysis	150 m
Wb	cloud base updraft, m⋅s−1	Hb (Eq. 5)	27%
S	cloud base max supersaturation, %	Tb, Pb, Wb, Nd (Eq. 1)	25% of S in percent
NCCN(S)	CCN at cloud base, cm−3	Nd, S by definition	30%

Validation of the Satellite-Retrieved CCN(S)

Cloud base S was obtained from Eq. 1, with N_db calculated by Eq. 2 and W_b calculated using Eq. 5. The calculated N_db is by definition equal to CCN(S) at cloud base. To compare with surface-based measurements, the concentration is corrected for the difference between air density at cloud base and at the ground, and then validated against the CCN(S) as measured by the ground-based instrument. This assumes that the thermals bring the surface air to cloud base without much change in the mixing ratio and properties of aerosol particles. This is a widely accepted assumption for vapor mixing ratio at thermally driven cloud bases in a well-mixed boundary layer, where the lifting condensation level is usually very similar to the actual cloud base height.

An initial comparison of the satellite-retrieved CCN to the SGP instrumental validation data (assuming no error in the instrument measured CCN) showed a slope of 0.74 for the regression line. A retrieval bias could be caused by a large number of factors, which are quantified in Error Analysis, but the largest potential source of error is inaccuracy in r_e. The observed 26% underestimate in CCN could have been caused by a 10% systematic overestimate in the retrieved r_e. This is quite probable, because MODIS-retrieved r_e was found to be larger by 10–15% than aircraft in situ measurements (34–36). An underestimate of satellite- versus surface-measured CCN can be also caused by a systematic decrease of CCN number concentration (N_CCN) between the surface and cloud base heights. This bias has to be corrected before calculating S by Eq. 1, because, otherwise, S would be overestimated. To stay on the conservative side, we applied only half of the bias correction and used here a reduction factor of 1.15 instead of 1.3, as proposed by Freud et al. (31), and applied it to all of the validation sites.

Validation cases were selected over the sites of the ARM sites of the SGP in Oklahoma, at Manacapuru near Manaus in the Amazon, and over the northeastern Pacific onboard the MAGIC ship. In addition, CCN measurements were obtained from the Amazon Tall Tower Observatory (ATTO) site 150 km to the northeast of Manaus (37). Data were obtained from the start of availability of VIIRS data in 2012 until early 2015. The case selection criteria were as follows: (i) Satellite overpass has to occur at a zenith angle between 0° and 45° to the east of the ground track, which is the sunny side of the clouds. For a specific location, these satellite views occur once or twice every 6 d. (ii) Convective clouds must occur and possess a vertical development that spans at least 6 K of cloud temperature from base to top, limiting to clouds with thickness >1 km. (iii) The clouds must not precipitate significantly (i.e., without a radar or lidar detectable rain shaft that reaches the ground). The precipitation causes cold pools that disconnect the continuity of the air between the surface and the cloud base. (iv) Cloud elements with indicated r_e > 18 μm are rejected automatically from the analysis that is likely to rain/drizzle heavily. (v) No obscuration from high clouds is allowed. An automatic detection of semitransparent clouds screens them from the selected area for analysis. (vi) Ground-based CCN data must be available.

The availability of CCN data from the ARM program at all of its three sites was severely limited due to data quality issues. Insufficient available time for stabilization of temperatures at low S caused the CCN readings at S ≤ 0.25% to be grossly underestimated or zero, and therefore they could not be used. The points with S > 0.25% were fit with a second-order polynomial that was forced through the origin, because CCN must be zero for S = 0. By extrapolation with this polynomial, we could extend the use of the data down to S = 0.2%. Cases with cloud base S < 0.2% were rejected. The operation of the ARM CCNCs was changed after August 2014 to allow sufficient time for stabilization at low S. This correction was applied to Manacapuru only by April 2015, however. These limitations did not apply to ATTO, and valid data from this site were available from May 2014 until January 2015.

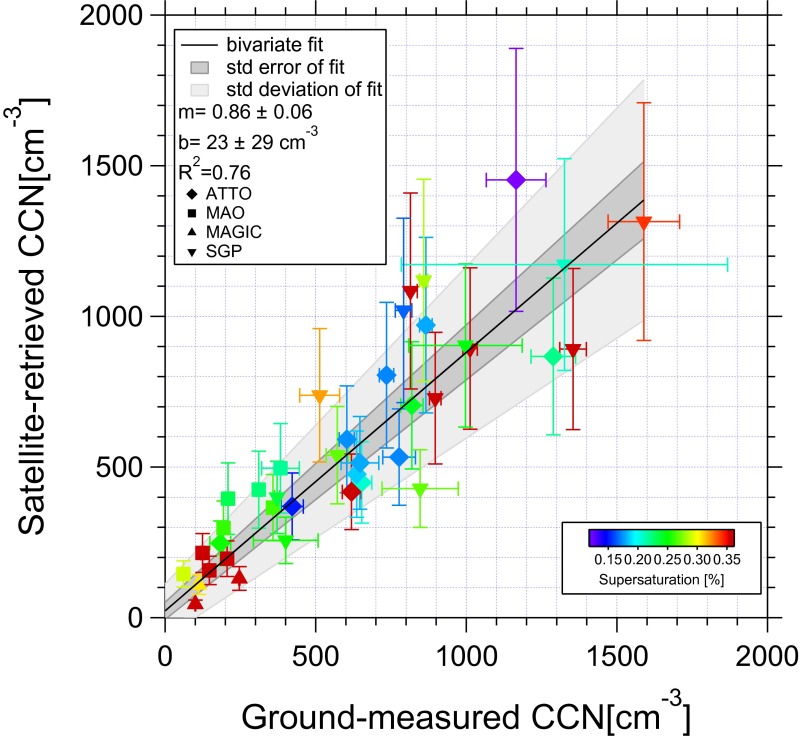
The results are shown in Fig. 3. Each point in the figure represents one satellite overpass over one ground-based CCNC. The CCN data from a time window of ±1 h around the overpass are taken to include several CCN(S) spectra at all measured supersaturations. Because of the much slower scanning rate of S at ATTO, a larger time window of ±1.5 h was taken there to include at least one full spectrum of CCN(S). The satellite analyzes clouds over an area of about 30 × 30 km around the ground measurement site, with some adjustments to incorporate the convective clouds in the vicinity. The satellite-retrieved CCN and S are compared with the instrument measurements as follows: (i) A scatter plot of the individual ground-based measurements of CCN concentrations (N_CCN) is plotted as a function of S. (ii) A second-order polynomial curve is fit to the points. The function is forced through the origin, because zero S must correspond to zero N_CCN. (iii) The N_CCN is taken from the polynomial fit at the same S that is retrieved from satellite at cloud base. The ±95% confidence interval of N_CCN at the value of satellite-retrieved S is calculated. (iv) The satellite-retrieved N_CCN is the satellite-retrieved N_db, corrected for the air density difference between cloud base and the surface.

Fig. 3.

The relationship between satellite-retrieved N_CCN and S at cloud base, and the ground-based instrument measurements of N_CCN at the same S. The slope and intercept of the best fit line are given in the key by m and b, respectively. The validation data are collected from the DOE/ASR sites on the SGP in Oklahoma and GOAmazon near Manaus, and over the northeast Pacific (MAGIC). In addition, data are obtained from the ATTO. The location is denoted by the marker shape, and S is shown by the color.

Results

Fig. 3 shows the relationships between the satellite retrievals of N_CCN and S at cloud base, and the ground-based measurements of N_CCN at the same S. There are several points worth noting. (i) The figure covers a large dynamic range of S for both low and high values N_CCN. (ii) The value of R² = 0.76 shows that the fit explains more than 3/4 of the variability between the satellite and ground-based measurements of CCN(S). (iii) There is a systematic underestimate bias of 14% in the satellite-retrieved CCN. It follows that the estimation errors decrease almost linearly with smaller N_CCN. (iv) The variation of the satellite with respect to the ground-based measurements is within 20–25% of the ground-based measurements. This includes the 14% bias error. (v) The SD of the fit is similar to the expected magnitude from the error sources of the satellite uncertainties in W_b, T_b, and r_e.

The methodology was converted into a procedure that can be applied to any specified rectangle in the VIIRS imagery, which contains surface thermally driven convective clouds, and provides as output the following parameters: T_b, P_b, H_b, W_b, N_db, and S. The value of N_db is equal to the CCN concentrations at the retrieved S at cloud base, and this value of CCN(S) is also an output parameter. As an illustrative example, this procedure was applied to a regular grid of 75 × 75 VIIRS Imager pixels (28 × 28 km at nadir) over the region of Houston during conditions of onshore flow of a tropical marine air mass. The results are shown in Fig. 4. The salient features are as follows: (i) There are very low CCN concentrations over the ocean. (ii) There is only a modest increase in CCN over the rural areas inland. (iii) The CCN concentrations more than triple over and downwind of the urban area compared with the cross-wind areas. (iv) S decreases over the urban area to less than half of the values over the rural areas. Therefore, CCN for the same S is enhanced by a factor much larger than 3. (v) The indicated CCN concentrations are similar in adjacent areas with similar conditions, indicating the robustness of the methodology.

Fig. 4.

Application of the methodology to the Houston area. The retrieval is done for a regular grid of 75 × 75 375-m VIIRS/Imager pixels (∼28 × 28 km at nadir). The numbers in each area are: top, CCN (per cubic centimeter); middle, S (percent); and bottom, cloud base temperature (degrees Celsius). Unstable clean tropical air mass flows northward (upward in the image) from the Gulf of Mexico. The Houston urban effect is clearly visible by more than tripled CCN concentrations over Houston and the reduction of S to less than half. This represents an even larger factor in enhancing CCN for the same S. A smaller effect is seen over the urban and industrial areas to the east of Houston. The color composite is red, green, and blue for the visible reflectance, 3.7-μm solar reflectance, and thermal temperature, respectively, as in Rosenfeld et al. (30). The Houston bay and beltways are marked by white lines.

Applications of Satellite-Retrieved Updrafts and CCN(S) to Reduced Climate Uncertainties

Here we showed the feasibility to retrieve CCN(S) from a single satellite passive sensor using clouds as CCN chambers, under certain conditions. There are still many challenges to overcome before it will be possible to do so for most cloud types. This requires the development of new satellite capabilities that will be able to provide more direct measurements of updraft speeds, such as measuring vertical motions of cloud elements by tracking their evolution with time. Here we attempt to open a window to the potential applications of such capability, with a few examples.

The sensitivity of cloud properties to N_CCN is logarithmic (38). This means that a small absolute change in N_CCN has a much larger impact during pristine than polluted conditions. Carslaw et al. (25) argued that the main sensitivity to anthropogenic aerosols occurs in areas that had N_CCN of 35–65 cm⁻³ during the preindustrial era. Satellite measurements show that an increase of more than 100 W⋅m⁻² in cloud radiative effect (CRE) can occur when N_d of marine shallow boundary layer clouds increases from 35 cm⁻³ to 65 cm⁻³, mainly due to increased cloud cover and cloud liquid water path. This is manifested as closing areas of open cellular convection (39). However, the satellite observed N_d is related to both W_b and CCN(S), as shown by Eq. 1. Therefore, there is a possibility that measurements of the large enhancement of CRE that were associated with increased N_d could also result from changes in W_b, which could be caused by changes of meteorology (40). For separating the roles of W_b and N_CCN in the determination of N_db, both W_b and N_CCN should be measured. As already discussed in Need for Global Measurements, using AOD as a proxy for N_CCN in the marine boundary layer clouds has several shortcomings. Because, among other problems, the correlation between AOD and N_CCN is not very close and because a column property like AOD is not necessarily representative of the CCN concentrations that affect growing clouds, the AOD approach allows only an order-of-magnitude estimate of N_CCN. On the other hand, combining W_b with N_db can provide CCN(S) with an uncertainty that can be quantified and is far better than the AOD approach. Having both W_b and CCN(S) will allow disentangling of the roles of these two factors in determining N_d and in the attribution of the related changes in CRE to aerosols.

Having satellite retrievals of both W_b and N_CCN will allow disentangling of their respective roles on determining N_d and the related precipitation-forming processes, rainfall amounts, and distribution of vertical latent heating. CCN(S) ingested by deep convective clouds can be estimated by using adjacent shallower nonprecipitating convective clouds in their upwind side. Adding CCN to deep convective clouds can invigorate them and incur more extensive anvils and respective positive radiative forcing (41–43). This can be quantified observationally using long-term surface aerosol, cloud, and meteorological measurements made at a single location in the SGP (41, 42), and also using global A-Train satellite products (44). These estimates of CRF (the change in CRE due to anthropogenic causes) are associated with aerosol-induced changes in cloud properties that do not differentiate the respective roles of aerosol and dynamics or meteorology but their joint effects.

Having global coverage of CCN(S) where we need them most—in conjunction with the clouds that ingest them—will provide input for regional and global simulations. The coincident retrieved cloud properties will constrain these models and provide us with realistic assessments of the CRE. The retrieved CCN(S) can be used for constraining aerosol production and transport models. This will allow separating the aerosols into natural and anthropogenic components more accurately. The application of such classified CCN(S) will facilitate calculating the anthropogenic aerosol-induced CRF, which will constitute a major reduction of the uncertainty in anthropogenic climate forcing. Developing methodologies for retrieving updrafts at clouds with elevated bases will further enhance these possibilities.

Conclusions

The feasibility of estimating CCN(S) and W_b of boundary layer clouds from the Suomi NPP polar-orbiting operational weather satellite was demonstrated with an accuracy of ±25% to ±30%, which is limited mostly by the accuracy in the retrieval of r_e. The validation was done in Oklahoma, the Amazon Basin, and the northeast Pacific Ocean. Our methodology is presently limited to boundary layer convective clouds of at least 1 km depth, which are not obscured by upper layer clouds, including semitransparent cirrus. This might limit its application in some regions of the world. Moreover, the limitation for small solar backscattering angles of <25° restricts the satellite coverage to 1/4 of the satellite swath width, or a view once every 4 d, on average. On the other hand, even for a regional coverage, it would be much more valuable to study the process of aerosol−cloud interactions rather than using single-point data as provided by ground-based observations.

A major advantage of using clouds as analog for CCN chambers relative to relying on the optical signal of the aerosols themselves is the fact that the optical signals (e.g., AOD and Ångstrom coefficient) vanish at very small aerosol concentrations, which is exactly where the relative changes in CCN concentrations matter most, or, in other words, where very small absolute changes in concentrations have very large impacts on clouds (16, 25). This is where the traditional remote sensing methods of aerosols break down, whereas the applicability of using clouds as CCN chambers remains intact, as evident by the lower left corner of Fig. 3. This has particular importance in the context of the quest for the significance of changes from the preindustrial era to the present background aerosols (25).

The retrieval of both CCN(S) and W_b allows, for the first time to our knowledge, disentangling of the roles of updrafts and CCN on cloud microphysical, precipitation, and radiative properties over climatically meaningful areas. Previously, the inability to separate these factors has been a major impediment to our ability to quantify the aerosol/cloud-mediated effects on Earth's energy budget, thus keeping high the uncertainty of this effect (1). Application of the new capabilities offered by our methodology is expected to allow a breakthrough in quantifying these effects and to substantially reduce the uncertainty in anthropogenic aerosol climate forcing, at least for boundary layer convective clouds.

Error Analysis

A direct comparison of the satellite- to ground-based CCN, assuming no errors in the CCNC measurements, shows a correlation coefficient of 0.88 and a slope of 0.9 (i.e., underestimate of 10%). The MAPE is ±30%. However, both satellite retrievals and CCNC measurements are subject to errors. Therefore, a bivariate regression has to be used for fitting two parameters with associated errors for both (45). The associated error for the satellite-retrieved CCN for a given S was taken as ±30%. The CCN instrument errors were taken as the ±95% confidence interval (i.e., ±2 SDs) of N_CCN for the individual cases, as described at the end of Estimation of Cloud Base Drop Concentrations. Both sets of errors are shown as error bars in Fig. 3.

The largest sensitivity is to errors in r_e, because, according to Eq. 2, the error in N_a is the cube of the error in r_e. The accuracy of MODIS-retrieved r_e is best when the 3.7-μm waveband is used (MODIS r_e is also available for 2.1-μm and 1.6-μm wavebands) in nondrizzling clouds; under these conditions, it showed the best agreement with aircraft measurements, with an uncertainty of 1 μm (46). The 3.7-μm-based r_e is also minimally affected by cloud inhomogeneities (47) because this band absorbs solar radiation much more strongly (48, 49). The VIIRS footprint area, which is sevenfold smaller than that of MODIS, further reduces the possibility of errors caused by cloud inhomogeneities. Our implementation to VIIRS is even more accurate than MODIS in the best of circumstances, because we use only pixels with visible reflectance >0.4 at backscattering angles (satellite zenith angle of 0–50 degrees). To avoid significant distortion of r_e by coalescence, we avoided heavily precipitating clouds at their tops (r_e 0> 18 μm). MODIS r_e is larger than aircraft in situ measurements by 10–15% (34–36). This is probably not a problem for retrieved r_e based on the VIIRS Imager (30), because it is lower by a similar amount with respect to MODIS r_e. The retrieval uncertainty of r_e itself is roughly ±10% (36). This translates to uncertainty of a factor of ±33% in N_a. This error alone is larger than the measured validation error of ±30% when assuming no errors in the ground-measured CCN, which includes many other error sources, as described next. This might serve as an indication that the error in the retrieved r_e from VIIRS is smaller than for MODIS, probably due to the much finer resolution.

The MAPE in cloud base temperature of ±1.1 °C propagates to a 5% error in N_a due to changing C(T_b,P_b) in Eq. 1. The error in W_b (Fig. 2) can be propagated to an error in N_a according to Twomey's approximation of

$$N_a=CCN{\left(S=1\mathrm{\%}\right)}^{2/\left(k+2\right)}{W}_b^{3k/\left(2k+4\right)},$$ [6]

where k is the slope of the CCN(S) spectrum on a log−log scale (50). Accordingly, a W_b MAPE of ±27% propagates to an error in N_a of only 7–13% for k = 0.5 and 1, respectively. The overall combined error is ±36%, as obtained by the calculation (0.33² + 0.05² + 0.13²)^0.5 = 0.36. This overall calculated error of ±35%, even before adding the CCN instrument uncertainty, is larger than the measured validation error of ±30% when assuming no errors in the ground-measured CCN. This discrepancy could be explained, for example, by reducing the r_e error from 10% to 8%.