F₁-ATPase conformational cycle from simultaneous single-molecule FRET and rotation measurements

Significance

The major source of ATP in life is ATP synthase, and its catalytic part is known to be the F₁ rotary motor. F₁’s structure and function have been characterized in spectacular detail by crystallography and single-molecule techniques, respectively. However, despite more than two decades of intense research, the correspondence of the observed functional states and crystal structures is uncertain. To match structures and states, we perform single-molecule fluorescence-based distance measurements and simultaneous rotary angle measurements on F₁-ATPase, and then exploit the wealth of structural data in their analysis. The resulting comprehensive view of the F₁’s ATPase cycle reveals the functional principles in the coupling of chemical reactions, stator conformations, and rotary angles for efficient ATP synthesis.

Abstract

Despite extensive studies, the structural basis for the mechanochemical coupling in the rotary molecular motor F₁-ATPase (F₁) is still incomplete. We performed single-molecule FRET measurements to monitor conformational changes in the stator ring-α₃β₃, while simultaneously monitoring rotations of the central shaft-γ. In the ATP waiting dwell, two of three β-subunits simultaneously adopt low FRET nonclosed forms. By contrast, in the catalytic intermediate dwell, two β-subunits are simultaneously in a high FRET closed form. These differences allow us to assign crystal structures directly to both major dwell states, thus resolving a long-standing issue and establishing a firm connection between F₁ structure and the rotation angle of the motor. Remarkably, a structure of F₁ in an ε-inhibited state is consistent with the unique FRET signature of the ATP waiting dwell, while most crystal structures capture the structure in the catalytic dwell. Principal component analysis of the available crystal structures further clarifies the five-step conformational transitions of the αβ-dimer in the ATPase cycle, highlighting the two dominant modes: the opening/closing motions of β and the loosening/tightening motions at the αβ-interface. These results provide a new view of tripartite coupling among chemical reactions, stator conformations, and rotary angles in F₁-ATPase.

ATP synthase (F₁F_o-ATPase) catalyzes ATP synthesis from ADP and P_i in cells. The isolated F₁ portion is called F₁-ATPase, because it also catalyzes the reverse reaction, ATP hydrolysis (1–3). The α₃β₃γ-catalytic core complex of F₁-ATPase (denoted F₁) is a rotary molecular motor in which three αβ-dimers are arranged around the central γ-shaft (4). Unidirectional rotation of γ is driven by the free energy derived from sequential ATP hydrolysis at catalytic sites in the three αβ-dimers (5–7). Under an external torque, F₁ synthesizes ATP coupled to the rotation of γ in the opposite direction (8). This reversible operation of F₁ is achieved by the tripartite mechanochemical coupling between chemical reactions at the catalytic sites of αβ, conformational changes in the stator ring-α₃β₃, and orientation of γ.

A combination of the rotation assay (5, 6) and single-molecule fluorescence imaging techniques (9) has led to a detailed picture of the coupling between chemical reactions in α₃β₃ and the rotary angles (10, 11). One ATP hydrolysis reaction in α₃β₃ drives discrete 80° + 40° substeps of γ in bacterial F₁ (7). The 80° substep is mainly driven by the binding energy of ATP (7, 9). The dwell before the 80° substep is, therefore, named the ATP waiting dwell. Release of the product, ADP, occurs before completion of the 80° substep (9, 10). The angle-dependent affinity of ADP suggests that the ADP release event also contributes part of the energy for the 80° substep (10). The dwell before the 40° substep is called the catalytic dwell; it consists of two rate-limiting events: ATP cleavage and release of the product, P_i (10, 12). The 40° substep is accompanied by a decrease of P_i affinity, with release that, in turn, generates torque (10). The coupling scheme between chemical reactions in α₃β₃ and the rotary angles has, therefore, been almost completely established (10).

In the coupling of chemical reactions and α₃β₃-conformations, the key concept is thought to be the binding change mechanism, in which three catalytic sites in F₁ undergo sequential transitions between conformational states with different affinities for nucleotides corresponding to different rotary angles (1). The binding change mechanism is supported by the first crystal structure of F₁, in which two βs adopt the closed form with nucleotides and the other β adopts the open form without a nucleotide (4). The 120° step of γ observed in the rotation assay further supports this mechanism (6).

However, we still face significant gaps in the structural ATPase cycle. Previous studies have suggested that F₁ should adopt at least two distinct conformational states for the ATP waiting dwell (ATP waiting form) and the catalytic dwell (catalytic form) based on rotation and tilting angles of γ (13). Furthermore, based on indirect evidence, it has been pointed out that the first crystal structure should represent the catalytic form or forms similar to the catalytic intermediate states (14–18). Although the crystal structures of the α₃β₃γ-complex differ from each other in terms of their nucleotide binding states and detailed configurations of the residues, their global structures are similar to the first crystal structure (19), which leaves the structure of the ATP waiting form unresolved. Closing this gap in the conformational cycle will deepen our understanding of the coupling between chemical reactions, α₃β₃-conformations, conformations, and rotary angles, not least by providing critical input into the theoretical modeling of F₁ (20–26).

Here, we use the FRET technique to elucidate the conformational transitions of α₃β₃-conformations in F₁. FRET involves excited-state energy transfer from one fluorescent dye (donor) to another (acceptor) through dipole–dipole interactions (27). Single-pair FRET measurements combined with single-molecule techniques have been used to investigate the dynamics of intramolecular conformational changes or intermolecular interactions at the single-molecule level (28–34), including for F_oF₁-ATP synthase (35–37). We perform single-molecule FRET measurement to monitor distance changes between two fluorescently labeled βs and simultaneously monitor the rotational steps of γ. The FRET data allow us to distinguish the ATP waiting form from the catalytic form and thus, relate these dwelling states to the respective crystal structures. A systematic comparison of the crystal structures reveals the structural basis of the ATPase cycle. This study provides a structural basis for tripartite coupling among chemical reactions, conformations in the stator, and rotary angles in bacterial F₁.

Results

Preparation of Fluorescently Labeled F₁ for Single-Pair FRET.

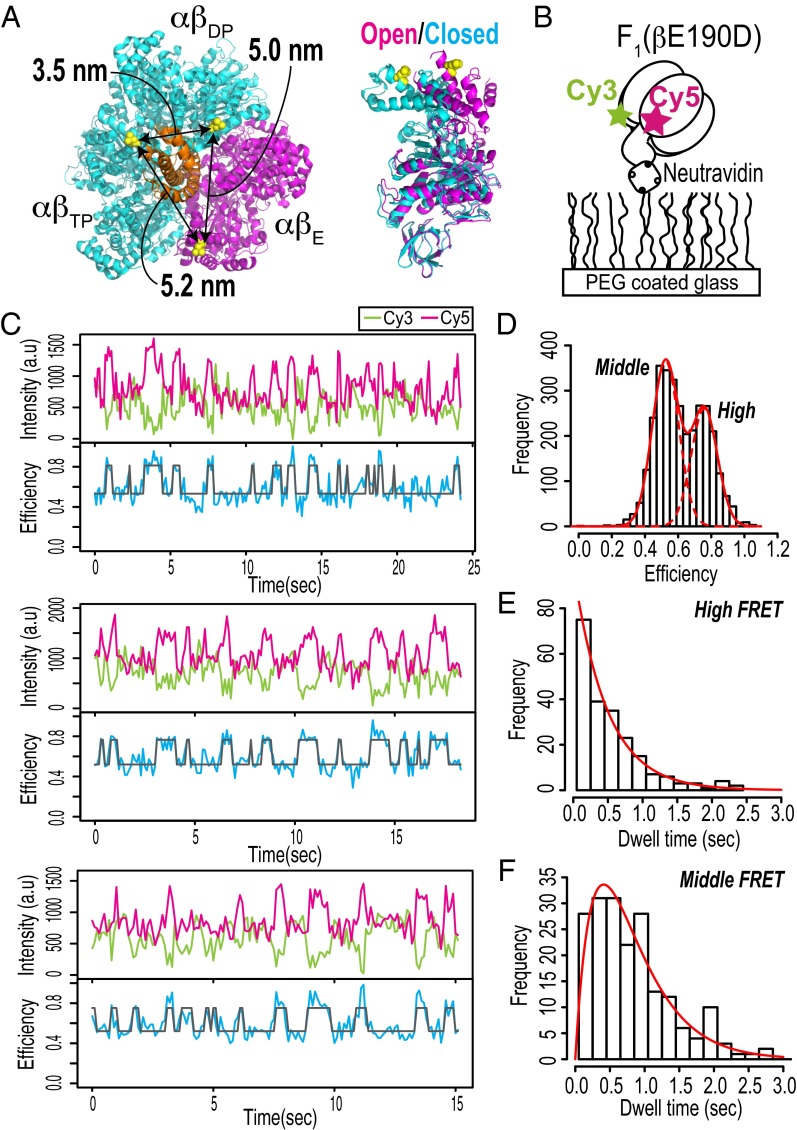
For single-pair FRET, we prepared F₁ from thermophilic Bacillus PS3 (TF₁) with βs specifically labeled with a single pair of Cy3 and Cy5. For specific labeling of TF₁ with thiol-reactive dyes, we constructed a cysteine mutant of β. We selected the cysteine mutation site in TF₁ based on the crystal structures of bovine F₁ (MF₁), which is known to be the first crystal structure (4) [referred to as the 1BMF structure based on Protein Data Bank (PDB) ID code 1BMF], and the ground-state structure (38) (referred to as the 2JDI structure based on PDB ID code 2JDI). βL402 in MF₁ follows a well-conserved amino-acid sequence DELSEED motif (residue number: 394–400) which has a contact with γ. The distances between the three Cβs of βL402 in the 2JDI structure are 3.5, 5.2, and 5.0 nm (Fig. 1A, Left). The βs in the 2JDI structure adopt two distinct conformations, namely the open form and the closed form (Fig. 1A, Right). Note that the subscripts to αβ and β correspond to the nomenclature for the first crystal structure (4). β_E is in the open form, whereas β_DP and β_TP are in the closed form. The 3.5-nm configuration is derived from the set of two closed forms, and the 5.2- and 5.0-nm configurations are derived from the set of open and closed forms. These β-configurations in the crystal structure were expected to produce sufficiently large changes in the distances between the two residues to be detectable by FRET. Note that not only the labeling sites of the protein but also, the sizes and orientations of the dyes determine the resulting interdye distances; therefore, the distances mentioned above do not necessarily represent the interdye distances. Taken together, βL398 in TF₁, which is equivalent to βL402 in MF₁, was selected as the cysteine mutation site. In addition, we constructed AviTag-F₁, in which AviTag, a biotinylation sequence, was inserted into the protrusion domain of γ and used to attach the probe bead to γ for monitoring the rotary angles (Materials and Methods). Finally, we obtained an F₁ molecule containing the cysteine mutants of βs and biotinylated-γ [AviTag-F₁(βL398C)].

Fig. 1.

Single-molecule FRET measurements of F₁. (A) Cysteine mutation sites for specific fluorescent labeling. The molecular structure is derived from bovine F₁ [PDB ID code 2JDI (38)]. βL402s in the 2JDI structure, which correspond to βL398s in thermophilic F₁, are shown as yellow spheres. (Right) The αβ-colors represent two distinct β-conformations: closed forms of β_DP and β_TP are shown in cyan, and an open form is shown in magenta; the γ-subunit is shown in orange. The distances between three Cβs of βL402 are indicated. (B) Schematic diagram of single-molecule FRET measurement. (C) Typical time trajectories of fluorescence intensities of Cy3 (donor; green) and Cy5 (acceptor; magenta) and FRET efficiency (blue). A two-state HMM fit to the FRET efficiency trace is shown in gray. The experiments were performed at 100 μM ATP. The recording rate was 10 frames per second. (D) Histogram of FRET efficiencies obtained from time series data (total of 19 molecules). The solid and dotted red lines represent a two-Gaussian fit (means of 0.52 and 0.76; variances of 0.0064 and 0.0064, respectively). (E and F) Histograms of dwell times in high and middle FRET states obtained from two-state HMM fits. The solid red lines in E and F are fits of (E) a single exponential for the high FRET state and (F) the convolution of two exponentials with same rate constant for the middle FRET state. The rate constants of the fits are 2.1 s⁻¹ for the high FRET state and 2.4 s⁻¹ for the middle FRET state.

Single-Molecule FRET Measurements of F₁ in Catalytic Dwells.

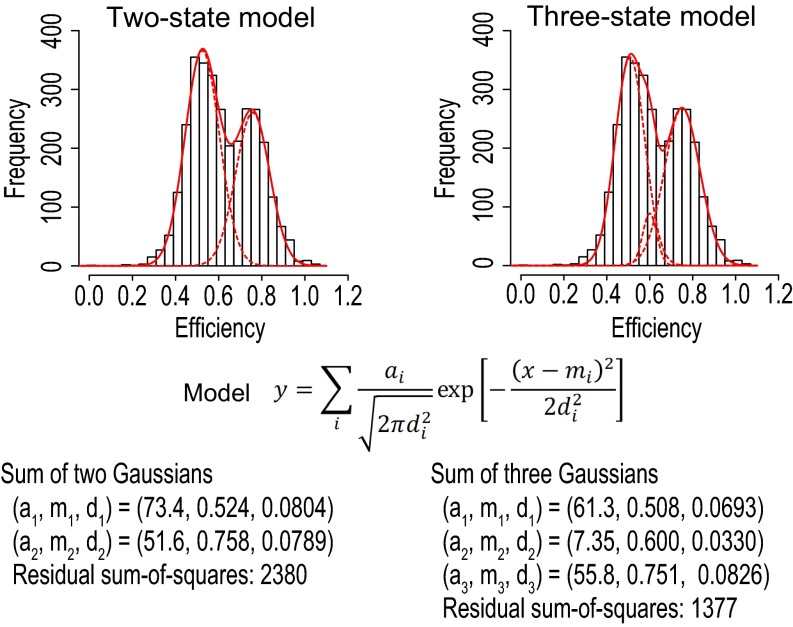
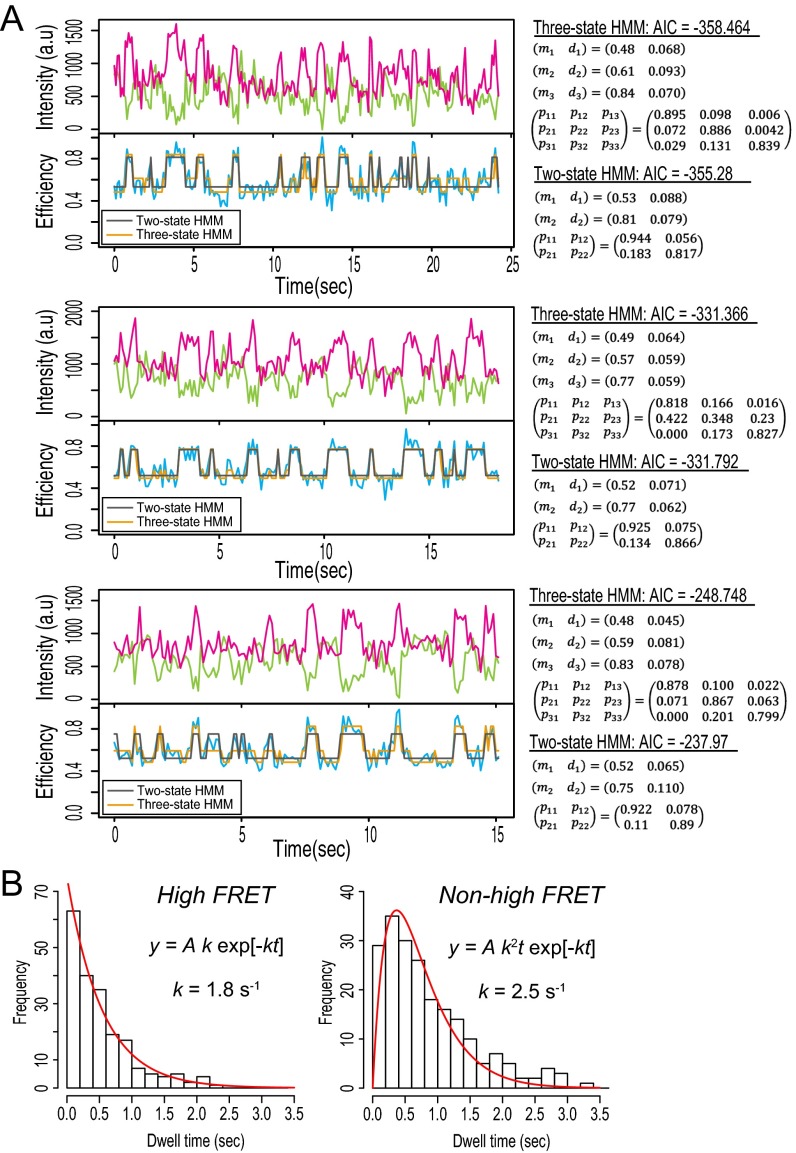
Previous studies based on cysteine cross-linking (14) and single-molecule studies (15–17) suggest that crystal structures, such as those of 1BMF and 2JDI, should represent the catalytic intermediate states. If this is the case and the ATP waiting dwell is short at high ATP concentration, then our prepared F₁ should exhibit significant FRET alternation corresponding to changes in the distance between dye attachment points from 3.5 to 5.2 and 5.0 nm as seen in the crystal structure (Fig. 1A). We investigated this point by performing single-molecule FRET measurements, taking advantage of mutation βE190D to prolong the lifetime of the catalytic dwell from a few milliseconds to hundreds of milliseconds. This mutation slows the ATP hydrolysis reaction ∼60-fold (to ∼3 s⁻¹) (12). F₁(βE190D)-Cy3Cy5s were immobilized on PEG-coated glass by biotin–streptavidin interactions (Fig. 1B). To make the events in the ATP waiting dwells undetectable at our time resolutions and thereby, highlight the events in the catalytic dwells, the experiments were performed at saturated ATP concentration (100 µM). The time series data showed anticorrelation between the donor and acceptor fluorescence intensities, indicating alternation of the FRET efficiency (Fig. 1C). A histogram of the FRET efficiencies indicates two subpopulations, with a high FRET state (0.76) and a middle FRET state (0.52) (Fig. 1D). The time trajectories of the FRET efficiencies were fitted by a two-state hidden Markov model (HMM) (39) (Fig. 1C), and the dwell time distributions of the high and middle FRET states were obtained (Fig. 1 E and F). The two-state approximation was a reasonable and minimum description of the single-molecule FRET data, first because the FRET efficiency histogram was reasonably fitted by a sum of two Gaussians relative to a sum of three Gaussians (Fig. S1) and second because the use of two- or three-state HMMs in data modeling hardly affected detection of the high FRET state (Fig. S2). The dwell time distribution of the high FRET state was fitted by a single-exponential curve, with a rate constant of 2.1 s⁻¹ (Fig. 1E). The dwell time distribution of the middle FRET state could not be fitted by a single-exponential curve, which suggests that the middle FRET state consists of more than one process (Fig. 1F). Based on these results and the three sets of configurations of the two βs in the 2JDI structure (Fig. 1A), a reasonable interpretation is that the high FRET state corresponds to the short configuration of the two βs, such as the 3.5-nm configuration in the 2JDI structure, whereas the middle FRET state includes the 5.2- and 5.0-nm configurations. Assuming that a pair of two βs sequentially adopts the 3.5-, 5.2-, and 5.0-nm configurations in the catalytic dwells and that the 5.2- and 5.0-nm distances are indistinguishable by FRET, the middle FRET state comprises two consecutive processes with the same rate constant. The probability density function in this case is a convolution of two single-exponential functions with the same rate constant, P(t) = tk²exp[−kt], where k is the rate constant (40). The dwell time distribution of the middle FRET state was fitted by the convolution function, with a rate constant of 2.4 s⁻¹. The rate constant of 2.1 s⁻¹ for the high FRET state and that of 2.4 s⁻¹ for the middle FRET state are comparable with the reported rate constant of 3 s⁻¹ (12). These data suggest a transition cycle in FRET states of high → middle → middle FRET, where each transition corresponds to rotational steps of 120°. The overall rotation rate is thus estimated to be one-third of these obtained rate constants (that is, 0.7–0.8 s⁻¹), which is consistent with the rotation rate of 0.6 s⁻¹ obtained by the rotation assay, for which the catalytic dwell was the rate-limiting step in the rotation (Table S1). Taken together, these results suggest that the overall structure in the catalytic dwell should resemble the 2JDI structure.

Fig. S1.

Comparison between fits by a sum of two Gaussians and a sum of three Gaussians to FRET efficiency histogram.

Fig. S2.

(A) Fittings by two- and three-state HMMs. (B) Dwell time analysis by the three-state HMM. (Left) The dwell time of the highest FRET state among the three states was fitted by single-exponential function of which the rate constant was 1.8 s⁻¹, which was consistent with 2.1 s⁻¹ for the high FRET state in the two-state HMM (main text). (Right) The combined dwell time of the remaining two FRET states was fitted by a convolution of two exponential functions of which the rate constant was 2.5 s⁻¹, which is consistent with 2.4 s⁻¹ for the middle FRET state in the two-state HMM (main text). AIC, Akaike Information Criterion.

Table S1.

Summary of statistics for experiment with F₁(βE190D)-Cy3Cy5 at 1 mM ATP

Molecule	Rotation rate (rotations per second)	Mean FRET efficiency ± SD (n = data points)			Games–Howell test*
		Dwell 1 (80°)†	Dwell 2 (200°)†	Dwell 3 (320°)†	1 and 2‡	1 and 3‡	2 and 3‡
A1	0.53	0.79 ± 0.17 (n = 178)	0.44 ± 0.13 (n = 183)	0.47 ± 0.20 (n = 240)	<0.01	<0.01	0.15
A2	0.53	0.75 ± 0.21 (n = 66)	0.42 ± 0.17 (n = 56)	0.52 ± 0.14 (n = 39)	<0.01	<0.01	<0.01
A3	0.47	0.72 ± 0.08 (n = 68)	0.56 ± 0.12 (n = 89)	0.49 ± 0.12 (n = 58)	<0.01	<0.01	<0.01
A4	0.77	0.82 ± 0.20 (n = 74)	0.46 ± 0.28 (n = 108)	0.46 ± 0.28 (n = 118)	<0.01	<0.01	0.98
A5	0.65	0.63 ± 0.20 (n = 148)	0.37 ± 0.23 (n = 175)	0.48 ± 0.22 (n = 130)	<0.01	<0.01	<0.01
A6	0.71	0.80 ± 0.17 (n = 99)	0.48 ± 0.20 (n = 119)	0.51 ± 0.19 (n = 60)	<0.01	<0.01	0.62
A7	0.39	0.75 ± 0.19 (n = 104)	0.49 ± 0.21 (n = 201)	0.51 ± 0.28 (n = 121)	<0.01	<0.01	0.62
A8	0.53	0.71 ± 0.28 (n = 142)	0.40 ± 0.19 (n = 104)	0.33 ± 0.35 (n = 82)	<0.01	<0.01	0.25
A9	0.73	0.83 ± 0.22 (n = 90)	0.53 ± 0.21 (n = 17)	0.55 ± 0.24 (n = 56)	<0.01	<0.01	0.9
A10	0.44	0.80 ± 0.27 (n = 66)	0.52 ± 0.33 (n = 110)	0.5 ± 0.21 (n = 31)	<0.01	<0.01	0.95
A11	0.40	0.81 ± 0.26 (n = 138)	0.60 ± 0.35 (n = 37)	0.52 ± 0.23 (n = 61)	<0.01	<0.01	0.45
A12	0.85	0.70 ± 0.17 (n = 52)	0.61 ± 0.24 (n = 21)	0.52 ± 0.27 (n = 30)	0.29	<0.01	0.44
	0.58 ± 0.15 (mean ± SD)	0.75 ± 0.06§	0.46 ± 0.07§	0.48 ± 0.07§

^*One-way ANOVA with Games–Howell posthoc test.

^†The rotary angles were defined as follows; the dwell taking the highest efficiency was at 80° of the rotary angle, and then, following dwells were at 200° and 320° in turn (main text).

^‡Numbers represent the indices assigned to the three dwells as shown in columns 3–5, and P values between the two dwells of the indicated indices are shown below.

^§Average and SEM of the total data points in all molecules.

Timing of Two-State Alternation of FRET in Catalytic Dwells Synchronizes with Rotational Steps.

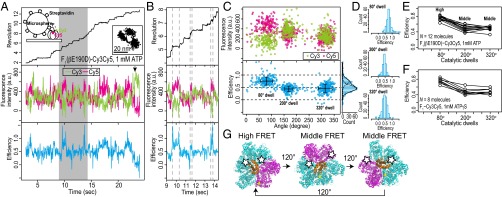
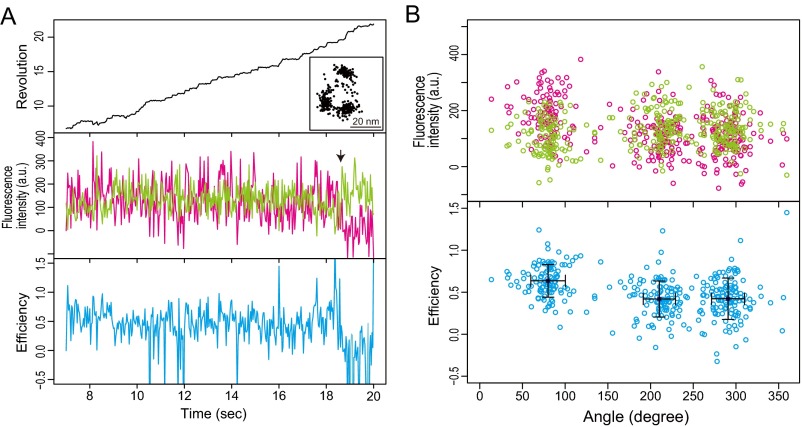
Two-state alternation of FRET in the catalytic dwells was observed by the single-molecule FRET experiments as described above (Fig. 1). However, it was unclear whether the timings of these alternations were synchronized with the rotational steps of γ. Simultaneous observation of the rotational steps of γ and the two-state alternation of FRET was, therefore, necessary. We performed simultaneous FRET and rotation measurements, in which the catalytic mutant F₁(βE190D)-Cy3Cy5 molecules were directly immobilized on a glass surface and streptavidin-conjugated beads were attached to their γ-components (Fig. 2A, Top, Left Inset). The experiments were performed at saturated ATP concentration (1 mM) to obtain the FRET signals and rotary angles in the catalytic dwells. The trajectory of the probe bead clearly showed three dwelling points in the catalytic dwell (Fig. 2A, Top, Right Inset). The rotation rate, 0.58 ± 0.15 rotations per second (mean ± SD; n = 12 molecules), was comparable with the previously reported rotation rate, for which the catalytic dwell was the rate-limiting step [0.9 rotations per second (12)]. The data show that FRET alternation is synchronized with the rotational steps (Fig. 2B). For data presentation, the dwell at the highest FRET efficiency is defined as 80° dwell, and the following dwells as 200° and 320° dwells. The timings of the two-state FRET alternation are synchronized with the rotational steps, and the middle FRET state continues over two rotational steps (Fig. 2 C and D). The mean values of the FRET efficiencies of the 80°, 200°, and 320° dwells are 0.75 ± 0.06, 0.46 ± 0.07, and 0.48 ± 0.07 (average ± SEM; n = 12 molecules), respectively (Fig. 2E). The differences between the mean values of the FRET efficiency for the 80° and 200° dwells and the differences between those of the 80° and 320° dwells are significant [P < 0.01 for 23 of 24 pairs in 12 molecules; one-way ANOVA with the Games–Howell posthoc test (Games–Howell test)] (Table S1). In contrast, the difference between the mean values of the FRET efficiency for the 200° and 320° dwells is not significant (P > 0.01 for 9 of 12 pairs in 12 molecules; Games–Howell test) (Table S1).

Fig. 2.

Simultaneous measurements of FRET and rotation between catalytic dwells. (A) Typical experiment with F₁(βE190D)-Cy3Cy5 at 1 mM ATP. Simultaneous time traces of (Top) revolution of probe bead (black line), (Middle) fluorescence intensities of Cy3 (green line) and Cy5 (magenta line), and (Bottom) FRET efficiency (blue line) are shown. The recording rate was 100 frames per second. The trajectory of the probe bead in the sample plane is shown (Top, Right Inset). The arrow denotes bleaching of Cy5 in A (Middle). The data are shown from the beginning of the fluorescence imaging after the bead imaging was started and stable rotation was confirmed. (B) Magnification of the gray box in A, showing timing of rotational steps and FRET alternation. (C) Correlations between rotary angles and fluorescence intensities of Cy3 (green dots) and Cy5 (magenta dots) and FRET efficiency (blue dots) during FRET events before acceptor photobleaching in A. The dwell with maximum mean FRET efficiency is defined as the 80° dwell, and the following dwells are defined as 200° and 320° dwells. Error bars are SDs of angle and efficiency at each dwell. (D) Histograms of FRET efficiency in the 80°, 200°, and 320° dwells. (E) Mean FRET efficiencies at three catalytic dwells in each molecule (total of 12 molecules). (F) Mean FRET efficiencies at three catalytic dwells in each molecule obtained from experiment with F₁-Cy3Cy5 in presence of 1 mM ATPγS (total of eight molecules). (G) Representation of interpretation of results. Molecular structures are the 2JDI structure. Colors of subunits are the same as in Fig. 1A. White stars represent donor or acceptor dyes.

To verify these findings, we performed simultaneous measurements using WT F₁ in the presence of ATPγS. ATPγS increases the waiting time in the catalytic dwell ∼35-fold from 2 to 70 ms for WT F₁ (12) and enables us to detect the FRET signals in the catalytic dwells with single-molecule fluorescence imaging. The measured rotation rate was 4.6 ± 1.1 rotations per second (mean ± SD; n = 8 molecules), which is consistent with the previously reported rotation rate when the catalytic dwell was the rate-limiting step [4.4 rotations per second at 2 mM ATPγS (12)]. Two-state alternation of FRET was synchronized with the rotational steps (Fig. S3). The mean values of FRET efficiency at the 80°, 200°, and 320° dwells were 0.73 ± 0.08, 0.48 ± 0.09, and 0.50 ± 0.09 (average ± SEM; n = 8 molecules), respectively (Fig. 2F). All differences between the mean values of the FRET efficiencies for 80° and 200° dwells and between those for 80° and 320° dwells are significant (P < 0.01 for 16 of 16 pairs in eight molecules; Games–Howell test) (Table S2). In contrast, the difference between the mean values of the FRET efficiencies for the 200° and 320° dwells was not significant (P > 0.01 for seven of eight pairs in eight molecules; Games–Howell test) (Table S2). The experiments with F₁-Cy3Cy5 in the presence of ATPγS, therefore, reinforce the findings obtained from the experiments with the mutant F₁(βE190D)-Cy3Cy5. We conclude that the FRET signals in the catalytic dwell are consistent with those expected from the 2JDI structure. Furthermore, the high FRET state represents the short-distance configuration of two βs, consistent with the 3.5-nm configuration in the 2JDI structure; by contrast, the middle FRET state represents configurations with distant pairs, consistent with either the 5.2- or 5.0-nm configuration (Figs. 1A and 2G).

Fig. S3.

(A) Typical data from the experiment with F₁-Cy3Cy5 at 1 mM ATPγS. The recording rate was 100 frames per second. Time trajectories of (Top) revolution of probe bead, (Middle) fluorescence intensities of Cy3 (green) and Cy5 (magenta), and (Bottom) FRET efficiency (blue) are shown. The trajectory of the probe bead in the sample plane is shown in A, Top, Inset. (A, Middle) The arrow indicates photobleaching of Cy5. The data are shown from the beginning of the fluorescence imaging after the bead imaging was started and stable rotation was confirmed. (B) Correlations between rotary angles and fluorescence intensities of Cy3 (green) and Cy5 (magenta) and FRET efficiency (blue) during FRET events before acceptor photobleaching in A. Error bars are SDs of each dwell.

Table S2.

Summary of statistics for experiment with F₁-Cy3Cy5 at 1 mM ATPγS

Molecule	Rotation rate (rotations per second)	Mean FRET efficiency ± SD (n = data points)			Games–Howell test*
		Dwell 1 (80°)†	Dwell 2 (200°)†	Dwell 1 (80°)†	1 and 2‡	1 and 3‡	2 and 3‡
B1	4.78	0.76 ± 0.27 (n = 84)	0.42 ± 0.33 (n = 75)	0.47 ± 0.32 (n = 78)	<0.01	<0.01	0.5
B2	4.70	0.81 ± 0.14 (n = 196)	0.49 ± 0.17 (n = 84)	0.54 ± 0.17 (n = 44)	<0.01	<0.01	0.24
B3	3.27	0.78 ± 0.12 (n = 95)	0.65 ± 0.17 (n = 34)	0.60 ± 0.18 (n = 44)	<0.01	<0.01	0.39
B4	4.40	0.71 ± 0.26 (n = 274)	0.39 ± 0.25 (n = 225)	0.45 ± 0.27 (n = 260)	<0.01	<0.01	0.05
B5	3.69	0.64 ± 0.18 (n = 111)	0.44 ± 0.19 (n = 109)	0.44 ± 0.23 (n = 124)	<0.01	<0.01	0.98
B6	3.77	0.74 ± 0.15 (n = 133)	0.46 ± 0.16 (n = 138)	0.47 ± 0.20 (n = 95)	<0.01	<0.01	0.94
B7	6.49	0.71 ± 0.14 (n = 86)	0.48 ± 0.16 (n = 90)	0.39 ± 0.20 (n = 92)	<0.01	<0.01	<0.01
B8	5.68	0.85 ± 0.23 (n = 100)	0.54 ± 0.28 (n = 90)	0.54 ± 0.26 (n = 81)	<0.01	<0.01	0.99
	4.60 ± 1.08 (mean ± SD)	0.73 ± 0.08§	0.48 ± 0.09§	0.50 ± 0.09§

^*One-way ANOVA with Games–Howell posthoc test.

^†The rotary angles were defined as follows; the dwell taking the highest efficiency was at 80° of the rotary angle, and then, following dwells were at 200° and 320° in turn (main text).

^‡Numbers represent the indices assigned to the three dwells as shown in columns 3–5, and P values between the two dwells of the indicated indices are shown below.

^§Average and SEM of the total data points in all molecules.

Distinction Between ATP Waiting Form and Catalytic Form.

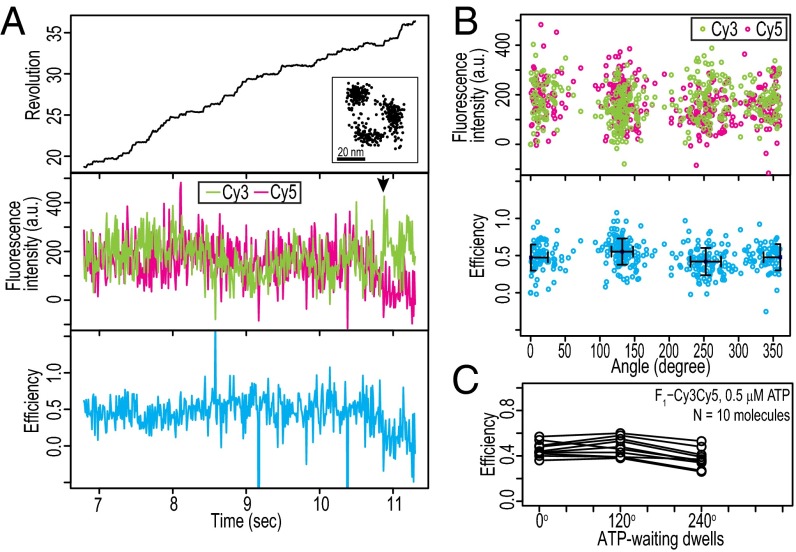
The β-configurations in the ATP waiting dwell were investigated at low ATP concentration with F₁-Cy3Cy5 (0.5 µM) (Fig. 3A). Because the catalytic dwelling rate of ∼500 s⁻¹ (7) was much faster than our recording rate of 100 frames per second, the catalytic events were not observed, and thus, three dwelling points in the trajectory of the probe bead were in the ATP waiting dwells (Fig. 3A, Top, Inset). The value of 3.6 ± 1.2 rotations per second (mean ± SD; n = 10 molecules) is consistent with previous studies [rotation rate V = V_max[ATP]/(K_m + [ATP]) = 4.2 rotations per second, where V_max = 80 rotations per second, K_m = 15 µM for bead rotation, and [ATP] = 0.5 µM] (7). Unlike in the catalytic dwell, in the ATP waiting dwell, the FRET signals did not show clear FRET efficiency alternations (Fig. 3 A and B). The mean value of the FRET efficiency in all three dwells was 0.46 ± 0.06 (average ± SEM; n = 10 molecules), which is significantly lower than for the high FRET state (∼0.75); 8 of 10 molecules had statistically significant differences among the mean values of the FRET efficiencies in the three dwells (P ≤ 0.01; Games–Howell test) (Table S3). We defined 240° as the rotary angle at which the mean of the FRET efficiency was minimum. The mean values of the FRET efficiencies of the 0°, 120°, and 240° dwells were 0.46 ± 0.06, 0.48 ± 0.07, and 0.39 ± 0.08, respectively (average ± SEM; n = 10 molecules) (Fig. 3C).

Fig. 3.

Absence of apparent FRET alternation in ATP waiting dwell. Typical examples of simultaneous measurements of FRET and rotation with F₁-Cy3Cy5 at 0.5 μM ATP. The recording rate was 100 frames per second. Time trajectories of (Top) revolution of probe bead (black line), (Middle) fluorescence intensities of Cy3 (green line) and Cy5 (magenta line), and (Bottom) FRET efficiency (blue line). The trajectory of the probe beads in the sample plane is shown in A, Top, Inset. The arrow denotes bleaching of Cy5 in A, Middle. The data are shown from the beginning of the fluorescence imaging after the bead imaging was started and stable rotation was confirmed. (B) Correlations between rotary angles and fluorescence intensities of Cy3 (green dots) and Cy5 (magenta dots) and FRET efficiency (blue dots) during FRET events before acceptor photobleaching in A. (C) Mean FRET efficiencies at three catalytic dwells in each molecule (total of 10 molecules). The dwell with minimum mean FRET efficiency is defined as 240° dwell, and the following dwells are defined as 0° and 120° dwell.

Table S3.

Summary of statistics for experiment with F₁-Cy3Cy5 at 0.5 µM ATP

Molecule	Rotation rate (rotations per second)	Mean FRET efficiency ± SD (n = data points)			Games–Howell test*
		Dwell 1 (80°)†	Dwell 2 (200°)†	Dwell 3 (240°)‡	1 and 2‡	1 and 3‡	2 and 3‡
C1	2.49	0.36 ± 0.32 (n = 84)	0.38 ± 0.27 (n = 44)	0.26 ± 0.30 (n = 24)	0.92	0.37	0.26
C2	5.05	0.43 ± 0.14 (n = 140)	0.48 ± 0.13 (n = 80)	0.35 ± 0.14 (n = 171)	0.03	<0.01	<0.01
C3	1.69	0.49 ± 0.15 (n = 744)	0.58 ± 0.14 (n = 197)	0.48 ± 0.16 (n = 94)	<0.01	0.8	<0.01
C4	4.82	0.43 ± 0.18 (n = 258)	0.43 ± 0.18 (n = 208)	0.34 ± 0.22 (n = 210)	0.95	<0.01	<0.01
C5	2.17	0.54 ± 0.16 (n = 283)	0.46 ± 0.18 (n = 111)	0.36 ± 0.18 (n = 195)	<0.01	<0.01	<0.01
C6	3.62	0.48 ± 0.17 (n = 146)	0.55 ± 0.17 (n = 146)	0.41 ± 0.18 (n = 111)	<0.01	<0.01	<0.01
C7	3.44	0.40 ± 0.20 (n = 436)	0.39 ± 0.20 (n = 353)	0.27 ± 0.22 (n = 406)	0.56	<0.01	<0.01
C8	4.35	0.42 ± 0.33 (n = 131)	0.39 ± 0.29 (n = 124)	0.37 ± 0.30 (n = 223)	0.81	0.42	0.81
C9	4.35	0.57 ± 0.24 (n = 138)	0.60 ± 0.22 (n = 117)	0.53 ± 0.26 (n =429)	0.57	0.23	0.01
C10	3.97	0.44 ± 0.20 (n = 442)	0.53 ± 0.20 (n = 418)	0.39 ± 0.21 (n = 399)	<0.01	<0.01	<0.01
	3.60 ± 1.15 (mean ± SD)	0.46 ± 0.06§	0.48 ± 0.07§	0.39 ± 0.08§

^*One-way ANOVA with Games–Howell posthoc test.

^†The rotary angles were defined as follows; the dwell taking the highest efficiency was at 80° of the rotary angle, and then, following dwells were at 200° and 320° in turn (main text).

^‡Numbers represent the indices assigned to the three dwells as shown in columns 3–5, and P values between the two dwells of the indicated indices are shown below.

^§Average and SEM of the total data points in all molecules.

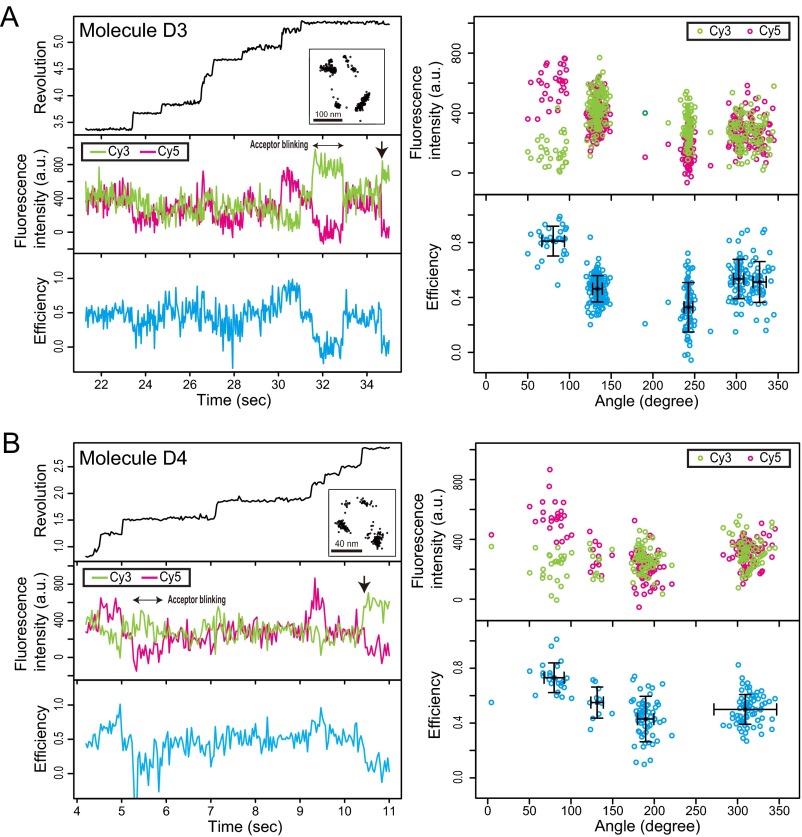
To observe FRET alternation in consecutive ATP waiting and catalytic dwells, we performed simultaneous observations of FRET and rotation at ATP concentrations of K_m [1 μM (12)]. The AviTag-F₁ that we used here did not enable us to observe clear 80° + 40° substeps, probably because the single-point attachment of a streptavidin-coated bead by a single AviTag resulted in decreased resolution of the rotary angles. To achieve double-point attachment of the bead, we used F₁ in which double-cysteine mutations were introduced into γ for biotinylation. We constructed the hybrid F₁(βE190D)-Cy3Cy5, in which the γ was doubly biotinylated and the βs were specifically labeled with Cy3 or Cy5 by replacing the βs of the biotinylated F₁ with fluorescently labeled βs (Materials and Methods). The hybrid F₁(βE190D)-Cy3Cy5 enabled us to observe the 80° + 40° substeps and the fluorescent signals of single-pair FRET during more than one rotation. The trajectories of the fluorescence intensities and FRET clearly showed alternation between high FRET efficiency (∼0.75) and middle FRET efficiency (∼0.5). The high FRET state was restricted to one of three catalytic dwells (Fig. 4 A–D, Fig. S4, and Table S4). These results are consistent with a series of two-state FRET alternations in the six dwell angles (Fig. 4E). The high FRET state was not observed in the ATP waiting dwells but was observed in one catalytic dwell. This finding is consistent with the experimental results as shown above. The high FRET state represents a short configuration, such as the 3.5-nm configuration in the 2JDI structure. In the 3.5-nm configuration, the two βs are in the closed form (Fig. 1A). Therefore, none of the β-pairs in the ATP waiting state adopt the short-distance configuration.

Fig. 4.

FRET alternation at six dwells. Typical examples with hybrid F₁(βE190D)-Cy3Cy5 at 1 µM ATP. The recording rate was 30 frames per second. (A and C) Time trajectories of (Top) revolution of probe bead (black line), (Middle) fluorescence intensities of Cy3 (green line) and Cy5 (magenta line), and (Bottom) FRET efficiency (blue line). The trajectory of the probe beads in the sample plane is shown in A, Top, Inset and C, Top, Inset. The arrow denotes bleaching of Cy5 in A, Middle and C, Middle. The data are shown from the beginning of the fluorescence imaging after the bead imaging was started and stable rotation was confirmed. (B and D) Correlations between rotary angles and fluorescence intensities of Cy3 (green dots) and Cy5 (magenta dots) and FRET efficiency (blue dots) during FRET events before acceptor photobleaching in A and C. (E) Mean FRET efficiencies at six dwells in each molecule (total of four molecules). The rotary angle in the dwell with maximum mean FRET efficiency is defined as the 80° dwell.

Fig. S4.

Data for molecules (A) D3 and (B) D4 from experiments with hybrid F₁(βE190D)-Cy3Cy5 (Table S4).

Table S4.

Summary of statistics for experiment with hybrid-F₁(βE190D)-Cy3Cy5 at 1 µM ATP

Molecule	Mean FRET efficiency ± SD (n = data points)
	Dwell (0°)	Dwell (80°)	Dwell (120°)	Dwell (200°)	Dwell (240°)	Dwell (320°)
D1*	0.46 ± 0.10 (n = 11)	0.75 ± 0.07 (n = 26)	0.58 ± 0.13 (n = 90)	0.43 ± 0.18 (n = 13)	0.38 ± 0.13 (n = 346)	0.46 ± 0.11 (n = 14)
D2*	0.56 ± 0.12 (n = 135)	0.80 ± 0.12 (n = 43)	0.50 ± 0.10 (n = 18)	0.34 ± 0.12 (n = 155)	0.49 ± 0.11 (n = 26)	0.52 ± 0.11 (n = 71)
D3†	0.51 ± 0.15 (n = 46)	0.81 ± 0.11 (n = 30)	0.46 ± 0.10 (n = 142)	NA	0.33 ± 0.18 (n = 79)	0.53 ± 0.14 (n = 61)
D4†	NA	0.73 ± 0.11 (n = 24)	0.55 ± 0.11 (n = 11)	0.43 ± 0.17 (n = 63)	NA	0.50 ± 0.11 (n = 75)
	0.51 ± 0.15‡	0.77 ± 0.15‡	0.52 ± 0.15‡	0.40 ± 0.15‡	0.40 ± 0.15‡	0.50 ± 0.15‡

^*The time series data in Fig. 4 A and C were derived from D1 and D2, respectively.

^†The data of D3 are also shown in Fig. S4A, and the data of D4 are also shown in Fig. S4B.

^‡Average and SEM of the total data points in all molecules.

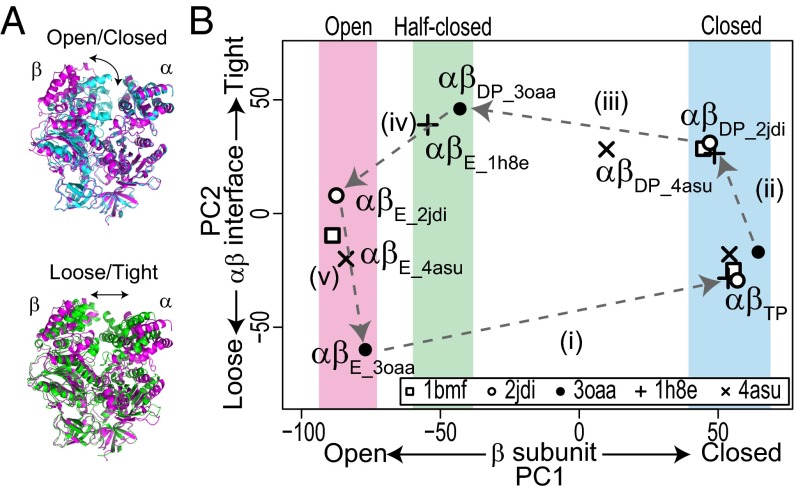
α₃β₃γ-Conformation of 3OAA Crystal Structure as ATP Waiting Form.

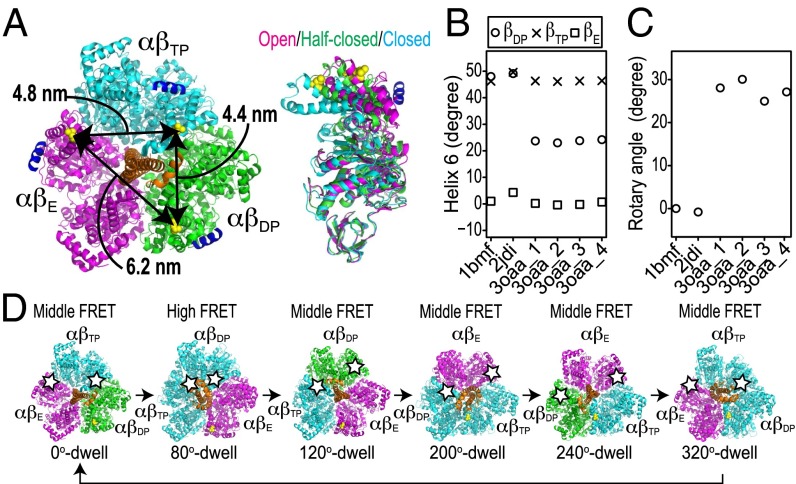
Unlike other crystal structures of F₁ containing the γ-subunit, in the 3OAA structure of Escherichia coli F₁ (EF₁) [PDB ID code 3OAA (41)], only one β-subunit is closed, and correspondingly, all three distances between the dye attachment points, βL388, are long: 4.4, 4.8, and 6.2 nm (Fig. 5A). Indeed, Cingolani and Duncan (41) suggested that 3OAA could represent the ATP waiting dwell. By contrast, in an earlier candidate for the ATP waiting form (21) [PDB ID code 2HLD (42)], the shortest dye attachment distance is 4.0 nm, intermediate between 3.5 nm of 2JDI and 4.4 nm of 3OAA. Consistent with this observation, Nam et al. (26) recently concluded that 2HLD is in a state intermediate between the catalytic and ATP waiting dwells. The model by Nam et al. (26) of the waiting state indeed has a comparably long minimum distance of 4.1 nm between the dye attachment points, although shorter than in 3OAA (Table S5).

Fig. 5.

The α₃β₃γ of crystal structure 3OAA as ATP waiting form. (A) The molecular structure of the α₃β₃γ-complex is derived from E. coli F₁ [PDB ID code 3OAA (41)]. βL388 in the 3OAA structure is shown as yellow spheres, indicating the fluorescent labeling sites. Colors of αβs represent three distinct β-conformations: the half-closed form of β_DP, the closed form of β_TP, and the open form of β_E are shown in green, cyan, and magenta, respectively; γ is shown in orange. Helix 6 of the β-subunits is shown in dark blue. (B) Projected orientation of helix 6 of each β in structures 1BMF, 2JDI, and 3OAA in a plane perpendicular to the rotation axis of γ. (C) Rotary angles of γ in structures 1BMF, 2JDI, and 3OAA. The rotary angle of structure 1BMF is defined as 0°. (D) Schematic diagrams of conformation transitions shown by FRET. Structure 3OAA (2JDI) correspond to dwells at 0°, 120°, and 240° (80°, 200°, and 320°). The dwell at the highest FRET efficiency defines the 80° angle. Stars represent donor or acceptor dyes.

Table S5.

Cβ-distances of fluorescent labeling sites in crystal structures

PDB ID code	βL402 distance βTP–βDP (nm)	βL402 distance βTP–βE (nm)	βL402 distance βDP–βE (nm)
1BMF	3.55	5.13	5.06
1H8E	3.62	5.08	4.48
2HLD*	3.99	5.26	5.39
2JDI	3.48	5.17	4.98
3OAA†	4.42	4.84	6.23
4ASU	3.91	5.12	5.42
4Z1M	3.85	5.04	5.26
Nam et al. (26)‡	4.14	5.25	5.78

^*For yeast F₁-ATPase, corresponding βL402 is used.

^†For Escherichia coli F₁-ATPase, corresponding βL388 is used.

^‡For the structure model from the molecular dynamics simulation with 2HLD (26), corresponding βL402 is used.

The 3OAA structure consists of α₃β₃γε, in which ε elongates and inserts into the gap between α₃β₃ and γ and therefore, is thought to be in the ε-inhibition state. A recent report suggested that ε-insertion induces the substep from the catalytic dwell to the ATP waiting dwell and may, therefore, induce conformational changes in the α₃β₃γ-complex in bacterial F₁ (43). The α₃β₃-conformation of the 3OAA structure is, therefore, a good candidate structure for the ATP waiting form. This hypothesis is strongly supported by two other measurements: the helix 6 tilt angles of βs and the rotary angles. Masaike et al. (17) measured the helix 6 tilt angles with single-molecule fluorescence polarization techniques. Their results are as follows. In the catalytic form, compared with the helix 6 of β_E, the helix 6 angles of both β_DP and β_TP rotate by about 40°; in the ATP waiting form, compared with the helix 6 of β_E, the helix 6 angles of β_DP and β_TP rotate about 20° and 40°, respectively. These helix 6 angles are consistent with those of the 1BMF, 2JDI, and 3OAA structures (Fig. 5B). Next, we evaluated the γ-orientations in the crystal structures. Compared with the rotary angles of the 2JDI and 1BMF structures, γ in the 3OAA structure rotates at about 30° in the ATP hydrolysis direction (Fig. 5C). The rotational step from the catalytic dwell to the ATP waiting dwell is ∼40° in the ATP hydrolysis direction in TF₁ (7, 12). Based on these measurements put together, the α₃β₃γ-complex of the 3OAA structure seems to capture the ATP waiting form, whereas the 2JDI and 1BMF structures represent the catalytic form (Fig. 5D), and 2HLD is in an intermediate state. A recent structure of the ε-inhibition state of TF₁ [PDB ID code 4XD7 (44)] also has consistently long distances: 4.7, 4.9, and 6.1 nm. However, its main difference from 3OAA—β_DP being open instead of half-closed—is likely a consequence of lacking nucleotides in all sites but β_TP.

Systematic Analysis of Crystal Structures of ATP Waiting and Catalytic Forms.

The single-molecule FRET results indicated the correspondence between the two major forms (the ATP waiting and catalytic forms) and the two representative crystal structures (the 3OAA and 2JDI structures), respectively. By filling in missing intermediates, we for the first time, to our knowledge, were able to scrutinize the structural basis of the ATPase cycle of F₁. To further identify responsible motions in the individual catalytic subunits, we performed a systematic comparison of the crystal structures with principal component analysis (PCA), which enabled us to quantitatively characterize the αβ-dimer conformations down to the levels of the opening/closing motions in β and the loosening/tightening motions at the αβ-interface (Fig. 6A) (19). These opening/closing and loosening/tightening motions in the αβ-dimer are closely related to chemical reactions, such as nucleotide binding and catalytic events (19, 23, 45–47). For the systematic structural comparison, we selected five representative crystal structures: PDB ID codes 1BMF (4), 1H8E (48), 2JDI (38), 3OAA (41), and 4ASU (49). The 1BMF, 3OAA, and 2JDI structures have already been mentioned. The 1H8E and 4ASU structures are thought to be the catalytic intermediate states, particularly in the product release step (48, 49). PCA identified two major axes, principal component 1 (PC1) and PC2, along which the structures can be best separated (Materials and Methods and Fig. 6B). The PC1 and PC2 axes represent the opening/closing motions in β and the loosening/tightening motions at the αβ-interface, respectively, as previously reported (19). The PC1–PC2 plot distinctly showed the uniqueness of each crystal structure. For example, αβ_DP of 3OAA is similar to αβ_E of 1H8E but has a more open form than αβ_DP of 2JDI on the PC1 axis. The αβ_DP of 4ASU is between those of the 2JDI and 3OAA structures on the PC1 axis. The form of αβ_E of the 3OAA structure is looser than that of the 2JDI structure on the PC2 axis. The αβ_E of the 4ASU structure is between those of the 2JDI and 3OAA structures on the PC2 axis. The αβ_TPs of the five crystal structures are very similar to each other in this analysis. Overall, the representation of the structures in the PC1–PC2 plane implies a five-step conformational transition cycle coupled with the ATP hydrolysis reaction cycle (Fig. 6B).

Fig. 6.

Systematic structural comparison of crystal structures representing ATP waiting and catalytic forms. (A) Two major conformational changes in αβ-dimer: (Upper) opening/closing motions in β and (Lower) loosening/tightening motions at αβ-interface. Molecular structures are αβ-dimers of 3OAA structure; αβ_E, αβ_DP, and αβ_TP are shown in magenta, green, and cyan, respectively. (B) Systematic structural comparison of F₁ crystal structures using PCA. Crystal structures used for analysis were PDB ID codes 1BMF, 2JDI, 3OAA, 1H8E, and 4ASU. Eigenvectors PC1 and PC2 obtained from PCA represent opening/closing motions in β and loosening/tightening motions at αβ-interface, respectively. Dashed arrows indicate the five-step transition cycle of αβ-conformation in the ATP hydrolysis direction.

Discussion

We investigated dynamic structural couplings in F₁-ATPase using single-molecule techniques and a systematic structural comparison. The experimental results indicate that two of three β-subunits take the nonclosed form in the ATP waiting dwell, unlike the case for the catalytic dwell. The criteria for the ATP waiting form revealed by this study and previous studies suggest that the α₃β₃γ-complex of the 3OAA structure is probably in the ATP waiting form among the reported crystal structures, whereas the 2JDI and 1BMF structures represent the catalytic form. ε-Inhibition, thus, seems to exploit conformational selection, trapping F₁ in the ATP waiting form along the functional cycle. The rotation assay of the bacteria F₁ with the ε-subunit suggested that the rotary angle in the ε-inhibition state is the same as that in the catalytic dwell (50–53), whereas the rotary angles of the crystal structures in the ε-inhibition state are the same as those of the ATP waiting dwell (41, 44). Resolving these contradictory findings may require an investigation of the ε-inhibited structure trapped in an active rotation assay.

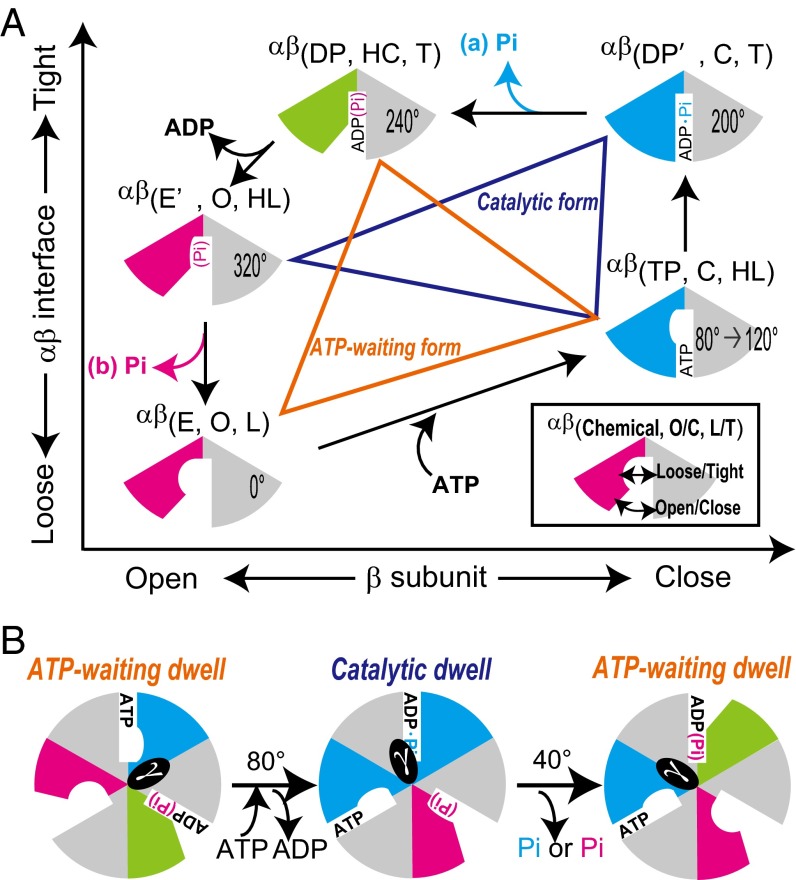
A systematic comparison of these representative crystal structures was used to quantitatively classify each αβ-dimer of the structures. The results suggest a conformational transition cycle coupled to the ATP hydrolysis reaction cycle. We, therefore, propose a comprehensive model involving tripartite coupling among chemical reactions, enzyme structures, and rotary angles in F₁ (Fig. 7). In the model, the αβ-conformations are categorized by three parameters [i.e., the nucleotide states, the open/closed states of β, and the loose/tight states at the αβ-interface represented by αβ (chemical state, open/closed state, and loose/tight state); empty (E), ATP-bound (TP), intermediate in ATP hydrolysis (DP′), ADP/P_i-bound (DP), and P_i (P_i-bound) in chemical states; open (O), half-closed (HC), and closed (C) in the open/closed states of the β-subunit; and loose (L), half-loose (HL), and tight (T) in the loose/tight states at the αβ interface]. The ATPase cycle of αβ consists of five steps as follows (Fig. 7A). (i) ATP binding event: the ATP binding induces not only the largest closing motion in β but also, tightening motion at the αβ-interface. (ii) ATP hydrolysis intermediate state: the loosening/tightening motions at the αβ-interface involve rearrangement of the catalytic core residues such as the arginine finger and impact the chemical reaction (19, 54). This rearrangement may also be critical for ATP synthesis. We note that, operating in reverse, the rotation of γ in the ATP synthesis direction under an external torque loosens the αβ-interface from αβ(DP′, C, and T) to αβ(TP, C, and HL), which inhibits hydrolysis of newly synthesized ATP. (iii) Completion of ATP hydrolysis event: in the transition from αβ(DP′, C, and T) to αβ(DP, HC, and T), opening motion of β from the closed state to the half-closed state is driven by ATP cleavage, but the product ADP is retained in αβ because of the tight state of the αβ-interface, αβ(DP, HC, and T), which corresponds to αβ_{DP_3OAA} and αβ_{E_1H8E}; αβ_{E_1H8E} is thought to be the conformational state of the posthydrolysis, preproduct release step (48), supporting our model. In terms of P_i release, two different ATPase reaction cycle schemes have been proposed [i.e., P_i is released before ADP (49), or P_i is the last product to be released (23, 55]. In the former scheme, P_i is released from αβ(DP′, C, T). (iv) ADP release event: the release of produced ADP induces additional opening motion in β from αβ(DP, HC, T) to αβ[empty or P_i bound (E′), O, HL]. In the alternative scheme of the P_i release event, the catalytic core residue in αβ(E′, O, HL) still holds the product P_i. (v) P_i release/isomerization event: the product P_i is released from αβ(E′, O, HL), with additional loosening motion at the αβ-interface as Okazaki and Takada (19) pointed out from their previous systematic structural comparison. This finding is further supported by the recently reported two crystal structures [PDB ID codes 4YXZ (56) and 4Z1M (57)], of which the αβ_E-dimers represent the chemical state related to the P_i release event. The αβ_E positions of 4YXW and 4Z1M in the PCA map are on the line connecting αβ_E of 2JDI and 3OAA (Fig. S5). This finding suggests that the P_i release event should be accompanied with loosening motion of the αβ_E-interface. In an alternative pathway, in which the product P_i is released before ADP, this loosening motion can be interpreted as isomerization of the αβ-conformation.

Fig. 7.

Model of tripartite coupling in F₁ between chemical reactions, stator conformation, and rotary angles. (A) Model of αβ-dimer coupling between nucleotide states and conformations based on results shown in Fig. 6B. αβ-Dimer is categorized into at least five states by three parameters (chemical states, open/closed states, and tight/loose states): E, TP, DP′, DP, and E′ in chemical states; O, HC, and C in open/closed states of β; and L, HL, and T in loose/tight states at αβ-interface. P_i is released from (A, a) αβ(DP′, C, T) or (A, b) αβ(E′, O, HL). Conformation sets of three αβ-dimers linked by orange lines and blue lines represent the ATP waiting and catalytic forms, respectively. Rotary angles are indicated, where αβ(E, O, L) defines 0°. (B) Models of ATP waiting form and catalytic form of F₁-ATPase with rotary angle transitions.

Fig. S5.

Systematic structure comparison including the structures with PDB ID codes 4YXW and 4Z1M.

Fig. 7B shows models of the ATP waiting and catalytic forms of F₁-ATPase with the rotary angles. The ATP waiting form is comprised of the conformation set of αβ(TP, C, HL), αβ(DP, HC, T), and αβ(E, O, L), whereas the catalytic form is comprised of the conformation set of αβ(TP, C, HL), αβ(DP′, C, T), and αβ(E′, O, HL) (Fig. 7A). These two conformation sets are consistent with the previously proposed β-conformation sets by Masaike et al. (17), in which three βs take the closed, half-closed, and open states in the ATP waiting form and the closed, closed, and open states in the catalytic form. The idea that the rotational steps of γ are driven by conformational changes coupled to chemical reactions in the stator α₃β₃ is generally accepted (21, 58, 59). The driving force of the 80° substep arises from ATP binding and ADP release events (10). These events are accompanied by two large conformational changes: the transitions from αβ(E, O, L) to αβ(TP, C, HL) and from the αβ(DP, HC, T) to αβ(E′, O, HL) (Fig. 7A). These conformational changes drive the 80° substep. The 40° substep is induced by P_i release in TF₁ (10). In our model, P_i release accompanies loosening motion at the αβ-interface in the transition from αβ(E′, O, HL) to αβ(E, O, L) or opening motion in β in the transition from αβ(DP′, C, T) to αβ(DP, HC, T). Therefore, the loosening motion at the αβ_E-interface or the closing motion of β_DP should affect the 40° substep. Additional studies, such as monitoring the loosening/tightening motions of the αβ-interface, are necessary to test our model in detail. In addition, simultaneous measurements of the conformational changes in α₃β₃ and rotations of γ with magnetic beads under controlled rotation should reveal the tripartite coupling in the ATP synthesis reaction.

Materials and Methods

AviTag-F₁.

The α₃β₃γ-subcomplex of F₁-ATPase was derived from thermophilic Bacillus PS3 (TF₁). We used α(C193S)₃β(His10 at N terminus)₃γ (referred to as WT F₁ in the text) and α(C193S)₃β(His10 at N terminus/E190D)₃γ [referred to as F₁(βE190D)]. AviTag is the biotinylation sequence (60). The AviTag sequence (GLNDIFEAQKIEWHE) was inserted between γA108 and γS109 for biotinylation (referred to as AviTag-F₁). AviTag-F₁(βL398C) or AviTag-F₁(βE190D/L398C) was expressed in E. coli, purified using His-Tag affinity chromatography, and labeled with Cy3–maleimide or Cy5–maleimide (GE Healthcare). The ratio of Cy3:Cy5:F₁ in the purified sample was ∼1:1:1 based on the absorption spectrum. Note that the preparation gives a mixture of F₁s with a single pair of Cy3 and Cy5 and F₁s with no fluorescent molecule, one fluorescent molecule, two molecules of the same dye, or three dyes. We, therefore, selected the data for F₁ with a single pair of Cy3 and Cy5.

Preparation of Hybrid F₁.

For biotinylation of the γ-subunit, we used F₁ with cysteine mutations introduced into its γ-subunit, α(C193S)₃β(His10 at N terminus)₃γ(S109C/I212C). The F₁ was expressed in E. coli, purified using His-Tag affinity chromatography, and then, biotinylated with biotin–maleimide (Dojindo Laboratories). We also introduced L398C mutations into pucβ(His10 at N terminus) and pucβ(His10 at N terminus/E190D) plasmids (referred to as βL398C and βE190D/L398C, respectively) using the megaprimer method. These β-subunits were expressed in E. coli, purified using hydrophobic interaction chromatography, and labeled with Cy3–maleimide or Cy5–maleimide (GE Healthcare). The Cy3-labeled β-subunit, the Cy5-labeled β-subunit, and the biotinylated F₁ were then mixed at a ratio of 10:10:1 and dissolved in a high-salt buffer [10 mM 3-morpholinopropanesulfonic acid (Mops), pH 7.0, 2 mM MgCl₂, 1 M KCl]. The sample was incubated overnight at 4 °C for β-exchange. The mixture was then subjected to ultrafiltration (Amicon Ultra; 10-kDa cutoff; Merck Millipore) for desalting and incubated at 37 °C for 1 h. Excess β was removed by gel filtration (Superdex 200HR 10/30; GE Healthcare). We obtained hybrid F₁ in which the γ-subunit was biotinylated and the β-subunits were labeled with Cy3 or Cy5. The ratio of Cy3:Cy5:F₁ was ∼1:1:1 based on the absorption spectrum. However, as mentioned above, this preparation gave a mixture of F₁s with single pairs of Cy3 and Cy5 molecules and other F₁s. We, therefore, selected the data from F₁ labeled with a single-pair fluorescent molecule.

Microscopy.

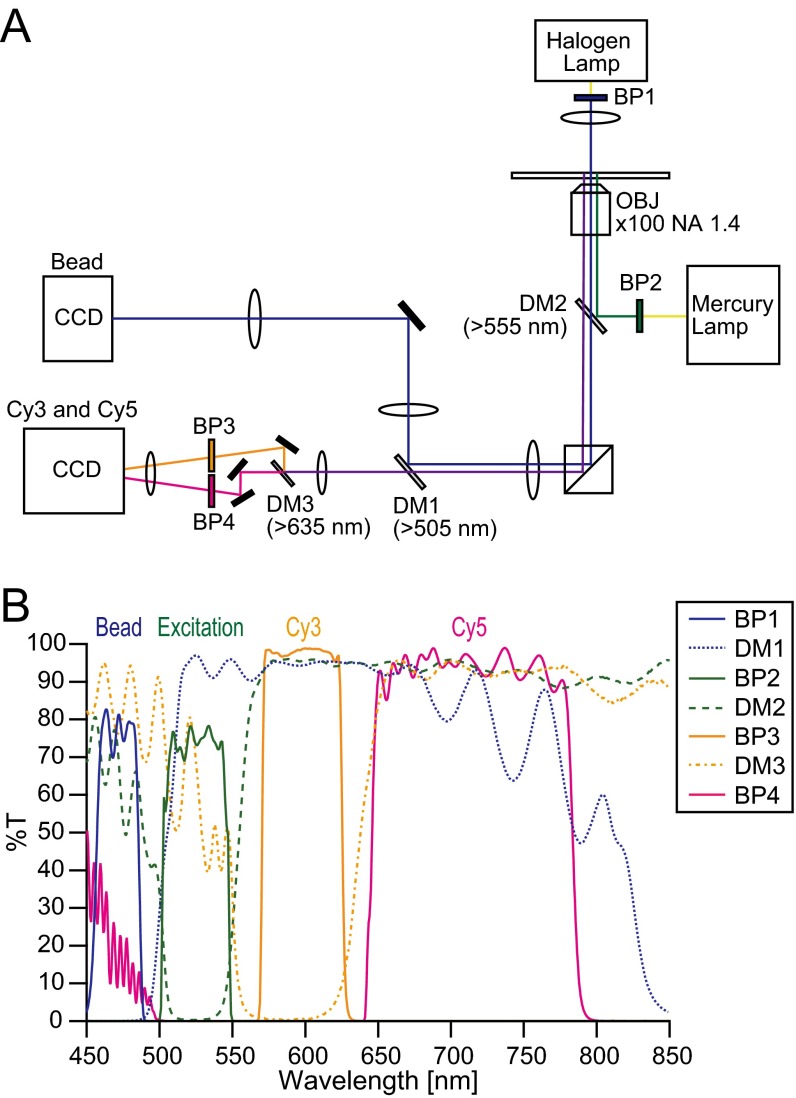
The rotation of polystyrene beads on the γ-subunit was visualized by center-stop dark-field microscopy (17) using an inverted microscope (IX71; Olympus) with an objective lens (Plan Apo 100× or 60×; N.A. 1.45; Olympus), a center stop (circular reticle with φ = 500 μm; Qioptiq Photonics GmbH & Co KG), a halogen lamp or a light-emitting diode (pE-100; center wavelength = 470 nm; CoolLED), and a CCD camera (Luca; Andor Technologies) (Fig. S6). Cy3 and Cy5 fluorescence was observed using the same microscopy system with epiillumination with a mercury lamp or an evanescent field with a 532-nm diode laser, a dual-view imaging system (DV2; Photometrics), and a CCD camera (iXon; Andor Technologies) (Fig. S6). To prevent cross-talk between the bead and the fluorescence signals, the wavelength for the bead imaging was much shorter than the Cy3 and Cy5 emission wavelengths, and thus, the bead imaging hardly affected the quality of the FRET imaging.

Fig. S6.

(A) Schematic drawing of optics for simultaneous measurement of FRET and rotation. (B) Wavelength properties of optical filters in A. BP, bandpass filter; DM, dichroic mirror; OBJ, objective.

Single-Molecule FRET Measurements.

If we assume that Cy3 and Cy5 are freely rotating on a timescale faster than the fluorescence lifetime, which means that the orientation factor κ² is 2/3 in the Förster distance equation, the Förster distance of this pair is ∼54–60 Å (30, 61). This Förster distance is suitable to detect the changes in the distances between the cysteine mutation sites of the βs.

PEG-coated cover glasses were made using the following procedure. Cover glasses (24 × 32 mm²) were cleaned with KOH and then, immersed in 1% (3-mercaptopropyl)triethoxysilane (Momentive) in 1% acetic acid for 45 min in an incubator at 90 °C. The silanized cover glasses were washed with distilled water and dried in the incubator. The dry silanized cover glasses were immersed in a mixture of 0.1 mg/mL biotin–PEG 5000–maleimide (Nektar Therapeutic) and 10 mg/mL mPEG 2000–maleimide (NOF Corporation) in 10 mM Hepes (pH 7.5). The reaction time was 2 h. The biotinylated PEG-coated cover glasses were washed and stored in water.

A flow chamber (5–8 μL) was made using a biotinylated PEG-coated cover glass (24 × 32 mm²) and an untreated cover glass (18 × 18 mm²). Streptavidin (1 mg/mL; Wako Pure Chemical Industries, Ltd.) was infused into the flow chamber. After incubation for 5 min, the excess streptavidin was washed out with 40 μL F₁ buffer (10 mM Mops, pH 7.0, 2 mM MgCl₂). Then, 20–50 pM AviTagF₁(βE190D)-Cy3Cy5 (40 μL) in F₁ buffer was infused into the flow chamber. After incubation for 5 min, the unbound F₁ was washed out with 40 μL F₁ buffer containing ATP, an ATP regeneration system (0.02 mg/mL creatine kinase, 0.082 mg/mL creatine phosphate), and an oxygen-scavenging system (4.5 mg/mL glucose, 0.32 mg/mL glucose oxidase, 20 U/mL catalase, 1% β-mercaptoethanol). Observations were made at 24 °C ± 2 °C.

Streptavidin-Conjugated Beads.

We used streptavidin-conjugated beads to observe rotation of the biotinylated γ-subunit. Streptavidin was conjugated with carboxylated polystyrene beads (diameter = 220 nm; Polyscience) using 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC; Thermo Scientific) and N-hydroxysulfosuccinimide (sulfo-NHS; Thermo Scientific). Briefly, the polystyrene beads (about 30 fmol) were diluted to 3 nM with F₁ buffer (10 mM Mops, pH 7.0, 2 mM MgCl₂) and then, reacted with EDC (1–4 mg/mL) and sulfo-NHS (1–4 mg/mL) for 30 min at room temperature. Excess EDC and sulfo-NHS were removed by centrifugation, and the pellet was dissolved in 10 mM Hepes, pH 8.0. Then, streptavidin (0.1 mg; Wako Pure Chemical Industries, Ltd.) was added to the bead solution and reacted for over 2 h at room temperature. The streptavidin-conjugated beads were purified by centrifugation.

Simultaneous Measurement of Single-Pair FRET and Rotation.

A flow chamber (5–8 µL) was made from a KOH-treated cover glass (24 × 32 mm²) and an untreated cover glass (18 × 18 mm²). The biotinylated and fluorescently labeled F₁ was diluted to 20–50 pM with F₁ buffer, then infused into the flow chamber, and incubated for 5 min. The unbound F₁s were washed out with 40 µL 10 mM potassium phosphate buffer, pH 7.0. Streptavidin-conjugated beads (diameter = 220 nm) in 10 mM potassium phosphate buffer (pH 7.0) were then infused into the flow chamber and incubated for 10 min. The unbound beads were washed out with 40 µL F₁ buffer containing ATP or ATPγS (Roche) with an ATP-regenerating system and an oxygen-scavenging system. Note that, in the assay with ATPγS, the ATP-regenerating system was not included in the assay buffer. Observations were made at 24 °C ± 2 °C.

Systematic Structure Comparison.

The analysis was performed as described previously (19). Five PDB files of F₁ were used: ID codes 1BMF (4), 1H8E (48), 2JDI (38), 4ASU (49) (bovine F₁), and 3OAA (41) (E. coli F₁). First, the sequences of α- and β-subunits were aligned using ClustalW. Second, we superimposed the αβ-structures with Cα-atoms, ignoring gap/insertion regions and missing residues. For the α-subunits, residues of bovine F₁ (E. coli F₁), namely 26–187 (26–187), 196–313 (188–305), 314–318 (310–314), 319–401 (322–404), and 410–508 (413–511), were used. For the β-subunits, residues of bovine F₁ (E. coli F₁), namely 10–25 (2–17), 26–126 (19–119), 129–206 (122–199), 213–245 (200–232), 247–387 (233–373), and 396–464 (382–450), were used. The superimposed coordinates were analyzed using PCA.