Stability versus exchange: a paradox in DNA replication

Abstract

Multi-component biological machines, comprising individual proteins with specialized functions, perform a variety of essential processes in cells. Once assembled, most such complexes are considered very stable, retaining individual constituents as long as required. However, rapid and frequent exchange of individual factors in a range of critical cellular assemblies, including DNA replication machineries, DNA transcription regulators and flagellar motors, has recently been observed. The high stability of a multi-protein complex may appear mutually exclusive with rapid subunit exchange. Here, we describe a multisite competitive exchange mechanism, based on simultaneous binding of a protein to multiple low-affinity sites. It explains how a component can be stably integrated into a complex in the absence of competing factors, while able to rapidly exchange in the presence of competing proteins. We provide a mathematical model for the mechanism and give analytical expressions for the stability of a pre-formed complex, in the absence and presence of competitors. Using typical binding kinetic parameters, we show that the mechanism is operational under physically realistic conditions. Thus, high stability and rapid exchange within a complex can be reconciled and this framework can be used to rationalize previous observations, qualitatively as well as quantitatively.

INTRODUCTION

Cells depend on an array of sophisticated multi-protein machines performing diverse functions, ranging from nucleic-acid metabolism to membrane transport. The grouping of enzymes with specialized functions within these assemblies leads to greater coordination, accuracy and efficiency, thus conferring evolutionary advantages. Textbook models often present these complexes as stable machines catalyzing sequential reactions repeatedly and for extended periods—much like devices we use in our everyday lives. However, the cellular world is restricted by a different set of operating principles. Many of these assemblies must operate continually to ensure cell survival, even in the face of altered protein levels or rare molecular configurations that could lead to stalling. These requirements demand a combination of high stability of the complex while allowing for rapid subunit exchange and reformation events. The design principles that allow molecular machines to balance these competing interests remain poorly understood.

A hallmark example of a dynamically operating system evolved to balance the competing demands of the molecular world within cells is the replisome, the machine responsible for copying DNA in all living organisms. Replisomes are composed of a series of individual proteins that together orchestrate a complex sequence of reactions to generate two daughter DNA molecules from one parent. A multitude of protein–protein interactions, displaying a wide variety of affinities from low pM to high μM, encode replisomes with rapidly evolving dynamics characterized by constant exchange and recycling of components. These kinetic properties are further modulated by changes in external conditions such as protein concentration and nucleotide availability.

Early studies revealed that replisomes are highly stable. Experiments on replication systems from bacteriophages T4 (1,2) and T7 (3), as well as Escherichia coli (4), have shown that replisomes continue operation for extended periods, even when challenged by dilution. However, more recent studies suggest that in the presence of DNA polymerases in solution, the polymerases associated with the replisome at the start of the reaction exchange with those in solution within tens of seconds to minutes (5–7). Exchange has also been observed between different types of polymerases (8–10), a mechanism that is thought to be key to the restart of replication after encounters with lesions in the DNA. These observations challenge the view of the replisome as a stable complex, rather suggesting a much more dynamic picture. It is, however, not clear what molecular mechanisms explain the seemingly contradictory observations of stability under dilution versus exchange.

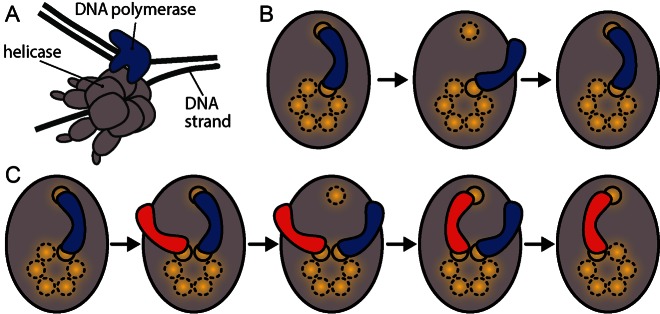
A qualitative explanation for how the replisome could balance stability with exchange emerges when considering several recent studies of polymerase dynamics and the molecular contacts that ensure their attachment within replisomes. The presence of multiple attachment points retaining the DNA polymerase within the replisome has previously been proposed to support polymerase exchange. Benkovic and coworkers suggested that a DNA polymerase from solution does not have to await complete dissociation of a replisome-bound polymerase before binding itself, but can bind to the complex while the original polymerase is still there, to later replace it at the site of DNA synthesis (5). Later, single-molecule visualization of DNA polymerase exchange (7,11) led us to suggest that multiple binding sites for polymerases within the replisome could—at least qualitatively—reconcile finding that a complex is highly stable under dilution with the observation that components exchange (12). The bacteriophage T7 replisome (Figure 1A), illustrates the central idea: The DNA polymerase (blue) associates with the replisome through two contacts: one with the hexameric helicase (gray; with six potential binding sites) and the other with the primer-template DNA (black; a single binding site). Dissociation of the original polymerase from either site still leaves it bound to the other site. In the absence of competing DNA polymerases in solution, the protein will simply rapidly re-bind, before unbinding from the second binding site leads to complete dissociation (Figure 1B). As a result, such multisite binding confers high stability under dilution. On the other hand, in the presence of competing polymerases in solution, a competitor can bind to one of the sites as soon as it is available (Figure 1C). This binding of a second protein can then be followed by either dissociation of the incoming polymerase and rebinding of the original to its secondary binding site, or a successful exchange of the original polymerase with the incoming one. This multisite competitive exchange mechanism reconciles both observations of stability under dilution and exchange under competition. While the details differ, the binding of additional polymerases beyond the two minimally needed to support synthesis on both daughter DNA strands appears to be a general feature of other replication systems: the bacteriophage T4 replisome can bind up to three polymerases (13), and also exhibit rapid exchange (5), and the E. coli replisome can bind three polymerases (14,15).

Figure 1.

Schematic of the multisite competitive exchange mechanism, supporting stability in the absence of competing binding molecules, and exchange in their presence. (A) The bacteriophage T7 replisome with the active DNA polymerase bound simultaneously to DNA and to one of six binding sites on the helicase. (B) Mechanism behind high stability in the absence of competing molecules. If a molecule (blue), which is bound to two sites, unbinds from only one site, it can rapidly rebind again. (C) Mechanism of exchange in the presence of competing molecules. If a competing molecule (red) binds to the complex, it can await unbinding of the originally bound molecule (blue) and potentially replace it.

The property of enhanced exchange under competitive conditions has been observed in many systems beyond DNA polymerases: The β clamp of the E. coli replisome is recycled in the absence of competition, while it is exchanged in the presence of β clamp in solution (16). Similarly, the eukaryotic single-stranded DNA-binding protein RPA exhibits prolonged binding under dilution but rapid exchange in the presence of competing single-stranded binding proteins (17). An entirely different example is provided by the bacterial flagellar motor, which needs to be rigid and stable to exert the required significant torque (18). Nevertheless, MotB, one of the subunits of the proton-dependent E. coli stator, exchanges rapidly with a membrane-bound pool of inactive and unbound MotB (19). Furthermore, a decreased time before dissociation of the DNA binding protein Fis has been observed when challenged by competing Fis or another DNA binding protein, HU. (20). The same observation has also been made for the DNA binding protein NHP6A being challenged by NHP6A (20). A decreased time before dissociation when challenged by competition has likewise been reported for the E. coli transcription regulator CueR, both in vitro (21) and in vivo (22). Clearly, the balance of stability versus exchange is a key operating principle for many essential molecular machines.

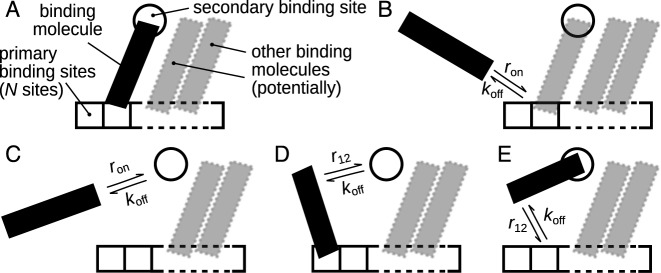
To understand how the arrangement of multiple binding sites within protein complexes could support both stability and exchange we developed a quantitative model. We consider an idealized system—inspired by the bacteriophage T7 replisome, but intended as a general framework for understanding the principles of multisite competitive exchange in many other protein assemblies—comprising two types of binding sites with a binding partner able to bind to either or both sites (Figure 2A). Similar mechanisms to ours have been recently proposed and mathematically analyzed (23,24), but differ in the basic picture they are describing and cannot be directly applied to the T7 replisome. We give analytic expressions for the dissociation time from the complex of an originally bound molecule, both in the absence (Figure 1B) and presence (Figure 1C) of competing molecules, providing insight into the general dependence on the kinetic parameters. Importantly, we show that the general mechanism is operational for physically reasonable parameters, thus suggesting that the multisite competitive exchange mechanism can indeed balance stability against exchange in multi-protein complexes.

Figure 2.

Reactions and corresponding rates for the multisite competitive exchange model. (A) Generalized multisite binding model. A molecule can bind to either or both of two types of binding sites. One of the binding site types has several, N, individual sites, to which several molecules (shaded) can bind. (B and C) Binding from solution to either a primary binding site (B) or the secondary binding site (C) occurs with rate r_on, while unbinding occurs with rate k_off. (D and E) Binding to either the secondary (D) or a primary (E) binding site when already bound to the other occurs with rate r₁₂; unbinding occurs with the same rate, k_off, as when unbinding to solution (cf. panel B and C).

MATERIALS AND METHODS

We formulate the model within a master equation formalism (25,26), where the probability, P_i(t), of the system being in a state i at time t is governed by the master equation

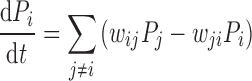(1)

Here 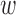_ij denotes the probability per unit time of transition from state j to state i given that it is in state j. For our cases, the system ultimately always end up in a specific final state (the state where the initially bound molecule has completely unbound), , and it is possible to define a mean life-time, τ_i, for a system starting in the initial state i. Following standard methods (25), one can show that the mean life-times fulfill

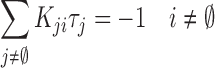(2)

which is valid for all i except the final state, 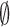, and where the summation omits the final state, 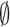. In Equation (2)

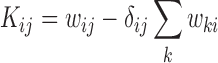(3)

For our cases, the transition probabilities, 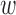_ij, are known, so K_ij is completely determined. Note also the reversal, compared to matrix multiplication, of the indices in the sum.

Equation (2) is a linear equation for the mean life-time from any initial state, and can be solved using standard methods. This allows us to write down explicit analytical solutions for all cases considered here. We used Mathematica (Wolfram Research, Inc., Champaign, IL, USA) to solve all equations.

The reaction schemes and explicit master equation systems considered in this work are somewhat verbose and have hence been delegated to the Supplementary Data (SD; Supplementary Figures S1, S4–S5 and Section Master Equation Systems).

RESULTS

Model

Our model is based upon the reactions defined in Figure 2, chosen to mimic polymerase binding and exchange within the bacteriophage T7 replisome. However, since we argue that many of the results have implications also for other systems, we have adopted a neutral nomenclature. We consider two types of binding sites in the complex, arbitrarily denoted primary and secondary, to which a molecule can simultaneously bind. We allow for several, N, primary binding sites, and only one secondary. In the T7 replisome the helicase provides the primary binding sites, its hexameric structure giving six sites (N = 6) representing the six acidic C-terminal tails that have been shown to bind the polymerase (27,28); the DNA primer-template provides the secondary binding site. Note that in deriving our results we assume that there is always at least one primary binding site, so N > 0 (and an integer) is an implicit requirement for all results presented below.

A molecule in solution can bind to either a primary (Figure 2B) or the secondary (Figure 2C) binding site with rate r_on (if the site is vacant). If a molecule is already bound to a primary binding site, it can subsequently bind to the secondary binding site (Figure 2D) with rate r₁₂ (again, if vacant) and vice versa for the secondary binding site (Figure 2E). A molecule can, however, not bind to two primary binding sites. Note that the order of binding is irrelevant and the terms primary and secondary are not meant to imply a particular order in time. We assume for simplicity that a bound molecule unbinds from either a primary or the secondary binding site with rate k_off, regardless of which site it is bound to and regardless of whether it is bound to both sites (Figure 2B–E). Note that the on rate, r_on, gives the total reaction rate and is not a microscopic rate constant. That is, we may write r_on = k_onc_bulk, where k_on is the microscopic rate constant and c_bulk the bulk concentration.

In relation to previous works, Cocco et al. consider several different models of molecules binding to DNA, focused on molecules with a large number of points of contact (10 or more), where the molecule must unbind successively from each binding site in order (23). Several primary binding sites (in our nomenclature; N > 1) have no correspondence in their models (and vice versa), and we do not assume that the molecule first unbinds from the primary and then the secondary site. Sing et al., on the other hand, consider a molecule binding at two points of contacts (24), but do not consider several (in our nomenclature) primary binding sites, an important element of the T7 replisome and which supplies an additional mechanism for exchange (see below). We also derive exact analytical expressions, rather than approximations, from which the whole regime of parameters may be studied. We hope these expressions may be of utility in future, for researchers to apply to related, and perhaps very different, systems.

For transparency, we have made several simplifications. The binding kinetics associated with a primary and the secondary site are assumed to occur with equal rates. The analysis could be generalized to the case of different affinities, but the results would be more complicated, impeding interpretation and obscuring the fundamental mechanisms. Also not included are cooperative (or anti-cooperative) effects, e.g., an increased (decreased) binding rate when several primary binding sites are already occupied (apart from prohibiting binding to an already occupied site). Such effects provide an alternative (not necessarily exclusive) mechanism for exchange, as has been observed for the E. coli single-stranded DNA binding protein (29).

The model is conceptually simple, but explicit listing of all states of the system and transitions among them requires significant space. The Methods section gives technical details on the solution and the SD shows full reaction schemes and equation systems (Supplementary Figure S1, S4–S5 and Section Master Equation Systems).

Stability under dilution

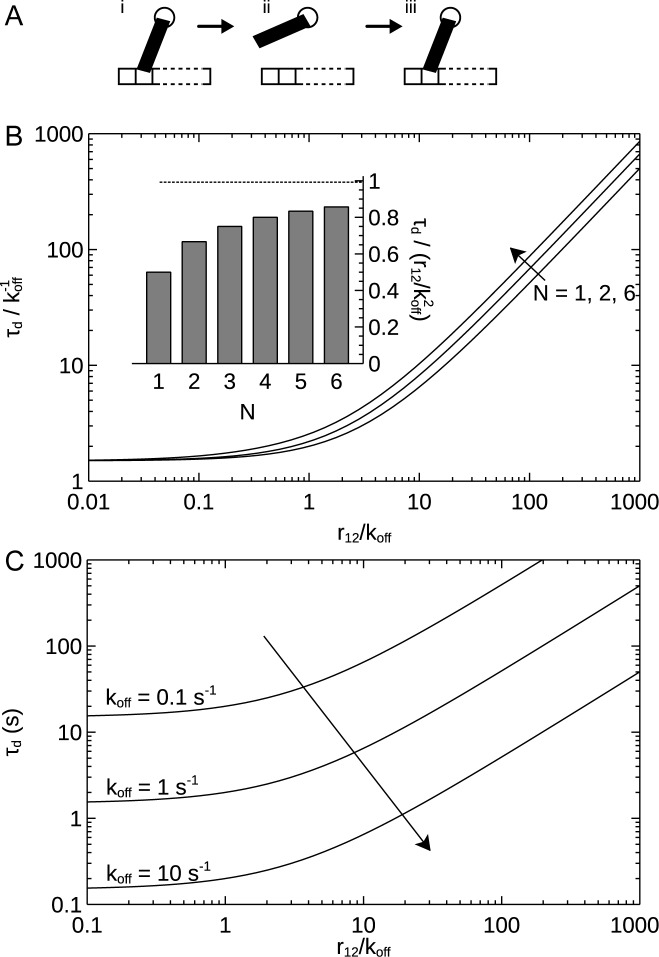
We start by considering the stability of a complex under infinite dilution, that is, the dissociation time of an already bound molecule in the absence of other competing molecules seeking to bind to the complex. The qualitative mechanism is illustrated in Figure 3A; when a molecule is bound to two sites (i), it can unbind from one (ii) while still remaining associated to the complex. If re-binding to the first site is rapid, simultaneous unbinding from the second is improbable and the most likely outcome is that the molecule simply re-binds (Figure 3A, iii). In this way the complex may be rendered stable, not due to particularly strong binding affinities, but rather due to the presence of two binding sites.

Figure 3.

Effect of multiple binding sites on stability in the absence of binding partners in solution (infinite dilution). (A) Schematic illustrating the mechanism of increased stability. (B) Dissociation time in dimensionless form with times measured in multiples of the dissociation time of a single site (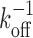). Arrow shows direction of increasing number of primary binding sites (N). (Inset) Dependence on the number of primary binding sites (when r₁₂/k_off is large). (Dotted line) Limit of an infinite number of primary binding sites. (C) Dissociation time in physical units. Arrow shows direction of increasing off rate (k_off). Only one primary binding site is considered (N = 1). Main graphs calculated using Equation (4); panel B inset using Equation (5).

The dissociation time is calculated using as initial state the molecule bound to both a primary and the secondary sites (Figure 3A, i), and determining the time it takes the molecule to completely unbind from the complex. We neglect binding from solution (r_on = 0) due to the absence of competing molecules (infinite dilution). The dissociation time is stochastic and we calculate its mean, τ_d. The calculation is described in Methods and the full reaction scheme and equation system can be found in SD [Supplementary Figure S1 and Equation (S1); the reaction scheme and results for completely general kinetic coefficients are given in Supplementary Figure S2 and Equation (S3–S4)]. The dissociation time is given by

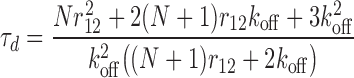(4)

Unsurprisingly, the dissociation time, τ_d, depends on both the unbinding rate, k_off, as well as the rate of re-binding, r₁₂. If there were only a single binding site (i.e., not both primary and secondary sites) then the dissociation time would clearly just be the inverse unbinding rate, 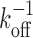. To facilitate comparison of different systems and show the general features, the results are thus presented in dimensionless form by expressing all times in terms of this rate. Since the dissociation time also depends on the number of primary binding sites, results are shown for several different numbers of primary binding sites (N = 1,2 and 6).

Figure 3B shows that the dissociation time is greatly enhanced if re-binding is rapid compared to unbinding (r₁₂/k_off is large) as suggested by the qualitative mechanism (Figure 3A). However, Figure 3B also gives the quantitative estimate that the stability of the complex is increased by an order of magnitude for each order of magnitude re-binding (r₁₂) is more rapid than unbinding (k_off)—a highly significant effect.

We can explicitly consider the regime in which re-binding is rapid compared to unbinding (r₁₂/k_off is large); to first non-vanishing order we find

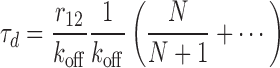(5)

This simple expression shows that the increase in stability is essentially given by the factor r₁₂/k_off, modulated by the number of primary binding sites, N. The general form of this result is preserved also when unbinding occurs with unequal rates depending upon if the molecule is attached to one or two types of sites [see Equation (S6)]. The straight lines for r₁₂/k_off > 20−30 in Figure 3B represent this regime. Interestingly, the dependence on the number of primary binding sites is rather weak (cf. the lines for different N in Figure 3B). The inset in Figure 3B shows explicitly the N/(N + 1) dependence, suggesting that beyond two to three sites there is little extra to be gained in stability by having additional sites. We may understand Equation (5) in terms of a quasi-steady-state approximation (cf. the Briggs-Haldane approximation to the Michaelis–Menten mechanism), as shown in SD (Section Stability under Dilution in the Limit of Rapid Re-Binding).

We may also explicitly study the opposite regime in which re-binding is slowly compared to unbinding (r₁₂/k_off is small), where we find to first non-vanishing order 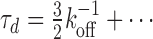Again, one finds a very similar result also when unbinding occurs with unequal rates depending upon if the molecule is attached to one or two types of sites [see Equation (S7)]. Naturally, there is no increase in stability under these conditions, and the results are independent of the number of primary binding sites. These observations are clearly consistent with Figure 3B, and can easily be understood in detail (Supplementary Figure S3). This may be used to evaluate the kinetic coefficient, k_off, experimentally, if one can argue that re-binding is slowly compared to unbinding so that this limit applies.

To illustrate the results more concretely, Figure 3C shows the dissociation time in physical units, showing that when re-binding is slow compared to unbinding, the stability is not significantly increased, while if re-binding is more rapid than unbinding, an increase in stability of many orders of magnitude can be achieved. Naturally, overall stability becomes lower as the rate of unbinding (k_off) increases (Figure 3C; arrow).

It is worthwhile to put this into a numerical perspective to later compare to a scenario with competing binding partners. Given an unbinding rate of a single site of k_off = 0.1 s⁻¹ and a re-binding rate of r₁₂ = 100 s⁻¹, the presence of a secondary binding site apart from a single primary site (N = 1) increases the mean dissociation time from 10 s to more than an hour (Supplementary Table S1 summarizes the outcomes). The effect is clearly significant and operational for physically realistic parameters.

Stability under competition from other binding molecules

We continue with the stability of the complex under competition from other molecules seeking to bind to it. In contrast to the case of stability under infinite dilution (above), the dependence on the number of primary binding sites is less trivial and the mathematics becomes more involved with a higher number of binding sites [e.g., see the full expression given for N = 2 in SD Equation (S13–S15)]. We consequently limit much of the explicit calculations to lower numbers of binding sites.

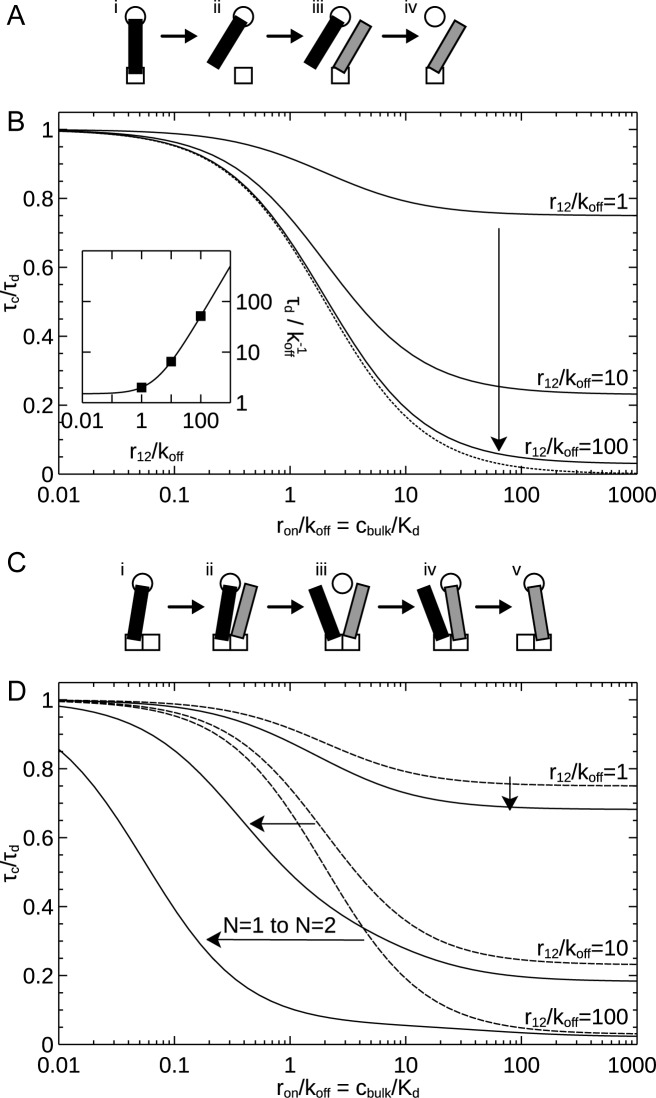
We start by considering the simplest case of only a single primary binding site (N = 1). Figure 4A illustrates the qualitative mechanism behind the lowered stability compared to the scenario in which no competing molecules are available: When a molecule is bound to both the primary and secondary binding site (i), the molecule can unbind from one site (ii) thus allowing a competing molecule to bind to it (iii). This event is only probable if binding from solution is sufficiently rapid; otherwise, the originally bound molecule would simply re-bind, and the situation would be the same as in the absence of competition (cf. Figure 3A). However, if the newly bound molecule remains long enough for the originally bound molecule to completely unbind (Figure 4A, iv), this mechanism allows complete exchange of the originally bound molecule.

Figure 4.

Effect of multiple binding sites on stability under competition. The exchange time (τ_c) is normalized to the dissociation time under dilution (τ_d), and is shown as a function of the binding rate of competitors from solution relative to the unbinding rate (r_on/k_off) or, equivalently, the bulk concentration of competitors over the dissociation constant (c_bulk/K_d). (A) Schematic illustrating the exchange mechanism available in the case of a single primary binding site. (gray) competing molecule. Naturally, the same process can take place on the secondary binding site. (B) Exchange time with one primary binding site (N = 1). Arrow shows direction of increased stability under dilution (r₁₂/k_off). Results calculated using Equations (4) and (6). (Dotted line) Approximation valid for a complex very stable against dilution (large r₁₂/k_off), calculated from Equation (7). (Inset) Dissociation time under dilution duplicated from Figure 3B. Symbols indicate parameters (values of r₁₂/k_off) considered in the main graph. (C) Schematic illustrating the novel mechanism present with several primary binding sites (N > 1). (D) Exchange time with two primary binding sites (N = 2). (Solid lines) Two primary binding sites. (Dashed lines) Results for one primary binding site duplicated from panel B; arrows indicate change from one to two sites. Results for N = 2 calculated using SD Equation (S13–S15).

The exchange time is calculated similarly to above, except that we now allow binding from solution (r_on > 0) and we consider as the final state any state in which the originally bound molecule is no longer bound, regardless of whether a competitor is bound or not. The calculation is described in Methods and the full reaction scheme and equation system are given in SD (Supplementary Figure S4 and Section Master Equation Systems). The mean exchange time is given by

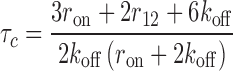(6)

The exchange time depends both on the strength of competition, as well as on how stable the complex is in the absence of competitors (i.e., under dilution). We measure the strength of competition with the binding rate from solution normalized to the unbinding rate (r_on/k_off) or, equivalently, the bulk concentration over the dissociation constant of a single site (c_bulk/K_d). To more explicitly show the impact of competition, the results have been normalized to the stability in the absence of competition (τ_d) and are shown for several different values of the parameters (r₁₂/k_off) that result in different stabilities under dilution (for ease of reference, the corresponding stability under dilution is duplicated, with identical values of the parameters indicated).

Figure 4B shows that when competition is weak (r_on/k_off is small)—either because the microscopic binding rate constant of the competitors is small, or because their concentration is low—the stability of the complex is not changed compared to that under dilute conditions, as expected. However, as competition is increased (r_on/k_off becomes larger)—either because the microscopic binding rate constant of the competitors is large, or because their concentration is increased well above the dissociation constant—the stability decreases progressively with increased competition. This is particularly notable with parameters that give a highly stable complex under dilution (r₁₂/k_off = 10 and 100 in Figure 4B), where the stability rapidly declines with increased competition. This observation is the key outcome of our model: a complex that binds a protein using two binding interactions is highly stable against dilution but is rendered unstable under competition.

To put this into physical units, let us use our previous numerical example with a single site unbinding rate k_off = 0.1 s⁻¹ and a re-binding rate of r₁₂ = 100 s⁻¹. This situation corresponds to r₁₂/k_off = 1000 and gave a dissociation time under dilute conditions of more than an hour (Supplementary Table S1). Figure 4B suggests that this stable complex can nevertheless be made to exchange at a time scale of 2  min, by having a bulk concentration of competing molecules 100-fold higher than the dissociation constant (Supplementary Table S1 summarizes the outcomes). Again, we find that the mechanisms are operational for physically realistic parameters.

Another interesting observation is that the exchange time reaches a lower plateau, that is, there exists a minimum time for how rapidly competitors can displace the originally bound molecule, even when competition is very strong (r_on/k_off is large in Figure 4B). We can study this regime by keeping r₁₂/k_off finite while expanding in k_off/r_on, giving 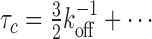This result agrees exactly with the stability under dilution in the slow re-binding limit. The explanation is that when competition is very strong, then as soon as the originally bound molecule has let go of a site a competitor will occupy it. In other words, the originally bound molecule will never re-bind, and the analysis of the limit that re-binding is slow under dilution applies (see Supplementary Figure S3 for details). In particular, this argument implies that the result is, in fact, valid for a general number of primary binding sites, N. Thus, the minimum time for displacing the originally bound molecule by competition is , regardless of the number of primary binding sites.

Interestingly, the effect of competition is larger for complexes that are more stable under dilute conditions; compare upon increasing competition the small decrease in relative stability of the unstable complex (r₁₂/k_off = 1) with the large decrease in relative stability of the much more stable complex (r₁₂/k_off = 100) (Figure 4B). This follows from the observation (previous paragraph) that the minimum displacement time of the originally bound molecule only depends on the unbinding rate, k_off. This implies that the response to increasing competition always tends to the same limit, which on a scale relative to the stability under dilution (Figure 4B) gives a higher effect of competition for a complex that is stable under dilution.

In the limit of a highly stable complex, we arrive at a particularly simple analytical result; keeping r_on/k_off finite while expanding in k_off/r₁₂, we find to first non-vanishing order

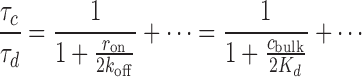(7)

which shows how the factor r_on/k_off = c_bulk/K_d determines the decrease in stability in a straightforward way. Figure 4B shows this result (dotted line), where it can also be observed how the approximation becomes increasingly better with increased stability (r₁₂/k_off is large). If a system warrants the underlying assumption (that the complex is highly stable against dilution), Equation (7) can be used to evaluate the dissociation constant, K_d, from corresponding experimental data in a straightforward manner. Note, however, that this result is only valid for one primary binding site (N = 1).

Turning to the case of two primary binding sites (N = 2), it is now possible that while the original molecule is still bound to both a primary and the secondary site (Figure 4C, i) a competitor binds to the empty primary site (ii). The competitor may then await the unbinding of the originally bound molecule from the secondary site (iii) and subsequently bind to it (iv). If the originally bound molecule then unbinds, full exchange has taken place (v). This provides an additional mechanism for exchange, apart from that present with a single primary binding site (Figure 4A).

As before, the calculation of the exchange time is described in Methods with the full reaction scheme and equation system in SD (Supplementary Figure S5 and Section Master Equation Systems); the final expression is, however, too long to reproduce here and can instead also be found in SD [Equation S(13-15)].

Figure 4D shows the exchange time with two primary binding sites (N = 2; solid lines) compared to the corresponding results for one site (N = 1; dashed lines) with the same normalizations as in Figure 4B. The presence of another primary binding site does not influence the general qualitative conclusions that increasing competition—either from a high microscopic binding constant of the competing molecule, or from a high concentration—decreases the stability of the complex, and that this effect is more pronounced for a complex that is stable against dilution (r₁₂/k_off large). However, it does change the quantitative behavior such that a complex with two primary binding sites is more susceptible to competition than a complex with a single primary binding site (arrows). This is in line with the existence of a new mechanism for displacement (Figure 4C) and is particularly large under conditions where the complex is stable against dilution (r₁₂/k_off large). Finally, we may corroborate the observation that there is a minimum time for replacing an originally bound molecule (the plateau for high r_on/k_off in Figure 4D).

DISCUSSION

We present here a quantitative model for the stability of multi-protein complexes in the absence and presence of competing binding molecules. The main outcome is that for physically realistic parameters, it is possible to have a complex that is highly stable under dilution, yet rapidly exchanges in the presence of competition. The molecular requirement to achieve such behavior is the presence of two points of interaction that retain a binding partner to a complex.

In more detail, we found that the stability under dilution of a complex with two types of binding sites can be increased by a factor of (r₁₂/k_off)N/(N + 1) by having a higher re-binding rate (r₁₂) compared to the unbinding rate (k_off). Such a scenario would increase the stability by orders of magnitude (Figure 3). On the other hand, a complex that is stable under dilution may exchange in the presence of competing molecules seeking to bind to it. The effect is large; when the (bulk) concentration of competing molecules is above the dissociation constant of a single site, the stability rapidly decreases (Figure 4B). Interestingly, the phenomena are positively correlated, that is, the more stable a complex is under dilution, the more prone to exchange it is under competition. We also found a very weak increase in stability against dilution with increasing number of primary binding sites beyond 2–3. For stability, it would thus appear less costly to evolve a rapid re-binding rate, r₁₂, rather than more binding sites.

While we stress the general nature of the multisite competitive exchange mechanism, it is useful to briefly quote numerical results for the bacteriophage T7 replisome (Figure 1A). Here, the unbinding rate from the helicase has been measured to be k_off = 1/(44 s) while the re-binding rate must at least be quicker than r₁₂ = 1 s⁻¹, because individual unbinding events are not observed (7). The unbinding rate from the primer is unknown, but let us use k_off = 0.1 s⁻¹ for both sites. For six binding sites (N = 6) we find a dissociation time in the absence of competition of 103 s, compared to approximately 125 s measured experimentally (7). Under competition we use the results for two binding sites. With a dissociation constant of K_d = 1 nM (and otherwise equal parameters) we find that a 10 nM bulk concentration of competitors decreases the life-time from 82 to 23 s, again in general agreement with experiments (7).

In our model simultaneous binding can only occur between one of six helicase binding sites and a single priming site. However, in reality polymerase binding to the helicase is likely to be more complex. Each subunit of the T7 gp4 helicase is known to have multiple distinct polymerase binding sites for leading-strand synthesis, lagging-strand synthesis and exchange (30). Whether all these sites can be simultaneously occupied or are mutually exclusive is not known, but given their close proximity it may be more useful to consider them as part of larger binding surfaces on the helicase as opposed to explicit sites. In this case, polymerase rearrangements on the helicase surface could lead to dynamic changes in the available binding surfaces in the absence of polymerase dissociation which could provide another means to enhance the stability of the polymerase-helicase association. Beyond these additional considerations, DNA itself may act more like an extended binding surface then a single-binding site, given that the lagging strand emerging from the helicase must be continuously sampled to locate sites for primer synthesis, multiple priming events may occur simultaneously and DNA sliding has been observed for several replication factors (31,32). While modeling these diverse behaviors will require more parameters and lead to more complexity, we expect these additional binding surfaces to function in the same way. In all cases, multiple points of contact provide both more stability in the absence of competition, and faster exchange in the presence of competing factors.

We may also compare our results to the increased dissociation rate with increasing competition reported experimentally for Fis binding to DNA (20). Previous efforts have modeled this using either 14 binding sites and a binding energy of 1.95k_BT (23), or two binding sites and a binding energy of 12.3k_BT (24), respectively; in both cases k_B is the Boltzmann constant and T the absolute temperature. Our model is rather formulated in terms of kinetic constants and since Fis binds two adjacent sites on the DNA we may proceed by assuming a single primary binding site (N = 1). Inverting Equation (7) then predicts a linear behavior of τ_d/τ_c with increasing concentration of competitors. Since τ_d is a constant, this implies a linear increase of the dissociation rate, 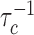, with increasing concentration of competitors, as indeed observed experimentally (20). From the same data, we may evaluate the dissociation constant of a single site to be K_d = 7.5 nM. Assuming diffusion-limited reaction kinetics, for which k_on ∼ 10⁹ M⁻¹s⁻¹, we can then estimate k_off = K_dk_on ∼ 7.5 s⁻¹. According to Equation (5) [which is valid in the same limit we are working in] 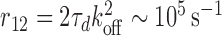, implying that the time-scale for re-binding to a second site after having unbound from one is around 10 ms. This is rather rapid, but still orders of magnitude slower than the time-scale given by the rotational diffusion coefficient of a molecule of size R = 1 nm (given by ηR³/(k_BT) ∼ 0.2 ns, where η is the viscosity of water).

As for the functionality of the multisite competitive exchange mechanism, we note that a complex with a single binding site would have a minimum time for a bound molecule to dissociate given by 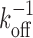, which cannot be overcome by increased competition. Consequently, if a bound molecule is on occasion needed to be removed swiftly, then this requirement would demand a high unbinding rate, k_off. However, rapid unbinding will obviously decrease the stability of the complex also in situations where it is desired. Having multiple binding sites satisfies these opposing demands—with limited compromises. With several binding sites, the minimum time to remove an initially bound molecule under competition increases only by a factor of order unity to 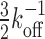, while giving a gain in stability of (r₁₂/k_off)N/(N + 1). In the case of DNA replication, having a stable complex allows for rapid replication of DNA, while rapid exchange allows DNA polymerases to be momentarily exchanged for specialized counterparts optimized for repair if damage is detected (8–10). Similarly, a stable flagellar motor allows efficient motion, while exchange could allow switching between different modes [many bacterial species possess more than one type of stator that give motors different functionalities (18)]. The dual nature of multi-protein complexes—high stability but with the possibility of exchange under competition—thus likely plays critical functional roles in the cell.

FUNDING

European Research Council [281098 to A.M.v.O.]; Dutch Science Foundation [680-47-607 to A.M.v.O.]. Funding for open access charge: European Research Council [281098 to A.M.v.O.].

Conflict of interest statement. None declared.