Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2016 Apr 22;44(10):4528–4538. doi: 10.1093/nar/gkw311

How topoisomerase IV can efficiently unknot and decatenate negatively supercoiled DNA molecules without causing their torsional relaxation

Eric J Rawdon 1,*,†, Julien Dorier 2,3,†, Dusan Racko 2,4,5, Kenneth C Millett 6, Andrzej Stasiak 2,4,*
PMCID: PMC4889953  PMID: 27106058

Abstract

Freshly replicated DNA molecules initially form multiply interlinked right-handed catenanes. In bacteria, these catenated molecules become supercoiled by DNA gyrase before they undergo a complete decatenation by topoisomerase IV (Topo IV). Topo IV is also involved in the unknotting of supercoiled DNA molecules. Using Metropolis Monte Carlo simulations, we investigate the shapes of supercoiled DNA molecules that are either knotted or catenated. We are especially interested in understanding how Topo IV can unknot right-handed knots and decatenate right-handed catenanes without acting on right-handed plectonemes in negatively supercoiled DNA molecules. To this end, we investigate how the topological consequences of intersegmental passages depend on the geometry of the DNA-DNA juxtapositions at which these passages occur. We observe that there are interesting differences between the geometries of DNA-DNA juxtapositions in the interwound portions and in the knotted or catenated portions of the studied molecules. In particular, in negatively supercoiled, multiply interlinked, right-handed catenanes, we detect specific regions where DNA segments belonging to two freshly replicated sister DNA molecules form left-handed crossings. We propose that, due to its geometrical preference to act on left-handed crossings, Topo IV can specifically unknot supercoiled DNA, as well as decatenate postreplicative catenanes, without causing their torsional relaxation.

INTRODUCTION

Bacterial DNA topoisomerase IV (Topo IV) is responsible for the decatenation of freshly replicated circular DNA molecules (1,2). Topo IV belongs to the type II DNA topoisomerases, which perform passages of two duplex DNA segments through each other. During the reaction, Topo IV binds first to one DNA region and then drives the passage of another DNA region through a transient cut introduced in the first region. After the passage, the transient cut is resealed (3). The passage is driven by the energy gained from ATP hydrolysis and is orchestrated by a complex sequence of conformational changes in the enzyme. Topo IV has to solve a particularly difficult problem. On one hand, Topo IV has to perform intersegmental passages resulting in the decatenation of freshly replicated circular double-stranded DNA molecules that wind around each other in a right-handed way (4–9). On the other hand, Topo IV should not perform intersegmental passages within interwound portions of supercoiled DNA molecules where the opposing DNA segments also wind around each other in a right-handed way (5). Locally, the structure of the regions where the catenated DNA molecules wind around each other are very similar to the plectonemic regions in negatively supercoiled DNA (see Figure 1). However, the topological consequences of passages are different. Passages between duplex segments belonging to two different molecules lead to their progressive decatenation, which is necessary for segregation of freshly replicated DNA molecules. On the other hand, intramolecular passages between duplex segments in plectonemically wound negatively supercoiled DNA molecules lead to their progressive relaxation, which is an undesired effect. Supercoiling is actively maintained by bacterial cells since, among other roles it plays, it is required to facilitate DNA replication and transcription (10). If Topo IV were efficient in relaxing negatively supercoiled DNA molecules, this relaxation would result in a metabolic short circuit. The relaxation of negatively supercoiled DNA molecules would be followed by the action of DNA gyrase that, using the energy gained from ATP hydrolysis, would act to reestablish the original level of negative supercoiling (11). Negatively supercoiled molecules then again would be relaxed by topoisomerase IV in a reaction that also uses ATP. Such a metabolic short circuit would be harmful for cells as it would deplete the available ATP.

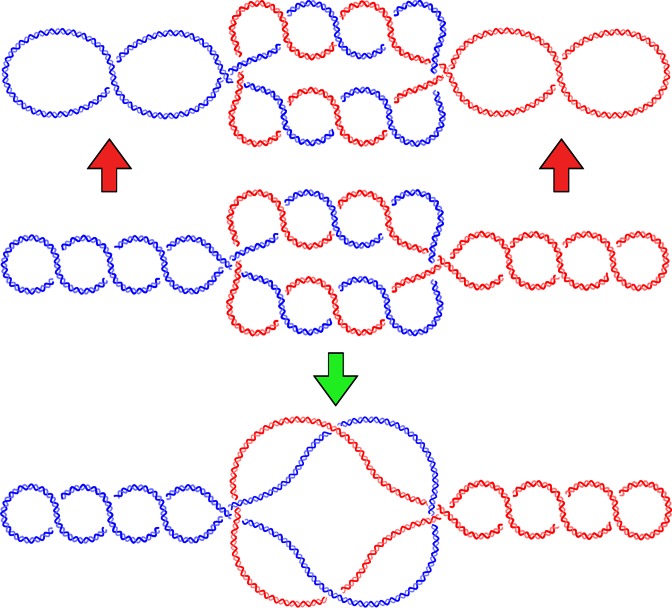
Figure 1.

Figure 1.

Open in a new tab

Topo IV needs to distinguish between right-handed intertwinings of DNA duplexes resulting from postreplicative catenation and those resulting from negative supercoiling. A schematic presentation of supercoiled postreplicative catenanes is shown in the center. Two newly replicated circular DNA molecules (red and blue) form multiply interlinked right-handed catenanes. The molecules also are supercoiled, which results in the formation of right-handed plectonemes. Local structural cues guide Topo IV to perform passages resulting in progressive decatenation (green arrow) and to avoid passages within the interwound portions (red arrows) that would result in a harmful relaxation of the negative supercoiling.

It has not yet been firmly established how Topo IV distinguishes between right-handed intertwinings of two duplex DNA regions in catenanes versus intertwinings in supercoiled DNA molecules.

In addition to its role in the decatenation of postreplicative catenanes, Topo IV (1,2) also plays an important role in the relaxation of positive supercoils arising ahead of active replication forks and also ahead of transcribing RNA polymerases (12,13). Without efficient relaxation of positive supercoiling, DNA replication and transcription would be strongly inhibited (12,14). Experiments performed in vitro showed that Topo IV is ∼20 times more active in the relaxation of positive supercoiling than in the relaxation of negative supercoiling (15). It has been proposed that these differences in the activity on positively and negatively supercoiled DNA result from the enzyme's preference for DNA juxtapositions in which the juxtaposed segments wind around each other in a left-handed way and have the geometry typical for the plectonemes formed in positively supercoiled DNA (4). In principle, such a preference should make Topo IV inefficient in resolving right-handed postreplicative catenanes. However, this is not the case. The puzzle as to how Topo IV can act efficiently on left-handed duplex-duplex windings in positively supercoiled DNA and still can be active in resolving right-handed postreplicative catenanes is known as the Topo IV paradox (6).

Topo IV also has the ability to unknot DNA molecules preferentially and thus to decrease the knotting level much below the level that would result from random intramolecular passages (16). While unknotting of DNA molecules may seem less vital than the decatenation of freshly replicated DNA molecules, DNA knots need to be removed efficiently by DNA topoisomerases or else the knots would interfere with transcription and DNA replication (17,18). In fact, DNA knots frequently form during the replication of circular DNA (19). Unknotting and decatenation of freshly replicated DNA molecules occur concomitantly in vivo and Topo IV is the enzyme involved in the two processes (20). The preferential targeting of DNA knots by Topo IV was proposed to result from enzyme selectivity for the juxtapositions involving strongly bent DNA (21–24). This proposal was confirmed when the solved structure of Topo IV bound to DNA revealed that the bound G segment is strongly bent within the protein (3). The G segment is the DNA region that is first bound by a topoisomerase and then cut to serve as the Gate for the passage of the T segment that is Transferred through the gate.

In bacterial cells, the DNA is bent significantly due to topological constraints such as supercoiling or catenation (see Figure 1). When Topo IV, binds to DNA, which is already bent, the lowest energy state is reached when the enzyme positions itself in such a way that the DNA bending due to supercoiling, knotting, or catenation is best accommodated into the enzyme binding site, which imposes DNA bending (25). The azimuthal orientation of Topo IV on the bent G segment is such that it only can capture potential T segments that are inside of the bend formed by the G segment (3). For the DNA-DNA passage, the T segment needs to be captured by the Topo IV before passing through the entry and exit gates of the enzyme. The passages can happen efficiently when the G segment, which determines the spatial orientation of Topo IV, and the T segment are in a suitable angular inclination with respect to each other. The dependence of Topo IV activity on the inclination or crossing angle (θ) between the G and T segment was investigated earlier (4,6,15). However, these earlier studies did not consider cases where the torsional tension due to supercoiling was acting on knotted and catenated DNA molecules as is the case of DNA in bacterial cells.

Topo IV's geometrical/structural selectivity for intersegmental passages was presumably under strong evolutionary pressure until it reached the best compromise between three requirements: (i) selective decatenation of negatively supercoiled DNA molecules without causing their torsional relaxation; (ii) selective unknotting of supercoiled DNA molecules without causing their torsional relaxation; (iii) efficient relaxation of positively supercoiled DNA but not of negatively supercoiled DNA.

Using numerical simulations, we investigate the possible geometrical selectivity of Topo IV that satisfies these three requirements.

MATERIALS AND METHODS

Metropolis Monte Carlo

We model circular DNA chains of length 3 kb and diameter 3 nm with bending and torsional stiffness. The diameter of 3 nm represents the effective diameter of DNA under conditions where DNA charges are strongly, but not completely, screened, such as is the case in vivo (26–28). Supercoiling was introduced by imposing various levels of linking number difference (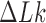Inline graphic).

DNA chains were modeled as circular beaded chains, each with N hard-core beads of diameter σ centered at the vertices 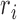Inline graphic of an equilateral polygon having N edges of length σ. For a given chain configuration, the total energy is defined as

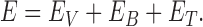graphic file with name M3.gif

The hard-core steric repulsion is given by

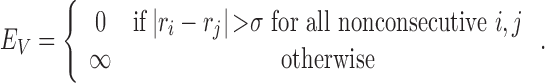graphic file with name M4.gif

The bending stiffness is imposed by the usual bending energy term

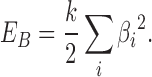graphic file with name M5.gif

where 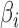Inline graphic is the bending angle

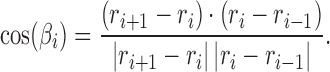graphic file with name M7.gif

Torsional stiffness is imposed by the energy term proposed by Vologodskii et al. (29)

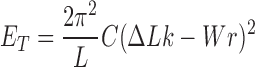graphic file with 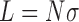name M8.gif

with Inline graphic the chain length, 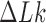Inline graphic the delta linking number, and 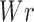Inline graphic the writhe of the chain (30).

To model 3 kb DNA chains, assuming a linear density of 3 bp/nm, we used the parameters listed below:

N = 334

σ = 3 nm

k = 17kBT

C = 72kBT nm

Inline graphic = −16.

The bending stiffness parameter k was chosen to give a persistence length LP ≈ 53 nm for a linear chain without torsional stiffness. The torsional rigidity constant C was taken in the range proposed by Vologodskii et al. (29). The linking number difference 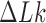Inline graphic was set to −16 since this value places simulated molecules in the middle of the supercoiling density ranges observed in DNA plasmids isolated from bacteria grown in various conditions (31). As mentioned in the discussion, the magnitude of supercoiling is reduced in vivo, but this change is balanced by the crowding effect (32).

To evaluate thermal equilibrium properties of the system, we generated an ensemble of chain configurations, distributed according to the Boltzmann distribution, using a Metropolis Monte Carlo algorithm (33) based on crankshaft moves, described earlier (34). Note that this type of crankshaft move conserves the distance between consecutive beads and the topology of the chain by preventing the rotating sub-chain from crossing other parts of the chain during the move.

For the knotted chains, after an initialization starting from the configuration given in Supplementary Figure S1A, the Monte Carlo algorithm was run for a total of 2.6 × 108 iterations (one iteration = N crankshaft moves, where N is the number of beads). After the first 107 iterations, sample configurations were saved every 105 iterations to be used later to evaluate the thermal averages of properties of interest. During the run, the squared radius of gyration of knotted supercoiled chains was measured every 1000 iterations, and the corresponding autocorrelation function was evaluated using the ‘blocking’ method (35). Supplementary Figure S2 (red points) presents the autocorrelation as a function of block size. A fit of exp(−n/τ) to these data gives an estimated correlation time τ for the squared radius of gyration on the order of 105 iterations, which means that the total number of Monte Carlo iterations corresponded approximately to 2600τ. This result suggests that enough independent configurations were obtained during the Monte Carlo run to sample thermal equilibrium.

For the two catenated chains, the system was initialized to the configuration shown in Supplementary Figure S1B, and the Monte Carlo algorithm was run for a total of 3.5 × 108 iterations. Sample configurations were saved every 105 iterations after the first 107 iterations. The autocorrelation function for the average squared radius of gyration per chain is shown in Supplementary Figure S2 (blue points), and the estimated correlation time is on the order of 2 × 105 iterations. Therefore, the total number of iterations corresponded approximately to 1700τ, which suggests a sufficiently equilibrated system of catenated, supercoiled chains.

Geometrical and topological characterization of DNA-DNA juxtapositions

In our simulations, DNA molecules are modeled as beaded chains where every bead corresponds to 8 bp. To analyze the juxtapositions, in which the G and T segments have sizes of about 50 bp, we analyzed subchains composed of seven beads each. For the geometrical analysis each seven bead-long subchain of modeled configurations was considered as a potential G segment and its geometry was approximated by a fixed angle bend formed by the two line segments starting at the center of the middle bead (M1) and ending at the two centers of the terminal beads (see Figure 2). As explained earlier, Topo IV positions itself on a G segment in such a way that it can only capture potential T segments that are located inside of the bend formed by the G segment. To account for this type of Topo IV's selectivity, we entered into the statistics only the DNA–DNA juxtapositions where the subchain S2 (representing the potential T segment) had an intersection point Ip with the surface spanning from the interior of the fixed angle bend that approximated the geometry of the G segment (see Figure 2). In addition, to reflect the fact that topoisomerases can only capture DNA segments that are very close to its surface, we somewhat arbitrarily decided that the distance between the middle bead M1 of the G segment and the intersection point Ip should not exceed 6 nm (i.e. 2σ). If there was more than one intersection point with the spanning surface determined by the bend of a given G segment, only the one closest to the vertex M1 was taken into account. In such a case the seven bead-long subchain S2 representing a potential T segment is then defined as the one whose middle vertex M2 is the vertex closest to the Ip. Subsequently, for the geometrical analysis, the subchain S2 was replaced by the fixed angle bend formed by the two line segments starting from vertex M2 and ending at the two terminal vertices of that chain. Once the pairs of potential G and T segments were defined, we characterized them geometrically and considered how the topology of the entire analyzed molecules changes upon intersegmental passage between these G and T segments.

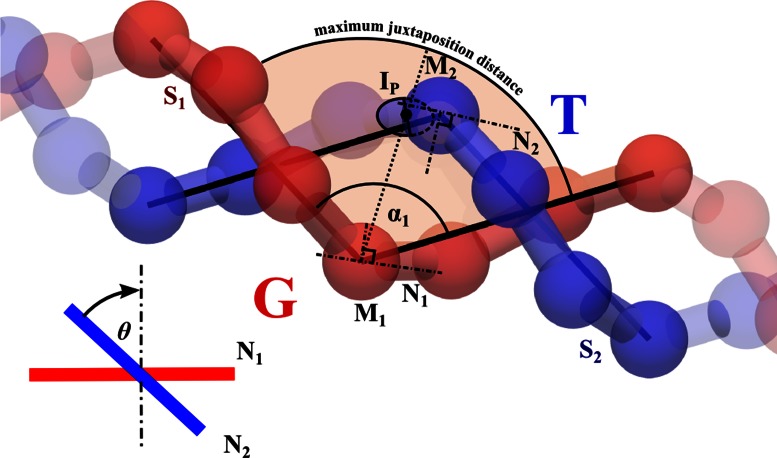
Figure 2.

Figure 2.

Open in a new tab

Geometry of juxtapositions. To facilitate the visibility of geometric characteristics of modeled beaded chains, which are composed of touching spheres, we have shrunk the actual beads and represented the chains as composed of beads and joining cylinders. In our models, the subchain S1 corresponds to the G segment, which is bound first by the topoisomerase and whose curvature, reflected by the angle α1, dictates how the topoisomerase is positioned on the DNA. This positioning, in turn, determines from which side and at which crossing angle θ, the T segment (subchain S2) can approach the G segment to be used for the passage. The geometries of seven bead-long subchains are approximated by fixed angle bends formed by two line segments connecting the center of the middle beads with the centers of the terminal beads. For each juxtaposition (see the Materials and Methods section for our criteria of juxtapositions), we determine the α1 angle and the chirality-dependent crossing angle θ. In the inset the tangentials N2 and N1 are shown along the direction that is perpendicular to both of them. In that projection, the θ angle is the smallest rotation angle that would be required to rotate the tangential closer to an observer (in this case N2) to make it perpendicular to the other tangential (in this case N1). If the direction of this rotation is clockwise, the crossing is right-handed and the θ angle is positive (see the Materials and Methods section for more details). For left-handed crossings, θ angles are negative and the direction of this rotation is counter-clockwise.

Geometrical analysis

We characterized several geometric characteristics of the analyzed juxtapositions. However, the ones that are likely to be used by topoisomerases in the selection of juxtapositions for strand passage, and were considered as such in several earlier papers (4,6,21,24), are the crossing angle θ and the bending angle α1. The crossing angle θ measures the inclination of the G segment, which is bound first by a topoisomerase, with respect to the subsequently captured T segment. As mentioned previously, the seven bead-long subchains that model the G and T segments are approximated first by fixed angle bends formed each by two straight-line segments (see Figure 2).

To measure the θ angle between these two bends, we define tangential lines N1 and N2 passing through middle vertex of each bend (M1 and M2, respectively). These tangential lines are perpendicular to bisecting lines of each bend and are in the planes defined by the respective bends (see Figure 2). We then follow the approach of Burnier, et al. (24). First, one finds the viewing direction that is perpendicular to both lines N1 and N2. Subsequently, one measures the θ angle, which is the smallest angular rotation (in a plane perpendicular to the viewing direction) of the line closer to the observer that would make that line perpendicular to the line that is further from the observer (see the inset in Figure 2). If that rotation is clockwise, the crossing is considered as right-handed and its angular value is given a positive sign. The θ angle can range from −90° to +90°, where negative and positive values indicate left- and right-handed crossings, respectively, and where the 0° value characterizes achiral, perpendicular crossings. It is important to mention that the θ angle notation used here is different than the θ angle used by Stone et al. (4) and results in a −90° shift. In our notation, right-handed and left-handed crossings have positive and negative θ values, respectively. The convention used by Stone et al. associates a positive sign to all θ angles and they range from 0° to 90° for left-handed crossings and from 90° to 180° for right-handed crossings.

The α1 bending angle, reflecting the bending angle of the G segment bound by a topoisomerase, is simply the included angle (≤180°) of a given bend that approximates the geometry of a given seven bead-long subchain (see Figure 2).

Topological analysis

For each geometrically characterized juxtaposition, we determined how intersegmental passage within the given juxtapositions changes the topology of the entire modeled DNA molecule. To this end, for every analyzed juxtaposition, we created a configuration resulting from a passage between juxtaposed segments. In the case of knotted, supercoiled molecules, we calculated the HOMFLY polynomial to determine the knot type of the configuration after the intersegmental passage (36,37). For supercoiled, catenated molecules, we calculated the catenation number, i.e. the linking number between the two molecules forming the catenane, to determine the topology of the catenane after the intersegmental passage.

RESULTS

Structure of negatively supercoiled DNA molecules forming right-handed trefoil knots

Trefoil knots are the simplest and the most frequent knots that can be formed in DNA plasmids in vitro (26,38) and also in vivo (19,39). Trefoil knots exist in right- and left-handed forms. In right-handed trefoil knots (+31 in standard knot notation), the DNA–DNA juxtapositions due to knotting are preferentially right-handed, as also is the case for juxtapositions in interwound portions of negatively supercoiled DNA molecules. For this reason, right-handed trefoil knots provide a bigger challenge than left-handed trefoil knots for the Topo IV to be able to direct its action to the knotted portion and to spare the interwound portion of the supercoiled DNA molecules. Since we wish to understand how Topo IV can distinguish between juxtapositions resulting from knotting and catention from the juxtapositions resulting from negative supercoiling, we first investigate the overall structure of supercoiled DNA molecules forming right-handed trefoils.

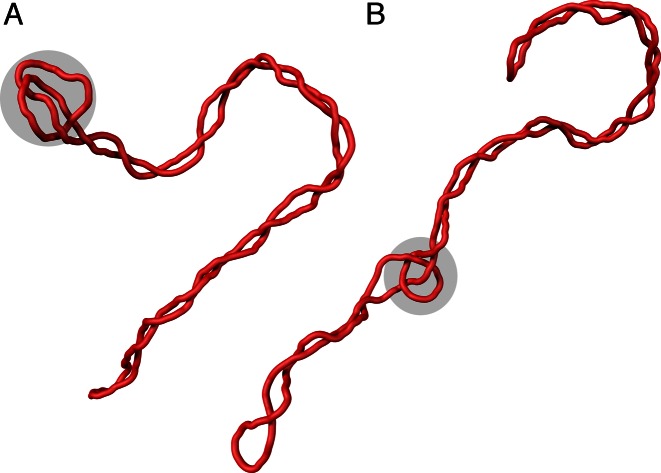
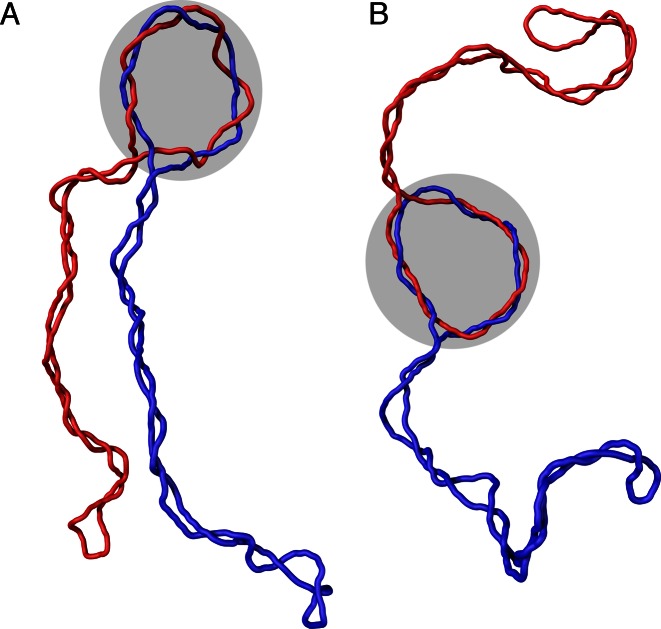
Figure 3 shows two characteristic snapshots of simulated negatively supercoiled DNA molecules forming right-handed trefoil knots. In the majority of cases, the knot is entropically tightened (40,41) and is localized at one of the apical loops of the supercoiled DNA molecules (Figure 3A). Presumably, the apical position of the knot decreases the elastic energy of the entire molecule. DNA portions in apical loops and in knotted regions are subject to bending stress since these regions have higher curvature than the rest of the molecule (42). Therefore, these regions have higher elastic energy than other portions of the molecule. When the elastic energy investment in the bending of one DNA region can be used both in an apical loop and the knotted portion, the number of strongly bent sites in a molecule is decreased, which in turn decreases the elastic energy of the entire molecule. Less frequently, we observe configurations with the knotted portion moving between the two apical loops (Figure 3B).

Figure 3.

Figure 3.

Open in a new tab

Simulation snapshots of negatively supercoiled DNA molecules forming right-handed trefoil knots. The modeled molecules correspond to plasmids with about 3000 bp and ΔLk = −16. The shaded regions indicate the position of the knotted portions of the modeled molecules. (A) A configuration with the knot localized in the apical loop of the supercoiled plasmid. (B) A configuration with the knotted portion moving between the two apical loops.

Crossing angle differences between knotted and interwound portions of knotted supercoiled DNA molecules

Visual analysis of DNA molecules shown in Figure 3 suggests that crossings between approaching segments in the knotted portions are closer to perpendicular than the crossings in the plectonemic portion of the molecules. To verify this observation, we measured the crossing angle θ for DNA–DNA juxtapositions, where the potential T segment was inside the bend formed by the potential G segment and determined the topological consequences of passages occurring at these juxtapositions (see Figure 2 and the Materials and Methods section for more details).

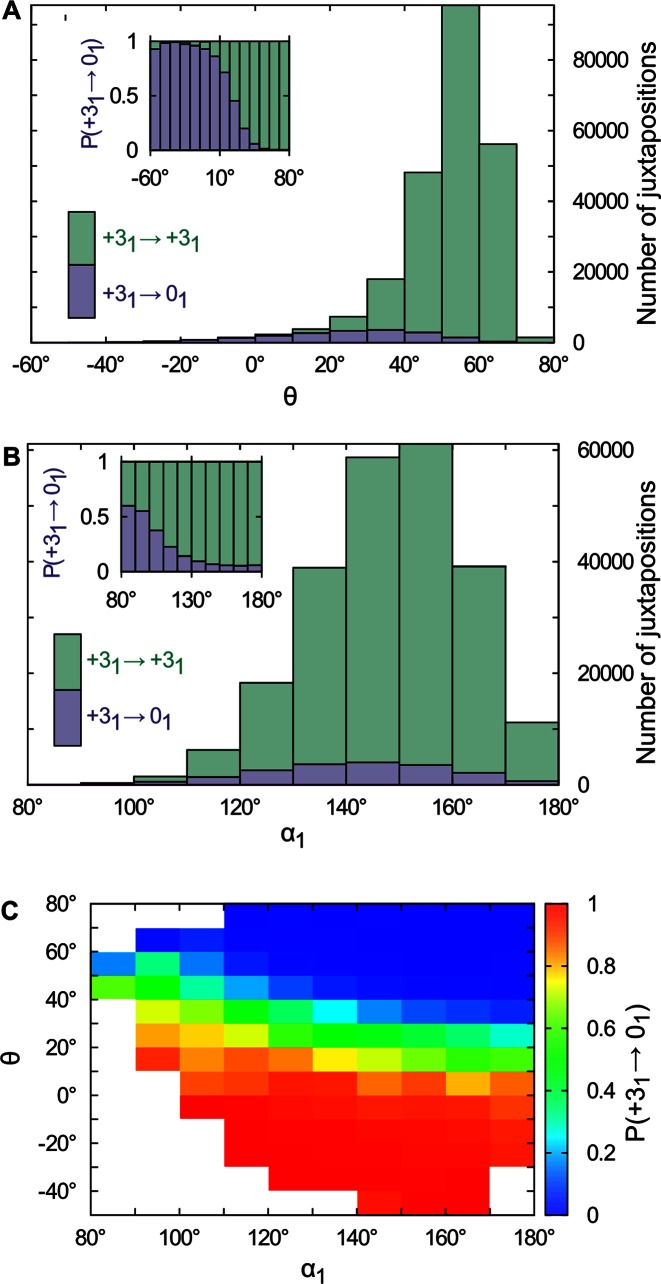
Figure 4A shows the distribution of the chirality-dependent θ angles in DNA-DNA juxtapositions observed in simulated negatively supercoiled DNA molecules forming right-handed trefoil knots, examples of which are shown in Figure 3. The height of the main histogram bars in Figure 4A corresponds to the observed number of juxtapositions within the corresponding θ angle range in the simulated DNA molecules. We can see that the most frequent juxtapositions are right-handed with the θ angle ranging between 50° and 60°. Such juxtapositions are expected for DNA molecules where the duplex regions wind around each other in a right-handed fashion (4). As can be seen in Figure 3, most of the DNA–DNA juxtapositions in these molecules are between duplexes forming the interwound portions of the molecules. The passages occurring between the interwound duplexes result in the undesired partial relaxation of DNA supercoiling and have no effect on knotting or unknotting of these molecules. The fraction of juxtapositions with this topological outcome is indicated in green within the individual histogram bars. The blue color indicates the fraction of juxtapositions that, upon internal passage, result in DNA unknotting. These juxtapositions can only form in the knotted portion of the molecules.

Figure 4.

Figure 4.

Open in a new tab

Geometrical and topological characterization of juxtapositions in the modeled supercoiled DNA molecules forming right-handed trefoil knots. (A) Main part: Raw data, a stacked histogram in which the heights of the histogram bars correspond to the total number of juxtapositions observed in the analyzed configurations falling within a given range of the θ angle. The colors indicate the fractions of the juxtapositions (within a given θ range) that, upon intersegmental passages, result either in unknotting (blue) or maintaining the original knot type (green). Juxtapositions that result in unknotting involve knotted portions of the molecules, whereas juxtapositions that maintain the original knot type are located within the interwound portions. Inset: The normalized histogram from the main part shows more directly that the fraction of juxtapositions that result in unknotting upon intersegmental passage approaches one for left-handed crossings with the θ angle ranging between −20° and −60°. (B) Main part: Raw data, a stacked histogram showing the distribution of the α1 angle in the analyzed juxtapositions. Color indications are the same as in panel A. Inset: Normalized histogram from the main part showing directly that Topo IV's selectivity for strongly bent G sites (smaller α1 angle) increases the probability of unknotting. (C) Probability of unknotting as a function of the α1 and θ angles. The color scale indicates the probability that a passage at juxtapositions with a given combination of α1 and θ angles results in unknotting. The regions with nonsufficient statistics (<10 entries) were left blank.

The topological outcome of passages occurring in given juxtapositions is therefore a strong hint or proxy for the localization of these juxtapositions and we use it as such in what follows. The main histogram in Figure 4A reveals that there is a difference in the distribution of the θ angle in the interwound and knotted portions of the molecules. This difference is better seen in the inset where the main histogram was normalized to bring each histogram bar to one. The normalized histogram clearly shows that if Topo IV were selective for the left-handed juxtapositions with the θ angle of about −40°, then nearly all passages would result in unknotting and there would be practically no undesired passages causing partial relaxation of supercoiled DNA molecules.

Differences between the bending angle of potential G segments in knotted and interwound portions of knotted supercoiled DNA molecules

Earlier observations of Topo IV bound to DNA (21) and earlier modeling studies of non-supercoiled knotted DNA molecules have suggested that Topo IV can unknot non-supercoiled DNA efficiently by acting preferentially at the juxtapositions involving strongly bent DNA regions (21,22,24,43). However, in bacteria DNA molecules are supercoiled. Therefore, it is important to check whether selection of bent DNA regions can also favor unknotting in supercoiled DNA molecules. Molecules shown in Figure 3 give an impression that the DNA portion in the knotted regions is more highly bent than in the plectonemic regions. A similar observation was made earlier (42) but it was not determined whether strand passages within DNA-DNA juxtapositions involving strongly bent DNA result in preferential unknotting of the supercoiled DNA molecules.

Figure 4B shows the distribution of the α1 angle, i.e. the bending angle of the potential G segments in our modeled supercoiled, knotted DNA molecules. As in Figure 4A, the height of the main histogram bars corresponds to the raw numbers of juxtapositions observed in our samples within a given range of the α1 angle. A close inspection of the main histogram reveals that the distribution of α1 angles in the knotted portions is shifted toward stronger bending and thus to smaller α1 angles than in the plectonemic portions of the molecules. This shift is seen much better in the inset, where each histogram bar from the main histogram is scaled to one. We can see that the proportion of juxtapositions that result in unknotting upon intersegmental passage increases as the α1 angle decreases. Therefore, by acting preferentially on juxtapositions with strongly bent DNA regions, Topo IV would be expected to increase, approximately 10-fold, its chances to unknot supercoiled DNA molecules when compared to acting on the juxtapositions with a weakly bent G segment. However, even for highly bent G segments, the probability of unknotting does not exceed 60%. In contrast, in juxtapositions with θ angle of about −40°, the probability of unknotting approaches one (see inset in Figure 4A).

The combined effects of two different geometric characteristics of DNA-DNA juxtapositions on the topological outcome of the strand passage

The geometrical selection of potential sites of action by topoisomerases is likely to be simultaneously affected by several geometric characteristics of DNA–DNA juxtapositions. In general, the configurations of the juxtapositions that best fit the DNA binding sites of the enzyme will be recognized with the highest probability. By combining several geometric characteristics of DNA–DNA juxtapositions, the topoisomerase's specificity for unknotting can be enhanced. However, it also is possible that if one selection criteria is fulfilled, the other may become less important. Figure 4C shows the complex effect of combining just two characteristics, i.e. the crossing angle θ and the bending angle α1, on the topological outcome of strand passage. The color code in Figure 4C (see the scale) indicates the probability with which juxtapositions with a given combination of the θ and α1 angles result in unknotting the supercoiled knotted DNA molecules. We can see that a relatively large region of the configuration space that predisposes DNA–DNA juxtapositions for very efficient unknotting lies in the favorable intersection of θ angles ranging from −20° to −60° and α1 angles ranging from 100° to 180°. However, very strong bending of the G segment increases the probability of unknotting regardless of the θ angle.

The structure of negatively supercoiled postreplicative DNA catenanes

As early as the 1980s, it was observed that just after replication, circular DNA molecules form multiply interlinked right-handed catenanes (8,9). This interlinking is a consequence of the right-handed helical structure of DNA (8). Of course, freshly replicated DNA molecules need to be decatenated rapidly and several different DNA topoisomerases participate in this process. From studies of bacterial systems, it is known that when freshly replicated DNA molecules are not yet covalently closed, and contain nicks and gaps, their decatenation can be performed by topoisomerase III (44). Topo III is a type I DNA topoisomerase that preferentially performs passages between single and double stranded regions of the DNA. The activity of DNA gyrase is needed for efficient decatenation by Topo III (45) and it was suggested that the action of DNA gyrase on nicked and gapped DNA can result in pushing the interlinks toward nicks and gaps (46). Once both freshly replicated molecules become covalently closed and supercoiled, Topo IV is responsible for their further decatenation (1). To investigate how Topo IV can efficiently decatenate supercoiled DNA molecules without relaxing their supercoiling, we performed simulations of multiply catenated supercoiled DNA molecules. The simulated molecules are interlinked with each other five times and have the supercoiling density typical for bacterial plasmids.

Figure 5 shows two examples of equilibrated configurations of the simulated catenanes. Similar to the confinement and localization of the knotted portions in supercoilied molecules (see Figure 3), the catenated portions are confined and tend to localize at the apical loops of supercoiled DNA molecules.

Figure 5.

Figure 5.

Open in a new tab

Simulation snapshots of negatively supercoiled DNA molecules forming right-handed catenanes. The modeled molecules correspond to plasmids with approximately 3000 bp, ΔLk = −16, and with the interlinking or catenation number +5. The shaded regions indicate the position of the catenated portions of the modeled molecules. (A and B) Configurations where the plectonemic portions join the catenated portion ‘in cis’ or ‘in trans’, respectively.

Negative crossing angles θ are strongly enriched in the catenated portions of negatively supercoiled, catenated DNA molecules

The configurations of negatively supercoiled, catenated DNA molecules shown in Figure 5 give the impression that the crossing angles in the catenated regions and in the plectonemically interwound portions of the molecules are quite similar to each other. To analyze in more detail possible differences between the θ angles of juxtapositions formed in the catenated or in interwound portions of the molecules, we characterized the geometry and the topological outcome of strand passages occurring at the given juxtapositions. As is the case in knotted DNA molecules, one can infer the location of a given juxtaposition from the topological outcome of passages between juxtaposed segments in that juxtaposition. If the passage in a given juxtaposition leads to a decrease in the catenation number of catenated molecules, the juxtaposition in question involves segments belonging to the region of catenation. On the other hand, strand passages in the juxtapositions located in the interwound portions result in molecules keeping the original catenation number. The raw data, stacked histogram in Figure 6A shows the total number of juxtapositions within a given interval of θ angles and also tells how many of them lie in the interwound and catenated portions of the molecules (indicated on the histogram with green and blue color, respectively). Upon normalization of each histogram bar to one (see the inset), we see that among the relatively rare juxtapositions with negative θ angle, there is strong domination of juxtapositions formed in the catenated portions since passages occurring within them lead to a decrease of the catenation number (topological change from the catenane 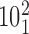Inline graphic to Inline graphic). This analysis shows that if Topo IV were selectively acting on juxtapositions with the θ angles ranging between −40° and −60°, the great majority of the passages would result in progressive decatenation of the DNA molecules. It is interesting to note that a similar range of θ angles also was optimal for the unknotting of supercoiled DNA molecules forming right-handed trefoil knots (see Figure 4).

Figure 6.

Figure 6.

Open in a new tab

Geometrical and topological characterization of juxtapositions in catenated supercoiled DNA molecules (such as those shown in Figure 5). (A) Main part: Raw data, a stacked histogram where the heights of histogram bars correspond to the total number of juxtapositions observed in the analyzed configurations and falling within a given range of the θ angle. The blue color indicates the fractions of the juxtapositions (within a given θ range) that result in decreasing the catenation number upon intersegmental passages, i.e. in passing from the torus type catenane with 10 crossings (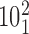Inline graphic) to the torus type of catenane with eight crossings (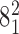Inline graphic). The green color indicates the fractions of juxtapositions that upon intersegmental passages result in maintaining the original catenane (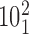Inline graphic) but cause undesired partial relaxation of the DNA supercoiling. Inset: The normalized histogram from the main part shows directly that the fraction of juxtapositions that result in unknotting upon intersegmental passages approaches one for left-handed crossings with the θ angles ranging between −40° and −60°. (B) Main part: Raw data, a stacked histogram showing the distribution of the α1 angle in the analyzed juxtapositions. The color indications are the same as for panel A. Inset. 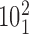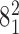The renormalized histogram from the main part shows directly that Topo IV's selectivity for strongly bent G sites (smaller α1 angle) can favor passages needed for progressive decatenation that, in this case, are passages from the catenane Inline graphic to Inline graphic. 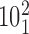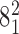(C) Probability of a passage from the catenane Inline graphic to Inline graphic as a function of α1 and θ angle. The regions with nonsufficient statistics (<10 entries) were left blank.

Preferential interaction with bent DNA regions can aid Topo IV in progressive decatenation of catenated supercoiled DNA molecules

The raw data histogram shown in Figure 6B shows that the most frequently observed α1 bending angles range from from 140° to 160° and that this is true for both the juxtapositions in the catenated and the interwound portions of the modeled DNA molecules. The normalized histogram (inset) reveals though that by selecting juxtapositions with more highly bent G segment (i.e. with a smaller α1 angle), Topo IV can increase the fraction of passages leading to progressive decatention. However, the effect is only moderate and other additional selection criteria would be needed to ensure highly specific decatenation.

Figure 6C shows the combined effect of the crossing angle θ and the bending angle α1 on the topological outcome of passages occurring in the juxtapositions within different angle ranges. 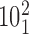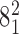The color scale indicates the probability that passages involving juxtapositions with a given geometric characterization results in a decrease of their catenation number from 5 to 4 and passage from catenanes with the topological notation Inline graphic to Inline graphic. We see that the θ angles ranging from −40° to −60° strongly predispose juxtapositions for progressive decatenation.

The location of juxtapositions that can be selected by Topo IV for decatenation-specific passages

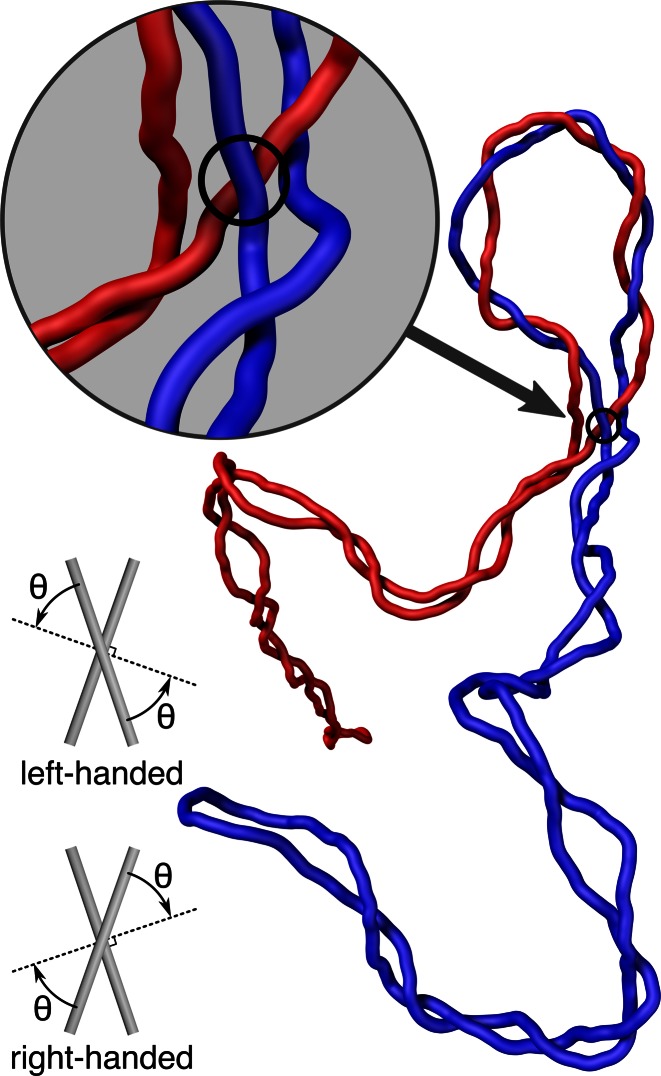
As is shown in Figure 6A, only a very small fraction of juxtapositions in catenated, supercoiled DNA molecules have left-handed crossings with the θ angle ranging from −40° to −60°. These juxtapositions are highly enriched in the catenated portions of the molecules and thus Topo IV's specificity for juxtapositions with such a geometry could result in targeted decatenation. In fact, Topo IV is likely to have such specificity since left-handed juxtapositions within this range of θ angle dominate in positively supercoiled DNA molecules that are preferentially recognized by Topo IV (4,15). To understand better how Topo IV can specifically decatenate negatively supercoiled right-handed catenanes, we investigated where the left-handed crossings with θ angles ranging from −40° to −60° are localized in these molecules. Our analysis reveals that these juxtapositions are preferentially located in the region where plectonemic portions of catenated molecules join the catenated portions (see Figure 7). As illustrated in Figure 7, one of the crossings formed in this region is left-handed, whereas all other crossings in the configuration are right-handed. In addition, this crossing is between segments belonging to two freshly replicated daughter molecules. Therefore, Topo IV, which shows a strong preference for left-handed crossings (4), can nevertheless very specifically decatenate right-handed catenanes formed by supercoiled DNA molecules since one specific crossing in these catenanes is frequently left-handed.

Figure 7.

Figure 7.

Open in a new tab

An equilibrated configuration of supercoiled, catenated DNA molecules. Notice that in the region where the plectonemic portions join the catenated portion, there is one juxtaposition (crossing) that is left-handed (see the magnified view), whereas all of the other crossings in the presented configuration are right-handed (see insets and Figure 3 for schematics of right- and left-handed crossings).

DISCUSSION

It has been a puzzle as to how Topo IV, which shows selectivity for left-handed crossings, can efficiently decatenate multiply interlinked right-handed catenanes. A partial answer to this question was provided by Stone et al. who measured the activity of Topo IV on right- and left-handed DNA braids (4). These measurements, combined with numerical simulations of DNA braids, led the authors to propose that Topo IV can act only on left-handed crossings, such as those omnipresent in positively supercoiled DNA. In addition, Stone et al. proposed that the left-handed crossings also can form in right handed catenanes provided that the catenanes have a low catenation number (4). A lack of supercoiling combined with a low catenation number give these catenated molecules enough structural freedom to be driven by thermal motion to occasionally form left-handed crossings. However, Stone et al. did not consider that freshly replicated molecules can have high catenation number and that these catenated DNA molecules get supercoiled before their decatenation (47). Therefore, it is important to investigate whether these additional structural constraints can prevent supercoiled DNA molecules with relatively high catenation number from forming left-handed crossings suitable for Topo IV-mediated decatenation.

Our numerical simulations of negatively supercoiled, catenated DNA molecules with relatively high catenation number show that the catenated region is highly confined in such molecules and that this confinement limits the possibility of forming short regions with left-handed windings within this region. However, in the regions where the plectonemic portions join the region of catenation, one observes the formation of individual left-handed juxtapositions involving segments of two catenated circular molecules (see Figure 7). Interestingly, the formation of these left-handed juxtapositions in right-handed catenanes is the natural consequence of the specific structure of multiply interlinked catenanes where each of the two catenated molecules is negatively supercoiled (see Figure 7). These left-handed juxtapositons form in regions where the plectonemic portions join the catenated portion and have crossing angles θ typical for positively supercoiled DNA. Importantly, left-handed crossings with θ angles typical for positively supercoiled DNA molecules appear very rarely in negatively supercoiled DNA, which explains how negatively supercoiled DNA can be protected from the Topo IV action. Without such protection, the Topo IV action would result in the continuous relaxation of the negative supercoiling.

Our simulation results support the original proposal of Stone et al. that Topo IV has a strong preference for left-handed juxtapositions with the θ angle ranging from −30° to −60° (4). However, the 2003 proposal of Stone et al. was challenged in 2009 by Neuman et al. (6). Using magnetic tweezers to wrap two DNA molecules around each other at different crossing angles, Neuman et al. concluded that the optimal crossing angle for Topo IV to act is very close to the achiral crossing, where two contacting segments are nearly perpendicular to each other (θ ≈ 0°) (6). However, the experimental setup used by Neuman et al. introduced a coupling between the θ angle and the α1 angle of enforced juxtapositions. Juxtapositions, where the approaching segments were nearly perpendicular to each other were also most likely to be strongly bent. As discussed in the introduction, Topo IV has high affinity to strongly bent sites. Therefore, we believe that the preference of Topo IV for juxtapositions with nearly perpendicular crossing angle θ observed in experiments by Neuman et al. was likely the result of the high affinity of Topo IV to strongly bent DNA and did not correctly reflect the enzyme's preference for a given θ angle. Interestingly, our simulations show that juxtapositions involving strongly bent G segments predispose knotted molecules for unknotting and catenated molecules for decatenation even when the θ angle is not in the −40° to −60° range.

The geometric selection of juxtapositions by Topo IV and other topoisomerases is likely to depend on several geometric characteristics of these juxtapositions. Earlier studies have shown that by selecting strongly bent DNA, Topo IV can efficiently unknot torsionally relaxed DNA molecules (21,22,24,43). Our simulation results show that the selection of θ angles in the range −40° to −60° aided by the preferential interaction with bent DNA sites can explain how Topo IV efficiently unknots and also decatenates negatively supercoiled DNA molecules without causing their torsional relaxation. In crystals where Topo IV interacts with G segments, these DNA regions are strongly bent (25). Although there are not yet any solved crystals in which the G and T segments are bound by Topo IV, our results lead us to anticipate that the θ angle between the G and T segments in such crystals will be between −40° and −60°.

Our study focused on the situation where the replication is already finished and both freshly replicated daughter DNA molecules, forming catenanes, are covalently closed and supercoiled. However, when the replication is not yet completed, the freshly replicated portions of circular DNA molecules form the so-called precatenanes (48). Since actively replicated DNA molecules accumulate positive supercoiling the precatenanes are expected to wind around each other in a right-handed fashion (5,48). As long as the replication is not finished, the freshly replicated portions forming precatenanes contain discontinuities in freshly synthesized strands and this precludes the precatenaes from accumulating torsional stress needed for supercoiling. For this reason, it is unlikely that right-handed precatenanes will form left-handed crossings of the type that we observe in the modeled supercoiled catenanes. Topo IV would be, therefore, unlikely to decatenate these precatenanes. However, we showed recently that gyrase action on nonsupercoiled catenanes is likely to promote topoisomerase III-mediated decatenation occurring at nicks and single stranded gaps (46). Such an activity is independent of the handedness of the interwinding of the contacting DNA segments and thus should also be efficient in promoting decatenation of right-handed precatenanes.

The modeling studies presented here did not account for the fact that DNA in bacterial cells interacts with histone-like proteins such as H-NS and HU (49). As a consequence of this interaction, part of the supercoiling of bacterial DNA is constrained and the magnitude of supercoiling density in vivo is roughly twice lower than in the deproteinized DNA isolated from bacterial cells (50–53). We did not account for this decrease of the magnitude of supercoiling density in vivo. However, our earlier modeling studies showed that conditions of high crowding, characteristic for bacterial nucleoids, naturally compensate for this decreased magnitude of supercoiling in vivo (32).

Supplementary Material

Supplementary Data
Click here for additional data file. (434.8KB, zip)
SUPPLEMENTARY DATA
supp_44_10_4528__index.html (842B, html)

FUNDING

Leverhulme Trust [RP2013-K-017 to A.S.]; Swiss National Science Foundation [31003A_138267 to A.S.]; United States National Science Foundation [1418869 to E.J.R.]. Funding for open access charge: The open access publication charge for this paper has been waived by Oxford University Press - NAR Editorial Board members are entitled to one free paper per year in recognition of their work on behalf of the journal.

Conflict of interest statement. None declared.

REFERENCES

  • 1.Zechiedrich E.L., Cozzarelli N.R. Roles of topoisomerase IV and DNA gyrase in DNA unlinking during replication in Escherichia coli. Genes Dev. 1995;9:2859–2869. doi: 10.1101/gad.9.22.2859. [DOI] [PubMed] [Google Scholar]
  • 2.Zechiedrich E.L., Khodursky A.B., Cozzarelli N.R. Topoisomerase IV, not gyrase, decatenates products of site-specific recombination in Escherichia coli. Genes Dev. 1997;11:2580–2592. doi: 10.1101/gad.11.19.2580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Schoeffler A.J., Berger J.M. DNA topoisomerases: harnessing and constraining energy to govern chromosome topology. Quart. Rev. Biophys. 2008;41:41–101. doi: 10.1017/S003358350800468X. [DOI] [PubMed] [Google Scholar]
  • 4.Stone M.D., Bryant Z., Crisona N.J., Smith S.B., Vologodskii A., Bustamante C., Cozzarelli N.R. Chirality sensing by Escherichia coli topoisomerase IV and the mechanism of type II topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2003;100:8654–8659. doi: 10.1073/pnas.1133178100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Schvartzman J.B., Stasiak A. A topological view of the replicon. EMBO Rep. 2004;5:256–261. doi: 10.1038/sj.embor.7400101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Neuman K.C., Charvin G., Bensimon D., Croquette V. Mechanisms of chiral discrimination by topoisomerase IV. Proc. Natl. Acad. Sci. U.S.A. 2009;106:6986–6991. doi: 10.1073/pnas.0900574106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Witz G., Stasiak A. DNA supercoiling and its role in DNA decatenation and unknotting. Nucleic Acids Res. 2010;38:2119–2133. doi: 10.1093/nar/gkp1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Sundin O., Varshavsky A. Terminal stages of SV40 DNA replication proceed via multiply intertwined catenated dimers. Cell. 1980;21:103–114. doi: 10.1016/0092-8674(80)90118-x. [DOI] [PubMed] [Google Scholar]
  • 9.Sundin O., Varshavsky A. Arrest of segregation leads to accumulation of highly intertwined catenated dimers: dissection of the final stages of SV40 DNA replication. Cell. 1981;25:659–669. doi: 10.1016/0092-8674(81)90173-2. [DOI] [PubMed] [Google Scholar]
  • 10.Wang J.C. Cellular roles of DNA topoisomerases: a molecular perspective. Nat. Rev. Mol. Cell Biol. 2002;3:430–440. doi: 10.1038/nrm831. [DOI] [PubMed] [Google Scholar]
  • 11.Bates A.D., Maxwell A. DNA Topology. Oxford: Oxford University Press; 2005. [Google Scholar]
  • 12.Khodursky A.B., Peter B.J., Schmid M.B., DeRisi J., Botstein D., Brown P.O., Cozzarelli N.R. Analysis of topoisomerase function in bacterial replication fork movement: use of DNA microarrays. Proc. Natl. Acad. Sci. U.S.A. 2000;97:9419–9424. doi: 10.1073/pnas.97.17.9419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Koster D.A., Crut A., Shuman S., Bjornsti M.A., Dekker N.H. Cellular strategies for regulating DNA supercoiling: a single-molecule perspective. Cell. 2010;142:519–530. doi: 10.1016/j.cell.2010.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Drolet M. Growth inhibition mediated by excess negative supercoiling: the interplay between transcription elongation, R-loop formation and DNA topology. Mol. Microbiol. 2006;59:723–730. doi: 10.1111/j.1365-2958.2005.05006.x. [DOI] [PubMed] [Google Scholar]
  • 15.Crisona N.J., Strick T.R., Bensimon D., Croquette V., Cozzarelli N.R. Preferential relaxation of positively supercoiled DNA by E. coli topoisomerase IV in single-molecule and ensemble measurements. Genes Dev. 2000;14:2881–2892. doi: 10.1101/gad.838900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Rybenkov V.V., Ullsperger C., Vologodskii A.V., Cozzarelli N.R. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science (New York, N.Y.) 1997;277:690–693. doi: 10.1126/science.277.5326.690. [DOI] [PubMed] [Google Scholar]
  • 17.Portugal J., Rodriguez-Campos A. T7 RNA polymerase cannot transcribe through a highly knotted DNA template. Nucleic Acids Res. 1996;24:4890–4894. doi: 10.1093/nar/24.24.4890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Deibler R.W., Mann J.K., Sumners D.W., Zechiedrich L. Hin-mediated DNA knotting and recombining promote replicon dysfunction and mutation. BMC Mol Biol. 2007;8:44. doi: 10.1186/1471-2199-8-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Sogo J.M., Stasiak A., Martinez-Robles M.L., Krimer D.B., Hernandez P., Schvartzman J.B. Formation of knots in partially replicated DNA molecules. J. Mol. Biol. 1999;286:637–643. doi: 10.1006/jmbi.1998.2510. [DOI] [PubMed] [Google Scholar]
  • 20.Lopez V., Martinez-Robles M.L., Hernandez P., Krimer D.B., Schvartzman J.B. Topo IV is the topoisomerase that knots and unknots sister duplexes during DNA replication. Nucleic Acids Res. 2012;40:3563–3573. doi: 10.1093/nar/gkr1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Vologodskii A.V., Zhang W., Rybenkov V.V., Podtelezhnikov A.A., Subramanian D., Griffith J.D., Cozzarelli N.R. Mechanism of topology simplification by type II DNA topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2001;98:3045–3049. doi: 10.1073/pnas.061029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Buck G.R., Zechiedrich E.L. DNA disentangling by type-2 topoisomerases. J. Mol. Biol. 2004;340:933–939. doi: 10.1016/j.jmb.2004.05.034. [DOI] [PubMed] [Google Scholar]
  • 23.Liu Z., Mann J.K., Zechiedrich E.L., Chan H.S. Topological information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by type-2 DNA topoisomerases. J. Mol. Biol. 2006;361:268–285. doi: 10.1016/j.jmb.2006.06.005. [DOI] [PubMed] [Google Scholar]
  • 24.Burnier Y., Weber C., Flammini A., Stasiak A. Local selection rules that can determine specific pathways of DNA unknotting by type II DNA topoisomerases. Nucleic Acids Res. 2007;35:5223–5231. doi: 10.1093/nar/gkm532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Lee I., Dong K.C., Berger J.M. The role of DNA bending in type IIA topoisomerase function. Nucleic Acids Res. 2013;41:5444–5456. doi: 10.1093/nar/gkt238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Rybenkov V.V., Cozzarelli N.R., Vologodskii A.V. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. U.S.A. 1993;90:5307–5311. doi: 10.1073/pnas.90.11.5307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Bednar J., Furrer P., Stasiak A., Dubochet J., Egelman E.H., Bates A.D. The twist, writhe and overall shape of supercoiled DNA change during counterion-induced transition from a loosely to a tightly interwound superhelix. Possible implications for DNA structure in vivo. J. Mol. Biol. 1994;235:825–847. doi: 10.1006/jmbi.1994.1042. [DOI] [PubMed] [Google Scholar]
  • 28.Leforestier A., Siber A., Livolant F., Podgornik R. Protein-DNA interactions determine the shapes of DNA toroids condensed in virus capsids. Biophys. J. 2011;100:2209–2216. doi: 10.1016/j.bpj.2011.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Vologodskii A.V., Levene S.D., Klenin K.V., Frank-Kamenetskii M., Cozzarelli N.R. Conformational and thermodynamic properties of supercoiled DNA. J. Mol. Biol. 1992;227:1224–1243. doi: 10.1016/0022-2836(92)90533-p. [DOI] [PubMed] [Google Scholar]
  • 30.Klenin K., Langowski J., Vologodskii A. Computational analysis of the chiral action of type II DNA topoisomerases. J. Mol. Biol. 2002;320:359–367. doi: 10.1016/S0022-2836(02)00447-3. [DOI] [PubMed] [Google Scholar]
  • 31.Sobetzko P., Travers A., Muskhelishvili G. Gene order and chromosome dynamics coordinate spatiotemporal gene expression during the bacterial growth cycle. Proc. Natl. Acad. Sci. U.S.A. 2012;109:E42–E50. doi: 10.1073/pnas.1108229109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Benedetti F., Japaridze A., Dorier J., Racko D., Kwapich R., Burnier Y., Dietler G., Stasiak A. Effects of physiological self-crowding of DNA on shape and biological properties of DNA molecules with various levels of supercoiling. Nucleic Acids Res. 2015;43:2390–2399. doi: 10.1093/nar/gkv055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H., Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087. [Google Scholar]
  • 34.Dorier J., Stasiak A. The role of transcription factories-mediated interchromosomal contacts in the organization of nuclear architecture. Nucleic Acids Res. 2010;38:7410–7421. doi: 10.1093/nar/gkq666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Flyvbjerg H., Petersen H.G. Error estimates on averages of correlated data. J. Chem. Phys. 1989;91:461–466. [Google Scholar]
  • 36.Freyd P., Yetter D., Hostle J., Lickorish W.B.R., Millett K.C., Ocneanu A. A new polynomial invariant of knots and links. Bull. Am. Math. Soc. 1985;12:239–246. [Google Scholar]
  • 37.Ewing B., Millett K.C. Progress in Knot Theory and Related Topics. Vol. 56. Paris: Herman; 1997. pp. 51–68. [Google Scholar]
  • 38.Dean F.B., Stasiak A., Koller T., Cozzarelli N.R. Duplex DNA knots produced by Escherichia coli topoisomerase-I—structure and requirements for formation. J. Biol. Chem. 1985;260:4975–4983. [PubMed] [Google Scholar]
  • 39.Deibler R.W., Rahmati S., Zechiedrich E.L. Topoisomerase IV, alone, unknots DNA in E. coli. Genes Dev. 2001;15:748–761. doi: 10.1101/gad.872301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Katritch V., Olson W.K., Vologodskii A., Dubochet J., Stasiak A. Tightness of random knotting. Phys. Rev. E. 2000;61:5545–5549. doi: 10.1103/physreve.61.5545. [DOI] [PubMed] [Google Scholar]
  • 41.Orlandini E., Stella A.L., Vanderzande C. The size of knots in polymers. Phys. Biol. 2009;6:025012. doi: 10.1088/1478-3975/6/2/025012. [DOI] [PubMed] [Google Scholar]
  • 42.Witz G., Dietler G., Stasiak A. Tightening of DNA knots by supercoiling facilitates their unknotting by type II DNA topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2011;108:3608–3611. doi: 10.1073/pnas.1016150108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Liu Z., Zechiedrich E.L., Chan H.S. Inferring global topology from local juxtaposition geometry: interlinking polymer rings and ramifications for topoisomerase action. Biophys. J. 2006;90:2344–2355. doi: 10.1529/biophysj.105.076778. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Nurse P., Levine C., Hassing H., Marians K.J. Topoisomerase III can serve as the cellular decatenase in Escherichia coli. J. Biol. Chem. 2003;278:8653–8660. doi: 10.1074/jbc.M211211200. [DOI] [PubMed] [Google Scholar]
  • 45.Usongo V., Tanguay C., Nolent F., Bessong J.E., Drolet M. Interplay between type 1A topoisomerases and gyrase in chromosome segregation in Escherichia coli. J. Bacteriol. 2013;195:1758–1768. doi: 10.1128/JB.02001-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Racko D., Benedetti F., Dorier J., Burnier Y., Stasiak A. Generation of supercoils in nicked and gapped DNA drives DNA unknotting and postreplicative decatenation. Nucleic Acids Res. 2015;43:7229–7236. doi: 10.1093/nar/gkv683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Martinez-Robles M.L., Witz G., Hernandez P., Schvartzman J.B., Stasiak A., Krimer D.B. Interplay of DNA supercoiling and catenation during the segregation of sister duplexes. Nucleic Acids Res. 2009;37:5126–5137. doi: 10.1093/nar/gkp530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Peter B.J., Ullsperger C., Hiasa H., Marians K.J., Cozzarelli N.R. The structure of supercoiled intermediates in DNA replication. Cell. 1998;94:819–827. doi: 10.1016/s0092-8674(00)81740-7. [DOI] [PubMed] [Google Scholar]
  • 49.Dorman C.J. Genome architecture and global gene regulation in bacteria: making progress towards a unified model? Nat. Rev. Microbiol. 2013;11:349–355. doi: 10.1038/nrmicro3007. [DOI] [PubMed] [Google Scholar]
  • 50.Pettijohn D.E., Pfenninger O. Supercoils in prokaryotic DNA restrained in vivo. Proc. Natl. Acad. Sci. U.S.A. 1980;77:1331–1335. doi: 10.1073/pnas.77.3.1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Bliska J.B., Cozzarelli N.R. Use of site-specific recombination as a probe of DNA structure and metabolism in vivo. J. Mol. Biol. 1987;194:205–218. doi: 10.1016/0022-2836(87)90369-x. [DOI] [PubMed] [Google Scholar]
  • 52.Bowater R.P., Chen D., Lilley D.M. Modulation of tyrT promoter activity by template supercoiling in vivo. EMBO J. 1994;13:5647–5655. doi: 10.1002/j.1460-2075.1994.tb06903.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Zacharias W., Jaworski A., Larson J.E., Wells R.D. The B- to Z-DNA equilibrium in vivo is perturbed by biological processes. Proc. Natl. Acad. Sci. U.S.A. 1988;85:7069–7073. doi: 10.1073/pnas.85.19.7069. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
Click here for additional data file. (434.8KB, zip)
SUPPLEMENTARY DATA
supp_44_10_4528__index.html (842B, html)
supp_gkw311_nar-00848-f-2016-File009.pdf (434.7KB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES