Protein Residue Contacts and Prediction Methods

Abstract

In the field of computational structural proteomics, contact predictions have shown new prospects of solving the longstanding problem of ab initio protein structure prediction. In the last few years, application of deep learning algorithms and availability of large protein sequence databases, combined with improvement in methods that derive contacts from multiple sequence alignments, have shown a huge increase in the precision of contact prediction. In addition, these predicted contacts have also been used to build three-dimensional models from scratch.

In this chapter, we briefly discuss many elements of protein residue–residue contacts and the methods available for prediction, focusing on a state-of-the-art contact prediction tool, DNcon. Illustrating with a case study, we describe how DNcon can be used to make ab initio contact predictions for a given protein sequence and discuss how the predicted contacts may be analyzed and evaluated.

1. Introduction

For protein structure prediction, ab initio methods are gaining importance because the well-established traditional method of template-based modeling is limited by the number of structural templates available in the Protein Data Bank [1]. Initially, fragment-based ab initio structure prediction tools like Rosetta [2] and FRAGFOLD [3] demonstrated great success. However, recent residue contact-based methods like EVFOLD [4] and CONFOLD [5] have shown a promising new direction for contact-guided ab initio protein structure prediction. Although the idea of predicting residue–residue contact maps and using them to predict three-dimensional (3-D) models was introduced around two decades ago [6, 7], the realization of that idea has only recently come into practice as many authors have shown how residue contacts can be predicted with reasonable accuracy [8, 9]. The primary interest in predicting residue–residue contacts has always been to use them to reconstruct 3-D models, although residue contacts are useful in drug design [10] and model ranking, selection and evaluation [11, 12] as well. In 2011, Debora et al. predicted the correct folds for 15 proteins using predicted contacts and secondary structures, and in 2014, Jones et al. reconstructed 150 globular proteins with a mean TM-score of 0.54 [4, 9]. Currently, the problem of correctly predicting contacts and using them to build 3-D models is largely unsolved, but the field of contact-based structure prediction is rapidly moving forward.

1.1. Definition of Contacts

Residue–residue contacts (or simply “contacts”) in protein 3-D structures are pairs of spatially close residues. A 3-D structure of a protein is expressed as x, y, and z coordinates of the amino acids’ atoms in the form of a pdb file,¹ and hence, contacts can be defined using a distance threshold. A pair of amino acids are in contact if the distance between their specific atoms (mostly carbon-alpha or carbon-beta) is less than a distance threshold (usually 8Å), see Fig. 1. In addition, a minimum sequence separation in the corresponding protein sequence is also usually defined so that sequentially close residues, which are spatially close as well, are excluded. Although proteins can be better reconstructed with carbon-beta (Cβ) atoms [13], carbon-alpha (Cα), being a backbone atom, is still widely used. The choice of distance threshold and sequence separation threshold also defines the number of contacts in a protein. At lower distance thresholds, a protein has fewer number of contacts and at a smaller sequence separation threshold, the protein has many local contacts. In the Critical Assessment of Techniques for Protein Structure Prediction (CASP) competition, a pair of residues are defined as a contact if the distance between their Cβ atoms is less than or equal to 8Å, provided they are separated by at least five residues in the sequence. In recent works by Jones et al., a pair of residues are said to be in contact if their Cα atoms are separated by at least 7Å with no minimum sequence separation distance defined [14].

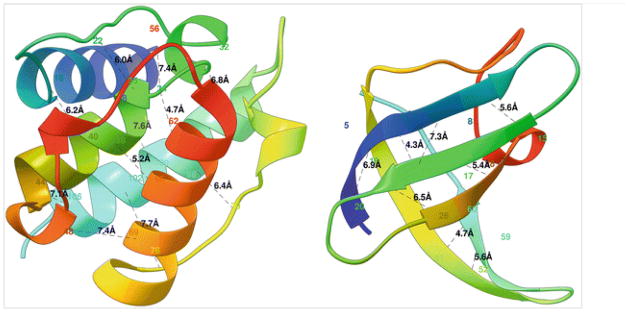
Fig. 1.

Two globular proteins with some contacts in them shown in black dotted lines along with the contact distance in Armstrong. The alpha helical protein 1bkr (left) has many long-range contacts and the beta sheet protein 1c9o (right) has more short- and medium-range contacts

1.2. Contact Evaluation

Realizing that the contacting residues which are far apart in the protein sequence but close together in the 3-D space are important for protein folding [15], contacts are widely categorized as short-range, medium-range, and long-range. Short-range contacts are those separated by 6–11 residues in the sequence; medium-range contacts are those separated by 12–23 residues, and long-range contacts are those separated by at least 24 residues. Most contact prediction assessment methods evaluate long-range contacts separately as they are the most important of the three and also the hardest to predict [16–18]. Depending upon the 3-D shape (fold), some proteins have a lot of short-range contacts while others have more long-range contacts, as shown in Fig. 1. Besides the three categories of contacts, the total number of contacts in a protein is also important if we are to utilize the contacts to reconstruct 3-D models for the protein. Certain proteins, such as those having long tail-like structures, have fewer contacts and are difficult to reconstruct even using true contacts while others, for example compact globular proteins, have a lot of contacts and can be reconstructed with high accuracy. Another important element of predicted contacts is the coverage of contacts, i.e., how well the contacts are distributed over the structure of a protein. A set of contacts having low coverage will have most of the contacts clustered in a specific region of the structure, which means that even if all predicted contacts are correct, we may still need additional information to reconstruct the protein with high accuracy.

Predicted contacts are evaluated using precision, i.e., the number of contacts that are correct out of all predicted contacts. For a lot of proteins, as few as 8 % of native contacts are sufficient to reconstruct the fold of proteins [19]. Moreover, all proteins do not have their number of contacts proportional to the sequence length. Hence, it is common to evaluate the top L/2 or just the top L/5 predicted contacts using precision, with L being the sequence length of the protein. Since short/medium-range contacts are relatively easier to predict (especially for proteins having beta-sheets), the CASP competition focuses on evaluating predicted long-range contacts. The evaluation of contact prediction using precision is simple and is currently being used widely, but it does not cover two important aspects: number of contacts and coverage. Regarding the number of contacts needed for accurate folding, the top 1 L contacts have shown to produce good results [5, 20], but the authors have suggested that the number of contacts needed can be specific to prediction methods. Moreover, predicted top L/5 contacts may be highly precise and sufficient in number, but can have a low coverage, such that they only cover a part of the protein and, thus, cannot capture the overall fold of the protein. Debora et al. attempted to qualitatively assess the coverage of contacts and Eickholt et al. discussed evaluating coverage using the idea of omitting neighboring contacts [4, 18], and yet, the question of how to decide coverage and number of predicted contacts to fold a protein remains unanswered.

1.3. Contact Evaluation in CASP Competition

In the contact prediction category of recent CASP competitions, where predictors are evaluated based on blind predictions, machine learning approaches and coevolution-derived approaches have shown the best performance. Among the target proteins, free-modeling (FM) category proteins are the hardest of all to predict because no tertiary structure templates are available for them, and CASP focuses on evaluating participating methods based on FM protein performance. The best contact prediction methods in CASP10 and CASP12, DNcon [21] and CONSIP2/metaPSICOV [22], have shown a precision of 20 and 27 %, respectively, for top L/5 long-range contact predictions on FM targets. Both of these sequence-based methods, DNcon and CONSIP2, rely on neural networks to make contact predictions. The improvement in CONSIP2 is observed because of the integration of correlated mutation-based features with other ab initio features.

2. Materials

Existing methods for residue contact prediction can be broadly classified into five categories based on the type of information they use to make predictions: (1) coevolution-derived information-based, (2) machine learning methods-based, (3) template-based, (4) physiochemical information-based, and (5) hybrid methods [23]. Other authors, however, have suggested different classifications. Di Lena et al. classify contact prediction approaches into four groups: (a) machine learning, (b) template-based, (c) correlated mutations, and (d) 3-D model-based [24]. Björkholm et al., on the other hand, suggest dividing classification into three categories: (a) machine learning, (b) template-based, and (c) statistical methods [25]. All suggested classifications take into account the two largest groups of contact prediction methods—machine learning-based and correlated mutation-based. Currently, methods that integrate these two approaches, like PconsC2 [26], CONSIP2 [27], and EPC-map [23], are being developed, and because of their integrated approach, it is difficult to distinguish them as machine learning-based or coevolution-based.

2.1. Machine Learning-Based Methods

Many machine learning algorithms have been applied to predict protein residue contacts, and the most recent ones based on deep learning methods have shown the best results. Early approaches to ab initio contact prediction used artificial neural networks [28–32], genetic algorithm [33, 34], random forest [35], hidden Markov model [25, 36], and support vector machines [37, 38]. Most recent approaches, however, focus on using deep learning architectures with and without including correlated mutation information [18, 24, 26]. Many of these methods, available online as web servers or downloadable, are listed in Table 1. These machine learning-based methods use a wide range of features as input including features related to local window of the residues, information about the residue type, and the protein itself. This includes features like secondary structure, sequence profiles, solvent accessibility, mutual information of sequence profiles, residue type information (polarity and acidic properties), sequence separation length between the residues under consideration, and pairwise information between all the residues involved.

Table 1.

Machine learning-based contact prediction methods

Method summary	Availability	Published
PconsC2 [26]—Integration of contact predictions from PSICOV, plmDCA, and deep learning techniques with other features	http://c2.pcons.net/ and downloadable at http://c.pcons.net	2014
DNcon [21]—Uses deep networks and boosting techniques making use of GPUs and CUDA parallel computing technology	http://iris.rnet.missouri.edu/dncon/	2012
CMAPpro [24]— Progressive refinement of contacts using 2D recursive neural networks, secondary structure alignment, and deep neural network architecture	http://scratch.proteomics.ics.uci.edu/	2012
ICOS [53]—Applies predicted structural aspects of proteins to a genetic algorithms-based rule learning system (BioHEL)	http://cruncher.ncl.ac.uk/psp/prediction/action/home	2012
Proc_s3 [35]—Uses a set of Random Forest algorithm-based models	http://www.abl.ku.edu/proc/proc_s3.html (under maintenance)	2011
NNcon [28]—Uses 2D-Recursive Neural Network (2D-RNN) models to predict general residue–residue contacts and specific beta contacts, and combines them	http://sysbio.rnet.missouri.edu/multicom_toolbox/tools.html (downloadable)	2009
FragHMMent [25]—A hidden Markov model (HMM)-based method	http://fraghmment.limbo.ifm.liu.se/	2009
SVMSEQ [38]—A support vector machine-based contact prediction server	http://zhanglab.ccmb.med.umich.edu/SVMSEQ/	2008
SVMcon [37]—Uses support vector machines to predict medium- and long-range contacts with profiles, secondary structure, relative solvent accessibility, contact potentials, etc., as features	http://sysbio.rnet.missouri.edu/multicom_toolbox/tools.html (downloadable)	2007
SAM-T06 [30]—Neural network is applied to calculate the probability of contact between residue positions along with a novel statistic for correlated mutation	http://www.soe.ucsc.edu/research/compbio/SAM_T06/T06-query.html (under maintenance)	2007
DISTILL [54]—The prediction of a contact map’s principal eigenvector (PE) from the primary sequence, followed by the reconstruction of the contact map from the PE and primary sequence	http://distillf.ucd.ie/distill/	2006
CORNET [32]—Based on neural networks with evolutionary information included in the form of sequence profile, sequence conservation, correlated mutations, and predicted secondary structures	http://gpcr.biocomp.unibo.it/cgi/predictors/cornet/pred_cmapcgi.cgi	1999

2.2. Coevolution-Derived Methods

Coevolution-derived methods are based on the principle of “correlated mutation,” which suggests that mutations are usually accompanied by joint mutation of other residues around the local structure in order to maintain the overall structure of the protein [39–41]. Early attempts to identify structural contacts from sequences performed poorly mainly because of (1) insufficient sequences in input multiple sequence alignments, (2) the issue of phylogenetic bias, and (3) indirect couplings mixed with direct couplings [42–44]. However, recently, methods based on direct coupling analysis (DCA) have been able to disentangle direct couplings and have shown considerable success by addressing the problem of correlation chaining, i.e., causation versus correlation issue. Some recent methods use message passing-based DCA (mpDCA [43]) and mean-field DCA (mfDCA [45]), while others use sparse inverse covariance methods (PSICOV [14]) and some more recent approaches use pseudo-likelihood-based optimization (plmDCA [46, 47]/gplmDCA [48] and GREMLIN [49]). In addition to the DCA methods, another set of methods based on mutual information (MI) have revived recently with new developments of their global statistical versions [50]. Some of these recent methods are summarized in Table 2. Most of these coevolution-derived methods accept multiple sequence alignment as input, which can be generated using methods like PSI-Blast at http://blast.ncbi.nlm.nih.gov/Blast.cgi, HHblits at http://toolkit.tuebingen.mpg.de/hhblits, or Jackhmmer at http://www.ebi.ac.uk/Tools/hmmer/search/jackhmmer.

Table 2.

Coevolution-derived contact prediction methods

Method summary	Availability	Published
EPC-map [23]—Evolutionary and physicochemical sources of information are combined to make predictions and, hence, work well even when only a few sequence homologs are present	http://compbio.robotics.tu-berlin.de/epc-map/	2014
MetaPSICOV [27]—Combines three approaches: PSICOV, FreeContact, and CCMpred	http://bioinf.cs.ucl.ac.uk/MetaPSICOV/	2014
CCMpred [55]—Performance optimized implementation of the pseudolikelihood maximization (PLM) algorithm using C and CUDA	https://bitbucket.org/soedinglab/ccmpred (downloadable)	2014
FreeContact [56]—Open source implementation of mfDCA and PSICOV	https://rostlab.org/owiki/index.php/FreeContact (downloadable)	2014
GREMLIN [49]—DCA with pseudolikelihood optimization but performs better even with fewer sequences	http://gremlin.bakerlab.org/submit.php	2013
plmDCA [46]—Pseudolikelihood optimization-based method using statistical properties of families of evolutionarily related proteins	http://plmdca.csc.kth.se/ (downloadable)	2013
CMAT [57]—Fully automated web server for correlated mutation analysis; performs homology search, multiple sequence alignment construction, sequence redundancy treatment, and calculates various correlated mutation score measures	http://binfolab12.kaist.ac.kr/cmat/analyze/	2012
mfDCA [45]—Computationally efficient implementation of direct coupling analysis	http://dca.rice.edu/portal/dca/	2011
EVCouplings [4]—Direct coupling analysis using maximum entropy model	http://evfold.org/	2011
MISTIC [58]—Mutual information (MI) theory with sequence-weighting techniques to improve predictability	http://mistic.leloir.org.ar/index.php	2009

2.3. Brief Overview of DNcon

Taking help of graphics processing units (GPUs) and CUDA parallel computing technology, DNcon [21], predicts residue–residue contacts using deep networks and boosting techniques. DNcon was trained and tested using 1426 proteins of which 1230 were used for training and 196 for testing. Multiple ensembles of deep networks were trained using several pairwise potentials, global features, and values characterizing the sequence between contact pairs for predicting medium/long-range contacts. Recently, DNcon’s performance was evaluated in various neighborhood sizes to find that it performs particularly well achieving an accuracy of 66 % for the top L/10 long-range contacts [18]. DNcon showed the best performance among the sequence-based contact predictors in the CASP9 experiment for top L/5 long-range contacts in the free-modeling category, which is the most difficult [17].

3. Methods

The overall steps for using a contact prediction web server (or a downloadable tool) are shown in Fig. 2. The first step in predicting contacts of a protein sequence is to search the input sequence against existing sequence databases and template databases. This is done to check if there are homologous templates and/or other sequences available. If we are really lucky, which is not usually the case, we will find that at least one good homologous template and many predictions about our input sequence can be derived from the template. If we are less lucky, we will find many homologous sequences, if not structural templates, suggesting that we can rely on coevolution-based tools based on the size of the multiple sequence alignment. However, many times the sequence becomes an ab initio target suggesting that we should focus on using sequence-based contact prediction tools. An appropriate contact prediction tool may be selected based on this analysis on availability of homologous sequences and structures. A contact prediction tool predicts contacts with a confidence score associated with each pair, and the predicted contacts are usually ranked according to this confidence score. Depending upon requirement, an appropriate number of contacts need to be selected, for example the top L/5 or top L/2 or top L. Below, we outline the steps that need to be executed to predict residue contacts using DNcon.

Fig. 2.

The process in predicting protein residue contacts

• 1Analyze the input sequence against template databases and sequence databases (for example at http://toolkit.tuebingen.mpg.de/hhpred and http://blast.ncbi.nlm.nih.gov/Blast.cgi) to check if any closely homologous template structures exist. If any such homologous templates are found, template-based contact prediction can generate better results [38, 51]. Instead, if a lot of homologous sequences are found (at least a few hundred), coevolution-derived methods can utilize the homologous sequences’ alignments to make accurate predictions.
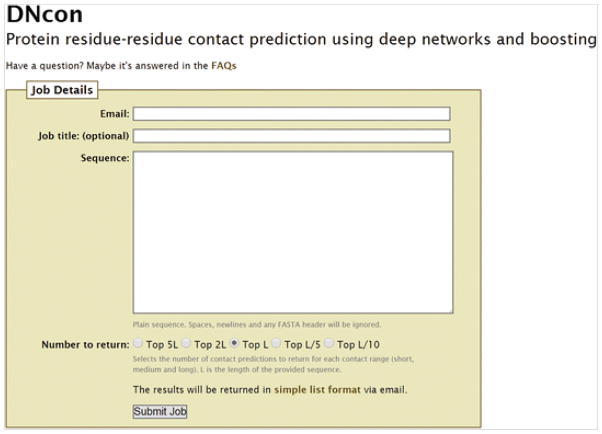
• 2Supply the input sequence to DNcon at http://iris.rnet.missouri.edu/dncon/filling the email address field as well (see Fig. 3). The generated results are sent through an email, and the contents of the email may be saved to a text file. Many other contact prediction servers, however, produce the results in RR format; the description of RR format is at http://predictioncenter.org/casprol/index.cgi?page=format#RR. The contacts predicted by DNcon web server (sent in email) are in a three-column format and the results are sorted according to the prediction confidence score. In each contact row, the first two numbers are residue numbers of the pair of residues predicted as a contact, and the last number is the confidence score of prediction with a score of 1.0 being the most confident prediction.
• 3Decide the minimum sequence separation and calculate the number of contacts required (top L/5, top L, etc.) and filter out all other contacts in the rank below.
• 4
  In the case that contacts are being predicted to evaluate the contact prediction server, precision may be calculated for the selected top contacts. For each predicted contact in the list, the user needs to check if the true distance between the two residues is less than the contact threshold. Specifically, for the contacts predicted by DNcon, the Euclidean distance between the two Cβ atoms of the two residues needs to be computed (also see Notes 1 and ²).

  $$\text{precision}=\frac{\text{number}\text{of}\text{correctly}\text{predicted}\text{contacts}}{\text{total}\text{number}\text{of}\text{predicted}\text{contacts}}$$
• 5The selected contacts may be further visualized within the native structure to observe the coverage of the predicted contacts. In USEF Chimera [52], this can be accomplished using the following steps:

  1. Convert the predicted text file’s contact rows into Chimera’s distance calculation commands, ignoring everything but the first two numbers. For example, “2 50 0.85” will become “distance :10@ca :11@ca”. For precise distance computations “ca” must be replaced by “cb” but since it is convenient to visualize using “ca” (carbon alpha) atoms, using ca atoms is perfectly fine if we only care about visualizing the coverage. Save these distance command rows in a text file, for example, “commands.txt”.

  2. Open the true structure (pdb file) in Chimera.

  3. Open the command line in Chimera from the Tools menu.

  4. Load the distance commands file, commands.txt, using the command “read full_path_to_comands.txt”.

Fig. 3.

A screenshot of DNcon web server at http://iris.rnet.missouri.edu/dncon/. By default, top L contacts are predicted

4. Case Study

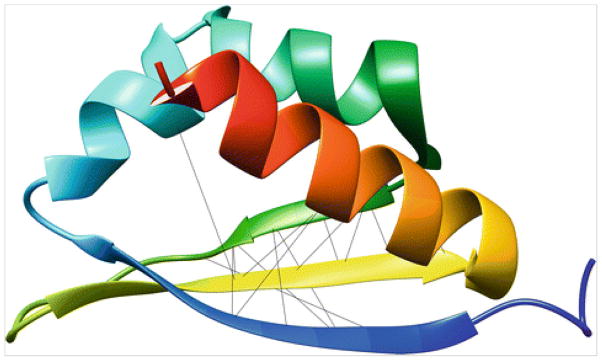
As a case study for using DNcon, consider a small globular protein “1wvn” of 74 residues (accessible at http://www.rcsb.org/pdb/explore/explore.do?structureId=1wvn), which is considered as one of the data sets in EVFOLD [4]. We supplied the sequence to DNcon and saved the contents received in email to the file: 1wvn.txt. It took about 45 min for the web server to send the results. For analysis, we evaluated top L/10 long-range contacts and top L/10 medium-range contacts, i.e., 74/10=7 contacts for each group. First we filtered out all contacts that have sequence separation less than 24 residues, and then we kept only the top seven contacts, to get the long-range contacts. Similarly, for medium-range contacts, we filtered out all contacts with sequence separation of less than 12 residues. In order to evaluate these top seven long- and top seven medium-range contacts, we computed the true distances between the Cβ atoms for each contact in the native structure. From Table 3, we find that the precision of top L/10 long-range contacts is 0.14 and the precision of top L/10 medium-range contacts is 0.86. Furthermore, to visualize how these contacts are distributed over the structure we converted this contact information into the Chimera’s distance command format (for example, “distance :10@ca :39@ca”) and wrote to a text file chimera.txt. After opening the native “pdb” in Chimera, we read the file from command line using the “read” command. Visualization (see Fig. 4) shows that most contacts are clustered around the beta sheet region of the protein.

Table 3.

Top L/10 long-range (left) and medium-range (right) contacts predicted by DNcon for the protein 1wvn and their true distance in the native structure

R1–R2	Sep	Conf	dpdb	R1-R2	Sep	Conf	dpdb
10–39	29	0.902	10.3	39–55	16	0.946	5.3
8–41	33	0.892	13.9	38–56	18	0.946	4.7
20–53	33	0.886	7.6	39–53	14	0.936	6.5
7–42	35	0.873	13.0	38–54	16	0.931	8.2
8–40	32	0.871	11.1	38–55	17	0.923	7.2
10–41	31	0.871	11.2	37–57	20	0.921	5.1
9–40	31	0.869	9.9	41–53	12	0.914	5.8
Precision			0.14	Precision			0.86

First, second, and third columns are the contacting residue pairs with sequence separation between them, and predicted confidence score, respectively. The last column, d_pdb, is the true distance in native structure. Precision is calculated for each category

Fig. 4.

Predicted top 14 long- and medium-range contacts highlighted in the native structure. The lines were shown using distance commands in USEF Chimera