Breaking Good: Accounting for Fragility of Genomic Regions in Rearrangement Distance Estimation

Abstract

Models of evolution by genome rearrangements are prone to two types of flaws: One is to ignore the diversity of susceptibility to breakage across genomic regions, and the other is to suppose that susceptibility values are given. Without necessarily supposing their precise localization, we call “solid” the regions that are improbably broken by rearrangements and “fragile” the regions outside solid ones. We propose a model of evolution by inversions where breakage probabilities vary across fragile regions and over time. It contains as a particular case the uniform breakage model on the nucleotidic sequence, where breakage probabilities are proportional to fragile region lengths. This is very different from the frequently used pseudouniform model where all fragile regions have the same probability to break. Estimations of rearrangement distances based on the pseudouniform model completely fail on simulations with the truly uniform model. On pairs of amniote genomes, we show that identifying coding genes with solid regions yields incoherent distance estimations, especially with the pseudouniform model, and to a lesser extent with the truly uniform model. This incoherence is solved when we coestimate the number of fragile regions with the rearrangement distance. The estimated number of fragile regions is surprisingly small, suggesting that a minority of regions are recurrently used by rearrangements. Estimations for several pairs of genomes at different divergence times are in agreement with a slowly evolvable colocalization of active genomic regions in the cell.

Introduction

Intuition, simplicity, and mistranslations of a so-called Nadeau–Taylor rule have converged to a standard mathematical model for genome rearrangements (inversions, translocations, fusions, fissions, transpositions): Rearrangements are operations acting on linear arrangements of genomic loci and all operations of the same type have the same probability to occur. For example, a usual computational problem is to ask for the minimum number of inversions—that is, reversions of the order of loci within subsegments—that are necessary to transform one order into the other. Sturtevant and Tan (1937) proposed in 1937 that, if the order of letters $L\hspace{0.17em}H\hspace{0.17em}F\hspace{0.17em}E\hspace{0.17em}B\hspace{0.17em}A\hspace{0.17em}D\hspace{0.17em}C\hspace{0.17em}K\hspace{0.17em}I\hspace{0.17em}J\hspace{0.17em}G\hspace{0.17em}M$ depicts the order of loci on the X chromosome of Drosophila melanogaster, while $A\hspace{0.17em}B\hspace{0.17em}C\hspace{0.17em}D\hspace{0.17em}E\hspace{0.17em}F\hspace{0.17em}G\hspace{0.17em}H\hspace{0.17em}I\hspace{0.17em}J\hspace{0.17em}K\hspace{0.17em}L$ depicts the order of orthologous loci in the X chromosome of Drosophila pseudoobscura, seven inversions are necessary to explain the differences between the two orders. In fact six is reachable but a statistician would ask for an estimation of the most probable number of inversions given an evolutionary model. In that case a possible answer is 7.6, if we apply the formula of Caprara and Lancia (2000), assuming equiprobability of inversions.

A consequent number of combinatorial (Fertin et al. 2009) or statistical (Eriksson 2004) variants of the genome rearrangement problem have been proposed, almost always supposing a uniform weight or probability for all inversions. We call such a model the “pseudouniform” model (also called “Random Breakage Model” in the literature). This model has de facto become the null model for the genome rearrangement problem. Growing biological evidence that genomic regions do not break uniformly at random in many genomes referred to this null hypothesis to reject it. There are, however, two major problems with it, independent from the biological validity of the uniform hypothesis.

The first problem is that the Nadeau–Taylor hypothesis does not naturally lead to the pseudouniform model despite their frequent confusion (Wang et al. 2006; Alekseyev and Pevzner 2010; Alexeev et al. 2015). Nadeau and Taylor (1984) formalized a uniform random law for rearrangement breakage locations on genetic maps, on which genes are points on a line, with distances between them. Switching to genome sequences, and knowing that breakages inside genes (Lemaitre et al. 2009) or some conserved intergenic regions (Mongin et al. 2009) are very often selected against, we can reasonably translate their conclusion into the following: Spontaneous rearrangements happen uniformly at random along the genomic sequence and are selected against in some regions, called “solid.” As a consequence, the probability to find a fixed rearrangement breakpoint in a “fragile” region, which is any region outside solid ones, is proportional to its size. In that context, modeling the genome by a permutation of solid regions where fragile regions are contracted is an oversimplification, because a uniform model does not stay uniform when contracting several objects of different sizes (fig. 1A). It is unrealistic, unlikely, and unstable to assume that fragile regions all have the same size and keep the same size during a rearrangement scenario, as in a pseudouniform model.

Fig. 1.—

Transformation of a genome into a permutation of genes. A uniform random breakage in the sequence (A) is not a uniform random breakage in the gene order (B) unless intergenes (the sequences between the subelements) are assigned a probability proportional to their size. Moreover, including these breakage probabilities supposes a rule for their redistribution after a rearrangement, leading to an evolutionary process on breakage probability distributions.

The second problem is that the pseudouniform model assumes that solid regions are known. In practice, comparing genome organizations begins with preparing homologous loci in different genomes, which can be either a selection of orthologous sets of genes or synteny blocks made from genes or genomic alignments (Sankoff and Nadeau 2003). However, real fragile regions could lie within such loci, and real solid regions could lie between two consecutive loci. This makes statistical estimations based on the pseudouniform model depend on the arbitrary choices of data preparation.

Despite these drawbacks, all statistical estimators of genome rearrangement distances based on a uniform model (Wang and Warnow 2001; Larget et al. 2002; Eriksen and Hultman 2004; Berestycki and Durrett 2006; Lin and Moret 2008; Biller et al. 2015) assume that fragile regions are known and all have the same probability of breakage. The same statement holds for simulators aimed at validating inference methods, whether they are ad hoc constructions implemented for the purpose of validating a single method, or less dedicated simulators (Dalquen et al. 2012) (but see a possible alternative with Knibbe et al. 2007; Biller et al. 2016).

Methodological work on deviations from a uniform model concerns giving a different weight to different types of events (Blanchette et al. 1996; Wang et al. 2006); designing models where inversions are weighted by their length, symmetry around a replication origin (Baudet et al. 2014), or by the proximity of their extremities in the cell (Berthelot et al. 2015; Swenson and Blanchette 2015); weighting breakage probabilities by chromatin state (Berthelot et al. 2015); or predicting the existence of hot regions for rearrangement breakages (Pevzner and Tesler 2003; Peng et al. 2006; Alexeev and Alekseyev 2015). The diversity of susceptibilities to rearrangements reflects genetic or epigenetic structural or functional constrains on genome arrangements and rearrangements, like the pattern of repetitions along the genome, chromatin structure, three-dimensional (3D) organization of chromosomes, regulation, replication, or cotranscription (Farré et al. 2015). Fragile breakpoint models (Peng et al. 2006; Alekseyev and Pevzner 2010; Alexeev and Alekseyev 2015) presented a decisive solution to the second concern on the pseudouniform model: Solid regions are uncorrelated from loci given in the input. Yet a constant probability of breakage is still assumed on the fragile regions.

Here, we propose a Markovian model without this homogeneity hypothesis (see the first part of the Results section). This model is called INFER, standing for “INversions in FragilE Regions.” It is defined on solid and fragile regions, where solid regions cannot break, and fragile regions break with given probabilities. The crucial points are that 1) the fragile regions of a genome do not necessarily have the same probability to break and that 2) breakage probabilities in fragile regions evolve together with the genome. We show that this model has an equilibrium distribution in which breakage probabilities are distributed according to a flat Dirichlet law. The INFER model contains as a particular case the truly uniform model—meaning uniform at the nucleotide level—in which fragile regions are broken with a probability proportional to their sizes. In this particular case, the equilibrium distribution of the model resembles the distribution of intergene sizes from diverse organisms (fig. 2).

Fig. 2.—

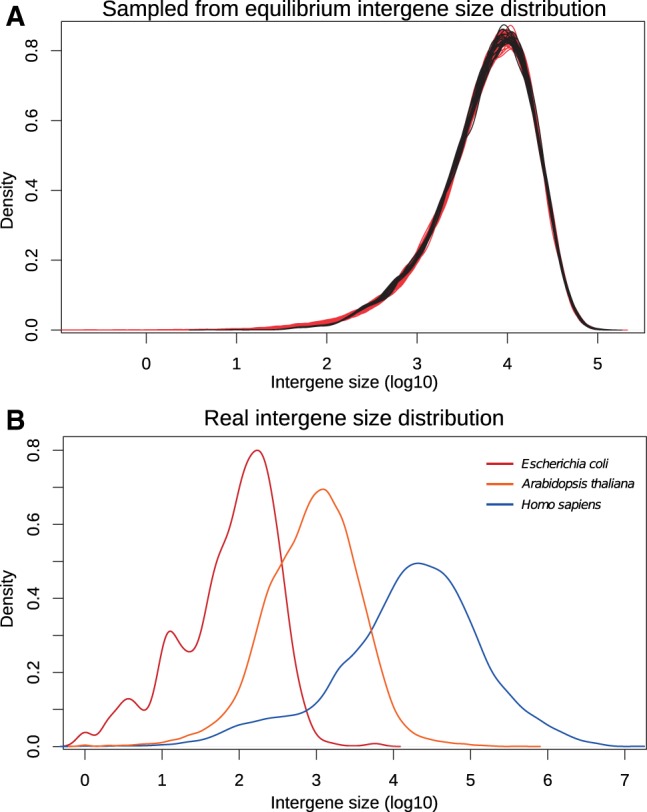
Density of the set of the logarithms (base 10) of intergene sizes from (A) simulated genomes (black) sampled from the Markov chain process starting from a genome with 10,000 solid regions and equally distributed breakage probabilities, applying 500,000 inversions as a burn-in, and then sampling breakage probabilities every 10,000 additional inversions, or sampled genomes (red) by picking values in an exponential distribution and normalizing; (B) real genomes, chosen among diverse model organisms: Homo sapiens (blue), Arabidopsis thaliana (orange), and Escherichia coli (red).

The INFER model can be used for statistical inference with or without the knowledge of the solid and fragile regions, whose number can be estimated, as well as with or without the knowledge of the breakage probabilities, which can be assumed to be distributed according to a Dirichlet law. In the second part of the Results section, we consider the case where the boundaries of the solid and fragile regions are known, as well as the breakage probability of each fragile region. We derive a first statistical estimator of the rearrangement distance between two genomes accounting different probabilities for fragile regions, based on the observed number of “common adjacencies” linking solid regions of both genomes. As expected, this estimator shows similar performances to pseudouniform-based estimators on simulations of a pseudouniform process, and incomparably better performances on simulations of the truly uniform process. This stresses that the two models are not equivalent and switches the null hypothesis from the pseudouniform to the uniform model.

However, as explained in the third part of the Results section, testing this estimator on real genomes revealed that fixing coding genes as solid and breakage probabilities proportional to intergene sizes leads to incoherent distance estimations, as they are systematically lower than a parsimony value. The uniform model, despite bringing an improvement over the pseudouniform model, is still not able to explain the mode of evolution in real genomes. This is coherent with the often observed fact that rearrangement breakage densities measured in genome comparisons are not homogeneous along genomes (among other possible references, see Ruiz-Herrera et al. 2006; Lemaitre et al. 2009; Mongin et al. 2009; Berthelot et al. 2015), or that some regions are recurrently used in evolutionary scenarios (Pevzner and Tesler 2003; Alekseyev and Pevzner 2007, 2010). Thus, we propose a second INFER-based estimator of the rearrangement distance between two genomes, this time considering the number of fragile regions unknown, as first proposed by Alexeev et al. (2015) and Alexeev and Alekseyev (2015), and their exact breakage probabilities unknown but distributed according to a flat Dirichlet law. As predicted by Pevzner and Tesler (2003), estimates of the number of fragile regions are surprisingly low, an order of magnitude lower than the number of intergenes, or even the number of regions with open chromatin. It gives the image of a genome organization in which a small measurable number of regions are recurrently used by rearrangements. We finally discuss the relevance of this model with respect to several genomic observations and the 3D conformation of chromosomes in the cell.

Results

In the first part we describe the INFER model and its stationary distribution. Then in the second part we show with simulations how it can be used with fixed known solid regions and breakage probabilities. In the third and last part, we show that on real genomes we have to assume that solid regions and breakage probabilities are unknown. We give estimates of some genomic distances, which are coherent with parsimony solutions (that is, higher or equal than the inversion distance), though the estimator theoretically allows for incoherence.

INFER, An Evolutionary Model Accounting for the Diversity of Fragile Regions, and Its Stationary Distribution

We model a genome by a signed permutation evolving by inversions. This captures a single linear chromosome but can be extended to genomes with several chromosomes or to circular chromosomes; however, this requires technical additions that we only develop in the supplementary material, Supplementary Material online, to keep the description clearer.

A genome $G=(\pi ,p)$ is made up of two components:

• a signed permutation π over $\{1,\dots ,n\}$, that is, an ordering of the elements of $\{1,\dots ,n\}$ where each element is given a sign, + or − (+ usually omitted), representing the reading direction of an element. The elements of the permutation are “solid regions,” which can be considered known (identified with coding genes for example) or not. Two additional fixed solid regions ${\pi }_0=0$ and ${\pi }_{n+1}=n+1$ are added to any permutation π. An “adjacency” is a pair of two consecutive regions, read in either directions ${\pi }_i{\pi }_{i+1}$ or $-{\pi }_{i+1}-{\pi }_i$.

• a vector p of $\tilde{n}=n+1$ breakage probabilities, $p_i>0,\hspace{0.17em}0\le i\le n$, with $\sum _i{p}_i=1$. Each number p_i denotes the probability to break in the “fragile region” between π_i and ${\pi }_{i+1}$ in the permutation π. Breakage probabilities can also be considered known (proportional to intergene sizes for example) or not.

Solid regions have no thickness, because solid region sizes have no importance for the calculations. However, when we compare the model with data, we suppose that they encompass genomic regions of diverse sizes. We suppose a homogeneity of breakage probability inside a fragile region, so fragile regions should not be too large.

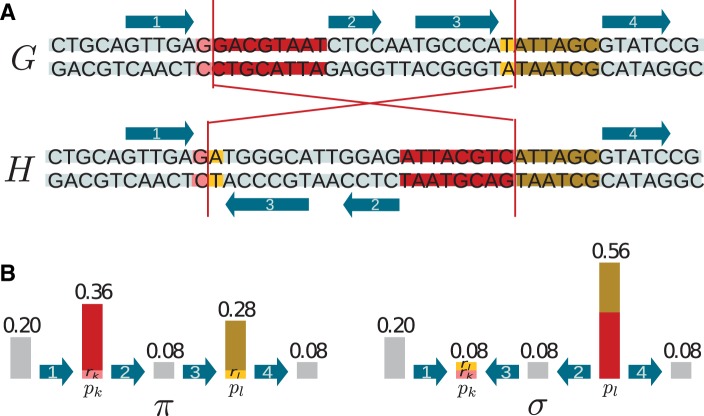
An “inversion” on a genome breaks two fragile regions according to their breakage probabilities, reverses the segment between them, and updates the breakage probabilities. More precisely, choose two fragile regions k and l with probability p_k and p_l. If k is equal to l, nothing is changed to the genome. Otherwise, suppose k < l then pick two numbers r_k and r_l uniformly at random respectively in $]0,p_k[$ and $]0,p_l[$. Reverse the segment ${\pi }_{k+1},\dots ,{\pi }_l$ in the permutation, flip all signs inside this segment, reverse the order of breakage probabilities between k + 1 and l − 1, and define new breakage probabilities $p_k=r_k+r_l$ and $p_l=p_k+p_l-r_k-r_l$ (fig. 1B). Through such an operation, n and $\sum _i{p}_i=1$ are invariant. A nonzero p_i cannot become zero, which prevents any absorbing state. This way of redistributing breakage probabilities is chosen to generalize the exchange of genetic material by intergenes if breakage probabilities are proportional to intergene sizes.

The evolutionary model INFER is defined as a Markov chain in which states are genomes and transitions are inversions. It is a symmetric Markov chain: The probability density from genome G to genome $G\prime$ is the same as the probability density of the reverse step (see supplementary material, Supplementary Material online, for the proofs). Hence it has a stationary distribution, which is a uniform distribution “over all genomes.” Thus, regardless of an initial genome, after a long evolutionary time, all possible genomes are equally probable, for all possible orderings of the solid regions and all possible breakage probability vectors for the fragile regions.

This uniform distribution restricted to the breakage probabilities corresponds to a flat Dirichlet distribution (the symmetric Dirichlet law with a single parameter α = 1). Importantly, this does not mean that all fragile regions have the same probability to break, as traditionally assumed in the pseudouniform model: Under the evolutionary process considered here, where breakage probabilities coevolve with genome organization, the vector where $p_1=p_2=\dots =p_{{\displaystyle \tilde{n}}}$ is a very special improbable and unstable state. Neither does it mean that individually breakage probabilities can be assumed to be taken from a uniform law. Sampling uniformly a vector $p=\left\{p_i\right\}$ of breakage probabilities (verifying $\sum _i{p}_i=1$) can be done by picking independently every p_i from an exponential law, and normalizing by the sum of all picked values.

We define the “uniform” model as the particular case of INFER where breakage probabilities are uniform at the nucleotide level, and thus proportional to the sizes of fragile regions at the region level. If ${\nu }_i\ge 0$ is the number of nucleotides between solid region π_i and solid region ${\pi }_{i+1}$, then $p_i=({\nu }_i+1)/{\sum }_{j=0}^n({\nu }_j+1)$, so that it is possible to break between any two pairs of nucleotides. In that case, the inversion breaks between two nucleotides and two fragile regions exchange part of their material (fig. 1A).

Note, as a curiosity, that in this particular case, the restriction of INFER to the set of breakage probabilities (or intergene sizes) is a generalized Sankoff–Ferretti (Sankoff and Ferretti, 1996) model of chromosome size evolution (De et al. 2001). It is also identical to the so-called top-swap Markov chain (Bhatnagar et al. 2007), which has been proved to converge fast. This means that sampling can either be achieved with the exponential law as described in the previous paragraph, or by letting the Markov chain run for a while from any starting point and sampling from its last steps. Figure 2A shows the distribution obtained with both sampling methods, which yield highly similar results. Rather than being concentrated on a single intergene size, this distribution spans a wide range of intergene sizes. This means that once the inversion process has reached its equilibrium, the genome is likely to encompass a diversity of intergene sizes, and thus a diversity of breakage probabilities. In other words, at any step of the process, some fragile regions are more fragile than others.

In contrast, in the pseudouniform model all p_i are equal to $\frac{1}{\tilde{n}}$, and stay equal all along the scenario, rather than being updated at each rearrangement.

Figure 2 compares an intergene size distribution sampled from the equilibrium distribution of the uniform model and some real intergene size distributions, chosen among diverse model organisms. The similarity between all curves (with scale differences due to genome sizes and gene numbers) suggests that inversions could participate in shaping intergene sizes. However, other major factors are duplications, insertions, deletions, regulation, recombination, and dispersion of insertion sequences or transposable elements. Providing a full explanation of whole distributions is out of the scope here, so we intentionally do not fit the real curves or estimate parameters from them. But the equilibrium obtained under our simple neutral inversion process is sufficiently close to real distributions from diverse organisms to serve our purpose here: It provides a mathematically grounded and realistic basis for estimating the rearrangement distance between two genomes.

Distance Estimators for Simulated Genomes with Known Fragile Regions

In this section, we use simulations and statistical estimators supposing that solid and fragile regions are given. On biological data this situation is theoretically possible if we consider that genes are solid and intergenes are fragile, or if fragility data along genomes are available.

The Behavior of Pseudouniform-based Distance Estimators

Because most statistical estimators are developed under a pseudouniform model, we first test whether they can be considered a good approximation under the uniform model. We use three standard estimators of the number of inversions between two genomes, given the relative order of orthologous loci, that were proposed in the literature (we tested several others—Caprara and Lancia 2000; Berestycki and Durrett 2006; Lin and Moret 2008; Alexeev and Alekseyev 2015—and none has a significantly different behavior). Their aim is, given two genomes, one evolved from the other by applying k inversions, to recover k. One tested estimator is the “inversion distance,” that is, the minimum number of inversions necessary to transform one genome into another (Hannenhalli and Pevzner 1999), noted ID. We also call it the estimator based on parsimony. A second is $\widetilde{DCJ}$ (Biller et al. 2015), a statistical estimator based on the expected number of common adjacencies between two genomes under a pseudouniform model. A “common adjacency” of two genomes G and $G\prime$ defined on the same elements is an adjacency present in both, in one reading direction or the other. The last estimator, which we call EH (Eriksen and Hultman, 2004), is a statistical estimator of the number of inversions based on the expected number of cycles of the so-called breakpoint graph (see supplementary material, Supplementary Material online), under the pseudouniform model.

In figure 3, we can see the average result of evolving 100 times a genome with n = 1000 solid regions by k inversions (k is on the x-axis), and computing the three estimates (values are on the y-axis). In figure 3A, the genomes are evolved using the pseudouniform model. We can see three phases in this graph, which correspond to well-known results (Berestycki and Durrett 2006)): From k = 0 to $k=n/2$, the three methods follow y = x and thus correctly recover k. Between $n/2$ and $O(n\log \hspace{0.17em}n)$, the inversion distance ID leaves the diagonal while the two statistical methods $\widetilde{DCJ}$ and EH give a rather good estimate. For $k>O(n\log \hspace{0.17em}n)$, the three methods saturate, that is, the final genome no longer depends on the initial genome and it becomes impossible to guess k.

Fig. 3.—

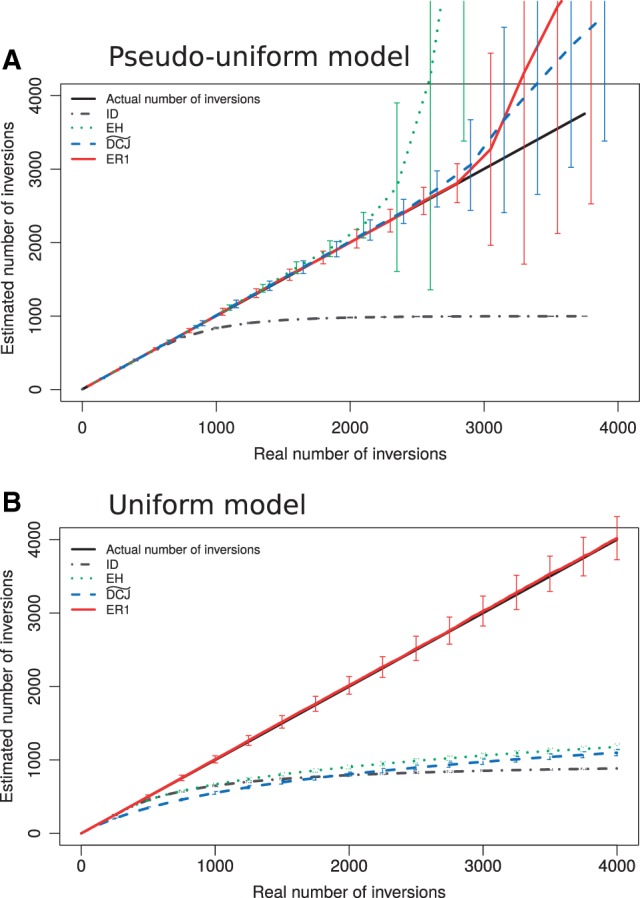
Behavior of rearrangement distance estimators on 100 simulations from a permutation of n = 1,000 elements evolved by inversions using (A) a pseudouniform model, and (B) a uniform model, with initial breakage probabilities drawn from a flat Dirichlet distribution. The real number k of inversions is on the x-axis, and the estimated number of inversions $\hat{k}$, according to several methods, is on the y-axis. It emphasizes that pseudouniform and uniform models are very different.

In figure 3B, genomes are evolved according to the uniform model, where an initial intergene size distribution is sampled from its equilibrium distribution. Now the behaviors are radically different: $\widetilde{DCJ}$ saturates very quickly, whereas EH and ID follow the y = x diagonal a bit longer but do not give the right answer as soon as $k>n/2$. Interestingly, EH is not estimating better than ID, while $\widetilde{DCJ}$ is worse for a large part of the simulation. Therefore, in that case, the parsimony estimation, which was the worst in figure 3A simulation, has the best position, although with low performance.

Thus, the pseudouniform model, under which almost all combinatorial and statistical rearrangement studies have been developed up to now, is not an adequate framework to build methods to recover the number of rearrangements from real data, even if they are assumed to occur under a neutral process without any additional biological constraints.

An INFER-based Distance Estimator: ER1

We now describe a first INFER-based estimator of the number of inversions separating two genomes. Similarly to several other studies (Berestycki and Durrett 2006; Alexeev and Alekseyev 2015), this estimator is based on expected values for some parameters of dynamic random graphs. Indeed, the INFER model of genome evolution is analogous to a model of random graph evolution. Identify $\tilde{n}=n+1$ fragile regions of a genome with the $\tilde{n}$ vertices of a graph: Each vertex has a weight, which is the region breakage probability. Each time an inversion between fragile regions i and j is applied on a genome, an edge between vertices i and j is added to the graph. This yields a Markov chain close to the standard Erdös–Rényi (Erdös and Rényi 1960) random graph evolution. The difference is that, in the Erdös–Rényi model, edges are taken uniformly at random, like in the pseudouniform model, whereas an edge ij is here added with probability $p_i{p}_j$, and p_i and p_j are updated as in the INFER model. Loops and multiple edges are allowed (see supplementary material, Supplementary Material online, for a full description of this analogy with a proof of good approximation).

Berestycki and Durrett (2006) remarked that the number of vertices minus the number of components of the graph approximates well the minimum number of inversions, and deduced an estimator under the pseudouniform model. Unfortunately, their method used the pseudouniform model and is hardly generalizable if fragile regions have different breakage probabilities. Indeed, although random graphs with prescribed degree distributions have been much studied (Chatterjee et al. 2011), there is no tractable general formula for the number of connected components of any random graph with k edges if they are not drawn from a uniform distribution.

There is, however, a way to compute an expected value for the number U of isolated vertices in a random graph with k edges, and it can be proven that this U is a good approximation of the number C of common adjacencies of genomes separated by k inversions (see supplementary material, Supplementary Material online). The expected number of isolated vertices in a random graph with $\tilde{n}$ vertices where k edges have been successively added is given by

$$E(U)=f_{\tilde{n},p}(k)\text{with}{f}_{\tilde{n},p}(k)=\sum _{i=0}^{\tilde{n}}(p_i^2+(1-p_i{)}^2{)}^k,$$ (1)

where the term inside the sum depicts both cases in which one vertex remains isolated after adding k edges: $p_i^2$ is the probability of creating a loop, and ${(1-p_i)}^2$ is the probability of adding an edge between any other two vertices. This formula is valid for any vector $p=\left\{p_i\right\}$ of breakage probabilities and can be used if p is given.

Our estimator of k as a function of the observed number C of common adjacencies consists in inverting the function f in Equation 1, as in a method of moments. We call it ER1, which stands for “Erdös–Rényi” with one observation (there is an ER2 in the sequel of the article):

$$\widehat{k}=f_{\tilde{n},p}^{-1}(C).$$ (ER1)

We do not know how to analytically invert f, but f is monotonous, twice derivable in k, so the equation can be efficiently solved numerically.

The practical behavior of this estimator can be observed in figure 3A and B. In figure 3A, where p was set to $\{p_i=\frac{1}{\tilde{n}}\}$ (pseudouniform model), we see a similar performance compared to $\widetilde{DCJ}$ and EH. In figure 3B, the breakage probabilities in the initial genome were randomly drawn from a flat Dirichlet distribution (equilibrium of the uniform model) and used in the estimation. We see that the estimator is keeping its accuracy up to values of k which are far above the saturation points of all other methods. Note that, as expected, ER1 performs better on simulations with the truly uniform model than on simulations with the pseudouniform model. Indeed, the truly uniform model implies a diversity of breakage probabilities (as long as there is a diversity in the lengths of fragile regions), which ER1 is designed to exploit. When there is a diversity of fragility levels across regions, some regions are not so prone to rearrangements and behave as slow evolving sites that keep the signal for a longer time. ER1 can thus exploit this signal to correctly infer the evolutionary distance even if k is large. On the contrary, in the pseudouniform model, all sites evolve at the same speed and the signal is lost more quickly.

A Distance Estimator for Real Genomes, with Unknown Fragile Regions

In this section, we suppose that fragility data are not available, which is the case for all real genome comparisons so far. Indeed, we first show that the identification of genes with solid regions and intergenes with fragile regions yields incoherent results on a uniform model. If fragile regions are not given, then their lengths are not given as well, and breakage probabilities are not known. So we leave the uniform model, and assume the INFER equilibrium distribution for breakage probabilities, independently of the size of fragile regions. Note that we do not estimate the positions of the fragile regions, but only their number. Anchors in the genome, which can be orthologous genes or synteny blocks, are still used as an input. Broken regions, which are a subset of regions between anchors, are necessarily fragile. But the estimated number of fragile regions can be higher or lower than the number of regions between anchors. Indeed, some segments may be hypothesized solid (anchors) whereas they are estimated (at least partly) fragile, and some segments may be hypothesized fragile, whereas they are estimated solid.

Why the Number of Solid and Fragile Regions Is Unknown

As inversion distance (ID) is the length of the most parsimonious scenarios to transform the initial genome into the final one, a necessary condition for an estimator to be valid is that the estimated number of inversions is equal to or higher than the inversion distance. For instance, in simulations of the uniform process (fig. 3B), it is always the case for our estimator, but not for $\widetilde{DCJ}$. This shows that estimation under a model on data generated with a different model can lead to incoherence. This feature can be used to test the model on data: If inversion distance is always higher than the estimator built under a certain model, this is a sign that this model and/or its parameters do not explain the data well.

We used this criterion to evaluate the behavior of the ER1 estimator on amniote genomes. Specifically, we computed the inversion distance and the ER1 distance estimations for all 21 pairs from 7 amniote genomes, at different evolutionary distances (human, chimp, macaca, mouse, horse, opossum and chicken, see Methods). This implies generalizing the model and the estimators to multiple chromosomes (see supplementary material, Supplementary Material online), and retrieving and filtering sets of pairs of orthologous genes for each pairwise comparison (see Methods). Results are summarized in figure 4. We identify coding genes with solid regions, and set the breakage probabilities either all equal (pseudouniform model) or proportional to the intergene sizes (uniform model)—that is, the number of nucleotides between the genes that are outside any gene, as detailed in Methods. All pairwise comparisons yield estimated distances which are smaller than the inversion distance. Estimations under the pseudouniform model systematically give impossible solutions, whereas the uniform model is already a decisive improvement. It emphasizes again that both models are not equivalent to explain the organizations of extant genomes. However, estimations under the uniform model still output values lower than the inversion distance. This tends to reject the particular case of the uniform model where fragile regions are exactly identified with intergenic regions, as accounting for amniote genome evolution, in agreement with several earlier results (among others Pevzner and Tesler (2003); Peng et al. 2006; Alekseyev and Pevzner 2007; Lemaitre et al. 2009; Mongin et al. 2009; Berthelot et al. 2015; Naville et al. 2015), although sometimes it is not clear whether the uniform or the pseudouniform model was rejected, or on which fragile regions a uniform or pseudouniform model should act.

Fig. 4.—

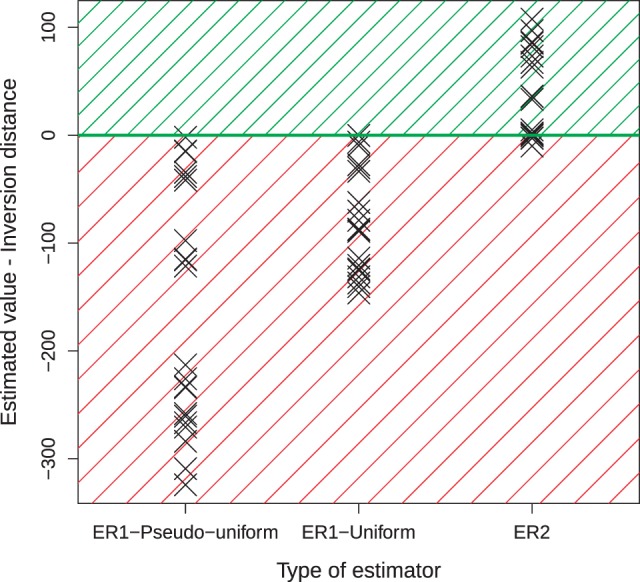
Difference between the estimation of the genomic distance and the inversion distance (y-axis), for statistical estimators with different parameters (number of solid regions and breakage probabilities) (x-axis). The points represent 21 pairwise amniote genome comparisons. Distance estimates are obtained from (ER1—pseudouniform), if solid regions are genes and intergene breakage probabilities p_is are all equal; (ER1—uniform), if solid regions are genes and p_is proportional to intergene sizes; (ER2), with a parameterized number $\tilde{n}$ of fragile regions, and breakage probabilities distributed in fragile regions according to a flat Dirichlet law. The difference should be nonnegative if the scenario is likely, given the parameters $\tilde{n}$ and $p_i$.

There are several possible explanations for the incoherence of ER1–pseudouniform and ER1–uniform. For example, it is possible that we do not model the right rearrangements. The inclusion of nonreciprocal translocations (sometimes called transpositions or block transpositions) of large genomic segments could modify the estimations (Alexeev et al. 2015). These rearrangements have rarely been reported for large segments (Schubert and Lysák 2011) and their prevalence is debated (Alexeev et al. 2015). Here we choose to ignore their effect. Also, it is possible that we do not define well the fragile regions by identifying them with intergenic regions. A uniform breakage model is still possible on a set of fragile regions taking other genetic or epigenetic factors into account. For example, we tried to define fragile regions as intergenic regions with open chromatin but this made the results worse (see supplementary material, Supplementary Material online). It is also possible that ER1 has some flaw that is visible on amniote genomes but not on simulations. We tested simulations on multichromosomal genomes, applying the same filters as in real genomes (see supplementary material, Supplementary Material online) to address possible differences as much as possible, and did not find any qualitative difference. The incoherence of ER1–pseudouniform and ER1–uniform can be finally explained and repaired by parameterizing n and fitting it to the data, as detailed below.

Coestimating the Distance and the Number of Fragile Regions: ER2

The number $\tilde{n}=n+1$ of fragile regions is a parameter of the model and it is not necessarily known in practice. If $\tilde{n}$ is not known, neither are the breakage probabilities. We cannot estimate all of them with only the observation of two genomes. Thus, in the following, we assume that breakage probabilities are distributed along the unknown $\tilde{n}$ fragile regions according to a flat Dirichlet distribution, because it is the stable distribution of the model. In this way, the distribution of breakage probabilities is the equilibrium of the model, but can deviate from the fragile region sizes, so it allows deviations from a uniform model. We then have to estimate both $\tilde{n}$ and the rearrangement distance k.

The ER2 estimator is based on two observations. The first is the number of broken regions $\tilde{n}-C$, where C is the number of common adjacencies. For this we need the estimation of C. In Equation 1, we have the expression of E(U) as a function of $\tilde{n}$, k, and {$p_i$}, which approximates E(C). If we suppose that the breakage probabilities are distributed according to a flat Dirichlet law, we get rid of the p_is using estimations of the moments of a flat Dirichlet distribution, and approximate E(U) by the following expression depending only on k and $\tilde{n}$ (see supplementary material, Supplementary Material online, for the algebraic transformations and computational issues).

$$\begin{array}{lll}C& \approx & E(U)=f_{\tilde{n},Dirichlet(\tilde{n})}\\ & \approx & f_{\tilde{n}}^{\prime }(k)=\tilde{n}{\sum }_{l=0}^{\infty }\frac{{(-2k)}^l}{{\Pi }_{u=0}^{l-1}(\tilde{n}+u)}\end{array}$$ (2)

This function alone is not sufficient to estimate two parameters k and $\tilde{n}$. So we make a second observation and compute its expected value: Let C₂ be the random variable which counts the number of “squares of adjacencies.” Comparing genomes G and $G\prime$ on the same elements, recall that an adjacency is a pair ab of consecutive signed elements, and that adjacency ab is considered the same as adjacency $-b-a$. A square of adjacencies consists of adjacencies ab and cd in G such that adjacencies a – c and – bd are observed in $G\prime$. It means that the breakpoint graph (see supplementary material, Supplementary Material online) forms a cycle with four vertices. This is the probable trace of one inversion on these adjacencies, while no other inversion used them.

Recall that the common adjacencies of G and $G\prime$ are identified with the number of isolated vertices in a random graph. Similarly, squares of adjacencies are often isolated edges in the same random graph (see supplementary material, Supplementary Material online), where an isolated edge is an edge xy whose extremities are different and not involved in another nonloop edge. The expected number of isolated edges in a random graph with $\tilde{n}$ vertices, when k edges are successively added, is given by

$$g_{\tilde{n},p}(k)=k\times \sum _{i=0}^{\tilde{n}}\sum _{j=0}^{\tilde{n}}{p}_i{p}_j\times {(p_i^2+p_j^2+{(1-p_i-p_j)}^2)}^{k-1}$$ (3)

which sums, over all possible edges, the probability that any edge is added once and its vertices never touched otherwise, allowing loops (i.e., edges whose two extremities are the same vertex).

By using this equation to approximate $E(C_2)$, performing a series of algebraic calculations, approximations, that are detailed in the supplementary material, Supplementary Material online, we obtain:

$$\begin{array}{ll}{g}_{\tilde{n},Dirichlet(\tilde{n})}(k)& \approx g_{\tilde{n}}^{\prime }(k)\\ & =k{\tilde{n}}^2\sum _{l=0}^{\infty }\sum _{m=0}^{\infty }\frac{{(-2(k-1))}^{l+m}(l+1)(m+1)}{{\Pi }_{u=0}^{l+m+1}(\tilde{n}+u)}\end{array}$$ (4)

Equations (2) and (4) describe E(C) and $E(C_2)$ as two functions of $\tilde{n}$ and k. Successive terms of the infinite sum can be computed iteratively, avoiding the linear products and allowing fast computations (see supplementary material, Supplementary Material online). The infinite sum has to be interrupted at some point for the computations.

With the observation of $\tilde{n}-C$ and C₂, we can estimate k and $\tilde{n}$ by numerically inverting the two functions $f\prime$ and $g\prime$. We call this the ER2 estimator, standing for Erdös–Rényi with two observations. Figure 5A shows the ability to estimate a close value for $\tilde{n}$ on simulations. Results obtained on the amniote genomes are depicted in figure 4 (ER2). This time, as we can expect from a plausible model, the estimated distance is larger or equal to the inversion distance given by the parsimony. Interestingly, the estimated number of fragile regions $\widehat{\tilde{n}}$ is systematically inferred an order of magnitude under the number of intergenes in the input.

Fig. 5.—

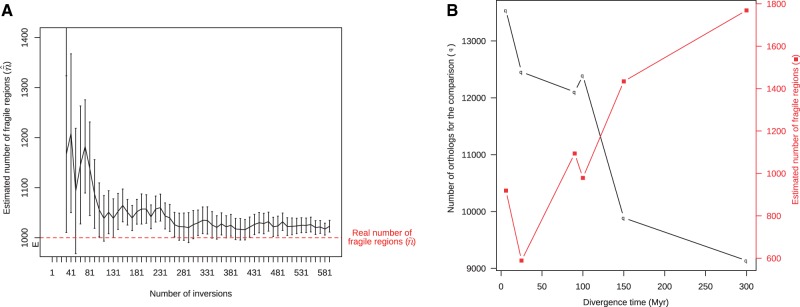
Estimations of the number of fragile regions ($\widehat{\tilde{n}}$). (A) On simulated data. A genome with n = 1000 genes is evolved 20 times with inversions, and the number of fragile regions ($\tilde{n}$) is estimated from the comparison of the initial and final genomes, using only the values for B and C₂. The estimator gets the right order of magnitude from $k=n/10$ rearrangements, but constantly slightly overestimates the real number. (B) On real data. Six pairwise amniote comparisons at different divergence time were used (human with chimpanzee, macaca, mouse, horse, opossum, and chicken). Although the number of available orthologs for the comparison is expectedly decreasing with divergence time (taken from lower bounds from paleontological studies; Benton and Donoghue 2007), the estimated number of fragile regions is increasing.

Figure 5B summarizes the obtained results. Although the number of intergenes, corresponding to the number of found one-to-one reliable nonoverlapping orthologs between species, is around 10⁴, $\widehat{\tilde{n}}$ varies from 589 to 1,769 depending on the compared pair of genomes. We tested the robustness of the ER2 estimator when the number of orthologous genes varies in input (see supplementary fig. S3, Supplementary Material online). We propose an interpretation of the difference between the number of intergenes and the number of fragile regions based on the 3D structure of chromosomes in the following section.

Methods

Mathematical developments are all included in the Supplementary Material online, including the transition matrix of INFER, which proves convergence to the equilibrium distribution, the analogy with random graph evolution, the estimators of random graph parameters, the description of breakpoint graphs, and multichromosomal genomes. Here we only detail how we retrieved real genomic data to test our estimators.

Intergene Sizes

For figure 2, we retrieved all gene coordinates of the Escherichia coli genome from Hogenom (Penel et al. 2009), and of the Arabidopsis thaliana and Homo sapiens genomes from Ensembl (Vilella et al. 2009). We ignored overlapping genes and reported only nonnegative intergene sizes. Then we reported the number of nucleotides between any pair of consecutive nonoverlapping genes, including centromeres, and adding telomeres (number of nucleotides from the extremity of a chromosome and the first gene from this extremity).

Intergene sizes used in the computation of breakage probabilities for the ER1 estimator are computed as the number of nucleotides which are not in a gene (according to the Ensembl coordinates) between two genes taken in the data set. As we filter the data, it is possible that there are some coding genes between two consecutive genes in the data set, so it can differ from the simple computation of the size of the region between two consecutive genes in the data set. We tried ER1 with both values and it did not make any qualitative difference in the results.

Anchors in Amniote Genomes

Gene coordinates and one-to-one orthologs were downloaded from the Ensembl Compara database (Vilella et al. 2009) (using Biomart). We filtered all genes whose coordinates intersect another gene in the data set, so all anchors are disjoint.

“Lonely genes”, that is, genes that are not involved in common adjacencies, are very often annotation artifacts that blur the inversion signal. Indeed ortholog identification has a false positive rate which very often results in lonely genes. We give several arguments for this in the supplementary material, Supplementary Material online, comparing the number of lonely genes in simulations and in biological data. Thus we remove from the data set all lonely genes. The remaining pairs of orthologs were used as anchors.

The breakage probabilities for the uniform model were then defined as the cumulated size of all intergenic regions between two anchors (as genes were filtered, a region between two genes can contain filtered coding genes). An alternative set of breakage probabilities has been computed as the quantity of open chromatin between markers.

Software Availability

A Python code for ER1 and ER2 is available upon request to the corresponding author. It takes as input two genomes in the form of a multichromosomal permutation, and optionally a vector p of breakage probabilities, and outputs the estimated rearrangement distance, the parsimony DCJ distance, and the estimated number of fragile regions.

Discussion

We successively discuss three main results: The construction of a sound model of evolution by inversions and its equilibrium distribution, the importance of including intergene sizes in the construction of a uniform breakage evolutionary model, and the generalization to nonuniform models, accompanied by statistical estimators of their parameters.

Slow and Fast Evolving Sites

Our first contribution is the elaboration of a model of genome evolution by inversions, where 1) the breakable regions of a genome are allowed to differ in their breakage probabilities and 2) those breakage probabilities coevolve with the order of solid regions. This dynamical process has an equilibrium distribution, which is the uniform distribution over all possible genomes. From the point of view of breakage probability distribution inside a genome, this is equivalent to a flat Dirichlet distribution for the probability vector p. Up to a normalization term, this means that under equilibrium, each breakage probability p_i can be considered distributed according to an exponential distribution, or a Gamma law with parameter 1.

We implemented our estimator ER2 with this parameter 1, because it is the equilibrium distribution of our model, which is the generalization of the Nadeau–Taylor model. However, this estimator could very well be implemented with a nonflat symmetric Dirichlet distribution for p, with any parameter α. Up to normalization, this would amount to have each breakage probability p_i follow a Gamma law with parameter α.

It is interesting to note that, concerning evolution of genomic sequences by substitutions, the introduction of a Gamma law differentiating sites according to their evolutionary rates has been a great progress in phylogenetic inference (Yang 1996). It allows us to give the adequate relative importance to different sites for carrying information about the recent (for fast evolving sites) or deep (for slow evolving sites) evolution.

This opens the path to using rearrangements in phylogeny with a finer model. Probably this would not go without modeling also the evolution of gene contents of genomes, because in reality, contrary to our simulations, the dynamics of gains and losses of genes affect the conservation of the gene order signal.

What Is a Uniform Model of Genomic Breakage?

The first mathematical studies on genome rearrangements were parsimonious reconstruction of inversion scenarios (Sturtevant and Novitski 1941; Hannenhalli and Pevzner 1999). In that context only gene orders matter. Permutations of genes have become a popular object to depict gene orders, and statisticians first constructed their models on permutations (Larget et al. 2002; Eriksen and Hultman 2004). But this was forgetting an important element, which would impact combinatorial or statistical modeling approaches.

The formulation by Nadeau and Taylor of the uniformity of breakage along genomes was that “rearrangement breakpoints are randomly distributed in mammalian genomes.” Genomes were accessible through genetic maps at that time, so genes were considered as point loci, without thickness, themselves distributed uniformly. Knowing more today about genome architectures, we have to interpret this hypothesis to formulate mathematical models. Signed permutation was a strange answer: It gave thickness to genes and removed it to intergenes. An alternative interpretation is to give a thickness to both: A uniform probability of breakage in intergenic regions at the nucleotide level.

We showed that forgetting intergene sizes (the pseudouniform way) leads to probabilistic models that are unable to perform better, and often perform worse, than parsimony on simulations with a truly uniform model in the sense of Nadeau and Taylor.

We argue for a switch of the null hypothesis, which should be uniform and not pseudouniform. Standard simulators of gene order evolution should adopt a uniform hypothesis in the absence of knowledge on biological constraints.

Towards a General Model for Genome Rearrangements

After clarifying what a uniform model is, our construction also allows for the exploration of deviations. Indeed, there is now a diversity of evidence for a complex distribution of rearrangement breakpoints inside genomes. We can summarize some of them as follows.

1. An excess of density in rearrangement breakpoints in mammalian genomes has been observed in small intergenes (Lemaitre et al. 2009; Mongin et al. 2009; Berthelot et al. 2015). It has been successively attributed to positive selection (Roberto et al. 2007), negative selection in larger intergenes (Peng et al. 2006; Mongin et al. 2009; Naville et al. 2015), fragility due to transcription and early replication activity (Lemaitre et al. 2009), or low chromatin condensation (Berthelot et al. 2015).

2. Correlations with various genomic elements have been reported, like repeated elements and GC content (Ruiz-Herrera et al. 2006; Farré et al. 2015). The causal role of repeated elements is evident is some cases, but in general it is unclear where these strong correlations come from. It has been hypothesized that all correlations can be explained by gene density (Berthelot et al. 2015).

3. Parsimonious estimations of rearrangement distances imply that some regions should be more often broken than others (Pevzner and Tesler 2003; Alekseyev and Pevzner 2007). This argument has been challenged (Bergeron et al. 2006; Sankoff 2006; Attie et al. 2011), but our study eventually supports this conclusion. These regions are supposed to be rearrangement hotspots, and have been hypothesized to have a limited lifespan (Alekseyev and Pevzner 2010).

4. Small inversions have been observed to be more frequent than large ones (McLysaght et al. 2000), which induce a concentration of couples of breakages.

5. A 3D positional bias of genomic regions has been invoked (Swenson and Blanchette 2015).

Alternatives to the (pseudo)uniform model are often called for (Farré et al. 2015), but precise formulations are rare. Pevzner and Tesler (2003) and Alexeev and Alekseyev (2015) proposed that a subset of intergenes should be considered fragile. Mongin et al. (2009) proposed that genomic regions between genes that are regulatory elements should be considered solid. Alekseyev and Pevzner (2010) described a birth and death process for the positions of fragile regions. Berthelot et al. (2015) observed that the density of breakage in mammalian genomes in an intergene i is proportional to ${\nu }_i^c$, where ν_i is the intergene size and c < 1 is a constant integrating chromatin density. They also proposed that fragility is assigned to couples of regions rather than, or in addition to, individual regions, which is also the idea proposed by Swenson and Blanchette (2015).

As remarked by Farré et al. (2015), none of these models can explain all the observations on its own. For example, obervations 1 and 3 are not implied one by another and models accounting for one do not necessarily account for the other. We tried to translate the chromatin condensation parameter of Berthelot et al. (2015) into a probability and to apply our estimator ER1 to it. It gave incoherent results like the pseudouniform model. This is not surprising because this power function ${\nu }_i^c$ with a number c close to zero has the effect of uniformizing the breakage probabilities with respect to intergene sizes. We also tried ER2 on the model proposed by Alexeev and Alekseyev (2015). Specifically, as in INFER, fragile regions are unknown, but the individual p_is are distributed according to a uniform law, which means $\left\{p_i\right\}$ is distributed according to a symmetric Dirichlet with a high parameter instead of a flat Dirichlet. In most amniote comparisons the distance estimation was lower than the parsimony (lower in 47% of the comparisons versus 14% for ER2), leading to impossible scenarios. In addition, the estimator proposed by Alexeev and Alekseyev (2015) does not perform better than parsimony on simulations from the uniform model. The intergenic breakage model (Peng et al. 2006; Becker and Lenhard 2007; Mongin et al. 2009), supposing that solid regions are long range regulation loci, would imply that a major part of the genome is under selection, including regions with various genomic features. This is not yet supported by regulation data (Farré et al. 2015).

The INFER model can capture both observations 1 and 3: The number of fragile regions is set to fit observation 3, and their probabilities are distributed so that inside fragile regions there is a diversity of breakage probabilities that are possibly correlated with genomic features. We partially account for observation 5, because it would explain the solidity of most of the genome, as it is not in contact regions (fig. 6). All our results and former observations are in agreement with the idea of a slowly evolvable colocalization of active genomic regions in the cell. Indeed, the increase in the number of fragile regions with evolutionary time (fig. 5) is coherent with the Turnover Fragile Breakage Model of Alekseyev and Pevzner (2010), supposing a birth and death of fragile regions. Yet observations 4 and 5 still point one of the most serious limitation to the INFER model.

Fig. 6.—

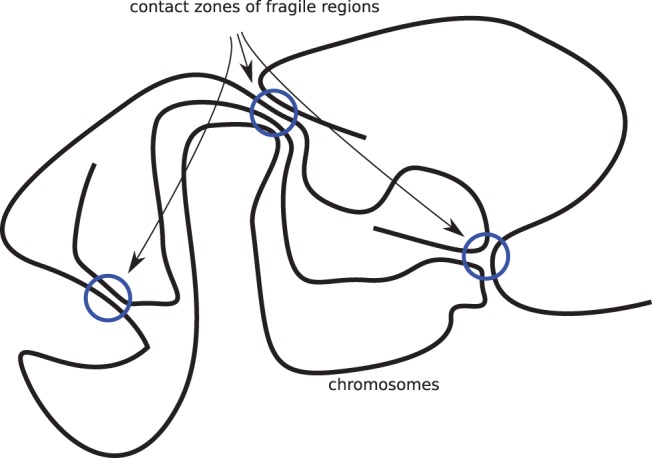
Chromosomes organized in territories in the cell. We conjecture that rearrangements happen mainly within pairs of breakpoints in contact zones. Two breakpoints may concern a single chromosome segment (small rearrangements) or different chromosome segments (large rearrangements), leading to two different modes of evolution.

Limits

INFER does not handle dependency between probabilities, as a model of 3D conformation would prescribe. Such a model would consist in drawing the genome as organized in loops and contact regions as in figure 6 (Bouwman and de Laat 2015). It would explain most of the observed deviations from the uniform model. As contact regions are regions of high transcriptional activity, it results in higher breakage density in gene dense regions (Lemaitre et al. 2009). As close regions in the genome are close also in 3D, small rearrangements are frequent. As most regions are in loops and are not in contact, the number of fragile regions is small.

Hence the limit to our approach is the independent choice of the two breakpoints for each rearrangement. This independent hypothesis allows for easier computations, but future work should aim at coupling or grouping adjacencies and modifying their breakage probabilities in function of their mates. The work of Berthelot et al. (2015) and Swenson and Blanchette (2015) provides a first modeling or combinatorial framework, but the statistical aspects are still to be developed.

Other limitations are that a breakage is often not at the resolution of a nucleotide, it would be more appropriate to speak about breakpoint regions (Lemaitre et al. 2009). Other ways to redistribute breakage probabilities after rearrangements could be considered.

Eventually, the model is dependent on the resolution at which we consider rearrangements. If the considered loci are coding genes, the smallest possible rearrangement is the inversion of one gene. As we filter lonely genes (see Methods), it has in fact the size of two genes. This can be variable along a genome and between genomes. For example, the precision will not be the same for amniote or yeast genomes. This can be important when the main deviations from the uniform model concern small rearrangements. The definition of small can vary with mean gene sizes.

Supplementary Material

Supplementary figures S1–S6 and methods are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).