Skip to main content
PMC home page
BMC Biochemistry logoLink to BMC Biochemistry
. 2004 Jul 19;5:10. doi: 10.1186/1471-2091-5-10

The molecular basis of electroporation

D Peter Tieleman 1,✉
PMCID: PMC489962  PMID: 15260890

Abstract

Background

Electroporation is a common method to introduce foreign molecules into cells, but its molecular basis is poorly understood. Here I investigate the mechanism of pore formation by direct molecular dynamics simulations of phospholipid bilayers of a size of 256 and of more than 2000 lipids as well as simulations of simpler interface systems with applied electric fields of different strengths.

Results

In a bilayer of 26 × 29 nm multiple pores form independently with sizes of up to 10 nm on a time scale of nanoseconds with an applied field of 0.5 V/nm. Pore formation is accompanied by curving of the bilayer. In smaller bilayers of ca. 6 × 6 nm, a single pore forms on a nanosecond time scale in lipid bilayers with applied fields of at least 0.4 V/nm, corresponding to transmembrane voltages of ca. 3 V. The presence of 1 M salt does not seem to change the mechanism. In an even simpler system, consisting of a 3 nm thick octane layer, pores also form, despite the fact that there are no charged headgroups and no salt in this system. In all cases pore formation begins with the formation of single-file like water defects penetrating into the bilayer or octane.

Conclusions

The simulations suggest that pore formation is driven by local electric field gradients at the water/lipid interface. Water molecules move in these field gradients, which increases the probability of water defects penetrating into the bilayer interior. Such water defects cause a further increase in the local electric field, accelerating the process of pore formation. The likelihood of pore formation appears to be increased by local membrane defects involving lipid headgroups. Simulations with and without salt show little difference in the observed pore formation process. The resulting pores are hydrophilic, lined by phospholipid headgroups.

Background

Electric fields can induce pore formation and other structural defects in lipid membranes, including cell membranes and skin [1,2]. Electroporation is widely used in the laboratory for gene transfection, introduction of polar and charged molecules such as dyes, drugs, proteins and peptides and also has applications in drug delivery in cancer treatment [3-8]. Electropermeabilized vesicles are more prone to fuse with cells and can be loaded with a wide range of (drug) molecules [9]. Most of our experimental understanding of electroporation is derived from experiments on black lipid membranes [10,11], and it is generally assumed that aqueous pores lined with phospholipid headgroups are created in the membrane [1,12]. Although several models are available that predict aspects of the size and spatial distributions of pores, the molecular basis of pore formation remains poorly understood. We have recently shown that pore formation by mechanical stress and by electric fields can be studied by detailed computer simulations [13]. Here I propose a mechanism for the molecular basis of electroporation based on extensive computer simulations of dioleoylphosphatidyl-choline (DOPC) bilayers in which the formation of water-filled pores can be followed at atomic resolution, and of a simpler system that allows detailed numerical analyses of the interactions of water with the electric field. Such simulations use a realistic description of the interactions between lipid and water atoms and have become a very powerful technique to study lipids and membrane proteins [14]. The results show, surprisingly, that the initial steps of pore formation do not seem to depend on the nature of the lipid headgroups but are determined by the increased likelihood of water defects in the membrane interior with increasing applied electric field.

Results

The main result of the simulations are the motions of all molecules involved during pore formation in phospholipid bilayers and in a water/octane system. In this section these primary results are described, while a more detailed numerical analysis of the same process is presented in the discussion.

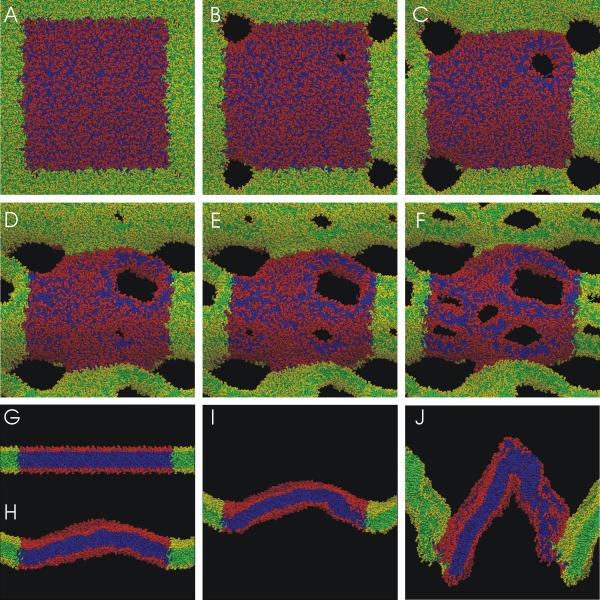
Figure 1 shows the effect of a strong electric field (of 0.5 V/nm) on a bilayer with initial dimensions of ca. 26 × 29 × 8 nm. The starting structure is planar and undulations form in the first 1.5 ns of the simulation (Fig. 1A,1B), which has also been observed in an equilibrium simulation of a bilayer half this size [15]. At around 1.6 ns the first pore forms, which rapidly widens. After 2 ns a second pore opens close to the first, and the bilayer becomes strongly curved. Over the course of the next 1.5 ns four more pores form, involving a large fraction of the lipids in the bilayer. The final structure is highly curved and has significant patches of exposed lipid chains in the regions with the highest curvature. This is shown by sideviews of the system in Fig. 1G,1H,1I. An animation of this simulation is given in the supplementary material. Pore sizes grow up to a diameter of ca. 10 nm.

Figure 1.

Figure 1

Open in a new tab

Top view of lipid bilayer of initially ca. 25 × 29 nm (2304) lipids at six different times during the simulation: A) 1700 ps, onset of first pore formation B) 2040 ps, second pore forming, C) 2600 ps, D) 2800 ps, E) 2990 ps, F) 3600 ps. Sideviews, showing the increasing curvature of the bilayer: G) 0 ps, H) 1700 ps, I) 2040 ps, J) 3600 ps. The simulation cell is periodic, so that effectively an infinite stack of bilayers is simulated, but only the central simulation cell is actually simulated. The lipids are shown as spacefilling, with red for the headgroups and blue for the chains in the central simulation cell. For clarity, parts of the periodic images in the x, y plane are also shown, with the headgroups in yellow and the chains in green. The potential is positive at the top of snapshots G-J relative to the bottom. In the same reference frame, views of snapshots A-F are from the top. Water is not shown. Molecular graphics images were made with VMD [37]. Animations of this event and of the events in figures 2 are available as supplementary material. The time in each snapshot is only given as an indication of how fast defects develop; because the process is stochastic the exact values are not reproducible.

This bilayer is an excellent model for a membrane due to its size, which allows substantial curvature and multiple pores. It consists of over 420,000 atoms, however, and is too large for extensive simulations under different conditions because of current computational limitations. I therefore turned to a smaller bilayer (45,000 atoms) and a water/octane system (ca. 7,000 atoms) to investigate the mechanism of pore formation in more detail.

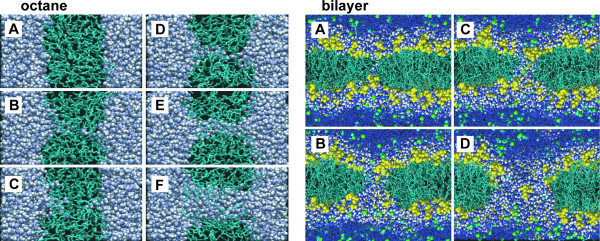
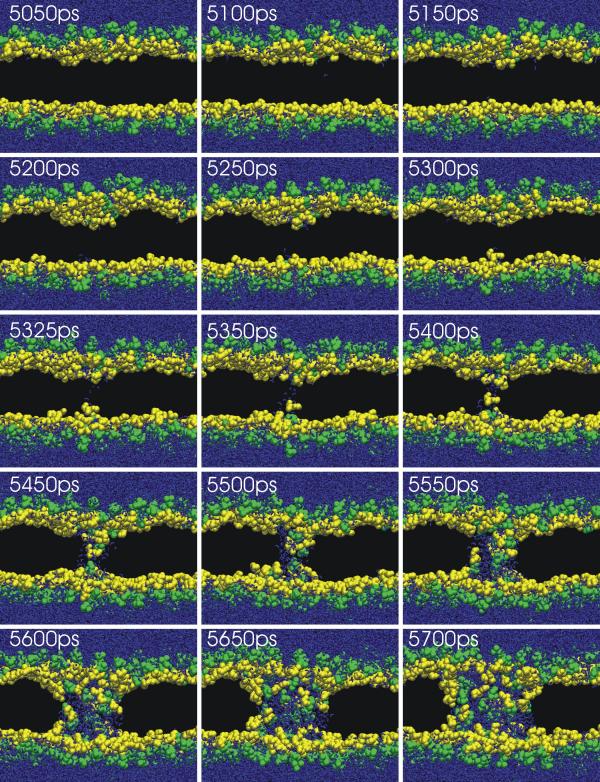
Figure 2 illustrates the process of pore formation in these two smaller systems. In both cases, water defects form at the interface between water and the hydrophobic part of the system. These defects grow in length, cross the full hydrophobic width either by themselves or by joining a similar defect from the opposite side, and rapidly expand into a water-filled pore. Animations of both processes are available as supplementary material. In the water/octane system pores form from small water defects at the interface. In the phospholipid bilayer pores also form from small water defects, but these defects occur more commonly near 'headgroup defects', where the choline group of the lipid is located near the glycerol backbone region. Figure 3 shows the pore formation process in more detail for the same phospholipid bilayer as in figure 2, but from a viewpoint further away from the pore. In the first snapshot (5050 ps) there is no clear sign of headgroup defects or other irregularities at the site of pore formation, only a few hundred picoseconds later. Water molecules are occasionally found in the interior of the membrane (e.g. 5100 ps, 5150 ps), which is normally, in the absence of applied electric fields, a very rare occasion. Such water molecules may form hydrogen-bonded chains of several water molecules, which do not have to lead to pores. At 5200 ps, 5250 ps, a deformation of the headgroups is seen, with water defects forming at the same time. The water defects begin to span the bilayer, and headgroups start moving towards this pore (5300 – 5400 ps). This pore then expands and become lined with lipid headgroups, although it takes some time before the headgroups are evenly distributed over the pore 'surface'. Although in the final snapshot at 5700 ps water is still exposed to lipid chains, this is not unlike the distribution of head groups in an unperturbed bilayer.

Figure 2.

Figure 2

Open in a new tab

Snapshots of pore formation in the water/octane system (left): A) 0 ps, B) 327 ps, C) 341 ps, D) 344 ps, E) 350 ps, F) 368 ps. The octane molecules are shown in cyan as bonds, the water molecules in blue and white as spacefilling. The potential is positive on the left side of each octane/water snapshot. Snapshots of pore formation in the DOPC bilayer, with an applied field of 0.5 V/nm in the presence of 1 M NaCl (right): A) 5330 ps, B) 5450 ps, C) 5500 ps, D) 5700 ps. The lipid headgroups are shown in yellow, the chains in cyan, chloride ions spacefilling in green, sodium ions in cyan; water is shown as dark blue and white spacefilling in the interface region and the pore, as dark blue bonds elsewhere. The potential is positive at the top of each snapshot relative to the bottom.

Figure 3.

Figure 3

Open in a new tab

A second series of snapshots of the same simulation as in Figure 2 (right), but viewed from further away so that the outside of the pore is visible rather than a cut through the pore. The series starts at 5050 ps, when there is no clear sign of pore formation yet. Ions and lipid chains are not shown for clarity. The lipid headgroups are divided in the choline part (green) and the phosphate/glycerol part (yellow). The potential is positive at the top of each snapshot relative to the bottom.

Discussion

The simulations give a graphical view of the pore formation process, but why do pores form in the first place?

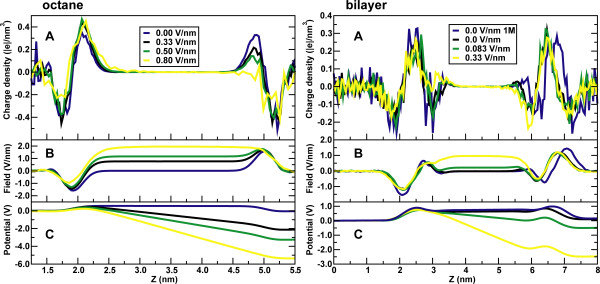
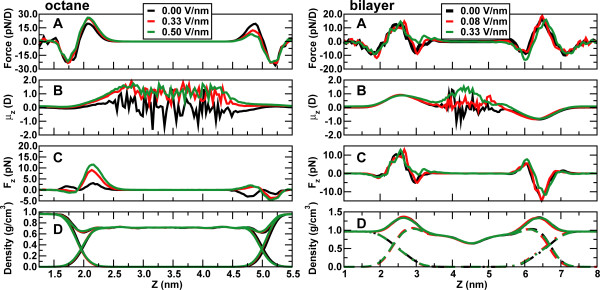
The water/octane system is simplest: the external field only interacts with the water molecules, as the model used for octane has no charges. In bulk water and in the absence of salt the applied field simply causes a small average orientation described by a Langevin function, with little effect on water properties, so we will focus on the octane/water interface. The water/octane interface is only a few tenths of a nm wide but because water molecules orient at this interface the charge density along the z-axis is not uniform, even in the absence of an applied field (Figure 4A). Interestingly, the features of the net charge distribution are very similar for water/octane, water/phospholipid and water/phospholipid/salt, despite the large difference in molecular structure of octane and lipid, and the potentially large effect of 1 M NaCl (Figure 4A).

Figure 4.

Figure 4

Open in a new tab

A) Charge density, B) electric field and C) electrostatic potential for water/octane at four different strengths of the applied field (left) and a lipid bilayer without salt for three different strengths of the applied field, and with salt at zero applied field (right). The properties in this figure and in figures 4 and 5 were calculated from simulations in which pores did not form, or else averaging as a function of the z-coordinate would not be possible.

For the purpose of interacting with electric fields water molecules can be approximated as a dipole. The force on a dipole is given by F = (μ•∇)E and is zero in a constant field. Of interest is the component of the force along the bilayer normal (the z-axis): 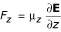Inline graphic. Here 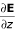Inline graphic is proportional to the charge density ρ(z), which can be calculated directly from the simulation. Figure 5A shows the gradient of the local electric field expressed as a force on a dipole oriented along the Z-axis with a magnitude of 1 D (the dipole moment of the SPC model used is 2.27 D).

Figure 5.

Figure 5

Open in a new tab

Interfacial properties of the water/octane (left) and water/phospholipid (right) interfaces as a function of applied external field. Shown are (A) the force on a hypothetical dipole with a strength of 1 D, pointing in the direction of the Z-axis, (B) the average orientation of water molecules along the Z-axis expressed as the magnitude of the dipole moment in Debye along the Z-axis, (C) the average force in the z-direction, calculated from the product of the average orientation and the field gradient, and (D) the density profile for the total density and the water or phospholipid components along the Z-axis. In the octane simulations, data shown have been averaged over the trajectory from 5 to 50 ns, with no pore formation occurring. In the phospholipid simulation data has been averaged over 0–20 ns for 0 M/0 V (which was already equilibrated under these conditions), 10–20 ns for 0 M/0.083 V, and 20–50 ns for 0 M/0.33 V.

This gradient depends on the strength of the applied field and on the left side increases as the applied field becomes stronger.

Without applied field the local field rapidly changes direction at the interface with approximately equal magnitudes. In the presence of an applied external field, as in electroporation experiments, the local field gradient is no longer symmetric for both interfaces. On one side, the field gradient increases with a higher external potential, on the other side it decreases. To amplify the effect of the increased gradient at the positive potential side, water molecules become strongly oriented in the presence of an external field so that both the projected dipole moment in the Z-direction and the field gradient forcing these dipoles into the membrane become larger (Figure 5B), and depending on the exact location the average force due to the gradient of the field acting on water dipoles (Figure 5C). For orientation, the density profiles, showing the density of different parts in the system as a function of Z, are also shown (Figure 5D).

Local fluctuations and hydrogen bonding facilitate the process of insertion; hydrogen bonding in a hydrophobic interior is stronger than in water, so that the probability of a defect growing is substantially larger than the probability of the initial formation of a defect. If the field gradient is the driving force for water defect formation it should be expected that defect formation from both sides is not equally likely because the field gradients are not symmetric.

Indeed the formation of pores in the simple water/octane system has a much higher chance of initiating from the positive side. In 100 simulations of water/octane with an applied field of 0.8 V/nm, pore formation occurred over 90 times from positive side, while in the remaining cases substantial defects from both sides combined to form the initial single file water defect spanning the octane phase. This is consistent with the small force at the right side (high Z) of the 0.5 V/nm octane/water simulation.

For the lipid bilayers the forces are more symmetric, and indeed in the small number of pore formation events observed water defects from both sides play a role. The effect of the external field on water orientation is similar in the bilayers compared to octane. On the positive side, the field causes a significant increase in water ordering, with the same direction as in water/octane despite the 'extra' negative peak at ca. 3 nm. On the negative side, the external field orders water molecules in the opposite direction than the interface does, and the average degree of orientation decreases. In fact, in the region with a water density of less than 10% of the bulk density, the orientation of water is reversed at higher fields compared to zero field.

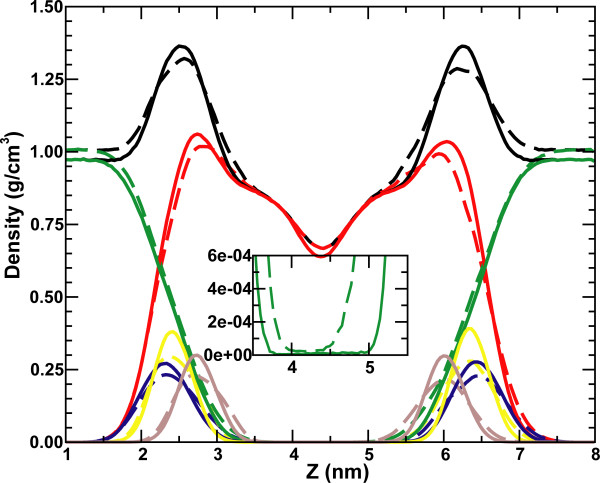
A graph of the density of the different groups (lipid, water, ions, as well as groups of atoms within the lipids) shows that the peak-to-peak distance of the lipid density profile does not change, but the individual groups become broader and water penetrates somewhat further into the membrane (Figure 6). This is consistent with experimental data that shows that the capacitance of a bilayer does not significantly decrease in the presence of an external potential difference, indicating the bilayer does not become significantly thinner [1]. The broadening of the water distribution towards the interior of the membrane, even though the absolute density of water in the hydrocarbon interior remains very low, still shows a significantly decreased barrier for water penetration. This is consistent with a change in the potential of mean force for water moving to the hydrophobic interior. The averaged total force on water molecules Fave(z) is related to the potential of mean force for water moving from bulk water to the hydrophobic phase as minus the derivative of the potential of mean force [16]. The average total force becomes less negative at the positive side, so that the potential of mean force indeed becomes less steep with applied field.

Figure 6.

Figure 6

Open in a new tab

Density profile, comparing the distribution of water, lipids, and elements of the lipid head groups in a simulation without external field (solid lines, averaged over 0–20 ns) and with an external field of 0.33 V/nm (dashed lines, averaged over 20–50 ns). Black is the total density, green water density, red lipid density, yellow phosphate density, blue choline density, and brown glycerol density.

Although the main focus of this paper is to address the question why pores form, the simulations give interesting suggestions about several experimental observations and hypotheses.

First, DNA can be transported into cells by electroporating their membranes. The molecular basis of this process is controversial; there currently appear to be two major hypotheses, without critical experiments to decide between them. In the first, DNA is transported through large stable pores that form without significant interaction with DNA and then reseal. A recent theoretical model supports this idea [17]. The second, more widely supported, hypothesis suggests that DNA is transported into cells by direct interaction with lipids and intermediates that involve a complex of lipid components and DNA. In this case, permeabilization by an electric field might cause a number of smaller pores that by themselves are not large enough to allow DNA transport but make the membrane amenable to structural modifications that allow translocation of DNA [4,18,19]. The simulation of the large bilayer gives holes that have a diameter of up to 10 nm, which would be sufficiently large to allow the transport of double-stranded DNA. This is not a definitive answer, however, because the electric field in the presence of pores might be higher than can be achieved in real cell experiments (see below), and it remains to be shown that pores of this size are reversible and will reseal when the electric field is removed. A recent molecular dynamics study by Leontiadou et al. investigated the stability of small pores in bilayers and established a minimum radius at which hydrophilic pores in dipalmitoylphosphatidylcholine bilayers could be stable [20], but the maximum radius to my knowledge is not known, although a recent model suggests it can be quite large [17].

The simulations also suggest an explanation of the experimental observations that lipid headgroup charge and ionic strength of the solution appear to have little effect on electroporation but that lipid tails, cholesterol and hydrophobic polymers do have a significant effect [21-23]. First, the simulations suggest that there is almost no salt effect because the contributions of these charges to the local field gradients at the interface practically cancel. Although no electroporation in bilayers with lipids with charged headgroups was simulated, this would be an interesting extension. The important contribution appears to be the added effect of the external field at the interface, regardless of the exact composition of the interface. Second, it can be expected that changes in the hydrophobic part of the membrane (e.g. changing lipid tails from palmitoyl-oleoyl to diphytanoyl or adding cholesterol) have a significant effect because the force required to move water into the hydrophobic interior will change. For lipids that are more densely packed the formation of water defects is likely to be less favourable. For longer lipids one might also expect that the formation of water defects spanning the bilayer is less likely. For lipid bilayers with structural defects, such as those caused by surfactants, electroporation would be expected to be easier because it is more favourable for water to penetrate. These hypotheses could be tested both experimentally and in further simulations. The simulations also suggest why coating the outside of bilayers with polymers can increase the resistance to pore formation: water defects would still form but the next stages in which lipid headgroups move in to form more stable headgroup lined pores is frustrated [24].

An interesting and experimentally useful observation is that electropermeabilized vesicles and cells are more prone to fusion [9]. The present simulations suggest a number of possible explanations for this, including higher curvature of these vesicles (analogous to the large bilayer), the metastable nature of the fusion pores, and increased hydrophobic surface area of electropermeabilized vesicles which would facilitate fusion. Fusion is difficult to study directly in full atomistic detail, but recently developed coarse-grained models of phospholipids have been used to investigate fusion between vesicles and could also be used to test these hypotheses [25,26].

Although the simulations presented here give unprecedented atomistic detail of the pore-formation process, they suffer from several limitations. These include both relatively obvious limits on the size of the simulation system and the length of the simulations, but also more subtle questions on the comparison to experimental data.

The largest bilayer simulated is initially ca. 25 × 29 nm in the plane of the membrane, but the z-dimension is much shorter, initially only 8 nm. As pores form, the bilayer deforms and 'folds' (Fig. 1). This folding is influenced by the periodic boundary conditions, because these allow independent changes in x and y, the plane of the membrane. While this is the most realistic choice of boundary conditions, both the magnitude and shape of structural fluctuations is affected by the requirement that the curvature at the boundaries is continuous on each side of the box. It is also possible to scale x and y together. This would maintain the shape of the bilayer, and would make the extreme curving observed in the present simulation impossible, although it would allow curvature in the form of a 'dimple'.

An important question is to what type of experiments the simulations correspond to in terms of the incorporation of an electric field. The voltage in the simulations is maintained at a constant value of the box length times the applied field, regardless of whether a pore is present or not. The simulations assume that the potential everywhere in the system due to the applied constant field is the same as the potential caused by electrodes at a large distance from the membrane in a black lipid membrane experiment. Figure 4 shows that this is reasonable for the case without pores, but the potential distribution inside the pores is too noisy to calculate accurately from the simulation for a detailed comparison with a continuum electrostatics model. Nonetheless, experiments under voltage clamp conditions measure the current as a function of time and show a jump in conductance as pores form, but are able to maintain the original voltage in the presence of pores until the membrane ruptures. Alternatively, measurements can be done under conditions of constant current, monitoring the voltage fluctuations. An interesting question that is outside the scope of this study is how planar lipid bilayer experiments relate to electroporation experiments on whole cells. A study by Hibino et al. showed that the membrane potential has a maximum value, presumably because large pores dissipate the transmembrane potential in whole-cell solutions [27].

Experimentally, the critical voltage that induces pore formation in a black lipid membrane is of the order of 0.25 – 0.50 V. In the case of an applied field of 0.4 V/nm the total potential difference across the membrane is approximately 3 V, or 5–10 times as much. However, pore formation can be induced by much higher fields in the simulations, while still showing the same characteristics, although at a faster time scale. Experimentally, the lifetime of a black lipid membrane is shorter when a stronger voltage is applied, but individual pore properties do not depend on the applied voltage [11]. It is likely pore formation in the simulations at lower potential differences would be slower but would still occur. A critical voltage cannot be determined from this type of simulations.

Exact correspondence in time scales between simulation and experiment cannot be expected because of the small size of the simulation membrane compared to experiment and the experimental time scales involved due to membrane capacitance and time resolution of the measurements [1]. It is also not possible to predict the distribution of pore sizes or their spatial distribution in a large membrane, although the simulation of the large bilayer shows that pores can be quite close to each other without affecting each other much, at least on a nanosecond time scale. Much more extensive simulations would be required to address the important issue of pore coalescence. The system would have to be so large and the simulations so long that this is probably not practical at the moment at this level of atomistic detail, although coarser lipid models could be used [28]. I am currently exploring this.

Conclusions

Detailed computer simulations of lipid bilayers in the presence of an external electric field have given an atomistic description of the process of electroporation. Pore formation is promoted by an increased likelihood of transmembrane water defects in the presence of an external electric field. Pores form even in octane layers, suggesting the primary role of water dipoles. Water defects are caused by the interaction of water dipoles with the electric field gradient at the water/lipid or water/octane interface. The presence or absence of salt has little effect on the process of pore formation. Pores in the lipid bilayers are lined by phospholipid headgroups. These results provide a better understanding of this fundamental process and form a basis for future work to investigate conditions that experimentally change electroporation phenomenology and to study transport through bilayer pores.

Methods

Bilayer simulations

A bilayer of 256 DOPC lipids and 11228 water molecules was simulated without salt with applied fields of 0 V/nm (20 ns), 0.33 V/nm (50 ns), 0.4 V/nm (20 ns, pore formation at 12–14 ns) and 0.5 V/nm (pore formation at ca. 3 ns). The same bilayer with 1 M NaCl (ions replacing water molecules, resulting in 10828 water molecules, 200 Na+ ions, and 200 Cl- ions) was simulated at 0 V/nm and 0.5 V/nm (pore formation after ca. 5 ns). In addition, a bilayer consisting of 2304 lipids and 101052 water molecules was simulated with an applied field of 0.5 V/nm (multiple pores form after ca. 2.5 ns).

Octane simulations

Water/octane simulations used a system of 182 octane and 1802 water molecules, in a box with a flexible height (ca. 6.6 nm) and an interface kept fixed at 4 × 4 nm. Simulations were 50 ns each with applied fields of 0 V/nm, 0.33 V/nm, and 0.5 V/nm (no pore formation), and 100 simulations with a field of 0.8 V/nm each until pore formation occurred, typically somewhere between 50 ps and 2 ns. The final equilibrium structure of the water/octane systems is one in which the octane slab is rotated 90 degrees, with its normal now along either the x or the y axis; this arrangement is a consequence of trying to minimize both the water/octane interface perpendicular to the applied field and minimizing the water/octane interfacial area and depends on the geometry of the box. For the present purpose of investigating the structure of the interface before pore formation and the early events of pore formation, up to the point where phospholipid headgroups would move in to line the pore, only the initial part of the water/octane simulations are relevant.

Phospholipid parameters were taken from the OPLS-based force field of Berger et al. [29] combined with GROMOS87 bonded parameters and parameters for the CH1 atoms in the double bonds. Parameter files are available from http://moose.bio.ucalgary.ca. Octane parameters were taken from the GROMOS96 force field 45a3 [30]. In both cases, methyl and methylene groups are treated as united atom, so that an octane molecule has 8 atoms and a DOPC lipid 54. In all simulations the temperature was set to 300 K using the weak coupling algorithm [31] with τT = 0.1 ps, and pressure to 1 bar independently in each dimension with τp = 1 ps (in z only for water/octane). This allows the dimensions of the system to change in normal fluctuations but also as a response to the applied electric field or pore formation. A 1 nm Coulomb cutoff combined with Particle-Mesh-Ewald was used for electrostatic interactions [32] with a 1 nm cutoff for Lennard-Jones interactions. In the case of a non-zero applied field the system has a net dipole moment, which results in a surface charge on the replicated systems. In vacuum this would require a correction, but because this surface charge is exactly balanced by the tin-foil boundaries used in the PME implementation this effect is zero. The time step was 2 fs except in the last 30 ns of the DOPC bilayer with no salt and a field of 0.33 V/nm, where it was 5 fs. This larger time step has no effect on the structure of a similar dipalmitoylphosphatidylcholine bilayer as determined by 150 ns simulations in which only the time step was varied [33]. The water model used was the Simple Point Charge model [34]. All simulations were performed using the GROMACS set of programs [35,36].

The charge density shown in Figure 4A and used to calculate the force on a dipole at the interface can be calculated directly from the simulation and is related to the potential through Poisson's equation which, averaged over the x, y plane, is: 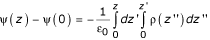Inline graphic where the second integration constant ψ(0) is chosen as 0 V in the middle of the water phase on the left side of the box at z = 0 and the first integration constant, the electric field E(0), is taken as 0 V/nm in the middle of water layer. Because of the applied field, the actual field in the middle of the water phase is not zero and the value E(0) could be taken as Ez divided by the experimental dielectric constant of water or the dielectric constant of the SPC water model under the conditions simulated. This choice makes no difference for the field gradient and has an effect of only ca. 7 mV in the case of the strongest applied field of 0.8 V/nm in water/octane, within the accuracy of the quoted values for the transmembrane potentials. The average field is shown in Figure 4B. The calculated potential drop across each system is the applied field times the length of the simulation box in the z-dimension, validating this simple approach (Figure 4C). In the bilayers, an applied field of 0.33 V/nm corresponds to a transmembrane potential of ca. 2.6 V. In octane, a field of 0.33 V/nm corresponds to a "transmembrane" potential of ca. 2 V. This potential difference remains the same in the presence of pores. I make the assumption that the potential distribution in the system in this case is still realistic, although I have only shown this explicitly for the case without pores (figure 4).

All systems use periodic boundary conditions in three dimensions, so that effectively a multilamellar stack of bilayers (or octane slabs) with infinite dimensions in the x, y plane is simulated.

Supplementary Material

Additional File 1

Animation of a large lipid bilayer of 2304 lipids, between t = 0 and t = 3680 ps. The simulation cell is shown in red (headgroups) and blue (chains); yellow and green lipids are periodic images shown for clarity only. Water is not shown.

Click here for file (2.5MB, mpg)
Additional File 2

Pore formation in octane, with an applied field of 0.8 V/nm. The left side of the octane is positive with respect to the right side. Octane is shown as bonds, water in space-filled representation. The final state is one in which the electric field gradient in the z-direction is minimized. The potential is positive on the left side relative to the right side.

Click here for file (2.4MB, mpg)
Additional File 3

Animation of pore formation in a DOPC bilayer with an applied field of 0.4 V/nm, corresponding to a transmembrane potential of ca. 3.2 V. The lipid chains have been omitted for clarity. Water in the interface and inside the membrane is shown as spacefilling, outside those zones in less detail in blue. The headgroups are shown as yellow sticks. The potential is positive at the top relative to the bottom.

Click here for file (8.1MB, mpg)
Additional File 4

Animation of pore formation in a DOPC bilayer with an applied field of 0.5 V/nm, corresponding to a transmembrane potential of ca. 4 V. The representation is the same as in movie 3; the additional sodium is shown as spacefilling cyan spheres, chloride as green spheres. The potential is positive at the top relative to the bottom.

Click here for file (5.4MB, mpg)

Acknowledgments

Acknowledgements

DPT is a Scholar of the Alberta Heritage Foundation for Medical Research. This work was supported by the Natural Sciences and Engineering Research Council of Canada. I thank the reviewers for their comments, as well as my group members and other colleagues for comments during the Biophysical Society annual meeting in 2004.

References

  1. Weaver JC, Chizmadzhev YA. Theory of electroporation: A review. Bioelectroch Bioener. 1996;41:135–160. doi: 10.1016/S0302-4598(96)05062-3. [DOI] [Google Scholar]
  2. Prausnitz MR, Bose VG, Langer R, Weaver JC. Electroporation of mammalian skin - a mechanism to enhance transdermal drug-delivery. Proc Natl Acad Sci U S A. 1993;90:10504–10508. doi: 10.1073/pnas.90.22.10504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Arap W, Pasqualini R, Ruoslahti E. Cancer treatment by targeted drug delivery to tumor vasculature in a mouse model. Science. 1998;279:377–380. doi: 10.1126/science.279.5349.377. [DOI] [PubMed] [Google Scholar]
  4. Rols MP, Delteil C, Golzio M, Dumond P, Cros S, Teissie J. In vivo electrically mediated protein and gene transfer in murine melanoma. Nat Biotechnol. 1998;16:168–171. doi: 10.1038/nbt0298-168. [DOI] [PubMed] [Google Scholar]
  5. Alper J. Drug delivery - Breaching the membrane. Science. 2002;296:838–839. doi: 10.1126/science.296.5569.838. [DOI] [PubMed] [Google Scholar]
  6. Golzio Muriel, Teissie Justin, Rols Marie-Pierre. Direct visualization at the single-cell level of electrically mediated gene delivery. Proc Natl Acad Sci U S A. 2002;99:1292–1297. doi: 10.1073/pnas.022646499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Olofsson J, Nolkrantz K, Ryttsen F, Lambie BA, Weber SG, Orwar O. Single-cell electroporation. Curr Opin Biotech. 2003;14:29–34. doi: 10.1016/S0958-1669(02)00003-4. [DOI] [PubMed] [Google Scholar]
  8. Langer R. Drug delivery and targeting. Nature. 1998;392:5–10. [PubMed] [Google Scholar]
  9. Ramos C, Bonato D, Winterhalter M, Stegmann T, Teissie J. Spontaneous lipid vesicle fusion with electropermeabilized cells. FEBS Lett. 2002;518:135–138. doi: 10.1016/S0014-5793(02)02676-5. [DOI] [PubMed] [Google Scholar]
  10. Winterhalter Mathias. Black lipid membranes. Curr Opin Colloid In. 2000;5:250–255. doi: 10.1016/S1359-0294(00)00063-7. [DOI] [Google Scholar]
  11. Melikov KC, Frolov VA, Shcherbakov A, Samsonov AV, Chizmadzhev YA, Chernomordik LV. Voltage-induced nonconductive pre-pores and metastable single pores in unmodified planar lipid bilayer. Biophys J. 2001;80:1829–1836. doi: 10.1016/S0006-3495(01)76153-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gehl J. Electroporation: theory and methods, perspectives for drug delivery, gene therapy and research. Acta Physiol Scand. 2003;177:437–447. doi: 10.1046/j.1365-201X.2003.01093.x. [DOI] [PubMed] [Google Scholar]
  13. Tieleman DP, Leontiadou H, Mark AE, Marrink SJ. Molecular dynamics simulation of pore formation in phospholipid bilayers by mechanical force and electric fields. J Am Chem Soc. 2003;124:6382–6383. doi: 10.1021/ja029504i. [DOI] [PubMed] [Google Scholar]
  14. Tieleman DP, Marrink SJ, Berendsen HJ. A computer perspective of membranes: molecular dynamics studies of lipid bilayer systems. Biochim Biophys Acta. 1997;1331:235–270. doi: 10.1016/S0304-4157(97)00008-7. [DOI] [PubMed] [Google Scholar]
  15. Lindahl E, Edholm O. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys J. 2000;79:426–433. doi: 10.1016/S0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Darve E, Pohorille A. Calculating free energies using average force. J Chem Phys. 2001;115:9169–9183. doi: 10.1063/1.1410978. [DOI] [Google Scholar]
  17. Smith KC, Neu JC, Krassowska W. Model of creation and evolution of stable electropores for DNA delivery. Biophys J. 2004;86:2813–2826. doi: 10.1016/S0006-3495(04)74334-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Sukharev SI, Klenchin VA, Serov SM, Chernomordik LV, Chizmadzhev Yu A. Electroporation and electrophoretic DNA transfer into cells. The effect of DNA interaction with electropores. Biophys J. 1992;63:1320–1327. doi: 10.1016/S0006-3495(92)81709-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Neumann E, Kakorin S, Tsoneva I, Nikolova B, Tomov T. Calcium-mediated DNA adsorption to yeast cells and kinetics of cell transformation by electroporation. Biophys J. 1996;71:868–877. doi: 10.1016/S0006-3495(96)79288-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Leontiadou H, Mark AE, Marrink SJ. Molecular dynamics simulations of hydrophilic pores in lipid bilayers. Biophys J. 2004;86:2156–2164. doi: 10.1016/S0006-3495(04)74275-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Diederich A, Bahr G, Winterhalter M. Influence of surface charges on the rupture of black lipid membranes. Phys Rev E. 1998;58:4883–4889. doi: 10.1103/PhysRevE.58.4883. [DOI] [Google Scholar]
  22. Koronkiewicz S, Kalinowski S. Influence of cholesterol on electroporation of bilayer lipid membranes: chronopotentiometric studies. Biochim Biophys Acta. 2004;1661:196–203. doi: 10.1016/j.bbamem.2004.01.005. [DOI] [PubMed] [Google Scholar]
  23. Genco I, Gliozzi A, Relini A, Robello M, Scalas E. Electroporation in Symmetrical and Asymmetric Membranes. Biochim Biophys Acta. 1993;1149:10–18. doi: 10.1016/0005-2736(93)90019-V. [DOI] [PubMed] [Google Scholar]
  24. Diederich A, Strobel M, Meier W, Winterhalter M. Viscosity- and inertia-limited rupture of dextran-supported black lipid membranes. J Phys Chem B. 1999;103:1402–1407. doi: 10.1021/jp982637z. [DOI] [Google Scholar]
  25. Stevens MJ, Hoh JH, Woolf TB. Insights into the molecular mechanism of membrane fusion from simulation: evidence for the association of splayed tails. Phys Rev Lett. 2003;91:188102. doi: 10.1103/PhysRevLett.91.188102. [DOI] [PubMed] [Google Scholar]
  26. Marrink SJ, Mark AE. The mechanism of vesicle fusion as revealed by molecular dynamics simulations. J Am Chem Soc. 2003;125:11144–11145. doi: 10.1021/ja036138+. [DOI] [PubMed] [Google Scholar]
  27. Hibino M, Itoh H, Kinosita K., Jr. Time courses of cell electroporation as revealed by submicrosecond imaging of transmembrane potential. Biophys J. 1993;64:1789–1800. doi: 10.1016/S0006-3495(93)81550-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Marrink SJ, de Vries AH, Mark AE. Coarse grained model for semiquantitative lipid simulations. J Phys Chem B. 2004;108:750–760. doi: 10.1021/jp036508g. [DOI] [Google Scholar]
  29. Berger O, Edholm O, Jahnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys J. 1997;72:2002–2013. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schuler LD, Daura X, van Gunsteren WF. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J Comp Chem. 2001;22:1205. doi: 10.1002/jcc.1078.abs. [DOI] [Google Scholar]
  31. Berendsen HJC, Postma JPM, van Gunsteren WF, Dinola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]
  32. Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A Smooth Particle Mesh Ewald Method. J Chem Phys. 1995;103:8577–8593. doi: 10.1063/1.470117. [DOI] [Google Scholar]
  33. Anezo C, de Vries AH, Holtje H-D, Tieleman DP, Marrink SJ. Methodological issues in lipid bilayer simulations. J Phys Chem B. 2003;107:9424–9433. doi: 10.1021/jp0348981. [DOI] [Google Scholar]
  34. Berendsen HJC, Postma JPM, van Gunsteren WF, Hermans J. Intermolecular Forces. Dordrecht, Reidel; 1981. Interaction models for water in relation to protein hydration; pp. 331–342. [Google Scholar]
  35. Berendsen HJC, van der Spoel D, van Drunen R. Gromacs - a message passing parallel molecular-dynamics implementation. Comput Phys Comm. 1995;91:43–56. doi: 10.1016/0010-4655(95)00042-E. [DOI] [Google Scholar]
  36. Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J Mol Model. 2001;7:306–317. [Google Scholar]
  37. Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J Mol Graph. 1996;14:33–8, 27-8.. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Additional File 1

Animation of a large lipid bilayer of 2304 lipids, between t = 0 and t = 3680 ps. The simulation cell is shown in red (headgroups) and blue (chains); yellow and green lipids are periodic images shown for clarity only. Water is not shown.

Click here for file (2.5MB, mpg)
Additional File 2

Pore formation in octane, with an applied field of 0.8 V/nm. The left side of the octane is positive with respect to the right side. Octane is shown as bonds, water in space-filled representation. The final state is one in which the electric field gradient in the z-direction is minimized. The potential is positive on the left side relative to the right side.

Click here for file (2.4MB, mpg)
Additional File 3

Animation of pore formation in a DOPC bilayer with an applied field of 0.4 V/nm, corresponding to a transmembrane potential of ca. 3.2 V. The lipid chains have been omitted for clarity. Water in the interface and inside the membrane is shown as spacefilling, outside those zones in less detail in blue. The headgroups are shown as yellow sticks. The potential is positive at the top relative to the bottom.

Click here for file (8.1MB, mpg)
Additional File 4

Animation of pore formation in a DOPC bilayer with an applied field of 0.5 V/nm, corresponding to a transmembrane potential of ca. 4 V. The representation is the same as in movie 3; the additional sodium is shown as spacefilling cyan spheres, chloride as green spheres. The potential is positive at the top relative to the bottom.

Click here for file (5.4MB, mpg)

Articles from BMC Biochemistry are provided here courtesy of BMC

RESOURCES