Statistical mechanical modeling of RNA folding: from free energy landscape to tertiary structural prediction

Abstract

In spite of the success of computational methods for predicting RNA secondary structure, the problem of predicting RNA tertiary structure folding remains. Low-resolution structural models show promise as they allow for rigorous statistical mechanical computation for the conformational entropies, free energies, and the coarse-grained structures of tertiary folds. Molecular dynamics refinement of coarse-grained structures leads to all-atom 3D structures. Modeling based on statistical mechanics principles also has the unique advantage of predicting the full free energy landscape, including local minima and the global free energy minimum. The energy landscapes combined with the 3D structures form the basis for quantitative predictions of RNA functions. In this chapter, we present an overview of statistical mechanical models for RNA folding and then focus on a recently developed RNA statistical mechanical model -- the Vfold model. The main emphasis is placed on the physics underpinning the models, the computational strategies, and the connections to RNA biology.

10.1 Introduction

RNA 3D structure, folding stability and kinetics underlie RNA functions. The 3D crystal structures of rRNAs and tRNAs have led to detailed mechanisms of protein synthesis in the ribosome machinery (Ban et al. 2000; Wimberly et al. 2000; Yusupov et al. 2001). Recent findings regarding the slow folding kinetics of self-splicing introns have revealed how their enzymatic activities arise from their global 3D folds (Hougland et al. 2005; Laederach et al. 2007; Pan and Woodson 1998; Waldsich and Pyle 2008; Woodson 2000; Zarrinkar and Williamson 1994). Theoretical and experimental analyses point to a close correlation between the efficacy of microRNA in gene regulation and the 3D structure and folding stability (Long et al. 2007; Kertesz et al. 2007) of the microRNA/target complex. RNA functions highlight the biological significance of RNA folding and the need for a predictive model for RNA folding.

Existing RNA folding theories mainly focus on secondary structures (Lu et al. 2006; Mathews et al. 2006; McCaskill 1990; SantaLucia and Turner 1997; Zuker 2003). However, RNA functions often involve structures and structural changes at the tertiary structural level. Phylogenetic modeling (Major et al. 1993; Massire et al. 1998; SantaLucia et al. 2004) as well as de novo methods (Das and Baker 2007; Das et al. 2007; Jonikas et al. 2009; Parisien and Major 2008; SantaLucia 2007; Shapiro et al. 2007; Tyagi and Mathews 2007) combined with atomic computations (Major et al. 1993; Masquida and Westhof 2006; Mathews et al. 2006) and experimental constraints (Deigan et al. 2009; Jonikas et al. 2009) have shown success in predicting RNA 3D structures. However, RNA function is determined not only by the minimum free energy state of the RNA, but also by the its folding stability and the potentially large conformational changes it can undergo. Understanding RNA function requires models that predict the full free energy landscape.

Recent developments in statistical mechanical modeling of RNA folding have led to successes in predicting RNA structures, folding stabilities and folding kinetics for structures with increasing complexity. The models provide quantitative predictions and novel insights for a variety of experiments and RNA functions such as programmed ribosomal frameshifting (Cao and Chen 2009), mRNA splicing (Cao and Chen 2006a), and microRNA gene regulation (Kertesz et al. 2007; Long et al. 2007). Despite the success of this approach, several key issues remain. These issues include the computation of the entropy for RNA tertiary folds and the extraction of the energy/entropy parameters for non-canonical tertiary interactions from thermodynamic data and known structures. The primary focus of this chapter is the application of methods based on statistical mechanics to predict RNA 3D structures and folding energy landscapes and to gain quantitative understanding of RNA functions.

10.2 Overview of computational models for RNA folding

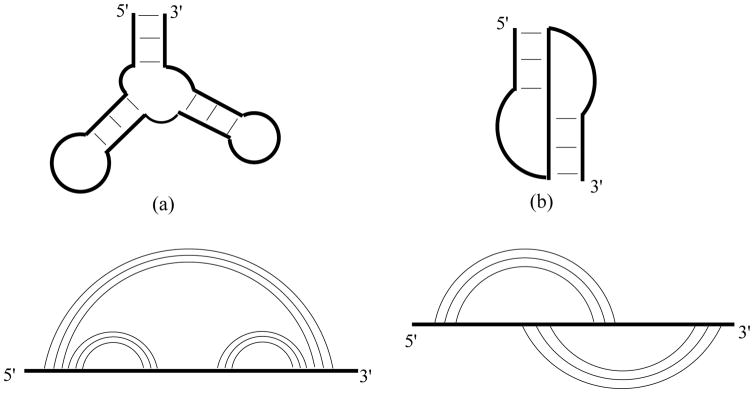
An RNA structure, defined by the nested Watson-Crick base pairs and the tertiary contacts contained in the 3D structure, can be conveniently represented by a polymer graph (Fig. 1). Such a graph (= a 2D structure) usually corresponds to many 3D conformations due to the flexible conformations of the single-stranded regions. Following Chastain and Tinoco (Chastain and Tinoco 1991), tertiary and secondary (2D) structures can be classified as the polymer graphs with and without cross-links, respectively.

Figure 1.

A 2D structure can be defined by a graph, which consists of vertices (representing nucleotide monomers), connected by curved links (representing base pairing), and straight lines (representing the backbone covalent bonds). Any two base pairs on the graph can be nested, (cross-)linked, or unrelated. RNA structures are described at the secondary and tertiary structural level. Shown in the figure are the 2D structures and the corresponding graphs for (a) a secondary structure containing three helices and (b) a pseudoknot (as a simple tertiary structure). In the pseudoknot structure, the nucleotides within a loop in the secondary structure pair with the nucleotides external to the loop.

Chemical and enzymatic reagents (Ehresmann et al. 1987) are highly effective structural probes for nucleic acids because the reactivity of a nucleotide can be sensitive to its local conformation and interactions, including base pairing and stacking, which are reflected in its solvent accessibility. Structure-probing experiments based on chemical and enzymatic reagents, such as the Selective 2′-Hydroxyl Acylation analyzed by Primer Extension (SHAPE) analysis (Watts et al. 2009) and synchrotron-generated hydroxyl radical footprinting (Petri and Brenowitz 1997), give direct information about base pairing and local structures. The experimental data provide useful input as structural constraints for the computational modeling of complete 3D structures. In parallel with these the experimental developments, de novo computational modeling of RNA folding shows continuous improvements in the accuracy of the predictions of RNA structures, including the structures for long RNA sequences. Table 1 shows a list of the computational models for RNA structure prediction from single sequence input. For structure predictions from sequence homology, see references provided in these citations: (Mathews and Turner 2002; Hofacker et al. 2002).

Table 1.

Computational models for RNA structure predictions.

Models	URL	References
	RNA secondary structure
Mfold	http://mfold.bioinfo.rpi.edu	Zuker 1989; Mathews et al. 1999a
Vienna software	http://rna.tbi.univie.ac.at	Rehmsmeier et al. 2004
Vfold	http://vfold.missouri.edu	Cao and Chen 2005
Sfold	http://sfold.wadsworth.org	Ding and Lawrence 2003
CONTRAfold	http://contra.stanford.edu/contrafold	Do et al. 2006
MC-Fold	http://www.major.iric.ca/MC-Fold	Parisien and Major 2008
	RNA pseudoknot
STAR	http://biology.leidenuniv.nl/~batenburg/STAR.html	Gultyaev et al. 1995
MPGAfold	http://www-lecb.ncifcrf.gov/~bshapiro/mpgaFold/mpgaFold.html	Shapiro and Wu 1997
pknotsRE	http://selab.janelia.org/software.html	Rivas and Eddy 1999
pknots-RG	http://bibiserv.techfak.uni-bielefeld.de/pknotsrg	Reeder and Giegerich 2004
NUPACK	http://nupack.org	& Dirks and Pierce 2003
ILM	http://cic.cs.wustl.edu/RNA	Ruan et al. 2004
Hotknots	http://www.cs.ubc.ca/labs/beta/Software/HotKnots	Ren et al. 2005
Vfold	http://vfold.missouri.edu	Cao and Chen 2006b
	RNA/RNA complexes
OligoWalk	http://rna.urmc.rochester.edu/software.html	Mathews et al. 1999b
DINAMelt	http://dinamelt.bioinfo.rpi.edu	Dimitrov and Zuker 2004
RNAhybrid	http://bibiserv.techfak.uni-bielefeld.de/rnahybrid	Rehmsmeier et al. 2004
PairFold	http://www.rnasoft.ca/cgi-bin/RNAsoft/PairFold/pairfold.pl	Andronescu et al. 2005
Vfold	http://vfold.missouri.edu	Cao and Chen 2006a
RNAup	http://www.tbi.univie.ac.at/~ivo/RNA	Mückstein, U. et al. 2006
NUPACK	http://nupack.org	Dirks et al. 2007

10.2.1 Secondary structures

RNA secondary structures contain no cross-links (non-nested interactions) in the corresponding graphs and thus permit use of efficient dynamic programming algorithms for conformational enumeration. Structural prediction algorithms based on free energy minimization (Mathews et al. 1999; Nussinov and Jacobson 1980; Williams and Tinoco 1986; Zuker 1989) can predict secondary structures, starting from a single sequence, with about 70% accuracy. Another type of approach to structural prediction is based on calculating the statistical mechanical partition function, which is an average over the conformational ensemble (Hofacker 2003; McCaskill 1990). The strategy is to determine the stable structures from the Boltzmann ensemble-averaged base pairing probabilities over all the possible base pairs. In 2003, Ding et al. developed a statistical sampling algorithm (Sfold) (Ding and Lawrence 2003) to predict RNA secondary structure. In the algorithm, 1000 structures are sampled based on the Boltzmann distribution. The cluster centroids of the 1000 structures give the predicted structures. The statistical sampling algorithm is found to give a better prediction than the free energy minimization method (Ding 2006).

While the above methods employ the same empirical thermodynamic parameters (the Turner rules) for secondary structural elements based on the nearest neighbour base pair interaction model, other models use knowledge-based scoring functions. For instance, the CONTRfold (Do et al. 2006) model uses the energy parameters derived from a training set and the MC-Fold (Parisien and Major 2008) model uses a scoring function that represents the probability of selecting a certain nucleotide cyclic motif (NCM) for the given sequence. The NCMs in the MC-Fold include the lone-pair loops and the double-stranded internal/bulge loops, which are extracted from known PDB structures. Benchmark tests show that CONTRfold and MC-Fold programs give better predictions than Mfold (Do et al. 2006, Parisien and Major 2008).

10.2.2 H-type pseudoknots --- free energy models

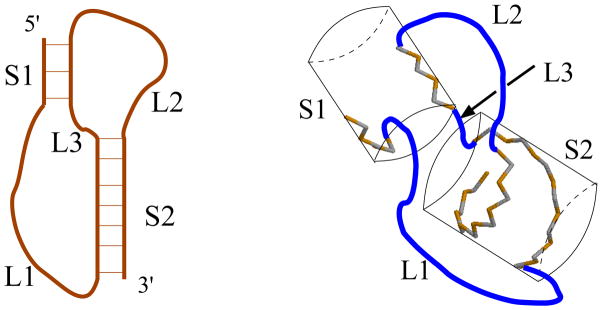
A general pseudoknot consists of two helical stems, S₁ and S₂, and three loops, L₁, L₂ and L₃ (see Fig. 2). Pseudoknots, which are neglected in most software for secondary structure prediction, play important structural and functional roles in many biochemical processes, such as viral replication (Brierley et al. 2007; Brierley et al. 2008; Draper 1990; Gesteland and Atkins 1996; Giedroc et al. 2000; Giedroc and Cornish 2009; Staple and Butcher 2005), human telomerase RNA activity (Chen and Greider 2005; Comolli et al. 2002; Qiao and Cech 2008; Shefer et al. 2007; Theimer and Feigon 2006) and metabolite-sensing riboswitches (Kang et al. 2009; Klein et al. 2009; Spitale et al. 2009).

Figure 2.

A 2D structure and the 3D conformations for a pseudoknot with inter-helix loop L₃.

The free energy for a pseudoknot is equal to the sum of the free energies for the helical stems and loops: ΔG_pk = ΔG_S1 + ΔG_S2 + ΔG_CS − TΔS_loops, where ΔG_S1 and ΔG_S2 are the free energies of stems S₁ and S₂ and ΔG_CS is the coaxial stacking energy between stems S₁ and S₂. While the helix free energies can be evaluated from the nearest-neighbor model based on the empirical thermodynamic parameters for base stacks, to determine the loop entropy ΔS_loops requires a physical model.

From statistical mechanics, ΔS_loops = −k_B ln Ω_Coil/Ω, where Ω is the number of the 3D conformations of the loops and Ω_Coil is the number of the corresponding coil conformations. The evaluation of the conformational entropy ΔS_loops is intrinsically a problem embedded in 3D space. The difficulty in the evaluation of the pseudoknot loop entropy comes from the conformational correlation between the loop and the helix. Specifically, the viability of a loop conformation is subject to the presence of the nearby helix due to the loop-helix excluded volume interaction and the end-to-end distance constraint of the loop set by the length of the helix. The presence of the nearby helix reduces the accessible space of the loop configuration, and thus decreases the number of the viable loop conformations.

The most frequently occurring pseudoknots in natural RNAs are the canonical H-type pseudoknots having a very short (single nucleotide) or completely absent inter-helix loop, L₃. For the canonical H-type pseudoknot, the helix stems S₁ and S₂ have a strong tendency to coaxially stack on each other to form a quasi-continuous helix. Applying polymer physics theory (Fisher 1966; Jacobson and Stockmayer 1950; Poland and Scheraga 1966), Gultyaev et al. proposed the following expressions for the loop entropy (Gultyaev et al. 1999):

$$\begin{array}{l}\mathrm{\Delta }{S}_{L_1}=A_{\mathit{major}}(S_2)+1.75k_{B}ln\left(1+N-N_{min\text{major}}(S_2)\right),\\ \mathrm{\Delta }{S}_{L_2}=A_{min\mathit{or}}(S_1)+1.75k_{B}ln\left(1+N-N_{min\text{minor}}(S_1)\right),\end{array}$$

where N _{min major} (S₂) and N _{min minor} (S₁) are the shortest allowed lengths for L₁ and L₂, respectively. The ad hoc fitting of known pseudoknots with the requirement that the pseudoknot be more stable than its hairpin components yielded estimates for the entropy parameters (Gultyaev et al. 1999).

In a canonical H-type pseudoknot, loops L₁ and L₂ span the major (narrow and deep) and the minor (shallow and wide) grooves of helices S₂ and S₁, respectively. Therefore, the two loops are highly asymmetric (Aalberts and Hodas 2005). Considering the loop asymmetry, Aalberts and Hodas (Aalberts and Hodas 2005) used the Gaussian chain approximation to derive the end-to-end distance distribution (between D and D+d) for an N-nt loop:

$$P_G(D,N)=4\pi D^{2}d{\left(\frac{3}{2\pi {Na}^2}\right)}^{3/2}{e}^{\frac{-3D^2}{2{Na}^2}}$$

where d = 0.1 Å and a = 6.2 Å. The total loop entropy is

$$\mathrm{\Delta }S=k_{B}ln[P_G(D_{L_1},L_1+1)P_G(D_{L_2},L_2+1)]$$

where D_L1 and D_L2 are the end-to-end distance for a L₁-nt loop L₁ and L₂-nt loop L₂, respectively. The end-to-end distances for L₁ and L₂ are determined by stems S₂ and S₁, respectively.

Based on the Gaussian chain approximation, Isambert and Siggia derived the loop entropy, ΔS, for a general three-loop (non-canonical) pseudoknot (Isambert and Siggia 2000, Isambert 2009):

$$\mathrm{\Delta }S=k_{B}ln\left({\alpha }^2\frac{e^{-A_1{S}_1^2-A_2{S}_2^2}}{D^{3/2}}\frac{e^{2A_3{S}_1{S}_2}-e^{-2A_3{S}_1{S}_2}}{4A_3{S}_1{S}_2}\right)$$

where D = L₁L₂ + L₁L₃ + L₂L₃, A₁ = 3(L₁ + L₂)/2abD, A₂ = 3(L₂ + L₃)/2abD, A₃ = 3(L₃/2abD and $S_{1,2}=\sqrt{d^2{sin}^2(\pi n_{1,2}/n_p)+h^2{(n_{1,2}/n_p)}^2}$. In the calculation, a = 6 Å, b = 1.5 nm, n_p=11, α = 0.0068, d = 4a, h = 5a and n_1,2 are the numbers of the base pairs in stems S₁ and S₂, respectively.

10.2.3 Pseudoknots --- structure prediction

The early computational methods for RNA pseudoknot prediction (Gultyaev et al. 1995) were based on the genetic algorithm (GA). These methods, such as the STAR (Gultyaev et al. 1995) and the MPGAfold (Shapiro and Wu 1997) models, predict the structures with the optimal kinetic accessibility instead of the ones with the lowest free energies. Other pseudoknot prediction methods based on stochastic simulations, such as the ILM (Ruan et al. 2004) and the Hotknots (Ren et al. 2005) models, can give low free energy structures. However, due to the nature of the stochastic conformational sampling, the predicted structure is not guaranteed to have the lowest free energy.

In 1999, Rivas and Eddy developed a dynamic programming method (pknotsRE) to predict pseudoknot structure (Rivas and Eddy 1999). Unlike the genetic algorithm and the other heuristic algorithms, the pknotsRE program, which uses a highly simplified energy function, is guaranteed to find the lowest energy pseudoknot. Later, with a more advanced pseudoknot energy model, Dirks and Pierce developed a partition function method (NUPACK) to predict pseudoknot structures (Dirks and Pierce 2003). In 2004, Reeder and Giegerich developed a new algorithm pknots-RG (Reeder and Giegerich 2004), which yields improved prediction than the original pknotsRE algorithm.

All the above algorithms use simplified nonphysical entropy parameters for pseudoknot loops. In 2006, Cao and Chen developed a physics-based pseudoknot prediction model based on a low-resolution structural representation, which is described below (Vfold, Cao and Chen 2006b). Benchmark tests indicate that the Vfold-based approach gives much improved predictions for pseudoknots compared to other models (Cao and Chen 2009).

10.2.4 RNA/RNA complexes

Functional RNAs often form complexes with RNA cofactors to perform catalytic and regulatory functions in a variety of RNA machineries, including ribozymes (Andronescu et al. 2005), spliceosomes (Staley and Guthrie 1998) and miRNA-argonaut complexes (Bartel 2009). Early computational models for RNA/RNA complexes, such as Hyther (Peyret et al. 1999), OligoWalk (Mathews et al. 1999), RNAhybrid (Rehmsmeier et al. 2004) and DINAMelt (Dimitrov and Zuker 2004), can give the structures and folding thermodynamics, such as the melting curves and binding affinities, for the simple, Watson-Crick paired RNA complexes. However, these models cannot treat the formation of intra-molecular base pairs in the binding process and thus cannot treat the interplay between the intra- and inter-molecular base pairing, which are known to be critical for many RNA catalytic and regulatory reactions.

In 2005, Andronescu et al. developed the PairFold program (Andronescu et al. 2005), which can explicitly account for both intra- and the inter-molecular base pairs. Tests on seventeen experimentally validated structures show an average correct accuracy 79%. The PairFold program is based on free energy minimization, thus does not predict thermodynamic stabilities, which are determined by the properties of the complete free energy landscape. In 2006, Cao and Chen (Cao and Chen 2006a) applied the Vfold model to predict RNA/RNA complexes based on the partition function method. The Vfold model predicts in addition to the native structure, all the local minima on the free energy landscape (i.e. meta-stable states) as well as thermodynamic properties such as melting curves. By using of a physical model for conformational sampling to obtain the entropy, as well as properly including non-Watson-Crick base pairs in the conformational ensemble, the Vfold model gives improved predictions. Later, based on partition function calculations, Mückstein et al. developed the RNAup algorithm (Mükstein et al. 2006) to compute the base “un-pairing” probability. The application of fundamental theory to the analysis of RNAi-target association led to more reliable predictions for the correlation between the RNAi efficiency and the RNAi-target binding energy. In 2007, Dirks et al. (Dirks et al. 2007) established a new partition function-based theory (NUPACK). A unique feature of the theory is its ability to treat multiple (> 2) nucleic acid strands.

Most of the above mentioned folding programs are restricted to structures without pseudo-knotted folds. Although PairFold can treat pseudo-knotted complexes, but not with high accuracy (Andronescu et al. 2005). In 2006, based on a number of heuristic approaches to the energy models, Alan et al. (Alan et al. 2006) applied the minimum free energy algorithm to search for the native structure of the pseudo-knotted complexes including the kissing loop complexes. Later, Chitsaz et al. (Chitsaz et al. 2009) and Huang et al. (Huang et al. 2009) used the partition function-based algorithm to calculate the structures and folding stabilities of pseudo-knotted complexes. Test of the algorithm by Chitsaz et al. showed that the algorithm can correctly predict the thermodynamic properties for RNA/RNA complexes such as the OxyS/fhlA complex (Chitsaz et al. 2009).

10.3 RNA tertiary structural folding --- from 2D low-resolution to 3D all-atom structures

The partition function stands at the center of statistical mechanical modeling. The partition function, Q, of an RNA molecule is the Boltzmann sum over all the possible structures:

$$Q=\sum _s{e}^{-\mathrm{\Delta }{G}_s/k_{B}T}$$ (10.1)

where s denotes an enumeration over all possible 2D structures (polymer graphs; see Fig. 1), ΔG_s is the energy of s and k_B = 1.99cal/K is the Boltzmann constant. The calculation of the partition function contains two key ingredients: sampling of all the possible conformations Σ_s and accurate evaluation of the free energy ΔG_s(= ΔH − TΔS) of each 2D structure s. Here ΔH and ΔS are the enthalpy and entropy for the given 2D structure s.

The empirical enthalpy and entropy parameters for base stacks and loops (Turner rules) form the foundation for RNA folding free energy prediction at the secondary structural level. However, even for simple secondary structures, the answers to many biologically significant questions require information that goes beyond these parameters. For example, the stability of a hairpin or internal loop is an average over many loop conformations which may involve a variety of sequence-dependent intra-loop contacts. The intra-loop contacts dramatically reduce the loop entropy. To understand and predict the loop entropy and stability for a given sequence, we must dissect the loop entropy for different loop structures with different intra-loop contacts. Empirical thermodynamic parameters such as Turner rules cannot give such entropies. What we need is a theory to calculate the entropy.

Furthermore, most existing RNA folding prediction algorithms are unable to account for the effect of the cross-linked (i.e., tertiary) contacts. One of the challenges comes from the entropy evaluation for tertiary folds. The success of the energy and entropy parameters for the secondary structure models relies on the additive nearest-neighbor (NN) model. For the conformational entropies, the NN model assumes that the entropy for a secondary structure is equal to the sum of the entropies of the subunits (loops, base stacks). Therefore, a parameter database for the different types of subunits would suffice for the calculation of the total free energy. However, the additivity rule for secondary structures is doomed to fail for tertiary folds. This is because the tertiary contacts (cross-links) between the different secondary structural motifs (helices, loops) cause inter-dependence between the (distant) motifs. As a result, even if we knew the entropies and free energies of the individual structural subunits, we would still be unable to predict the entropy and the free energy of a tertiary structure. Therefore, a meaningful database for the tertiary energy parameters, such as a list of the entropy parameters for loops, must consider the influence of other subunits. This, in fact, makes the experimental determination of the parameters impossible. What we need rather is a first principles model. The recently developed model, called “Vfold”, is such a model.

10.3.1 The Vfold model

While predictions of the structure and full free energy landscape may not be possible at the high resolution atomic scale level, what is well within reach is to parse the complexity into two parts: To use low-resolution models to account for the complete conformational ensemble by treating the atomic details implicitly, and then to construct atomistic 3D (native and alternative) structures from the low-resolution models. Given the huge conformational space available to an RNA molecule, such a multi-scale approach has several distinctive advantages:

1. At the low-resolution level, many experimental questions are not concerned with the specific locations of the hydrogen or nitrogen atoms; instead, they are far more concerned with the global fold, backbone flexibility, and the potential for large structural rearrangements, as investigated by small angle X-ray or neutron scattering and other low-resolution techniques (Chauhan et al. 2005; Deigan et al. 2009; Gherghe et al. 2009; Russell et al. 2002).

2. The key issue in prediction of the tertiary structural folding concerns the entropy of the global fold, which is largely determined by low-resolution properties such as the excluded volume and the chain connectivity effects. The reduced complexity of the low-resolution model allows us to maintain the rigor in physical principles when accounting for these properties. As a result, use of a low-resolution model enables first principles calculations for chain entropy, free energy, and the full free energy landscape for any given sequence.

3. The low-resolution structure provides a useful scaffold for the final all-atom folding model through structural refinements.

4. The predicted structure will provide highly needed guidance for experiments. For example, in NMR structural determinations of RNA, a severe limitation is that sequential resonance assignments rely heavily on Nuclear Overhauser Effect (NOE) data to establish connectivities (“NOE walks”), which often requires several months of data collection and analysis. The information on the nucleotide spatial proximity from the predicted (low-resolution) structure can provide useful constraints for enhancement in the efficiency and accuracy of resonance assignments.

Vfold is a recently developed low-resolution model based on the virtual bond representation of RNA conformation (Cao and Chen 2005; Cao et al. 2010; Chen 2008). As shown in Fig. 3a, the P-O₅-C₅-C₄ and the C₄-C₃-O₃-P dihedrals tend to be planar and rigid, because the torsional angles about the C₅-O₅ and C₃-O₃ bonds tend to remain in the relatively rigid trans (t) state,. Therefore, the original six-torsion nucleotide backbone can be reduced to two “virtual bonds” spanning P to C₄ and C₄ to the next P in the chain (Olson and Flory 1972; Olson 1975; Olson 1980). Calculations on the nucleotide atomic structures show that each virtual bond has a length of 3.9 Å. The third virtual bond (C₄-N₁ for primidine or C₄-N₉ for purine) represents the orientation of the base. In addition, a survey of known RNA structures suggests that the distance between the N₁ (in pyrimidines) or N₉ (in purines) and C₄ atoms stays close to 3.9 Å and the torsion angle between plane P_i-C₄-P_i+1 and P_i-C₄-N₁ (N₉), close to the g⁻¹ isomeric state. Thus, the C₄-N₁ (N₉) virtual bond is quite rigid. The three-vector virtual bond model leads to the following Vfold model for RNA folding:

Figure 3.

(a) Each nucleotide has two backbone virtual bonds P-C₄-P (blue) and a sugar-base virtual bond (red) C₄-N₁ for primidine or C₄-N₉ for purine. (b) An RNA conformation can be generated through random walks of the virtual bonds in a diamond lattice. In the diamond crystal the four carbon atoms are located at the vertices and center of a tetrahedron. Four such tetrahedral connected at their vertices fit in a cube. Repetition of such cubes side by side generates a diamond lattice.

1. The virtual bond structure for a helix is constructed from the atomic coordinates of an A-form RNA helix (Arnott and Hukins 1972).

2. The ensemble of virtual bond structures for loop conformations are generated by using the usual gauche⁺ (g⁺), trans (t) and gauche⁻ (g⁻) rotational isomeric states for a polymer. A survey on the existing known structures shows that such rotational isomeric states can well represent RNA loop conformations (Cao and Chen 2005; Duarte and Pyle 1998; Duarte et al. 2003; Richardson et al. 2008). The three isomeric states can be realized in the diamond lattice. Therefore, the virtual bonds of loop conformations are configured on the diamond lattice, where each lattice bond is a virtual bond (see Fig. 3b).

3. At the helix-loop junction, we fit the virtual bonds onto the diamond lattice with the minimum RMSD.

The Vfold model is fundamentally different from any of the simplified models such as the simple square or cubic lattice models used in other folding theories. Vfold is a realistic atomistic structural model because the virtual bonds are the realistic, physical P-C₄ and the C₄-P bonds in the structure, and the discretization (diamond lattice) of the virtual bond configurations for loop conformations is based on the principles of polymer physics as well as known RNA structures. So the Vfold model can directly predict experimentally measurable and biologically relevant structures and stabilities. The Vfold package is available for Windows and Unix users (to be released; URL: http://vfold.missouri.edu/chen-software02.html). For pseudo-knotted folds, the CPU time (t seconds) for the Vfold-based structural prediction grows with the sequence length (l nucleotides) as ln (t) ≈ −24.3 + 7.7 ln (l) on a Intel(R) Xeon(R) CPU 5150 @ 2.66GHz on Dell EM64T cluster system. The most time-consuming part of the computation is the enumeration of the different stems and loops (2D structures).

10.3.2 Pseudoknot structure and stability

The predictive power of the Vfold model is shown by its ability to compute the entropy for complex folds such as a 3-loop pseudoknot (Fig. 2). The computation involves three steps:

1. All the possible helix orientations are generated through the enumeration of (virtual bond) conformations of the loop L₃.

2. For each helix orientation, because the probability for a loop bumping into another loop is relatively small, the loops can be treated with the independent loop approximation (Cao and Chen 2009; Chen and Dill 2000; Poland and Scheraga 1970): The total conformational count (Ω) for the 3-loop system can be estimated as the product of the conformational count (Ω_{loop Li}) for each loop.

   $$\mathrm{\Omega }={\prod }_{\mathrm{i}}{\mathrm{\Omega }}_{\mathit{loop}{\mathrm{L}}_{\mathrm{i}}};{\mathrm{S}}_{\text{loop}}=k_{B}ln\mathrm{\Omega }$$ (10.2)

   This approach is remarkable because it reduces the 3-loop conformational enumeration into conformational enumeration for one loop at a time, resulting in a dramatic reduction in the computer time from T(Σ_nL_n) to Σ_nT(L_n), where L_n is the length of the n-th loop and T(L) is the computer time for counting conformations for a loop of length L.

3. The volume exclusion between a loop and the helices (grooves) is the key to the evaluation of the loop entropy. In the Vfold model, this can be explicitly taken into account by disallowing overlapping virtual bonds when the loop conformations are generated in the virtual bond diamond lattice.

The Vfold model leads to loop entropy parameter tables for canonical (Cao and Chen 2006a) 2-loop H-type pseudoknots and non-canonical 3-loop H-type pseudoknot (Cao and Chen 2009). Table 1 gives the entropy parameters for the canonical (2-loop) H-type pseudoknot. For the non-canonical (3-loop) H-type pseudoknot, the entropy tables are deposited at http://rnajournal.cshlp.org/content/15/4/696/suppl/DC1 (Cao and Chen 2009).

These loop entropy parameters allow for calculations of the folding free energy for a given pseudoknot (Cao and Chen 2006b; Cao and Chen 2009; Chen 2008). For example, for the 3-loop pseudoknot shown in Fig. 4, the free energy is ΔG = ΔG₁ + ΔG₂ − TΔS(S₁, S₂, L₁, L₂, L₃) = (−7.1) kcal/mol + (−6.3) kcal/mol + k_BT (14.2) = −4.6 kcal/mol, where S₁ and S₂ denote the length of stems 1 and 2 and L₁, L₂ and L₃ are the lengths of loops 1, 2 and 3, respectively. The entropy parameter ΔS(S₁, S₂, L₁, L₂, L₃) is transcribed from Table S1 of this reference: (Cao and Chen 2009).

Figure 4.

The evaluation of the free energy for a 3-loop (non-canonical) H-type pseudoknot using the loop entropy parameters in Table S1 of reference (Cao and Chen 2009) and the Turner rule (Serra and Turner 1995).

Application of the Vfold model to the structure prediction of a pool of biologically significant RNA molecules ranging in length from 28 to 91 nucleotides (Ren et al. 2005) indicates that the Vfold model gives significant improvements in the accuracy of the predictions as compared to other existing RNA folding models (Cao and Chen 2009). Furthermore, the successful implementation of the Vfold-predicted entropy parameters in several other software packages indicates that their use can indeed lead to significantly improved accuracy in pseudoknot structural prediction (Andronescu et al. 2010; Sperschneider and Datta 2010; Liu et al. 2010). The calculation of entropies of more complex pseudo-knotted structure is computationally demanding (Cao and Chen 2006a; Cao and Chen 2009). Monte-Carlo simulation may be a potentially useful method to generate virtual bond conformations for the evaluation of the entropy and free energy of more complex structures (Zhang et al. 2008; Zhang et al. 2009).

10.3.3 Loop-stem base triple interactions

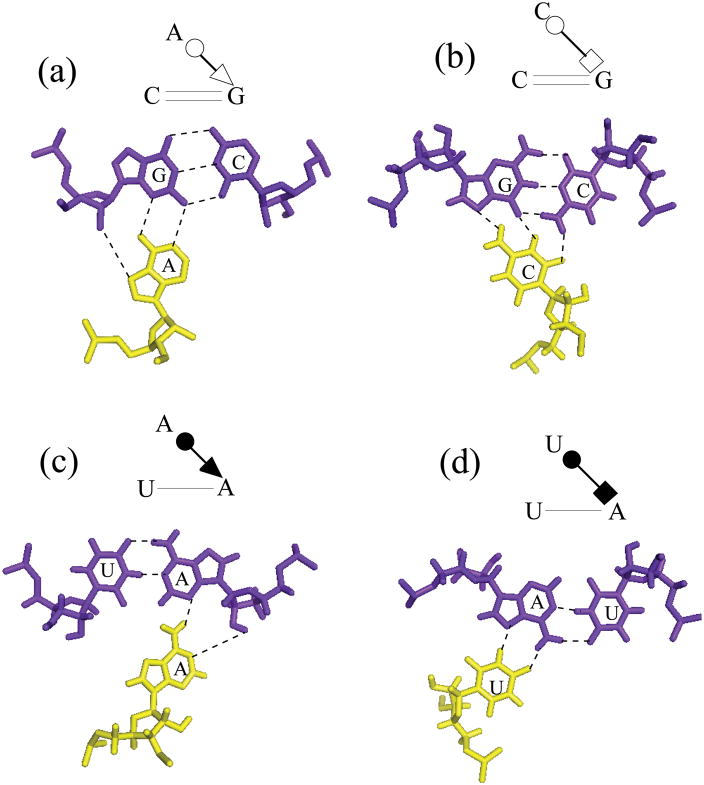
In RNA pseudoknots, the close spatial proximity between loops and stems facilitates formation of the tertiary contacts between loop and stem nucleotides. Specifically, a nucleotide in the loop surrounding the major or minor groove is prone to form base triple interactions with a base pair in the helix stem (see Figs. 5a & b). Analysis of the known X-ray structures reveals a large number of non-canonical tertiary interactions in RNA molecules (Xin et al. 2008). These tertiary interactions include A-minor motifs first identified in ribosomal RNA (Nissen et al. 2001), the base triples seen by X-ray in the pseudoknots (Su et al. 1999) and the ribose zipper interactions originally found in group I introns (Cate et al. 1996). Non-canonical tertiary interactions can be critical for the stabilization of the structures and RNA biological functions. For instance, mutations that disrupt the base triples can dramatically reduce the biological activity of telomerase (Theimer et al. 2005) and the efficiency of ribosomal frameshifting (Cornish et al. 2005; Kim et al. 1999; Su et al. 1999).

Figure 5.

(a) Human telomerase RNA (hTR) pseudoknot contains 2 base triples (blue dashed lines) between loop L2 and helix stem S1 and 3 base triples between loop L1 and helix stem S2 (Theimer et al. 2005). (b) The atomic configuration for the base triple between U9 and the U22-A39 base pair. (c) Theory-experiment test for the melting thermodynamics of five experimentally measured pseudoknot molecules: PLRV and PEMV-1 (Nixon et al. 2002), BWYV and the U8 variant (Nixon and Giedroc 2000), ScYLV. The melting of these molecules show two apparent transitions. The melting at the lower temperature $T_m^3$ and the higher temperature $T_m^2$ usually correspond to the disruption of the loop-stem tertiary contacts and the secondary structure, respectively. In the theoretical predictions, the salt-dependent helix stability (in 1M NaCl) is modified according to the experimental condition (0.5 KCl, PH 7.0) by using empirical formulas (SantaLucia 1998; Tan and Chen 2006). (d) The predicted (lowest free energy) 2D structure for the ScYLV pseudoknot agrees exactly with the NMR structure (Cornish et al. 2005, PDB: 1YG3). The red lines denote the loop-stem base triples.

There are eight different types of base triples in the known pseudoknot structures, A.G-C), A.(C-G), C⁺.(G-C), C⁺.(C-G), U.(A-U), U.(U-A), A.(A-U) and A.(U-A). These base triples belong to different geometric families, defined by the families to which their component basepairs belong (Almakarem et al. submitted 2011). Fig. 6 shows four types of geometric families based on the nomenclature proposed by Leontis and Westhof (Leontif and Westhof 2001). For example, A.(G-C), C⁺.(G-C), A.(A-U) and U.(A-U) belong to cis WW/trans SW, cis WW/trans HW, cis WW/cis SW and cis WW/cis HW geometric families, respectively. According to the protonation properties, the eight base triples can be further classified into two types: the protonated [C⁺.G-C) and C⁺.(C-G)] and the unprotonated base triples. The classification is based on the fact that the protonated base triples are more stable than the unprotonated base pairs (Cornish et al. 2005) due to strong electrostatic interactions.

Figure 6.

Configurations of four base triples (a) A.(G-C), (b) C⁺.(G-C), (c) A.(A-U) and (d) U.(A-U). They belong to cis W.W./trans S.W., cis W.W./tran H.W., cis W.W./cis S.W. and cis W.W./cis H.W. geometric families, respectively (Leontif and Westhof 2001; Almakarem et al. submitted 2010).

Computational prediction of the non-canonical tertiary interactions is extremely difficult because of the lack of accurate energy parameters for tertiary interactions and the higher conformational complexity and the larger size of the conformational space (Das and Baker 2007; Ulyanov et al. 2007; Yingling and Shapiro 2006). Yingling and Shapiro predicted the base triples in the human telomerase RNA (hTR) pseudoknot using molecular dynamics simulations (Yingling and Shapiro 2006). Though the predicted structure is not exactly consistent with the NMR structure (Kim et al. 2008), the simulation was able to provide useful insights into the interplay between bulge formation and the base triple interactions in telomerase RNAs. Molecular dynamics simulation often relies on the initial input of the 3D structure. In contrast, the Vfold model, which uses the nucleotide sequence as the only input information, does not require any additional structural information.

The Vfold-based prediction of loop-stem tertiary interactions involves the following steps:

1. Through explicit enumeration of the virtual bond conformations, the Vfold model gives the loop entropy ΔS_loops as a function of loop length, helix length, and assignments of base triples (Figs. 5ab). Based on the Vfold-predicted entropy parameter set, for a given structure that contains loop-stem tertiary contacts, the free energy ΔG can be evaluated as

   $$\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\mathit{helix}}-T\mathrm{\Delta }{S}_{\mathit{loop}}+{\sum }_{i=1}^n(\mathrm{\Delta }{h}^{(i)}-T\mathrm{\Delta }{s}^{(i)})$$

   where Δh⁽ⁱ⁾ and Δs⁽ⁱ⁾ are the enthalpy and entropy parameters for loop-stem contact i.

2. Theory-experiment comparisons for different systems with loop-stem contacts allow us to extract Δh and Δs parameters. As the lowest order approximation, we assume two sets of (Δh, Δs) parameters for protonated and non-protonated base triples, respectively. Fitting the melting curves for different pseudoknots that contain loop-stem base triples (Giedroc and Cornish 2009; Nixon et al. 2002; Nixon and Giedroc 2000) converged on the same set of (Δh, Δs) parameters (Fig. 5c) below:

   $$(\mathrm{\Delta }h,\mathrm{\Delta }\mathrm{s})=(-7\text{kcal}/\text{mol},-19\text{cal}/\text{mol.K})\text{for}(\mathrm{A}\text{or}\mathrm{U}).(\text{A-U}\text{or}\text{U-A})\text{and}(\mathrm{A}).(\text{C-G}\text{or}\text{G-C})$$ (10.3)

   $$\text{and}=(-14\text{kcal}/\text{mol},-38\text{cal}/\text{mol}/\mathrm{K})(\text{pH}7.0)\text{for}{\mathrm{C}}^{+}.(\text{C-G}\text{or}\text{G-C})$$ (10.4)

The above Vfold approach has led to accurate predictions for the loop-stem tertiary contacts and thermodynamic stabilities for a series of experimentally determined pseudo-knotted structures (Fig. 5c) (Cao et al. 2010).

10.3.4 All-atom 3D RNA structures

Predicting RNA 3D structure is not a solved problem (Das and Baker 2007; Ding et al. 2008; Jonikas et al. 2009; Jossinet and Westhof 2005; Parisien and Major 2008; Shapiro et al. 2007; Tan et al. 2006). Currently, challenges include adequate treatment of the problem of conformational sampling (Das and Baker 2007) and the evaluation of the energetic parameters for tertiary contacts (Ding et al. 2008; Parisien and Major 2008). The Vfold model (Cao et al. 2010) can successfully predict the 2D structures of pseudoknots, including loop-stem tertiary interactions. The Vfold model-predicted virtual bond structure provides a scaffold for the construction of all-atom models of the 3D structure. The prediction of the all-atom 3D structure from the Vfold-predicted 2D structures involves the following three steps (see Fig. 7):

Figure 7.

(a) The Vfold-predicted Watson-Crick base pairs for the 2D structure of BWYV pseudoknot. (b) The predicted 3D low-resolution (virtual bond) structure built from the predicted 2D structure. (c) The all-atom 3D structure built from the virtual bond structure. (d) the all-atom structure refined by Amber 9. The figure is adopted from Ref. (Cao et al. 2010). The root mean square deviation (RMSD) between the experimental structure (PDB code: 473d; in sand color) and the predicted structure (in purple-blue color) is 2.7Å over all-heavy atoms.

1. Adding all atoms to the virtual bond structure. For nucleotides in each predicted helix, atoms are added according to the A-form helix atomic structure. The 3D conformations of the loop are generated from a combined fragment-based and diamond lattice-based method: the coordinates of the red nuclotides are adopted from the PEMV-1 fragment (PDB ID: 1KPX) and the remaining two nucleotides (blue) are generated by self-avoiding random walks on the diamond lattice. The method can effectively reduce the numbers of loop conformations to a few low-energy viable conformations. For nucleotides in the predicted loop conformations, atoms can be added using helix nucleotides as templates, by aligning the P, C₄ and N_1,9 atoms with those in of a nucleotide in a helix. This step results in an “atomistic version” of the Vfold structure.

   The product of this initial refinement step is a pre-refined atomic structure. The pre-refined structure may contain some atoms/groups that clash sterically with each other. Such steric clashes can be readily resolved by the subsequent molecular dynamics simulation in the next step.

2. Energy minimization of the whole atomistic structure using AMBER molecular dynamics simulations. With the above pre-refined structure as the initial state, molecular dynamics energy minimization with the AMBER molecular dynamics package (Case et al. 2005; Case et al. 2006; Cornell et al. 1995; Pearlman et al. 1995) yield reliable predictions for all-atom 3D structures. In the energy minimization, the negative charges on phosphates are neutralized by Na⁺ cations added to the solution. The nonbonded interactions are truncated at 12 Å. Water molecules are treated by the standard TIP3P model included in AMBER software.

As shown in Fig. 7, the above strategy gives reliable predictions for the all-atom 3D structures for simple tertiary folds such as pseudoknots.

10.4 Quantitative prediction for RNA function --- −1 programmed ribosomal frameshifting

A −1 programmed ribosomal frameshift occurs when the reading frame is shifted by one nucleotide. The change of the reading frame causes the production of multiple proteins. Ribosomal frameshifting is a mechanism used by many RNA viruses to regulate the relative number of copies of viral proteins (gag and pol). Maintaining a normal ratio of gag and gag-pol proteins is critical for viral replication. Alteration in frameshifting efficiency could lead to an abnormal ratio of gag and gag-pol proteins, resulting in reduction or elimination of viral replication (Dinman et al. 1998).

The ribosomal frameshifting machinery consists of three coupled components (see Figs. 8a and b): (a) the slippery sites (nucleotides in blue color) with the sequence XXXYYYZ, where X can be any nucleotide, Y is A or U and Z is A, U or C, (b) a spacer (black thick line) that connects the 5′ slippery sites and the 3′ mRNA structure, and (c) the 3′ mRNA structure which can fold into a pseudoknot structure (nucleotides in red color). According to the mechanical model for frameshifting (Hansen et al. 2007; Namy et al. 2006; Plant et al. 2003), the pseudoknot blocks the entrance of the mRNA into the ribosome and causes ribosomal pausing. During ribosomal pausing, the 3′→5′ movement of the tRNA in the A/T to A/A aa-tRNA accommodation process can generate a tension force in the spacer (Plant et al. 2003; Yusupova et al. 2001). The tension, if sufficiently strong, could break the codon-anticodon pair of the 0 frame, causing a 5′→3′ shift by one nucleotide of the mRNA chain and the subsequent shift of the codon-anticodon pair by one nucleotide.

Figure 8.

A schematic diagram for the −1 ribosomal frameshifting induced by an RNA pseudoknot. The slippery sites of mRNA (blue nucleotides) is shifted in the 5′→3′ direction by one nucleotide, which results in the reading frame to be shifted from the original (a) 0 frame to the new (b) −1 frame. The translated codons are (XXY,YYZ) in the 0 frame (a) and (XXX,YYY) (b) in the shifted −1 frame.

The three components of the ribosomal frameshifting machinery are coupled through the spacer length m: the tension force in the spacer is a function of spacer length, which varies with the folding-unfolding of the downstream mRNA. The tension force in the spacer is also dependent on the end-to-end distance X of the spacer, which increases from 3.3 nm to 4.3 nm in the 3′→5′ movement of the tRNA. If the downstream mRNA structure is robust against the large tension force, the spacer would more likely be subject to a large tension to induce frameshifting before unfolding of the downstream mRNA structure occurs. Otherwise, unfolding of the downstream mRNA structure would cause the relaxation of the tension, reducing the likelihood of frameshifting.

Quantitative prediction of ribosomal frameshifting requires modeling of the folding stability and the structure of the frameshifting machinery. The partition function for the 3-component frameshifting machinery is Q(m,X)=Q_ds Q_ss Q_codon. Here Q_ds, Q_ss, and Q_codon are the partition functions of the 3′ downstream mRNA structure (“structured” region, excluding the 5′ and 3′ tails), the (single-stranded) spacer of length m and end-to-end distance X, and the codon-anticodon base-pairing duplex (in the slippery region), respectively. While Q_ss and Q_codon can be evaluated using the extensible freely jointed chain model (EFJC) (Gerland et al. 2004; Hyeon and Thirumalai 2005; Liphardt et al. 2001; Smith et al. 1996; Strick et al. 2000) and the nearest neighbor model (Serra and Turner 1995), respectively, the computation of Q_ds requires a statistical mechanical model such as the Vfold model. The tension force predicted from the partition function is given by F(X)=dΔG(X)/dX = −k_BT d ln Σ_mQ(m, X)/dX.

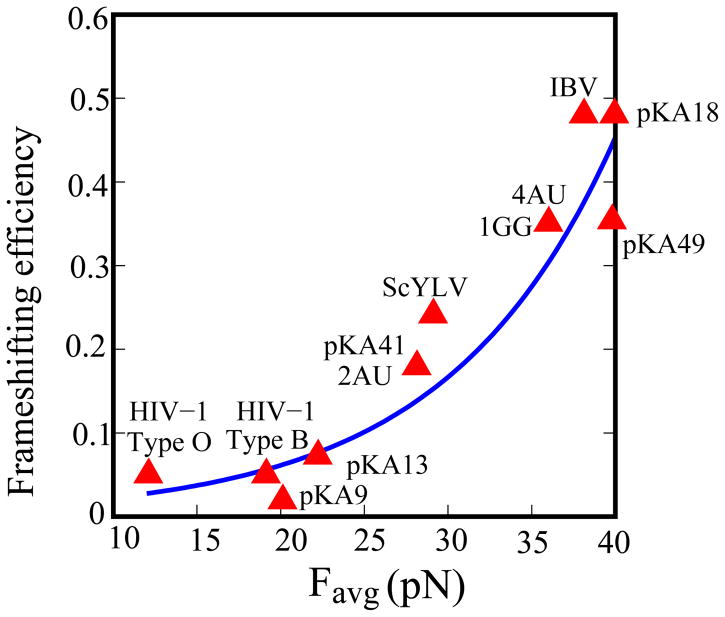
The Vfold modeling for the system leads to an analytical relationship between the frameshifting efficiency and the mean tension force; see Fig. 9. It should be noted that recent single-molecule experimental data yields a highly similar relationship (Chen et al. 2009). Furthermore, because the experimental measurement (Chen et al. 2009) for human telomerase RNA and the Vfold-based theoretical predictions (Cao and Chen 2008) involve different frame-shifting systems, the fact that similar analytical relationships are derived from independent theoretical and experimental studies suggests that the quantitative results for the frame-shifting efficiency may be valid for a variety of systems.

Figure 9.

The correlation between the frameshifting efficiency (η) and the mean force F_avg from X=3.3 nm to 4.3 nm. We fitted a analytical expression (the blue thick line) for the correlation: η ≈ 0.0083e^0.1F_avg. The experimental data of the frameshifting efficiency is adopted from references (Brierley et al. 1991; Napthine et al. 1999) for IBV and its mutant (pKA18, 1GG, 2UU, pKA41, 3AU, 4AU, pKA49, pKA13 and pKA9), reference (Dulude et al. 2002) for HIV-1 type B, reference (Baril et al. 2003) for HIV-1 type O and reference (Cornish et al. 2005) for ScYLV.

10.5 Conclusions

For a long time, the bottleneck for RNA tertiary structural folding has been the inability to treat the free energy, especially the entropy, of structures with non-nested, long-range (tertiary) contacts between nucleotides distant in the 2D structure. Recent advances in the construction of low-resolution conformational models allow us to predict the entropy and the full free energy landscape for RNA tertiary global folds, as well as the 2D structures for the local and the global free energy minima. These 2D structures can further provide scaffolds for the construction of all-atom 3D models of the stable and metastable RNA folds through molecular dynamics calculations. Comparisons between theoretical predictions and experimental data for the 2D and 3D structures and the folding thermodynamics suggest that the statistical mechanical approach is reliable. One of the key factors that contribute to the predictive power of the statistical mechanical models is the rigorous conformational sampling/entropy.

With the rapidly growing size of the database of the experimentally measured RNA structures, fragment-based methods show promise, especially when the homologous conformations of modular components of the RNA of interest can be identified in the PDB database (Cao et al. 2011; Das and Baker 2007; Parisien and Major 2008). However, compared to the number of the deposited protein structures in the PDB database, the number of known RNA structures remains relatively small. Therefore, fragment-based methods for RNA 3D prediction may fail if no known homologous conformations can be found in the PDB database. In that case, a de novo construction of the (low-resolution) conformations (especially for the junctions/loops regions) is the only viable approach. The Vfold model introduced in this chapter is one such model that can build the conformations de novo.

The current form of the Vfold theory can successfully treat pseudo-knotted folds. However, the problem of predicting more complex pseudo-knotted folds, such as the internal ribosome entry site (IRES) of the cricket paralysis-like viruses (Filbin and Kieft 2009) and other larger tertiary folds, remains. Further development of the model should go beyond the simple loop-stem base triples by including more complex tertiary interactions, such as tetraloop-receptor interactions and kissing loop interactions (Chitsaz et al. 2009; Huang et al. 2009).

Table 2.

Entropy parameters for loops L₁ and L₂. In the table, an entropy parameter ΔS_loop is given in the form of −ΔS_loop/k_B, where k_B is the Boltzmann constant. The * entries in the Table indicate the loop conformations that cannot be realized in the diamond lattice but may be viable for a realistic pseudoknot. These loop conformations usually have a long stem and short loop. For the entropies of these restricted loops, we use the values of the minimal loop for the same helix length. The table is adapted from reference (Cao and Chen 2006a).

Stem size (bp)	Loop size (nt)
	1	2	3	4	5	6	7	8	9	10	11	12
(S2)	L1 (across the major groove of S2)
2	-	-	-	6.2	6.4	6.4	6.6	6.8	6.9	7.1	7.2
3	-	6.4*	6.4*	6.4	6.6	6.6	6.8	6.9	7.1	7.3	7.5
4	4.5*	4.5*	4.5	5.4	5.6	6.0	6.3	6.6	6.9	7.1	7.3
5	2.3	4.4	4.6	5.7	6.0	6.5	6.9	7.2	7.5	7.8	8.0
6	2.3	4.4	4.8	5.8	6.0	6.5	6.8	7.1	7.4	7.6	7.8
7	2.3	4.4	5.0	5.9	6.2	6.8	7.0	7.3	7.6	7.8	8.0
8	-	4.4	5.2	5.7	6.4	6.7	7.1	7.3	7.5	7.7	7.9
9	-	5.5*	5.5	6.4	6.7	7.2	7.5	7.9	8.1	8.3	8.5
10	-	6.9*	6.9*	6.9	7.5	7.7	8.1	8.3	8.6	8.8	8.9
11	-	-	-	-	8.7	8.8	8.9	9.1	9.2	9.3	9.3
12	-	-	-	-	9.8	9.2	9.5	9.6	9.7	9.8	9.8
(S1)	L2 (across the major groove of S1)
2	-	-	-	7.6	7.0	7.0	7.1	7.2	7.3	7.4	7.5	7.7
3	-	6.5*	6.5*	6.5	6.6	6.7	6.9	7.1	7.2	7.4	7.6	7.7
4	-	-	9.2*	9.2*	9.2	8.9	8.9	8.9	9.0	9.0	9.1	9.2
5	-	-	-	9.8*	9.8*	9.8	9.1	8.9	8.8	8.8	8.8	8.8
6	-	-	-	11.9*	11.9*	11.9*	11.9	11.0	10.4	10.1	9.9	9.8
7	-	-	-	-	12.4*	12.4*	12.4*	12.4	11.4	11.0	10.7	10.5
8	-	-	-	-	12.1*	12.1*	12.1*	12.1	11.6	11.4	11.2	11.1
9	-	-	-	-	-	13.7*	13.7*	13.7*	13.7	12.6	12.0	11.5
10	-	-	-	-	-	13.7*	13.7*	13.7	12.7	12.2	11.8	11.5
11	-	-	-	-	-	-	-	-	15.9	14.1	13.0	12.4
12	-	-	-	-	-	-	-	-	18.7	15.8	14.2	13.2