Universality of Human Microbial Dynamics

Abstract

The recent realization that human-associated microbial communities play a crucial role in determining our health and well-being^1,2 has led to the ongoing development of microbiome-based therapies³ such as fecal microbiota transplantation^4,5. Thosemicrobial communities are very complex, dynamic⁶ and highly personalized ecosystems^3,7, exhibiting a high degree of inter-individual variability in both species assemblages⁸ and abundance profiles⁹. It is not known whether the underlying ecological dynamics, which can be parameterized by growth rates, intra- and inter-species interactions in population dynamics models¹⁰, are largely host-independent (i.e. “universal”) or host-specific. If the inter-individual variability reflects host-specific dynamics due to differences in host lifestyle¹¹, physiology¹², or genetics¹³, then generic microbiome manipulations may have unintended consequences, rendering them ineffectual or even detrimental. Alternatively, microbial ecosystems of different subjects may follow a universal dynamics with the inter-individual variability mainly stemming from differences in the sets of colonizing species^7,14. Here we developed a novel computational method to characterize human microbial dynamics. Applying this method to cross-sectional data from two large-scale metagenomic studies, the Human Microbiome Project^9,15 and the Student Microbiome Project¹⁶, we found that both gut and mouth microbiomes display pronounced universal dynamics, whereas communities associated with certain skin sites are likely shaped by differences in the host environment. Interestingly, the universality of gut microbial dynamics is not observed in subjects with recurrent Clostridium difficile infection¹⁷ but is observed in the same set of subjects after fecal microbiota transplantation. These results fundamentally improve our understanding of forces and processes shaping human microbial ecosystems, paving the way to design general microbiome-based therapies¹⁸.

The underlying dynamics of a microbial ecosystem, i.e. the ecological interactions that govern its change, equilibrium and stability, can be represented by a population dynamic model

$${\stackrel{.}{\mathit{x}}}^{(\nu )}=\mathit{f}\left({\mathit{x}}^{(\upsilon )};{\mathrm{\Theta }}^{(\upsilon )}\right),$$ (1)

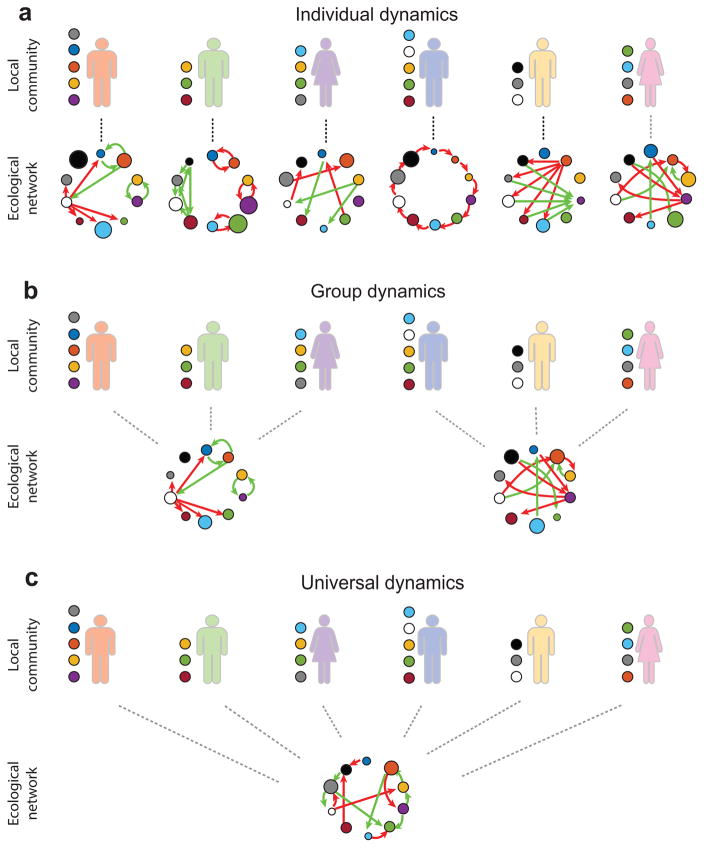
which describes the time-dependent abundance profile ${\mathit{x}}^{(v)}(t)=\left(x_1^{(v)}(t),\dots ,x_N^{(v)}(t)\right)$ of N microbial species present in a particular body site of subject υ. Here, f (x^(υ); Θ^(υ)) is typically a nonlinear function and Θ^(υ) captures all the ecological parameters, i.e. growth rates, intra- and inter-species interactions. Those parameters may generally depend on host-independent factors, e.g. biochemical processes and microbial metabolic pathways¹⁹; and host-specific ones, e.g. nutrient intake²⁰ and host genetic make-up¹³. Three fundamental cases could represent the dynamics of M healthy subjects: a)Individual dynamics, where the ecological parameters are different in different subjects, i.e. Θ⁽¹⁾ ≠ ⋯ ≠ Θ^(M); b)Group dynamics, where subjects can be classified into K groups (K ≪ M) based on certain host factors and subjects in the same group share the same set of parameters, i.e. Θ^(υ) = Θ^P for all subjects in group P (P = 1,⋯,K); c)Universal dynamics, where all the subjects share the same set of parameters, i.e. Θ^(ν) = Θ for all subjects. If we represent the ecological parameters, e.g. the inter-species interactions, in a directed weighted ecological network, the above three cases can be easily visualized (see Fig. 1).

Figure 1. Alternative scenarios of microbial dynamics across different healthy subjects.

Microbial dynamics captured by (1) is simply characterized by an ecological network, where nodes represent species (with node sizes proportional to growth rates) and edges represent inter-species interactions (with green/red arrows represent excitatory/inhibitory interactions, respectively). Different subjects typically have different species assemblages, represented by colored circles near each subject. a, The underlying dynamics/network is unique for each subject. b, Subjects within the same group share the same dynamics/network that is significantly different from that of other groups. c, Different subjects have the same underlying dynamics/network.

Despite its critical consequences, we don’t know which case best represents the microbial ecosystems of healthy individuals. Addressing this question is crucial for developing microbiome-based therapies^3,18. Indeed, if the dynamics are universal, the inter-personal variability stems solely from the different assemblages of colonizing species in different individuals. Then we can design general interventions to control the microbial state (in terms of species assemblage and abundance profile) of different individuals. In contrast, if the dynamics are strongly host-specific, we must design truly personalized interventions, which must consider not only the unique microbial state of an individual but also the unique dynamics of the underlying microbial ecosystem. In addition, host-specific dynamics, if exist, raise a major safety concern for FMT because the healthy microbiota, though stable in the donor’s gut, may be shifted to an undesired state in the recipient’s gut.

The ideal approach to addressing this fundamental question would be to infer the dynamic model captured by (1)for a large number of healthy individuals from temporal metagenomic data, and then compare the system parameters Θ^(υ) directly. However, empirical parameterization of the exact functional form of f (x^(υ); Θ^(υ)) is extremely difficult for complex ecological systems. Furthermore, inferring the system parameters typically requires high-quality time series data and well-designed experiments to ensure the system parameters are identifiable²¹. Such datasets are not currently available. A conventional correlation analysis of cross-sectional data cannot address this question either, because it only captures effective (or indirect) interactions and is subject to spurious correlations due to the compositionality of relative abundances in genomic survey data²².

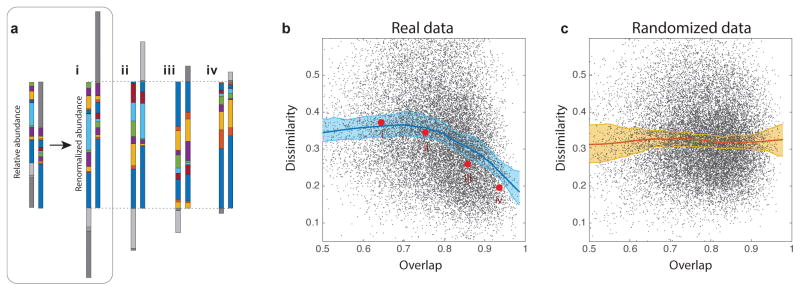
To overcome these issues, we developed a novel method to detect “fingerprints” of universal microbial dynamics. This is achieved by restricting ourselves to answer the question of “whether the dynamics are universal or not”, rather than the broader and harder question of “what are the dynamics”. The key idea is that when comparing microbial communities (samples) from different subjects, we distinguish between two contributors to the inter-individual variability: the difference in species assemblages and the difference in abundance profiles. We quantify those two contributors by: O(x̃,ỹ), the overlap of the species assemblages, calculated from the relative abundances of the shared species; and D(x̂,ŷ), the dissimilarity between the renormalized abundance profiles of the shared species (see Methods section). Note that the two measures (overlap and dissimilarity) are not apriori dependent on each other. Indeed, D(x̂,ŷ) is mathematically not constrained by any value of O(x̃,ỹ) > 0 (see SI Sec.1.2.1 for the proof). Hence any constraints of D(x̂,ŷ) by O(x̃,ỹ) observed from real data deserve our attention and may have ecological interpretations (see Fig. 2a,b).

Figure 2. Higher overlap of microbial communities is associated with lower dissimilarity.

a, Four gut microbial sample pairs (i–iv)represented by stacked bars at the genus level. For each sample pair, their shared genera are colored while non-shared genera are shown in gray. b, DOC(in dark blue) of gut microbial sample pairs from the HMP study (M = 190 samples). Gray dots represent all the 17,955 sample pairs. c, DOC (in dark red) of the randomized samples is flat. In (b) and (c), and throughout the paper, shaded area indicates the range of the 94% confidence intervals (see Methods section).

To systematically compare samples from a given microbiome dataset, we first calculate the overlap and dissimilarity of all the sample pairs and represent each sample pair as a point in the Dissimilarity-Overlap plane. We then perform nonparametric regression and bootstrap sampling to calculate the average Dissimilarity-Overlap Curve (DOC) and its confidence interval (see Fig. 2b and Methods section). In the case of (i) individual dynamics; or (ii) universal dynamics but without inter-species interactions, a flat DOC is expected (see SI Sec. 1.2.3). In contrast, for systems with universal dynamics and inter-species interactions, we expect the corresponding DOC to display a characteristic feature: a negative slope in the high-overlap region, i.e. abundance profiles of sample pairs become more similar as their overlap becomes higher(see SI Sec. 1.2 and Extended Data Fig. 1). A negative slope can also be seen in the DOC of microbial communities characterized by group dynamics. The existence of such group dynamics however can be easily detected by standard ordination techniques and clustering analysis^23,24 and hence ruled out (see Data Extended Fig. 2). Note that the DOC analysis described above is not affected by the compositionality of the genomic survey data and requires neither time series data nor any apriori knowledge of the specific ecological dynamics. Instead, it only relies on a few reasonable assumptions (see Methods).

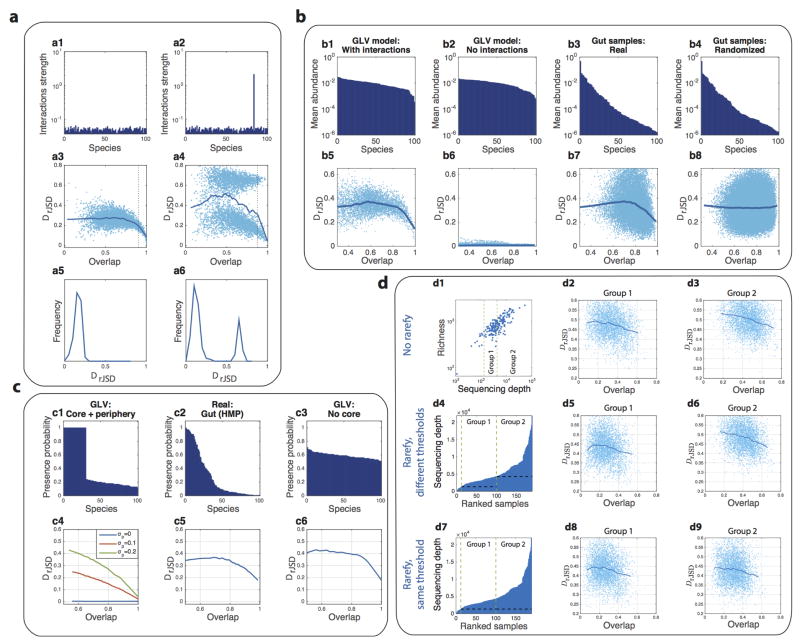
To verify our DOC analysis, we first applied it to synthetic data generated from the canonical Generalized Lotka-Volterra (GLV) model, which has been used for predictive modeling of the intestinal microbiota^25–27. Extended Data Fig. 3 shows that in the case of universal dynamics with strong inter-species interactions, the DOC displays a clear negative slope in the high-overlap region. In contrast, in the case of individual dynamics or universal dynamics without inter-species interactions, a flat DOC is observed.

To directly verify the DOC analysis using real data, we analyzed longitudinal gut microbial samples of four healthy individuals from two microbiome studies^11,28. For each individual, we expect a highly universal microbial dynamics throughout the period of measurement, i.e. the ecological parameters Θ^(ν) of the corresponding microbial community are largely time-invariant. We found that the DOCs of all four subjects show a clear negative slope in the high-overlap region (Extended Data Fig. 4), consistent with our expectation.

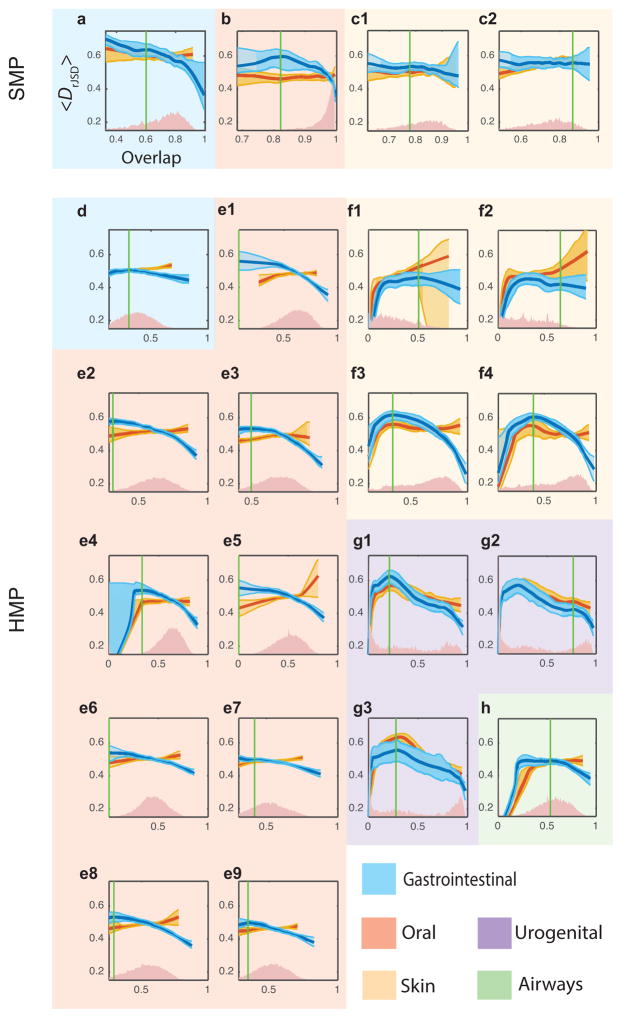
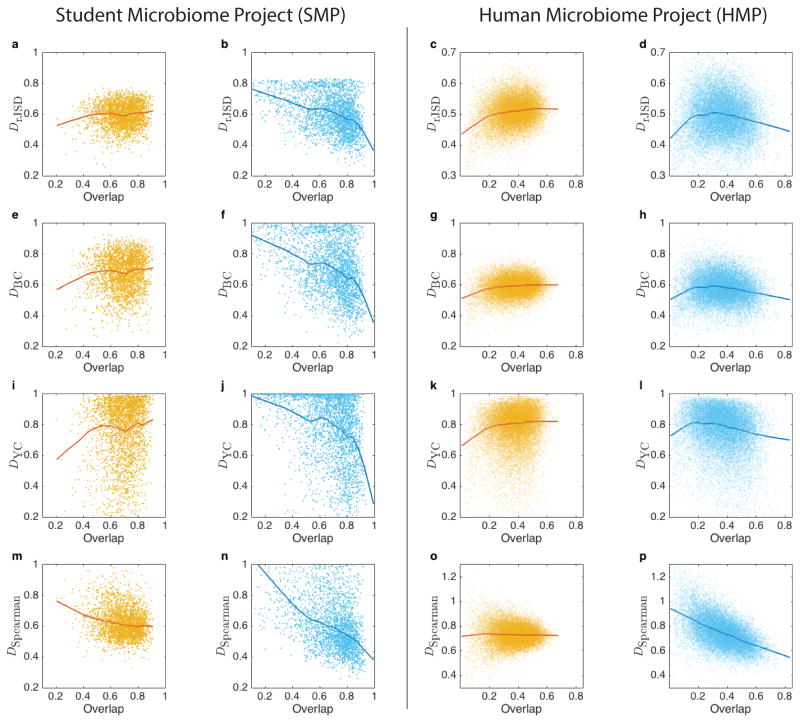
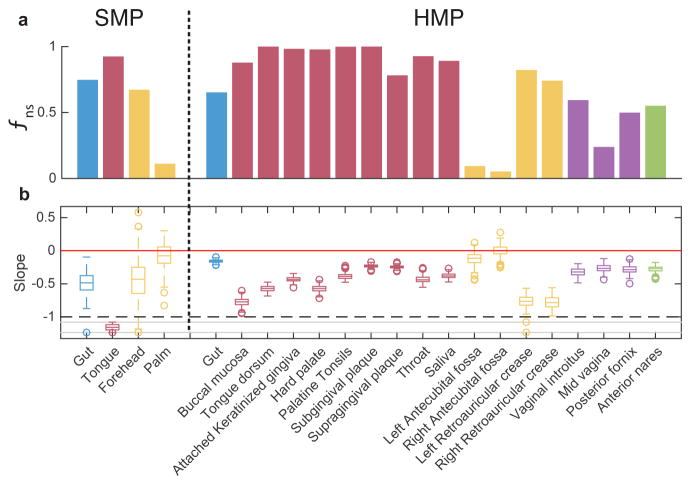
Next, we systematically analyzed cross-sectional microbial samples of different body sites from two large-scale metagenomic studies, the Human Microbial Project (HMP)^9,15 and the Student Microbiome Project (SMP)¹⁶. The results were shown in Fig. 3 and Extended Data Fig. 5. In Fig. 3, for each body site the DOCs calculated from real and randomized samples are shown in dark blue and red, respectively. The overlap distributions of the real between-subjects sample pairs are shown in red. Note that the characteristic overlap in a particular body site is different in the two studies. For example, the average overlap between HMP gut samples is about 0.4 and between SMP samples is about 0.75. To account for this fact and to fairly compare the DOCs across different body sites and different studies, we used two different measures to quantify the universality (see Methods). Interestingly, though these two measures quantify different features of the DOC analysis, the body sites stratification pattern is consistent across the two measures and the two studied datasets (Extended Data Fig. 6). In particular, the negative slope of DOC is most significantly observed in samples from the gut and mouth and least observed in samples from hand skin (palm and elbow). These findings strongly suggest the existence of universal dynamics characterized by inter-species interactions in the gut and mouth microbiomes.

Figure 3. Detecting universality of microbial dynamics in different body sites.

We calculated DOCs for real (dark blue) and randomized samples (dark red) of two datasets: (1) SMP- a, gut, b, tongue, c1, forehead skin, c2, palm skin; (2) HMP – d, gut, e1, tongue dorsam, e2, attached keratinized gingiva, e3, buccal mucosa, e4, hard palate, e5, palatine tonsils, e6, subgingival plaque, e7, supergingival plaque, e8, throat, e9, saliva, f1,2, left/right antecubital fossa, f3,4, left/right retroauricular crease, g1, vaginal introitus, g2, mid vagina, g3, posterior fornix, h, anterior nares. The vertical green line represents the “change point” (see Methods section).

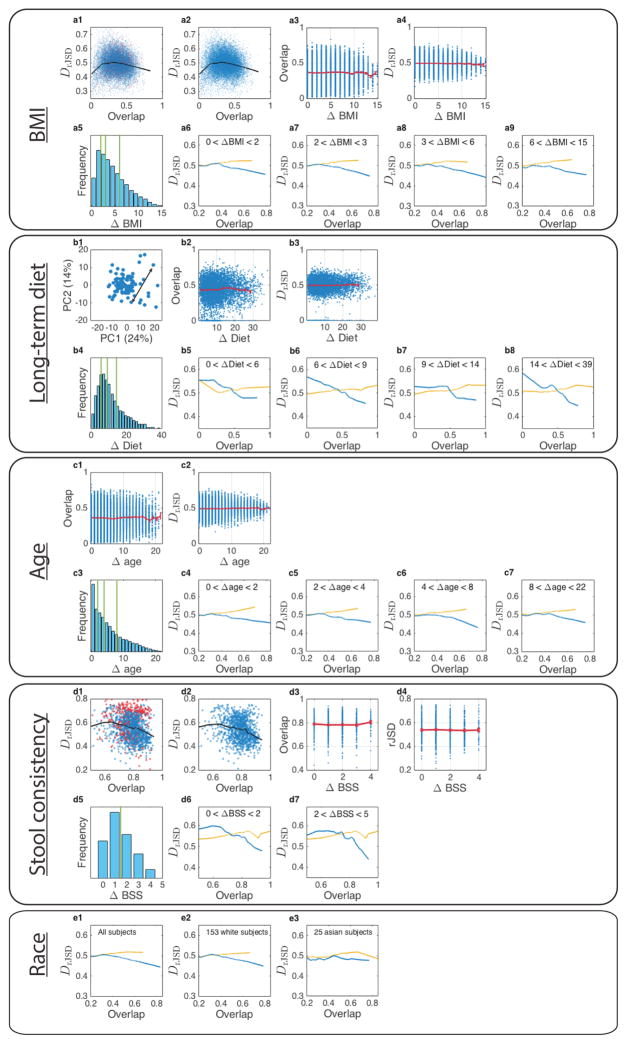
An alternative explanation for the observed negative slope of the DOC for gut and mouth microbiomes of healthy subjects could be that some host factors not only select for the presence of certain microbes but also drive their relative abundances by enforcing certain optimally adapted compositions. To test this alternative explanation, we systematically analyzed microbial samples while controlling for the effect of several leading candidates for potential confounding factors, e.g. body mass index, age, long-term dietary pattern and stool consistency. We found that as long as their values are in the normal range those factors cannot explain the observed DOC pattern (see Extended Data Figs. 7,8). Hence, the alternative explanation for the negative slope in DOC is unlikely to be true. Of course, with currently available datasets we cannot possibly account for all other confounders, e.g. drugs, genetics, inflammation, or combinations of them. More datasets will be needed to test this intriguing alternative explanation.

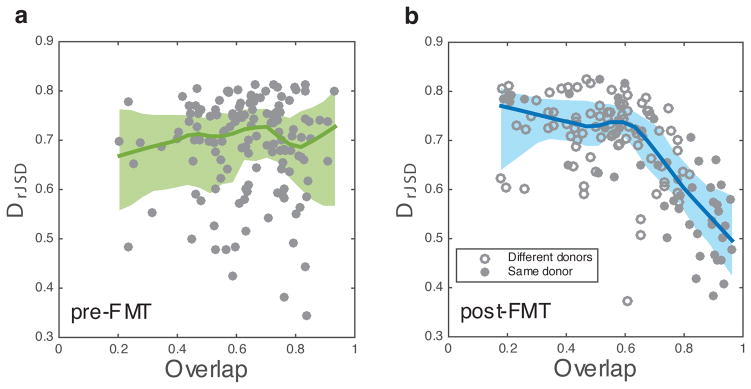
The above results of healthy subjects raise an interesting question: Does the universality of microbial dynamics also exist in subjects with disrupted microbiomes? To address this question, we applied the DOC analysis to microbial samples of 17 subjects with recurrent Clostridium difficile infection (rCDI) and the same set of subjects after FMT¹⁷. Clostridium difficile is an opportunistic pathogen that causes disease worldwide and greatly increases morbidity and mortality in hospitalized patients. Fortunately, FMT is very efficacious in treating patients with rCDI, with pronounced clinical improvement even after a single treatment²⁹. Interestingly, we found that the dissimilarity between rCDI subjects is largely independent of their species overlap, rendering a flat DOC (Fig. 4a). In contrast, after FMT (median, 4 days) the DOC displays a pronounced negative slope in the high-overlap region (Fig. 4b), suggesting a universal gut microbial dynamics. FMT treatments show the flexibility of microbial communities and their adaptation to composition changes. Our result suggests that this adaptive behavior may be associated with the observed universal microbial dynamics after FMT.

Figure 4. DOC analysis of human subjects with rCDI.

a, Before FMT, the DOC (dark green line) of the rCDI subjects is nearly flat. b, After FMT, the DOC (dark blue line) displays a pronounced negative slope in the high-overlap region. We denoted a subject pair as a solid (or hollow) circle if the two subjects received FMT from the same donor (or two different donors), respectively. Interestingly, solid circles spread over a wide range of overlap values, suggesting that even if two subjects share the same donor, their post-FMT microbiomes may still display strong inter-individual variability.

Finally, we anticipate that applying our DOC analysis to subjects with other diseases (especially non-gastrointestinal diseases) or infants at different developmental stages will offer deeper insights into how dynamical processes shape human microbial ecosystems. The developed DOC analysis can also be directly applied to other microbial ecosystems, e.g. soil, ocean, lakes, phyllosphere/rhizosphere and fermenters microbiome, to detect the universality of the underlying ecological dynamics (see Extended Data Fig. 9). This sheds light on the design of more advanced methods to extract dynamical information from microbial data.

Methods

Overlap between species assemblages

Consider two microbial samples, represented by two abundance vectors x = (x₁,…,x_N) ∈ ℝ^N and y = (y₁,…,y_N) ∈ ℝ^N. For genomic survey data of the human microbiome, only the relative abundances are known. Hence, we are dealing with the relative abundance profiles x̃ = (x̃₁,…,x̃_N) and ỹ = (x̃₁,…,x̃_N), where ${\stackrel{\sim }{x}}_i\equiv \frac{x_i}{{\sum }_{j=1}^N{x}_j}$ and ${\stackrel{\sim }{y}}_i\equiv \frac{y_i}{{\sum }_{j=1}^N{y}_j}$. To quantify the similarity of the species assemblages (sets) of the two samples, denoted as X = {i|x_i > 0} and y = {i|y_i > 0}, we defined the overlap measure

$$O(\stackrel{\sim }{\mathbf{x}},\stackrel{\sim }{\mathbf{y}})\equiv \sum _{i\in S}\frac{{\stackrel{\sim }{x}}_i+{\stackrel{\sim }{y}}_i}{2},$$

where S ≡ X ∩ Y is the set of shared species present in both samples. In case S is empty, O(x̃, ỹ) = 0. If S = {1,…N}, i.e. all the species in X and Y are shared, then O(x̃, ỹ) = 1, but the abundance profiles x̃ and ỹ can still be very different. In the extreme case when the relative abundance is the same for all species in X and Y, the overlap measure can be written as a function of the classical Jaccard index. Yet, there are many advantages of using the overlap measure, instead of the Jaccard index, in our analysis (see SI Sec. 1.1.4).

Dissimilarity between abundance profiles

To compare the abundance profiles of two samples, we first renormalize the relative abundances of only the shared species (set S), yielding x̃ = {x̃_i}_i∈S and ỹ = {ỹ_i}_i∈S. Here ${\widehat{x}}_i\equiv \frac{{\stackrel{\sim }{x}}_i}{{\sum }_{j\in S}{\stackrel{\sim }{x}}_j}=\frac{x_i/{\sum }_{k\in X}{x}_k}{{\sum }_{j\in S}{x}_j/{\sum }_{k\in X}{x}_k}=\frac{x_i}{{\sum }_{j\in S}{x}_j}$ and ŷ_i is defined similarly. This way we remove the spurious dependence between the relative abundances of the shared and the non-shared species. More importantly, this renormalization assures that the calculated dissimilarity measure is mathematically independent of the overlap measure (see SI Sec. 1.2.1). The dissimilarity is then evaluated via the root Jensen-Shannon Divergence (rJSD) measure

$$D(\widehat{\mathbf{x}},\widehat{\mathbf{y}})=D_{\text{rJSD}}(\widehat{\mathbf{x}},\widehat{\mathbf{y}})\equiv {\left[\frac{D_{KL}(\widehat{\mathbf{x}},\mathbf{m})+D_{KL}(\widehat{\mathbf{y}},\mathbf{m})}{2}\right]}^{\frac{1}{2}}$$

where $\mathbf{m}\equiv \frac{\widehat{\mathbf{x}}+\widehat{\mathbf{y}}}{2}$ and $D_{\text{KL}}(\widehat{\mathbf{x}},\widehat{\mathbf{y}})\equiv {\sum }_{i\in S}{\widehat{x}}_{i}log\frac{{\widehat{x}}_i}{{\widehat{y}}_i}$ is the Kullback-Leibler divergence between x̂ and ŷ. The dissimilarity can also be evaluated via any other classical dissimilarity measures in ecology and biology, e.g. Bray-Curtis Dissimilarity, Yue-Clayton Dissimilarity, and the negative Spearman correlation (see Extended Data Fig. 5). In this work, we focused on rJSD because it is a distance metric that satisfies non-negativity, identity, symmetry and triangle inequality (see SI Sec.1.1.1). Comparing sample pairs based on phylogenetic information, e.g. using weighted- and unweighted-UniFrac³⁰ as quantitative and qualitative measures, respectively, has the potential to provide better insight on the communities’ dissimilarity-overlap behavior. However, since the weighted- and unweighted-UniFrac are not independent, they cannot be trivially integrated into our DOC analysis.

Dissimilarity-Overlap Curve (DOC)

To systematically compare sample pairs with a wide range of overlap values and analyze their dissimilarity-overlap relations, we calculate the overlap and dissimilarity of all the sample pairs from a given set of microbiome samples and represent each sample pair as a point in the Dissimilarity-Overlap plane. We then use the robust LOWESS (locally weighted scatterplot smoothing) method, a standard non-parametric regression method that is resistant to outliers, to calculate the DOC.

To get the confidence interval, we use the following bootstrap technique: (1) From a dataset of M samples we calculate the overlap and dissimilarity of the M(M − 1)/2 sample pairs, represented as M(M − 1)/2 points in the Overlap-Dissimilarity plane. (2) In each bootstrap realization, we resample a new set k = {k₁,…,k_M} from the M original samples with replacement. Some of the original samples might not be included and a few might be sampled more than once. (3) We create a new cloud of points C: a point associated with sample pair (i,j) is included in C only if both i,j ∈ k, while a point is chosen several times if the sample i or j were resampled more than once in k. (4)A new DOC is calculated for C using the robust LOWESS method. We set the smoothing parameter (“span”) to be 0.2.(5) We repeat steps (2)–(4) T times to create T DOCs. (6) The 3 and 97 percentiles of the T curves represent the 94% confidence interval for the DOC. In this work, we chose T = 100.

Assumptions of the DOC Analysis

There are two reasonable assumptions underlying the DOC analysis. First, the abundance profiles of the samples should represent the steady states of the microbial ecosystem and hence the fixed points of the underlying dynamics that satisfy ẋ = 0. This assumption is fairly reasonable because human gut microbiota is a relatively resilient ecosystem³, and until the next large perturbation (e.g. antibiotic administration or dramatic dietary change) is introduced, the system remains stable for months and possibly even years^11,28,31. Second, if two communities have the same species assemblages and the same abundance profile (steady state), then the two communities have the same microbial dynamics. Mathematically, this is not necessarily true, because different dynamical systems can give rise to an identical steady state or fixed point. Yet, given the large number of species and all the other levels of complexity in their interactions, the possibility of having different dynamics with the same fixed point is very unlikely. Indeed, universal dynamics is the most plausible explanation for the observed pattern, i.e. the negative slope of DOC in the high-overlap region.

Limitations of the DOC Analysis

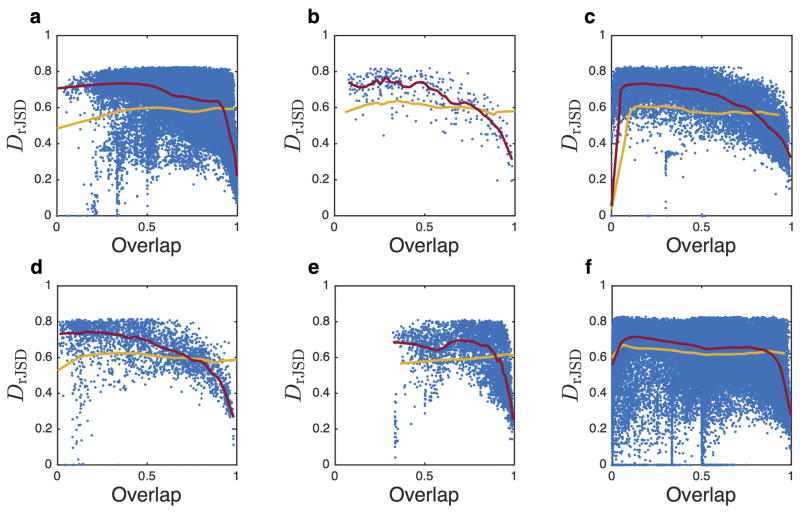
We point out that for overlap values close to zero, a positive slope may occur as the artifact of dissimilarity between relative abundance profiles with small number of species (see Fig. 3 e4, f1–4, g1–3, h, Extended Data Fig. 10, and SI Sec. 1.1.3).

We also emphasize that a flat DOC does not completely rule out the possibility of universal dynamics. For example, the DOC of the gut microbiome samples of rCDI patients is flat (Fig. 4a). There are two possibilities. First, the universality of microbial dynamics found in healthy subjects (Fig. 3a,d) is completely lost in the rCDI subjects, due to the infection or/and the dysbiosis caused by the extensive inciting antibiotic treatment. Second, the possibly universal microbial dynamics of the rCDI subjects are just undetectable by the DOC analysis. This could be due to the extremely liquid stool samples of the rCDI subjects that suffer from diarrhea, as stool consistency has been found to be strongly correlated with the gut microbiota compositions^32,33. It is also possible that the abundance profiles of rCDI subjects are drastically varying over time and hence do not represent the steady states of the underlying microbial ecosystem (though a murine infection model doesn’t seem to support this hypothesis³⁴).

If true multi-stability exists, i.e. multiple stable states (abundance profiles) are associated with the same set of species present in the same environment, then our DOC analysis may not detect it. However, true multi-stability in human-associated microbial communities has not been demonstrated experimentally, partially because any subtle differences in the species assemblages can drive those microbial communities³⁵.

In sum, our DOC analysis hence detects universal dynamics under certain conditions. More precisely, it provides a means of discriminating dynamics into universal or possibly universal.

Universality Measures and Statistical Test

Note that the DOCs of different datasets/studies must be compared with caution, especially if the microbial samples were preprocessed by different pipelines³⁶, e.g. with different OTU clustering thresholds, or different OTU picking methods, etc. As shown in Fig. 3, the characteristic overlap in a particular body site is different in the two studies. For example, the average overlap between HMP gut samples is about 0.4 and between SMP samples is about 0.75. To account for this fact and to fairly compare the DOCs across different body sites and different studies, we used two different measures to quantify the universality:

1. f_ns. For each cohort we determined the fraction of data points for which the DOC displays a negative slope, denoted as f_ns. Specifically, for a given DOC calculated from a cohort of M microbial samples, we first detected the “change point” O_c such that $\frac{\mathrm{d}y(O)}{\mathrm{d}O}<0$ for any O > O_c, where y(O) is a smoothed curve of the DOC (e.g. using the default “smooth” function of Matlab with moving average over 5 neighbors). Then, f_ns is defined as

   $$f_{\text{ns}}\equiv \frac{\text{number}\text{of}\text{sample}\text{pairs}\text{with}O>O_{\mathrm{c}}}{\text{total}\text{number}\text{of}\text{sample}\text{pairs}}.$$

   In Fig. 3a–h this is the area of the overlap distribution to the right of the green vertical line, which represents the change point, the minimal overlap above which a negative slope is observed. The results of f_ns for different body sites are shown in Extended Data Fig. 6a.

2. p-value. To estimate the slope of the DOC, we used a linear mixed-effects model, which explicitly takes into account the fact that those data points in the Dissimilarity-Overlap plane are not completely independent (because each sample affects (n − 1) data points). To avoid any potential biases due to the detection of change point, we use data points with overlap larger than the median value, that is 50% of all the data points, for all the datasets (from all the body sites). We repeated this step for 200 bootstrap realizations. The distributions of the slopes for different body sites are shown in Extended Data Fig. 6b. We than calculated the one-tailed p-value as the fraction of bootstrap realizations with a non-negative slope. Benjamini and Hochberg procedure was used to calculate the false discovery rate (FDR) for multiple comparisons.

We emphasize that those two measures are complementary. In the first measure (f_ns), we consider the existence of a negative slope and ask what is the fraction of data points that support it. In the second measure, we consider a fixed fraction of data points (50%) and asked whether a significant negative slope is observed. Interestingly, though these two measures quantify different features of the DOC analysis, the body sites stratification pattern is consistent across the two measures and the two studied datasets (see Extended Data Fig. 6).

Population Dynamics model

The GLV model represents the dynamics of N interacting species as a set of ordinary differential equations: $\frac{{dx}_i}{dt}=r_i{x}_i+{\sum }_{j=1}^N{a}_{ij}{x}_i{x}_j$, i = 1, N. Here, r_i is the intrinsic growth rate of species i, a_ij is the interaction strength between species j and i and $a_{ii}{x}_i^2$ (with a_ii < 0) represents the logistic growth term. We considered a microbial “sample” as a steady state of a GLV model parameterized by the growth rate vector r = {r_i} ∈ R^N and the interaction matrix A = (a_ii) ∈ R^N×N and we set N = 100 and a_ii = − 1 in our simulations. We generated different “cohorts”, each consists of M = 100 “samples”. The GLV models differ from each other in their specific parameters (r_i and a_ij). To achieve that, for each cohort, we first constructed a “base” GLV model (r^★, A^★) as follows: $r_i^{★}$ is randomly chosen from the uniform distribution 𝕆 (0,1). $a_{ij}^{★}$ is randomly chosen from the normal distribution ℕ (0, (σ̃σ_max)²), σ̃ varies between 0 and 1, σ_max is the maximal interaction strength allowed to ensure stability of the ecological system (here σ_max = 0.1). Then, different GLV models (ν = 1,…,M) are generated as random variations of this base model with $r_i^{\nu }={\phi }_i^{\nu }{r}_i^{★}$ and $a_{ij}^{\nu }={\varphi }_{ij}^{\nu }{a}_{ij}^{★}$ where both ${\phi }_i^{\nu }$ and ${\varphi }_{ij}^{\nu }$ are randomly chosen from a uniform distribution 𝕆 (1 − δ, 1 + δ) so that the expected values of the parameters of those models in the same cohort are the same as the base model, i.e. E[r]_ν = r^★ and E[A]_ν = A^★. In other words, all the samples of the same cohort are generated from GLV models that share the same structure and sign pattern of the base interaction matrix A^★. As δ → 0 the model parameters become identical in all the GLV models of the same cohort. Thus, δ̃ ≡ 1 − δ quantifies the “universality” of the dynamics of those models. Finally, for each cohort, the 100 samples (steady states) were generated by integrating the GLV differential equations with random initial conditions (both initial assemblage and abundance profile are randomly chosen).

Human microbiome datasets analyzed in this work

Longitudinal microbiome datasets

(1) Two time series of gut microbiome consist of 336 and 131 stool samples, respectively. A 16S rRNA gene-based dataset, variable region V4, analyzed here at the OTU level. For detailed description of this dataset see ref. ²⁸. The data is available at http://qiita.ucsd.edu under study ID 550. (2) Two time series of gut microbiome consist of 299 and 180 stool samples, respectively. A 16S rRNA gene-based dataset, variable region V4, analyzed here at the OTU level. For detailed description of this dataset see ref.¹¹. The data is available in the European Bioinformatics Institute (EBI) European Nucleotide Archive (ENA) under the nucleotide accession number ERP006059.

Cross-sectional microbiome datasets

In order to quantitatively compare the universality of microbial dynamics in different body sites, we used two large-scale microbiome datasets:(1) Human Microbiome Project (HMP)^9,15. A 16S rRNA gene-based dataset, variable regions V3 to V5, of the human microbiome from 239 healthy subjects. The data is available at http://hmpdacc.org/ and was detailed inref.^9,15. This dataset covers 18 body sites in five areas: the oral cavity (nine sites: saliva (M = 262), tongue dorsum (M = 291), palatine tonsils (M = 285), keratinized gingiva (M = 289), hard palate (M = 275), buccal mucosa (M = 287), throat (M = 283), and sub- and supragingival plaques ( M = 283 and M = 289, respectively)), the gut (one site: stool (M = 297)), the vagina (three sites: introitus (M = 115), mid-vagina (M = 124), and posterior fornix (M = 124)), the nasal cavity (one site: anterior nares (M = 230)), and the skin (four sites: left and right antecubital fossae (M = 161 and M = 171, respectively) and retroauricular creases (M = 240 and M = 257, respectively)). Full protocols are available on the HMP DACC website (http://hmpdacc.org/HMMCP). OTU level was used for our analysis. We used a single sample from each subject. In case more than one sample is available, we used the first visit. (2) Student Microbiome Project (SMP). A 16S rRNA gene-based dataset, variable region V4 from 85 college-aged adults. The dataset covers four body sites: gut (M = 72), tongue (M = 79), forehead skin (M = 78) and palm skin (M = 60). In case there are multiple samples measured for one subject, we used the sample from the first visit. For detailed description of this dataset seeRef.¹⁶. The data is available at https://github.com/gregcaporaso/student-microbiome-project/tree/master/otu-tables.

In order to rule out several leading candidates of confounding factors in our DOC analysis, we analyzed two additional datasets: (3) A data set of healthy volunteers (M = 98) from the Cross-sectional Study of Diet and Stool Microbiome Composition (COMBO). Diet information was collected using two questionnaires that queried recent diet (“Recall”) and habitual long-term diet (food frequency questionnaire; “FFQ”). Stool samples were collected, and DNA samples were analyzed by 454/Roche pyrosequencing of the variable region V1–V2 of the 16S rDNA gene segments. Samples were analyzed at the OTU taxonomic level. For detailed description of this dataset see Ref.³⁷.(4) A dataset of healthy women (M = 53), aged 20–55 years (median 42.5), as part of the Flemish Gut Flora Project (FGFP). Stool consistency levels using Bristol Stool Scale (BSS)scores were self-reported. The V4 region of the 16S rDNA gene was sequenced. Samples were analyzed at the OTU taxonomic level. For detailed description of this dataset see Ref.³³.

Clinical trial dataset

Stool samples of patients with recurrent Clostridium difficile infection (rCDI): before and after fecal microbiota transplantation (FMT). This clinical trial was approved by the Partners Human Research Committee as well as by the US Food and Drug Administration (FDA) (Investigational New Drug application number 15199) and registered at Clinical Trials.gov (NCT01704937). Informed consent was obtained from all participants. Microbial samples from 17 patients with rCDI were analyzed in the groups of “pre-FMT” and “post-FMT”. Only subjects for whom both pre- and post-FMT samples are available were included. In case where more than one post-FMT samples is available we included only the first one (median, 4 days after FMT). The V4 region of the 16S rRNA gene was sequenced using an Illumina MiSeq. Samples were analyzed at the OTU level. For detailed description of this dataset see ref.¹⁷.

Code availability

The Matlab code for computing the DOC and the universality measures as well as an example dataset (i.e. the dataset used to generate Fig. 2b) are freely available at the project webpage:http://scholar.harvard.edu/yyl/doc.

Extended Data

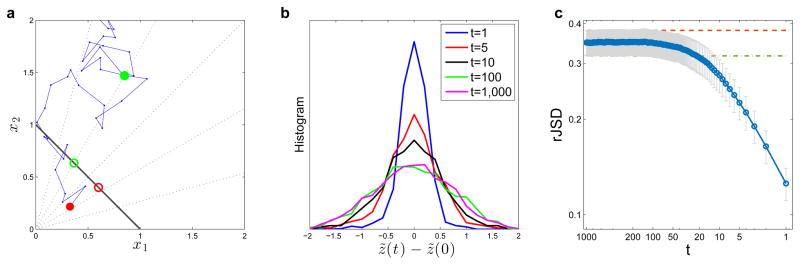
Extended Data Figure 1. Displacement of normalized N-dimensional random walks.

a, Trajectory of a 2-dimensional random-walk represents the absolute abundance of two species x_1, x₂. The initial state is marked by a red circle and the first 100 steps are shown. The solid black line is the 1-dimensional simplex upon which the locations are projected to obtain the relative abundances x̃₁, x̃₂. The dotted lines starting at the origin represent the projection process: all the points in a dotted line have the same relative abundances and they are all projected to the intersection of the dotted line and the simplex (e.g. the solid red and green circles are projected to the red and green open circles, respectively). We define a new coordinate z̃(t) ≡ x̃₂(t)− x̃₁(t) for the location of normalized relative abundance on the simplex. The displacement of the normalized random walk after t steps is then z̃(t) − z̃(0), where z̃(0) is the projected location of the initial state (see, as an example, the distance between the green and the red open circles in a). b, Distributions of displacement of an ensemble of 1,000 random walks after t steps (t=1, 5, 10, 100, 1000). For small t, the displacement distributions depend on t, while for large t (t=100, 1000) the distributions are the same. c, Symbols represent the average displacement of 1,000 N-dimensional normalized random walks (here we set N=50), measured as D_rJSD, and the error-bars represent the standard deviation. Each random walk is forced to stay on the positive orthant, i.e. if $x_i^{(t)}<0$ we set $x_i^{(t)}=0$ . The D_rJSD was calculated using all N coordinates, setting $x_i^{(t)}={10}^{-4}$ as a pseudo count for $x_i^{(t)}=0$. Where t is small, the distance grows with increasing t, however, the distance saturates for large t. The dashed red and green lines represent the average distance between two random locations (green) and between the final locations (x^(t=1,000)) of the random walks (red).

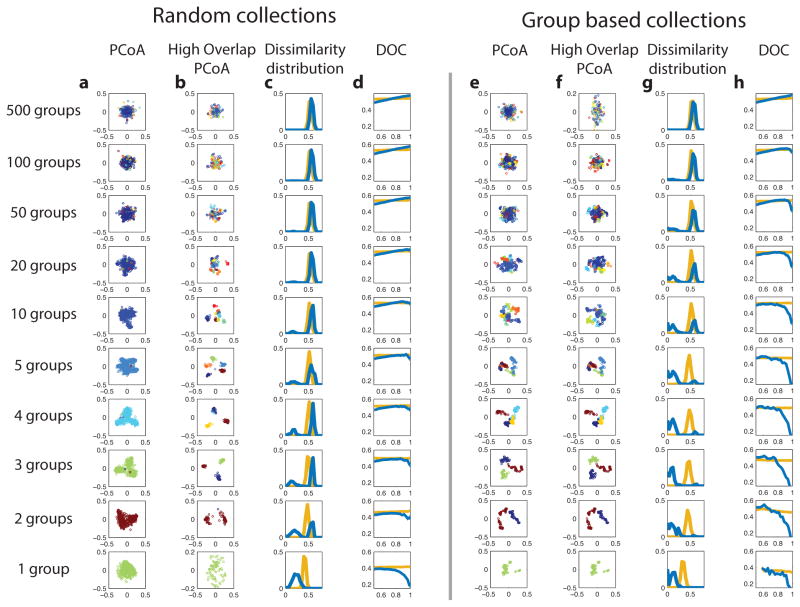
Extended Data Figure 2. Detection of group dynamics using ordination technique.

In each raw, 500 synthetic samples were generated. Samples in the same group were taken from the steady states of the same GLV model of 100 species. The initial species assemblages were determined in two scenarios: at random (columns a–d) or based on the group (e–h). In the latter scenario, in each group the species were first randomly ordered and then in each of the samples the first f species were selected and the other been removed (f is randomly chosen from a uniform distribution 𝕆(20,100)). In columns a and e, a standard ordination technique, i.e. the principal coordinate analysis (PCoA), was applied. All 500 samples were shown in the plane of the first two principal coordinates (using rJSD as the distance metric) and coloured according to their group. In columns b and f only the samples that have high overlap (>0.95) with at least one other sample were shown. Columns c and g show the dissimilarity distributions P(rJSD) between the high-overlap sample pairs. Columns d and h show the DOCs. The ordination technique successfully detects the existence of group dynamics (especially when the number of groups is small). We anticipate that the group dynamics can also be detected by classical clustering analysis. In the scenario of random collections, the PCoA of high-overlap samples, i.e. samples that have high overlap (>0.95) with at least one other sample, is doing better than the PCoA of all samples to detect group dynamics, especially for a small number (2~10) of groups. Moreover, for a small number of groups, the dissimilarity distributions P(rJSD) can distinguish between the two scenarios of initial assemblage selection: random or group-based. The ordination technique cannot distinguish between the cases of 500 groups (“individual dynamics”) and single group (“Universal dynamics”). Those cases can be distinguished by the DOC analysis.

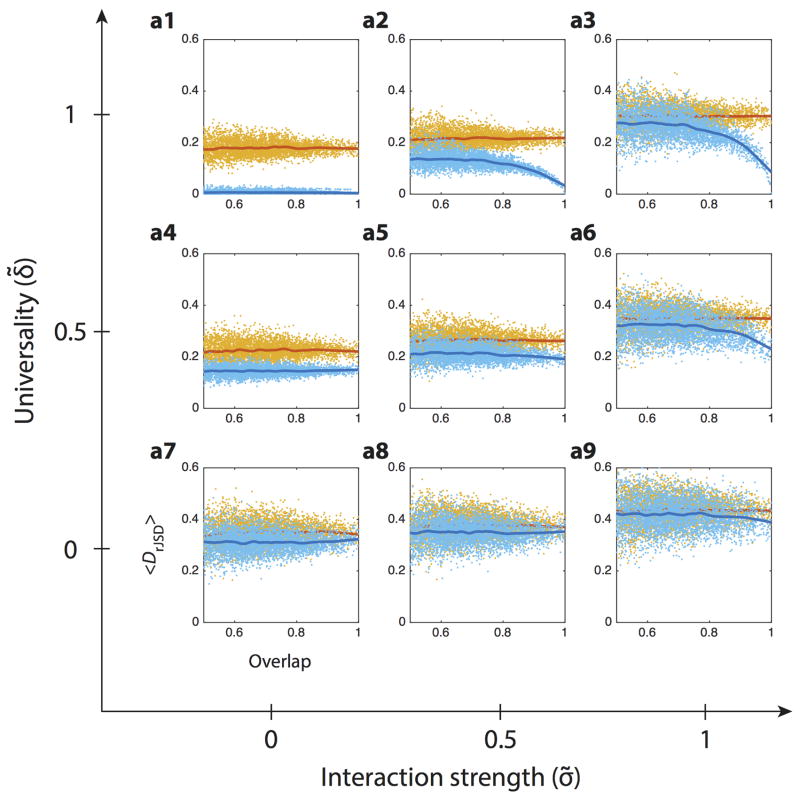
Extended Data Figure 3. Detecting universality in population dynamics models.

Synthetic microbial samples were calculated as steady states of Generalized Lotka-Volterra (GLV) models (see Methods section). The GLV models are generated as “cohorts” (100 models in each cohort) with different levels of i) inter-species interaction strength; and ii) universality, tuned by the parameters σ̃ and δ̃, respectively (see Methods section). In each of the 100 models, a random fraction f of the species (f ~ 𝕆(0,0.8)) was initially removed, and the remaining species were initiated with random abundance (x ~ 𝕆(0,1)). The Dissimilarity-Overlap points of sample pairs in each cohort and of the corresponding randomized samples are shown in light blue and yellow respectively. The solid curves represent the DOCs calculated using the robust LOWESS method. The DOC of “cohorts” generated by GLV models without inter-species interactions (a1, a4, a7) is flat even in the high-overlap region. This is because, without inter-species interactions, for any sample pair the presence or absence of unique (i.e. non-shared) species has no effect on the shared ones. A flat DOC is also observed in the case of individual dynamics (a7, a8, a9), where a higher overlap between sample pairs does not lead to more similar abundance profiles. However, in the case of universal dynamics with strong inter-species interactions (e.g. a3), the DOC displays a clear negative slope in the high-overlap region.

Extended Data Figure 4. DOC analysis of gut microbiome samples from longitudinal studies.

In plots a–d, sample pairs are selected from four different subjects, with number of samples: M_a = 299, M_b = 180, M_c = 336, M_d = 131, respectively. The mean DOCs (calculated from 100 bootstrap realizations using the robust LOWESS method) of each subject and the corresponding randomized samples are shown in dark blue and yellow, respectively. The shaded area indicates the range of the 94% confidence intervals. The overlap distributions are shown in red. For all the four subjects, a clear negative slope of the DOC is observed at the high-overlap region, indicating a largely time-invariant or universal dynamics for each subject throughout the measurement period. This is in marked contrast with the flat DOC of the null model (See SISec. 1.3). The secondary peak of lower overlap samples in b (overlap ≈ 0.8) is of sample pairs from two different periods, before and after a Salmonella infection, which represent two distinct microbial steady states and thus exhibit a flat DOC. This is consistent with our assumption of time-invariant microbial dynamics for a given healthy individual.

Extended Data Figure 5. DOC analysis of gut microbiome samples is consistent across different studies and different dissimilarity measures.

For two microbiome samples, the dissimilarity of their abundance profiles over shared species can be evaluated by different measures. Weighted measures, such as root Jensen-Shannon Divergence (rJSD), Bray-Curtis (BC) dissimilarity and Yue-Clayton (YC) dissimilarity should be applied to the renormalized abundance profiles, to ensure mathematical independency between the overlap and the dissimilarity measures. Rank-based dissimilarity measures, e.g. negative Spearman Correlation (nSC), can be directly applied without renormalization. We used the four dissimilarity measures (rJSD, BC, YC and nSC) to calculate the DOC (using robust LOWESS)of gut microbiome samples from two studies: the HMP and SMP. In all cases, we observed a pronounced negative slope in the DOC (dark-blue curve) of real sample pairs (light-blue points) and a flat DOC (orange curve) for the pairs of randomized samples (yellow points).

Extended Data Figure 6.

a, The fraction of data for which a negative slope is observed in Fig. 3. Note that for overlap values close to zero (e.g., Fig. 5 d, f1–4, g1–3) a positive slope occur as the artifact of dissimilarity between relative abundance profiles with small number of species (See SI Sec. 1.1.3). For gut and mouth, a negative slope of DOC is observed in the two data sets for a broad range of overlap, indicating a significant universality of microbial dynamics in those habitats. In contrast, the negative slope of DOC in the hand’s skin microbiome is observed only for small part of the sample pairs. b, Box plot of the slope of DOC calculated from 200 bootstrap realizations. The slope is calculated by fitting a linear mixed-effects model for data points with overlap larger than the median. The one-tailed p-value is then calculated as the fraction of bootstrap realizations with a non-negative slope. The Benjamini-Hochberg procedure was used to calculate the false discovery rate (FDR) for multiple comparisons. The null hypothesis of non-negative slope is rejected for all body sites (p < 10⁻²) except four skin sites: forehead (p = 0.099), palm (p = 0.377) in the SMP study and left/right antecubital fossa in the HMP study (p = 0.099 and p = 0.495).

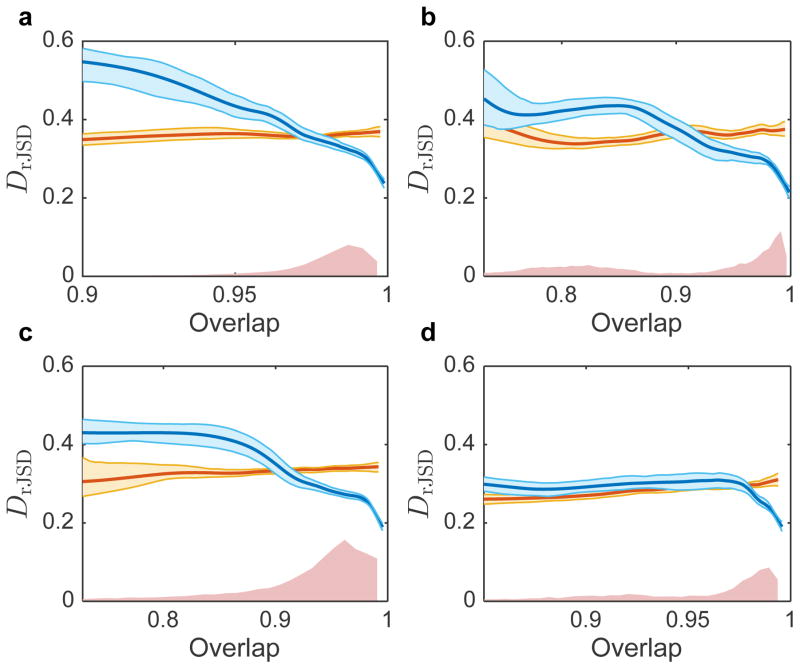
Extended Data Figure 7. Effects of various host factors on the DOC analysis.

a, The effect of body mass index (BMI) on the DOC analysis. a1, DOC analysis of all gut microbiome sample pairs among 190 subjects from the HMP study. Red points represent samples pairs associated with at least one obese subject (with BMI > 30). a2, Same as shown in a, but 13 obese subjects with BMI > 30 were excluded. a3, blue points represent the gut microbiome samples’ overlap and ΔBMI. The red curve is the average (error bars represent the s.e.m.). a4, dissimilarity versus ΔBMI. a5, distribution of ΔBMI values, divided to four groups of equal number of pairs. a6–a9, DOC analysis of the sample pairs in each group. b, The effect of diet on the DOC analysis. b1, Diet difference (ΔDiet)between two subjects is defined as the Euclidean distance between their associated diet scores in the two leading principal components PC₁ and PC₂. In total there are M = 97 healthy subjects in the Cross-sectional Study of Diet and Stool Microbiome Composition (COMBO) study³⁷. b2, overlap versus ΔDiet. Blue points represent the overlap and ΔDiet of all gut microbiome pairs among the 97 subjects from the COMBO study. The red curve is the average (error bars represent the s.e.m.). b3, dissimilarity versus ΔDiet. b4, distribution of ΔDiet values, divided to four groups of equal number of pairs. b5–b8, DOC analysis of the pairs in each group. c, The effect of age on the DOC analysis. c1, overlap versus ΔDiet. Blue points represent the overlap and ΔAge of all gut microbiome samples pairs between the 190 subjects from the HMP study. The red curve is the average (error bars represent the s.e.m.). c2, dissimilarity versus ΔAge. c3, distribution of ΔAge values, divided to four groups of equal number of pairs. c4–c7, DOC analysis of the pairs in each group. d, The effect of stool consistency on the DOC analysis. d1, DOC analysis of all sample pairs. In this dataset the subjects have BSS values between 1 and 6. The points (sample pairs) associated with subjects with BSS = 6 (at least one subject has BSS = 6)are colored in red. The black line is the DOC. d2, DOC analysis of all subjects with BSS < 6. d3–d4, among all subjects with 1 ≤ BSS ≤ 5, the overlap and the dissimilarity are independent on ΔBSS. d5, Distribution of ΔBSS values for the 46 subjects with 1 ≤ BSS ≤ 5. d6, DOC analysis of the pairs with similar BSS values, 0 ≤ ΔBSS ≤ 1 and (d7) pairs with more different BSS values, 2 ≤ ΔBSS ≤ 4. In both cases, a clear negative slope of the DOC isobserved. e, The effect of race on the DOC analysis. e1, All subjects (M = 190), e2, White subjects (M = 153) and e3, Asian (M = 25). Note that in the HMP study, stool samples were collected from 153 White, 10 Black, 25 Asian, and 2 subjects with other races.

Extended Data Figure 8. DOC analysis under special conditions.

a, The effect of strongly interacting species. A comparison of two GLV models of 100 species with random inter-species interactions. The system parameters were fixed for all the simulated samples (M = 100), representing maximal universality. In a1, all species have the same characteristic interaction strength, while in a2, the inter-species interactions of one species are significantly stronger than all other species, representing a strongly interacting species. The presence/absence of the strongly interacting species dramatically affect (either directly or indirectly) the abundance profile of many other species leading to a pronounced secondary cloud of points in the Dissimilarity-Overlap plane (a4). The effect is the most pronounced in the region of high overlap (top 5%) pairs, and can be detected by looking at their dissimilarity distributions (a5–a6). b, DOC behaves the same for samples with uniform or skewed abundance distribution. b1, b2, Samples were generated from the steady states of the GLV model with largely uniform abundance distribution (determined mainly by the species growth rates). In the case of interacting species (b1), a negative slope of the DOC is observed but not in the case of noninteracting species (b2). b3, Real samples from the gut (from the HMP study, genus level) exhibit a high level of alpha-diversity and a very skewed abundance distribution. A negative slope of the DOC in the high-overlap region is observed. b4, The randomized samples preserve the abundance distribution of the real samples but the effect of inter-species interactions is removed, leading to a flat DOC. c, Effect of core species and non-interacting periphery species. c1, Samples were generated as steady states of the GLV model with N = 100 species. The parameters of the GLV model were fixed for all the samples, representing maximal universality. The initial species assemblages were chosen as follows: 30 species were present in all the samples, representing a set of “core species”, and the other 70 “peripheral” species were present with lower probability (mean 0.18, min 0.12, and max 0.24). c2, Presence probability of real gut microbial samples, from the HMP at the genus level. Only one genus (Bacterioides) is present in all the samples. c3, Species presence probability in a GLV model where all species are present with average probability 0.6. c4, The effect of the interactions of the peripheral species. In the GLV model, the inter-species interactions among the core species (“core-core”) has a characteristic strength σ_core = 0.15, and both the “periphery-periphery” and the “periphery-core” interactions have a characteristic strength σ_p. When σ_p = 0, i.e. the peripheral species do not interact with the core species, the DOC is flat. When σ_p > 0, the DOC has a negative slope. c5–c6, In the case of real gut microbiome samples as well as the GLV model without core species, the DOC has a negative slope in the high-overlap region. d, The effect of sequencing depth on the DOC analysis. d1, Richness (number of present OTUs) vs. sequencing depth of 190 HMP gut samples. 12 subjects with less than 1,300 reads/sample were excluded and the remaining 178 were assigned into two groups of n = 89 subjects, with average sequencing depth 3,019 and 8,640 reads/sample, respectively. d2, d3, The characteristic overlap between samples of Group 1 is smaller than between samples of Group 2. However, DOC analysis of each group shows a clear negative slope. d4–d6, Samples of each group were rarefied prior to analysis with minimal community size of 1,317 and 4,333 in Group 1 and Group 2 respectively, as represented by the black dashed lines in d4. d7–d9, Samples of both groups were rarefied prior to analysis with the same minimal community size of 1,317, as represented by the black dashed line in d7.

Extended Data Figure 9. DOC analysis of longitudinal microbiome data from six lakes in Germany³⁸.

(Data downloaded from http://qiita.microbio.me, Study ID: 945). a. ‘Stechlin’ (M = 440); b. ‘Haus’ (M = 26); c. ‘Tiefwaren’ (M = 164); d. ‘Melzer’ (M = 68); e. ‘Breiter Luzin’ (M = 89); f. ‘Fuchskuhle’ (M = 355). Blue points represent the dissimilarity-overlap values of sample pairs from the same lake. The DOCs of real samples from each lake and that from the corresponding randomized samples are calculated using robust LOWESS and shown in red and yellow, respectively. For all the six lakes, a clear negative slope is observed for the DOCs of real samples, suggesting universal or time-invariant microbial dynamics for each lake. Differences in the DOC shapes (e.g. the moderate DOC slope in b, c and d, in contrast with the steep DOC in a, e and f) deserve a systematic study of those microbial ecosystems. This example clear demonstrates the applicability of DOC analysis to general microbial ecosystems, e.g. soil, ocean, rizosphere/phyllosphere, fermenters, etc.

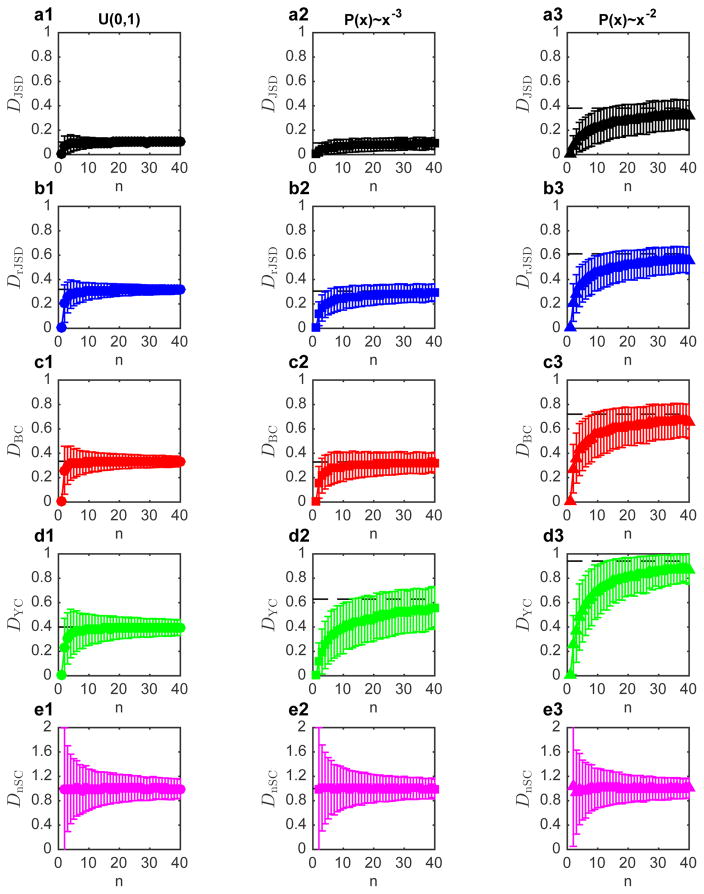
Extended Data Figure 10. Average dissimilarity between two normalized random vectors.

Two indepdent vectors x, y of n elements randomly choosen from uniform distribution u (0,1) were generated and then normalized ${\widehat{x}}_i\equiv \frac{x_i}{{\sum }_{j=1}^n{x}_j}$ and ${\widehat{y}}_i\equiv \frac{y_i}{{\sum }_{j=1}^n{y}_j}$ . (Note that in practice all n elements are always shared in x and y, since zeros are very unlikely). The dissimilarity D(x̂, ŷ) is then calculated using the five dissimilarity measures (D_JSD, D_rJSD, D_BC, D_YC and D_nSC). Average dissimilarity and standard deviations of 1,000 pairs are shown in a1, b1, c1, d1 and e1, for the different measures. The horizontal black dashed line represents the average dissimilarity for n = 100. For all the measures here, the dissimilarity displays no n-dependence for n > 15, while D_nSC is n-independent for any n > 0. Similar analysis was performed for vectors whose elements were chosen from power-law distributions P(x)~x^−α with α = 3 (a2, b2,c2,d2ande2)and P(x)~x^−α with α = 2 (a3, b3, c3, d3 and e3).