Immunoglobulin Classification Using the Colored Antibody Graph

Abstract

The somatic recombination of V, D, and J gene segments in B-cells introduces a great deal of diversity, and divergence from reference segments. Many recent studies of antibodies focus on the population of antibody transcripts that show which V, D, and J gene segments have been favored for a particular antigen, a repertoire. To properly describe the antibody repertoire, each antibody must be labeled by its constituting V, D, and J gene segment, a task made difficult by somatic recombination and hypermutation events. While previous approaches to repertoire analysis were based on sequential alignments, we describe a new de Bruijn graph–based algorithm to perform VDJ labeling and benchmark its performance.

1. Introduction

The antibody molecule is comprised of two pairs of two distinct proteins: the heavy and light chains. In humans, there exist a single heavy chain locus, and two light chain loci. These heavy and light chains pair with one another to form a “Y”-shaped protein structure. The tips of this immunoglobulin (Ig) molecule interact and bind to different antigens within one's body, signaling an immune response. Unlike typical transcripts within eukaryotic cells, the heavy and light chain transcripts are not directly taken from exonic segments of the individual's genome. Instead, there are three distinct classes of exon-esque gene segments, termed the variable (V), diversity (D), and joining (J) gene segments. Each of these classes of gene segments contains many different variants encoded in an individual's genome. The light chain transcript contains only V and J gene segments, while the heavy chain transcript contains V, D, and J gene segments. Both heavy and light chains also contain a constant (C) gene segment that does not contribute to combinatorial diversity.

Unlike typical exonic splicing, which is precise, somatic recombination of antibody gene segments is inexact, with the exonuclease removing several base-pairs from each end of the gene segments. Ligation of D to J, and subsequently DJ to the V gene segment, is also imprecise with deoxynucleotidyl transferase (TdT) incorporating non templated base pairs into the resulting gene (Desiderio et al., 1984); a process known as V(D)J recombination. In addition to the variability induced by somatic recombination, somatic hypermutation (SHM) events introduce additional deviations from germline gene segments. The end result of this process is a B-cell that produces a single type of antibody, a monoclonal antibody (mAb). This increased variability allows for a larger search space of antibody configurations to be explored for specificity to a particular antigen. While this is advantageous from the perspective of our immune system's adaptability to foreign substances, analysis of these highly variable immunoglobulin genes becomes difficult.

Repertoire construction forms the basis for the analysis of antibodies; characterizing the pool of gene segments that were selected for a particular antigen. A prerequisite step for repertoire analysis is the labeling of V, D, and J gene segments for the read of each heavy and light chain. This VDJ labeling problem can be described as the following: given reference gene-segment sets , , , 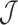and a read, return the “most likely” labels 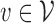, , 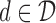and 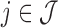for this read. Despite this problem being easily described, it remains unclear how to design an adequate and easy-to-compute likelihood estimator for VDJ classification. As a result, this classification can be difficult and error prone, particularly for the heavy chain. While all described approaches also operate on the light chain, we focus on the heavy chain due to its difficulty in correctly identifying composite gene segments.

Existing tools for repertoire characterization rely on aligning reads against the reference sequences of V, D, and J gene segments from the organism in question (Weinstein et al., 2009; Arnaout et al., 2011; Chen et al., 2012; Jiang et al., 2013). This strategy is exemplified by IMGT-VQUEST (Brochet et al., 2008) (the most widely used VDJ classification tool) and other tools (Volpe et al., 2006; Gaéta et al., 2007; Wang et al., 2008; Ye et al., 2013; Souto-Carneiro et al., 2004; Ohm-Laursen et al., 2006). Most of these tools rely on an iterative approach where first the best matching V gene segment is identified, then J, and finally D. This specific order of alignments (from V to J to D gene segment) is appealing because it starts from the longest (and thus resulting in the most confident alignment) gene segment and ends with the shortest (and thus resulting in the least confident alignment) gene segment. However, it also suffers from uncertainties in alignment (there are usually multiple optimal alignments) and sequential dependencies in the iterative alignment (at each step, previously matched nucleotides are removed from future alignments).

To address this sequential dependency bias shortcoming, we describe a colored de Bruijn graph–based approach, which leverages the current understanding of V(D)J structuring of antibody transcripts. Similarly to recent attempts to remove biases of previous alignment-based approaches in genomics applications, we now introduce the concept of de Bruijn graph to immunoinformatics. Iqbal et al. (2012) introduced the colored de Bruijn graph for identifying variants across genomes; we repurpose this approach for use with antibodies. The resulting algorithm IgGraph does away with the sequential nature of iterative alignment and provides accurate labeling of reads. IgGraph is shown to perform well on both real immunoglobulin sequencing (Ig-seq) datasets, and simulated datasets with varying levels of deviations from reference gene segments. At the same time, we show that the problem of VDJ classification is far from being resolved as the leading tools produce remarkably different results when applied to large Ig-seq datasets.

2. Methods

2.1. Antibody sequencing and the CDRs

The transcripts of the heavy/light chains can be sequenced using reverse primers located in constant regions, and forward primers located at different positions of the different V gene segments. Sequencing of these transcripts can then be performed after PCR amplification. The VDJ region of heavy chains is approximately 110 amino acids (330 bp), which is why the previous literature favored the Roche 454 platform due to its larger read lengths of approximately 450 bp. However, with Illumina's increasing read length and throughput, recent and future studies face the challenge of analyzing large repertoires with millions of reads (Safonova et al., 2015).

The heavy and light chains have three subsequences, termed complementary determining regions (CDRs) due to the role they play in defining a particular antibody's antigen binding specificity. These CDRs, denoted CDR1, CDR2, and CDR3, while located along the length of each immunoglobulin chain, are in close spacial proximity at the physical “tips” of the antibody structure. The location at the junction, along with exonucleotide chewback and nontemplated nucleotide addition, all contribute to the larger variability in CDR3 length. Since CDR1 and CDR2 are located entirely within the V gene segment, they are only subjected to somatic hypermutation.

2.2. V/D/J antibody segments

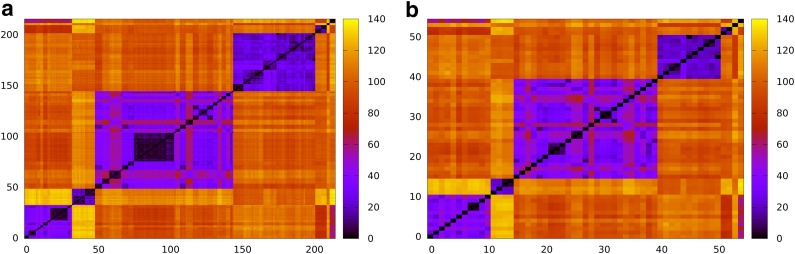
In all, 213 V, 30 D, and 13 J gene segments are annotated as functional (and complete) in the international ImMunoGeneTics (IMGT) database (Robinson et al., 2013). Of these 213 V gene segments, many are allelic variants of one another, differing in a few nucleotides from another allelic variant of the same gene. High similarity between these allelic variants adds complexity to the problem of VDJ classification. Even after collapsing allelic variants to their consensus sequences (that results in only 55 consensus V gene segments), there are still many similar fragments between these consensus sequences. Figure 1a visualizes similarities between 213 V gene segments and Figure 1b visualizes similarities between 55 consensus V gene segments.

FIG. 1.

Edit distances between (a) 213 human V gene segments (alleles) and (b) 55 consensus V gene segments. The consensus V gene segments illustrate that, even after collapsing highly similar allelic variants into consensus V gene segments, many of the 55 consensus V gene segments remain similar to each other.

2.3. Simulating antibodies

To generate simulated data that properly represent the challenge of VDJ labeling from reads, we needed to simulate the VDJ somatic recombination events that drive the diversity of the CDR3 region of antibodies. Unfortunately, there are no publicly available antibody simulators, despite many existing tools having used simulated antibody sequences to demonstrate performance (Arnaout et al., 2011; Volpe et al., 2006; Wang et al., 2008). To this end, a simulated monoclonal antibody (smAb) is generated by the process detailed in Supplementary Figure 1 (available online at www.liebertpub.com/cmb): selecting a V, D, and J gene segment to comprise our smAb; exonuclease chewback on the 3′ V, 5′ and 3′ D, and 5′ J segments; and finally, nontemplated nucleotide addition to these same regions. To simulate these biological processes, empirical distributions for exonuclease chewback length (Jackson et al., 2004), as well as composition and length distributions for nontemplated nucleotide additions (Basu et al., 1983), were used. Using this process to create a smAb, we are able to generate datasets with labeled V/D/J segments with simulated biological diversity.

These smAbs can then be sampled using a read simulator to further introduce sequencing errors. The Grinder (Angly et al., 2012) read simulator can be used to generate Illumina and 454 reads. Additionally, we also want to generate datasets of smAbs with a fixed number of deviations from the germline sequence, that is, mutations. To this end, positions along the V gene segment were selected from a distribution of mutations created from 23,051 annotated IMGT sequences. These positions were selected without replacement to ensure a fixed divergence from germline references. The V, D, and J gene segments from humans were collected from the IMGT database (Robinson et al., 2013) as the basis for the simulation of each smAb.

2.4. Canonical antibody graph

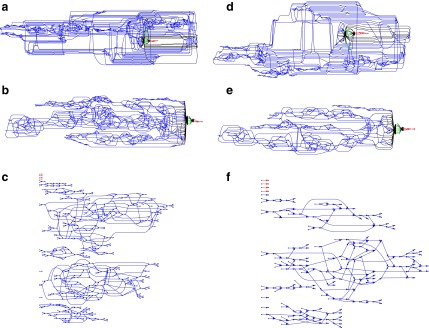
The canonical antibody graph is created by constructing a de Bruijn graph of each set of V, D, and J gene segments, and creating an artificial joining of nodes at the V/D and D/J segments. Figure 2 shows multiple versions of this graph for different parameters 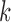. The differences when creating the canonical antibody graph with either all alleles (left) or all consensus gene segments (right) is shown. The arcs in this graph are colored blue for V gene segments, green for D gene segments, and red for J gene segments. The arcs artificially joining gene segments are colored black. This canonical antibody graph was created for three values of 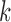to show the connectivity between the different sets of reference gene segments. The graph constructed with 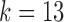shows sharing of 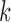-mers between V and D gene segments, as well as among different V genes. The parameterization of 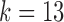results in a very complicated graph; this complexity of the visual representation is partially exacerbated by the graph visualization layout algorithm. It is the relative comparison of complexity between the graphs in Figure 2 that is meaningful.

FIG. 2.

The canonical antibody graph for different values of 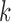(arcs corresponding to the V, D, and J gene segments are colored blue, green, and red, respectively) constructed for all alleles (left) and all consensus gene-segments (right). All nonbranching paths are collapsed to a single arc, and at each junction, a dummy node is created to connect V gene segments to D gene segments, and D gene segments to J gene segments; these arcs are colored black. These graphs are constructed with 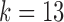(a and d), 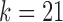(b and e), and 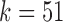(c and f). Panel (b) shows V, D, and J gene segments completely separated, while (a) shows considerably more sharing of arcs in the V segments, and some shared in the D gene segments. Increasing the value of 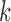(c) greatly simplifies the relationship among V gene segments. This is not a feasible parameter for our purposes (as no D segments are captured) but does show the complexity of V gene segments. In the case of 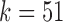, the graph becomes disconnected (and green edges disappear), since it exceeds the length of the longest D gene segment.

2.5. Antibody graph

Given a set of reads 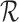from mAbs, we construct the de Bruijn graph (termed antibody graph) over the 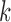-mers of these reads in the following manner. Nodes in this graph represent all 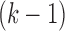-mers over the set of reads 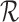. Nodes 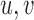are connected by a directed edge (arc) 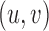if 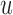is a prefix, and 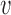is a suffix of some 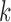-mer in a read from 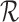. More on applications of the de Bruijn graphs for assembly can be found in Compeau et al. (2011).

We can also incorporate IMGT reference gene segments into the antibody graph. Reference gene segments 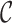can be added to the antibody graph and considered as “colored” reads. For example, the human antibody graph has 213 + 30 + 13 = 256 colors (corresponding to 213 V, 30 D, and 13 J gene segments). In comparison, the mouse antibody graph has 242 V, 27 D, and 8 J gene segments, for a total of 277 colors. A total of 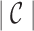reference gene segments are added to the antibody graph in a similar manner as the (virtual) reads, with an additional data structure. Each arc along a reference read path 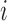is assigned the color 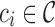. A hash of arcs to a set of colors, 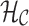, is maintained as each reference sequence is added to the graph. The hash can then be queried given an arc 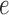, for example, 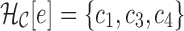, to retrieve all the colors present on that arc. Edges from reads are assigned a special “noncolored” symbol representing their lack of color (shown as black edges in subsequent examples).

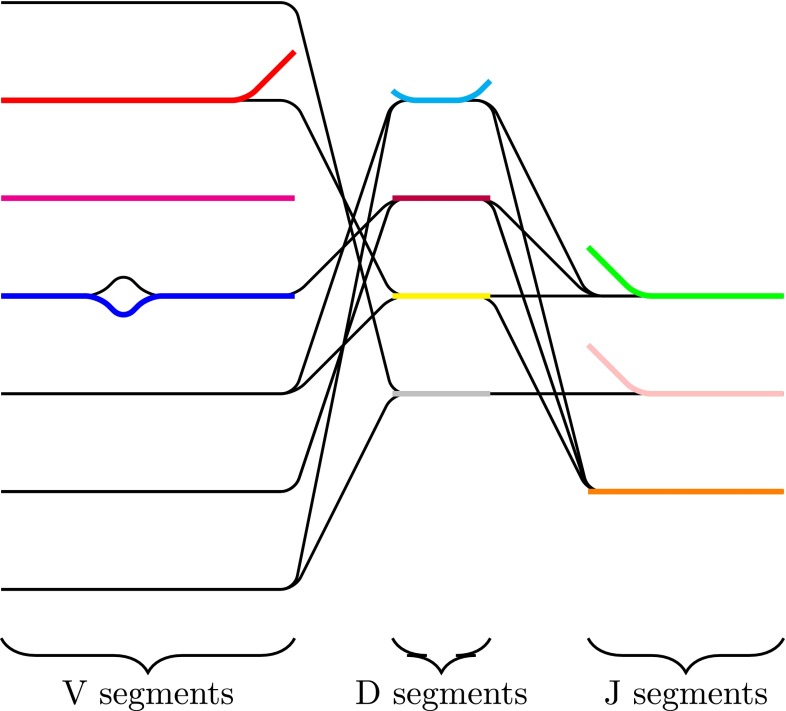
The antibody graph incorporating reference gene segments is termed the colored antibody graph. This graph represents the sequenced mAb repertoire and their similarity to reference gene segments; an idealized depiction of this graph is shown in Figure 3.

FIG. 3.

Colored antibody graph. An idealized colored antibody graph built over the reads, with reference gene segments represented as distinct colors. Imperfect overlay of reference gene segments at V/D and D/J segments is common. Also detectable is the divergence of V-segments from their references, helpful in determining differences in CDR1 and CDR2 regions.

2.6. Color profile

The coloring of the antibody graph relies on common structures in de Bruijn graphs referred to as bulges and tips (Compeau et al., 2011) that will help us to repaint black edges into colors corresponding to reference gene segments. Given a set of reference gene segments 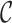, a 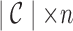color profile matrix 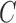can be constructed for a read of length 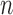, representing the associations of each color to each position of the read. At first glance, it is unclear how to assign new colors to arcs on the black path 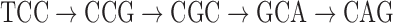in Figure 4. However, one can note that this path forms a bulge with the colored path 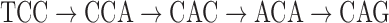that we will use for coloring the black path as described below. A similar approach is applied to tips, such as 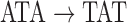. Construction of the color profile matrix is accomplished by considering each color 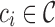, and traversing each arc 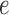from read 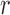, noting when 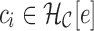. This condition determines the value at 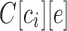, the cell in the color profile matrix for the color and position, which is updated to note the match/mismatch with color 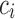at the position of arc 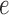. Figure 4 shows an example graph with 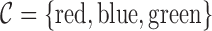, and a single read depicted with black arcs. In this example, read arcs (in black) 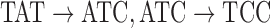, and 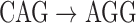are shared with different reference segments; the contents of 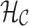for these arcs are shown in the figure. It is worthy to note in this example that reference segments share arcs, for example, red and green sharing three arcs, something that is common for allelic variants of V gene segments. This color profile represents an abstraction for scoring the reference gene segments to a read .

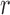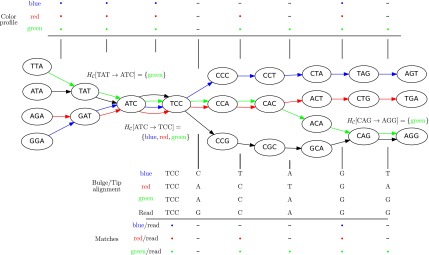
FIG. 4.

An example antibody graph with three reference segments, colored by red, blue, and green arcs. A single read is shown here with black arcs. The color hash 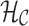is shown for the three arcs from the read that are shared with reference gene segments, 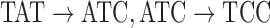and 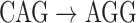. Bulge/tip traversal and color assignment is shown below the graph, for example, to obtain the matching for the green reference, the green/black bulge is traversed, and marginals are aligned. Tips are also traversed, shown here with red and blue references. Matching/mismatching nucleotides are noted for each colored reference to the read at the bottom of the figure. Matches are noted with a • and mismatches with a −.

2.7. Color propagation

Deviations from reference gene segments create bulges and tips (Pevzner et al., 2004; Zerbino and Birney, 2008). A bulge is created when a read deviates from a reference gene segment and is not near either end. A tip is created when this deviation occurs near either end of a reference gene segment or read. The assignment of each color to the read can be greatly affected by bulges and tips between a read and a colored reference sequence. This particularly effects V gene segments due to somatic hypermutations, as such, we must ensure the color propagates through these arcs such that small differences between a read and a gene segment do not result in a “loss of color.” Bulges arising from mutations in the V gene segments are traversed, and the color profile is adjusted accordingly. Figure 5a shows color propagation for a de Bruijn graph constructed with 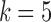when a single reference segment (red arc color), and a single read (black arcs), have a single nucleotide variation between them. Above each red arc is the arc marginal (last nucleotide of the corresponding 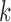-mer) for the reference, similarly, below each black arc is the marginal for the read.

FIG. 5.

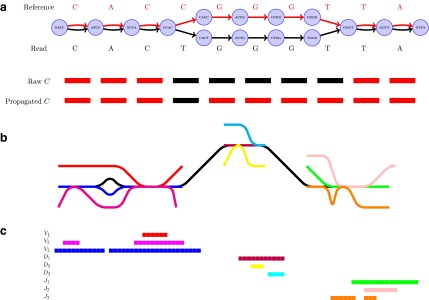
Color propagation and colored antibody graph with single read. (a) Color propagation example. Two sequences with a single nucleotide difference between them: GATCCACTGGGTTA (read shown by black edges) and GATCCACCGGGTTA (reference shown by red edges). The de Bruijn graph in this example is created with 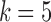. Edges shared between the two sequences are colored red and black. A single nucleotide difference creates five mismatches in the color profile of this read, shown as the “Raw” 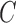. IgGraph traverses this bulge and propagates the color to reduce the number of mismatches to the single nucleotide difference, shown as “Propagated” 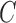. (b) A single read (shown in black) along with V, D, and J gene segments shown as different colors. Shared 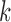-mers between the read and different gene segments are shown as merged paths, while divergences are shown as bulges and tips. (c) The 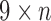color profile matrix for the example is shown. Each row represents one of nine gene segments, and each column is a different position in the read. From this matrix, we can score each row to select the V, D, and J labels for the read.

The information contained in the arc marginal aids us in creating the color profile of a read. In our example (Fig. 5a), this matrix is of dimension 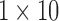, since we have only a single color in our set of colors 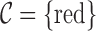, and a fragment represented by 10 arcs. Two different color profiles are shown in Figure 5a, a “Raw” and a “Propagated.” These color profiles are shown with red/black rectangles denoting matches/mismatches over each position, that is, each arc marginal. If we merely traverse the arcs of the read, we would obtain the color profile “Raw” showing five mismatches, colored black, in 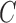. If we instead traverse the bulge, that is, traverse both the read and reference paths, we obtain the subsequences of the read and reference over the bulge. These subsequences can then be aligned to fill in the color profile and only report a single mismatch, shown as “Propagated” in Figure 5a. A similar propagation is performed for tips from the read/reference that could be caused by mutations in the first and/or last 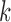base pairs. Figure 4 depicts the traversal of bulges and tips, and their subsequent color propagation. The full color profile, after color propagation, is shown at the top of the figure, aligned with the arcs of the read.

Using the colored antibody graph, we label each read's V, D, and J gene segments for repertoire analysis. Figure 5b depicts a single read, shown in black, with multiple colored reference gene segments sharing some subsequences. A single read can be traversed to create the color profile for that read. This profile consists of all the colors that paint the path of the read, that is, all the reference gene segments that share some 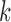-mer with the read. Figure 5c shows the 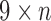color profile matrix 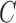for the example represented by the nine (three V, three D, and three J) reference gene segments, and 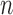positions. From this color profile matrix, we can select the top 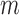scoring gene segments for each V, D, and J gene segment set. Scoring each row of this matrix, by a variety of scoring schemes described below, will allow us to select the top gene segments.

2.8. Scoring the color profile

To utilize the color profile 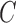, a scoring scheme must be defined. A simple scoring scheme with match and mismatch values can be used for the D and J gene segments, as they exhibit far fewer mutations. In this simple case, the most popular color can be selected as the reference label. The V gene segments frequently contain many mutations, some having known associated motifs (Rogozin and Kolchanov, 1992; Dörner et al., 1998; Clark et al., 2006). Rogozin and Kolchanov (1992) first exposed the RGYW motif, and Doerner et. al., (1998) showed the inverse motif, WRCY, also promotes mutations. As a result, the simple scoring does not leverage this additional information and thus does not perform well on V gene segments. However, this information can be easily incorporated into the model to improve gene segment labeling. Mutations in the V gene segments are known to be positionally dependent (Clark et al,. 2006), with fewer occurring in framework regions and more in CDR regions. This is incorporated with discovered 4-mer motifs into a probabilistic score. At each position in the scoring matrix, 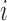, there is an event of either a mutation or a match. There is an associated 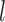-mer 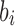and a read position 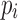. From these, the probability of an event 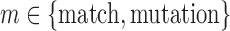is 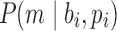. We compute the probability of the read 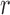, arising from reference 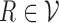, with each reference being equally likely as .

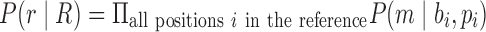The computation of 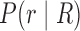can be performed over a row 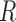of color profile , 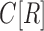. Each column 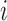of 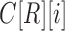provides us with positional information, 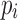, and its surrounding sequence context. In the uncommon cases when bulge/tip color propagation is unable to resolve differences in the sequences, we must assume that all differences arise from mutations without any reference sequence context. This is computed for all references in the V gene segment set .

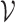The probabilities for mutation and matching events are computed from 23,051 human IMGT annotated sequences, resulting in 67,108 mutation events and 1,487,059 matching events. Any events that include an indel from the alignment of read to reference are discarded. Once probabilities for each reference (i.e., color) are computed, a rank score is associated with each color. The top-ranked colors, cumulatively comprising a certainty cutoff, are all awarded a tie for top rank. Each other color is assigned the rank of its probability; only the top-ranked colors are returned.

3. Results

3.1. Datasets

In order to test the labeling performance of the IgGraph, two approaches were utilized: simulating datasets of smAbs with varying levels of divergence, and testing on three Ig-seq datasets. Comparison on simulated datasets is deemed as supervised since ground truth labels are known. Comparison on Ig-seq datasets is computed on similarity of predictions by different tools since ground truth cannot be known, that is, unsupervised evaluation.

Obtaining true labels for real data (like the Stanford S22 dataset) is difficult and error prone. We thus include Stanford S22 dataset as an example of real Ig-seq data, all of which are shown in Table 1, and compare predictions on it in an unsupervised manner.

Table 1.

Table of Datasets Used for Benchmarking

Dataset	Sequencing	No. unique entries	Size (MB)
Simulated Ig	Simulated	2 000	1.1
Stanford S22 (Jackson et al., 2010)	Roche 454	13 153	3.4
Mouse Ig-seq (Halemano et al., 2014)	Illumina MiSeq	204 462	80.0
Human Ig-seq (Safonova et al., 2015)	Illumina MiSeq	3 099 967	1 173.0

Simulated datasets are evaluated in a supervised manner, and real datasets are compared in an unsupervised manner.

While the datasets of real Ig-seq data are invaluable, they are likely to be biased in favor of certain V/D/J gene segments selected for by the immune system (Supplementary Fig. S5). This bias is not a desirable property when benchmarking a tool. Rather, we wish to test performance on all combinations of gene segments, so an ideal dataset will have a uniform distribution of VDJ usage (Supplementary Fig. S7). The simulated dataset was generated by using V, D, and J gene segments from human reference gene segments, using the method described in Supplementary Figure S1. The distributions of exonuclease chewback, nucleotide additions, and V(D)J combinations are represented across the datasets. Furthermore, each dataset included a fixed number of mutations per smAb, testing the ability to perform VDJ classification at varying degrees of divergence from the reference gene segment. Considering a single read, it can be labeled by one, or more, reference gene segments. Ideally, only a single segment should be returned. However, there are occasions when exonuclease chewback makes unique identification infeasible. We select the maximum number of gene segments to return, above which we return no label (Supplementary Figs. S8 and S9).

We attempted to benchmark as many tools as possible, and while many exist (Gaëta et al., 2007; Brochet et al., 2008; Ye et al., 2013; Wang et al., 2008; Souto-Carneiro et al., 2004; Volpe et al., 2006; Ohm-Laursen et al., 2006), few are available for download, and only IgBlast is able to be run on the large number of sequences produced by current Ig-seq experiments. This is likely the cause for why so many analyses of Ig-seq experiments produce their own approaches to VDJ classification (Weinstein et al., 2009; Jiang et al., 2011; Arnaout et al., 2011; Wine et al., 2013; Halemano et al., 2014). Even for IgBlast, while scaling well to process millions of Ig-seq reads, its output was not immediately usable and a wrapper parser had to be written to convert its output to a more concise format. Other tools only provide a web-based interface (Brochet et al., 2008; Ohm-Laursen et al., 2006; Souto-Carneiro et al., 2004), which have varying limitations on the number of sequences, none of which could handle the mouse or human Ig-seq datasets, as listed in Table 1. The lack of usable, efficient, and standardized tools suggest the potential usefulness of IgGraph for this increasingly used analysis of Ig-seq datasets.

3.2 Performance on Ig-seq datasets

In order to compare the predicted classes of various tools, we separate comparisons on labeled data (i.e., simulated data) and unlabeled data (i.e., Ig-seq datasets). Comparisons on labeled data are supervised and reported as accurate. Unlabeled data is compared in an unsupervised manner and reported as the Jaccard index over two sets 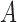and 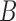, computed as 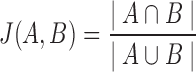. Both alleles and genes are compared using the Jaccard index (Jaccard, 1908), as are partitions. Clusters based on the junction sequences, as reported by the tools, are compared using the Fowlkes–Mallows index (Fowlkes and Mallows, 1983). Further explanation of the tool used for this comparison is described in the supplement.

Table 2 shows the runtimes of different tools over the datasets. iHMMune was not run on the Stanford S22 dataset since predictions were available (Jackson et al., 2010). IgGraph is able to process the large Ig-seq datasets now being generated, as evidenced by the CPU time required for the human Ig-seq dataset. Reducing the CPU time from 102 hours when using IgBlast to 27 hours when using IgGraph. The unsupervised comparison of all pairs of tools is shown in Table 3. The full pairwise comparisons for the Stanford S22 dataset are shown in Supplementary Figure S6. Predictions between IgGraph and IgBlast are very similar for J alleles/genes, while less similar for V alleles/genes. The predictions for D alleles/genes is an area where the predictions of the two tools diverge the most. Clone partitioning also differs greatly between the two tools, particularly for the Stanford S22 dataset and human Ig-seq dataset, but are similar for the mouse Ig-seq dataset. Clone partitions are defined by the reported CDR3 sequences (for IgGraph) or the reported junction sequences (post-processed from the output of IgBlast).

Table 2.

Table of Runtimes for Each Tool on the Datasets Tested

Dataset	Tool	CPU time (sec)	Time per entry (sec)
Simulated Ig	IgGraph	54	0.027
	IgBlast	151	0.075
	iHMMune	3,724	1.862
Stanford S22	IgGraph	191	0.014
	IgBlast	641	0.048
	iHMMune	NA	NA
Mouse Ig-seq	IgGraph	10,311	0.050
	IgBlast	20,114	0.098
Human Ig-seq	IgGraph	99,813	0.032
	IgBlast	367,545	0.118

iHMMune-align was not run on the Stanford S22 dataset, but was analyzed using the published predictions. iHMMune-align was not run on the mouse Ig-seq and human Ig-seq datasets due to its high estimated run time from its time per entry on the simulated Ig dataset.

Table 3.

Table of Ig-seq Datasets Showing Pairwise Comparison Using Unsupervised Evaluation Criteria

		Alleles					Genes
Dataset	Tools	IGHV	IGHD	IGHJ	Total	Clone cluster	IGHV	IGHD	IGHJ	Total
	IgBlast - IgGraph	0.944	0.824	0.983	0.774	0.153	0.960	0.824	0.983	0.787
Stanford S22	IgBlast - iHMMune	0.739	0.878	0.921	0.696	—	0.903	0.889	0.923	0.862
	iHMMune - IgGraph	0.814	0.771	0.921	0.674	—	0.913	0.781	0.923	0.766
Mouse Ig-seq	IgBlast - IgGraph	0.948	0.426	0.947	0.426	0.997	0.948	0.426	0.947	0.426
Human Ig-seq	IgBlast - IgGraph	0.936	0.583	0.951	0.526	0.563	0.945	0.594	0.954	0.541

Criteria for allele and gene levels is Jaccard index, while Fowlkes-Mallows is used to compare the clone clusterings.

3.3. Performance on simulated datasets

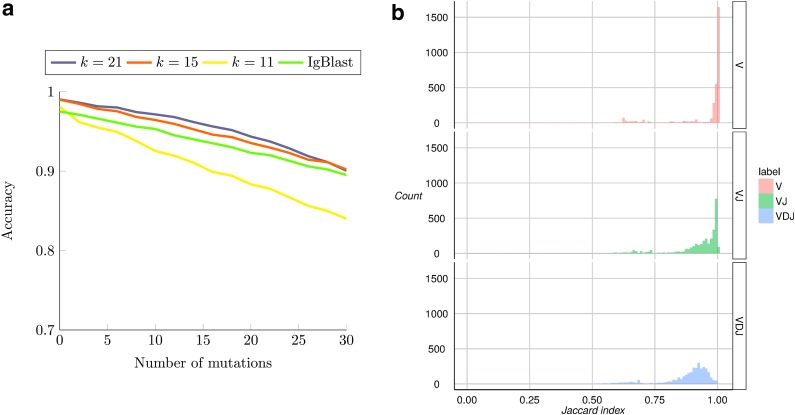
To evaluate the performance of IgGraph in the case when somatic hypermutations (SHM) are prevalent, we generated simulated datasets of smAbs with increasing numbers of mutations, ranging from 0 up to 30. In these datasets, a mutation is a change to a nongermline nucleotide with uniform probability, it is not meant to simulate true motifs found within antibodies. Mutations were selected only along the V gene segment, as sampled from our mutation distribution obtained from IMGT data. Figure 6a shows the V gene segment performances of each mutation dataset with an even number of mutations (datasets with an odd number are used for parameter selection [Supplementary Fig. S9]) when the divergence from the germline increases. The difference in performance between these parameterizations with varying 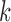-mer sizes correlates with the complexity of the canonical antibody graph shown in Figure 2. With more nodes shared with using the smaller 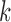, reconstruction is more difficult. The green curve shows the performance of IgBlast on these same datasets when run with default parameters. While IgGraph with 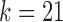and 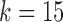outperform IgBlast, the 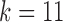parameterization does underperform when reference divergence is increased.

FIG. 6.

Labeling and partitioning comparison. Panel (a) shows the accuracy of IgGraph for V gene segments when a fixed number of mutations are inserted in each smAb V gene segment. Only datasets with an even number of mutations are plotted. The blue, orange, and yellow curves represent IgGraph results with parameterizations of 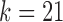, , 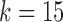and 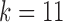, respectively. The green curve represents the IgBlast tool run with default parameters. (b) Jaccard index over partitions. The similarity of the partitioning for range sets of V, VJ, and VDJ gene segments are measured by computing the Jaccard index for predictions from IgGraph and IgBlast for each sequence.

One option is to provide multiple values of 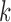for the different V, D, and J gene segments; since larger values for 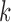perform better for V and J, while smaller values of 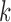are required for recovering many D gene segments. This can be done by creating the graph for each gene segment type and one or more reads, as described previously. The resulting accuracies, for pairs of values of 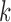for V/J and D on a simulated dataset are shown in Supplementary Figure S12.

3.4. VDJ partitioning comparison

Partitioning an input read into the germline genesegments is a useful output for VDJ classification. To adequately compare the similarity in partitioning between the tools, a dataset of 7,532 antibody sequences was downloaded from the IMGT database. This approach of using a collection of unlabeled, experimentally derived sequences for comparison was employed in previous approaches (Gaëta et al., 2007; Ye et al., 2013). This set was selected by collecting all fully annotated, human heavy chain antibody sequences in the IMGT database whose length ranged from 350 to 500 bp.

Figure 6b shows the similarities in partitioning between IgBlast and IgGraph as the Jaccard index between the partitioning ranges considered. For each tool, each range of positions for V, D, and J is considered a set, and the Jaccard index over two sets 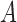and 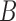is computed, 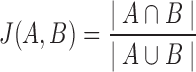. While there are differences between the two tools where the partitions are drawn, they are largely similar. As the difficulty in labeling gene segments increases, so too do the differences between the reported partitions.

4. Discussion

We presented a new IgGraph approach to VDJ gene segment labeling for immunoglobulin transcripts. Our colored antibody graph departs from the alignment-based methods (IMGT, SoDA, IgBlast, and others) and HMM-based methods (iHMMune-align). Recently, colored de Bruijn graphs have been used to identify genomic variants (Iqbal et al., 2012); we repurpose and extend this idea to identify immunoglobulin gene segments. Further, our approach utilizes a scoring model for V gene segments that considers mutation motifs and position dependence, something that many other tools do not model. iHMMune-align is one of the few that explicitly model known mutation motifs, however, they do so in a static fashion. Our scoring is based on probabilities learned from IMGT data, discovering known, and potentially novel, mutation motifs.

We have shown that our approach performs well on simulated datasets and on real Ig-seq datasets. While this approach performs well, it does have its limitations, namely the reliance on sufficiently large 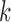-mers. This is of concern particularly for small D gene segments, as there must be some 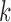-mers that match on these segments that have been shortened by exonuclease chewback. However, selecting too small a value for 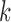to ensure coverage on D gene segments can create an overly complicated graph, potentially connecting 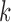-mers in V gene segments to those in J gene segments. While we do not observe any significant reductions in performance in either our simulated datasets or real ones due to this, this can limit the potential applications, namely to T-cell receptors (TCR). TCRs share the same V/D/J structure as immunoglobulins, but in humans have only two D gene segments, 12 and 16 bp long. While some approaches may claim to recover these D gene segments, our colored antibody graph will likely be unable to as long as exonuclease chewback sufficiently reduces its length.

Acknowledgments

This work was supported by the U.S. National Institutes of Health grant 2-P41-GM103484 from the National Center for Research Resources.

Author Disclosure Statement

No competing financial interests exist.