Admixture, Population Structure, and F-Statistics

Abstract

Many questions about human genetic history can be addressed by examining the patterns of shared genetic variation between sets of populations. A useful methodological framework for this purpose is F-statistics that measure shared genetic drift between sets of two, three, and four populations and can be used to test simple and complex hypotheses about admixture between populations. This article provides context from phylogenetic and population genetic theory. I review how F-statistics can be interpreted as branch lengths or paths and derive new interpretations, using coalescent theory. I further show that the admixture tests can be interpreted as testing general properties of phylogenies, allowing extension of some ideas applications to arbitrary phylogenetic trees. The new results are used to investigate the behavior of the statistics under different models of population structure and show how population substructure complicates inference. The results lead to simplified estimators in many cases, and I recommend to replace F₃ with the average number of pairwise differences for estimating population divergence.

FOR humans, whole-genome genotype data are now available for individuals from hundreds of populations (Lazaridis et al. 2014; Yunusbayev et al. 2015), opening up the possibility to ask more detailed and complex questions about our history (Pickrell and Reich 2014; Schraiber and Akey 2015) and stimulating the development of new tools for the analysis of the joint history of these populations (Reich et al. 2009; Patterson et al. 2012; Pickrell and Pritchard 2012; Lipson et al. 2013; Ralph and Coop 2013; Hellenthal et al. A simple and intuitive approach that has quickly gained in popularity are the F-statistics, introduced by Reich et al. (2009) and summarized in Patterson et al. (2012). In that framework, inference is based on “shared genetic drift” between sets of populations, under the premise that shared drift implies a shared evolutionary history. Tools based on this framework have quickly become widely used in the study of human genetic history, both for ancient and for modern DNA (Green et al. 2010; Reich et al. 2012; Lazaridis et al. 2014; Allentoft et al. 2015; Haak et al. 2015).

Some care is required with terminology, as the F-statistics sensu Reich et al. (2009) are distinct, but closely related to Wright’s fixation indexes (Wright 1931; Reich et al. 2009), which are also often referred to as F-statistics. Furthermore, it is necessary to distinguish between statistics (quantities calculated from data) and the underlying parameters (which are part of the model) (Weir and Cockerham 1984).

In this article, I mostly discuss model parameters, and I therefore refer to them as drift indexes. The term F-statistics is used when referring to the general framework introduced by Reich et al. (2009), and Wright’s statistics are referred to as F_ST or f.

Most applications of the F-statistic framework can be phrased in terms of the following six questions:

1. Treeness test: Are populations related in a tree-like fashion (Reich et al. 2009)?

2. Admixture test: Is a particular population descended from multiple ancestral populations (Reich et al. 2009)?

3. Admixture proportions: What are the contributions from different populations to a focal population (Green et al. 2010; Haak et al. 2015)?

4. Number of founders: How many founder populations are there for a certain region (Reich et al. 2012; Lazaridis et al. 2014)?

5. Complex demography: How can mixtures and splits of population explain demography (Patterson et al. 2012; Lipson et al. 2013)?

6. Closest relative: What is the closest relative to a contemporary or ancient population (Raghavan et al. 2014)?

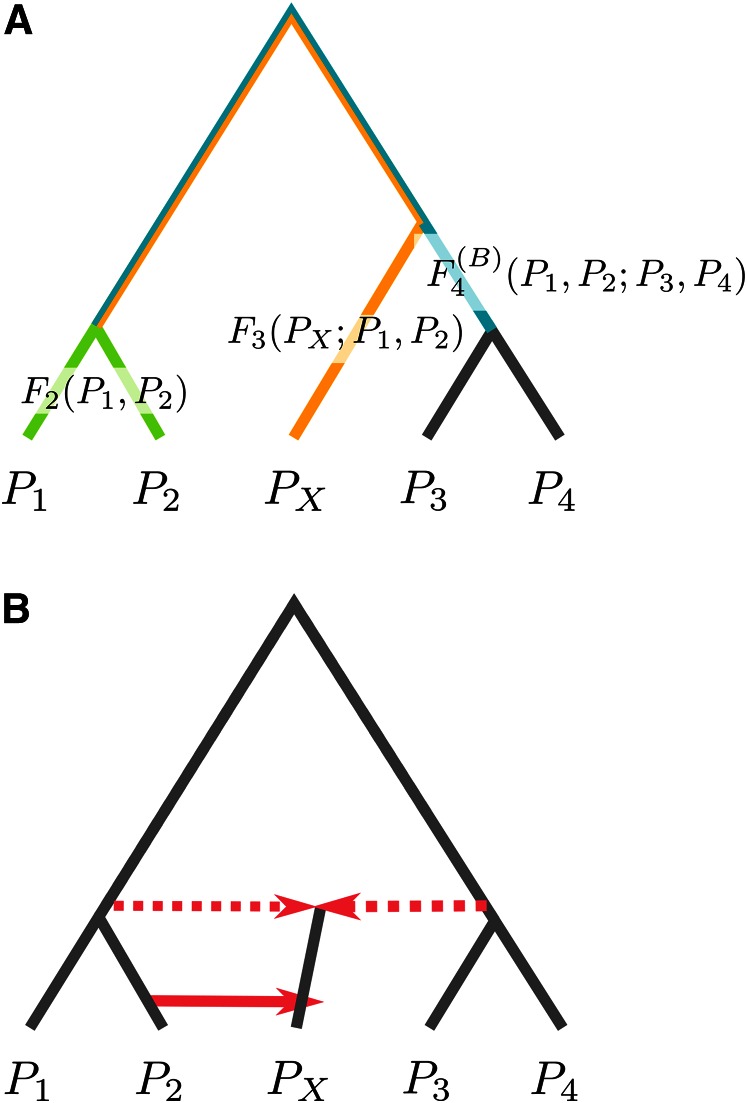
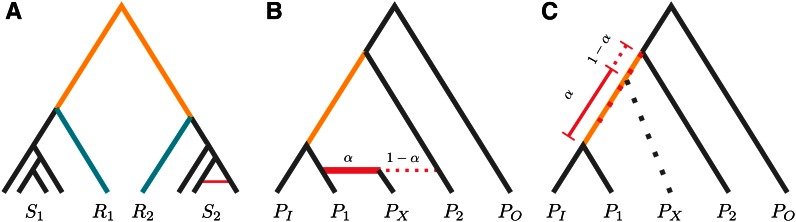
The demographic models under which these questions are addressed, and that motivated the drift indexes, are called population phylogenies and admixture graphs. The population phylogeny (or population tree) is a model where populations are related in a tree-like fashion (Figure 1A), and it frequently serves as the null model for admixture tests. The branch lengths in the population phylogeny correspond to how much genetic drift occurred, so that a branch that is subtended by two different populations can be interpreted as the “shared” genetic drift between these populations. The alternative model is an admixture graph (Figure 1B), which extends the population phylogeny by allowing edges that represent population mergers or a significant exchange of migrants.

Figure 1.

(A) A population phylogeny with branches corresponding to F₂ (green), F₃ (yellow), and $F_4^{\left(\mathrm{B}\right)}$ (blue). (B) An admixture graph extends a population phylogeny by allowing gene flow (red, solid line) and admixture events (red, dotted line).

Under a population phylogeny, the three F-statistics proposed by Reich et al. (2009), labeled F₂, F₃, and F₄, have interpretations as branch lengths (Figure 1A) between two, three, and four taxa, respectively. Assume populations are labeled as P₁, P₂, …. Then

• F₂(P₁, P₂) corresponds to the path on the phylogeny from P₁ to P₂.

• F₃ (P_X; P₁, P₂) represents the length of the external branch from P_X to the (unique) internal vertex connecting all three populations. Thus, the first parameter of F₃ has a unique role, whereas the other two can be switched arbitrarily.

• $F_4^{\left(\mathrm{B}\right)}$ (P₁, P₂; P₃, P₄) represents the internal branch from the internal vertex connecting P₁ and P₂ to the vertex connecting P₃ and P₄ (Figure 1A, blue).

If the arguments are permuted, some F-statistics will have no corresponding internal branch. In particular, it can be shown that in a population phylogeny, one F₄ index will be zero, implying that the corresponding internal branch is missing. This is the property that is used in the admixture test. For clarity, I add the superscript $F_4^{\left(\mathrm{B}\right)}$ if I need to emphasize the interpretation of F₄ as a branch length and $F_4^{\left(\mathrm{T}\right)}$ to emphasize the interpretation as a test statistic. For details, see the F₄ subsection in Methods and Results.

In an admixture graph, there is no longer a single branch length corresponding to each F-statistic, and interpretations are more complex. However, F-statistics can still be thought of as the proportion of genetic drift shared between populations (Reich et al. 2009). The basic idea exploited in addressing all six questions outlined above is that under a tree model, branch lengths, and thus the drift indexes, must satisfy some constraints (Buneman 1971; Semple and Steel 2003; Reich et al. 2009). The two most relevant constraints are that (i) in a tree, all branches have positive lengths (tested using the F₃-admixture test) and (ii) in a tree with four leaves, there is at most one internal branch (tested using the F₄-admixture test).

The goal of this article is to give a broad overview on the theory, ideas, and applications of F-statistics. Our starting point is a brief review on how genetic drift is quantified in general and how it is measured using F₂. I then propose an alternative definition of F₂ that allows us to simplify applications and study them under a wide range of population structure models. I then review some basic properties of distance-based phylogenetic trees, show how the admixture tests are interpreted in this context, and evaluate their behavior. Many of the results that are highlighted here are implicit in classical (Wahlund 1928; Wright 1931; Cavalli-Sforza and Edwards 1967; Felsenstein 1973, 1981; Cavalli-Sforza and Piazza 1975; Slatkin 1991; Excoffier et al. 1992) and more recent work (Patterson et al. 2012; Pickrell and Pritchard 2012; Lipson et al. 2013), but often not explicitly stated or given in a different context.

Methods and Results

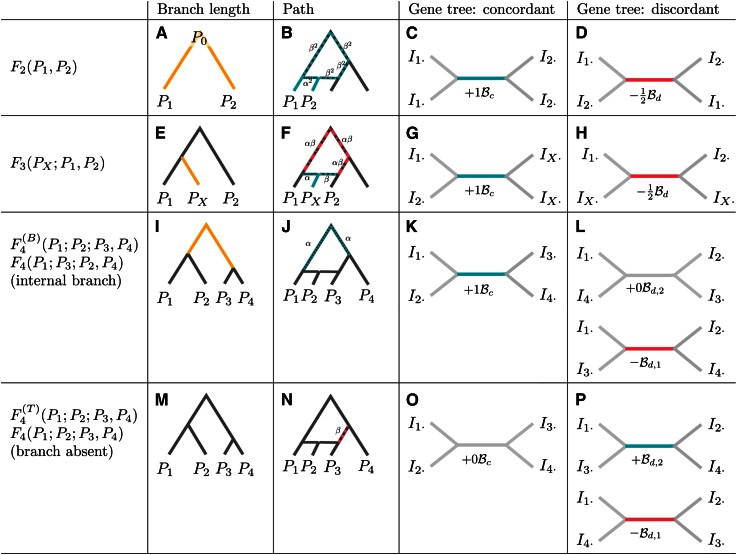
The next sections discuss the F-statistics, introducing different interpretations and giving derivations for some useful expressions. A graphical summary of the three interpretations of the statistics is given in Figure 2, and the main formulas are summarized in Table 1.

Figure 2.

Interpretation of F-statistics. F-statistics can be interpreted as branch lengths in a population phylogeny (A, E, I, and M), as the overlap of paths in an admixture graph (B, F, J, and N, see also Figure S1), and in terms of the internal branches of gene genealogies (see Figure 4, Figure S2, and Figure S3). For gene trees consistent with the population tree, the internal branch contributes positively (C, G, and K), and for discordant branches, internal branches contribute negatively (D and H) or zero (L). F₄ has two possible interpretations; depending on how the arguments are permuted relative to the tree topology, it may reflect either the length of the internal branch [I–L, $F_4^{\left(\mathrm{B}\right)}$] or a test statistic that is zero under a population phylogeny [M–P, $F_4^{\left(\mathrm{T}\right)}$]. For the admixture test, the two possible gene trees contribute to the statistic with different sign, highlighting the similarity to the D-statistic (Green et al. 2010) and its expectation of zero in a symmetric model.

Table 1. Summary of equations.

Drift Measure	F2 (P1, P2)	F3 (PX; P1, P2)	F4(P1, P2, P3, P4)
Definition	$\mathrm{E}\left[{\left(p_1-p_2\right)}^2\right]$	$\mathrm{E}\left(p_X-p_1\right)\left(p_X-p_2\right)$	$\mathrm{E}\left(p_1-p_2\right)\left(p_3-p_4\right)$
F2	—	$\frac{1}{2}\left(F_2\left(P_1,P_X\right)+F_2\left(P_2,P_X\right)-F_2\left(P_1,P_2\right)\right)$	$\frac{1}{2}\left(F_2\left(P_1,P_4\right)+F_2\left(P_2,P_3\right)-F_2\left(P_1,P_3\right)-F_2\left(P_2,P_4\right)\right)$
Coalescence times	$2\mathrm{E}{T}_{12}-\mathrm{E}{T}_{11}-\mathrm{E}{T}_{22}$	$\mathrm{E}{T}_{1X}+\mathrm{E}{T}_{2X}-\mathrm{E}{T}_{12}-\mathrm{E}{T}_{XX}$	$\mathrm{E}{T}_{14}+\mathrm{E}{T}_{23}-\mathrm{E}{T}_{13}-\mathrm{E}{T}_{24}$
Variance	$\text{Var}\left(p_1-p_2\right)$	$\text{Var}\left(p_X\right)+\text{COV}\left(p_1,p_2\right)-\text{COV}\left(p_1,p_X\right)-\text{COV}\left(p_2,p_X\right)$	$\text{COV}\left(\left(p_1-p_2\right),\left(p_3,p_4\right)\right)$
Branch length	$2{\mathrm{ℬ}}_{\mathrm{c}}-{\mathrm{ℬ}}_{\mathrm{d}}$	$2{\mathrm{ℬ}}_{\mathrm{c}}-{\mathrm{ℬ}}_{\mathrm{d}}$	$B_c-B_d\hspace{0.17em}\text{or}\hspace{0.17em}\text{as}\hspace{0.17em}\text{admixture}\hspace{0.17em}\text{test}:\hspace{0.5em}{B^{\prime }}_d-B_d$

A constant of proportionality is omitted for coalescence times and branch lengths. Derivations for F₂ are given in the main text, and F₃ and F₄ are a simple result of combining Equation 16 with Equations 20b and 24b. ${\mathrm{ℬ}}_{\mathrm{c}}$ and ${\mathrm{ℬ}}_{\mathrm{d}}$ correspond to the average length of the internal branch in a gene genealogy concordant and discordant with the population assignment, respectively (see Gene tree branch lengths section).

Throughout this article, populations are labeled as P₁, P₂, … , P_i, … . Often, P_X will denote an admixed population. The allele frequency p_i is defined as the proportion of individuals in P_i that carry a particular allele at a biallelic locus, and throughout this article I assume that all individuals are haploid. However, all results hold if instead of haploid individuals, an arbitrary allele of a diploid individual is used. I focus on genetic drift only and ignore the effects of mutation, selection, and other evolutionary forces.

Measuring genetic drift—F₂

The purpose of F₂ is simply to measure how much genetic drift occurred between two populations, i.e., to measure genetic dissimilarity. For populations P₁ and P₂, F₂ is defined as

$$F_2(P_1,P_2)=F_2(p_1,p_2)=\mathrm{E}{(p_1-p_2)}^2$$ (1)

(Reich et al. 2009). The expectation is with respect to the evolutionary process, but in practice F₂ is estimated from hundreds of thousands of loci across the genome (Patterson et al. 2012), which are assumed to be nonindependent replicates of the evolutionary history of the populations.

Why is F₂ a useful measure of genetic drift? As it is infeasible to observe changes in allele frequency directly, the effect of drift is assessed indirectly, through its impact on genetic diversity. Most commonly, genetic drift is quantified in terms of (i) the variance in allele frequency, (ii) heterozygosity, (iii) probability of identity by descent, (iv) correlation (or covariance) between individuals, and (v) the probability of coalescence (two lineages having a common ancestor). In the next sections I show how F₂ relates to these quantities in the cases of a single population changing through time and a pair of populations that are partially isolated.

Single population:

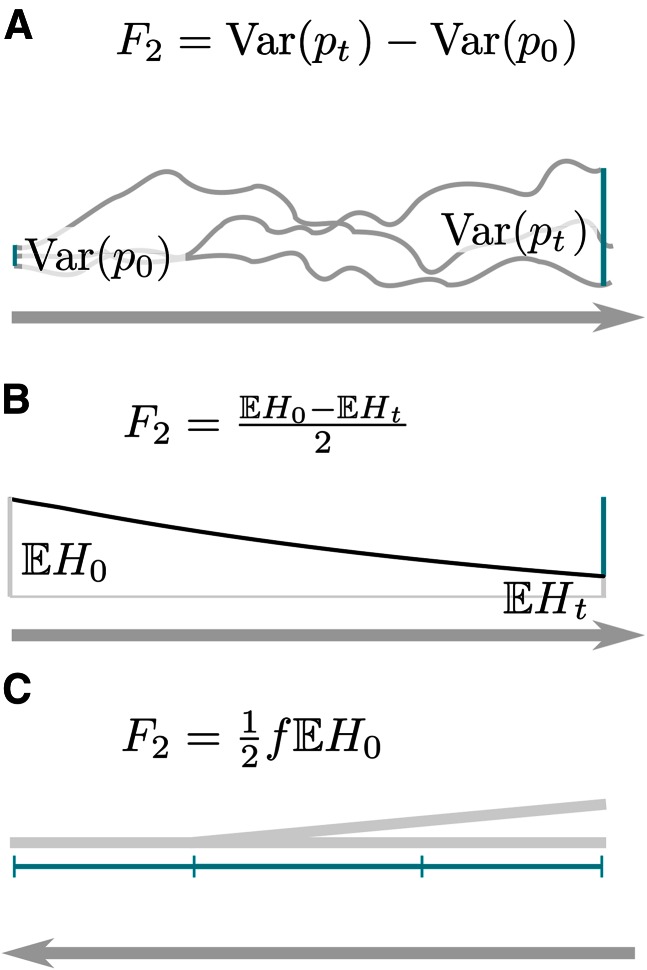
I assume a single population, measured at two time points (t₀ and t), and label the two samples P₀ and P_t. Then F₂ (P₀, P_t) can be interpreted in terms of the variances of allele frequencies:

$$\begin{array}{c}{F}_2\left(P_t,P_0\right)=\mathrm{E}\left[{\left({\mathit{p}}_{\mathit{t}}–p_0\right)}^2\right]\\ =\mathrm{Var}\left(p_t–p_0\right)+\mathrm{E}{\left[\left({\mathit{p}}_{\mathit{t}}–p_0\right)\right]}^2\\ =\mathrm{Var}\left(p_t\right)+\mathrm{Var}\left(p_0\right)–2\mathrm{COV}\left(p_0,p_t\right)\\ =\mathrm{Var}\left(p_t\right)+\mathrm{Var}\left(p_0\right)–2\mathrm{COV}\left(p_0,p_0+\left(p_t–p_0\right)\right)\\ =\mathrm{Var}\left(p_t\right)–\mathrm{Var}\left(p_0\right).\end{array}$$ (2)

Here, I used $\mathrm{E}\left[{\mathit{p}}_{\mathit{t}}–p_0\right]=\mathrm{COV}\left(p_0,p_t–p_0\right)=0$ to obtain lines three and five. It is worth noting that this result holds for any model of genetic drift where the expected allele frequency is the current allele frequency and increments are independent. For example, this interpretation of F₂ holds also if genetic drift is modeled as a Brownian motion (Cavalli-Sforza and Edwards 1967).

An elegant way to introduce the use of F₂ in terms of expected heterozygosities H_t (Figure 3B) and identity by descent (Figure 3C) is the duality

$${\mathrm{E}}_{p_t}\left[p_t^{n_t}|p_0,n_t\right]={\mathrm{E}}_{n_0}\left[p_0^{n_0}|p_0,n_t\right].$$ (3)

This equation is due to Tavaré (1984), who also provided the following intuition: Given n_t individuals are sampled at time t, let E denote the event that all individuals carry allele x, conditional on allele x having frequency p₀ at time t₀. There are two components to this: First, the frequency will change between t₀ and t, and then all n_t sampled individuals need to carry x.

Figure 3.

Measures of genetic drift in a single population. Shown are interpretations of F₂ in terms of (A) the increase in allele frequency variance; (B) the decrease in heterozygosity; and (C) f, which can be interpreted as probability of coalescence of two lineages or the probability that they are identical by descent.

In a diffusion framework,

$$\mathrm{\mathbb{P}}\left(\mathit{E}\right)={\displaystyle {\int }_0^1{y}^{n_t}\mathrm{\mathbb{P}}\left({\mathit{p}}_{\mathit{t}}=y|p_0,n_t\right)dy}=\mathrm{E}\left[{\mathit{p}}_t^{{\mathit{n}}_{\mathit{t}}}|p_0,n_t\right].$$ (4)

On the other hand, one may argue using the coalescent: For E to occur, all n_t samples need to carry the x allele. At time t₀, they had n₀ ancestral lineages, who all carry x with probability p₀. Therefore,

$$\mathrm{\mathbb{P}}\left(\mathit{E}\right)={\displaystyle \sum _{i=1}^{n_0}{p}_0^i\mathrm{\mathbb{P}}\left({\mathit{n}}_{\mathrm{0}}=i|p_0,n_t\right)}=\mathrm{E}\left[{\mathit{p}}_{\mathrm{0}}^{{\mathit{n}}_0}|p_0,n_t\right].$$ (5)

Equating (4) and (5) yields Equation 3.

In the present case, the only relevant cases are n_t = 1,2, since

$$\begin{array}{l}\mathrm{E}\left[{\mathit{p}}_{\mathit{t}}^{\mathrm{1}}|p_0;n_t=1\right]=p_0\\ \mathrm{E}\left[{\mathit{p}}_{\mathit{t}}^{\mathrm{2}}|p_0;n_t=2\right]=p_{0}f+p_0^2\left(1-f\right),\end{array}$$

where f is the probability that two lineage sampled at time t coalesce before time t₀.

This yields an expression for F₂ by conditioning on the allele frequency p₀,

$$\begin{array}{c}\mathrm{E}\left[{\left({\mathit{p}}_{\mathrm{0}}-p_t\right)}^2|p_0\right]=\mathrm{E}\left[{\mathit{p}}_{\mathrm{0}}^{\mathrm{2}}|p_0\right]-\mathrm{E}\left[\mathrm{2}{\mathit{p}}_{\mathit{t}}{p}_0|p_0\right]+\mathrm{E}\left[p_t^2|p_0\right]\\ =p_0^2-2p_0^2+p_{0}f+p_0^2\left(1-f\right)\\ =f{p}_0\left(1-p_0\right)\\ =\frac{1}{2}f{H}_0,\end{array}$$

where H₀ = 2p₀ (1 – p₀) is the heterozygosity. Integrating over $\mathrm{\mathbb{P}}\left({\mathit{p}}_{\mathrm{0}}\right)$ yields

$$F_2\left(P_0,P_t\right)=\frac{1}{2}f\mathrm{E}{H}_{\mathrm{0}}$$ (6)

and it can be seen that F₂ increases as a function of f (Figure 3C). This equation can also be interpreted in terms of probabilities of identity by descent: f is the probability that two individuals are identical by descent in P_t given their ancestors were not identical by descent in P₀ (Wright 1931), and $\mathrm{E}{\mathit{H}}_{\mathrm{0}}$ is the probability two individuals are not identical in P₀.

Furthermore, $\mathrm{E}{\mathit{H}}_{\mathit{t}}=\left(1-f\right)\mathrm{E}{\mathit{H}}_{\mathrm{0}}$ (equation 3.4 in Wakeley 2009) and therefore

$$\mathrm{E}{\mathit{H}}_{\mathrm{0}}-\mathrm{E}{H}_t=\mathrm{E}{H}_0\left(1-\left(1-f\right)\right)=2{\mathit{F}}_{\mathrm{2}}\left(P_t,P_0\right),$$ (7)

which shows that F₂ measures the decay of heterozygosity (Figure 3A). A similar argument was used by Lipson et al. (2013) to estimate ancestral heterozygosities and to linearize F₂.

These equations can be rearranged to make the connection between other measures of genetic drift and F₂ more explicit:

$$\mathrm{E}{H}_t=\mathrm{E}{H}_0-2F_2\left(P_0,P_t\right)$$ (8a)

$$=\mathrm{E}{H}_0-2\left(\mathrm{Var}\left(p_t\right)-\mathrm{Var}\left(p_0\right)\right)$$ (8b)

$$=\mathrm{E}{H}_0\left(1-f\right).$$ (8c)

Pairs of populations:

Equations 8b and 8c describing the decay of heterozygosity are–of course–well known by population geneticists, having been established by Wright (1931). In structured populations, very similar relationships exist when the number of heterozygotes expected from the overall allele frequency, $H_{\mathrm{obs}}$ is compared with the number of heterozygotes present due to differences in allele frequencies between populations H_exp (Wahlund 1928; Wright 1931).

In fact, already Wahlund showed by considering the genotypes of all possible matings in two subpopulations (table 3 in Wahlund 1928) that for a population made of two subpopulations with equal proportions, the proportion of heterozygotes is reduced by

$$H_{\mathrm{obs}}=H_{\exp }-2{\left(p_1-p_2\right)}^2$$

from which it follows that

$$F_2\left(P_1,P_2\right)=\frac{\mathrm{E}{\mathit{H}}_{\exp }-\mathrm{E}{H}_{\mathrm{obs}}}{2}.$$ (9)

Furthermore, $\mathrm{Var}\left(p_1-p_2\right)=\mathrm{E}{\left({\mathit{p}}_{\mathrm{1}}-p_2\right)}^2-{\left[\mathrm{E}\left(p_1-p_2\right)\right]}^2,$ but $\mathrm{E}\left(p_1-p_2\right)=0$ and therefore

$$F_2\left(P_1,P_2\right)=\mathrm{Var}\left(p_1-p_2\right).$$ (10)

Finally, the original definition of F₂ was as the numerator of F_ST (Reich et al. 2009), but F_ST can be written as $F_{\mathrm{ST}}=2{\left(p_1-p_2\right)}^2/\mathrm{E}{H}_{\exp },$ from which follows

$$F_2\left(P_1,P_2\right)=\frac{1}{2}{F}_{\mathrm{ST}}\mathrm{E}{H}_{\exp }.$$ (11)

Covariance interpretation:

To see how F₂ can be interpreted as a covariance, define X_i and X_j as indicator variables that two individuals from the same population sample have the A allele, which has frequency p₁ in one and p₂ in the other population. If individuals are equally likely to be sampled from either population,

$$\begin{array}{c}\mathrm{E}{X}_i=\mathrm{E}{X}_j=\frac{1}{2}{p}_1+\frac{1}{2}{p}_2\\ \mathrm{E}{X}_i{X}_j=\frac{1}{2}{p}_1^2+\frac{1}{2}{p}_2^2\\ \mathrm{COV}\left(X_i,X_j\right)=\mathrm{E}{X}_i{X}_j-\mathrm{E}{X}_i\mathrm{E}{X}_j\\ =\frac{1}{4}{\left(p_1-p_2\right)}^2=\frac{1}{4}{F}_2\left(P_1,P_2\right).\end{array}$$

Justification for F₂:

The preceding arguments show how the usage of F₂ for both single and structured populations can be justified by the similar effects of F₂ on different measures of genetic drift. However, what is the benefit of using F₂ instead of the established inbreeding coefficient f and fixation index F_ST? Recall that Wright motivated f and F_ST as correlation coefficients between alleles (Wright 1921, 1931). Correlation coefficients have the advantage that they are easy to interpret, as, e.g., F_ST = 0 implies panmixia and F_ST = 1 implies complete divergence between subpopulations. In contrast, F₂ depends on allele frequencies and is highest for intermediate-frequency alleles. However, F₂ has an interpretation as a covariance, making it simpler and mathematically more convenient to work with. In particular, variances and covariances are frequently partitioned into components due to different effects, using techniques such as analysis of variance and analysis of covariance (e.g., Excoffier et al. 1992).

F₂ as branch length:

Reich et al. (2009) and Patterson et al. (2012) proposed to partition “drift” (as previously established, measured by covariance, allele frequency variance, or decrease in heterozygosity) between different populations into contribution on the different branches of a population phylogeny. This model has been studied by Cavalli-Sforza and Edwards (1967) and Felsenstein (1973) in the context of a Brownian motion process. In this model, drift on independent branches is assumed to be independent, meaning that the variances can simply be added. This is what is referred to as the additivity property of F₂ (Patterson et al. 2012).

To illustrate the additivity property, consider two populations P₁ and P₂ that split recently from a common ancestral population P₀ (Figure 2A). In this case, p₁ and p₂ are assumed to be independent conditional on p₀, and therefore $\mathrm{COV}\left(p_1,p_2\right)=\mathrm{Var}\left(p_0\right).$ Then, using (2) and (10),

$$\begin{array}{c}{F}_2\left(P_1,P_2\right)=\mathrm{Var}\left(p_1-p_2\right)=\mathrm{Var}\left(p_1\right)+\mathrm{Var}\left(p_2\right)-2\mathrm{COV}\left(p_1,p_2\right)\\ =\mathrm{Var}\left(p_1\right)+\mathrm{Var}\left(p_2\right)-2\mathrm{Var}\left(p_0\right)\\ =F_2\left(P_1,P_0\right)+F_2\left(P_2,P_0\right).\end{array}$$

Alternative proofs of this statement and more detailed reasoning behind the additivity assumption can be found in Cavalli-Sforza and Edwards (1967), Felsenstein (1973), Reich et al. (2009), and Patterson et al. (2012).

Lineages are not independent in an admixture graph, and so this approach cannot be used. Reich et al. (2009) approached this by conditioning on the possible population trees that are consistent with an admixture scenario. In particular, they proposed a framework of counting the possible paths through the graph (Reich et al. 2009; Patterson et al. 2012). An example of this representation for F₂ in a simple admixture graph is given in Supplemental Material, Figure S1, with the result summarized in Figure 2B. Detailed motivation behind this visualization approach is given in Appendix 2 of Patterson et al. (2012). In brief, the reasoning is as follows: Recall that $F_2\left(P_1,P_2\right)=\mathrm{E}\left(p_1-p_2\right)\left(p_1-p_2\right)$ and interpret the two terms in parentheses as two paths between P₁ and P₂, and F₂ as the overlap of these two paths. In a population phylogeny, there is only one possible path, and the two paths are always the same; therefore F₂ is the sum of the length of all the branches connecting the two populations. However, if there is admixture, as in Figure 2B, both paths choose independently which admixture edge they follow. With probability α they will go left, and with probability β = 1 − α they go right. Thus, F₂ can be interpreted by enumerating all possible choices for the two paths, resulting in three possible combinations of paths on the trees (Figure S1), and the branches included will differ, depending on which path is chosen, so that the final F₂ is made of an average of the path overlap in the topologies, weighted by the probabilities of the topologies.

However, one drawback of this approach is that it scales quadratically with the number of admixture events, making calculations cumbersome when the number of admixture events is large. More importantly, this approach is restricted to panmictic subpopulations and cannot be used when the population model cannot be represented as a weighted average of trees.

Gene tree Interpretation:

For this reason, I propose to redefine F₂, using coalescent theory (Wakeley 2009). Instead of allele frequencies on a fixed admixture graph, coalescent theory tracks the ancestors of a sample of individuals, tracing their history back to their most recent common ancestor. The resulting tree is called a gene tree (or coalescent tree). Gene trees vary between loci and will often have a different topology from that of the population phylogeny, but they are nevertheless highly informative about a population’s history. Moreover, expected coalescence times and expected branch lengths are easily calculated under a wide array of neutral demographic models.

In a seminal article, Slatkin (1991) showed how F_ST can be interpreted in terms of the expected coalescence times of gene trees,

$$F_{\mathrm{ST}}=\frac{\mathrm{E}{T}_{\mathrm{B}}-\mathrm{E}{T}_{\mathrm{W}}}{\mathrm{E}{T}_{\mathrm{B}}},$$

where $\mathrm{E}{T}_{\mathrm{B}}$ and $\mathrm{E}{T}_{\mathrm{W}}$ are the expected coalescence times of two lineages sampled in two different populations and the same population, respectively.

Unsurprisingly, given the close relationship between F₂ and F_ST, an analogous expression exists for F₂ (P₁, P₂): The derivation starts by considering F₂ for two samples of size 1. I then express F₂ for arbitrary sample sizes in terms of individual-level F₂ and obtain a sample-size independent expression by letting the sample size n go to infinity.

In this framework, I assume that mutation is rare such that there is at most one mutation at any locus. In a sample of size 2, let $I_i$ be an indicator random variable that individual i has a particular allele. For two individuals, F₂ (I₁, I₂) = 1 implies I₁ = I₂, whereas F₂ (I₁, I₂) = 0 implies I₁ ≠ I₂. Thus, F₂(I₁, I₂) is another indicator random variable with the parameter equal to the probability that a mutation happened on the tree branch between I₁ and I₂.

Now, instead of a single individual I₁, consider a sample of n₁ individuals: $P_1=\left\{I_{1,1,}{I}_{1,2},\mathrm{\dots },I_{1,n_1}\right\}.$ The sample allele frequency is ${\widehat{p}}_1=n_1^{-1}{\displaystyle {\sum }_i{I}_{1,i}}.$ And the sample F₂ is

$$\begin{array}{c}{F}_2\left({\widehat{p}}_1,I_2\right)=F_2\left(\frac{1}{n_1}{\displaystyle \sum _{i=1}^{n_1}{I}_{1,i},I_2}\right)=\mathrm{E}{\left(\frac{1}{n_1}{\displaystyle \sum _{i=1}^{n_1}{I}_{1,i}-I_2}\right)}^2\\ =\mathrm{E}\left[\frac{1}{n_1^2}{\displaystyle \sum I_{1,i}^2+\frac{2}{n_1^2}}{\displaystyle \sum I_{1,i}{I}_{1,j}-\frac{2}{n_1}}{\displaystyle \sum I_{1,i}{I}_2+I_2^2}\right]\\ =\mathrm{E}\left[\frac{1}{n_1}{\displaystyle \sum I_{1,i}^2-\frac{2}{n_1}}{\displaystyle \sum I_{1,i}{I}_2+\frac{n_1}{n_1}}{I}_2^2\right]\\ +\mathrm{E}\left[\frac{2}{n_1^2}{\displaystyle \sum I_{1,i}{I}_{1,j}-\frac{n_1-1}{n_1^2}}{\displaystyle \sum I_{1,i}^2}\right].\end{array}$$

The first three terms can be grouped into n₁ terms of the form F₂ (I_1,i, I₂), and the last two terms can be grouped into $\left({}_2^{n_1}\right)$ terms of the form F₂ (I_1,i, I_1,j), one for each possible pair of samples in P₁.

Therefore,

$$F_2\left({\widehat{p}}_1,I_2\right)=\frac{1}{n_1}{\displaystyle \sum _i{F}_2\left(I_{1,i},I_2\right)-\frac{1}{n_1^2}}{\displaystyle \sum _{i\mathrm{<}j}{F}_2\left(I_{1,i},I_{1,j}\right)},$$ (12)

where the second sum is over all pairs in P₁. This equation is equivalent to equation 22 in Felsenstein (1973).

As $F_2\left({\widehat{p}}_1,{\widehat{p}}_2\right)=F_2\left({\widehat{p}}_2,{\widehat{p}}_1\right),$ I can switch the labels and obtain the same expression for a second population $P_2=\left\{I_{2,i},i=0,\mathrm{\dots },n_2\right\}.$ Taking the average over all I_2,j yields

$$\begin{array}{c}{F}_2\left({\widehat{p}}_1,{\widehat{p}}_2\right)=\frac{1}{n_1}{\displaystyle \sum _i{F}_2\left(I_{1,i},I_{2,j}\right)}\\ -\frac{1}{n_1^2}{\displaystyle \sum _{i<j}{F}_2\left(I_{1,i},I_{1,j}\right)}-\frac{1}{n_2^2}{\displaystyle \sum _{i<j}{F}_2\left(I_{2,i},I_{2,j}\right)}.\end{array}$$ (13)

Thus, I can write F₂ between the two populations as the average number of differences between individuals from different populations, minus some terms including differences within each sample.

Equation 13 is quite general, making no assumptions on where samples are placed on a tree. In a coalescence framework, it is useful to make the assumptions that all individuals from the same population have the same branch length distribution; i.e., $F_2\left(I_{x_1,i},I_{y_1,j}\right)=F_2\left(I_{x_2,i},I_{y_2,j}\right)$ for all pairs of samples (x₁, x₂) and (y₁, y₂) from populations P_i and P_j. Second, I assume that all samples correspond to the leaves of the tree, so that I can estimate branch lengths in terms of the time to a common ancestor T_ij. Finally, I assume that mutations occur at a constant rate of $\mathit{\theta }/2$ on each branch. Taken together, these assumptions imply that $F_2\left(I_{i,k},I_{j,l}\right)=\mathit{\theta }\mathrm{E}{\mathit{T}}_{\mathit{ij}}$ for all individuals from populations P_i, P_j. this simplifies (13) to

$$F_2\left({\widehat{p}}_1,{\widehat{p}}_2\right)=\mathit{\theta }\mathrm{\times }\left(\mathrm{E}{\mathit{T}}_{\mathrm{12}}-\frac{1}{2}\left(1-\frac{1}{n_1}\right)\mathrm{E}{T}_{11}-\frac{1}{2}\left(1-\frac{1}{n_2}\right)\mathrm{E}{T}_{22}\right),$$ (14)

which, for the cases of n = 1, 2, was also derived by Petkova et al. (2014). In some applications, F₂ might be calculated only for segregating sites in a large sample. As the expected number of segregating sites is $\left(\mathit{\theta }/2\right)T_{\mathrm{tot}}$ (with T_tot denoting the total tree length), taking the limit where $\mathit{\theta }\to \mathit{0}$ is meaningful (Slatkin 1991; Petkova et al. 2014):

$$F_2\left({\widehat{p}}_1,{\widehat{p}}_2\right)=\frac{2}{T_{\mathrm{tot}}}\mathrm{\times }\left(\mathrm{E}{\mathit{T}}_{\mathrm{12}}-\frac{1}{2}\left(1-\frac{1}{n_1}\right)\mathrm{E}{T}_{11}-\frac{1}{2}\left(1-\frac{1}{n_2}\right)\mathrm{E}{T}_{22}\right).$$ (15)

In either of these equations, $2/T_{\mathrm{tot}}$ or θ acts as a constant of proportionality that is the same for all statistics calculated from the same data. Since interest is focused on the relative magnitude of F₂ or whether a sum of F₂ values is different from zero, this constant has no impact on inference.

Furthermore, a population-level quantity is obtained by taking the limit when the numbers of individuals n₁ and n₂ go to infinity:

$$F_2\left(P_1,P_2\right)=\underset{n_1,n_2,\to \mathrm{\infty }}{\lim }{F}_2\left({\widehat{p}}_1,{\widehat{p}}_2\right)=\mathit{\theta }\left(\mathrm{E}{\mathit{T}}_{\mathrm{12}}-\frac{\mathrm{E}{T}_{11}+\mathrm{E}{T}_{12}}{2}\right).$$ (16)

Unlike F_ST, the mutation parameter θ does not cancel. However, for most applications, the absolute magnitude of F₂ is of little interest, since only the sign of the statistics is used for most tests. In other applications F-statistics with presumably the same θ (Reich et al. 2009) are compared. In these cases, θ can be regarded as a constant of proportionality and will not change the theoretical properties of the F-statistics. It will, however, influence statistical properties, as a larger θ implies more mutations and hence more data.

Estimator for F₂:

An estimator for F₂ can be derived using the average number of pairwise differences π_ij as an estimator for θT_ij (Tajima 1983). Thus, a natural estimator for F₂ is

$${\widehat{F}}_2\left(P_1,P_2\right)={\mathit{\pi }}_{\mathrm{12}}-\frac{{\mathit{\pi }}_{\mathrm{11}}+{\mathit{\pi }}_{\mathrm{22}}}{2}.$$ (17)

Strikingly, the estimator in Equation 17 is equivalent to that given by Reich et al. (2009) in terms of the sample allele frequency ${\widehat{p}}_i$ and sample size n_i:

$$\begin{array}{c}{F}_2\left(P_1,P_2\right)={\mathit{\pi }}_{12}-{\mathit{\pi }}_{\mathrm{11}}/2-{\mathit{\pi }}_{\mathrm{22}}/2\\ =\left[{\widehat{p}}_1\left(1-{\widehat{p}}_2\right)+{\widehat{p}}_2\left(1-{\widehat{p}}_1\right)\right]\\ -\hspace{0.17em}{\widehat{p}}_1\left(1-{\widehat{p}}_1\right)\frac{n_1}{n_1-1}-{\widehat{p}}_2\left(1-{\widehat{p}}_2\right)\frac{n_2}{n_2-1}\\ ={\widehat{p}}_1\left(1-1-\frac{1}{n_1}\right)+{\widehat{p}}_2\left(1-1-\frac{1}{n_2}\right)-2{\widehat{p}}_1{\widehat{p}}_2\\ +{\widehat{p}}_1^2\left(1-\frac{1}{n_1-1}\right)-{\widehat{p}}_2^2\left(1-\frac{1}{n_2-1}\right)\\ =\left({\widehat{p}}_1-{\widehat{p}}_2\right)-\frac{{\widehat{p}}_1\left(1-{\widehat{p}}_1\right)}{n_1-1}-\frac{{\widehat{p}}_2\left(1-q2\right)}{n_2-1}.\end{array}$$

The last line is the same as equation 10 in the appendix of Reich et al. (2009).

However, while the estimators are identical, the underlying modeling assumptions are different: The original definition considered only loci that were segregating in an ancestral population; loci not segregating there were discarded. Since ancestral populations are usually unsampled, this is often replaced by ascertainment in an outgroup (Patterson et al. 2012; Lipson et al. 2013). In contrast, Equation 17 assumes that all markers are used, which is the more natural interpretation for sequence data.

Gene tree branch lengths:

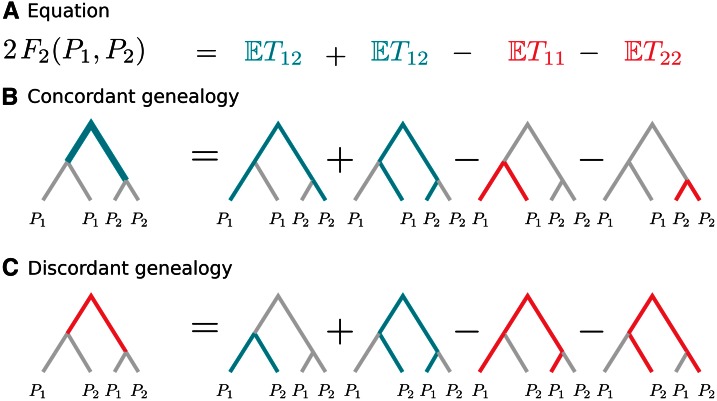
An important feature of Equation 16 is that it depends only on the expected coalescence times between pairs of lineages. Thus, the behavior of F₂ can be fully characterized by considering a sample of size 4, with two random individuals taken from each population. This is all that is needed to study the joint distribution of T₁₂, T₁₁, and T₂₂ and hence F₂. By linearity of expectation, larger samples can be accommodated by summing the expectations over all possible quartets.

For a sample of size 4 with two pairs, there are only two possible unrooted tree topologies: one, where the lineages from the same population are more closely related to each other [called concordant topology, ${\mathcal{T}}_{\mathrm{c}}^{\left(\mathrm{2}\right)}$] and one where lineages from different populations coalesce first [which I refer to as discordant topology, ${\mathcal{T}}_{\mathrm{d}}^{\left(\mathrm{2}\right)}$]. The superscripts refers to the topologies being for F₂, and I discard them in cases where no ambiguity arises.

Conditioning on the topology yields

$$\begin{array}{c}{F}_2\left(P_1,P_2\right)=\mathrm{E}\left[F_2\left(P_1,P_2\right)|\mathcal{T}\right]\\ =\mathrm{\mathbb{P}}\left({\mathcal{T}}_{\mathrm{c}}\right)\mathrm{E}\left[F_2\left(P_1,P_2\right)|{\mathcal{T}}_{\mathrm{c}}\right]+\mathrm{\mathbb{P}}\left({\mathcal{T}}_{\mathrm{d}}\right)\mathrm{E}\left[F_2\left(P_1,P_2\right)|{\mathcal{T}}_{\mathrm{d}}\right].\end{array}$$

Figure 4 contains graphical representations for $\mathrm{E}\left[{\mathit{F}}_{\mathrm{2}}\left(P_1,P_2\right)|{\mathcal{T}}_{\mathrm{c}}\right]$ (Figure 4B) and $\mathrm{E}\left[{\mathit{F}}_{\mathrm{2}}\left(P_1,P_2\right)|{\mathcal{T}}_{\mathrm{d}}\right]$ (Figure 4C), respectively.

Figure 4.

(A–C) Schematic explanation of how F₂ behaves conditioned on a gene tree. (A) Equation with terms corresponding to the branches in the tree below. Blue terms and branches correspond to positive contributions, whereas red branches and terms are subtracted. Labels represent individuals randomly sampled from that population. External branches cancel out, so only the internal branches have nonzero contribution to F₂. In the concordant genealogy (B), the contribution is positive (with weight 2), and in the discordant genealogy (C), it is negative (with weight 1). The mutation rate as constant of proportionality is omitted.

In this representation, T₁₂ corresponds to a path from a random individual from P₁ to a random individual from P₂, and T₁₁ represents the path between the two samples from P₁.

For ${\mathcal{T}}_{\mathrm{c}}$ the internal branch is always included in T₁₂, but never in T₁₁ or T₂₂. External branches, on the other hand, are included with 50% probability in T₁₂ on any path through the tree. T₁₁ and T₂₂, on the other hand, consist only of external branches, and the lengths of the external branches cancel.

On the other hand, for ${\mathcal{T}}_{\mathrm{d}},$ the internal branch is always included in T₁₁ and T₂₂, but only half the time in T₁₂. Thus, they contribute negatively to F₂, but only with half the magnitude of ${\mathcal{T}}_{\mathrm{c}}.$ As for ${\mathcal{T}}_{\mathrm{c}},$ each T contains exactly two external branches, cancelling the external branches from T₁₂.

An interesting way to represent F₂ is therefore in terms of the internal branches over all possible gene genealogies. Denote the unconditional average length of the internal branch of ${\mathcal{T}}_{\mathrm{c}}$ as ${\mathrm{ℬ}}_{\mathrm{c}}$ and the average length of the internal branch in ${\mathcal{T}}_{\mathrm{d}}$ as ${\mathrm{ℬ}}_{\mathrm{d}}.$ Then, F₂ can be written in terms of these branch lengths as

$$F_2\left(P_1,P_2\right)=\mathit{\theta }\left(\mathrm{2}{\mathrm{ℬ}}_{\mathrm{c}}-1{\mathrm{ℬ}}_{\mathrm{d}}\right),$$ (18)

resulting in the representation given in Figure 2, C and D.

As a brief sanity check, consider the case of a population without structure. In this case, the branch length is independent of the topology and ${\mathcal{T}}_{\mathrm{d}}$ is twice as likely as ${\mathcal{T}}_{\mathrm{c}}$ and hence ${\mathrm{ℬ}}_{\mathrm{d}}=2{\mathrm{ℬ}}_{\mathrm{c}},$ from which it follows that F₂ will be zero, as expected in a randomly mating population

This argument can be transformed from branch lengths to observed mutations by recalling that mutations occur on a branch at a rate proportional to its length. F₂ is increased by doubletons that support the assignment of populations (i.e., the two lineages from the same population have the same allele), but reduced by doubletons shared by individuals from different populations. All other mutations have a contribution of zero.

Testing treeness

Many applications consider tens or even hundreds of populations simultaneously (Patterson et al. 2012; Pickrell and Pritchard 2012; Haak et al. 2015; Yunusbayev et al. 2015), with the goal to infer where and between which populations admixture occurred. Using F-statistics, the approach is to interpret $F_2\left(P_1,P_2\right)$ as a measure of dissimilarity between P₁ and P₂, as a large F₂ value implies that populations are highly diverged. Thus, the strategy is to calculate all pairwise F₂ indexes between populations, combine them into a dissimilarity matrix, and ask whether that matrix is consistent with a tree.

One way to approach this question is by using phylogenetic theory: Many classical algorithms have been proposed that use a measure of dissimilarity to generate a tree (Fitch et al. 1967; Saitou and Nei 1987; Semple and Steel 2003; Felsenstein 2004) and what properties a general dissimilarity matrix needs to have to be consistent with a tree (Buneman 1971; Cavalli-Sforza and Piazza 1975), in which case the matrix is also called a tree metric (Semple and Steel 2003). Thus, testing for admixture can be thought of as testing treeness.

For a dissimilarity matrix to be consistent with a tree, there are two central properties it needs to satisfy: First, the length of all branches has to be positive. This is strictly not necessary for phylogenetic trees, and some algorithms may return negative branch lengths (e.g. Saitou and Nei 1987); however, since in our case branches have an interpretation of genetic drift, negative genetic drift is biologically nonsensical, and therefore negative branches should be interpreted as a violation of the modeling assumptions and hence of treeness.

The second property of a tree metric important in the present context is a bit more involved: A dissimilarity matrix (written in terms of F₂) is consistent with a tree if for any four populations P_i, P_j, P_k, and P_l,

$$F_2\left(P_i,P_j\right)+F_2\left(P_k,P_l\right)\le \max \left(F_2\left(P_i,P_k\right)+F_2\left(P_j,P_l\right),F_2\left(P_i,P_l\right)+F_2\left(P_j,P_k\right)\right);$$ (19)

that is, if the sums of pairs of distances are compared, two of these sums will be the same, and no smaller than the third one. This theorem, due to Buneman (1971, 1974), is called the four-point condition or sometimes, more modestly, the “fundamental theorem of phylogenetics.” A proof can be found in Semple and Steel (2003, Chap. 7).

Informally, this statement can be understood by noting that on a tree, two of the pairs of distances will include the internal branch, whereas the third one will not and therefore be shorter. Thus, the four-point condition can be colloquially rephrased as “any four-taxa tree has at most one internal branch.”

Why are these properties useful? It turns out that the admixture tests based on F-statistics can be interpreted as tests of these properties: The F₃ test can be interpreted as a test for the positivity of a branch and the F₄ as a test of the four-point condition. Thus, the working of the two test statistics can be interpreted in terms of fundamental properties of phylogenetic trees, with the immediate consequence that they may be applied as treeness tests for arbitrary dissimilarity matrices.

An early test of treeness, based on a likelihood ratio, was proposed by Cavalli-Sforza and Piazza (1975): They compared the likelihood of the observed F₂ matrix to that induced by the best-fitting tree (assuming Brownian motion), rejecting the null hypothesis if the tree likelihood is much lower than that of the empirical matrix. In practice, however, finding the best-fitting tree is a challenging problem, especially for large trees (Felsenstein 2004), and so the likelihood test proved to be difficult to apply. From that perspective, the F₃ and F₄ tests provide a convenient alternative: Since treeness implies that all subsets of taxa are also trees, the ingenious idea of Reich et al. (2009) was that rejection of treeness for subtrees of sizes 3 (for F₃) and 4 (for F₄) is sufficient to reject treeness for the entire tree. Furthermore, tests on these subsets also pinpoint the populations involved in the non-tree-like history.

F₃: Three population statistic

In the previous section, I showed how F₂ can be interpreted as a branch length, as an overlap of paths, or in terms of gene trees (Figure 2). Furthermore, I gave expressions in terms of coalescence times, allele frequency variances, and internal branch lengths of gene trees. In this section, I give analogous results for F₃.

Reich et al. (2009) defined F₃ as

$$F_3\left(P_X;P_1,P_2\right)=F_3\left(p_X;p_1,p_2\right)=\mathrm{E}\left(p_X-p_1\right)\left(p_X-p_2\right)$$ (20a)

with the goal to test whether P_X is admixed. Recalling the path interpretation detailed in Patterson et al. (2012), F₃ can be interpreted as the shared portion of the paths from P_X to P₁ with the path from P_X to P₁. In a population phylogeny (Figure 2E) this corresponds to the branch between P_X and the internal node. Equivalently, F₃ can also be written in terms of F₂ (Reich et al. 2009):

$$F_3\left(P_X;P_1,P_2\right)=\frac{1}{2}\left(F_2\left(P_X,P_1\right)+F_2\left(P_X,P_2\right)-F_2\left(P_1,P_2\right)\right).$$ (20b)

If F₂ in Equation 20b is generalized to an arbitrary tree metric, Equation 20b is known as the Gromov product in phylogenetics (Semple and Steel 2003). The Gromov product is a commonly used operation in classical phylogenetic algorithms to calculate the length of the portion of a branch shared between P₁ and P₂ (Fitch et al. 1967; Felsenstein 1973; Saitou and Nei 1987), consistent with the notion that F₃ is the length of an external branch in a population phylogeny.

In an admixture graph, there is no longer a single external branch; instead all possible trees have to be considered, and F₃ is the (weighted) average of paths through the admixture graph (Figure 2F).

Combining Equations 16 and 20b gives an expression of F₃ in terms of expected coalescence times:

$$F_3\left(P_X;P_1,P_2\right)=\frac{\theta }{2}\left(\mathrm{E}{T}_{1X}+\mathrm{E}{T}_{2X}-\mathrm{E}{T}_{12}-\mathrm{E}{T}_{XX}\right).$$ (20c)

Similarly, an expression in terms of variances is obtained by combining Equation 2 with Equation 20b,

$$F_3\left(P_X;P_1,P_2\right)=\mathrm{Var}\left({\mathit{p}}_{\mathit{X}}\right)+\mathrm{COV}\left(p_1,p_2\right)-\mathrm{COV}\left(p_1,p_X\right)-\mathrm{COV}\left(p_2,p_X\right),$$ (20d)

which was also noted by Pickrell and Pritchard (2012).

Outgroup F₃ statistics:

A simple application of the interpretation of F₃ as a shared branch length are the “outgroup” F₃ statistics proposed by Raghavan et al. (2014). For an unknown population P_U, they wanted to find the most closely related population from a panel of k extant populations $\left\{P_i,i=1,2,\mathrm{\dots ,}k\right\}.$ They did this by calculating F₃ (P_O; P_U, P_i), where P_O is an outgroup population that was assumed widely diverged from P_U and all populations in the panel. This measures the shared drift (or shared branch) of P_U with the populations from the panel, and high F₃ values imply close relatedness.

However, using Equation 20c, the outgroup F₃ statistic can be written as

$$F_3\left(P_{\mathrm{O}};P_{\mathrm{U}},P_i\right)\mathrm{\propto }\mathrm{E}{T}_{\mathrm{UO}}+\mathrm{E}{T}_{i\mathrm{O}}-\mathrm{E}{T}_{\mathrm{U}i}-\mathrm{E}{T}_{\mathrm{OO}}.$$ (21)

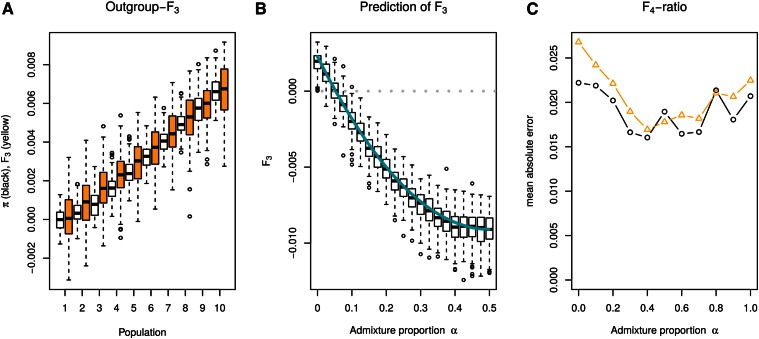
Of these four terms, $\mathrm{E}{T}_{\mathrm{UO}}$ and $\mathrm{E}{T}_{\mathrm{OO}}$ do not depend on P_i. Furthermore, if P_O is truly an outgroup, then all $\mathrm{E}{T}_{i\mathrm{O}}$ should be the same, as pairs of individuals from the panel population and the outgroup can coalesce only once they are in the joint ancestral population. Therefore, only the term $\mathrm{E}{T}_{\mathrm{U}i}$ is expected to vary between different panel populations, suggesting that using the number of pairwise differences, ${\pi }_{\mathrm{U}i},$ is largely equivalent to using F₃ (P_O; P_U, P_i). I confirm this in Figure 5A by calculating outgroup F₃ and ${\pi }_{i\mathrm{U}}$ for a set of increasingly divergent populations, with each population having its own size, sample size, and sequencing error probability. Linear regression confirms the visual picture that ${\pi }_{i\mathrm{U}}$ has a higher correlation with divergence time (R² = 0.90) than F₃ (R² = 0.73). Hence, the number of pairwise differences may be a better metric for population divergence than F₃.

Figure 5.

Simulation results. (A) Outgroup F₃ statistics (yellow) and ${\pi }_{iU}$(white) for a panel of populations with linearly increasing divergence time. Both statistics are scaled to have the same range, with the first divergence between the most closely related populations set to zero. F₃ is inverted, so that it increases with distance. (B) Simulated (boxplots) and predicted (blue) F₃ statistics under a simple admixture model. (C) Comparison of F₄ ratio (yellow triangles, Equation 29) and ratio of differences (black circles, Equation 31).

F₃ admixture test:

However, F₃ is motivated and primarily used as an admixture test (Reich et al. 2009). In this context, the null hypothesis is that F₃ is nonnegative; i.e., the null hypothesis is that the data are generated from a phylogenetic tree that has positive edge lengths. If this is not the case, the null hypothesis is rejected in favor of the more complex admixture graph. From Figure 2F it may be seen that drift on the path on the internal branches (red) contributes negatively to F₃. If these branches are long enough compared to the branch after the admixture event (blue), then F₃ will be negative. For the simplest scenario where P_X is admixed between P₁ and P₂, Reich et al. (2009) provided a condition when this is the case (equation 20 in supplement 2 of Reich et al. 2009). However, since this condition involves F-statistics with internal, unobserved populations, it cannot be used in practical applications. A more useful condition is obtained using Equation 20c.

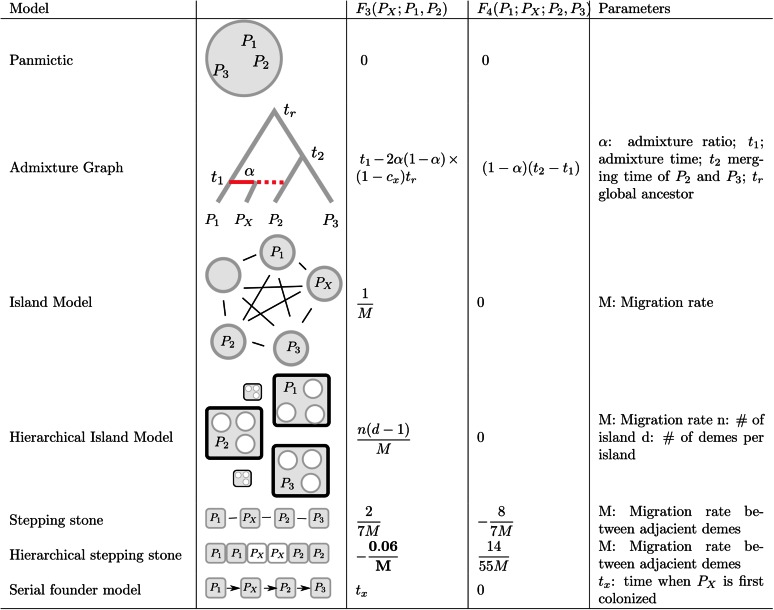
In the simplest admixture model, an ancestral population splits into P₁ and P₂ at time t_r. At time t₁, the populations mix to form P_X, such that with probability α, individuals in P_X descend from individuals from P₁, and with probability (1 − α), they descend from P₂ (see Figure 7 for an illustration). In this case, F₃ (P_X; P₁, P₂) is negative if

$$\frac{1}{\left(1-c_x\right)}\frac{t_1}{t_r}\mathrm{<}2\alpha \left(\mathrm{1-}\alpha \right),$$ (22)

where c_x is the probability two individuals sampled in P_X have a common ancestor before t₁. For a randomly mating population with changing size N(t),

$$c_x=1-\exp \left(-{\displaystyle {\int }_0^{t_1}\frac{1}{N\left(s\right)}ds}\right).$$

Thus, the power of F₃ to detect admixture is large (1) if the admixture proportion α is close to 50%; (2) if the ratio between the times of the original split and the time of secondary contact is large; and (3) if the probability of coalescence before the admixture event in P_X is small, i.e., the size of P_X is large.

Figure 7.

Expectations for F₃ and F₄ under select models. The constant factor $\mathit{\theta }/2$ is omitted.

A more general condition for negativity of F₃ is obtained by considering the internal branches of the possible gene tree topologies, analogously to that given for F₂ in the Gene tree branch lengths section. Since Equation 20c includes $\mathrm{E}{T}_{XX},$ only two individuals from P_X are needed and one each from P₁ and P₂ to study the joint distribution of all terms in (20c). The minimal case therefore contains again just four samples (Figure S2).

Furthermore, P₁ and P₂ are exchangeable, and thus there are again just two distinct gene genealogies, a concordant one ${\mathcal{T}}_{\mathrm{c}}^{\left(\mathrm{3}\right)}$ where the two lineages from P_X are most closely related and a discordant genealogy ${\mathcal{T}}_{\mathrm{d}}^{\left(\mathrm{3}\right)}$ where the lineages from P_X merge first with the other two lineages. A similar argument to that for F₂ shows (presented in Figure S2) that F₃ can be written as a function of just the internal branches in the topologies,

$$F_3\left(P_X;P_1,P_2\right)=\theta \left(2{\mathrm{ℬ}}_{\mathrm{c}}-{\mathrm{ℬ}}_{\mathrm{d}}\right),$$ (23)

where ${\mathrm{ℬ}}_{\mathrm{c}}$ and ${\mathrm{ℬ}}_{\mathrm{d}}$ are the lengths of the internal branches in ${\mathcal{T}}_{\mathrm{c}}^{\left(\mathrm{3}\right)}$ and ${\mathcal{T}}_{\mathrm{d}}^{\left(\mathrm{3}\right)},$ respectively, and similar to F₂, concordant branches have twice the weight of discordant ones. Again, the case of all individuals coming from a single populations serves as a sanity check: In this case ${\mathcal{T}}_{\mathrm{d}}$ is twice as likely as ${\mathcal{T}}_{\mathrm{c}},$ and all branches are expected to have the same length, resulting in F₃ being zero. However, for F₃ to be negative, note that ${\mathrm{ℬ}}_{\mathrm{d}}$ needs to be more than two times longer than ${\mathrm{ℬ}}_{\mathrm{c}}.$ Since mutations are proportional to ${\mathrm{ℬ}}_{\mathrm{d}}$ and ${\mathrm{ℬ}}_{\mathrm{c}},$ F₃ can be interpreted as a test whether mutations that agree with the population tree are more than twice as common as mutations that disagree with it.

I performed a small simulation study to test the accuracy of Equation 22. Parameters were chosen such that F₃ has a negative expectation for α > 0.05, and I find that the predicted F₃ fitted very well with the simulations (Figure 5B).

F₄: Four population study

The second admixture statistic, F₄, is defined as

$$F_4\left(P_1,P_2;P_3,P_4\right)=F_4\left(p_1,p_2;p_3,p_4\right)=\mathrm{E}\left[\left(p_1-p_2\right)\left(p_3-p_4\right)\right]$$ (24a)

(Reich et al. 2009). Similarly to F₃, F₄ can be written as a linear combination of F₂,

$$F_4\left(P_1,P_2;P_3,P_4\right)=\frac{1}{2}\left(F_2\left(P_1,P_4\right)+F_2\left(P_2,P_3\right)-F_2\left(P_1,P_3\right)-F_2\left(P_2,P_4\right)\right),$$ (24b)

which leads to

$$F_4\left(P_1,P_2;P_3,P_4\right)=\frac{\theta }{2}\left(\mathrm{E}{T}_{14}+\mathrm{E}{T}_{23}-\mathrm{E}{T}_{13}-BE{T}_{24}\right).$$ (24c)

As four populations are involved, there are 4! = 24 possible ways of arranging the populations in Equation 24a. However, there are four possible permutations of arguments that will lead to identical values, leaving only six unique F₄ values for any four populations. Furthermore, these six values come in pairs that have the same absolute value and a different sign [i.e., $F_4\left(P_1,P_2;P_3,P_4\right)=-F_4\left(P_1,P_2;P_4,P_3\right)$], leaving only three unique absolute values, which correspond to the three possible tree topologies. Of these three, one F₄ can be written as the sum of the other two, leaving just two independent possibilities:

$$F_4\left(P_1,P_2;P_3,P_4\right)+F_4\left(P_1,P_3;P_2,P_4\right)=F_4\left(P_1,P_4;P_2,P_3\right).$$

As for F₃, Equation 24b can be generalized by replacing F₂ with an arbitrary tree metric. In this case, Equation 24b is known as a tree split (Buneman 1971), as it measures the length of the overlap of the branch lengths between the two pairs. As there are two independent F₄ indexes for a fixed tree, there are two different interpretations for the F₄ indexes. Consider the tree from Figure 1A: $F_4\left(P_1,P_2;P_3,P_4\right)$can be interpreted as the overlap between the paths from P₁ to P₂ and from P₃ to P₄. However, these paths do not overlap in Figure 1A, and therefore F₄ = 0. This is how F₄ is used as a test statistic. On the other hand, $F_4\left(P_1,P_3;P_2,P_4\right)$ measures the overlap between the paths from P₁ to P₃ and from P₂ to P₄, which is the internal branch in Figure 1A, and will be positive.

It is cumbersome that the interpretation of F₄ depends on the ordering of its arguments. To make the intention clear, instead of switching the arguments around for the two interpretations, I introduce the superscripts (T) (for test) and (B) (for branch length):

$$F_4^{\left(\mathrm{T}\right)}\left(P_1,P_2;P_3,P_4\right)=F_4\left(P_1,P_2;P_3,P_4\right)$$ (25a)

$$F_4^{\left(\mathrm{B}\right)}\left(P_1,P_2;P_3,P_4\right)=F_4\left(P_1,P_3;P_2,P_4\right).$$ (25b)

Four-point condition and F₄:

Tree splits, and hence F₄, are closely related to the four-point condition (Buneman 1971, 1974), which, informally, states that a (sub)tree with four populations will have at most one internal branch. Thus, if data are consistent with a tree, $F_4^{\left(\mathrm{B}\right)}$will be the length of that branch, and $F_4^{\left(\mathrm{T}\right)}$will be zero. Figure 2, I–L, corresponds to the internal branch and Figure 2, M–P, to the “zero” branch.

Thus, in the context of testing for admixture, testing that F₄ is zero is equivalent to checking whether there is in fact only a single internal branch. If that is not the case, the population phylogeny is rejected. This statement can be generalized to arbitrary tree metrics: The four-point condition (Buneman 1971) can be written as

$$F_2\left(P_1,P_2\right)+F_2\left(P_3,P_4\right)\le \min \left[F_2\left(P_1,P_3\right)+F_2\left(P_2,P_4\right),F_2\left(P_1,P_4\right)+F_2\left(P_2,P_3\right)\right]$$ (26)

for any permutations of the samples. This implies that two of the sums need to be the same and larger than the third one. The claim is that if the four-point condition holds, at least one of the F₄ values will be zero, and the others will have the same absolute value.

Without loss of generality, assume that

$$\begin{array}{l}{F}_2\left(P_1,P_2\right)+F_2\left(P_3,P_4\right)\le F_2\left(P_1,P_3\right)+F_2\left(P_2,P_4\right)\\ F_2\left(P_1,P_3\right)+F_2\left(P_2,P_4\right)=F_2\left(P_1,P_4\right)+F_2\left(P_2,P_3\right).\end{array}$$

Simply plugging this into the three possible F₄ equations yields

$$\begin{array}{l}{F}_4\left(P_1,P_2;P_3,P_4\right)=0\\ F_4\left(P_1,P_3;P_2,P_4\right)=k\\ F_4\left(P_1,P_4;P_2,P_3\right)=-k,\end{array}$$

where $k=F_2\left(P_1,P_3\right)+F_2\left(P_2,P_4\right)-F_2\left(P_1,P_2\right)+F_2\left(P_3,P_4\right).$

It is worth noting that the converse is false. If

$$\begin{array}{l}{F}_2\left(P_1,P_2\right)+F_2\left(P_3,P_4\right)\mathrm{>}{F}_2\left(P_1,P_3\right)+F_2\left(P_2,P_4\right)\\ F_2\left(P_1,P_3\right)+F_2\left(P_2,P_4\right)=F_2\left(P_1,P_4\right)+F_2\left(P_2,P_3\right),\end{array}$$

the four-point condition is violated, but $F_4\left(P_1,P_2;P_3,P_4\right)$ is still zero, and the other two F₄ values have the same magnitude.

Gene trees:

Evaluating F₄ in terms of gene trees and their internal branches, there are three different gene tree topologies that have to be considered, whose interpretation depends on whether the branch length or test-statistic interpretation is considered.

For the branch length [$F_4^{\left(\mathrm{B}\right)}$], the gene tree corresponding to the population tree has a positive contribution to F₄, and the other two possible trees have a zero and negative contribution, respectively (Figure S3). Since the gene tree corresponding to the population tree is expected to be most frequent, F₄ will be positive and can be written as

$$F_4^{\left(B\right)}=\theta \left({\mathrm{ℬ}}_c-{\mathrm{ℬ}}_d\right).$$ (27)

This equation is slightly different from those for F₂ and F₃, where the coefficient for the discordant genealogy was half that for the concordant genealogy. Note, however, that F₄ includes only one of the two discordant genealogies. Under a tree, both discordant genealogies are equally likely (Durand et al. 2011), and thus the expectation of F₄ will be the same.

In contrast, for the admixture test statistic [$F_4^{\left(\mathrm{T}\right)}$], the contribution of the concordant genealogy will be zero, and the discordant genealogies will contribute with coefficients −1 and +1, respectively and thus the expectation of F₄ as a test statistic

$$F_4^{\left(T\right)}=\theta \left(B_c-{B^{\prime }}_d\right)$$ (28)

is zero under the null hypothesis. Furthermore, the statistic is closely related to the ABBA-BABA or D-statistic also used to test for admixture (Green et al. 2010; Durand et al. 2011), which includes a normalization term and conditions on alleles being derived. In our notation the expectation of D is

$$E\left[D\right]=\frac{{B^{\prime }}_d-B_d}{{B^{\prime }}_d+B_d}$$

and thus, $F_4^{\left(\mathrm{T}\right)}$ and D are different test statistics for the same null hypothesis.

Rank test:

Two major applications of F₄ use its interpretation as a branch length. First, the rank of a matrix of all F₄ statistics is used to obtain a lower bound on the number of admixture events required to explain data (Reich et al. 2012). The principal idea of this approach is that the number of internal branches in a genealogy is bounded to be at most n − 3 in an unrooted tree. Since each F₄ is a sum of the length of tree branches, all F₄ indexes should be sums of n − 3 branches or n − 3 independent components. This implies that the rank of the matrix (see, e.g., section 4 in McCullagh 2009) is at most n − 3, if the data are consistent with a tree. However, admixture events may increase the rank of the matrix, as they add additional internal branches (Reich et al. 2012). Therefore, if the rank of the matrix is r, the number of admixture events is at least r − n + 3.

One issue is that the full F₄ matrix has size $\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)\mathrm{\times }\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)$ and may thus become rather large. Furthermore, in many cases only admixture events in a certain part of the phylogeny are of interest. To estimate the minimum number of admixture events on a particular branch of the phylogeny, Reich et al. (2012) proposed to find two sets of test populations S₁ and S₂ and two reference populations for each set R₁ and R₂ that are presumed unadmixed (see Figure 6A). Assuming a phylogeny, all $F_4^{\left(\mathrm{B}\right)}$ (S₁, R₁; S₂, R₂) will measure the length of the same branch, and all $F_4^{\left(\mathrm{T}\right)}$ (S₁, R₁; S₂, R₂) should be zero. Since each admixture event introduces at most one additional branch, the rank of the resulting matrix will increase by at most one, and the rank of either the matrix of all $F_4^{\left(\mathrm{T}\right)}$ or the matrix of all $F_4^{\left(\mathrm{B}\right)}$ may reveal the number of branches of that form.

Figure 6.

Applications of F₄. (A) Visualization of rank test to estimate the number of admixture events. F₄ (S₁, R₁, S₂, R₂) measures a branch absent from the phylogeny and should be zero for all populations from S₁ and S₂. (B) Model underlying admixture ratio estimate (Green et al. 2010). P_X splits, and the mean coalescence time of P_X with P_I gives the admixture proportion. (C) If the model is violated, α measures where on the internal branch in the underlying genealogy P_X (on average) merges.

Admixture proportion:

The second application is by comparing branches between closely related populations to obtain an estimate of mixture proportion or how much two focal populations correspond to an admixed population (Green et al. 2010):

$$\alpha =\frac{F_4\left(P_{\mathrm{O}},P_{\mathrm{I}};P_X,P_1\right)}{F_4\left(P_{\mathrm{O}},P_{\mathrm{I}};P_2,P_1\right)}.$$ (29)

Here, P_X is the population whose admixture proportion is estimated; P₁ and P₂ are the potential contributors, where I assume that they contribute with proportions α and 1 − α, respectively; and P_O, P_I are reference populations with no direct contribution to P_X (see Figure 6B). P_I has to be more closely related to one of P₁ or P₂ than the other, and P_O is an outgroup.

The canonical way (Patterson et al. 2012) to interpret this ratio is as follows: The denominator is the branch length from the common ancestor population from P_I and P₁ to the common ancestor of P_I with P₂ (Figure 6C, yellow line). The numerator has a similar interpretation as an internal branch (Figure 6C, red dotted line). In an admixture scenario (Figure 6B), this is not unique and is replaced by a linear combination of lineages merging at the common ancestor of P_I and P₁ (with probability α) and lineages merging at the common ancestor of P_I with P₂ (with probability 1 − α).

Thus, a more general interpretation is that α measures how much closer the common ancestor of P_X and P_I is to the common ancestor of P_I and P₁ and the common ancestor of P_I and P₂, indicated by the red dotted line in Figure 6C. This quantity is defined also when the assumptions underlying the admixture test are violated and, if the assumptions are not carefully checked, might lead to misinterpretations of the data. In particular, α is well defined in cases where no admixture occurred or in cases where either one of P₁ and P₂ did not experience any admixture.

Furthermore, it is evident from Figure 6 that if all populations are sampled at the same time, $\mathrm{E}{T}_{\mathrm{O}X}=\mathrm{E}{T}_{\mathrm{O}1}=\mathrm{E}{T}_{\mathrm{O}2}=\mathrm{E}{T}_{\mathrm{OI}},$ and therefore

$$\mathit{\alpha }=\frac{\mathrm{E}{T}_{\mathrm{I}1}-\mathrm{E}{T}_{\mathrm{I}X}}{\mathrm{E}{T}_{\mathrm{I}1}-\mathrm{E}{T}_{\mathrm{I}2}}.$$ (30)

Thus,

$$\mathit{\alpha }=\frac{{\pi }_{\mathrm{I}1}-{\pi }_{\mathrm{I}X}}{{\pi }_{\mathrm{I}1}-{\pi }_{\mathrm{I}2}}$$ (31)

is another estimator for α that can be used even if no outgroup is available. I compare Equations 29 and 31 for varying admixture proportions in Figure 5C, using the mean absolute error in the admixture proportion. Both estimators perform very well, but (31) performs slightly better in cases where the admixture proportion is low. However, in most cases this minor improvement possibly does not negate the drawback that Equation 31 is applicable only when populations are sampled at the same time.

An area of recent development is how these estimates can be extended to more populations. A simple approach is to assume a fixed series of admixture events, in which case admixture proportions for each event can be extracted from a series of F₄ ratios (Lazaridis et al. 2014, SI 13). A more sophisticated approach estimates mixture weights using the rank of the F₄ matrix, as discussed in the Rank test section (Haak et al. 2015, SI 10). Then, it is possible to estimate mixture proportions, using a model similar to that introduced in the program structure (Pritchard et al. 2000), by obtaining a low-rank approximation for the F₄ matrix.

Population structure models

Here, I use Equation 16 together with Equations 20b and 24b to derive expectations for F₃ and F₄ under some simple models.

Panmixia:

In a randomly mating population (with arbitrary population size changes), P₁ and P₂ are taken from the same pool of individuals and therefore $\mathrm{E}{T}_{12}=\mathrm{E}{T}_{11}=\mathrm{E}{T}_{22}\mathrm{,E}{F}_2=\mathrm{E}{F}_3=\mathrm{E}{F}_4=0.$

Island models:

A (finite) island model has D subpopulations of size 1 each. Migration occurs at rate M between subpopulations. It can be shown (Strobeck 1987) that $\mathrm{E}{T}_{11}=\mathrm{E}{T}_{22}=D\text{(...), and}\mathrm{E}{T}_{12}$ satisfies

$$\mathrm{E}{T}_{\text{12}}=\frac{1}{\left(D-1\right)M}+\frac{D-2}{D-1}\mathrm{E}{T}_{\text{12}}+\frac{1}{D-1}\mathrm{E}{T}_{\text{11}}$$ (32)

with solution $\mathrm{E}{T}_{\text{12}}=\text{1}+M^{-\text{1}}.$ This results in the equation in Figure 7. The derivation of coalescence times for the hierarchical island models is marginally more complicated, but similar. It is given in Slatkin and Voelm (1991).

Admixture models:

These are the models for which the F-statistics were originally developed. Many details, applications, and the origin of the path representation are found in Patterson et al. (2012). For simplicity, I look at the simplest possible tree with four populations, where P_X is admixed from P₁ and P₂ with contributions α and $\beta =\left(1-\alpha \right),$ respectively. I assume that all populations have the same size and that this size is 1. Then,

$$\begin{array}{c}{F}_3\left(P_X;P_1,P_2\right)\mathrm{\propto }\mathrm{E}{T}_{1X}+\mathrm{E}{T}_{2X}-\mathrm{E}{T}_{12}-\mathrm{E}{T}_{XX}\\ =\left(\mathit{\alpha }{t}_1+\mathit{\beta }{t}_r+1\right)+\left(\mathit{\alpha }{t}_r+\mathit{\beta }{t}_1+1\right)-t_r-1\\ -\hspace{0.17em}{\mathit{\alpha }}^{2}1-{\left(1-\mathit{\alpha }\right)}^{2}1-2\alpha \left(1-\mathit{\alpha }\right)\left[\left(1-c_x\right)t_r+1\right]\\ =t_1-2\alpha \left(1-\mathit{\alpha }\right)\left(1-c_x\right)t_r.\end{array}$$ (33)

Here, c_x is the probability that the two lineages from P_X coalesce before the admixture event.

Thus, F₃ is negative if

$$\frac{t_1}{\left(1-c_x\right)t_r}\mathrm{<}2\alpha \left(1-\mathit{\alpha }\right),$$ (34)

which is more likely if α is large, the admixture is recent, and the overall coalescent is far in the past.

For F₄, omitting the within-population coalescence time of 1,

$$\begin{array}{c}{F}_4\left(P_1{P}_X;P_2,P_3\right)=\mathrm{E}{T}_{12}+\mathrm{E}{T}_{3X}-\mathrm{E}{T}_{13}-\mathrm{E}{T}_{2X}\\ =t_r+\mathit{\alpha }{t}_r+\mathit{\beta }{t}_{23}-t_r-\mathit{\alpha }{t}_r\mathit{-\beta }{t}_{2X}\\ =\mathit{\beta }\left(t_2-t_1\right).\end{array}$$

Stepping-stone models:

For the stepping-stone models, I have to solve the recursions of the Markov chains describing the location of all lineages in a sample of size 2. For the standard stepping-stone model, I assumed there were four demes, all of which exchange migrants at rate M. This results in a Markov chain with the following five states: (i) lineages in same deme, (ii) lineages in demes 1 and 2, (iii) lineages in demes 1 and 3, (iv) lineages in demes 1 and 4, and (v) lineages in demes 2 and 3. Note that the symmetry of this system allows collapsing some states. The transition matrix for this system is

$$\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 2M& 1-3M& M& 0& 0\\ 0& M& 1-3M& M& M\\ 0& 0& 2M& 1-2M& 0\\ 2M& 0& 2M& 0& 1-4M\end{array}\right).$$ (35)

Once lineages are in the same deme, the system terminates as the time to coalescence time is independent of the deme in isotropic migration models (Strobeck 1987) and cancels from the F-statistics.

Therefore, the vector v of the expected time until two lineages are in the same deme is found using standard Markov chain theory by solving v = (I − T)⁻¹)1, where T is the transition matrix involving only the transitive states in the Markov chain (all but the first state), and 1 is a vector of 1’s.

Finding the expected coalescence time involves solving a system of five equations. The terms involved in calculating the F-statistics (Table 1) are the entries in v corresponding to these states.

The hierarchical case is similar, except there are six demes and 10 equations. Representing states as lineages being in demes (same), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (3, 4),

$$\left(\begin{array}{cccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 2M& 1-3M& M& 0& 0& 0& 0& 0& 0& 0\\ 0& M& 1-3M& M& 0& 0& M& 0& 0& 0\\ 0& 0& M& 1-3M& M& 0& 0& M& 0& 0\\ 0& 0& 0& M& 1-3M& M& 0& 0& M& 0\\ 0& 0& 0& 0& 2M& 1-2M& 0& 0& 0& 0\\ 2M& 0& M& 0& 0& 0& 1-4M& M& 0& 0\\ 0& 0& 0& M& 0& 0& M& 1-4M& M& M\\ 0& 0& 0& 0& 2M& 0& 0& 2M& 1-4M& 0\\ 2M& 0& 0& 0& 0& 0& 0& 2M& 0& 1-4M\end{array}\right).$$

As in the nonhierarchical case, solving this system yields all pairwise coalescence times. Then, all I have to do is average the coalescence times over all possibilities; e.g.,

$$\mathrm{E}{T}_{1X}=\frac{v_2+v_3+v_6+v_7}{4}.$$ (36)

For F₄, I assume that demes 1 and 2 are in P₁, demes 3 and 4 are in P_X, and demes 5 and 6 correspond to P₂ and P₃, respectively.

Range expansion model:

I use a serial founder model with no migration (Peter and Slatkin 2015), where I assume that the expansion is recent enough such that the effect of migration after the expansion finished can be ignored. Under that model, I assume that samples P₁ and P₂ are taken from demes D₁ and D₂, with D₁ closer to the origin of the expansion and populations with high identification numbers even farther away from the expansion origin. Then $\mathrm{E}\hspace{0.17em}T12=t1+\mathrm{E}T11,$ where $\mathrm{E}t1$ is the time required for a lineage sampled farther away in the expansion to end up in D₁. (Note that t₁ depends only on the deme that is closer to the origin.) Thus, for three demes,

$$\begin{array}{c}{F}_3\left(P_2;P_1,P_3\right)\mathrm{\propto }\mathrm{E}{T}_{12}-\mathrm{E}{T}_{13}+\mathrm{E}{T}_{23}-\mathrm{E}{T}_{22}\\ \mathrm{\propto }\mathrm{E}{T}_{11}+t_1-\mathrm{E}{T}_{11}-t_1+\mathrm{E}{T}_{22}+t_2-\mathrm{E}{T}_{22}\\ \mathrm{\propto }{t}_2\end{array}$$

and

$$\begin{array}{c}{F}_4^{\left(\mathrm{T}\right)}\left(P_1,P_2;P_3,P_4\right)\mathrm{\propto }\mathrm{E}{T}_{13}-\mathrm{E}{T}_{14}+\mathrm{E}{T}_{24}-\mathrm{E}{T}_{23}\\ \mathrm{\propto }\mathrm{E}{T}_{11}+t_1-\mathrm{E}{T}_{11}-t_1+\mathrm{E}{T}_{22}+t_2-\mathrm{E}{T}_{22}-t_2\\ =0.\end{array}$$

More interesting is

$$\begin{array}{c}{F}_4^{\left(\mathrm{B}\right)}\left(P_1,P_2;P_3,P_4\right)\mathrm{\propto }\mathrm{E}{T}_{12}-\mathrm{E}{T}_{14}+\mathrm{E}{T}_{34}-\mathrm{E}{T}_{23}\\ \mathrm{\propto }\mathrm{E}{T}_{11}+t_1-\mathrm{E}{T}_{11}-t_1+\mathrm{E}{T}_{33}+t_3-\mathrm{E}{T}_{22}-t_2\\ \mathrm{\propto }\mathrm{E}{T}_{33}+t_3-\mathrm{E}{T}_{22}-t_2.\end{array}$$

A hierarchical stepping-stone model, where demes are combined into populations, is the only case I studied (besides the admixture graph) where F₃ can be negative. This effect indicates that admixture and population structure models may be the two sides of the same coin: Admixture is a (temporary) reduction in gene flow between individuals from the same population. Finally, for a simple serial founder model without migration, I find that F₃ measures the time between subsequent founder events.

Simulations

Simulations were performed using ms (Hudson 2002). Specific commands used are

ms 466 100 -t 100 -r 10 100000 -I 12 22 6 61 49 57 33 43 34 40 84 13 24 -en 0 2 7.2 -en 0 3 .2 -en 0 4 .4 -en 0 5 .2 -en 0 6 4.4 -en 0 7 3.2 -en 0 8 4.8 -en 0 9 0.2 -en 0 10 3.2 -en 0 11 0.2 -en 0 12 0.7 -ej 0.01 2 1 -ej 0.02 3 1 -ej 0.04 4 1 -ej 0.06 5 1 -ej 0.08 6 1 -ej 0.10 7 1 -ej 0.12 8 1 -ej 0.14 9 1 -ej 0.16 10 1 -ej 0.18 11 1 -ej 0.3 12 1

for the outgroup F₃ statistic (Figure 5A). Sample sizes and population sizes were picked randomly, but kept the same over all 100 replicates. Additionally, I randomly assigned each population an error rate uniformly between 0 and 0.05. Errors were introduced by adding additional singletons and flipping alleles at that rate.

For Figure 5B, the command was

ms 301 100 -t 10 -I 4 100 100 100 1 -es 0.001 2 $ALPHA -ej 0.03 2 1 -ej 0.03 5 3 -ej 0.3 3 1 -ej 0.31 4 1

with the admixture proportion $ALPHA set to increments of 0.025 from 0 to 0.5, with 200 data sets generated per $ALPHA.

Finally, data for Figure 5C were simulated using

ms 501 100 -t 50 -r 50 10000 -I 6 100 100 100 100 100 1 -es 0.001 3 $ALPHA -ej 0.03 3 2 -ej 0.03 7 4 -ej 0.1 2 1 -ej 0.2 4 1 -ej 0.3 5 1 -ej 0.31 6 1

Here, the admixture proportion $ALPHA was varied in increments of 0.1 from 0 to 1, again with 200 data sets generated per $ALPHA.

F₃ and F₄ statistics were calculated using the implementation from Pickrell and Pritchard (2012).

Estimation and testing

In this article, I focused almost exclusively on the theoretical properties of the F-statistics, glancing over the statistical problems of how they are estimated. Many procedures are implemented in the software package ADMIXTOOLS and described in Patterson et al. (2012). Alternatively, the software package treemix (Pickrell and Pritchard 2012) contains lightwight alternatives for calculating F₃ and F₄ statistics. Both use a block-jackknife approach to estimate standard errors, taking linkage between markers into account.

Discussion

There are three main ways to interpret F-statistics: In the simplest case, they represent branches in a population phylogeny. In the case of an admixture graph, the idea of shared drift in terms of paths is most convenient. Finally, the expressions in terms of coalescence times and the lengths of the internal branches of gene genealogies are useful for more complex scenarios. This last interpretation makes the connection to the ABBA-BABA statistic explicit and allows the investigation of the behavior of the F-statistics under arbitrary demographic models.

If drift indexes exist for two, three, and four populations, should there be corresponding quantities for five or more populations (e.g., Pease and Hahn 2015)? Two of the interpretations speak against this possibility: First, a population phylogeny can be fully characterized by internal and external branches, and it is not clear how a five-population statistic could be written as a meaningful branch length. Second, all F-statistics can be written in terms of four-individual trees, but this is not possible for five samples. This seems to suggest that there may not exist a five-population statistic as general as the three F-statistics I discussed here, but they will still be useful for questions pertaining to a specific demographic model.

A well-known drawback of F₃ is that it may have a positive expectation under some admixture scenarios (Patterson et al. 2012). Here, I showed that F₃ is positive if and only if the branch supporting the population tree is longer than the two branches discordant with the population tree. Note that this is (possibly) distinct from the probabilities of tree topologies, although the average branch length of the internal branch in a topology and the probability of that topology are frequently strongly correlated. Thus, negative F₃ values indicate that individuals from the admixed population are likely to coalesce with individuals from the two other populations, before they coalesce with other individuals from their own population!

For practical purposes, it is useful to know how the admixture tests perform under demographic models different from population phylogenies and admixture graphs and in which cases the assumptions made for the tests are problematic. In other words, under which demographic models is population structure distinguishable from a tree? Equation 16 enables the derivation of expectations for F₃ and F₄ under a wide variety of models of population structure (Figure 7). The simplest case is that of a single panmictic population. In that case, all F-statistics have an expectation of zero, consistent with the assumption that no structure and therefore no population phylogeny exists. Under island models, F₄ is also zero, and F₃ is inversely proportional to the migration rate. Results are similar under a hierarchical island model, except that the number of demes has a small effect. This corresponds to a population phylogeny that is star-like and has no internal branches, which is explained by the strong symmetry of the island model. Thus, looking at different F₃ and F₄ statistics may be a simple heuristic to see whether data are broadly consistent with an island model; if F₃ values vary a lot between populations, or if F₄ is substantially different from zero, an island model might be a poor choice. When looking at a finite stepping-stone model, F₃ and F₄ are both nonzero, highlighting that F₄ (and the ABBA-BABA D-statistic) is susceptible to migration between any pair of populations. Thus, for applications, F₄ should be used as an admixture test only if there is good evidence that gene flow between some pairs of the populations was severely restricted.

Overall, when F₃ is applicable, it is remarkably robust to population structure, requiring rather strong substructure to yield false positives. Thus, it is a very striking finding that in many applications to humans, negative F₃ values are commonly found (Patterson et al. 2012), indicating that for most human populations, the majority of markers support a discordant gene tree, which suggests that population structure and admixture are widespread and that population phylogenies are poorly suited to describe human evolution.

Ancient population structure was proposed as possible confounder for the D-statistic and F₄ statistic (Green et al. 2010). Here, I show that nonsymmetric population structure such as in stepping-stone models can lead to nonzero F₄ values, showing that both ancestral and persisting population structure may result in false positives when assumptions are violated.

Furthermore, I showed that F₂ can be seen as a special case of a tree metric and that using F-statistics is equivalent to using phylogenetic theory to test hypotheses about simple phylogenetic networks (Huson et al. 2010). From this perspective, it is worth raising again the issue pointed out by Felsenstein (1973) of how and when allele-frequency data should be transformed for within-species phylogenetic inference. While F₂ has become a de facto standard, different transformations of allele frequencies might be useful in some cases, as both F₃ and F₄ can be interpreted as tests for treeness for arbitrary tree metrics.

This relationship provides ample opportunities for interaction between these currently diverged fields: Theory (Huson and Bryant 2006; Huson et al. 2010) and algorithms for finding phylogenetic networks such as Neighbor-Net (Bryant and Moulton 2004) may provide a useful alternative to tools specifically developed for allele frequencies and F-statistics (Patterson et al. 2012; Pickrell and Pritchard 2012; Lipson et al. 2013), particularly in complex cases. On the other hand, the tests and different interpretations described here may be useful to test for treeness in other phylogenetic applications, and the complex history of humans may provide motivation to further develop the theory of phylogenetic networks and stress its usefulness for within-species demographic analyses.