Actomyosin Cortical Mechanical Properties in Nonadherent Cells Determined by Atomic Force Microscopy

Abstract

The organization of filamentous actin and myosin II molecular motor contractility is known to modify the mechanical properties of the cell cortical actomyosin cytoskeleton. Here we describe a novel method, to our knowledge, for using force spectroscopy approach curves with tipless cantilevers to determine the actomyosin cortical tension, elastic modulus, and intracellular pressure of nonadherent cells. We validated the method by measuring the surface tension of water in oil microdrops deposited on a glass surface. We extracted an average tension of T ∼ 20.25 nN/μm, which agrees with macroscopic experimental methods. We then measured cortical mechanical properties in nonadherent human foreskin fibroblasts and THP-1 human monocytes before and after pharmacological perturbations of actomyosin activity. Our results show that myosin II activity and actin polymerization increase cortex tension and intracellular pressure, whereas branched actin networks decreased them. Interestingly, myosin II activity stiffens the cortex and branched actin networks soften it, but actin polymerization has no effect on cortex stiffness. Our method is capable of detecting changes in cell mechanical properties in response to perturbations of the cytoskeleton, allowing characterization with physically relevant parameters. Altogether, this simple method should be of broad application for deciphering the molecular regulation of cell cortical mechanical properties.

Introduction

The cortical actin cytoskeleton lies just beneath the cell plasma membrane to define cell shape and mechanical properties, and thus plays a key role in cellular processes such as migration and morphogenesis (1), and contributes to the macroscale mechanics of tissues. The organization of filamentous actin and myosin II molecular motor contractility is known to modify the mechanical properties of the cell cortex (2, 3). For example, a recent study has shown that during cytokinesis, the regulation of cortical tension by myosin II motor activity and actin crosslinkers is essential for shape changes (4). Moreover, the highly contractile actin cortex in cancer cells is the main factor that drives cell bleb formation and unregulated amoeboid motility (5, 6, 7). However, it is unclear how these mechanical properties are interrelated and regulated by specific molecular pathways to achieve controlled cellular processes.

The physical parameters that contribute to cell mechanical properties include cortical tension, intracellular pressure, and elasticity. Various methods have been used to determine the values of these parameters. Cellular cortical tension, intracellular pressure, and/or elastic modulus have been measured by micropipette aspiration (6), parallel glass microplate compression (8), membrane tether pulling with an optical trap (9), and atomic force microscopy (AFM) (10, 11, 12). Micropipette aspiration and parallel glass microplate compression, although accurate and easy to implement on virtually any microscope, are highly invasive, as both require large deformations of the cortex for long time periods (13) that are likely to activate mechanosensitive signal transduction cascades that may feedback to alter cortical mechanics (14). Optical trapping to pull tethers is less invasive (15), but supplies only a very localized point measurement. Furthermore, optical traps measure an effective tension, resulting in ambiguous interpretations that are problematic for characterization of cortical mechanics.

Current AFM techniques are accurate; however, they require rather complex theory for large strains (16), complicated contact mechanics for different tip geometries (11, 17), determination of the complete cell shape via high-resolution imaging systems (18), and/or compensation for cantilever tilt by custom modification of equipment and probes (16, 18). For example, nonlinearities in mechanical properties and geometry due to large deformations were needed to properly be taken into account to extract the surface tension of giant unilamellar vesicles undergoing compression using a tipless AFM cantilever (16). Recently, the cortical tension was determined for the germ-layer organization in zebrafish and the lamellipod of adherent Ptk-1 rat-kangaroo kidney cells by AFM force-distance (F-Z) curves with cantilevers with attached microbeads (11) or sharp probes (17), respectively, requiring careful consideration of the tip geometry. Additionally, the imaging of the deformed shape of HeLa cells undergoing mitosis when compressed using an AFM equipped with a tipless cantilever to apply large forces for long time periods was required for the estimation of the time-varying hydrostatic pressure (12, 18). Lastly, it has been shown, by using the AFM with tipless cantilevers, that progressive accumulation of myosin II and stable F-actin increases the cortical tension and intracellular pressure of the mitotic cell cortex, but the method requires the application of large deformations and forces (few micrometers and tens of nanoNewtons) (19). Together, these studies show the potential of AFM to measure a broader spectrum of cellular mechanical properties with reduced intervention, but a complex analysis and/or equipment modification was required. Therefore, a simpler AFM method that allows the quantification of cortical tension, elastic modulus, and internal pressure by applying 10–100 times lower force eliminates the need for large deformation theory and the need to reconstruct the entire shape of the cell, thus allowing a wide array of applications.

Here we describe the use of standard AFM force-distance curves to measure actomyosin cortex mechanical properties of living nonadherent cells. A soft, flat, and tipless rectangular cantilever was used to slightly deform a nonadherent cell. We developed a theoretical mechanics framework to determine the cortical tension and elastic modulus as well as the intracellular pressure of nonadherent cells. We initially validated the method using water microdrops suspended in oil deposited on a glass substrate. We then used the method to measure the actin cortex mechanics of untreated primary human foreskin fibroblast (HFF) cells and treated with 1) Blebbistatin, 2) Calyculin-A (CA), 3) Latrunculin-A (LatA), and 4) CK-666 pharmacological agents, which each cause a different molecular perturbation to the actomyosin cortex. This method is capable of detecting changes in the mechanical properties of the cortical actin when using these treatments. We believe this present method will be useful in deciphering the molecular regulation of cortical mechanics.

Materials and Methods

Preparation of water microdrops

Glass slides are handled on their edges and cleaned with 70% ethanol using a soft Kimwipe cloth (Kimtech Science/Kimberly-Clark, New Milford, CT). A 200 μL drop of olive oil was first deposited on slide. We used a P-97 Flaming/Brown Micropipette Puller (Sutter Instrument, Hercules, CA) to generate a glass micropipette to deliver microdrops into the oil drop. A glass micropipette with an inner diameter of ∼2–3 μm connected to a 1 mL syringe delivered ∼10 μL in 1–2 s to get the desired microdrop size (radii of ∼5–10 μm). Lastly, we waited ∼30 min to let the water microdrops settle on the glass surface.

HFF cell culture and preparation

HFF cells were obtained from the American Type Culture Collection (ATCC, Manassas, VA) and maintained at 37°C and 5% CO₂ in Dulbecco’s Modified Eagle’s Medium supplemented with 10% fetal bovine serum, 20 mM HEPES pH 7.4, 1 mM Sodium Pyruvate, 1× GlutaMAX, and 1× Antibiotic-Antimycotic (all from Life Technologies, Carlsbad, CA). Cells were trypsinized using 0.25% trypsin/EDTA (Life Technologies) and plated in glass-bottom petri dishes (Willco Wells, Amsterdam, The Netherlands) to <70% confluence. After ∼5 min of plating, the cells were placed on the AFM stage to perform measurements before cell spreading occurred.

Human monocyte cell culture and preparation

THP-1 human monocytes were obtained from ATCC, and maintained at 37°C and 5% CO₂ in Roswell Park Memorial Institute 1640 medium (RMPI 1640; Life Technologies) supplemented with 10% of heat-inactivated fetal bovine serum (Life Technologies), and 2 mM L-Glutamine (Life Technologies). To weakly adhere the monocytes to glass-bottom petri dishes (Willco Wells), we precoated the dishes with low concentrations of polyHEMA (Sigma-Aldrich, St. Louis, MO) or poly-L-lysine (Sigma-Aldrich). A solution of 2 mL containing 1.5 μg/mL of polyHEMA in 95% ethanol was deposited on the dish and left to dry overnight inside a sterile incubator at 37°C. For poly-L-lysine dish preparation, a solution of 2 mL of 0.01% poly-L-lysine was deposited on the dish, and after ∼5 min the solution was removed by aspiration and the surface was thoroughly rinsed. Then the dish was allowed to dry at room temperature inside a sterile biological safety cabinet overnight. Cells were plated in precoated dishes to <70% confluence and immersed in the culture medium buffered with 20 mM HEPES pH 7.4 (Life Technologies). After ∼30 min of plating, the cells were placed on the AFM stage to perform measurements.

Cell treatments

The following pharmacological drugs were used: 20 μM Blebbistatin (Toronto Research Chemicals, North York, Ontario, Canada), 100 nM Calyculin-A (Sigma-Aldrich), 25 nM and 100 nM Latrunculin-A (Life Technologies), and 50 μM CK-666 (Sigma-Aldrich). For treatment experiments, we added the drugs to the cells in suspension before plating them. Then, we plated the treated cells in glass-bottom petri dishes and immediately moved the cells to the AFM sample stage.

Atomic force microscopy

Microdroplet measurements were performed using a Catalyst AFM system (Bruker, Santa Barbara, CA) mounted on an inverted Axio Observer Z1 Microscope System (Carl Zeiss, Göttingen, Germany) with a 40× (0.6 NA, Plan Apochromat) objective lens (Carl Zeiss) and an ORCA-R2 digital charge-coupled device camera (Hamamatsu Photonics, Hamamatsu, Japan) placed on a vibration isolation table (Kinetic Systems, Boston, MA). Live cell measurements were performed using a Bioscope II AFM System (Veeco Metrology, Santa Barbara, CA) mounted on an inverted Eclipse TE2000-E Microscope System (Nikon, Melville, NY) placed on a vibration isolation table (Kinetic Systems). The inverted microscope was controlled by the software MetaMorph (Molecular Devices, Sunnyvale, CA). Bright field images were captured using a 40× (1.4 NA, Plan Apo PH) objective lens (Nikon) and a QuantTEM:512SC electron-multiplying charge-coupled device camera (PhotoMetrics, Tucson, AZ). A heating stage was used to maintain physiological temperature of cells during measurements. A tipless rectangular silicon nitride AFM cantilever (HQ:CSC38/tipless/Cr-Au, MikroMasch, Tallinn, Estonia) was used for all measurements. The effective spring constant of the cantilever was calibrated using the thermal noise fluctuations method (20). Calibrated spring constants for cantilever used in microdrops and cells experiments were 0.2–0.35 and 0.085–0.11 N/m, respectively. Once the sample was placed in the AFM sample stage, the cantilever was positioned in liquid far above the sample surface and allowed to thermally equilibrate. For static force-distance curves, we identified the cell of interest using the inverted microscope and brought the cantilever in close proximity to the surface. The cantilever was then pressed on the cell surface and retracted to generate the F-Z curve. Ten successive force curves, with a 10 s wait between each curve to let the specimen return to the initial undeformed configuration, were acquired in the same location for both microdrops and cells using 2 μm ramps with up to ∼100 nm indentation at 0.5 Hz (velocity-dependent compression 2 μm/s) and 4 μm ramps with up to ∼1 μm indentation at 0.5 Hz (velocity-dependent compression 4 μm/s), respectively. The trigger force for all measurements performed in this work on microdrops and cells was ∼10 and ∼1 nN, respectively.

Spinning disk confocal fluorescence microscopy

Dual-color spinning disk confocal fluorescence microscopy in fixed nonadherent HFF cells was performed using a 100× (1.4 NA, Plan Apo PH) oil immersion objective lens (Nikon) on an inverted Eclipse Ti microscope combined with the Perfect Focus System (both by Nikon), equipped with a CSU-X1-A3 spinning disk confocal scan head (Yokogawa, Tokyo, Japan), and controlled by the software MetaMorph (Molecular Devices). Immunofluorescence images were captured using a CoolSNAP MYO cooled charge-coupled device camera (PhotoMetrics) operated in the 12-bit digitization mode. Images were acquired using the 488- and 561-nm lasers in the red and green channels.

AFM data analysis

All AFM force-distance curve analyses were performed using a custom script written with the software MATLAB (The MathWorks, Natick, MA). Before importing curves to MATLAB for analysis, each recorded curve was individually preconditioned by offsetting the y axis to 0 and reformatted to a text file format using the NanoScope Analysis software (Bruker). We initially discarded force curves that presented one of the following issues: 1) large slope due to hydrodynamic drag in the region of the curve before initial contact point, 2) noisy approach curves due to acoustic environmental vibrations, and/or 3) jumps in the curve due to cantilever slippage or moving cells. For initial contact estimation, user-dependent determination for the initial guess, followed by a linear slope-fitting algorithm, was employed to find the point where a substantial change in slope of the force curve occurred. This method does not require a priori assumptions about the material and geometrical properties of the object. For fitting the approach curve data obtained on water-in-oil microdrops and nonadherent cells, we used Z distances between 0–100 nm and 0–400 nm, respectively. The curves that had poor fit R² < 90% were also rejected and discarded from the analysis. Statistical analysis and data plotting were performed using the software GraphPad Prism 6 (GraphPad Software, San Diego, CA). Data statistical analysis for two case groups was performed with an unpaired two-tailed student’s t or a one-way analysis-of-variance test.

Images data analysis

Bright field images obtained for each cell during AFM experiments were analyzed using the software ImageJ (National Institutes of Health, Bethesda, MD) to estimate their radius before deformation. All confocal image analyses were performed using the image analysis software Fiji (http://fiji.sc/) (21) to measure the actin cortex thickness and density. Statistical analyses and data plotting were performed using the software GraphPad Prism 6 (GraphPad Software). Data statistical analysis for the two case groups was performed with an unpaired, two-tailed Student’s t-test.

Actomyosin cortex thickness measurements

The FusionRed-CAAX (Evrogen, Moscow, Russia) plasmid was transfected into HFF cells by electroporation using an Amaxa Nucleofector II (Lonza, Basel, Switzerland). (FusionRed-CAAX is a mammalian expression vector with the 20-amino-acid farnesylation signal sequence from c-Ha-Ras that mediates protein prenylation, and thus targets the fluorescent protein into the inner leaflet of the plasma membrane.) Nonadherent HFF cells were fixed using 4% paraformaldehyde (Electron Microscopy Sciences, Fort Washington, PA) in cytoskeleton buffer (50 mM imidazole, 50 mM KCl, 0.5 mM MgCl₂, 0.1 mM EDTA, 1 mM EGTA at pH 6.8) for 20 min at room temperature. The actin cytoskeleton was stained with Alexa-Fluor 488 conjugated-phalloidin (Life Technologies) at 1:250 for 1 h at room temperature in cytoskeleton buffer. Spinning disk confocal images through the central Z-plane of the cell were then acquired. To correct for background, fluorescence intensity within a region of interest drawn inside the cytoplasm was measured and used for manually correcting background. Fluorescence intensity line scans from background-corrected images of Alexa-Fluor 488 phalloidin and FusionRed-CAAX that were approximately symmetric around the peak were used to calculate the distance between peaks. The actin cortex thickness was then estimated using the equation reported by Clark et al. (22): $h=2\left(X_m=X_c\right)$, where $X_m$ is the center of the membrane and $X_c$ is the center of the cortex.

Myosin II and F-actin density measurements

The nonadherent HFF cells-fixation procedure was kept the same. Mouse monoclonal anti-myosin II regulatory light chain antibody (MLC; Sigma-Aldrich) was used at a 1:250 dilution overnight at 4°C in blocking buffer solution (150 mM NaCl, 20 mM HEPES pH 7.4, 5 mM EDTA, 0.1% Triton X-100, 1% BSA, and 1% fish gelatin). An Alexa-Fluor 564 conjugated secondary antibody (Life Technologies) was used in blocking buffer at a 1:400 dilution for 2 h at room temperature. Samples were extensively washed using wash buffer (150 mM NaCl, 20 mM HEPES pH 7.4, 5 mM EDTA, and 0.1% Triton X-100) before imaging. For cortical myosin II and F-actin density measurements, anti-MLC and Alexa-Fluor 564 phalloidin staining were measured using a 5-pixel-wide line drawn along the cortex and the mean fluorescence intensities were measured. Additionally, background fluorescence was measured by selecting a region outside the cell. The normalized myosin II and F-actin densities were then calculated as the mean fluorescence intensity at the cortex minus background fluorescence.

Results

Theory for measurement of tension, pressure, and elasticity of spherical samples

We present a new method, to our knowledge, to measure the mechanics of soft spherical specimens deposited on an infinitely rigid substrate by using F-Z curves obtained with a tipless soft AFM probe. The main advance of our proposed method is the realization that for low strains (small deformations, i.e., <10%, compared to the initial specimen radius), the surface tension can be estimated by a simple force balance relating the applied cantilever force with the hydrostatic pressure excess inside the specimen and the corresponding surface tension (Fig. 1). In addition, such small deformations induced a very small contact area between the cantilever and the soft spherical specimen, which allowed the approximation of the deformation profile from a sphere to a slightly flattened ellipsoid, eliminating the necessity of measuring the deformed contact area (18). Moreover, by applying the law of Laplace, we can relate the measured tension directly to the hydrostatic pressure. Additionally, we can determine the elastic modulus (Young’s modulus) of spherical samples containing a measurable cortex thickness by relating the tensile stress to Hooke’s law. Lastly, a low-strains regime allows the linearization of the mechanics theory. Accordingly, we derived expressions for the aforementioned mechanical properties (the derivation of the formulae can be found in Text S1 in the Supporting Material):

$$T=\frac{k_c}{\pi }\left(\frac{1}{\raisebox{1ex}{$Z$}\!\left/ \!\raisebox{-1ex}{$d$}\right.-1}\right),$$ (1)

$$P=\frac{2T}{R},$$ (2)

$$E=\frac{\pi R{T}^2}{2h{k}_{c}d},$$ (3)

where T is the surface tension, P is the hydrostatic pressure, E is the elastic Young’s modulus, k_c is the calibrated effective cantilever spring constant, Z is the Z-piezo extension distance, d is the cantilever deflection, R is the sample radius, and h is the cortex thickness.

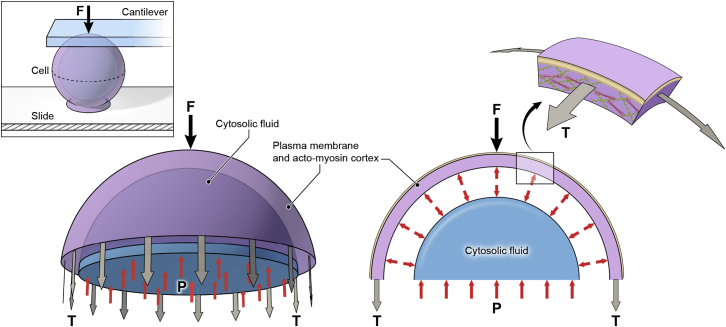
Figure 1.

Free body diagram of the top section of a nonadherent cell. The applied cantilever normal force (F) is balanced by: 1) the net contractile force generated from the cortical tension (T) and 2) the hydrostatic pressure excess (P) of the incompressible cytosolic fluid. The gap between the cytosolic fluid and the actomyosin cortex is not real, but just illustrates that hydrostatic pressure acts in all directions. Note that the substrate does not contribute to the force balance if tension and pressure balance are taken in the upper-half of the cell. In the actomyosin cortex zoom, the red filaments illustrate the myosin II minifilaments and the green filaments are the actin filaments. To see this figure in color, go online.

For AFM mechanical property measurements of nonadherent cells, the main assumptions that allow the use of this method are: 1) the induced deformation is small compared to the cell radius (≤10% R), thus creating negligible contact area compared to cell radius; 2) a viscoelastic contribution is negligible; 3) the cytoplasmic elasticity and cortex bending are negligible; 4) a low-strain regime behaves almost linearly; 5) the weak adhesions and small deviation from sphericity have a negligible effect; and 6) the volume, hydrostatic pressure, and tension are all constant during AFM ramp.

Model validation: measuring surface tension and hydrostatic pressure of water microdrops suspended in oil

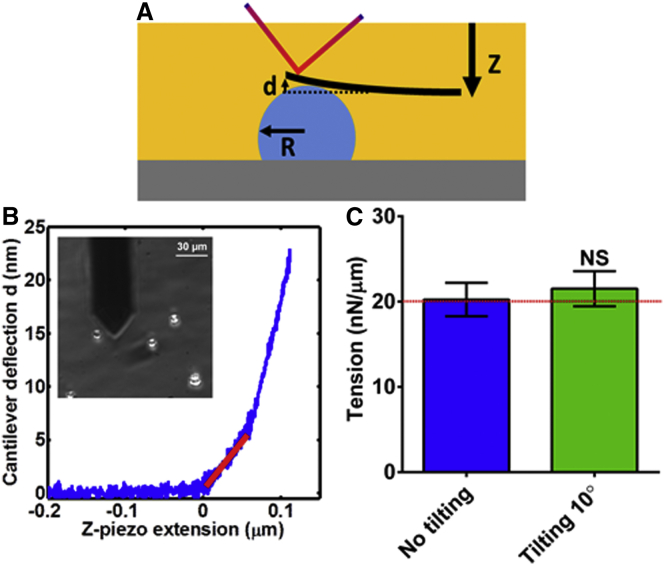
To validate our method, we first measured the surface tension and hydrostatic pressure of water microdrops in oil deposited on glass. Using a moderately soft tipless cantilever k_c ∼ 0.34 N/m, we pushed on 16 microdrops over three independent experiments (Fig. 2 A). Fig. 2 B shows a typical force-distance curve on a microdrop. We then fitted the slope of the force-distance curve in the low indentation region (red slope in Fig. 2 B), because this method is applicable to small deformations (see Text S1 in the Supporting Material), and used Eqs. 1 and 2 to estimate the surface tension and hydrostatic pressure. The calculated mean surface tension for the microdrops, using Eq. 1, was T = 20.25 ± 1.95 (mean ± SD) nN/μm, in good agreement with reported macroscopically measured tension T = 20 nN/μm (23) (Fig. 2 C). The fact that the computed surface tension of water-in-oil microdrops compared well with reported values supports the plausibility of the method. Also, the mean internal hydrostatic pressure of the microdrops with measured radii of R = 7.4 ± 2.2 μm was calculated by using Laplace’s pressure law (Eq. 2), P = 6.6 ± 0.67 kPa (Figs. S1 and S2). Together, the extracted values of surface tension and hydrostatic pressure confirm the ability of this method to measure the mechanical properties of spherical objects with high precision.

Figure 2.

Estimation of surface tension and hydrostatic pressure of water-in-oil microdrops. (A) Schematic representation of a water-in-oil microdrop deposited on glass being slightly deformed by a tipless AFM cantilever. When deforming the microdrop, changes in laser (red line) location in the photodetector are acquired and transformed to deflection in length units. The depicted parameters represent: d is the cantilever deflection, Z is the piezo movement, k_c is the cantilever spring constant, and R is the microdrop radius. (B) Acquired force-distance curve on a water microdrop. (Inset) Bright field image of the microdrops to record location as well as determine the radius. The red slope in the plot shows the linear region that is fitted to determine the surface tension and the hydrostatic pressure of each microdrop. (C) Determined surface tension for nontilting and 10° tilting conditions. No significant statistical differences were found between both conditions (p > 0.05). The red dashed line represents the previous reported macroscale measurement for surface tension of T = 20 nN/μm, which is in excellent agreement with our measurements. To see this figure in color, go online.

The AFM microcantilever has an inherent angle of ∼10°; consequently, it does not deform the sample symmetrically, as would standard parallel microplate compression methods (8, 16, 18). To test the performance of the proposed method and prove that this small angle does not provide any significant artifact to the measured mechanical properties, we increased the angle of the microcantilever with respect to the water-in-oil microdrops by an additional 10°. Thus we modified our current AFM setup by placing a custom-made wedge with a 10° tilt underneath the AFM head, as previously described in Gavara and Chadwick (24). For the tilted condition, the measured mean surface tension for 10 microdrops was not statistically significantly different than the aforementioned nontilted value (21.5 ± 2.1 pN/μm vs. 20.25 ± 1.95 nN/μm, p > 0.05) (Fig. 2 C). In conclusion, the method can be used without the difficulty of correcting for the cantilever angle, as would be required by other methods (16, 18).

Actomyosin cortical tension, elastic modulus, and intracellular pressure of nonadherent cells

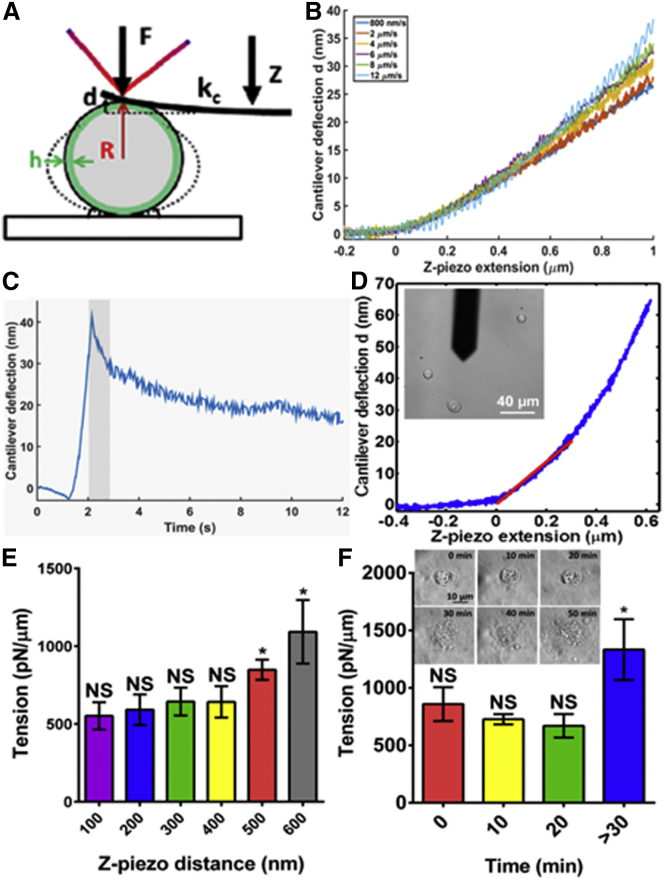
We next sought to determine whether this method is applicable on nonadherent cells, thus we tested the validity of the main assumptions to see if they are satisfactorily fulfilled (see Fig. 4 A):

• 1)Small deformations (≤10% R) induce small contact area between cantilever and nonadherent cell. To examine this assumption, we performed calculations showing that indeed at these small deformations <400 nm (compressive force ∼1 nN), the contact radius that formed between the flat cantilever and the spherical cell is <3% of the cell middle radius (see Text S3 in the Supporting Materials and Methods for details). Moreover, recently it has been shown that compressive forces <5 nN are too small to create sufficient deformation compatible for light microscopy detection and generates excessive errors in the estimation of the contact radius (25). Accurate determination of the contact area is limited by the diffraction limit of the light microscope (∼200 nm).
• 2)Viscoelastic contributions are negligible for typical experimental loading rates (velocity-dependent compression). We showed that on nonadherent HFF cells, viscous losses are negligible for typical loading rates ranging from 800 nm/s to 12 μm/s (frequency 0.1–1.5 Hz) because compressive force curves deviate negligibly from each other at small deformations (see Figs. 4 B and S3). Additionally, stress-relaxation experiments performed for small deformations with a compressive velocity of 4 μm/s, show further evidence that the viscoelastic contribution is small for the approach curves, because the fast decay of the force is <20% of the maximum force (see Fig. 4 C). Thus, we confirm that the actomyosin cortex is indeed viscoelastic, as observed by Humphrey et al. (26) and Gardel et al. (27). However, if the mechanical perturbations are small and rapid compared to the relaxation time constant τ, strain energy will be stored and the cortex will behave elastically. Furthermore, previous work showed that compressive curves collected at short timescales with the approach speed regime at 1 Hz are rapid enough to minimize viscous behavior (28). Consequently, it is safe to assume that viscoelastic contributions are negligible in this work because acquired measurements are faster than slow stress relaxation timescales <0.1 Hz (29, 30), but slower than acoustic frequencies <1 kHz, which are known to induce viscoelastic and inertial effects (31, 32).
• 3)Cytoplasmic elasticity and cortex bending is negligible. We performed calculations to show that cytoplasmic elastic response is ≤7% of the cortical elastic response. To justify the assumption that there is a negligible elastic response from the cytoplasm, we can show that the elastic energy to deform the cytoplasm is a small fraction of the elastic energy to deform the cortex: $U_{\text{cyto}}/U_{\text{cortex}}\approx {\pi }^2{E}_{\text{cyto}}R\left(16T\right)=0.007-0.07$ (see Text S4 in the Supporting Materials and Methods for details). The contribution of bending forces to cortical mechanical properties is highly dependent on the length scale that the measurement is performed, and is poorly understood for cells. For nonadherent HFF cells, we measured the bending-to-tensile forces ratio using Eq. S13 (see Text S2 in the Supporting Material) in the range of 0.01–0.05% (Table S1), which signifies >2 orders-of-magnitude smaller than adherent cells. The results are in line with previously reported works showing that the bending forces contribution plays a significant role for actin cortices when measured at small length scales (radius of curvature of few 10s of nanometers) (17, 33); nevertheless, the radius of curvature by using the proposed method on nonadherent cells is in the range of micrometers. This result confirms that for nonadherent cells, bending forces are negligible and cortical actomyosin contractility is dominated by tensile forces.
• 4)The low-strain regime behaves almost linearly. Most theories for cell mechanics in the low-strain regime behave linearly, in contrast to high strains where mechanical and geometrical nonlinearities dominate (34). To prove this and show that our method is not arbitrary, we measured the cortical tension of HFF cells (n = 25) for deformations ranging from 0 to 600 nm (see Fig. 4 E). Deformations from 0 to 400 nm showed a good agreement with no statistical significant differences between each other (p < 0.05), whereas at larger deformations 500 and 600 nm, the extracted tension increased monotonically and showed significant differences from smaller deformation measurements (p > 0.05). This increase could be possibly due to contributions from the nucleus, geometrical and mechanical nonlinearities, and inaccuracy of the ellipsoidal deformation model for large deformations. Additionally, we have made calculations to further show that the model can fit nonlinear data up to ∼400 nm for the force curve obtained on nonadherent cells. The issue raised concerns as to the shape of the force-distance curve, which is clearly nonlinear and therefore limits the use of the model, which cannot fit the entire curve. The exact force balance equation (Eq. S4 and see Text S1 in the Supporting Material) can only fit the data up to 400-nm Z distance as shown in Fig. S6. So the model should not be pushed beyond 400 nm; beyond that, the model is unreliable.
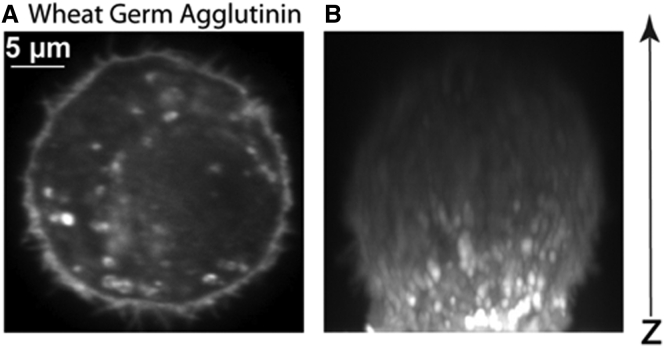
• 5)The effects of the weak adhesion and small deviation from spherical configuration on the measurements are negligible. To test for the contributions made by these effects on nonadherent HFF cells (Fig. 3 A), we initially needed to ensure that the shape of the cells was approximately spherical. We utilized cells that had just begun to weakly adhere to the glass-bottom dish shortly after plating. We labeled the plasma membrane with fluorescent Alexa-Fluor 568-conjugated wheat germ agglutinin that labels the glycocalyx on the cell surface, and collected confocal Z-stacks to image the nonadherent HFF cells deposited on glass (Fig. 3 B). Three-dimensional reconstructions of the Z-slices showed that cells adopt a spherical shape, likely maintained by actomyosin cortical tension, similar to surface tension pulling a water drop into a sphere in oil. We then measured the cortical tension of untreated HFF cells at different spreading stages with times 0, 10, 20, and >30 min (Fig. 4 F). We plated and incubated HFF cells for 5 min before AFM experiments. Zero time is when the first measurement was acquired on a rounded weakly adhered HFF cell. It can be clearly observed that the method shows good agreement with no statistical significant differences on estimated cortical tension up to 30 min spreading time. For larger times, when the cell has flattened to less than a hemisphere, the theory no longer applies. Thus, for a spreading stage with lamellipodia and filopodial projections, adhesions do affect the balance of forces and their contributions cannot be ignored. Previous work showed that the mechanical parameters of spreading MDCK II cells do not significantly change within the first 10–20 min of cell adhesion and spreading, but after ∼20 min a decrease in mechanics (adhesion released cortical prestress) is observed, and finally after 30 min a significant increase is observed due to cell adherence and large spherical shape deviations (35). Therefore, for AFM experiments, we analyzed data on cells early in time that exhibit weak adhesion and small spherical geometry deviation.
• 6)The cell volume, intracellular hydrostatic pressure, and cortical tension are constant during AFM ramp. This is usually of standard practice for cell mechanics theory because the volumes of the undeformed and deformed shapes are equal; therefore the cell behaves like a uniform incompressible fluid (36). Furthermore, it has been shown that there is no outflow of cytosolic fluid or inflow of extracellular fluid through the semipermeable plasma membrane when slightly deformed (37). Also, at rapid small deformations, the AFM cantilever does not alter the internal pressure of cells, because, by the Law of Laplace, intracellular pressure is proportional to tension and the actomyosin cortical tension remains constant. Thus, the cell volume, the intracellular pressure, and the cortical tension are assumed to be unperturbed because the AFM force curve is acquired at a much faster timescale (time <1 s) compared to the actual timescale of actomyosin cortex remodeling or water movement through the plasma membrane (using a timescale of minutes (37).

Figure 4.

Applicability of the method to nonadherent HFF cells. (A) Schematic representation of a nonadherent cell being slightly deformed by a tipless AFM cantilever. When deforming the spherical cell, changes in laser location in the photodetector are acquired and transformed to deflection in length units. F is the applied normal force, d is the cantilever deflection, Z is the piezo movement, k_c is the cantilever spring constant, R is the initial cell radius, and h is the cortical actin thickness. (B) Velocity-dependent compression force curves performed on the same HFF cell. Successive curves show negligible viscous losses with negligible deviation from each other for deformations <∼400 nm. (C) Typical stress-relaxation curve performed on a nonadherent untreated HFF cell. The tipless cantilever approaches and is pushed against the spherical cell until a deformation of ∼500 nm is reached, then the cantilever is held at a constant height for 10 s. The marked area shows the comparison of rapid compression 4 μm/s (equal to 1 s compression of cell) to the region of fast decay in force immediately after holding the cantilever height constant. The decay is moderately small, ≤20% the maximum force. (D) Acquired force-distance curve on a HFF cell. (Inset) Bright field image of the HFF cells to identify the location and viability as well as to determine the cell radius. The red slope in the plot shows the linear region that is fitted to determine the actin cortex tension and the intracellular pressure of each cell. (E) Cortical actomyosin tension of untreated HFF cells extracted at different Z-piezo distances from 0 to 600 nm. It can be observed that from 100 to 400 nm these are not statistically different (p > 0.05) in extracted cortex tension, confirming that our method is robust for quantitatively estimating the mechanical properties for small deformations. For Z-distance of 500 nm or greater, the estimated tension increases, demonstrating significant differences using a one-way analysis-of-variance test (p < 0.05). (F) Cortical actomyosin tension of untreated HFF cells measured at different spreading stages. The progressive cell spreading and adhesion is observed by phase contrast (inset). At early stages (time 0–20 min) there are no statistically significant differences (p > 0.05) in extracted cortical tension, confirming that weak adhesion contributions are negligible. However, when cells exhibit lamellipodia and filopodia projections, the measured tension significantly increases—demonstrating that adhesion contribution cannot be ignored at advanced spreading stages (time >30 min). To see this figure in color, go online.

Figure 3.

Nonadherent HFF cells shape is approximately spherical. (A) A representative midplane cross-section view showing the circular shape of a primary HFF cell stained with fluorescently conjugated wheat germ agglutinin for marking the glycocalyx on the plasma membrane imaged by confocal microscopy. (B) Z-stacks were collected to show the spherical shape of the nonadherent cells, satisfying an important assumption for the method to be valid on nonadherent cells.

Therefore, we can safely assume that in our experiments the response of nonadherent HFF cells is approximately elastic, and behaves almost linearly at small deformations. Taken together, all these assumptions supported by previous works or validated herein allow the development of an easy and simple methodological approach using commercially available biological AFM systems, giving us confidence that the method is appropriate to quantify the actomyosin cortex tension, the elastic modulus, and the intracellular pressure of individual nonadherent cells.

To determine the role of actomyosin cortex activity on the cortical mechanical properties on nonadherent cells, we chose pharmacological drugs and dosages that would cause a specific perturbation in a physiological relevant way. We decided to treat cells with the following pharmacological drugs: 20 μM Blebbistatin, and either 100 nM CA, 25 or 100 nM LatA, or 50 μM CK-666. Blebbistatin inhibits myosin II molecular motor ATPase activity, which in turn dramatically reduces cell contractility (38). LatA inhibits actin polymerization by sequestering G-actin monomers and results in a decrease in cortical actin filaments (39). CA inhibits myosin II light chain protein phosphatases 1 and 2A, thus enhances myosin II phosphorylation, and consequently increases contractility (40). Lastly, CK-666 is a small molecule that binds the Arp2/3 complex causing actin filament debranching and inhibits actin nucleation (41, 42). Immunolocalization of myosin II at the actin cortex after drug treatments showed that no treatment significantly affected myosin II density (Fig. S7, A–D). Thus, the results indicate that cortical actomyosin perturbations by the low dose of pharmacological drug use herein are, indeed, physiologically relevant and reduce off-target effects.

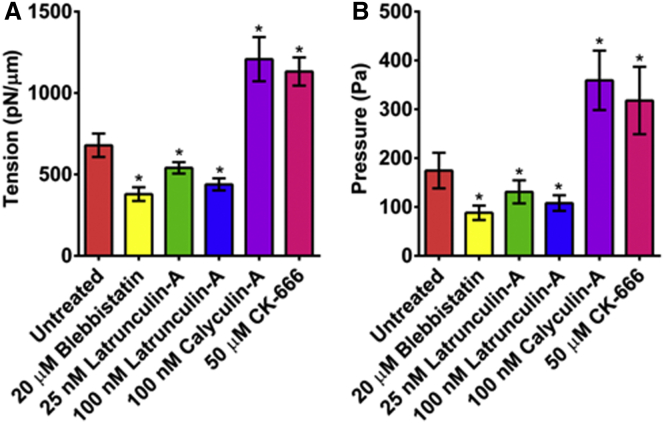
We next sought to test the hypothesis that nonadherent cells cortical mechanical properties were affected by actomyosin cortex activity. To test this, the cortical mechanical properties of living nonadherent HFFs and THP-1 monocytes cells were measured by performing quasi-static AFM force spectroscopy shortly after plating, and actomyosin cortical activities were perturbed by the above drugs. Using a soft tipless cantilever with calibrated effective spring constant k_c ∼ 0.09 N/m, we measured untreated HFF and monocyte cells (n = 25 and n = 20, respectively), and cells treated with either 20 μM blebbistatin (n = 21 and n = 18, respectively). Additionally, HFF cells were treated with 100 nM CA (n = 29), or 25 or 100 nM LatA (n = 26 or 28, respectively), or 50 μM CK-666 (n = 28) over 2–3 independent experiments for each condition. We then measured the cortical actomyosin tension for each perturbation by using Eq. 1. The results for nonadherent HFF cells are represented in Fig. 5 A. Compared to untreated control HFF cells (679 ± 72 pN/μm), the mean cortex tensions were statistically significantly reduced by ∼50, ∼20, and ∼40% by treatment with 20 μM blebbistatin, 25 nM LatA, and 100 nM LatA, respectively (379 ± 42, 540 ± 35, and 439 ± 37 pN/μm, p < 0.05). In contrast, cortex tension was approximately twofold higher in the CA- and CK-666-treated cells compared to untreated HFF cells (1208 ± 136 and 1132 ± 87 pN/μm, p < 0.05). Interestingly, CK-666 results indicate that branched actin networks reduce cortical tension possibly due to the preference of myosin II interaction on polymerized actin filaments rather than branched ones. Moreover, in line with the results on HFFs, the cortical tension of monocytes is dramatically reduced after the addition of the pharmacological drug blebbistatin (143 ± 23 vs. 292 ± 45 pN/μm, p > 0.05) (Fig. S5 C). These results show that inhibition of myosin II motor activity or actin polymerization decreases cortical tension, while increasing myosin II activity and inhibition of actin branching increases cortical tension, indicating that actomyosin contractility promotes cortex tension. The results also demonstrate the sensitivity of the method by measuring changes in actomyosin cortical tension with incremental changes in drug concentration.

Figure 5.

Determination of nonadherent HFF cells’ cortical actomyosin tension and intracellular pressure after pharmacological drug treatments. (A) Cortical actomyosin tension after drug treatments perturbing the cortex. (B) Intracellular pressure after treatments. All treated cases were found to have statistically significant differences versus untreated cases (p < 0.05). To see this figure in color, go online.

We next determined the intracellular pressure of the HFF cells using the Laplace’s Law equation (Eq. 2). We used the estimated mean cortex tension value and measured the radius for each cell from a bright field image. The mean cell radii for untreated, blebbistatin, CA, 25 nM LatA, 100 nM LatA, and CK-666 treated HFF cells were 8 ± 1.5, 8.7 ± 1.1, 6.9 ± 0.8, 8.5 ± 1.3, 8.3 ± 1, and 7.4 ± 1.4 μm, respectively (Fig. S4). The significant reduction in mean cell radii of CA-treated cells agrees with the observation that an increase in cortical tension leads to a reduction in cell surface area (43). Fig. 5 B presents the results of the intracellular pressure for each condition. Similar to results for cortical tension, this showed that compared to control (175 ± 36 Pa), mean intracellular pressures were ∼50, ∼25, and ∼40% lower in the blebbistatin-, 25 nM LatA- and 100 nM LatA-treated cells (88 ± 15, 131 ± 24, and 108 ± 16 Pa, p < 0.05). The intracellular pressures were approximately twofold higher in the CA- and CK-666 treated cells than in the untreated ones (359 ± 61 and 318 ± 69 Pa, p < 0.05). These results indicate that inhibiting contractility decreases pressure, whereas enhancing cortical actomyosin contractility increases intracellular pressure.

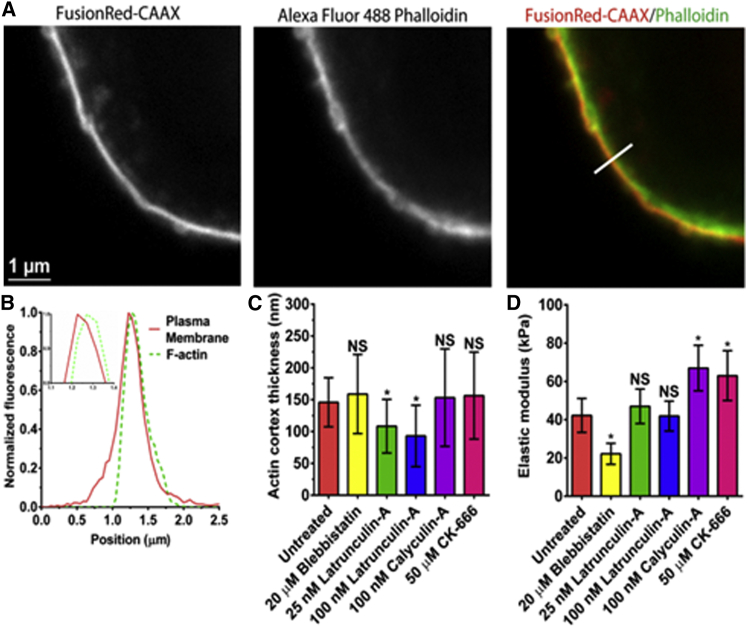
For cortex elastic modulus estimation, using Eq. 3, we needed to determine the actin cortex tension and cell radius as well as the cortex thickness. To measure the cortex thickness, we utilized a slightly modified version of the method described by Clark et al. (22) in which nonadherent HFF cells were transiently transfected by the plasma membrane marker FusionRed-CAXX, which targets the inner leaflet; then fixed, labeled for F-actin with Alexa-Fluor 488 phalloidin, and imaged using confocal fluorescence microscopy (see Materials and Methods) (Fig. 6 A). After background corrections, a line scan of the membrane and actin cortex was created to extract the membrane and actin fluorescent intensity curves; both curves display a symmetric Gaussian-like shape (Fig. 6 B). Then, by fitting a Gaussian function to both curves and determining the distance between the peak centers of these two curves, we estimated the actin cortex thickness for each condition. The mean cell cortex thickness was not affected when nonadherent HFF cells were treated with either blebbistatin or CK-666, but LatA significantly reduced the cortical thickness (Fig. 6 C). These results demonstrate that inhibition of actin polymerization reduces actin cortex thickness, but at the LatA drug concentrations used, the cortex remained intact. Calculation of the mean cortex elastic modulus showed that blebbistatin-treated cells were ∼50% lower than the untreated ones (22 ± 5 vs. 42 ± 9 kPa, p < 0.05). The elastic moduli were ∼1.5-fold higher in the CA- and CK-666 treated cells than in the untreated ones (67 ± 12 and 63 ± 13, p < 0.05). Interestingly, CK-666 results indicate that the presence of branched actin networks softens the cortex. Surprisingly, the mean cortex elastic modulus was the same for 25- and 100-nM LatA-treated and untreated cells (47 ± 9 and 42 ± 8 vs. 42 ± 9 kPa, p > 0.05), indicating that low levels of cortical actin are sufficient to maintain cortex elasticity (Fig. 6 D).

Figure 6.

Determination of actin cortex thickness and elastic moduli after pharmacological drug treatments. (A) A representative fixed nonadherent HFF cell, transiently transfected with the plasma membrane marker FusionRed-CAAX and labeled for F-actin with Alexa-Fluor 488 phalloidin, were imaged by confocal microscopy. (B) Normalized fluorescence intensity peaks of actin and membrane extracted by line scan after background corrections. (C) Calculated actin cortex thickness, h, between cells after drug treatments using the method of Clark et al. (22). All cases were found to have no statistically significant differences (p > 0.05), except for LatA treatments (p < 0.05). (D) Cortical actomyosin elastic modulus after treatments perturbing the cortex. All cases were found to have statistically significant differences (p < 0.05), except for LatA treatments (p > 0.05). To see this figure in color, go online.

The results reveal that myosin II activity and actin polymerization increase cortex tension and intracellular hydrostatic pressure, whereas branched actin networks decrease them. Interestingly, actin polymerization has no effect on cortex stiffness, while myosin II activity stiffens the cortex and branched actin networks soften it.

Discussion

We show that three mechanical properties—cortex tension, elastic modulus, and intracellular pressure—can be extracted on nonadherent HFFs and monocyte cells by a gentle AFM method compatible with any commercially available AFM system for biological applications. Our method uses quasi-static F-Z curves, the most common AFM approach for determining mechanical properties of live cells (10, 44). Additionally, it uses tipless AFM cantilevers to avoid the complexity of accounting for tip geometry, and to deform the whole cell. An additional strength of the proposed method is that, as demonstrated, it can be used without the difficulty of correcting for the cantilever angle. Moreover, it does not involve simultaneous AFM measurements and imaging of the entire cell, as required by other methods (12, 18). Lastly, the measured mechanical properties using this method compare excellently to cell mechanics measurements using other approaches (Table 1) (6, 10, 11, 18, 45). Together, this shows that this simple method should be of broad application to a wider array of applications for the mechanistic dissection of molecular pathways that control cortical mechanical properties.

Table 1.

Comparison of Extracted Mechanical Properties of the Proposed Method with Existing Approaches

Reference	Approach	Cell	Cortex Tension (pN/μm)	Intracellular Pressure (Pa)	Cortex Elastic Modulus (kPa)
this work	AFM F-Z compression tipless	nonadherent HFFs	679 ± 72	175 ± 36	42 ± 9
Fischer-Friedrich et al. (18)	AFM constant height	HeLa interphase/ metaphase	170 ± 130/ 1600 ± 500	40 ± 30/ 400 ± 120	NA
Tinevez et al. (6)	micropipette aspiration	suspended L929 fibroblasts	413.6 ± 15.2a	NA	NA
Krieg et al. (11)	AFM indentation colloidal tip	germ-layer progenitors from zebrafish	54.5 ± 8.6b	NA	NA
Rotsch and Radmacher (10)	AFM indentation sharp tip	adherent 3T3 and NRK fibroblasts	NA	NA	10–100
Bausch et al. (45)	twisting microbeads	adherent NIH/3T3 fibroblasts	NA	NA	20–40c

Different experimental techniques allow estimation of mechanical properties. The described method is the only one capable of extracting the three physical parameters, with values agreeing with other methods. Otherwise specified data is represented as mean ± SD. NA, not applicable.

^aMean ± standard error.

^bMedian ± median absolute deviation.

^cMean of extracted shear modulus.

Our drug treatment experiments confirmed that actin and myosin II both regulate the cortex tension and intracellular pressure, but, surprisingly, show that myosin II plays a more significant role than actin in regulating cortical elasticity. By inhibiting myosin II ATPase motor activity using blebbistatin, the active contractile force of the motor was significantly reduced, consequently decreasing the three mechanical properties. Recently, it has been shown that treatments of cells with high concentrations of blebbistatin for long incubation times result in stiffening of nonadherent cells from a decrease in myosin II-mediated actin turnover (46), while the more physiologically relevant smaller concentrations and shorter timescales we used here decrease myosin II-mediated actin prestress, increasing the cortical mechanics, which is in line with our results. The cortical mechanical properties increase when selective inhibition of protein phosphatases 1 and 2A is achieved by the addition of CA, which consequently enhances myosin II activity and drives an increase in contractility (40). Moreover, the mechanical properties increase when inhibiting the Arp2/3-mediated actin branching by the addition of CK-666, possibly favoring formin-mediated actin bundling that could effectively increase the interaction of individual myosin II motors on more actin filaments (47, 48). Finally, by inhibiting actin polymerization using LatA, the cortex tension and intracellular pressure reduce due to a decrease in actin filament density, and this is confirmed by a ∼50–60% reduction in phalloidin fluorescence intensity on LatA-treated cells compared to untreated nonadherent HFF cells (Fig. S7 D). However, the level of cortex elastic modulus remains relatively the same as untreated cells. LatA does not interfere with motor activity, but decreases actin filament density, thus there is less actin for myosin II to interact with Ayscough et al. (39), demonstrating that low levels of cortical actin are sufficient to maintain the cortex elasticity. Collectively, these results show that cellular mechanical properties are modified when the cortical actomyosin is perturbed, suggesting that cell mechanics are directly regulated by actomyosin.

A significant advance of our method is that it allows determination of the cortex elastic modulus, which we measured to be ∼40 kPa in HFF cells. Until now, the cortex elastic modulus has been poorly understood with various studies reporting widely different results. Previously reported values of the elastic modulus of adherent fibroblasts have ranged from 1 to 100 kPa (10, 45, 49, 50), which is a very large range for such an important physical property. Measurements using torsional magnetic microbeads deposited on the cell membrane show that the actin cortex elastic modulus is E ∼ 1–50 kPa (45). However, results from another study using the same technique, but now modeling the actin cortex as a soft-glassy material, suggest that the cortex elastic modulus is in the lower range E ∼ 1 kPa (50). Previous AFM and twisting microbeads methods were very localized studies that only measure the Young’s modulus modeling the cortical layer as an infinite isotropic elastic half-space (51). Thus, the finite thickness of the cortex layer was not considered as was done here. Our present method only slightly deforms the whole spherical cell containing a relatively homogeneous actomyosin cortex (52) instead of an adherent cell where the cortex distribution is extremely heterogeneous (53).

A potential application of this method could be for determining the mechanics of isolated nuclei. In recent years, there is increased interest in understanding a number of mechanical effects involving the nucleus, including nuclear envelope dynamics (54), nuclear lamina and chromatin interactions (55), cytoskeleton tensional contributions to nucleus homeostasis (56), nucleus deformation for cells under high three-dimensional confinement microenvironments (57), and nucleus mechanical breakage (58). For example, a previous study using the AFM to measure the influence of lamin-A on the stiffness of isolated Xenopus oocyte nuclei showed that lamina layer mechanics were important for nucleus integrity (59). Additionally, using micropipette aspiration to deform the nucleus of an A549 cell showed that the response of the lamina is highly viscoelastic, considering a combination of elastic component from Lamin-B and a more dominant viscous component from Lamin-A (60). Therefore, we strongly believe our method can be used to give further breath to understanding outstanding cellular biology questions similar to this, that were heretofore not possible.

In conclusion, our method to measure the mechanics of individual nonadherent eukaryotic cells opens the door for full characterization of the cortical actomyosin layer mechanical properties to dissect its function in determining cell shape and motility. Recently, cortical tension and intracellular pressure were shown to be predictive of leader-bleb-based migration (7). We believe this method will be useful to other research studying similar types of cell migration. The ability of the proposed method to measure single cell actomyosin cortex tension, elastic modulus, and intracellular pressure with only one fast force curve (1 s) is of major significance. For this reason, we predict that the proposed method will help to unveil further evidence of differences in mechanical properties that underlay cellular processes and disease progression, therefore, reinforcing the importance of AFM in cellular mechanobiology.

Author Contributions

A.X.C.-R., J.S.L., C.M.W., and R.S.C. conceived and designed the experiments; A.X.C.-R. performed all the AFM research experiments; J.S.L. performed all the spinning disk confocal experiments; A.X.C.-R. analyzed the AFM data; J.S.L. analyzed the spinning disk confocal data; A.X.C.-R. and J.S.L. prepared the figures; A.X.C.-R., C.M.W., and R.S.C. cowrote the article; and all authors discussed the results and reviewed the article.

Editor: Christopher Yip.

Supporting Citations

References (61, 62, 63) appear in the Supporting Material.