Abstract
Motivation: Structured sparse canonical correlation analysis (SCCA) models have been used to identify imaging genetic associations. These models either use group lasso or graph-guided fused lasso to conduct feature selection and feature grouping simultaneously. The group lasso based methods require prior knowledge to define the groups, which limits the capability when prior knowledge is incomplete or unavailable. The graph-guided methods overcome this drawback by using the sample correlation to define the constraint. However, they are sensitive to the sign of the sample correlation, which could introduce undesirable bias if the sign is wrongly estimated.
Results: We introduce a novel SCCA model with a new penalty, and develop an efficient optimization algorithm. Our method has a strong upper bound for the grouping effect for both positively and negatively correlated features. We show that our method performs better than or equally to three competing SCCA models on both synthetic and real data. In particular, our method identifies stronger canonical correlations and better canonical loading patterns, showing its promise for revealing interesting imaging genetic associations.
Availability and implementation: The Matlab code and sample data are freely available at http://www.iu.edu/∼shenlab/tools/angscca/.
Contact: shenli@iu.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Sparse canonical correlation analysis (SCCA) (Chen and Liu, 2012; Chen et al., 2012; Du et al., 2014; Lin et al., 2013; Parkhomenko et al., 2009; Witten et al., 2009), is a powerful bi-multivariate analysis technique (Vounou et al., 2010). It has recently become a popular method in brain imaging genetics studies to identify bi-multivariate associations between single nucleotide polymorphisms (SNPs) and imaging quantitative traits (QTs).
SCCA was initially proposed by Witten et al. (2009) and Witten and Tibshirani (2009) in the analysis of gene expression data. This first SCCA model introduced the -norm (lasso) term into the traditional CCA model to make both canonical loadings sparse. The penalized matrix decomposition (PMD) technique was used to solve this sparse learning problem. For a group of correlated features, lasso tends to randomly select only one feature from the group, and often cannot recover all the relevant and correlated features. Witten et al. (2009) and Witten and Tibshirani (2009) also proposed the fused lasso based SCCA, which takes into account the spatial correlation among features. Thus, neighboring features tend to be selected together to help discover regional structures.
In order to accommodate other types of structures in the data, several structured SCCA methods (Chen et al., 2013; Chen and Liu, 2012; Chen et al., 2012; Du et al., 2014, 2015; Lin et al., 2013; Witten et al., 2009; Witten and Tibshirani, 2009; Yan et al., 2014) arise recently. We group these SCCA methods into two kinds according to their distinct regularization terms. One kind used the group lasso penalty, and the other kind used the graph/network-guided fused lasso penalty to conduct feature selection and feature grouping. The first kind, i.e. the group lasso based SCCA, required prior knowledge to define the group structure. Lin et al. (2013) incorporated the priori knowledge into the SCCA model with a group lasso regularizer, where the same PMD technique was used to identify non-overlapping group structure. Du et al. (2014) proposed S2CCA using group lasso, and incorporated both the covariance matrix information and the priori knowledge information to discover group-level bi-multivariate associations. The KG-SCCA (Yan et al., 2014) was an extension of S2CCA (Du et al., 2014), which also employed the group lasso to constrain one canonical loading. This type of SCCA methods may not be useful when the biological priori knowledge is incomplete or unavailable. Of note, it is a hard task to provide precise prior knowledge in real biomedical studies.
The second kind of structured SCCA methods use graph/network-guided fused lasso penalties. These methods can perform well on any given priori knowledge. In case the prior knowledge is not available, these methods can also work via using the sample correlation to define the graph/network constraint. Chen et al. (2013) proposed ssCCA using a graph-guided fused -norm penalty for one canonical loading of the taxa based on their relationship on a phylogenetic tree. Chen et al. (2012) proposed a network-guided fused lasso based SCCA which penalized every pair of features by the -norm of . It could be viewed as an extension to the fused lasso based SCCA without demanding the features being ordered. Du et al. (2015) proposed GN-SCCA which penalizes the -norm of . These two SCCA methods could only handle the positively correlated features. Chen and Liu (2012) proposed an improved network-structured SCCA (NS-SCCA) by incorporating the sign of the sample correlation within features. NS-SCCA penalized the -norm of to tune a similar weight value for ui and uj if , or dissimilar if . The aforementioned KG-SCCA (Yan et al., 2014) employed -norm of on one canonical loading. Most of these SCCA methods used the data-driven correlation as the network constraint, while some incorporated prior knowledge to define the network constraint (Chen and Liu, 2012; Yan et al., 2014). In the data-driven mode, they were dependent on the sign of the pairwise sample correlation to identify the hidden structure pattern. Unfortunately, this can introduce additional estimation bias since the sign of the correlations can be wrongly estimated due to possible graph/network misspecification caused by noise (Yang et al., 2012).
We focus on the data-driven mode in this paper. We first propose a novel structured penalty using the pairwise difference of absolute values between features, which is an improved GraphNet penalty (Grosenick et al., 2013). Then we introduce our novel structured SCCA model coupled with an effective SCCA algorithm, i.e. SCCA using the absolute value based GraphNet (AGN-SCCA). Our contributions are summarized as follows. (i) The new regularizer penalizes the difference between the absolute values of the coefficients no matter whether their correlations are positive or negative. Thus it could tune both positively and negatively correlated features to have similar weights despite the correlation signs. (ii) AGN-SCCA could reduce estimation bias due to its independence to the signs of sample correlation, and thus has better performance and generalization ability than those methods dependent on sample correlation signs. (iii) We provide a quantitative upper bound for the grouping effect of AGN-SCCA and prove that the algorithm is guaranteed to converge fast. (iv) On both synthetic and real imaging genetic data, AGN-SCCA yields higher or comparable correlation coefficients, and generates more accurate and cleaner patterns than three competing methods, i.e. L1-SCCA (CCA with lasso) (Witten et al., 2009; Witten and Tibshirani, 2009) FL-SCCA (CCA with fused lasso) (Witten et al., 2009; Witten and Tibshirani, 2009) and NS-SCCA (Chen and Liu, 2012).
2 Methods
In this paper, we use the boldface lowercase letter to denote a vector, and use the boldface uppercase one to denote a matrix. represents the ith row of matrix M. We use and to denote the SNP data and the QT data originating from the same population. The SCCA model proposed in (Witten et al., 2009; Witten and Tibshirani, 2009) can be defined as follows:
| (1) |
where and are constraints for controlling the model sparsity, and typical constraints include lasso (Chen et al., 2012; Parkhomenko et al., 2009; Witten et al., 2009; Witten and Tibshirani, 2009) and fused lasso (Witten et al., 2009; Witten and Tibshirani, 2009).
2.1 The new penalty
Grosenick et al. (2013) have extended the traditional elastic net regularizer to a more general form, which is named GraphNet, i.e.
| (2) |
where M is a matrix, and are tuning parameters. Note that GraphNet becomes the elastic net if (Grosenick et al., 2013). Typical GraphNet studies (Du et al., 2015; Grosenick et al., 2013) have , where L is the Laplacian matrix of a graph. Let be the graph formed by our sample correlation matrix A. Let D be a diagonal degree matrix with the following diagonal entries: . The Laplacian matrix L is defined as (Grosenick et al., 2013). When , the GraphNet term can be transferred and written as:
| (3) |
It is easy to see that this penalty only puts emphasis on the positively correlated features, and does not take into consideration the negatively correlated features. To address this issue, we introduce a novel penalty which uses the pairwise difference between absolute values instead, i.e. . SCCA requires two penalties, one for each canonical loading. Thus, we propose the following new penalties:
| (4) |
where and depend on the pairwise sample correlation of X and Y respectively. and are used to control the model sparsity.
In accordance to the form of GraphNet, we rewrite the penalty and call it absolute value based GraphNet penalty,
| (5) |
where and are Laplacian matrices of the correlation matrices of X and Y respectively.
The main motivations for proposing are as follows. First, if we have some priori knowledge, e.g. the pathway information about genetic markers, each pairwise penalty encourages and to be similar. This makes sure that the two markers have a high probability to be selected together if they are connected on the graph. Second, if the priori knowledge is unavailable, every pairwise term will be imposed to encourage for both positively and negatively correlated features based on the strength of their sample correlations, which will be supported by Theorem 1. Third, genetic (or imaging) markers in the same pathway (or brain circuitry) could play different roles for a specific disease. That is, some markers could be significant, while others could be irrelevant. Therefore, we impose lasso to assure additional sparsity.
2.2 AGN-SCCA model and proposed algorithm
By imposing the novel GraphNet penalty into a CCA model, we obtain our AGN-SCCA model.
| (6) |
Note that we utilize and , which embraces the covariance structure of the data in our model. The strength of this strategy has been demonstrated by our prior S2CCA work (Du et al., 2014).
Using Lagrange multiplier method, we define the Lagrangian below,
| (7) |
where are the Lagrange multipliers, which are also called dual variables.
According the Lagrange duality, the Lagrangian can represent problem Eq. (6) as the following unconstrained one,
| (8) |
Now that there is no constraint term in Lagrangian , it is easy to solve Eq. (8) than Eq. (6). Given the optimal dual variables , we could obtain the solution by taking derivative regarding u and v respectively, and let both of them be zero.
| (9) |
However, the new proposed penalty is non-differentiable at zero value owning to the -norm term and the absolute value based GraphNet term. Thus we use the sub-gradient in Eq. (9) instead, and obtain the following (if , the ith element of diagonal matrix is not available. So we regularize the element in as (ζ is a very small positive number) when . Then the objective function regarding u is . It is easy to prove that will reduce to problem (7) regarding u when . Those can also be regularized by the same strategy),
| (10) |
| (11) |
where is a diagonal matrix with the ith element as , and is a diagonal matrix with the jth element as . is a diagonal matrix with the k1th element as , where is the k1th row of the Laplacian matrix . Similarly, is the diagonal matrix with the k2th element as , and is the k2th row of the Laplacian matrix .
Both and depend on u; and both and depend on v. Since u and v are unknown, we propose an effective iterative algorithm called AGN-SCCA to solve this problem. Algorithm 1 shows the pseudocode. In each iteration, the algorithm first fixes v to calculate u and then fixes u to calculate v. This procedure repeats until it converges.
Computational analysis. Step 4 and Step 7 are the key steps of Algorithm 1. To assure the efficiency, we solve a system of linear equations with quadratic complexity to update u and v other than computing the matrix inverse with cubic complexity. Step 10 is a simple operation to rescale the results. So, the whole procedure is efficient and runs fast. Moreover, the algorithm is guaranteed to converge, as shown in Theorems 2 and 3.
Algorithm 1.
The AGN-SCCA Algorithm
Require:
Ensure:
Canonical loadings u and v.
1: Initialize ; and only on the training set;
2: while not converged do
3: while not converged regarding u do
4: Solve u according to Eq. (10)
5: end while
6: while not converged regarding v do
7: Solve v according to Eq. (11)
8: end while
9: end while
10: Scale u so that , and v so that .
2.3 The grouping effect analysis
It is important to investigate the grouping effect of the a structured learning method in handling high-dimensional data (Zou and Hastie, 2005). Although many structured SCCA methods have been proposed and could recover structure pattern practically. None of them provides a theoretical bound for the grouping effect. In this work, we have the following theorem which provides a qualitative theoretical bound in grouping correlated features.
Theorem 1 Given two datasets X and Y, and the pre-tuned parameters . Let be the solution to our SCCA problem of Eqs. (10) and (11). Without loss of generality, we consider the uith and ujth feature are only linked to each other on the graph, i.e. . Let ρij is the sample correlation between them, is their edge weight. Then the estimated canonical loading u satisfies,
| (12) |
and the estimated canonical loading v satisfies,
| (13) |
where is the weight between the ith and jth feature of v, and is their sample correlation coefficient.
The proof of this theorem can be found in Appendix A (See Supplementary File). Theorem 1 not only provides an upper bound for the difference between the canonical loading paths of the ith and jth features when they are positively correlated, but also provides a quantitative description when they are negatively correlated. If , the higher correlation two features have, the smaller difference there is between their coefficients. While if , a smaller value will generate a closer-to zero value for the sum of their coefficients. This is desirable because AGN-SCCA can estimate the coefficients with equal amplitude except signs for two negatively correlated features. This quantitative description for the grouping effect demonstrates that our novel structured SCCA is suitable for sparse structure learning.
2.4 The convergence analysis
We have the following theorems regarding the Algorithm 1.
Theorem 2 The problem Eq. (8) is lower bounded by –1.
Theorem 3 In each iteration, the AGN-SCCA algorithm monotonously decreases the objective value till it converges.
The proofs are provided in Appendix B and C (See Supplementary File) due to space limitation. Since the objective value keeps deceasing during the iteration, and the problem has the lower bound, the proposed algorithm is guaranteed to converge to a local optimum.
In our implementation, we set the stopping criterion of Algorithm 1 as and , where τ is a predefined estimation error. In this paper, is empirically set based on experiments.
3 Experiments
3.1 Experimental setup
3.1.1 Benchmarks
We chose three existing SCCA methods for comparison in this study, one is the state-of-the-art method NS-SCCA (network-structured CCA) (Chen et al., 2013), and the other two methods are the L1-SCCA (CCA with lasso) and FL-SCCA (CCA with fused lasso). The latter two can be found in package PMA (the PMA software package implements both L1-SCCA and FL-SCCA, and they are widely used as benchmark algorithms. See http://cran.r-project.org/web/packages/PMA/for details), which is widely used for SCCA studies. We do not compare our method with KG-SCCA (Yan et al., 2014) due to two reasons: (i) KG-SCCA uses -norm on one canonical loading (similar to S2CCA), uses -norm of on the other (similar to NS-SCCA), and requires predefined group and network structures. (ii) NS-SCCA uses the -norm of , which is supposed to be more reasonable in sparse learning than KG-SCCA since -norm is a sparse constraint but -norm is not. Therefore we include NS-SCCA instead of KG-SCCA as a competing method. We also do not compare our method with GN-SCCA (Du et al., 2015) because it only focuses on the positively correlated features. In addition, ssCCA (Chen et al., 2013), CCA-SG (CCA-sparse group) (Lin et al., 2013) and S2CCA (Du et al., 2014) are opted out, since they are knowledge-guided methods and applicable only when priori knowledge is available.
3.1.2 Parameter tuning
According to Eqs. (10) and (11), we have six parameters to be tuned. Obviously, this is very time consuming by blind grid search. Thus we here employ some tricks to speed up the tuning procedure. The major difference between the traditional CCA and SCCA is the penalty terms. On one hand, SCCA and CCA will yield similar results if the parameters are too small. On the other hand, SCCA will over-penalize the result when the parameters are too large. Thus a neither too large nor too small parameter is more reasonable. As a result, we tune these parameters from [, 10°, 101, 102]. All the parameters are tuned through the nested 5-fold cross-validation where and denote the jth subset of the input data (testing set), and and mean the canonical loadings estimated from the training set. We choose the as the tuned optimal parameters. For efficiency purpose, these parameters are only tuned from the first run of the cross-validation strategy. That is, the parameters are tuned when the first four folds are used as the training set. Then we directly use the tuned parameters for all the remaining experiments. Though this could limit the performance for the rest of the experiments, we find that it will not affect the performance significantly from the results which will be shown later. All these methods utilize the same partition during cross-validation to make a fair comparison.
3.2 Results on synthetic data
We simulate four different datasets with different properties in this study, and we expect the diversity could make sure a thorough comparison. The true signals and the strengths of correlation coefficients within these data are distinct. As a simulation of a large p small n problem, we here set the number of observations be smaller than the number of features, i.e. n = 80, p = 100 and q = 120. The generation procedure is similar to that in (Chen and Liu, 2012) except for the last step: (i) We create u and v separately according the predefined structure. (ii) We generate a latent variable . (iii) We generate X with the entry: , where , and Y with the entry: , where . (iv) For the first group of nonzero coefficients in u, we change the first half of their signs. At the same time, we also change the signs of the corresponding data. As a result, we still have where and are the data matrix and coefficients after the sign swap. Note that these synthetic data are order-independent, and thus this setup is equivalent to randomly change a portion of signs for coefficients u (Yang et al., 2012). For the Y side, we do the same. The details of the four datasets are as follow. (i) The first two datasets have the same signal structure, i.e. the same group structure regarding u and v. But their correlation coefficients are different. The correlation coefficient of the first dataset is 0.52, while that of the second dataset is 0.17. (ii) The third dataset is different from the first two datasets in its group structure regarding u and v. Its correlation coefficient is 0.58. (iii) The fourth dataset is different from all the above three datasets in its group structure regarding u and v. Its correlation coefficient is 0.51. The true signal of each dataset can be observed from the first row in Figure 1.
Fig. 1.
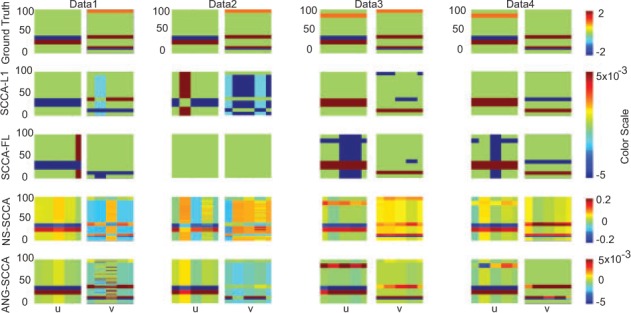
Canonical loadings estimated on four synthetic datasets. The first column is for Dataset 1, and the second column is for Dataset2, and so forth. For each dataset, the estimated weight of u is shown on the left figure, and v is on the right. The first row is the ground truth, and each remaining one corresponds to a method: (1) Ground Truth. (2) L1-SCCA. (3) FL-SCCA. (4) NS-SCCA. (5) AGN-SCCA
In Table 1, we present the estimated correlation coefficients from both training and testing data, and their differences from the true correlation coefficients (i.e. the numbers in parentheses). We use the boldface to highlight the highest value as well as those that are not significantly smaller than the highest value. For the training set, we observe that our method obtains the best correlation coefficients on Dataset 2 and Dataset 3, and it is only slightly smaller than the best method on the rest of the two datasets. Though AGN-SCCA does not obtain the highest for every dataset, it is not statistically different from the best method. If we consider the true correlation coefficients, we observe that AGN-SCCA and L1-SCCA are two methods which have smaller estimation errors. That is, both AGN-SCCA and L1-SCCA identify more accurate correlation coefficients than FL-SCCA and NS-SCCA regarding the training results. For the testing set, AGN-SCCA outperformed the competing methods on Dataset 3, and was not significantly different from the best method on the remaining datasets. Besides, AGN-SCCA’s estimation error is the smallest for Datasets 2–4, which means it performs better than the competing methods regarding the prediction performance. Generally, this is more interesting since the testing performance is more important than the training results. These results show that AGN-SCCA either outperforms or performs similarly to those competing methods in terms of estimated correlation coefficients.
Table 1.
5-fold cross-validation results on synthetic data: the estimated correlation coefficients of each individual fold and their MEAN are shown
| Methods | Dataset 1 (cc = 0.52) | MEAN | Dataset 2 (cc = 0.17) | MEAN | Dataset 3 (cc = 0.58) | MEAN | Dataset 4 (cc = 0.51) | MEAN | AVG. Error | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training results | |||||||||||||||||||||||||
| L1-SCCA | 0.51 | 0.56 | 0.50 | 0.47 | 0.59 | 0.53 (+0.01) | 0.25 | 0.12 | 0.26 | 0.18 | 0.25 | 0.21 (0.04) | 0.51 | 0.51 | 0.53 | 0.51 | 0.56 | 0.52 (-0.06) | 0.44 | 0.49 | 0.46 | 0.49 | 0.51 | 0.48 (-0.03) | 0.03 |
| FL-SCCA | 0.50 | 0.56 | 0.49 | 0.47 | 0.59 | 0.52 (0.00) | NaN | NaN | NaN | NaN | NaN | NaN | 0.51 | 0.53 | 0.56 | 0.59 | 0.56 | 0.55 (-0.03) | 0.50 | 0.54 | 0.47 | 0.55 | 0.54 | 0.52 (0.05) | 0.05 |
| NS-SCCA | 0.38 | 0.45 | 0.33 | 0.37 | 0.48 | 0.40 (-0.12) | 0.23 | 0.14 | 0.22 | 0.16 | 0.21 | 0.19 (0.02) | 0.32 | 0.36 | 0.39 | 0.47 | 0.40 | 0.39 (-0.19) | 0.28 | 0.48 | 0.45 | 0.38 | 0.41 | 0.40 (-0.11) | 0.11 |
| AGN-SCCA | 0.61 | 0.63 | 0.13 | 0.55 | 0.64 | 0.51 (-0.01) | 0.27 | 0.16 | 0.33 | 0.21 | 0.26 | 0.25 (0.08) | 0.47 | 0.58 | 0.60 | 0.56 | 0.60 | 0.56 (-0.02) | 0.45 | 0.54 | 0.46 | 0.55 | 0.53 | 0.51 (0.00) | 0.03 |
| Testing Results | |||||||||||||||||||||||||
| L1-SCCA | 0.57 | 0.16 | 0.65 | 0.71 | 0.12 | 0.44 (-0.08) | 0.39 | 0.40 | 0.13 | 0.26 | 0.02 | 0.24 (0.07) | 0.57 | 0.57 | 0.55 | 0.60 | 0.40 | 0.54 (-0.04) | 0.58 | 0.40 | 0.71 | 0.32 | 0.14 | 0.43 (-0.08) | 0.07 |
| FL-SCCA | 0.57 | 0.16 | 0.66 | 0.70 | 0.16 | 0.24 (-0.28) | NaN | NaN | NaN | NaN | NaN | NaN | 0.58 | 0.58 | 0.50 | 0.31 | 0.45 | 0.48 (-0.10) | 0.63 | 0.42 | 0.79 | 0.40 | 0.30 | 0.51 (0.00) | 0.14 |
| NS-SCCA | 0.49 | 0.15 | 0.16 | 0.70 | 0.39 | 0.48 (-0.04) | 0.01 | 0.32 | 0.57 | 0.22 | 0.02 | 0.23 (0.06) | 0.42 | 0.15 | 0.32 | 0.48 | 0.30 | 0.33 (-0.25) | 0.01 | 0.14 | 0.78 | 0.38 | 0.19 | 0.30 (-0.21) | 0.14 |
| AGN-SCCA | 0.60 | 0.24 | 0.31 | 0.74 | 0.32 | 0.44 (-0.08) | 0.25 | 0.07 | 0.18 | 0.28 | 0.01 | 0.16 (-0.01) | 0.73 | 0.60 | 0.45 | 0.50 | 0.56 | 0.57 (-0.01) | 0.58 | 0.26 | 0.77 | 0.39 | 0.19 | 0.44 (-0.07) | 0.04 |
The difference (numbers in parentheses) between the estimated correlation coefficients and the true ones, and their average estimated error area also shown. ’NaN’ means a method fails to estimate a pair of canonical loadings. ‘0.00’ means a very small value. The highest values and those that are NOT significantly worse (t-test with p-value smaller than 0.05) are shown in boldface.
We show the estimated canonical loadings of four SCCA methods in Figure 1. As we can see, none of these methods could generate stable results for the small-n-large-p problem when using cross-validation strategy. They still exhibit group structures for the estimated canonical loadings. However, neither L1-SCCA nor FL-SCCA can accurately recover the true signals. They cannot identify those coefficients with signs swapped. Thus they treat the positively and negatively correlated features with no difference. NS-SCCA and AGN-SCCA successfully recognize the coefficients whose signs are changed. The reason is that AGN-SCCA uses the absolute difference between the coefficients, and NS-SCCA takes advantage of the sign of sample correlation. Note the sign of sample correlation depends on the signal-to-noise ratio (SNR), and it is likely to be wrong due to a high proportion of noise. Therefore, for the three datasets with high correlations (Dataset 1, Dataset 3 and Dataset 4), NS-SCCA could exhibit a similar pattern to AGN-SCCA with respect to the canonical loadings. While for the second dataset whose correlation is small, AGN-SCCA outperforms NS-SCCA in terms of the structure pattern, especially for the canonical loading v. In order to make this clear, we also calculate the AUC (area under ROC curve) to present the performance regarding the canonical loadings pattern in Table 2 with those best values marked in bold. We observe that both structured SCCA, i.e. AGN-SCCA and NS-SCCA, perform consistently better than L1-SCCA and FL-SCCA. Our AGN-SCCA obtains the best scores in most runs except on few folds, especially for the canonical loadings v.
Table 2.
The AUC (area under the curve) of estimated canonical loadings on synthetic data: the AUC of each individual fold and their MEAN are shown
| Methods | Dataset 1 (cc = 0.52) | MEAN | Dataset 2 (cc = 0.17) | MEAN | Dataset 3 (cc = 0.58) | MEAN | Dataset 4 (cc = 0.51) | MEAN | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimated Canonical Loading u | ||||||||||||||||||||||||
| L1-SCCA | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.80 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 |
| FL-SCCA | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | NaN | NaN | NaN | NaN | NaN | NaN | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.83 | 1.00 | 1.00 | 1.00 | 0.97 |
| NS-SCCA | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.80 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 |
| AGN-SCCA | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.67 | 1.00 | 1.00 | 1.00 | 1.00 | 0.93 |
| Estimated Canonical Loading v | ||||||||||||||||||||||||
| L1-SCCA | 0.83 | 0.33 | 0.83 | 0.83 | 0.83 | 0.73 | 0.33 | 0.00 | 0.00 | 0.33 | 0.00 | 0.13 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| FL-SCCA | 0.67 | 0.63 | 0.67 | 0.67 | 0.67 | 0.66 | NaN | NaN | NaN | NaN | NaN | NaN | 0.67 | 0.67 | 0.67 | 0.83 | 0.67 | 0.70 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| NS-SCCA | 0.67 | 0.67 | 0.33 | 0.67 | 0.67 | 0.60 | 0.33 | 0.00 | 0.00 | 0.28 | 0.00 | 0.12 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| AGN-SCCA | 1.00 | 0.72 | 0.59 | 0.67 | 1.00 | 0.80 | 0.33 | 0.00 | 0.33 | 0.67 | 0.00 | 0.27 | 0.67 | 1.00 | 1.00 | 1.00 | 1.00 | 0.93 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
‘NaN’ means the AUC is not available. The best MEAN values of each fold are shown in boldface.
In summary, the AGN-SCCA not only estimates the most accurate correlation coefficients in most cases, but also identifies the signal locations with the best accuracy in all the cases. These promising results reveal that our method outperforms the competing methods, showing that it can handle a range of synthetic datasets with distinct structures and correlations.
3.3 Results on real neuroimaging genetics data
Apart from the synthetic data, it is essential to evaluate our method on real neuroimaging genetics data. Real imaging genetics data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). For up-to-date information, see www.adni-info.org.
The genotyping and baseline amyloid imaging data (preprocessed [11C] Florbetapir PET scans) of 283 non-Hispanic Caucasian participants were downloaded from the ADNI website (adni.loni.usc.edu). The amyloid imaging data were preprocessed according to the steps in (Yan et al., 2014), and then pre-adjusted by regressing out the effects of the baseline age, gender, education and handedness. Using the voxel-based imaging data, we extracted 191 ROI level mean amyloid measurements, where the ROIs were defined by MarsBaR AAL atlas. For the genotyping data, we included 58 SNP markers within the APOE gene, including the APOE e4 SNP rs429358 (i.e. the best-known AD genetic risk factor) (Ramanan et al., 2014). We aim to evaluate the associations between the amyloid data and the APOE SNP data using the proposed method.
In Table 3, we present the correlation coefficients estimated by the four different SCCA methods via 5-fold cross-validation strategy. As we can see, AGN-SCCA can not only identify the strongest correlation on the training set, but also outperform those competing methods on the testing set. Although all methods yield acceptable correlation coefficients, AGN-SCCA significantly and consistently outperforms other SCCA methods, demonstrating its capability in identifying strong imaging genetic associations.
Table 3.
5-fold cross-validation results on real data: the estimated correlation coefficients of each individual fold and their MEAN are shown
| Methods | Training results | MEAN | Testing results | MEAN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1-SCCA | 0.57 | 0.56 | 0.56 | 0.56 | 0.54 | 0.56 | 0.46 | 0.54 | 0.53 | 0.49 | 0.63 | 0.53 |
| FL-SCCA | 0.51 | 0.48 | 0.50 | 0.50 | 0.48 | 0.49 | 0.38 | 0.51 | 0.45 | 0.44 | 0.56 | 0.47 |
| NS-SCCA | 0.53 | 0.50 | 0.53 | 0.51 | 0.50 | 0.52 | 0.41 | 0.42 | 0.37 | 0.42 | 0.62 | 0.45 |
| AGN-SCCA | 0.61 | 0.59 | 0.59 | 0.59 | 0.58 | 0.59 | 0.48 | 0.59 | 0.57 | 0.52 | 0.65 | 0.56 |
The best value and those that are NOT significantly worse (t-test with p-value smaller than 0.05) are shown in boldface.
We also show the canonical loadings estimated from the training set in Figure 2 using the heat maps. In Figure 2, each row refers to a method. The estimated u, containing weights for genetic markers, is shown on the left panel and the estimated v, containing weights for the imaging markers, is shown on the right. For the canonical loading u, AGN-SCCA only identified the APOE e4 SNP rs429358, i.e. the best-known AD genetic risk factor. L1-SCCA and FL-SCCA also discovered the APOE e4 SNP, but reported much more additional SNPs than AGN-SCCA. Thus their results are not as sparse as AGN-SCCA. NS-SCCA also identified many SNPs which is hard to interpret. For the v side, we can observe that FL-SCCA fused the results of L1-SCCA because of its pairwise smoothness penalty. However, their results consists of too many signals, making them hard to interpret. NS-SCCA identified even more signals than FL-SCCA and L1-SCCA due to its pairwise smoothness imposed on the whole graph, which is suboptimal for biomarker discovery.
Fig. 2.
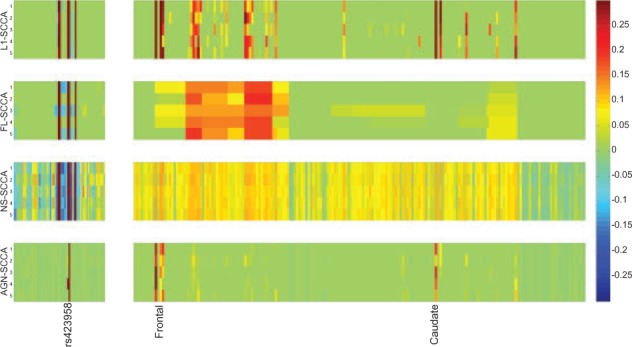
Canonical loadings estimated on real imaging genetics dataset. Each row corresponds to an SCCA method: (1) L1-SCCA. (2) FL-SCCA. (3) NS-SCCA. (4) AGN-SCCA. For each method, the estimated weights of u are shown on the left panel, and those of v are on the right
As a result, we could see that AGN-SCCA exhibits a very clean pattern and reports very few relevant imaging signals, including frontal and caudate regions that are known to be related to AD (Jiji et al., 2013). In short, the proposed AGN-SCCA algorithm successfully discovered a biologically meaningful associations between APOE SNP rs429358 and the amyloid accumulations at the AD related brain regions. This demonstrates that AGN-SCCA can not only reveal strong imaging genetic associations, but also identify meaningful and relevant genetic and imaging markers.
4 Conclusion
We have proposed a novel structured regularization term using the pairwise difference between absolute values of two weights, and incorporated it into a SCCA framework. This proposed structured SCCA model, named as AGN-SCCA, aims to discover any group or network structure laying behind the data. We have demonstrated that AGN-SCCA has strong upper bound of grouping effect, and have developed an iterative procedure with proven convergence.
The existing structured SCCA methods either use the group lasso (Du et al., 2014; Lin et al., 2013; Yan et al., 2014) or the graph/netwrok-guided fused lasso (Chen et al., 2013; Chen and Liu, 2012; Chen et al., 2012; Du et al., 2015; Yan et al., 2014) to model the structure information. The first type of methods rely on prior knowledge to define the group structure, and the prior knowledge is sometimes unavailable in real applications. The latter type of methods can perform well on any given priori knowledge. In case the prior knowledge is not available, these methods can also work via using the sample correlation to define the graph/network constraint. However, they depend on the sign of sample correlation being defined in advance, which could be wrongly estimated due to possible graph/network misspecification caused by noise (Yang et al., 2012).
Our proposed SCCA is different from those previously published ones in the following aspects: (i) AGN-SCCA employs a novel absolute value based GraphNet penalty, and it does not require to estimate the sign of sample correlation. (ii) The AGN-SCCA could tune positively correlated features as well as negatively correlated ones to have similar weights despite the correlation signs. (iii) AGN-SCCA has a strong theoretical upper bound for the grouping effect, and the corresponding algorithm is guaranteed to converge fast.
We have compared AGN-SCCA with three competing SCCA methods with different penalty functions, including L1-SCCA, FL-SCCA and NS-SCCA, using both synthetic data and real imaging genetics data. The experimental results demonstrate the following: (i) For the estimated correlation coefficients, AGN-SCCA obtained the best or comparable results on the synthetic data, and significantly outperformed the competing methods on the real data. (ii) For the estimated canonical loadings, AGN-SCCA yielded better canonical loading pattern on both synthetic data and real data, especially on the real data where it produced much cleaner patterns than the competing methods. By discovering a strong association between the APOE SNP data and the amyloid accumulation data in an AD study, AGN-SCCA demonstrated itself as a promising structured SCCA method. The theoretical convergence and upper bound of the grouping effect further reveal that AGN-SCCA is of efficiency and effectiveness in identifying meaningful bi-multivariate associations in brain imaging genetics studies. In this work, we only tested AGN-SCCA while using data-driven covariance structure as the graph/network constraint. In the future, we will apply the AGN-SCCA model to more general cases and test its performance when priori knowledge is available.
Supplementary Material
Acknowledgements
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Funding
At Indiana University, this work was supported by the National Institutes of Health [R01 LM011360 to L.S. and A.J.S., U01 AG024904 to M.W., RC2 AG036535 to M.W., R01 AG19771 to A.J.S., P30 AG10133 to A.J.S., UL1 TR001108 to A.S., R01 AG 042437 to P.C., and R01 AG046171 to R.K.], the National Science Foundation [IIS-1117335 to L.S.], the United States Department of Defense [W81XWH-14-2-0151 to T.M., W81XWH-13-1-0259 to M.W., and W81XWH-12-2-0012 to M.W.], and the National Collegiate Athletic Association [Grant No. 14132004 to T.M.]. At University of Texas at Arlington, this work was supported by the National Science Foundation [CCF-0830780 to H.H., CCF-0917274 to H.H., DMS-0915228 to H.H., and IIS-1117965 to H.H.]. At University of Pennsylvania, the work was supported by the National Institutes of Health [R01 LM011360 to J.M., R01 LM009012 to J.M., and R01 LM010098 to J.M.].
Conflict of Interest: none declared.
References
- Chen J. et al. (2013) Structure-constrained sparse canonical correlation analysis with an application to microbiome data analysis. Biostatistics, 14, 244–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Liu H. (2012) An efficient optimization algorithm for structured sparse cca, with applications to eqtl mapping. Stat. Biosci., 4, 3–26. [Google Scholar]
- Chen X. et al. (2012). Structured sparse canonical correlation analysis. In: AISTATS.
- Du L. et al. (2014). A Novel structure-Aware Sparse Learning Algorithm for Brain Imaging Genetics. MICCAI, Boston, MA, pp. 329–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du L. et al. (2015). Gn-scca: Graphnet based sparse canonical correlation analysis for brain imaging genetics In: Guo Y. et al. , (eds), Brain Informatics and Health, Springer, London, UK, pp. 275–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosenick L. et al. (2013) Interpretable whole-brain prediction analysis with graphnet. NeuroImage, 72, 304–321. [DOI] [PubMed] [Google Scholar]
- Jiji S. et al. (2013) Segmentation and volumetric analysis of the caudate nucleus in alzheimer’s disease. Eur. J. Radiol., 82, 1525–1530. [DOI] [PubMed] [Google Scholar]
- Lin D. et al. (2013) Correspondence between fMRI and SNP data by group sparse canonical correlation analysis. Med. Image Anal., 18, 891–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkhomenko E. et al. (2009) Sparse canonical correlation analysis with application to genomic data integration. Stat. Appl. Genet. Mol. Biol., 8, 1–34. [DOI] [PubMed] [Google Scholar]
- Ramanan V.K. et al. (2014) APOE and BCHE as modulators of cerebral amyloid deposition: a florbetapir pet genome-wide association study. Mol. Psychiatry, 19, 351–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vounou M. et al. (2010) Discovering genetic associations with high-dimensional neuroimaging phenotypes: a sparse reduced-rank regression approach. NeuroImage, 53, 1147–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D.M., Tibshirani R.J. (2009) Extensions of sparse canonical correlation analysis with applications to genomic data. Stat. Appl. Genet. Mol. Biol., 8, 1–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D.M. et al. (2009) A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics, 10, 515–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J. et al. (2014) Transcriptome-guided amyloid imaging genetic analysis via a novel structured sparse learning algorithm. Bioinformatics, 30, i564–i571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang S. et al. (2012). Feature grouping and selection over an undirected graph In: Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, pp. 922–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H., Hastie T. (2005) Regularization and variable selection via the elastic net. J. R. Stat. Soc.: Ser. B (Stat. Methodol.), 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


