Transmit Array Spatial Encoding (TRASE) using broadband WURST pulses for RF spatial encoding in inhomogeneous B₀ fields

Abstract

Transmit Array Spatial Encoding (TRASE) is a promising new MR encoding method that uses transmit RF ($B_1^{+}$) phase gradients over the field-of-view to perform Fourier spatial encoding. Acquisitions use a spin echo train in which the transmit coil phase ramp is modulated to jump from one k-space point to the next. This work extends the capability of TRASE by using swept radiofrequency (RF) pulses and a quadratic phase removal method to enable TRASE where it is arguably most needed: portable imaging systems with inhomogeneous B₀ fields. The approach is particularly well-suited for portable MR scanners where (a) inhomogeneous B₀ fields are a byproduct of lightweight magnet design, (b) heavy, high power-consumption gradient coil systems are a limitation to siting the system in non-conventional locations and (c) synergy with the use of spin echo trains is required to overcome intra-voxel dephasing (short $T_2^{\ast }$) in the inhomogeneous field. TRASE does not use a modulation of the B₀ field to encode, but it does suffer from secondary effects of the inhomogeneous field. Severe artifacts arise in TRASE images due to off-resonance effects when the RF pulse does not cover the full bandwidth of spin resonances in the imaging FOV. Thus, for highly inhomogeneous B₀ fields, the peak RF power needed for high-bandwidth refocusing hard pulses becomes very expensive, in addition to requiring RF coils that can withstand thousands of volts. In this work, we use swept WURST RF pulse echo trains to achieve TRASE imaging in a highly inhomogeneous magnetic field (ΔB₀/B₀ ~ 0.33% over the sample). By accurately exciting and refocusing the full bandwidth of spins, the WURST pulses eliminate artifacts caused by the limited bandwidth of the hard pulses used in previous realizations of TRASE imaging. We introduce a correction scheme to remove the unwanted quadratic phase modulation caused by the swept pulses. Also, a phase alternation scheme is employed to mitigate artifacts caused by mixture of the even and odd-echo coherence pathways due to defects in the refocusing pulse. In this paper, we describe this needed methodology and demonstrate the ability of TRASE to Fourier encode in an inhomogeneous field (ΔB₀/B₀ ~ 1% over the full FOV).

1. Introduction

A growing body of research explores the use of lightweight, low-field, portable magnetic resonance relaxometers and imaging systems for medical applications and materials analysis. Single sided scanners [1] such as the NMR-MOUSE [2] use portable permanent magnets for profiling and relaxometry. The NMR-MOUSE magnet's rapid field decay over the sensitive region is used to create 1D profiles of samples such as human skin [3]. The NMR-MOUSE's capability has been extended to 2D [4] and 3D imaging [5], however the device can only image thin samples and is not applicable to brain imaging. Other approaches based on single-sided and “inside-out” magnets have been used for rock porosity analysis in oil well prospecting [6] and for assessing properties of soil and food [1]. Adding Fourier encoding to these systems in directions other than the readout (projection) direction is made difficult by the extremely inhomogeneous field.

A major difference between portable NMR systems and conventional MRI scanners is that, in the former, the main B₀ field is usually inhomogeneous. This concession can dramatically reduce the complexity of the device, thus minimizing weight, cost, and power requirements and enhancing portability. But this inhomogeneity introduces two significant obstacles to performing Fourier imaging with conventional B₀ gradient encoding. First, the bandwidth of spins in the sample may become too broad to be excited by typical RF pulses (e.g. hard pulses) at safe RF power levels. Second, to perform traditional Fourier readout spatial encoding (and/or slice selection), the applied linear B₀ gradients must dominate the variations in the background B₀ field. Phase encoding in a spin echo sequence has been demonstrated in highly inhomogeneous fields [7], but 2D and 3D encoding with pure phase encoding are time-consuming since only one k-space point is acquired per echo, and moreover the need for gradient coils and power amplifiers can limit portability.

Nonetheless, light-weight, inhomogeneous MR scanners based on arrays of permanent magnets have been proposed as portable devices for human imaging. In one such approach [8], the background B₀ field variation is used as a “built-in” gradient field for acquiring generalized spin echo projections of the sample that can be reconstructed using iterative matrix solvers. This system still requires a method of encoding along the axis of rotation and the B₀ inhomogeneity (short $T_2^{\ast }$) requires the use of spin echo acquisitions.

Methods for creating long spin echo trains in highly inhomogeneous fields have been demonstrated using frequency-swept pulses that excite and refocus all spins over the sample with dramatically lower peak power levels compared to hard pulses [9,10]. In Ref. [9], frequency-swept pulses were played in a CPMG spin echo train to acquire echoes from a sample with a 120 kHz linewidth in an inhomogeneous B₀ field. Compared with hard pulses, the frequency-swept pulses provided a 3-fold or greater signal enhancement and corresponding increase in the spectral width of the acquired data (Fourier transform of the echoes).

Frequency-swept RF pulses have also been used as key components of spatial encoding schemes that provide improved robustness to B₀ inhomogeneity, including MRI by steering resonance through space (STEREO) [11] and spatiotemporally-encoded MRI (SPEN) [12–16]. Both methods use swept RF pulses to excite and/or refocus different Larmor frequency isochromats at different times. The focal point of the resulting quadratic phase profile is then steered across the object during readout using linear encoding gradients. While these methods show significant promise, they still rely on slewed linear B₀ gradient systems whose coils must overcome the B₀ inhomogeneities and whose power amplifiers and cooling systems are an encumbrance to remote siting and portability. Further, while they are being pursued for use in inhomogeneous fields, this class of methods has only been experimentally demonstrated with modest inhomogeneities (i.e. ~ 100s of Hz) [11,12].

The Bloch–Siegert shift imparted by off-resonant RF pulses has been recently exploited for frequency [17] and phase [18] encoding using pure transmit RF field ($B_1^{+}$) spatial encoding. In this approach, an RF coil with a spatially varying $B_1^{+}$ amplitude along the encoding direction is used (typically a linear profile). When an off-resonant RF pulse is played on such a coil after spin excitation by a uniform $B_1^{+}$ coil, the spin phase becomes a function of position and can be used for spatial encoding. While early results in relatively homogeneous B₀ fields show promise, the utility of the method for highly inhomogeneous fields is limited by the trade-off between Bloch–Siegert encoding efficiency and off-resonance performance.

In the present work, we show that Transmit Array Spatial Encoding (TRASE) [19], a recently-introduced $B_1^{+}$ spatial encoding method, can be adapted for imaging in highly inhomogeneous B₀ fields without the use of external imaging gradients. TRASE uses $B_1^{+}$ phase gradients produced by tailored RF transmit coils to impart a progressively increasing spatial phase modulation to each echo in a spin echo train. The center point of each echo is a sample in k-space with the echo-train traversing a line in k-space (for 1D TRASE) analogous to conventional phase encoding with linear B₀ gradients. TRASE can be performed along any dimension for 1D, 2D, or 3D imaging using appropriate coils for generating $B_1^{+}$ phase gradients along each desired encoding direction. This allows image formation without using conventional B₀ imaging gradients. High-resolution 2D TRASE images acquired in a 0.2 Tesla homogeneous field display comparable image quality to conventional B₀ gradient encoded images [20].

The TRASE method is best-suited for low field imaging where specific absorption rates (SAR) are lower, allowing long spin echo trains without significant RF heating. Adding to its versatility, TRASE is compatible with the use of parallel RF receive arrays [21] and parallel imaging approaches [22,23] for accelerated imaging using undersampled k-space data. Moreover, even though TRASE is a type of phase encoding, un-encoded signal outside the FOV does not alias into the image as a wrapping artifact, but instead manifests as line artifacts in the corner of the image [24]. Finally, since TRASE switches only RF gradient fields, it has the benefit of being silent.

TRASE is particularly appealing for portable MR systems since it only uses the transmit RF system for spatial encoding. This reduces or eliminates the need for high power gradient amplifiers as well as heavy, noisy gradient coils and their associated water cooling. The result is a dramatically simplified imaging system. As an independent encoding mechanism, TRASE can be used in highly inhomogeneous B₀ fields without requiring that the $B_1^{+}$ phase gradient dominate the variation in B₀. This stands in contrast to other methods that have been proposed for portable MRI systems, such as STEREO [11], which still rely on a B₀ gradient system for spatial encoding.

Although TRASE appears well-suited for portable imagers and their spatially inhomogeneous fields, the excitation and refocusing pulses must cover the bandwidth of the spins in the imaging volume. If the full spin bandwidth is not covered, then off-resonance effects degrade performance by introducing flip angle and phase errors to spin isochromats outside the pulse bandwidth. Bloch simulations show that significant TRASE artifacts arise for refocusing pulse flip angles of less than 150° [25]. A recent paper states that for echo trains of hard pulses with duration t_p, “good” TRASE performance is achieved for sample bandwidths on the order of 0.1/t_p and “fair” performance was noted for bandwidths on the order of 0.2/t_p [20]. The authors suggest that TRASE could benefit from composite refocusing pulses, but do not explore the topic experimentally.

For proof-of-concept 1D imaging, we target a bandwidth of 30 kHz in a highly inhomogeneous human head-sized permanent magnet (ΔB₀/B₀ ~ 1%) [7]. For this field inhomogeneity, the use of hard pulses would require impractical peak power. For example, to achieve “fair” TRASE performance a refocusing pulse length of ~6 μs would be required. This corresponds to an 83 kHz (1.9 mT) peak field, about 2 orders of magnitude higher than the field achievable using the body RF coil of conventional clinical scanners.

In this work, we demonstrate a method for overcoming off-resonance artifacts in TRASE imaging by replacing hard pulses with WURST frequency-swept pulses in the spin echo train [8]. The swept pulses minimize flip angle and phase errors resulting from the range of B₀ fields across the FOV. However, the WURST pulses introduce a quadratic phase across the excitation bandwidth. To mitigate the effect of this phase in TRASE imaging, we introduce a simple phase correction method to remove the quadratic phase modulation imparted by the swept pulses to even-numbered echoes in the train. This renders the entire echo train compatible with TRASE spatial encoding. We show experimental 1D TRASE images of two water phantoms in a field with a peak inhomogeneity range of 30 kHz. Some results were previously presented in abstract form [26].

2. Theory

In this section, we briefly review the use of RF pulses with linear frequency sweeps (quadratic phase sweeps) on the signal phase in a spin echo train. We then discuss a simple correction method for removing the unwanted quadratic phase modulation from even-numbered echoes in the train, restoring a conventional echo shape and making the entire spin echo train usable for TRASE imaging.

As described by Kunz [27], when frequency-swept excitation and refocusing pulses are applied in the presence of a static inhomogeneous B₀ field, they impart a frequency-dependent phase to the spins. Assuming a symmetric frequency sweep around the Larmor frequency, the relevant phase of the spin isochromats following the π/2 excitation pulse is:

$${\varphi }_{exc}\left(f\right)=\pi f^2∕R_{exc}$$ (1)

and the phase imparted by the π refocusing pulse is:

$${\varphi }_{ref}\left(f\right)=2\pi f^2∕R_{ref},$$ (2)

where f is the frequency offset from the Larmor frequency and R is the RF pulse frequency sweep rate. Because the refocusing pulse inverts the phase profile imparted by the excitation pulse, the overall phase after an excitation pulse followed by a single refocusing pulse is:

$$\varphi \left(f\right)=-\pi f^2∕R_{exc}+2\pi f^2∕R_{ref}.$$ (3)

The quadratic phase imparted by the pulse pair vanishes if the sweep rates are set to R_ref = 2R_exc. For simple linear frequency sweeps, this condition is typically met by setting the duration of the refocusing pulse to be half the duration of the excitation pulse.

In swept pulse spin echo trains, this sweep rate condition (R_ref = 2R_exc) cancels quadratic phase in odd-numbered echoes, leaving these echoes with only conventional B₀-based phase modulations. However, the quadratic phase modulation remains on even-numbered echoes. Here, the frequency-domain signal is multiplied by the quadratic phase profile (ϕ_ref) applied by the last, uncancelled refocusing pulse [28]. Likewise, the time-domain signal is convolved by the time-domain quadratic phase function [28]. Since the shape of the quadratic phase function is preserved under the Fourier transform, the time domain function is also a quadratic phase “chirp” kernel proportional to exp(i2πβt²), where coefficient β depends on the sweep rate of the refocusing pulse.

Time-domain convolution of the echo with this kernel leads to smearing of the signal across the readout window, such that the shape of the time-domain signal comes to approximate the histogram of spin frequencies in the inhomogeneous B₀ field (i.e., a projection of the sample if the inhomogeneity originated from a gradient field). This effect is due to each Larmor frequency isochromat refocusing at a different point in time. Spin echoes acquired in this manner have been called “spectral echoes” [9] because of their resemblance to the frequency spectrum of the sample. The width of the spectral echo in the time domain depends on the bandwidth of the spins over the sample and the sweep rate of the RF pulse. The faster the pulse is swept, the narrower the time delay between excitation and refocusing of the isochromats, and the shorter the duration of the resulting spectral echo. Spatial quadratic phase profiles applied by RF pulses and/or nonlinear B₀ fields have been proposed in the past to perform slice selection [29], “phase scrambling” for dynamic range compression during signal reception [30], and reduced FOV imaging [31–33]. While spectral echoes are useful for some applications, they cannot be directly used with TRASE imaging.

Assuming the acquisition window is wide enough to capture the full “bandwidth” of the spectral echo, then convolution of the conventional echo with the chirp kernel is an information-preserving transform. To restore a conventional echo shape, the quadratic phase modulation can be removed in one of two ways: (a) convolution by the complex conjugate of the chirp kernel in the time domain, or (b) division by the quadratic phase profile in the frequency domain [32]. The second operation is equivalent to subtracting out the phase difference between the Fourier transforms of two successive echoes in the train, which removes the phase imparted by the frequency-swept pulse while retaining the phase contributed by the intended encoding schemes.

Spectral echoes that have been transformed into conventional echoes can be used for TRASE imaging. However, the success of the quadratic phase removal depends on the echo train consisting of interleaved conventional (odd) and spectral (even) echoes with no mixture of the two. In ordinary spin echo trains that satisfy the CPMG conditions [34], defects in the refocusing pulse lead to multiple spin echo and stimulated echo pathways, which all refocus at the same time and constructively interfere to form a conventional echo shape. Unfortunately, in frequency-swept echo trains, defects in the refocusing pulse flip angle can lead to “mixing” of the conventional and spectral echoes. This complicates the quadratic phase removal and leads to image artifacts with TRASE. However, this problem can be largely avoided through careful choice of a pulse phase alternation scheme for each group of four successive echoes, as described in Section 3.

To implement quadratic phase removal in the frequency domain, the signal acquired in the nth readout, denoted w_n, is first Fourier transformed to yield $W_n=\mathcal{F}\left\{w_n\right\}=a_n{e}^{i{\varphi }_n}$, where $\mathcal{F}$ is the Fourier transform operator. The phase correction is then computed as the difference in Fourier domain phase of the first two echoes in the train: (ϕ₂ – ϕ₁). This phase difference corresponds to the extra phase modulation applied by the second swept refocusing pulse. This term is subtracted in the Fourier domain from the phase of all even-numbered echoes in the train and the result is inverse Fourier transformed to generate the set of phase-corrected echoes, denoted ŵ_n. A phase factor of π is additionally applied to remove the effects of the pulse phase-alternation scheme. The correction applied to echoes in each group of four is thus described as follows:

$${\widehat{w}}_n=\{\begin{array}{cc}{w}_n,\hfill & n=1,5,9,\dots \hfill \\ {\mathcal{F}}^{-1}\left\{a_n{e}^{i({\varphi }_n-({\varphi }_2-{\varphi }_1))}\right\},\hfill & n=2,6,10,\dots \hfill \\ w_n{e}^{i\pi },\hfill & n=3,7,11,\dots \hfill \\ {\mathcal{F}}^{-1}\left\{a_n{e}^{i({\varphi }_n-({\varphi }_2-{\varphi }_1))}\right\}{e}^{i\pi },\hfill & n=4,8,12,\dots \hfill \end{array}\phantom{\}}$$ (4)

For noisy data, it may be advantageous to fit the phase difference (ϕ₂ – ϕ₁) to a second-order polynomial (weighted by the magnitude of the spectrum at each point) in order to limit noise propagation.

The phase correction term can also be calculated directly based on the sweep rate of the refocusing pulses: $e^{-i({\varphi }_2-{\varphi }_1)}=e^{-i2\pi f^2∕R_{ref}}$. The Fourier transform of the echo is multiplied by this phase correction factor and then inverse Fourier transformed to obtain the corrected echo. Equivalently, the time-domain echo can be convolved with the chirp kernel that is the Fourier transform of the phase correction:

$${\mathcal{F}}^{-1}\left\{e^{-i2\pi f^2∕R_{ref}}\right\}=\sqrt{\frac{R_{ref}}{2}}{e}^{i\pi ∕4}{e}^{-i\pi R_{ref}{t}^2∕2}$$ (5)

When implementing the convolution numerically, it is necessary to divide by the number of elements in the echo signal multiplied by the number of elements in the chirp kernel. In either domain, care must be taken in computing the phase correction analytically, since it does not account for timing errors in the pulse sequence (which translate the quadratic phase profile relative to the echo time origin) or other defects.

3. Methods

WURST pulses are a close approximation to the simplest frequency swept pulse: a rectangular amplitude envelope with linear frequency sweep. The WURST pulse deviates from this basic swept pulse by softening the rising and falling edge with an amplitude taper and therefore reduces ringing in the off-resonance spin response. Hyperbolic secant swept pulses [35], an alternative pulse shape option, give sharper frequency band transitions than WURST pulses; this provides advantages for applications such as slice selection. Moreover, hyperbolic secant pulses can be paired in a way that cancels the quadratic phase modulation in the first echo [10]. However, hyperbolic secant pulses are not as efficient as WURST pulses for very wide bandwidths (as proposed here), and therefore tend to be longer. Since TRASE imaging relies on long echo trains, it is important to use the shortest refocusing pulses possible to minimize image artifacts caused by T₂-decay. For signals acquired in the presence of strong gradients, if the echo spacing becomes too long, TRASE imaging performance may also be limited by the diffusion weighting [1]. For these reasons, the choice of WURST pulses for TRASE imaging in an inhomogeneous field is motivated by the need to optimize pulse efficiency; the sharpness of the band edge transitions of the spin isochromats is not important in this application.

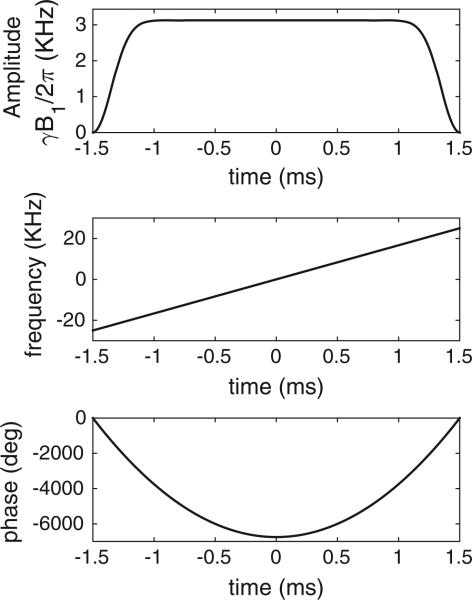
A WURST pulse pair is used to demonstrate the properties of frequency-swept spin echo trains in a highly inhomogeneous field using a large bottle phantom (following the experiments in Ref. [8]). The refocusing pulse design (Fig. 1) uses a WURST-40 amplitude envelope [36] and a linear frequency sweep of R = 50 kHz over pulse duration τ_ref = 3 ms to adequately cover the 30 kHz bandwidth (Fig. 2). The excitation has the same envelope and sweep width but with twice the pulse duration to satisfy the previously described sweep rate condition for quadratic phase cancellation. The peak pulse amplitudes are γB_1,exc/2π = 780 Hz and γB_1,ref/2-π = 3.12 kHz. In addition, a second pulse pair is designed with an R = 25 kHz sweep width and half the pulse duration for efficient 1D TRASE imaging of smaller, structured phantoms with narrower spin frequency histograms. The reduced sweep width enables shorter pulse lengths and reduced echo spacing, limiting blurring from T₂-decay. This is advantageous for high-resolution TRASE imaging, where long echo trains are necessary.

Fig. 1.

Profile of WURST-40 refocusing pulse design. Sweep width is 50 kHz, pulse duration is 3 ms, peak γB₁/2π is 3.12 kHz, and amplitude taper coefficient is 40. The excitation pulse uses the same profile but with duration 6 ms and γB₁/2π = 780 Hz.

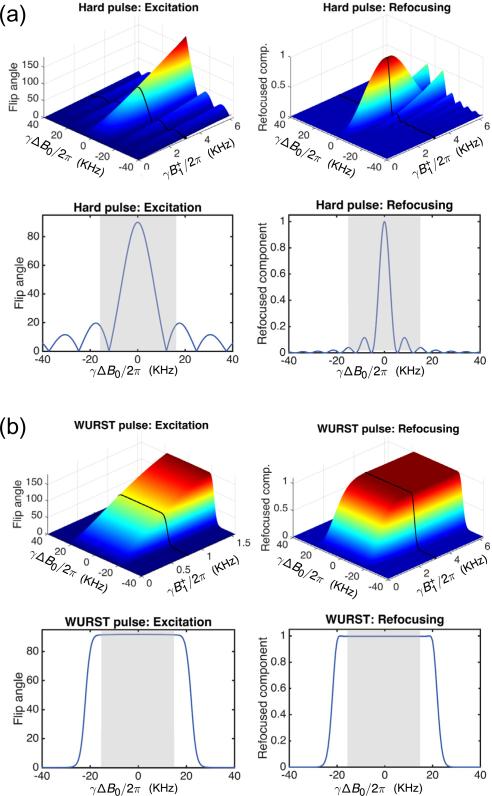
Fig. 2.

Simulated flip angle and refocused component as a function of off-resonance (ΔB₀) and transmit RF amplitude deviation ($\Delta B_1^{+}$) for hard pulses and 50 kHz WURST pulses. The 1D plots correspond to the black lines on the 2D plots at the nominal $B_1^{+}$ values used in experiments. The target B₀ bandwidth of 30 kHz is indicated with gray shading in the 1D profile plots. (a) Hard pulse pair (80 μs and 160 μs, the shortest achievable pulse lengths with the available amplifier and coil hardware). Hard pulse performance degrades rapidly with both B₀ and $B_1^{+}$ variation, motivating the use of swept WURST pulses. (b) The WURST pulse pair (described in Fig. 1) covers the desired excitation bandwidth. The WURST refocusing pulse amplitude is chosen to lie is in the adiabatic regime ($\mid B_1^{+}\mid >d{B}_1∕dt$). Refocusing pulse errors can create multiple coherence pathways in the echo train and “mixing” of conventional and spectral echoes (see Fig. 4). As a precaution against this effect, the refocusing pulse phase is alternated in the echo train to prevent a mixture of conventional and “spectral” echoes.

Fig. 2 shows Bloch simulations of the 50 kHz sweep width WURST excitation and refocusing pulse pair along with the shortest hard pulse pair achievable with the same hardware. The Bloch simulations use 2 × 2 rotation matrices specified by Cayley–Klein parameters to represent the action of the RF pulse on magnetization at each time point and isochromat [37]. The simulation time step is chosen so that no spin isochromat undergoes a rotation of more than 15° during the interval. Each pulse is simulated over an 80 kHz bandwidth for a range of $B_1^{+}$ amplitudes. The accuracy of refocusing pulses is evaluated using the refocused component [38]. A refocused component amplitude of unity for a particular isochromat means that the transverse spins are flipped symmetrically about the intended refocusing axis and are independent of B₀ inhomogeneity.

The simulations show that while a hard excitation pulse achieves a 90° flip angle only at the center of the spin bandwidth, the WURST pulse achieves a nearly-uniform 90° flip angle over the entire 30 kHz bandwidth (indicated in gray). The difference in the refocused component between hard pulses and WURST pulses is even more pronounced. In addition to covering the entire target bandwidth, the WURST refocusing pulse is also more robust to $B_1^{+}$ amplitude deviations in the adiabatic regime, where $\mid B_1^{+}\mid >d{B}_1∕dt$. The refocused component is therefore relatively insensitive to flip angle errors within the adiabatic regime, reducing the likelihood of artifacts in TRASE images.

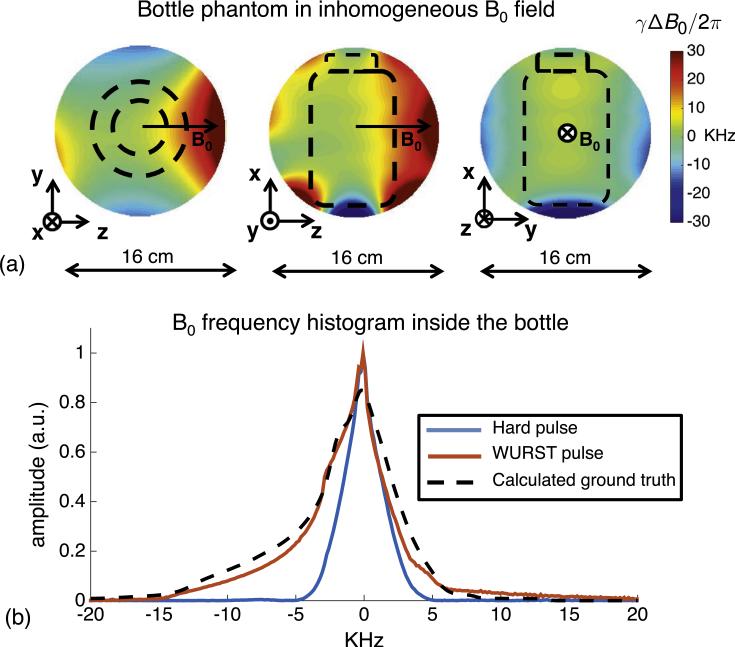
All experiments are performed in an inhomogeneous Halbach cylinder permanent magnet previously described in Ref. [8]. The average B₀ field strength and center frequency of the magnet are 77 mT and 3.29 MHz, respectively. The imaging field-of-view (FOV) is a 16 cm diameter sphere. The B₀ field vector is oriented along the Halbach cylinder's diameter (z-direction), and TRASE encoding is performed along the cylinder axis (x-direction). Data are acquired with a single-channel Tecmag Apollo console (Houston, Texas, USA). The 1D TRASE images in Figs. 9 and 10 are acquired using a custom-built TRASE array of two transmit coils. The frequency histogram and spin echo train data from the large bottle phantom in Figs. 3 and 8 are acquired using a solenoid coil whose region of homogeneous $B_1^{+}$ amplitude is larger than that of the TRASE coil array.

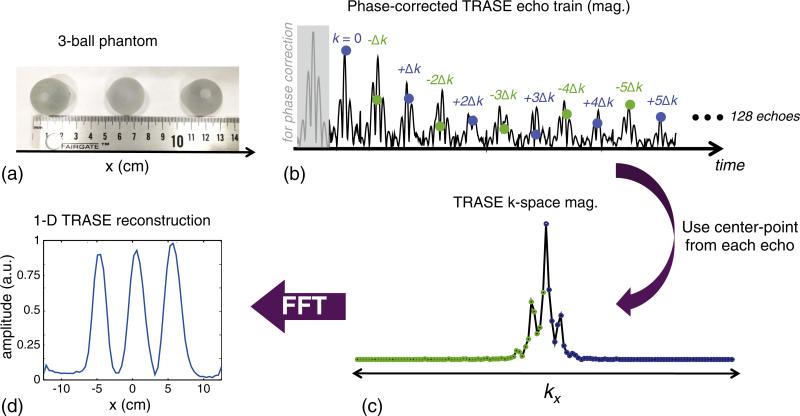
Fig. 9.

Experimental 1D TRASE imaging performed using single-shot WURST spin echo train in an inhomogeneous field. (a) Three-ball tap water-filled phantom used in experiment. The balls are 2.54 cm in diameter (1″) and the gap between them is also 2.54 cm. The full width of the phantom is 12.7 cm. (b) The first 12 echoes out of 128 echo train that have been corrected with the quadratic phase correction procedure. An extra echo at the beginning (gray shaded) of the train is acquired with no TRASE phase modulation and is used to perform the phase correction on the even-numbered echoes in the train. The mid-point of each 96-point echo is used as the TRASE k-space sample since the echo mid-point is modulated only by TRASE and not by the inhomogeneous B₀ field. (c) 1D k-space formed by re-ordering the mid-points of each echo. (d) The 1D image magnitude formed from the k-space data. The projections of the three balls are clearly visible in the 25 cm field-of-view 1D image. Sequence parameters: τ_exc = 3 ms, R_exc = 25 kHz/3 ms, peak γB_1,exc/2π = 650 Hz, τ_ref = 1.5 ms, R_ref = 25 kHz/1.5 ms, peak γB_1,ref/2π = 2.6 kHz, echo spacing = 7.6 ms, TR = 2.5 s, readout duration = 2.4 ms, echo train length = 128, echo train duration = 972.8 ms, sampling bandwidth = 40 kHz, number of averages = 96.

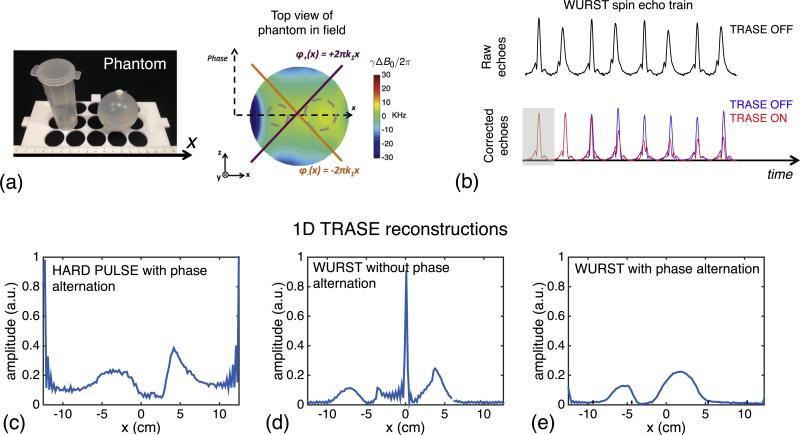
Fig. 10.

Experimental comparison of WURST pulses, hard pulses, and the two different refocusing pulse phasing schemes for 1D imaging. (a) Tap-water phantom comprised of 3 cm wide cylinder and 5 cm diameter sphere. (b) Echo train without (raw) and with (corrected) quadratic phase removal. The effect of turning on the TRASE modulation is also shown. (c–e) 1D images reconstructed from the hard pulses and WURST pulse trains. The WURST reconstructions are shown with and without phase alternation of the RF pulses. (c) Hard pulse TRASE image. As expected, the projections formed using hard pulses with TRASE modulation are severely distorted due to flip angle and phase errors caused by the limited bandwidth of the hard pulses (80 μs and 160 μs for excitation and refocusing pulses). Hard pulse results without phase alternation (not shown) are even more distorted. (d) WURST image without phase alternation. Refocusing pulse defects can cause mixing of conventional and spectral echo types for echoes in the train (see Fig. 4), corrupting the reconstruction. (e) WURST image with phase alternation. The phase alternation mitigates coherence pathway problems, producing a higher fidelity TRASE image. WURST sequence parameters: τ_exc = 3 ms, R_exc = 25 kHz/3 ms, peak γB_1,exc/2π = 650 Hz, τ_ref = 1.5 ms, R_ref = 25 kHz/1.5 ms, peak γB_1,ref/2π = 2.6 kHz, echo spacing = 7.6 ms, TR = 2.5 s, readout duration = 2.4 ms, echo train length = 128, echo train duration = 972.8 ms, sampling bandwidth = 40 kHz, number of averages = 96. Ignoring the relatively minor T₂ and diffusion weightings, the effective spatial resolution is approximately FOV/128 = 25/128 = 0.2 cm.

Fig. 3.

Measured B₀ variation with respect to a 9 cm dia., 14 cm long bottle phantom (shown in outline). The ΔB₀/B₀ over the bottle is about 1%. A solenoid volume coil is used for excitation and signal reception. (a) B₀ maps in the 3 orthogonal planes. (b) Frequency histogram of signal inside the bottle (obtained from Fourier transforms of spin echoes) after a hard-pulse pair (80 μs and 160 μs) or a WURST pulse pair (6 ms and 3 ms, sweep width = 50 kHz). For comparison, the dotted black curve shows the calculated ground truth histogram, which is expected if all of the spins inside the bottle were perfectly excited and refocused. When WURST pulses are used for excitation and refocusing, the area of the projection is increased by 70% as compared with hard pulses. The WURST projections also better agree with the simulated ground truth projection.

Fig. 8.

Experimental demonstration of phase correction method to change spectral echoes to a conventional echo shape in the phantom with an inhomogeneous B₀ field. Data are acquired using the same 9 cm dia., 14 cm long bottle phantom as in Figs. 3 and 4. The spin echo train uses phase alternation (noted in subscript) on the refocusing pulses but no TRASE modulation applied. The difference in echo amplitude between even and odd echoes is attributed to $B_1^{+}$ field variations over the large volume of the sample within the TRASE coil. Sequence parameters: τ_exc = 6 ms, R_exc = 50 kHz/6 ms, peak γB_1,exc/2π = 780 Hz, τ_ref = 3 ms, R_ref = 50 kHz/3 ms, peak γB_1,ref/2π = 3.12 kHz, echo spacing = 10 ms, TR = 2.5 s, readout duration = 6.4 ms, sampling bandwidth = 40 kHz, number of averages = 8.

The B₀ field map over the three cardinal planes is shown in Fig. 3 along with a calculated histogram (dashed-line) of spin frequencies over the volume of a bottle phantom (9 cm diameter, 14 cm length) inside the magnet. More than 35 kHz of field variation exists over the spherical imaging volume, providing ΔB₀/B₀ ~ 1%. The ground-truth histogram shown in Fig. 3 is calculated from a set of axial B₀ field maps acquired at 1 cm intervals along x using a Hall-effect probe mounted to a computer-controlled positioning arm. Overlaid on the calculated histogram are experimental histograms (projections) of the bottle phantom obtained by Fourier transforming spin echo readouts obtained using both the hard and the 50 kHz sweep WURST pulse pairs. The WURST pulse histogram corresponds well to the calculated histogram, and the area under the curve is 70% greater than the area of the hard pulse histogram, demonstrating much better coverage of the isochromats within the bottle phantom.

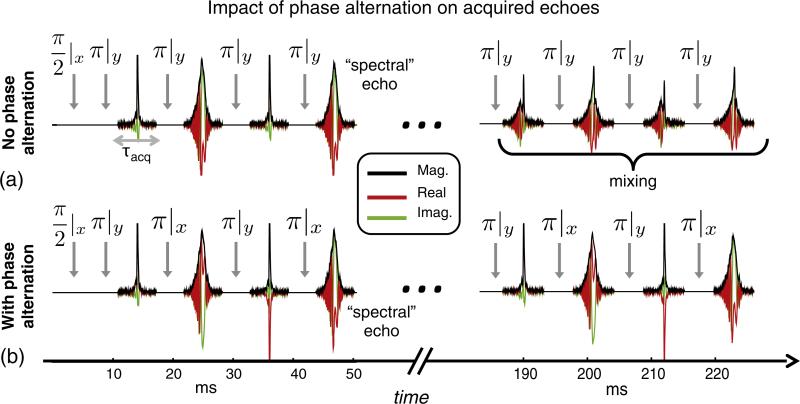
Fig. 4 shows the effect of phase alternation on the echo train, comparing no alternation and a scheme with a 90° difference between successive refocusing pulses (used in Ref. [9]). In the first pulse sequence, with no phase alternation (Fig. 4a), effects from experimental imperfections (i.e. refocusing pulse flip angle errors) accumulate and create stimulated echoes and other coherences later in the echo train. This causes a mixture of conventional and spectral echoes, which complicates the quadratic phase correction method described above. To mitigate this problem, the phase alternation scheme [9,39] shown in the second pulse sequence (Fig. 4b) is used to create two separate coherence pathways, effectively separating the conventional and spectral echoes along the entire echo train. The full pulse phase scheme including cycling over multiple TRs [9] is described in the Fig. 4 caption.

Fig. 4.

Spin echo train acquired from bottle phantom in the inhomogeneous B₀ field using WURST swept pulses. Since R_ref = 2R_exc, the quadratic phase modulation is removed from the first echo. Because the same R_ref is used on all refocusing pulses, the quadratic phase is also removed from subsequent odd-numbered echoes. However, even-numbered echoes retain a quadratic phase. This creates “spectral echoes” in which different isochromats refocus at different times depending on where they occur in the frequency sweep. This causes the echo shape to resemble a projection of the object. (a) Without phase alternation all RF refocusing pulses use the same phase (noted in the subscripts). Errors in the refocusing pulse flip angle lead to mixing of the conventional and spectral echoes in later echoes. This renders the data difficult to use with TRASE. (b) With the chosen phase alternation scheme, the refocusing pulse phase alternates between 0° and 90°. This forms two coherence pathways and maintains better separation between the spectral and conventional echoes. To limit spin history effects between TRs, the phase of the excitation pulse, refocusing pulse pairs, and receiver is varied every four TRs as follows: ϕ_exc = [0,180,90,270], ϕ_ref1 = [90,90,0,0], ϕ_ref2 = [0,0,90,90], ϕ_acq = [90,270,180,0].

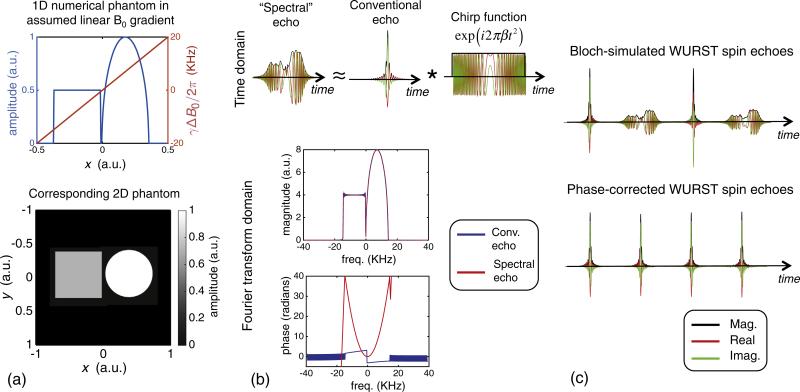
In Fig. 5, a Bloch simulation illustrates the proposed quadratic phase correction method for restoring spectral echoes to conventional echoes when the previously described 50 kHz sweep WURST pulses are used. Echoes from a numerical phantom with two features are simulated in a linear B₀ gradient field traversing a 40 kHz bandwidth over the field of view (~30 kHz over the phantom). The shape of the spectral echo resembles a projection of the phantom in the linear gradient; this correspondence is easier to see for the simulated linear gradient than for the experimental inhomogeneous B₀ field.

Fig. 5.

1D Bloch simulation and method of restoring the spectral echoes from the smearing caused by the quadratic phase. (a) Numerical phantom and its 1D projection. A linear variation in ΔB₀ field was assumed. (b) Echoes simulated using the 1D phantom. The spectral echo is represented as a convolution of a conventional echo with a temporal chirp function. Real and imaginary components and magnitudes are shown. In the Fourier transform domain, the magnitude spectrum of the two echo types look almost identical. However, the phase of the conventional echo is relatively flat while the spectral echo has a quadratic phase profile. (c) The conventional echo shape is restored by subtracting the difference between the phase profiles of the two echo types in the Fourier transform domain, and then transforming back to the time. A π phase shift is also applied to the third and fourth echoes to compensate for the effects of the RF pulse phase alternation scheme (see Fig. 4). After the phase correction, all echoes in the train have a conventional echo shape. As long as the readout window is long enough to contain the entire spectral echo, the transform is information-preserving. Simulated parameters: τ_exc = 6 ms, R_exc = 50 kHz/6 ms, peak γB_1,exc/2π = 780 Hz, τ_ref = 3 ms, R_ref = 50 kHz/3 ms, peak γB_1,ref/2π = 3.12 kHz, echo spacing = 10 ms, TR = 2.5 s, readout duration = 6.4 ms.

As discussed previously, the time domain spectral echo can be described as a convolution of the conventional echo with a temporal chirp function whose scaling parameter, β, depends on the sweep rate of the WURST pulse (Fig. 5b top). In the Fourier transform domain, the two echo types have essentially the same magnitude (some Gibbs ringing is seen due to the finite duration of the spectral echo readout window) but the phases differ by a quadratic offset over the spin bandwidth (Fig. 5b bottom). To restore the spectral echoes to conventional echoes, the difference between the phase of the Fourier-transformed conventional and spectral echoes is subtracted out, and the signals are inverse Fourier transformed back to the time domain (Fig. 5c). The equivalent operation can be performed in the time domain by convolving the spectral echo with an appropriately scaled, conjugated version of the quadratic phase chirp function (Eq. (5)).

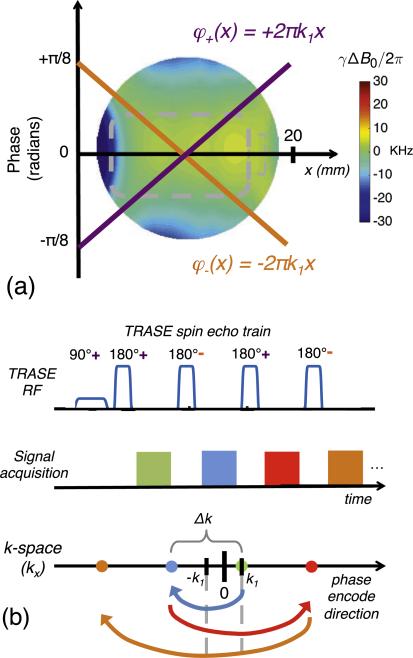
The procedure for performing 1D TRASE phase encoding with two $B_1^{+}$ phase gradients is illustrated in Fig. 6, but is more fully described in Refs. [19,20]. While TRASE can in general be performed using any two distinct $B_1^{+}$ phase profiles, we assume two equal and opposite phase ramps in this work described by slopes +2πk₁ and −2πk₁. These phase ramps are designed to reach a maximum phase dispersion of π/8 at the edge of the FOV of the image, and determine the TRASE k-space origins: +k₁ and −k₁. The first echo in the WURST spin echo train is refocused with the positive $B_1^{+}$ phase slope, and has applied phase-weighting +k₁. When the sign of phase gradient is flipped for the second refocusing pulse, the phase of the acquired echo is reflected across the −k₁ origin. The third pulse has positive phase gradient and in turn reflects the k-space trajectory across the +k₁ origin. Each successive pulse thereby has the effect of adding Δk = 4k₁ to the trajectory. Because the spacing between points is equal to 4k₁, the result is that FOV = 1/Δk = 1/4k₁. The value 4k₁ is analogous to the gradient moment of a phase encoding step, γG₀Δt, which is the k-space distance traversed by a conventional B₀ gradient with amplitude G₀ and pulse duration Δt, where γ is the gyromagnetic ratio.

Fig. 6.

TRASE k-space encoding using opposite sign, spatially linear $B_1^{+}$ phase ramps, which alternate between even and odd numbered spin echoes. (a) The two switchable $B_1^{+}$ phase slopes applied by a specialized transmit coil array over the FOV. (b) k-space is traversed by alternating the sign of the phase ramp between successive echoes in a spin echo train. For a conventional coil with no phase ramp the spin-echo reflection point is at k = 0. For the TRASE coil with a phase ramp described by φ₊(x) = +2π k₁x, the reflection point is +k₁. If the pulse is played with a second phase ramp described by φ₋(x) = −2π k₁x, the reflection point is −k₁. The signal of the first echo records the k = +k₁ because the excitation imparts a phase of +k₁ and the refocusing pulse reflects this around the origin for this phase ramp (+k₁) leaving it at k₁. The second refocusing pulse (a “−” pulse), reflects the signal around its origin (−k₁) as shown by the blue arrow, leaving the signal at k = −3k₁. The third refocusing pulse is a “+” pulse and thus reflects about +k₁ leaving the signal at k = +5k₁. Defining Δk = 4k₁ allows us to interpret the resultant sampling pattern as Cartesian sampling with a FOV = 1/Δk and a spatial resolution of FOV/ETL where ETL is the echo train length. Figure adapted from Ref. [19].

In order to perform the quadratic phase correction in the experimental implementation of TRASE with WURST pulses, the sign of the TRASE phase slope is not flipped until the third refocusing pulse in the echo train (not shown in Fig. 6). Therefore the first two echoes have no TRASE phase encoding and any phase differences between the two echoes are attributable to the quadratic phase profile imparted by the WURST refocusing pulse. As such, the phase difference between the Fourier transforms of the two echoes is used for quadratic phase removal, restoring all spectral echoes in the train to conventional echoes.

At the echo refocusing time, TE, phase terms from the inhomogeneous B₀ field are completely refocused by the spin echo, leaving only modulation caused by the TRASE phase encoding along with T₂ decay and a very small diffusion weighting. To form a 1D projection of the object using TRASE, a k-space vector is assembled by reordering the mid-points of each phase-corrected echo in the train (Fig. 6b). The 1D image is then formed by taking the Fourier transform of the TRASE k-space vector.

Equivalently, the on-resonance component can be obtained by integrating the Fourier transform of each echo in the train. The resulting points are then and re-ordered to form TRASE k-space. While this is mathematically equivalent to taking the mid-point of the echo under ideal circumstances, it has the advantage of being less sensitive to timing errors in the pulse sequence.

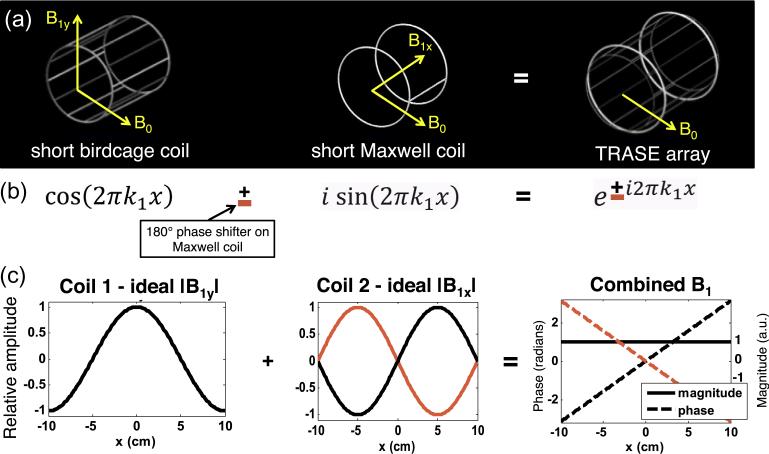
To realize a TRASE gradient $B_1^{+}$ field, a two-channel transmit array was designed that consists of two nested cylindrical coils (Fig. 7) [40]. In the spirit of the TRASE coil in Ref. [41], we combine a “cosine” $B_1^{+}$ amplitude coil in spatial quadrature with a “sine” $B_1^{+}$ amplitude coil to generate a linear phase ramp between −π/8 and π/8 across the FOV. Coil 1 is a short 4-turn birdcage coil (12 rungs, 18 cm diam., 22 cm length) that produces a $B_1^{+}$ field pointed along y with a cosine shape variation along x, $B_{1y}^{+}=\mid B_{1xy}^{+}\mid \cos \left(2\pi k_{1}x\right)$. The use of multiple turns in the birdcage coil, previously described in Ref. [42], increases the $B_1^{+}$ efficiency of the coil, reducing the RF power requirements. Coil 2 is a 10-turn Maxwell coil (22 cm diam., 18 cm length). The Maxwell coil produces a $B_1^{+}$ field pointed along x with a sine shape variation along x, $B_{1x}^{+}=\mid B_{1xy}^{+}\mid \sin \left(2\pi k_{1}x\right)$. The coils are tuned to the Larmor frequency (3.29 MHz) and decoupled with a toroidal transformer (S₂₁ = −15 dB isolation).

Fig. 7.

Design of experimental TRASE transmit coil with uniform $B_1^{+}$ amplitude and linear phase along the encoding direction. The B₀ field is transverse to the axis of the cylindrical TRASE coil array. (a) The coil array is realized as a multi-turn birdcage coil with a nested Maxwell pair coil. (b) The coils are designed to approximate the cosine and sine terms of Euler's equation for a linear phase ramp. The sign of the phase ramp can be flipped by applying a 180 deg. phase shift to the Maxwell coil RF transmit path. (c) The birdcage coil generates a transverse field (B_1y) with cosine amplitude variation over the FOV (x direction), while the Maxwell coil generates a longitudinal field (B_1z) with approximately sine amplitude variation. Four turns of wire are used in each birdcage rung to provide increased $B_1^{+}$ field for minimizing the needed swept RF pulse duration. The coils are decoupled to S₁₂ = −15 dB using a toroidal transformer to cancel the mutual inductance.

Fig. 7 shows the ideal relative magnitude of B_1x and B_1y from the two coils over the 20 cm encoded field-of-view. When the two coils are driven to produce an equal $\mid B_{1xy}^{+}\mid$ amplitude and their fields vary according to the same spatial frequency, k₁, they produce the desired $B_1^{+}$ field, $B_1^{+}\left(x\right)=\mid B_{1xy}^{+}\mid e^{+i2\pi k_{1}x}$ (uniform magnitude and linear phase). To control the sign of the $B_1^{+}$ phase gradient, a 180° phase shifter is added in the Maxwell coil RF path. Pulses with the 180° phase shift produce a negative phase gradient, $B_1^{+}\left(x\right)=\mid B_{1xy}^{+}\mid e^{-i2\pi k_{1}x}$, which allows for a sign change on every other refocusing pulse in TRASE echo trains. The birdcage coil is used for signal reception since it has a more uniform $B_1^{+}$ amplitude than the Maxwell coil over the phantom VOI. The $B_1^{+}$ magnitude and phase of each coil are separately mapped using a small field probe on a computer-controlled positioning arm to measure S₂₁ between each coil and the probe. The two measurements are weighted proportional to the RF transmit voltage applied to each coil and combined to create a B₁ map for the TRASE array coil (see Supplemental Fig. 1). This map is used to determine the FOV suitable for TRASE imaging.

Because of the low Larmor frequency of 3.29 MHz and the wide pulse bandwidths of 25 kHz and 50 kHz (~1% of the Larmor frequency), care must be taken to ensure that the coil is impedance matched across the entire bandwidth to avoid errors for off-resonant spins. A 10 ohm resistor is added to each of the two coils to decrease the quality factor (Q) and widen the impedance match of the coil so that RF energy is transmitted evenly across the entire pulse bandwidth.

The two TRASE coils are driven by two independent RF power amplifiers (Tomco, Stepney, Australia). To implement the ${B_{1x}}^{+}$ sign change, the small-signal RF input to one of the amplifiers is phase shifted using a PIN-diode actuated lumped-element 180° phase shifter. This approach eliminates the need for a high-power phase shifter and unequal power divider, as used for TRASE imaging in Ref. [41]. A length of coaxial cable is added to one of the transmit paths to equalize the temporal RF phase at the inputs to the two TRASE coils (as measured on a network analyzer). A high-power directional coupler is used to measure the incident and reflected RF power in each of the two paths. The power balance between the two TRASE coils is adjusted by adding attenuators to the signal input to the Maxwell coil RF power amplifier until the desired TRASE $B_1^{+}$ phase slope is achieved across the FOV.

Experimental TRASE 1D images are acquired on two simple tap water phantoms. T₁ and T₂ of the tap water is measured with a Bruker Minispec mq20 relaxometer (Billerica, MA, USA) at 7.5 MHz to assess the impact of relaxation on the TRASE images.

TRASE spin echo image data are acquired using the WURST pulses as well as hard pulses for comparison. The two pulse phasing schemes described in Fig. 4 are also compared. The WURST pulse sweep width is set to 25 kHz. The single-shot echo train length (and number of TRASE k-space points) is 128. The excitation pulse duration is 3 ms and the refocusing pulse duration is 1.5 ms. Peak RF power γB₁/2π is 650 Hz for excitation and 2.6 kHz for refocusing. The readout sampling bandwidth is set to 40 kHz and 96 samples are acquired. The width of the spectral echoes depends on the WURST refocusing pulse sweep rate. For the pulse used here, the 2.4 ms acquisition window is wide enough to capture all signals in the spectral echoes that refocus at different points in time. The acquisition window and WURST pulse duration set the minimum echo spacing at 7.6 ms, corresponding to an echo train length of 972.8 ms for 128 echoes. The TR is set to 2.5 s and 96 averages are acquired for a total acquisition time is 240 s. Unfortunately, a suitable linear B₀ gradient coil is unfeasible for projection imaging in the highly inhomogeneous low field scanner. Consequently, we are not able to acquire a reference 1D image to use as ground truth (as in Refs. [19,20]).

The diffusion weighting in the CPMG echo train is estimated using the following equation [1],

$$\frac{1}{T_{diff}}=\frac{1}{12}{\gamma }^2{G}_0^{2}D{t}_{TE}^2$$ (6)

where $\frac{1}{T_2^{\prime }}=\frac{1}{T_2}+\frac{1}{T_{diff}}$ and D is assumed to be 2.3e–5 cm²/s for tap water [1]. While this equation only describes the diffusion weighting of the CPMG component, and coherences such as stimulated echoes have a different (and potentially larger) diffusion weighting, we take this to be a reasonable approximation for our CPMG experiment, since care has been taken to minimize the signal contribution of unwanted coherences. To estimate the “worst-case” maximum possible diffusion weighting, we consider spins at the edge of the region-of-interest at a radius of approximately 8 cm from the magnet isocenter, where the local B₀ field variation is approximately 5000 Hz/cm. We also calculate the average diffusion weighting over the full FOV. Finally, TRASE image reconstruction is simulated on a 1D numerical phantom with and without blurring due to relaxation and diffusion.

4. Results

The T₁ and T₂ values for the tap water used in the imaging phantoms were measured to be 3400 ms and 2500 ms, respectively, at 7.5 MHz. Given the relative insensitivity of T₂ to field strength, this T₂ value is taken to be a reasonable approximation to T₂ at our experimental Larmor frequency of 3.3 MHz. For areas of objects extending to the edge of the 8 cm spherical FOV, Eq. (4) yields an effective relaxation constant of T′₂ = 1962 ms, corresponding to only 7% extra signal attenuation at the end of the 972.8 ms echo train. Similarly, the average frequency gradient over the FOV is estimated to be 2500 Hz/cm, yielding an average T′₂ = 2338 ms (only 2% extra attenuation at the end of the echo train). Since these values of T′₂ are still considerably longer than the 972.8 ms echo train used to acquire the TRASE data, the impact of the diffusion weighting on the signal intensity is quite modest for our experimental parameters. Supplemental Fig. 2 shows that the combined effect of T₂ decay and the worst-case diffusion weighting causes only a minor blurring of the object (shown with the orange arrow).

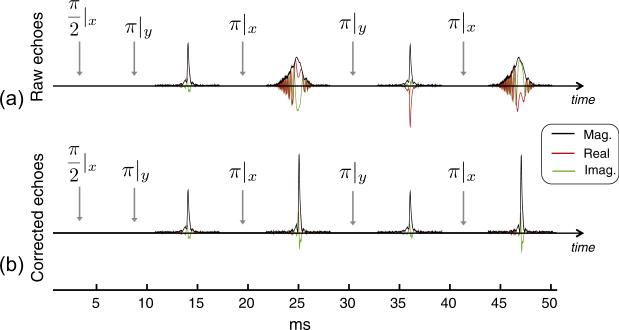
Experimental validation of the quadratic phase correction method is shown in Fig. 8. The first four echoes of a WURST echo train acquired on a large bottle phantom are plotted. The spectral echoes (Fig. 8a) show the characteristic broadening caused by the refocusing of each isochromat at different time points, resembling a 1D projection of the bottle phantom in the inhomogeneous B₀ field. The projection shape roughly corresponds to the histogram of frequencies within the bottle shown in Fig. 3. When the spectral echoes are Fourier transformed and the quadratic phase is subtracted out, their time-domain shape is restored to that of a conventional echo (Fig. 8b), as previously shown in simulations in Fig. 5. The third and fourth echo (and multiples of those echoes later in the train) are further multiplied by exp(iπ) to compensate for the −π phase offset applied by the phase alternation of the refocusing pulses.

Measured $B_1^{+}$ amplitude and phase field maps for the TRASE array coil are plotted in Supplemental Fig. 1 for the three cardinal planes with 5% delta contours overlaid. The phase gradient varies between approximately −π/8 and +π/8 over a distance of 20 cm. This nominally determines the TRASE Δk step size and the corresponding encoding FOV of 20 cm. However, the $B_1^{+}$ amplitude drops off sharply toward the edge of the TRASE axis and also in the plane transverse to this axis. As discussed below, $B_1^{+}$ amplitude variation greater than ~10% can cause echo train defects and TRASE image artifacts. So although the phase gradient is capable of encoding a FOV of 20 cm, the usable axial FOV is limited to ~13 cm due to the $B_1^{+}$ amplitude roll-off. In the y and z directions, $B_1^{+}$ is deemed sufficiently uniform over a roughly ±2 cm region. Consequently, the phantoms used for TRASE imaging are restricted to the 4 cm × 4 cm × 13 cm rectangular VOI overlaid on the plots in gray.

Fig. 9 shows 1D TRASE imaging performed on a phantom made up of three 2.54 cm dia. (1″) tap water-filled spheres separated by a gap of 2.54 cm (12.7 cm total spatial extent). Fig. 9b shows experimental data in which spectral echoes have been converted to conventional echoes using the proposed phase correction method. The effect of TRASE phase encoding is easily seen in the shape of the echoes, which no longer all have the same shape and whose mid-points no longer follow a smooth T₂-decay curve. TRASE k-space (Fig. 9c) is formed by rearranging the mid-points of each echo in the train. The k-space data is Fourier transformed to generate a 1D image (Fig. 9d) that clearly shows the position of the three balls within this FOV. The FOV estimated from the TRASE coil phase slope is 20 cm, however this FOV places the balls slightly too close together (closer to ~4 cm) along the x axis. We have therefore used the known position of the balls to infer the effective FOV to be 25 cm for the TRASE coil, and we have set the x axis in the plot accordingly. We note that this method is commonly used for calibration; B₀ gradient coil sensitivity is often measured using projections of an object of known size. Ignoring the minor effect of T₂ and diffusion, the nominal spatial resolution is the TRASE FOV (set by the slope of the coil phase gradient) divided by the echo train length: ~25 cm/128 = 0.2 cm.

While Fig. 9 shows results using the appropriate RF pulses, phase corrections, and phase alternation scheme, Fig. 10 demonstrates the importance of these choices. The TRASE data in Fig. 10 was acquired on the cylinder-and-sphere water phantom (Fig. 10a). For this phantom, the WURST echo train is shown before and after phase-correction (Fig. 10b). The corrected train is then overlaid with and without TRASE phase encoding enabled for the first eight echoes in the train, highlighting the spin dephasing caused by the TRASE phase gradient. The 1D image obtained from hard pulse data (Fig. 10c) shows severe off-resonance effects resulting in distorted shapes for the two objects in the FOV as well as a large “DC” artifact created by un-encoded spins (at the edge of the FOV). Severe artifacts also result when data is acquired using WURST pulses without phase alternation (Fig. 10d). In this case, the shape of the two objects is distorted and the DC artifact occurs in the center of the FOV rather than the edge. By contrast, when phase alternation is used with the WURST pulses (Fig. 10e), the projections show the expected correspondence to the shape and size of the phantoms as well as the distance between them. There is still a DC component artifact at the edge of the FOV, but it is greatly attenuated.

5. Discussion

Initial 1D image results demonstrate that TRASE can be adapted to perform spatial encoding in highly inhomogeneous B₀ fields. When hard pulses (used in previous realizations of TRASE) are replaced by WURST pulses and suitable phase alternation and phase correction are applied, 1D TRASE images acquired in the inhomogeneous field are markedly improved (Figs. 9 and 10). Our extension of the TRASE method thus substantially mitigates off-resonance effects on image quality, which the inventors of TRASE anticipated in Ref. [20] as a chief obstacle to widespread adoption of the method.

The phase correction method introduced here allows spectral echoes to be used for populating one half of k-space. For TRASE imaging, we implement the phase correction by taking the difference between the phase of the Fourier transform of the first two echoes in the train (and optionally fitting this difference to a polynomial). We note that while this approach has the advantage of being “auto-calibrating”, it may be unsuitable for data with poor SNR. In the latter case, the quadratic phase profile should be calculated analytically and applied to the Fourier transform of the spectral echoes (or equivalently, applied as a convolution in the time-domain).

Given that TRASE is synergistic with lightweight, low-field imaging systems, where it may not be practical to achieve a highly uniform B₀ field, our results represent a significant advance toward developing this application with TRASE. However, the results also show that there is room for further refinement of the TRASE-WURST acquisition and reconstruction. For example, a modest DC component still exists in the projections in Figs. 9 and 10 at the edge of the FOV, most likely arising from spin coherence pathways that are not properly excited and/or refocused in the echo train. Therefore, these spins are not properly encoded by the TRASE phase gradient. Additionally, in Fig. 8, the even and odd phase-corrected echoes show differences in amplitude that can arise from $\mid B_1^{+}\mid$ spatial variation over the sample. In TRASE data, this can create a bias offset between the positive and negative halves of the acquired TRASE k-space data, causing artifacts.

Bloch simulations show that the echo amplitude alternation in Fig. 8 can arise from $B_1^{+}$ variations over the large bottle phantom. Supplemental Fig. 3 displays echoes that are simulated using the same RF pulses and sequence parameters as the large bottle experiment in Fig. 8. For simplicity, a rectangular 1D phantom is used and a linear $B_1^{+}$ field with ±10% variation over the phantom is assumed. Simulations are compared for an inhomogeneous quadratic B₀ field with ~25 kHz variation over the phantom as well as for a uniform B₀ field. In the latter case, an artificial $T_2^{\ast }$ weighting is added to permit echo formation for purposes of illustration. The $B_1^{+}$ amplitude variation creates echo amplitude differences consistent with those observed for the large bottle phantom in Fig. 8. Specifically, the phase-corrected spectral echoes show a higher peak amplitude than the conventional echoes. Altering the excitation flip angle does not reproduce the alternating echo amplitude effect. For the TRASE array coil used in this work, $B_1^{+}$ roll-off near the edge of the coil limits the usable FOV to ~13 cm. In practice, the coil's limited impedance match bandwidth may also contribute to the effective $B_1^{+}$ variation applied to spin isochromats in the sample.

We note that the even/odd echo amplitude variation effect is a separate phenomenon from the “mixing” of conventional and spectral echoes that occurs when the refocusing pulse is not in the adiabatic regime. However, as illustrated in Fig. 4, the echo mixing effect is readily circumvented through the use of phase alternation to separate the coherence pathways of the conventional and spectral echoes.

A disadvantage of using WURST pulses instead of hard pulses is the longer pulse duration and corresponding increase in echo spacing, which increases attenuation of high frequency k-space points by T₂-decay. For our proof-of-concept experiments, we used tap water phantoms with T₂ greater than the entire echo train duration, minimizing the impact of T₂-decay and isolating to the extent possible the effect of TRASE phase modulation on the signal intensity and the TRASE image quality. In practice, for in vivo brain imaging, where T₂ is much shorter, there is a trade-off between the desired image resolution and the amount of available RF power (and hence the minimum pulse duration) [20]. For our experiments at a Larmor frequency of 3.3 MHz (0.078 T), we estimate T₁ and T₂ based on published measurements made between 0.08 T and 0.5 T, as summarized in Table 1.

Table 1.

A summary of previously published T₁ and T₂ measurements at low magnetic field strengths for gray matter, white matter, and cerebrospinal fluid.

Tissue type	T1 (ms)	B0 (T)	Ref.	T2 (ms)	B0 (T)	Ref.
Gray matter	500	0.08	[43]	60	0.2	[44]
				55-74	0.5	[45]
White matter	250	0.08	[43]	42	0.2	[44]
				64	0.5	[45]
Cerebrospinal fluid	4360	0.15	[46]	1760	0.15	[46]

Given these approximate T₂ values for brain tissue at low field, the 128-echo, 972.8 ms echo train used in this work would suffer heavy attenuation of high-frequency TRASE k-space points acquired late in the echo train, leading to severe blurring. However, as a mitigating circumstance, we note that the practical use of TRASE for brain slice encoding would not require 128 slices. Acquiring a more modest number of slices, such as 32, would yield a more tractable echo train length of 243 ms, greatly reducing the blurring.

In principle there are ways to overcome the limit imposed on resolution by T₂, albeit at the cost of increased scan time. For example, as suggested in Refs. [19,47], if a new TRASE coil is designed with a doubled phase gradient slope, it can be used to acquire two separate echo trains (with reduced FOVs) that can be interleaved to encode the full FOV. The two separate echo trains would be acquired with an opposite order of the alternating coil phase gradients. While each of these echo trains will generate aliased images due to the reduced FOV (increased Δk), the interleaved dataset will encode the full FOV. This approach will be explored in future work and improvements in resolution will be assessed.

While simple swept WURST pulses are used in this proof-of-concept to demonstrate TRASE in an inhomogeneous B₀ field, there is a whole class of composite, shaped, adiabatic, and optimal control pulses that could be explored for enabling TRASE imaging of broadband samples [48]. To take one promising example, “symmetric phase-alternating” composite refocusing pulses with equal duration to a narrowband hard pulse have been shown to provide increased CPMG signal amplitudes from samples with wide bandwidths [49]. These refocusing pulses work most efficiently when their imperfections are compensated by an “axis-matched” excitation pulse [48].

The bandwidth of the TRASE transmit coil array imposes another constraint on the use of TRASE in highly inhomogeneous B₀ fields. While resistive Q-spoiling overcomes this limitation for purposes of the present work, in general this solution may be impractical since it decreases the efficiency of the coil. A more elegant approach is to add a high-Q resonant circuit between the RF amplifier and the RF coil and inductively couple this circuit to the resonant coil. If the two resonant circuits are appropriately overcoupled, the bandwidth is increased with only a modest impact on coil efficiency across the band. The approach is used in Ref. [50] for widening receive coil bandwidth (by a factor of 5), but it is equally applicable to transmit coils. Another potential solution is to use untuned transmit coils and custom RF power amplifiers, an approach that has recently been explored for low field imaging [51].

Improved decoupling and orthogonality of the two TRASE coil's fields could also improve performance. In the echo train data acquired here, the amplitude of the even and odd-numbered RF pulses in the echo train had to be adjusted slightly (a few percent) to account for the effect of an undesired concomitant ${B_{1y}}^{+}$ field component generated by the Maxwell coil (collinear with the desired birdcage ${B_{1y}}^{+}$ field). The ratio of Maxwell to birdcage ${B_{1y}}^{+}$ in the center of the FOV is approximately 25%. If left uncompensated, this ${B_{1y}}^{+}$ field impacts the refocusing pulse accuracy and the resulting TRASE image quality. However, varying the refocusing pulse does not completely compensate the effects of the Maxwell ${B_{1y}}^{+}$ field because the field varies spatially over the VOI. In future work, we will strive for improved decoupling of the TRASE coils and better orthogonality between the field components generated by each coil (${B_{1x}}^{+}$ and ${B_{1y}}^{+}$). As TRASE phase gradient coils are still a relatively recent innovation, there is a large space of potential designs to explore. We plan to explore different coil geometries and wire patterns – such as designs based on the target-field method [52] – in the hopes of minimizing concomitant fields and maximizing the FOV usable for TRASE imaging. However, as the present topic is the use of swept pulses to enable TRASE in an inhomogeneous B₀ field, we considered the Maxwell-birdcage coil sufficient for proof-of-concept broadband TRASE imaging in spite of its obvious flaws.

In this work, TRASE image reconstruction is performed using a simple Fourier transform. However, improved image fidelity could potentially be achieved by incorporating $B_1^{+}$ phase gradient nonlinearity [53], $\mid B_1^{+}\mid$ variations, and T₂-decay into the forward model encoding matrix. Generalized image reconstruction then proceeds using an iterative matrix solver such as the conjugate gradients algorithm [54]. In addition to reducing image artifacts, the generalized reconstruction would allow TRASE encoding to be incorporated into flexible encoding schemes that also use B₀ gradient encoding with linear and/or nonlinear fields, a hybrid approach that our group has begun exploring for low field imaging [40]. Using a single encoding matrix to explicitly account for the actual $B_1^{+}$ and/or B₀ field profiles provides maximum freedom for designing acquisition schemes. This in turn has the potential to relax the requirements on hardware design for low field scanners.

6. Conclusion

Proof-of-concept 1D images show that TRASE phase encoding in a highly inhomogeneous B₀ field is possible with ordinary RF power levels and a simple spin echo pulse sequence using WURST swept RF pulses. TRASE imaging is successfully demonstrating on phantoms with spin bandwidths too wide to be accurately refocused by hard pulses (ΔB₀/B₀ ~ 0.3%). Using a correction method, we compensate for the quadratic phase modulation imparted by the swept WURST pulses, enabling the entire echo train to be used for TRASE. While WURST pulses are longer than hard pulses and lengthen the echo train, increasing blurring from T₂-decay, this limitation can in principle be partially overcome by interleaving multiple spin echo trains that each acquire different subsets of k-space. The swept pulse TRASE approach is generalizable to 2-D and 3-D encoding using RF transmit arrays with $B_1^{+}$ phase gradients along each encoding direction. TRASE provides pure $B_1^{+}$ encoding that is independent of the B₀ field and thus does not need to dominate B₀ field variation over the sample, as in conventional B₀ slice-select and readout gradient encoding. TRASE therefore provides an appealing option for MRI spatial encoding for portable low-field applications, where it reduces weight, cost, size, and power requirements on system design.