Estimating the Mechanical Behavior of the Knee Joint during Crouch Gait: Implications for Real-Time Motor Control of Robotic Knee Orthoses

Abstract

Individuals with cerebral palsy frequently exhibit crouch gait, a pathological walking pattern characterized by excessive knee flexion. Knowledge of the knee joint moment during crouch gait is necessary for the design and control of assistive devices used for treatment. Our goal was to 1) develop statistical models to estimate knee joint moment extrema and dynamic stiffness during crouch gait, and 2) use the models to estimate the instantaneous joint moment during weight-acceptance. We retrospectively computed knee moments from 10 children with crouch gait and used stepwise linear regression to develop statistical models describing the knee moment features. The models explained at least 90% of the response value variability: peak moment in early (99%) and late (90%) stance, and dynamic stiffness of weight-acceptance flexion (94%) and extension (98%). We estimated knee extensor moment profiles from the predicted dynamic stiffness and instantaneous knee angle. This approach captured the timing and shape of the computed moment (root-mean-squared error: 2.64 Nm); including the predicted early-stance peak moment as a correction factor improved model performance (root-mean-squared error: 1.37 Nm). Our strategy provides a practical, accurate method to estimate the knee moment during crouch gait, and could be used for real-time, adaptive control of robotic orthoses.

I. Introduction

Cerebral palsy (CP) is the most common child onset movement disorder [1]. Many individuals with CP exhibit crouch gait, a pathological walking pattern characterized by excessive bilateral knee flexion and elevated knee extensor joint moments [2]. This pattern increases the energy cost of walking [3], is associated with joint pain and pathology [4], and typically precipitates ambulatory decline in adulthood [5]. Wearable robotic devices, such as power-assist knee orthoses, may be a potentially viable non-invasive treatment option to compensate for or ideally to improve crouch gait.

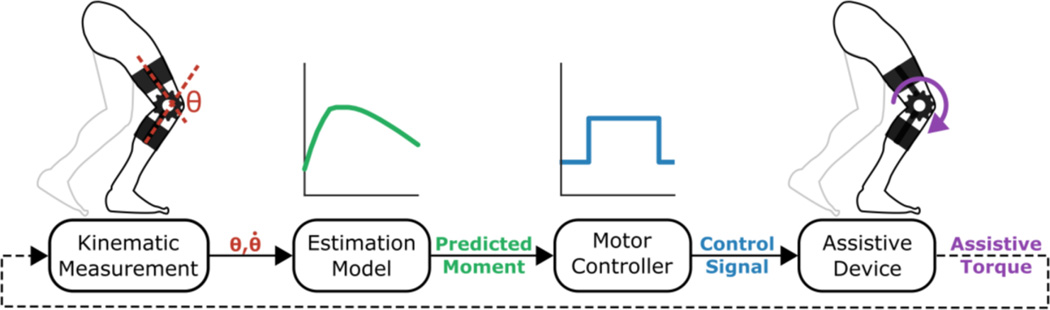
Understanding the mechanical behavior of the knee during crouch gait on an individual basis is necessary for the design and control of assistive devices because appropriately specifying the magnitude and timing of assistive torque is critical for eliciting a favorable biomechanical response. Knowledge of an individual’s dynamic knee stiffness and peak or instantaneous knee moments during crouch gait would be useful for fine-tuning the spring-damper elements in quasi-passive orthoses [6] and customizing the motor control or assist settings of wearable robotic devices, which typically rely on joint moment feedback [7–9]. A measure of the instantaneous (i.e. real-time) internal joint moment would be particularly useful for motor controllers used in gait assistance because it would allow the adaptive application of an assistive torque as a percentage of the internal joint moment (Figure 1), an approach currently being pursued by the authors.

Figure 1.

A framework for utilizing the estimated instantaneous knee extensor moment in the adaptive control of a robotic knee orthosis. On-board sensors measure the knee joint kinematics, which are input into an estimation model to determine the instantaneous internal knee joint moment. The predicted moment is used by the motor controller to specify the necessary control signals to elicit the motor torque for the desired level of assistance as a percentage of the internal knee joint moment.

Using motorized assistance to treat crouch gait may have several possible outcomes because of the complex and multifaceted causes of this pathological gait pattern; an accurate estimation of knee joint moment may be beneficial regardless of the underlying etiology. Some individuals with crouch gait are unable to completely straighten their legs due to muscle tightness, spasticity, and/or contractures. In these cases it may be desirable for a robotic device to provide assistance that improves mobility without fully alleviating the crouched posture. Knowledge of the instantaneous joint moment during their unassisted crouch gait pattern would be useful for controlling a device under this scenario. For individuals who are capable of responding to a device which straightens the leg (e.g. weakness based crouch), an exoskeleton may be used to complement existing muscle activity to elicit a less crouched, corrected gait. In these cases, knowledge of the instantaneous joint moment during their baseline gait pattern could be used to standardize the amount of extension assistance among subjects. Ultimately, if an exoskeleton is used in a long-term rehabilitation paradigm, maintenance of muscle activity would be critical throughout treatment to avoid further weakening of the knee extensors. Knowledge of the knee joint moment during the modified gait pattern could be used to adjust the amount assistance in order to maintain a targeted amount of muscle activity that can hopefully be progressively decreased as strength increases.

While joint moments can be computed via gait analysis and modeling [2], this approach requires post-hoc computational analysis and is generally confined to a research laboratory because it requires expensive equipment and lengthy experimental procedures that limit utility for implementation in real world settings. It should be possible to estimate the kinetic behavior of the knee during crouch gait from statistical models based on anthropometric and kinematic relationships. Lower-extremity joints exhibit a coupling between kinematics and kinetics during walking in unimpaired individuals; portions of this coupling can be described as quasi-constant slope phases separated by transition periods [10]. Statistical models have been used to estimate the spring-like behavior (i.e. dynamic or quasi stiffness) of the knee during weight acceptance of normal walking [11], and quadriceps muscle force during crouch gait [12]. Fortunately, joint angles can be readily measured outside of a laboratory setting using wearable sensors (i.e. goniometer), video analysis, or other affordable motion sensors [13].

The first goal of this study was to establish the moment-angle relationships of the knee during mild to moderate crouch gait and develop general form statistical models describing the key features of these relationships based on readily obtainable measures. We focused on the extrema of the knee extensor moment and dynamic stiffness during weight acceptance, as these parameters were deemed most relevant to the customization of clinical treatment and assistive devices. Our second goal was to evaluate the utility of applying the statistical models to estimate the instantaneous joint moment during weight-acceptance, which has implications for the design of motor control strategies for wearable robotic devices used in crouch gait rehabilitation. To accomplish these goals, we used experimental walking biomechanics data and computational modeling to quantify knee joint angles and moments during walking in patients with CP who would potentially qualify as candidates to use a powered exoskeleton. Next, we utilized this data set to establish statistical models that account for the variability of the mechanical behavior of the knee among patients with CP based on anthropometric and kinematic parameters.

II. METHODS

A. Subject and Experimental Data

We used experimental walking biomechanics data from 10 subjects with spastic diplegic CP. The data were collected at Gillette Children’s Specialty Healthcare, and made publically available on SimTK.org [14, 15]. The parents, guardians, and/or subjects in the dataset provided informed written consent prior to data collection. We selected participants from this dataset based on the following criteria: 1) they had at least one clean individual limb force plate strike, and 2) they walked with mild to moderate crouch gait (minimum knee flexion angle during stance between 15° and 50°). Participants had less than 30° of tibial or femoral torsion deformity. Participant information for the 10 subjects (of the 20) that met our criteria is presented in Table 1.

Table I.

Anthropometric, kinematic, stiffness, and stiffness linear fit data for each participant.

Subject	Leg Length (m)	Weight (kg)	Speed (m·s−1)	θWA (°)	ΔθWA (°)	θMS (°)	θLS (°)	kF (Nm/deg)	kE (Nm/deg)	kF Fit (R2)	kE Fit (R2)
1	0.67	28.2	0.94	31	6	15	22	2.10	0.78	0.92	0.95
2	0.71	23.1	0.67	36	12	24	26	1.72	1.39	0.99	0.95
3	0.80	78.5	0.75	49	9	45	52	7.90	4.17	0.95	0.97
4	0.67	21.1	0.90	56	12	31	42	3.34	0.91	0.95	0.94
5	0.73	28.7	1.21	51	6	36	43	5.09	1.35	0.97	0.98
6	0.60	26.1	1.05	40	9	24	23	1.98	1.35	0.99	0.94
7	0.57	21.3	0.88	27	9	17	18	1.15	0.82	0.98	0.99
8	0.67	29.0	0.87	39	8	31	34	2.26	1.48	0.94	0.99
9	0.64	50.8	0.95	44	18	25	28	3.19	2.54	0.98	0.99
10	0.66	28.0	1.12	34	7	19	27	2.62	1.50	0.96	0.98

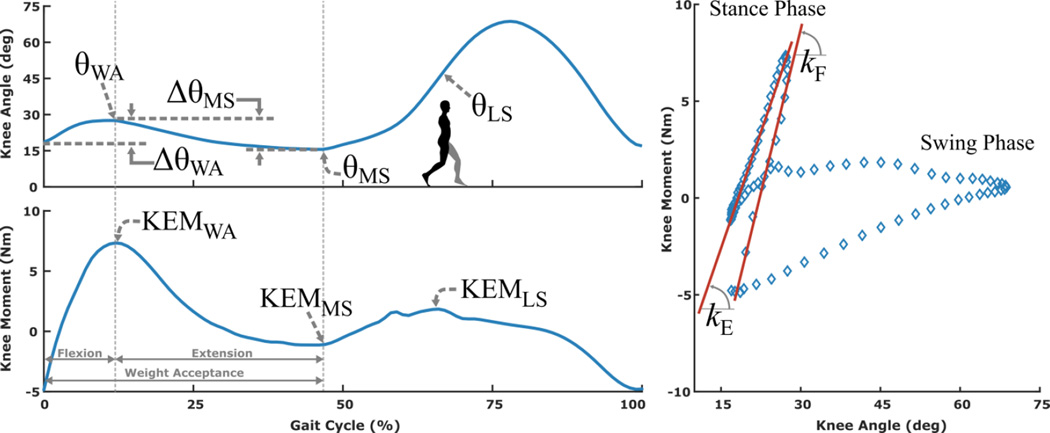
Where θ_WA is defined as the peak knee flexion angle during weight acceptance, Δθ_WA is defined as the knee angle range of motion from heal strike to the weight acceptance peak, θ_MS is defined as the minimum knee flexion angle during stance, θ_LS is defined as the knee angle at contralateral heal strike, k_F is defined as the dynamic stiffness of the knee during weight acceptance flexion, and k_E is defined as the dynamic stiffness of the knee during weight acceptance extension. Weight acceptance was defined as the period from foot strike through the end of the knee extension phase that follows the period of knee flexion in early stance (Figure 2).

The experimental procedures for this dataset, reported in greater detail previously [14, 15], were as follows: reflective markers were placed on lower-extremity landmarks using a standard protocol [16]. Participants walked across the motion capture space barefoot, without assistance, and at their self-selected speeds. Ground reaction forces were collected from 4 in-ground force plates (AMTI, Watertown, MA, USA). Marker trajectories were measured using 12 motion capture cameras (Vicon, Oxford, UK).

B. Computational Analysis

We used OpenSim [17] to calculate joint kinematics and kinetics from each experimental walking trial. First, a 19 degree of freedom (DOF) musculoskeletal model [18, 19] was scaled for each participant using anthropometric measures (segment lengths and body mass). Lower-extremity DOF included revolute ankle joints, a 1-DOF coupled knee mechanism with translations and rotations of the tibia prescribed by the knee angle, and ball and socket hip joints. Joint angles were determined using the method of inverse kinematics, which minimizes the error between experimental and virtual marker trajectories. Joint moments were computed using the method of inverse dynamics, which solves the Newton-Euler equations of motion and determines the generalized forces necessary to reproduce each simulated walking trial based on the inertial properties of the model and the measured external ground reaction forces.

The joint kinematics and kinetics computed in OpenSim were normalized to percent gait cycle. The peak knee extensor moments during early and late stance were found by taking the maximum values during 0–20% and 40–60% of the gait cycle, respectively; the minimum knee extensor moment for mid stance was found by taking the minimum during 20–40% of the gait cycle.

To estimate the dynamic stiffness of the knee during the flexion phase of weight acceptance, we applied a linear fit to the moment-angle data points from the point of minimum knee extension moment to the point of maximum knee extension moment (Figure 2). To estimate the dynamic stiffness of the knee during the extension phase of weight acceptance, we applied a linear fit to the moment-angle data points from the point of maximum knee extensor moment to the first subsequent (local) minimum. Collectively, these knee joint parameters computed from inverse dynamics were used as the ground truth for our predictive statistical models as described below.

Figure 2.

Knee joint angle (top) and moment (middle) during the gait cycle, and moment-angle curve (bottom) for a representative participant. The kinematic parameters used as predictors in the statistical model development are noted in the knee joint angle plot (top), where θ_WA is defined as the peak knee flexion angle during weight acceptance, Δθ_WA is defined as the knee angle range of motion from heal strike to the weight acceptance peak, θ_MS is defined as the minimum knee flexion angle during stance, θ_LS is defined as the knee angle at contralateral heal strike. In the moment-angle plot (right), dynamic stiffness was defined as the slope of the best fit line during weight-acceptance flexion (k_F) and extension (k_E). Since the moment angle relationships are different between stance and swing, embedded foot switches or pressure sensors could be used to distinguish between these phases.

C. Statistical Model Building

For our general form models describing knee extensor moment extrema and dynamic loading stiffness, we limited our set of predictors to measures that could be readily obtained in a clinical setting or via simple wearable sensors; body mass, leg length, walking speed, and knee joint kinematics. Kinematic parameters included the peak knee angle during weight acceptance (θ_WA), knee angle range of motion from heel strike to the weight acceptance peak (Δθ_WA), the minimum knee flexion angle during stance (θ_MS), and the knee angle at contralateral heal strike (θ_LS) (Figure 2). In keeping with the analytical decomposition of the knee moment, the kinematic parameters used in each model were constrained to the temporal region of the predicted kinetic feature. For example, only weight acceptance kinematic parameters were included in the predictor set for weight acceptance kinetic features. We used stepwise linear regression to establish a least-squares fit of the response data such that only significant predictors (p<0.05) were included in each final statistical model. To avoid overfitting and improve model adoptability, we limited our fitted models to non-quadratic terms and excluded interactions. In total, we fit five linear regression equations, one each for weight acceptance peak knee moment (KEM_WA), mid-stance minimum knee moment (KEM_MS), late stance peak knee moment (KEM_LS), flexion dynamic stiffness (k_F), and extension dynamic stiffness (k_E). We evaluated the predictive performance of each model by conducting a 10-fold leave one out cross-validation, whereby we sequentially removed the data from one participant at a time, fit the model with data from the remaining nine participants, and then tested the model on the absent participant. We computed the root mean squared error (RMSE) between the values predicted by the regression model and those computed from inverse dynamics in OpenSim. The RMSE were used to evaluate the predictive performance of the regression models, and we then reported the grand average RMSE across the 10-fold cross validation (CV RMSE).

D. Estimating the Instantaneous Knee Moment Profile

In addition to models predicting knee moment extrema and dynamic stiffness, we developed two additional models to predict the knee extensor moment profile during the weight acceptance phase of the gait cycle (profile estimation models 1 and 2). Accurate assessment of the knee moment profile during weight acceptance is critical for specification of a powered knee orthosis because of the precise timing necessary to sharply increase knee extensor torque during weight transfer followed by a sharp decease to maintain forward momentum [20]. In the case of crouch gait from CP, accurately predicating this profile for each individual is even more critical since these individuals typically show the largest deviations from non-impaired populations at the knee [2].

For wearable robotic applications, onboard sensors (e.g. joint angle encoders) can be used to measure joint position. Therefore, we defined the flexion and extension phases of weight-acceptance based on the knee joint angle and time derivatives. The instant of peak knee flexion angular velocity following foot contact was defined as the starting point for the flexion phase. We found this to be a strong indicator of when the knee joint moment switches from flexion to extension following heel strike.

In profile estimation model 1 (equation 1), the knee extensor moment during flexion and extension was calculated using the instantaneous change in knee angle and the predicted dynamic knee stiffness for weight acceptance flexion and extension, respectively. Profile estimation model 1 estimated the knee extensor moment as follows:

$$KEM(t)=\{\begin{array}{cc}\hfill k_F{\sum }_{t=1}^{n\mathit{\text{Flex}}}{\theta }_t-{\theta }_{t-1},& \mathit{\text{flexion}}\hfill \\ \hfill KEM(n\mathit{\text{Flex}})-k_E{\sum }_{t=1}^{n\mathit{\text{Ext}}}{\theta }_{t-1}-{\theta }_t,& \mathit{\text{extension}}\hfill \end{array}$$ (1)

where k_F represents the predicted dynamic stiffness during flexion, k_E represents the predicted dynamic stiffness during extension, θ represents the knee joint angle, KEM(nFlex) is the knee extensor moment calculated at the end of the flexion phase, and t represents the t^th time step. The transition from the flexion phase to the extension phase (nFlex) occurred when the angular velocity changed signs (negative during flexion to positive during extension).

In model 1, the predicted moment during the extension phase relies on the accurate prediction of the knee extensor moment at the end of flexion (i.e. KEM(nFlex)). Thus, errors in the estimated moment during flexion may propagate during extension. For example, if the knee moment is under predicted during the flexion phase, it will remain under predicted during extension.

To address this issue, we developed profile estimation model 2 (equation 2), which incorporated a correction factor at the flexion-extension transition. During flexion, the knee extensor moment was calculated using the instantaneous change in knee angle and the predicted flexion dynamic knee stiffness as in model 1. At the flexion-extension transition, we used the predicted first peak of the knee extensor moment (KEM_WA) to estimate the peak moment at the end of flexion. As such, KEM(nFlex) was set to KEM_WA at this transition, and the knee extensor moment during extension was calculated using the instantaneous change in knee angle and the predicted extension dynamic knee stiffness, again as in model 1. Profile estimation model 2 estimated the knee extensor moment as follows:

$$KEM(t)=\{\begin{array}{cc}\hfill k_F{\sum }_{t=1}^{n\mathit{\text{Flex}}}{\theta }_t-{\theta }_{t-1},& \mathit{\text{flexion}}\hfill \\ \hfill KE{M}_{WA},& \mathit{\text{transition}}\hfill \\ \hfill KE{M}_{WA}-k_E{\sum }_{t=1}^{n\mathit{\text{Ext}}}{\theta }_{t-1}-{\theta }_t,& \mathit{\text{extension}}\hfill \end{array}$$ (2)

where k_F represents the predicted dynamic stiffness during flexion, k_E represents the predicted dynamic stiffness during extension, θ represents the knee joint angle, KEM_WA represents the predicted first peak of the knee extensor moment, and t represents the t^th time step.

For both profile estimation models, we specified the end of the extension phase (nExt) when either the angular position of the knee during the extension phase reached the angle of the knee at heel strike or the angular velocity became positive. The predicted moments were constrained to non-negative (i.e. extensor) values.

The RMSE between the estimated and computed instantaneous knee extensor moment profiles during weight-acceptance was used to evaluate the predictive performance of each model.

E. Analysis of Step by Step Variability

Since step to step variability may be present in crouch gait, we sought to evaluate the accuracy of our predictive equations and profile estimation models on an additional gait cycle for two subjects. We selected an additional clean force plate strike (heel strike through weight acceptance) for a subject with moderate (Subject 5) and mild (Subject 10) crouch gait. The experimental data for these strides, which were not used in the statistical model building, were used to predict the weight acceptance peak knee moment, dynamic stiffness, and knee moment profiles using estimation models 1 and 2.

III. RESULTS

The knee joint moment-angle relationships exhibited approximately linear behavior during weight acceptance flexion and extension. The range of R² values for the linear fits of these relationships (i.e. dynamic stiffness) were between 0.92–0.99 during flexion and 0.94–0.99 during extension (Table 1).

The general statistical models for prediction of knee extensor moment extrema and dynamic stiffness are presented in Table 2. The stepwise linear regression analysis found that only body weight and the relevant kinematic parameters were significant predictors to the response values; walking speed and leg length were not found to be significant predictors and were excluded from all models. All of the final statistical models explained at least 90% of the response value variability as indicated by adjusted R² values (Table 2).

Table II.

Statistical models for predicting knee joint moment features during crouch gait.

Knee Moment Feature	Predictive Equation	Adj. R2	CV RMSE	p
Weight Acceptance Peak (KEMWA, Nm)	KEMWA= −25.0 + 0.55·W + 0.41·θWA + 0.99 ·ΔθWA	0.99	1.78	<0.001
Mid-Stance Minimum (KEMMS, Nm)	KEMMS = 7.64 + 0.026·W·θMS	0.93	4.61	<0.001
Late Stance Peak (KEMLS, Nm)	KEMLS = −25.4 + 0.50·W + 0.86·θLS	0.90	3.80	<0.001
Flexion Stiffness (kF, Nm/deg)	KF = −2.33 + 0.082·W + 0.11·θWA − 0.20·ΔθWA	0.94	0.53	<0.001
Extension Stiffness (kE, Nm/deg)	KE = 0.21 + 0.055·W + 1.37·θWA − 1.38·θMS− 1.38· ΔθMS	0.98	0.23	<0.001

Where θ_WA is defined as the peak knee flexion angle during weight acceptance, Δθ_WA is defined as the knee angle range of motion from heal strike to the weight acceptance peak, θ_MS is defined as the minimum knee flexion angle during stance, and θ_LS is defined as the knee angle at contralateral heal strike. Adj. R² refers to R² value for each predictive equation adjusted for the number of predictors in the model. CV RMSE refers to the grand average RMSE across the 10-fold leave one out cross-validation.

Dynamic knee stiffness was positively associated with body-weight and crouch severity, and negatively associated with knee range of motion. Peak knee extensor moments were positively associated with body-weight and crouch severity.

The most accurate model describing the extrema of the knee extensor moment was that of the weight acceptance peak (R²: 0.99), while the least accurate was that of the late stance peak (R²: 0.90); the accuracy for the mid-stance minimum was in-between the two (R²: 0.93). The model describing the dynamic stiffness during weight acceptance extension (R²: 0.98) was slightly more accurate than during weight acceptance flexion (R²: 0.94).

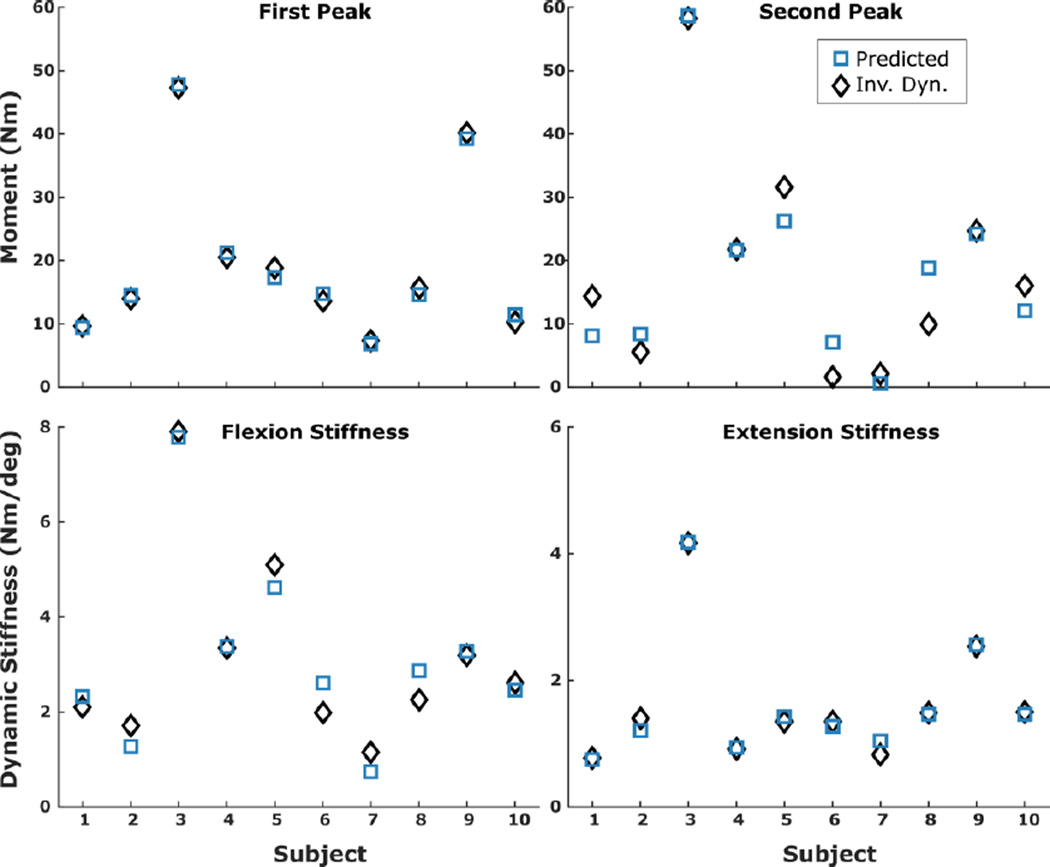
In terms of accuracy, the peak extensor moment (KEM_WA) showed the lowest CV RMSE (1.78 Nm) while mid-stance minimum (KEM_MS) had the highest CV RMSE (4.61 Nm) (Table 2). The CV RMSE was 0.53 Nm/deg for the flexion stiffness (k_F) and 0.23 Nm/deg for the extension stiffness (k_E). Comparisons between the predicted and inverse dynamics-computed first and second peak knee extensor moment and flexion and extension dynamic stiffness for each subject are presented in Figure 3.

Figure 3.

Peak knee extensor moments during weight acceptance (top left) and late stance (top right), and dynamic stiffness during weight acceptance flexion (bottom left) and extension (bottom right) computed using inverse dynamics (squares) and predicted from the respective statistical model (diamonds).

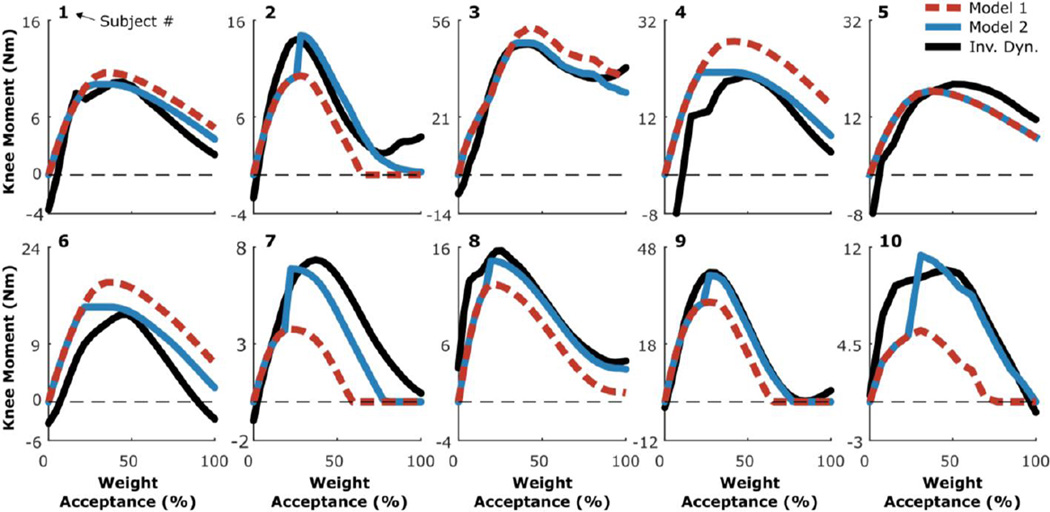
Both of the estimation models used to predict the instantaneous knee extensor moment profile captured the timing and general shape (i.e. rise and fall) of the moments computed from inverse dynamics. Comparisons of the estimated profiles and those computed from inverse dynamics are presented in Figure 4. Estimation model 2, which had an average RMSE of 1.4 Nm across all of the participants, was more accurate than estimation model 1, which had an average RMSE of 2.6 Nm. Individual RMSE values for each model are reported in Table 3.

Figure 4.

Knee joint moment waveforms during weight-acceptance computed using inverse dynamics (solid black lines) and predicted from estimation models 1 (dashed red lines) and 2 (solid blue lines). The numbers above each plot signify subject number.

Table III.

Profile estimation model performances.

Subject	Model 1 RMSE (Nm)	Model 2 RMSE (Nm)
1	0.9	0.5
2	2.7	1.7
3	4.0	2.3
4	4.5	2.3
5	1.3	1.3
6	3.8	2.1
7	1.8	0.9
8	2.5	1.0
9	3.5	1.1
10	1.4	0.5
Avg	2.6	1.4

The predicted knee joint moment features for the additional gait cycle in the “step by step” analysis were of similar accuracy to the gait cycles of those subjects used in the full analysis (Table IV). The RMSE for profile estimation models 1 and 2 were 4.8 and 2.9, respectively, for the second gait cycle from subject 5. The RMSE for profile estimation models 1 and 2 were 1.3 and 1.2, respectively, for the second gait cycle from subject 10.

Table IV.

Step by step variability and prediction performance.

	Subject 5		Subject 10
	Step 1	Step 2	Step 1	Step 2
Weight Acceptance Peak (Nm)	17.3 (18.8)	17.6 (21.3)	11.4 (10.2)	8.8 (8.2)
Flexion Stiffness (Nm/deg)	4.6 (5.1)	2.5 (3.3)	2.5 (2.6)	2.1 (2.2)
Extension Stiffness (Nm/deg)	1.4 (1.3)	1.2 (0.9)	1.3 (1.5)	1.5 (1.0)

Values are presented as predicted (actual). Subject 5 exhibited moderate crouch gait, while subject 10 exhibited mild crouch gait.

IV. DISCUSSION

In this study, we used experimental biomechanics data and an inverse dynamics approach to establish the kinematic-kinetic coupling relationships of the knee during crouch gait in CP. We utilized these relationships to develop a set of statistical models based on clinically available measures to estimate features of the knee extensor moment, including peak moment values and dynamic knee stiffness. We found R² values between 0.90 and 0.99 for the general form predictive equations, which included both kinematic and anthropometric parameters. We also developed models based on the predicted knee moment features to estimate the knee moment profile during crouch gait weight-acceptance, which can be calculated in real-time.

Computing the knee extensor moment during walking via instrumented gait analysis is challenging in CP patients and is typically unobtainable outside of clinical or research gait laboratory settings. Our approach aims to provide the ability to estimate important features of the knee moment profile without the need for computational analysis or recording single limb ground reaction forces. In building our predictive equations, we constrained our set of predictors to anthropometric and kinematic parameters that can be measured with wearable sensors or in a clinical setting with minimal equipment and those which are included in the analytical decomposition of the knee moment.

Surprisingly, walking speed and leg length were not significant predictors in any of the equations, and were therefore eliminated in the stepwise regression analysis. The effects of walking speed and leg length were likely small compared to the effects of the kinematic knee parameters and body weight. We used data where participants walked at only their self-selected speeds, which may further explain these findings. The performance of our statistical models during walking at non-self-selected walking speeds warrants further investigation.

Similar to the behavior of the knee in unimpaired individuals [11], we found that the moment-angle relationship of the knee during the flexion and extension phases of weight-acceptance were approximately linear during crouch gait (the R² values were between 0.92 and 0.99). We utilized the predictive equations to estimate the knee extension moment profile, which can be calculated in real-time based on the instantaneous change in knee angle. We evaluated one estimation model based solely on dynamic stiffness (profile estimation model 1), and another that incorporated a first peak correction factor (profile estimation model 2). We found that both estimation models captured the general characteristics of the knee extensor moment, while the model that utilized a correction factor for the first peak (model 2) resulted in the most accurate predictions. The second estimation model corrected for compounding errors that resulted when the moment predicted from the flexion-region dynamic stiffness underestimated or overestimated the peak moment at the flexion-extension transition. The predicted first peak of the knee extensor moment (KEM_WA) was used as the correction factor because our predictive equation for that parameter was highly accurate (Table 2, R²=0.99, RMSE = 1.15Nm) and it demonstrated a potential to correct errors in the instantaneous moment due to prediction errors of the weight acceptance flexion stiffness.

The results of this study have implications for the design or modification of passive knee orthoses aimed to assist individuals with crouch gait. Since we found that the moment-angle relationships remained approximately linear during crouch gait, this suggests that passive knee orthoses used in this population could utilize elastic or spring to store and return energy during the flexion and extension phases of weight-acceptance, respectively. A device based on this concept has been proposed and tested in non-impaired individuals [6]. Our equations used to predict knee joint stiffness may aid the specification and individual customization of the spring stiffness used in such a device.

Powered orthoses used for gait assistance typically utilize joint moment feedback-based motor controllers [7–9]. For rehabilitation in individuals with CP, where some locomotor function remains, assistive devices should supplement, but not replace, existing function in order to maintain muscle strength. Applying an assistive torque as a percentage of the instantaneous internal joint moment may prove critical for long-term training and rehabilitation of the neuromuscular system. Our predictive equations may be used in a framework for utilizing the estimated instantaneous knee extensor moment in the control of robotic knee orthoses (Figure 1), where the magnitude of assistive torque adapts to the magnitude of the internal joint moment.

The step by step variability analysis suggests that the predictive equations and estimation models are able handle normal perturbations that may occur during walking in crouch gait. However, a change in knee kinematics and kinetics as a result of motorized assistance may affect the accuracy of our estimation models. During walking in able-bodied individuals with an assistive exoskeleton that provided external stiffness to the knee joint, Shamaei et al. found that the combined dynamic stiffness of the knee and device remains invariant when the external assistive stiffness is provided up to ~80% of the internal knee stiffness [21]. Their finding, combined with the strong performance of our estimation models across a reasonably wide range of knee angles, provides confidence in the ability our proposed approach to accurately determine the internal knee moment when motorized assistance may result in altered kinematics while treating crouch gait. This must be tested experimentally, and is something we will evaluate in our ongoing research.

Researchers have used surface electromyography based approaches to estimate joint moments during a variety of tasks, including the knee joint moment during walking in individuals with [22] and without [23] CP. While electromyography based approaches have implications for motor control algorithms, they may have limited practicality outside of a research laboratory due to challenges associated with electrode placement, such as limited use duration, re-calibration, and motion artifact from clothing and/or the orthosis. The approach outlined in the present study may have improved practicality because it does not require instrumented calibration and utilizes sensors customarily already included in robotic devices, such as a motor encoder.

We found that our statistical models were able to estimate the kinetic behavior of the knee with similar accuracy compared to prior studies in able-bodied adults [11], and other estimation paradigms [22]. The results of our cross-validation provide a high level of confidence in the reported predictive equations. Still, the relatively small sample size was a limitation of this study. It is possible that certain crouch gait variations were not included in our analysis. Therefore, the generalizability of our findings to individuals with knee behavior not encompassed by the type or range of parameters in our sample remains unknown and should be interpreted with caution. Future studies encompassing larger and more diverse datasets (e.g. additional subjects, walking conditions, etc.) would be beneficial.

V. CONCLUSSION

This study established the moment-angle coupling relationships of the knee during crouch gait and developed a set of predictive equations to estimate key features of the knee joint moment during the stance phase based on kinematic and anthropometric measures. Only anthropometric and kinematic measures were included in the statistical models, which allow clinicians, technicians, and/or orthotists to estimate features of a patient’s knee moment without requiring instrumented gait analysis and post-hoc analysis. We demonstrated the utility of our statistical models and presented a practical approach to estimate the instantaneous knee extensor moment based on predicted knee joint dynamic stiffness and peak moment. The predictive models reported in this study have implications for assessing and improving the treatment of crouch gait.

Biographies

Zachary F. Lerner received the Ph.D. degree in biomedical engineering from Colorado State University, Fort Collins, CO, in 2015. He is currently a postdoctoral fellow in the Functional and Applied Biomechanics Section in the Rehabilitation Medicine Department, Clinical Center, National Institutes of Health, Bethesda, MD.

Diane L. Damiano received the Ph.D. degree in research methods/biomechanics from the University of Virginia, Charlottesville, in 1993. She is currently the Chief of the Functional and Applied Biomechanics Section in the Rehabilitation Medicine Department, Clinical Center, National Institutes of Health, Bethesda, MD.

Thomas C. Bulea received the Ph.D. degree in biomedical engineering from Case Western Reserve University, Cleveland, OH, in 2012. He is currently a staff scientist in the the Functional and Applied Biomechanics Section in the Rehabilitation Medicine Department, Clinical Center, National Institutes of Health, Bethesda, MD.