Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jun 21;6:28055. doi: 10.1038/srep28055

Effect of ionic radii on the Curie temperature in Ba1-x-ySrxCayTiO3 compounds

A Berenov 1,a, F Le Goupil 1, N Alford 1
PMCID: PMC4914972  PMID: 27324841

Abstract

A series of Ba1-x-ySrxCayTiO3 compounds were prepared with varying average ionic radii and cation disorder on A-site. All samples showed typical ferroelectric behavior. A simple empirical equation correlated Curie temperature, TC, with the values of ionic radii of A-site cations. This correlation was related to the distortion of TiO6 octahedra observed during neutron diffraction studies. The equation was used for the selection of compounds with predetermined values of TC. The effects of A-site ionic radii on the temperatures of phase transitions in Ba1-x-ySrxCayTiO3 were discussed.

Introduction

Perovskites with the general formula: Ba1-x-ySrxCayTiO3 (BSCT) show enhancement of several properties (e.g dielectric, piezoelectric1, electrocaloric2 response) in the vicinity of Curie temperature, TC, where a cubic to tetragonal phase transition occurs and could be strong contenders for Pb-free ferroelectric materials3. As a result, the ability to optimize chemical composition of BSCT compounds in order to shift TC to the desired operating temperature range is important from a practical point of view. Several decades of research have established some of the key parameters that influence the TC in perovskites: chemical composition of A- and B-sites in ABO3 perovskites4, A to B nonstoichiometry ratio5, lattice parameters6, tolerance factor7, average mass of A-site ions8, 18O/16O isotope ratio9, grain size10, annealing temperature11, hydrostatic pressure12, strain in thin film13. Nevertheless there is still a lack of simple guidelines for the selection of the materials compositions with predetermined value of TC.

The average ionic radius, <rA–site>, of A-site ions has a strong effect on the TC especially in Ba1-xSrxTiO3 compounds where TC decreases linearly with Sr doping. This decrease is usually explained by the substitution of Ba ions by smaller Sr ions resulting in the observed linear decrease of the TC with lattice parameter in Ba1-xSrxTiO3 (a or 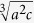Inline graphic) for cubic or tetragonal phases, respectively)6. Similarly, the decrease TC with applied hydrostatic pressure12 was explained by the pressure induced decrease of the unit cell volume14.

Another parameter affecting TC is the A-site cation disorder which can be quantified by variance, σ2, as follows15

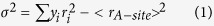graphic file with name srep28055-m2.jpg

where ri and yi–ionic radii and occupancy of A-site of element i, respectively. The linear increase of the TC with σ2 in BSCT has been observed when the average ionic radius was kept constant16. In other perovskite or perovskite related structures, the increase of σ2 was shown to decrease the metal-insulator transition temperature in manganites15 and decrease critical current in YBCO-type superconductors17. In this work we evaluated the effects of average ionic radius (ionic radii in 12 fold coordination were used18) and ionic radii variance of A-site ions in the perovskite lattice on the phase transitions in BSCT compounds.

A series of compounds (see Table 1) were prepared by a conventional solid-state reaction synthesis with starting chemicals BaCO3 (Alfa Aesar, 99.95%), CaCO3 (Alfa Aesar, 99.95%), SrCO3 (Alfa Aesar, 99.99%) and TiO2 (PI-KEM Ltd., 99.9%) calcined at 1300 °C for 10 hrs. Three series of compounds were prepared: series A where <rA–site> was fixed at 1.551 Å and σ2 was varied from 0.0066 to 0.0125 Å2, series B where both <rA-site> and σ2 were varied, series C where both <rA-site> and σ2 were varied in order to maintain constant TC as described below. Chemical composition was confirmed by ICP-OES analysis (DV 200 OES, Perkin Elmer). XRD (X’PERT MPD, PANalytical) showed that all specimens were single phase tetragonal perovskites (4 mm s.g.) at room temperature except for Ba0.78Ca0.22TiO3 where a weak peak belonging to CaTiO3 was observed (see Supplementary Fig. S1). This composition is close to the temperature dependent Ca solubility limit of 16% at 1300 °C19, 25% at 1430 °C20 and 1549 °C21. A good agreement between the values of the lattice parameters of Ba1-xSrxTiO3 with those reported in the literature22 was observed. For the series A the increase of variance resulted in a slight decrease of the a lattice parameter and increase of the c lattice parameter whereas the c/a ratio showed an increase. Dense pellets (>92% dense) were prepared by sintering at 1450 °C. The average grain size was 30–65 μm as observed by SEM (JSM 6400, JEOL) and shown in Supplementary Fig. S2. DSC measurements (DSC200 F3, Netzch) during 5 K/min heating showed well defined peaks at TR-O, TO-T and TC which correspond to consecutive phase transitions during heating from rhombohedral (3 m) to orthorhombic (mm2) to tetragonal (4 mm) and, finally, to cubic (m3 m) structures, respectively (see Supplementary Fig. S3 and Supplementary Table S4).

Table 1. Crystallographic parameters of studied samples.

Composition  < rA–site> (Å) δ2 (Å2) a (Å) c (Å) c/a
Series A
 Ba0.65Sr0.35TiO3 1.5505 0.0066 3.9657(1) 3.9739(1) 1.0021
 Ba0.69Sr0.24Ca0.07TiO3 1.5505 0.0085 3.9655(4) 3.9831(8) 1.0044
 Ba0.74Sr0.12Ca0.15TiO3 1.5506 0.0105 3.9633(6) 3.9938(8) 1.0077
 Ba0.78Ca0.22TiO3 1.5506 0.0125 3.9631(7) 4.0066(9) 1.0110
Series B
 Ba0.8Sr0.2TiO3 1.5760 0.0046 3.9804(1) 4.0045(4) 1.0061
 Ba0.6Sr0.2Ca0.2TiO3 1.5220 0.0126 3.9500(1) 3.9640(5) 1.0036
 Ba0.9Ca0.1TiO3 1.5830 0.0066 3.9784(1) 4.0236(1) 1.0114
 Ba0.85Sr0.1Ca0.05TiO3 1.5795 0.0056 3.9793(2) 4.0149(2) 1.0089
 Ba0.78Sr0.1Ca0.12TiO3 1.5606 0.0092 3.9696(2) 4.0043(2) 1.0088
 Ba0.75Sr0.1Ca0.15TiO3 1.5525 0.0105 3.9609(2) 3.9956(3) 1.0088
 Ba0.7Sr0.1Ca0.2TiO3 1.5390 0.0124 3.9576(2) 3.9884(2) 1.0078
Series C
 Ba0.68Sr0.32TiO3 1.5559 0.0063 3.9688(1) 3.9795(3) 1.0027
 Ba0.62Sr0.28Ca0.1TiO3 1.5359 0.0098 3.9580(1) 3.9683(4) 1.0026
Open in a new tab

The dielectric properties were evaluated by HP 4263B LCR with 0.3 V/mm ac signal at 0.1–100 kHz. The thermal hysteresis observed between heating and cooling runs was less than 3 K. Dielectric permittivity, εr, peaked at TC and showed humps at TR-O and TO-T (Fig. 1). No frequency dependence of εr was observed. The tanδ showed clear peaks positioned slightly below (by less than 10 K) the temperatures of the corresponding phase transitions. The estimated error in the determination of temperatures of phase transitions is 1.5 K and a good agreement was observed between the values of TC, TR-O and TO-T determined from DSC and LCR measurements. Both TR-O and TO-T decreased with Ca doping and no TR-O and TO-T were observed in the samples with more than 20 and 15% of Ca doping, respectively, in agreement with the literature23,24. TC increases linearly with the tetragonal distortions in the lattice (expressed as c/a ratio) regardless of the chemical composition of samples (Supplementary Fig. S5). The εr data located 10–20 K above TC were fitted to the Curie-Weiss law (Table 2). The value of T0 determined from the fitting, was smaller than TC suggesting a first order phase transition in all studied samples.

Figure 1. Temperature dependence of permittivity and loss tangent of Ba0.69Sr0.24Ca0.07TiO3 at 0.1, 1, 10 and 100 kHz.

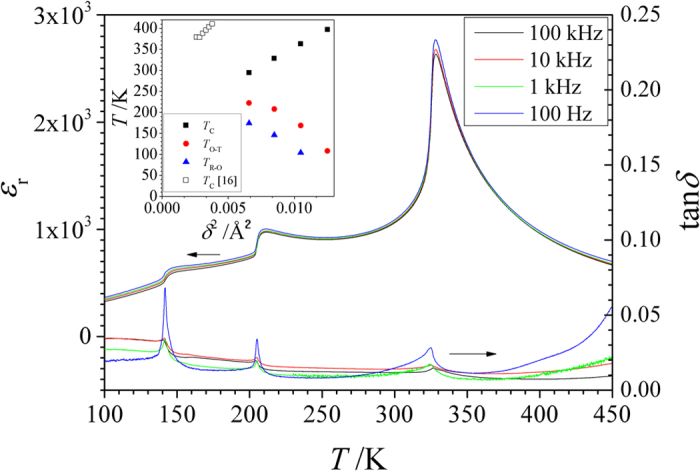
Figure 1

Open in a new tab

Measurements were performed during 1 K min−1 heating. Inset shows temperatures of phase transitions in BSCT compounds (series A) as a function of σ2.

Table 2. The results of dielectric measurements of studied compounds.

Composition TR-O (K) TO-T (K) TC (K) εrm T0 (K) γ
Series A
 Ba0.65Sr0.35TiO3 174 222 294 2566 271 1.09
 Ba0.69Sr0.24Ca0.07TiO3 146 208 328 2635 289 1.03
 Ba0.74Sr0.12Ca0.15TiO3 104 167 363 6132 351 1.12
 Ba0.78Ca0.22TiO3 NA NA 397 4049 373 1.19
Series B
 Ba0.8Sr0.2TiO3 187 253 343 4483 322 1.11
 Ba0.6Sr0.2Ca0.2TiO3 NA NA 324 2692 301 1.18
 Ba0.9Ca0.1TiO3 148 231 411 2994 385 1.27
 Ba0.85Sr0.1Ca0.05TiO3 172 250 378 4251 365 1.15
 Ba0.78Sr0.1Ca0.12TiO3 134 206 375 3697 360 1.21
 Ba0.75Sr0.1Ca0.15TiO3 NA 170 373 3161 357 1.25
 Ba0.7Sr0.1Ca0.2TiO3 NA 94 363 3826 353 1.24
Series C
 Ba0.68Sr0.32TiO3 176 229 304 3737 269 1.08
 Ba0.62Sr0.28Ca0.1TiO3 124 184 311 9564 309 1.18
Open in a new tab

It has been shown that the increase of cation disorder results in the formation of relaxor type behavior25. As a result a modified Curie-Weiss law26 was used to fit the data

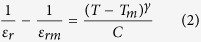graphic file with name srep28055-m3.jpg

where εrm is the permittivity at TC, γ is exponent which is expected to be 1 for classical ferroelectrics and 2 for relaxors. Relatively low values of γ measured in this work (1.03–1.27), the lack of frequency dependence of εr and the closeness of the peaks on εr and δ temperature curves, suggested that all compounds investigated showed typical ferroelectric behavior. The linear increase of the TC with the σ2 was observed (inset Fig. 1). The observed 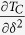Inline graphic slope was slightly larger (17252 K Å−1) than previously reported (14500 K Å−1) for BSCT compounds with <rA−site>  = 1.594 Å16. TT-O and TR-O showed a monotonic decrease with σ2.

Recently a combined effect of the average ionic radii and cation variance on the phase transition temperature in perovskite (alkaline earth doped rare earth manganites) and perovskite related (cuprate superconductors) compounds was proposed27. For example, a linear decrease of the metal-insulator transition temperature with the increase of the 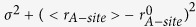Inline graphic function was observed in a large number of manganites28. 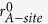Inline graphic is the ionic radius of the “ideal” non-distorted cubic perovskite which can be calculated from geometrical considerations as 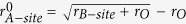Inline graphic where rB−site and rO are ionic radii of B and O ions in ABO3 perovskite, respectively. An empirical hard sphere ionic model has been proposed28 where the increase in σ2 and 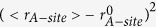Inline graphic determined BO6 octahedra tilting in perovskites with the tolerance factor, t, less than 1 and introduced strain like energy term affecting the temperature of phase transition. Similar hard sphere ionic model was applied to the perovskites studied in this work with the t > 1. In this case the lattice distortions caused by ion size mismatch relieved not by BO6 octahedra tilting but by shifting of oxygen ions leading to the distortion of BO6 octahedra29. In the model the ferroelectricity was assumed to be caused by the shift of Ti ions in the direction of equatorial oxygen in TiO6 octahedra however the results of local-structure refinements in Sr doped BaTiO3 suggested 4 site distribution of Ti ions in tetragonal and 8 site distribution in cubic phases with the site splitting of ≈0.2 Å29,30. In the ideal non-distorted cubic perovskite (t = 1) Ti and O ions were closely packed and no shift of Ti ions from the centrosymmetric positions were possible (Fig. 2(a)). An increase of <rA–site> by the introduction of larger A-site ions (σ2 = 0 Fig. 2(b)) or an increase of σ2 by the introduction of cation disorder (<rA–site>  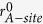= Inline graphic Fig. 2(c)) was likely to enlarge TiO6 octahedra and allowed Ti ions to shift from the centrosymemtric position at T < TC by the distance d. From the geometrical considerations:

Figure 2.

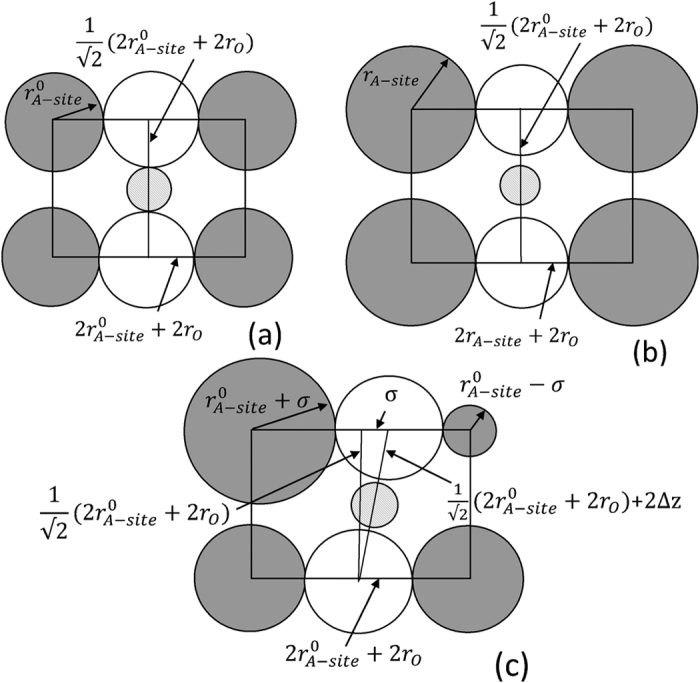
Figure 2

Open in a new tab

Schematic representation of (110) planes in the ideal cubic perovskite with 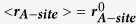Inline graphic and σ2 = 0 (a), in the cubic perovskite with Inline graphic and σ2 = 0 (b) and in the cubic perovskite with Inline graphic and σ2 > 0 (c). Grey, white, and patterned circles represent A-site ions, O and Ti ions, respectively.

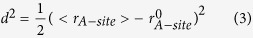graphic file with name srep28055-m10.jpg

and (assuming 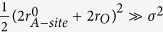Inline graphic)

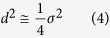graphic file with name srep28055-m12.jpg

for the former (Fig. 2(b)) and later (Fig. 2(c)) cases, respectively. It has been shown both empirically31 and theoretically32,33 that TC depends on the atomic displacement of B-site cations, d, as TC ~ d2.

As a result an increase of the TC with both 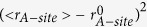Inline graphic and σ2 was expected. However a poor correlation of values of TC with 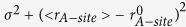Inline graphic function was observed for the samples studied in this work (Supplementary Fig. S6) presumably due to the assumptions used in the suggested simple model (spherical non polarizing ions, cubic perovskite structure in the ferroelectric phase, neglect of off centered Ca ions, etc.) and a modified empirical function 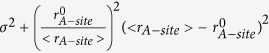Inline graphic was suggested.

The TC of all studied samples showed a linear correlation with the modified function regardless of the cation composition on A-site (Fig. 3) as follows:

Figure 3.

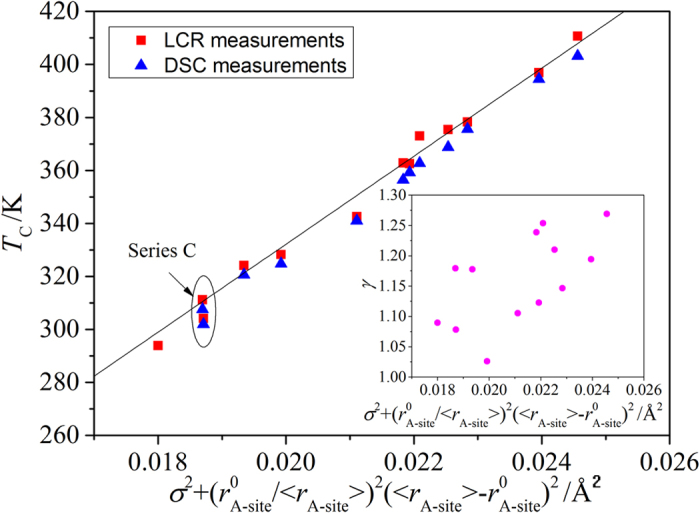
Figure 3

Open in a new tab

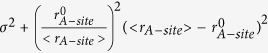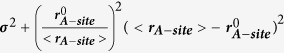TC as a function of Inline graphic. Solid line is a fit to equation 3. Inset shows γ as function of Inline graphic.

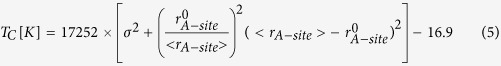graphic file with name srep28055-m16.jpg

Although the proposed simple model appeared to qualitatively explain the empirical relationship of σ2 and <rA−site> with TC, a detailed model is required to relate ionic radii of individual ions with the following factors influencing ferroelectricity in titanate perovskites: magnitude of Ti off centering in TiO6 octahedra, the direction of the Ti off centering and contributions from A-site ions displacements. Recent studies of local structure provided vital information on the influence of Ca and Sr substitution in BaTiO3 on the above mentioned parameters29,30,34. The magnitude of Ti off centering was found to decrease monotonically with Sr doping in BaTiO3 as TiO6 octahedra became more regular and reduced in volume29,30,35. This effect is usually associated with the observed decrease of TC upon Sr doping. The effect of Ca doping on TiO6 octahedra remains controversial. It was shown that Ca doping decreased the average volume of TiO6 octahedra whereas the degree of distortions in TiO6 network increased35. The volume of some TiO6 octahedra was found to be close to the one of BaTiO3 even when 30% Ca was introduced on A-site. On the other hand the increase of the volume of TiO6 octahedra with the increasing number of neighboring Ca ions and concurrent increase of the Ti displacement was reported30. The direction of Ti ions displacement was found to be aligned at ≈33° with respect to the c axis in BaTiO329. Sr doping increased this angle of alignment to 39° in Ba0.8Sr0.2TiO3 and 54° (Ti displacement along (111) direction) in Ba0.5Sr0.5TiO3. As a result the c-axis component of polarization diminished lowering the value of TC. Ca doping appeared to induce an opposite effect as the direction of Ti ions displacement was closely aligned with c axis in Ba0.7Ca0.3TiO330. No Sr off-centering was observed in Ba1-xSrxTiO3 materials resulting in an isotropic relaxation of oxygen ions around the A-site thus providing no additional contribution to specimen polarisation29,30. Ca off-centering was experimentally observed by EXAFS in CaTiO334 and Ba1-xCaxTiO3 (0 < x < 0.5)30, by XANES in Ba1-xCaxTiO3 (x = 0.02, 0.05)36 compounds and theoretically predicted in Ba0.875Ca0.125TiO324 and Ba1-xCaxTiO335. If Ca off-center displacements occur in the same direction as TiO6 distortions this additional contribution to polarization results in the increased values of TC. The direction of Ca off-centering were reported along [111]30, [001]35,36 or [113]24 directions. Furthermore Ca displacements were shown to facilitate Ti displacements inside TiO6 octahedra further enhancing ferroelectic behaviour30. It is possible to speculate that the increase of A-site cation disorder (expressed as σ2) could facilitate the shift of smaller A-site cations from the centrosymmetric positions in order to relieve an associated bond strain. A model was proposed that assumed two competitive effects active during Ca doping in Ba1-xCaxTiO3: the shrinkage of TiO6 octahedra resulting in smaller Ti displacements (and possibly away from the c-axis direction) and the increase of the number of off-centered Ca ions. This mode described experimentally observed TC dependence reasonably well35. Similar A-site driven ferroelectricity was found in perovskites with the t < 1 where the introduction of smaller ions (e.g. Li in K0.5Li0.5NbO337 and Lu in (La,Lu)MnNiO638 stabilized off-centering of A-site ion (thus inducing ferroelectric state) over tilting of BO6 octahedra3.

The observed increase of TC with σ2 and decrease of TC with <rA–site> are in agreement with previous results16. A weak increase of γ with 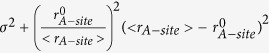Inline graphicwas observed (inset Fig. 3) presumably due to the increased degree of cation disorder. In order to evaluate whether this simple empirical equation (5) consisting of tabulated values of ionic radii, could be used for the selection of compositions with specific values of TC, two compounds (series C) were prepared with an intended TC of 35 °C. The Ca doping on A site, y, in Ba1-x-ySrxCayTiO3 was fixed at y = 0 and 0.1, respectively. A good agreement between the intended and measured values of TC were observed (31 °C for 0 and 37 °C for 0.1 Ca doped samples).

Neutron diffraction data were collected at room temperature on several samples using the high resolution powder diffractometer, HRPD, at the ISIS neutron facility, Rutherford Appleton Laboratories, UK. Diffraction patterns were recorded over the time-of-flight range 31–125 ms, corresponding to a d-spacing range 0.65–2.58 Å, or 0.85–3.89 Å, for patterns collected in the back-scattering and 90 degree detector banks, respectively. The patterns were recorded to a total incident proton beam of about 60 μA h. The neutron patterns from back scattered and 90 degree banks were fitted simultaneously by Rietveld profile refinement method using Gsas II software39. The data were refined in P4 mm space group with the following atomic positions: Ti (0, 0, 0), Ba/Sr/Ca (0.5, 0.5, z), O1 (0, 0, z), O2 (0, 0.5, z). Due to strong correlation, atomic positions and isotropic thermal factors for A-site cations were not refined independently. As a result we were unable to model Ca ion off-centering ions as discussed above. The cation occupancies were fixed according to the results of the chemical analysis and the full oxygen occupancy was assumed. The following parameters were refined: background coefficients, scale factors, diffractometer constant, peak shape, anisotropic strain, atomic positions and isotropic displacement parameters. The results of the refinements are given in the Table 3. As a function 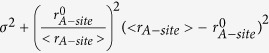Inline graphic increased, one Ti-O1 bond monotonically increased whereas another Ti-O1 bond decreased leading to the distortion of TiO6 octahedra (Fig. 4). As a result a linear increase of the squared atomic displacement of Ti ions from the centrosymemtric position, d2, is observed (inset Fig. 4).

Table 3. Refined parameters obtained from Rietveld refinements on neutron data.

Parameter Series A Series B Series C
Ba0.69Sr0.24Ca0.07TiO3 Ba0.74Sr0.12Ca0.15TiO3 Ba0.78Ca0.22TiO3 Ba0.8Sr0.2TiO3 Ba0.6Sr0.2Ca0.2TiO3 Ba0.68Sr0.32TiO3
a (Å) 3.96435(3) 3.96279(3) 3.96231(7) 3.97818(4) 3.94981(4) 3.96849(3)
c (Å) 3.98716(5) 3.99661(4) 4.00921(9) 4.00558(6) 3.97230(7) 3.98159(4)
z (A-site) 0.514(2) 0.512(14) 0.509(2) 0.512(2) 0.511(3) 0.519(2)
Uiso(A-site) (Å2) 0.0056(2) 0.0097(2) 0.0073(3) 0.0079(2) 0.0106(2) 0.0070(2)
Uiso (Ti) (Å2) 0.0033(4) 0.0071(3) 0.0050(4) 0.0071(4) 0.0064(5) 0.0042(4)
z (O1) 0.530(2) 0.5332(1) 0.536(1) 0.527(1) 0.529(2) 0.529(1)
Uiso (O1) (Å2) 0.0079(6) 0.0115(4) 0.0100(5) 0.0098(5) 0.0140(7) 0.0093(5)
z (O2) 0.029(1) 0.030(1) 0.031(1) 0.029(1) 0.029(2) 0.031(1)
Uiso (O2) (Å2) 0.0058(3) 0.0101(2) 0.0080(3) 0.0087(3) 0.0095(3) 0.0071(3)
wRp 4.11 4.34 5.90 4.17 4.11 4.15
Ti-O1 (Å) 1.876(6) 1.866(4) 1.861(5) 1.873(5) 1.870(7) 1.875(5)
Ti-O1 (Å) 2.111(6) 2.131(4) 2.148(5) 2.133(5) 2.102(7) 2.107(5)
Ti-O2 (Å) 1.9856(3) 1.9851(2) 1.9850(3) 1.9924(3) 1.9782(4) 1.9881(3)
Ti-O-Ti (°) 173.2(3) 173.0(2) 172.9(3) 173.4(3) 173.4(4) 172.9(2)
A-O1 (Å) 2.8039(1) 2.8034(1) 2.8039(2) 2.8143(1) 2.7938(1) 2.8604(7)
A-O2 (Å) 2.767(3) 2.762(3) 2.756(3) 2.774(3) 2.753(4) 2.778(3)
A-O2 (Å) 2.857(4) 2.862(3) 2.882(4) 2.872(3) 2.850(4) 2.844(3)
Open in a new tab

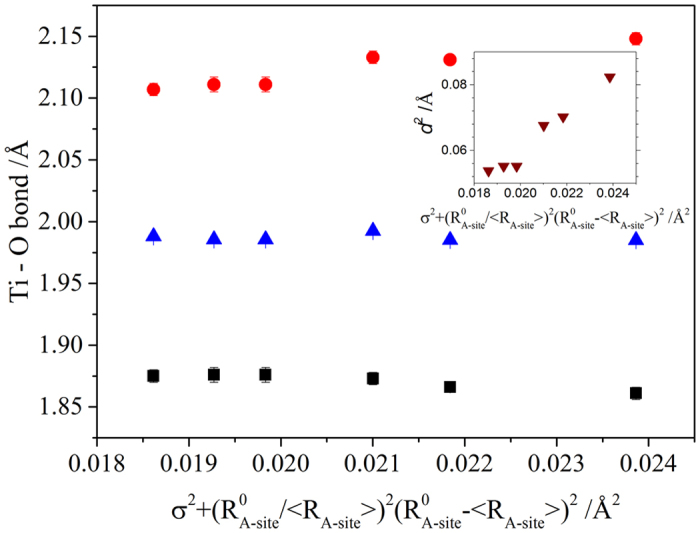
Figure 4.

Figure 4

Open in a new tab

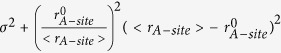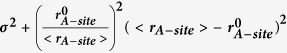Ti-O bond lengths as a function of Inline graphic. Inset shows d2 as function of Inline graphic.

Figure 5 shows the TC as a function of 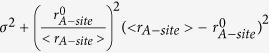Inline graphic in a large number of Ba1-x-ySrxCayTiO3 with the tolerance factor greater than 1 reported in the literature over the last 60 years12,20,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59. A strong linear correlation is observed with some scatter of data presumably due to compositional inhomogeneity (including partial substitution of Ca on B site52), annealing conditions5, thermal hysteresis during the measurements43, etc. In datasets44,46 that showed a deviation from the observed empirical trend, frequency dependences of εr was observed in heavily doped Ca samples. As a result we suggest that the observed empirical equation (5) is valid for typical ferroelectrics.

Figure 5.

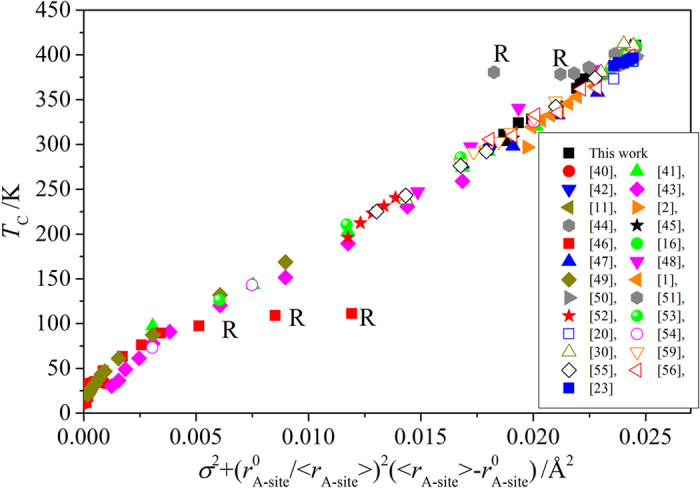
Figure 5

Open in a new tab

TC as a function of 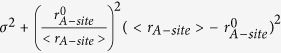Inline graphic for samples studied in this work and reported in the literature. R denotes samples with relaxor type behavior.

It is interesting to consider the effect of Ca doping on TC in Ba1-yCayTiO3 compounds. It has been shown that Ca doping on A-site results in first slight increase of TC with up to 8% Ca doping followed by a decrease20,30,44,51, whereas even small extend of Ca doping on B site resulted in a drastic decrease of TC51,57,58 (Fig. 6). From the proposed model the introduction of smaller Ca ions in BaTiO3 resulted in the increase of σ2 and the decrease of 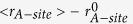Inline graphic thus exhibiting opposite effects on the values of TC. As a result Tc is expected to show the maximum with Ca doping. When the TC data was replotted as a function of 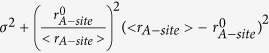Inline graphic a monotonic increase of TC was observed (inset to Fig. 6) regardless of Ca doping on A- or B-sites (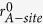Inline graphic increased with Ca doping on the Ti-site). Furthermore our preliminary results showed that the correlation similar to (5) exists in Zr and Sn doped titanates. As a result it is possible that the observed empirical correlation (5) is valid for the families of titanates with A- and B-sites doped by isoelectronic ions. At the same time the proposed model is expected to break down when the ion shape cannot be considered spherical, for example when the stereochemically active electron lone pairs (Pb2+, Bi3+) or partially filled orbitals (La3+) are present as shown in Supplementary Fig. S7.

Figure 6.

Figure 6

Open in a new tab

TC as a function of Ca doping and Inline graphic (inset).

The temperatures for rhombohedral to orthorhombic, TR-O, and orthorhombic to tetragonal, TO-T, transitions in BSCT are shown in Fig. 7(a,b), respectively. For compounds containing only Ba and Sr on the A-site, a linear increase of the transition temperatures with Inline graphic was observed. The Ca containing samples showed negative deviation of TR-O and TO-T from the linear trends of Ba1-xSrxTiO3 compounds (marked as ΔT on Fig. 7(a,b)). ΔT increased linearly with Ca doping, y, regardless of Sr and Ba content (insets to Fig. 7 (a,b)). The following empirical equations were proposed:

Figure 7.

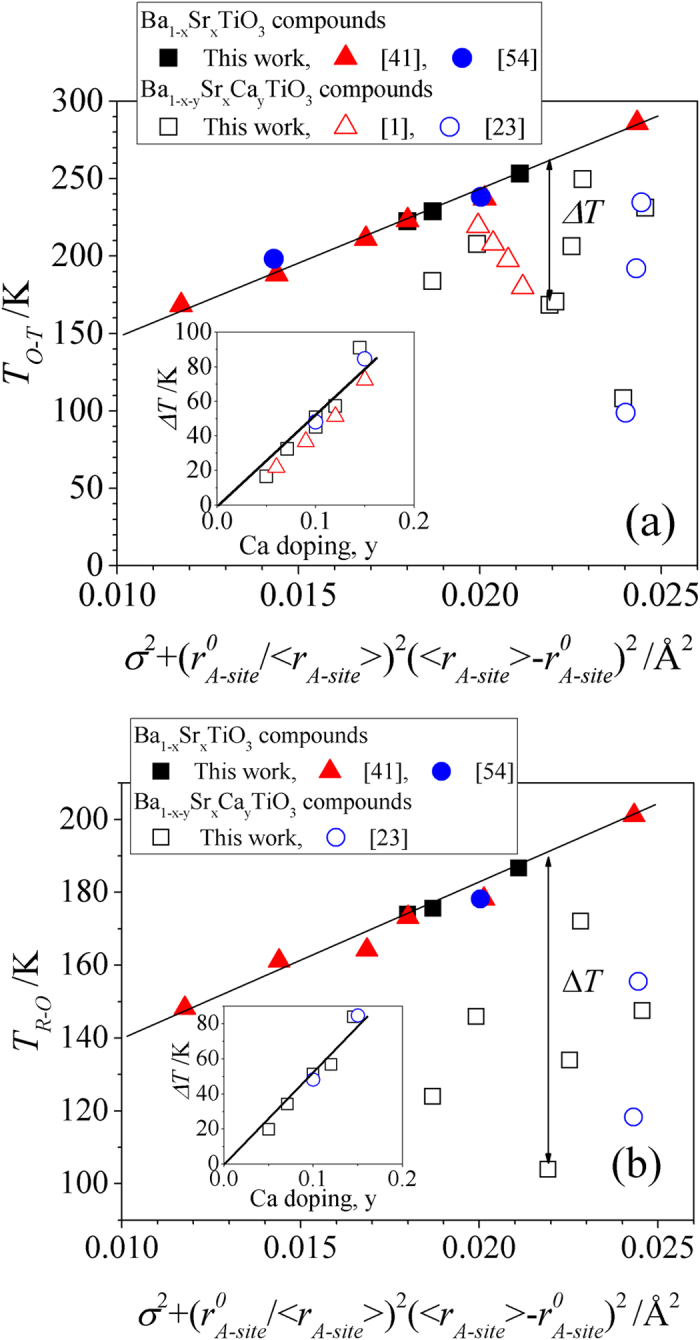
Figure 7

Open in a new tab

Temperatures of orthorhombic to tetragonal transition, TO-T, (a) and rhombohedral to orthorhombic transition, TR-O, (b) as function of 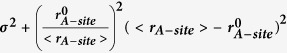Inline graphic. The temperature deviation, ΔT, of Ca containing samples (Ba1-x-ySrxCayTiO3, open symbols) from line for only Ba, Sr containing compounds (Ba1-xSrxTiO3, solid symbols). Insets show ΔT as a function of Ca doping, y. Solid lines are guides to eye.

for orthorhombic to tetragonal transition (y < 0.2)

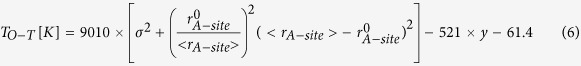graphic file with name srep28055-m24.jpg

for rhombohedral to orthorhombic transition (y < 0.15)

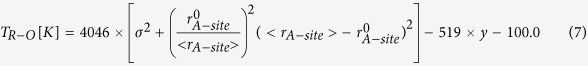graphic file with name srep28055-m25.jpg

In conclusion we demonstrated a combined effect of average ionic radii and cation variance on TC a Ba1-x-ySrxCayTiO3 ferroelctric perovskites. TC increased linearly with σ2 and <rA–site>. A set of empirical equations was proposed which allowed the estimation of temperature of phase transitions in alkaline-earth titanates based on the tabulated values of ionic radii. This provides simple guidelines for a selection of compounds with required values phase transitions temperatures (TC, TR-O and TO-T) in Ba1-x-ySrxCayTiO3 perovskites.

Additional Information

How to cite this article: Berenov, A. et al. Effect of ionic radii on the Curie temperature in Ba1-x-ySrxCayTiO3 compounds. Sci. Rep. 6, 28055; doi: 10.1038/srep28055 (2016).

Supplementary Material

Supplementary Information
srep28055-s1.pdf (665.2KB, pdf)

Acknowledgments

The authors would like to acknowledge the EPSRC (grant EP/G060940/1) and STFC for financial support. Data underlying this article can be accessed on Zenodo at http://dx.doi.org/10.5281/zenodo.53983, and used under the Creative Commons Attribution licence.

Footnotes

Author Contributions A.B. prepared samples, collected and analysed X-ray diffraction, ICP, DSC and dielectric data, performed Rietveld refinements and F.L.G. performed neutron measurements. N.A. supervised the project. All authors contributed in writing of the manuscript.

References

  1. Wang J., Zhang X., Zhang J., Li H. & Li Z. Dielectric and piezoelectric properties of (1−x)Ba0.7Sr0.3TiO3−xBa0.7Ca0.3TiO3 perovskites. J. Phys. Chem. Solids 73, 957–960 (2012). [Google Scholar]
  2. Lin G. C., Xiong X. M., X. Z. J. & Wei Q. Latent heat study of phase transition in Ba0.73Sr0.27TiO3 induced by electric field. J. Therm. Anal. Calorim. 81, 41–44 (2005). [Google Scholar]
  3. Rödel J. et al. Perspective on the Development of Lead-free Piezoceramics. J. Amer. Ceram. Soc. 92, 1153–1177 (2009). [Google Scholar]
  4. Hennings D., Schnell A. & Simon G. Diffuse ferroelectric phase transitions in Ba(Ti1-yZry)O3 ceramics. J. Amer. Ceram. Soc. 65, 539–544 (1982). [Google Scholar]
  5. Lee S., Rossetti G. A., Liu Z.-K. & Randall C. A. Intrinsic ferroelectric properties of the nonstoichiometric perovskite oxide Ba1−xTi1−yO3−x−2y. J. Appl. Phys. 105, 093519 (2009). [Google Scholar]
  6. Zhang L., Zhong W. L., Wang Y. G. & Zhang P. L. The cell volume effect in barium strontium titanate. Solid State Commun. 104, 263–266 (1997). [Google Scholar]
  7. Eitel R. E. et al. New high temperature morphotropic phase boundary piezoelectrics based on Bi(Me)O3–PbTiO3 ceramics. Jap. J. Appl. Phys. 40, 5999 (2001). [Google Scholar]
  8. Nakamura T., Shan Y. J., Sun P.-H., Inaguma Y. & Itoh M. Discrimination of ferroelectrics from quantum paraelectrics among perovskite titanates ATiO3 and (A′1/2 A′′1/2)TiO3. Ferroelectrics 219, 71–81 (1998). [Google Scholar]
  9. Hidaka T. Isotope effect on the ferroelectric phase transitions in BaTiO3, SrTiO3 and PbTiO3. Ferroelectrics 283, 11–22 (2003). [Google Scholar]
  10. Zhong W. L. et al. Phase transition in PbTiO3 ultrafine particles of different sizes. J. Phys. Cond. Matt. 5, 2619 (1993). [Google Scholar]
  11. Li W., Xu Z., Chu R., Fu P. & Hao J. Sol-gel synthesis and characterization of Ba1-xSrxTiO3 ceramics. J. Alloys Compound. 499, 255–258 (2010). [Google Scholar]
  12. Samara G. A. Pressure and temperature dependences of the dielectric properties of the perovskites BaTiO3 and SrTiO3. Phys. Rev. 151, 378–386 (1966). [Google Scholar]
  13. Haeni J. H. et al. Room-temperature ferroelectricity in strained SrTiO3. Nature 430, 758–761 (2004). [DOI] [PubMed] [Google Scholar]
  14. Yamanaka T., Hirai N. & Yutaka K. Structure change of Ca1-xSrxTiO3 perovskite with composition and pressure Amer. Mineralogist 87, 1183–1189 (2002). [Google Scholar]
  15. Rodriguez-Martinez L. M. & Attfield J. P. Cation disorder and size effects in magnetoresistive manganese oxide perovskites. Phys. Rev. B 54, R15622–R15625 (1996). [DOI] [PubMed] [Google Scholar]
  16. Sinclair, D. C. & Attfield P. J. The influence of A-cation disorder on the Curie temperature of ferroelectric ATiO3 perovskites. Chem. Comm., 16, 1497–1498 (1999). [Google Scholar]
  17. MacManus-Driscoll J. L. et al. Systematic enhancement of in-field critical current density with rare-earth ion size variance in superconducting rare-earth barium cuprate films. Appl. Phys. Lett. 84, 5329–5331 (2004). [Google Scholar]
  18. Shannon R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A32, 751–767 (1976). [Google Scholar]
  19. Tiwari V. S., Singh N. & Pandey D. Structure and properties of (Ba,Ca)TiO3 ceramics prepared using (Ba,Ca)TiO3 ceramics I, crystallographic and microstructural studies. J. Amer. Ceram. Soc. 77, 1813–1818 (1994). [Google Scholar]
  20. McQuarrie M. & Behnke F. W. Structural and dielectric studies in the system (Ba, Ca)(Ti, Zr)O3. J. Amer. Ceram. Soc. 37, 539–543 (1954). [Google Scholar]
  21. DeVries R. C. & Roy R. Phase equilibria in the system BaTiO3—CaTiO3. J. Amer. Ceram. Soc. 38, 142–146 (1955). [Google Scholar]
  22. Navi N. U. et al. Thermochemistry of (CaxSr1-x)TiO3, (BaxSr1-x)TiO3, and (BaxCa1-x)TiO3 perovskite solid solutions. J. Amer. Ceram. Soc. 95, 1717–1726 (2012). [Google Scholar]
  23. Zhu X. N., Zhang W. & Chen X. M. Enhanced dielectric and ferroelectric characteristics in Ca-modified BaTiO3 ceramics. AIP Advances 3, 082125 (2013). [Google Scholar]
  24. Fu D., Itoh M., Koshihara S.-y., Kosugi T. & Tsuneyuki S. Anomalous Phase Diagram of Ferroelectric (Ba,Ca)TiO3 Single Crystals with Giant Electromechanical Response. Phys. Rev. Lett. J1-PRL 100, 227601 (2008). [DOI] [PubMed] [Google Scholar]
  25. Puli V. S. et al. Barium zirconate-titanate/barium calcium-titanate ceramics via sol–gel process: novel high-energy-density capacitors. J. Phys. D: Appl. Phys. 44, 395403 (2011). [Google Scholar]
  26. Uchino K. & Nomura S. Critical exponents of the dielectric constants in diffused-phase-transition crystals. Ferroelec. Lett. 44, 55–61 (1982). [Google Scholar]
  27. Attfield J. P. A Simple approach to lattice effects in conducting perovskite-type oxides. Chem. Mater. 10, 3239–3248 (1998). [Google Scholar]
  28. Rodríguez-Martínez L. M. & Attfield J. P. Disorder-induced orbital ordering in L0.7M0.3MnO3 perovskites. Phys. Rev. B 63, 024424 (2000). [Google Scholar]
  29. Levin I., Krayzman V. & Woicik J. C. Local structure in perovskite Ba1-xSrxTiO3: Reverse Monte Carlo refinements from multiple measurement techniques. Phys. Rev. B 89, 024106 (2014). [Google Scholar]
  30. Levin I., Krayzman V. & Woicik J. C. Local-structure origins of the sustained Curie temperature in (Ba,Ca)TiO3 ferroelectrics. Appl. Phys. Lett. 102, 162906 (2013). [Google Scholar]
  31. Abrahams S. C., Kurtz S. K. & Jamieson P. B. Atomic displacement relationship to Curie temperature and spontaneous polarization in displacive ferroelectrics. Phys. Rev. 172, 551–553 (1968). [Google Scholar]
  32. Deng H.-Y., Lam C. H. & Huang H. An atomistic approach to the dielectric modes of BaTiO3 and SrTiO3. Solid State Commun. 151, 474–477 (2011). [Google Scholar]
  33. Grinberg I. & Rappe A. M. Local structure and macroscopic properties in PbMg1∕3Nb2∕3O3-PbTiO3 and PbZn1∕3Nb2∕3O3-PbTiO3 solid solutions. Phys. Rev. B 70, 220101 (2004). [Google Scholar]
  34. Krayzman V. et al. Ca K-edge X-ray absorption fine structure in BaTiO3-CaTiO3 solid solutions. J. Appl. Phy. 113, 044106 (2013). [Google Scholar]
  35. Dawson J. A., Sinclair D. C., Harding J. H. & Freeman C. L. A-Site Strain and Displacement in Ba1-xCaxTiO3 and Ba1-xSrxTiO3 and the Consequences for the Curie Temperature. Chem. Mater. 26, 6104–6112 (2014). [Google Scholar]
  36. Okajima T., Yasukawa K. & Umesaki N. Local structure of Ca dopant in BaTiO3 by Ca K-edge X-ray absorption near-edge structure and first-principles calculations. J. Electron. Spectrosc. Relat. Phenom. 180, 53 (2010). [Google Scholar]
  37. Bilc D. I. & Singh D. J. Frustration of Tilts and A-Site Driven Ferroelectricity in KNbO3-LiNbO3 Alloys. Phys. Rev. Lett. 96, 147602 (2006). [DOI] [PubMed] [Google Scholar]
  38. Singh D. J. & Park C. H. Polar Behavior in a Magnetic Perovskite from A-Site Size Disorder: A Density Functional Study. Phys. Rev. Lett. 100, 087601 (2008). [DOI] [PubMed] [Google Scholar]
  39. Toby B. H. & Von Dreele R. B. GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystal. 46, 544–549 (2013). [Google Scholar]
  40. Bednorz J. G. & Müller K. A. Sr1-xCaxTiO3: An XY quantum ferroelectric with transition to randomness. Phys. Rev. Lett. 52, 2289–2292 (1984). [Google Scholar]
  41. Berbecaru C. et al. Ceramic materials Ba1-xSrxTiO3 for electronics–Synthesis and characterization. Thin Solid Films 516, 8210–8214 (2008). [Google Scholar]
  42. Kang D.-S., Han M.-S., Lee S.-G. & Song S.-H. Dielectric and pyroelectric properties of barium strontium calcium titanate ceramics. J. Eur. Ceram. Soc. 23, 515–518 (2003). [Google Scholar]
  43. Lemanov V. V., Smirnova E. P., Syrnikov P. P. & Tarakanov E. A. Phase transitions and glasslike behavior in Sr1-xBaxTiO3. Phys. Rev. B 54, 3151–3157 (1996). [DOI] [PubMed] [Google Scholar]
  44. Mitsui T. & Westphal W. B. Dielectric and X-ray studies of CaxBa1-xTiO3 and CaxSr1-xTiO3. Phys. Rev. 124, 1354–1359 (1961). [Google Scholar]
  45. Naik R. et al. Temperature dependence of the Raman spectra of polycrystalline Ba1-xSixTiO3. Phys. Rev. B 61, 11367–11372 (2000). [Google Scholar]
  46. Sakamoto N., Wang R. & Itoh M. Effects of A-site ion size mismatch on dielectric properties of SrTiO3. Ferroelectrics 262, 131–136 (2001). [Google Scholar]
  47. Syamaprasad U., Galgali R. K. & Mohanty B. C. Dielectric properties of the Ba1−xSrxTiO3 system. Mater. Lett. 7, 197–200 (1988). [Google Scholar]
  48. Yun S. & Wang X. Dielectric properties of (Ba1-2xSrxCax)TiO3 ferroelectric ceramics. J. Electroceram. 21, 585–588 (2008). [Google Scholar]
  49. Wang R., Inaguma Y. & Itoh M. Dielectric properties and phase transition mechanisms in Sr1−xBaxTiO3 solid solution at low doping concentration. Materials Research Bulletin 36, 1693–1701 (2001). [Google Scholar]
  50. Zhang L. et al. Comment on the use of calcium as a dopant in X8R BaTiO3-based ceramics. Appl. Phys. Lett. 90, 142914 (2007). [Google Scholar]
  51. Zhang L. L., Wang X. S., Yang W., Liu H. & Yao X. Structure and relaxor behavior of BaTiO3-CaTiO3-SrTiO3 ternary system ceramics. J. Appl. Phys. 104, 5 (2008). [Google Scholar]
  52. Zheng R. K. et al. Effects of Ca doping on the Curie temperature, structural, dielectric, and elastic properties of Ba0.4Sr0.6-xCaxTiO3 (0 < = x < = 0.3) perovskites. J. Appl. Phys. 98, 084108 (2005). [Google Scholar]
  53. Zhou L., Vilarinho P. M. & Baptista J. L. Dependence of the structural and dielectric properties of Ba1-xSrxTiO3 ceramic solid solutions on raw material processing. J. Eur. Ceram. Soc. 19, 2015–2020 (1999). [Google Scholar]
  54. Alexandru H. V., Berbecaru C., Ioachim A., Nedelcu L. & Dutu A. BST solid solutions, temperature evolution of the ferroelectric transitions. Appl. Surf. Sci. 253, 354–357 (2006). [Google Scholar]
  55. Fu C., Yang C., Chen H., Wang Y. & Hu L. Microstructure and dielectric properties of BaxSr1−xTiO3 ceramics. Mater. Sci. Eng. B 119, 185–188 (2005). [Google Scholar]
  56. Cheng X. & Shen M. Enhanced spontaneous polarization in Sr and Ca co-doped BaTiO3 ceramics. Solid State Commun. 141, 587–590 (2007). [Google Scholar]
  57. Park J. G., Oh T. S. & Kim Y. H. Dielectric properties and microstructural behaviour of B-site calcium-doped barium titanate ceramics. J. Mater. Sci. 27, 5713–5719 (1992). [Google Scholar]
  58. Zhuang Z. Q., Harmer M. P., Smyth D. M. & Newnham R. E. The effect of octahedrally-coordinated calcium on the ferroelectric transition of BaTiO3. Mater. Res. Bull. 22, 1329–1335 (1987). [Google Scholar]
  59. Bai Y., Han X. & Qiao L. Optimized electrocaloric refrigeration capacity in lead-free (1-x)BaZr0.2Ti0.8O3-xBa 0.7Ca0.3TiO3 ceramics. Appl. Phys. Lett. 102, 252904 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep28055-s1.pdf (665.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES