Robust functional clustering of ERP data with application to a study of implicit learning in autism

Abstract

Motivated by a study on visual implicit learning in young children with Autism Spectrum Disorder (ASD), we propose a robust functional clustering (RFC) algorithm to identify subgroups within electroencephalography (EEG) data. The proposed RFC is an iterative algorithm based on functional principal component analysis, where cluster membership is updated via predictions of the functional trajectories obtained through a non-parametric random effects model. We consider functional data resulting from event-related potential (ERP) waveforms representing EEG time-locked to stimuli over the course of an implicit learning experiment, after applying a previously proposed meta-preprocessing step. This meta-preprocessing is designed to increase the low signal-to-noise ratio in the raw data and to mitigate the longitudinal changes in the ERP waveforms which characterize the nature and speed of learning. The resulting functional ERP components (peak amplitudes and latencies) inherently exhibit covariance heterogeneity due to low data quality over some stimuli inducing the averaging of different numbers of waveforms in sliding windows of the meta-preprocessing step. The proposed RFC algorithm incorporates this known covariance heterogeneity into the clustering algorithm, improving cluster quality, as illustrated in the data application and extensive simulation studies. ASD is a heterogeneous syndrome and identifying subgroups within ASD children is of interest for understanding the diverse nature of this complex disorder. Applications to the implicit learning paradigm identify subgroups within ASD and typically developing children with diverse learning patterns over the course of the experiment, which may inform clinical stratification of ASD.

1. Introduction

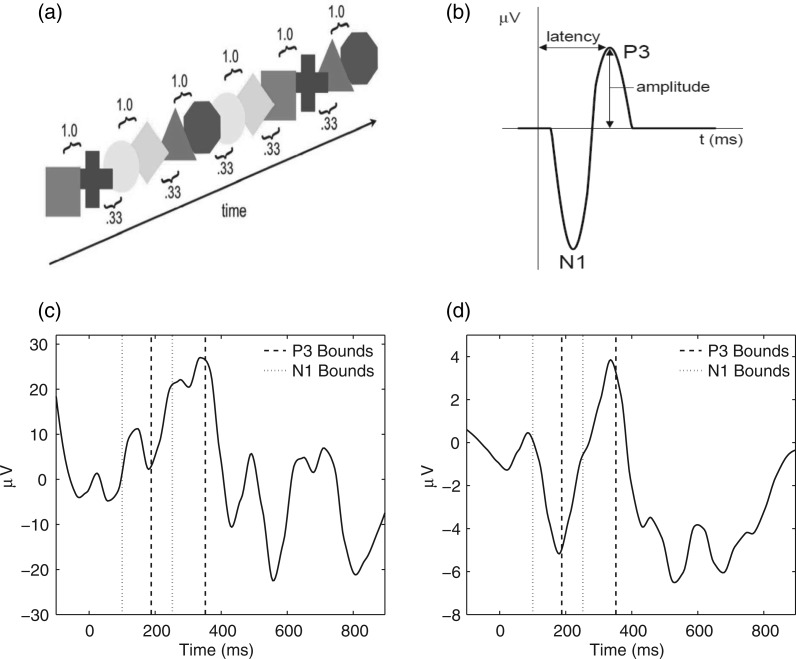
Electroencephalography (EEG) is a non-invasive method for measuring spontaneous electrical activity across brain regions over time. As a method to identify neural function and cognitive states, it has been studied in diverse biomedical settings including epilepsy, sleep disorders, multiple sclerosis, brain tumors, schizophrenia, and bipolar disorder (Tierney and others, 2012). Here we consider an application to a study of visual implicit learning in young children with Autism Spectrum Disorders (ASDs) (Jeste and others, 2015). ASD has a highly heterogeneous presentation, making it difficult to tease apart underlying mechanistic pathways to core deficits. The goal of this paper is to provide insights into those pathways through a better understanding of implicit learning, defined as the detection of regular patterns in one's environment without a conscious awareness to learn. Age-matched 2–5-year-old typically developing (TD) and ASD children were presented with a continuous sequence of six colored shapes organized into three shape pairs (Figure 1(a)). Shapes within pairs appeared in the same order but the pairs themselves occurred in random order. Transitions within a shape pair were labeled “expected” since they could be learned and transitions between shape pairs were “unexpected” since they could not be predicted.

Fig. 1.

(a) The sequence of shape pairs in the implicit learning paradigm. (b) The ERP waveform containing the P3 and N1 phasic components from the implicit learning study. (c) ERP waveform from a single subject, condition, electrode, and trial in the right frontal region of the scalp after preprocessing. (d) The average of the first 30 consecutive ERP waveforms for the same subject, electrode, and condition.

EEG signals, time-locked to visual stimuli (e.g. presentation of colored shapes), result in event-related potential (ERP) waveforms containing the P3 and N1 phasic components shown in Figure 1(b). While the focus is on the P3 and N1 components in this particular paradigm, other phasic components may be studied in different applications. The P3 peak of the ERP waveform is thought to be related to cognitive processes such as decision-making, while the N1 dip represents early category recognition (Bugli and Lambert, 2006; Jeste and others, 2015). Implicit learning is assessed through differences in the amplitude (size of the peak) and latency (time when the peak occurs) of the ERP components between the expected and unexpected conditions.

It is natural to seek inference about potential differences in ERP variation between TD and ASD groups in the implicit learning paradigm (Jeste and others, 2015). However, ASD is a heterogeneous syndrome characterized by impairments in social communication and the presence of restricted interests and repetitive behaviors. Hence, in addition to contrasting learning patterns of TD and ASD groups, identifying subgroups within ASD children with distinct learning patterns is also of interest for understanding the diverse nature of this complex disorder. We therefore propose a robust functional clustering (RFC) algorithm to more finely grain learning patterns within TD and ASD children. The term “robust” refers to the proposed algorithm's ability to make maximal use of the existing structural information on covariance heterogeneity of ERPs induced by data quality issues to improve clustering accuracy even in small samples.

Typical analysis of ERP data focuses on summaries of key components, such as peak amplitude and latency. Specifically, to increase the low signal-to-noise ratio (SNR) in raw ERP data, the waveforms resulting from repeated stimuli (referred to as trials) are averaged for each subject so that the ERP components are identifiable. Hasenstab and others (2015) proposed a meta-preprocessing step for the analysis of ERP data, based on a moving average, which increases the SNR of the observed ERPs while preserving changes in ERPs across trials. Meta-preprocessing retains valuable longitudinal information which is lost by the common practice of averaging ERP trajectories across all trials. Capturing these trends is especially important in settings such as our motivating example, where patterns of learning correspond by definition to changes of ERP features across trials. However, an important issue with the meta-preprocessed functional ERP components is covariance heterogeneity, due to removed trials. Trials resulting in low data quality, commonly encountered in experiments involving young children, are removed in the data cleaning steps. This leads to the averaging of different numbers of waveforms in the sliding windows during meta-preprocessing, and hence to covariance heterogeneity in the functional data. We propose a novel clustering algorithm for the functional data produced by the meta-preprocessing step (consisting of ERP components obtained over trials of the experiment for each subject), which accounts for the known source of covariance heterogeneity in the trajectories induced by data quality issues, setting it apart from previously proposed functional clustering algorithms.

Clustering or classification of functional data typically involves either regularization or filtering. Regularization involves discretization of the time interval followed by the application of standard multivariate clustering or classification methods. Because the resulting data are high-dimensional and highly correlated, a regularization constraint is typically applied to the covariance structure in model-based methods (Yeung and others, 2001; Fraley and Raftery, 2002; Samé and others, 2011). Filtering methods work by projecting each curve onto a finite-dimensional set of basis functions, such as B-splines or functional principal component analysis (FPCA), and then applying standard clustering or classification algorithms to the resulting basis coefficients (James and Sugar, 2003; Serban and Wasserman, 2005; Delaigle and others, 2012; Gattone and Rocci, 2012). Serban and Jiang (2012) extended filtering-based functional approaches to hierarchical data structures using multilevel FPCA in the context of hard and soft clustering.

Chiou and Li (2007, 2008) introduced another filtering method, k-centers functional clustering (FC), based on FPCA to identify homogeneous clusters within the sample sharing a cluster-specific mean function and a cluster-specific covariance surface. We build on this approach to incorporate the known covariance heterogeneity in the meta-preprocessed functional data into the proposed clustering algorithm. First, we identify induced covariance subsets within each diagnostic group with similar low quality data patterns over time (trials of the ERP experiment). Fixing the covariance subsets, trajectories are clustered according to the estimated mean trends where covariance subset and cluster memberships are allowed to differ. Mean trajectory and covariance surface estimates are updated iteratively in a non-parametric fashion, where cluster memberships are updated in a reclassification step based on a non-parametric random effects model. We further extend the proposed RFC for multilevel functional data to be applicable to the meta-preprocessed ERP components obtained from multiple electrodes on the scalp.

The remainder of the paper is organized as follows. Section 2 describes the cleaning and meta-preprocessing of ERP data in detail. Section 3 provides background on FPCA and introduces the proposed RFC algorithm for single- and multilevel functional data. Section 4 applies the proposed RFC to the autism study and compares the results with those obtained from alternative algorithms including FC of Chiou and Li (2007). We study the performance of the proposed algorithm in extensive simulations summarized in Section 5 and conclude with a brief discussion (Section 6).

2. Description of the data cleaning and meta-preprocessing steps and the resulting multilevel functional data

In the motivating study of implicit learning, EEG data were recorded for 120 trials per condition (expected/unexpected) for each of the 34 TD and 37 ASD children at 128 electrodes. The EEG signals were sampled at 250 Hz, producing 250 within-trial time points per waveform, spanning 1000 ms. Despite the standard preprocessing steps (see Hasenstab and others, 2015 for more details), the ERP data has a small SNR, making it difficult to identify components, such as peak amplitudes and latency, on trial-specific ERPs. Figure 1(c) displays a single ERP waveform for one subject from a single trial recorded in the right frontal region of the scalp. The P3 peak and N1 dip are unrecognizable due to the low SNR. Typical analysis of averaging across all ERP trials in order to increase the SNR to a level where features are identifiable leads to a loss of longitudinal information about potentially important changes over the course of the experiment. Hence the meta-preprocessing of Hasenstab and others (2015), utilizing a moving average of ERPs across sliding trial windows, is necessary to extract meaningful longitudinal information on features of the ERP curves. Figure 1(d) displays the meta-preprocessed ERP (an average of 30 ERP waveforms from adjacent trials) where the P3 peak and N1 dip are easily recognized due to the increased SNR. Components of interest such as peak amplitudes are extracted from these averaged ERP waveforms (see Hasenstab and others, 2015 for details).

In addition to identifying the magnitudes of the key ERP components over trials, the meta-preprocessing provides information on the variance of the extracted components. EEG experiments involving young children tend to have larger amounts of trials with low quality data due to head movements or lack of cooperation. Hence, the number of ERPs averaged in the sliding windows during meta-preprocessing may not be the same, introducing a known form of covariance heterogeneity in the ERP components. Components extracted from ERPs averaged over a smaller number of trials will have larger variance. For illustration of the methods, we consider P3 peak amplitude trajectories between the 5th and 60th trials of the experiment, where implicit learning is thought to be maximal, and analyze data from the four electrodes in the right frontal region of the scalp. The considered data are multilevel (electrodes nested in subjects) on P3 amplitude difference trajectories between expected and unexpected conditions and the number of averaged ERPs. We first cluster the multilevel functional data on the number of averaged ERPs to determine the induced covariance subsets (see Section 4 for details), which are assumed to be known in the proposed RFC algorithm outlined below.

3. Robust functional clustering

Our work builds on the FC algorithm proposed by Chiou and Li (2007). The original formulation of FC assumes identical mean and covariance cluster membership. This assumption of within-cluster covariance homogeneity may not be warranted in meta-preprocessed ERP data. Hence, we aim to make use of the covariance subset information induced in the meta-preprocessing step due to data quality issues. We consider 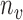covariance subsets, but we do not require subset membership to necessarily overlap with cluster membership in the proposed RFC, which clusters trajectories according to mean trends. Even though the covariance subsets are known, the covariance surfaces cannot be estimated with unknown cluster membership of the functional trajectories. Hence the proposed algorithm involves an iterative mean and covariance update to estimate cluster structures. These cluster structures are used for updating cluster memberships via predictions based on a non-parametric random effects model of the truncated Karhunen–Loève (K-L) expansions. We introduce basic principles in Section 3.1 and the RFC algorithm in Section 3.2.

3.1. Functional model

The observed functional trajectory for subject 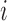, , 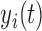is assumed to be a realization of a stochastic process, 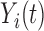, defined in a Hilbert space of square integrable functions 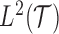, 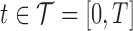with the norm 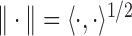, where 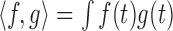for two functions 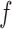and 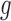. The random function has smooth and continuous mean 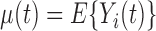and covariance 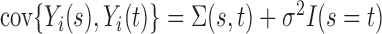, leading to the K-L expansion, 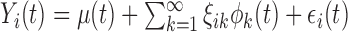, where 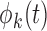are the eigenfunctions associated with covariance 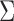and corresponding eigenvalues 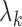such that 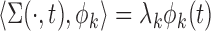and 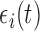is measurement error with mean zero and variance 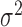. The eigenfunctions are orthonormal, i.e. 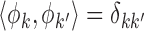, where 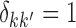when 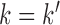and 0 when 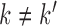. The eigenvalues are assumed in non-increasing order 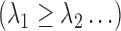such that their sum is finite. The scores 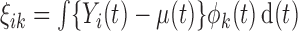are the projections of 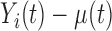in the direction of the 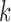th eigenfunction 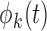and are uncorrelated with 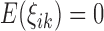and .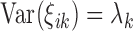

To allow for granularity in the foregoing model, we allow subclusters within each of the overarching diagnostic groups (i.e. ASD and TD). Specifically, we assume that 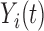is sampled from a mixture of stochastic processes, with cluster membership indexed by 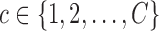. To account for covariance heterogeneity, we allow for covariance subsetting, indexed by 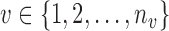, which may be different from cluster membership. Conditioning on cluster membership 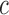and covariance subset 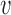, means and covariances of the subprocesses are given as 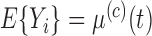, , 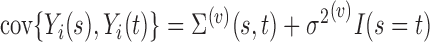respectively. The measurement error 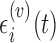has mean zero and variance 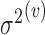for covariance subset 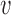. We note that, for full generality, measurement error can be allowed to change across covariance subsets, but in practice one will often contain it to be the same across 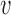. It is assumed that each subprocess has a K-L expansion with corresponding mean function 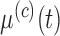and eigenvalues 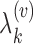and corresponding eigenfunctions 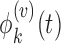such that 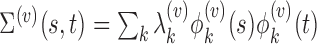, 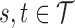and .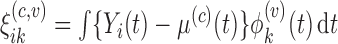

The updating of the cluster membership in the proposed RFC will utilize functional predictions based on the non-parametric random effects model, 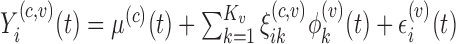. Methods for selecting the number of components 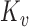include cross-validation (Yao and others, 2005), Akaike's Information Criterion (Yao and others, 2005), and percentage of variance explained (Chiou and Li, 2008; Di and others, 2009). We found that choosing components to explain 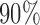of the variation works well in our applications. For a trajectory 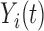from covariance subset 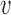, 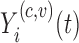will be the truncated K-L expansion and hence will be a good approximation o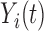f if 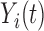actually belongs to cluster 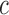, but may match poorly if the current cluster assignment is incorrect. Hence, the cluster membership updating will compare an observed curve for subject 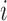, 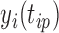(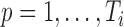), from covariance subset 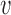to its estimated predictions 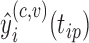from each of the 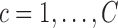clusters and assign cluster membership according to the criterion .

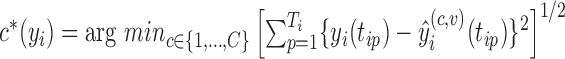3.2. RFC algorithm

Single-level RFC Algorithm

1. Fit the FPCA model to the entire sample and cluster the leading 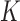scores 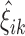using k-means to initialize mean clusters , .

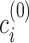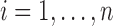2. For each subject 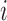belonging to covariance subset 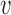and assigned to mean cluster 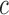during iteration :

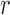   1. Estimate 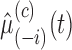, , 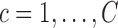using all subjects assigned to mean cluster 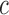in iteration 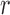while leaving out the 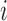th subject.
   2. Estimate 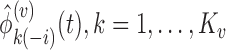, using all mean centered trajectories of subjects who belong to the covariance subset 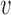, while leaving out the 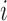th subject.
   3. Estimate 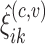, for the mean clusters 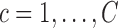and the covariance subset .
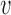   4. Calculate predictions for the mean clusters 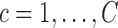and the covariance subset 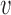via .
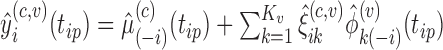   5. Assign the 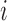th subject to mean cluster

      

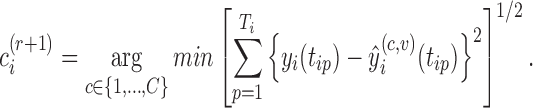
3. Repeat Step 2 until no curve is reclassified.

The proposed RFC algorithm for single-level data is summarized in the above table. Note that covariance subset assignments do not change throughout the algorithm; only the mean clusters are updated in each iteration. Clusters are initialized in Step 1. Note that if the initial clusters are far from the true clustering, this could adversely affect cluster quality and the RFC may converge to a local optimum. Hence, robustness to initial clustering results should be studied in applications. Given the initial clustering results, we estimate predictions for the 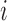th subject's trajectory from all clusters 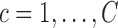(Step 2(a)–(d)). Model components are estimated (details are deferred to the supplementary material available at Biostatistics online) while leaving out the 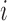th subject to avoid bias in the model predictions. While the covariance components themselves, such as the eigenfunctions and eigenvalues, are not associated with mean clusters, their estimates will be associated with multiple mean clusters since mean centered trajectories are used in the estimation of both 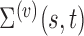and 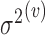(Step 2(b)). Nevertheless, covariance estimates are not indexed by these sets of mean clusters for ease of notation. When estimating FPCA model components, only the mean functions of the cluster containing subject 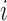need to be re-estimated. In addition, the eigenfunction estimates need to be estimated only for one covariance subset, the subset that contains the 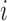th subject's trajectory. Scores can be estimated based on the leave-one-out mean and eigenfunction estimates for 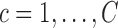, based on the estimated projection 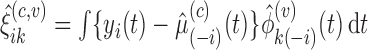for dense functional data. For sufficiently large sample sizes, one may ignore the leave-one-curve out procedure when calculating predictions 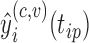in order to significantly reduce computational time, assuming negligible bias. Finally, the sum in Step 2(e) is taken over all observation time points for subject 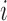, but different weighting schemes can be implemented if observation times in certain intervals are thought to be more informative than others in determining cluster membership.

As with other clustering algorithms, RFC requires the number of clusters (and covariance subsets) to be known a priori. In our applications, we set both the number of clusters and covariance subsets to two due to limitations in sample size (there are 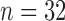and 34 children in the TD and ASD groups, respectively, after removal of outliers). Readers are referred to Li and Chiou (2011) for an extensive discussion on methods for selecting the number of clusters in the context of functional data. In addition, the bandwidth choices in the estimation of the mean functions and covariance surfaces may have an effect on the performance of the clustering, since the cluster memberships, hence possibly the smoothness levels of the mean and covariance functions, dynamically change across iterations. We defer discussions on the selection of the smoothing bandwidths to Section 4 and the supplementary material (available at Biostatistics online).

Chiou and Li (2007) discuss identifiability conditions for their FC algorithm and show that the cluster eigenspaces cannot be subsets of each other; there cannot be two identical cluster mean functions and that if a cluster mean function belongs to its own cluster's eigenspace, then another mean function cannot belong to that same eigenspace. Note that unlike our proposed RFC, the FC algorithm of Chiou and Li assumes that all curves within a cluster have the same covariance and uses both mean and covariance differences to identify clusters. In contrast, the proposed RFC clusters functional trajectories only based on differences in mean trends, since cluster and covariance subset memberships do not necessarily overlap. Hence identifiability conditions for the proposed RFC include that (1) the cluster mean functions cannot be the same and that (2) the cluster mean functions cannot lie in any covariance subset eigenspace. Note that the identifiability of the covariance subsets (via the assumption that eigenspaces cannot be subsets of each other) is no longer needed for RFC, since the covariance subsets are assumed to be known a priori. However, while cluster mean functions lying in their own eigenspaces is not a problem for FC, where FC cluster and covariance subset memberships overlap, it poses an identifiability issue for RFC, where memberships do not necessarily overlap. Since the first identifiability condition is standard, we examine only the second condition through simulation studies (Section 5).

We also extend the proposed RFC algorithm to multilevel functional data. Multilevel functional data refers to functional data collected in a hierarchy of units such as subject-specific ERP feature trajectories observed at multiple electrodes (subunits) on the scalp. Let 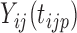denote a functional response observed for subject 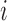, on subunit 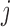at time point 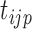, 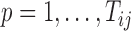. Total functional variation in 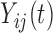, , 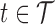can be decomposed via functional analysis of variance (FANOVA) such that 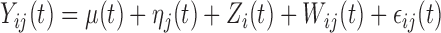, where 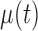and 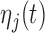are fixed functional effects that represent the overall mean function and subunit (e.g. electrode-specific) shifts, respectively; 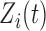and 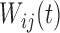are the subject- and subunit-specific deviations, respectively; and 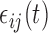is measurement error with mean zero and variance 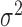(Di and others, 2009). The deviations 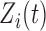and 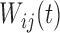are assumed to be uncorrelated mean zero stochastic processes. 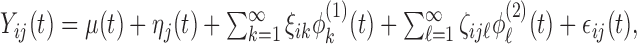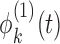As with the K-L decompositions for the single-level functional data, decomposition across both levels of variation results in where and 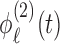are level 1 and level 2 eigenfunctions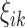, and and 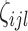are subject-specific scores with mean zero and variance 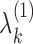and 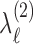, respectively. Note that 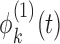and 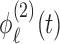may not be mutually orthogonal. The above formulation models the dependency between subunit-specific trajectories within a subject, while still allowing covariance surfaces within subunits to be different from covariance surfaces across subunits. In this application, we consider multilevel functional data from four electrodes in the right frontal region of the scalp. However, we note that more complex FANOVA models can be developed with additional layers in the multilevel structure (e.g. electrodes nested within multiple brain regions). Similarly to the single-level case, we assume that 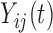is sampled from a mixture of subprocesses with cluster means and induced covariance subsets. Cluster membership updates still utilize functional predictions based on the estimated non-parametric truncated multilevel random effects model and cluster allocation is performed based on a multilevel extension of the single-level distance-based criterion. A detailed summary of the multilevel RFC extension is included in the supplementary material (available at Biostatistics online).

4. Application to the implicit learning study

We utilize the proposed multilevel RFC algorithm to cluster P3 amplitude difference trajectories within ASD and TD groups. Following the data cleaning and meta-preprocessing steps, differences in amplitudes are computed for each trial between expected and unexpected conditions; trials which do not have valid data for both conditions are considered missing. To determine the covariance subsets, the number of ERPs (from sliding windows in the moving average) are further averaged across conditions, where the number of ERPs are observed to be quite similar for the two conditions. Five subjects are removed as outliers prior to analysis. Two of the removed subjects (one in each diagnostic group) did not have observed data until trial 20 of the experiment, and the remaining three subjects had amplitude differences more than 2 standard deviations away from their respective group means for most of the trials. Covariance subsetting is determined by clustering the multilevel functional trajectories of the number of averaged ERPs. A k-means clustering is applied to the level 1 scores in the multilevel FPCA decompositions. Due to small sample sizes in both the TD and ASD groups (32 and 34 children in TD and ASD groups, respectively), we explore two clusters and two covariance subsets via RFC.

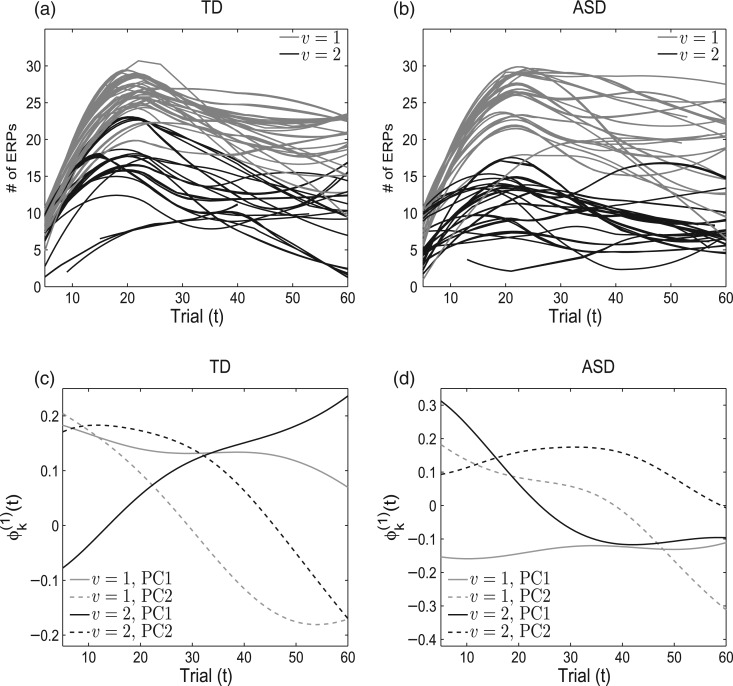
The number of averaged ERPs from all 4 electrodes are plotted in Figures 2(a) and (b) for the two covariance subsets identified within the TD and ASD groups. Lower numbers of averaged ERPs correspond to higher variance. The numbers of averaged ERPs increase to their maximum value of 30 around trial 20 in the first covariance subset. The separation between covariance subsets is larger in the ASD group with respect to shapes and magnitudes of the trajectories due to lower numbers of averaged ERPs, suggesting stronger covariance heterogeneity. The second covariance subset within ASD has consistently low numbers of averaged ERPs across the first 60 trials. In contrast, the trajectories in the second covariance subset within TD are more similar in shape to those in the first covariance subset but with smaller magnitudes. These observations are consistent with the estimated covariance subset eigenfunctions (Figures 2(c) and (d)) obtained after the estimation of the cluster means via RFC. The estimated leading eigenfunction for the second covariance subset within TD shows that much of the variability in the trajectories is observed at later trials, where the number of averaged ERPs decrease. Nevertheless, the estimated leading eigenfunctions differ more in ASD than the TD group. The major differences are in the earlier trials, where the second covariance subset within ASD has lower numbers of averaged ERPs.

Fig. 2.

The number of averaged ERP trajectories from the two covariance subsets for the TD (a) and ASD (b) children. Estimated eigenfunctions for the two covariance subsets are given in plots (c) and (d) where the gray and black trajectories correspond to the covariance subset index and the solid and dashed lines represent the first and second principal components, respectively.

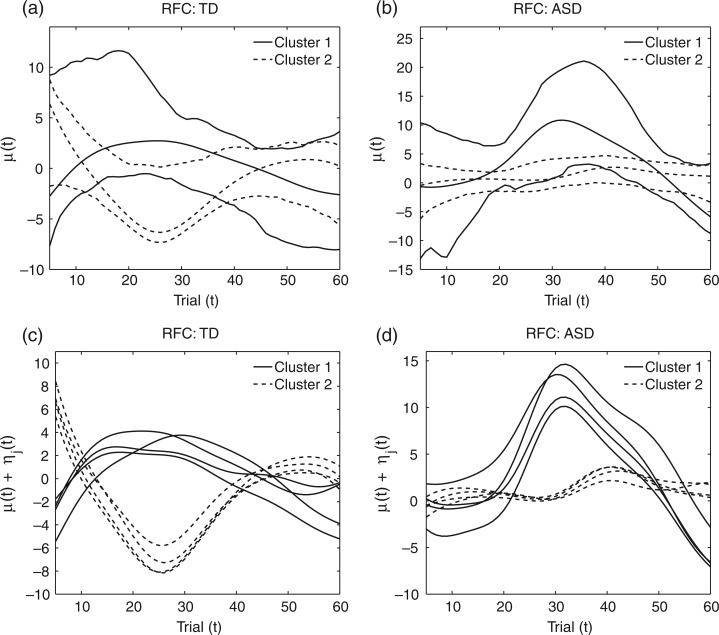
Estimated cluster means and 90% bootstrap bands obtained from the RFC algorithm are shown in Figures 3(a) and (b) for the TD and ASD groups, respectively. Bandwidths for the mean and covariance smooths are selected using generalized cross-validation and visual assessment to maximize cluster quality, where selected bandwidths are 5 and 10 for mean and covariance smoothing, respectively. A sensitivity analysis, where different bandwidths across iterations were selected by generalized cross-validation, yielded similar results. The percentile confidence bands are based on 200 bootstrap samples chosen with replacement from TD and ASD subject-specific ERP data. The data cleaning and meta-preprocessing steps are applied to the resampled ERP data followed by covariance subsetting and RFC clustering. Hence, in addition to assessing the variability in the proposed RFC algorithm, the bootstrap procedure also includes variability associated with the meta-preprocessing of the data and sampling variation within the TD and ASD groups. While resulting confidence intervals are wide, given the small sample sizes of our application, we note that the shapes of the cluster mean trajectories are fairly preserved in the bootstrap bands. Bootstrap clusters are mapped to the cluster means of the original sample such that the distance between them is minimized. The percentage of times a subject is assigned to their original mean cluster over the 200 bootstrap runs is averaged across all subjects to be used as a measure of RFC cluster consistency. Despite the small sample size of the groups, RFC clustering is found to be fairly consistent, its subjects in the bootstrap sample being assigned their original clusters 76% and 77% of the time for the TD and ASD groups, respectively. In addition to the plots of the estimated cluster means, Figures 3(c) and (d) display the electrode-specific cluster means which are quite similar within clusters, implying small within-subject between-electrode variation. Hence, we further display amplitude difference trajectories smoothed across electrodes in the top rows of Figures 4 and 5 for the TD and ASD groups, respectively.

Fig. 3.

The estimated cluster mean functions obtained from RFC for the TD (a) and ASD (b) groups along with 90% bootstrap confidence bands. The estimated electrode-specific cluster mean functions are also plotted for the TD (c) and ASD (d) groups.

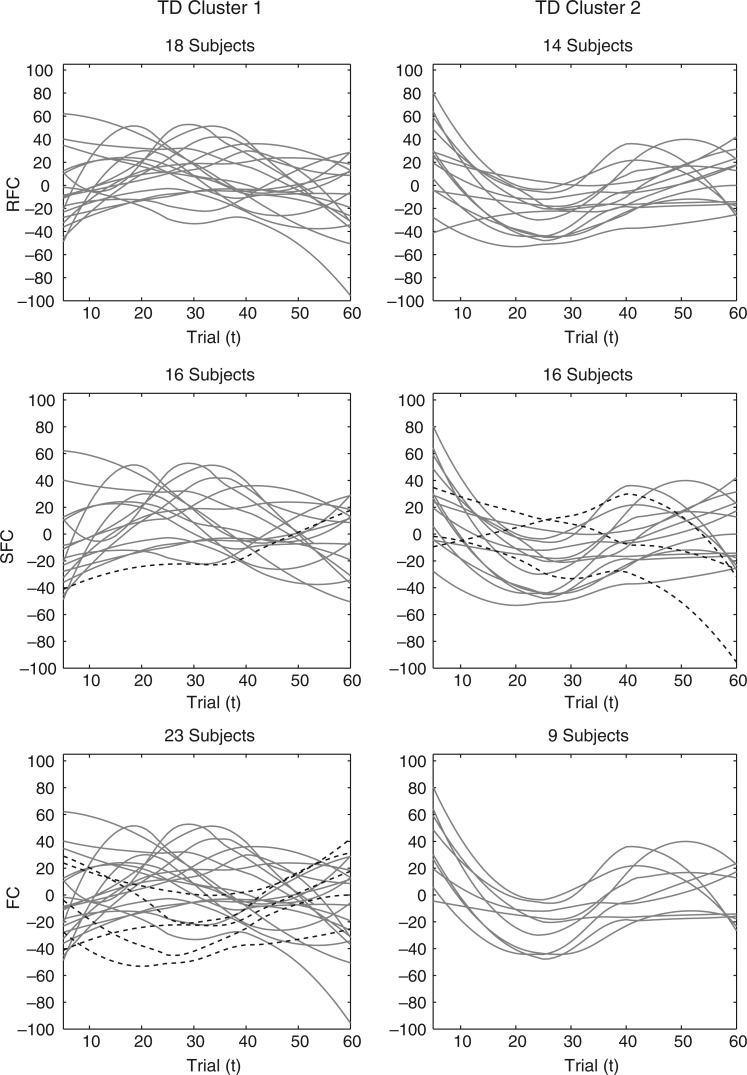
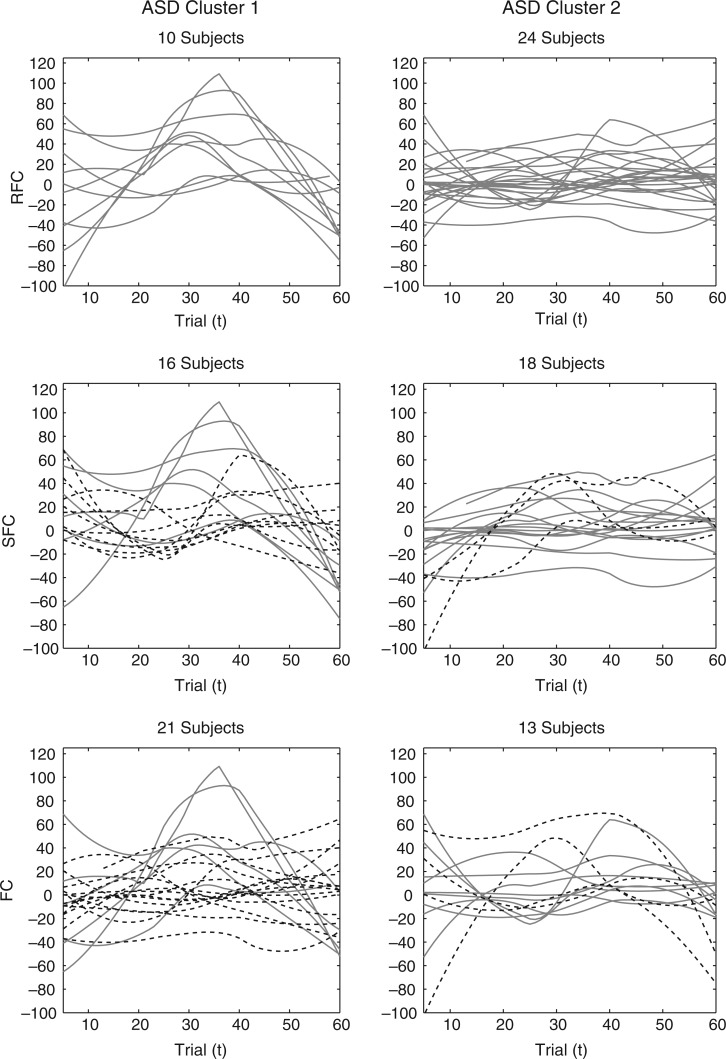
Fig. 4.

The smoothed P3 amplitude difference trajectories across electrodes for each algorithm (row) and cluster (column) within the TD group. The trajectories in SFC and FC with different clustering assignment from the proposed RFC are given dashed.

Fig. 5.

The smoothed P3 amplitude difference trajectories across electrodes for each algorithm (row) and cluster (column) within the ASD group. The trajectories in SFC and FC with different clustering assignment from the proposed RFC are given dashed.

The TD group contains two clusters with roughly equal numbers of children showing condition differentiation in opposing positive and negative directions, while the ASD group comprises a subgroup of children 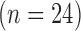with a flat mean condition differentiation and another subgroup 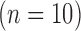with a positive mean differentiation pattern (Figures 3(a) and (b)). While the average pattern over the two subgroups within the TD and ASD groups are consistent with previous findings (Hasenstab and others, 2015), with a negative overall mean differentiation pattern for TD and a positive overall mean pattern for ASD, they identify diverse subgroups within each diagnostic group, implying that not all TD and ASD children display opposing trends of condition differentiation. In fact, most children in the ASD group are in the cluster with a flat differentiation pattern indicating little or no implicit learning, while others differentiate positively between the conditions, similar to roughly half of the TD children. RFC analysis shows that the negative differentiation pattern of half of the TD children is not shared by children with ASD. These findings provide novel insights into the diversity of implicit learning patterns within each group, while also enabling comparisons across groups.

The RFC clustering results are further compared with clusters obtained via a simpler version of the algorithm that assumes a single covariance subset [referred to as the single subset functional clustering (SFC)] and a multilevel extension of the FC algorithm of Chiou and Li (2007). Smoothed amplitude difference trajectories across electrodes from all clustering algorithms are also displayed in Figures 4 and 5. For the TD group, SFC yields similar clustering results to RFC with a few differences in cluster assignments and an equal subject split across clusters. In contrast, the SFC results are quite different from RFC for the ASD group, allocating several of the subjects from the cluster with the flat mean to the cluster with the positive mean. This is consistent with the prior observations where trajectories of the number of averaged ERPs and estimated eigenfunctions confirm that the ASD group displays higher covariance heterogeneity than the TD group, which makes the single covariance subset assumption of SFC harder to justify. The clustering results from FC are different from those obtained from RFC in both the TD and ASD groups. For the TD group, FC assigns subjects from the cluster with the negative mean to the cluster with the positive mean. For the ASD group, FC assigns almost half of the subjects from the cluster with the flat mean to the cluster with the positive mean. The FC algorithm clusters subject trajectories according to both the mean and covariance trends. Hence, due to the covariance heterogeneity in the TD and ASD groups, FC is unable to robustly identify clusters according to differences in the mean trends. We also compare the three clustering algorithms within the TD and ASD groups using multilevel extensions to multiple internal cluster validation metrics: the Davies–Bouldin, Calinski–Harabasz, and Silhouette indices. Indices show that RFC achieves a better cluster separation over the other two algorithms within each diagnostic group and differences across the three algorithms are greater in the ASD group (details on the results are deferred to the supplementary material available at Biostatistics online). Performance of the three clustering algorithms are further compared via simulations (Section 5).

5. Simulation studies

We study the performance of the proposed RFC compared with FC and SFC, and study the performance of the algorithm under the second non-identifiability condition outlined in Section 3.2, that the cluster mean functions lie in the same or different covariance subset eigenspaces. We summarize the findings in this section and defer the simulation details including the selection of smoothing bandwidths to the supplementary material (available at Biostatistics online). We conducted simulations under five scenarios. The first two cases correspond to the second non-identifiability condition with cluster mean functions lying in the eigenspace of the same covariance subset (case 1) and different covariance subsets (case 2). The cluster and covariance subset memberships are not assumed to be identical. The last three simulation scenarios correspond to the assumptions of RFC, SFC, and FC, respectively: that the cluster and covariance subset memberships are not identical (case 3); that there is a single covariance subset for the entire sample (case 4); and cluster and covariance subset membership are set to be the same (case 5). All three algorithms perform poorly in the first two simulation cases of non-identifiability conditions, since the cluster means lying in the eigenspace of the covariance subsets is also a non-identifiable case for SFC and FC with non-overlapping cluster and covariance subset memberships. RFC outperforms SFC and FC in the third simulation case, improving cluster quality by incorporating the known covariance heterogeneity into the clustering of the mean trends. When the covariance groups are highly similar (simulation case 4), all three algorithms perform equally well as expected. In case (5), where cluster and covariance subset membership overlap and there are multiple covariance subsets, RFC is almost as effective in finding clusters as FC and SFC is unable to recosver clusters.

6. Discussion

We proposed a novel clustering algorithm (RFC) that is designed to integrate existing structural information on covariance heterogeneity in the sample into clustering, leading to improvements in cluster accuracy even in small samples. In our data application, the known covariance heterogeneity arises during the preprocessing steps designed to address data quality issues and is quantified by the longitudinal data available on the number of averaged ERPs (during meta-preprocessing) which are further clustered to determine covariance subsets. Similar situations can arise in brain imaging applications where data analysis typically follows a long set of preprocessing procedures that may introduce covariance heterogeneity. Another example would be clustering of concatenated data where the goal may be to cluster according to mean trends robust to possible covariance heterogeneity introduced by the different data sources or data collection methods. A second point of novelty in the proposal is the extension to multilevel functional data where developments are especially designed for clustering longitudinal trends in ERP experiments from multiple electrodes. Coupled with the previously proposed meta-preprocessing step, the proposed RFC is the only algorithm to date that can cluster longitudinal trends effectively within an ERP experiment. Finally, the proposed methodology leads to novel scientific insights into the diversity of implicit learning patterns within and across ASD and TD children.

Note that the proposed RFC algorithm relies on consistent estimation of the cluster and covariance subset components such as the mean functions, covariance surfaces, eigenfunctions, and eigenscores. Even though the asymptotic consistency of the model components has been established in Yao and others (2005) and model components for multilevel functional data have been studied extensively in simulation studies, finite sample performance of these estimators may affect the performance of the RFC. Another issue is the consistency of the cluster and covariance subset components based on observations from estimated clusters. Almost sure convergence of cluster means for the classical k-means clustering algorithm was established by Pollard (1981) for multivariate data. Chiou and Li (2007) point out that owing to the complexity of convergence and slower convergence rates for estimating cluster means and covariance subset eigenfunctions in functional data, consistency results for FC need development of further technical results. Similarly, consistency of RFC requires further research.

Supplementary material

Supplementary Material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by the grant R01 GM111378-01A1 (D.S., D.T., C.S.) from the National Institute of General Medical Sciences and the graduate research fellowship grant DGE-1144087 (K.H.) from the National Science Foundation.