The effect of chirality and steric hindrance on intrinsic backbone conformational propensities: tools for protein design

Abstract

The conformational propensities of amino acids are an amalgamation of sequence effects, environmental effects and underlying intrinsic behavior. Many have attempted to investigate neighboring residue effects to aid in our understanding of protein folding and improve structure prediction efforts, especially with respect to difficult to characterize states, such as disordered or unfolded states. Host–guest peptide series are a useful tool in examining the propensities of the amino acids free from the surrounding protein structure. Here, we compare the distributions of the backbone dihedral angles (φ/ψ) of the 20 proteogenic amino acids in two different sequence contexts using the AAXAA and GGXGG host–guest pentapeptide series. We further examine their intrinsic behaviors across three environmental contexts: water at 298 K, water at 498 K, and 8 M urea at 298 K. The GGXGG systems provide the intrinsic amino acid propensities devoid of any conformational context. The alanine residues in the AAXAA series enforce backbone chirality, thereby providing a model of the intrinsic behavior of amino acids in a protein chain. Our results show modest differences in φ/ψ distributions due to the steric constraints of the Ala side chains, the magnitudes of which are dependent on the denaturing conditions. One of the strongest factors modulating φ/ψ distributions was the protonation of titratable side chains, and the largest differences observed were in the amino acid propensities for the rarely sampled α_L region.

Introduction

Amino acid conformational preferences can aid our understanding of protein conformational ensembles in the unfolded and denatured states of globular proteins (Dill and Shortle, 1991; Gillespie and Shortle, 1997; Voelz et al., 2010; Meng et al., 2013), the ‘native’ states of intrinsically disordered proteins (Fawzi et al., 2005; Uversky, 2013), and in the misfolded ensembles that precede protein aggregation (Fawzi et al., 2005; Bowler, 2012; Uversky, 2013). Secondary and tertiary structural interactions stabilize the ensemble of conformations present in the native, folded state. However, the intrinsic preferences that underlie the conformational preferences of nonnative states are less well understood. In addition, our understanding of the link between an amino acid sequence and the fold topology that sequence will assume is limited (Sánchez et al., 2006). This sensitivity to the amino acid sequence is illustrated by the designed heteromorphic proteins GA98 and GB98, which have all-α and α/β folds, respectively, but whose sequences differ by only a single residue (He et al., 2012). Conformational propensities of amino acids depend on sequence, intrinsic behavior, and structural and chemical environment; hence, parsing the specific effects of different contexts on amino acid propensities remains a great challenge. In order to understand the dependence of amino acid conformational propensities on sequence, we must first isolate the intrinsic propensities. As many unfolding experiments are performed at high temperature or in chaotropic solvents (Gattin et al., 2009; Ghosh et al., 2013; Silva-Lucca et al., 2013; Tischer and Auton, 2013; Roy and Bagchi, 2014; Ahmad et al., 2015), we must also determine how environmental conditions modulate those propensities. A strategic approach that examines intrinsic behavior in different host systems can provide a more detailed understanding of the factors that modulate amino acid propensities, in turn providing a better understanding of protein folding, unfolding, nonfolding, and misfolding.

The sterically accessible φ/ψ regions of polypeptide chains were first estimated using simple definitions of van der Waals contact distances and bond angles and were validated by the conformations of protein structures known at that time (Ramachandran et al., 1963). Since these original studies, the definitions of sterically accessible regions in φ/ψ space now include infrequently sampled conformations (Porter and Rose, 2011; Zhou et al., 2011). Polymer physics models of amino acid intrinsic propensities predict that residues in the ‘random coil’ state sample φ/ψ space without preference for any conformational region and independently of their nearest neighbors (Flory, 1969; O'Connell et al., 1999; Pappu et al., 2000). In these models, the random coil state of amino acids refers to sampling where the amino acids have complete access to all sterically allowed conformations, do not participate in secondary or tertiary interactions, and have solvent exposed side chains (Toal and Schweitzer-Stenner, 2014). However, experimental and theoretical investigations demonstrate that the 20 proteogenic amino acids possess intrinsic preferences for conformational regions in φ/ψ space (Avbelj et al., 2006; Beck et al., 2008; Schweitzer-Stenner, 2009; Mirtič et al., 2014; Schweitzer-Stenner and Toal, 2014; Toal and Schweitzer-Stenner, 2014; Towse et al., 2014, 2016).

Two major strategies are used to model the intrinsic conformational preferences of amino acids: coil libraries and small, unstructured peptides. Coil libraries excise coil regions, simply defined as sequences adopting neither α-helical nor β-sheet structure, from X-ray crystal structures to define intrinsic conformational preferences (Fitzkee et al., 2005; Jha et al., 2005; Tamiola et al., 2010; Jiang et al., 2013). However, such libraries determine φ/ψ preferences from short sequences whose conformations are biased by the structural context provided by the surrounding protein structure and, therefore, such libraries do not represent intrinsic propensities (Jiang et al., 2013). Host–guest peptide series using a small number of residues circumvent these issues by preventing secondary or tertiary interactions from biasing conformational preferences. However, enough residues need to be present to adequately model the protein chain. For example, intrinsic conformational preferences obtained from dipeptide models account for only a single neighboring residue and do not reflect the intrinsic behavior of amino acids within a polypeptide chain (Oh et al., 2012a,b). In addition, although the commonly used host–guest GGXGG pentapeptides are of sufficient length to provide the intrinsic propensities in the context of a chain of amino acids while allowing the greatest conformational freedom, the simple Gly-host lacks the backbone chirality present for the majority of residues in a true polypeptide chain (Avbelj et al., 2006; Beck et al., 2008; Vymětal et al., 2013; Schweitzer-Stenner and Toal, 2014). Thus, while the GGXGG series is a good model for amino acid intrinsic propensities in the simplest polypeptide chains, the Ala-host residues in the AAXAA series provide a more realistic model of the intrinsic propensities of an amino acid within the simplest of chiral l-protein sequences. However, there has been concern that Ala induces artificially high levels of helix both in experiments and simulations. While Ala is frequently found in α-helices, its ability to induce helical content is reduced drastically in small peptides. For example, Firestine et al. demonstrated this in the KKA_nKKGY model system, where significant helical content was observed only when n ≥ 9 (Firestine et al., 2008). With respect to simulations, many molecular dynamics (MD) force fields induce excessive helicity. Experimental estimates are ∼20% for Ala₃-, Ala₄- and Ala₅-based peptides (Firestine et al., 2008; Jiang et al., 2013); other common force fields produce high helical contents for such systems except for GROMOS: 13.1% (GROMOS53a6), 57.5% (CHARMM27 with CMAP), 62.3% (AMBER03), 94.2% (AMBER99), and 97.6% (AMBER94) (Best et al., 2008). The average helix content for our blocked AAAAA peptide simulations is 19.4% (Towse et al., 2016), which is in very good agreement with experiment.

Challenges in modeling the intrinsic conformational propensities of amino acids are echoed in the computational design of loops and other flexible regions in proteins (Hu et al., 2007). Difficulties in modeling loop regions may be attributed to several sources. First, these regions may adopt multiple conformational regions that interconvert on timescales from nanoseconds to milliseconds (Benson and Daggett, 2008; Gu et al., 2015). Second, regular patterns of secondary structure do not stabilize loop structure; instead, interactions between the loop, solvent, and the surrounding protein environment all contribute to the structure and dynamics of loops (Zimmermann and Jernigan, 2012; Papaleo et al., 2016). Third, many computational design strategies rely on an initial target conformation obtained from the PDB. The crystal environment necessary to solve protein structures via X-ray crystallography frequently bias loop structures and mask the true dynamic conformations(s) of the loop in solution. This results in a mismatch between the template for design and the true structure(s) (Fiser et al., 2000; Sellers et al., 2008; Messih et al., 2015). Finally, the conformational ensemble and dynamics of loop regions are more sensitive to mutation; thus, even highly similar sequences may possess distinct conformations and dynamics, rendering the use of templates in loop design less useful (Ceruso et al., 2003; Papaleo et al., 2016). In such cases, the intrinsic conformational preferences of amino acids play a greater role in determining loop dynamics. As flexible loops are intimately connected to the dynamics and functions of proteins, correct modeling of flexible loops and linkers is crucial to improving the accuracy and sophistication of computationally designed proteins. Knowledge of amino acid conformational propensities and the sensitivity of those propensities to environment and backbone chirality should aid in the computational design of flexible regions in proteins.

Our two independent studies of the GGXGG and AAXAA host–guest series reveal a dependence on structural and environmental contexts on amino acid intrinsic propensities (Beck et al., 2008; Towse et al., 2016). Not only are the intrinsic propensities different from the amino acid propensities within folded proteins (Beck et al., 2008), but the intrinsic propensities also show sensitivity to environment (Towse et al., 2016). These initial studies were experimentally validated and demonstrate the power of MD simulations to provide atomistic detail of heterogeneous conformational ensembles (Beck et al., 2008; Towse et al., 2016). Here, we performed a comparative study of the φ/ψ propensities of the guest ‘X’ residues in the GGXGG and AAXAA host–guest series. For this study, we extended our earlier GGXGG simulations (Beck et al., 2008) by performing longer simulations and performing simulations in 8 M urea to match conditions in our recent AAXAA study (Towse et al., 2016), allowing us to determine the environmental sensitivity of the GGXGG propensities. By comparing these new and more extensive GGXGG simulations with the AAXAA simulations, we have determined the effects of two factors on intrinsic propensities: backbone chirality and simple sterics provided by C_β methyl groups.

Materials and methods

MD simulations of host–guest pentapeptides

GGXGG pentapeptide simulations were previously performed for 100 ns in water at 298 K. However, both the alternative protonation states of titratable amino acids and the side-chain chirality of Thr were neglected in this earlier study. The Thr residue previously studied was the rarer allo-form with chirality inverted at the C_β position (Beck et al., 2008). Here, we extended the existing GGXGG simulations to be consistent in length with the AAXAA simulations, which required longer times to converge, and simulated new models for the additional protonation states and Thr. We also simulated GGXGG series peptides under thermally denaturing and chemically denaturing conditions. End-capped (N-acetylated, C-amidated) GGXGG peptides containing all 20 amino acids were built with extended conformations (φ/ψ angles set to 180° and −180°, respectively) and simulated under three conditions: water at 298 K, 8 M urea at 298 K, and water at 498 K. Where necessary, we generated additional pentapeptides for both neutral and acidic protonation states (Asp, Ash, Glu, Glh). Three individual simulations of His were performed for each possible protonation state: Hid (δH), Hie (εH), and Hip (both δH and εH protonated). Cysteine was modeled in the reduced state (-CH₂-SH, denoted Cyh). The simulation and analysis procedures used for the AAXAA series (Towse et al., 2016) were also used here to ensure a direct comparison of φ/ψ sampling between the AAXAA and GGXGG peptides.

Simulations were performed using the in lucem molecular mechanics (ilmm) package (Beck et al. 2000–2016) with the Levitt et al. force field (Levitt et al., 1995), the microcanonical NVE (constant number of particles, volume and energy) ensemble, and the flexible three-center (F3C) water model (Levitt et al., 1997). Nonbonded interactions were treated with an 8-Å force-shifted cutoff (Beck et al., 2005), and explicit solvent molecules were used for both 8 M urea (Zou et al., 2002; Day and Daggett, 2005) and water (Levitt et al., 1997) simulations. The F3C water model is fully flexible and lacks a fictitious H–H bond in contrast to other commonly used models, resulting in better agreement with experiment for both the structural and dynamic properties of water (Levitt et al., 1997). To obtain 8 M urea solvent boxes, water molecules in a pre-solvated peptide system were randomly substituted with urea molecules. Both water and 8 M urea solvent systems at 298 K were simulated with a box size that reproduced the experimental densities, 0.9970 g/mL and 0.7813 g/mL, respectively. For the simulations at 498 K, the density was set to the reduced density for that temperature, 0.829 g/mL (Kell, 1967).

To assess convergence, multiple simulations were performed of the GGAGG, GGGGG, and GGWGG peptides in 8 M urea and of the GGAGG peptides in water at 298 and 498 K. All simulations were performed for a minimum of time consistent with requirements to reach convergence as determined for AAXAA (Towse et al., 2016): 1 μs in 8M urea (1.5 μs for Ala, Tyr and Gly); 600 ns in water at 298 K; and 100 ns in water at 498 K (200 ns for Ala). The total simulation time for both GGXGG and AAXAA was 106 µs.

Calculation of conformational propensities

Populations were calculated for the four quadrants of the conformational φ/ψ space and for specific conformational regions, defined as α_R: −100° ≤ φ ≤ −30°, −80° ≤ ψ ≤ −5°; near-α_R: −175° ≤ φ ≤ −100°, −55° ≤ ψ ≤ −5°; α_L: 5° ≤ φ ≤ 75°, 25° ≤ ψ ≤ 120°; β: −180° ≤ φ ≤ −50°, 80° ≤ ψ ≤ −170°; P_IIL: −110° ≤ φ ≤ −50°, 120° ≤ ψ ≤ 180°; and P_IR: −180° ≤ φ ≤ −115°, 50° ≤ ψ ≤ 100°. An additional β region, named non-polyproline β (nPβ), was defined as the area of the β region that does not overlap with either P_IIL or P_IR. Populations were calculated as percentages to account for the different trajectory lengths. φ/ψ frequency distributions were generated using two-dimensional histograms with 5° × 5° bins, and correlations between the distributions were taken to form similar correlation matrices.

Comparison with NMR

The various parameterizations and simulation methodologies present in modern force fields and simulation packages can affect the distributions of conformational propensities (Vymětal et al., 2013). Consequently, we strive to compare our simulations with experiment whenever possible. Experimental validation of the AAXAA simulations has been reported using experimental chemical shifts acquired in 8 M urea at 298 K, pH 2.5, for the AAXAA series. Here, we assessed the experimental agreement of the GGXGG simulations using experimental data for the GGXGG series also acquired in 8 M urea at 298 K, pH 2.5 (Schwarzinger et al., 2000). Experimental GGXGG chemical shifts were obtained from the Biological Magnetic Resonance database (BMRB code: 4747) (Schwarzinger et al., 2000; Ulrich et al., 2008). A random 1% selection of structures (5000 structures) from the production dynamics portion of the GGXGG trajectories, previously shown to be representative of the full ensemble of conformations generated (Towse et al., 2016), were used to calculate the ¹H, ¹⁵N and ¹³C chemical shifts using SHIFTX2 (Han et al., 2011). As no homology models exist for these pentapeptide systems, only the SHIFTX+ component of SHIFTX2 was used to calculate the chemical shifts.

Results

We previously reported the intrinsic conformational preferences of the 20 naturally occurring amino acids within the GGXGG host under native conditions (water at 298 K) for 100 ns (Beck et al., 2008) and the AAXAA host under native (water at 298 K) and denaturing conditions (water at 498 K and 8 M urea at 298 K) (Towse et al., 2016). Here, we report the effect of chirality and simple steric effects of the neighboring Ala C_β methyl groups on the conformational sampling of guest residues in native (water at 298 K) and denaturing (8 M urea at 298 K and water at 498 K) conditions. To draw direct comparisons between our GGXGG and AAXAA pentapeptide systems (Beck et al., 2008; Towse et al., 2016), we extended the GGXGG trajectories under native conditions from 100 ns to 600 ns and performed simulations of the GGXGG peptides under denaturing conditions. Additionally, we have performed simulations of the protonated states of glutamate (Glh), aspartate (Ash), and three protonated forms of histidine (the neutral Hid and Hie states and the diprotonated, positively charged Hip) in the Gly-host.

Equilibrium sampling of conformational space

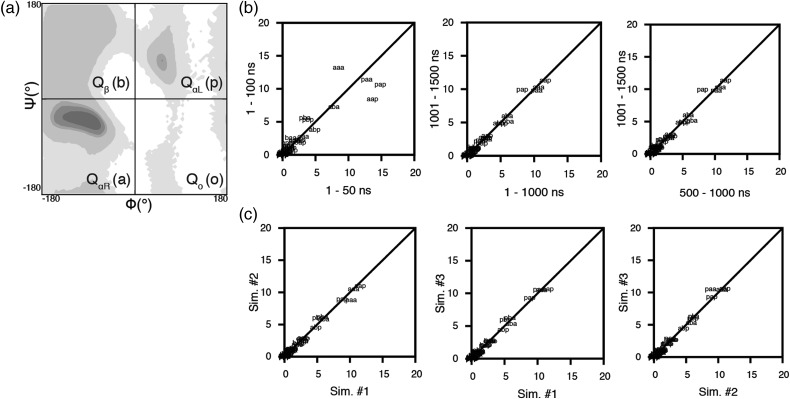
To assess the intrinsic conformational sampling of the guest amino acids, MD simulations of the GGXGG host–guest pentapeptides, where X is any of the 20 proteogenic amino acids, were performed under native, control (water, 298 K), thermally denaturing (water, 498 K), and chemically denaturing (8 M urea, 298 K) conditions. To obtain meaningful φ/ψ statistics, we confirmed that our simulations reached an equilibrium distribution with stable population frequencies to ensure Boltzmann sampling had been achieved. We assumed that each pair of φ/ψ dihedral angles of the three central residues can occupy four possible states that correspond to the four quadrants of Ramachandran space, which results in a total of 64 possible conformations of the three central residues. We compared the fraction of the ensemble spent in each of the four quadrants of Ramachandran space across different portions of the trajectory and between independent replicate simulations. All simulations converged with respect to the sampling of Ramachandran space (Beck et al., 2008; Towse et al., 2016; see Supplementary Figs S1 and S2). Convergence was monitored between replicate simulations of GGAGG, GGGGG, and GGWGG as well as across different trajectory windows for all GGXGG peptide simulations (Fig. 1, Supplementary Table SI). The production dynamics portion of the trajectories, after the point of convergence, was used for analysis and to compare the intrinsic sampling of the central guest residues in the Gly- and Ala-based systems across native, thermally denaturing, and chemically denaturing conditions. Comparison of the extended Gly-based peptide simulations in water at 298 K to the 100 ns trajectories previously published shows that the intrinsic conformational propensities were retained with little variation, further demonstrating Boltzmann sampling was achieved (Beck et al., 2008).

Fig. 1.

Convergence of the population of conformational states sampled by the three central residues shown for GGAGG in 8 M urea at 298 K. (a) Quadrants of Ramachandran space used to define the 64 conformational states: a (Qα_R, right-handed α-helical): –φ, –ψ; b (Qβ, β): –φ, +ψ; p (Qα_L, left-handed α-helical): +φ, +ψ; o (Q_o, other): +φ, –ψ. (b) Comparison of the sampling of the 64 conformational states of run #1 of GGAGG across different portions of the trajectory. (c) Comparison of the sampling of the 64 conformational states of all three simulations of GGAGG.

To ensure that the GGXGG simulations captured experimentally valid ensembles, we calculated NMR chemical shifts for the production dynamics using SHIFTX2 and compared them against experimental data obtained of the same peptides in 8 M urea (Schwarzinger et al., 2000; Han et al., 2011). As the NMR experiment provides chemical shifts that are an average over all molecules root mean squared deviations (RMSD) between the simulated and experimental chemical shifts were also calculated to compare the average chemical shifts over the MD ensembles and those obtained by experiment. Previously, we showed agreement between the AAXAA peptide simulations and experimental AAXAA NMR observables, with excellent correlation coefficients between calculated and experimental chemical shifts (R > 0.99) (Towse et al., 2016). Here, we also obtained highly satisfactory individual correlations (R ≥ 0.94, Table I) between the GGXGG simulations and experimental data for all nuclei except for H_N, for which little dispersion in the range of values contributed to the low correlation coefficient (Table I). The correlation coefficient between the GGXGG simulations and experimental data when all nuclei were considered was excellent (R > 0.99, Table I) with an RMSD of 0.72 ppm (Table I).

Table I.

Correlations between experimental and calculated NMR chemical shifts for the GGXGG series in 8 M urea

Nucleus	R	n	RMSD (ppm)
HN	0.77	19	0.20
Hα	0.94	20	0.07
Hβ1	>0.99	4	0.06
Hβ2	>0.99	16	0.10
Hβ3	0.99	16	0.09
NH	0.97	19	1.36
Cα	0.99	20	0.69
Cβ	>0.99	19	1.14
C′	0.95	20	0.64
Overall	>0.99	153	0.72

Experimental data for the GGXGG peptides were determined by Schwarzinger et al. (2000) in 8 M urea at pH 2.3. Calculated NMR chemical shifts were obtained using SHIFTX2 (see Materials and Methods) for the 8 M urea MD simulations.

Neighboring residues do not alter coverage of φ/ψ space

The coverage of φ/ψ space for the Gly guest residue (79–81%) was independent of host residue and simulation environment. Steric overlap of the backbone atoms restricts the remaining 20% of φ/ψ space as initially determined by Ramachandran (Ramachandran et al., 1963; Table II). The addition of heavy atoms to the side chain of guest residues reduced the coverage of φ/ψ space by 32% on average. Across all conditions, the average change in coverage of φ/ψ space between AAXAA and GGXGG was ∼2%, with the largest differences observed for Hip, Tyr, Ile and Thr. This did not apply to Pro, which sampled the smallest area of φ/ψ space (<20% across all conditions). The sampling of the remaining non-Gly residues showed that they all accessed φ/ψ space to the same degree (mean 48–52%), irrespective of environment, with the β-branched residues at the lower end of the coverage range due to the increased steric clashes (Table II).

Table II.

Coverage of φ/ψ space by Gly- and Ala-based pentapeptide systems in control and denaturing conditions

Residue	Water 298		8 M urea		Water 498 K
	GGXGG (%)	AAXAA (%)	GGXGG (%)	AAXAA (%)	GGXGG (%)	AAXAA (%)
Ala	59 ± 1a	61a	61 ± 1a	63 ± 2a	62 ± 1a	62a
Arg	48	50	52	50	50	53
Asn	46	50	46	49	52	53
Asp	38	37	37	36	51	52
Ash	43	44	45	46	48	50
Cys	52	56	54	53	54	53
Gln	48	50	49	50	53	53
Glu	48	50	50	49	51	51
Glh	49	48	50	53	53	52
Gly	79	81	80a	81a	79	79
Hid	50	50	53	51	52	55
Hie	52	51	54	52	53	54
Hip	40	52	46	53	51	50
Ile	34	39	37	39	38	39
Leu	49	50	49	51	48	52
Lys	48	50	51	48	50	52
Met	50	51	53	49	51	53
Phe	49	51	48	49	51	50
Pro	16	13	16	15	19	18
Ser	53	51	53	55	55	54
Thr	38	39	35	36	41	42
Trp	50	50	50 ± 2a	53 ± 1a	52	53
Tyr	47	53	50	44	51	53
Val	37	38	34	40	41	40
Meanb	48 ± 7	49 ± 11	49 ± 7	52 ± 13	51 ± 6	52 ± 10

^aAverages across triplicate simulations; standard deviations omitted when they were <0.5%.

^bMean coverage is calculated excluding glycine and proline values.

Within a host series, there were no appreciable differences in the coverage of φ/ψ space except for the different protonation states of Asp and His. The negative charge on the Asp side chain that would be present at neutral pH reduced the area sampled compared with its protonated state, Ash. This was also true of the di-protonated His residue (Hip), which sampled less than the Hid and Hie forms. However, under thermally denaturing conditions, the restriction of backbone sampling by the charged Asp and Hip residues was no longer observed. These two exceptions aside, the largest difference across the environments was for residues in the AAXAA series, where a change in the coverage was 2–3% greater than that observed for residues in the Gly-based hosts.

Intrinsic propensities are weakly host-dependent

Under native-state conditions, water at 298 K, the sampling of the GGXGG and AAXAA host–guest pentapeptides was not random and the guest residues exhibited intrinsic conformational propensities in both hosts (Fig. 2, Supplementary Tables SII and SIII). To determine differences in these conformational propensities, percentage populations were calculated in the four quadrants of the φ/ψ plots and within seven defined conformational regions that correspond to elements of secondary structure in folded proteins (Fig. 3a). We take the Gly-based peptides to reflect the ‘true’ intrinsic propensities of the amino acids; and, deviations from these values in the Ala-based peptides reflect the simple steric effects of the side-chain methyl group of the Ala-host residues and the backbone chirality imposed by their presence (Supplementary Table SIV).

Fig. 2.

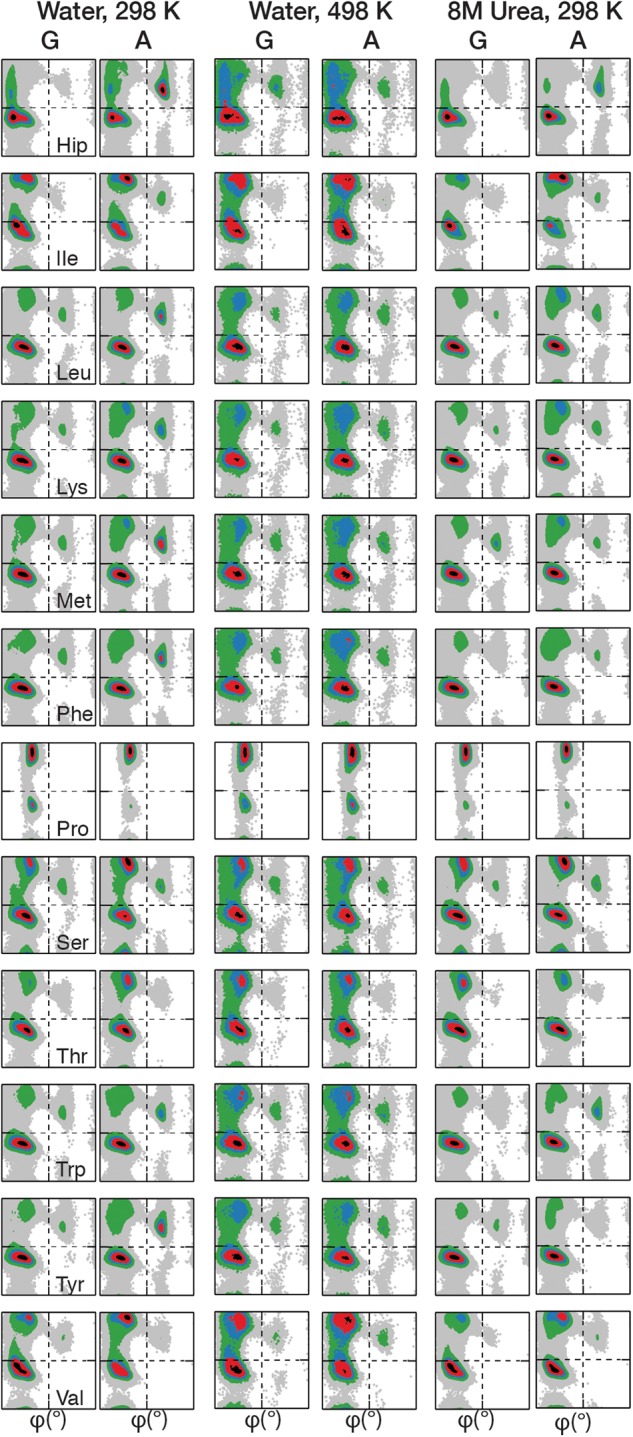
Ramachandran plots of the guest residues (‘X’) in the GGXGG (G) and AAXAA (A) hosts. Plots have been prepared for all peptides under three environmental conditions: water at 298 K, water at 498 K, and 8 M urea at 298 K. Plots have been normalized to the maximally populated bin of each plot and colored by increasing percentage population from gray to black: 0 = white; 0 < grey < 0.05; 0.05 ≤ green < 0.2; 0.2 ≤ blue < 0.4; 0.4 ≤ red < 0.8; 0.8 ≤ black.

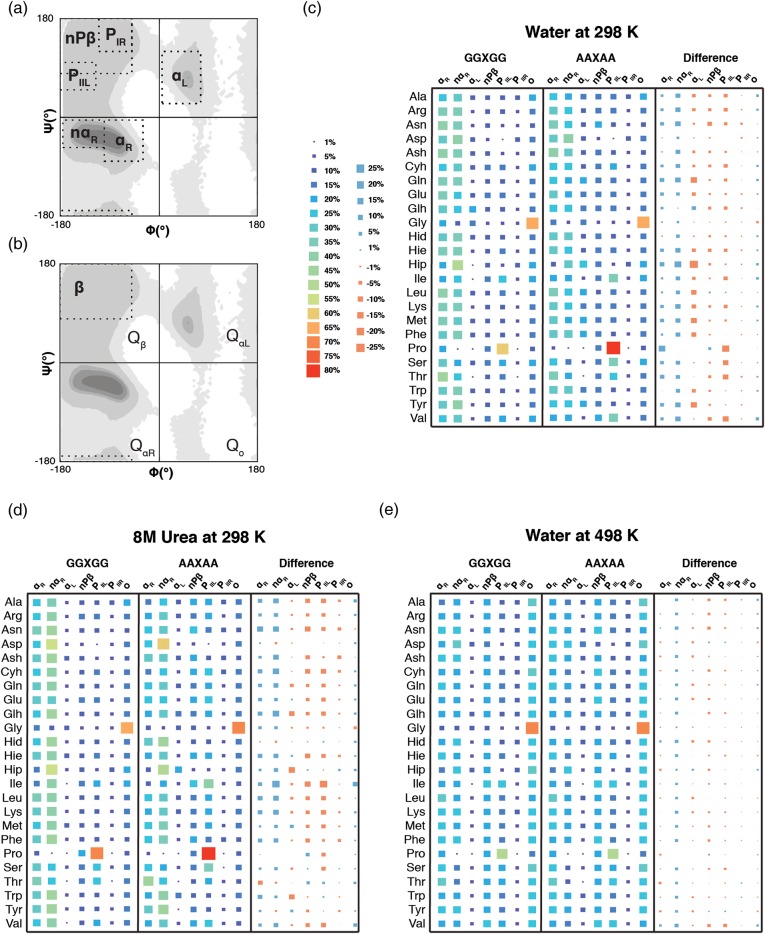
Fig. 3.

Differences in the fractional populations of conformational regions between GGXGG and AAXAA peptides in three environmental contexts. (a) Ramachandran plots are provided that outline the seven conformational regions as defined in Materials and Methods: α_R, near-α_R, α_L, non-Pβ, P_IIL, P_IR, and o, and (b) the four quadrants and broadly defined β region. (b–d) Hinton diagram of the population of conformational states of the guest residues in the GGXGG and AAXAA peptides as well as the differences in sampling between the two peptide series under native (c), chemically denaturing (d), and thermally denaturing (e) conditions.

Correlations of the φ/ψ frequency distributions showed little change in the overall sampling trends by a given residue due to the identity of the host (Table III). This was consistent with our finding that the additional steric effects of the Ala C_β methyl group did not reduce the accessibility of φ/ψ space (Table II). Although similar broad biases towards particular conformational regions on the Ramachandran plots were observed (Fig. 2), differences in sampling were immediately discernable from the φ/ψ quadrant populations (Supplementary Tables SII–SIV). In Ala-hosts, the greatest population resided in the Qα_R for all residues except Pro, the β-branched Ile and Val residues and Ser, which showed preferential sampling of Qβ. In the GGXGG series, this discrimination between these three residues and the others did not exist, all non-Pro residues predominantly sampled Qα_R. Closer examination of the populations shows that for all residues there was a greater population in Qα_R when in Gly-hosts versus the Ala-hosts. The reduced steric constraints of the Gly neighbors increased the favorability of even Pro, known for its dominance of the β and P_IIL regions, to sample Qα_P regions.

Table III.

Correlation coefficients^a between AAXAA and GGXGG ϕ/ψ frequency distributions

Guest residue	Water 298 K	8 M urea 298 K	Water 498 K
Ala	0.94	0.90	0.93
Arg	0.96	0.97	0.96
Asn	0.97	0.91	0.96
Asp	0.99	0.99	0.97
Ash	0.98	0.96	0.97
Cys	0.96	0.88	0.96
Gln	0.88	0.96	0.96
Glu	0.97	0.96	0.96
Glh	0.97	0.89	0.96
Gly	0.97	0.90	0.88
Hid	0.99	0.99	0.96
Hie	0.96	0.95	0.96
Hip	0.74	0.94	0.96
Ile	0.94	0.68	0.97
Leu	0.96	0.95	0.98
Lys	0.95	0.94	0.97
Met	0.92	0.97	0.97
Phe	0.96	0.97	0.97
Pro	0.94	0.98	0.99
Ser	0.91	0.96	0.96
Thr	0.94	0.96	0.97
Trp	0.98	0.95	0.96
Tyr	0.92	0.99	0.97
Val	0.89	0.94	0.94

^aPearson's correlation coefficient was calculated as the correlation of population frequencies in each of the 5148 (72 × 72) bins in ϕ/ψ space.

Two residues that showed little difference between the hosts were Gly and Asp. In both Ala- and Gly-hosts, the quadrant populations of the Gly guest residue were almost indistinguishable. Both the broad sampling of φ/ψ space by Gly and the population of the conformational regions within the quadrants were retained; Gly showed very little response to the change in host residue (Fig. 2, Supplementary Tables SII–SIV). Similarly, Asp showed a <3% difference in sampling across the quadrants as well as the individual conformational regions. In most cases, there were only marginal differences (<10%) observed in the populations of the conformational regions for the majority of guest residues in the Gly- and Ala-hosts consistent with the high correlations between the overall φ/ψ distributions (Table III, Supplementary Tables SII–SIV).

Overall, the preferences for the α_R and near-α_R regions were robust, and the greater sampling in these regions by the Gly-based peptides, greatest in near-α_R, echoed the distinct increases in the Qα populations observed. In contrast, guest residues in Ala-based peptides had larger populations in the α_L, non-Pβ, and P_IIL regions. The difference in the populations of the P_IR and ‘other’ regions was negligible, suggesting that sampling in these regions was less dependent on the host residue.

Bulky hydrophobic, β-branched, and aromatic residues play important roles in guiding protein folding (Frank et al., 2002) and in the formation of interaction sites for intrinsically disordered proteins (Espinoza-Fonseca, 2012). The β-branched residues Ile and Val had below-average sampling of structures in the Qα quadrant in both Gly- and Ala-hosts and above-average sampling in the β quadrant. Thr did not share this behavior with the other β-branched residues; instead, Thr had the highest sampling of the α_R conformational region in both Ala- and Gly-host peptides (Supplementary Tables SII–SIV). And, as the volume of the guest residue increased close to the main chain, e.g. the increased steric constraints at the C_β position for the orientation of the Ser side chain, the β-branched residues and the cyclic imino acid Pro, so did the preference for β structures (Supplementary Tables SII–SIV). Most residues sampled the P_IIL region to a greater extent in the Ala-host than in the Gly-host; however, this behavior did not apply to the aromatic residues Phe, Trp and Tyr.

To determine whether the differences in sampling between the two peptide systems was the result of altered intra-molecular contacts, we calculated ensemble averaged atomic contacts in three categories: main-chain–main-chain contacts, side-chain–side-chain contacts, and main-chain–side-chain contacts. No backbone atom pairs formed hydrogen bonds for >5% of the total simulation, and the introduction of Ala neighbors did not change the frequency of hydrogen bond formation by >2% for any individual hydrogen bond (Supplementary Fig. S3). Similarly, there was no change in the formation or duration of contacts made between the guest residue and the peptide backbone under any condition.

The Ala-host introduces additional side-chain–side-chain contacts between the guest residues and their nearest neighbors; however, the formation of these additional contacts did not correlate with changes in φ/ψ distributions. We found that the side-chain contacts formed in the Ala peptides were equivalent under both native and thermally denaturing conditions (Supplementary Fig. S3). Since the φ/ψ distributions between AAXAA and GGXGG were similar under thermally denaturing conditions, we concluded that intra-molecular contacts were not directly responsible for changes in φ/ψ distributions. We found no significant differences in intra-molecular hydrogen bonding, hydrophobic interactions, or nonspecific interactions.

Conformational propensities are sensitive to protonation state

Comparison of the sampling behavior of the Glu/Glh, Asp/Ash and Hie/Hid/Hip residue sets showed just how great an effect protonation could have (Fig. 4). In the Ala-host system, protonation can appreciably change the conformational propensities of a residue. Although not so apparent with the Glu/Glh pair (R = 0.98), the effect of protonation was more substantial for Asp via a larger β population (increase ∼13%) due to the increased sampling of extended structures by Ash (Fig. 4, Supplementary Table SV).

Fig. 4.

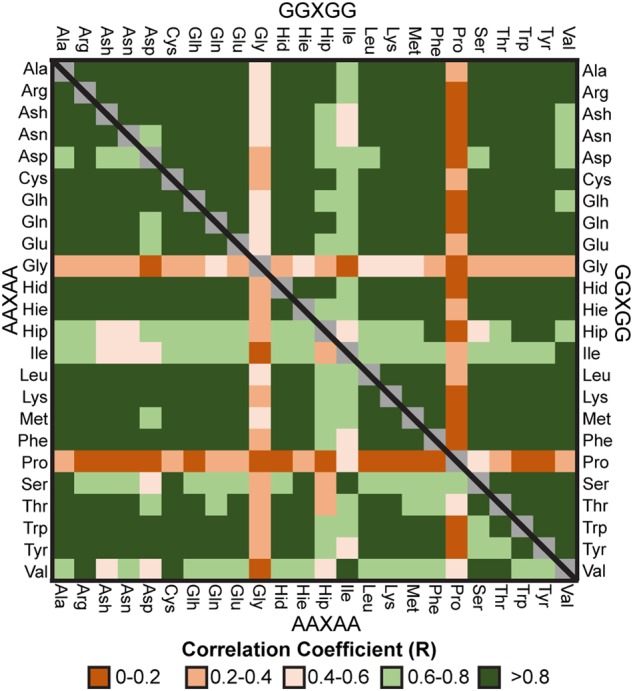
Correlation matrix for GGXGG and AAXAA simulations in native conditions (water, 298 K) using the Pearson correlation coefficients calculated between φ/ψ frequency distributions for the central guest residue. Legend for the matrix element colors is inset.

The effect of protonation was more pronounced for His (R < 0.7). The Hie (εH) and Hid (δH) protonation states exhibited similar φ/ψ sampling (R = 0.96) with only marginal changes observed in Qβ coincident with an offset between the stabilization of the near-α_R and P_IIL regions dependent on whether the δN or εN was protonated (Table III). However, diprotonated His (Hip, δH and εH) showed a distinct mirroring effect, where Hid and Hie showed a significant preference for α_R over α_L (α_R: 27%, α_L: 8%) and Hip showed almost the exact opposite (α_R: 9%, α_L: 25%). Protonation had a lesser effect on the His and Asp sampling in the Gly-hosts, and instead showed more pronounced changes for the Glu/Glh residue pair. As observed for His in the Ala-host, a distinct change in preference for the α_L region occurred for protonated Glu (Glu: 6%, Glh: 20%) (Fig. 3, Supplementary Tables SII–SIV).

Steric effects of alanine neighbors under denaturing conditions

The difference in sampling of the guest residues in GGXGG and AAXAA under chemically denaturing conditions was marginally greater than the difference in sampling under native conditions (Fig. 3, Supplementary Table SIX). We previously showed that in AAXAA under chemically denaturing conditions, the conformational preferences observed under native conditions are largely retained in 8 M urea at 298 K. As was observed for residues in the Ala system, residues in the Gly system under chemically denaturing conditions primarily sampled structures in Qα_P, although more expanded helical structures were sampled in 8 M urea, reflected by the increases in sampling in the near-α_P region. As in native conditions, the guest residues in GGXGG peptides sampled Qα_R structure to a greater extent than in AAXAA peptides, which sampled the α_L, nPβ and P_IIL regions more (Supplementary Tables SVI–SVIII). Chemical denaturation destabilized the α_L region and promoted sampling of the P_IIL region. The nPβ and P_IIL regions had the greatest difference in sampling between the AAXAA and GGXGG host systems (Supplementary Table SVIII). Chemical denaturation increased the impact of neighboring Ala groups on the sampling of guest residues, leading to slightly greater differences in sampling between AAXAA and GGXGG.

The sampling of φ/ψ space increased further at high temperature, and residues had diminished preferences for one conformational region over another (Fig. 3e). Under thermally denaturing conditions, the difference in sampling of the guest residues in GGXGG and AAXAA hosts indicated a lack of host-residue-dependent sampling propensities (Fig. 3e, Supplementary Table SVIII). In both peptide systems, thermally denaturing conditions reduced intrinsic propensities for any single conformational region and led to increased sampling of extended β structures. This made the φ/ψ distributions of the two peptide systems virtually indistinguishable from one another.

Discussion

The coverage of φ/ψ space for any given residue was invariant for the majority of guest residues in the Gly- and Ala-based systems, appearing insensitive to the introduction of the neighboring Ala residues, irrespective of the conditions. This led us to two conclusions. First, the additional side-chain interactions in the AAXAA system pose no great steric restriction to the regions of φ/ψ space that can be sampled. Second, there is no significant consequence from enforcing backbone chirality on the extent of φ/ψ sampling by the central guest residue. It is the relative free energy of regions of φ/ψ space that changes in response to the neighboring residues and conditions, not the area that can be sampled. Consequently, populations shift and conformational propensities can change.

Under native conditions, the populations of the seven defined conformational regions of the guest residues were weakly dependent on their host peptide. Residues with titratable side chains, however, did display some sensitivity to host sequence and environment. The protonation state of the amino acids with titratable side chains can have important consequences for electrostatic interactions in protein folding (Shen, 2010). Although the sampling of Asp was insensitive to host peptide sequence, the sampling protonated and amide counterparts of Asp (Ash and Asn, respectively) did show sensitivity to the host peptide sequence. The contrast in the sampling between Asp, Ash and Asn, which have side chains of similar geometry and size, shows how side-chain charge affected intrinsic sampling. This contrasting behavior was not as prominent for the Glu/Glh/Gln set where the functional groups are located farther away from the main chain. The distinct sampling of the Glu/Glh, Asp/Ash and Hie/Hid/Hip residue sets showed just how great an effect protonation could have, suggesting that protonation sensitive behaviors could contribute to the nature of electrostatic interactions in protein folding. A common conformational effect of protonation was to increase α_L structures and was dependent on both the identity of the titratable residue side chain and that of the neighboring residues. This shift to α_L is coincident with the increased frequency of α_L in active sites where it is believed the unusual structure at this position places residues in a functional pose (Novotny and Kleywegt, 2005). Moreover, this sensitivity to host correlates with observations that the pKa of certain residues, e.g. Glu78 and Glu172 in Bacillus circulans xylanase, is dependent on the concerted action of conserved residues in active sites (Joshi et al., 2001).

Access to the denatured state ensemble is commonly accomplished through the use of co-solvents such as urea (Das and Mukhopadhyay, 2009) or elevated temperatures. Under thermally denaturing conditions, guest residues were essentially insensitive to their host peptide and they sampled φ/ψ space similarly. This similar sampling of φ/ψ space suggests that the thermal energy at 498 K exerts a greater influence over the φ/ψ distributions than the other factors guiding intrinsic propensities. Under these conditions, the guest residues traverse φ/ψ space with ease as barriers separating conformational states are lowered. The guest residues also have reduced preferences for conformational regions with broad, shallow distributions. Under chemically denaturing conditions, the sampling of the guest residues was more dependent on the host peptide and varied by guest residue type. The presence of urea molecules allows for distinct solute–solvent interactions, which could lead to the stabilization of certain conformational regions via the formation of solute–solvent interaction networks. Overall, the host-dependent sampling differences, though weak, were distinct among the native, elevated temperature, and 8 M urea conditions, and led us to conclude that neighbor-dependent intrinsic propensities in natively unfolded states, under physiological conditions, differ from those under harsher denaturing conditions. The sensitivity of the sequence-dependent conformational preferences, and the conformational preferences themselves, to environmental conditions, of these simple peptide models agrees with the finding that the chemically denatured state ensembles of proteins differ from physiological unfolded states (Arcus et al., 1994, 1995; Bond et al., 1997; Das and Mukhopadhyay, 2009; Meng et al., 2013).

Conclusions

Here we have quantified the difference in φ/ψ distributions of the naturally occurring amino acids within two sequence contexts, GGXGG and AAXAA, and across three environmental conditions. Due to the achirality of Gly, the GGXGG series is a model for the true intrinsic propensities of the amino acids and provides a baseline on which to build an understanding of how sequence contexts can modulate amino acid propensities. The AAXAA series also provides a model for the intrinsic propensities of the amino acids, but intrinsic to their tethering within a chiral protein chain. Hence, the differences observed here reveal how the introduction of chirality and simple sterics into the polypeptide chain alters amino acid conformational propensities.

Loops in proteins frequently serve more complex functions than simply connecting elements of secondary structure. For example, loops serve as active sites in enzymes, bind small molecules, participate in protein–protein interactions, and can aid in the allosteric regulation of protein dynamics (Papaleo et al., 2016). Thus, accurate design of loops may be instrumental in the success of computational and experimental protein design studies. To this end, this study provides insight into physically realistic models of intrinsic conformational preferences under different conditions. We have previously incorporated these propensities into the design of amyloid inhibiting peptides (Hopping et al., 2014). We anticipate that the intrinsic propensities of neighboring group effects determined here, in combination with our fragment library (Rysavy et al., 2014), may be exploited in the design of small peptides and in the design of flexible components of proteins.

Authors’ contributions

V.D. designed and supervised the research. M.C.C. and C.-L.T. performed the research and analyzed the data. All authors contributed to the writing of the manuscript.

Supplementary data

Supplementary data are available at PEDS online.

Funding

This work was supported by the US National Institutes of Health, General Medical Sciences grant GM 50789 to V.D. We thank the National Energy Research Scientific Computing Center, supported by the DOE Office of Biological Research, which is supported by the US Department of Energy under contract no. DE-AC02-05CH11231, for providing computing time.