Modeling Patterns of Activities using Activity Curves

Abstract

Pervasive computing offers an unprecedented opportunity to unobtrusively monitor behavior and use the large amount of collected data to perform analysis of activity-based behavioral patterns. In this paper, we introduce the notion of an activity curve, which represents an abstraction of an individual’s normal daily routine based on automatically-recognized activities. We propose methods to detect changes in behavioral routines by comparing activity curves and use these changes to analyze the possibility of changes in cognitive or physical health. We demonstrate our model and evaluate our change detection approach using a longitudinal smart home sensor dataset collected from 18 smart homes with older adult residents. Finally, we demonstrate how big data-based pervasive analytics such as activity curve-based change detection can be used to perform functional health assessment. Our evaluation indicates that correlations do exist between behavior and health changes and that these changes can be automatically detected using smart homes, machine learning, and big data-based pervasive analytics.

1. Introduction

Many pervasive computing applications such as home automation, activity aware interventions, and health assessment require analyzing and understanding activity-based behavioral patterns. The performance of such applications depends on the ability to correctly learn a model of general daily activity behavior from a large amount of data and be able to predict when such daily behavior is likely to continue or change. These big data-based approaches to activity modeling can then in turn be used to provide effective activity-aware services such as improved healthcare.

Activity recognition lies at the heart of any pervasive computing approach to modeling behavioral routines. An activity recognition algorithm maps a sensor reading or sequence of readings to a corresponding activity label. In order to answer general questions related to daily activity patterns, such information needs to be transformed to a higher-level representation. For example, questions such as how average daily activity patterns have changed over a year, or generally what hours did a particular individual sleep last month are difficult to answer using raw output from activity recognition algorithms. However, many pervasive computing applications such as home automation and health assessment require answering such questions.

Obtaining higher-level representations or models of activities has several additional advantages. Higher-level representations can abstract variations in day-to-day activity routines. For example, wake-up times in the morning may be slightly different each day even if the overall routine is fairly stable. Additionally, such representations simplify the task of modeling an individual’s daily routine and at the same time make visualization and interpretation of daily activity routines easy. Collecting big data sets over long periods of time allows us to abstract activity models over such daily variations. As we will demonstrate in this paper, such representations aid with the process of identifying long-term changes in a behavioral routine.

For example, consider the following description highlighting aspects of an individual’s routine at two different points in time:

• Month of March 2012 : Sleep at 10:00 PM, get up at 6:00 AM, eat breakfast at 7:00 AM, eat lunch at 12:00 PM, go out for a walk at 4:00 PM, and dine at 8:00 PM.

• Month of September 2013 : Sleep at 8:00 PM, wake up frequently during the night, get up at 10:00 AM, no breakfast, eat lunch at 11 AM, no going out for a walk, and dine at 7:00 PM.

Note that each of these sample activity-based descriptions is aggregated over a one-month period and therefore describes a general routine that is maintained over a prolonged period of time. Based on these descriptions we also note changes in the routine from the first observation to the second. From this example, we can infer that by September 2013 the observed individual was experiencing disturbances in sleep, was skipping meals, and stopped exercising. Determining if the overall daily activity patterns has changed may be difficult based only on the raw sensor data or even based on event-by-event labels from an activity recognition algorithm. Such questions can be more easily answered by comparing two higher-level representations of these activity patterns.

In our current work, we propose a novel activity curve to model an individual’s generalized daily activity routines. The activity curve modeling algorithm uses activity-labeled sensor events to learn a higher-level representation of the individual’s regular routine. These activity labels are automatically-recognized using an activity recognition algorithm. We also introduce a Permutation-based Change detection in Activity Routine (PCAR) algorithm to compare activity curves between different time points in order to detect changes in an activity routine. To validate our algorithm, we make use of longitudinal smart home sensor data collected by monitoring everyday behavior of residents over two years. Finally, we demonstrate how the activity curve and the PCAR algorithm can be used to perform important pervasive computing tasks such as automated assessment of an individual’s functional health.

2. Related work

The work that we describe in this paper is unique in its ability to automatically characterize behavioral routines based on recognized activities and to detect changes in generalized routines over time. However, other work has focused on alternative approaches to recognizing and discovering daily activity routines and two-sample tests to detect changes between two sample populations similar to the core component of the proposed PCAR algorithm. Additionally, other studies have investigated the relationship between changes in activity patterns and changes in health using the statistical and visualization techniques.

Discovering activity routines

Researchers have studied the problem of automated discovery and recognition of daily activity routines using the data collected from wearable sensors [1, 2], GPS signals [3] and mobile phones [4] using algorithms such as topic modeling [1] and collaborative filtering [5]. In these approaches, raw sensor data are converted to a bag-of-words representation which contains the histogram of activity label occurrences or histogram of location/proximity information. Data from wearable sensors can be used to discover daily routines such as having lunch and brushing teeth [1]. Similarly, data from mobiles phones can be used to recognize routines such as commuting to office and working.

In contrast to these earlier works that focus on discovering and recognizing daily activity routines from sensor data, our focus is to model the discovered and recognized daily activity routines using an activity curve model. The proposed activity curve model is a generic model that can be calculated both from the output of an activity recognition algorithm as well as using the algorithms mentioned in the aforementioned studies. Furthermore, our proposed model facilitates answering more complex questions related to activity routines such as whether changes in an activity routine have occurred or not. In our current work, the proposed activity curve model uses the output from an activity recognition algorithm.

Visualization of activity routines

Researchers have proposed visualization techniques to visualize daily activity patterns. For example, Galambos et al. [6, 7] developed methods to visualize activity level, time spent away from home, deviations in activities of daily living, and behavioral patterns. Similarly, other researchers have developed techniques to visualize deviations in activity routines and behavioral patterns using smart home sensors [8, 9]. These methods provide a tool to understand sensor-monitoring data and to study daily activity routines. However, these approaches rely on manual inspection of the data in order to make any higher-level conclusions regarding daily routines.

Two-sample test

The two-sample test is a widely used statistical analysis tool to compare between two sample populations. Classical two-sample tests such as the t-test are used to compare the means of two populations having the same or different variances. However, the t-test is a parametric test that is limited to comparing between two Gaussian distributions. Other examples of non-parametric classical versions of two-sample tests are the Wald-Wolfowitz runs test, the Anderson-Darling test and the Kolmogorov-Smirnov test [10].

Recently, Maximum Mean Discrepancy (MMD) was proposed as another non-parametric two-sample test technique [11]. MMD compares the means of two distributions in a universal reproducing kernel Hilbert space and has superior performance to several of the classic two-sample tests. However, the superior performance of MMD relies on a valid choice of a kernel and kernel width, and recommendations have been made in the literature for obtaining optimal performance with MMD [12]. Similarly, the Least Squares Sample Test (LSTT) technique has been proposed in the literature to make use of permutation to perform two-sample tests [13]. In the LSTT based two-sample test, divergence is estimated using the density ratio estimation technique and the permutation-based technique is used to test the significance of the estimated divergence. Such permutation-based tests are preferable because they are data-centric approaches that make inferences directly from data.

The proposed PCAR algorithm detects significant changes in activity curves based on a permutation-based two-sample test using symmetric Kullback-Liebler divergence as a distance metric. Our proposed method to detect changes in activity routines has some similarities with activity tracking algorithms that have been previously proposed [14, 15]. These proposed activity-tracking algorithm discovers and tracks changes in sensor sequence patterns for the purpose of adapting home automation strategies. In contrast, our method tracks changes in the distribution of automatically-recognized activity patterns.

Relationship between changes in activity routines and health

Researchers have developed functional assessment algorithms based on different parameters of everyday abilities. These researchers have studied correlations between everyday abilities and corresponding standard clinical measurements. Researchers have correlated sensor measurements of sleep patterns, gait, activity rhythms, indoor activities and outings, and mobility with standard clinical measurements such as MMSE and self-report data. For example, Paavilainen et al. [16] compared the changes in circadian rhythm of activities of older adults living in nursing homes with clinical observations of the health status of subjects. In other work, Robben et al. [17, 18, 19] studied the relationship between different high-level features representing the location and transition patterns of an individual’s indoor mobility behavior, namely the frequency, duration and times being carried out, with the Assessment of Motor and Process Skills (AMPS) scores [20]. Other researchers have studied the relationship between walking speed and the amount of in-home activity among healthy older adults and older adults with Mild Cognitive Impairment (MCI) [21]. These researchers found out that coefficient of variation in the median walking speed was higher in the MCI group as compared with the healthy group. However, none of these works considered parameters reflecting the performance of activities of daily living.

Other researchers have developed functional assessment algorithms based on performance of an individual in a fixed set of activities. They have correlated the performance in these activities with the direct observation of participants completing the ADLs. In one such work, Dawadi et al.[22, 23] proposed learning algorithms to obtain activity performance measures of simple and complex ADLs from sensor data and correlated them with validated performance measures derived from direct observation of participants completing the ADLs. They also studied the relationship between sensor-detected activity performance measures and overall cognitive health. In another work, Hodges et al. [24] correlated sensor events gathered during a coffee-making task with an individual’s neuropsychological score. Similarly, in an another research effort by Riboni et al.[25] researchers developed a Fine-grained Abnormal BEhavior Recognition (FABER) algorithm to detect abnormal behaviour using a statistical-symbolic technique. These researchers hypothesize that such abnormal activity routines may indicate the onset of early symptoms of cognitive decline.

3. Activity curve

An activity curve is a model that represents an individual’s generalized activity routine. We are interested in modeling activity routines for a day-long period but this time period can be changed as needed. The activity curve uses automatically-recognized activity labels to express daily behavioral characteristics based on the timing of recognized activities.

We assume that a continuous sequence of time-stamped sensor events is available. We use an activity recognition algorithm to annotate each of these sensor events with an activity label. Activity recognition algorithms map a sequence of sensor events {e₁, e₂, …, e_n} onto the corresponding activity label A_i, where the label is drawn from the predefined set of activity classes A = {A₁, A₂, …, A_n}.

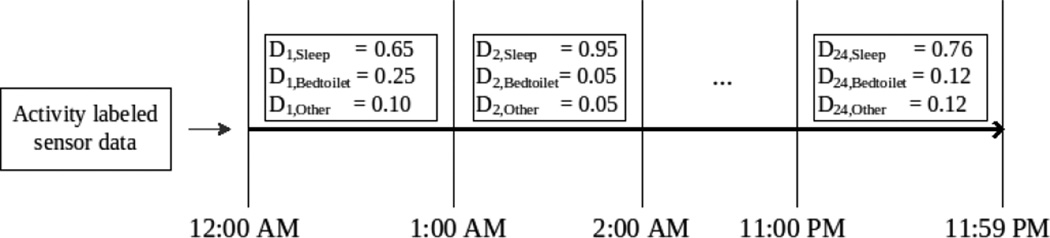
We note that prevalence of common activities differs by the time of day. For example, the “sleep” activity dominates the prevalent distribution of activities at midnight and the “cook breakfast” and “eat breakfast” activities dominate the early morning hours. To capture such differences in activity patterns throughout the day, we segment the day-long observation period into m equal-size consecutive windows, or time intervals, and define probability distributions over activities, or activity distributions, for each of these time intervals (see Figure 1 for an example). An activity curve is a compilation of these activity distributions for the entire day-long period.

Figure 1.

Example activity distributions calculated at 60 minute time intervals. The figure models three possible activities: sleep, bed toilet transition, and an “other” activity. An activity curve is thus the compilation of all of these activity distributions.

We also note that our activity routines tend to vary from one day to the next. For example, we may wake up at 6:30 AM and eat breakfast at 7:15 AM one day while we might wake up at 7:30 AM and eat breakfast at 8:00 AM the next day. In order to generalize our model over such day-to-day variations in activity routines, we will define the notion of an aggregated activity curve that is calculated over an aggregation window of x days.

Definition 1

Given a time interval t, an activity distribution models the daily routine based on the predefined set of activities A as a probability distribution over activities in A. The probability distribution can be estimated from sample data based on the normalized time an individual spends on a predefined set of n activities during time intervals t as observed during one or more days.

An activity distribution for time interval t is a n-element set D_t = {d_t,1, d_t,2, …, d_t,n} whose length is equal to that of the activity set A. The i^th element in an activity distribution, d_t,i, represents the probability of performing activity A_i during time interval t.

To model a person’s overall daily activity routine, we use m activity distributions corresponding to each of the m time intervals. We can then construct an activity curve by collecting activity distributions that model daily activity patterns at all different times of the day.

Definition 2

An activity curve C is the compilation of activity distributions D_t ordered by time interval t.

The length of an activity curve is m. We refer to the model that compiles activity distributions as an “activity curve” because if we consider the activity distribution of activity A_i for all time intervals 1, 2, …, m, these activity distributions form a curve that represents the “fraction of a time” that an individual is likely to perform activity A_i over successive time intervals.

We calculate an aggregated activity distribution D̂_t for time interval t by aggregating activity distributions D_k,t(1 ≤ k ≤ x) over an aggregation window of x days. If D_1,t, D_2,t,…, D_x,t are activity distributions for the t^th time interval aggregated over a window of x days and follow normal distributions, then we can define an aggregated activity distribution as follows.

Definition 3

An aggregated activity distribution D̂_t at time interval t is the maximum likelihood estimate of the mean that is obtained from activity distributions D_k,t(1 ≤ k ≤ x) that fall within an aggregation window of size x.

We can write the aggregated activity distribution D̂_t at time interval t as show in Equation 1.

$${\hat{\mathbf{D}}}_t=\sum _{k=1}^x\frac{{\mathbf{D}}_{k,t}}{x}$$ (1)

Definition 4

An aggregated activity curve is the compilation of aggregated activity distributions obtained over an aggregation window of size x.

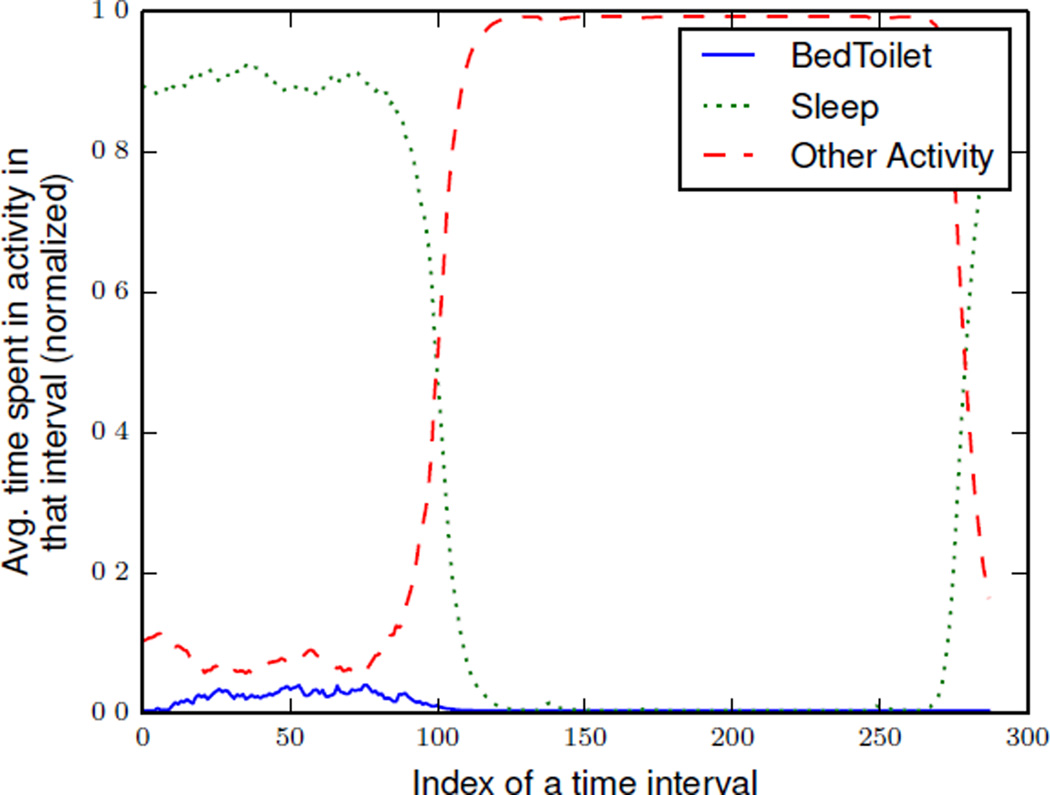
If Σ = {C₁, C₂, C₃, …, C_x} is a set of activity curves over an aggregation window of size = x days, we can represent an aggregated activity curve over Σ as C^Σ. The aggregated activity curve C^Σ compiles the aggregated activity distributions, D̂_t. Figure 2 illustrates an example of an aggregated activity curve that models three different activities: sleep, bed toilet transition, and other.

Figure 2.

An example aggregated activity curve that models three different activities: sleep, bed toilet transition, and an “other” activity. This sample aggregated activity curve was derived using x= three months of actual smart home data. Aggregated activity distributions were calculated at 5 minute time intervals, (m = 288). In this graph, the time interval at index 0 represents 12:00 AM.

4. Activity distribution distance

We calculate the distance between two activity distributions using the Kullback-Leibler (KL) divergence measure. We assume that the activity distributions model the same activity set A for the same time interval size and aggregation window size. The KL divergence between two activity distributions D₁ = {d_1,1, d_1,2, …, d_1,i, …, d_1,n} and D₂ = {d_2,1, d_2,2, …, d_2,i, …, d_2,n} is defined as shown in Equation 2.

$$D_{KL}({\mathbf{D}}_1\Vert {\mathbf{D}}_2)=\sum _{i=1}^n{d}_{1,i}\text{ log}\frac{d_{1,i}}{d_{2,i}}$$ (2)

We note that the standard KL distance metric is a non-symmetric measure of the differences between two probability distributions D₁ and D₂. Therefore, we use a symmetric version of the Kullback-Leibler divergence between activity distributions D₁ and D₂, which is defined as shown in Equation 3. Throughout the remainder of the paper, our discussion of KL divergence will refer to this symmetric version of the KL divergence measure.

$$S{D}_{KL}({\mathbf{D}}_1\Vert {\mathbf{D}}_2)=D_{KL}({\mathbf{D}}_1\Vert {\mathbf{D}}_2)+D_{KL}({\mathbf{D}}_2\Vert {\mathbf{D}}_1)$$ (3)

Before defining the distance between two activity curves C₁ and C₂ of length m, we first need to align the activity distributions in the activity curves (this is described in Section 6). As a result of the alignment step, we obtain a vector of alignment pairs Γ = (p, q) of length l = |Γ| that aligns an activity distribution at time interval p (1 ≤ p ≤ m) of activity curve C₁ with activity distribution at time interval q (1 ≤ q ≤ m) of activity curve C₂.

We calculate the total distance, SD_KL(C₁‖C₂), between two activity curves, C₁ and C₂, as the sum of distances between each aligned activity distribution for the two activity curves, as shown in Equation 4.

$$S{D}_{KL}(C_1\Vert C_2)=\sum _{\alpha =1}^{l}S{D}_{KL}({\mathbf{D}}_{1,p}\Vert {\mathbf{D}}_{2,p})\text{ such that }{\mathbf{\Gamma }}_{\alpha }=(p,q)$$ (4)

where D_1,p and D_2,q are the activity distributions that belong to activity curves C₁ and C₂ at time intervals p and q, respectively.

5. Determining the size of an aggregation window

Daily activity routines are performed differently from one day to the next. As a result, the daily activity curve that models these activity routines will vary from one day to the next. We want to calculate an aggregated activity curve that generalizes over minor day-to-day variations while still capturing the typical routine behavior. When determining the appropriate size of an aggregation window, our goal is to find the smallest possible number of days that is considered stable. We determine that an aggregated activity curve is stable if the shape of the curve remains mostly unchanged when more days are added to the aggregation window. By keeping the aggregation window small, our model can be more sensitive to significant changes in routine behavior. If the window is too small it will not be general enough to encompass normal variations in daily routines. We propose Algorithm 1 to determine the minimum length of an aggregate window that is required to calculate a stable, representative aggregated activity curve for a particular time interval. We choose the minimum aggregate window size x_min such that no smaller window would ensure the stability criterion.

To determine the ideal aggregation window size, we start with a window of size x = 2 and consider the corresponding aggregated activity curve C^Σ, aggregated from the set of individual activity curves Σ = {C₁, …, C_x}. We estimate the distance between $C_x^{\mathrm{\Sigma }}$ and $C_{x+1}^{\mathrm{\Sigma }}$. If the distance is greater than a predefined threshold T, we increase the window size. Therefore, if $S{D}_{KL}(C_x^{\mathrm{\Sigma }}\Vert C_{x+1}^{\mathrm{\Sigma }})<T$ and $S{D}_{KL}(C_{x+1}^{\mathrm{\Sigma }}\Vert C_{x+2}^{\mathrm{\Sigma }})<T$, then x is selected as the representative aggregation window size, otherwise we increase size of the aggregation window by one and repeat the process. This process is shown in Algorithm 1.

Algorithm 1.

Aggregation Size(Σ, T)

1:	// Calculate the minimum size of an aggregation window.
2:	Σ = {C1, C2,…, CN} for each of the N days in the input data.
3:	// Return the minimum aggregation window size.
4:	initialize x = 2
5:	repeat:
6:	Create $C_x^{\mathrm{\Sigma }}$, aggregated activity curve for window size x.
7:	Create $C_{x+1}^{\mathrm{\Sigma }}$, aggregated activity curve for window size x + 1.
8:	Create $C_{x+2}^{\mathrm{\Sigma }}$, aggregated activity curve for window size x + 2.
9:	Compute d1 = distance between two aggregated activity curves $S{D}_{KL}(C_x^{\mathrm{\Sigma }}\Vert C_{x+1}^{\mathrm{\Sigma }})$.
10:	Compute d2 = distance between two aggregated activity curves $S{D}_{KL}(C_{x+1}^{\mathrm{\Sigma }}\Vert C_{x+2}^{\mathrm{\Sigma }})$.
11:	if d1 > T and d2 > T, then x = x + 1
12:	else return x
13:	until x < N

6. Activity curve alignment

In order to compute similarity (or distance) between two activity curves, we need to compare each of the activity distributions that belong to these two activity curves. However, we first need to determine which pairs of distributions to compare by considering alternative distribution alignment techniques. Activity curve alignment can be performed based on aligning the same time of day between two curves. Alternatively, we can try to maximally align the activity occurrences between two curves before performing such a comparison. Here we provide details for these two alignment techniques that we use in our work.

6.1. Time interval-based activity curve alignment

The time interval-based activity curve alignment technique presumes that distributions between two curves should be aligned based on time of day and thus aligns activity distributions between two activity curves if the time intervals are the same. In essence, this method does not make any extra effort to align activities that occur at different times in the distribution, but simply compares the activity distributions based on time of day alone.

If C₁ and C₂ are two activity curves of length m, the time interval-based activity distribution alignment method aligns the corresponding activity distributions using a vector of alignment pairs, Γ = (r, r). This technique aligns an activity distribution at time interval r (1 ≤ r ≤ m) of activity curve C₁ with activity distribution at time interval r (1 ≤ r ≤ m) of activity curve C₂.

6.2. Dynamic time warping-based activity curve alignment

A person’s routine may be relatively stable, even though there are minute changes in the time an activity occurs or the duration of a particular activity. For example, an individual may sleep at 10:00 PM one day, an hour earlier at 9:00 PM the next day, an hour later at 11:00 PM a few days later, and eventually go back to sleeping at 10:00 PM. Aligning activity distributions using dynamic time warping allows us to maximally align common activities before comparing two activity curves. Such an alignment accommodates activity time changes that are shifted temporally backward (for example, an hour earlier), forward (for example, an hour later), expanded (longer duration), compressed (shorter duration), or not changed at all from one day to another. We optimize activity alignment using Dynamic Time Warping(DTW) to align distributions between two activity curves.

Dynamic time warping finds an optimal alignment or warping path between activity curves. This optimal warping path has minimal total cost among all possible warping paths. We use the symmetric KL distance metric that we previously mentioned to compute this warping path. The warping path has the following three main properties:

• Boundary property: The first and last elements (activity distributions) from the two activity curves are always aligned with each other.

• Monotonicity property: Paths are not allowed to move backwards.

• Step size property: No activity distributions are omitted from the curve alignment.

We also note that due to the monotonicity property, DTW does not allow backward alignments. However, as we have seen in practice, activity distributions can be shifted temporally backward and/or temporally forward. Therefore, we modify the standard approach to perform two independent iterations of DTW:

• In forward dynamic time warping, we start from the first activity distribution and move forward in time toward the last activity distribution to find an optimal alignment between activity curves that are similar in the forward time direction.

• In backward dynamic time warping, we start from the last activity distribution and move backward in time toward the first activity distribution to find an optimal alignment between activity curves that are similar in the backward time direction.

If C₁ and C₂ are two activity curves of length m, the DTW-based activity distribution alignment outputs two alignment vectors, Γ_forward = (u, υ) of length l_forward, and Γ_backward = (r, s) of length l_backward, respectively. The forward DTW aligns an activity distribution from curve C₁ at time interval u (1 ≤ u ≤ m) with an activity distribution from curve C₂ at time interval υ (1 ≤ υ ≤ m). Similarly, the backward DTW aligns an activity distribution from curve C₁ at time interval r (1 ≤ r ≤ m) with an activity distribution from curve C₂ at time interval s (1 ≤ s ≤ m). The DTW method outputs whichever vector, Γ_forward or Γ_backward, that results in the maximal alignment between the two distributions and thus minimize the difference. We will utilize these two different alignment techniques in our PCAR algorithm to detect changes between two aggregated activity curves and calculate change scores.

7. PCAR

Based on our notion of an activity curve, we now introduce our Permutation-based Change Detection in Activity Routine (PCAR) algorithm. This algorithm identifies and quantifies changes in an activity routine. PCAR operates on the assumption that daily activities are scheduled according to a routine and are not scheduled randomly. For example, we regularly “wake up”,“bathe” and “have breakfast” in the morning and “dine” and “relax” in the evening. In contrast, we rarely dine in the middle of night. Such regularities are useful, for example, to determine if there are significant changes in lifestyle behavior that might indicate changes in cognitive or physical health.

7.1. Permutation-based two-sample test

PCAR identifies significant changes in an activity routine using a two-sample permutation test [26]. The permutation-based technique provides a data-driven approach to calculate an empirical distribution of a test statistic. The empirical distribution of a test statistic is obtained by calculating the test statistic after randomly shuffling (rearranging) the data a specified number of times. The permutation-based test is exact if the joint distributions of rearranged samples are the same as the joint distribution of the original samples. In other words, the samples are exchangeable when the null hypothesis is true. This type of test allows us to determine the significant difference between two aggregated activity curves.

We use a permutation-based test to perform a two-sample homogeneity test. In a two-sample homogeneity test, we test the null hypothesis that the two samples come from the same probability distribution versus the alternate hypothesis that they come from different probability distributions.

7.2. Changes in activity distributions

We use the permutation-based two-sample test to determine whether there is a significant change among a set of activity distributions at a particular time interval. We formulate the null hypothesis that the set of activity distributions comprising two activity curves are identical versus the alternative hypothesis that the set of activity distributions is significantly different between the two aggregated activity curves.

We test the hypothesis of a significant change between two aggregated activity distributions, D̂_1,t and D̂_2,t.

• Calculate the test statistic: Calculate the test statistic Dist_t = SD_KL(D̂_1,t‖ D̂_2,t) between the two aggregated activity distributions.

• Permutation: Randomly shuffle individual activity distributions between the two aggregated distributions and recalculate the aggregated distributions D̂_1,t and D̂_2,t. Calculate the KL divergence between the new aggregated activity distributions Dîst_t = SD_KL(D̂_1,t‖ D̂_2,t). Repeat the process a specified number of times to obtain an empirical distribution of KL divergence (the test statistic), Dîst_t.

• Significance testing: To test if a significant difference exists between D̂_1,t and D̂_2,t calculate the p-value by calculating the number of times the test statistic from the permuted sample is equal to or greater than the original test statistic Dist_t, in the empirical distribution Dîst_t. If a small p-value is obtained, reject the null hypothesis in favor of alternative hypothesis. This is shown in Equation 5.

  $$p_{\mathit{\text{perm}}}=\frac{\#{\mathit{\text{Dîst}}}_t>{\mathit{\text{Dist}}}_t}{\#\text{permutations}}$$ (5)

where Dîst_t is the empirical distribution of the test statistic at the t^th time interval. We reject the null hypothesis that no changes have occurred at a significance level of α = 0. 01.

7.3. Changes in activity curves

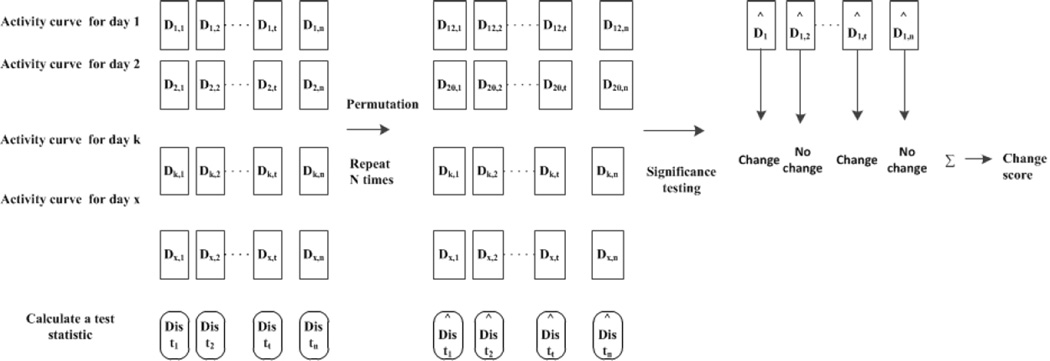
We now extend the technique of detecting significant changes between activity distributions to quantify the difference in activity routine observed from two separate aggregation windows, W₁ and W₂, each of size x days. To do this, PCAR counts the total number of significant differences between the individual activity distributions within window W₁ and the distributions within window W₂ to output a change score that quantifies the significant changes observed among the activity curves. Figure 3 demonstrates the three main steps involved in detecting changes in an activity curve using the permutation-based method.

Figure 3.

The permutation-based steps to detect changes in the activity curve. The first step is to compute the test statistic from the original samples. In the second step, the samples are rearranged N times and the test statistic is calculated for each arrangement. In the third step, significance testing is performed by comparing the test statistic obtained from the original (unpermuted) set of data with the the test statistic obtained from the permuted data. Finally, a change score is calculated by counting the number of significant changes in activity distributions.

PCAR calculates a sum, S, over changes that are detected between activity curve distributions for each individual time interval. In order to identify the time intervals at which changes in the activity distributions comprising the aggregated activity curves are deemed significant, PCAR performs the following steps:

• Permutation: Calculate the empirical distributions of the test statistic (KL divergence) by permuting and comparing the individual activity distributions within the two aggregation windows W₁ and W₂ at each time interval using the method summarized in Algorithm 2.

• Alignment: Calculate the two aggregated activity curves C₁ and C₂ using the activity distributions aggregated for each time interval over windows W₁ and W₂. Align curves C₁ and C₂ using one of the alignment techniques described in the previous section to generate the alignment vector Γ = (u, υ).

• Calculate the test statistic: For each alignment pair (u, υ) ∈ Γ, calculate the test statistic Dist_u,υ between the aggregated activity distribution at time interval u of activity curve C₁ and the aggregated activity distribution at time interval υ of C₂.

• Significance testing: To test if there is a significant change between activity distributions at time intervals u and υ, calculate the p-value based on the the number of times the test statistic from the permuted sample is equal to or greater than the original test statistic. The steps are summarized in Algorithm 3.

We note that we compare at least m activity distributions during this process where m is the number of aggregated activity distributions in an activity curve. To control the False Discovery Rate (FDR) at level α*(α* = 0.01), we apply the Benjamini-Hochberg (BH) method [27]. The BH method first orders the p-values, p₍₁₎, p₍₂₎, …, p_(k), …, p_(m), in ascending order and for a given value of α*, the BH method finds the largest k such that $p_{(k)}\le k\times \frac{{\alpha }^{*}}{m}$. The BH algorithm rejects the null hypothesis corresponding to p_(i) if i ≤ k. If a significant change is detected between aligned activity distributions, PCAR increments its change score, S, by one. PCAR generates two different change scores based on the alignment techniques that are employed: either the same index alignment or the DTW-based alignment.

8. Use of activity curves for smart functional assessment: A case study

An activity curve model provides a big data-based tool for representing a longer-term behavioral model. Such a tool is valuable for a variety of applications including human automation, health monitoring, and automated health assessment. In this section, we explain how the activity curve model and the PCAR algorithm can be instrumental in performing automated functional assessment.

Activities of daily living such as sleeping, grooming, and eating are essential everyday functions that are required to maintain independence and quality of life. Decline in the ability to independently perform these ADLs has been associated with a host of negative outcomes, including placement in long-term care facilities, shortened time to conversion to dementia, and poor quality of life for both the functionally impaired individuals and their caregivers [28, 29, 30].

Algorithm 2.

Empirical Distribution(Σ₁, Σ₂, N_P)

1:	// Build empirical distribution Dîst of the test statistic.
2:	Σ1, Σ2 = two sets of activity curves
3:	Np = number of permutations
4:	initialize Dîst as Np × m matrix	▷ m is # activity distributions in the activity curves
5:	initialize i = 0
6:	while i < Np do :
7:	Shuffle the activity curves.
8:	Generate aggregated activity curves CΣ1 and CΣ2 by aggregating the distributions in Σ1, Σ2
9:	Using the time interval-based alignment technique, align the two aggregated activity curves to obtain an alignment vector Γ
10:	for all alignment pairs (u, u) in Γ do :
11:	Find a distance SDKL(D1,u‖D2,u) between uth activity distributions in two activity curves.
12:	Insert SDKL (D1,u‖D2,u) to empirical distribution Dîst at location [i, u].
13:	end for
14:	i = i+1
15:	end while
16:	return Dîst

We use smart home sensor data to derive activity curves that model the activity routines of a smart home resident. Our PCAR algorithm detects changes in those activity routines. We note that changes in ADL patterns are one of the many forms of behavioural changes that are frequently associated with changes in cognitive and physical health. We hypothesize that activity curve will allow us to detect changes in ADL patterns which possibly can provide valuable information about a change in the health condition. To validate our automated assessment technique, we utilize smart home sensor data that was collected from real world smart home test beds with older adult residents. We apply robust activity recognition algorithms [31, 32] to label these sensor-monitored data with the corresponding activity labels.

Algorithm 3.

PCAR(Σ₁, Σ₂, Dîst)

1:	Σ1, Σ2 = two sets of activity curves
2:	//Return a change score S
3:	C1 = Aggregate Activity Curves(Σ1)
4:	C2 = Aggregate Activity Curves(Σ2)
5:	Γ = Align Curves(C1, C2)
6:	for all alignment pairs (u, υ) in Γ do :
7:	Calculate SDKL(D1,u‖D2,υ) between activity distribution D1,u ∈ C1 and D2,υ ∈ C2.
8:	Perform significance testing of estimated distance by querying Dîst.
9:	if change is significant :
10:	S = S + 1
11:	end for
12:	return S

8.1. Synthetic dataset

First, we validate the performance of the proposed PCAR algorithm by running it on a synthetic activity curve. We create a synthetic activity curve by compiling synthetic activity distributions. The synthetic activity distribution models the patterns of two activities, an arbitrary activity A and an “other” activity.

We generate synthetic activity distributions for each time interval t for N days by applying the following three steps. Here l represents the length of each time interval.

• Generate a random value p (0 ≤ p ≤ l), which represents the average time that is spent in performing activity A during time interval t.

• Generate two vectors, S and S′, each of length N. Generate the vector S from a normal distribution i.e. S ~ Normal(p, 1). Each element of vector S′ is generated by subtracting the corresponding value in S from l i.e l − s ∈ S′.

• Create an activity distribution that models patterns of two activities at a time interval t. The elements of the activity distribution is [s, l −s]. We combine these individual synthetic activity distributions at different time intervals into activity curves. When we introduce an activity change, we multiply the average time spent performing an activity A by a constant factor in each time interval.

Using the aforementioned method, we create two different sets of activity curves. The first set Y does not contain any changes and another different set of daily activity curves Z contains changes in all activity distributions every 90 days. We run the PCAR algorithm on an aggregated activity curve of size 90 days using the time interval index alignment. PCAR successfully detects all changes in the dataset where activity changes were made and does not produce any false positives in the synthetic dataset that does not contain changes.

8.2. Experimental setup

Next, we demonstrate how PCAR can be used to detect changes in real smart home data. For this study, we recruited 18 single-resident senior volunteers from a retirement community and installed smart home sensors in their homes [33]. The smart home sensors unobtrusively and continuously monitor resident activities. We continuously collected raw sensor events for an extended period (~ 2 years) from all of the residents. At the same time, standardized clinical, cognitive, and motor tests were administered biannually to the residents.

8.3. Participants

Participants included 18 senior residents (5 females, 13 males) from a senior living community. All participants were 73 years of age or older, and had a mean level of education of 17.52 years. At baseline, participants were classified as cognitively healthy (N=7), at risk for cognitive difficulties (N=7) or experiencing cognitively difficulties (N=4). One participant in the cognitively compromised group met the criteria for dementia [34], while the other three individuals met the criteria for mild cognitive impairment (MCI) [35].

8.4. Smart home test bed

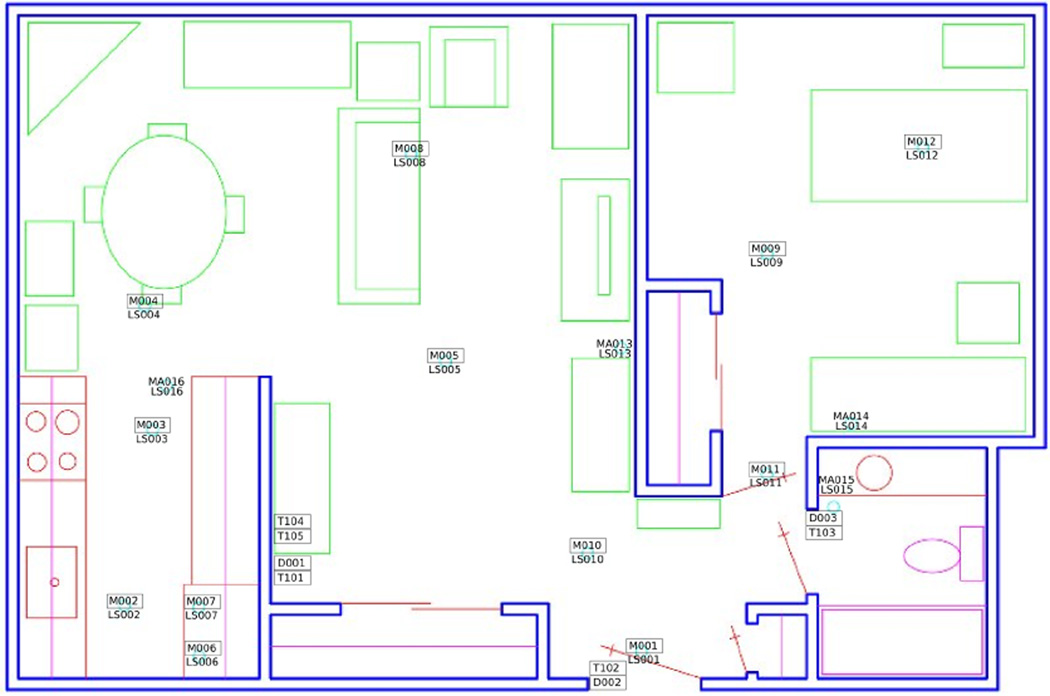
The 18 smart home test beds are single-resident apartments, each with at least one bedroom, a kitchen, a dining area, and one bathroom. The sizes and layouts of these apartments vary from one apartment to another. The apartments are equipped with combination motion/light sensors on the ceilings and combination door/temperature sensors on cabinets and doors. Figure 4 shows the layout and sensor placement for one of the smart home test beds.

Figure 4.

Smart home floor plan and sensor layout.

The residents perform their normal activities in their smart apartments, unobstructed by the smart home instrumentation. While residents carry out their daily routines, sensors continuously monitor their behavior. The middleware collects the sensor events and stores them on a database server. Figure 5 provides a sample of the raw sensor events that are collected and stored. Each sensor event is represented by four fields: date, time, sensor identifier, and sensor message. The raw sensor data does not contain activity labels. We use an activity recognition algorithm, described in the next section, to map individual sensor events to corresponding activity labels.

Figure 5.

Activity annotated sensor data. Sensors IDs starting with M are motion/light sensors and IDs starting with D are door/temperature sensors. Each sensor event is annotated with an activity label.

8.5. Activity recognition

Activity recognition algorithms label activities based on readings (or events) that are collected from the smart environment, mobile device, or other sensors. As described earlier, the challenge of activity recognition is to map a sequence of sensor events onto a value from a set of predefined activity labels. These activities may consist of simple ambulatory motion, such as walking and sitting, or complex activities of daily living, such as cooking and eating, depending upon what type of underlying sensor technologies and learning algorithms are used.

Our activity recognition algorithm, AR [31, 32], recognizes activities of daily living, such as cooking, eating, and sleeping using streaming sensor data from environmental sensors such as motion sensors and door sensors. These motion and door sensors are discrete-event sensors with binary states (On/Off, Open/Closed). Human annotators label one month of sensor data from each home with predefined activity labels to provide ground truth for training and evaluating the algorithm. The inter-annotator reliability (Cohen’s Kappa) values of the labeled activities in the sensor data ranged from 0.70 to 0.92, which is considered moderate to substantial. The trained model is then used to generate activity labels for unlabeled sensor data.

AR identifies activity labels in real time as sensor event sequences are observed. We accomplish this by moving a sliding window over the data and using the sensor events within the window to provide a context for labeling the most recent event in the window. The window size is dynamically calculated based on the current sensor and each event within the window is weighted based on its time offset and mutual information value relative to the last event in the window. This allows events to be discounted that are likely due to other activities being performed in an interwoven or parallel manner. We calculate the feature vector using accumulated sensor events in a window. The feature vector contains information such as time of the first and last sensor events, temporal span of the window, and influences of all other sensors on the sensor generating the most recent event based on mutual information. Currently, AR recognizes the activities we monitor in this project with 95% accuracy based on 3-fold cross validation with the data we are analyzing in this paper. An example of activity-labeled sensor data is presented in Figure 5.

8.6. Activities

Using the AR algorithm, we recognize seven different activities of daily living: sleep, bed-to-toilet, cook, eat, personal hygiene, leave home, relax, and an “other” activity. In our datasets, the relax activity includes watching television, reading, and/or napping that typically takes place in a favorite chair or location where the resident spends time doing these activities.

One of the activities that we assess in this case study, sleep, is a particularly important clinical construct that both clinicians and caregivers are interested in understanding [36]. Sleep problems in older adults can affect cognitive abilities [37, 38] and have been associated with decreased functional status and quality of life [39, 40]. Moreover, individuals with dementia often experience significant disruption of the sleep-wake cycle [41].

On the other hand, all basic activities of daily living (e.g., eating, grooming) and instrumental activities of daily living (IADLs; e.g., cooking, managing finances) are fundamental to independent living. We postulate that like sleep, changes in any of these activities may indicate changes in cognitive or physical health. Data indicate that subtle difficulties in everyday activity completion (e.g., greater task inefficiencies, longer activity completion times) occur with increased age [42]. Clinical studies have also demonstrated that individuals diagnosed with MCI experience greater difficulties (e.g., increased omission errors) completing everyday activities when compared with healthy controls [43, 44, 45, 46]. Furthermore, with incidence of severe cognitive problems such as AD, individuals have difficulty in both initiating and completing basic activities [47]. Thus, clinicians argue the importance of understanding the course of functional change given the potential implications for developing methods for both prevention and early intervention [48, 42].

Finally, our AR algorithms places all other activities into an “other” category. This category includes all remaining activities that we are not distinguishing and analyzing separately in this case study. Thus, in our current work, we analyze daily patterns of 7 activities of daily living and the “other” activity using activity recognition algorithms and analyze them using the PCAR algorithm.

8.7. Standard neuropsychological tests

Clinical tests were administered every six months to residents of our smart home test beds. As detailed in Table 1, these tests included Timed Up and Go Test (TUG) and a global measure of cognitive status (RBANS). The administered clinical tests are standardized and validated measures that provide indication of mobility-based health and cognitive health. Table 1 provides a brief description of each clinical test and the measure that was employed from each test. Using repeated measurements obtained from biannual clinical tests, we create a clinical longitudinal dataset that contains these two measurement variables (features).

Table 1.

Variables in standard clinical dataset

Variable name	Type	Description
TUG	Numeric	Timed Up and Go Test[49]. This test measures basic mobility skills. Participants are tasked with rising from a chair, walking 10 feet, turning around, walking back to the chair and sitting down. The TUG measure represents the time it took participants to complete the task.
RBANS	Numeric	Repeatable Battery for the Assessment of Neuropsychological Status[50]. This global measure of cognitive status was developed to identify and characterize cognitive decline in older adults.

9. Experimental results

9.1. Preprocessing

We use two different preprocessing techniques to preprocess activity curves.

• Mean smoothing: We run a mean smoothing filter of size 3 on activity distributions comprising the activity curve to smooth out noise and minor variations. In this step, we replace the estimate at time interval t with the average estimate of activity distributions at times t − 2, t − 1, and t.

• Add-One smoothing: Activity distributions for certain activities can be zero. For example, we rarely eat and cook at midnight so activity distributions of these activities at midnight are often zero. We perform add-one smoothing on all of the elements of activity distributions. In add-one smoothing, we add a constant α = 1 in every elements of the activity distributions. Add-one smoothing technique is often used in natural language processing to smooth unigram estimates and has an effect of removing zero entries.

9.2. Studying aggregated activity curve

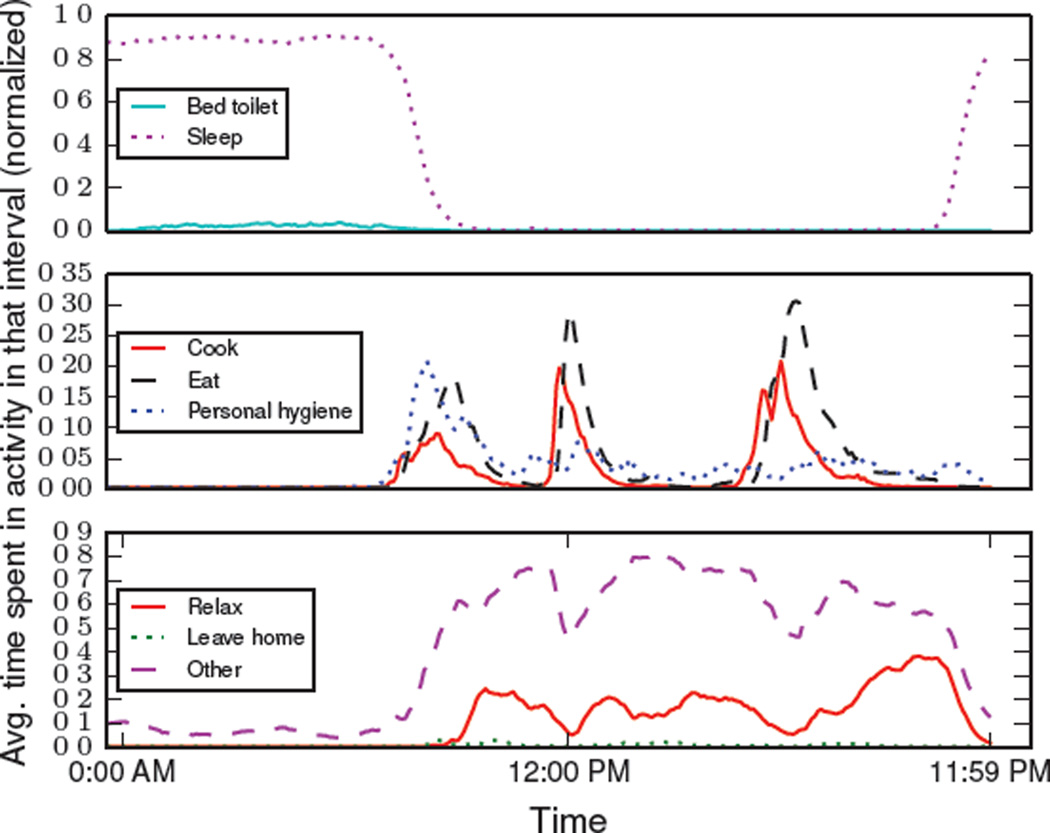
Figure 6 is an example aggregated activity curve that models eight different activities, including seven recognized activities(i.e., sleep, bed toilet transition, eat, cook, relax, personal hygiene) and an “other” activity. This sample aggregated activity curve was derived using an aggregation window of size x = three months based on actual single resident smart home sensor data and 5 minute time intervals. We observe that this smart home resident usually goes to sleep at around 9:00 PM and wakes up at around 7:00 AM. We also observe that the resident exhibits a fairly fixed schedule for eating breakfast, lunch, and dinner.

Figure 6.

An example of aggregated activity curve that models eight different activities. This sample aggregated activity curve was derived using x = three months of actual smart home data. Aggregated activity distributions were calculated at 5 minute time intervals, (m = 288)

9.3. Comparing activity distributions

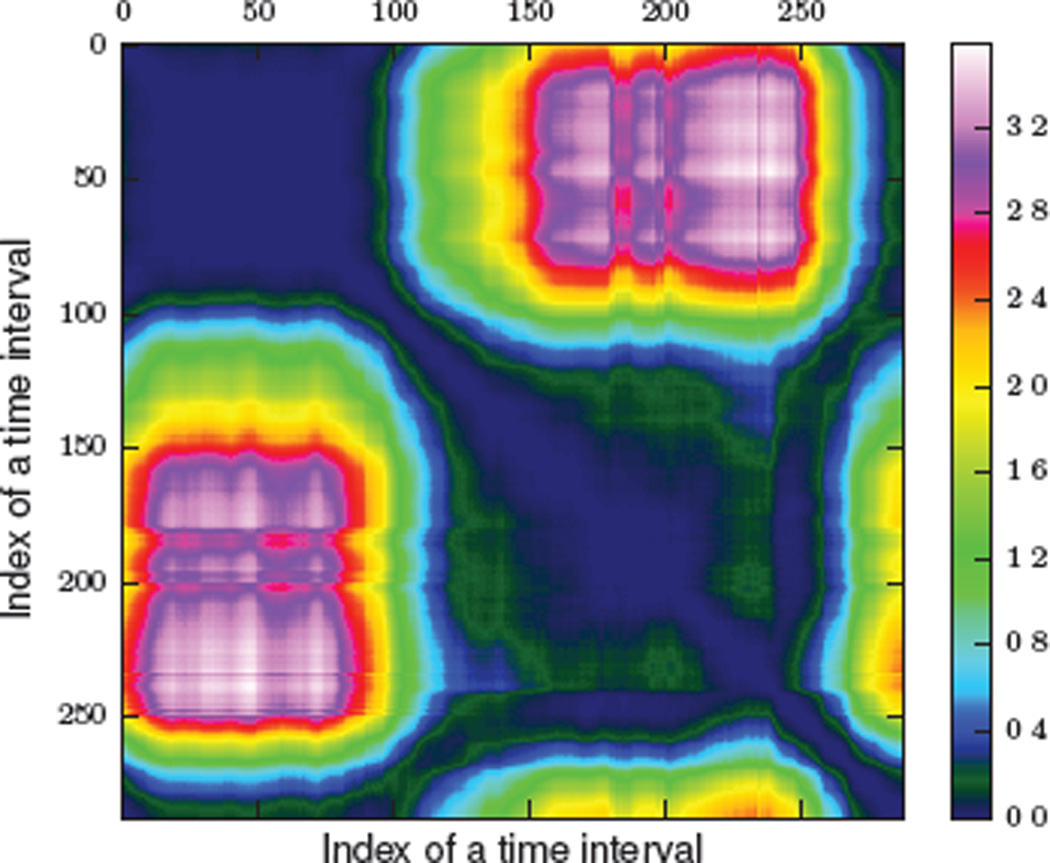
For most individuals, our activities follow a common pattern based on factors such as time of day. Thus, the activity distributions that model activities at different time intervals belonging to different times of a day will be different. In our first experiment, we assess whether our proposed activity curve can capture such differences in activity distributions. We calculate an aggregated activity curve for five-minute time intervals using the first three months of activity-annotated sensor data from one of our smart homes. We calculate a pairwise distance (symmetric KL divergence) matrix between activity distributions from this aggregated activity curve. We plot this pairwise distance matrix in a heat map shown in Figure 7.

Figure 7.

Heat map of the pairwise distance matrix between activity distributions of an aggregated activity curve using KL distance. The size of the time interval is 5 minutes. Index 0 represents 12:00 AM.

From the heat map in Figure 7, we observe that the distance between activity distributions varies according to the time of day. We observe that the darkest colors appear along the diagonal when we compare activity distributions for the same time of day. In contrast, we observe that the hottest colors (greatest distance) occurs when comparing activities at midnight (when the resident typically sleeps) to activities in mid-afternoon when the resident is quite active. Additionally, we also see different clusters emerge (for instance, between times 0 and 100) corresponding to times of day. These observations provide intuitive visual evidence that the activity curve is capturing generalizable differences in activity routine at various times of the day.

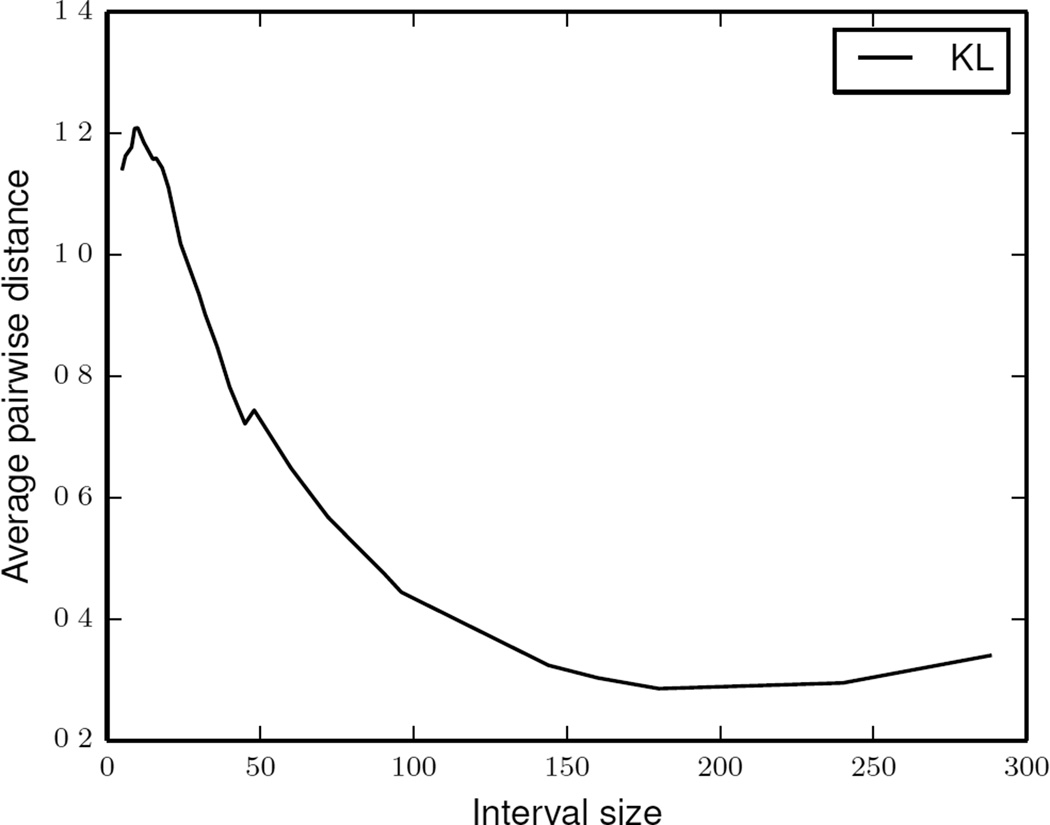
In the next experiment, we study how the activity distribution distances within an activity curve (the y axis in Figure 8) change as a function of the time interval size (the x axis). For this experiment, we calculated an average pairwise distance between activity distributions within aggregated activity curve for each time interval size. We observe that as the time interval increases, the average pairwise distance between daily activity distributions decreases. Such a decrease in distances is observed because activity distributions at larger sized time intervals are overwhelmed by activities that take larger duration (such as sleep). As a result, smaller differences between such activity distributions are harder to detect.

Figure 8.

Average intra-curve pairwise KL distance as a function of time interval size.

9.4. Aggregation Window Size

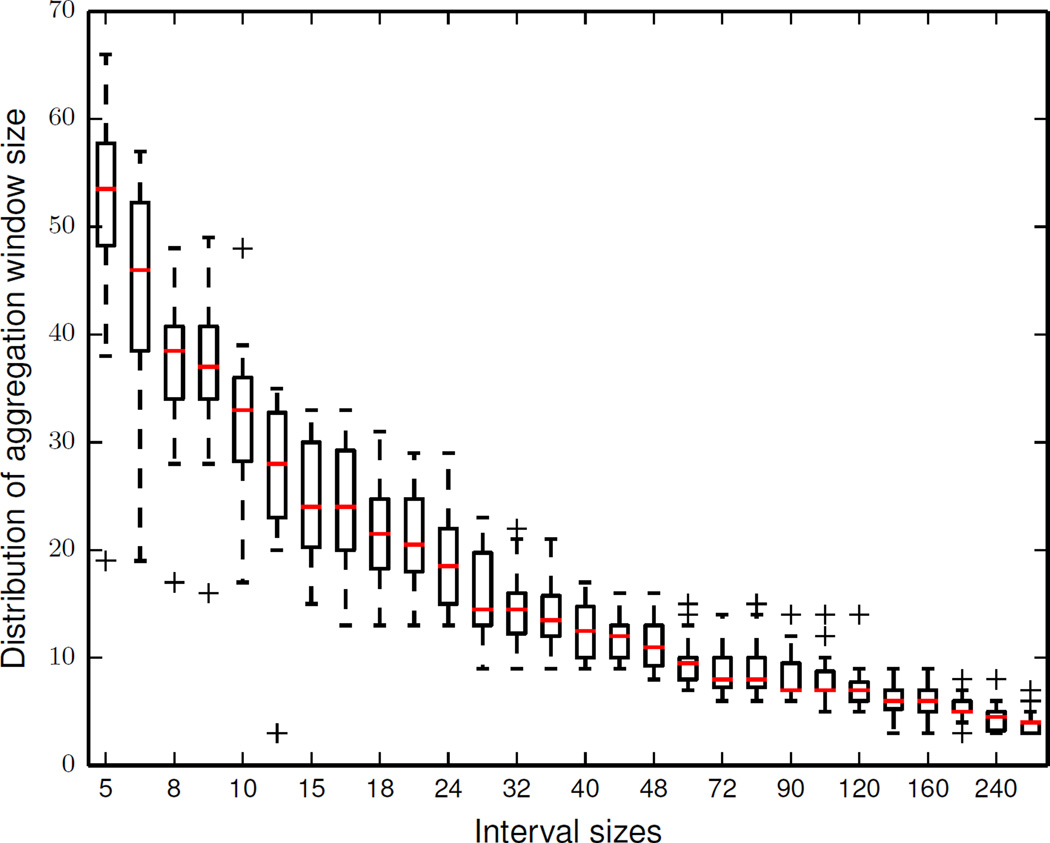
In the next experiment, we determine the minimum length of an aggregation window that is required to calculate a stable aggregated activity curve for our smart home data. Figure 9 shows the variations in the length of an aggregate window at different interval sizes calculated using all the available sensor data. We observe that the length of the aggregation window is larger for the smaller interval sizes and smaller for the larger interval sizes. We can explain such differences in length of the aggregation window based on the observations we made between average pairwise distances and interval sizes in Figure 9. At larger interval sizes, activity distributions are dominated by activities that take a long time to complete (such as sleep). Thus, the distance between two activity distributions for such activity curves are significantly lower than the distance between two activity distributions for activity curves at smaller time intervals. Hence, we obtain a stable activity curve using a smaller aggregation window size for larger interval sizes.

Figure 9.

Distribution of aggregation window size vs. interval sizes.

9.5. Change scores and correlations

In this section, we study the strength of the correlations between the changes detected in activity routines by the PCAR algorithm and the corresponding standard clinical scores (RBANS and TUG) for a smart home resident. Specifically, we calculate correlations between change scores calculated by applying PCAR on activity curves derived using activity labeled smart home sensor data and corresponding clinical scores ensuring that each pair of the smart home change score and clinical score was observed at around the same time.

Algorithm 4.

Behavior And Health Correlation(t)

1:	// t = testing time points
2:	// Return correlation coefficient
3:	Behavior Change Scores = []
4:	Clinical Change Scores = []
5:	i = 0
6:	repeat
7:	Σi = Aggregate Activity Curves At Time(ti + 3 months)
8:	Σi+1 = Aggregate Activity Curves At Time(ti+1 − 3 months)
9:	Dîst = Empirical Distribution(Σi, Σi+1, NP)
10:	S1 = PCAR (Σi, Σi+1, Dîst)
11:	S2 = Clinical Scores(ti, ti+1)
12:	Append(S1, Behavior Changes Scores)
13:	Append(S2, Clinical Changes Scores)
14:	i = i + 1
15:	until
16:	return Correlation(S1, S2)

To obtain such correlations, we first calculate aggregated activity curves for two three-month aggregation windows, W₁ and W₂. Next, we apply PCAR to these activity curves to obtain a smart home-based change score. We also obtain clinical scores measured at time points, t₁ and t₂. We repeat this step for all available pairs of consecutive testing time points for all 18 residents. Finally, we calculate Pearson correlation and Spearman rank correlation between the activity change scores and the corresponding clinical scores to evaluate the strength of the relationship. The process is summarized in Algorithm 4.

To evaluate our automated health correlation based on smart home data, we derived correlation coefficients between change scores obtained from the smart home-based activity curve model with the standard health clinical scores (TUG and RBANS scores). To conduct this experiment, we ran 1500 permutation iterations and derived change scores for both alignment techniques. We repeated the experiments for different time interval sizes.

As a baseline for comparison, we generated random change scores by randomly predicting a change between activity distributions instead of using the PCAR algorithm. Table 2 and 3 list the correlations between these two scores for different time interval sizes.

Table 2.

Pearson(r) and Spearman rank (rho) correlations between activity change scores and RBANS scores.

	Time interval change score		DTW score		Random scores
intervalsize	r-RBANS	rho-RBANS	r-RBANS	rho-RBANS	r-RBANS	rho-RBANS
5	0.00	−0.10	0.11	−0.04	0.10	0.06
6	−0.01	−0.13	0.06	−0.10	0.14	0.14
8	−0.01	−0.16	0.04	−0.08	−0.06	0.00
9	−0.03	−0.19	0.03	−0.09	0.09	0.11
10	−0.03	−0.15	−0.03	−0.13	−0.07	−0.10
12	−0.04	−0.17	−0.03	−0.13	−0.07	−0.07
15	−0.04	−0.14	−0.05	−0.16	0.11	0.26
16	−0.04	−0.13	−0.04	−0.14	−0.19	−0.19
18	−0.06	−0.18	−0.08	−0.13	0.02	0.04
20	−0.04	−0.18	−0.03	−0.12	−0.16	−0.13
24	−0.04	−0.18	−0.03	−0.16	0.05	0.04
30	−0.07	−0.20	−0.01	−0.17	−0.06	−0.11
32	−0.04	−0.20	0.01	−0.19	0.20	0.19
36	−0.04	−0.21	0.01	−0.17	0.06	0.01

Table 3.

Pearson(r) and Spearman rank (rho) correlations between activity change scores and TUG scores.

	Time interval index score		DTW score		Random scores
intervalsize	r-TUG	rho-TUG	r-TUG	rho-TUG	r-TUG	rho-TUG
5	0.27	0.28	0.27	0.43**	−0.21	−0.06
6	0.28*	0.31*	0.27	0.40**	−0.09	−0.03
8	0.32*	0.39**	0.33*	0.37*	−0.09	−0.12
9	0.31*	0.35*	0.24	0.25	−0.15	−0.06
10	0.33*	0.31*	0.29*	0.37*	0.10	0.12
12	0.35*	0.33*	0.30*	0.30*	0.18	0.15
15	0.33*	0.34*	0.31*	0.40**	0.06	−0.06
16	0.34*	0.38*	0.30*	0.35*	−0.03	−0.10
18	0.32*	0.29*	0.29*	0.27	−0.17	−0.07
20	0.32*	0.35*	0.29*	0.28*	0.19	0.12
24	0.35*	0.29*	0.31*	0.23	−0.10	−0.13
30	0.33*	0.24	0.28	0.27	−0.15	−0.15
32	0.33*	0.28*	0.28*	0.32*	−0.15	−0.13
36	0.32*	0.28*	0.28	0.31*	0.01	0.03

^*p < 0.05,

^**p < 0.005

We make the following observations:

• We obtain statistically significant correlations between activity change scores and TUG scores (Table 3)

• No correlations exist between activity change scores obtained from random predictions and TUG scores.

• No correlations exist between smart home based activity change scores and RBANS scores.

• Often, the strength of correlations at larger time interval sizes is weak because at larger time intervals activities are either dominated by sleep activity or other activity. Hence, changes in activity distributions at large time intervals are comparatively harder to detect.

9.6. Continuous change scores

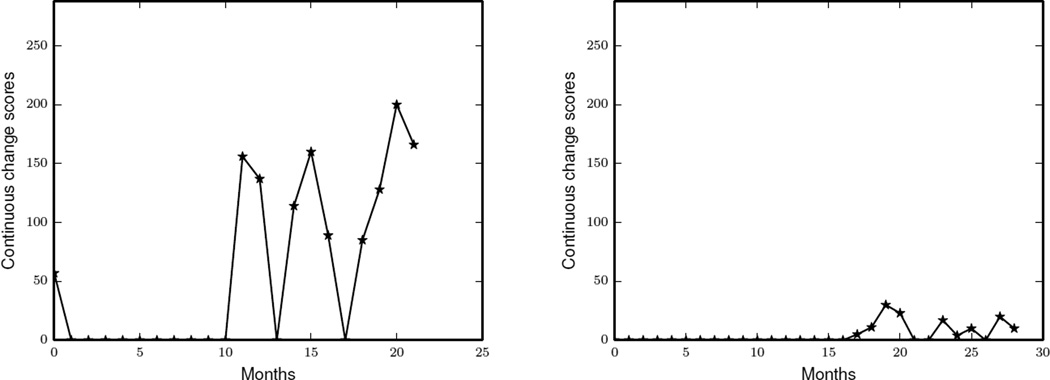
In the previous section, we predicted change scores at six month intervals to correlate the smart home-based behavior change scores with changes in standard clinical scores. We can also calculate these change scores more frequently by running the PCAR algorithm on the activity curves that lies within a sliding window of size six months and shifting this sliding window by one month (30 days). We will refer to such frequent change scores as continuous change scores. We can use continuous change scores to monitor the “performance” of a smart home resident’s everyday behavior.

Figure 10 shows how the continuous change scores of two smart home residents have varied with time. Each point in a plot represents a total change score obtained by using the PCAR algorithm to compare behavior six months prior with current behavior. First, we plot continuous change scores of a resident whose health status has declined (Figure 10). We observe that after a year, the total change score of this resident started to fluctuate. Such fluctuations indicate changes in the average daily routines of this resident. Similarly, we plot continuous change scores of another resident whose health has been in excellent condition for the entire data collection period (Figure 10). We observe that the PCAR algorithm detects very few changes in the average daily routines of this resident.

Figure 10.

The continuous change scores of two residents calculated by running PCAR algorithm on a sliding window of 6 months with an aggregation window size of 30 days.

9.7. Individual activity change

The change scores calculated in the previous sections quantify overall changes in average daily routines for the entire collection of know activities. In this experiment, we can quantify total changes in the average daily routines of some specific activities by running PCAR algorithm on a reduced activity set. The elements in this reduced activity set are activities that we want to monitor and the “other activities” class is used to represent all of the remaining activities. For example, if we want to monitor sleep and bed to toilet activities, we put three elements (sleep, bed to toilet and other) in the reduced activity set. Using this reduced set of activity, we can use PCAR to obtain continuous change scores.

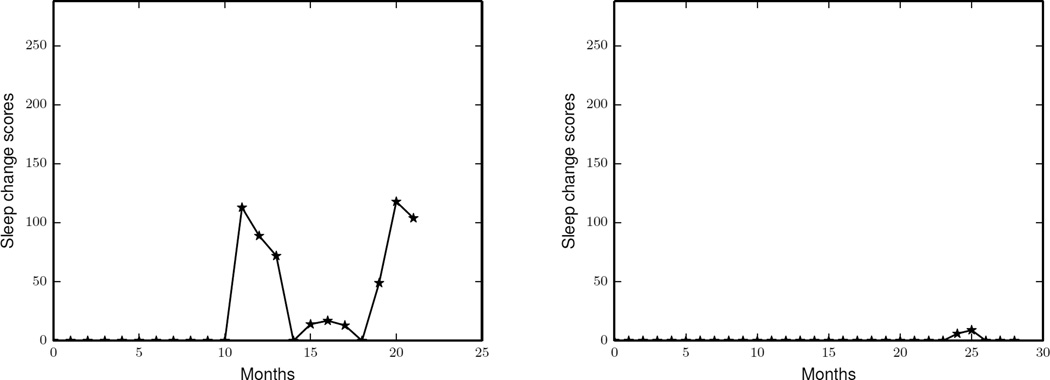
Figure 11 shows the continuous sleep change scores of the same two smart home residents for whom we studied the continuous change scores in Figure 10. We see that PCAR detected changes in the overall sleep routine of the first resident while it does not detect any sleep routine changes for the other resident.

Figure 11.

The continuous sleep change scores of two residents calculated by running PCAR algorithm on a sliding window of 6 months with an aggregation window size of x = 30 days.

9.8. Discussions

In this work, we proposed an activity curve model to represent daily activity-based behavior routines. The proposed activity curve models the activity distributions of the activities at different times of a day. Using the activity curve model, we developed the PCAR algorithm to identify and quantify changes in the activity routines. We validated our model by performing experiments using synthetic data and longitudinal smart home sensor data. PCAR is able to represent behavior patterns through big data analysis.

The current activity model considers activity distributions using different interval sizes. In our future work, we will build a hierarchical activity curve model to combine the activity distributions at different time interval sizes. Further, while performing experiments with an activity curve model, we chose a subset of activities that are considered important in daily life. In the future, we will extend our experiments to include larger pool of daily activities. We also note that the activities that did not fit into these seven predefined categories were termed “other”. We note that the “other” data is very large, complex, and represents important activities that we will add to our activity vocabulary in future work.

We developed the PCAR algorithm to quantify changes in an activity routine. PCAR makes use of a smart home sensor data of an individual collected over a period to quantify changes in the activity routine and outputs change scores. This algorithmic approach is important because activity routines vary among individuals.

9.9. Conclusion

In this paper, we studied the relationship between the output from the PCAR algorithm and the standard clinical and physical health scores. We found moderate correlations between the change scores and standard TUG scores. However, we found that the correlations between smart home-based change scores and standard cognitive scores (RBANS) were not as strong as we expected because the majority of the older adults for whom we analyzed the data are healthy older adults. We note that clinicians have frequently argued for the existence of a relationship between changes in ADL patterns and changes in the health. We want to use our idea of an activity curve to detect changes in ADL patterns which possibly can be associated with a change in cognitive and physical health conditions. Similarly, we also demonstrated methods to evaluate the “average performance” of a smart home resident by continuously monitoring changes in the overall daily routine as well as a set of specified activities.

The work described here confirms that pervasive computing methods can be used to correlate an individual’s behavior patterns and clinical assessment scores. In our future work, we will explore visualization tools for the activity curve model and we will further investigate how clinicians and caregivers can utilize the results of this method so that they can make informed decisions.