Mechanism of extracellular ion exchange and binding-site occlusion in the sodium-calcium exchanger

Abstract

Na⁺/Ca²⁺ exchangers utilize the Na⁺ electrochemical gradient across the plasma membrane to extrude intracellular Ca²⁺, and play a central role in Ca²⁺ homeostasis. Here, we elucidate their mechanisms of extracellular ion recognition and exchange through a structural analysis of the exchanger from Methanococcus jannaschii (NCX_Mj) bound to Na⁺, Ca²⁺ or Sr²⁺ in various occupancies and in an apo state. This analysis defines the binding mode and relative affinity of these ions, establishes the structural basis for the anticipated 3Na⁺:1Ca²⁺ exchange stoichiometry, and reveals the conformational changes at the onset of the alternating-access transport mechanism. An independent analysis of the dynamics and conformational free-energy landscape of NCX_Mj in different ion-occupancy states, based on enhanced-sampling molecular-dynamics simulations, demonstrates that the crystal structures reflect mechanistically relevant, interconverting conformations. These calculations also reveal the mechanism by which the outward-to-inward transition is controlled by the ion-occupancy state, thereby explaining the emergence of strictly-coupled Na⁺/Ca²⁺ antiport.

Introduction

Na⁺/Ca²⁺ exchangers (NCX) play physiologically essential roles in Ca²⁺ signaling and homeostasis^1-4. NCX catalyzes the uphill extrusion of intracellular Ca²⁺ across the cell membrane, by coupling this process to the downhill permeation of Na⁺ into the cell^5,6, with a 3 Na⁺ to 1 Ca²⁺ stoichiometry^6-11. This reaction is, however, inherently reversible, its direction being dictated only by the transmembrane electrochemical ion gradients ¹. The mechanism of NCX proteins is therefore highly likely to be consistent with the alternating-access model of secondary-active transport¹². The basic functional unit for ion transport in NCX consists of ten membrane-spanning segments^13,14, comprising two homologous halves. Each of these halves contains a highly conserved region, referred to as α-repeat, known to be important for ion binding and translocation^15,16; in eukaryotic NCX, the two halves are connected by a large intracellular regulatory domain^2,15,17,18, which is absent in microbial NCX^15,19 (Supplementary Fig. 1).

Despite a long history of physiological and functional studies, the molecular mechanism of NCX has been elusive, owing to the lack of structural information. Our recent atomic-resolution structure of NCX_Mj from Methanococcus jannaschii provided the first view of the basic functional unit of an NCX protein²⁰. This structure shows the exchanger in an outward-facing conformation and reveals four putative ion-binding sites, denominated internal (S_int), external (S_ext), Ca²⁺-binding (S_Ca) and middle (S_mid), clustered in the center of the protein and occluded from the solvent²⁰ (Fig. 1a-b). With similar ion exchange properties to those of its eukaryotic counterparts^20,21, NCX_Mj provides a compelling model system to investigate the structural basis for the specificity, stoichiometry and mechanism of the ion-exchange reaction catalyzed by NCX. In this study, we set out to determine the structures of outward-facing wild-type NCX_Mj in complex with Na⁺, Ca²⁺ and Sr²⁺, at various concentrations. These structures reveal the mode of recognition of these ions, their relative affinities, and the mechanism of extracellular ion exchange, for a well-defined, functional conformation in a membrane-like environment. An independent analysis based on molecular-dynamics simulations demonstrates that the structures capture mechanistically relevant states. These calculations also reveal how the ion occupancy state of the outward-facing exchanger determines the feasibility of the transition to the inward-facing conformation, thereby addressing a key outstanding question in secondary-active transport, namely how the transported substrates control the alternating-access mechanism.

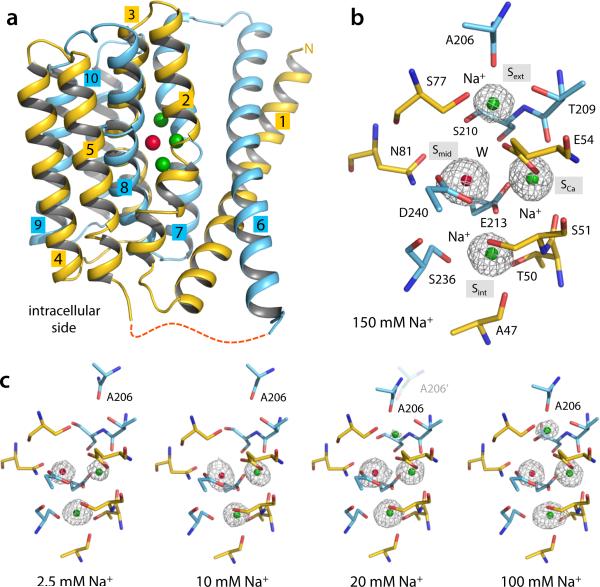
Figure 1.

Na⁺ binding to outward-facing NCX_Mj. (a) Overall structure of native outward-facing NCX_Mj from crystals grown in 150 mM Na⁺. N- and C-terminal halves are colored yellow and cyan, respectively. Colored spheres represent the bound Na⁺ (green) and water (red). (b) Structural details and definition of the four central binding sites. Only residues flanking these sites are shown for clarity (same for all other figures). The electron density (grey mesh, 1.9 Å F_o-F_c ion omit map contoured at 4σ) at S_mid was modeled as water (red sphere) and those at S_ext, S_Ca and S_int as Na⁺ ions (green spheres). Further details are shown in Supplementary Fig. 1. (c) Concentration-dependent change in Na⁺ occupancy (see also Table 1). All F_o – F_c ion-omit maps are calculated to 2.4 Å and contoured at 3σ for comparison. The displacement of A206 reflects the [Na⁺]-dependent conformational change from the partially open to the occluded state (observed at low and high Na⁺ concentrations, respectively). At 20 mM Na⁺, both conformations co-exist. No significant changes were observed in the side-chains involved in ion or water coordination at the S_Ca, S_int and S_mid sites.

Results

Extracellular Na⁺ binding

The assignment of the four central binding sites identified in the previously reported NCX_Mj structure²⁰ was hampered by the presence of both Na⁺ and Ca²⁺ in the protein crystals. To conclusively clarify this assignment, we first set out to examine the Na⁺ occupancy of these sites without Ca²⁺. Crystals were grown in 150 mM NaCl using the lipidic cubic phase (LCP) technique²⁰. The crystallization solutions around the LCP droplets were then slowly replaced by solutions containing different concentrations of NaCl and EGTA (Methods). X-ray diffraction of these soaked crystals revealed a Na⁺-dependent variation in the electron-density distribution at sites S_ext, S_Ca and S_int, indicating a Na⁺ occupancy change (Fig. 1c). Occupancy refinement indicated two Na⁺ ions bind to S_int and S_Ca at low Na⁺ concentrations (Fig. 1c), with a slight preference for S_int (Table 1). Binding of a third Na⁺ to S_ext occurs at higher concentrations, as no density was observed there at 10 mM Na⁺ or lower (Fig. 1c); S_ext is however partially occupied at 20 mM Na⁺, and fully occupied at 150 mM (Fig. 1c). The Na⁺ occupation at S_Ca, compounded with the expected 3Na⁺:1Ca²⁺ stoichiometry, implies our previous assignment of the S_mid site must be re-evaluated. Indeed, two observations indicate that a water molecule rather than a Na⁺ ion occupies S_mid, as was predicted in a recent simulation study²². First, the electron density at S_mid does not depend significantly on the Na⁺ concentration. Second, the protein coordination geometry at S_mid is clearly suboptimal for Na⁺ (Supplementary Fig. 1d). The water molecule at S_mid forms hydrogen-bonds with the highly conserved Glu54 and Glu213 (Supplementary Fig. 1d), stabilizing their orientation to properly coordinate multiple Na⁺ ions at S_ext, S_Ca and S_int. It can be inferred from this assignment that Glu54 and Glu213 are ionized, while Asp240, which flanks S_mid (and is replaced by Asn in eukaryotic NCX) would be protonated, as indicated by the abovementioned simulation study²².

Table 1.

Concentration-dependent Na⁺ occupancy of outward-facing NCX_Mj

Sites \ [Na+]	2.5 mM	10 mM	20 mM	100 mM	150 mM
Sint	0.84	0.92	0.99	0.96	1.00
SCa	0.75	0.87	0.97	1.00	1.00
Sext	-	-	0.59	0.79	0.93
Total	1.58	1.79	2.55	2.75	2.93
Conformation	Partially open	Partially open	Mixed	Occluded	Occluded

Na⁺-dependent conformational change

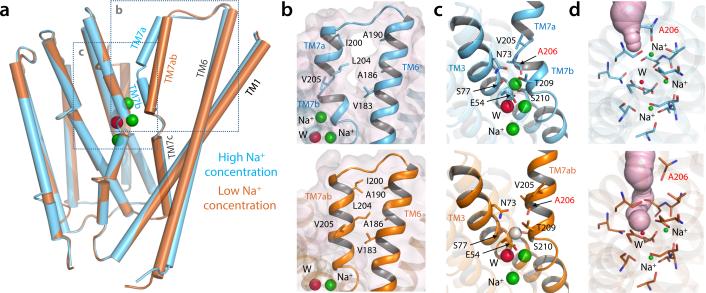
The NCX_Mj structures in various Na⁺ concentrations also reveal that Na⁺ binding to S_ext is coupled to a subtle but important conformational change (Fig. 2). When Na⁺ binds to S_ext at high concentrations, the N-terminal half of TM7 is bent into two short helices, TM7a and TM7b (Fig. 2a). TM7b occludes the four central binding sites from the external solution, with the backbone carbonyl of Ala206 coordinating the Na⁺ ion (Fig. 2b-d). However, when S_ext becomes empty at low Na⁺ concentrations, TM7a and TM7b become a continuous straight helix (Fig. 2a), and the carbonyl group of Ala206 retracts away (Fig. 2b-d). TM7a also forms hydrophobic contacts with the C-terminal half of TM6. These contacts are absent in the structure with Na⁺ at S_ext, in which there is an open gap between the two helices (Fig. 2b). This difference is noteworthy because TM6 and TM1 are believed to undergo a sliding motion, relative to the rest of the protein, when the transporter switches to the inward-facing conformation²⁰. The straightening of TM7ab also opens up a passageway from the external solution to S_ext and S_mid, while S_Ca and S_int remain occluded (Fig. 2d). Thus, the structures at high and low Na⁺ concentrations represent the outward-facing occluded and partially open states, respectively. This conformational change is dependent on the Na⁺ occupancy of S_ext and occurs when Na⁺ already occupies S_int and S_Ca. Our crystallographic titration experiment indicates that the K_1/2 of this Na⁺-driven conformational transition is ~20 mM. At this concentration, S_ext is partially occupied and the NCX_Mj crystal is a mixture of both the occluded and partially open conformations. This structurally-derived Na⁺ affinity agrees well with the external Na⁺ concentration required for NCX activation in eukaryotes¹. The finding that the Na⁺ occupancy change from 2 to 3 ions coincides with a conformational change of the transporter also provides a rationale to the Hill coefficient of the Na⁺-dependent activation process in eukaryotic NCX^1,7,8,11.

Figure 2.

Na⁺-occupancy dependent conformational change in NCX_Mj. (a) Superimposition of the NCX_Mj crystal structures obtained in high (100 mM, cyan cylinders) and low (10 mM, brown cylinders) Na⁺ concentrations. (b) Close-up view of the interface between TM6 and TM7ab in the NCX_Mj structures obtained at high and low Na⁺ concentrations (top and lower panels, respectively). Residues forming van-der-Waals contacts in the structure at low Na⁺ concentration are shown in detail. (c) Close-up view of the Na⁺-binding sites. The vacant S_ext site in the structure at low Na⁺ concentration is indicated with a white sphere. Residues surrounding this site are also indicated; note A206 (labeled in red) coordinates Na⁺ at S_ext via its backbone carbonyl oxygen. (d) Extracellular solvent accessibility of the ion binding sites in the structures at high and low [Na⁺]. Putative solvent channels are represented as light-purple surfaces.

Extracellular Ca²⁺ and Sr²⁺ binding and their competition with Na⁺

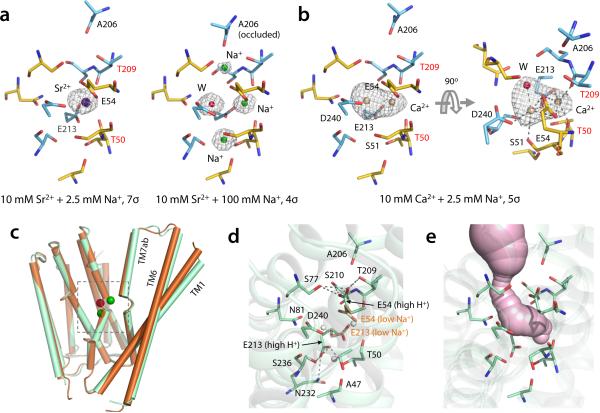
To determine how Ca²⁺ binds to NCX_Mj and competes with Na⁺, we first titrated the crystals with Sr²⁺ (Methods). Sr²⁺ is transported by NCX similarly to Ca^{2+ 23,24}, and is distinguishable from Na⁺ by its greater electron-density intensity. Protein crystals soaked with 10 mM Sr²⁺ and 2.5 mM Na⁺ revealed a strong electron-density peak at site S_Ca, indicating binding of a single Sr²⁺ ion (Fig. 3a). The Sr²⁺-loaded NCX_Mj structure adopts the partially open conformation observed at low Na⁺ concentrations. Binding of Sr²⁺, however, excludes Na⁺ entirely. Crystal titrations with decreasing Sr²⁺ or increasing Na⁺ demonstrated that Sr²⁺ binds to the outward-facing NCX_Mj with low affinity, and that it can be out-competed by Na⁺ even at low concentrations (Supplementary Note 1 and Supplementary Fig. 2a-b). Thus, in 100 mM Na⁺ and 10 mM Sr²⁺, Na⁺ completely replaced Sr²⁺ (Fig. 3a) and reverted NCX_Mj to the Na⁺-loaded, fully occluded state.

Figure 3.

Divalent cation binding and apo structure of NCX_Mj. (a) A single Sr²⁺ (dark blue sphere) binds at S_Ca in crystals titrated with 10 mM Sr²⁺ and 2.5 mM Na⁺ (see also Supplementary Fig. 2). Residues involved in Sr²⁺ coordination are labeled. There are no significant changes in the side-chains involved in ion coordination, relative to the Na⁺-bound state. T50 and T209 (labeled in red) coordinate Sr²⁺ through their backbone carbonyl-oxygen atoms. High Na⁺ concentration (100 mM) completely displaces Sr²⁺ and reverts NCX_Mj to the occluded state (right panel). The contour level of the F_o – F_c omit map of the structure at high Na⁺ concentration was lowered (to 4σ) so as to visualize the density from Na⁺ ions and H₂O. (b) Ca²⁺ (tanned spheres) binds either to S_Ca or S_mid in crystals titrated with 10 mM Ca²⁺ and 2.5 mM Na⁺ (see also Supplementary Fig. 2). The relative occupancies are 55% and 45%, respectively. (c) Superimposition of NCX_Mj structures obtained at low Na⁺ concentration (10 mM) and pH 6.5 (brown) and in the absence of Na⁺ and pH 4 (light green), referred to as apo state. (d) Close-up view of the ion-binding sites in the apo (or high H⁺) state. The side chains of E54 and E213 from the low Na⁺ structure are also shown (light brown) for comparison. White spheres indicate the location S_int, S_mid S_Ca. (e) Extracellular solvent accessibility of the ion-binding sites in apo NCX_Mj.

Similar titration experiments showed that Ca²⁺ and Sr²⁺ binding to NCX_Mj are not exactly alike The electron density distribution from crystals soaked in high Ca²⁺ and low Na⁺, indicates that Ca²⁺ can bind to S_mid as well as S_Ca, with a preference for S_Ca (Fig. 3b). Binding of Ca²⁺ to both sites simultaneously is highly improbable due to their close proximity, and at least one water molecule can be discerned coordinating the ion (Fig. 3b). The partial Ca²⁺ occupancy at S_mid is likely caused by Asp240, which flanks this site and can in principle coordinate Ca²⁺. Previous functional and computational studies, however, indicate Asp240 becomes protonated during transport²². Indeed, in most NCX proteins Asp240 is substituted by Asn, which would likely weaken or abrogate Ca²⁺ binding to S_mid. S_Ca is therefore the functional Ca²⁺ site. Similarly to Sr²⁺, Ca²⁺ binds with low affinity to outward-facing NCX_Mj and can be readily displaced by Na⁺ (Supplementary Note 1 and Supplementary Fig. 2c). This finding is consistent with physiological and biochemical data for both eukaryotic NCX and NCX_Mj indicating that the apparent Ca²⁺ affinity is much lower on the extracellular than the cytoplasmic side^21,23,25-27. Specifically, our crystallographic titration assay indicates Ca²⁺ binds with sub-millimolar affinity, in good agreement with the external apparent Ca²⁺ affinities deduced functionally for cardiac NCX (K_m ~ 0.32 mM)²⁶ and NCX_Mj (K_m ~ 0.175 mM).²¹

Taken together, these crystal titration experiments demonstrate that the four binding sites in outward-facing NCX_Mj exhibit different specificity: S_int and S_ext are Na⁺ specific whereas S_Ca, previously hypothesized to be Ca²⁺ specific²⁰, can also bind Na⁺, confirming our earlier simulation study²², as well as Sr²⁺; S_mid can also transiently accommodate Ca²⁺ but during transport S_mid is most likely occupied by water. The ion-binding sites in NCX_Mj can therefore accommodate up to three Na⁺ ions or a single divalent ion, and occupancy by Na⁺ and Ca²⁺ (or Sr²⁺) are mutually exclusive, as was deduced for eukaryotic exchangers¹.

A structure of NCX_Mj without Na⁺ or Ca²⁺ bound

An apo state of outward-facing NCX_Mj is likely to exist transiently in physiological conditions, despite the high amounts of extracellular Na⁺ (~150 mM) and Ca²⁺ (~2 mM). We were able to determine an apo-state structure of NCX_Mj, by crystallizing the protein at lower pH and in the absence of Na⁺ (Methods). This structure is similar to the partially open structure with two Na⁺ or either one Ca²⁺ or one Sr²⁺ ion, with two noticeable differences. First, TM7ab along with the extracellular half of the TM6 and TM1 swing further away from the protein core (Fig. 3c), resulting in a slightly wider passageway into the binding sites. Second, Glu54 and Glu213 side chains rotate away from the binding sites and appear to form hydrogen-bonds with residues involved in ion coordination in the fully Na⁺-loaded structure (Fig. 3d). Although the binding sites are thus fully accessible to the external solution (Fig. 3e), the lack of electron density therein indicates no ions or ordered solvent molecules. This apo structure might therefore represent the unloaded, open state of outward-facing NCX_Mj. Alternatively, this structure might capture a fully protonated state of the transporter, to which Na⁺ and Ca²⁺ cannot bind. Such interpretation would be consistent with the computer simulations reported below. Indeed, transport assays of NCX_Mj have shown that even in the presence of Na⁺ or Ca²⁺, low pH inactivates the transport cycle²².

Ion occupancy determines the free-energy landscape of NCX_Mj

That secondary-active transporters are able to harness an electrochemical gradient of one substrate to power the uphill transport of another relies on a seemingly simple principle: they must not transition between outward- and inward-open conformations unless in two precise substrate occupancy states. NCX must be loaded either with 3 Na⁺ or 1 Ca²⁺, and therefore functions as an antiporter; symporters, by contrast, undergo the alternating-access transition only when all substrates and coupling ions are concurrently bound, or in the apo state. The reason why only specific occupancy states permit this transition in a given system, thereby determining its biological function, remains unclear. To examine this central question, we sought to characterize the conformational free-energy landscape of NCX_Mj and to examine its dependence on the ion-occupancy state, using molecular dynamics (MD) simulations. This computational analysis was based solely on the published structure of NCX_Mj²⁰, independently of the crystallographic studies described above. As it happens, the results confirm that the structures now available are representing interconverting states of the functional cycle of NCX_Mj, while revealing how the alternating-access mechanism is controlled by the ion-occupancy state.

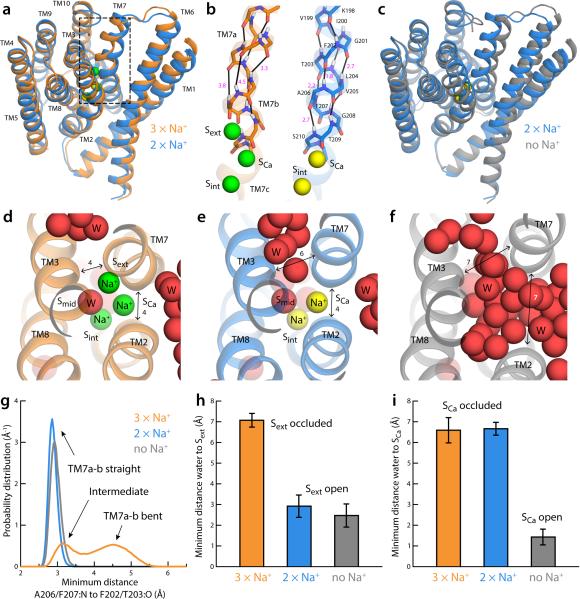
A series of exploratory MD simulations was initially carried out to examine what features of the NCX_Mj structure might depend on the ion-binding sites occupancy. Specifically, we first simulated the outward-occluded form, in the ion configuration we previously predicted²², now confirmed by the high-Na⁺ crystal structure described above (Fig. 1b). That is, Na⁺ ions occupy S_ext, S_Ca, and S_int, while D240 is protonated and a water molecule occupies S_mid. The Na⁺ ion at S_ext was then relocated from the site to the bulk solution (Methods), and this system was then allowed to evolve freely in time. The Na⁺ ions at S_Ca and S_int were displaced subsequently, and an analogous simulation was then carried out. These initial simulations revealed noticeable changes in the transporter, consistent with those observed in the new crystal structures. The most notable change upon displacement of Na⁺ from S_ext was the straightening of TM7ab (Fig. 4a). When 3 Na⁺ ions are bound, TM7ab primarily folds as two distinct, non-collinear α-helical fragments, owing to the loss of the backbone carbonyl-amide hydrogen-bonds between F202 and A206, and T203 and F207 (Fig. 4b). This distortion occludes S_ext from the exterior (Fig. 4d, 4h-i) and appears to be induced by the Na⁺ ion itself, which pulls the carbonyl group of A206 into its coordination sphere (Fig. 4g). With S_ext empty, however, TM7ab forms a canonical α-helix (Fig. 4a-b, 4g), thereby creating an opening between TM3 and TM7, which in turn allows water molecules from the external solution to reach into S_ext (Fig. 4e, 4h-i), i.e. the transporter is no longer occluded. Displacement of Na⁺ from S_Ca and S_int induces further changes (Fig. 4c). The most noticeable is an increased separation between TM7 and TM2 (Fig. 4f), previously brought together by concurrent backbone interactions with the Na⁺ ion at S_Ca (Fig. 4d-e). TM1 and TM6 also slide further towards the membrane center, relative to the outward-occluded state (Fig. 4c). Together, these changes open a second aqueous channel leading directly into S_Ca and S_int (Fig. 4f, Fig. 4h-i). The transporter thus becomes fully outward-open.

Figure 4.

Spontaneous changes in the structure of outward-occluded, fully Na⁺-occupied NCX_Mj (PDB code 3V5U²⁰) upon sequential displacement of Na⁺. (a) Representative simulation snapshots of NCX_Mj (Methods) with Na⁺ bound at S_ext, S_Ca and S_int (orange cartoons, green spheres) and with Na⁺ bound only at S_Ca and S_int (marine cartoons, yellow spheres) (b) Close-up of the backbone of the N-terminal half of TM7 (TM7ab), in the same Na⁺ occupancy states depicted in (a). Black lines indicate (i, i + 4) carbonyl-amide pairs along the helix; specific O-N distances are indicated, in Å (magenta). (c) Representative simulation snapshots (same as above) with Na⁺ bound at S_Ca and S_int (marine cartoons, yellow spheres) and without any Na⁺ bound (grey cartoons). (d) Close-up of the ion-binding region in the fully Na⁺-occupied state. Approximate distances between TM2, TM3 and TM7 are indicated in Å. (e) Close-up of the ion-binding region in the partially Na⁺-occupied state. (f) Close-up of the ion-binding region in the Na⁺-free state. (g-i) Analytical descriptors of the changes just described, calculated from the simulations of each Na⁺-occupancy state depicted in panels (a-f). These descriptors were employed as collective variables in the Bias-Exchange Metadynamics simulations (Methods). (g) Probability distributions of an analytical descriptor of the backbone hydrogen-bonding pattern in TM7ab (Eq. 2). (h) Mean value (with standard deviation) of a quantitative descriptor of the solvent accessibility of the S_ext site (Eq. 1). (i) Mean value (with standard deviation) of a quantitative descriptor of the solvent accessibility of the S_Ca site (Eq. 1).

To more rigorously characterize the influence of the ion-occupancy state on the conformational dynamics of the exchanger, we carried out a series of enhanced-sampling MD calculations designed to reversibly simulate the transition between the outward-occluded and fully outward-open states, and thus quantify the free-energy landscape encompassing these states (Methods). As above, we initially examined three occupancy states, namely with Na⁺ in S_ext, S_Ca and S_int, with Na⁺ only at S_Ca and S_int, and without Na⁺.

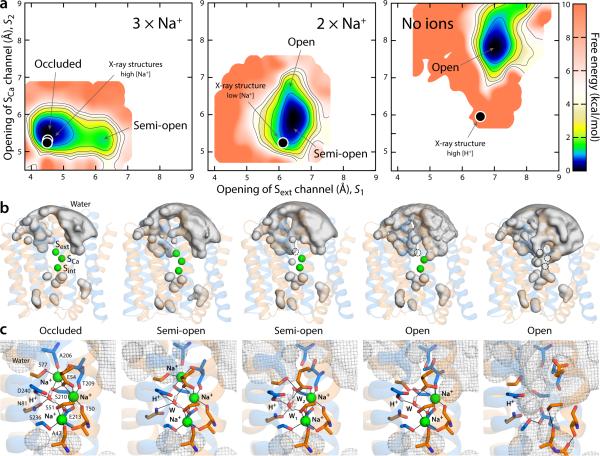
These calculations demonstrate that the Na⁺ occupancy state of the transporter has a profound effect on its conformational free-energy landscape. When all Na⁺ sites are occupied, the global free-energy minimum corresponds to a conformation in which the ions are maximally coordinated by the protein (Fig. 5a, 5c); TM7ab is bent and packs closely with TM2 and TM3, and so the binding sites are occluded from the solvent (Fig. 5b). At a small energetic cost, however, the transporter can adopt a metastable ‘half-open’ conformation in which TM7ab is completely straight and S_ext is open to the exterior (Fig. 5a, 5b). The Na⁺ ion at S_ext remains fully coordinated, but an ordered water molecule now mediates its interaction with A206:O, relieving the strain on the F202:O–A206:N hydrogen-bond (Fig. 5c). This semi-open conformation is nearly identical to that found to be the most probable when Na⁺ occupies only S_Ca and S_int (2 × Na⁺, Fig. 5a), demonstrating that binding (or release) of Na⁺ to S_ext occurs in this metastable conformation. Interestingly, this doubly occupied state can also access conformations in which the second aqueous channel mentioned above, i.e. leading to S_Ca between TM7 and TM2 and over the gating helices TM1 and TM6, also becomes open (Fig. 5b-c). Crucially, though, the free-energy landscape for this partially occupied state demonstrates that the occluded conformation is no longer energetically feasible (Fig. 5a). Displacement of the two remaining Na⁺ ions from S_Ca and S_int further reshapes the free-energy landscape of the transporter (No ions, Fig. 5a), which now can only adopt a fully open state featuring the two aqueous channels (Fig. 5b-c). The transition to the occluded state in this apo state is again energetically unfeasible.

Figure 5.

Thermodynamic basis for the proposed mechanism of substrate control of the alternating-access transition of NCX. (a) Calculated conformational free-energy landscapes for outward-facing NCX_Mj, for two different Na⁺-occupancy states, and for a state with no ions bound. The free energy is plotted as a function of two coordinates, each describing the degree of opening of the aqueous channels leading to the S_ext and S_Ca sites, respectively (see Methods). Contours correspond to 1 kcal/mol intervals. Black circles map the X-ray structures of NCX_Mj obtained at high and low Na⁺ concentration, as well as that at low pH, reported in this study. (b) Density isosurfaces for water molecules within 12 Å of the ion-binding region (grey volumes), for each of the major conformational free-energy minima in each ion-occupancy state. Na⁺ ions are shown as green spheres. The two inverted-topology repeats in the transporter structure (transparent cartoons) are colored differently (TM1-5, orange; TM6-10, marine). (c) Close-up views of the ion-binding region in the same conformational free-energy minima. Key residues involved in Na⁺ and water coordination (W) are highlighted (sticks, black lines). The water-density maps in (b) is shown here as a grey mesh. Note D240 is protonated, while E54 and E213 are ionized²².

From a mechanistic standpoint, it is satisfying to observe how the open and semi-open states are each compatible with two different Na⁺ occupancies, explaining how sequential Na⁺ binding to energetically accessible conformations (prior to those binding events) progressively reshape the free-energy landscape of the transporter; by contrast, the occluded conformation is forbidden unless the Na⁺ occupancy is complete. This processivity is logical since three Na⁺ ions are involved, but also implies that in the Ca²⁺-bound state, which includes a single ion, the transporter ought to be able to access all three major conformations, i.e. the outward-open state, in order to release (or re-bind) Ca²⁺, but also the occluded conformation, and thus the semi-open intermediate, in order to transition to the inward-open state. By contrast, occupancy by H⁺, which as mentioned are not transported, might be compatible with a semi-open state as well as with the fully open conformation, but should not be conducive to occlusion.

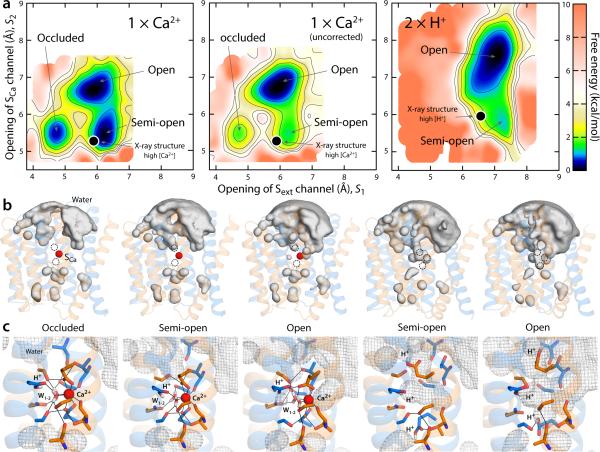
To assess this hypothesis, we carried out enhanced-sampling simulations for the Ca²⁺ and H⁺-bound states of outward-facing NCX_Mj analogous to those described above for Na⁺ (see Supplementary Note 2 and Supplementary Fig. 3-4 for details on how the structures of the Ca²⁺-bound state was predicted). The calculated free-energy landscape for Ca²⁺-bound NCX_Mj confirms the hypothesis outlined above (1 × Ca²⁺, Fig. 6a): consistent with the fact that NCX_Mj transports a single Ca²⁺, the occluded, dehydrated conformation is one of the major energetic minima, but clearly the exchanger can also adopt the semi-open and open states that would be required for Ca²⁺ release and Na⁺ entry, via either of the aqueous access channels that lead to S_ext and S_Ca (Fig. 6b-c). By contrast, protonation of Glu54 and Glu213 makes the occluded conformation energetically unfeasible, consistent with the fact that NCX_Mj does not transport protons; in this H⁺-bound state, though, the exchanger can adopt the semi-open conformation captured in the low pH, apo crystal structure (2 × H⁺, Fig. 6a-c).

Figure 6.

Thermodynamic basis for the proposed mechanism of substrate control of the alternating-access transition of NCX. (a) Calculated free-energy landscapes for outward-facing NCX_Mj, for the Ca²⁺ and the fully protonated state. The free energy is plotted as in Fig. 5. For Ca²⁺, a map is shown in which a correction for the charge-transfer between the ion and the protein is introduced, alongside the uncorrected map (see Supplementary Notes 3-4 and Supplementary Fig. 5-6). The uncorrected map overstabilizes the open state relative to the semi-open and occluded because it also overestimates the cost of dehydration of the ion, once it is bound to the protein (this effect is negligible for Na⁺). Black circles map the crystal structures obtained at high Ca²⁺ concentration and at low pH (or high H⁺) reported in this study. (b) Water-density isosurfaces analogous to those in Fig. 5 are shown for each of the major conformational free-energy minima in the free-energy maps. The Ca²⁺ ion is shown as a red sphere; the protein is shown as in Fig. 5. (c) Close-up views of the ion-binding region in the same conformational free-energy minima. Key residues involved in Ca²⁺ and water coordination (W) are highlighted (sticks, black lines). The water-density maps in (b) are shown here as a grey mesh. In the occluded state with Ca²⁺ bound, helix TM7ab bends in the same way as in the fully occupied Na⁺ state, as the carbonyl of Ala206 forms a hydrogen-bonding interaction with Ser210.

Taken together, this systematic computational analysis of outward-facing NCX_Mj clearly demonstrates that the alternating-access and ion-recognition mechanisms in this Na⁺/Ca²⁺ exchanger are coupled through the influence that the bound ions have on the free-energy landscape of the protein, which in turn determines whether or not the occluded conformation is energetically feasible. This occluded conformation, which is a necessary intermediate between the outward and inward-open states, and which entails the internal dehydration of the protein, is only attainable upon complete occupancy of the binding sites.

Discussion

The alternating-access hypothesis implicitly dictates that the switch between outward- and inward-open conformations of a given secondary-active transporter must not occur unless the appropriate type and number of substrates are recognized. This control mechanism is functionally crucial, as it precludes the backflow of the species that is transported uphill, and also prevents the dissipation of the driving electrochemical gradients. It is however also non-trivial: antiporters, for example, do not undergo the alternating-access transition without a cargo, but this is precisely how membrane symporters reset their transport cycles. Similarly puzzling is that a given antiporter will undergo this transition upon recognition of substrates of different charge, size and number. Yet, when multiple species are to be co-translocated, by either an antiporter or a symporter, partial occupancies must not be conducive to the alternating-access switch. Here, we have provided novel insights into this intriguing mechanism of conformational control through structural studies and quantitative molecular simulations of a Na⁺/Ca²⁺ exchanger.

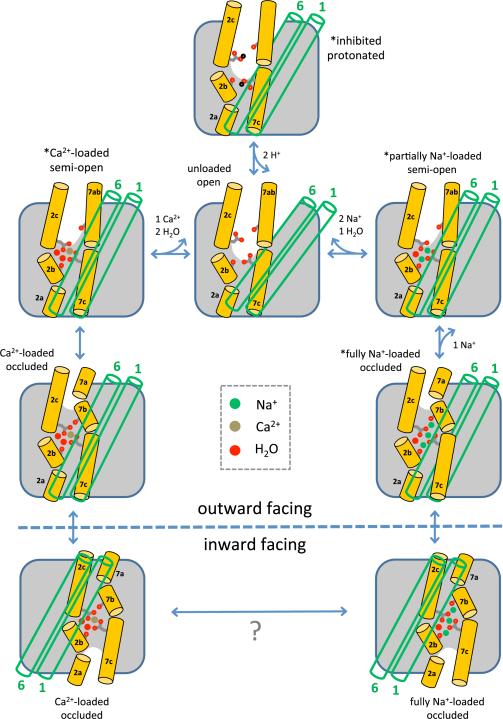
Specifically, our studies of NCX_Mj reveal the mechanism of forward ion exchange (Fig. 7). The internal symmetry of outward-facing NCX_Mj and the inward-facing crystal structures of several Ca²⁺/H⁺ exchangers^20,28-30 indicate that the alternating-access mechanism of NCX proteins entails a sliding motion of TM1 and TM6 relative to the rest of the transporter. Here, we demonstrate that conformational changes in the extracellular region of the TM2-TM3 and TM7-TM8 bundle precede and are necessary for the transition, and are associated with ion recognition and/or release. The most apparent of these changes involves the N-terminal half of TM7 (TM7ab); together with more subtle displacements in TM2 and TM3, this change in TM7ab correlates with the opening and closing of two distinct aqueous channels leading into the ion-binding sites from the extracellular solution. Interestingly, the bending of TM7 associated with the occlusion of the ion-binding sites also unlocks its interaction with TM6, and thus enables TM6 and TM1 to freely slide to the inward-facing conformation. We anticipate that the intracellular ion-exchange process involves analogous conformational changes.

Figure 7.

Structural mechanism of extracellular forward ion exchange in NCX. The carbonyl groups of Ala47 (on TM2b) and Ala206 (on TM7b), and the side chains of Glu54 (on TM2c) and Glu213 (on TM7c) are highlighted; these are four of the key residues for ion chelation and conformational changes. The green open cylinders represent the gating helices TM1 and TM6. Asterisks mark the states whose crystal structures have been determined in this study. These states and their connectivity can also be deduced from the calculated free-energy landscapes, which also reveal a Ca²⁺-loaded outward-facing occluded state, and an unloaded, fully open state.

The crystal structures of NCX_Mj reported here, with either Na⁺, Ca²⁺, Sr²⁺ or H⁺ bound, capture the exchanger in different conformational states. These states can only represent a subset among all possible, but they ought to reflect inherent preferences of the transporter, modulated by the experimental conditions. For example, in the crystal of NCX_Mj in LCP, the extracellular half of the gating helices (TM6 and TM1) form a lattice contact, which might ultimately restrict the degree of opening of the ion-binding sites in some cases (e.g. in the apo, low pH structure). Nonetheless, the calculated free-energy landscapes, derived without knowledge of the experimental data, reassuringly confirm that the crystallized structures correspond to mechanistically relevant, interconverting states. The simulations also demonstrate how this landscape is drastically re-shaped upon each ion-binding event. Indeed, we show that it is the presence or absence of the occluded state in this landscape that explains the antiport function of NCX_Mj and its 3Na⁺:1Ca²⁺ stoichiometry. We posit that a similar principle might govern the alternating-access mechanism in other transporters; that is, we anticipate that for both symporters and antiporters, it is the feasibility of the occluded state, encoded in the protein conformational free-energy landscape and its dependence on substrate binding, that ultimately explains their specific coupling mechanisms.

In multiple ways, our findings provide an explanation for, existing functional, biochemical and biophysical data for both NCX_Mj and its eukaryotic homologues. The striking quantitative agreement between the ion-binding affinities inferred from our crystallographic titrations and the K_m and K_1/2 values previously deduced from functional assays has been discussed above. Consistent with that finding, mutations that have been shown to inactivate or diminish the transport activity of NCX_Mj and cardiac NCX^16,31-34 perfectly map to the first ion-coordination shell in our NCX_Mj structures (Supplementary Fig. 4c-d). The crystallographic data also provides the long-sought structural basis for the ‘two-site’ model proposed to describe competitive cation binding in eukaryotic NCX^8,35, underscoring the relevance of these studies of NCX_Mj as a prototypical Na⁺/Ca²⁺ exchanger. Specifically, our crystal titrations suggest that, during forward Na⁺/Ca²⁺ exchange, sites S_int and S_Ca, which Ca²⁺ and Na⁺ compete for, can be grouped into one; Na⁺ binding to these sites does not require high Na⁺ concentrations, and two Na⁺ ions along with a water molecule (at S_mid) are sufficient to displace Ca²⁺, explaining the Hill coefficient of ~2 for Na⁺-dependent inhibition of Ca²⁺ fluxes³⁵. The S_ext site, by contrast, might be thought as an activation site for inward Na⁺ translocation, since this is where the third Na⁺ ion binds at high Na⁺ concentration, enabling the transition to the occluded state. Interestingly, binding of Ca²⁺ to S_mid appears to be also possible, but available evidence indicates that this event transiently blocks the exchange cycle²². Indeed, structures of NCX_Mj bound to Cd²⁺ or Mn²⁺, both of which inhibit transport, show these ions at S_mid²⁰; by contrast, Sr²⁺ binds only to S_Ca, and accordingly, is transported by NCX similarly to calcium^23,24.

Lastly, our theory that occlusion of NCX_Mj is selectively induced upon Ca²⁺ or Na⁺ recognition is consonant with a recent analysis of the rate of hydrogen-deuterium exchange (HDX) in NCX_Mj, in the presence or absence of these ions³¹, in conditions that favor outward-facing conformations^20,21. Specifically, saturating amounts of Ca²⁺ or Na⁺ resulted in a noticeable slowdown in the HDX rate for extracellular portions of the α-repeat helices. We interpret these observations as reflecting that the solvent accessibility of the protein interior is diminished upon ion recognition, consistent with our finding that opening and closing of extracellular aqueous pathways to the ion-binding sites depend on ion occupancy state. In addition, the increased compactness of the protein tertiary structure in the occluded state would also slow down the dynamics of the secondary-structure elements, and thus further reduce the HDX rate. Our data would also explain the observation that the reduction in the HDX rate is comparable for Na⁺ and Ca²⁺, as well as the finding that the degree of deuterium incorporation remains non-negligible even under saturating ion concentrations. As the calculated free-energy landscapes show, Na⁺ and Ca²⁺ induce the occlusion of the transporter in a comparable manner, and yet the ion-bound states retain the ability to explore conformations that are partially or fully open to the extracellular solution, precisely so as to be able to unload and re-load the substrates.

Methods

Protein expression, purification and crystallization

NCX_Mj was expressed, purified and crystallized as previously described²⁰. Briefly, the NCX_Mj gene with a C-terminal hexa-histidine tag was subcloned into the pQE60 vector and expressed in Escherichia coli BL21(DE3)plysS. Harvested cells were homogenized and incubated in buffer containing 50 mM HEPES pH 7.2, 50 mM NaCl, 12 mM KCl, 10 mM CaCl2, 40 mM DDM. After incubation at room temperature (RT) for 3.5 hours, the supernatant was collected by centrifugation and loaded onto a Talon Co²⁺ affinity column (Clontech). The non-specifically bound contaminates on the column were washed with buffer containing 50 mM HEPES pH 7.2, 50 mM NaCl, 12 mM KCl, 10 mM CaCl2, 15 mM imidazole, and 1 mM DDM. The bound NCX_Mj was eluted by increasing the imidazole concentration to 300 mM. The eluate was treated with thrombin to remove the hexa-histidine tag and dialyzed against 20 mM HEPES pH 7.2, 50 mM NaCl, 12 mM KCl, 10 mM CaCl₂, and 1 mM DDM at RT overnight. After overnight digestion the sample was loaded onto a second Co²⁺ affinity column to remove any free hexa-histidine tag and contaminant proteins. NCX_Mj in the flow-through was collected and further purified by gel filtration using a Superdex-200 (10/300) column (GE Healthcare) in 20 mM HEPES pH 7.2, 50 mM NaCl, 12 mM KCl, 10 mM CaCl₂ and 0.5 mM DDM. The purified protein was then concentrated to 40 mg/ml for crystallization.

Native NCX_Mj was crystallized using the lipidic cubic phase (LCP) technique, as previously described^20,36. Concentrated NCX_Mj was first reconstituted into 1-oleoyl-rac-glycerol (Sigma) in a protein:lipid weight ratio of 1:1.5, using the two-syringe method³⁶. Protein-laden LCP droplets of 35 nL were dispensed onto Corning 96-well protein-crystallization plates and overlaid with 5 μL of precipitant solution containing 40-42% PEG 400, 100 mM MES pH 6.5, 100 mM NaAc. Crystals were observed after 48 hours and grew to full size after 2 weeks. The native crystals belong to space group P2₁2₁2₁ with a cell dimension of a=49.5Å, b=72.9Å and c=96.2Å, and contain one subunit per asymmetric unit. As the LCP droplet accounts for less than 1% of the total crystallization volume, the salt composition in the crystallization condition was determined mainly by the overlaying solution, and estimated to have 150 mM Na⁺ (from MES buffer and NaAc) and 30 μM Ca²⁺ (from LCP droplet). In these concentration conditions (high Na⁺ and low Ca²⁺) Ca²⁺ does not bind to NCX_Mj (as shown in our crystallographic titration experiments) and thus this native crystal structure represents NCX_Mj in 150 mM Na⁺. The native crystals were used in all subsequent titration experiments to define low-Na⁺, Ca²⁺ and Sr²⁺-loaded structures.

To obtain the apo crystal form, the protein was first purified in a solution containing 20 mM Hepes-Tris pH 7.2, 100 mM NMDG, 10 mM CaCl₂ and 0.5 mM DDM. The crystals were obtained in LCP with crystallization solution containing 200 mM KAc, pH 4.0, 35% PEG400. The apo NCX_Mj crystals belong to space group C2 with a cell dimension of a=164.2Å, b=46.8Å, c=97.0 Å and β=106.2°, and contain two protein subunits per asymmetric unit.

Crystal titrations

Once the native crystals reached their full size, the crystallization solutions overlaying lipid/protein droplets were gradually replaced by titration solutions through multiple steps of solution exchange. In general, 2-3 μL of existing crystallization solutions (normally in 5 μL) were replaced by the same volume of titration solutions, followed by overnight equilibration. The same procedures were repeated 6-10 times until the ion components in the crystal drops reached the targeted concentrations. For titration experiments to define concentration-dependent Na⁺ binding, the titration solutions contained 100 mM MES-Tris pH 6.5, 44% PEG400, 10 mM EGTA and a 100 mM mixture of NaAc and CsAc, in the following proportions: 100 mM CsAc; 90 mM CsAc and 10 mM NaAc; 80 mM CsAc and 20 mM NaAc; and 100 mM NaAc. Note that Cs⁺ does not bind NCX proteins and is commonly used as a Na⁺ substituent to maintain the ionic strength of the solutions. As complete removal of Na⁺ would deteriorate the crystals, we had to maintain a minimum Na⁺ concentration of about 2.5 mM in the crystal drops. The final Na⁺ concentrations in this set of titration experiments were about 2.5, 10, 20 and 100 mM, respectively. It is worth noting that the observed Na⁺-dependent conformational change occurs while the proteins are in crystal form and embedded in lipid.

In the titration experiments carried out to define the mode of divalent cation binding and competition with Na⁺, the soaking solutions contained 100 mM MES-Tris pH 6.5, 44% PEG400, 100 mM mixture of CsAc and NaAc and various concentrations of XCl₂, where X=Ca²⁺ or Sr²⁺, in the following proportions: 100 mM CsAc and 10 mM XCl₂; 100 mM CsAc and 1 mM XCl₂; 100 mM CsAc and 0.1 mM XCl₂; 90 mM CsAc, 10mM NaAc and 10mM XCl₂; and 100 mM NaAc and 10 mM XCl_2. After multiple steps of solution exchanges, the final soaking conditions contained 0.1, 1, or 10 mM of X²⁺ together with 2.5 mM Na⁺; or 10 mM X²⁺ together with 2.5, 10 or 100 mM Na⁺.

Data collection and structure determination

After soaking crystals were mounted on 100-μm Mitegen Microloops and frozen in liquid nitrogen. All diffraction data were collected at the Advanced Photon Source (APS) GM/CA-CAT beamlines 23ID-B or 23ID-D using a beam size of 35 μm × 50 μm. Data were processed and scaled using HKL2000³⁷ and the structures were determined by molecular replacement in PHASER³⁸ using our previously published NCX_Mj structure (PDB code 3V5U)²⁰ as a search model. Model building was completed using COOT³⁹ and structure refinement was performed with PHENIX⁴⁰. The data sets from crystals soaked in solutions containing 2.5 to 100 mM Na⁺ were collected using an X-ray wavelength of 1.033Å; the crystal grown with 150 mM Na⁺, and those soaked with Ca²⁺ and Sr²⁺ solutions, were obtained with a wavelength of 0.9793 Å. Lastly, the data from the crystal grown at low pH with no Na⁺ or Ca²⁺ were collected with a 2.0-Å wavelength beam. The resulting statistics for data collection and refinement are shown in Tables 2-4. All structure figures were prepared in PyMOL (The PyMOL Molecular Graphics System, Version 1.5.0.4 Schrödinger, LLC.). The ion passageways in low- and high-Na⁺ structures as well as the apo state were analyzed using the program CAVER⁴¹. Due to the variation in diffraction resolution and intensity among crystals, ion-occupancy comparisons were made on the basis of the diffraction data obtained in the titration experiments scaled against a common reference data before map calculation. The NCX_Mj crystal obtained with 2.5 mm Na⁺ only was used as the reference.

Table 2.

Data collection and refinement statistics for the NCX_Mj structures obtained from crystals soaked with varying amounts of Na⁺, and no Ca²⁺, and at low pH and no Na⁺ or Ca²⁺.

[Na+]	2.5 mM PDB 5HWX	10 mM PDB 5HWY	20 mM PDB 5HXC	100 mM PDB 5HXE	150 mM PDB 5HYA	0 mM PDB 5HXH
Data collection
Space group	P212121					C2
Cell dimensions
a, b, c (Å)	49.70, 72.28, 95.78	46.21, 71.97, 95.63	49.75, 72.56, 95.78	49.77, 72.85, 96.36	49.49, 72.88, 96.21	164.18, 46.83, 96.96
α, β, γ (°)	90, 90, 90	90, 90, 90	90, 90, 90	90, 90, 90	90, 90, 90	90, 106.20, 90
Resolution (Å)	2.40 (2.44-2.40)	2.10 (2.14-2.10)	2.10 (2.14-2.10)	2.28 (2.32-2.28)	1.90 (1.93-1.90)	2.80 (2.85-2.80)
Rsym (%)	9.4 (99.4)	9.3 (69.8)	10.5 (99.6)	9.9 (56.3)	8.6 (88.0)	10.5 (94.3)
I/σI	24.2 (1.8)	24.3 (2.7)	20.6 (1.9)	15.9 (2.8)	32.9 (2.4)	17.7 (1.2)
CC1/2	(0.625)	(0.819)	(0.602)	(0.722)	(0.786)	(0.561)
Completeness (%)	99.8 (99.1)	99.9 (100)	99.9 (99.8)	96.4 (98.6)	98.9 (97.8)	99.9 (99.9)
Redundancy	6.9 (6.7)	6.1 (6.0)	7.1 (7.0)	3.4 (3.3)	9.3 (8.9)	7.1 (5.7)
Refinement
Resolution (Å)	50-2.4	50-2.1	50-2.1	50-2.3	50-1.9	50-2.80
No. reflections	13977	19254	20739	15767	27923	21489
Rwork/Rfree	0.21/0.25	0.19/0.22	0.19/0.23	0.19/0.24	0.179/0.207	0.20/0.26
No. atoms
Protein	2206	2274	2366	2229	2229	4410
Ligand/Ion	56/3	154/2	161/5	162/6	257/4	121/2
Water	18	36	67	67	100	39
B-factors
Protein	53.25	34.28	34.91	39.75	26.05	42.98
Ligand/Ion	62.94/47.70	55.86/31.75	55.25/36.47	58.24/38.93	46.11/22.13	54.29/63.47
Water	58.12	41.16	46.97	49.74	37.80	33.17
R.m.s deviations
Bond lengths (Å)	0.004	0.006	0.008	0.003	0.006	0.003
Bond angles (°)	0.819	0.915	1.269	1.024	0.966	0.705

Values in parenthesis are for highest resolution shell. 5% of the data was used in the R_free calculation. ‘Ligand’ atoms are from lipids, PEG400 and acetates.

Table 4.

Data collection and refinement statistics for the NCX_Mj structures obtained from crystals soaked with varying amounts of Na⁺ and Ca²⁺.

[Ca2+] / [Na+]	10 mM / 2.5 mM PDB 5HXR	1 mM / 2.5 mM N/A*	0.1 mM / 2.5 mM N/A*	10 mM / 10 mM N/A*
Data collection
Space group	P212121
Cell dimensions
a, b, c (Å)	49.70, 72.52, 96.94	49.80, 72.26, 95.80	49.48, 72.47, 96.30	49.88, 72.22, 96.10
α, β, γ (°)	90, 90, 90	90, 90, 90	90, 90, 90	90, 90, 90
Resolution (Å)	2.45 (2.49-2.45)	2.65 (2.70-2.65)	2.40 (2.44-2.40)	2.20 (2.24-2.20)
Rsym (%)	11.8 (94.2)	11.1 (92.1)	11.2 (91.3)	10.3 (99.1)
I/σI	24.4 (1.6)	20.9 (1.6)	20.4 (1.6)	22.4 (1.8)
CC1/2	(0.611)	(0.696)	(0.632)	(0.549)
Completeness (%)	99.7 (100.0)	99.9 (100.0)	99.2 (100.0)	99.7 (100.0)
Redundancy	7.8 (7.8)	7.0 (6.5)	6.9 (7.0)	7.1 (7.1)
Refinement
Resolution (Å)	50-2.45	50-2.65	50-2.40	50-2.2
No. reflections	12996	10548	13736	18080
Rwork/Rfree	0.22/0.26	0.22/0.28	0.20/0.26	0.19/0.24
No. atoms
Protein	2211	2225	2228	2284
Ligand/Ion	114/3	130/3	162/3	164/4
Water	16	20	42	57
B-factors
Protein	64.97	71.22	53.50	45.16
Ligand/Ion	78.98/60.53	90.03/72.90	70.67/45.53	69.09/42.92
Water	68.57	81.02	64.12	55.45
R.m.s deviations
Bond lengths (Å)	0.002	0.004	0.002	0.004
Bond angles (°)	0.630	1.143	0.686	0.650

Values in parenthesis are for highest resolution shell. 5% of the data was used in the R_free calculation. ‘Ligand’ atoms are from lipids, PEG400 and acetates.

^*These structures are virtually identical to that resolved with 10 mM Ca²⁺ and 2.5 mM Na⁺ (PDB 5HXR), except for the weakened electron-density signal for the divalent ion, and were therefore not deposited in the PDB.

Conventional molecular dynamics (MD) simulations

Conventional (i.e. not enhanced) MD simulations were carried out with NAMD 2.7-2.9 ⁴² at constant temperature (298 K), pressure (1 atm), and membrane surface area (~69 Ų per lipid),and with periodic boundaries in all directions. All calculations used the standard CHARMM27/CMAP force field^43,44, except for NBFIX corrections for the interaction between carboxylate-oxygens and Na⁺ interaction²² or Ca²⁺ (Supplementary Note 3, Supplementary Fig. 5). Electrostatic interactions were calculated using PME with a real-space cut-off of 12 Å; the same cut-off distance was used for all van der Waals interactions.

Five ion-occupancy states of the transporter were considered, namely with 3 Na⁺, 2 Na⁺, 2 H⁺ or 1 Ca²⁺, and with no ions bound; in all cases Asp240 is protonated²². For the 3×Na⁺ state, we reanalyzed a 200-ns trajectory of NCX_Mj reported previously²². NCX_Mj had been embedded in a POPC lipid membrane using GRIFFIN⁴⁵. The initial configuration of the 2×Na⁺ state was generated from an equilibrated configuration of 3×Na⁺ state, from which the Na⁺ ion at S_ext was displaced by means of a slow alchemical transformation that annihilates the bound ion and recreates it in the bulk solution (in the same simulation box). The resulting 2×Na⁺ state was simulated for 250 ns. Similarly, the state with no Na⁺ bound was generated from an equilibrated configuration of the 2×Na⁺ state, from which the remaining Na⁺ ions were displaced; this state was again simulated for 250 ns. For the 2×H⁺ state, an initial configuration was generated from an equilibrated configuration of the 3×Na⁺ state, by gradually annihilating the Na⁺ ions from the binding sites and creating protonated E54 and E213 side chains; concurrently, acetic acid molecules in the bulk solution (in the same simulation box) were deprotonated and Na⁺ ions introduced. A second initial configuration of the 2×H⁺ state was obtained from an equilibrated configuration of the simulation with no ions bound, by slowly transforming deprotonated E54 and E213 into their protonated form, while doing the opposite to acetic acid molecules in the bulk solution. These two initial configurations of the 2×H⁺ state were then equilibrated for 800 ns. All annihilation/creation simulations were carried out using the FEP module of NAMD; and comprised 32-50 intermediate simulations of 400 ps each, for each transformation. A soft-core van der Waals potential with a radius-shifting coefficient of 2 Ų was used. The annihilated Na⁺ ions were confined within their corresponding binding sites using flat-bottom distance restraints. Specifically, the Na⁺ in S_ext was concurrently maintained within 4 Å of E54:Cδ, A206:C, S77:Cβ, T209:Cβ and S210:Cβ. The Na⁺ ions in S_Ca and S_int were concurrently kept within 4 Å of the E213:Cδ and A47:C, respectively. The Na⁺ ions and acetic acid molecules in the bulk solution were kept at a distance greater than 37 Å from the membrane center. Finally, the initial configuration of the Ca²⁺ state was generated on the basis of the published NCX_Mj X-ray structure²⁰ by placing Ca²⁺ in the S_Ca site and two water molecules coordinating Ca²⁺ at and near the S_mid site, so as to satisfy the expected coordination geometry (see Supplementary Note 2, Supplementary Fig. 3-4). This configuration was initially equilibrated through a series of simulations in which RMSD-based restraints of gradually diminishing strength were applied to the protein Cα atoms as well the side-chains involved in Ca²⁺ coordination. A 250 ns equilibration was then carried without any restraints.

Enhanced-sampling MD simulations

Free-energy landscapes were calculated using Bias-Exchange Well-Tempered Metadynamics (BE-WT-MetaD)^46,47, using GROMACS4.5.5/PLUMED^48,49. The force-field and simulation conditions were equivalent to those employed in the unbiased MD simulations. The accumulated simulation time for each of the ion-occupancy states studied was 1.6 μs. Each of these calculations consisted of 16 concurrent, interdependent simulations (or replicas); in 15 of these replicas, a WT-MetaD biasing potential was applied on different subsets of collective variables, as specified below, while the remaining replica was unbiased. Attempts to exchange coordinate configurations among replicas were made every 2-5 ps, using the Metropolis criterion⁴⁶. The inputs for each calculation were equilibrated configurations extracted from the unbiased MD simulations.

The choice of collective variables to be biased in the BE-WT-MetaD simulations was also based on analysis of the unbiased MD trajectories (Fig. 4g-i). Specifically, to enhance the reversible opening and closing of the water channels reaching from the extracellular bulk solution into either the S_ext or the S_Ca binding sites, we employed the following time-dependent collective variable (Fig. 4h-i):

$$V_{1,2}\left(t\right)=\frac{\beta }{\ln {\sum }_i\exp \{\beta ∕r_i\left(t\right)\}}$$ (Eq. 1)

where r_i denotes the distance between the oxygen atom of each water molecule in the system i and the center of the binding site considered (V₁ for S_ext,V₂ for S_Ca), and β is 10-100 nm. When the binding site was occupied, the ion was used to define its center. If the site was empty, its center was defined as the center-of-mass of the oxygen atoms coordinating the ion if bound. Bound water molecules at or near S_mid (coordinating the Na⁺ or Ca²⁺ ions) were not considered.

To enhance the reversible formation and disruption of selected backbone hydrogen bonds in TM7ab (Fig. 4g), we used an analogous collective variable:

$$V_3\left(t\right)=\frac{\beta }{\ln {\sum }_{ij}\exp \{\beta ∕r_{ij}\left(t\right)\}}$$ (Eq. 2)

In this case, the index i denotes atoms P202:O and T203:O, while the index j denotes atoms A206:N and P207:N. To preclude the artificial unraveling of TM7ab driven by this bias, an upper-bound V₃^max equal to 0.7 nm was imposed with a boundary potential of the form k (V₃(t) – V₃^max)⁴ if V₃(t) > V₃^max, where k = 10⁵ nm⁻⁴ kJ/mol. In addition, to control the bending and straightening of TM7ab more globally, we used the following path-collective variables⁵⁰:

$$V_4\left(t\right)=\frac{\exp \{-\lambda d_1\left(t\right)\}+2\exp \{-\lambda d_2\left(t\right)\}}{\exp \{-\lambda d_1\left(t\right)\}+\exp \{-\lambda d_2\left(t\right)\}}$$ (Eq. 3)

$$V_5\left(t\right)=-\frac{1}{\lambda }\ln [\exp \{-\lambda d_1\left(t\right)\}+\exp \{-\lambda d_2\left(t\right)\}]$$ (Eq. 4)

where d₁ and d₂ denote the mean-square-differences between the conformation of TM7ab and either the straight or bent conformations, respectively, and λ = 100 nm⁻². Note that V ₄ is by definition confined between a lower (V₄ ~ 1) and upper bound (V₄ ~ 2)⁵⁰; to confine the exploration of V₅, an upper value V₅^max of 0.020-0.025 nm² was imposed with boundary potential of the form k (V₅(t) – V₅^max)⁴ if V₅(t) > V₅^max, where k = 10¹¹ nm⁻⁸ kJ/mol. The mean-square-differences d₁ and d₂ comprise the backbone atoms of residues 198-211 as well as the side chain carbon atoms of residues P207 and L211.

A boundary potential was also applied to confine the ions and water molecule bound to S_ext, S_Ca, S_int and S_mid to their corresponding binding sites. Specifically, the variable confined was:

$$V_{\mathrm{c}}\left(t\right)=\sum _i\frac{1-{[r_i\left(t\right)∕r_0]}^8}{1-{[r_i\left(t\right)∕r_0]}^{10}}$$ (Eq. 5)

where r_i denotes the distance between the ion and each of its coordinating oxygen atoms; r₀ was set to 0.24 nm for the Na⁺ ions, and to 0.30 nm for Ca²⁺. Note that the upper-bound value of V_c is, by definition, approximately the coordination number in the bound state, whereas V_c becomes 0 as the ion becomes unbound. For the Na⁺ ion bound to S_ext and S_int, therefore, a lower bound value V_c^min = 4.3 was imposed with potential of the form k (V_c(t) – V_c^min)⁴ when V_c(t) < V_c^min, where k = 2500 kJ/mol. An analogous restraint was used for the Na⁺ ion at S_Ca, with V_c^min = 4.75. Similarly, for the Ca²⁺ ion at S_Ca a lower bound value V_c^min = 7.4 was imposed with a potential of the form k (V_c(t) – V_c^min)² when V_c(t) < V_c^min, with k = 400 kJ/mol. Note that these restraints do not perturb the chemical structure of the ion-coordination sphere when the ion is bound, i.e. V_c(t) > V_c^min. The displacement of the bound water molecules in the ion-coordination sphere by equivalent water molecules in the solvent was prevented similarly.

The specific sets of collective variables biased in each of the replica WT-MetaD simulations, as well as further details on the biasing potentials introduced, are specified in Supplementary Table 1.

Derivation of conformational free-energy landscapes

To translate the data gathered in the BE-WT-MetaD simulations into conformational free-energy landscapes, we sought to identify a low-dimensional representation of the data that is nevertheless also intuitive and representative. We ultimately settled on two structure-based descriptors of the degree of opening of the each of the aqueous channels leading to the ion-binding sites (Fig. 4), defined as:

$$S_{1,2}=\frac{\beta }{\ln {\sum }_{ij}\exp \{\beta ∕r_{ij}\}}$$ (Eq. 6)

where r_ij denotes a set of pairwise distances for specific Cα atoms in the protein, for a given simulation snapshot. For S₁, index i refers to the Cα of residues 198 to 209 in TM7, while index j refers to those in residues 66 to 80 and 290 to 297, in TM3 and TM10, respectively. For S₂, index i refers to the Cα of residues 51 to 64 in TM2, while index j refers to those in residues 177 to 193 and 198 to 209, in TM6 and TM7, respectively. Therefore, S₁ describes the effective separation between TM7 and TM3/TM10, on the extracellular half of the protein, and thus reports on the accessibility to the S_ext site. Analogously, S₂ measures the separation between TM2 and TM6-TM7, also on the extracellular side, and thus reports on the accessibility to S_Ca.

The conformational free energy of NCX_Mj as a function of S₁ and S₂ was then computed for each ion-occupancy state separately (Figs. 5a, 6a). These landscapes were obtained through reweighting of the biased probability distribution from the BE-WT-MetaD sampling, using the WHAM method⁵¹; through this approach we combine the statistics gathered in all replicas, and can consider alternate free-energy projections^49,52,53.

To correct the landscape calculated for the Ca²⁺-bound state (Fig. 6a) on account of the excess amount of charge transferred from the ion to the protein (Supplementary Note 4, Supplementary Fig. 6), we reprocessed all the sampling obtained during the original BE-WT-MetaD simulations, introducing in the WHAM equations a re-weighting factor w for each configuration X:

$$w\left(\mathit{X}\right)\propto \exp \left\{-\frac{U_{\mathrm{c}}\left(\mathit{X}\right)-U\left(\mathit{X}\right)}{k_{\mathrm{B}}T}\right\}$$ (Eq. 7)

where U denotes the ‘uncorrected’ CHARMM27/NBFIX potential-energy function, and U_c denotes the corrected function. To calculate U_c (X), the charge of Ca²⁺ was reduced to +1.8e from its standard value of +2e, and the difference was distributed among the surrounding protein residues (as specified in Supplementary Note 4). To minimally alter the charge-distribution used in the original CHARMM27 force-field, the charge added to each protein atom was proportional to the absolute value of its uncorrected charge.

The statistical errors for all free-energy landscapes are provided in Supplementary Fig. 7.

Derivation of representative structures and water-density maps

Representative structures and water-density iso-surfaces (Fig. 5b-c, Fig. 6b-c) were derived for each BE-WT-MetaD simulation by clustering all sampling⁵⁴ in the multi-dimensional space of V₁, V₂, and V₄ (Eq. 1-3), plus a descriptor S₃ of the proximity between TM6-TM7 and TM2-TM3/TM10, on the extracellular side of the protein. More precisely:

$$S_3=\sum _{ij}\frac{1-{[r_{ij}\left(t\right)∕r_0]}^8}{1-{[r_{ij}\left(t\right)∕r_0]}^{12}}$$ (Eq. 8)

where r₀ = 7.5 Å, and r_ij denotes a specific set of pairwise Cα distances, for a given simulation snapshot. Similarly to S₁ and S₂ (Eq. 6), index i refers to Cα atoms in the extracellular halves of TM6 and TM7, while index j refers to Cα atoms in the extracellular halves of TM2, TM3, and TM10. We thus obtained⁵⁴ ~2,000 clusters for each of the simulation systems (using RMSD cut-off values of 1.3 Å for V₁ and V₂, 0.1 Å for V₄; and 6.25 Å for S₃). Using the WHAM equations, we calculated the relative free energy of each of these clusters, and then identified the major basins in this space with the MCL method^55,56 (with p = 1.4.) Water occupancy maps were calculated for each of these major free-energy basins, only using the sampling gathered by the unbiased replicas.

Table 3.

Data collection and refinement statistics for the NCX_Mj structures obtained from crystals soaked with varying amounts of Na⁺ and Sr²⁺.

[Sr2+] / [Na+]	10 mM / 2.5 mM PDB 5HXS	1 mM / 2.5 mM N/A*	0.1 mM / 2.5 mM N/A*	10 mM / 10 mM N/A*	10 mM / 100 mM N/A#
Data collection
Space group	P212121
Cell dimensions
a, b, c (Å)	49.52, 72.35, 96.00	49.76, 72.62, 95.62	49.80, 72.27, 94.84	49.67, 72.46, 96.43	49.88, 72.43, 95.91
α, β, γ (°)	90, 90, 90	90, 90, 90	90, 90, 90	90, 90, 90	90, 90, 90
Resolution (Å)	2.80 (2.85-2.80)	2.90 (2.95-2.90)	2.54 (2.58-2.54)	2.30 (2.34-2.30)	2.50 (2.54-2.50)
Rsym (%)	12.3 (88.0)	12.3 (91.0)	11.9 (88.5)	13.7 (95.8)	10.9 (96.8)
I/σI	19.0 (1.8)	19.2 (1.6)	21.5 (1.9)	18.4 (1.6)	19.7 (1.8)
CC1/2	(0.674)	(0.686)	(0.768)	(0.420)	(0.767)
Completeness (%)	98.8 (90.4)	94.9 (96.1)	99.9 (100.0)	99.8 (99.9)	99.6 (99.7)
Redundancy	6.5 (5.4)	6.7 (6.9)	7.1 (6.8)	6.2 (4.5)	5.9 (6.0)
Refinement
Resolution (Å)	50-2.80	50-2.90	50-2.54	50-2.3	50-2.5
No. reflections	8927	7611	11483	16488	12665
Rwork/Rfree	0.22/0.27	0.22/0.27	0.23/0.26	0.20/0.25	0.21/0.24
No. atoms
Protein	2227	2249	2217	2271	2223
Ligand/Ion	110/2	133/3	155/3	101/3	104/6
Water	10	2	5	34	17
B-factors
Protein	61.55	67.82	60.83	46.42	56.75
Ligand/Ion	74.56/63.32	85.56/70.47	80.33/90.41	64.79/38.25	71.27/53.50
Water	59.22	61.31	68.58	51.39	55.07
R.m.s deviations
Bond lengths (Å)	0.004	0.005	0.005	0.007	0.003
Bond angles (°)	0.887	1.076	0.963	1.057	0.733

Values in parenthesis are for highest resolution shell. 5% of the data was used in the R_free calculation. ‘Ligand’ atoms are from lipids, PEG400 and acetates.

^*These structures are virtually identical to that resolved with 10 mM Sr²⁺ (PDB 5HXS), except for the weakened electron-density signal for the divalent ion, and were therefore not deposited in the PDB.

^#This structure is virtually identical to that resolved with 100 mM Na⁺ without Ca²⁺ or Sr²⁺ (Table 1, PDB 5HXE) and was therefore not deposited in the PDB.