Flow-driven cell migration under external electric fields

Abstract

Electric fields influence many aspects of cell physiology, including various forms of cell migration. Many cells are sensitive to electric fields, and can migrate toward a cathode or an anode, depending on the cell type. In this paper, we examine an actomyosin-independent mode of cell migration under electrical fields. Our theory considers a one-dimensional cell with water and ionic fluxes at the cell boundary. Water fluxes through the membrane are governed by the osmotic pressure difference across the cell membrane. Fluxes of cations and anions across the cell membrane are determined by the properties of the ion channels as well as the external electric field. Results show that without actin polymerization and myosin contraction, electric fields can also drive cell migration, even when the cell is not polarized. The direction of migration with respect to the electric field direction is influenced by the properties of ion channels, and are cell-type dependent.

Electric fields are important in many aspects of cell dynamics, even for non-excitable tissue cells. During development, electric fields are responsible for tissue patterning and cell migration [1]. The mechanism that couples electrical signals to cell movement is not understood [2]. The classic mechanism of cell migration on two-dimensional (2-D) substrates combines actin-driven protrusions with myosin contraction [3]. A similar mechanism has been proposed for galvanotaxis, where electrically induced downstream signal pathways could regulate actomyosin dynamics [2] [Fig. 1(a)]. Here, the direction of cell migration depends on the orientation of the external electric fields and the cell type [2]. However, water permeation and ion fluxes across the cell membrane [4, 5] can also drive cell movement and cell bleb formation [6] in an actomyosin-independent manner. This water-ion coupling leads to a natural connection among actin-independent cell motility, electric fields, and galvanotaxis. In this work, we explore this connection and develop a flow-driven model of cell migration under a prescribed external electric potential difference. We consider a 1-D configuration [Fig. 1(b)], and explore properties of membrane ion channels that affect migration under the proposed mechanism. Since ion channel properties have implications on the pathophysiology of cells [7], results of our model can be used to explain actin-independent movement of cancer cells such as glioblastoma [8].

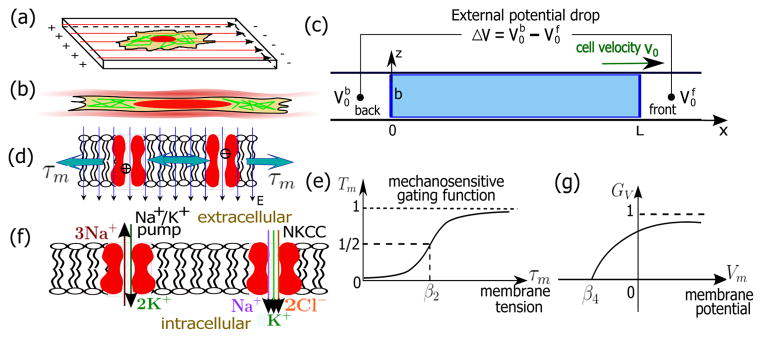
FIG. 1.

(Color online). Schematics of the model and membrane channels in cells. (a) Cartoon of a 2-D cell under an electric field. (b) Cartoon of a confined 1-D cell in a microchannel. (c) Diagram and the coordinate system of a 1-D cell model in an applied external voltage drop, ΔV. The coordinate system moves with the cell so that x ∈ [0, L] represent the cell body. z ∈ [0, b] in the width direction. $V_0^{\mathrm{b}/\mathrm{f}}$ is the extracellular electric potential at the back/front of the cell. The cell velocity is assumed positive when the cell moves towards the positive x–direction. (d) Schematics of the tension-gated passive channels that transport ions along the potential difference across the membrane. (e) The mechanosensitive gating function, T_m, follows a Boltzmann distribution and ranges from 0 to 1. (f) Cartoons of the Na⁺/K⁺ pumps and Na⁺-K⁺-Cl⁻ cotransporters (NKCC). (g) Voltage dependence function, G_V, of the Na⁺/K⁺ pumps that ranges from 0 to 1.

The 1-D cell model is illustrated in Fig. 1(c). We consider a cell with length L, width b, and depth w occupying the entire cross section of a narrow channel. The coordinate system moves with the cell body so that x ∈ [0, L] represents the domain of the cell for all times. Four ionic species, Na⁺, K⁺, Cl⁻, and A⁻, are considered. Na⁺, K⁺, and Cl⁻ are the most abundant ions in the cells, and are transportable across the cell membrane through specific channels. A⁻ represents negatively charged molecules that are not permeable through the membrane. Since most proteins are negatively charged, A⁻ is proportional to the total protein number in the cell. Here, we set the valence of these proteins to be −1. The cytoplasm is approximately electro-neutral so that electroosmosis is neglected and Σ_n z_nc_c,n(x) = 0, where c_c,n is the intracellular ionic concentration (in molars) of each species; n ∈ {Na⁺,K⁺, Cl⁻,A⁻} and z_n is the valency of each ionic species. We use the subscript ‘c/0’ to represent variables associated with the intra-/extracellular domain and the superscript ‘b/f’ to denote the back/front end of the cell. For example, $V_0^{\mathrm{b}}$ is the extracellular electric potential at the back end of the cell.

The cell membrane is permeable to water due to aquaporins. The chemical potential of water, Ψ = p − Π, is a combination of the hydrostatic pressure, p, and the osmotic pressure, Π. The water flux through the membrane is proportional to ΔΨ = Ψ_c − Ψ₀. We take the convention that the flux is positive from outside to inside so that the flux per unit cross-sectional area is

$$J_{\text{water}}^{\mathrm{b}/\mathrm{f}}=-{\alpha }^{\mathrm{b}/\mathrm{f}}(\mathrm{\Delta }{p}^{\mathrm{b}/\mathrm{f}}-\mathrm{\Delta }{\mathrm{\Pi }}^{\mathrm{b}/\mathrm{f}}),$$ (1)

where α^b/f is the water permeability constant that depends on the density of the aquaporins on the membrane. The osmotic pressure is related to the total ion concentration by Π_c/0 = RT Σ_n c_c/0,n, where RT is the gas constant times the absolute temperature. The osmotic pressure difference across the membrane will regulate the cell volume [5]. Here we assume constant cell volume because simulations with different cell volumes did not lead to qualitatively different results.

In this problem, water is assumed to be stationary with respect to a fixed frame. The transported water through the cell membrane contributes to the displacement of the membrane and thus determines the velocity of cell migration, v₀. Therefore, at steady state with constant cell size $J_{\text{water}}^{\mathrm{f}}=-J_{\text{water}}^{\mathrm{b}}=v_0$. From Eq. 1 we have

$$\mathrm{\Delta }{p}^{\mathrm{f}}=\mathrm{\Delta }{\mathrm{\Pi }}^{\mathrm{f}}-v_0/{\alpha }^{\mathrm{f}},\mathrm{\Delta }{p}^{\mathrm{b}}=\mathrm{\Delta }{\mathrm{\Pi }}^{\mathrm{b}}+v_0/{\alpha }^{\mathrm{b}},$$ (2)

which expresses Δp^b/f in terms of ΔΠ^b/f and v₀.

To obtain ΔΠ^b/f, the intracellular ion distribution must be solved. We consider ion dynamics for Na⁺, K⁺, Cl⁻, and A⁻. In the frame of the cell body, the electrodiffusion equation for the ions is ∂c_c,n/∂t = −∂J_n/∂x, where J_n is the intracellular ion flux for each species, given by $J_n=-D_n{\partial }_x{c}_{c,n}-D_n\frac{z_{n}F}{RT}{c}_{c,n}{\partial }_x{V}_c-{\overline{v}}_f{c}_{c,n}$, where D_n is the diffusion constant, F is the Faraday’s constant, and V_c is the intracellular electric potential. v̄_f is the averaged cross-sectional fluid velocity in the frame of the cell body; v̄_f = −v₀ by assumption.

At steady-state, J_n’s must be constant in space; they are determined by the boundary conditions of ion fluxes through the membrane channels at the two ends of the cell. In general, ions are both passively and actively transported across membranes. Passive ionic transport is carried out by ion channels and ionic transporters, some of which are gated by membrane tension [τ_m, Fig. 1(d)]. Active transport is carried out by ion pumps, which utilize chemical energy (ATP) to transport ions against a chemical potential gradient.

The passive ion fluxes are proportional to the electrochemical potential difference of ions across the membrane, i.e., $J_{n,p}^{\mathrm{b}/\mathrm{f}}=G_{0,n}^{\mathrm{b}/\mathrm{f}}{T}_m^{\mathrm{b}/\mathrm{f}}\left(\mathit{RT}ln{\mathrm{\Gamma }}_n^{\mathrm{b}/\mathrm{f}}-z_{n}F{V}_m^{\mathrm{b}/\mathrm{f}}\right)$, where n ∈ {Na⁺, K⁺, Cl⁻} since A⁻ is impermeable to the membrane. ${\mathrm{\Gamma }}_n^{\mathrm{b}/\mathrm{f}}=c_{0,n}^{\mathrm{b}/\mathrm{f}}/c_{c,n}^{\mathrm{b}/\mathrm{f}}$ is the ratio of extra-and intra-cellular ion concentration at the cell boundary. $V_m^{\mathrm{b}/\mathrm{f}}=V_c^{\mathrm{b}/\mathrm{f}}-V_0^{\mathrm{b}/\mathrm{f}}$ is the membrane potential. $G_{0,n}^{\mathrm{b}/\mathrm{f}}$ is a constant depending on the property and density of channels; $G_{0,n}^{\mathrm{b}}$ and $G_{0,n}^{\mathrm{f}}$ can be different for a polarized cell. T_m ∈ (0, 1) is a mechanosensitive gating function [Fig. 1(e)] that follows a Boltzmann distribution, i.e., T_m = [1+e^{−β₁ (τ_m−β₂)}]⁻¹, where β₁ and β₂ are constant.

Another passive channel to consider is the Na⁺-K⁺-Cl⁻ cotransporter (NKCC) [Fig. 1(f)] because it, along with its isoforms, is widely expressed in various cell types [9]. The NKCC simultaneously transports one Na⁺, one K⁺, and two Cl⁻ into the cell under physiological conditions, the flux of which can be written as [10]

$$\begin{array}{l}{J}_{\text{NKCC},\text{Na}}^{\mathrm{b}/\mathrm{f}}=J_{\text{NKCC},\mathrm{K}}^{\mathrm{b}/\mathrm{f}}=\frac{1}{2}{J}_{\text{NKCC},\text{Cl}}^{\mathrm{b}/\mathrm{f}}\\ ={\alpha }_{\text{NKCC}}^{\mathrm{b}/\mathrm{f}}RT\left(ln{\mathrm{\Gamma }}_{\text{Na}}^{\mathrm{b}/\mathrm{f}}+ln{\mathrm{\Gamma }}_{\mathrm{K}}^{\mathrm{b}/\mathrm{f}}+2ln{\mathrm{\Gamma }}_{\text{Cl}}^{\mathrm{b}/\mathrm{f}}\right),\end{array}$$ (3)

where ${\alpha }_{\text{NKCC}}^{\mathrm{b}/\mathrm{f}}$ is a transport rate constant independent of the membrane tension. Since NKCC is electrically neutral, its flux is independent of the membrane potential.

For the active ionic fluxes, we consider the Na⁺/K⁺ pump, a ubiquitous and important ion pump in animal cells. It exports three Na⁺ ions and intakes two K⁺ ions per ATP unit [Fig. 1(f)]. Because the overall flux is positively charged, the activity of the pump depends on the membrane potential [11]. In addition, the flux depends on the concentrations of Na⁺ and K⁺ [7, 12] and saturates at high concentration limits [7]. By decoupling the dependence of the voltage and ion concentration, as a modification of existing models [7, 13], we assume that the flux of Na⁺ and K⁺ through the Na⁺/K⁺ pump is

$$J_{\text{Na}/\mathrm{K},\text{Na}}^{\mathrm{b}/\mathrm{f}}=-\frac{3}{2}{J}_{\text{Na}/\mathrm{K},\mathrm{K}}^{\mathrm{b}/\mathrm{f}}=-{\alpha }_{\text{ATP}}^{\mathrm{b}/\mathrm{f}}{G}_V^{\mathrm{b}/\mathrm{f}}{c}_{\text{ATP}}^{\mathrm{b}/\mathrm{f}}\times {\left(1+{\alpha }_{\text{Na}/\mathrm{K},\text{Na}}^{\mathrm{b}/\mathrm{f}}{\mathrm{\Gamma }}_{\text{Na}}^{\mathrm{b}/\mathrm{f}}\right)}^{-3}{\left(1+{\alpha }_{\text{Na}/\mathrm{K},\mathrm{K}}^{\mathrm{b}/\mathrm{f}}/{\mathrm{\Gamma }}_{\mathrm{K}}^{\mathrm{b}/\mathrm{f}}\right)}^{-2},$$ (4)

where ${\alpha }_{\text{ATP}}^{\mathrm{b}/\mathrm{f}}$ is a transport rate constant, $c_{\text{ATP}}^{\mathrm{b}/\mathrm{f}}$ is the concentration of ATP. ${\alpha }_{\text{Na}/\mathrm{K},\text{Na}}^{\mathrm{b}/\mathrm{f}}$ and ${\alpha }_{\text{Na}/\mathrm{K},\mathrm{K}}^{\mathrm{b}/\mathrm{f}}$ are two constants. The exponents 3 and 2 are the Hill’s coefficients of Na⁺ and K⁺, respectively. Eq. 4 ensures that the flux is zero when either $1/{\mathrm{\Gamma }}_{\text{Na}}^{\mathrm{b}/\mathrm{f}}$ or ${\mathrm{\Gamma }}_{\mathrm{K}}^{\mathrm{b}/\mathrm{f}}$ goes to zero; the flux saturates if $1/{\mathrm{\Gamma }}_{\text{Na}}^{\mathrm{b}/\mathrm{f}}$ and ${\mathrm{\Gamma }}_{\mathrm{K}}^{\mathrm{b}/\mathrm{f}}$ go to infinity. $G_V^{\mathrm{b}/\mathrm{f}}$ captures the voltage-dependence of the pump activity [11] and is expressed as [Fig. 1(g)] G_V = 2[1 + e^{−β₃(V_m−β₄)}]⁻¹ − 1 if V_m ≥ β₄ and G_V = 0 otherwise, where β₃ and β₄ are constant.

Combining the contributions from the passive channels and active pump, the total ion fluxes through the back and front membranes for the four species are $J_{\text{Na}}^{\mathrm{b}/\mathrm{f}}=J_{\text{Na},p}^{\mathrm{b}/\mathrm{f}}+J_{\text{NKCC},\text{Na}}^{\mathrm{b}/\mathrm{f}}+J_{\text{Na}/\mathrm{K},\text{Na}}^{\mathrm{b}/\mathrm{f}},J_{\mathrm{K}}^{\mathrm{b}/\mathrm{f}}=J_{\mathrm{K},p}^{\mathrm{b}/\mathrm{f}}+J_{\text{NKCC},\mathrm{K}}^{\mathrm{b}/\mathrm{f}}+J_{\text{Na}/\mathrm{K},\mathrm{K}}^{\mathrm{b}/\mathrm{f}},J_{\text{Cl}}^{\mathrm{b}/\mathrm{f}}=J_{\text{Cl},p}^{\mathrm{b}/\mathrm{f}}+J_{\text{NKCC},\text{Cl}}^{\mathrm{b}/\mathrm{f}}$, and $J_{\mathrm{A}}^{\mathrm{b}/\mathrm{f}}=0$. Then we have the boundary conditions for J_n’s, i.e., $J_n{\mid }_{x=0}=J_n^{\mathrm{b}}$ and $J_n{\mid }_{x=L}=-J_n^{\mathrm{f}}$. The minus sign in the last relation is due to the convention that $J_n^{\mathrm{b}/\mathrm{f}}$ is positive inwards.

To obtain the water flux across the membrane, the distribution of hydrostatic pressure is needed. At the micro-scale, the fluid inertia can be neglected and the lubrication theorem applies. In the frame of the cell body the depth-wise averaged fluid velocity is v_f (z) = (1/2η)(∂p_c/∂x)(z² − bz), where η is the dynamic viscosity of the intracellular fluid. By assumption we have ${\overline{v}}_f=b^{-1}{\int }_0^b{v}_f(z)dz=-v_0$ so that v₀ = (b²/12η)∂p_c/∂x. Then p_c|_x=L = p_c|_x=0 + (12η/b²)v₀L. When the extracellular hydrodynamic and osmotic pressures are unpolarized at the two ends of the cell, with Eq. 2, v₀ can be solved as $v_0={\sum }_n(c_{c,n}^{\mathrm{f}}-c_{c,n}^{\mathrm{b}})/\gamma$, where γ = (1/α^f + 1/α^b + 12ηL/b²)/RT.

The existence of an intracellular hydrostatic pressure gradient and fluid flow will generate stresses on the cell membrane. Here we assume that the membrane moves with the cell. For cells in confined channels, the cell membrane also contacts the channel lateral wall and experiences friction. Hence, the tension balance in the membrane is [τ_m(x + dx) − τ_m(x)] = η∂_zv_fz=bdx + ξ_wv₀dx, where ξ_w is the coefficient of friction between the membrane and the channel wall. At the back of the cell, the force balance of the membrane gives the boundary condition $\mathrm{\Delta }{p}^{\mathrm{b}}=2{\tau }_m^{\mathrm{b}}/b$. The tension is then τ_m(x) = bΔp^b/2 + (6η/b + ξ_w) v₀x. Using Eq. 2, we can solve the membrane tension at the back and front of the cell as ${\tau }_m^{\mathrm{b}}=b(\mathrm{\Delta }{\mathrm{\Pi }}^{\mathrm{b}}+v_0/{\alpha }^{\mathrm{b}})/2$ and ${\tau }_m^{\mathrm{f}}={\tau }_m^{\mathrm{b}}+(6\eta /b+{\xi }_w)v_{0}L$, respectively. These tension values determine the gating function, T_m.

The cell velocity depends on the properties of ion channels at the two ends of the membrane. The model predicts that a polarized cell can migrate under zero electric potential drop (ΔV = 0), with a direction determined by the direction of cell polarization. For example, when ${\alpha }_{\text{NKCC}}^{\mathrm{b}}>{\alpha }_{\text{NKCC}}^{\mathrm{f}},{\alpha }_{\text{ATP}}^{\mathrm{b}}<{\alpha }_{\text{ATP}}^{\mathrm{f}}$, or $G_{0,n}^{\mathrm{b}}<G_{0,n}^{\mathrm{f}}$, solute moves in the positive x–direction, and the fluid follows solute movement by osmosis. In this case, the cell move towards the negative x–direction. This is reminiscent of solute-fluid coupling in fluid absorbing epithelia [14, 15].

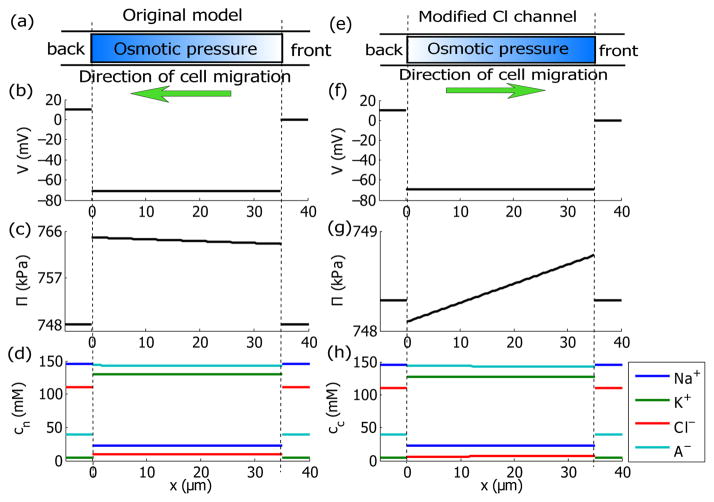
When an unpolarized cell is placed in a 10 mV potential drop, the model predicts that the cell migrates toward the back [Fig. 2(a)] with a speed of 19 nm/s. The membrane potential is about −70 mV [Fig. 2(b)]. The direction of cell migration is mainly determined by polarized intracellular osmotic pressure, which is higher at the back [Fig. 2(c)]. The predicted intracellular concentration of K⁺ is about 100 mM higher than those of Na⁺ and Cl⁻ [Fig. 2(d)]. This concentration difference across ion species is found to be electrophysiologically important [16]. We can modulate the ion fluxes of Na⁺, K⁺, and Cl⁻ by adjusting the transport coefficients of the membrane channels. When the activity of the Na⁺/K⁺ pump or the NKCC is either reduced or increased by 2 orders (based on the parameters in Tab. I in the SM), the cell is still predicted to migrate towards the back. This persistence in the migration direction was also seen in the experiments by Allen et al. [2] wherein the ion fluxes through the membrane were manipulated but the cell did not reorient. When the passive ion transport coefficients for Cl⁻, $G_{0,\text{Cl}}^{\mathrm{b}/\mathrm{f}}$, are increased by 1 order of magnitude, however, our model predicts a reorientation of cell migration [Fig. 2(e)] with a speed 10 nm/s. The membrane potential remains polarized [Fig. 2(f)] but the ion distribution is in favor of a higher intracellular osmotic pressure at the front [Fig. 2(g)]. The predicted cell re-orientation can be explained by a perturbative expansion derived in the supplemental material (SM). A comparison between the analytic result and numerical solution is shown in the SM as well.

FIG. 2.

(Color online). Model predictions for a cell under a given external electric potential drop ΔV = 10 mV. x ∈ [0, L] represents the intracellular domain and the outside represents the extracellular domain at the two ends. (a–d) Predictions for an unpolarized cell with the membrane channel properties provided in Tab. I in the Supplemental Material. The cell migrates towards the negative x–direction at 19 nm/s. (e–h) Predictions for the same cell but with $G_{0,\text{Cl}}^{\mathrm{b}/\mathrm{f}}$ increased by one order. The cell migrates towards the positive x–direction at 10 nm/s. (a) and (e) Cartoons of a migrating cell with non-uniform distribution of intracellular osmotic pressure. (b) and (f) Spatial distribution of electric potentials. (c) and (g) Spatial distribution of osmotic pressure. (d) and (h) Spatial distribution of ion concentrations for Na⁺, K⁺, Cl⁻, and A⁻.

We consider the three passive channels, the NKCC, and the Na⁺/K⁺ pump as the primary pathways for transmembrane ionic transport. Many other channels and transporters are expressed in various cell types as well, and many of them have been implicated in cell migration [17]. It may be of interest, and is indeed not difficult to incorporate this complexity into our modeling framework. We do emphasize, however, that the physical principles discussed here should still be relevant even with this added complexity.

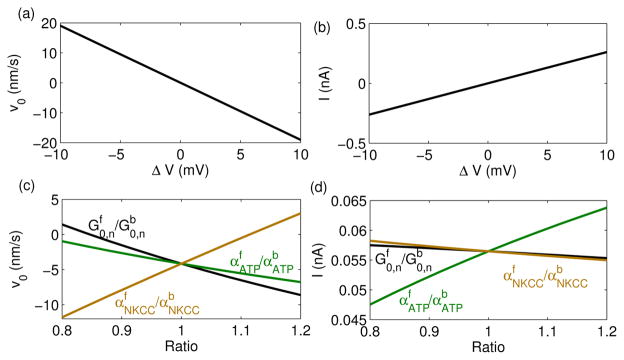
The model predicts that the intracellular potential drop across the two ends, $V_c^{\mathrm{b}}-V_c^{\mathrm{f}}$, is at least one order lower than the external potential drop ΔV [Fig. 2(b, f)], consistent with the small perturbation approximation. As a result, the difference between $V_m^{\mathrm{b}}$ and $V_m^{\mathrm{f}}$ follows closely with ΔV, which affects the intracellular ion distribution through the passive channels. Indeed, the model predicts that the velocity of the cell varies with ΔV in an almost linear fashion [Fig. 3(a)], consistent with Eq. 6 in the SM. In contrast with the 1-D model prediction, a 2-D experiment showed that the direction of an electric field reorients the cell, but the strength of the field had no influence on the cell velocity [2]. This difference may be due to polarization dynamics of the cell because membrane channels and pumps will redistribute and polarize based on environmental cues [2, 4]. Hence, the cell polarization, the environmental cues, and the cellular responses are correlated. In our 1-D model, we have assumed a static polarization by setting the ratio of channels/pumps fluxes at the two ends and predict the cell velocity accordingly [Fig. 3(c)]. In cells, this polarized distribution of membrane channels may come from vesicle trafficking and recycling of membrane from the back to the front. A simple derivation for the polarized channels/pumps distribution is included in the SM.

FIG. 3.

(Color online). (a–b) Cell Velocity and the net current through the cell as functions of the external electric potential drop ΔV. See Tab. I in the SM for the parameters. (c–d) Cell Velocity and the net current through the cell under ΔV = 2 mV. For each line, the ratio of $G_{0,n}^{\mathrm{f}}/G_{0,n}^{\mathrm{b}},{\alpha }_{\text{ATP}}^{\mathrm{f}}/{\alpha }_{\text{ATP}}^{\mathrm{b}}$, or ${\alpha }_{\text{NKCC}}^{\mathrm{f}}/{\alpha }_{\text{NKCC}}^{\mathrm{b}}$ is varied while the other parameters are kept same. The ratios are obtained when the channel properties at the back membrane are fixed as in Tab. I while those at the front membrane varies.

I = bwF Σ_n z_nJ_n is the net ionic current through the cell; it can be calculated as a function of ΔV and polarization ratios [Fig. 3(b,d)]. This current depends on the effective resistance imposed by the membrane channels, such as the density of channels and the rate of ion transport of each channel, and is thus a potential measure of the physiological or pathological state of a cell. Indeed, the measurement of current or the estimation of the effective resistance has implications on other biophysical contexts, including the electrical property of epithelium and the coupled solute-solvent flow within it[14]. In our model [Fig. 2(a–d)], the flux through each passive channel or active pump is about 10⁻¹⁷ mol/μm²/s, corresponding to ~10⁷ ions/μm²/s. Under normal conditions a passive channel (an active pump) transports ~10⁷ (~10⁴) ions per second [18]; then the model implies that around 1 passive channel (10³ active pumps) per μm² are needed to support the total flux and cell migration.

The predicted cell velocity in our model is on the order of 10 nm/s, comparable to velocities of actin-based cell migration [19]. If actin is involved, then there could be mechanical coupling between water flow and actin network dynamics. For instance, the hydrostatic pressure gradient and the membrane tension gradient could influence actin polymerization and determine direction of actin protrusion. These complex questions require further investigation and are beyond the scope of the current paper.

In this work we adopt a flow-driven mechanism to develop a physical model of cell migration under an external electric field. The model can also predict the cell migration velocity under different osmotic conditions, similar to the predictions of an electro-neutral model [4] (see SM). In this work, we have considered constant extracellular concentrations of Na⁺, K⁺, and Cl⁻; voltages are changed independently. Different predictions are expected if voltages are controlled by a set of ions involving Na⁺, K⁺, or Cl⁻. In general, charge transport, osmolarity, and water flow are all coupled in the complex biophysics of the cell, and may drive cell migration and active cell shape changes in different environments.