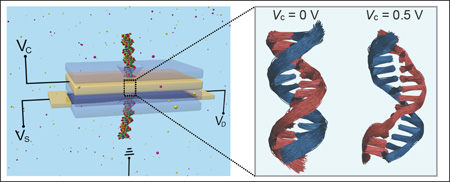
Abstract
Nanopores offer sensors for a broad range of nanoscale materials, in particular ones of biological origin like single- and double-stranded DNA or DNA-protein complexes. In order to increase single-molecule sensitivity, it is desirable to control biomolecule motion inside nanopores. In the present study, we investigate how in case of a double-stranded DNA the single-molecule sensitivity can be improved through bias voltages. For this purpose we carry out molecular dynamics simulations of the DNA inside nanopores in an electrically biased metallic membrane, by using molecular dynamics simulations. Stabilization of DNA, namely a reduction in thermal fluctuations, is observed under positive bias voltages, while negative voltages bring about only negligible stabilization. For positive biases the stabilization arises from electrostatic attraction between the negatively charged DNA backbone and the positively charged pore surface. Simulations on a teardrop-shape pore show a transverse shift of DNA position toward the sharp end of the pore under positive bias voltages, suggesting the possibility to control DNA alignment inside nanopores through geometry shaping. The present findings open a feasible and efficient route to reduce thermal noise, and in turn, enhance the signal-to-noise ratio in single-molecule nanopore sensing.
Keywords: solid-state nanopore, DNA sequencing, molecular dynamics, biosensor, stabilization
Graphical abstract
In the past two decades, fast and inexpensive genome sequencing has become a rapidly growing research area.1–5 DNA sequencing using solid-state nanopores (SSNs), inspired by their biological counterparts,6–10 holds great promise for genomic applications as a potentially cost-effective, rapid and scalable technology.11–15 SSN devices are made of a thin membrane containing one or multiple nanometer-sized pores, through which DNA molecules are translocated under an electric field across the membrane.16–25 The passing nucleotides in the DNA molecule interact with the membrane, enabling the detection, and potentially the identification of individual nucleotides. Typical detection methods include measuring ionic current blockades from DNA dwelling in the nanopore,7 measuring electrostatic potential changes across a membrane capacitor caused by the passage of DNA charges,13 and monitoring transverse tunnelling currents owing through nucleotides sandwiched between two membrane electrodes.26
Despite many efforts, no practical DNA sequencing experiments using SSNs have been reported so far; detecting a real-time discernible signal for the nucleotides in a DNA strand as the molecule is translocated through SSNs remains a challenging task. One of the primary impediments is the low signal-to-noise ratio due to thermal fluctuations of DNA bases, ions and water inside SSNs. In particular, the noise from variations in DNA structural conformation inside a nanopore may offset the signal induced by each nucleotide, largely weakening the sensing sensitivity of the nanopore device. Therefore, in order to ensure the effective operation of a nanopore device in single-molecule sensing applications, a scenario to control the motions of biomolecules in SSNs is highly desirable. In biological protein nanopores, the control of motion and translocation velocity of DNA can be achieved by using a processive enzyme, thereby enabling their applications in DNA sequencing,27 mapping of DNA methylation28 and measurement of DNA position within the nanopore with subangstrom precision.29
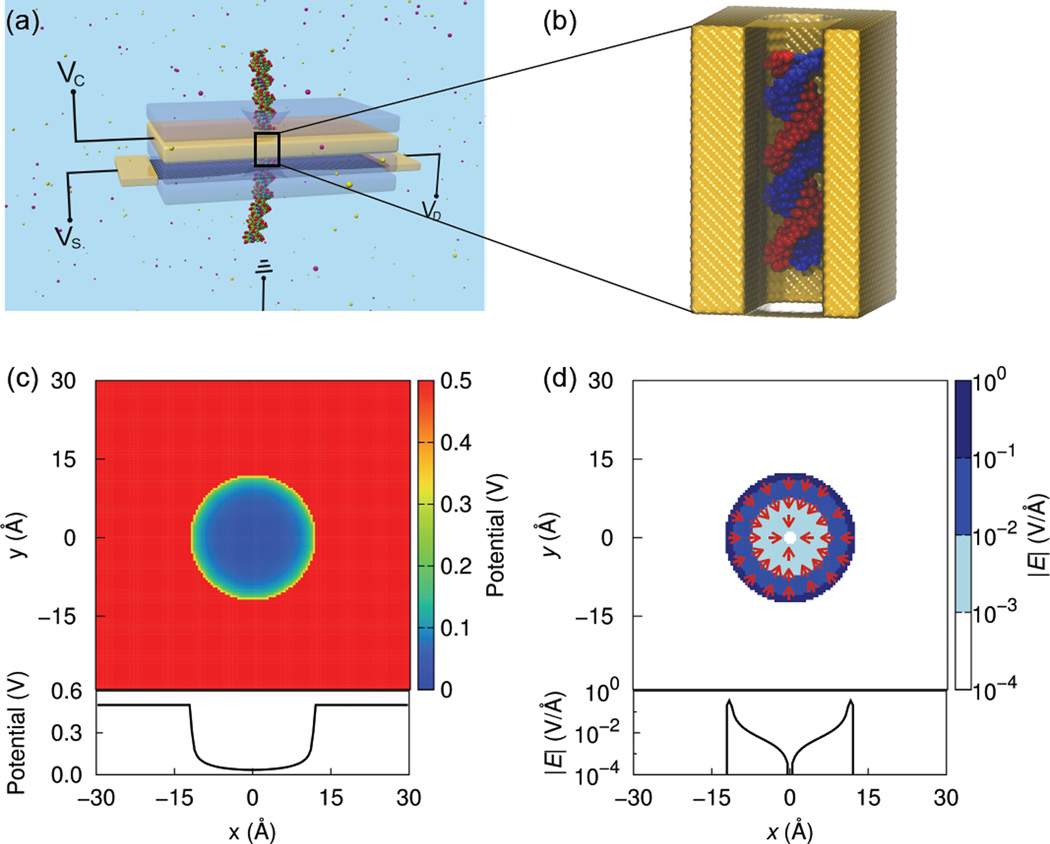
In SSNs, a possible strategy to control molecule motions is the use of a multi-layered membrane transistor containing a motion-control electrode layer,30 as shown in Fig. 1a, which shapes the electrostatic landscape in the nanopore to reduce the stochastic fluctuations of the interior biomolecules. To explore this possibility, we carried out computational studies that first self-consistently solve for the electrostatic potential arising from the biased motion-control layer containing two types of nanopores, one with a cylindrical cross section and a second one with a teardrop-shape cross section. We then performed a series of molecular dynamics simulations to determine the effect of the generated electrostatic potential on the motion of a double-stranded DNA (dsDNA) in the nanopore. The results show that DNA fluctuations can be reduced by positive voltage biases higher than 0.5 V, suggesting a promising strategy to stabilize DNA inside nanopores. The reduction of DNA fluctuations could lower the conformational noise in the nucleotide signal measured by a secondary sensing membrane layer, and in turn, improve the sensitivity of nucleotide detection and identification.
Figure 1.
(a) Schematic of a prototypical multilayer transistor with a nanopore for DNA manipulation and detection. A metallic control layer (yellow), sandwiched between two insulating oxide layers (blue), is biased at a voltage VC. A conducting sensing membrane such as a graphene monolayer, biased at VD and VS, is used to detect the passing DNA molecule. The system is biased with respect to a common ground. (b) System of molecular dynamics simulations in this study. The system consists of a dsDNA confined within a nanopore in a metallic membrane. To render the DNA molecule visible, the front part of the membrane is left transparent. (c,d) Electrostatic potential (c) and magnitude of electric field (d), in the x, y-plane (top panel) and along a line across the nanopore diameter (bottom panel), of a 0.5 V biased cylindrical nanopore. Arrows denote the directions of local electric fields.
Results and Discussion
We first consider, as shown in Fig. 1a, a nanopore in a stacked membrane with a cylindrical cross-section and 2.4 nm diameter. In a typical device, the metallic motion-control layer of the stacked membrane is biased at a control voltage, VC, and isolated from the sensing membrane (e.g., graphene) by an oxide layer such as SiO221 or Al2O331. In the later case, a multi-layered graphene-Al2O3 membrane was fabricated through alternately depositing the layers of graphene and Al2O3 onto a substrate31. The control voltage is varied from −0.75 V to 0.75 V by applying Dirichlet boundary conditions to the electrode layer, as described in Methods. The control voltage, as well as source (VS) and drain (VD) voltages across the sensing membrane, are set with respect to a common ground30.
Figures 1c and 1d show the electrostatic potential and the associated electric field, respectively, in a plane perpendicular to the nanopore axis and at an electrode voltage of 0.5 V. The potential is constant within the metallic interior, but drops rapidly after crossing the pore boundary, due to the large screening of Cl− ions that are attracted by the positively charged pore surface. The potential along a line through the nanopore center is shown in the bottom panel of Fig. 1c. The potential is nearly zero in most regions inside the pore, while a fast drop near the pore surface is observed, leading to a strong local electric field on the order of 0.1 V/Å (Fig. 1d). Besides, the local electric field at every point inside the pore points uniformly to the pore center (Fig. 1d). At negative electrode biases, the fields and potentials are identical in magnitude but opposite in sign to those for positive voltages.
The calculated potential was then incorporated in MD simulations to determine its influence on the motion of a dsDNA molecule confined in the pore (Fig. 1b). In Figs. 2a and 2b, we show center of mass (CM) positions of the DNA molecule in the xy-plane for each frame in the last 50 ns of 70 ns simulation trajectories at positive and negative voltages, respectively. At zero electrode bias, the DNA positions at different times spread almost uniformly inside the pore, as no significant interaction between the pore and the DNA molecule exists. We also note that, the center point, around which the DNA resides, deviates slightly from the pore center by 0.2 Å, which accounts for about 0.8% of the pore diameter (2.4 nm), due to limited sampling of possible DNA conformations in the MD simulations. At positive voltages (Fig. 2a), on the other hand, the DNA CM positions become more localized around a specific location in the pore, indicating damping of the DNA motion. This location is also not exactly at the pore center because of the slight randomness in conformational change in response to applied voltages. The reduction of DNA fluctuations is discernible through the backbone spread in the overlapped DNA conformations obtained from the MD trajectory at 0.5 V (middle panel in Fig. 2c), which is thinner than that in the voltage-free case (left panel). Such a stabilization effect produced by positive voltages is the consequence of electrostatic attraction between the positively charged pore surface and the negatively charged DNA backbone. In addition, larger positive electrode voltages reduce the area within which the DNA CM is found (Fig. 2a), suggesting that larger voltages reduce the motion of the DNA molecule more strongly.
Figure 2.
Scatter diagram showing center of mass positions of dsDNA in the last 50 ns of the 70 ns simulation trajectory at (a) positive and (b) negative voltages. (c) Overlapped conformations of the DNA in a 5 ns MD trajectory at 10 ps intervals under voltage biases of 0 (left), 0.5 (middle), −0.5 V (right).
At negative voltages, however, the DNA still fluctuates greatly, as indicated by the broad distribution of DNA CM positions (Fig. 2b) and the thicker backbone spread in the DNA conformations (right panel in Fig. 2c). The DNA was compressed significantly in the lateral direction due to strong repulsion between the negatively charged pore surface and the DNA backbone. Because DNA is a soft biological molecule, it does not necessarily achieve a perfect symmetric configuration around the pore center after the compression (see the right panel in Fig. 2c, for instance). As a result, the scattering of DNA CM positions is centered at a random position, but very close to the pore center. Such randomness in the DNA positions is further supported by another independent series of simulations (see Fig. S1 in Supporting Information), where the DNA CM positions are quite different from those obtained in the above simulations at the same negative voltages. The only difference between the two groups of simulations lies in the seed of a random number generator that was used to assign the initial velocity of each atom in the system.
Figures 3a and 3c show the root mean square deviation (RMSD) profiles of all non-hydrogen atoms of the central portion of the dsDNA from the starting conformation, namely nucleotides between the 6th and 17th base-pair of the 22 base-pairs, under positive and negative electrode voltages, respectively. In the voltage-free case, the DNA RMSD fluctuates around an average value of 2.1 Å during the whole simulation (black curve in Figs. 3a or 3c), with a high moving standard deviation ranging from 0.2 to 0.5 Å (black curve in Figs. 3b or 3d). When a positive voltage VC = 0.25 V is applied to the electrode, the overall RMSD profile (red) fluctuates around a relatively larger average displacement of ~3.5 Å from the starting conformation of the DNA (Fig. 3a), with a moving standard deviation between 0.15 and 0.3 Å that is reduced compared to the voltage-free case (Fig. 3b). The conformational change is attributed to the lateral expansion of the dsDNA in the x, y-plane of the cylindrical pore that is induced by electrostatic attraction between the positively charged pore surface and the negatively charged DNA backbone. As the positive voltage further increases to VC = 0.5 V, the DNA RMSD profile exhibits an enhanced conformational change from the starting DNA structure with an average displacement of ~4.7 Å (green). In parallel, the moving standard deviation of the RMSD profile at this voltage is significantly reduced compared to VC values at 0.25 and 0 V, indicating that the thermal fluctuation of dsDNA is greatly inhibited (see also middle panel in Fig. 2c). When the positive voltage is increased to 0.75 V (blue curve in Fig. 3a), the dsDNA exhibits comparable RMSD values to those at 0.5 V voltage, indicating that the lateral expansion of the DNA becomes saturated. However, the decreased moving standard deviation observed at 0.75 V electrode voltage suggests that higher positive voltages achieve stronger stabilization (blue curve in Fig. 3b). The stabilization at positive voltages is induced by the adhesion of DNA to the pore surface. Once adhered, the DNA molecule cannot detach easily from the pore surface unless a non-positive voltage is applied, as we document now.
Figure 3.
(a,c) RMSDs of all non-hydrogen atoms of the central portion of the dsDNA, namely nucleotides between the 6th and 17th base-pair of the 22 base-pairs, from the starting DNA conformation in MD simulations at positive (a) and negative (c) bias voltages. The thick lines represent moving average over 100 data points. (b,d) Moving standard deviation over 100 data points of RMSD for positive (b) and negative (d) voltages.
In sharp contrast to the positive electrode biases, no evident stabilization effect is observed when negative voltages are applied to the membrane, as indicated by the large fluctuations in RMSD profiles for all negative voltages (Figs. 3c and 3d). However, the RMSD values are also increased at these negative voltages from the voltage-free case, the increase being induced by the lateral shrinkage of DNA due to electrostatic repulsion between the negatively charged pore surface and DNA backbone (see also right panel in Fig. 2c). In all cases for negative voltages, the moving standard deviation displays no significant dependence on voltage strength (Fig. 3d), further indicating that negative voltages cannot effectively stabilize the DNA.
A quick response to changes in electrode voltage is of significance in applications where real-time and precise manipulation of biological molecules is required. To assess the possibility, we simulated the response of a DNA molecule to a pulsed voltage of 0.5 V, namely a voltage turned on and off repeatedly every 30 ns, as depicted in Fig. 4a. Figures 4b and 4c show the moving average and standard deviation of the RMSD of a dsDNA molecule from the initial configuration, respectively. When the voltage is turned on, the lower fluctuations in RMSD profile (Fig. 4b), validated by a lower standard deviation (Fig. 4c), indicate the stabilization of DNA in the nanopore. When the voltage is turned off, the DNA reverts, as expected, to a configuration with lower RMSDs, but larger fluctuations. When the positive voltage is turned on again, the fluctuations are again suppressed. In addition, it is worth mentioning that the stabilization is achieved within 1 ns after turning on the voltage, indicating the ability of a real-time and precise manipulation to DNA motion.
Figure 4.
Controllable stabilization of DNA by a pulsed voltage of 0.5 V. (a–c) Voltage applied to the electrode (a), calculated RMSD from the starting configuration (b) and the associated standard deviation (c) versus simulation time.
In all above simulations, a circular pore was considered to confine DNA and generate the potential landscape for DNA stabilization. As expected, the dwelling area of the DNA CM positions inside such a symmetric pore is approximately circular (Fig. 2). In realistic experiments, however, a fabricated pore hardly turns out to be a perfect cylinder. For instance, nanopores drilled into solid-state membranes, by focused ion beams,32 high-energy electron beams33 or dielectric breakdown,34 adopt cross-sections that are irregularly shaped and not symmetric around the pore center. In this context, one may wonder if a pore with a lower spatial symmetry can achieve a customized control on the DNA conformation. For this purpose, we consider a teardrop-shape pore to assess the influence of THE pore geometry on DNA behaviour, as shown in Fig. 5a. In Figs. 5b and 5c, we show the electrostatic potential and electric field for a teardrop-shape nanopore, respectively, at a positive electrode voltage of 0.5 V. Potential and electric field are no longer symmetric in the x-direction, but rather, decay more slowly away from the sharp end (left) than from the smooth end (right) of the tear-drop circumference. When the obtained potential is applied to the DNA molecule, a strong DNA localization occurs again, as seen from the concentrated distribution of CM positions (green dots in Fig. 5d) compared to the voltage-free case (black dots in Fig. 5d). In addition, it is worth noting that the DNA moves slightly leftward to approach the sharp end under the positive voltage, mainly due to the relatively higher magnitude and slower decay of the potential/electric field on the left side of the pore. At a negative voltage of VC=−0.5 V, the inhibition of DNA fluctuation and the leftward movement of DNA center are insignificant compared to the positive voltage case. The demonstrated controllable alignment of DNA inside shaped nanopores is of critical importance in DNA sensing applications where a high-sensitivity DNA sensing emerges only when DNA bases are aligned along a specific direction, for example, perpendicular to the owing direction of the transverse current.35
Figure 5.
Customized control of DNA alignment through pore geometry shaping. (a) Geometry of the cross-section of the teardrop-shape nanopore simulated in the present study. (b,c) Electrostatic potential (b) and magnitude of electric field (c) of the teardrop-shape nanopore at 0.5 V electrode voltage, in the x, y-plane (top panel) and along a line across the center and the sharp end of the pore (bottom panel). The nanopore center is defined as x, y = 0,0 and depicted as a star. (d) Scatter diagram showing center of mass positions of DNA in MD simulations at electrode voltages of 0, 0.5 and −0.5 V.
Conclusions
In summary, we suggest the use of a biased nanopore to quench DNA conformational fluctuations by combining self-consistent electrostatic potential calculations and molecular dynamics simulations. We found that DNA molecules are stabilized by imposing positive voltages higher than 0.5 V on the nanopore electrodes. The reduction of DNA fluctuations is attributed to the electrostatic attraction between the negatively charged DNA backbone and the positively charged pore surface. No evident conformational response of DNA occurs at negative electrode voltages. The use of a teardrop-shape pore yields also a teardrop-shape distribution of DNA positions, which shrinks significantly and shifts slightly toward the sharp end of the pore under positive electrode voltages. The present findings open a simple and efficient route to control motions of biological molecules inside nanopores to improve the signal-to-noise ratio, which is highly desirable for nanopore sensing applications.
Methods
Our methodological approach outlined here includes calculation of the electrostatic potential arising from various voltage biases at the motion-control electrode layer and subsequent classic MD simulations of DNA fluctuations under the obtained potentials, which were applied to the DNA molecule via the grid force module of NAMD2.36
Electrostatic Potential Calculations
The electrostatic potential ϕ inside a nanopore filled up with electrolytic solution was obtained by solving the Poisson equation in three dimensions
| (1) |
where ε(r) is the position-dependent dielectric constant, i.e., ε = 78 in water and ε → ∞ at the metal electrode. The right-hand-side charge term includes ions in solution (K+ and Cl−), which are described assuming a Boltzmann equilibrium, namely through13
| (2) |
where cK+ and cCl− are the local ion concentrations of K+ and Cl−, and c0 is the molar concentration of the solution, taken to be 0.3 M.
The system was discretized within a Cartesian box onto a non-uniform, rectilinear grid. Neumann boundary conditions were imposed on the sides of the box,
| (3) |
while the top and bottom of the box were subjected to Dirichlet boundary conditions,
| (4) |
All electrode points were also subjected to Dirichlet conditions, with the potential ϕ set to the given bias voltage.
Eqn. 1 can be solved self-consistently using a number of methods. In the present study, we adopted a Newton-Multigrid37–39 method that discretizes the system onto a 129 × 129 × 129 point uniform grid. Starting from the finest grid, Jacobi relaxation was performed to obtain an initial guess for the solution ϕ. Then, the solution was interpolated and relaxed on subsequently coarser grids to smooth out high-frequency errors. Finally, the error to the solution was relaxed and interpolated on finer grids until the original, fine-grid solution was corrected. Once the solution ϕ was obtained, it was re-inserted back into the Poisson equation, and this process was repeated until the desired convergence was reached. A full description of the exact procedure followed has been provided earlier.37–39
Molecular Dynamics Simulations
A dsDNA helix containing 22 base-pairs of dA-dT was constructed by the X3DNA program.40 For the sake of simplicity, we placed the DNA strand, subjected to mathematical boundaries representing the confinement of DNA in a cylindrical or tear-drop shape nanopore, in a water box. Inclusion of a real material as the motion-control layer, such as copper or gold, would alter the stabilization behaviour demonstrated here; in some cases, the stabilization effect may be promoted due to the strong intrinsic interaction between the pore and DNA molecule.
K+ and Cl− ions were randomly added to the water box to make the system charge neutral and achieve an ion concentration at 0.3 M. All simulations were carried out with NAMD 2.9,36 and visualized and analyzed with VMD.41 A Langevin thermostat was adopted to maintain constant temperature at 300 K. Periodic boundary conditions were imposed to all directions and, thereby, an infinitely long nanopore was obtained in the z-direction. DNA was described with the CHARMM2742 force field and water was modelled by the TIP3P43 water model. A time step of 2 fs was used in all simulations. The particle-mesh-Ewald method44 was employed to treat the long-range electrostatic interactions. van der Waals energies were calculated using a cut-off of 12 Å. After a 5000-step energy minimization, the system was initially equilibrated for 2 ns as an NPT ensemble, in which the Langevin piston method45 was used to control the pressure at 1 atm. The calculated potential through Eqn. 1 was then applied to the DNA only in the MD simulations, as the redistribution of ions and water by the potential has already been taken into account in the Poisson-Boltzmann solution of Eqn. 1. At a given voltage, each simulation was run for 70 ns as an NVT ensemble for data analysis.
Supplementary Material
Acknowledgments
This work was supported by grants from Oxford Nanopore Technology, the Seeding Novel Interdisciplinary Research Program of the Beckman Institute, National Institutes of Health grant 9P41GM104601 and National Science Foundation grants PHY0822613 and PHY1430124. The authors gratefully acknowledge also supercomputer time provided through the Extreme Science and Engineering Discovery Environment (XSEDE) grant MCA93S028 and by the University of Illinois at Urbana-Champaign on the TAUB cluster.
Footnotes
Supporting Information Available
Additional simulation results showing the randomness of DNA position distribution at negative electrode voltages. This material is available free of charge via the Internet at http://pubs.acs.org/.
Contributor Information
Klaus Schulten, Email: kschulte@ks.uiuc.edu.
Jean-Pierre Leburton, Email: jleburto@illinois.edu.
References
- 1.Taber KAJ, Dickinson BD, Wilson M. The Promise and Challenges of Next-Generation Genome Sequencing for Clinical Care. JAMA Intern. Med. 2014;174:275–280. doi: 10.1001/jamainternmed.2013.12048. [DOI] [PubMed] [Google Scholar]
- 2.Schadt EE, Turner S, Kasarskis A. A Window into Third-Generation Sequencing. Hum. Mol. Gen. 2010;19:R227–R240. doi: 10.1093/hmg/ddq416. [DOI] [PubMed] [Google Scholar]
- 3.Branton D, Deamer DW, Marziali A, Bayley H, Benner SA, Butler T, Di Ventra M, Garaj S, Hibbs A, Huang X, Jovanovich SB, Krstic PS, Lindsay S, Ling XS, Mastrangelo CH, Meller A, Oliver JS, Pershin YV, Ramsey JM, Riehn R, et al. The Potential and Challenges of Nanopore Sequencing. Nat. Biotechnol. 2008;26:1146–1153. doi: 10.1038/nbt.1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Venkatesan BM, Bashir R. Nanopore Sensors for Nucleic Acid Analysis. Nature Nanotech. 2011;6:615–624. doi: 10.1038/nnano.2011.129. [DOI] [PubMed] [Google Scholar]
- 5.Schloss JA. How to Get Genomes at One Ten-Thousandth the Cost. Nat. Biotechnol. 2008;26:1113. doi: 10.1038/nbt1008-1113. [DOI] [PubMed] [Google Scholar]
- 6.Bezrukov SM, Vodyanoy I, Brutyan RA, Kasianowicz JJ. Dynamics and Free Energy of Polymers Partitioning into a Nanoscale Pore. Macromolecules. 1996;29:8517–8522. [Google Scholar]
- 7.Kasianowicz JJ, Brandin E, Branton D, Deamer DW. Characterization of Individual Polynucleotide Molecules using a Membrane Channel. Proc. Natl. Acad. Sci. USA. 1996;93:13770–13773. doi: 10.1073/pnas.93.24.13770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Akenson M, Branton D, Kasianowicz JJ, Brandin E, Deamer DW. Microsecond Time-Scale Discrimination among Polycytidylic Acid, Polyadenylic Acid, and Polyuridylic Acid as Homopolymers or as Segments Within Singe RNA Molecules. Biophys. J. 1999;77:3227–3233. doi: 10.1016/S0006-3495(99)77153-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kumar S, Tao C, Chien M, Hellner B, Balijepalli A, Robertson JW, Li Z, Russo JJ, Reiner JE, Kasianowicz JJ, Ju J. PEG-Labeled Nucleotides and Nanopore Detection for Single Molecule DNA Sequencing by Synthesis. Sci. Rep. 2012;2 doi: 10.1038/srep00684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Reiner JE, Balijepalli A, Robertson JW, Campbell J, Suehle J, Kasianowicz JJ. Disease Detection and Management via Single Nanopore-Based Sensors. Chem. Rev. 2012;112:6431–6451. doi: 10.1021/cr300381m. [DOI] [PubMed] [Google Scholar]
- 11.Xie P, Xiong Q, Fang Y, Qing Q, Lieber CM. Local Electrical Potential Detection of DNA by Nanowire-Nanopore Sensors. Nature Nanotech. 2012;7:119–125. doi: 10.1038/nnano.2011.217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Howorka S, Siwy Z. Nanopore Analytics: Sensing of Single Molecules. Chem. Soc. Rev. 2009;38:2360–2384. doi: 10.1039/b813796j. [DOI] [PubMed] [Google Scholar]
- 13.Gracheva ME, Xiong A, Aksimentiev A, Schulten K, Timp G, Leburton J-P. Simulation of the Electric Response of DNA Translocation through a Semiconductor Nanopore-Capacitor. Nanotechnology. 2006;17:622–633. [Google Scholar]
- 14.Li J, Gershow M, Stein D, Brandin E, Golovchenko J. DNA Molecules and Configurations in a Solid-State Nanopore Microscope. Nat. Mater. 2003;2:611–615. doi: 10.1038/nmat965. [DOI] [PubMed] [Google Scholar]
- 15.Carlsen AT, Zahid OK, Ruzicka J, Taylor EW, Hall AR. Interpreting the Conductance Blockades of DNA Translocations through Solid-State Nanopores. ACS Nano. 2014;8:4754–4760. doi: 10.1021/nn501694n. [DOI] [PubMed] [Google Scholar]
- 16.Sathe C, Zou X, Leburton J-P, Schulten K. Computational Investigation of DNA Detection using Graphene Nanopores. ACS Nano. 2011;5:8842–8851. doi: 10.1021/nn202989w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Skinner GM, van den Hout M, Broekmans O, Dekker C, Dekker NH. Distinguishing Single- and Double-Stranded Nucleic Acid Molecules using Solid-State Nanopores. Nano Lett. 2009;9:2953–2960. doi: 10.1021/nl901370w. [DOI] [PubMed] [Google Scholar]
- 18.Dekker C. Solid-State Nanopores. Nature Nanotech. 2007;2:209–215. doi: 10.1038/nnano.2007.27. [DOI] [PubMed] [Google Scholar]
- 19.Wanunu M, Sutin J, McNally B, Chow A, Meller A. DNA Translocation Governed by Interactions with Solid-State Nanopores. Biophys. J. 2008;95:4716–4725. doi: 10.1529/biophysj.108.140475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schneider GF, Kowalczyk SW, Calado VE, Pandraud G, Zandbergen HW, Vandersypen LMK, Dekker C. DNA Translocation through Graphene Nanopores. Nano Lett. 2010:3163–3167. doi: 10.1021/nl102069z. [DOI] [PubMed] [Google Scholar]
- 21.Merchant CA, Healy K, Wanunu M, Ray V, Peterman N, Bartel J, Fischbein MD, Venta K, Luo Z, Johnson ATC, Drndić M. DNA Translocation through Graphene Nanopores. Nano Lett. 2010;10:2915–2921. doi: 10.1021/nl101046t. [DOI] [PubMed] [Google Scholar]
- 22.Garaj S, Hubbard W, Reina A, Kong J, Branton D, Golovchenko JA. Graphene as a Subnanometre Trans-Electrode Membrane. Nature. 2010;467:190–193. doi: 10.1038/nature09379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Qiu H, Guo W. Detecting ssDNA at Single-Nucleotide Resolution by Sub-2-Nanometer Pore in Monoatomic Graphene: A Molecular Dynamics Study. Appl. Phys. Lett. 2012;100:083106. [Google Scholar]
- 24.Liu K, Feng J, Kis A, Radenovic A. Atomically Thin Molybdenum Disulfide Nanopores with High Sensitivity for DNA Translocation. ACS Nano. 2014;8:2504–2511. doi: 10.1021/nn406102h. [DOI] [PubMed] [Google Scholar]
- 25.Qiu H, Sarathy A, Leburton J-P, Schulten K. Intrinsic Stepwise Translocation of Stretched ssDNA in Graphene Nanopores. Nano Lett. 2015;15:8322–8330. doi: 10.1021/acs.nanolett.5b03963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zwolak M, Ventra MD. Electronic Signature of DNA Nucleotides via Transverse Transport. Nano Lett. 2005;5:421–424. doi: 10.1021/nl048289w. [DOI] [PubMed] [Google Scholar]
- 27.Manrao EA, Derrington IM, Laszlo AH, Langford KW, Hopper MK, Gillgren N, Pavlenok M, Niederweis M, Gundlach JH. Reading DNA at Single-Nucleotide Resolution with a Mutant MspA Nanopore and Phi29 DNA Polymerase. Nat. Biotechnol. 2012;30:349–353. doi: 10.1038/nbt.2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Laszlo AH, Derrington IM, Brinkerhoff H, Langford KW, Nova IC, Samson JM, Bartlett JJ, Pavlenok M, Gundlach JH. Detection and Mapping of 5-Methylcytosine and 5-Hydroxymethylcytosine with Nanopore MspA. Proc. Natl. Acad. Sci. USA. 2013;110:18904–18909. doi: 10.1073/pnas.1310240110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Derrington IM, Craig JM, Stava E, Laszlo AH, Ross BC, Brinkerhoff H, Nova IC, Doering K, Tickman BI, Ronaghi M, Mandell JG, Gunderson KL, Gundlach JH. Subangstrom Single-Molecule Measurements of Motor Proteins using a Nanopore. Nat. Biotechnol. 2015;33:1073–1075. doi: 10.1038/nbt.3357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Girdhar A, Sathe C, Schulten K, Leburton J-P. Graphene Quantum Point Contact Transistor for DNA Sensing. Proc. Natl. Acad. Sci. USA. 2013;110:16748–16753. doi: 10.1073/pnas.1308885110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Venkatesan BM, Estrada D, Banerjee S, Jin X, Dorgan VE, Bae M-H, Aluru NR, Pop E, Bashir R. Stacked Graphene-Al2O3 Nanopore Sensors for Sensitive Detection of DNA and DNA–Protein Complexes. ACS Nano. 2011;6:441–450. doi: 10.1021/nn203769e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gershow M, Golovchenko JA. Recapturing and Trapping Single Molecules with a Solid-State Nanopore. Nature Nanotech. 2007;2:775–779. doi: 10.1038/nnano.2007.381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Storm AJ, Chen JH, Ling XS, Zandergen HW, Dekker C. Fabrication of Solid-State Nanopore with Single-Nanometre Precision. Nat. Mater. 2003;2:537–540. doi: 10.1038/nmat941. [DOI] [PubMed] [Google Scholar]
- 34.Yanagi I, Akahori R, Hatano T, Takeda K-i. Fabricating Nanopores with Diameters of Sub-1 nm to 3 nm using Multilevel Pulse-Voltage Injection. Sci. Rep. 2014;4:5000. doi: 10.1038/srep05000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Girdhar A, Sathe C, Schulten K, Leburton J-P. Tunable Graphene Quantum Point Contact Transistor for DNA Detection and Characterization. Nanotechnology. 2015;26:134005. doi: 10.1088/0957-4484/26/13/134005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable Molecular Dynamics with NAMD. J. Comp. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Trottenberg U, Oosterlee CW, Schuller A. Multigrid. Academic press; 2000. [Google Scholar]
- 38.Briggs WL, McCormick SF. A Multigrid Tutorial. Siam; 2000. [Google Scholar]
- 39.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C (2Nd Ed.): The Art of Scientific Computing. New York, NY, USA: Cambridge University Press; 1992. [Google Scholar]
- 40.Lu X-J, Olson WK. 3DNA: A Software Package for the Analysis, Rebuilding and Visualization of Three-Dimensional Nucleic Acid Structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Humphrey W, Dalke A, Schulten K. VMD – Visual Molecular Dynamics. J. Mol. Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 42.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher IWE, et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 43.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 44.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 45.Feller SE, Zhang Y, Pastor RW, Brooks BR. Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995;103:4613–4621. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.