Cellular Contraction and Polarization Drive Collective Cellular Motion

Abstract

Coordinated motions of close-packed multicellular systems typically generate cooperative packs, swirls, and clusters. These cooperative motions are driven by active cellular forces, but the physical nature of these forces and how they generate collective cellular motion remain poorly understood. Here, we study forces and motions in a confined epithelial monolayer and make two experimental observations: 1) the direction of local cellular motion deviates systematically from the direction of the local traction exerted by each cell upon its substrate; and 2) oscillating waves of cellular motion arise spontaneously. Based on these observations, we propose a theory that connects forces and motions using two internal state variables, one of which generates an effective cellular polarization, and the other, through contractile forces, an effective cellular inertia. In agreement with theoretical predictions, drugs that inhibit contractility reduce both the cellular effective elastic modulus and the frequency of oscillations. Together, theory and experiment provide evidence suggesting that collective cellular motion is driven by at least two internal variables that serve to sustain waves and to polarize local cellular traction in a direction that deviates systematically from local cellular velocity.

Introduction

During wound repair, embryonic development, and cancer invasion, cells migrate in cooperative packs (1, 2, 3) that generate swirls (4, 5) and waves (6, 7). Our understanding of how cellular forces generate these collective behaviors is limited, but recent experiments have offered some clues. First, within a confluent monolayer cells tend to migrate along orientations of minimal intercellular shear stress (8, 9, 10); cell-cell junctions along these orientations carry appreciable normal stresses but only minimal shear stresses. Second, far from any boundary, each cell exerts local tractions upon its substrate that tend to align with the direction of local motion (8, 11); near a boundary, by contrast, tractions tend to align systematically toward the cell-free boundary regardless of the direction of local cellular motion (11).

Some previous theoretical models (12, 13, 14, 15), but not all (16), have recognized that local tractions can align in a direction that deviates transiently, but not systematically, from that of the local velocity. This transient misalignment has been modeled by introducing noisy fluctuations around a tendency toward realignment (15, 17) or via an internal variable that regulates the correlation between traction and velocity (12, 13, 14). Here, we provide further evidence that each cell polarizes so as to apply local traction in a direction that can deviate systematically from its local velocity, and that this systematic deviation is a general property of collective cellular motion. If local traction and local velocity are not aligned, it follows logically that tractions cannot result solely from viscous friction between the moving cell and its motionless substrate; rather, tractions must be regulated by variables in addition to velocity (12, 13, 14).

To identify state variables that control cellular motion and propulsive forces, we study oscillating collective waves of cellular motion that are known to arise spontaneously in a confined epithelial monolayer (7). Oscillations in passive mechanical systems result from the exchange of elastic potential energy and inertial kinetic energy. Previous work has established that cell layers behave elastically (6) but have negligible inertia (13, 14, 15). To account for the collective oscillations of cellular motion, we therefore propose an internal variable that provides an effective inertia in the sense that it sets a timescale for turnover in intracellular contractile tension (14). To account for the local angular deviation between cell traction and velocity, we propose a second internal variable that we call cell polarization. Using a minimal physical model, we show that these two internal state variables account for both the experimentally observed oscillatory waves of motion and local systematic angular deviation between cell traction and velocity. We conclude that the collective modes of cellular motion result from an interplay between cell contraction and polarization.

Materials and Methods

Cell culture

Madin-Darbvy canine kidney type II cells, expressing GFP with a nuclear localization signal (pAcGFP1-Nuc vector, Clontech), were supplied by A. Pegoraro and D. Weitz (Harvard University). The cells were maintained in low-glucose Dulbecco’s modified Eagle’s medium (12320-032; Life Technologies, Carlsbad, CA) with 10% fetal bovine serum (Corning) and 1% penicillin-streptomycin (Sigma-Aldrich. St. Louis, MO) in an incubator at 37°C and 5% CO₂.

Preparation of polyacrylamide substrates

Polyacrylamide gels with Young’s modulus of 6 kPa and thickness of 100 μm were polymerized by preparing a solution of 5.5% weight/volume (w/v) acrylamide (Biorad Laboratories, Hercules, CA), 0.20% w/v bisacrylamide (Biorad Laboratories), 0.014% w/v fluorescent particles (diameter 0.5 μm, carboxylate-modified; Life Technologies), 0.05% w/v ammonium persulfate (Biorad Laboratories), and 1/2000 volume/volume TEMED (Biorad Laboratories). The gel solution was pipetted onto no. 1.5 glass bottom dishes (In Vitro Scientific, Mountain View, CA), a glass coverslip (no. 1 thickness, 18-mm diameter circle) was placed on top, and the dishes were centrifuged upside down so that the fluorescent particles collected at the top surface of the gel. The gels were functionalized with type l rat tail collagen (BD Biosciences, Franklin Lakes, NJ; 0.01 mg/mL, 1 mL per 18-mm diameter gel) using the covalent cross-linker sulfo-SANPAH (Pierce Biotechnology, Waltham, MA) as described previously (18).

Micropatterning expanding and confined cellular islands

Masks were prepared with circular holes (diameter 700 μm) using standard techniques in soft lithography similar to those described previously (6). Silicon-photoresist masters were custom fabricated (MicroFit, Seongnam-si, Gyeonggi-do, Korea), and polydimethylsiloxane (PDMS) (Sylgard 184, Dow Corning, Midland, MI) was poured onto the masters to cure overnight on a hot plate at 80°C. The PDMS masks were sterilized with 70% ethanol and incubated at 37°C in 2% Pluronic F-127 (Sigma-Aldrich) for 4 h to prevent cell adhesion to the masks. For expanding islands, masks were placed on the collagen-coated polyacrylamide gels, and a 200 μL droplet of cell suspension (4 × 10⁵ cells total) was placed on each mask. The gels were transferred to a 37°C/5% CO₂ incubator for 45 min for the cells to adhere to the collagen. Afterward, the 200 μL droplets were aspirated off of the PDMS masks, the masks were removed with tweezers, and the gels were rinsed with phosphate-buffered saline (PBS) before addition of 3 mL fresh medium. For confined islands, masks were placed onto the polyacrylamide gels before functionalizing with collagen, thus leaving a circular island of collagen to which the cells adhered. Imaging of the cell monolayers began approximately 1 h after seeding and continued for ∼30 h.

Microscopy

Images of the cells, nuclei, and beads were captured every 20 min using phase-contrast (for cells) or fluorescent (for nuclei and beads) microscopy using a DMI6000B microscope with a 5× NA 0.12 objective and a DFC345FX CCD camera (Leica Microsystems, Wetzlar, Germany). Fluorescent particles and cell nuclei were imaged with fluorescence; cells were imaged with phase contrast. The imaging environment was maintained at 37°C/5% CO₂ in a heated enclosure (PeCon, Erbach, Germany). For experiments with expanding cellular islands a 2 × 2 grid of images was captured and stitched together using the freely available Fiji distribution of ImageJ (http://fiji.sc/Fiji) (19). After each time-lapse experiment, cells were removed from the polyacrylamide substrates by incubating in 0.05% trypsin for 20 min, and images of the fluorescent particles were collected; these images captured a stress-free reference state of the polyacrylamide substrates for subsequent computation of tractions.

Measuring cell velocity and rate-of-strain

The velocity fields were measured using custom particle image velocimetry (also called digital image correlation) software of phase contrast images written in Matlab (The Mathworks, Natick, MA). Interrogation windows of 64 × 64 pixels were used; this window size allowed for a spatial resolution of ∼16 pixels (14 μm). Boundaries of the cell islands were detected automatically using a previously described protocol (20). The rate-of-strain tensor was computed by numerically differentiating the velocity fields in space.

Traction force microscopy and monolayer stress microscopy

Displacements of the particles were measured using digital image correlation, and tractions exerted between the cell layer and its substrate were computed using unconstrained Fourier transform traction microscopy (21) taking into account the effects of finite substrate thickness (18, 22). From these measured tractions we computed the distribution of internal stresses within the cell layer using monolayer stress microscopy (MSM) (8, 23).

MSM rests upon the main assumptions that the cell layer is flat, continuous and thin. Regardless of material properties of the cell layer, including any effects of nonlinearity and viscoelasticity, Newton’s laws in one dimension demand that these internal stresses and boundary traction stresses must always remain in precise balance, and the MSM solution in that case is therefore exact (8, 23). In two dimensions, matters are slightly more complicated, because the Poisson effect makes the solution inexact. Nevertheless, the sensitivity to the Poisson effect has been shown to be quite small, and the solution has been shown to be insensitive to a remarkably wide range of assumptions about material properties of the cell layer itself, its nonlinearity, and its viscoelasticity (8, 23); this finding was further validated independently by Zimmermann et al. (17), who used a particle-based simulation to show that the stresses in the simulation are recovered by MSM with a high degree of accuracy. In two dimensions, three independent components of the stress tensor within the monolayer are obtained by solving three coupled equations. Two of those equations describe force balance, making no assumptions about the properties of the monolayer (8, 23). The third equation is the compatibility of the deformation field. (For more information, see the Supporting Material.) Displacements, tractions, and stresses are measured at the same spatial resolution as the velocity field, 14 μm.

Measuring cell area and density

The position of each cell’s nucleus was computed from the fluorescent images of nuclei using the watershed transform in Matlab. For each cell, the distance between its nucleus and the nuclei of the nearest six neighbors was computed and averaged; this distance was taken to be the diameter of that cell. From each cell’s diameter, its area was computed. Density is computed by taking the inverse of the cell area. To compute the gradient in density, each 3 × 3 window of data points is fit to a linear equation in the x direction and to a second linear equation in the y direction. The slopes give the derivatives in the x and y directions, respectively.

Chemical treatments

Chemical treatments were blebbistatin (20 μM), U0126 (10 μM), and epidermal growth factor (EGF) (20 ng/mL). Blebbistatin and U0126 were dissolved in dimethyl sulfoxide (DMSO); EGF was dissolved in PBS. Blebbistatin and U0126 stock solutions were 20 mM and 10 mM, respectively. They were diluted by a factor of 1000 when added to the medium, leading to a DMSO concentration of 0.1% in the cell culture medium. All comparisons were made to matching concentrations of a vehicle control (DMSO or PBS).

Statistics

Statistical comparisons were made using the nonparametric Wilcoxon rank sum test in Matlab.

Results

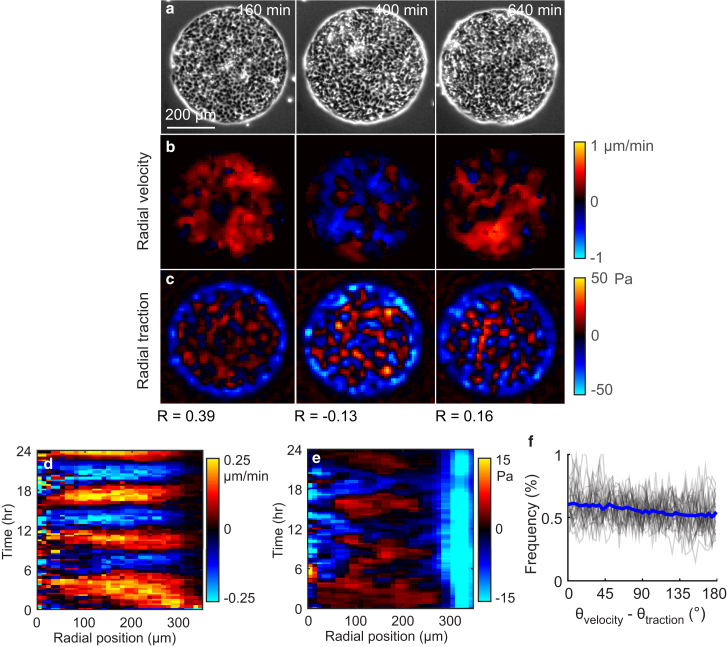
To investigate the relationship between cellular tractions and velocities, we confined monolayers of Madin-Darby canine kidney cells to circular islands (diameter 700 μm) of adhesive collagen type I. We measured cell velocities with particle image velocimetry and simultaneously measured tractions with traction force microscopy (18, 21, 22) (Fig. 1; Fig. S1). Similar to reports in a previous study (7), we observed sustained oscillations of inward and outward cellular motion comprising waves with a period of ∼6 h (Fig. 1 b; Movie S1). To visualize the data at all points in space and time, we averaged the velocity data over the azimuthal angle to collapse all spatial data onto a single axis specifying the radial position. We then plotted the data over time to generate a kymograph. As shown in the kymograph of velocity (Fig. 1 d), the cellular motion was highly coordinated with standing waves of outward and inward collective motion, similar to seiches observed in lakes or other confined bodies of water.

Figure 1.

Tractions do not align with local cellular motions. (a) Phase-contrast images of a confined cell monolayer. Time zero corresponds to the first image collected. (b and c) The radial components of velocity (b) and traction (c) are uncorrelated with one another. At some time points (e.g., 160 min), the Pearson’s correlation coefficient, R, is positive, and at other time points (e.g., 400 min) it is negative. (d) The kymograph shows the radial velocity as a function of position and time. Red and blue bands indicate oscillating outward and inward motion. (e) Kymograph of radial traction showing that cells at the perimeter apply tractions that point inward, whereas cells within the bulk apply tractions that oscillate between inward and outward. (f) Histogram of the angle between the velocity and traction vectors. Each gray line shows a single point in time for the cell island; the blue line shows all points in time. To see this figure in color, go online.

Surprisingly, even though the monolayer velocity varied little with the radial position at a given time, tractions were organized in a standing wave with finite wavelength (Fig. 1 e). Although the tractions at the perimeter of the island pointed radially inward, tractions at any point within the bulk of the island oscillated radially inward and outward over time akin to the velocity field. At the perimeter of the island, all cells applied inward-pointing tractions (Fig. 1 c), indicating that these cells pulled themselves toward the exterior free space, a behavior called kenotaxis (11). However, across the island, the correlation between traction and velocity was negligible (the typical correlation coefficient magnitude was |R| < 0.1; Fig. 1, b and c). Furthermore, the angles between the directions of velocity and traction showed a nearly uniform distribution across the monolayer (Fig. 1 f), indicating that the orientation of each cell’s traction is not linked solely to its velocity.

To investigate further the relationship between traction and velocity, we considered cellular motion within an expanding cellular island wherein the cells were not restricted by a boundary. We seeded cells onto a mask with 700 μm holes placed atop a compliant polyacrylamide gel coated with collagen type I. As shown previously (4), removing this mask induces cell migration into the newly created free space. Upon sensing the free space created by mask removal, cells located at the perimeter of the island migrated first, and their outward motion caused cells just inside the perimeter to follow (Fig. S2). Over time, more and more cells began to move, creating a wave of radial motion that propagated from the perimeter to the center of the island (Fig. S2, b and d), similar to the waves of motion observed for cells in a rectangular monolayer (6). Much like the cells in the confined islands, the cells near the perimeter of the expanding islands applied inward tractions to pull themselves toward free space (Fig. S2, c and e). For cells in the bulk of the expanding island, however, we observed no alignment between directions of traction and velocity (Fig. S2 f).

These findings suggest that cells tend to apply local propulsive forces in a direction that can deviate systematically from the direction of local cellular motion. In the specific case of cells near the edge of the freely expanding monolayer, local tractions and velocities were aligned, but elsewhere they were not. Why this independence of orientations? In contrast to previous models (24, 25) which predict that cells apply traction along a gradient of cellular density, our data showed no correlations between the orientations of cellular tractions, velocities, or gradients in number density (Fig. S3).

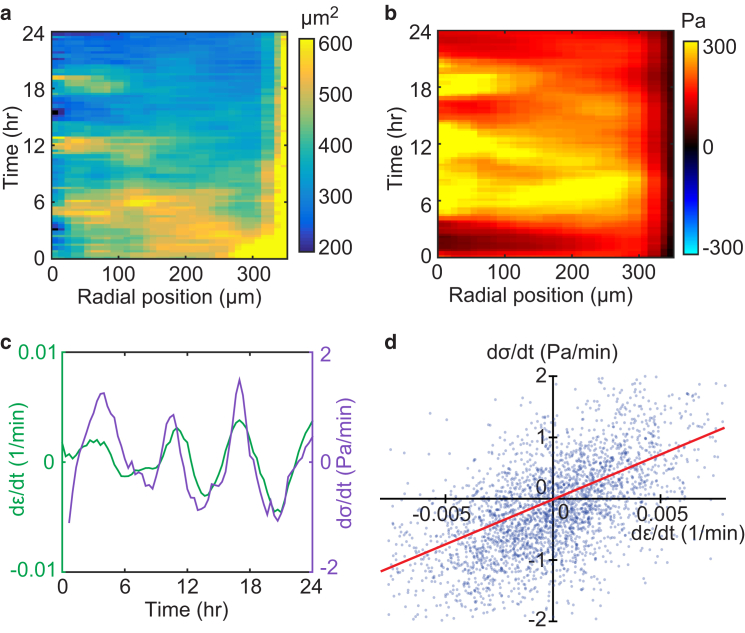
We tracked the position of each cell’s nucleus to compute the average distance between each nucleus and its neighbors; from these distances, we then computed the local area covered by each cell. Within the confined islands, cellular areas increased as cells collectively moved outward and then decreased as they moved inward (Fig. 2 a). We compared the cellular areas to the stresses within the monolayer, which we measured using MSM (8, 23). MSM applies the principle of force equilibrium to the cell monolayer to compute the in-plane monolayer stresses from the cell-to-substrate tractions. We found that the tension σ (defined as the mean of the two principal stresses within the cell monolayer) periodically increased and decreased with the same frequency as the radial waves in cellular velocity and with the same phase as the cellular area (Fig. 2 b), thus implying an elastic relationship. To investigate further the elastic behavior of the monolayer, we examined the relationship between stress and strain rate, and found no correlation (Fig. S4). The lack of correlation implied that viscous contributions to the monolayer stress are negligible. We then compared the time derivative of stress to the strain rate. Specifically, we plotted the time derivative of the tension (dσ/dt) and the trace of the strain-rate tensor (dε/dt), which were well correlated over time along a single radial position (Fig. 2 c). The correlation is further evident by a scatter plot (Fig. 2 d). The elastic modulus K of the cell monolayer is given by the slope of a line fit to the scatter plot, K = 113 ± 28 Pa (mean ± SD of n = 8 islands).

Figure 2.

Elastic behavior of the cell monolayer. (a) The oscillatory motion causes expansion and contraction of each cell, shown by the oscillations in the kymograph of cell area. (b) Contractile tension within the monolayer oscillates in phase with the cell areas. (c) The area strain rate (dε/dt, defined as the trace of the rate-of-strain tensor) and the time derivative of tension (dσ/dt) are computed by averaging around a circle 100 μm from the center of the island and plotting over time. dε/dt and dσ/dt are well correlated (Pearson’s correlation coefficient R = 0.77). (d) A scatter plot of dσ/dt versus dε/dt for all cell positions at all times shows a positive correlation (R = 0.59). The slope of a linear fit (red line) is equal to the effective elastic modulus of the monolayer, given by K = 152 Pa for this cell island. Experiments for n = 8 islands give an average value of K = 113 ± 28 Pa (mean ± SD). The kymograph of velocity for this cell monolayer is shown in Fig. 1d. To see this figure in color, go online.

Similarly, cells in a freely expanding island displayed elastic behavior. As an island expanded due to outward migration, each cell within that island became stretched, thereby increasing its area (Fig. S5, a and b). Similar to the confined islands, when cells increased in area, the tension consequently increased (Fig. S5 c). As above, when we plotted dσ/dt against dε/dt, the data were well correlated for a single radial position (Fig. S5 d) and for all positions within the island (Fig. S5 e). For the expanding islands, we found a modulus of K = 62 ± 17 Pa (mean ± SD of n = 7 islands). Our findings thus demonstrated that both confined and expanding cellular monolayers behave as an elastic material, albeit with different elastic moduli.

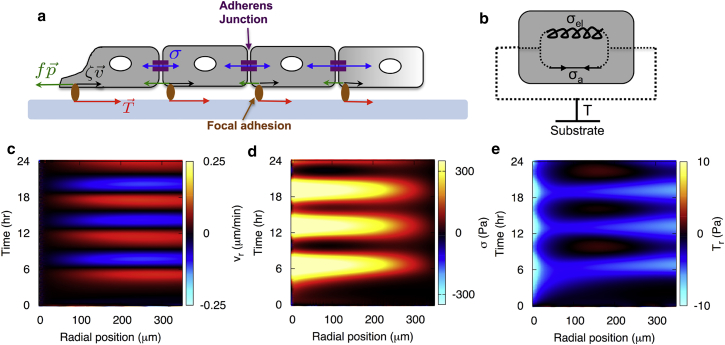
To examine the internal variables that generate cellular polarization and oscillatory waves, we developed a minimal physical model, which describes the monolayer as an elastic continuum with a displacement field $\overrightarrow{u}\left(\overrightarrow{r},t\right)$. The assumption of elastic behavior is supported by our data and those of others (6, 26) that show a linear relationship between the rate of stress and the rate of strain. As in a previously described one-dimensional model of an expanding cell monolayer (14), we couple this displacement field to a scalar field $c\left(\overrightarrow{r},t\right)$ describing the concentration of a chemical signal controlling cell contractility, as elaborated below. In addition, we introduce a dimensionless vector polarization field, $\overrightarrow{p}\left(\overrightarrow{r},t\right)$, whose magnitude describes the local degree of polarization in the cell layer. The orientation of $\overrightarrow{p}$ defines the local direction of the propulsive thrust internally generated by each cell through its adhesion to the substrate (Fig. 3 a) (12, 13, 14, 15). The traction exerted by the cell layer on its substrate is therefore the difference between the viscous friction and the thrust,

$$\overrightarrow{T}=\zeta {\partial }_{\text{t}}\overrightarrow{u}-f\overrightarrow{p},$$ (1)

where ζ describes viscous friction with the substrate and f is the strength of the coupling between cell polarization and thrust (Fig. 3 a). The motivation for introducing the polarization field comes from our experimental data described above, which show that local cell traction is not aligned with local cell velocity, indicating that there must be an additional internal driving force in the equation of motion for the monolayer. The dynamics of the cell monolayer is overdamped and is governed by the force-balance equation,

$$h{\partial }_j{\sigma }_{ij}=T_i,$$ (2)

where h is the thickness of the monolayer, and σ_ij is the tensor describing the in-plane stresses within the cellular monolayer, with the Latin indices representing in-plane spatial coordinates. The monolayer stress tensor σ_ij consists of stresses exerted by elastic and active elements within the cell and connected in parallel. As such, ${\sigma }_{ij}={\sigma }_{ij}^{\text{el}}+{\sigma }_{ij}^{\text{a}}$, where ${\sigma }_{ij}^{\text{el}}$ is the stress tensor of a linearly elastic material (27) (see the Supporting Material) and ${\sigma }_{ij}^{\text{a}}$ is the active stress due to intracellular contractile signaling (Fig. 3 b). We take this to be of the form ${\sigma }_{ij}^{\text{a}}=\beta \text{log}\left(c/c_0\right){\delta }_{ij}$, where δ_ij is the Kronecker delta, and β > 0 controls the strength of the active contractile stresses. The active stress arises from a distribution of contractile force dipoles generated by myosin clusters cross-linking actin filaments in the cytoskeleton. In general, the stress contains both an isotropic term representing an active contractile tension (i.e., a negative pressure) and an anisotropic term proportional to the local polarization. Here, we neglect this anisotropic component, having verified that it does not change the behavior described below. We also neglect, for simplicity, nonlinear elasticity of the monolayer (13). The active stresses might be generated, for example, by a chemical reaction such as ATP hydrolysis, described by a concentration field, c, representing the concentration of phosphorylated myosins, with the equilibrium value given by c₀ (14). Eq. 2 is supplemented by equations governing the dynamics of the internal variables c and $\overrightarrow{p}$. The concentration of the chemical is described by a reaction-advection equation,

$${\partial }_{\text{t}}c+\nabla ·\left(c{\partial }_{\text{t}}\overrightarrow{u}\right)=-\frac{1}{\tau }\left(c-c_0\right)+\alpha c_0\nabla ·\overrightarrow{u},$$ (3)

where τ is the timescale of relaxation to equilibrium and α > 0 is the rate of production of the chemical due to cellular stretching. Thus, in agreement with the experimental data (Fig. 2) and previous results for single cells (28) and multicellular monolayers (26), a local increase in cell area generates a local increase in the contractile stress ${\mathbf{\sigma }}^{\text{a}}$ (and vice versa). It is instructive to note that for small changes in c around its equilibrium value, Eq. 3 essentially describes the dynamics of active monolayer stress that is similar to a Maxwell constitutive model for intercellular stress proposed by Lee and Wolgemuth (12). Here, in addition, we consider an elastic contribution to the active stress, described by the term α. The dynamics of the polarization field is given by

$${\partial }_{\text{t}}{p}_i=a\left(1-{\left|\overrightarrow{p}\right|}^2\right)p_i+\kappa {\nabla }^2{p}_i+w{\partial }_{i}c/c_0,$$ (4)

where α > 0 controls the rate of relaxation to a homogeneously polarized cell monolayer, and κ controls the strength of nearest-neighbor alignment of the polarization field. The active coupling w > 0 describes the rate of alignment of cell polarization with the gradients in the concentration field, such that local cell motion is propelled over time toward regions of high contractility. It is useful to compare our model to those of (12) and (13). The model of (13) is very similar to the one used here. Both models describe a tissue as an active elastic medium in terms of coupled equations for displacement field, polarization, and an internal scalar degree of freedom describing a deformation-induced chemical signal. Our model is a minimal version of that of (13), where many of the nonessential nonlinearities and anisotropies are ignored. In (12), in contrast, the authors describe the tissue as a fluid and retain the anisotropic part of the active stress proportional to polarization. Internal dynamics is introduced by assuming that the stress is viscoelastic, with dynamics described by a Maxwell model. This has a similar effect to our assumption of relaxational dynamics for the chemical signal that controls the isotropic active stress. Both introduce an additional timescale that provides an effective inertia for the overdamped monolayer, be it a liquid or an elastic medium. Less direct is the comparison with the work by Basan et al. (15), who propose a particle model and assume a tendency toward alignment between cell polarization and velocity, which leads to an overall antialignment between traction and cell velocity, which does not agree with our experimental data.

Figure 3.

Minimal physical model capturing the wave-like motion and the distribution of traction of the cell monolayer. (a) Schematic of the forces acting on the cell monolayer. Tractions exerted by the monolayer on the substrate point inward (red arrows) at the monolayer edge and balance the forces due to viscous friction, $\zeta \mathit{v}$ (black arrows), and propulsion, $f\overrightarrow{p}$ (green arrows). The monolayer is in mechanical equilibrium, such that the tractions are locally balanced by the divergence of the monolayer stress, $T_i=h{\partial }_j{\sigma }_{ij}$. (b) Constitutive elements of the mechanochemical model. The elastic and active elements exert stresses in parallel, and a local gradient in stress is balanced by the traction exerted by the cell on the substrate. (c) Kymograph of radial velocity in the cell monolayer captures the experimentally observed collective inward and outward cellular motions. (d) Kymograph of cellular tension in the monolayer, which increases and decreases periodically with the same frequency as the velocity. (e) Kymograph of radial traction. See Table S1 for a complete list of the model parameter values. To see this figure in color, go online.

By solving the coupled system given by Eqs. 2–4, assuming in-plane circular symmetry, we applied this model to the confined monolayers in our experiments (see the Supporting Material). The results are displayed in a series of kymographs showing the spatiotemporal evolution of the radial velocity, the monolayer tension, and the traction (Fig. 3, c–e). The model quantitatively captured multiple aspects of our experimental data, namely, that the monolayer’s velocity field alternated between inward and outward motion (Fig. 3 c) with a time period equal to that of the oscillations in the monolayer tension (Fig. 3 d). This wave-like motion is predicted by the model to arise through the chemomechanical feedback between the mechanical strain and the internal state variable c (14, 29). In the limiting case c = c₀, when the deformation $\overrightarrow{u}$ is only coupled to $\overrightarrow{p}$, no oscillatory behavior is observed (Fig. S6, d–f). However, if the deformation $\overrightarrow{u}$ is coupled to c only, the traction is proportional to velocity, which contradicts our experimental observations (Fig. S6, a–c). This indicates that the polarization field, $\overrightarrow{p}$, is crucial to capture the misalignment between traction and velocity. Thus, coupling of the deformation $\overrightarrow{u}$ to both c and $\overrightarrow{p}$ is required to capture the experimentally observed distribution of tractions, which pointed inward at the exterior of the cell island and oscillated between outward and inward within the bulk of the island (Fig. 3 e).

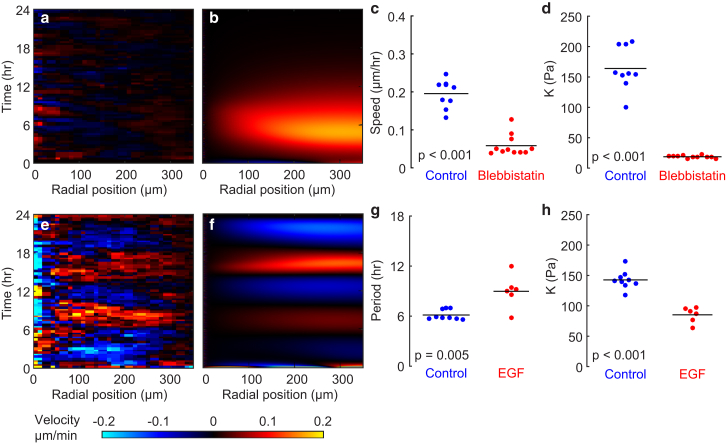
To test the model’s prediction that a feedback between mechanical strain and cellular contraction generates collective oscillations, we inhibited contraction with the myosin II inhibitor blebbistatin (20 μM). For an expanding island, blebbistatin has no effect on the speed of migration (6), but in confined islands, blebbistatin reduced each cell’s speed (Fig. 4, a and c). Further, blebbistatin eliminated the multicellular oscillations (Fig. 4 a; Movie S2), and reduced the modulus K to ∼20 Pa (Fig. 4 d). This observation is consistent with our model, which predicts that the coupling between strain and contractility yields an effective modulus $K\approx B+\alpha \tau \left(\beta +fw/2ah\right)$ (14), larger than the modulus B of the monolayer in the absence of contractility. Removing the coupling between strain and contractility by setting α = 0 eliminated the oscillatory waves in our model (Fig. 4 b). These findings suggest that the elasticity is primarily active: the oscillations in motion cause oscillations in cellular strain, which, through active contraction, cause oscillations in tension. To further test this, we sought to connect changes in elasticity with the motion. We found that EGF (20 ng/mL) increased the period of oscillation (Fig. 4, e and g; Movie S3). In an oscillatory system, modulus and period are inversely related, and in accord with increasing the period, treatment with EGF decreased the modulus K (Fig. 4 h). When we reduced the magnitude of the constants that couple tension and strain, α and β, we saw, similarly, an increase in the period of oscillations (Fig. 4 f). From these findings—that the waves require contraction and that the period depends inversely on modulus—we conclude that the elasticity is not passive in nature; rather, it is the result of myosin-driven contractility within the cell.

Figure 4.

The waves of collective motion and elasticity in the monolayer depend on the contractile activity of the cells. (a) Kymograph of radial velocity after treatment with blebbistatin shows reduction in speed and elimination of oscillatory waves of radial motion. (b) Simulated kymograph of radial velocity using the model with no feedback between strain and contractility (α = 0) also shows elimination of waves. (c and d) Treatment with blebbistatin reduces root mean-square speed of cells by a factor of ∼4 (c) and reduces the modulus K to a nearly negligible value (d). (e) Kymograph of radial velocity for an island treated with EGF (20 ng/mL). (f) Simulated kymograph with reduced values of the parameters α and β. (g) Compared with the control, EGF increased the period of oscillation. (h) Relative to the control, treatment with EGF decreased the effective elastic modulus, K. For the plots in (c), (d), (g), and (h), each dot corresponds to a different cell island. p-values are computed using a rank-sum statistical test. To see this figure in color, go online.

Discussion

Here, we have studied motions and forces in a confined monolayer of epithelial cells. Spontaneous oscillations arise wherein cells alternate between outward and inward correlated motions that resemble the sloshing seiches that are observed in confined bodies of water. The direction of local cellular velocity is generally independent of the direction of local traction, thus indicating that the relationship between force and motion requires additional state variables. Two cellular state variables, the concentration of contractile elements and the polarization of cell motion, were introduced to reproduce the experimental results. The coupling between the cellular strain and chemical concentration generates effective inertia, which, together with cellular elasticity, supports the oscillatory waves of motion observed in the experiments. Decreasing the elastic modulus with EGF increased the period of oscillation (Fig. 4, g and h), in agreement with the theory.

Elasticity of the monolayer has been previously attributed to a passive spring-like behavior of the cytoskeleton, its contractile apparatus, and cell-cell adhesions (6, 7). In contrast, our model now incorporates a feedback between cellular strain and contractility such that a local increase in cell area induces larger contractility. This mechanism is consistent with recent experiments on single cells (28) and multicellular clusters (26, 30), which show that cells with larger area are more contractile than cells with smaller area. When we suppressed cell contractility with the myosin-II inhibitor blebbistatin, the elastic modulus decreased by an order of magnitude (Fig. 4 d), and the waves were suppressed (Fig. 4 a). From this observation we conclude that the elasticity required to generate the waves is not simply a passive spring-like behavior; rather, it results from the active contractile elements inside the cell (26). Adding blebbistatin reduced the average cell speed in these confined islands, but such a reduction in speed is unlikely to be the mechanism that inhibits the oscillations in cellular motion. A previous study showed that blebbistatin in an expanding cellular island has no effect on cell speed, but it does eliminate propagating waves of contractile tension (6). This observation agrees with our finding that active cell contraction is required to generate the oscillatory waves.

The molecular mechanisms that link changes in cellular stretching to changes in contractile tension are unknown, but theoretical studies (13) and experimental evidence point to ERK MAP kinase (ERK1/2) as being associated with extension of muscle tissue (31) and stretching of stress fibers (32). Moreover, when a monolayer begins to expand into free space, a wave of ERK1/2 phosphorylation propagates from the monolayer’s free edge into the bulk (33, 34) at a speed approximately the same as that of the waves of cellular motion that occur in our experiments of expanding cellular islands (Fig. S2 d) and have been reported elsewhere (6). This slow-moving wave results not from damage to the monolayer, but rather from the free space offered to the monolayer’s edge (34). When we inhibited ERK1/2 with U0126 (10 μM), the effective modulus decreased by a factor of 2, and collective oscillations were suppressed (Fig. S7; Movie S4).

Collective cellular oscillations similar to the ones described here have been reported by Deforet et al. (7), who performed stochastic particle-based simulations that balanced the forces of inertia, friction, intercellular adhesions, and active propulsion. In their simulation, each cell was given a tendency to adapt its velocity to that of its nearest neighbors. Although the model by Deforet et al. and the one presented here are both based on local force-balance, they differ in spirit. Instead of simulating the dynamics of individual cells, we propose a continuum model formulated in terms of a few coarse-grained fields such as traction and velocity, which are measured directly in the experiments. Our model contains only a small number of parameters that represent effective material properties of the monolayer and describe the combined effect of a number of signaling pathways. The model makes testable predictions that provide a way of correlating the macroscopic parameters of the theory with specific pathways.

Oscillatory or wavelike motion requires second-order differential equations in time, corresponding to the tradeoff between two independent timescales. The dynamics of cellular monolayers is overdamped, hence governed by a first-order differential equation, with a single timescale determined by the interplay of viscous friction and elasticity. Until now, the origin of the second timescale required for oscillatory behavior has remained mysterious. Deforet et al. accounted for the second timescale by introducing cellular inertia (7). Serra-Picamal et al. accounted for the second timescale by assuming that stretched cells became fluidized (i.e., they flowed under tensile forces) for a specified period of time (6). There is evidence that cells fluidize when stretched and unstretched quickly (35, 36, 37), but whether stretches due to slow cellular motion induce fluidization remains an open question. Our model and experiments point to a second timescale that comes from the mechanochemical feedback (13) between the local strain and the rate of change in contractile tension. This feedback mechanism results in self-sustained periods of stiffening and fluidization in the cell monolayer (14).

Dynamics of the chemical concentration c does not explain the apparent independence between the local orientations of traction and velocity (Fig. 1 f; Figs. S2 f and S8). Whereas Kim et al. showed that velocity and tractions do not align near a boundary (11), we show here that an angle of misalignment between traction and velocity occurs even in the absence of a boundary. The histogram of the angle between traction and velocity at all points in time (Fig. 1 f, blue line) shows a very small peak near zero, indicating a slight tendency for cells to pull on the substrate in the same direction that they move. This occasional alignment between motion and traction is consistent with the presence of a viscous drag exerted by the moving cells onto the substrate, as described by our model and those of others (12, 13, 14, 15). In these models, the viscous-drag term connects tractions to motion, and thus, our observation of occasional alignment between traction and velocity serves as a confirmation of this connection.

To account for the deviation between the local directions of traction and velocity, we propose a vector polarization field that locally directs the cellular motion. Other theoretical models have also incorporated a cell polarization field defining the orientation of an anisotropic dipole-like contractile stress (12), with dynamics governed by general nonlinear hydrodynamic equations of polar liquid crystals (13, 38). In contrast, our work considers a minimal model where cell polarization does not generate shear stresses, in agreement with our experimental data that show an isotropic distribution of the monolayer stress field (Fig. S9). Importantly, we identify two physical mechanisms that control the dynamics of cell polarization. First, cells tend to polarize their traction toward free space, consistent with kenotaxis (11). Our model accounts for kenotaxis in the first term on the righthand side of Eq. 4, which tends to polarize the monolayer toward free space. Second, the polarization field evolves in time so as to locally align toward regions of high contractile tension in the monolayer (Fig. S10). These two tendencies are required to reproduce the spatial patterning of the traction field (Figs. 1 e and 3 e), and they provoke the question of what molecular mechanism generates the polarization. The cytoskeletal protein merlin may be involved, as the feedback between merlin and Rac1 has been shown to direct formation of lamellipodia in collective cellular migration (9). If merlin indeed polarizes the cells, it is likely only one of several molecular mechanisms controlling the forces that drive collective cellular motion.

Here, we have found that the various biological mechanisms controlling the waves of collective motion combine together to relate force and motion through two physical variables, one controlling intracellular contractility and the other controlling polarized cell motion. These two state variables are present within each cell, but perhaps even more striking is the fact that each cell coordinates these state variables with its neighbors to generate emergent waves of correlated motion that span multiple cell diameters. Emergent phenomena like these multicellular waves control the motion and final positioning of the cellular collective, and thus, they are likely to play a key role in development and disease. The two internal variables that we describe here—cell contraction and polarization—provide a framework for further investigation.

Author Contributions

J.N., S.B., M.C.M., J.B., and J.J.F designed the research. J.N. performed the experiments. S.B. and K.J.C.U. performed the simulations. B.G., H.J., Y.P., and J.S. developed experimental protocols. J.N., S.B., K.J.C.U., B.G. M.C.M., J.B., and J.J.F. discussed the results. J.N., S.B., M.C.M., and J.J.F wrote the manuscript.

Editor: Charles Wolgemuth.

Supporting Material

Movie S1. Oscillations of Motion in a Cell Monolayer

(Left) Phase contrast. (Right) Nuclei expressing green fluorescent protein.

Movie S2. Motion of a Cell Monolayer Treated with Blebbistatin

(Left) Phase contrast. (Right) Nuclei expressing green fluorescent protein.

Movie S3. Motion of a Cell Monolayer Treated with EGF

(Left) Phase contrast. (Right) Nuclei expressing green fluorescent protein.

Movie S4. Motion of a Cell Monolayer Treated with U0126

(Left) Phase contrast. (Right) Nuclei expressing green fluorescent protein.