Hierarchical dynamics of informational patterns and decision-making

Abstract

Traditional studies on the interaction of cognitive functions in healthy and disordered brains have used the analyses of the connectivity of several specialized brain networks—the functional connectome. However, emerging evidence suggests that both brain networks and functional spontaneous brain-wide network communication are intrinsically dynamic. In the light of studies investigating the cooperation between different cognitive functions, we consider here the dynamics of hierarchical networks in cognitive space. We show, using an example of behavioural decision-making based on sequential episodic memory, how the description of metastable pattern dynamics underlying basic cognitive processes helps to understand and predict complex processes like sequential episodic memory recall and competition among decision strategies. The mathematical images of the discussed phenomena in the phase space of the corresponding cognitive model are hierarchical heteroclinic networks. One of the most important features of such networks is the robustness of their dynamics. Different kinds of instabilities of these dynamics can be related to ‘dynamical signatures’ of creativity and different psychiatric disorders. The suggested approach can also be useful for the understanding of the dynamical processes that are the basis of consciousness.

1. Introduction

(a). Informational patterns, metastable states, and sequential dynamics

Mind dynamics, i.e. human cognitive activity is the interaction of sequential mental processes organized in a hierarchical manner. In turn, mental hierarchical dynamics are generated by the hierarchy of the brain functional networks [1–3]. The idea of formalizing sequential order in neuroscience was first formulated by Lashley for behaviour [4], and soon became popular. In fact, the performance of any mental function can be seen as a sequence of metastable states, informational patterns, that switch in a serial order. The existence of metastable informational patterns arises in the context of functionally coupled active brain areas across the whole brain [5,6]. Such patterns qualitatively change not only with the changing of specific cognitive/behavioural tasks but they also depend on the stage of the performance, i.e. they sequentially change in time [7,8].

Many cognitive functions are based on the same key dynamical principles. One such universal principle can be formulated as this: thinking, music improvization, speech, and other cognitive functions are the result of sequential switching of different informational patterns representing different modes of activity in distributed functional networks [9,10]. Using this perspective, we present a novel approach for the understanding, description, and prediction of hierarchical cognitive processes based on the analyses of the phase space topology and the bifurcations of metastable state networks. We suggest and analyse here dynamical images in the mental phase space such as (i) binding hierarchical networks, (ii) chunking hierarchy, and (iii) the interaction between them. Based on this approach, we specifically discuss decision-making (DM) dynamics.

(b). The dynamical images of cognitive and behavioural hierarchy in cognitive phase space

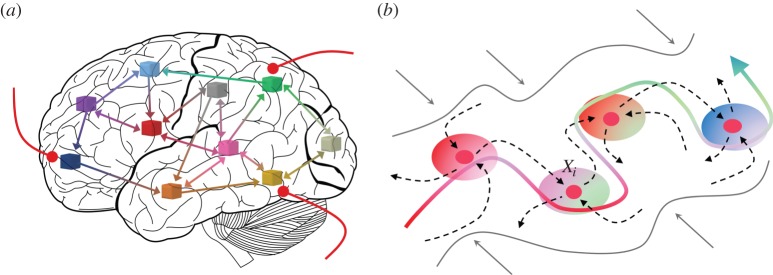
In this paper, we consider the hierarchical dynamics of cognitive networks that represent different mental activities not in a physical brain space, as in [11–13], but in a cognitive space, i.e. in the phase space of the corresponding dynamical model that describes such a process. As imaging experiments show, the performance of complex cognitive activities, like speech generation and perception, requires the collaboration of several basic cognitive networks (e.g. [14]; figure 1a). The nature of many elementary cognitive functions is dynamical and their corresponding activity is transient in time. There is a known mathematical image that can represent robust transient neural processes in the phase space—known as stable heteroclinic channels (SHCs) [15–18]. The building blocks of such channels are metastable states, saddle sets, connected by unstable separatrices (figure 1b). Metastable states represent perceptional or memory informational patterns in the brain. The robustness of SHCs is provided by the competitive interaction of agents, variables, that evolve sequentially to create a chain of metastable states. A winnerless competition (WLC), i.e. a permanent competition with different temporal winners, based on asymmetric inhibition [19] can be the origin of SHCs. If the dimension of the unstable separatrices of the saddles in such a chain is larger than one, heteroclinic channels form a heteroclinic network that can represent the dynamics of complex cognitive functions like speech generation, music improvization, figure skating dynamics, and others [18].

Figure 1.

(a) Global brain network whose activity can be represented in the cognitive space by robust stable heteroclinic channels (SHCs). (b) SHC that includes a chain of metastable states, informational patterns. The gradient colours in the vicinity of each metastable state represent the combination of brain elements that generate the corresponding pattern. Dashed lines with arrows represent the stable and unstable separatrices of the mestastable states, which determine the structure of the information flow. (Online version in colour.)

Most human thoughts involve consideration of events that happened in the past and play a fundamental role in planning what to do in the future. Recalling the past and imagining the future are dynamically linked as items in a joint sequential network. The recall of a sequence of events—episodic memory (EM), for which a specific time and context are connected, is a hierarchical dynamical process that must be robust and reproducible. We argue that the origin of this process is a WLC between the remembered items, or patterns, and new items at all levels of the informational hierarchy. The hierarchy of such competition includes binding and chunking processes, which suggest a decision is based on previous experience and learning. Here we analyse a modelling framework of such processes. In the context of this approach, we also address the investigation of dynamical diversity and brain network multifunctionality, emotion–cognition interaction and the relationship between hierarchical instabilities and different disorders.

In the following section, we offer a metaphor and the associated mathematical formalism for itinerant neuronal processing that can be associated with higher cognitive functions such as short-term memory, attention, and DM. Our treatment implies some abstraction and the relationship between the dynamical behaviours we use to illustrate the ideas and cognitive function are heuristic. However, there are several fundamental insights provided by this approach. In particular, we will illustrate that any distributed (macroscopic) activity at the whole brain scale can be described in terms of modes or patterns of activity whose time-varying fluctuations can be modelled in terms of SHCs easily implemented in generalized Lotka–Volterra (GLV) dynamics. By nesting in hierarchical fashion the normal form for these dynamics, one can describe sequential patterns of neuronal activity that are selected and contextualized in a way that is remarkably reminiscent of mnemonic, attentional, and DM processes. The resulting formalism provides not only a computational architecture for higher cognitive functions in the brain but could also be used as the basis of observation models (e.g. dynamic causal modelling) to quantify structured yet itinerant brain dynamics elicited during memory tasks and DM.

2. From perception to behavioural decision through sequential episodic memory

(a). Neurobiology of sequential memory: prediction and decision-making

Sequential EM represents memory of autobiographic experiences and specific events in time serial order. A chunk of such events is called an episode. The memory about a specific episode—what, where, and when—and the associated emotions can be explicitly recalled by a cognitive goal or sensory information [20]. The network of integrated memory of multiple episodes, episodic working memory (EWM), plays a key role in the prediction of future events in similar situations. When we remember the past or envision the future, events usually come to our mind in an organized sequence, i.e. an episode. Anatomically, the network that supports EM includes the hippocampal and ventral medial prefrontal cortex, the striatum, and other brain areas [21–23]. Thus, EM is a distributed dynamical process providing the representation of events that happened in the past and that can be used for the prediction of the future [24].

The human mind generates effective predictions within the constraints of our own action repertoire. This makes the prediction compatible for the sensory and motor systems' representations [25], and also explains the origin of the differences between prediction of an event actor in the episode and an observer [26–28].

(b). How to build a dynamical model of behavioural decision

Our previous experience usually helps us when we have to make a difficult decision based on uncertain or confusing information (see, e.g. [29]). Learning from experience alters the DM network and thus our mind is able to quickly categorize our perception and make a decision to carry out appropriate actions. Depending on the environmental information, a choice based on previous experience can be unconscious/automatic, or additional complementary sensory information can be consciously used for re-evaluation. These two behavioural reactions are encoded and performed in distinct human brain networks [30].

In the following section, we build a DM model based on the simplest evaluation of the information effectiveness that we gather from EM. The actual sequence of events will be just compared with ‘positive’ episodes that happened in the past. With the term ‘positive’ episodes we mean the sequence of events in the past that ended with a successful decision. When creating a DM model we also have to keep in mind the role of attentional selection. In functional neuroimaging studies of episodic retrieval (ER), activations in prefrontal, parietal, anterior cingulate, and thalamic regions are typically attributed to ER processes [31]. Attention and memory are intricately linked. Cabeza et al. [32] hypothesized and proved that attention may stabilize informational patterns of cognitive states. It is not clear how novel episodes are connected with previous episodic memories and then used for future DM. There must be intermediary processes that use memory as a basis to generate future-oriented decisions. We name such processes EWM controlled by goal-directed attentional selection.

(c). Dynamical coding: winnerless competition principle and informational patterns

One of the prevailing concepts related to information processing in the brain is dynamical cell assembly coding [33]. This concept is based on the fact that task-related, time-scaled dynamic modulations of large groups of neurons—a dynamical cell assembly—spontaneously organizes and is linked temporarily by the nearly coincident timing of spikes from cooperative neurons showing correlated firing with each other. We characterize these assemblies as spatio-temporal modes. For example, in the rat gustatory cortex, each taste is represented by specific sequential orders in the chain that can be considered as alternating switching between these modes—informational patterns [34]. Such style of dynamical coding, which is quite common in nature, is typically based on a WLC principle and can be interpreted in the framework of kinetic ecological models, the simplest of which is a Lotka–Volterra (LV) equation [35,36]. The mathematical image in the corresponding phase space of such coding is a SHC. We are going to use variants of this basic LV equation on each level of the hierarchical model that we wish to build.

Internally generated sequences are very important in learning and executing goal-directed DM [37]. Modern progress in neural recording technology allows the characterization of brain informational patterns. On the population level, 'these dynamics are usually low dimensional [38]. Such low-dimensional cooperative dynamics are the result of coherent activity of many elements that form modes and can be extracted by techniques such as principal component analysis [39,40]. The spatial patterning contains detailed information about the environment and the person's mental states. Pattern-based functional magnetic resonance imaging (fMRI) analyses enable a detailed characterization of content-based information processing in the human brain [41,42].

(d). Basic kinetic model

In many cases, it is possible to represent the temporal and spatial aspects of the brain modes separately by two variables: R(t) and Q(r). Thus, we have:

2.1

where Pⁱ(r, t) is the ith spatio-temporal pattern (brain mode) based on the set of discrete coordinates r in the brain space, Qⁱ(r) is correspondingly the spatial structure of the ith pattern, X_i(t) characterizes the temporal evolution of the cooperative dynamics of the ith pattern in the ensemble, and N is the number of informational patterns. One can suppose that X_i(t) for each pattern mode satisfies a kinetic equation up to second order. If, as the result of this inferential process, the spatial structure of the modes is known, after factorization the basic kinetic model can be written in the form of GLV equations:

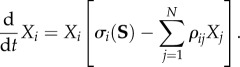2.2

Here σ_i(S) is a parameter that represents the mode excitation, ρ_ij is the cognitive inhibition matrix between the modes, and S is the input that captures the sources of internal or external excitation. The interaction of different modalities like emotion and cognition, which is important for the understanding of normal and pathological mental dynamics, can be described by the same type of equations [43,44]. It is important to emphasize that Pⁱ(r,t) may have a different sense relating to the performance of different cognitive, behavioural, tasks. In particular, the intrinsic dynamics of Pⁱ(r,t) can be complex and it can include several brain subnetworks like perceptual, memory, and motor brain circuits. These complex dynamics can often be represented as a sequence of events, thus model (2.2) in the same or in a generalized form is convenient for its analysis and, in particular, for the description of episodic memory.

(e). Hierarchical model of action-based decision-making. Episode formation: chunking

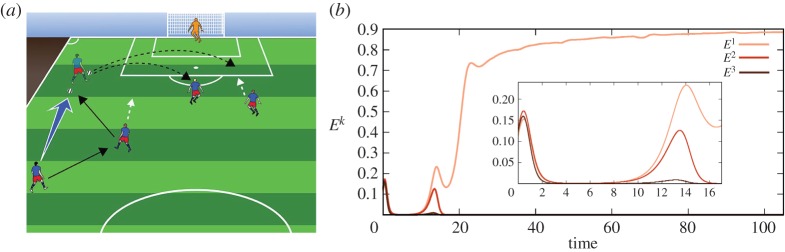
Let us consider the behaviour of a goalkeeper trying to predict who in the opposing team is going to shoot on a soccer goal. To make the problem clear, suppose that there are three or four attackers and the defenders cannot prevent their manoeuvres. The goalkeeper knows from previous games with the same team some of the favourite moves of each of the attackers: number nine prefers to kick the ball to the low left angle of the goal, number seven likes to kick the ball to the centre of the goal and numbers 10 and five usually make kicks to the right low and upper angle of the goal, respectively. According to this knowledge, the goalkeeper jumps to the left or right goal posts or stays in the centrum when he is able to predict who among the attackers will get the ball with the best chance. Such probabilistic prediction depends on the sequential dynamics of present and previous episodes, i.e. graphs of the previous ball passes that are recalled from the goalkeeper's EM (figure 2a). The usual styles of the attacker group behaviour are: chaotic exchanging of the soccer ball between the players, rhythmic exchange, or an attempt to attack the goal individually by one of the players. All these possibilities are represented in his mind by different dynamical images and can be easily compared with the beginning of the present episode induced by visual information from the field.

Figure 2.

(a) Typical attacking pattern, ball passing, in a soccer field. The goalkeeper has to predict who will make the final kick to make a decision on his jump to reach the ball in the current play. (b) Example of past episode interaction during the recall from EM. Variables E^k represent the kth episode in the past according to system (2.3)–(2.6), i.e. a particular play in the past. In this example, episode 1 prevails. Inset shows a blow up of time 0–17 arb. units where the past episodes are being evaluated/compared with the present episode according to equation (2.6). Parameters for this simulation are listed in the electronic supplementary material. (Online version in colour.)

The experienced human brain (after learning) is wired in a way that we are able, even unconsciously, to make the best decisions based on environment information. When sensory signals excite specific mental modes, other modes act as comparators to estimate the similarity of the new episode with those in the EM. This is the case in our example, action-based DM. When the similarity parameter reaches a winner-take-all (WTA) bifurcation threshold, a decision is made. As we mentioned earlier, the motor cortex is involved in corresponding DM modes and realizes the decision directly (see also [45]).

Following the logic of this example, our hierarchical model has to contain four levels of dynamics—today's sequence of passes that continue after making the decision, sequences of passing in the past, the level of the opponent team's activity forming the episodes (the chunking level), and the EWM level that is controlled by the beginning of the present episode. In the brain, the frontal lobes may be responsible for such controlling function [46,47]. The dynamics on all these levels can be described by equations that have a similar form to (2.2). Thus, our hierarchical network model is the following set of coupled equations:

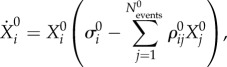2.3

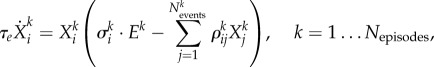2.4

2.5

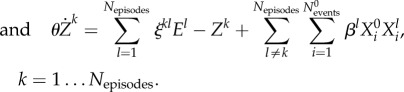2.6

Here 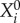is a group of variables that describe events that form the present episode, 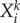represents the ith event from the kth episode, E^k describes the kth episode in the past. An event in this model describes a pass (an elementary action) in our soccer example, while an episode corresponds to a sequence of passes, i.e. a play. Z^k is responsible for the chunking of the episode, i.e. the hierarchical organization of the passes to build a successful play. ξ^kl describes the level of competition of the episodes in their chunking organization due to the limited EM capacity. Matrices 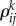are responsible for the inhibitory interactions that support the event transient sequential dynamics, and β^lX⁰X^l characterizes the controlling function that is used to select from the past experience the most probable event for the future of the present episode, which helps to make the best decision.

(f). Model simulations

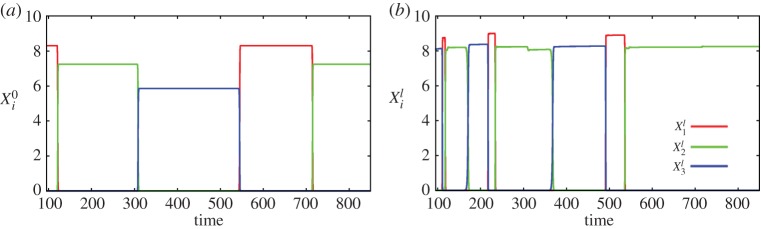
Figure 2b shows the mutual interaction of past episodes recalled from the EM under the action of the beginning of the present episode (see systems (2.3)–(2.6)). In our soccer example, an episode is built from a sequence of passes corresponding to a particular play. As one can see in figure 2b, the episode closest to today's unfinished episode is episode 1, which prevails in the competition (WTA dynamics). In figure 3a, we represent the event dynamics corresponding to the beginning of the present episode, i.e. the current play. This play is being compared to the past episodes (plays) from the EM (see equation (2.6)) to make the best move choice based on the most probable event. Figure 3b shows the event dynamics corresponding to the winning episode 1. Colours in this figure represent different event dynamics (different player activities). As one can see in figure 3b, after some passes, the ‘green’ player keeps the ball for a longer time and with higher probability makes the final kick. This is the basis for the goalkeeper's prediction. As the goalkeeper knows from previous experience, the green player's favourite kick is to the right upper angle. Thus, probably the best decision for the goalkeeper is to jump to this location.

Figure 3.

(a) Time series of the event dynamics for the non-finished present episode (equation (2.3)). (b) Event dynamics for the winning episode (episode 1, cf. figure 2b) from the episodic memory. Parameters for this simulation are listed in the electronic supplementary material. (Online version in colour.)

3. Episodic and emotional memory binding

(a). The role of emotion in autobiographical memory

The traditional theory of declarative (biographical) memory distinguishes between general knowledge (semantic memory) and memory for events [20]. However, these two forms of memory are interdependent [48,49]. In particular, Renoult et al. [49] introduced personal semantics (PS) memory. PS concerns knowledge of one's past and, like EM, PS is a personal feature (i.e. not culturally shared). Their studies indicate that these forms of memory can affect each other both at encoding and at retrieval. Interdependence or binding episodic and semantic memory is a key feature of memory from the past for the prediction of future events and DM.

Perceptual processing enhances memory for emotional information. It correlates with our own experience—we remember exciting- or emotionally charged events much better than boring ones. A recent fMRI study investigated the neural mechanisms of this effect by testing how neural activations during emotional memory retrieval are influenced by the prior encoding strategy [50]. The participants incidentally encoded emotional and neutral pictures under instructions to attend to either semantic or perceptual properties of each picture. Recognition memory was tested two days later. The results illustrate how encoding orientations yield alterations in the amygdala and hippocampus to retrieve emotional memories.

Let us create here a hierarchical dynamical model that can describe such cognitive information processing phenomena. To be clear, we consider an illustrative example. Suppose you are a famous sportsman and have been invited as a guest on a figure skating championship. A couple of months later, the editor of some sport magazine asks you to share your impression about the best skater in that championship with the readers. Then, you check in your memory a few episodes of good skaters, but it is difficult to say who was best. You are almost ready to decline editor's request. However, from a nearby café you hear a Gershwin melody. At that moment you remember in detail one of the episodes—it was based on Gershwin's Rhapsody in Blue. You then recall the skater's performance—how well he/she did the triple-toe-loop, and how good the sequence of elements was organized in chunks, you remembered the facial expressiveness, the costumes, and beautiful correlation of movements and music. Suddenly, it becomes easy to write about this skater.

Musical information can be associated with emotional and semantic information (associative memory) [51]. Koelsch et al. [52] have elegantly shown that short musical pieces with particular characteristics can prime the semantic language memory system, thus yielding faster and more efficient recognition of specific words (for review, see [53]).

(b). Modality binding inside the episodes

The dynamical image of the transient dynamics of a modality is a SHC as we discussed earlier. To be robust, such a channel has to be formed by metastable states with one-dimensional unstable separatrices [15,36]. When we consider multidimensional sequential dynamics, the situation is different. For example, to comprehend and describe the skater's behaviour, we have to share attention among, at least, three modalities—e.g. technical ability, art component, and emotions. The mathematical image of this in the cognitive phase space is a binding network as shown in figure 4a. Each rib in such a network represents a different modality [54]. Such a network can be robust in the case when the metastable states form ribs that are characterized not by one- but two-dimensional unstable separatrices. In the general case, the unstable separatrix can be multidimensional (see electronic supplementary material, figure S1).

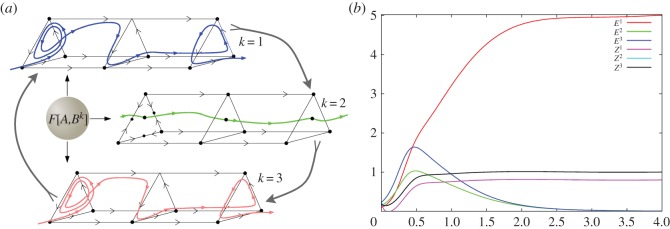
Figure 4.

(a) Three episode interaction in EWM under the action of an external stimulus (equation (3.4)). The episodes demonstrate different dynamics that correspond to attention sharing (green trace) and attention switching (blue and pink traces). (b) Evolution of the episodes (E^k). The chunking variables (Z^k) are also plotted. In this example, episode E¹ prevails in the WTA dynamics given by the systems ((3.3)–(3.5)), see parameters in the electronic supplementary material. (Online version in colour.)

A recent study in humans has shown that functional connections in the brain are more stable within modalities than across modalities [55]. In our binding model discussed in a later section, we choose a stronger interaction inside of the individual modality than the interaction between modalities (see connectivity matrices in the electronic supplementary material).

Attention selection can lead to different dynamical regimes of modality interaction. The upper and bottom panels in figure 4a illustrate a strong interaction between modalities like odour, taste, and aftertaste while wine tasting. In this case, the interaction is strong enough and leads to complex dynamics involving switching of attention between modalities. The middle panel in figure 4a illustrates the coexistence of interacting modalities: attention is shared nearly identically between different modalities continuously in time. In both cases, each event includes binding patterns of different modalities [56].

The generalized equations (2.3)–(2.6) with several modality binding episodes can be written in the following form with three levels of hierarchy:

(i) Binding M modalities

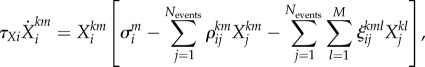3.1

where i,j = 1, … , N_events m = 1, … , M (different modalities). 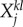is the lth modality component of the jth event in the kth episode. For example, we can have three episodes with six events and three modalities each, which results in 18 metastable patterns. ρ_ij is the matrix responsible for the competition among the different events within the same modality. Episodes are the result of the unification of sequences of events with three modalities each. Matrix 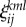characterizes the competition between different modalities inside the kth episode. For simplicity in our simulations, we will use the same value for all modalities. This value depends on attention: switching attention among different modalities corresponds to larger values of ξ. The sharing of attention corresponds to small values of ξ.

(ii) Episode dynamics

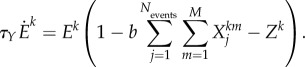3.2

In the case in which all modalities symmetrically interact with each other, we can rewrite the equation as

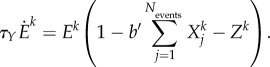3.3

(iii) EWM dynamics under an emotional cue

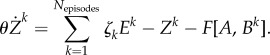3.4

Here Z^k is a chunking variable for the kth episode as before. θ is a time constant and ζ_k is the kth component of the projection vector for the episodes. F is a focusing function that is characterized by the distance d(A,B^k) between matrices :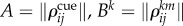

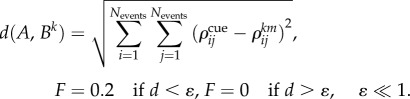3.5

We can consider that the origin of the matrices 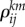is a learning process.

The information recalling from the EWM depends on the incoming stimuli, e.g. an emotional auditory input in our case, which controls WM dynamics (equation (3.4) and figure 4; electronic supplementary material, figure S2).

In the skater example, attention is shared between the modalities that represent in the cognitive space the binding episodic-emotion memory network. In general, not only each episode is a sequential structure of chunks events, but each event is a sequence of binding modes of different modalities. In this example, these modalities could be behaviour, personal semantic (music and artistic expression), and emotion.

Figure 4b illustrates an example of WTA dynamics of EWM recall as described by equations ((3.1)–(3.5)). In this example, modality 1 prevails. The sportsman can now write about this skater.

4. Hierarchical information connection: role of heteroclinic instabilities

Similar to complex brain networks [57], cognitive or mind networks are composed of ‘modules’. Such modules can be considered as an interconnected hierarchical heteroclinic network. These modules and the whole networks are dynamical and represent the performance of cognitive processes through phase trajectories along time. The analyses of the dynamical nature of hierarchical cognitive networks and the potential mechanisms underlying their interactions help to clarify the answer to intriguing problems such as the cognitive information capacity or the stability and robustness of goal-dependent performance. The request for robustness is fundamentally contradictory to the request for sensitivity of the sequential transient dynamics to informational signals from the environment. The solution to this contradiction comes naturally to a heteroclinic network because noise and an informational signal differently influence its topology. In these networks, the concepts are hierarchically nested by the level of abstraction and can be ordered on universal temporal hierarchies like binding and chunking that control their ‘Lego’-like combinations.

We have shown above that cognitive processes such as DM and prediction can be represented as hierarchical heteroclinic networks that exchange information because the unstable separatrices of the metastable state-informational patterns connect different levels of the hierarchy as in figure 4. Metastable patterns can gather plenty of information about specific events, images, or concepts.

The quantitative description of the hierarchical temporal information processing requires the definitions of (i) the information exchange value and (ii) the level of the unpredictability. Let us introduce the value information exchange on one metastable state as

4.1

where 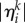is the distance between the chosen trajectory and the ith pattern (saddle point) in the direction of the kth unstable separatrix, 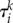is the exit time from the saddle point vicinity and 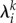is the corresponding eigenvalue of the saddle state.

Summarizing all information exchange among all modalities on the ith event, the information that the cognitive trajectory gets after passing the ith event—i.e. reading the metastable patterns that are bound on the ith event—is

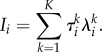4.2

In fact, this formula is the generalization of the Kolmogorov–Sinai entropy expression to non-stationary hierarchical processes.

We suggest that there is a dynamical bridge between the temporal hierarchy and the anatomical hierarchy of the brain. Our theory provides a framework for explaining a wide range of cognitive dynamics, including behaviour, by universal principles (see also [58–61]).

At the same time, the discussed approach helps to understand the dynamical nature of consciousness. Our consciousness is not our body nor our brain, but the dynamical sequence of information patterns that the brain global networks encode and the mind processes. In this sense, we can say that in our examples the goalkeeper's behaviour is automatic (subconscious). On the contrary, the reporter behaviour is conscious—he/she is talking with himself/herself, has doubts and finally after consulting his/her own episodic memory makes a decision.

5. Discussion

(a). Creativity and instabilities of cognitive networks dynamics

When our brain performs a standard cognitive function such as the generation of a specific motor programme that is determined by an environmental cue, the cognitive dynamics follows one of the familiar sequences of behavioural informational patterns. Cognitive networks in such cases are often not hierarchical. Instability of metastable patterns in these cases leads to losing information processing robustness and is limited by the processing capacity like in the case with sequential working memory [62]. However, even for perceptional goals, our brain uses hierarchical networks [63] as in the case of the integration or binding of different information modalities. Another example is chunking networks that deal with episodes formed by events. As we have seen above, the skeleton of hierarchical cognitive networks can emerge when different groups of information patterns are connected with each other by unstable separatrices. The dimension of such connections depends on the number of unstable separatrices and determines the complexity of hierarchical cognitive networks.

One of the most challenging problems related to cognitive instabilities is creativity. The non-linear dynamical approach to creativity considers it as the processes responsible for producing effective novelty, as well as the control mechanisms that confirm novelty production and the fact that it does not contradict mental health. Merely novel information displays surprise and incongruity, but it must also be meaningful. The corresponding multidimensional dynamical models can be based on the general cognitive principles discussed above: transitivity, existence of metastable states, robustness, and sensitivity to available information. In dynamical language, new brain instabilities produce new metastable patterns and make autobiographic memory much richer. In the canonic model (2.1), this means increasing the dimension of the model and the number of agents involved in the cognitive process. In the cognitive phase space, the additional instabilities and the increasing of the dimensionality lead to the appearance of absolutely new, fresh sequences of informational patterns that represent new music, dance, etc. Brain hierarchical networks that are responsible for creativity, e.g. music composition, are hierarchical and complex. They include the implementation of autobiographic memory—episodic and semantic, i.e. a reconstructive process, which is known to be critically dependent on the hippocampus.

As it is well known, emotion is a primary motivator for creative behaviour, but only recently the dynamical origin of this phenomena, i.e. the interaction between the neural systems involved in creativity and those involved in emotion, has been studied [64,65]. In particular, in [65], McPherson et al. showed that the activity in the prefrontal cortex and other brain areas involved in creativity is highly modulated by the emotional context. Thus, emotion and creativity are tightly bound. Another hierarchical process, chunking, is also present in the music creation process, which highly relies on event segmentation [66].

Two processes are crucially important for creativity: (i) some level of mental instability to drop the traditional view and approaches and (ii) rich enough semantic and EM. The importance of a low instability level is often connected with ‘unpredictability on the edge of chaos’ [67]. At the edge of chaos, the metastable patterns are maximally novel while still connected to patterns in the ordered regime, and thus are most likely to manifest the combination of novelty and utility that is the stamp of creativity. A similar concept was used to separate semantic network processes in people with disorders such as Asperger's syndrome, schizophrenia, and healthy people [68]. Such processes can also be theoretically analysed in the framework of the set of canonic models (2.1) that we proposed above (see also [69]).

Creative evaluation activates both the executive and default networks. New research has proposed that creative thought involves similar cognitive mechanisms as other forms of goal-directed, self-generated cognition [70]. The default network influences the generation of candidate ideas, but the control network can constrain this process to meet task-specific goals. Executive and default networks have shown positive functional connectivity throughout creative thinking [71]. In fact, our creativity is a binding process between goal-generated and free thoughts [72].

The instabilities that are responsible for creativity may also lead to pathological mental activity [73]. The connection between nearly pathological behaviours and creativity is produced because they share some personality features, such as cognitive disinhibition [74], which can arise from the activity of the same cognitive networks.

6. Conclusion

The dynamical origin of mental functions such as attention control, DM, episodic and semantic memories, sequence learning, and many others are still not fully understood. The approach discussed in this paper includes the universal mathematical language, fundamental modelling principles, and canonic models of key dynamical phenomena such as binding, chunking, and multilevel hierarchical organization of cognitive processes which include timing in a natural way. In fact, we have formulated here a basis for a future qualitative dynamical theory of cognition. This theory allows the analysis of the main bifurcations that control transitions between normal and pathological behaviour or thinking and to find key parameters of the dynamics of specific goal-dependent cognitive functions.

Data accessibility

The models described in this work can be easily implemented in dedicated code or in any simulation platform. All parameters used to obtain the data discussed in this work are available in the electronic supplementary material.

Authors' contributions

P.V. and M.I.R. conceived the models, generated and analysed the data, and wrote the manuscript. Both authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

P.V. was supported by MINECO/FEDER DPI2015-65833-P and TIN2012-30883. M.I.R. acknowledges support from ONR grant nos. N00014310205 and N00014-13-1-0678.