Chiral modes and directional lasing at exceptional points

Significance

Exceptional points (EPs) emerge when a system with loss or gain is tuned such that its eigenvalues and the corresponding eigenstates coalesce. By operating close to two EPs, we achieved a dynamic control of the rotation direction of light in a whispering-gallery-mode (WGM) resonator. This enabled us to tune the emission direction of a WGM microlaser from bidirectional, when the system is away from the EPs, to unidirectional emission at EPs and to reverse the emission direction by moving from one EP to the other. This feature provides WGM resonators new functionalities useful for lasing, sensing, optomechanics, and cavity quantum electrodynamics. Our findings will help to develop novel technologies for controlling the light flow on-chip and could affect scientific fields beyond optics.

Abstract

Controlling the emission and the flow of light in micro- and nanostructures is crucial for on-chip information processing. Here we show how to impose a strong chirality and a switchable direction of light propagation in an optical system by steering it to an exceptional point (EP)—a degeneracy universally occurring in all open physical systems when two eigenvalues and the corresponding eigenstates coalesce. In our experiments with a fiber-coupled whispering-gallery-mode (WGM) resonator, we dynamically control the chirality of resonator modes and the emission direction of a WGM microlaser in the vicinity of an EP: Away from the EPs, the resonator modes are nonchiral and laser emission is bidirectional. As the system approaches an EP, the modes become chiral and allow unidirectional emission such that by transiting from one EP to another one the direction of emission can be completely reversed. Our results exemplify a very counterintuitive feature of non-Hermitian physics that paves the way to chiral photonics on a chip.

Chirality lies at the heart of the most fascinating and fundamental phenomena in modern physics like the quantum Hall effect (1), Majorana fermions (2), and the surface conductance in topological insulators (3) as well as in p-wave superconductors (4). In all of these cases chiral edge states exist, which propagate along the surface of a sample in a specific direction. The chirality (or handedness) is secured by specific mechanisms, which prevent the same edge state from propagating in the opposite direction. For example, in topological insulators the backscattering of edge states is prevented by the strong spin-orbit coupling of the underlying material.

Transferring such concepts to the optical domain is a challenging endeavor that has recently attracted considerable attention. Quite similar to their electronic counterparts, the electromagnetic realizations of chiral states typically require either a mechanism that breaks time-reversal symmetry (5) or one that gives rise to a spin-orbit coupling of light (6–8). Because such mechanisms are often not available or difficult to realize, alternative concepts have recently been proposed, which require, however, a careful arrangement of many optical resonators in structured arrays (9, 10).

Here, we demonstrate explicitly that the above demanding requirements on the realization of chiral optical states propagating along the surface of a system can all be bypassed by using a single resonator with non-Hermitian scattering. The key insight in this respect is that a judiciously chosen non-Hermitian outcoupling of two near-degenerate resonator modes to the environment leads to an asymmetric backscattering between them [an effect that has been ignored in previous models based on coupled mode theory (11)] and thus to an effective breaking of the time-reversal symmetry that supports chiral behavior (12). More specifically, we show that a strong spatial chirality can be imposed on a pair of whispering-gallery modes (WGMs) in a resonator in the sense of a switchable direction of rotation inside the resonator such that these modes can be tuned to propagate in either the clockwise (cw) or the counterclockwise (ccw) direction.

In our experiment we achieved this on-demand tunable modal chirality and directional emission, using two scatterers placed in the evanescent field of a resonator (13). When varying the relative positions of the scatterers, the modes in the resonator change their chirality periodically, reaching maximal chirality and unidirectional emission at an exceptional point (EP)—a feature that is caused by the non-Hermitian character of the system (12, 14–21) and does not require the breaking of reciprocity.

Experimental Setup and Characterization

Our setup consists of a silica microtoroid WGM resonator that allows for the in- and outcoupling of light through two single-mode optical fiber waveguides (Fig. 1 and SI Appendix, Fig. S1). The major and the minor diameters of the resonator were $\sim 82\mu \text{m}$ and $\sim 8\mu \text{m},$ respectively, and the height of the silicon pillar holding the microtoroid above the surface of the wafer was $\sim 60\mu \text{m}.$ The resonator had a quality factor $Q\sim 3.9\times {10}^7$ at the resonant wavelength of 1,535.8 nm. To probe the scatterer-induced chirality of the WGMs, we used two silica nanotips as Rayleigh scatterers whose relative positions (i.e., relative phase angle β) and sizes (determined by the volume of the nanotips within the evanescent field of the WGM) within the WGM field were controlled by nanopositioners. The sizes of the nanotips used in the experiments ranged from tens of nanometers to several hundreds of nanometers.

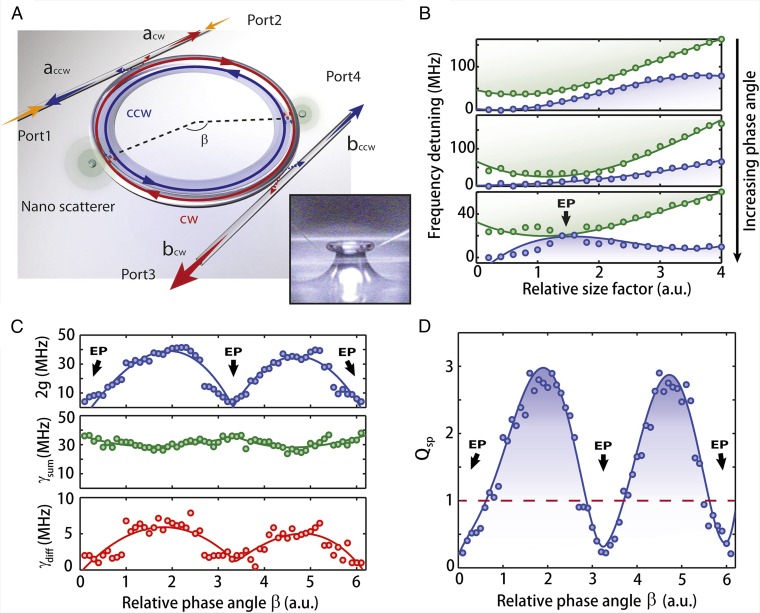
Fig. 1.

Experimental configuration and the effect of scatterers. (A) Illustration of a WGM resonator side-coupled to two waveguides, with the two scatterers enabling the dynamical tuning of the modes. cw and ccw are the clockwise and counterclockwise rotating intracavity fields. ${\text{a}}_{\text{cw}\left(\text{ccw}\right)}$ and ${\text{b}}_{\text{cw}\left(\text{ccw}\right)}$ are the field amplitudes propagating in the waveguides. β is the relative phase angle between the scatterers. Inset shows the optical microscope image of the microtoroid resonator, the tapered fiber waveguides (horizontal lines), and the two silica nanotips denoting the scatterers (diagonal lines on the left and right side of the resonator). (B) Varying the size and the relative phase angle of a second scatterer helps to dynamically change the frequency detuning (splitting) and the linewidths of the split modes revealing avoided crossings (Top) and an EP (Bottom). (C) Effect of β on the frequency splitting $2g,$ difference ${\gamma }_{\text{diff}},$ and sum ${\gamma }_{\text{sum}}$ of the linewidths of split resonances when relative size of the scatterers was kept fixed (SI Appendix, Figs. S3–S5). (D) Effect of β on the splitting quality factor $Q_{\text{sp}}.$ At the EP, the splitting quality factor $Q_{\text{sp}}$ approaches zero because the splitting $2g$ goes to zero (C, Top) whereas the total dissipation ${\gamma }_{\text{sum}}$ remains finite (C, Middle). Circles denote the experimental data, and the solid lines are the best fit using a theoretical model (SI Appendix, S1: Two-Mode-Approximation (TMA) Model and the Eigenmode Evolution and S2: Experimental Observation of an EP by Tuning the Size and Position of Two Scatterers).

First, using only the waveguide with ports 1 and 2 (Fig. 1A), we determined the effect of the sizes and positions of the scatterers on the transmission spectra. With the first scatterer entering the mode volume, we observed frequency splitting in the transmission spectra due to scatterer-induced modal coupling between the cw and ccw traveling modes. Subsequently, the relative position and the size of the second scatterer were tuned to bring the system to an EP (Fig. 1 B–D and SI Appendix, Figs. S2–S5) that is a non-Hermitian degeneracy (19–21) identified by the coalescence of the complex frequency eigenvalues and the corresponding eigenstates.

As has recently been realized, EPs act as a veritable source of nontrivial physics in a variety of systems (14–18, 22–27). Associated to an EP is an intrinsic chirality (16, 28) that appears in our system as a limiting case of perfect chirality. Depending on the amount of initial splitting introduced by the first scatterer and β, tuning the relative scatterer size brought the resonance frequencies (real part of eigenvalues) closer to each other, and then either an avoided crossing or an EP was observed (Fig. 1 B and D and SI Appendix, Figs. S4 and S5). At the EP both the frequency splitting $2g$ and the linewidth difference ${\gamma }_{\text{diff}}$ of the resonances approach zero, whereas the sum of their linewidths ${\gamma }_{\text{sum}}$ remains finite (Fig. 1 C and D and SI Appendix, Figs. S4 and S5). The splitting quality factor (29), $Q_{\text{sp}}=4g/{\gamma }_{\text{sum}},$ which is defined as the ratio of the frequency splitting to the half of the sum of the linewidths of the split resonances, reaches its minimum at the EP (Fig. 1D).

An EP not only leads to a perfect spectral overlap between resonances, but also forces the two corresponding modes to become identical (19–21). This can be understood as follows. Due to asymmetric backscattering in the vicinity of an EP, the two modes become chiral; i.e., both modes have a dominant contribution (cw or ccw). Moreover, they are mainly copropagating; i.e., the dominant contribution is the same in both cases. For example, both modes can have a large ccw component and only a small cw component. Approaching the EP leads to an even more decreasing cw component. At the EP the cw component vanishes, basically due to destructive interference. Both modes, considered as two-dimensional vectors (ccw, cw = 0), are then collinear. Only one independent eigenvector exists at the EP. Correspondingly, a pair of two counterpropagating WGMs observed in closed Hermitian resonators turns into a pair of copropagating modes with a chirality that increases the closer the system is steered to the EP (12, 30, 31) (SI Appendix, Figs. S6–S8).

Modal Chirality and Asymmetric Backscattering at an EP

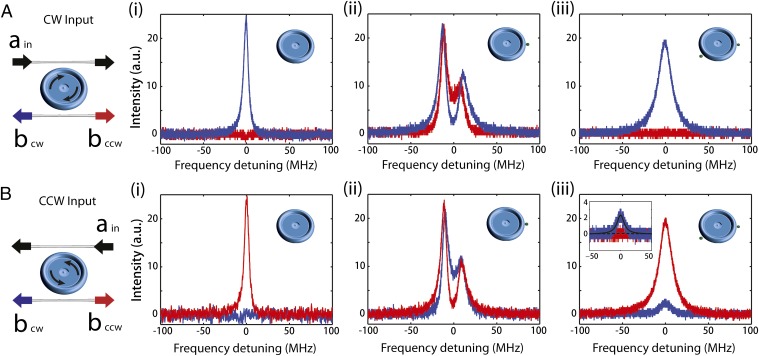
To investigate the modal chirality in detail we used both of the waveguides and monitored the transmission and reflection spectra at the output ports of the second waveguide for injection of light from two different sides of the first waveguide (Fig. 2). In the absence of the scatterers, when light was injected in the cw direction, a resonance peak was observed in the transmission and no signal was obtained in the reflection port (Fig. 2 A, i). Similarly, when the light was injected in the ccw direction, the resonance peak was observed in the transmission port with no signal in the reflection port (Fig. 2 B, i). When only one scatterer was introduced, two split resonance modes were observed in the transmission and reflection ports regardless of whether the signal was injected in the cw or the ccw direction (Fig. 2 A, ii and B, ii), implying that the field inside the resonator is composed of modes traveling in both cw and ccw directions. When the second scatterer was introduced and its position and size were tuned to bring the system to an EP, we observed that the transmission curves for injections from two different sides were the same but the reflection curves were different (Fig. 2 A, iii and B, iii): The reflection shows a pronounced resonance peak for the ccw input, whereas this peak vanishes for the cw input. This asymmetric backscattering (reflection) is the defining hallmark of the desired chiral modes (12, 30, 31), for which we provide here to our knowledge the first direct measurement in a microcavity (SI Appendix, S4: Chirality Analysis and Comparison Between the Lasing and the Transmission Models and Fig. S9).

Fig. 2.

Experimental observation of scatterer-induced asymmetric backscattering. (A and B) When there is no scattering center in or on the resonator, light coupled into the resonator through the first waveguide in the cw (A, i) [or ccw (B, i)] direction couples out into the second waveguide in the cw (A, i) [or ccw (B, i)] direction: the resonant peak in the transmission and no signal in the reflection. (A, ii and B, ii) When a first scatterer is placed in the mode field, resonant peaks are observed in both the transmission and the reflection regardless of whether the light is input in the cw (A, ii) or in the ccw (B, ii) direction. (A, iii and B, iii) When a second scatterer is suitably placed in the mode field, for the cw input there is no signal in the reflection output port (A, iii), whereas for the ccw input there is a resonant peak in the reflection, revealing asymmetric backscattering for the two input directions. Inset in B, iii compares the two backscattering peaks in A, iii and B, iii. Estimated chirality is −0.86.

Chirality and Directionality in a WGM Resonator

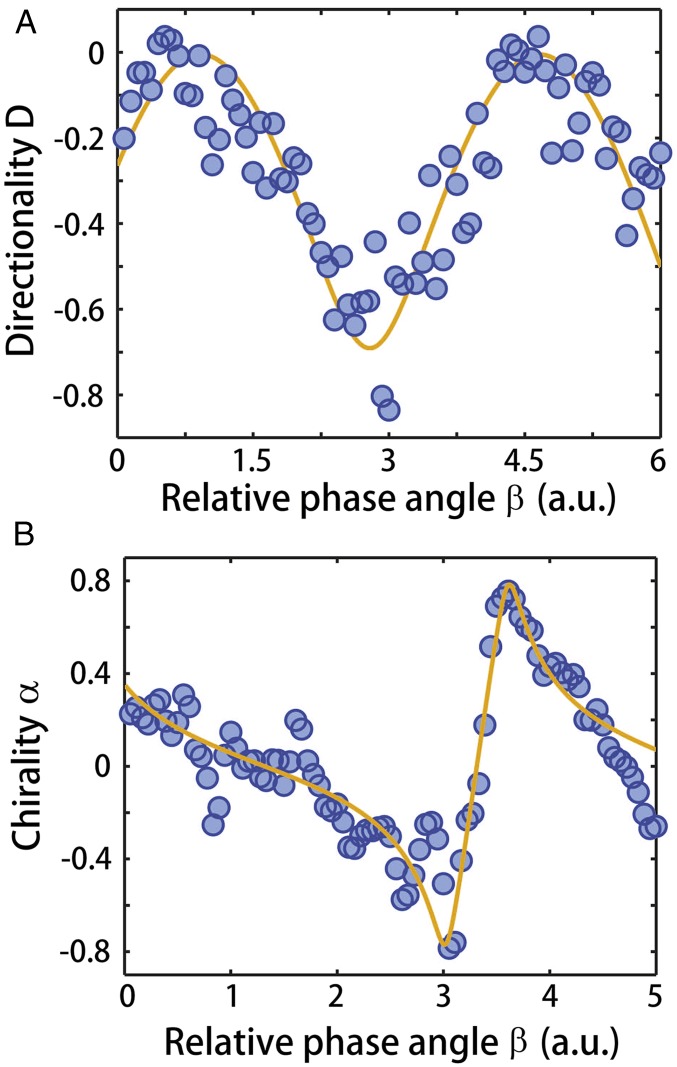
The crucial question to ask at this point is how the “chirality”—an intrinsic property of a mode that we aim to demonstrate—can be distinguished from the simple “directionality” (or sense of rotation) imposed on the light in the resonator just by the biased input. To differentiate between these two fundamentally different concepts based on the experimentally obtained transmission spectra, we determined the chirality and the directionality of the field within the WGM resonator, using the following operational definitions: The directionality defined as $D=\left(\sqrt{I_{\text{bccw}}}-\sqrt{I_{\text{bcw}}}\right)/\left(\sqrt{I_{\text{bccw}}}+\sqrt{I_{\text{bcw}}}\right)$ simply compares the difference of the absolute values of the light amplitudes measured in the ccw and cw directions without correcting for the direction from which the light is injected (Figs. 1A and 2). We observed that varying the relative distance between the scatterers changed this directionality, but the initial direction, that is the direction in which the input light was injected, remained dominant (Fig. 3A).

Fig. 3.

Controlling directionality and intrinsic chirality of whispering-gallery modes. (A and B) Directionality D (A) and chirality α (B) of the WGMs of a silica microtoroid resonator as a function of β between the two scatterers. The directionality D given in A was obtained when the input light was injected in the cw direction. For the input in the ccw direction, the results for D are similar but with opposite sign. Note that chirality α is an intrinsic quantity that is independent of the injection direction of the input light. The solid lines are obtained from the theoretical transmission model (SI Appendix, S4: Chirality Analysis and Comparison Between the Lasing and the Transmission Models and S5: Directionality Analysis for the Biased Input Case in the Transmission Model and Eqs. S16–S20) with the parameters set as $V_1=1.50-i0.10$ and $V_2=0.608-i0.099$ for A and $V_1=1.50-i0.10$ and $V_2=1.165-i0.675$ for B.

The intrinsic chirality of a resonator mode is a quantity that is entirely independent of any input direction and therefore not as straightforward to assess experimentally. One can, however, get access to the chirality α through the intensities measured in the used four-port setup as $\alpha =\left(\sqrt{I_{14}}-\sqrt{I_{23}}\right)/\left(\sqrt{I_{14}}+\sqrt{I_{23}}\right),$ where $I_{jk}$ denotes the intensity of light measured at the kth port for the input at the jth port (Fig. 1A and SI Appendix, S3: Emission and Chirality Analysis for the Lasing Cavity and S4: Chirality Analysis and Comparison Between the Lasing and the Transmission Models and Fig. S1). Note that to obtain α the reflection intensities obtained for injections from two different sides are compared. The chirality thus quantifies the asymmetric backscattering, similar to what is shown in Fig. 2 A, iii and B, iii. If the backscattering is equal for both injection sides ($I_{14}=I_{23}$), the chirality is zero, implying symmetric backscattering and orthogonal eigenstates. In the case where backscattering for injection from one side dominates, the chirality approaches 1 or $-1,$ depending on which side is dominant. The extreme values $\alpha =\pm 1$ are, indeed, possible only when the eigenvalues and eigenvectors of the system coalesce, that is, when the system is at an EP. By changing the relative phase angle between the scatterers, we obtained quite significant values ($\alpha =\pm 0.79$) of chirality with both negative and positive signs (Fig. 3B). The strong chiralities observed in Fig. 3B are linked to the presence of two EPs, each of which can be reached by optimizing β and the relative size factor such that asymmetric scattering is maximized for one of the two injection directions (SI Appendix, S1: Two-Mode-Approximation (TMA) Model and the Eigenmode Evolution and S4: Chirality Analysis and Comparison Between the Lasing and the Transmission Models and Figs. S2, S6, S7, and S9).

Controlling Emission Direction of a WGM Microlaser at EPs

Finally, we addressed the question of how this controllably induced intrinsic chirality can find applications and lead to new physics in the sense that the intrinsic chirality of the modes is fully brought to bear. The answer is to look at lasing in such devices because the lasing modes are intrinsic modes of the system. Previous studies along this line were restricted to ultrasmall resonators on the wavelength scale (32, 33), where modes were shown to exhibit a local chirality, no connection to asymmetric backscattering could be established, and chirality could not be controlled in situ.

Here, using a microcavity laser with a diameter being multiple times the wavelength ($>50\lambda$), we achieved a global and dynamically tunable chirality that we can directly link to the non-Hermitian scattering properties of the resonator. We used an Erbium (${\text{Er}}^{3+}$) doped silica microtoroid resonator coupled to only the first waveguide, which was used both to couple into the resonator the pump light to excite ${\text{Er}}^{3+}$ ions and to couple out the generated WGM laser light. With a pump light in the 1,450-nm band, lasing from ${\text{Er}}^{3+}$ ions in the WGM resonator occurred in the 1,550-nm band. Because the emission from Erbium ions couples into both the cw and ccw modes and the WGM resonators have a rotational symmetry, the outcoupled laser light typically does not have a predetermined outcoupling direction in the waveguide. With a single nanotip in the mode field, these initially frequency degenerate modes couple to each other, creating split lasing modes. Using another nanotip as a second scatterer, we investigated the chirality in the WGM microlaser by monitoring the laser field coupled to the waveguide in the cw and ccw directions. For this situation the parameters α and D from above can be conveniently adapted to determine the chirality of lasing modes based on the experimentally accessible quantities (SI Appendix, S2: Experimental Observation of an EP by Tuning the Size and Position of Two Scatterers–S5: Directionality Analysis for the Biased Input Case in the Transmission Model). Note that for the lasing modes chirality and directionality are equivalent as they both quantify the intrinsic dynamics of the laser system. We observed that by tuning the relative distance between the scatterers, the chirality of the lasing modes and with it the directional outcoupling to the fiber can be tuned in the same way as shown for the passive resonator (Fig. 3).

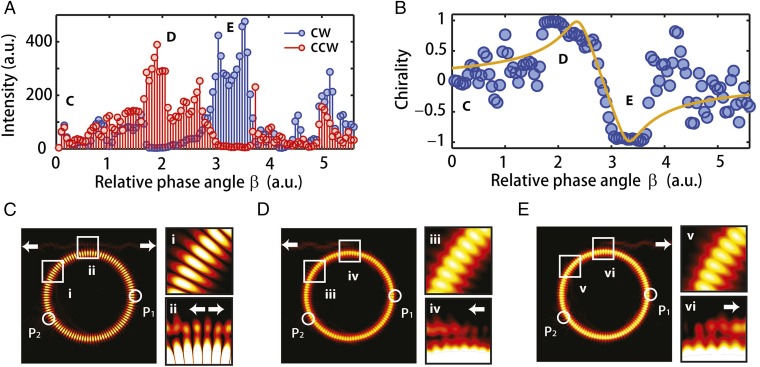
As depicted in Fig. 4A, depending on the relative distance between the scatterers one can have a bidirectional laser or a unidirectional laser, which emits only in the cw or the ccw direction. For the bidirectional case, one can also tune the relative strengths of emissions in cw and ccw directions. As expected, the chirality is maximal ($\pm 1$) for the relative phase angles where strong unidirectional emission is observed (Fig. 4B), and chirality is close to zero for the angles where bidirectional emission is seen. This confirms that by tuning the system to an EP the modes can be made chiral and hence the emission direction of lasing can be controlled: In one of the two EPs, emission is in the cw direction and in the other EP the emission is in the ccw direction. Thus, by transiting from one EP to another EP the direction of unidirectional emission is completely reversed—an effect demonstrated to our knowledge for the first time here. The fact that the maximum possible chirality values for the lasing system are reached here very robustly can be attributed to the fact that the nonlinear interactions in a laser tend to reinforce a modal chirality already predetermined by the resonator geometry (34).

Fig. 4.

Scatterer-induced mirror-symmetry breaking in a WGM microlaser at an EP. In a WGM microlaser with mirror symmetry the intracavity laser modes rotate both in cw and ccw directions and thus the outcoupled light is bidirectional and chirality is zero. The scatterer-induced symmetry breaking allows tuning both the directionality and the chirality of laser modes. (A) Intensity of light outcoupled into a waveguide in the cw and ccw directions as a function of β. Regions of bidirectional emission and fully unidirectional emission are seen. (B) Chirality as a function of β. Transitions from nonchiral states to unity ($\pm 1$) chirality at EPs are clearly seen. Unity chirality regions correspond to unity unidirectional emission regions in A. The solid line is obtained from the theoretical lasing model (SI Appendix, S3: Emission and Chirality Analysis for the Lasing Cavity and S4: Chirality Analysis and Comparison Between the Lasing and the Transmission Models and Eqs. S10–S12) with the parameters set as $V_1=1.50-i0.10$ and $V_2=1.485-i\mathrm{0.14.}$ (C–E) Finite-element simulations revealing the intracavity field patterns for the cases labeled C–E in A and B. Results shown in C–E were obtained for the same size factor but different β: (C) 2.628 rad, (D) 2.631 rad, and (E) 2.626 rad. $P_1$ and $P_2$ denote the locations of the scatterers. For a quantitative comparison between the experimental data and the simulations, the latter would have to be extended along the lines of ref. 34 to include also nonlinear effects as well as possible corrections stemming from the 3D nature of the experimental setup.

To relate this behavior to the internal field distribution in the cavity, we also performed numerical simulations that revealed that when the intracavity intensity distribution shows a standing-wave pattern with a balanced contribution of cw and ccw propagating components and a clear interference pattern, the emission is bidirectional, in the sense that laser light leaks into the second waveguide in both the cw and ccw directions (Fig. 4C). However, when the distribution does not show such a standard standing-wave pattern but an indiscernible interference pattern, the emission is very directional, such that the intracavity field couples to the waveguide only in the cw or the ccw direction, depending on whether the system is at the first or the second EP (Fig. 4 D and E). We confirmed that the presence or absence of an interference pattern in the field distribution was also linked with a bidirectional or a unidirectional transmission, respectively, observed in Fig. 3 for the passive resonator (SI Appendix, S5: Directionality Analysis for the Biased Input Case in the Transmission Model and Fig. S10).

Conclusions and Discussions

We have demonstrated chiral modes in whispering-gallery-mode microcavities and microlasers via geometry-induced non-Hermitian mode couplings. The underlying physical mechanism that enables chirality and directional emission is the strong asymmetric backscattering in the vicinity of an EP that universally occurs in all open physical systems. We believe that our work will lead to new directions of research and to the development of WGM microcavities and microlasers with new functionalities. In addition to controlling the flow of light and laser emission in on-chip micro- and nanostructures, our findings have important implications in cavity quantum electrodynamics for the interaction between atoms/molecules and the cavity light. They may also enable high-performance sensors to detect nanoscale dielectric, plasmonic, and biological particles and aerosols (35–38) and be useful for a variety of applications such as the generation of optical beams with a well-defined orbital angular momentum (39) and the topological protection in optical delay lines (9, 10, 40).