Range expansions transition from pulled to pushed waves as growth becomes more cooperative in an experimental microbial population

Significance

Species undergo range shifts in response to changing climate or following an introduction to a new environment. Invasions often incur significant economic cost and threaten biodiversity. Ecological theory predicts two distinct types of expansion waves, pulled and pushed, depending on the degree of cooperativity in the population. Although pulled and pushed invasions differ dramatically in how population-level properties such as the expansion rate depend on the organism-level properties such as rates of growth and dispersal, these theoretical predictions have not been tested empirically. Here, we use a microbial model system to perform these tests and demonstrate that pulled and pushed waves can be distinguished based on their dynamics.

Abstract

Range expansions are becoming more frequent due to environmental changes and rare long-distance dispersal, often facilitated by anthropogenic activities. Simple models in theoretical ecology explain many emergent properties of range expansions, such as a constant expansion velocity, in terms of organism-level properties such as growth and dispersal rates. Testing these quantitative predictions in natural populations is difficult because of large environmental variability. Here, we used a controlled microbial model system to study range expansions of populations with and without intraspecific cooperativity. For noncooperative growth, the expansion dynamics were dominated by population growth at the low-density front, which pulled the expansion forward. We found these expansions to be in close quantitative agreement with the classical theory of pulled waves by Fisher [Fisher RA (1937) Ann Eugen 7(4):355–369] and Skellam [Skellam JG (1951) Biometrika 38(1-2):196–218], suitably adapted to our experimental system. However, as cooperativity increased, the expansions transitioned to being pushed, that is, controlled by growth and dispersal in the bulk as well as in the front. Given the prevalence of cooperative growth in nature, understanding the effects of cooperativity is essential to managing invading species and understanding their evolution.

From a local disturbance by an invasive species to the global expansion of the biosphere after an ice age, range expansions have been a major ecological and evolutionary force (1, 2). Range expansions and range shifts are becoming increasingly frequent due to the deliberate introduction of foreign species (3, 4), unintentional introductions caused by global shipping (5), and temperature changes associated with climate change (6, 7). Many invasions disturb ecosystem functions, reduce biodiversity, and impose significant economic costs (8, 9). The interest in invasion forecasting and management resulted in a substantial effort to develop predictive mathematical models of range expansions (4, 10–13), but empirical tests of these models have been less extensive.

Species invade new territory through a combination of dispersal and local growth. Mathematically, these dynamics can be described by a variety of models depending on the details of the species ecology or simplifying assumptions (14). For example, the invasion of house finches in North America has been successfully modeled with integrodifference equations (4). Continuous reaction–diffusion equations have been used to describe the expansion of trees following the end of an ice age and the expansion of muskrats from central Europe (15), whereas metapopulation models with disjoint patches of suitable habitat and discrete generations are more appropriate for certain butterflies living in temperate climates (16). One of the great achievements of mathematical ecology is the discovery that all these diverse models of population expansion can be divided into two broad classes of pulled and pushed expansions with very different properties.

The class of the expansion is determined by how the per capita growth rate depends on population density (17–19). Whereas some populations experience only intraspecific competition and grow best at very low densities, others exhibit an Allee effect and grow best at intermediate densities, due to intraspecific cooperation, higher chances of finding mates, or other factors (20–23). These Allee effects may be weak (reduced but positive growth rate at low density) or strong (inability to survive at low density). Pulled expansions occur when Allee effects are small, and the expansion velocity depends only on the growth rate at low densities and the rate of dispersal. Such expansions are dominated by the dynamics at the very edge of the expanding wave front, which effectively pulls the wave forward (17, 18, 24). As a result, pulled invasions are known to be sensitive to demographic fluctuations and lead to rapid loss of genetic diversity because the population size at the expansion edge is very small (25–29). When the Allee effect is more severe, including but not restricted to the case of strong Allee effects, the expansions are pushed. In contrast to the simple and universal theory of pulled expansions, the velocity and other properties of pushed expansions depend on the per capita growth rate at all population densities, and thus are sensitive to all of the details of the species ecology (17, 18, 24).

Because direct observations of the Allee effect are often challenging, it is important to find alternative ways to distinguish pulled and pushed expansions. Unfortunately, these two invasion classes share many generic properties. In particular, both expansions advance as population waves that move at constant velocity and maintain a constant shape of the expansion front. Even the qualitative shape of the expansion front is the same for pulled and pushed waves because population densities decay exponentially at the expansion edge in both cases (17, 18). Thus, one needs quantitative rather than qualitative comparison between theory and observations to distinguish pulled and pushed waves.

Although high-quality quantitative data on range expansions is often limited, several studies have successfully tested theories of range expansions in natural and laboratory populations. Veit and Lewis (4) could accurately describe the spread of house finches in North America by incorporating an Allee effect and long-distance dispersal. Importantly, this was one of the early studies highlighting the difference between pulled and pushed invasions. Lewis and Kareiva (30) had earlier shown that the rate of spread also depends on the initial spatial abundance profile of the invader. Melbourne and Hastings (31) have carried out a very detailed comparison between theory and experiment for a laboratory population of flour beetles and showed that the unavoidable heterogeneity of the founding organisms leads to large variation in the rate of spread between replica populations. At the microscopic scale, Wakita et al. (32) tested the expected relation between the rate of spread and nutrient availability in Escherichia coli, and Giometto et al. (33) used the theory of pulled waves to describe the expansion of tetrahymena in linear channels. All of these studies, however, focused only on the rate of invasion and did not test theoretical predictions for the shape of the invading fronts. More importantly, these studies were conducted in a single environment and did not attempt to distinguish pulled and pushed expansions, in part because there was no experimental population that could undergo both pulled and pushed expansions.

Experimental microbial populations are a tractable system to study ecological phenomena without the overwhelming complexity of the natural world. However, such experiments can guide our thinking, show which theoretical predictions may be observable in nature (34, 35), and help develop new models (36). For example, range expansions of microbial populations have revealed the dependence of the invasion velocity on the supply of resources (37) and demographic stochasticity (33). Experiments with microbes have also demonstrated the strong effect of range expansion on competition (38–44) and neutral evolution via the founder effect or gene surfing (45, 46). In this study, we focus on expansions with and without the Allee effect and quantify their differences. Because it is possible to control and measure population sizes in microbial populations over a few orders of magnitude, our experimental system is particularly well-suited for studying the shape of the expansion fronts, as well as for future investigations on the rates of diversity loss and effects of habitat fragmentation such as invasion pinning (47, 48).

To recreate a range expansion in the laboratory, we used a metapopulation of budding yeast Saccharomyces cerevisae. Yeast grows best at low densities on simple sugars such as glucose or galactose but has a well-characterized Allee effect in the disaccharide sucrose (49–52). Sucrose is digested cooperatively because the yeast cells secrete an enzyme to hydrolyze extracellular sucrose into glucose and fructose, which are then transported into the cell. Higher cell densities facilitate the utilization of glucose, and therefore the growth rate of yeast on sucrose is maximum at intermediate population densities, where glucose utilization is high but competition is not yet strong. Importantly, the strength of the Allee effect can be controlled by tuning the relative concentrations of glucose and sucrose in the growth medium. Using this experimental system, we tested nontrivial properties of invasions including the exponential spatial decay of population density at the front. We then observed the transition from pulled to pushed expansion waves as the Allee effect was made more severe and found signatures of this transition in the expansion velocity and front shape. Our work confirms that Allee effects substantially affect invasion dynamics and demonstrates that pushed and pulled invasions can be distinguished by quantitative measurements.

Results

Experimental System.

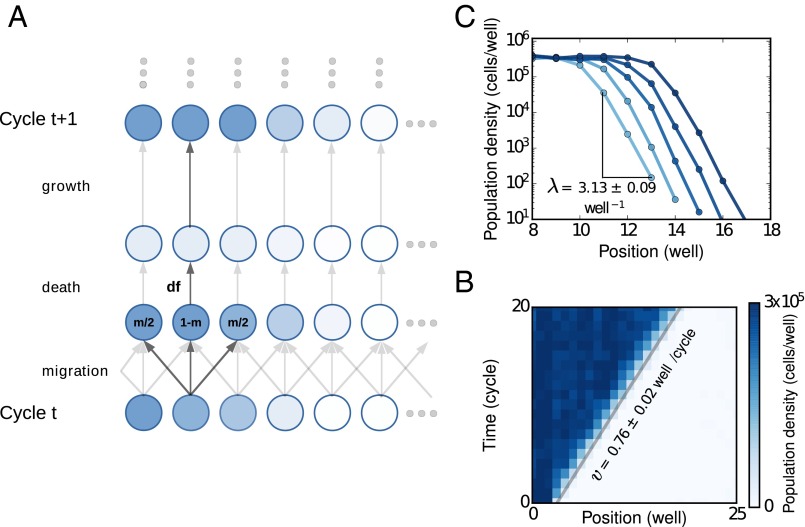
To study range expansions, we allowed the yeast populations to expand in one dimension along the columns of a 96-well plate. Each well represented a patch of suitable environment in a metapopulation where growth and death cycles occurred via a resupply of nutrients and dilution. Dispersal was achieved via exchange of small volumes of the growth media, corresponding to the migration rate (m), between the nearest wells (Fig. 1A and SI Appendix, Fig. S14). The experiments were started with a steep exponential initial population density profile, and after the profiles equilibrated over a few cycles we used flow cytometry to measure the density profiles of the emergent waves. This allowed us to measure with high accuracy the velocity ($v$) and the spatial decay rate of the exponential front ($\lambda$) over multiple orders of magnitude of population density (Fig. 1 B and C).

Fig. 1.

Theoretical predictions for the velocity and spatial density profile of pulled and pushed waves were quantitatively tested in metapopulations of budding yeast, S. cerevisae, in a controlled experimental setup. (A) Yeast populations expanded along the columns of a 96-well plate. The experiments were started with an exponentially decaying spatial density profile. After every growth cycle of 4 h, cells were diluted into fresh media (dilution factor, df) and dispersal was achieved by transferring small amounts of media to neighboring wells along the columns. (B) Optical density measurements at the end of each cycle revealed an emergent wave traveling at constant velocity. (C) At later times, after allowing the fronts to equilibrate, the density profiles were also measured using flow cytometry. These high-resolution measurements at the low density fronts showed exponential fronts extending over four orders of magnitude in density. The spatial decay rate, λ, was estimated by averaging over density profiles over the last few cycles, after the expansion wave had equilibrated. The profiles measured using flow cytometry were also used to measure the velocity more accurately (Materials and Methods).

Range expansions of yeast in our metapopulations are well described by a simple model incorporating growth and nearest-neighbor dispersal. Assuming that an unconnected population starting at some density $n$ grows to a final density given by $g_{\mathrm{\Delta }t}\left(n\right)$ in one cycle of length $\mathrm{\Delta }t$, the dynamics in connected populations, which have dispersal followed by growth, are given by

$$n_{t+\mathrm{\Delta }t,x}=g_{\mathrm{\Delta }t}\left(n_{t,x}+D_{eff}\frac{\mathrm{\Delta }t}{\mathrm{\Delta }{x}^2}\left(n_{t,x+\mathrm{\Delta }x}+n_{t,x-\mathrm{\Delta }x}-2n_{t,x}\right)\right).$$ [1]

Here, $t$ and $x$ are time and position, $\mathrm{\Delta }t$ and $\mathrm{\Delta }x$ are time of the dilution cycles and separation between the wells, and $D_{eff}$ is the dispersal rate determined by how much fluid is exchanged between the wells (see SI Appendix, Eq. S12 for the relationship between $D_{eff}$ and the experimental parameter, $m$). Note that, in the limit of small $\mathrm{\Delta }t$ and $\mathrm{\Delta }x$, this discrete model is equivalent to the well-known equation proposed by Fisher, Kolmogorov, and Skellam to describe biological invasions:

$$\frac{\partial n}{\partial t}=D\frac{{\partial }^{2}n}{\partial x^2}+nr\left(n\right).$$ [2]

Thus, our experiments can be viewed as both mimicking metapopulation dynamics typical for many ecosystems and approximating the continuous dynamics frequently assumed in mathematical ecology.

The dynamics of pulled expansions are completely determined by linearized growth [$g_{\mathrm{\Delta }t}\left(n_{t,x}\right)\approx n_{t,x}{e}^{r_0\mathrm{\Delta }t};r_0=r(n=0)$] and the expansion velocity is given by

$$v_{lin}={\min }_{\lambda >0}\left\{\frac{1}{\lambda \mathrm{\Delta }t}\ln \left[e^{r_0\mathrm{\Delta }t}\left[1+\frac{D_{eff}\mathrm{\Delta }t}{\mathrm{\Delta }{x}^2}\left(\cosh \left(\lambda \mathrm{\Delta }x\right)-1\right)\right]\right]\right\}\approx 2\sqrt{r_{0}D},$$ [3]

where the population density at the front decays exponentially with a rate $\lambda$, such that the velocity is minimized (SI Appendix, Eq. S10). In the limit of vanishing $\mathrm{\Delta }t$ and $\mathrm{\Delta }x$, this gives the classic Fisher velocity, $v=2\sqrt{r_0{D}_{eff}}$, and the spatial decay rate of the population density at the expansion edge, $\lambda =\sqrt{r_0/D_{eff}}$.

In sharp contrast, the knowledge of linearized growth is not sufficient to determine the velocity of a pushed expansion, because immigration from fast-growing regions behind the front increases the rate of invasion. Therefore, the deviations between the velocity and decay rate observed in the experiment and the corresponding values given by Eq. 3 indicate that the expansion is pushed, not pulled. In our analysis, we use this difference between the observed expansion velocity and the linearized growth velocity to distinguish between pulled and pushed waves.

Testing the Theory of Pulled Waves.

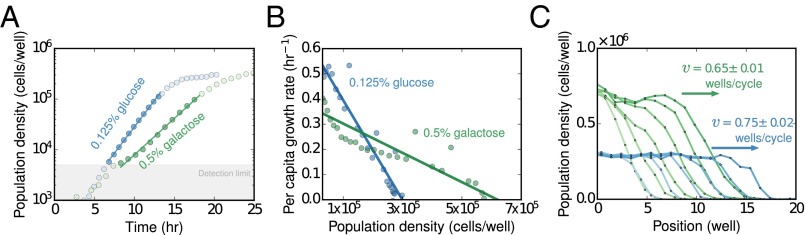
A surprising prediction for pulled waves is that the emergent properties of the wave front, its velocity $\left(v\right)$ and spatial decay rate ($\lambda$), depend on the per capita growth rate of the population only at low density, $r_0$, and not at higher densities. To the first order, $v\propto \sqrt{r_0}$, and consequently, an apparently healthy population that grows to a very high carrying capacity can in fact be a poor invader if it grows slowly, compared with a fast-growing population that saturates at lower densities. To test this hypothesis, we compared the range expansion of S. cerevisae in two different media: 0.125% glucose and 0.5% galactose. In both media, growth was exponential at low densities (Fig. 2A), but the two carbon sources showed a trade-off between faster low-density growth versus higher carrying capacity. Specifically, yeast cells initially grew at a faster rate in glucose but saturated to a lower carrying capacity compared with galactose (Fig. 2B). Furthermore, there was not a measurable Allee effect in either medium (SI Appendix, Fig. S2), and so we expected the expansions in both media to be pulled, and hence dependent only on the low-density growth rate. Consistent with the pulled-wave prediction, the resulting expansion waves indeed had a higher velocity in glucose, even though the bulk grew to a larger density in galactose (Fig. 2C).

Fig. 2.

In pulled waves, expansion velocity depends on the growth rate only at low densities irrespective of the carrying capacity. (A) A population of S. cerevisae grows exponentially at low densities in 0.125% glucose and 0.5% galactose. Growth rate at low densities is higher on 0.125% glucose compared with 0.5% galactose and decreases monotonically in both environments. (B) The galactose environment has a higher carrying capacity compared with glucose. The two environments thus show a trade-off between the low-density growth rate and the carrying capacity. (C) Although the galactose environment is more favorable in terms of the total nutrient availability (carrying capacity), expansions are faster in glucose because the populations grow faster in glucose at low density.

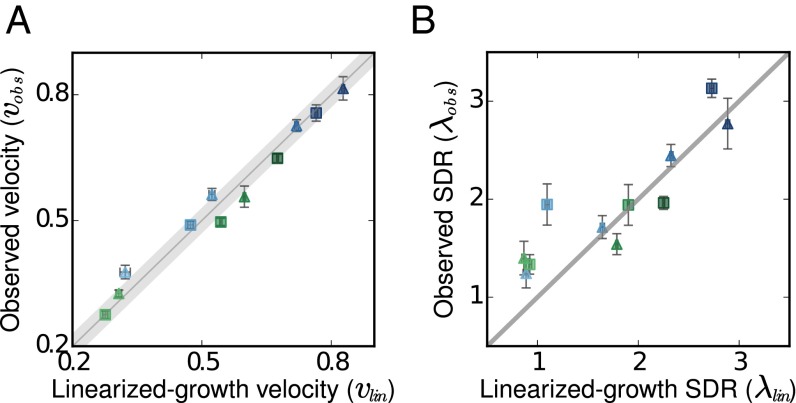
To further quantify the qualitative agreement with theory that we observed above, we repeated the range-expansion experiment in a wide range of environmental conditions, with the same two media, 0.125% glucose or 0.5% galactose. We varied the migration rate (m = 0.4, m = 0.5) and the death rate (dilution factors of 2, 2.5, 3.3, and 4), which resulted in invasion velocities ranging from 0.2 wells per cycle up to 0.9 wells per cycle. Because the growth rate at very low densities needs to be known accurately, flow cytometry was used to count the number of divisions (fold growth) that cells undergo over the course of each 4-h cycle (SI Appendix, Figs. S2 and S10). We found excellent agreement between the experimentally observed velocities and the linearized growth velocities predicted based on the rates of dispersal and growth at low densities alone (Fig. 3A). Although this agreement is expected given the near-logistic growth in glucose and galactose, it provides a quantitative confirmation of the theory of pulled waves.

Fig. 3.

For pulled waves, the growth rate at low density is sufficient to determine the emergent wave properties quantitatively. Over a wide range of environmental conditions, the observed expansion velocities and the spatial decay rates (SDR) of the population density at the front closely match the predictions based on the measured low-density growth rate. (A) Predicted and observed velocities in two different media are shown (glucose in blue, galactose in green). The migration rate (triangles: m = 0.5, squares: m = 0.4) and the death rate (darker colors are smaller death rates) were varied. Independently measured growth rates, only at low densities, in the two different media were sufficient to predict the velocities accurately. (B) A similar comparison for the spatial decay rates (λ, well⁻¹) also shows close agreement for steep predicted fronts (large λ). However, shallow predicted fronts deviated slightly from predictions, which may be a consequence of the long relaxation time to equilibrium for such fronts. x-axis error bars: SEM of the measured low-density growth rates, propagated to the errors in predicted velocity (A) and spatial decay rate (B). y-axis error bars: (A) SD of velocity measured for five different thresholds, and (B) SD in spatial decay rate measured over three different regions of the front.

A similar comparison between the observed and predicted spatial decay rates was more challenging due to stochastic effects and long equilibration times. Stochastic effects appear due to the small number of individuals at the front and create much larger deviations between the deterministic theory (Eq. 1) and the actual population dynamics for the spatial decay rate compared to the velocity (SI Appendix, Fig. S4). These deviations are known to make the fronts steeper (larger λ) (53, 54). Instead of using the analytical approximations that account for the stochastic effects, we chose a more direct and precise approach to test the theory of pulled waves. Because the distinction between pulled and pushed waves lies only in the degree to which the growth dynamics can be linearized, we performed individual-based simulations that included demographic fluctuations using only the growth rate measured at low densities. For pulled, but not pushed, waves the observed velocity and spatial decay rates must match simulations. As expected for expansions in glucose and galactose environments, the observed spatial decay rate was generally close to simulated values, confirming that these expansions are pulled (Fig. 3B). However, moderate deviations were observed under some experimental conditions. All four of these outliers occurred when the predicted spatial exponent was much smaller than that of the initial profile. As a result, these expansion profiles required a much longer time to reach their equilibrium shape and could still be out of equilibrium by the end of our experiments. Thus, the observed deviations might be due to insufficient observation time rather than the deviations from the theory of pulled waves.

Expansions Transition from Pulled to Pushed as Cooperativity Increases.

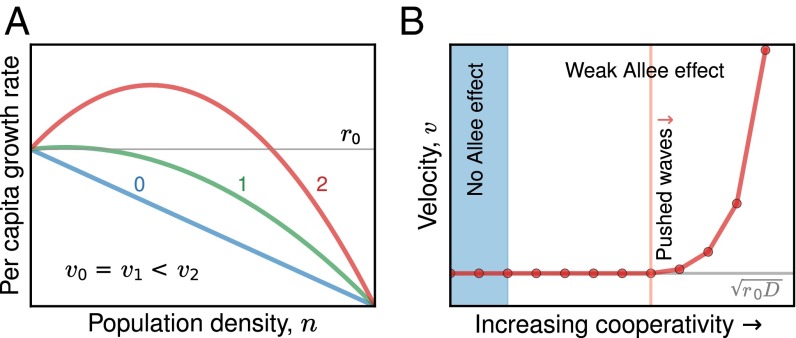
Populations in which the per capita growth rate decreases monotonically with increasing density always expand as pulled waves (55); similarly, expansions of populations with a strong Allee effect are always pushed (17). However, populations with a weak Allee effect may be either pulled or pushed, depending on the magnitude of the Allee effect (Fig. 4A). Thus, the transition from pulled to pushed waves occurs at some intermediate magnitude of the Allee effect, within the weak Allee effect regime (Fig. 4B).

Fig. 4.

Expansions transition from pulled to pushed waves at an intermediate strength of Allee effect within the weak regime. (A) Three different growth profiles displaying increasing magnitude of Allee effect (growth profile 0 is purely logistic; 1 and 2 have a weak Allee effect), but with the same low-density growth rate. Unlike pulled waves, the velocities of expansion in the three cases are not the same. In particular, both logistic (0) and the less-severe Allee effect (1) result in pulled waves with the same velocity, given by $2\sqrt{r_{0}D}$. In contrast, condition 2, with a larger but still weak Allee effect, leads to a pushed wave with velocity greater than $2\sqrt{r_{0}D}$. (B) In a generic model of the Allee effect (SI Appendix, Eq. S13), it can be shown that the transition from pulled to pushed waves occurs at a threshold magnitude of Allee effect that is different from the onset of a weak Allee effect. B shows the theoretical prediction for expansion velocity as the magnitude of the Allee effect (difference between maximal and low density per capita growth rate) is increased slowly, keeping the growth rate at low density constant. No change is seen in the dynamics of the expansion when a weak Allee effect is introduced. However, as the magnitude of the Allee effect is increased further, the expansion dynamics undergo a transition at a threshold magnitude of the Allee effect (vertical red line). The red curve is the actual expansion velocity, and the gray line is the velocity of a pulled wave with the same low density growth rate, r₀.

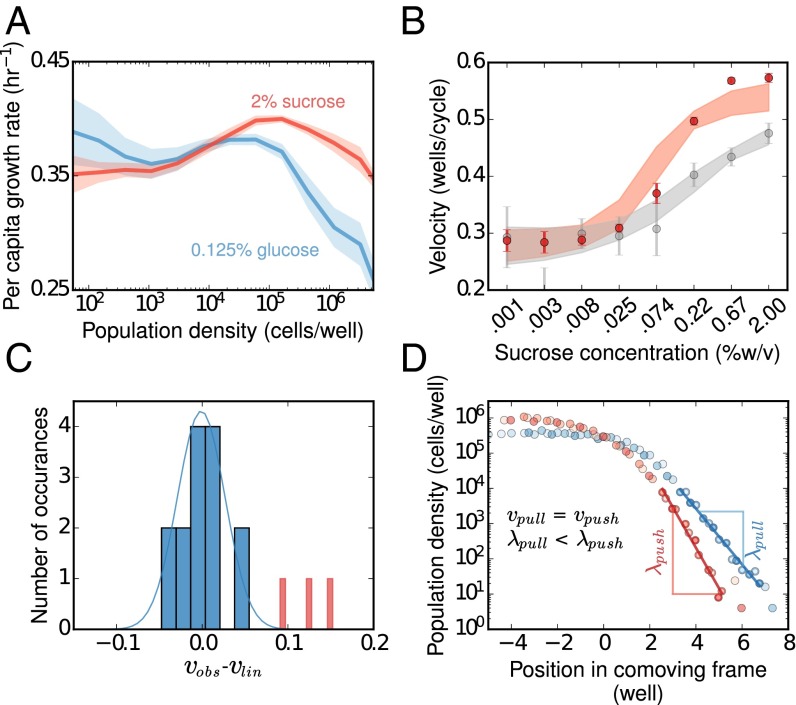
To study this transition from pulled to pushed waves with increasing magnitude of the Allee effect, we studied the expansion of yeast when growing on the sugar sucrose, where growth is known to be cooperative. In our experiments, low-density growth rate measurements in 2% sucrose showed an Allee effect over densities ranging from ∼10³ to 10⁵ cells per well, where the per capita growth rate increased with cell density (Fig. 5A). We note that this region of inverse density dependence is two orders of magnitude below the carrying capacity. As a result, the Allee effect would not have been visible with optical density measurements alone, and it was only revealed by fold-growth measurements using flow cytometry—a situation that parallels the difficulty of detecting Allee effects in natural populations. We show below that even this weak Allee effect was sufficient to make the expansion in 2% sucrose pushed instead of pulled.

Fig. 5.

Populations expand as pulled waves when Allee effect is small, but a large Allee effect makes populations expand faster than predicted based on linearized growth. (A) Experimental measurement of growth rates in sucrose (red) and glucose (blue). The growth rate in glucose decreases monotonically with increasing population density, and thus exhibits no Allee effect. In contrast, the per capita growth rate in sucrose increases with population density (between 10³ and 10⁵ cells per well) and thus exhibits a weak Allee effect. (B) By adding sucrose to the growth media, we increased the strength of the Allee effect (SI Appendix, Fig. S6) and observed a transition from pulled to pushed waves. Below sucrose concentration of 0.025%, observed expansion velocities (red dots) matched pulled-wave predictions based on linearized-growth (gray dots). For higher sucrose concentrations, we observed a significant deviation in observed velocities from the linearized growth velocities, indicating that expansions had become pushed. The error bars on the measured velocity (red points) are SD. Error bars are obtained on the linearized growth velocities (in gray) by bootstrapping on the growth rate measurements at low density. The observed velocities match well with the predictions of a mechanistic model (SI Appendix, section 4) shown in red shading. The model also captures the transition from pulled to pushed waves as the deviation between observed and linearized-growth velocities (gray shading) around sucrose concentration of 0.025%. The width of the shaded regions is the SD of simulation results for 89 parameter sets obtained by bootstrapping over the growth rate measurements and fitting the model to it. (C) The data at low sucrose concentrations (0.001, 0.003, and 0.008%; pulled regime) in blue and high sucrose concentrations (0.22, 0.67, and 2.0%; pushed regime) in red demonstrates the statistical significance of our results. When the Allee effect is small the difference in observed and linearized growth velocities is indistinguishable from zero, but the difference is large and highly significant for a large Allee effect (P = 0.0015). (D) Pushed waves are expected to have steeper profiles than pulled waves when expanding at the same velocity (and with the same migration rate). We found that a pulled wave in 0.125% glucose (blue) and a pushed wave in 2% sucrose (red) have approximately equal velocities, and, as expected, population densities declined much faster in space for the pushed wave.

We tuned the magnitude of the Allee effect by modulating the amount of sucrose in the media. As the sucrose concentration is increased, the growth rate at very low densities increases slowly, because only a fraction of the hydrolysis products can be captured by the cells before they diffuse away (SI Appendix, Fig. S5). In contrast, the maximal per capita growth rate, observed at intermediate cell densities, increases much more rapidly because dense populations use sucrose more efficiently (SI Appendix, Fig. S10). As a result, the magnitude of the Allee effect, measured as the difference between the low-density and the maximal per capita growth rate, increases with increasing sucrose concentration (SI Appendix, Fig. S6). Because the migration rates were known and the low-density growth rates were measured, we could directly compute the linearized growth velocity in each of the environments and compare it to the experimentally measured rate of invasion. For sucrose concentrations below ∼0.025%, the observed velocities were close to the linearized growth velocities, indicating that the expansions were pulled. However, as the Allee effect increased in magnitude, the observed and linearized growth velocities started to differ, reflecting the transition to pushed expansions (Fig. 5B).

To confirm that the observed differences between the pushed and the pulled waves were statistically significant, we focused on expansions in glucose (pulled waves) and three sucrose concentrations: 0.22%, 0.67%, and 2% (pushed waves). Whereas the velocities of pulled waves fluctuated in a small region around the linearized growth velocities due to demographic and environmental stochasticity, the expansion velocities at high sucrose concentrations were much larger than, and well separated from, the corresponding linearized growth velocities (P = 0.0015; Fig. 5C). Thus, our experiments indeed demonstrated a transition from pulled to pushed waves.

A mechanistic model of yeast growth further confirmed that the departure from the theory of pulled waves resulted from an Allee effect due to the cooperative breakdown of sucrose (SI Appendix, section 3). Briefly, we assume that yeast cells consume glucose and grow following Monod kinetics. Small amounts of glucose are present initially, but the bulk of glucose is produced through sucrose hydrolysis with a rate proportional to the total yeast concentration. The collective hydrolysis gives rise to an increasing Allee effect with increasing sucrose concentration, and the model generically predicts a transition from pulled to pushed waves (SI Appendix, Fig. S7). We inferred the model parameters from the measurements of yeast growth rates across different cell densities and sucrose concentrations (SI Appendix, section 4). The model, thus parameterized, predicted expansion velocities that closely matched our experimental observations (Fig. 5B), demonstrating that the transition from pulled to pushed waves was indeed caused by a greater Allee effect at higher sucrose concentrations. Further supporting this conclusion, our estimates of the model parameters agreed well with previous measurements (SI Appendix, Table S1).

To demonstrate an important difference between pulled and pushed waves, we compared a pulled expansion in glucose to a pushed expansion in sucrose with the same velocity and dispersal rate. If both waves are pulled, the density profiles must have identical spatial decay rates, but if the expansion in sucrose is pushed, then it must have a steeper front. Keeping all other experimental parameters the same, the two media allowed such a comparison: 0.125% glucose and 2% sucrose. The low-density growth rate in 0.125% glucose was marginally higher than in 2% sucrose (Fig. 5A), and the velocity of expansion in both the glucose and sucrose environments was nearly the same within measurement error. However, the spatial decay rates of the wave fronts were very different for the two waves. As predicted, the wave profile in sucrose was steeper than that in glucose, providing additional support to our finding that expansion in sucrose was a pushed wave (Fig. 5D) and demonstrating that the differences in the decay rates can also be used for distinguishing pushed from pulled expansions.

Discussion

Although range expansions have been studied extensively in ecology, many theoretical predictions remain untested. Because pulled and pushed waves appear qualitatively similar, with a constant expansion velocity and exponential fronts, expansions are often assumed to obey the universal theory of pulled waves. Our study provides a proof of principle that pulled and pushed waves can be distinguished with quantitative measurements. We demonstrated that these two classes of expansions can be empirically distinguished based on the violation of the expected relationship between the velocity and either the front shape or the low-density growth rate. At the same time, our work also shows that such measurements are difficult even in controlled laboratory settings.

Distinguishing between pushed and pulled expansions is important for forecasting invasion dynamics and understanding species evolution. Predicting the rate of colonization may be particularly challenging for pushed waves because they can advance slowly in the beginning due to an Allee effect but accelerate later as the bulk density increases (47, 56). Pushed waves are also expected to have slower rates of neutral evolution and diversity loss compared with pulled expansions (26, 57). The conservation strategies to limit pulled and pushed invasions could also be very different. For pulled waves, the best way to limit the expansion is to eradicate the invaders at the very edge of the expansion. In contrast, a balanced eradication strategy over the entire invasion front is more effective for pushed waves (47, 58).

Beyond the specific results described above, our work established a tractable experimental system where many ecological and evolutionary scenarios or theories can be tested. Given the increasing rate of range shifts, it is important to experiment with how populations respond to unavoidable changes in their spatial distribution as well as to specific ecological perturbations designed as mitigation measures. Laboratory microbial systems could be very useful for studying such phenomena in greater detail, complementing more realistic but less tractable field studies.

Some questions that can be immediately investigated in our experimental system are the response of invasions to environmental fragmentation and the effects of range expansions on species evolution. Habitat fragmentation is likely to increase due to anthropogenic activities and might be especially important for species moving to barely hospitable regions as they escape the warming climate. Theory predicts that pushed, but not pulled, waves can become pinned or stuck in a fragmented environment, yet empirical tests of this prediction are scarce. Species evolution also depends critically on whether it invades as a pulled or a pushed wave. For example, the founder effect has a much greater role in pulled compared with pushed invasions. Quantitative experiments in controlled laboratory settings are likely to provide valuable insights into these important phenomena.

Materials and Methods

Strains.

The yeast strain used is the same as the cooperator strain in ref. 59, derived from haploid cells BY4741 [mating type a, European Saccharomyces Cerevisiae Archive for Functional Analysis (EUROSCARF)]. It has a yellow fluorescent protein (yEYFP) expressed constitutively by the TEF1 promoter inserted into the HIS3 locus using the backbone plasmid pRS303.

Experimental Protocols.

All cultures were grown at 30 °C in standard synthetic media (yeast nitrogen base and complete supplement mixture). The two media used for pulled wave experiments had 0.125% glucose and 0.5% galactose. The media used for studying the transition from pulled to pushed waves consisted of 0.008% background glucose (to reduce the sensitivity of the low-density growth rate to sucrose hydrolysis), in addition to 2, 0.67, 0.22, 0.07, 0.025, 0.008, 0.003, and 0.001% sucrose. All concentrations throughout the text are in percent weight per volume.

All experiments were performed in 200-μL batch culture in BD Biosciences Falcon 96-well Microtest plates. Range expansions were carried out along the columns of the plate, in 24- to 32-well-long landscapes. Migrations and dilutions were performed every 4 h using the Tecan Freedom EVO 100 robot. Plates were not shaken during growth. This resulted in a slightly lower growth rate and yield (58) compared with measurements in a platereader (compare Fig. 2 and SI Appendix, Fig. S2). Optical densities were measured on the robot before every dilution cycle in the Tecan Sunrise platereader with 600-nm light. Cell densities for selected cycles were also measured in the MacsQuant flow cytometer after dilution in phosphate buffered saline (PBS), using the yellow fluorescence channel. Preliminary growth rate measurements on glucose and galactose were performed using overnight optical density measurements every 15 min. The more sensitive low-density growth rate measurements were performed in 96-well plates without shaking, by measuring initial and final cell densities over four dilution cycles of 4 h each, and ignoring the first two cycles for transient effects. Cultures were started at different initial densities for these measurements (SI Appendix, Fig. S10).

In the analysis, front positions were determined as the interpolated well position where the density (as measured by flow cytometry) crossed a fixed threshold. These were then used to calculate the velocity of expansion. The final velocity was obtained by averaging over multiple thresholds ranging between 100 and 1,000 cells per well. The thresholds were chosen so as to be sensitive to the dynamics at low density but at the same time not too low to be affected by Poisson errors in cell counting. Spatial decay rates were measured after translating the profiles at different times so that they coincide, and using the combined data to obtain a reliable fit to the exponentially decaying profile (Fig. 5D).