A method to decipher pleiotropy by detecting underlying heterogeneity driven by hidden subgroups applied to autoimmune and neuropsychiatric diseases

Abstract

There is growing evidence of shared risk alleles between complex traits (pleiotropy), including autoimmune and neuropsychiatric diseases. This might be due to sharing between all individuals (whole-group pleiotropy), or a subset of individuals within a genetically heterogeneous cohort (subgroup heterogeneity). BUHMBOX is a well-powered statistic distinguishing between these two situations using genotype data. We observed a shared genetic basis between 11 autoimmune diseases and type 1 diabetes (T1D, p<10⁻⁴), and 11 autoimmune diseases and rheumatoid arthritis (RA, p<10⁻³). This sharing was not explained by subgroup heterogeneity (corrected p_BUHMBOX>0.2, 6,670 T1D cases and 7,279 RA cases). Genetic sharing between seronegative and seropostive RA (p<10⁻⁹) had significant evidence of subgroup heterogeneity, suggesting a subgroup of seropositive-like cases within seronegative cases (p_BUHMBOX=0.008, 2,406 seronegative RA cases). We also observed a shared genetic basis between major depressive disorder (MDD) and schizophrenia (p<10⁻⁴) that was not explained by subgroup heterogeneity (p_BUHMBOX=0.28 in 9,238 MDD cases).

INTRODUCTION

Recent studies have demonstrated that many diseases share risk alleles^1–4 and exhibit significant coheritability^5–7. Coheritability studies are defining the relationship between complex traits, and providing new insights into disease mechanisms. Critically, as the number of phenotypes studied with genetics expands in the context of emerging deeply phenotyped population-wide cohorts⁸, including the Precision Medicine Initiative⁹, coheritablity between traits will become even more apparent. In the genomic era, methods for detecting coheritability have moved beyond traditional approaches such as twin or family studies^{10, 11}. Now, alternative approaches using genome-wide association study (GWAS) data from unrelated individuals are widely used. Polygenic risk score approaches^{3, 12, 13} build genetic risk scores (GRSs) for one phenotype and test their association with a second phenotype. Mixed-model approaches^{5, 6, 14} can estimate the genetic covariance between two traits on the observed scale. Genetic covariance can be used to calculate genetic correlation and coheritability⁶. Cross-trait LD Score regression (LDSC) utilizes linkage disequilibrium (LD) and summary statistics obtained from GWAS to estimate genetic correlation attributable to SNPs⁷. In addition, the p-values of independent SNPs associated with multiple phenotypes can be tested for a significant deviation from the null distribution². These approaches have been applied to demonstrate significant shared genetic structure among many phenotypes^{5, 7, 15} including autoimmune² and neuropsychiatric diseases^{3, 6, 13}. The observed coheritability and genetic sharing suggests the possibility of pleiotropy, defined here as the sharing of risk alleles across traits at specific loci or at a genome-wide level. An example of pleiotropy is the PTPN22 variant R620W, which is associated with multiple autoimmune diseases¹⁶.

Shared risk alleles across diseases can be driven by all individuals or by a subset of individuals. In the former, the sharing is clearly driven by pleiotropy (whole-group pleiotropy). In the latter, only a subset of individuals is genetically similar to another disease. We call this subgroup heterogeneity – a situation where a patient cohort consists of genetically distinct subgroups that may or may not result in distinct symptom profiles and treatment outcomes. Subgroup heterogeneity can occur in the context of misclassifications (e.g. cases with atypical clinical presentations for a different disease are erroneously included), molecular subtypes (e.g. two different etiologies cause a disease, resulting in a subset of cases that share pathogenesis with a different disease), asymmetric causal relationships (e.g. one disease causes another disease, resulting in a subset of cases that also have the causal disease; often called mediated pleiotropy), or ascertainment bias (e.g. cases also affected with a different disease are more likely to come to clinical attention and be included in the study). These situations result in a subset of cases that is genetically similar to another disease, creating shared genetic structure¹⁷. Indeed, there is now evidence that misclassifications^18–21, etiological diversity²², and ascertainment bias²³ are prevalent across certain human diseases, leading to the conclusion that significant heterogeneity may exist^24–27. Since the potential contribution of subgroup heterogeneity to any genetic sharing observed between diseases represents a critical disease insight, statistical methods are needed to distinguish subgroup heterogeneity from whole-group pleiotropy. For the purposes of this paper, we will use the term pleiotropy to refer to whole-group pleiotropy and heterogeneity to refer to subgroup heterogeneity.

RESULTS

Overview of BUHMBOX

Genetic sharing between disease A (D_A) and disease B (D_B) could be due to pleiotropy, but could also be due to heterogeneity (i.e. a subset of D_A cases are genetically more similar to D_B cases). If we calculated GRSs for D_A cases using D_B-associated loci and their effect sizes (GRS_B), the mean of GRS_B would be statistically different between D_A cases and controls under either pleiotropy or heterogeneity. Under pleiotropy, some D_B risk alleles impose D_A risk, and D_B risk alleles will be enriched in D_A cases compared to controls. Under heterogeneity, a subset of D_A cases will have genetic characteristics of D_B, and therefore D_B risk alleles will also be enriched in those individuals. In both situations, the enriched D_B risk alleles in D_A cases will result in an increased mean GRS_B in individuals that are D_A cases. For the same reasons, if we calculated the r_g of D_A and D_B using cross-trait LDSC⁷ in this scenario, the r_g would be positive under both pleiotropy and heterogeneity.

To detect heterogeneity, even in the presence of pleiotropy, we developed BUHMBOX (Breaking Up Heterogeneous Mixture Based On Cross-locus correlations). Our method tests for the presence of heterogeneous subgroups (i.e. D_B-like cases) in an otherwise homogenous phenotype (i.e. D_A). To do this, BUHMBOX requires (1) a list of known D_B-associated SNPs with corresponding risk alleles, risk allele frequencies, and effect sizes, and (2) individual-level genotype data for D_B SNPs in D_A cases. BUHMBOX leverages the fact that in the setting of heterogeneity, D_B risk alleles have higher allele frequencies only in a specific subset of D_A cases. In contrast, under true pleiotropy, D_B risk alleles are expected to have higher allele frequencies across all D_A cases (Figure 1). If D_B risk alleles are enriched in one subgroup, the expected correlations of risk allele dosages between loci will be consistently positive (for details see Supplementary Table 1 and Supplementary Note). BUHMBOX combines these pairwise correlations into one statistic and tests for it; heterogeneity can lead to a significant BUHMBOX test statistic. In contrast, the lack of true heterogeneity or insufficient power to detect the presence of heterogeneity (type II error) can lead to a non-significant BUHMBOX test statistic. Insufficient power occurs when the number of D_A cases, heterogeneity proportion, or number of known risk alleles and/or their effect sizes for D_B are small.

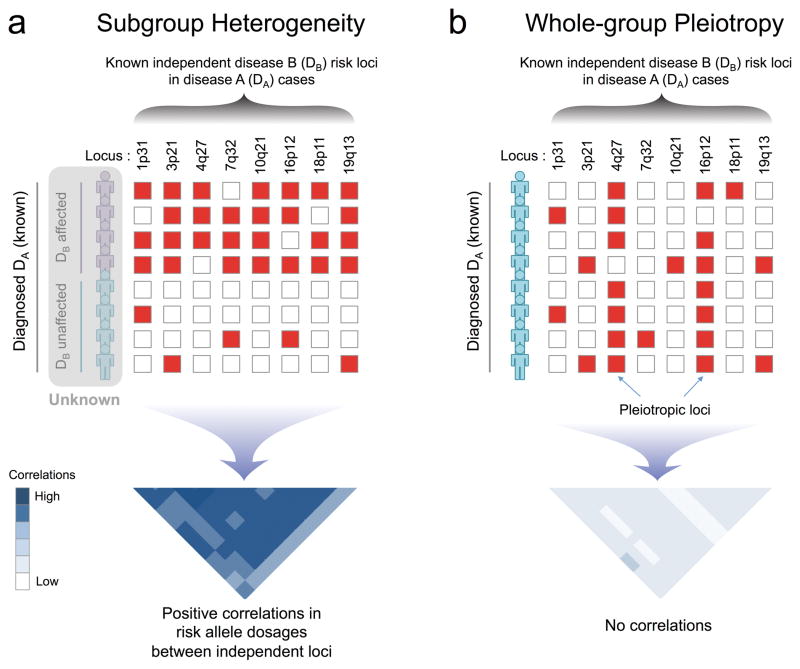
Figure 1. Overview of BUHMBOX.

(a) Under the scenario of subgroup heterogeneity, risk alleles of disease B (D_B)-associated loci will be enriched in a subgroup of disease A (D_A) cases, producing positive correlations between D_B risk allele dosages from independent loci. (b) Under the scenario where there is no heterogeneity and D_A and D_B share alleles due to pleiotropy (i.e. whole-group pleiotropy), D_B risk alleles will be uniformly distributed and have no correlations. Red boxes: risk alleles; white boxes: non-risk alleles.

BUHMBOX discriminates between heterogeneity and pleiotropy

To demonstrate that BUHMBOX detects heterogeneity (even in the presence of pleiotropy), we conducted simulations with the following parameters: sample size of D_A case individuals (N), number of risk loci associated to D_B (M), and the proportion of D_A cases that actually show genetic characteristics of D_B (heterogeneity proportion, or π). To simulate realistic distributions of effect sizes and allele frequencies, we sampled odds ratio (OR) and risk allele frequency (RAF) pairs from reported associations in the GWAS catalog²⁸ (Online Methods).

To characterize the false positive rate (FPR) of BUHMBOX we simulated 1,000,000 studies (N=2,000 and M=50) where there was no heterogeneity (π=0, Online Methods) or pleiotropy. BUHMBOX obtained a 5.1% FPR at p<0.05; it also obtained appropriate FPRs at a wide range of statistical significance thresholds (p<0.05 to 0.0005, Supplementary Table 2).

To evaluate the FPR of BUHMBOX where there actually was pleiotropy without heterogeneity (π=0), we simulated 1,000 studies (N=2,000 and M=50) assuming D_A and D_B shared 10% of risk loci (five loci). We quantified the proportion of instances where BUHMBOX and GRS approaches obtained p-values smaller than the threshold p<0.05. GRS appropriately demonstrated 64.8% power to detect shared genetic structure. BUHMBOX demonstrated an appropriate false positive rate of 4.3% to detect heterogeneity (Supplementary Figure 1).

Finally, to evaluate BUHMBOX’s power to detect heterogeneity we repeated these simulations assuming there was no pleiotropy, but that there was indeed subtle heterogeneity. We assumed that 10% of D_A cases were actually D_B (π=0.1). Here, BUHMBOX demonstrated 81.7% power to detect heterogeneity at p<0.05 (Supplementary Figure 1). The GRS approach demonstrated 100% power to detect shared genetic structure. Note that the power difference of the GRS approach in the pleiotropy and heterogeneity simulations is because of the stochastic chance that sampled effect sizes of all five loci may be small in the pleiotropy simulation; in simulations where we fixed the OR (1.25) and RAF (0.3) for all loci, the power of GRS was similar: 91.8% in pleiotropy and 92.0% in heterogeneity.

Together, these simulations illustrate that BUHMBOX is sensitive to heterogeneity but robust to pleiotropy, while the GRS detects both scenarios and cannot discriminate between the two. Thus, BUHMBOX complements methods for detecting pleiotropy by helping to interpret shared genetic structure (Supplementary Table 1).

Weighting pairwise correlations increases power

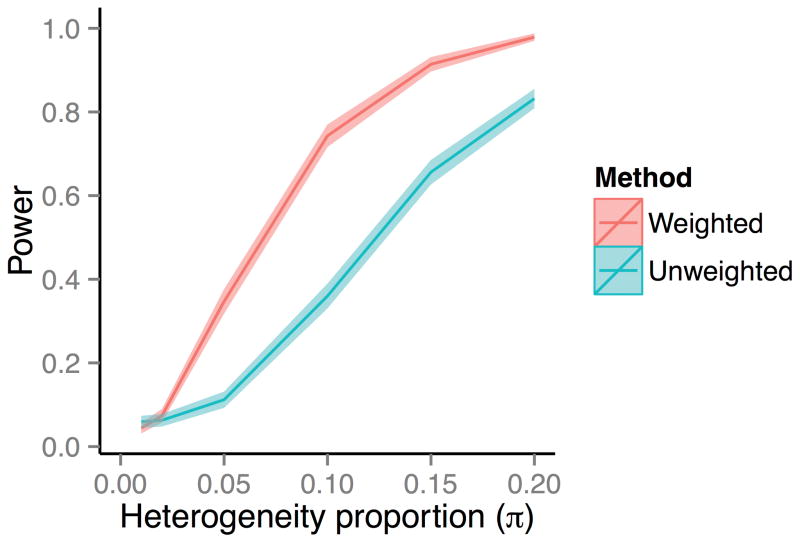
BUHMBOX combines multiple pairwise correlations into one statistic. A pair of loci with larger allele frequencies and effect sizes will show larger expected correlation given the same π, and may be more informative than other pairs of loci (Supplementary Figure 2). We hypothesized that accounting for this unequal information between SNP pairs could increase power. We defined a scheme to weight pairwise correlations between loci as a function of their effect sizes and allele frequencies (Online Methods). In simulations we observed substantial power gain with this weighting scheme. Assuming 1,000 cases and 50 loci, we compared the BUHMBOX power implemented with and without weighting correlations (equation (12) in Supplementary Note). Across a wide range of π we observed that weighting dramatically increased power (Figure 2). For example, at π=0.1 the weighted implementation of BUHMBOX obtained 74% compared to the unweighted implementation which obtained only 36% power.

Figure 2. Power gain by weighting SNPs by allele frequency and effect size.

We compared the statistical power of BUHMBOX with a weighting scheme that optimally weights correlations between SNPs (weighted) to an alternative approach that weights correlations uniformly (unweighted; equation (12) in Supplementary Note). We simulated 1,000 case individuals and assumed 50 risk loci, whose OR and RAFs were sampled from the GWAS catalog. Colored bands denote 95% confidence intervals of power estimates.

Power is proportional to number of samples and loci

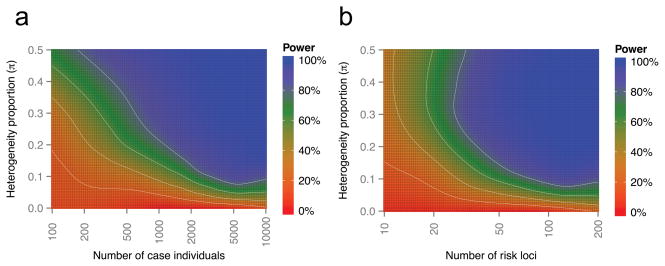
The statistical power of BUHMBOX is a function of many factors including sample size N of the cases we are testing for heterogeneity in, heterogeneity proportion π, number of loci M for the coheritable disease, RAF, and OR. We sampled pairs of RAF and OR from the GWAS catalog. Given a sample size of N=2,000 cases and 2,000 controls, assuming π=0.2 and 50 risk loci, BUHMBOX achieved 92% power at p<0.05 (Figure 3). As many GWAS now consist of more than 2,000 cases, and many diseases are approaching 50 known associated loci²⁸, BUHMBOX is currently well powered to detect a moderate amount heterogeneity (π=0.2) for many human traits. Modest heterogeneity is more challenging to detect at this sample size; power decreased to 67% at π=0.1 and to 38% at π=0.05. Power can be augmented with larger sample size (Figure 3) and larger effect sizes (Supplementary Figure 3). Power can also be increased by including large numbers of loci with even nominal evidence of association in addition to established genome-wide significant loci (Supplementary Note and Supplementary Figure 4).

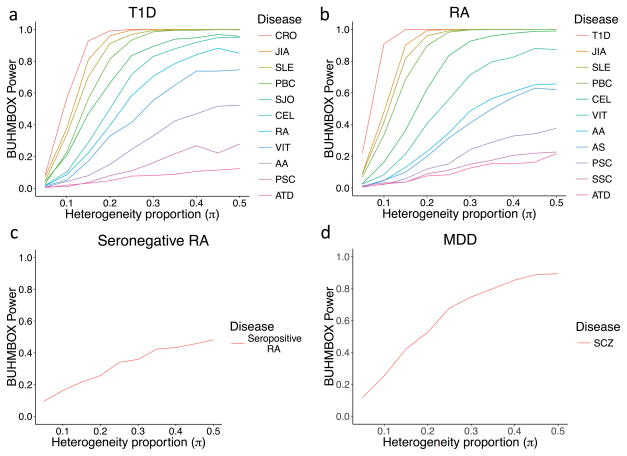
Figure 3. BUHMBOX power analysis.

Power of BUHMBOX for detecting heterogeneity as a function of the number of risk loci, number of case samples, and the proportion of samples that actually have different phenotype (heterogeneity proportion, π). We assume that we have the same number of controls as cases. White lines denote 20, 40, 60, and 80% power. (a) Power as a function of number of case individuals and heterogeneity proportion, when the number of risk loci is fixed at 50. (b) Power as a function of number of risk loci and heterogeneity proportion, when the case sample size is fixed at 2,000.

Controlling for linkage disequilibrium

Although BUHMBOX adequately controlled the FPR when loci were truly independent, we were concerned that long-range LD between apparently independent loci may introduce false positives²⁹. To ensure BUHMBOX was robust to LD, we implemented the following strategies: (1) stringent LD-pruning of D_B loci to exclude SNPs with r²>0.1, and (2) accounting for any remaining residual LD by assessing the relative increase of correlations in cases compared to controls (delta-correlations). We evaluated these strategies by measuring FPR using the RA Immunochip Consortium data³⁰. In 1,000 different loosely pruned (r²<0.5) SNP sets constructed using the Sweden EIRA data (Online Methods), the FPR without using delta-correlations was high (22.4% at p<0.05). Applying delta-correlations reduced this FPR to 9.5%. When we used stringent pruning (r²<0.1), FPR was appropriately controlled (FPR 5.9% and FPR 5.3% with and without delta correlations, respectively). Although LD pruning alone was sufficiently effective for FPR control in this simulation, we used both strategies throughout the paper to be conservative.

Accounting for population stratification

Another potential confounding factor is population stratification. If population stratification exists, weak correlations between unlinked loci may occur, leading to inappropriate significance. If similar population stratification exists in cases and controls, the use of delta-correlations mitigates this effect. To more aggressively control for the effect of stratification at the individual level, we implemented BUHMBOX to regress out principal components (PCs) from risk allele dosages before calculating correlation statistics. To evaluate this strategy, we simulated extreme population stratification using HapMap³¹ data (60 CEU and 60 YRI founders as cases, and 90 JPG+CHB founders as controls; λ_GC=26.5). Unsurprisingly, in 5,000 randomly sampled sets of independent SNPs we observed an inflated BUHMBOX FPR (14.1% at p<0.05). After regressing the effect of ten PCs from risk allele dosages, we observed that the FPR was appropriately controlled (5.7% at p<0.05). As an additional test under a more realistic scenario, we merged genotype data from Northern Europe (Sweden EIRA cohort; 2,762 cases/1,940 controls) and Southern Europe (Spain cohort; 807 cases/399 controls) in the RA Immunochip Consortium case-control dataset³⁰ (Online Methods) to create a highly stratified dataset. In 1,000 sets of randomly sampled independent SNPs, we observed an inflation of the FPR (8.6% at p<0.05); this was appropriately corrected (5.9% at p<0.05) when we regressed out the effect of ten PCs.

Application to autoimmune diseases

Autoimmune diseases share genetic loci^{2, 4, 32–36}, clustering in specific immune pathways^{2, 27, 36}. We used the GRS approach to evaluate shared genetic structure between autoimmune diseases, and then applied BUHMBOX to assess heterogeneity. We obtained individual-level genotype data from the Type 1 Diabetes Genetics Consortium (T1DGC) UK case-control cohort (6,670 cases and 9,416 controls)³⁷ and the RA Immunochip Consortium’s six RA case-control cohorts (7,279 seropositive RA cases and 15,870 controls)³⁰ (Online Methods). We evaluated genetic sharing between a spectrum of autoimmune diseases with T1D and RA. We obtained associated independent loci for all 18 autoimmune diseases (r²<0.1, including MHC SNPs) from ImmunoBase (see URLs and Supplementary Table 3), and tested the association of GRSs for these autoimmune diseases with T1D and RA case status.

We observed substantial genetic sharing between autoimmune diseases. T1D demonstrated significant sharing with alopecia areata (AA), autoimmune thyroid disease (ATD), celiac disease (CEL), Crohn’s disease (CRO), juvenile idiopathic arthritis (JIA), primary biliary cirrhosis (PBC), primary sclerosing cholangitis (PSC), RA, Sjögren’s syndrome (SJO), systemic lupus erythematosus (SLE), and vitiligo (VIT) (positive association, p<10⁻⁴). RA exhibited significant sharing with AA, ankylosing spondylitis (AS), ATD, CEL, JIA, PBC, PSC, SLE, systemic sclerosis (SSC), T1D and VIT (p<10⁻³). Overall, GRSs showed significant positive associations for 11 autoimmune diseases each in T1D and RA cohorts, respectively (GRS p<2.9×10⁻³ [=0.05/17 correcting for 17 diseases tested]; Table 1, Supplementary Table 4). We considered only these traits for subsequent analyses.

Table 1. Summary of genetic overlap using GRS and BUHMBOX.

Only the traits that have significant GRS p-values in positive directions are shown. Significant GRS p-value indicates evidence of shared genetic structure; significant BUHMBOX p-value indicates evidence of heterogeneity. See Supplementary Table 4 for the full results for all traits tested.

Cohort data	Test trait	#SNP	GRS p-value	GRS Beta (95% CI)	BUHMBOX p-value	BUHMBOX power at π=0.20
T1D	AA	10	1.4 × 10−120	0.76 (0.69 – 0.82)	0.83	0.15
	ATD	7	1.4 × 10−31	0.48 (0.40 – 0.56)	0.30	0.05
	CEL	38	2.2 × 10−35	0.32 (0.27 – 0.38)	0.16	0.50
	CRO	119	2.4 × 10−05	0.08 (0.04 – 0.11)	0.54	0.99
	JIA	22	3.6 × 10−151	0.44 (0.40 – 0.47)	0.37	0.96
	PBC	19	1.1 × 10−12	0.16 (0.11 – 0.20)	0.18	0.82
	PSC	12	4.1 × 10−26	0.38 (0.31 – 0.45)	0.91	0.08
	RA	68	6.6 × 10−89	0.55 (0.49 – 0.60)	0.45	0.40
	SJO	7	3.9 × 10−146	0.53 (0.49 – 0.57)	0.84	0.66
	SLE	16	1.1 × 10−83	0.44 (0.39 – 0.48)	0.79	0.91
	VIT	12	2.5 × 10−90	0.59 (0.53 – 0.65)	0.14	0.33
RA	AA	10	1.5 × 10−22	0.28 (0.22 – 0.34)	0.71	0.23
	AS	24	6.1 × 10−04	0.10 (0.04 – 0.15)	0.19	0.20
	ATD	7	3.9 × 10−20	0.34 (0.27 – 0.41)	0.57	0.08
	CEL	38	6.4 × 10−20	0.21 (0.17 – 0.26)	0.57	0.63
	JIA	22	8.9 × 10−125	0.36 (0.33 – 0.39)	0.61	0.99
	PBC	19	1.5 × 10−13	0.15 (0.11 – 0.19)	0.83	0.90
	PSC	12	6.2 × 10−14	0.24 (0.18 – 0.31)	0.46	0.12
	SLE	16	4.3 × 10−06	0.10 (0.05 – 0.14)	0.34	0.96
	SSC	5	9.6 × 10−10	0.22 (0.15 – 0.29)	0.08	0.09
	T1D	53	9.6 × 10−207	0.43 (0.40 – 0.46)	0.29	1.00
	VIT	12	1.8 × 10−11	0.18 (0.12 – 0.23)	0.02	0.41
Seroneg.RA	Seropos.RA	14	1.1 × 10−10	0.30 (0.21 – 0.39)	0.008	0.26
MDD	SCZ	90	1.5 × 10−5	0.17 (0.09 – 0.24)	0.28	0.53

AA, Alopecia areata; AS, Ankylosing spondylitis; ATD, Autoimmune thyroid disease; CEL, celiac disease; CRO, Crohn’s disease; JIA, juvenile idiopathic arthritis; MS, multiple sclerosis; PBC, primary biliary cirrhosis; PSC, primary sclerosing cholangitis; SJO, Sjögren’s syndrome; SLE, systemic lupus erythematosus; SSC, Systemic sclerosis; UC, ulcerative colitis; VIT: Vitiligo; MDD, major depressive disorder; SCZ, schizophrenia; Seroneg., seronegative; Seropos., seropositive.

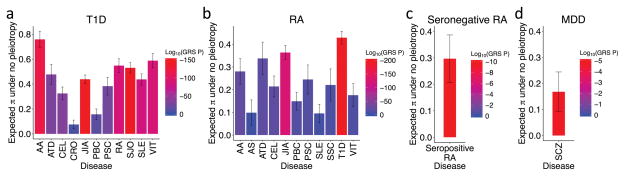
To evaluate the degree of heterogeneity necessary to achieve the observed genetic sharing for these autoimmune diseases, we calculated the GRS regression coefficient, which we previously showed approximates the expected heterogeneity proportion π³⁸ assuming no pleiotropy. Based on the GRS coefficients, we observed π estimates ranging from 0.08–0.76 across the different autoimmune diseases in T1D and from 0.10–0.43 in RA (Figure 4, Table 1).

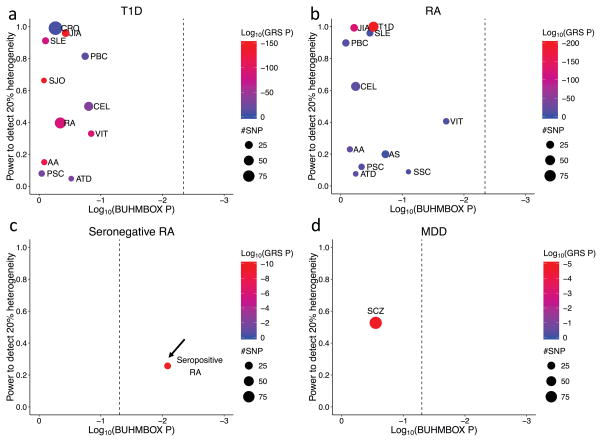
Figure 4. Genetic sharing between autoimmune diseases and psychiatric disorders.

In (a) and (b), we show only the diseases that have significantly positive GRS p-values out of the 17 tested. Y-axis denotes the expected heterogeneity proportion (π) to explain observed genetic sharing. Vertical bars indicate 95% confidence intervals. Heterogeneity proportion estimates are based on GRS analysis, assuming no pleiotropy for (a) T1D, (b) RA, (c) seronegative RA, and (d) MDD.

We estimated the power of BUHMBOX to detect heterogeneity, correcting for 11 tests (p<4.5×10⁻³). BUHMBOX was well powered for some autoimmune traits; at π=0.2, four traits had >90% power for T1D, and four traits had >90% power for RA (Figure 5). Despite this, we observed no evidence of heterogeneity at all (corrected p>0.2; Figure 6, Table 1). Our findings suggest that autoimmune diseases share similar risk alleles and pathways with T1D and RA, and not by subgroups of genetically similar cases resulting from misclassifications or molecular subtypes.

Figure 5. Statistical power of BUHMBOX to detect heterogeneity.

We calculated power by performing 1,000 simulations with corresponding sample size, number of risk alleles, risk allele frequencies, and odds ratios. To calculate power for (c) and (d), we used a significance threshold of 0.05. For (a) and (b), the threshold was adjusted using the Bonferroni correction accounting for 11 tests in T1D and RA, respectively.

Figure 6. BUHMBOX results.

We show only diseases with significantly positive GRS p-values (for complete results for all traits tested, see Supplementary Table 4). Significant GRS p-values indicate evidence of shared genetic structure; significant BUHMBOX p-value indicates evidence of heterogeneity. Point size represents the number of D_B-associated SNPs included in the analysis. Dashed vertical lines denote the Bonferroni-adjusted significance threshold for the BUHMBOX test statistic. Arrow indicates significant BUHMBOX test statistic.

Application to subtype misclassifications in RA

RA consists of two subtypes, seropositive and seronegative, with distinct clinical outcomes and MHC associations³⁸. These two subtypes are classified by whether patients are reactive to anti-CCP antibody. While anti-CCP testing is specific, its lack of sensitivity can result in some seropositive RA patients being misclassified as seronegative RA²⁰. We previously demonstrated that there is shared genetic structure between seropositive and seronegative RA using the GRS approach³⁸, which could imply misclassifications of up to 26.3% between the two RA subtypes.

We used BUHMBOX to evaluate whether seropositive RA misclassifications are present in a seronegative RA cohort. We used the seronegative RA cohort (2,406 cases/15,870 controls) from the RA Immunochip Consortium³⁰. Among 68 RA-associated independent loci, we chose SNPs that are associated to seropositive RA (p<5×10⁻⁸) but not seronegative RA (p>5×10⁻⁸) in our Immunochip data. This criterion resulted in 14 specific loci exclusively associated to seropositive RA (Supplementary Table 3). The seropositive RA GRS was significantly associated with seronegative RA case status (β=0.30, p=1.1×10⁻¹⁰). The regression coefficient (β=0.30) represents an upper bound for π (Figure 4). BUHMBOX suggested that heterogeneity was indeed present (p=0.008, Figure 6, Table 1, Supplementary Table 4), consistent with potential subtype misclassifications. As a more stringent test, we selected SNPs based on between-RA-subtype heterogeneity test results; for this test we obtained p-values by assigning seropositive RA as cases and seronegative RA as controls. We chose SNPs that are associated to seropositive RA (p<5×10⁻⁸) and show nominally significant between-RA-subtype heterogeneity (p<0.05, Supplementary Table 3). Applying BUHMBOX to these 12 loci still showed significant heterogeneity within the seronegative RA cohort (p=0.017).

Application to major depressive disorder and schizophrenia

Current definitions of psychiatric disorders reflect clinical syndromes, with overlapping clinical features. As a result, psychiatric diagnoses for a patient may change as their symptoms evolve²¹. In addition to the potential for misdiagnosis, a subset of true MDD cases may be genetically more similar to schizophrenia. If heterogeneity with respect to schizophrenia risk alleles exists among MDD cases, then genetic studies would suggest evidence of coheritability between the two disorders¹⁷ as has been observed in previous studies^{3, 6, 7}. The unintentional inclusion of “schizophrenia-like” MDD cases, due to diagnostic misclassification or genetically distinct subgroups, has been acknowledged and explored as a potential source of bias in coheritability studies by previous investigators^{3, 17}.

We used BUHMBOX to test for a subgroup of “schizophrenia-like” cases in MDD. If a subset of MDD cases are misdiagnosed and in fact have schizophrenia, or are more genetically similar to schizophrenia, we would expect to see subgroup heterogeneity among MDD cases with respect to schizophrenia risk loci. We first evaluated evidence of shared genetic structure among 90 known schizophrenia associated loci³⁹ (Supplementary Table 3) in 9,238 MDD cases and 7,521 controls from the Major Depressive Disorder Working Group of the Psychiatric Genomics Consortium⁴⁰ (Supplementary Table 5). Consistent with previous findings (Supplementary Table 6)^{3, 6,7}, the GRS was associated with MDD case status (p=1.54×10⁻⁵) indicating shared genetic structure (Figure 4). For the GRS analysis we used a refined subset of the total sample (6,382 MDD cases and 5,614 controls), excluding samples that overlapped with the schizophrenia GWAS³⁹ (Online Methods). Application of cross-trait LDSC⁷ to estimate the genetic correlation obtained further evidence of shared genetic structure between MDD and SCZ (r_g=0.47, SE=0.07, p=1.61×10⁻¹⁰), of similar magnitude to previous reports⁷. However, the BUHMBOX p-value was not significant (p=0.28), indicating no excess positive correlations among schizophrenia loci within MDD cases (Figure 6, Supplementary Table 4). Our findings suggest no evidence of a subgroup of schizophrenia-like MDD cases. However, we note that we lacked adequate statistical power to detect heterogeneity in the context of a small heterogeneity proportion. Given the MDD sample size and the number of currently known schizophrenia risk loci, there was 53% power at π=0.20 but only 25% power at π=0.10 (Figure 5).

DISCUSSION

BUHMBOX can distinguish whether shared genetic structure between traits is the consequence of heterogeneity or pleiotropy based on SNP genotype data alone. It can help to interpret recent observations of shared genetic structures in complex traits including autoimmune, neuropsychiatric, and metabolic diseases. The intuition behind BUHMBOX is that if heterogeneity exists, independent loci will show non-random positive correlations. Hence, correcting for population structure and long-range LD is critical for this approach to be effective. We emphasize that it is necessary to appropriately interpret the source of heterogeneity, which will depend on the biological and clinical relationship between the two traits. We provide detailed information to guide interpretation in the Supplementary Note.

We demonstrated that genetic sharing between autoimmune diseases is due to pleiotropy, noting that for a few traits we had only modest power (Figure 5). One notable exception was seronegative RA, which might contain misclassified seropositive RA cases. The results presented here demonstrate that seronegative RA is a heterogeneous phenotype with respect to genetic overlap with seropositive RA, bringing clarity to an ongoing debate about the nature of this disease. In contrast we were underpowered to draw more definitive conclusions as to whether a subset of MDD cases are genetically similar to schizophrenia cases; as MDD cohorts increase in size we will be able to reassess more accurately whether smaller proportions of heterogeneity might partially explain observed coheritability. Our results are consistent with recent analyses concluding that pleiotropy between psychiatric diseases is unlikely explained by misclassifications alone¹⁷.

We showed that the power of BUHMBOX is a function of sample size, heterogeneity proportion π, and the number, effect sizes and allele frequencies of loci. Power for subtle heterogeneity (π<0.1) in current datasets is limited. But, in future studies, increasing sample size and number of known associated loci will augment power. One potential strategy to augment power is to use a polygenic modeling^{3, 12, 13} approach, including a larger number of SNPs with less stringent significance thresholds (Supplementary Note and Supplementary Figure 4).

BUHMBOX has certain key caveats. First, it is designed to detect a specific type of heterogeneity resulting from the presence of a subgroup comprising a known second trait. Thus, BUHMBOX cannot currently be applied agnostically to detect the presence of heterogeneity within a dataset. Second, BUHMBOX requires prior knowledge of associated loci and their effect sizes. For diseases with few known loci, BUHMBOX may perform suboptimally. Also, if known effect size estimates are inaccurate, power may decrease because appropriate weighting is crucial (Figure 2). Third, BUHMBOX requires individual-level genotype data for a limited number of loci. Fourth, BUHMBOX can be sensitive to confounding factors. We recommend careful control of LD and population structure using LD pruning and PCs. Fifth, interpretation of the BUHMBOX test statistic is not simplistic. Positive findings indicate the presence of heterogeneity but cannot distinguish between the various causes of this (e.g. misclassifications, molecular subtypes, mediated pleiotropy, ascertainment bias), and negative findings may indicate no heterogeneity or low power. To aid interpretation, BUHMBOX provides a power calculation based on sample size and risk allele information, but it may not always be accurate. For example, if pleiotropy and heterogeneity co-exist, power may be overestimated. Sixth, if the heterogeneity proportion π is small (e.g. 0.05), BUHMBOX’s ability to detect heterogeneity is limited. We expect that π will vary between situations, and further clinical and biological investigations are necessary to uncover true π. Finally, there is the unlikely possibility that real epistasis can manifest as positive signal for BUHMBOX. Broadly, BUHMBOX can be thought of as capturing a specific form of epistasis where risk alleles correlate positively within the additive model. As such, if this specific form of epistasis occurs naturally between D_B-associated SNPs, and if this epistasis structure is shared with D_A, it has the potential to create a significant BUHMBOX test result and confound these analyses. However, this specific type of epistasis seems unlikely; were it present, application of BUHMBOX using D_B-associated SNPs in D_B cases to detect apparent “heterogeneity” might yield a significant result.

When comparing BUHMBOX to existing approaches, we focused on the GRS method. However, the results of our comparison also apply to other existing methods such as mixed-model-based approaches^{5, 6} and LD-score-based approaches⁷, which are similar to the GRS approach in the sense that they detect both pleiotropy and heterogeneity. We expect that BUHMBOX will complement any of these methods to facilitate interpretation of observed genetic sharing between traits. Our statistical approach may be extended to have application beyond heterogeneity, including identification of missing heritability resulting from this type of heterogeneity⁴¹. These applications will become more feasible as functional annotations of SNPs advance in the coming years.

ONLINE METHODS

Genetic risk score approach

Given M independent risk loci associated to D_B, we calculated the GRS of individual i as

$${\mathit{GRS}}_i=\sum _{j=1}^M{x}_{ij}{\beta }_j$$

where x_ij is individual i’s risk allele dosage at marker j, and β_j is the effect size (log odds ratio) of risk allele at marker j for disease D_B. The GRS approach calculates GRSs for all individuals and associates GRSs to the case/control status of D_A. In the logistic regression framework for associating GRSs and D_A status, we can obtain the regression coefficient for GRS (β_GRS). We previously showed that β_GRS approximates the proportion of D_A cases that are genetically D_B (heterogeneity proportion π), if we assume is no pleiotropy and the GRS association is solely driven by a subgroup³⁸. Thus, β_GRS represents an upper bound of π.

The BUHMBOX approach

To detect heterogeneity within D_A cases driven by a subgroup that is genetically similar to D_B patients, we utilize the following procedure:

1. Prepare genotype data of D_A cases and controls, and information about SNPs associated to D_B (risk allele, RAF, and OR).

2. Prune SNPs associated to D_B based on LD in control samples (excluding SNPs with r²>0.1 or within ±1Mb of other SNPs)

3. Obtain risk allele dosages of pruned SNPs from D_A cases and controls

4. Regress out PCs from risk allele dosages to obtain residual dosages, each locus at a time

5. Calculate R, the correlation matrix of residual dosages of risk alleles in N cases with D_A and R′, in N′ controls

6. Calculate Y, a z-score matrix from delta-correlations:

   $$\mathbf{Y}=\sqrt{\frac{N·N^{\prime }}{N+N^{\prime }}})\mathbf{R}-{\mathbf{R}}^{\prime })$$
7. Calculate the BUHMBOX statistic:

   $$S_{\mathit{BUHMBOX}}=\frac{{\sum }_{i<j}{w}_{ij}{y}_{ij}}{\sqrt{{\sum }_{i<j}{w}_{ij}^2}}$$
   where y_ij is the element in Y at row i and column j. Given M pruned SNPs, (i,j) iterates M(M−1)/2 non-diagonal elements of Y. The w_ij term is a weighting function that is designed to maximize power, such that (equation (13) in Supplementary Note):

   $$w_{ij}=\frac{\sqrt{p_i(1-p_i)p_j(1-p_j)}({\gamma }_i-1)({\gamma }_j-1)}{(({\gamma }_i-1)p_i+1)(({\gamma }_j-1)p_j+1)}$$

   where p_i is RAF of SNP i, and γ_i is the OR of SNP i for D_B. The BUHMBOX statistic follows N(0,1) under the null hypothesis. We calculate the significance of this statistic as a positive one-sided test; the p-value is p_BUHMBOX = 1 − Φ(S_BUHMBOX) where Φ is the cumulative density function of the standard normal distribution. In the context of heterogeneity, excessive positive correlations among D_B risk alleles in D_A cases result in p_BUHMBOX < α. See Supplementary Table 1 for a comparison of BUHMBOX and GRS approaches. The BUHMBOX test statistic was inspired by previous work deriving covariance between correlation estimates⁴² and on combining dependent estimates^{43, 44}. For details of the intuition, derivation, optimization, and interpretation of the BUHMBOX test statistic, see Supplementary Note.

Code availability

BUHMBOX has been fully implemented as a publicly available R script (see URLs).

Power and false positive rate simulations

Given sample size of D_A cases (N), proportion of D_A cases that actually show genetic characteristics of D_B (heterogeneity proportion π), and number of risk loci associated to D_B (M), we simulated studies to estimate power of our method as follows. To simulate a reasonable joint distribution of RAFs and ORs, we downloaded the GWAS catalog (as of 29 April 2014). Among all binary traits in the catalog, we selected traits with ≥50 reported SNPs resulting in 22 traits with 1,480 SNPs. From these SNPs, we sampled M pairs of RAF (p) and their corresponding OR (γ). To simulate genotypes, we set the RAF of a subgroup (Nπ individuals) to γp/((γ−1)p+1) and p for the other subgroup (N(1−π) individuals), because Nπ individuals can be thought of as D_B cases. Within each subgroup, we generated genotypes assuming that risk alleles are distributed according to the Hardy-Weinberg equilibrium (HWE) and risk loci are independent. We assumed HWE in cases because we assumed an additive disease model. Then we applied BUHMBOX to calculate the p-value. We repeated this 1,000 times to approximate power as the proportion of simulations with p-values ≤0.05. We evaluated power for different values of N, M, and π.

Under the assumption that the loci are independent, the FPR simulation was equivalent to the power simulation described above with the only difference being that π was set to zero, which forced the null hypothesis. We measured the FPR by assuming N=1,000 and M=20, and constructing 1,000,000 such studies.

Linkage disequilibrium simulations

To simulate realistic LD, we used chromosome 22 data from control individuals in the Swedish EIRA cohort of the RA dataset (2,762 cases/1,940 controls)³⁰. We assigned half of control individuals as cases and the rest as controls. To generate 1,000 random sets of SNPs, we began from all SNPs and thinned the SNP set by 10-fold with different seed numbers using PLINK⁴⁵ (with the command --thin 0.1). We then pruned each of the 1,000 datasets using PLINK⁴⁵ with r² criterion of 0.5 or 0.1.

Population stratification simulations

To assess the effects of population stratification, we conducted two sets of simulations. First, used data from HapMap³¹ release 23 data (60 CEU founders, 60 YRI founders, and 90 JPT+CHB founders) setting CEU+YRI as cases and JPT+CHB as controls. We calculated PCs after LD pruning (r²<0.1). For D_B SNPs we randomly selected 5,000 sets of 22 independent SNPs; we selected a single SNP from each autosome. Second, we used genotype data from a Northern Europe RA cohort (Swedish EIRA; 2,762 cases/1,940 controls) and a Southern Europe cohort (Spain; 807 cases/399 controls) from the RA dataset³⁰. For this simulation we used SNPs that we had generated for LD simulations (described above, thinned from Swedish EIRA chromosome 22 with criterion r²<0.1), by setting them as cases and adding Spain samples as controls.

Application to specific phenotypes

Type 1 diabetes dataset

To evaluate pleiotropy and heterogeneity between 18 autoimmune diseases and T1D, we applied GRS and BUHMBOX approaches to the UK case-control dataset provided by the T1DGC³⁷, which consisted of a total of 16,086 samples (6,670 cases and 9,416 controls) from three collections: (1) cases from the UK-GRID, (2) shared controls from the British 1958 Birth Cohort and (3) shared controls from Blood Services controls (data release 4 February 2012, hg18). The samples were collected from 13 regions. All samples were collected after obtaining informed consent, and were genotyped on the Immunochip array. GRS and BUHMBOX analyses were conducted using the region index as covariates.

Rheumatoid arthritis dataset

To evaluate pleiotropy and heterogeneity between 18 autoimmune diseases and RA, we used the RA Immunochip consortium data from six RA case-control cohorts (UK, US, Dutch, Spanish, Swedish Umea, and Swedish EIRA)³⁰. To evaluate pleiotropy to autoimmune diseases, we used 7,279 seropositive RA cases and 15,870 controls. To evaluate misclassifications of RA subtypes, we used 2,406 seronegative RA samples and the same controls. Seropositive and seronegative RA patients were defined in each cohort using standard clinical practices to assess whether patients were reactive to anti-CCP antibody³⁸. All samples were obtained with informed consent, and were collected through institutional review board approved protocols. All individuals self-reported as white and of European descent. Samples were genotyped with the Immunochip array. We merged the data of six cohorts into one, and used binary variables representing cohorts as well as 10 PCs as covariates in the analysis.

Defining autoimmune risk loci

We accessed ImmunoBase (7 June 2015 version) to define genome-wide significant risk loci for 18 autoimmune diseases. We did not include inflammatory bowel disease, due to its redundancy with Crohn’s disease and ulcerative colitis. For each of the 18 autoimmune diseases analyzed we pruned the list of index SNPs obtained from ImmunoBase in PLINK⁴⁵ with options --r2 --ld-window-r2 0.1, using the 1000 Genomes Phase 1 European reference panel for LD. For all pairs of SNPs with r²>0.1, we kept the most strongly associated SNP. To ensure completely independent risk loci we also removed SNPs annotated as being located in the same chromosomal region in ImmunoBase, again keeping the most strongly associated index SNP (Supplementary Table 3). When a locus was not in the Immunochip datasets, we looked for a proxy (r²>0.2) based on the 1000 Genomes data.

Major depressive disorder dataset

We used BUHMBOX to investigate the relationship between MDD and schizophrenia, which have been previously reported to share genetic etiology based on polygenic risk scoring³ and coheritability analyses⁶. The full MDD sample analyzed comprised nine GWAS datasets collected from eight separate studies (Supplementary Table 5) as previously described⁴⁰. All samples were collected through institutional review board approved protocols and were obtained with informed consent. Independence of the training (SCZ) and target (MDD) datasets is crucial in GRS analyses; GRSs are constructed using effect size estimates obtained using allele frequency differences between cases and controls in the training GWAS, and overlapping cases or controls will therefore bias the association of GRSs to the target dataset in the positive direction. In contrast the BUHMBOX test statistic is based on the correlation of risk allele dosages among cases, which is orthogonal to allele frequency differences in cases and controls, and is therefore not inflated by sample overlap. Thus, for the GRS analysis individual MDD samples (four cases, 886 controls) that overlapped with those in the schizophrenia GWAS³⁹ were removed from the analysis; three GWAS cohorts with an insufficient number of independent control samples (N<5) were also removed from the analysis. GRS analyses were conducted in each of the remaining six GWAS datasets (Supplementary Table 5), followed by meta-analysis of the GRS. To obtain the overall GRS effect size (β) and test statistic we used the inverse-variance weighted fixed effects method. For BUHMBOX, we used the full dataset; analyses were conducted in each of the nine GWAS datasets (Supplementary Table 5) followed by meta-analysis. Because the BUHMBOX statistic is a z-score, we meta-analyzed BUHMBOX results across the datasets using the standard weighted sum of z-score approach, where z-scores are weighted by the square root of the sample size.

Defining schizophrenia risk loci

Schizophrenia associated SNPs were selected as those showing genome-wide significant association with schizophrenia (p<5×10⁻⁸) in the most recent Psychiatric Genomics Consortium³⁹ GWAS. For schizophrenia associated SNPs not directly genotyped in the MDD GWAS datasets, we selected proxy SNPs as those with the highest r² from the list of all proxies with r²>0.2 using the 1000 Genomes Phase 1 European reference panel. Of the 97 schizophrenia associated SNPs (11 indels were not considered in our analysis), 90 LD-independent SNPs (r²>0.1, distance to each other is >1Mb) were available for analysis in the MDD GWAS datasets either via direct genotyping or by a proxy SNP (see Supplementary Table 3 for a detailed list of SNPs).