Contribution of Charged Groups to the Enthalpic Stabilization of the Folded States of Globular Proteins

Abstract

In this paper we use the results from all atom MD simulations of proteins and peptides to assess individual contribution of charged atomic groups to the enthalpic stability of the native state of globular proteins and investigate how the distribution of charged atomic groups in terms of solvent accessibility relates to protein enthalpic stability. The contributions of charged groups is calculated using a comparison of nonbonded interaction energy terms from equilibrium simulations of charged amino acid dipeptides in water (the “unfolded state”) and charged amino acids in globular proteins (the “folded state”). Contrary to expectation, the analysis shows that many buried, charged atomic groups contribute favorably to protein enthalpic stability. The strongest enthalpic contributions favoring the folded state come from the carboxylate (COO⁻) groups of either Glu or Asp. The contributions from Arg guanidinium groups are generally somewhat stabilizing, while ${\text{NH}}_3^{+}$ groups from Lys contribute little toward stabilizing the folded state. The average enthalpic gain due to the transfer of a methyl group in an apolar amino acid from solution to the protein interior is described for comparison. Notably, charged groups that are less exposed to solvent contribute more favorably to protein native-state enthalpic stability than charged groups that are solvent exposed. While solvent reorganization/release has favorable contributions to folding for all charged atomic groups, the variation in folded state stability among proteins comes mainly from the change in the nonbonded interaction energy of charged groups between the unfolded and folded states. A key outcome is that the calculated enthalpic stabilization is found to be inversely proportional to the excess charge density on the surface, in support of an hypothesis proposed previously.

1 Introduction

Variation in solvent accessible areas, packing density, or van der Waals and electrostatic interactions has been traditionally used to account for changes in protein stability upon amino acid mutations or under different environmental conditions. A quantitative understanding of the factors contributing to protein native-state stability remains an important goal, with benefits for advancing protein design efforts and understanding human disease. Studies to define the origins of structural stability are particularly relevant due to the implication of stability as a causative effect in disease causing mutations. A decrease in protein stability by 1 to 3 kcal/mol can be a major factor contributing to monogenic human disease (1–3).

At physiological temperatures, the native structure of most globular proteins is only marginally stable. The folded state is enthalpically but not entropically favored relative to the unfolded random-coil state, however the enthalpy and entropy of unfolding on a per residue basis vary in magnitude among globular proteins (4). The variation in the residue-specific entropy of unfolding is understood to arise primarily from differences in amino acid composition of buried residues, and can be rationalized in terms of changes in solvation of protein surface area and hydrophobicity (5). In contrast, the physical origin of the specific enthalpy of unfolding is not well understood (6,7).

Recently, a computational analysis of protein compressibility showed a correlation involving the distribution of charged atoms between the surface and interior of the protein (8); together, the results inferred an unexpected relationship between the enthalpy of unfolding and this charge distribution whereby the per-residue change in enthalpy upon protein unfolding, ΔH^U, decreases (the folded state is less stable) as the fraction of charged atoms located on the protein surface increases. We postulated that the variation among proteins in ΔH^U is due to differences in the excess of surface charged atoms but in a counter-intuitive way: a more uniform distribution of charge between the surface and interior stabilizes protein structure. Here, we test this postulate by estimating the enthalpic stability from all atom molecular dynamics (MD) simulations.

The change in solution free energy upon protein folding has three primary sources: a) the favorable decrease in free energy due to the formation of intraprotein interactions; b) the change in free energy due to the disruption of amino acid–water interactions (or desolvation) of all amino acids that are buried in the protein core or only partially exposed to water in the protein folded state, and c) the change in the free energy of the solvent due to solvent reorganization and structural collapse. The focus of this investigation is to estimate the enthalpic contribution of charged amino acids, Asp, Glu, Arg, and Lys, to protein folded state stability as a function of solvent accessibility and the spatial distribution of charged groups.

While there is a general agreement that burial of hydrophobic amino acids in the protein interior is a major driving force for protein folding and stability, the contributions from charged atomic groups and hydrogen bonding to protein folded state stability has been a much debated issue. Total or partial desolvation of charged and polar groups upon protein folding is widely regarded as a limiting step in protein folding. Some researchers (9–14) have favored a stabilizing contribution from salt bridges and side chain - side chain hydrogen bonds (15), while others have contended that hydrogen bonding and salt bridges make an unfavorable contribution (16–18). Transfer of a salt bridge between charged atomic groups from water to a nonpolar environment was found to be destabilizing by 10 to 16 kcal/mol (19). Nonetheless, the increase in the number of salt bridges in the native structure of the thermophilic proteins has been regarded as an indicator that, salt bridges could stabilize the protein folded state (6, 20) and that intraprotein electrostatic interactions are responsible for the increased stability of thermophilic proteins (21).

Quantitative measurements of salt bridge contributions to the stability of proteins also lend contradictory results. Salt bridges stabilize the folded state of T4 lysozyme by 5 to .5 kcal/mol depending on the experimental system and the location of the salt bridge (22, 23). Certain salt bridges substantially stabilize the folded state of T4 lysozyme, but ionic interactions at the solvent exposed surface have little or no contribution to stabilization. In other cases surface salt bridges were found to add several kcal/mol to protein stability (24). On the other hand, buried salt bridges were reported to destabilize a coiled-coil protein and Arc repressor protein by 2 to 4 kcal/mol (25,26). Thus experimental studies of salt bridges submit opposing conclusions of stabilization and destabilization of the protein folded state.

In an earlier study of protein compressibility (8), we linked the enthalpy of unfolding per residue to the excess charge on the protein surface and found that globular proteins that have lower excess charge (more charges buried) are enthalpically more stable in the folded state. The excess charge, δ_xs, is the difference between protein surface charge density and the charge density in the protein interior. The inverse relationship between the excess charge and the change in solution enthalpy upon protein unfolding was observed for experimental data from a set of 16 globular proteins. We hypothesized that protein folded state stabilization is partially due to a gain in enthalpy from favorable electrostatic interactions between buried charges as a result of optimal charge distributions evolved to stabilize buried charge in globular proteins. A goal of the present work is to test this hypothesis and investigate the origin of the empirical correlation between the distribution of buried charged groups in native proteins and protein folded state stability.

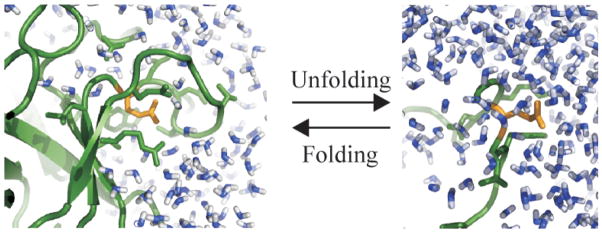
We use the results from all atom MD simulations of proteins and peptides to assess individual contribution of charged atomic groups to the enthalpic stability of the native state of globular proteins and investigate how the distribution of charged atomic groups in the protein tertiary structure influences their contribution to protein enthalpic stability. The net contribution of each charged atomic group is estimated as a sum of two components: a) the change in the nonbonded interaction energy of charged amino acids between the unfolded state modeled by solvated dipeptides and the folded state of globular proteins; and b) the change in the enthalpy of the hydration water due to the collapse of the hydration shells formed by charged atomic groups and subsequent release of certain water molecules to the bulk solvent in the process of protein folding. The concept is illustrated in Figure 1, where a carboxylate group from GLU (in gold), is shown in a protein folded state environment (on the left side of the scheme), and an unfolded state environment (on the right). The analysis shows that most native, charged atomic groups have significant contributions to protein enthalpic stability. While solvent reorganization/release has favorable contributions to folding for all charged atomic groups, the variation in folded state stability among proteins comes mainly from the change in the nonbonded interaction energy of charged amino acids between the unfolded and folded states.

Figure 1.

The change in the local environment of charged groups upon protein unfolding: a carboxylate group from GLU (in gold) in a protein folded state environment (ribbon diagram, in green), on the left side of the scheme, and in an unfolded state environment (on the right). Water molecules in the folded and unfolded states are shown in blue.

The carboxylate (COO⁻) groups from Glu and Asp are the leaders in enhancing the folded state stability. The guanidinium groups from Arg are somewhat stabilizing, while an ${\text{NH}}_3^{+}$ group from Lys is only marginally stabilizing the folded state. The average enthalpic gain due to the transfer of a methyl group in an apolar amino acid from solution to the protein interior is described for comparison. The trend in stabilization by the type of charged group is consistent with the distribution of the relative numbers of charged groups as a function of the degree of solvent exposure. Charged groups that are less exposed to solvent contribute more to protein native state enthalpic stability than charged groups that are exposed and the calculated cumulative effect of charge is inversely proportional to the excess charge density, δ_xs.

2 Theory and Computational Methods

2.1 Model Systems

The contributions of individual atomic groups to the enthalpic stability of the folded state were assessed from a comparison of their enthalpy in the folded and unfolded states. The atomic groups considered here are the side-chain carboxylate groups of Asp and Glu (COO⁻), the guanidinium group of Arg (Gu); the side-chain amino group of $\text{Lys}({\text{NH}}_3^{+})$; the charged Ca²⁺ ions in α-lactalbumin and trypsin. The apolar group is the methyl group, -CH₃, in ALA, VAL, LEU and ILE. The unfolded state of the protein is modeled here as charged- or apolar dipeptides, CH₃-CO-XXX-NH-CH₃, where XXX is Glu, Asp, Arg, Lys, Ala, Val, Leu, Ile, and the corresponding dipeptides are glud, aspd, argd, lysd, alad, vald, leud and iled, respectively. This definition of the unfolded state assumes that the unfolded state is a random coil, an ensemble of conformations in which the amino acid chain is highly hydrated and individual residues do not interact with each other. The backbone dihedral angles of the dipeptides are not fixed; they exhibit both α and β/PPII (stretched) conformations with relative populations specific to each dipeptide.

The folded state corresponds to the native states of four globular proteins: trypsin, ribonuclease A, hen egg-white lysozyme and α-lactalbumin. The total number of charged atomic groups in the four proteins is 104. Of these, 28% are COO⁻(Asp), 16% are COO⁻(Glu), 17% are from Arg and the rest of 38% are ${\text{NH}}_3^{+}$ groups from Lys. In vertebrates, 23% of amino acids are charged amino acids (27) and the relative composition in the charged category is: 26% are Asp, 25% are Glu, 18% are Arg and 31% are Lys. Therefore, our set of proteins is a reasonably representative set.

2.2 Change in Enthalpy upon Protein Unfolding

The net contribution of each atomic group to the change in enthalpy upon protein unfolding, ΔH^U, is a sum of two quantities: a) the change in the enthalpy of the charged group, g, due to a change in the local environment for transfer from the folded state to the unfolded state, $\mathrm{\Delta }{H}_g^U$; and b) the change in the enthalpy of the hydration water molecules that are released to the bulk upon protein folding, $\mathrm{\Delta }{H}_h^U$:

$$\mathrm{\Delta }{H}^U=\mathrm{\Delta }{H}_g^U+\mathrm{\Delta }{H}_h^U.$$ (1)

If ΔH^U > 0, the atomic group contributes favorably to protein folding. The sum of ΔH^U over all atomic groups in a protein corresponds to the unfolding enthalpy.

2.2.1 Local Environment of Charged Groups, $\mathrm{\Delta }{H}_g^U$

$\mathrm{\Delta }{H}_g^U$ of an atomic group is estimated from the difference between the time-average nonbonded energy (a sum of the electrostatic and van der Waals terms) in the unfolded state modeled by the dipeptide solution, $<E_{nb}^{g,\mathit{dipep}}>$, and the corresponding energy in the folded state, $<E_{nb}^{g,\mathit{prot}}>$

$$\mathrm{\Delta }{H}_g^U=1/2(<E_{nb}^{g,\mathit{dipep}}>-<E_{nb}^{g,\mathit{prot}}>).$$ (2)

where < … > represents the time average. In this approximation, the difference between the covalent bonding energies in the folded and unfolded states is assumed to be negligible.

The nonbonded energy of an atomic group, $E_{nb}^g$, in either the native protein or dipeptide solution, is a time average of the pairwise sum over the van der Waals and electrostatic interactions of all atoms in the atomic group, n_g, with the protein (or dipeptide) and the solvent molecules within a specified cutoff distance:

$$<E_{nb}^g>=<\sum _{i=1}^{n_g}\sum _{j\ne i}^m(E_{\mathit{vdW}}(r_{ij})+E_{\mathit{elec}}(r_{ij}))>$$ (3)

where m is the number of all atoms within the cutoff distance.

2.2.2 Solvent Reorganization, $\mathrm{\Delta }{H}_h^U$

The second term in Eq. 1, $\mathrm{\Delta }{H}_h^U$, is the change in solvation water enthalpy due to changes in the solvation shells around charged groups upon protein folding. The released water molecules become bulk water molecule in the peptide solution. Water molecules in the vicinity of proteins are “reorganized” with respect to the bulk water, and the corresponding radial distribution functions show structure up to 8 Å away from charged atomic groups (28). Three hydration shells are formed: the first hydration shell extends from 0 to 3.2 Å, a second shell is evident between 3.2 and 6 Å, and a less pronounced third hydration shell is formed between 6 and 8 Å

To calculate the change in hydration water enthalpy and account for its release from the dipeptide surface in the unfolded state, we estimate the average numbers of water molecules in the first, second and third hydration shells for each charged groups in the dipeptide solution ( $N_w^{1st},N_w^{2nd},N_w^{3rd}$), and the difference in the nonbonded energy of a water molecule in each hydration shell relative to bulk water: $\mathrm{\Delta }{H}_w^{1st},\mathrm{\Delta }{H}_w^{2nd}$, and $\mathrm{\Delta }{H}_w^{3rd}$. The average change in enthalpy for each water molecule in a hydration shell, $\mathrm{\Delta }{H}_w^{\mathit{shell}}$, is calculated as follows:

$$\mathrm{\Delta }{H}_w^{\mathit{shell}}=1/2(<E_{nb}^{\mathit{shell}}>/N_w^{\mathit{shell}}-<E_{nb}^w>),$$ (4)

where $<E_{nb}^{\mathit{shell}}>$ and $<E_{nb}^w>$ are the average nonbonded energy of hydration-shell water molecule and a bulk water molecule, respectively, in the dipeptide solution. <E_nb > is according to Eq. 3. $N_w^{1st},N_w^{2nd},N_w^{3rd}$ are calculated from post-processing the trajectories. $N_w^{1st}$ is the average number of water molecules in a spherical shell extending to 3.2 Å from a charged group in the peptide solution. To estimate $N_w^{2nd}$, we calculated the number of water molecules in a spherical shell between 3.2 and 6 Å around the charged group excluding water molecules that belong to the first hydration shell of other polar or apolar groups. In the same manner, $N_w^{3rd}$ is calculated to include water molecules between 6 and 8 Å from the charged group, excluding water molecules that are in the first hydration shell of apolar or polar groups. The maximum change in solvation water enthalpy for release of all hydration water molecules from the surface of the charged group when the protein folds, $\mathrm{\Delta }{H}_h^{\mathit{max}}$ is estimated as:

$$\mathrm{\Delta }{H}_h^{\mathit{max}}=N_w^{1st}\ast \mathrm{\Delta }{H}_w^{1st}+N_w^{2nd}\ast \mathrm{\Delta }{H}_w^{2nd}+N_w^{3rd}\ast \mathrm{\Delta }{H}_w^{3rd}.$$ (5)

For charged groups that are not completely buried upon protein folding, the actual $\mathrm{\Delta }{H}_h^U$ is less than $\mathrm{\Delta }{H}_h^{\mathit{max}}$. The solvent reorganization contribution can be estimated by factoring in the fractional degree of charge burial, 1 − SE, where SE is the fractional exposure of the charged group to solvent (a definition of SE is given below). Therefore:

$$\mathrm{\Delta }{H}_h^U=(1-SE)\ast \mathrm{\Delta }{H}_h^{\mathit{max}}.$$ (6)

2.3 Fractional Solvent Exposure for Atomic Groups

The nonbonded energy of each atomic group depends on its specific microenvironment, the sum of all the interactions with the neighboring atomic groups. We distinguish “environments” according to the location of the charged groups: from fully buried in the protein to gradually exposed to the solvent on the protein surface. The peptide environment is taken here to be similar to the environment encountered by the charged groups in the unfolded protein.

The fractional degree of exposure to solvent, SE (in %), is the ratio of the time average solvent accessible surface area exposed by an atomic group in the folded protein, < SA^g,prot >, and the time average solvent accessible surface area exposed by the same charged group in the corresponding dipeptide, < SA^g,dipep >:

$$SE=<S{A}^{g,\mathit{prot}}>/<S{A}^{g,\mathit{dipep}(g)}>\ast 100.$$ (7)

The time average SA for each atomic group is calculated from the time series of MD simulations using CHARMM (29) with a probe radius of 1.4 Å (using the algorithm of Lee and Richards (30)).

2.4 Molecular Dynamics Simulations

Equilibrium MD simulations for four proteins and 8 dipeptides were performed using CHARMM (29). A solvated Ca²⁺ ion that is found buried in both trypsin and α-lactalbumin, was also simulated in the ”unfolded” state. The main simulation boxes contained 3500 to 5000 explicit water molecules (1100 water molecules were included in the dipeptide and ion solutions) as well as charge neutralizing counterions. Additional Na⁺ and Cl⁻ molecules were added up to a final salt concentration of 0.166 M. Periodic boundary conditions and the particle mesh Ewald method (31) for calculating electrostatic interactions were used with a 2 fs time step for the integration of the equations of motion, in an NPT ensemble. Charged atomic groups have protonation states corresponding to pH 7, with the exception of Glu35 in HEW lysozyme. Other details of the simulations were as reported earlier (32, 33). 2 ns MD equilibrium simulation trajectories were post analyzed and snapshots 10 fs apart were used to calculate the nonbonded energies of charged groups.

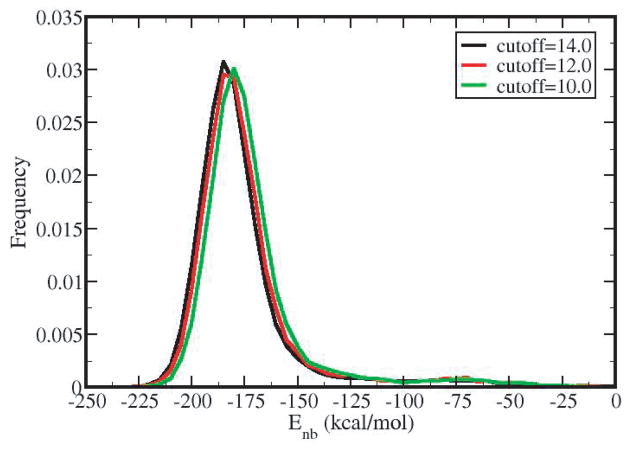
Distributions of nonbonded energies are shown in Figure 2 for the example of the COO⁻ group in glud and using a 10, 12, or 14 Å cutoff distance. The distributions are well converged. The time-averaged nonbonded energy is −180.0 kcal/mol for 10 Å, −182.5 kcal/mol for 12 Å and −184.0 kcal/mol for 14 Å. Our analysis utilizes the time-average nonbonded energy values, which for the well converged E_nb distributions observed in this study, are effectively equivalent to the most likely nonbonded energy; average nonbonded energies are within 1 kcal/mol from the most likely energies. Non-bonded energy cut-offs were set to 14 Å and all images within 18 Å were included in the calculation.

Figure 2.

The influence of cut-off distance on the distribution of the nonbonded energies for the carboxylate group in glud: 10 Å (black curve), 12 Å (red curve) and 14 Å (green curve). The time-averaged nonbonded energy is −180 kcal/mol for 10 Å, −182.5 kcal/mol for 12 Å and −184 kcal/mol for 14 Å. The results presented in this study are calculated using a nonbonded cutoff distance of 14 Å

3 Results

3.1 Distribution of Charged Groups as a Function of Solvent Exposure

The positions of the four types of charged atomic groups in the protein structure in terms of solvent exposure (Eq. 7) are summarized in Table 1. The level of solvent exposure, SE, for charged atomic groups is divided in five categories: less or equal to 20% exposed (SE_0–20), between 20 and 40% (SE_20–40), between 40 and 60%(SE_40–60), between 60 and 80%(SE_60–80), and between 80 and 100% (SE_80–100) solvent exposed. The fraction of charged atomic groups, $f_{SE}^i$, is the ratio between the number of charged atomic groups of type i for each SE range, and the total number of atomic groups of type i, multiplied by 100.

Table 1.

Numbers of charged atomic groups as a function of their exposure to solvent, SE (in %) in the protein folded state. N^g is the number of charged groups of type g with the indicated solvent exposure.

Group	Protein	${\mathrm{N}}_{0-100}^g$	${\mathrm{N}}_{0-20}^g$	${\mathrm{N}}_{20-40}^g$	${\mathrm{N}}_{40-60}^g$	${\mathrm{N}}_{60-80}^g$	${\mathrm{N}}_{80-100}^g$
COO− (ASP)	TRPS	6	4	0	1	0	1
	RBNA	5	2	1	0	2	0
	HLYSO	7	1	3	2	1	0
	ALACTA	11	3	3	1	3	1
	ΣNg	29	10	7	4	6	2
	$f_{SE}^g$		34	24	14	21	7
COO− (GLU)	TRPS	4	2	0	1	0	1
	RBNA	5	0	2	1	1	1
	HLYSO	1	0	0	0	1	0
	ALACTA	7	0	2	2	0	3
	ΣNg	17	2	4	4	2	5
	$f_{SE}^g$		12	24	24	12	28
Gu (ARG)	TRPS	2	0	1	0	1	0
	RBNA	4	1	1	1	1	0
	HLYSO	11	1	1	3	3	3
	ALACTA	1	0	0	0	0	1
	ΣNg	18	2	3	4	5	4
	$f_{SE}^g$		11	17	22	28	22
${\text{NH}}_3^{+}(\text{LYS})$	TRPS	14	1	1	4	6	2
	RBNA	10	1	1	4	1	3
	HLYSO	5	0	0	1	4	0
	ALACTA	11	1	1	2	6	1
	ΣNg	40	3	3	11	17	6
	$f_{SE}^g$		7.5	7.5	27.5	42.5	15
All Crg	ΣΣNg	104	17	17	23	30	17
All Crg	$f_{SE}^{\mathit{tot}}$	-	17	16	23	30	16

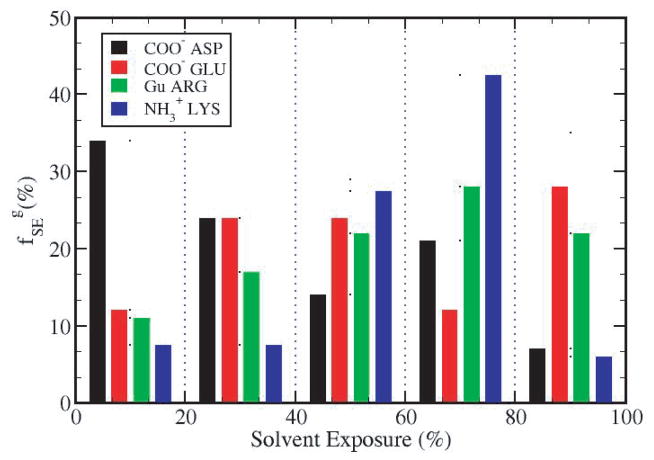
The distribution of the charged groups by type as a function of solvent exposure is shown in Figure 3. For the proteins studied here, the carboxylate group Asp has the highest percentage of buried groups (58%) with less than 40% within SE_0–40 (see also Tables 3S through 6S). By contrast, Lys amino groups are largely solvent exposed and not buried; 42.5% fall within the range of SE_60–80 while only 15% have less than 40% SE. These data indicate that on average, the basic amino acids Lys and Arg tend to position themselves closer to the protein-water interface than the acidic amino acids Asp and Glu.

Figure 3.

Distribution of charged groups in terms of solvent exposure. The fraction of each type of charged groups, $f_{SE}^g(\text{in}\%)$ as a function of SE values in the ranges indicated along the abscissa. COO⁻ (Asp)- black bars, COO⁻(Glu)- red bars, Gu(Arg) - green bars and ${\text{NH}}_3^{+}(\text{Lys})-\text{blue}\text{bars}$. The total number of groups for each type is over the four proteins used in this study.

3.2 Unfolded State Protein Enthalpy

The time-averaged values $<E_{nb}^{g,\mathit{dipep}(g)}>$ and < SA > for the charged groups in aspd, glud, argd and lysd, the methyl groups in alad, vald, leud, iled, and the Ca²⁺ ion were evaluated from distributions from 2 ns MD simulations. (Table 2S, Supplementary Material). The methyl group values range from −13.2 kcal/mol for leud to 2.2 kcal/mol for alad. Thus, methyl groups of vald, leud, iled (γ) have negative energies while the side chain in alad and iled (δ) have weakly unfavorable nonbonded interactions with its environment. The charged groups have strong, favorable interaction energies ranging from −72 kcal/mol for the guanidinium group in argd to −201 kcal/mol for the carboxylate group in aspd. The carboxylate group in glud has a nonbonded interaction energy of −184 kcal/mol and the ${\text{NH}}_3^{+}$ group in lysd −86 kcal/mol.

3.3 Contributions of Apolar Groups to the Enthalpy of Unfolding from the Change in Local Environment, $\mathrm{\Delta }{H}_g^U$

To provide a basis of comparison for the enthalpy of charged groups, the enthalpy change for apolar methyl groups upon protein folding was evaluated from the difference of nonbonded interaction energy of methyl groups in apolar dipeptide molecules (alad, vald, leud, iled) and that of the corresponding apolar amino acids, Ala, Val, Leu and Ile in folded proteins (Eq. 2). The average $\mathrm{\Delta }{H}_g^U$ for a methyl group is 1.3 kcal/mol and varies with the amino acid in which the methyl group is embedded as well as its position in the protein structure (Table 1S, Supplementary Material). The enthalpic gain for a side chain methyl group in Ala ranges from 0.8 to 1.5 kcal/mol, from 0 to 0.6 kcal/mol for Val, from 1 to 1.9 kcal/mol for Ile, and from 0.6 to 1.1 kcal/mol for Leu. The variation observed here is consistent with the site specific differences in contributions of apolar groups to protein stability from experiment (10), whereby the local environment, as characterized by the number of methyl and methylene groups in the neighborhood of a specific methyl group, was found to influence the free energy change upon folding.

3.4 Contributions to the Enthalpy of Unfolding Due to Solvent Reorganization, $\mathrm{\Delta }{H}_h^U$

The change in number of bound water molecules as a result of the increase in protein SA upon unfolding is accounted for with $\mathrm{\Delta }{H}_h^U$ calculated from the nonbonded energy differences of a water molecule in pure solvent and one in each hydration shell, plus an estimate of the number of hydration water molecules (see Theory and Computational Methods). Values for each hydration shell of $N_w^{1st},N_w^{2nd},N_w^{3rd};<E_{nb}^{1st}>,<E_{nb}^{2nd}><E_{nb}^{3rd}>;\mathrm{\Delta }{H}_w^{1st},\mathrm{\Delta }{H}_w^{2nd},\mathrm{\Delta }{H}_w^{3rd}$; and the maximum change in solvent enthalpy due to reorganization for a fully buried charged group, $\mathrm{\Delta }{H}_h^{\mathit{max}}$, are listed in Table 7S, Supplementary Material. $\mathrm{\Delta }{H}_w^{\mathit{shell}}$ depends on the nonbonded energy of a water molecule in pure solvent, which is $<E_{nb}^w>=-9.2\mathit{kcal}/\mathit{mol}$. $\mathrm{\Delta }{H}_h^{\mathit{max}}$ ranges from 1.1 to 2.4 kcal/mol.

While water molecules in the first hydration shell of charged groups have lower $<E_{nb}^{1st}>$ than bulk water molecules (by 1 to 3 kcal/mol, Table 7S) due to strong charge-dipole interactions between the charged atomic groups and water molecular dipoles, water molecules in the second and third hydration shells have unsatisfied hydrogen bonding capabilities so $<E_{nb}^{2nd}>$ and $<E_{nb}^{3rd}>$ are greater than $<E_{nb}^w>$. The combined result of the integrated effects for the loss of hydration shells is a net favorable enthalpy gain upon protein folding. The contribution of solvent reorganization/release favors protein folding but differentiates among charged atomic groups; the maximum gain in enthalpy upon complete burial of a charged group is from ASP, which contributes 2.4 kcal/mol towards the folded state stability. Complete burial of the same group from GLU, or the charged groups of arginine and lysine gains in solvent enthalpy 1.7, 1.9 and 1.1 kcal/mol, respectively. Estimates from vald for the maximum change in the enthalpy due to water molecules near apolar groups (Table 7S, last row) indicate that the change is similar in magnitude (approximately 2.4 kcal/mol) as that for charged groups, even though the mechanism that generates the change is different. Water in the first and third hydration shells of apolar groups have a less favorable nonbonded interaction energy than average waters, while water molecules in the second hydration shells have a more favorable interaction energy.

3.5 Charged Group Enthalpy of Unfolding, $\mathrm{\Delta }{H}^U=\mathrm{\Delta }{H}_g^U+\mathrm{\Delta }{H}_h^U$

The enthalpic contributions to protein unfolding (Eq. 1) summed over the charged groups from either asp, glu, arg or lys residues in each of the four proteins are shown in Table 2 as a function of SE. The individual residue contributions are provided in Tables 3S to 6S (Supplementary Material) along with residue values for $<E_{nb}^g>$, < SA >, SE, $\mathrm{\Delta }{H}_g^U$, and $\mathrm{\Delta }{H}_h^U$. Values for ΔH^U summed over residue type in each of the four proteins (Table 2) are largely positive in sign, so that the enthalpic contribution from charged groups generally stabilizes the folded state. Integrated over all degrees of solvent exposure (i.e. SE_0–100), the residue sums for ΔH^U are positive except for only two cases: Glu residues in HLYSO (−0.8 kcal/mol) and Lys residues in ALACTA (−1.8 kcal/mol).

Table 2.

Enthalpy of unfolding, change due to charged groups, upon protein unfolding, $\mathrm{\Delta }{H}^U=\mathrm{\Delta }{H}_g^U+\mathrm{\Delta }{H}_h^U(\text{kcal}/\text{mol})$, summed over charged groups of a given type as a function of exposure to solvent, SE, (in %). Group averages, $\overline{\mathrm{\Delta }{H}^U}$, are averages over each charged group type in the indicated SE range, from the 4 proteins. Global averages, $\stackrel{\sim }{\mathrm{\Delta }{H}^U}$, are averages over all charged groups in 4 proteins in the indicated SE range.

Group	Protein	ΔHU
		0–100	0–20	20–40	40–60	60–80	80–100
g= COO− (ASP)	TRPS	+30.7	+16.0	0	+14.5	0	+.2
	RBNA	+33.1	+8.4	+14.0	+.9	+9.8	0.0
	HLYSO	+33.8	+9.9	8.7	+14.3	+.9	0.0
	ALACTA	+38.4	+29.9	+15.8	+1.3	−2.9	−5.7
	ΣΔHU	+136.0	+64.2	+38.5	+31.0	+7.8	−5.5
	ΣNg	29	10	7	4	6	2
	$\overline{\mathrm{\Delta }{H}^U}$	+4.7	+6.4	+5.5	+7.8	+1.3	−2.8
g= COO− (GLU)	TRPS	+27.9	+24.4	0.0	+4.4	0.0	+.9
	RBNA	+18.5	0.0	+19.1	−2.1	−2.3	+3.8
	HLYSO	−.8	0.0	0.0	0.0	−.8	0.0
	ALACTA	+1.6	0.0	+3.0	+3.9	0.0	−5.3
	ΣΔHU	+49.0	+24.4	+22.1	+6.2	−3.1	−.6
	ΣNg	17	2	4	4	2	5
	$\overline{\mathrm{\Delta }{H}^U}$	+2.9	+12.2	+5.5	+1.4	−1.6	−.1
g= Gu(ARG)	TRPS	+2.1	0.0	.1	0.0	+2.0	0.0
	RBNA	+9.0	+2.5	+3.4	+2.8	+.3	0.0
	HLYSO	+12.6	+5.0	+1.6	+7.8	+1.7	−1.6
	ALACTA	+5.2	0	0	0	0	+5.2
	ΣΔHU	+28.9	+7.5	+5.1	+10.6	+4.0	+3.6
	ΣNg	18	2	3	4	5	4
	$\overline{\mathrm{\Delta }{H}^U}$	+1.6	+3.8	+1.7	+2.7	+.8	+.9
$\mathrm{g}={\text{NH}}_3^{+}(\text{LYS})$	TRPS	+8.7	+2.4	−1.3	+6.3	−.2	+1.7
	RBNA	+.6	−1.3	−3.3	+5.7	−1.0	+.6
	HLYSO	+1.7	0.0	0.0	+1.6	.1	0.0
	ALACTA	−1.8	+.1	−3.2	−.1	+3.5	−2.1
	ΣΔHU	+9.2	+1.2	−7.8	+13.5	+2.4	+.2
	ΣNg	40	3	3	11	17	6
	$\overline{\mathrm{\Delta }{H}^U}$	+.2	+.4	−2.6	+1.2	.03
All	ΣΣΔHU	223.1	97.3	57.9	61.3	11.1	−2.3
All	ΣΣNg	104	1917	17	23	30	17
All Ave	$\stackrel{\sim }{\mathrm{\Delta }{H}^U}$	2.1	5.7	3.4	2.7	.4	−.2

The global average of ΔH^U over all charged groups, $\stackrel{\sim }{\mathrm{\Delta }{H}^U}$, is 2.1 kcal/mol (Table 2, last row), a combination of $\stackrel{\sim }{\mathrm{\Delta }{H}_g^U}=1.3\text{kcal}/\text{mol}$ for protein environmental effects and $\stackrel{\sim }{\mathrm{\Delta }{H}_h^U}=1.9\text{kcal}/\text{mol}$ for solvent reorganization (Tables 8S and 9S, Supplementary Material). These charged group global averages are similar to those for methyl enthalpy changes, which are $\stackrel{\sim }{\mathrm{\Delta }{H}_g^U}=1.3\text{kcal}/\text{mol}$ and $\stackrel{\sim }{\mathrm{\Delta }{H}_h^U}=2.4\text{kcal}/\text{mol}$. Nonetheless the variation among charged groups is considerably larger than that of methyl groups (Tables 3S to 6S). While methyl groups in apolar amino acids have favorable contributions to the enthalpy of the protein folded state, irrespective of solvent exposure (Table 1S), the charged atomic groups have both favorable and unfavorable contributions to protein folding.

The listings in Tables 3S to 6S also indicate from the positive $\mathrm{\Delta }{H}_h^U$ values associated with individual charged groups from the four proteins that formation of hydration shells at the surface of the unfolded protein has the effect of increasing enthalpy. Thus, in addition to the well known increase in entropy upon the release of hydration water molecules during folding, the loss of hydration water molecules also favors folding for enthalpic reasons, which has been noted previously (35). Nonetheless, $\mathrm{\Delta }{H}_h^U$ is generally smaller in magnitude (2.4 kcal/mol) than $\mathrm{\Delta }{H}_g^U$, which ranges from −5 to 13 kcal/mol.

3.5.1 Carboxylate Group in Asp

Asp residues exhibit the strongest enthalpic interactions stabilizing the folded state. ΔH^U for all Asp residues (SE from 0 to 100) is greater than 30 kcal/mol in the case of all four proteins (Table 2). Based on these representative globular proteins, carboxylate groups from Asp contribute on average $\overline{\mathrm{\Delta }{H}^U}=4.7\mathit{kcal}/\mathit{mol}$ to protein folded-state stability. The fully buried COO⁻ group of Asp176 contributes ΔH^U = 9.9 kcal toward stabilization of TRPS folded state. This gain in enthalpic stability is more than twice the average enthalpic gain due to the transfer of a CH₃ group from water in the hydrophobic core of a protein (see above). By example that opposite effects on stability can occur, we note that a different buried COO⁻ group in TRPS, the COO⁻ of Asp171 (Table 3S), has ΔH^U = −2.6 kcal/mol and contributes unfavorably to the folded state of trypsin.

3.5.2 Carboxylate Group in Glu

Glu carboxylate groups have $\overline{\mathrm{\Delta }{H}^U}=2.9\text{kcal}/\text{mol}$ and can strongly stabilize tertiary structure, although to a somewhat lesser extent than those of Asp. The COO⁻ group in glud has a less weaker interaction with the solvent (−184 kcal/mol) than its counterpart in the aspd (−201 kcal/mol). This difference is likely due to the more hydrophobic nature of the glutamic acid (it has an extra CH₂ group). As part of a protein however, the COO⁻ group of the glutamic acid can contribute as much favorable enthalpy as that of an aspartic acid. A buried glutamic acid, Glu52, COO⁻ contributes 13.7 kcal/mol to the enthalpy of protein unfolding, and thus favors folding almost four times as much as an average methyl group, while the surface exposed charged group from Glu167 contributes only 0.9 kcal/mol.

3.5.3 Guanidinium Group in Arg

The average effect of the guanidinium group of arg residues to protein stability is slightly favorable by 1.6 kcal/mol (Table 2). Protein folding induces both positive and negative changes in enthalpy with values from different arg residues ranging from +5.2 kcal/mol for the charged group from Arg11 in α-lactalbumin (Table 6S) to −2.2 kcal/mol for the charged group from Arg128 (in HEW lysozyme).

3.5.4 The ${\text{NH}}_3^{+}$ Group in Lys

Unlike other charged groups, the average contribution of the ${\text{NH}}_3^{+}$ group of Lys is close to negligible: $\overline{\mathrm{\Delta }{H}^U}=0.2\text{kcal}/\text{mol}$ (Table 2). The folded-state environments are energetically similar to that of solvated Lys, with $\overline{\mathrm{\Delta }{H}_g^U}=-0.2\text{kcal}/\text{mol}$ (Table 8S).

3.6 Charged Atomic Groups and Solvent Exposure

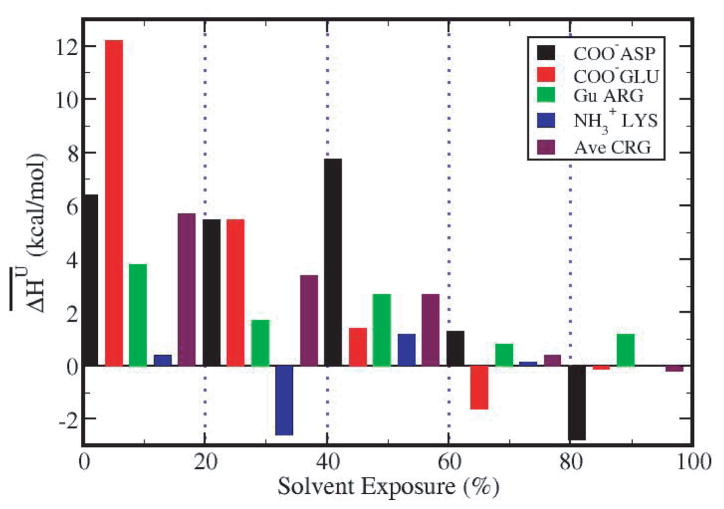
The group average contributions from different charged group types with given solvent exposure (Table 2), $\overline{\mathrm{\Delta }{H}^U}$, are plotted as a function of solvent exposure in Figure 4. The major stabilizing contributions are from the buried COO⁻ groups of Glu (red) and Asp (black) with SE less than 60%. In particular, the COO⁻ groups from Glu, which are less than 20% exposed to solvent, contribute an average 12.2 kcal/mol. By contrast, groups with more than 60% of their surface exposed to solvent have on a much smaller contribution to protein stability. The trend in $\overline{\mathrm{\Delta }{H}^U}$ for types of charged groups is roughly consistent with their frequency of occurrence as a function of SE. Comparison of Figures 3 and 4 finds higher frequency for greater stabilization in the folded state, as expected. 58% of Asp, 36% of Glu and 28% of Arg charged groups are more than 40% buried, while 85% of Lys charged groups are largely exposed to water.

Figure 4.

Average contribution to protein unfolding enthalpy for charged group type, $\overline{\mathrm{\Delta }{H}^U}$, as a function of solvent exposure, SE (in %): COO⁻(Asp)- black bars; COO⁻(Glu)- red bars; Gu(Arg) - green bars; ${\text{NH}}_3^{+}(\text{Lys})-\text{blue}\text{bars}$.

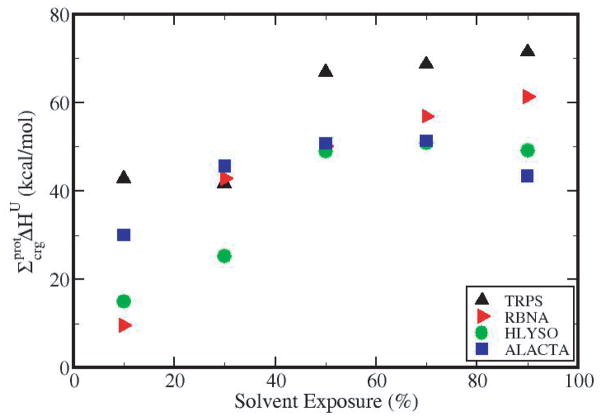
The cumulative contribution of all charged groups of a protein to ΔH^U, ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$, as a function of solvent exposure is shown in Figure 5. For the four proteins studied here, the cumulative contribution increases up to SE 40–60%, then plateaus or decreases slightly with the addition of the charged groups near the surface. Overall, charged groups contribute 43.4 kcal/mol to the stability of ALACTA, 49.2 kcal/mol for HLYSO, 61.3 kcal/mol for RBNA, and 71.4 kcal/mol for TRPS.

Figure 5.

Cumulative contribution of buried charged groups to the folded state enthalpy as a function of solvent exposure by protein, ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$ for 4 proteins: TRPS (black, triangle up symbols), RBNA (red, right triangles), HLYSO (green circles) and ALACTA (blue squares).

3.7 Correlation between ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$ and the Excess Charge Density, δ_xs

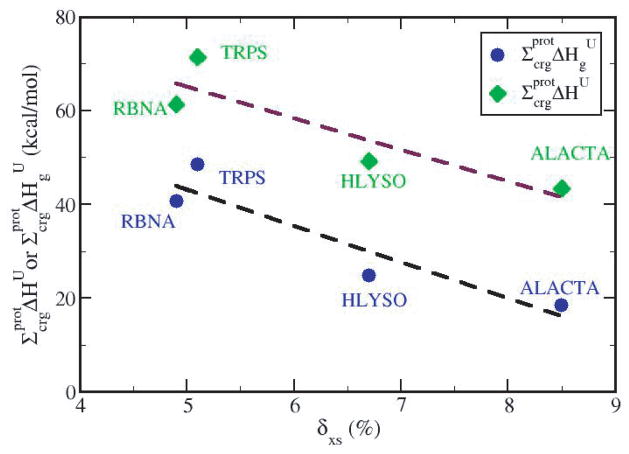
In an earlier paper (8) we linked protein folded state stability to the excess charge on the protein surface, and found that globular proteins with lower excess charge, or a more uniform charge distribution, have a more positive unfolding enthalpy per residue and thus are enthalpically more stable. The negative correlation between excess charge, δ_xs, and experimental ΔH^U values was shown for a set of 16 globular proteins (see Figure 5 in (8)). To establish a causal relationship in this correlation, we examine here whether enthalpies calculated from only charged groups exhibit this trend. Figure 6 shows ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$, and the contributions from environmental change only, ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}_g^U$, as a function of δ_xs for all charged groups in the four proteins as determined in this study. The inverse correlation observed here for ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$ from charged residues alone supports the postulate that differences among proteins in the specific enthalpy of unfolding are due to the spatial distribution of charge. Because most of the stabilizing effect related to charged groups comes from groups that are largely buried, the relationship observed with experimental data in protein folded state stability, showing increased protein stability with decreasing excess charge, is at least in part due to optimized nonbonded interactions between charged groups with the environment in the native protein folded state.

Figure 6.

Total protein-based enthalpy contributions, ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$, from charged groups as a function of excess charge density for each protein (green diamonds and maroon dashed linear regression best fit) and the contributions from environmental change only, ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}_g^U$ (blue circles and black dashed linear regression best fit).

It is interesting to note that the contribution from solvent reorganization, even though substantial (approximately 22 kcal/mol for each protein), does not influence the variation in stability among proteins, as shown by the two almost parallel best fits in Figure 6. The correlation coefficient for the linear fit of ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$ (upper line, Figure 6) is −0.89, and of ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}_g^U$ (lower line, Figure 6) is −0.93. Therefore, when comparing relative stabilities of globular proteins, the enthalpy gain due to solvent release around charged groups appears to provide an approximately constant enhancement to the specific ${\sum }_{\mathit{crg}}^{\mathit{prot}}\mathrm{\Delta }{H}^U$.

4 Discussion and Conclusions

The energetic analysis of protein charged groups reported here was motivated by a surprising empirical correlation observed between the folded-state spatial distribution of charged groups and the residue-specific enthalpic stability of globular proteins (8). We sought to determine if the enthalpic contribution of charged groups to ΔH^U increasingly favors the folded state as the fraction of buried charged residues increases. If so, the tertiary structures of proteins with more uniform charge distributions should provide a basis for learning what is needed to reduce the substantial energetic penalty that arises from the removal of charged groups from an aqueous environment. Such information can be exploited in future protein design. A key outcome of this study is that the estimated enthalpy due to charged groups for different proteins was found to be inversely related to the excess surface charge δ_xs (Figure 6), and thus the results support the hypothesis that buried charge lowers native protein enthalpy and a causal effect for the correlation (8).

Since the publication by Murphy, Privalov and Gill (4) correlating heat capacity with the entropy and enthalpy of protein unfolding, the basis for differences among globular proteins in the entropy per residue of unfolding is known to be the amount of buried apolar surface area (34). Nevertheless, proteins with large amounts of buried apolar surface do not gain stability regardless of the larger entropy favoring folding, and the origin of the compensating enthalpy was unclear (7,34,36). Studies of compressibility (8, 37,38) identified relationships with the unfolding enthalpy and entropy similar to those of heat capacity, and suggested a rationale based on charge distribution for variations in enthalpy of native, folded proteins (8). The calculated energies reported here confirm this rationale by demonstrating that enthalpic stability is gained by strong, favorable electrostatic interactions generated when charged groups are located in the interior as well as on the protein surface. Increasing numbers of buried charged groups necessarily opposes burying apolar surface, and thus changes in specific enthalpy by this mechanism would be compensated by opposing ones in the entropy per residue. Further, attributing differences in the specific thermodynamic properties of proteins to charged residues is reasonable because the variation in the fraction of charged residues is relatively large compared to that for uncharged polar and apolar residues (8).

We find that a number of buried charged groups make significant, favorable contributions to structural stability. The main argument against structural stabilization by charges buried in a protein interior is the large penalty for desolvation, and the experimental measures of free energy of transfer between water and organic solvents (19). On the other hand, it is well recognized that protein interiors are not a homogeneous, hydrophobic medium; numerous uncharged polar groups and some charged polar groups compose electrostatic networks and specific local environments shielded from solvent (34, 39). The question is whether the local environments can compensate sufficiently for the loss of water around a charged group. This study finds that the set of buried charged groups from four globular proteins exhibits a large range of $\mathrm{\Delta }{H}_g^U$ values that span both favorable and unfavorable contributions to the total enthalpy of unfolding. $\mathrm{\Delta }{H}_g^U$ for individual charged groups range from 14 kcal/mol to −3 kcal/mol (supplemental Tables 3–6), with the average over all groups examined here equal to 2.1 kcal/mol (Table 2), near the value 1.3 kcal/mol averaged over CH₃ apolar groups (supplemental Table 1). The different types of charged groups vary in their tendency for being buried; carboxylate groups are most likely to be buried while amino groups are the least likely. Moreover, the interactions of buried Glu and Asp carboxylate groups are found to be overall lower energy than buried Arg and Lys basic groups (Table 2). Indeed, the most favorable contributions for COO⁻ groups occur for fully buried groups, SE_0–20. Thus, many environments are indeed sufficient to overcome the desolvation penalty and the total contribution for all charged groups favors the folded state.

What is the explanation for the variations in $\mathrm{\Delta }{H}_g^U$ for a given type of charged group with similar solvent exposure? While a rigorous explanation is likely complex, we suggest a simple assessment of the local electrostatic environment may explain how to accommodate a charged group upon protein folding. The number of charged groups and the net charge, $Q_i^{\mathit{tot}}$, was evaluated for a spherical region centered on the group of interest and of radius $R=\mathit{5}\mathit{Å}:Q_{\mathit{tot}}^i\approx \sum q_j(R<5\mathit{Å})$. The conjecture is that a local $Q_{\mathit{tot}}^i\approx 0$, generated from two or more groups in addition to the central group, creates a “good neighborhood,” and the atomic group is likely to provide a positive contribution to the enthalpy of folding. This premise is supported by several examples in trypsin. Glu52 is buried yet has one of the largest favorable contributions to the protein folded state enthalpy: +12 kcal/mol (Table 3S). A 5 Å-radius sphere surrounding this group includes five charged groups (Arg49, Asp53, Glu59, Glu62, Arg99) and a Ca²⁺ ion with a net charge of Q_tot = 0, making a good neighborhood for embedding a charged group. The carboxylate group of Glu62 from the same cluster of charges contributes +9 kcal/mol and its local neighborhood contains six charged groups (Arg49, Glu52, Asp53, Glu59, Arg99, Lys125) and a total charge Q_tot = −1e. On the other hand, Asp171 contributes −5 kcal/mol and this destabilization derives from six charged groups (Lys125, Lys136, Lys170, Asp176, Lys200) within 5 Å but with a net positive charge of +2e. A more extensive analysis is underway to establish a quantitative relationship between the structural features of a local environment and the contribution to the folded state stability.

Experimental analysis of the effect of buried charged amino acids on protein structural stability has generated conflicting conclusions. Experimental mutagenesis of buried charged groups have an intrinsic limitation in that substitution of a given residue, or residue pair for a salt bridge, can disrupt the structure and impact local interactions of many atomic groups, charged and uncharged. As a result, factors other than simple removal of charge come into play. By contrast, the computational approach from MD simulations taken here allowed a direct analysis of the energetics.

The occurrence of both positive and negative $\mathrm{\Delta }{H}_g^U$ values explains certain conflicting results from mutagenesis studies; depending on which salt bridges are mutated, measurements would indicate either stabilizing or destablizing effects. In addition, engineering charged residues into a structure for stability likely requires long range analysis of the full structure rather than simple pairwise mutation of proximal residues with appropriate geometry for substitution of a salt bridge. Our study suggests that engineering attempts to design buried charged groups into a protein (24, 40, 41) can benefit by consideration of the carefully crafted network of interactions that have evolved in native proteins with uniform charge distribution, perhaps by development of parameters like $Q_i^{\mathit{tot}}$.