Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 5;6:29184. doi: 10.1038/srep29184

Monolayer MoS2 Bandgap Modulation by Dielectric Environments and Tunable Bandgap Transistors

Junga Ryou 1, Yong-Sung Kim 1,2,a, Santosh KC 3, Kyeongjae Cho 3,b
PMCID: PMC4932597  PMID: 27378032

Abstract

Semiconductors with a moderate bandgap have enabled modern electronic device technology, and the current scaling trends down to nanometer scale have introduced two-dimensional (2D) semiconductors. The bandgap of a semiconductor has been an intrinsic property independent of the environments and determined fundamental semiconductor device characteristics. In contrast to bulk semiconductors, we demonstrate that an atomically thin two-dimensional semiconductor has a bandgap with strong dependence on dielectric environments. Specifically, monolayer MoS2 bandgap is shown to change from 2.8 eV to 1.9 eV by dielectric environment. Utilizing the bandgap modulation property, a tunable bandgap transistor, which can be in general made of a two-dimensional semiconductor, is proposed.

Atomically thin two-dimensional (2D) semiconductors have attracted a great deal of attention for their superior properties in electronic devices. Monolayer (ML) molybdenum disulfide (MoS2) has shown high electron mobility of about 217 cm2 V−1 s−1 and an excessively high current on/off ratio of an order of 108 in a field effect transistor (FET)1,2. However, the superior properties have been achieved only with a supporting substrate and a gate dielectric in a top gate FET structure, such as the HfO2/MoS2/SiO2 stack1,2. Without the top gate high-k dielectric, large reduction of the electron mobility has been reported1,2,3, and it has been believed to be due to the environmental dielectric screening (EDS) effect suppressing the Coulomb scattering of carriers with charged impurities in the 2D semiconductors2,4. The EDS effect has also been reported to change the defect level with the band gap and induce deep- to shallow-level transition of dopants, enhancing the carrier concentrations significantly and the electrical conductivities5. Furthermore, the exciton binding energies have also been reported to be affected by the EDS effect strongly in 2D semiconductors6,7.

A moderate bandgap size is a determining characteristic property of a semiconductor. Nonetheless, an accurate evaluation of the bandgap in low dimensional semiconductors has not been as simple as in conventional bulk semiconductors. It is well established that the bandgap size of MoS2 layers has a strong dependence on the number of layers. Furthermore, in a spatially isolated low dimensional system (e.g. freestanding 2D semiconductors), the strong unscreened Coulomb interaction (through the space outside of the 2D materials) makes the quasiparticle (QP) renormalization of electrons huge. Within the GW approximation, the electronic bandgap of a freestanding ML MoS2 has been predicted to be about 2.8 eV (refs 8, 9, 10, 11, 12). Due to the strong exciton binding (~1 eV)8,9,10,11,12, the optical bandgap has been obtained to be about 1.8 eV from the photoluminescence (PL) and optical absorption experiments13, which agree with the theoretical Bethe-Salpeter-Equation (BSE) calculations9,10,11,12. Since the exciton binding energy is large, the measured optical bandgaps are not accurate representation of semiconductor bandgap, determined by the energy difference between valence and conduction band edges. Eliminating the excitonic effect, the measurements of the electronic bandgap have given diverse results. With intercalated potassium (K) in a bulk MoS2, a quasi ML MoS2 has been fabricated from a bulk MoS2, and a direct bandgap of 1.86 eV at the K valley has been measured using angle-resolved photo-emission spectroscopy (ARPES)14. For a chemical vapor deposition (CVD) grown ML MoS2 on a Au(111) substrate, the ARPES bandgap of about 1.39 eV has been measured, which is very small15. In scanning tunneling spectroscopy (STS) measurements, the bandgap of a ML MoS2 on graphite substrate has been measured to be 2.15 eV (ref. 16) and that on a bilayer graphene to be 2.16 eV (ref. 17), which are larger than other measured values, but still significantly lower than the predicted GW value of 2.8 eV (refs 8, 9, 10, 11, 12). In a ML MoS2 phototransistor that has the Al2O3/MoS2/SiO2 stack structure, the electronic transport bandgap of the ML MoS2 has been measured to be 1.8 eV, in which the optically excited excitons are separated to generate electron and hole carriers by applying the source and drain bias voltages18. As such, the measured electronic bandgap sizes have been in a wide range (1.39–2.16 eV), and the bandgap changes have been speculated to be introduced by the EDS10,15,17 or carrier-induced bandgap renormalization19 effect. Nevertheless, the measured bandgap sizes are significantly smaller than the accurate GW bandgap of 2.8 eV. These findings indicate that the traditional concept of assigning a well-defined bandgap size for a specific semiconductor (e.g., 1.1 eV for Si) as a fundamental material property may not be applicable to 2D semiconductors, and that the electronic bandgap may have strong dependence on the environments. Considering the fundamental role of the bandgap size in electronic device applications, it is critical to develop a fundamental and quantitative understanding on how the environmental effects change the bandgap sizes of 2D semiconductors.

In this study, as a representative 2D semiconductor, we investigate the bandgaps of a ML MoS2 with various environments based on GW calculations, and predict a wide range of bandgap size determined by the strong effects on the ML MoS2 embedded in a device structure. The bandgap of ML MoS2 is found to change by the surrounding medium according to the dielectric constant (κE) of the environment. Specifically, the GW bandgap changes from 2.8 eV of freestanding MoS2 down to about 1.9 eV for MoS2 in a sandwich structure between two high-k dielectrics. On the other hand, the bandgap changes down to 2.2 eV for a supported structure on ultrahigh-κE dielectrics. These GW bandgap changes are continuous functions of dielectric constant of the surrounding medium. Based on this finding, it is suggested that there should be transport barriers to electrons and holes in the ML MoS2 channel between near the metallic contacts and near the gate dielectric in a device structure, because of the different screening environments (and correspondingly different bandgap sizes) surrounding the ML MoS2. When the barriers are controlled by an external source, a tunable bandgap transistor can be made possible utilizing the environment-dependent property of the 2D semiconductors.

Results and Discussion

DFT and GW bandgaps of ML MoS2 with environments

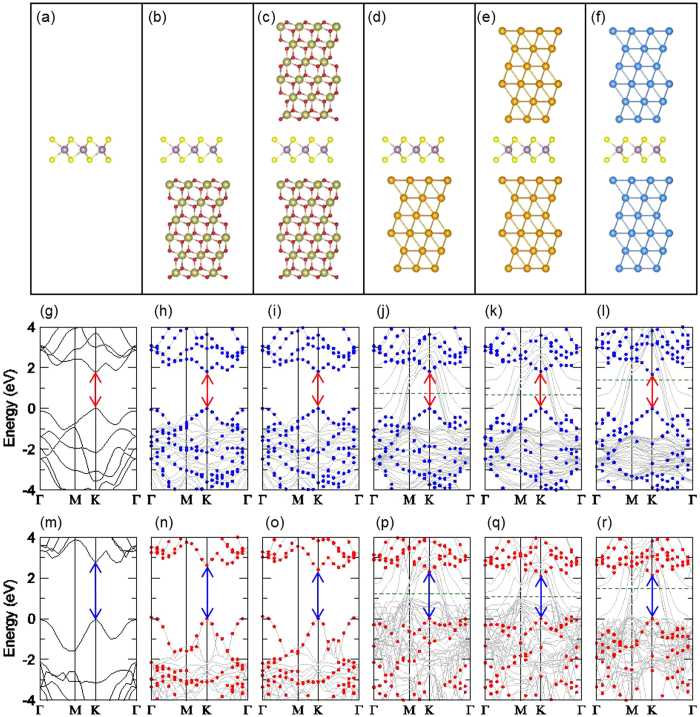
First, we consider five ML MoS2 model systems with different dielectric environments for full DFT and GW calculations: (A) a freestanding ML MoS2 surrounded by vacuum, (B) ML MoS2 on a HfO2 substrate, (C) ML MoS2 sandwiched by HfO2, (D) ML MoS2 on a Au substrate, and (E) ML MoS2 sandwiched by Au. We construct the model atomic structures for the five systems as shown in Fig. 1a–e. The details of the structures are described in the Supplementary Materials. The calculated band structures within the local density approximation (LDA) are plotted in Fig. 1g–k. The LDA band structures indicate that the ML MoS2’s have a direct bandgap of 1.8 eV at the K valley irrespective of the environments. The electronic structure analysis shows that the orbitals of the valence band maximum (EV) and the conduction band minimum (EC) at the K valley are characterized as the Mo 4d atomic orbitals. These atomic orbitals are located in the middle of the three atomic layers of ML MoS2 layer, and they have negligible hybridization with the orbitals of the nearby surrounding materials that interacts with the ML MoS2 through the van der Waals gap. The LDA bandgap at the K valley is about 1.8 eV agreeing with previous DFT calculations and found to remain unchanged with different environments. For the metallic Au environments (Fig. 1j,k), the Au related states (6s) are found inside the bandgap of the ML MoS2, but they can be clearly distinguished from the ML MoS2 states (shown as blue dots). Within the LDA, the Au 5d states are found inside the valence bands of the ML MoS2, and the Fermi level (EF) is found to be located at EV + 0.8 eV or EC − 1.0 eV.

Figure 1. Atomic structures and electronic band structures.

Figure 1

Open in a new tab

(a–f) Atomic structures of the freestanding ML MoS2 (a), ML MoS2 on HfO2 substrate (b), ML MoS2 sandwiched by HfO2 (c), ML MoS2 on Au metallic substrate (d), ML MoS2 sandwiched by Au (e), and ML MoS2 sandwiched by Ag (f). The Mo, S, Hf, O, Au, and Ag atoms are indicated by the purple, yellow, gold, red, yellow, and blue color balls, respectively. (g–l) Calculated LDA band structures of the freestanding ML MoS2 (g), ML MoS2 on HfO2 (h), ML MoS2 sandwiched by HfO2 (i), ML MoS2 on Au (j), ML MoS2 sandwiched by Au (k), and ML MoS2 sandwiched by Ag (l). The blue filled dots (g–l) indicate the projected states to the ML MoS2. (m–r) Calculated GW band structures of the freestanding ML MoS2 (m), ML MoS2 on HfO2 (n), ML MoS2 sandwiched by HfO2 (o), ML MoS2 on Au (p), ML MoS2 sandwiched by Au (q), and ML MoS2 sandwiched by Ag (r) are shown. The red filled dots (m–r) indicate the projected states to the ML MoS2. The arrows (g–r) indicate the direct bandgap at the K valley of the ML MoS2. The Fermi levels of the Au and Ag containing systems (j–l,p–r) are indicated by the green dashed lines.

The calculated GW band structures of the ML MoS2 with the same environments are plotted in Fig. 1m–q. They also show that the ML MoS2 has a direct bandgap at the K valley irrespective of the environments, as in the case of the LDA. The direct bandgap at the K valley of the freestanding ML MoS2 (Fig. 1m) is 2.8 eV in GW, close to the previous calculations8,9,10,11,12. The GW bandgap of the ML MoS2 on HfO2 (Fig. 1n) is calculated to be 2.6 eV, and that of the ML MoS2 sandwiched by HfO2 (Fig. 1o) is 2.4 eV, which are smaller than that of the freestanding ML MoS2 (2.8 eV). Since the electronic orbital hybridization between the MoS2 and the nearby HfO2 dielectric is negligible, as shown in the LDA results (Fig. 1h,i), the main cause of the bandgap reduction in the GW calculations is expected to be the EDS effect on the QP bandgap renormalization. The size of the bandgap reduction is significant, up to by 0.4 eV, in the presence of HfO2 layers. The ML MoS2 on the Au metallic substrate (Fig. 1p) is found to have a direct bandgap of 2.3 eV at the K valley in the GW calculations, and the ML MoS2 sandwiched by the Au layers (Fig. 1q) has a GW bandgap of 2.1 eV. The bandgap reduction is even more significant, up to by 0.7 eV, by the metallic Au environments.

GW bandgaps of ML MoS2 with effective medium

In order to investigate the primary effect of EDS on the bandgap of ML MoS2, we incorporate the effective environmental dielectric constant (κE) into the dielectric matrix of the screened Coulomb (W) interaction in GW calculations. Details of the procedure are described in the Supplementary Materials. With this approach that includes the EDS effectively in GW, there are several advantages besides making it possible to study separately the EDS effect: reducing the computational costs of GW calculations with environments, and making it possible to include additional polarizability into the screened Coulomb (W) interaction. Note that the dielectric effect of liquid medium on ML MoS2 bandgap can be modeled by the effective dielectric medium. The quasiparticle renormalization in the GW approximation (Fig. 1m-r) includes only the electronic contribution of screening into the screened Coulomb (W) interaction. Since high-κE dielectrics such as HfO2 (ε0 ≅ 26) usually have large ionic contribution (ε0−ε∝ ≅ 21) to the dielectric screening, the renormalization of electrons in the ML MoS2 would be further modified by the ionic screening of the surrounding materials. However, this ionic screening effect is neglected in the GW calculations of the band structures shown in Fig. 1n–r. In order to include such an ionic contribution of screening explicitly, the GW plus the lattice polarization effect (LPE) can be applied to the calculation of the bandgap renormalization. In some ionic solids, the inclusion of the LPE has been reported to lead to a large shrinkage of the bandgap20,21,22. Compared to full GW + LPE, effective dielectric medium method provide an alternative efficient approach to include full dielectric effects on the MoS2 bandgap.

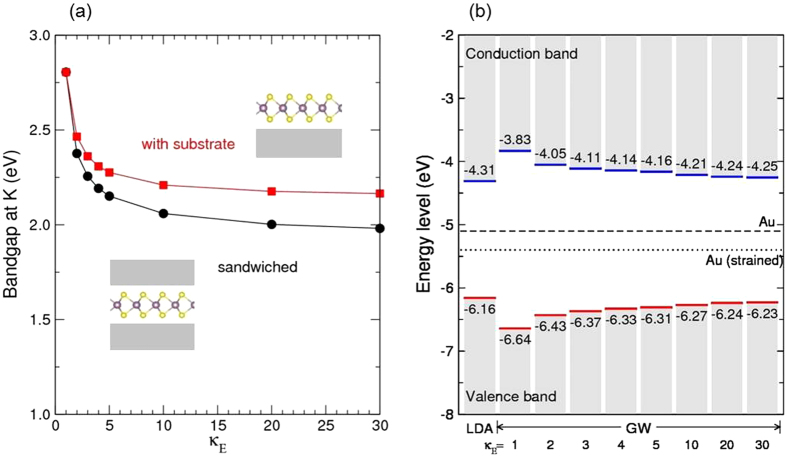
The calculated GW bandgaps of ML MoS2 with an effective dielectric constant (κE) of the environments are plotted as a function of the κE in Fig. 2a. With κE = 1, the ML MoS2 represents the freestanding isolated one in vacuum, and the GW bandgap is found to be 2.8 eV at the K valley. With increasing the dielectric constant, κE, the GW bandgap is found to drop rapidly down. With the one-side dielectric, in such a case of the supported ML MoS2 on a substrate, the GW bandgap is found to reduce down to about 2.2 eV with a ultrahigh-κE dielectric (at κE = 30). With the both-side dielectric, as in a typical top-gate FET structure, the GW bandgap of the ML MoS2 is found to be smaller down to about 1.9 eV with a ultrahigh-κE dielectric of κE = 30. It is notable that the bandgap reduction is very rapid in the range 1 < κE < 5, and most of the bandgap reduction, about 80%, occurs with κE = 5. Thus, the presence of a moderate dielectric material in vicinity of a ML MoS2, can strongly affect the bandgap renormalization in the ML MoS2, even though it is not an ultrahigh-κE dielectric.

Figure 2. Bandgap and absolute band edge levels.

Figure 2

Open in a new tab

(a) Calculated GW bandgaps at the K valley of the ML MoS2 on a substrate (red) and in a sandwich structure (black), as a function of the effective dielectric constant κE of the environment. (b) Calculated absolute GW band edge levels of the ML MoS2 sandwiched by the effective dielectric media having κE. They are compared to the absolute band edge levels in LDA. The work function levels of Au (at −5.1 eV) and the strained (used in our calculations) Au (at −5.4 eV) are indicated by the dashed and dotted line, respectively.

The experimentally measured bandgap of 2.15 eV in STS16 for the ML MoS2 on graphite substrate is close to the obtained asymptotic value of 2.2 eV for the one-side dielectric, and the STS bandgap of 2.16 eV for the ML MoS2 on a bilayer graphene substrate17 is also close the value. The measured ARPES bandgap of 1.86 eV for the K-intercalated MoS2 (ref. 14) is close to the obtained bandgap of ML MoS2 embedded in high-κE dielectric (1.9 eV). The measured ARPES bandgap of 1.39 eV for the ML MoS2 on Au substrate15 indicates a rather strong interaction at the interface, as shown in our previous metal-MoS2 interface study18. The measured bandgap of 1.8 eV for the ML MoS2 in the Al2O3/MoS2/SiO2 stacked top-gate FET19 is closer to the asymptotic value of 1.9 eV obtained for the both-side dielectric system. An additional reduction of the bandgap may be possible by the carrier-induced renormalization of bandgap20 in n-type ML MoS2 FET.

Absolute band edge levels of ML MoS2 with environments

We now investigate the absolute band edge levels (relative to vacuum level) of ML MoS2 with including the EDS effect. Figure 2b shows the band edge levels of ML MoS2 in LDA and those in GW with various κE. The EV and EC in LDA are found to be −6.16 and −4.31 eV, respectively, which are close to the previous LDA calculations (−5.98 and −4.29 eV)23. The absolute GW band edge levels are obtained using the bandgap center alignment scheme23, and the obtained EV and EC in GW with κE = 1 are −6.64 and −3.83 eV, respectively, in good agreement with the previous GW calculations (−6.50 and −3.74 eV, respectively)23. The calculated GW band edge levels with κE plotted in Fig. 2b show that the EV increases up and the EC decreases down monotonically with increasing κE, approaching the LDA values of EV and EC with ultrahigh-κE.

For the (strained) Au metal, the work function (5.4 eV) level is located at EV + 0.8 eV or EC − 1.1 eV with the LDA band edge levels. They agree with those obtained in our atomistic GW calculations (EV + 0.8 eV or EC − 1.0 eV) (Fig. 1j,k). In the atomistic GW calculations, the EF is found to be located at EV + 1.0 eV or EC − 1.3 eV in the Au supported structure and at EV + 0.9 eV or EC − 1.2 eV in the Au sandwiched structure (Fig. 1p,q). If we use the GW band edge levels without EDS (κE = 1), the Au work function level is located at EV + 1.2 eV or EC − 1.6 eV, which is far from the atomistic GW calculations (EV + 0.9 eV or EC − 1.2 eV, as shown in Fig. 1q). When we use the GW band edge levels with ultrahigh-κE (says κE = 30), the Au work function level of EV + 0.8 eV or EC − 1.1 eV is close to the atomistic GW results (EV + 0.9 eV or EC − 1.2 eV) (Fig. 1q). Note that within the GW, the Au 5d states are found to emerge inside the bandgap of ML MoS2 (Fig. 1p,q), which is in contrast to the LDA results (Fig. 1j,k). Although both the LDA and GW results indicate that the Au work function level is located deep inside the bandgap of ML MoS2, and some experiments have shown that Au produces n-type Schottky contacts to ML MoS2 (refs 24,25). Au has been typically used as a n-type contact metal to MoS2 (refs 1,26,27), which may be due to the Fermi level pinning at the interface near to the EC of MoS2 (refs 18,27, 28, 29).

In our calculations, the Au(111) slab is strained by +9.6% (tensile) to match in lattice to the 1 × 1 ML MoS2. In order to match the lattice constant of Au with the MoS2 within a few % of strain, a larger supercell, for example 2 × 2 Au(111) slab and √3 × √3R30° MoS2 with 5.0% of compressive strain, is required with the number of atoms exceeding 33, with which the GW calculation is computationally demanding. One effect of the tensile strain on the Au(111) slab is lowering the Fermi level with smaller band dispersions, and the work function of the strained Au(111) is 5.4 eV, while that of the unstrained Au(111) is 5.1 eV, as indicated in Fig. 2b. In both cases, the Fermi level crosses the Au(111) 6s-bands and is located inside the MoS2 bandgap. Both are metallic with the 6s Fermi electrons, having the infinite static dielectric constants. Since the quasi-particle bandgap dependence on the dielectric constant is very weak with the large static dielectric constant, less than 0.1 eV when κE > 10 (see Fig. 2a), the quasi-particle bandgap of the ML MoS2 is not expected to be significantly altered by the applied strain on the Au(111). We check another metallic slab, Ag(111), to test the quasi-particle bandgap of ML MoS2 with metallic screening. The Ag(111) slab is strained by 9.4% (tensile) to match with the 1 × 1 ML MoS2. The calculated band structures of the ML MoS2 with Ag(111) in the sandwich structure are shown in Fig. 1l (LDA) and Fig. 1r (GW). The obtained GW bandgap of the ML MoS2 is 2.11 eV with the metallic Ag(111) environment, which is nearly the same to the GW bandgap (2.09 eV) of the ML MoS2 with the metallic Au(111).

Bandgaps of ML MoS2 in FET

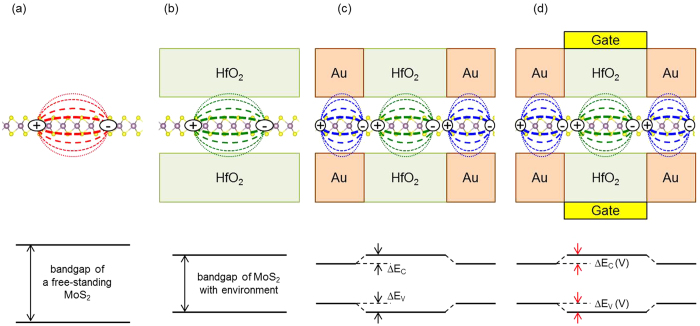
Figure 3 illustrates the effect of EDS on the bandgap of ML MoS2 in various environments. In an isolated freestanding ML MoS2, the strong Coulomb interaction (through the free space) between electrons makes the QP renormalization of electrons huge leading to a large bandgap (Fig. 3a). However, with a dielectric environment, the Coulomb interaction between electrons in the ML MoS2 is additionally screened, and the QP bandgap of the ML MoS2 is correspondingly reduced (Fig. 3b representatively for the both-side HfO2 dielectrics). In a typical top-gate FET device structure, a channel is located between a substrate and a gate dielectric. The channel is also connected with metallic contacts in the source and drain regions. Such typical device structure is shown in Fig. 3c with the metallic contact regions (representatively both-side Au) at both ends and the channel region with nearby dielectrics (representatively both-side HfO2) in the central region. For this structure, the EDS effect surrounding the ML MoS2 should be different for the source/drain and channel region. The different EDS strengths of metal and gate dielectric would result in different bandgaps in different regions. Under the metallic source/drain contact regions, the electronic bandgap should be smaller than in the channel region between the gate dielectric and the substrate. According to our atomistic GW calculations, the bandgaps in the source and drain regions with the both-side Au contacts are 2.1 eV, while the bandgap in the channel region with the both-side HfO2 dielectrics is 2.4 eV. The EV and EC offsets (ΔEC and ΔEV) in the ML MoS2 channel are 0.1 and 0.2 eV, respectively. It indicates that there are an electronic transport barrier (ΔEC) of 0.2 eV from the source to the channel, and a hole transport barrier (ΔEV) of 0.1 eV, even though the ML MoS2 channel itself is homogeneous atomically, due to the different EDS effects (see bottom in Fig. 3c). This type of environmentally induced barriers has not been known, and can be important in low-dimensional electronic devices. Especially, they can play a role of suppressing off-state leakage current in FET by blocking the minority carrier transport.

Figure 3. Schematic figures of screening and band diagrams.

Figure 3

Open in a new tab

(a) Strong Coulomb interaction (weak screening) between electrons (red lines) in the freestanding ML MoS2 and the wide bandgap. (b) Moderate Coulomb interaction (moderate screening) between electrons (green lines) in ML MoS2 with both-side (HfO2) dielectric environments and the reduced bandgap. (c) Weak Coulomb interaction (strong screening) between electrons (blue lines) in ML MoS2 with both-side metallic (Au) environments, in conjunction with the ML MoS2 with both-side (HfO2) dielectric environments. The band offsets are indicated in the band diagram below, which act as transport barriers to electrons (ΔEC) and holes (ΔEV). (d) A hypothetical device structure composed of a ML MoS2 sandwiched by Au metallic contacts at both the ends and a dielectric material in the central region, of which the dielectric constant [κE(V)] is variable with the electric field applied by the gate voltage (V). The band diagram shows the tunable transport barriers to electrons [ΔEC(V)] and holes [ΔEV(V)].

If the κE of the gate dielectric can be controlled externally, both the electron and hole transport barriers can be controlled, as schematically illustrated in Fig. 3d. In this tunable bandgap FET, both the hole and electron transport barriers can be controlled by the gate, which is the main difference from the conventional FET that controls only the band offsets between the source/drain and the channel (and thus the transport barrier of only one type of carrier). Such tunable bandgap is highly desirable to optimize and design a novel electronic device, and bilayer graphene has been utilized to realize the tunable bandgap FET, in which the bandgap is varied by an external electric field to break the inversion symmetry of the bilayer graphene30. While the bilayer graphene system is highly restrictive in symmetry, the bandgap tuning by EDS can be applied generally to low dimensional semiconductors without any symmetry requirements. A challenge to realize the tunable bandgap FET by EDS is on controlling the environmental (gate) dielectric constant (κE) externally. Recently, the electrically controlled dielectric materials utilizing ferroelectric properties have been suggested31, and such ferroelectric materials32,33,34,35 can be promising as gate dielectric materials in the EDS-based tunable bandgap FET. Polar instability at the phase transition36 can be also utilized to vary the dielectric constant, and distance control from the gate dielectric to the 2D semiconductor channel can be another way to control the EDS externally, which can function as an electromechanical device.

Conclusions

Electronic bandgap of a 2D semiconductor, ML MoS2, depends on the nearby dielectric environments, through the screened QP renormalization of electrons in the ML MoS2. The bandgap tends to reduce with increasing the environmental dielectric constant. In a ML MoS2 FET, the vicinity of metallic contacts gives smaller bandgap than that of the gate dielectric, and there should be valence and conduction band offsets between the regions. The band offsets can play a role of barriers to electron and hole transports through the channel. Utilizing the environment-dependent property of the bandgap, a tunable bandgap FET is suggested, which operates with the bandgap controlled by an external source to control the electron and hole transport barriers.

Methods

Density-Functional Theory and GW Calculations

The mean-field density-functional theory (DFT) calculations were performed with the Quantum-Espresso code with the local density approximation (LDA)37. The kinetic energy cutoff for the plane-wave basis expansion of the wave-functions was 40 Ry. The 24 × 24 × 1 k-point sampling in the hexagonal Brillouin zone (BZ) of the 1 × 1 ML MoS2 was used. The GW calculations were performed with the BerkeleyGW code38,39. The kinetic energy cutoff for the plane-wave basis expansion of the dielectric matrix was 6 Ry. The number of conduction bands used in the calculations of the static irreducible random phase approximation (RPA) polarizability and the Coulomb-hole self-energy was 100 for the free-standing 1 × 1 ML MoS2. For the 1 × 1 ML MoS2 with the HfO2 and Au environments, the number of conduction bands used was around 700. The limited number of conduction bands can affect the GW eigenvalues at the M point in the hexagonal BZ40, but those at the K point converge fast with respect to the number of conduction bands. When we used more number of conduction bands, and the GW bandgaps at K were not significantly affected. The generalized plasmon pole (GPP) approximation was used for the frequency dependence of the dielectric matrix. We applied slab truncation scheme for the Coulomb interaction to minimize the supercell interaction for the free-standing ML MoS2 and the ML MoS2 with the HfO2 environments.

Model Atomic Structures

The 1 × 1 hexagonal unit cell for the ML MoS2 was used. The lattice constant was fixed to 3.16 Å, which is the LDA optimized value for the free-standing ML MoS2. With the 1 × 1 in-plane periodicity of the ML MoS2, the HfO2 was modeled by the O-terminated 1 × 1 HfO2(111) slab, and the Au was modeled by the 1 × 1 Au(111) slab. With these interface structures, the HfO2 and Au slabs are hydrostatically strained by −8.5% (compressive) and +9.6% (tensile), respectively, to match their lattice constants to that of the ML MoS2 (3.16 Å). The atomistic environments are only model systems that represent dielectric and metallic environments. Six Hf atomic layers were used for the HfO2 dielectric slab, and six Au atomic layers were used for the Au metallic slab, as shown in Fig. 1b–e in the main article. For all the interfaces, we used the interface spacing of 2.975 Å (between the atomic layers), which was chosen arbitrary as the same to the interlayer spacing between the MoS2 layers in bulk 2H-MoS2. The vacuum thickness of about 12 Å in the supercell was used. The ideal (as-cleaved) atomic structures for the HfO2 and Au slabs were used to see only the electronic EDS effect.

Additional Information

How to cite this article: Ryou, J. et al. Monolayer MoS2 Bandgap Modulation by Dielectric Environments and Tunable Bandgap Transistors. Sci. Rep. 6, 29184; doi: 10.1038/srep29184 (2016).

Supplementary Material

Supplementary Information
srep29184-s1.pdf (373.1KB, pdf)

Acknowledgments

Y.S.K. acknowledges the support by Korea Evaluation Institute of Industrial Technology (KEIT) funded by the Ministry of Trade, Industry and Energy (MOTIE) (Project No. 10050296: Large scale (over 8”) synthesis and evaluation technology of 2-dimensional chalcogenides for next generation electronic devices), and the use of the computing facilities through the Strategic Supercomputing Support Program from Korea Institute of Science and Technology Information (No. KSC-2015-C2-046). This work was also supported in part by the Center for Low Energy Systems Technology (LEAST), one of six centers supported by the STARnet phase of the Focus Center Research Program (FCRP), a Semiconductor Research Corporation program sponsored by MARCO and DARPA.

Footnotes

Author Contributions J.R., S.K.C. and Y.-S.K. performed the DFT and GW calculations. Y.-S.K. and K.C. conducted this research. All the authors contribute to writing this manuscript.

References

  1. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011). [DOI] [PubMed] [Google Scholar]
  2. Radisavljevic B. & Kis A. Mobility engineering and a metal–insulator transition in monolayer MoS2. Nat. Mater. 12, 815–820 (2013). [DOI] [PubMed] [Google Scholar]
  3. Novoselov K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jena D. & Knar A. Enhancement of carrier mobility in semiconductor nanostructures by dielectric engineering. Phys. Rev. Lett. 98, 136805 (2007). [DOI] [PubMed] [Google Scholar]
  5. Noh J.-Y., Kim H., Park M. & Kim Y.-S. Deep-to-shallow level transition of Re and Nb dopants in monolayer MoS2 with dielectric environments. Phys. Rev. B 92, 115431 (2015). [Google Scholar]
  6. Lin Y. et al. Dielectric screening of excitons and trions in single-layer MoS2. Nano Lett. 14, 5569–5576 (2014). [DOI] [PubMed] [Google Scholar]
  7. Kylänpää I. & Komsa H.-P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B 92, 205418 (2015). [Google Scholar]
  8. Cheiwchanchamnangij T. & Lambrecht W. R. L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 85, 205302 (2012). [Google Scholar]
  9. Ramasubramaniam A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012). [Google Scholar]
  10. Komsa H.-P. & Krasheninnikov A. V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B 86, 241201 (2012). [Google Scholar]
  11. Shi H., Pan H., Zhang Y.-W. & Yakobson B. I. Quasiparticle band structures and optical properties of strained monolayer MoS2 andWS2. Phys. Rev. B 87, 155304 (2013). [Google Scholar]
  12. Qiu D. Y., da Jornada F. H. & Louie S. G. Optical spectrum of MoS2: Many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013). [DOI] [PubMed] [Google Scholar]
  13. Splendiani A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
  14. Eknapakul T. et al. W. Electronic structure of a quasi-Freestanding MoS2 monolayer. Nano Lett. 14, 1312–1316 (2014). [DOI] [PubMed] [Google Scholar]
  15. Miwa J. A. et al. Electronic structure of epitaxial single-Layer MoS2. Phys. Rev. Lett. 114, 046802 (2015). [DOI] [PubMed] [Google Scholar]
  16. Zhang C., Johnson A., Hsu C.-L., Li L.-J. & Shih C.-K. Direct imaging of band profile in single layer MoS2 on graphite: Quasiparticle energy gap, metallic edge states, and edge band bending. Nano Lett. 14, 2443–2447 (2014). [DOI] [PubMed] [Google Scholar]
  17. Ugeda M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014). [DOI] [PubMed] [Google Scholar]
  18. Gong C., Colombo L., Wallace R. M. & Cho K. The unusual mechanism of partial Fermi level pinning at metal-MoS2 Interfaces. Nano Lett. 14, 1714–1720 (2014). [DOI] [PubMed] [Google Scholar]
  19. Lee H. S. et al. MoS2 nanosheet phototransistors with thickness-modulated optical energy gap. Nano Lett. 12, 3695–3700 (2012). [DOI] [PubMed] [Google Scholar]
  20. Liang Y. & Yang L. Carrier plasmon induced nonlinear band gap renormalization in two-dimensional semiconductors. Phys. Rev. Lett. 114, 063001 (2015). [DOI] [PubMed] [Google Scholar]
  21. Bechstedt F., Seino K., Hahn P. H. & Schmidt W. G. Quasiparticle bands and optical spectra of highly ionic crystals: AlN and NaCl. Phys. Rev. B 72, 245114 (2005). [Google Scholar]
  22. Vidal J., Trani F., Bruneval F., Marques M. A. L. & Botti S. Effects of electronic and lattice polarization on the band structure of delafossite transparent conductive oxides. Phys. Rev. Lett. 104, 136401 (2010). [DOI] [PubMed] [Google Scholar]
  23. Liang Y., Huang S., Soklaski R. & Yang L. Quasiparticle band-edge energy and band offsets of monolayer of molybdenum and tungsten chalcogenides. Appl. Phys. Lett. 103, 042106 (2013). [Google Scholar]
  24. Walia S. et al. Characterization of metal contacts for two-dimensional MoS2 nanoflakes. Appl. Phys. Lett. 103, 232105 (2013). [Google Scholar]
  25. Fontana M. et al. Electron-hole transport and photovoltaic effect in gated MoS2 Schottky junctions. Sci. Rep. 3, 1634 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Liu K.-K. et al. Growth of large-area and highly crystalline MoS2 thin layers on insulating substrates. Nano Lett. 12, 1538–1544 (2012). [DOI] [PubMed] [Google Scholar]
  27. Neal A. T., Liu H., Gu J. & Ye P. Metal contacts to MoS2: A two-dimensional semiconductor. IEEE Device Research Conf. 65–66 (2012). [Google Scholar]
  28. Das S., Chen H.-Y., Penumatcha A. V. & Appenzeller J. High performance multilayer MoS2 transistors with scandium contacts. Nano Lett. 13, 100–105 (2013). [DOI] [PubMed] [Google Scholar]
  29. Chuang S. et al. MoS2 P-type transistors and diodes enabled by high work function MoOx contacts. Nano Lett. 14, 1337–1342 (2014). [DOI] [PubMed] [Google Scholar]
  30. Zhang Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009). [DOI] [PubMed] [Google Scholar]
  31. Kong L. B. et al. Electrically tunable dielectric materials and strategies to improve their performances. Progress in Materials Science 55, 840–893 (2010). [Google Scholar]
  32. Lines M. & Glass A. Principles and Applications of Ferroelectrics and Related Materials. Clarendon Press, Oxford (1979).
  33. Cohen R. E. Origin of ferroelectricity in perovskite oxides. Nature 358, 136–138 (1992). [Google Scholar]
  34. Eglitis R. I., Borstel G., Heifets E., Piskunov S. & Kotomin E. Ab initio calculations of the BaTiO3 (100) and (110) surfaces. J. Electroceram. 16, 289–292 (2006). [Google Scholar]
  35. Zhang J. M., Cui J., Xu K. W., Ji V. & Man Z. Y. Ab initio modeling of CaTiO3 (110) polar surfaces. Phys. Rev. B 76, 115426 (2007). [Google Scholar]
  36. Pradhan S. & Roy G. S. Study the crystal structure and phase transition of BaTiO3 – A pervoskite. Researcher 5, 63–67 (2013). [Google Scholar]
  37. Giannozzi P. et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Physics: Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
  38. Deslippe J. et al. BerkeleyGW: A massively parallel computer package for the calculation of the quasiparticle and optical properties of materials and nanostructures. Comput. Phys. Commun. 183, 1269 (2012). [Google Scholar]
  39. Hedin L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 139, A796 (1965). [Google Scholar]
  40. Hybertsen M. S. & Louie S. G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 34, 5390 (1986). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep29184-s1.pdf (373.1KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES