Predicting the growth of nanoscale nuclei by histotripsy pulses

Abstract

Histotripsy is a focused ultrasound therapy that ablates tissue through the mechanical action of cavitation. Histotripsy-initiated cavitation activity is generated from shocked ultrasound pulses that scatter from incidental nuclei (shock scattering histotripsy), or purely tensile ultrasound pulses (microtripsy). The Yang/Church model was numerically integrated to predict the behavior of the cavitation nuclei exposed to measured shock scattering histotripsy pulses. The bubble motion exhibited expansion only behavior, suggesting that the ablative action of a histotripsy pulse is related to the maximum size of the bubble. The analytic model of Holland and Apfel was extended to predict the maximum size of cavitation nuclei for both shock scattering histotripsy and microtripsy excitations. The predictions of the analytic model and the numerical model agree within 2% for fully developed shock scattering histotripsy pulses (>72 MPa peak positive pressure). For shock scattering histotripsy pulses that are not fully developed (<72 MPa), the analytic model underestimated the maximum size by less than 5%. The analytic model was also used to predict bubble growth nucleated from microtripsy insonations, and was found to be consistent with experimental observations. Based on the extended analytic model, metrics were developed to predict the extent of the treatment zone from histotripsy pulses.

1. Introduction

Histotripsy is an ablative form of therapeutic ultrasound (Maxwell et al 2012, Khokhlova et al 2015), which is under development for the treatment of prostate pathologies (Roberts 2014), liver cancer (Vlaisavljevich et al 2013), and deep vein thrombosis (Maxwell et al 2009). The therapy relies on the mechanical action of cavitation, although the bubble dynamics vary depending on the insonation scheme. Shockwave-induced heating generates boiling of the tissue (Khokhlova et al 2006), whereas tensile pressure waves expand endogenous cavitation nuclei. The cavitation nuclei are thought to have nanometer-sized gaseous cores (Maxwell et al 2013) that undergo a ‘Blake-like’ growth (Leighton 1994). Shocked histotripsy pulses scatters from activated cavitation nuclei, and constructively interfere with the subsequent cycles of the insonation (Maxwell et al 2011). Additional microbubbles are generated in the regions of constructive interference, resulting in the formation of a microbubble cloud for this ‘shock scattering’ form of histotripsy. Shock scattering ultrasound pulses have a fundamental frequency between 750 kHz and 1 MHz, are 5–20 cycles in pulse duration, and are delivered at a pulse repetition frequency (PRF) of 10 Hz–1 kHz (Khokhlova et al 2015). Between 10³–10⁴ pulses at peak rarefactional pressures of 15–25 MPa, and peak positive pressures in excess of 80 MPa are required for tissue ablation (Maxwell et al 2012). A ‘microtripsy’ pulse, in contrast, is composed primarily of a single tensile period that generates individual bubbles within the focal region (Maxwell et al 2013, Lin et al 2014a). The operational frequency of mictotripsy is between 345 kHz and 3 MHz (Vlaisavljevich et al 2015b), the PRF is less than 10 Hz, and 10² pulses are required for tissue ablation (Wang et al 2012). Peak rarefactional pressures in excess of 25 MPa are required to initiate cavitation (Maxwell et al 2013). Tissue appears completely homogenized after both shock scattering histotripsy and microtripsy exposure, resulting in primarily acelluar debris (Maxwell et al 2012).

Expansion of the cavitation nuclei is critical to initiate histotripsy therapy, regardless of the insonation type. For shock scattering histotripsy, the growth of nuclei is required to initiate scattering for microbubble cloud formation. Microtripsy requires the growth of individual bubbles for tissue ablation. Numerical computations have been developed to predict bubble activation under histotripsy excitation (Kreider et al 2011, Vlaisavljevich et al 2015b), due to the complex interaction between the bubble and the excitation waveform. In order to gauge the likelihood of inertial cavitation, an analytic model was developed which allowed for a heuristic understanding of the physical processes involved (Appel 1986, Holland and Apfel 1989), and served as the basis for a regulatory standard for diagnostic ultrasound (Apfel and Holland 1991).

Standard preclinical data is reviewed by the U.S. Food and Drug Administration (FDA) for focused ultrasound therapies that rely on thermal ablation (Harris 2009). No FDA standards currently exist for mechanically ablative therapies like histotripsy, which halts its progression through the regulatory process and into the clinics. Thus, there is a need for metrics to development of regulatory standards for histotripsy. A model that helps predict the location of histotripsy ablation and reveals the physical processes responsible for the therapeutic action of histotripsy are well understood and predictable would guide the development of regulatory metrics.

An analytic theory is developed here to predict the expansion of cavitation nuclei for shock scattering histotripsy. The predictions of the analytic model will be compared to numerical computation of bubble oscillations in a viscoelastic medium exposed to a shock scattering histotripsy pulse. An experimentally measured shockwave from a shock scattering histotripsy source is used as the time-dependent excitation pressure. The analytic model will also be extended to mictrotripsy pulses, and the predicted maximum size will be compared to measured values available in the literature. Based on these models, metrics will be developed to predict the treatment zone of histotripsy pulses.

2. Methods

2.1. Numeric model

The radial oscillations of cavitation nuclei in soft tissue were calculated by numerical integration of the Yang/Church model (2005). An adaptive fourth-order Runga–Kutta algorithm was implemented in MATLAB^® (The Mathworks, Natick, MA, USA), employing the function ‘ode15s’ to carry out the integration. The Yang/Church model has the form:

$$\left(1-\frac{\stackrel{.}{R}}{c}\right)R\ddot{R}+\left(1-\frac{\stackrel{.}{R}}{c}\right)\frac{3}{2}{\stackrel{.}{R}}^2=\left(1+\frac{\stackrel{.}{R}}{c}\right)\frac{p_{\mathrm{w}}(\stackrel{.}{R},R,t)}{\rho }+\frac{R}{\rho c}\frac{\partial p_{\mathrm{w}}}{\partial t}$$ (1)

where R is the time dependent bubble radius, the diacritic dot denotes the temporal derivative, c is the sound speed of the viscoelastic medium (1540 m s⁻¹), and ρ is the medium density (1000 kg m⁻³). The pressure at the bubble wall, p_w, is defined in terms of the properties of the viscoelastic medium:

$$p_{\mathrm{w}}=\left(P_0+\frac{2\sigma }{R_0}\right){\left(\frac{R_0}{R}\right)}^{3\kappa }-\frac{2\sigma }{R}-\frac{4\mu \stackrel{.}{R}}{R}-\frac{4G}{3}\left[1-{\left(\frac{R_0}{R}\right)}^3\right]-P_0-p_{\text{AC}}(t)$$ (2)

where P₀ is the ambient pressure (0.1 MPa), R₀ is the initial radius of the air-filled cavitation nucleus. Unless otherwise specified, the following values of the medium properties were used: surface tension, σ = 0.056 N m⁻¹ (Holland and Apfel 1989, Church et al 2015), dynamic viscosity, μ = 0.005 kg m⁻¹ s⁻¹ (Holland and Apfel 1989, Church et al 2015), and shear modulus, G = 30 kPa (Cao et al 2013).

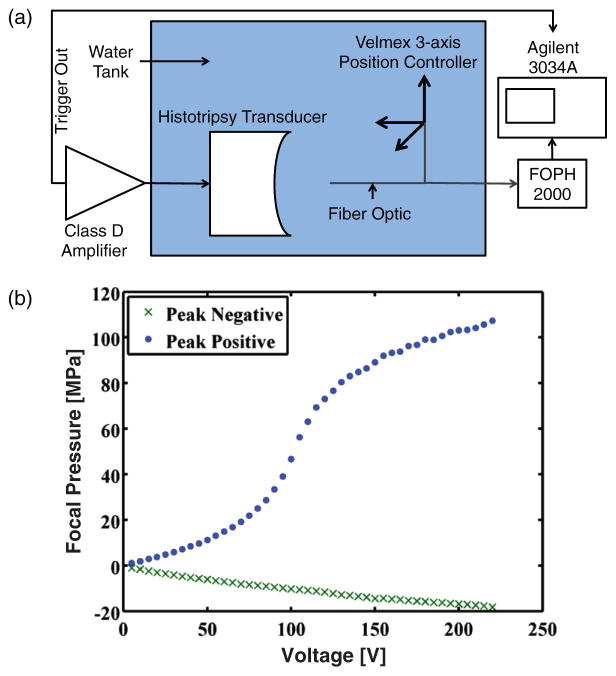
The time-dependent source term in (2), p_AC, was implemented with an experimentally measured histotripsy pulse (figure 1(a)). A 1 MHz transducer (Imasonic, Voray sur l’Ognon, France) driven by a custom-built class D amplifier (Hall and Cain 2006) was used to generate shocked histotripsy pulses in a tank of degassed (14% dissolved oxygen saturation), filtered water (0.2 μm pore size). The transducer was highly focused, with a 9 cm focal length and 10 cm aperture (f number 0.9). A short pulse duration (5 μs) and low PRF (1 Hz) were employed to reduce the likelihood of cavitation or standing waves. The nonlinear field of the transducer was mapped with a fiber optic hydrophone (FOPH 2000, RP Acoustics, Leutenbach, Germany) affixed to a three-axis positioning system (NF90 motor controllers, Velmex, Inc., Bloomfield, NY). Pressure waveforms were recorded at the focus, averaged over 128 histotripsy pulses, and stored for analysis offline. The averaged waveforms were deconvolved using time-domain impulse response data to recover bandwidth of the pulse up to 150 MHz (Kreider et al 2013). Histotripsy pulses with shockwave amplitudes up to 107 MPa were recorded before the tip of the FOPH was destroyed (figure 1(b)).

Figure 1.

(a) Set-up diagram for measuring shocked histotripsy pulses with fiber optic hydrophone. (b) Measured peak positive (blue dots) and peak negative (green x) of the histotripsy pulse as a function of input voltage from the class D amplifier.

2.2. Analytic model to predict maximum bubble size

2.2.1. Analytic model derivation for microtripsy

Holland and Apfel (1989) developed an analytic model to predict the maximum size of a bubble exposed to a single cycle of sinusoidal excitation:

$$R_{\text{MAX}}=\left[R_0+\sqrt{\frac{2P_0\xi }{9\rho }}\tau \right]{\left[\frac{\xi P_0}{3p_{\text{EFF}}}+1\right]}^{1/3}$$ (3)

where ξ and τ are defined in Holland and Apfel (1989), and P₀, R₀, and ρ are as defined in section 2.1. The effects of surface tension, viscosity, and inertia are accounted for in equation (3), but not tissue elasticity. The effective pressure in (3), p_EFF, acts as a ‘Blake brake’ to arrests the growth of the bubble. Holland and Apfel assumed that the pressure was slowly varying as the bubble approached its maximum size, and set p_EFF = P₀. This assumption is reasonable for insonations without an appreciable compressional phase, such as microtripsy (Maxwell et al 2013, Lin et al 2014a, Vlaisavljevich et al 2015a). It should be noted that the frequency dependence of the insonation is embedded in ξ and τ of (3). Microtripsy insonations do not have strong nonlinear components (Lin et al 2014b), and thus the insonation center frequency should be employed for (3).

2.2.2. Analytic model derivation for shock scattering hisototripsy

The pressure changes rapidly as the bubble approaches its maximum size for shock scattering histotripsy (figure 2), and the effective pressure can no longer assumed to be the ambient pressure. The effective pressure for shockwave excitation can be determined through considering the conservation of energy as the bubble approaches its maximum size. Apfel (1981) expresses this energy conservation as:

$$2\pi \rho [R^3{\stackrel{.}{R}}^2-R_{\mathrm{r}}^3{\stackrel{.}{R}}_{\mathrm{r}}^2]=\frac{4\pi p_{\text{EFF}}}{3}[R^3-R_{\mathrm{r}}^3]$$ (4)

Figure 2.

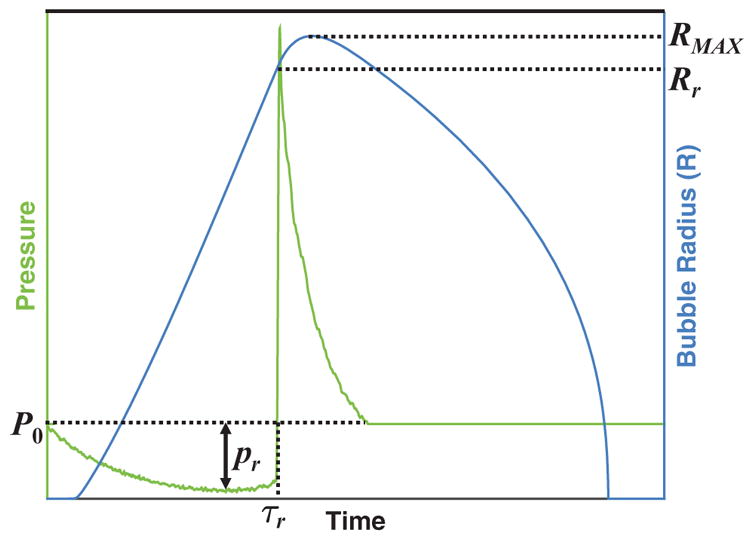
Schematic of bubble size (right hand ordinate) as a function of time when subject to a single cycle of a shocked histotripsy pulse (left hand ordinate). ‘R_r’ corresponds to the radius of the bubble at time τ_r, when the excitation pressure transitions from tensile to compressional (i.e. the shockwave front). The effective pressure for the analytic model, equation (3), is set to the magnitude of the rarefactional pressure, |p_r|, for shock scattering histotripsy. The frequency dependence inherent in the analytic model is dependent on the duration of the rarefactional phase of the acoustic pressure, τ_r, via equation (7).

In (4), R_r is the bubble radius at the end of the rarefactional phase of the acoustic pressure (figure 2). Solving (4) for Ṙ² yields:

$${\stackrel{.}{R}}^2=\frac{2p_{\text{EFF}}}{3\rho }\left[1-{\left(\frac{R_{\mathrm{r}}}{R}\right)}^3\right]+{\left(\frac{R_{\mathrm{r}}}{R}\right)}^3{\stackrel{.}{R}}_{\mathrm{r}}^2$$ (5)

When the bubble reaches its maximum size, the bubble wall velocity will be zero. Equating the right hand side of (5) to zero and taking the differential with respect to R yields the following expression for p_EFF

$$p_{\text{EFF}}=\frac{3\rho }{2}{\stackrel{.}{R}}_{\mathrm{r}}^2$$ (6)

Thus the effective pressure depends upon the bubble wall velocity as the acoustic pressure transitions from tensile to compressional. The bubble wall velocity is maximized at the end of the rarefaction pressure, as shown in figure 3, and can be estimated following Apfel (1981) as ${\stackrel{.}{R}}_{\mathrm{r}}=\sqrt{\frac{2\mid p_{\mathrm{r}}\mid }{3\rho }}$. Substituting this wall velocity into (6) yields p_EFF = |p_r| for shockwave excitation.

Figure 3.

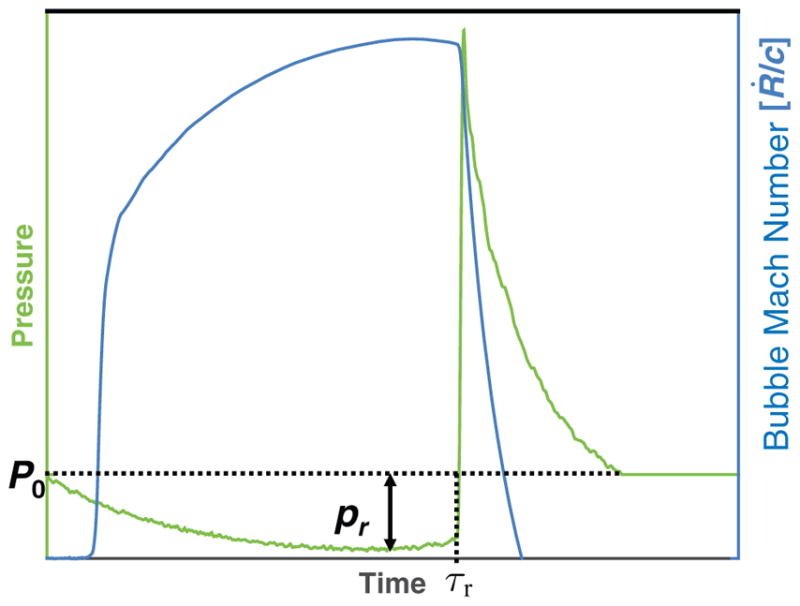
Numerically computed bubble Mach number (ratio of bubble wall velocity, Ṙ, and medium sound speed, c) displayed on the right hand ordinate as a function of time when subject to a single shockwave (left hand ordinate). Note the bubble wall velocity is maximized temporally at, τ_r, the shock front.

The tensile phase duration of the shockwave determines the period of forced bubble expansion. Holland and Apfel (1989) assumed that the tensile and compressional phases of the waveform were of equal duration, and embedded the duration of forced expansion in terms of the fundamental frequency within the variables ξ and τ of (3). For nonlinear shockwave formation, the tensile and compressional phases are not of equal duration (Canney et al 2008). To account for the extended period of forced bubble expansion properly, the frequency embedded in ξ and τ of (3) is defined as:

$$f=\frac{1}{2{\tau }_{\mathrm{r}}}$$ (7)

where τ_r is the tensile period of the shockwave, as shown in figure 3.

3. Results

3.1. Numerical computation

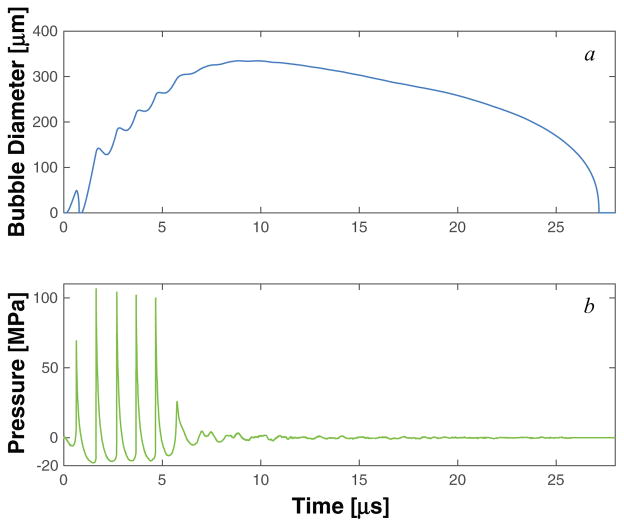
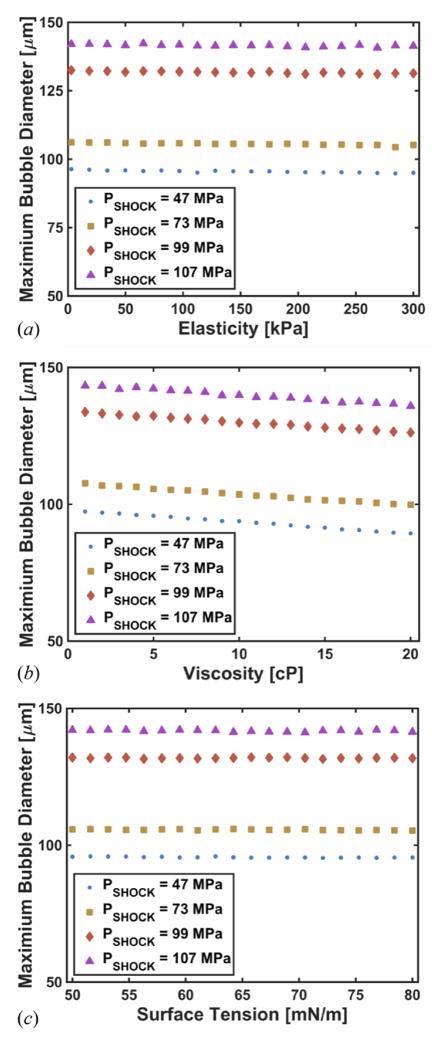
Numerical calculations were done for nuclei with diameters between 2 nm and 2 μm, although there was very little variation in the response for nuclei larger than 10 nm diameter. A representative measured histotripsy pulse and the corresponding calculated response of a 100 nm microbubble nucleus to the pulse are shown in figures 4. The bubble expands and undergoes an inertial collapse over the first cycle of the pulse. The subsequent cycle of the histotripsy pulse is fully shocked, and the bubble undergoes explosive growth. During the first fully developed shockwave of the histotripsy pulse (i.e. the second cycle of the histotripsy pulse), the maximum size was observed to be only weakly dependent on either the viscoelastic properties of the medium (figure 5) or the initial nucleus size (figure 6(a)).

Figure 4.

The response of cavitation nuclei to histotripsy excitation using the Yang/Church model, equation (1), is shown in panel a. The experimentally measured waveform used as the excitation source in the computation is shown in panel b. The initial diameter of the cavitation nuclei was 100 nm.

Figure 5.

Numerically computed maximum bubble diameter as a function of elasticity (a), viscosity (b), and surface tension (c). The diameter of the initial cavitation nuclei was 100 nm for all calculations, and the amplitude of the histotripsy pulse, P_SHOCK, is indicated in the legend.

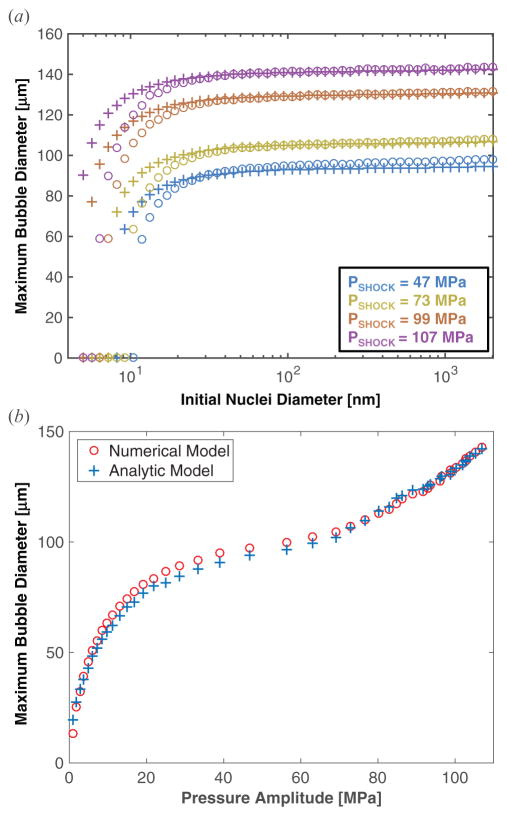
Figure 6.

(a) Maximum size of the bubble as a function of initial size for both numerical integration of the Yang/Church model (open circles) and the analytic theory (crosses). In equation (3), p_EFF = |p_r|. The shock amplitude, P_SHOCK, is indicated in the legend. (b) Maximum size of the bubble as a function of amplitude of a single cycle of the histotripsy pulse for both numerical integration of the Yang/Church model (open, red circles) and the analytic theory (blue crosses). The initial diameter of the cavitation nucleus was 100 nm. In equation (3), p_EFF = |p_r|.

The subsequent behavior of the bubble over the remainder of the histotripsy pulse depends on the pulse amplitude (figure 7). The growth rate, defined as the change in bubble size per cycle, is shown as a function of the peak rarefactional pressure of the histotripsy pulse in figure 8. For peak rarefactional pressures in excess of 14.7 MPa, the bubble dynamics are dominated by the rarefactional phase of the histotripsy pulse. The impact of the compressive shockwaves only slightly retards the bubble growth, and the bubble size increases linearly during each cycle (r² > 0.99). The bubble continues to grow after the completion of the histotripsy pulse because of the bubble wall momentum, and collapses under atmospheric pressure. For peak rarefactional pressures less than 14.7 MPa, the bubble exhibits explosive growth during the first fully developed shockwave. Sustained growth of the bubble was not observed during the remainder of the pulse (figure 7).

Figure 7.

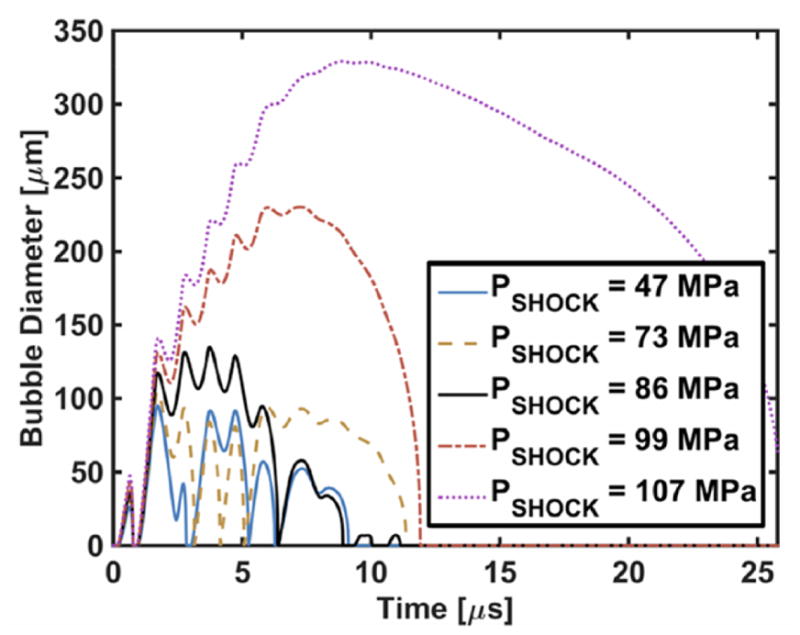
The response of a cavitation nucleus to histotripsy excitation using the Yang/Church model equation (1). The initial diameter of the cavitation nuclei was 100 nm. The shock amplitudes of the histotripsy pulse, P_SHOCK, are indicated in the legend, and have corresponding peak rarefactional pressures of 10.3, 11.7, 13.9, 16.2, and 18.3 MPa, respectively.

Figure 8.

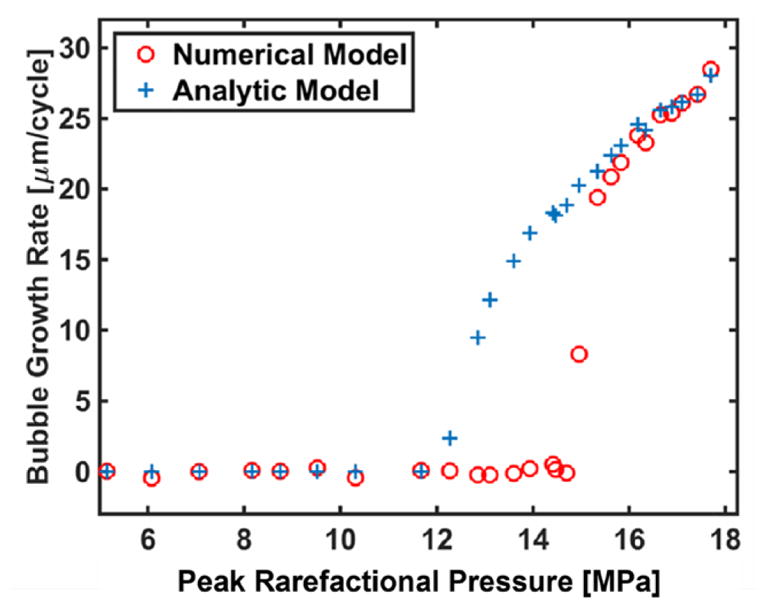
Bubble growth rate after the first fully developed shockwave of the histotripsy pulse based on numerical integration of the Yang/Church model (open circles) and the analytic predictions from equation (9) (crosses). The analytic theory predicts continual bubble growth for peak rarefactional pressures greater than 12.3 MPa, whereas the numerical model predicts continual bubble growth for peak rarefactional pressures greater than 14.7 MPa. The initial diameter of the cavitation nucleus was 100 nm. No difference in the threshold for continual bubble was observed for bubble diameters in the range of 10 nm to 2000 nm with the numerical computation.

3.2. Comparison of numerical model and analytic theory

3.2.1. Shock scattering histotripsy

The maximum size of the resulting bubble as a function of the amplitude of the histotripsy pulse is shown in figure 6(b) for both the analytic theory, (3), and the numerical model. The excitation pressure for the numerical model was the second cycle of the measured histotripsy pulse. The effective pressure was set to the magnitude of the rarefactional pressure in the analytic calculation. Excellent agreement is seen between the analytic theory and the numerical model for fully developed shockwaves (i.e. pressure amplitudes greater than 72 MPa). This agreement holds for initial cavitation nuclei larger than 10–20 nm, as seen in figure 6(a). The analytic model overestimates the maximum size for cavitation nuclei smaller than 10–20 nm, depending on shockwave amplitude. When the shockwave is not fully developed, the analytic model underestimates the maximum size of the bubble by less than 5% (figure 6(b)).

Beyond the first fully developed shockwave, the growth rate of the bubble depends on the amplitude of the histotripsy pulse, as shown in figure 7. For bubbles much larger than their initial size, the Yang/Church model, (1), reduces to:

$$R\ddot{R}+\frac{3}{2}{\stackrel{.}{R}}^2=-\frac{p_{\text{AC}}(t)}{\rho }$$ (8)

The bubble size increases linearly during each cycle because the time-averaged bubble wall acceleration is zero. Setting R̈ = 0 in (8), the time-averaged bubble growth rate can be approximated as:

$$\langle \stackrel{.}{R}\rangle =\sqrt{\frac{-2\langle p_{\text{AC}}(t)\rangle }{3\rho }}$$ (9)

where the angled brackets indicate a time-averaged quantity. The predicted bubble growth rate using (9) is shown along with the growth rate predicted by the full numerical computation, (1), in figure 8. The threshold for continual bubble growth during the histotripsy pulse occurs when the time-averaged pressure is negative in (9). As shown in figure 8, (9) underestimates the threshold for continual bubble growth by 16.3% compared to the numerical model (threshold peak rarefactional pressure of 12.3 MPa for (9) versus 14.7 MPa for the numerical model). Above 14.7 MPa peak rarefactional pressure, the bubble growth rate predicted by (9) is within 10% of the numerical computation.

3.2.2. Microtripsy

Recent studies by Vlaisavljevich et al (2015b) have determined the dependence of the maximum size of bubble growth for microtripsy insonation as a function of frequency. These measurements are shown along with the predictions of the analytic model in figure 9. The effective pressure for the analytic model was set to P₀ (0.1 MPa). The microbubble nuclei diameter was set to 4 nm, similar to that predicted by Vlaisavljevich et al (2015b). Good agreement is seen between the experimental measurements and the analytic theory at 345 kHz and 500 kHz. The analytic theory overestimates the maximum size for frequencies by 27% (30 μm) at 1.5 MHz, and 15% (15 μm) at 3 MHz.

Figure 9.

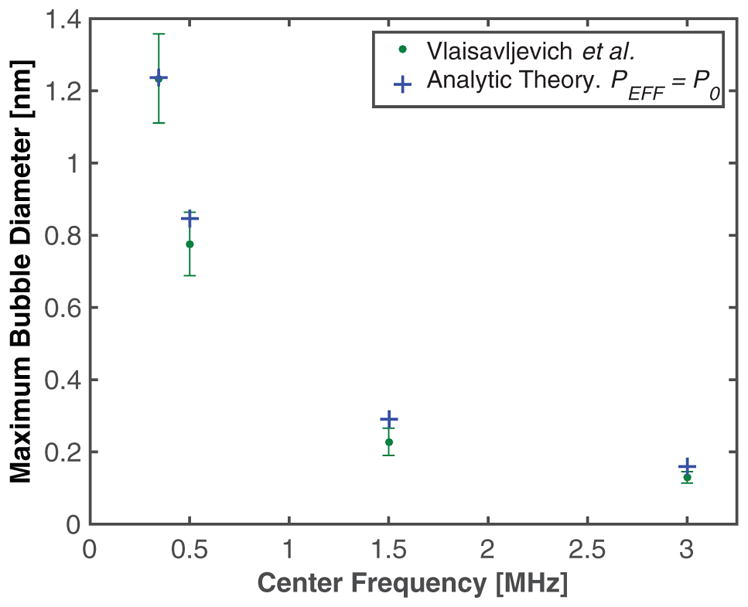
Maximum size of cavitation nuclei excited by microtripsy pulse as a function of frequency. The green dots are measured values, (table 2E = 1.2 kPa, from Vlaisavljevich et al (2015b)), and the blue crosses are the predictions of the analytic model. Because shockwave formation is minimized in microtripsy pulses, In p_EFF = |P₀|. (or ‘Blake Brake’) in equation (3). The initial cavitation nuclei diameter was 4 nm.

3.3. A metric to predict the maximum diameter of bubble expansion

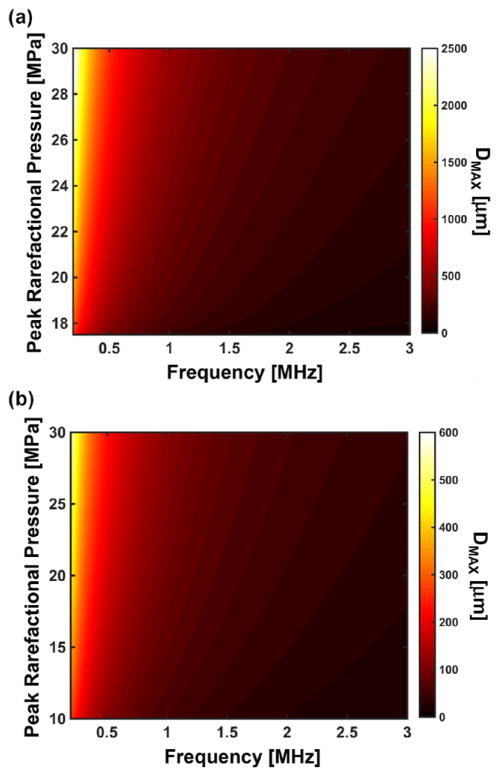
The bubble maximum diameter is independent of initial size for nuclei larger than 20 nm for shock scattering histotripsy (figure 6(a)), and for nuclei larger than 5 nm for microtripsy (figure 10). Thus, evaluation of the analytic model at 5 nm initial diameter or 20 nm initial diameter would provide an upper limit to the predicted maximum bubble diameter for microtripsy and shock scattering histotripsy, respectively. At these limiting initial diameters, the analytic model appears to be well behaved as a function of pressure and frequency (figure 11). Using the curve fitting tool ‘cftool’ in MATLAB^®, the maximum bubble diameter was fit in the least squares sense to a three-parameter model of the form:

$$D_{\text{MAX}}=a_1{\left|p_{\mathrm{r}}\right|}^{a_2}{f}^{a_3}$$ (10)

where D_MAX is the maximum bubble diameter in micrometers, |p_r| is the magnitude of the peak rarefactional pressure in MPa, f is the fundamental frequency of the histotripsy pulse in MHz, and a₁, a₂, and a₃ are fitting parameters. The values for the fitting parameters, along with the coefficient of determination, are shown in table 1. For both shock scattering histotripsy and microtripsy pulses, the maximum diameter is inversely proportional to the frequency (a₃ = −1 for both types) and directly proportional to the rarefactional pressure (a₂ = 0.56 for shock scattering histotripsy and a₂ = 1.17 for microtripsy).

Figure 10.

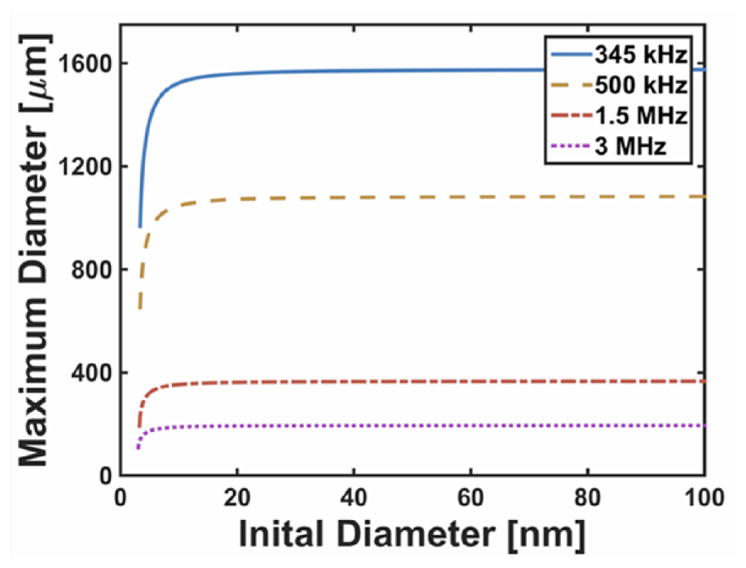
Analytic prediction of the maximum bubble size of cavitation nuclei as a function of the initial size. The effective pressure was set to P₀ in equation (3), and the insonation conditions are as reported in Vlaisavljevich et al (2015b). Note that the Blake threshold was not exceeded for nuclei smaller than approximately 3 nm in diameter, resulting in complex results in the analytic theory. Physically, this means that bubble growth is not possible for such small nuclei at these insonation conditions.

Figure 11.

Predicted maximum bubble diameter (D_MAX) for a 5 nm nucleus exposed to a single cycle microtripsy pulse (a) and a 20 nm nucleus exposed to a single cycle shock scattering histotripsy pulse (b). For each insonation type, the maximum bubble size is independent of the initial nuclei size for nuclei larger than the limiting size (5 nm for microtripsy and 20 nm for shock scattering histotripsy). Note that growth of the nuclei will only occur for pressures greater than the Blake threshold (Holland and Apfel 1989). Note also the peak rarefactional pressure range is difference for nuclei exposed to microtripsy pulses (a) and histotripsy pulses (b).

Table 1.

Coefficients of the three-parameter fit in equation (8), for the frequency and pressure dependence of the maximum size for shock scattering histotripsy and microtripsy. Goodness-of-fit parameters, coefficient of determination (r²) and the root mean square error (RSME), of the fit are also shown.

Histotripsy type	a1	a2	a3	r2	RMSE (μm)
Shock scattering	18.18	0.56	−1.00	0.999	0.62
Microtripsy	9.89	1.17	−1.00	0.998	23.90

Microtripsy nucleates individual bubbles with little to no cloud formation (Maxwell et al 2013), and (10) can be directly applied to predict the maximum size of the microtripsy ablation zone. Additional steps must be taken to predict the treatment zone for shock scattering histotripsy.

3.4. Prediction of the axial extent of the microbubble cloud

Shock scattering histotripsy requires the formation of a microbubble cloud for tissue ablation (Xu et al 2005). The precipitating event of the creation of a microbubble cloud is the continued growth of the nucleated bubble which scatters a portion of the incident shockwave geometrically (Maxwell et al 2011). The amplitude of the mth harmonic, p_m, in a shockwave is given by (Hamilton and Blackstock 1998):

$$p_m=\frac{P_{\text{SHOCK}}}{m\pi }$$ (11)

where P_SHOCK is the compressional amplitude of the shockwave. As the bubble grows, more harmonics will be scattered, and constructive interference with the subsequent rarefactional phase in the histotripsy pulse will be increased. The transient interference zone in the scattered field will support nucleation of a bubble cloud if the intrinsic cavitation threshold, P_INTRIN is exceeded. Vlaisavljevich et al (2015a) have measured this threshold experimentally for fundamental frequencies between 345 kHz and 3 MHz, and found the intrinsic pressure threshold for spontaneous nucleation is 26–28 MPa over this frequency range. The lowest harmonic of the incident shock, m_min, which contributes to constructive interference at the intrinsic cavitation threshold for soft tissue, can be computed as:

$$m_{min}=\text{floor}\left(\frac{P_{\text{SHOCK}}}{\mathrm{\Delta }{P}_{\text{INTRIN}}\pi }\right)+1$$ (12)

where ΔP_INTRIN = P_INTRIN − |p_r|. The bubble radius, R_SCAT, required to scatter harmonic m_min geometrically is (Anderson 1950):

$$R_{\text{SCAT}}=\frac{c}{2\pi m_{min}{f}_0}$$ (13)

where f₀ is the fundamental frequency of the histotripsy pulse. The size of the nucleated bubble after n cycles, R_n, can be computed using R_MAX via (3) or (10) and the bubble growth rate via (9):

$$R_n=R_{\text{MAX}}+\langle \stackrel{.}{R}\rangle (n-1)$$ (14)

Solving (14) for n and substituting R_SCAT into R_n, the critical cycle number, n_crit, required for the bubble to grow to the geometrical scattering limit is:

$$n_{\text{crit}}=\frac{R_{\text{SCAT}}-R_{\text{MAX}}}{\langle \stackrel{.}{R}\rangle }+1$$ (15)

Once the critical number of cycles has been reached, the axial growth rate of the cloud is approximately λ/3 per subsequent cycle (Maxwell et al 2011), where λ is the wavelength of the fundamental frequency of the histotripsy pulse. The predicted axial extent of the microbubble cloud is:

$$L_{\text{AX}}=(n_{\text{pulse}}-n_{\text{crit}})\lambda /3$$ (16)

where n_pulse is the number of cycles in the incident histotripsy pulse. Note that if n_crit exceeds n_pulse, L_AX is negative. Physically this means that the pulse duration was shorter than the time required to initiate geometric scattering, and a cloud was unable to form. In the absence of microbubble cloud formation (i.e. n_pulse is less than n_crit), the damage is restricted to the size of the nucleated bubble after at the completion of the histotripsy pulse:

$$L_{\text{AX}}=2[R_{\text{MAX}}+\stackrel{.}{R}(n_{\text{pulse}}-1)]$$ (17)

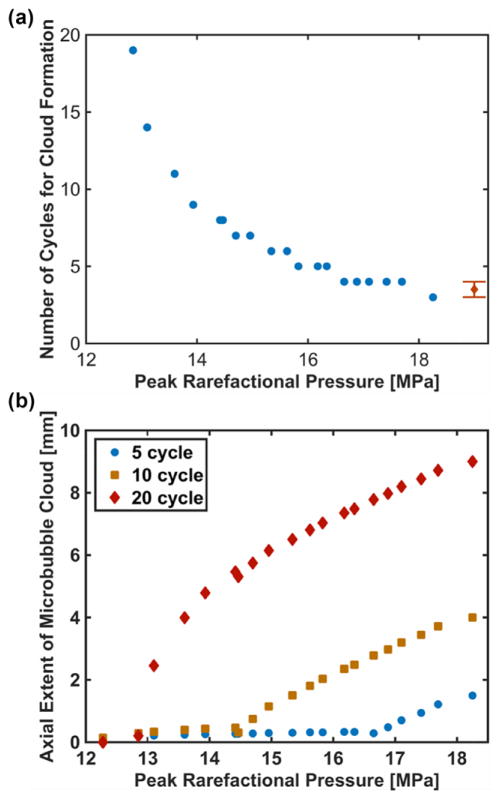
As an example, the predicted critical cycle number and axial extent of the microbubble cloud for waveforms used in this study is shown in figure 12. Using high speed videography, Maxwell et al (2011) found 3–4 cycles were required to initiate cloud formation for a 1 MHz histotripsy pulse with compressional and rarefactional pressures of 85 and 19 MPa, respectively. This number of cycles appears consistent with n_crit using (15) shown in figure 12(a).

Figure 12.

(a) Predicted critical number of cycles prior to microbubble cloud formation determined using (15). Maxwell et al (2011) observed that between 3–4 cycles were required to initiate microbubble cloud formation at 19 MPa peak rarefactional pressure (diamond). (b) Predicted axial extent of microbubble cloud using equation (16) when the number of cycles required for cloud formation was less than the pulse duration, and equation (17) when the number of cycles required for cloud formation was greater than the pulse duration. The pulse duration is indicated in the legend. A histotripsy pulse with a fundamental frequency of 1 MHz was employed for these computations.

4. Discussion

4.1. Validity of numerical model

In this study, both analytic and numerical models were employed to investigate the growth of cavitation nuclei for ‘cavitation-based’ histotripsy excitations (Maxwell et al 2012). The use of experimentally measured excitation waveforms in the numerical computations generated several features consistent with experimental observation. Using high speed videography, Maxwell et al (2011) observed that bubbles undergo a rapid expansion, followed by inertial collapse during the first cycle of a shocked histotripsy pulse. The bubble expanded gradually over the remainder of the pulse. The maximum diameter of the bubble after the first few cycles of the pulse was 80–180 μm. For similar histotripsy exposure conditions, this behavior is reflected in numerical integration of the Yang/Church model shown in figure 4. The rarefaction amplitude of the first cycle of the pulse is smaller than the subsequent cycles due to the finite damping of the transducer. Consequently, bubble growth is stunted during the first cycle. After the first cycle, the tension in the shocked histotripsy pulse induces a ‘Blake-like’ growth of the bubble for peak rarefactional pressures in excess of 14.7 MPa (figures 7 and 8). The growth is not sufficiently retarded by the shocks to induce collapse before the subsequent tensile pressure phase. This expansion-only behavior of the acoustically activated nuclei suggest that bubble expansion, and not collapse, may be the dominant mechanism of the therapy. The expansion only behavior also suggests that the scattering of shockwaves is due to passive reflection of the incident shock from the bubble, and not a diverging pressure wave generated by an inertial collapse. The numerically computed maximum diameter after three cycles of the histotripsy pulse is 183 μm, similar to that measured by Maxwell et al.

The maximum size of the bubble is weakly dependent on the initial size for nuclei larger than 10–20 nm, as seen in figure 6(a). Other numerical studies have also seen a weak dependence of the maximum size of bubbles on the initial size with shockwave excitation (Church 1989, Iloreta et al 2008). The weak dependence of the maximum size on the initial size also suggests the insonation frequency only weakly influences the cavitation dynamics (Leighton 1994) for histotripsy excitations. Vlaisavljevich et al (2015a) found the threshold for microbubble cloud formation was 26 to 28 MPa between 345 kHz and 3 MHz. However, a subsequent study found that the maximum size of the bubble generated by microtripsy pulses was inversely proportional to frequency (Vlaisavljevich et al 2015b), as indicated in figure 9.

4.2. Analytic prediction of maximum bubble size

The analytic theory appears consistent with numerical calculations of shock scattering histotripsy insonations after the shockwave is fully developed (figure 6). There was a disparity between the analytic theory and numerical calculations for nuclei smaller than 10–20 nm. Surface tension is the dominant mechanism retarding the growth of such small nuclei (Holland and Apfel 1989), and dictates the Blake threshold (Leighton 1994). In some instances the rarefactional pressure did not exceed the Blake threshold, and the analytic theory predicted complex maximum bubble sizes. The physical interpretation is that such small nuclei would not grow, and would not contribute to the therapeutic action of histotripsy. Good agreement was seen between the analytic model and numerical computations for nuclei larger than 20 nm diameter. The maximum diameter continued to depend weakly on the initial nucleus size, which may be of interest for boiling histotripsy applications (Khokhlova et al 2011). At acoustic pressure amplitudes below a fully developed shockwave (<72 MPa peak positive pressure), the assumptions for the effective pressure for shockwave excitation are no longer valid (figure 6(b)). Despite this erroneous assumption, the analytic theory and numerical model still agree within 5% for nuclei larger than 10–20 nm.

It should be noted that Iloreta et al (2007) also developed an analytic expression to predict the maximum size of microbubble nuclei from shockwave excitation. The expression of Iloreta et al was derived by empirically fitting the results of numerical calculations for bubbles exposed to shockwave lithotripsy pulses, and is dependent on both the peak positive and peak rarefactional pressures of the shockwave. The model developed in this study only requires knowledge of the peak rarefactional pressure, which can be directly measured in castor oils (Maxwell et al 2013), or via linear summation of element by element calibrations (Lin et al 2014a). The peak positive pressure, however, cannot be measured directly for therapeutic insonation conditions, and must be estimated with numerical models (Canney et al 2008).

For microtripsy insonation, the analytic theory appears to overestimate the bubble size for microtripsy frequencies greater than 1 MHz (figure 9). Large, potentially nonlinear compressional components are present for these waveforms (figure 1 of Vlaisavljevich et al (2015a)). In this case, the ambient pressure slightly underestimates the effective pressure in (3) and overestimates the maximum bubble diameter by 27%. The cavitation nucleus diameter was set to 4 nm in figure 9, similar to that assumed by Vlaisavljevich et al. The maximum size is strongly dependent on the initial size for nuclei smaller than 5 nm (see figure 10), and independent of the initial size for nuclei larger than 5 nm. Predictions of the analytic model for the maximum size became complex for nuclei diameters smaller than 3 nm. The maximum tension for the measured waveforms, 18.3 MPa, is not sufficient to exceed the Blake threshold, and no growth would occur for nuclei less than 3 nm in diameter. If nuclei between 3 and 5 nm diameter were present in the medium, evaluation of the analytic model at 5 nm initial diameter would provide an upper limit to the predicted maximum bubble size.

Some care must be taken in applying (3) based on the insonation type. For a microtripsy pulse, where little to no compressional phase is present, p_EFF = P₀. Because of the strong shockwave present in shock scattering histotripsy, p_EFF = |p_r|. Additionally, the elongation of the tensile portion of the nonlinear shockwave must be accounted for in the frequency dependence embedded in ξ and τ of (3).

4.3. Continual bubble growth during shockwave excitation

For shock scattering histotripsy, the bubble experienced continual growth over the duration of the histotripsy pulse for peak rarefactional pressures in excess of 14.7 MPa (figure 8). The onset of continual bubble growth appears to be a necessary, but not sufficient, condition for shockwave scattering (figure 12). Thus, the treatment mechanism of shocked histotripsy pulses appears to be due to two separate mechanisms. Below the threshold for continual bubble growth, individual bubbles grow to a fixed size but are not sufficiently large to initiate geometric scattering of the shockwave. Above the threshold for unbounded growth, there is an increased likelihood for microbubble cloud formation due to shockwave scattering depending on the maximum size of the bubble.

The bubble growth rate can be estimated using (9), assuming the wall velocity is constant (i.e. R̈ = 0). The threshold predicted by (9) for unbounded growth occurs when the time-averaged excitation waveform is less than 0, which underestimates the threshold by ~16.3% compared to the numerical model (figure 8). Although the discrepancy between the analytic model and numerical model appears large, a difference of 16.3% is within the accuracy of most hydrophones used to calibrate focused ultrasound sources (Harris 2005). At peak rarefactional pressures between the threshold predicted by (9) (12.3 MPa) and the threshold predicted by the numerical model (14.7 MPa), the motion of the bubble wall is highly nonlinear and cannot be treated analytically. Thus, histotripsy pulses intended to use shockwave scattering to initiate lesion formation should operate at pressures at least a factor of 16.3% greater than the threshold predicted by (9).

4.4. Metrics to predict the extent of bubble activity

A pressure and frequency dependent metric was developed to predict the upper limit for the maximum bubble diameter for shock scattering histotripsy and microtripsy (see (10)). The utility of predicting the maximum bubble size depends on the type of histotripsy insonation. Microtripsy nucleates individual bubbles with little to no cloud formation (Maxwell et al 2013). The spatial extent of the treatment zone directly correlates with the location of bubble activity (Lin et al 2014a). The cavitation dynamics of are dominated by bubble growth driven by the rarefactional phase of the histotripsy pulse. Thus, (10) or (3) can be directly applied to predict the maximum size of the ablation zone.

For shock scattering histotripsy, (10) predicts the size of the bubble after the first cycle of the pulse. Equation (16) can be employed to estimate the axial extent of the microbubble cloud, and requires calculation of the bubble growth rate via during the histotripsy pulse. Equation (9) can be used to calculate the bubble growth rate, but underestimates the threshold for bubble growth during the histotripsy pulse. Hence, the axial extent of the microbubble cloud will be overestimated for pressures near the threshold for continual bubble growth predicted by (9), and will depend on the pulse duration. Pulses with peak rarefactional pressures less than 14.7 MPa require between 6 and 19 cycles for the bubble to grow large enough to scatter the incident pulse geometrically (figure 12(a)). Equation (16) will overestimate the axial extent of the microbubble cloud for pulse durations longer than 6 cycles close to the threshold for continual bubble growth. Pulses shorter than 6 cycles require large bubble growth rates to initiate geometric scattering size within the duration of the pulse. Thus, pressure amplitudes well in excess of the threshold for bubble growth are required, and (16) is sufficient to estimate the axial extent of the microbubble cloud (figure 12(b)).

The entire waveform shape is required to predict the growth rate of the incidental bubble during shockwave excitation. The FDA requires characterization of the focal zone for therapeutic ultrasound systems (Harris 2006). Numerical modeling can accurately predict the field at the transducer focus under operating conditions where hydrophone damage would be inevitable (Canney et al 2008, Maruvada et al 2015). Application of (16) is limited to prediction of the microbubble cloud (and therefore lesion) along the axial dimension of the histotripsy transducer. The lateral extent of the cloud has been shown to be confined to 1–2 mm extent, and does not vary appreciably with pulse duration (Maxwell et al 2011). In addition, the model proposed here needs careful validation against the dimensions of tissue ablation in pre-clinical studies.

4.5. Limitations of the study

There are several aspects of this study that limit the generalizability of these findings. The amplitude of the measured shockwave maybe underestimated due to spatial averaging of the fiber and the bandwidth of the system (Canney et al 2008). Furthermore, the size of the bubble is assumed to be much smaller than the wavelength of the excitation pressure for the Yang/Church model, which is not the case for shockwave excitation. Nevertheless, the numerical computations appear to agree both qualitatively and quantitatively with experimental observations. It should be noted the formation of the microbubble cloud would shield the histotripsy pulse from bubbles distal to the source. This shielding would affect the accuracy of the numerical calculation after the formation of the microbubble cloud in figures 4 and 7. The analytic model takes into account surface tension, viscosity, and the inertial of the fluid (Holland and Apfel 1989). The influence of elasticity is neglected, which appears to significantly reduce the size of the bubble for Young’s moduli larger than 20 kPa (Vlaisavljevich et al 2015b).

5. Conclusions

Mechanical ablation from cavitation-based histotripsy can be initiated via shock scattering or microtripsy. In either case, the spatial extent of the cavitation is key to estimating the spatial extent of the treatment zone. While bubble oscillations can be calculated numerically, the expansion only behavior observed for shock scattering histotripsy excitation suggests that the maximum size of the bubble is the dominant feature of interest. An extension of the analytic model developed by Holland and Apfel was found to be consistent with the predictions of the numerical model for shockwave excitations, and with experimental observations of microtripsy. The implementation and applicability of the analytic model depends on the insonation type. Nevertheless, the analytic models developed in this manuscript allow for a straightforward calculation of the maximum extent of microbubble activity during histotripsy pulses.