Bayes and the Law

Abstract

Although the last forty years has seen considerable growth in the use of statistics in legal proceedings, it is primarily classical statistical methods rather than Bayesian methods that have been used. Yet the Bayesian approach avoids many of the problems of classical statistics and is also well suited to a broader range of problems. This paper reviews the potential and actual use of Bayes in the law and explains the main reasons for its lack of impact on legal practice. These include misconceptions by the legal community about Bayes’ theorem, over-reliance on the use of the likelihood ratio and the lack of adoption of modern computational methods. We argue that Bayesian Networks (BNs), which automatically produce the necessary Bayesian calculations, provide an opportunity to address most concerns about using Bayes in the law.

1. Introduction

The use of statistics in legal proceedings (both criminal and civil) has a long, but not terribly well distinguished, history that has been very well documented in (Finkelstein, 2009; Gastwirth, 2000; Kadane, 2008; Koehler, 1992; Vosk and Emery, 2014). The earliest reported case of a detailed statistical analysis being presented as evidence was in the Howland case of 1867 that is discussed in detail in (Meier and Zabell, 1980). In this case Benjamin Peirce attempted to show that a contested signature on a will had been traced from the genuine signature, by arguing that their agreement in all 30 downstrokes was extremely improbable under a binomial model. Meier and Zabell highlight the use and abuse of the “product rule” in Peirce’s evidence for multiplying probabilities of independent events. In any case, the court found a technical excuse not to use the evidence.

The historical reticence to accept statistical analysis as valid evidence is, sadly, not without good reason. When, in 1894, a statistical analysis was used in the Dreyfus case it turned out to be fundamentally flawed (Kaye, 2007). Not until 1968 was there another well documented case, (People v. Collins, 438 P. 2d 33 (68 Cal. 2d 319 1968), 1968) in which statistical analysis played a key role. In that case another flawed statistical argument further set back the cause of statistics in court. The Collins case was characterised by two errors:

• 1)It underestimated the probability that some evidence would be observed if the defendants were innocent by failing to consider dependence between components of the evidence; and
• 2)It implied that the low probability from the calculation in 1) was synonymous with innocence (the so-called ‘prosecutors’ fallacy).

Since then the same errors (either in combination or individually) have occurred in well reported cases such as R v Sally Clark (Forrest, 2003; Hill, 2005), R v Barry George (Fenton et al., 2013a), Lucia de Berk (Meester et al., 2007). Although original ‘bad statistics’ used in each case (presented by forensic or medical expert witnesses without statistical training) was exposed through ‘good statistics’ on appeal, it is the ‘bad statistics’ which leaves an indelible stain. Yet, the role of legal professionals (who allow expert witnesses to commit the same well known statistical errors repeatedly) is rarely questioned.

Hence, although the last 40 years has seen considerable growth in the use of statistics in legal proceedings, its use in the courtroom has been mostly restricted to a small class of cases where classical statistical methods of hypothesis testing using p-values and confidence intervals are used for probabilistic inference. Yet, even this type of statistical reasoning has severe limitations as discussed extensively in (Royal Statistical Society, 2015; Ziliak and McCloskey, 2008), including specifically in the context of legal and forensic evidence (Finkelstein, 2009; Vosk and Emery, 2014). In particular:

• The use of p-values can also lead to the prosecutor’s fallacy since a p-value (which says something about the probability of observing the evidence given a hypothesis) is often wrongly interpreted as being the same as the probability of the hypothesis given the evidence (Gastwirth, 2000).

• Confidence intervals are almost invariably misinterpreted since their proper definition is both complex and counter-intuitive (indeed it is not properly understood even by many trained statisticians) (Fenton and Neil, 2012).

The poor experience – and difficulties in interpretation - with classical statistics means that there is also strong resistance to any alternative approaches. In particular, this resistance extends to the Bayesian approach, despite the fact that the Bayesian approach is especially well suited for a broad range of legal reasoning (Fienberg and Finkelstein, 1996).

Although the natural resistance within the legal profession to a new statistical approach is one reason why Bayes has, to date, made only minimal impact, it is certainly not the only reason. Many previous papers have discussed the social, legal and logical impediments to the use of Bayes in legal proceedings (Faigman and Baglioni, 1988; Fienberg, 2011; Tillers and Green, 1988; Tribe, 1971) and in more general policy decision making (Fienberg and Finkelstein, 1996). However, we contend that there is another rarely articulated but now dominant reason for its continued limited use: it is because most examples of the Bayesian approach have oversimplified the underlying legal arguments being modelled in order to ensure the computations can be carried out manually. While such an approach may have been necessary 20 years ago it no longer is with the advent of easy-to-use and efficient Bayesian network algorithms and tools (Fenton and Neil, 2012) This continuing over-simplification is an unnecessary and debilitating burden.

The paper is structured as follows: Section 2 describes the basics of Bayes (and Bayesian Networks) for legal reasoning, covering the core notion of the likelihood ratio. Section 3 reviews the actual use of Bayes in the law. Section 4 describes why, in our view, Bayes has made such a minimal impact, while Section 5 explains what can be done to ensure it gets the exploitation we feel it deserves. We draw throughout primarily on English language sources and most cases cited are in English speaking countries (normally with a jury system). Most are from the UK and USA. The paper focuses on the use of Bayes and hence does not attempt to describe the broader use of statistics in the law which is well covered by the books (Aitken and Taroni, 2004; Fienberg, E, 1989; Zeisel and Kaye, 1997).

2. Basics of Bayes for legal reasoning

We start by introducing some terminology and assumptions that we will use throughout:

• A hypothesis is a statement (typically Boolean) whose truth value we seek to determine, but is generally unknown - and which may never be known with certainty. Examples include:

  • ○
    “Defendant is innocent of the crime charged” (this is an example of an offense level hypothesis also called the ultimate hypothesis, since in many criminal cases it is ultimately the only hypothesis we are really interested in)
  • ○
    “Defendant was the source of DNA found at the crime scene” (this is an example of what is often referred to as a source level hypothesis (Cook et al., 1998a))

• The alternative hypothesis is a statement which is the negation of a hypothesis.

• A piece of evidence is a statement that, if true, lends support to one or more hypotheses.

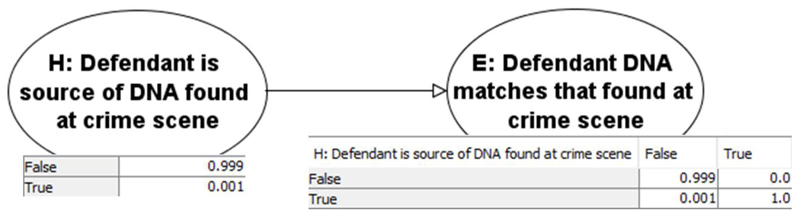
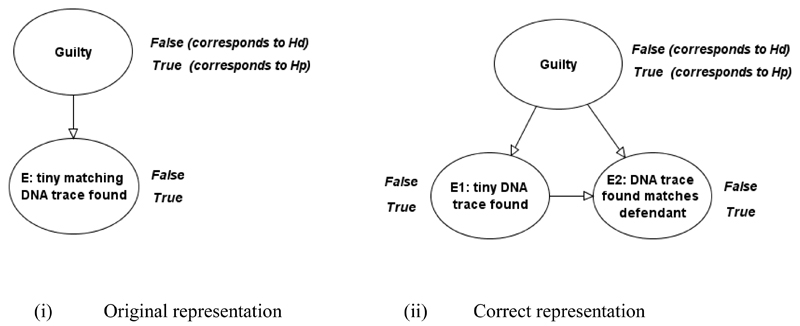
The relationship between a hypothesis H and a piece of evidence E can be represented graphically as in the example in Figure 1 where we assume that:

• The evidence E is a DNA trace found at the scene of the crime (for simplicity we assume the crime was committed on an island with 10,000 people who therefore represent the entire set of possible suspects)

• The defendant was arrested and some of his DNA was sampled and analysed

Figure 1. Causal view of evidence, with prior probabilities shown in tables. This is a very simple example of a Bayesian Network (BN).

The direction of the causal structure makes sense here because H being true (resp. false) can cause E to be true (resp. false), while E cannot ‘cause’ H. However, inference can go in both directions. If we observe E to be true (resp. false) then our belief in H being true (resp. false) increases. It is this latter type of inference that is central to all legal reasoning since, informally, lawyers and jurors normally use the following widely accepted procedure for reasoning about evidence:

• Start with some (unconditional) prior assumption about the ultimate hypothesis H (for example, the ‘innocent until proven guilty’ assumption equates to a belief that “the defendant is no more likely to be guilty than any other member of the population”).

• Update our prior belief about H once we observe evidence E. This updating takes account of the likelihood of the evidence.

This informal reasoning is a perfect match for Bayesian inference where the prior assumption about H and the likelihood of the evidence E are captured formally by the probability tables shown in Figure 1. Specifically, these are the tables for the prior probability of H, written P(H), and the conditional probability of E given H, which we write as P(E | H). Bayes’ theorem provides the formula for updating our prior belief about H in the light of observing E to arrive at a posterior belief about H which we write as P(H | E). In other words Bayes calculates P(H | E) in terms of P(H) and P(E | H). Specifically:

$$P(H|E)=\frac{P(E|H)P(H)}{P(E)}=\frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|not\hspace{0.17em}H)P(not\hspace{0.17em}H)}$$

The first table (the probability table for H) captures our knowledge that the defendant is one of 10,000 people who could have been the source of the DNA. The second table (the probability table for E | H) captures the assumptions that:

• The probability of correctly matching a DNA trace is one (so there is no chance of a false negative DNA match). This probability P(E | H) is called the prosecution likelihood for the evidence E.

• The probability of a match in a person who did not leave their DNA at the scene (the ‘random DNA match probability’) is 1 in 1,000. This probability P(E | not H) is called the defence likelihood for the evidence E.

With these assumptions, it follows from Bayes’ theorem that, in our example, the posterior belief in H after observing the evidence E being true is about 9%, i.e. our belief in the defendant being the source of the DNA at the crime scene moves from a prior of 1 in a 10,000 to a posterior of 9%. Alternatively, our belief in the defendant not being the source of the DNA moves from a prior of 99.99% to a posterior of 91%.

Note that the posterior probability of the defendant not being the source of the DNA is very different from the random match probability of 1 in 1,000. The incorrect assumption that the two probabilities P(not H | E) and P(E | not H) are the same characterises what is known as the prosecutor’s fallacy (or the error of the transposed conditional). A prosecutor might state, for example, that “the probability the defendant was not the source of this evidence is one in a thousand”, when actually it is 91%. This simple fallacy of probabilistic reasoning has affected numerous cases (Balding and Donnelly, 1994; Fenton and Neil, 2011), but can always be avoided by a basic understanding of Bayes’ Theorem. A closely related, but less common, error of probabilistic reasoning is the defendant’s fallacy, whereby the defence argues that since P(not H | E) is still low after taking into account the prior and the evidence, the evidence should be ignored.

Unfortunately, people without statistical training – and this includes most highly respected legal professionals – find Bayes’ theorem both difficult to understand and counter-intuitive (Casscells and Graboys, 1978; Cosmides and Tooby, 1996). Legal professionals are also concerned that the use of Bayes requires us to assign prior probabilities. In fact, an equivalent formulation of Bayes (called the ‘odds’ version of Bayes) enables us to interpret the value of evidence E without ever having to consider the prior probability of H. Specifically, this version of Bayes’ tells us:

• the posterior odds of H are the prior odds of H times the likelihood ratio

where the Likelihood Ratio (LR) is simply the prosecution likelihood of E divided by the defence likelihood of E, i.e.

• $\frac{P(E|H)}{P(E|\text{not}\hspace{0.17em}H)}$

In the example in Figure 1 the prosecution likelihood for the DNA match evidence is 1, while the defence likelihood is 1/1,000. So the LR is 1,000. This means that, whatever the prior odds were in favour of the prosecution hypothesis, the posterior odds must increase by a factor of 1,000 as a result of seeing the evidence. In general, if the LR is bigger than 1 then the evidence results in an increased posterior probability of H (with higher values leading to the posterior probability getting closer to 1), while if it is less than 1 it results in a decreased posterior probability of H (and the closer it gets to zero the closer the posterior probability gets to zero). If the LR is equal to 1 then E offers no value since it leaves the posterior probability is unchanged.

The LR is therefore an important and meaningful measure of the probative value of evidence. In our example the fact that the DNA match evidence had a LR of 1000 meant the evidence was highly probative in favour of the prosecution. But as impressive as that sounds, whether or not it is sufficient to convince you of which hypothesis is true still depends entirely on the prior P(H). If P(H) is, say 0.5 (so the prior odds are evens 1:1), then a LR of 1000 results in posterior odds of 1000 to 1 in favour of H. That may be sufficient to convince a jury that H is true. But if P(H) is very low - as in our example (9999 to 1 against) - then the same LR of 1000 results in posterior odds that still strongly favour the defence hypothesis by 10 to 1.

Notwithstanding this observation (and other problems with the LR that we discuss in Section 4) the fact that it does determine the probative value of evidence and can be calculated without reference to the prior probability of H, has meant that it has become a potentially powerful application of Bayesian reasoning in the law. Indeed, the CAI (Case Assessment and Interpretation) method (Cook et al., 1998b; Jackson et al., 2013) has the LR at its core. By forcing expert witnesses to consider both the prosecution and defence likelihood of their evidence – instead of just one or the other – it also avoids most common cases of the prosecutor’s fallacy.

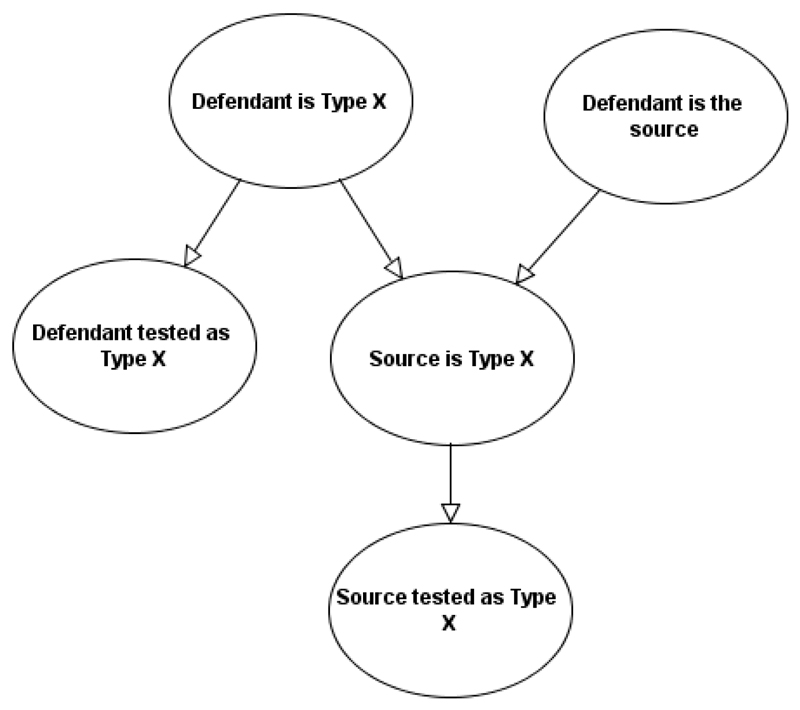
While Bayes’ Theorem provides a natural match to intuitive legal reasoning in the case of a single hypothesis H and a single piece of evidence E, practical legal arguments normally involve multiple hypotheses and pieces of evidence with complex causal dependencies. For example, even the simplest case of DNA evidence strictly speaking involves three unknown hypotheses and two pieces of evidence with the causal links shown in Figure 2 (Dawid and Mortera, 1998; Fenton et al., 2014) once we take account of the possibility of different types of DNA collection and testing errors (Koehler, 1993a; Thompson et al., 2003).

Figure 2. Bayesian network for DNA match evidence. Each node has states true or false.

Moreover, there are further crucial hypotheses not shown in Figure 2 (a full version of the model is provided in the supplementary material (Fenton et al., 2015)) such as: “Defendant was at the scene of the crime” and the ultimate hypothesis “Defendant committed the crime”. These are only omitted here because, whereas the law might accept a statistical or forensic expert reasoning probabilistically about the source of the forensic evidence, it is presupposed that any probabilistic reasoning about the ultimate hypothesis is the province of the trier of fact, i.e., the judge and/or the jury.

With or without the additional hypotheses, Figure 2 is an example of a Bayesian Network (BN). As in the simple case of Figure 1, to perform the correct Bayesian inference once we observe evidence we need to know the prior probabilities of the nodes without parents and the conditional prior probabilities of the nodes with parents. Assuming that it is possible to obtain suitable estimates of these prior probabilities, the bad news is that, even with a small number of nodes, the calculations necessary for performing correct probabilistic inference are far too complex to be done manually. Moreover, until the late 1980’s there were no known efficient computer algorithms for doing the calculations. This is the reason why, until relatively recently, only rather trivial Bayesian arguments could realistically be used in legal reasoning.

However, algorithmic breakthroughs in the late 1980s made it possible to perform correct probabilistic inference efficiently for a wide class of Bayesian networks and tools (Lauritzen and Spiegelhalter, 1988; Pearl, 1988). These algorithms have subsequently been incorporated into widely available graphical toolsets that enable users without any statistical knowledge to build and run BN models (Fenton and Neil, 2012). Moreover, further algorithmic breakthroughs have enabled us to model an even broader class of BNs, namely those including numeric nodes with arbitrary statistical distributions (Neil et al., 2007). These breakthroughs are potentially crucial for modelling legal arguments.

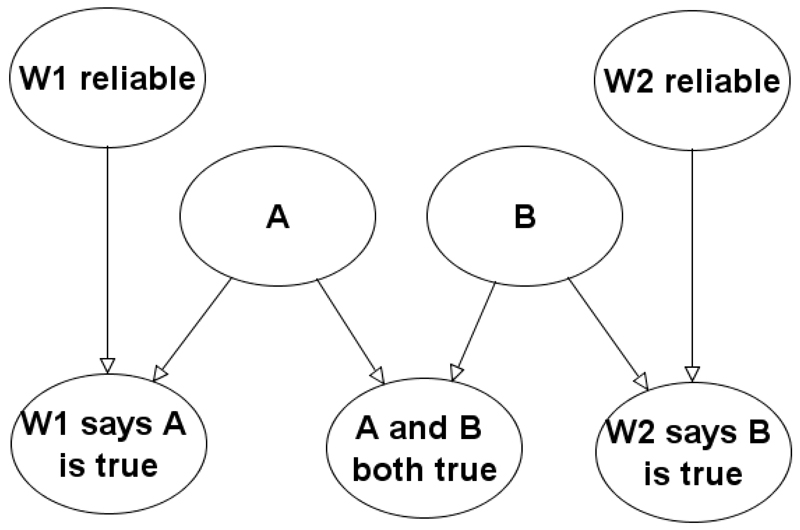
To show the simple power of BNs, we consider an example of how they can address claims made in several works, such as (Cohen, 1977) that probabilistic reasoning is inconsistent with legal reasoning because it leads to paradoxes. These claims have been challenged by Bayesians such as Dawid who paraphrased Cohen’s classic conjunction paradox as follows (Dawid, 1987):

• Suppose that A and B are independent disputed issues of fact, and that the plaintiff produces two independent witnesses: W1 attesting to A’s occurrence, and W2 to B’s occurrence. The witnesses are both regarded as 70% reliable. We infer, on the witnesses’ testimony, that Pr(A)=Pr(B)=0.7 whence Pr(C)=0.49. On Cohen’s analysis the suit succeeds; on a ‘Pascalian’ analysis, it fails. But each witness clearly offered positive support for the plaintiff. How can it be that their combined support undermines his case? Does this paradox not show that Cohen’s analysis is to be preferred?

Dawid provides a first-principles Bayesian argument to show that there is no paradox. The argument, which for non-mathematicians would be very hard to understand, is based on exposing hidden assumptions, notably that what the witness actually says about the fact is dependent on both whether the fact is true or not and whether the witness is reliable or not. No BN model is mentioned, but the underlying BN model is the one shown in Figure 3. The idea that the interpretation of any witness evidence must take account of the accuracy of the witness is a fundamental idiom (the evidence accuracy idiom) proposed in the general BN modelling approach of (Fenton et al., 2013b).

Figure 3. BN Model for the conjunction paradox.

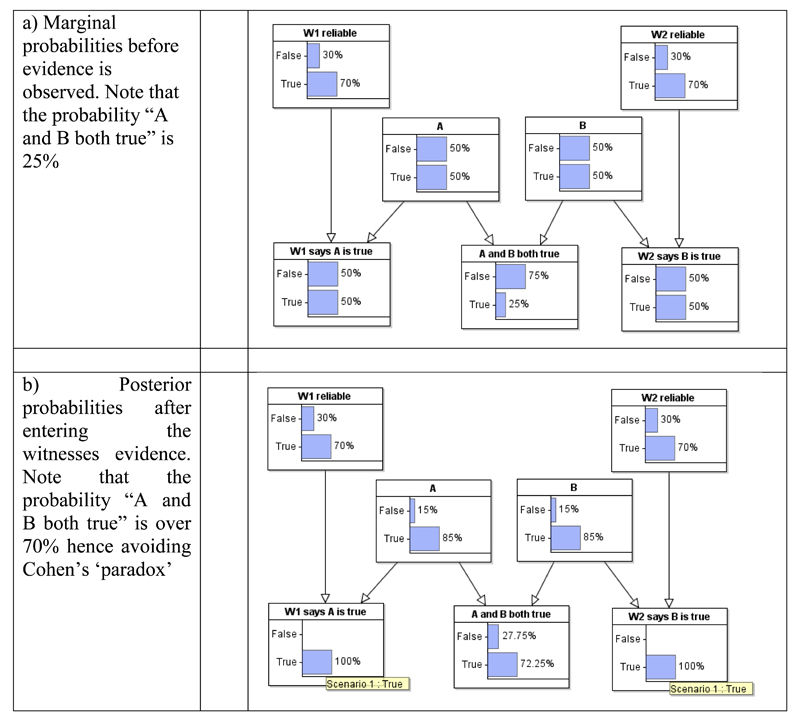
Simply running this model with different prior conditional probability values (for example using the free software (Agena Ltd, 2015) or (University of Pittsburg, 2015)) produces all the necessary results. For example, if we assume:

• The priors for the nodes W1, W2 are 70:30 for True/False

• The priors for nodes A, B are 50:50 True/False

• The conditional probability for the nodes representing what the witnesses say are as shown in Table 1:

Table 1. Conditional probability table for the nodes representing what the witnesses say.

Witness reliable	True		False
Fact	True	False	True	False
Witness says face is True	1	0	0.5	0.5
Witness says face is False	0	1	0.5	0.5

Then the result of running the model pre and post observations of the witness evidence are shown in Figure 4(a) and (b) respectively. This replicates all the complex calculations and formulae in (Dawid, 1987) and makes the argument much simpler and easier to understand.

Figure 4. Running the model before and after observing the witness evidence.

Moreover, in contrast to the argument in (Dawid, 1987), the BN approach is also scalable as explained in (Fenton et al., 2015) in the sense that it can easily incorporate further assumptions that would make the Bayesian updating impossible to do manually. The supporting material for this paper (Fenton et al., 2015) provides further detailed examples of the use of BNs.

3. Context and Review of Bayes in legal proceedings

To put the role of Bayesian reasoning in legal proceedings in context, we consider actual uses of Bayes in court according to a classification of cases that involve:

• Hypothesis testing of specific ‘dubious’ behaviour (discussed in Section 3.1)

• Determining extent to which ‘trait’ evidence helps with identification (Section 3.2)

• Using forensic evidence to infer the cause of effects (Section 3.3)

• Combining multiple pieces of statistical evidence (Section 3.4)

• Combining multiple pieces of diverse evidence (Section 3.5)

Additionally, Section 3.5 considers cases where Bayesian solutions have been used indirectly or retrospectively.

3.1. Hypothesis testing of specific ‘dubious’ behaviour

The vast majority of reported cases of explicit use of statistics in legal proceedings fall under this classification which, in (Fenton et al., 2015), we further sub-classify into:

• Any form of class discrimination and bias

• Any form of fraud/cheating

• Possession of illegal materials/substances

The review of such cases in (Fenton et al., 2015) shows that depressingly few involve explicit use of Bayes, and that where Bayes was used it was often misunderstood. For example, in Marks v Stinson 1994 (discussed in detail in (Fienberg and Finkelstein, 1996)) the Appeal Court judge relied heavily on the testimony of three statistical experts – one of whom used an explicitly Bayesian argument to compute the posterior probability that Marks had won the election based on a range of prior assumptions. Fienberg and Finkelstein assert that the judge misinterpreted the evidence provided by the experts and, because the Bayesian expert had used a range of prior values to examine the sensitivity of assumptions, “his calculations were subject to an even greater misinterpretation that that of the other experts”. So, although the judge did not dispute the validity of the use of Bayes, this was a clear example of how Bayesian reasoning can be misunderstood.

Typically, where there is sufficient relevant data, classical statistical hypothesis testing rather than Bayes has been used to determine whether the null hypothesis of ‘no dubious behaviour’ can be rejected at an appropriate level of significance. This is despite the known problems of interpreting the resulting p-values and confidence intervals, which the use of the Bayesian approach to hypothesis testing avoids (Fenton and Neil, 2012; Press, 2002). The potential for misinterpretation is enormous (Vosk and Emery, 2014). For example, in (U.S ex. Rel. DiGiacomo v Franzen, 680 F.2d 515 (7th Cir.), 1982) a forensic expert quoting a p-value from a study published in the literature interpreted it as the probability that each of the head hairs found on the victim were not the defendants. Sadly, there is a lack of awareness among statisticians that modern tools (such as those discussed in Section 2) make it possible to easily perform the necessary analysis for Bayesian hypothesis testing.

3.2. Determining extent to which ‘trait’ evidence helps with identification

This classification refers to all cases in which statistical evidence about ‘traits’ in the broadest sense (as defined in (Fenton et al., 2014)) is used. So traits range from ‘forensic’ physical features like DNA (coming from different parts of the body), fingerprints, or footprints, through to more basic features such as skin colour, height, hair colour or even name. But it could also refer to non-human artefacts (and their features) related to a crime or crime scene, such as clothing and other possessions, cars, weapons, glass, soil etc.

Any statistical use of trait evidence requires some estimate (based on sampling or otherwise) of the trait incidence in the relevant population. Much of the resistance to the use of such evidence is due to concerns about the rigour and validity of these estimates – with the errors made in the case of (People v. Collins, 438 P. 2d 33 (68 Cal. 2d 319 1968) , 1968) still prominent in many lawyers’ minds.

Nevertheless, the rapid growth of forensic statistics in the last 25 years has a led to a corresponding increase in the use of statistical trait evidence. This includes not just DNA, but also glass, paint, fibres, soil, fingerprints, handwriting, ballistics, bite marks, earmarks, and footwear. It is not surprising, therefore, that almost all of the publicised use of Bayes in legal proceedings relates to this class of evidence.

Its use in presenting trait evidence (as recommended, for example in (Aitken and Taroni, 2004; Balding, 2004; Collins and Morton, 1994; Dawid and Mortera, 2008; Evett and Weir, 1998; Evett et al., 2000; Jackson et al., 2013, 2006)) has been most extensive in respect of DNA evidence for determining paternity (Aitken and Taroni, 2004; Collins and Morton, 1994; Fung, 2003; MARSHALL et al., 1998). For example (see (North Carolina, 2009)), North Carolina’s court of appeals and supreme court have upheld the admissibility of genetic paternity test results using Bayes theorem with a 50% prior, non-genetic probability of paternity, citing cases: (Cole v. Cole, 74 N.C.App. 247, 328 S.E.2d 446, aff’d, 314 N.C. 660, 335 S.E.2d 897 (per curiam), 1985), (State v. Jackson, 320 N.C. 452, 358 S.E.2d 679, 1987), (Brown v. Smith, 137 N.C.App. 160, 526 S.E.2d 686, 2000). In contrast to the 50% prior recommended by North Carolina, in Plemel v Walter 1987 (discussed in (Fienberg and Finkelstein, 1996)) the need to present results against a range of priors was recommended; indeed this was also recommended in the criminal case (State of New Jersey v J.M. Spann, 130 N.J. 484: 617 A. 2d 247, 1993).

Outside of paternity testing the primary use of the LR in presenting DNA evidence has been to expose the prosecutor’s fallacy in the original statistical presentation of a random match probability. Notable examples in the UK of this scenario are the rape cases of (R v Deen, 1994), (R v Alan James Doheny and Gary Adams, 1996; Robertson and Vignaux, 1997), (R v Adams [1996] 2 Cr App R 467, [1996] Crim LR 898, CA and R v Adams [1998] 1 Cr App R 377, 1996); in each case an Appeal accepted the Bayesian argument showing that there was the potential to mislead in the way the DNA match evidence against the defendants had been presented by the prosecution at the original trial. Similar uses of the LR for presenting DNA evidence being accepted as ‘valid’ have been reported in New Zealand and Australia (Fenton et al., 2015; Thompson et al., 2001).

It is worth noting that the interpretation of DNA match probabilities is critically dependent on the context for the match and, in particular, serious errors of probabilistic reasoning may occur in cases (such as People v Puckett, USA 2008) where the match arises from a database search. In such cases Bayesian reasoning can again avoid errors (Balding and Donnelly, 1996; Meester and Sjerps, 2003).

It is difficult to determine the extent to which the LR for presenting forensic evidence other than DNA has been used in courts. Although mostly unreported, we know of cases involving glass, fibres and soil matches, while articles now promote its use in fingerprint evidence (Alberink et al., 2014; Nuemann et al., 2011). The most impressive well-publicised success concerns its use in relation to firearm discharge residue (FDR) in (R. v. George, EWCA Crim 2722, 2007); the use of the LR in the appeal – showing that the FDR evidence had ‘no probative value’ was the reason granted for a retrial (in which George was found not guilty) with the FDR evidence deemed inadmissible. The appeal court ruling in this case (along with our concerns about the over-simplistic use of the LR that we return to in Section 4) is discussed in detail in (Fenton et al., 2013a).

However, while the R v George appeal judgment can be considered a major success for the use of Bayes, the 2010 UK Court of Appeal Ruling - known as (R v T, 2010) - dealt it a devastating blow. The ruling quashed a murder conviction in which the prosecution had relied heavily on footwear matching evidence presented using Bayes and the LR. Specifically, even though there was recognition that it was used for this purpose in Netherlands, Slovenia and Switzerland) points 86 and 90 of the ruling respectively assert:

“We are satisfied that in the area of footwear evidence, no attempt can realistically be made in the generality of cases to use a formula to calculate the probabilities. The practice has no sound basis”.

“It is quite clear that outside the field of DNA (and possibly other areas where there is a firm statistical base) this court has made it clear that Bayes’ theorem and likelihood ratios should not be used”

Given its potential to change the way forensic experts analyse and present evidence in court, there have been numerous articles criticising the ruling (Aitken and many other signatories, 2011; Berger et al., 2011; Morrison, 2012; Nordgaard et al., 2012; Redmayne et al., 2011; Robertson et al., 2011; Sjerps and Berger, 2012). These papers recognise that there were weaknesses in the way the expert presented the probabilistic evidence (in particular not making clear that likelihood ratios for different aspects of the evidence were multiplied together to arrive at a composite likelihood ratio), but nevertheless express deep concern about the implications for the future presentation, by experts, of forensic evidence. The papers recognise positive features in the ruling (notably that experts should provide full transparency in their reports and calculations) but they provide compelling arguments as to why the main recommendations stated above are problematic. Unfortunately, as we explain in Section 4, the ruling is beginning to have a devastating impact on the way some forensic evidence is presented with experts deliberately concealing or obfuscating their calculations.

While most reported cases of the prosecutor’s fallacy relate to poor presentation of trait evidence, it is not the only way it occurs. In R v Sally Clark, Clark was convicted for the murder of her two young children who had died one year apart (Forrest, 2003; Nobles and Schiff, 2005). To counter the hypothesis that the children had died as a result of Sudden Infant Death Syndrome (SIDS) the prosecution’s expert witness Roy Meadow stated that there was “only a 1 in 73 million chance of both children being SIDS victims”. This figure wrongly assumed two SIDS deaths in the same family were independent and was presented in a way that may have led the jury into the prosecutor’s fallacy. These errors were exposed by probability experts during the appeal and they also used Bayes to explain the impact of failing to compare the prior probability of SIDS with the (also small) probability of double murder (Dawid, 2005; Hill, 2005). Clark was freed on appeal in 2003.

3.3. Forensic evidence to infer the cause of effects

While most uses of Bayesian reasoning with forensic evidence have been in the context of matching/identification as explained in Section 3.2, it is often the case that forensic evidence is used to infer the causes of effects (which, as is made clear in (Dawid et al., 2015) is treated as being different from the effects of causes). For example, items such as blood spatter are used to infer time of death and the cause of death (James et al., 2005), while a range of medical evidence is used in cases such as SIDS deaths to determine cause of death. (Dawid et al., 2015) explain why Bayesian methods are crucial for interpreting this type of evidence.

3.4. Combining multiple pieces of statistical evidence

Where there are multiple pieces of statistical evidence (such as trait evidence) involved in a case there is a need for careful probabilistic analysis taking account of potential dependencies between different pieces of evidence. Bayes is ideally suited to such an analysis, but sadly the failure to recognise this has led to many very well publicised errors. For example, in the Collins case the original statistical analysis failed to account for dependencies between the various components of the trait evidence. Similarly, in R v Clark the above mentioned figure of 1 in 73 million for the probability of two SIDS deaths in the same family was based on an unrealistic assumption that two deaths would be independent events. More generally courts have failed to properly understand what (Fienberg and Finkelstein, 1996) refers to as:

‘…cases involving a series of events or crimes and a related legal doctrine for the admissibility of evidence on ‘similar events’.

The Lucia de Berk case (Meester et al., 2007) is a classic example of this misunderstanding, whereby a prosecution case is fitted around the fact that one person is loosely connected to a number of related events. People die in hospitals and it is inevitable that there will be instances of individual nurses associated with much higher than normal death rates in any given period of time. The extremely low probability P(evidence | not guilty) – which without any real evidence that the defendant has committed a crime tells us very little – is used to drive the prosecution case. Another very similar case (currently subject to an appeal based on precisely these concerns) is that of Ben Geen who was also a nurse convicted of multiple murders and attempted murder (Gill, 2014).

(Fienberg and Kaye, 1991) describe a number of earlier cases and note that, despite the fact that Bayes is especially well suited since P(H | evidence) increases as more similar events are included in the evidence, in none of them was a Bayesian perspective used.

3.5. Combining multiple pieces of diverse evidence

The idea that different pieces of (possibly competing) evidence about a hypothesis H are combined in order to update our belief in H is central to all legal proceedings. Yet, although Bayes is the perfect formalism for this type of reasoning, it is difficult to find any well reported examples of the successful use of Bayes in combining diverse evidence in a real case. There are two reasons for this. One is to do with the lack of awareness of tools for building and running BN models that enable us to do Bayesian inference for legal arguments involving diverse related evidence. The second (not totally unrelated to the first) is due to the spectacular failure in one well publicised case where Bayes was indeed used to combine diverse competing evidence.

The case was that of (R v Adams [1996] 2 Cr App R 467, [1996] Crim LR 898, CA and R v Adams [1998] 1 Cr App R 377, 1996) already referred to above in connection to the misleading presentation of DNA evidence. This was a rape case (discussed in detail in (Donnelly, 2005)) in which the only prosecution evidence was that the defendant’s DNA matched that of a swab sample taken from the victim. The defence evidence included an alibi and the fact that the defendant did not match the victim’s description of her attacker. At trial the prosecution had emphasised the very low random match probability (1 in 200 million) of the DNA evidence. The defence argued that if statistical evidence was to be used in connection with the DNA evidence, it should also be used in combination with the defence evidence and that Bayes Theorem was the only rational method for doing this. The defence called a Bayesian expert (Prof Peter Donnelly) who explained how, with Bayes, the posterior probability of guilt was much lower when the defence evidence was incorporated. The appeal rested on whether the judge misdirected the jury as to the evidence in relation to the use of Bayes and left the jury unguided as to how that theorem could be used in properly assessing the statistical and non-statistical evidence in the case. The Appeal was successful and a retrial was ordered, although the Court was scathing in its criticism of the way Bayes was presented, stating:

• “The introduction of Bayes’ theorem into a criminal trial plunges the jury into inappropriate and unnecessary realms of theory and complexity deflecting them from their proper task.

• The task of the jury is … to evaluate evidence and reach a conclusion not by means of a formula, mathematical or otherwise, but by the joint application of their individual common sense and knowledge of the world to the evidence before them”

At the retrial it was agreed by both sides that the Bayesian argument should be presented in such a way that the jury could perform the calculations themselves (a mistake in our view). The jury were given a detailed questionnaire to complete to enable them to produce their own prior likelihoods, and calculators to perform the necessary Bayesian calculations from first principles. Adams was, however, again convicted. A second appeal was launched (based on the claim that the Judge had not summed up Donnelly’s evidence properly and had not taken the questionnaire seriously). This appeal was also unsuccessful, with the Court not only scathing about the use of Bayes in the case but essentially ruling against its future use.

While the subsequent R v T ruling in 2010 dealt a devastating blow for the use of Bayes in presenting forensic (non DNA) evidence, the ruling against the use of Bayes in R v Adams is actually far more damaging. This is because it rules against the very use where Bayes has the greatest potential to simplify and clarify complex legal arguments. The fact that the complex presentation of Bayes in the case was (rightly) considered to be its death knell is especially regrettable given that in 1996 the tools for avoiding this complexity were already widely available.

3.6. Cases where Bayesian solutions have been used indirectly or retrospectively

While there is a shortage of well publicised success stories for the use of Bayes in actual legal proceedings, there is no shortage of retrospective studies of real cases where statistics may or may not have been used in the actual trial or appeal, but where it has been argued that a Bayesian approach would have been useful to improve understanding (and expose flaws) (Aitken & Taroni 2004; Balding 2004; Good 1995; Kadane 2008; Lucy & Schaffer 2007; Redmayne 1995; Schneps & Colmez 2013; Taroni et al. 2014). Certain cases have, unsurprisingly, attracted numerous retrospective Bayesian analyses, notably the case of Collins (Dawid, 2005; Edwards, 1991; Finkelstein and Fairley, 1970), O J Simpson (Good, 1995; Thompson, 1996) and Sacco and Vanzetti (Fenton et al., 2013b; Hepler et al., 2007).

Bayes has also played an indirect (normally unreported) role in many cases. Based just on our own experience (and on that of colleagues) as expert consultants to lawyers, we know of dozens of cases in which Bayes was used to help lawyers in the preparation and presentation of their cases. Because of confidentiality (and sometimes sensitivity) this work normally cannot be publicised. There are rare exceptions such as (Kadane, 1990) who describes his proposed Bayesian testimony in an age discrimination case (settled before trial); some of the work we have been able to make public retrospectively is R v Levi Bellfield 2007-08 (Fenton and Neil, 2011) and B v National Health Service 2005 (Fenton and Neil, 2010).

4. Why Bayes has had minimal impact in the law

The review in Section 3 leaves little doubt that the impact of Bayes in the Law has been minimal. To understand how minimal, it is illustrative to consider the 350-page National Research Council report on “Strengthening Forensic Science in the United States” (National Research Foundation, 2009). This important committee report has had a major impact in the US with regard to the lack of data and statistical support for many forms of forensic evidence. However, it does not contain a single mention of Bayes, and it contains just one footnote reference to likelihood ratios. In contrast, in the UK a number of published guidelines recommend the use of LRs extensively for forensic evidence presentation (Jackson et al., 2013; Puch-Solis et al., 2012). However, the use of such methods is actually likely to decrease following rulings such as RvT.

In this section we explain what we consider to be the reasons for continued resistance to Bayes in the law.

4.1. Standard resistance to the use of Bayes

There is a persistent attitude among some members of the legal profession that probability theory has no role to play at all in the courtroom. Indeed, the role of probability – and Bayes in particular – was dealt another devastating and surprising blow in a 2013 UK Appeal Court case ruling (Nulty & Ors v Milton Keynes Borough Council, 2013) (discussed in (Spiegelhalter, 2013)). The case was a civil dispute about the cause of a fire. Originally, it was concluded that the fire had been started by a discarded cigarette, although this seemed an unlikely event in itself because the other two explanations were even more implausible. The Appeal Court rejected this approach, effectively arguing against the entire Bayesian approach to measuring uncertainty by asserting essentially that there was no such thing as probability for an event that has already happened but whose outcome is unknown. Specifically Point 37 of the ruling asserted (about the use of such probabilities):

I would reject that approach. It is not only over-formulaic but it is intrinsically unsound. The chances of something happening in the future may be expressed in terms of percentage. Epidemiological evidence may enable doctors to say that on average smokers increase their risk of lung cancer by X%. But you cannot properly say that there is a 25 per cent chance that something has happened … Either it has or it has not.

Although it is easy to show the irrationality of this viewpoint (see, for example (Fenton and Neil, 2012)) supporters of it often point to the highly influential paper (Tribe, 1971), which was written as a criticism of the prosecutor’s presentation in (People v. Collins, 438 P. 2d 33 (68 Cal. 2d 319 1968) , 1968). While Tribe’s article did not stoop to the level of the ‘no such thing as probability’ argument, it is especially sceptical of the potential use of Bayes’ Theorem since it identifies the following concerns (Berger, 2014; Fienberg and Finkelstein, 1996) that are especially pertinent for Bayes:

• That an accurate and/or non-overpowering prior cannot be devised.

• That in using statistical evidence to formulate priors jurors might use it twice in reaching a posterior

• That not all evidence can be considered or valued in probabilistic terms.

• That no probability value can ever be reconciled with “Beyond A Reasonable Doubt”

• That due to the complexity of cases and non-sequential nature of evidence presentation, any application of Bayes would be too cumbersome for a jury to use effectively and efficiently.

• That probabilistic reasoning is not compatible with the law, for policy reasons. In particular, that jurors are asked to formulate an opinion of the defendant’s guilt during the prosecutor’s case, which violates the obligation to keep an open mind until all evidence is in.

Although many of Tribe’s concerns have long been systematically demolished in (Edwards, 1991; Koehler, 1992) and more recently in (Berger, 2014; Tillers and Gottfried, 2007), the arguments against are far less well known among legal professionals than those in favour.

4.2. LR models are inevitably over-simplified

We believe that much of the recent legal resistance to Bayes is due to confusion, misunderstanding, over-simplification and over-emphasis on the role of the LR. The issues (dealt with in depth in the recent papers (Fenton, 2014; Fenton et al., 2014, 2013a)) are summarised in what follows.

The simplest and most common use of the LR – involving a single piece of forensic trace evidence for a single source level hypothesis – can actually be very complex as already explained in Section 2 (where Figure 2, rather than Figure 1 is the correct model). Even if we completely ignore much of the context (including issues of reliability of trace sample collection/storage and potential testing errors) the LR may still be difficult or even impossible to elicit because somehow we have to factor in to the hypothesis Hd (defendant is not the source of the DNA trace) every person other than the defendant who could have been the source (potentially every other person in the world) (Balding, 2004; Nordgaard et al., 2012). For example, P(E | Hr) is much higher than P(E | Hu) where Hr is the hypothesis “a close relative of the defendant is the source of the trace” and Hu is the hypothesis “a totally unrelated person is the source”

This means that, in reality, Hd is made up of multiple hypotheses that are difficult to articulate and quantify. The standard pragmatic solution (which has been widely criticised (Balding, 2004)) is to assume that Hd represents a ‘random person unrelated to the defendant’. But not only does this raise concerns about the homogeneity of the population used for the random match probabilities, it also requires separate assumptions about the extent to which relatives can be ruled out as suspects.

It is not just the hypotheses that may need to be ‘decomposed’. In practice, even an apparently ‘single’ piece of evidence E actually comprises multiple separate pieces of evidence, and it is only when the likelihoods of these separate pieces of evidence are considered that correct conclusions about probative value of the evidence can be made. This is illustrated in Example 1. In the light of these observations it is perhaps not surprising that (Wagenaar, 1988) had difficulties in getting the judge to interpret his LR descriptions.

• Example 1: Consider the evidence E: “tiny matching DNA trace found”. Suppose that the DNA trace has a profile with a random match probability of 1/100 (such relatively ‘high’ match probabilities are common in low-template samples). Assuming H_p and H_d are the prosecution and defence hypotheses respectively, it would be typical to assume that

  • $\text{P}(E\hspace{0.17em}|\hspace{0.17em}{H}_{\text{p}})=1$

  and that

  • $\text{P}(E\hspace{0.17em}|\hspace{0.17em}{H}_{\text{d}})=1/100$

  leading to a LR of 100, thus indicating quite strong support for the prosecution hypothesis. However, the evidence E actually comprises two separate pieces of evidence:

  • E1: tiny DNA trace found
  • E2: DNA trace found matches defendant

In particular, this makes clear the relevance of finding only a tiny trace of DNA when larger amounts would be expected to have been left by the person who committed the crime. So, actually P(E | Hp) will be much smaller than 1, because we would expect substantial amounts of DNA to be found, rather than just a tiny trace. To elicit all the necessary individual likelihood values, and to carry out the correct Bayesian calculations needed for the overall LR in situations such as this, we again need to turn to BNs as shown in Figure 5.

Figure 5. Modelling complex evidence in a BN.

The oversimplistic model fails to capture the relevance of the fact that the trace was tiny. If the defendant were guilty it is expected that the investigator would have found significant traces of DNA. The significance of the tiny trace is properly captured by separating out E1 in the second model. A reasonable conditional probability table for E1 is shown in Table 2.

Table 2. Conditional probability table for E1.

Guilty	False	True
False	0.5	0.999
True	0.5	0.0010

The conditional probability table for E2 shown in Table 3 uses the same RMP information as was used in the oversimplified model.

Table 3. Conditional probability table for E2.

Guilty	False		True
E1: tiny DNA trace found	False	True	False	True
False	1.0	0.99	1.0	0.0
True	0.0	0.01	0.0	1.0

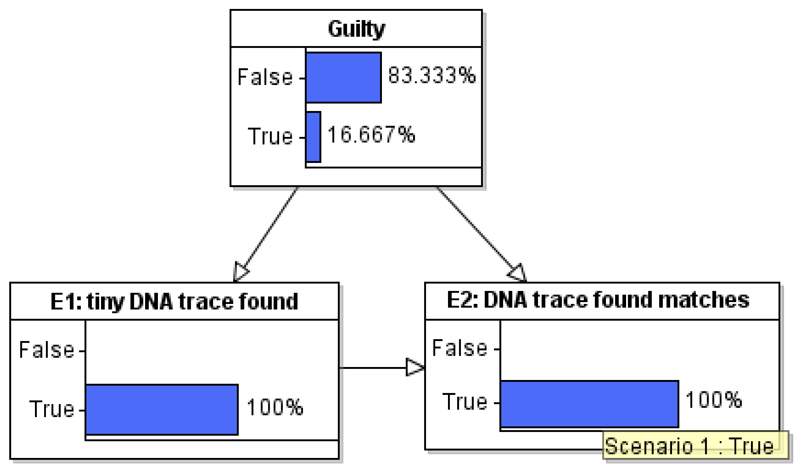
Calculating the overall LR manually in this case is much more complex, so we go directly to the result of running the model in a BN tool with E2 set as true (and the prior odds of guilt set at 50:50 again). This is shown in Figure 15. The LR is just the probability of guilty divided by the probability of not guilty, which is 0.2. So the evidence supports the defence hypothesis rather than the prosecution.

This example also indicates the importance of taking account of absence of evidence.

4.3. Exhaustiveness and mutual exclusivity of hypotheses is not respected in all LR uses

The most powerful assumed benefit of the LR is that it provides a valid measure of the probative value of the evidence E in relation to the alternative hypotheses H_p (prosecution hypothesis) and H_d (defence hypothesis). But when we say the evidence E “supports the hypothesis H_p” what we mean is that the “posterior probability of H_p after observing E is greater than the prior probability of H_p” and “no probative value” means the “posterior probability of H_p after observing E is equal to the prior probability of H_p”. The proof of the meaning of probative value in this sense relies both on Bayes’ theorem and the fact that H_p and H_d are mutually exclusive and exhaustive – i.e. are negations of each other (H_d is the same as “not H_p”) (Fenton et al., 2013a). If H_p and H_d are mutually exclusive but not exhaustive then the LR tells us absolutely nothing about the relationship between the posterior and the priors of the individual hypotheses as explained in Example 2.

• Example 2: In the game of Cluedo there are 6 people at the scene of a crime (3 men and 3 women). One woman, Mrs. Peacock, is charged with the crime (so H_p is “Mrs. Peacock guilty”). The prosecution provides evidence E that the crime must have been committed by a woman. Since P(E| H_p) = 1 and P(E| not H_p) = 2/5 the LR is 2.5 and so clearly the evidence is probative in favour of the prosecution. However, if the defence is allowed to focus on an alternative hypothesis H_d that is not “not H_p” say “Miss Scarlet guilty” then P(E| H_d) = 1. In this case the defence can argue that the LR is 1 and so has no probative value. But while the evidence does not distinguish between the (non-exhaustive) H_p and H_d, it certainly is probative for Hp.

We already noted that it may be very difficult in practice to elicit P(E | H_d) where H_d is simply the negation of H_p because H_d may encompass too many options. The inevitable temptation is to ‘cherry pick’ an H_d which seems a reasonable alternative to H_p for which P(E | H_d) can be elicited. Example 3 and the arguments in Fenton, Berger, et al. 2013) show the dangers in such an approach. Indeed, it was shown that the “LR = 1 implies evidence has no probative value” argument that was the key in the R v Barry George appeal may have been compromised by precisely this problem. Similarly, it has also been noted that the failure to choose appropriate (mutually exclusive and exhaustive) hypotheses in the arguments used by Bayesians to expose the flaws in the R v Sally Clark case may have exaggerated the scale of the problem (Fenton, 2014).

It is especially confusing (and even disturbing) that the Guidelines (Jackson et al., 2013; Roberts et al., 2013) specify that the LR requires two mutually exclusive but not necessarily exhaustive hypotheses. While this may make life more convenient for its primary target audience (i.e. forensic scientists) it can severely compromise how lawyers and jurors should interpret the results.

It is also important to note that an additional danger in allowing H_d to be something different from “not H_p” is that, in practice, forensic experts may come up with an H_d that is not even mutually exclusive to H_p. This was also shown to be a real problem in the transcript of the R v Barry George appeal (Fenton et al., 2013a). Two hypotheses that are not mutually exclusive may both be true and in such circumstances the LR is meaningless.

4.4. The ‘prior misconception’

The LR is popular with forensic experts precisely because it can be calculated without having to consider any prior probabilities for the hypotheses (Press, 2002). But this is something of a misconception for two reasons. First, the LR actually tells us nothing about the probability that either hypothesis is true, no matter how high or low it is. We can only make conclusions about such (posterior) probabilities if we know the prior probabilities. Although this observation has been well documented (Fenton, 2011; Meester and Sjerps, 2004; Triggs and Buckleton, 2004) this issue continues to confound not just lawyers, but also forensic experts and statisticians. An indication of the extent of the confusion can be found in one of the many responses by the latter community to the RvT judgement. Specifically, in the otherwise excellent position statement (Aitken and many other signatories, 2011) is the extraordinary point 9 that asserts:

“It is regrettable that the judgment confuses the Bayesian approach with the use of Bayes’ Theorem. The Bayesian approach does not necessarily involve the use of Bayes’ Theorem.”

By the “Bayesian approach” the authors are specifically referring to the use of the LR, thereby implying that the use of the LR is appropriate, while the use of Bayes’ Theorem may not be.

The second reason why it is a misconception is because it is impossible to specify the likelihoods P(E | H_p) and P(E | H_d) meaningfully without knowing something about the priors P(H_p), P(H_d), This is because (in strict Bayesian terms¹) we say the likelihoods and the priors are all conditioned on some background knowledge K and it follows that, without an agreed common understanding about this background knowledge, we can end up with vastly different LRs associated with the same hypotheses and evidence. This is illustrated in Example 3.

• Example 3. Suppose the evidence E in a murder case is: “DNA matching the defendant is found on victim”. While the prosecution likelihood P(E | H_p) might be agreed to be close to one, there is a problem with the defence likelihood, P(E | H_d). For DNA evidence such as this, the defence likelihood is usually assumed to be the random match probability (RMP) of the DNA type. This can typically be as low as one in a billion. But consider two extreme values that may be considered appropriate for the prior P(H_p), derived from different scenarios used to determine K :

  • a)
    P(H_p) = 0.5, where the defendant is one of two people seen grappling with the victim before one of them killed the victim;
  • b)
    P(H_p) = 1/40 million.where nothing is known about the defendant other than he is one of 40 million adults in the UK who could have potentially committed the crime.

  Whereas a value for P(E | H_d) = RMP seems reasonable in case b), it is clearly not in case a). In case a) the defendant’s DNA is very likely to be on the victim irrespective of whether or not he is the one who killed the victim. This suggests a value of P(E | H_d) close to 1. It follows that, without an understanding about the priors and the background knowledge, we can end up with vastly different LRs associated with the same hypotheses and evidence.

4.5. The LR for source level hypotheses tells us nothing about offense level hypotheses

Even when hypotheses are mutually exclusive and exhaustive, there remains the potential during a case to confuse what in (Cook et al., 1998a) were referred to as source-level and offence-level hypotheses Sometimes one may mutate into another through slight changes in the precision with which they are expressed. A LR for the source-level hypotheses will not in general be the same as for the offence-level hypotheses.

In (Fenton et al., 2013a) it is shown (using BNs that model dependencies between different hypotheses and evidence) that it is possible that an LR for a piece of evidence E that strongly favours one side for the source-level hypotheses can actually strongly favour the other side for the offence-level hypotheses even though both pairs of hypotheses seem very similar. Similarly, an LR that is neutral under the source-level hypotheses may actually be significantly non-neutral under the associated offence-level hypotheses. Once again these issues were shown to be a real problem in the transcript of the R v Barry George appeal (Fenton et al., 2013a).

4.6. Confusion about LR being expressed on a verbal scale

The UK Forensic Science Service Guide (Puch-Solis et al., 2012) recommends that, to help lawyers and jurors understand the significance of a LR, it should be presented on an equivalent verbal scale. This recommendation (criticised in (Mullen et al., 2014)) contrasts with US courts that have advised against verbal scales and instead recommended that posterior probabilities should be provided based on a range of priors for the given LR. We believe that the US Courts approach is correct, but recognise that in the UK explicit use of numerical LRs are increasingly snubbed following the RvT judgment.

As part of our own legal advisory/expert witness work we have examined numerous expert reports in the last five years (primarily, but not exclusively from forensic scientists). These reports considered different types of match evidence in murder, rape, assault and robbery cases. The match evidence includes not just DNA, but also handprints, fibre matching, footwear matching, soil and particle matching, matching specific articles of clothing, and matching cars and their number plates. In all cases there was some kind of database or expert judgement on which to estimate frequencies and ‘random match’ probabilities, and in most cases there appears to have been some attempt to compute the LR. However, in all but the DNA cases, the explicit statistics and probabilities were not revealed in court – in several cases this was as a direct result of the RvT ruling which has effectively pushed explicit use of numerical LR ‘underground’. Indeed, we have seen expert reports that contained the explicit data being formally withdrawn as a result of RvT. This is one of the key negative impacts of RvT - we feel it is extremely unhelpful that experts are forced to suppress explicit probabilistic information.

4.7. Continued use of manual methods of calculation

Despite the multiple publications applying BNs to legal arguments, even many Bayesian statisticians are either unaware of these breakthroughs or are reluctant to use the available technology. Yet, if one tries to use Bayes theorem ‘manually’ to represent a legal argument one of the following results is inevitable:

1. To ensure the calculations can be easily computed manually, the argument is made so simple that it no longer becomes an adequate representation of the legal problem.

2. A non-trivial model is developed and the Bayesian calculations are written out and explained from first principles and the net result is to totally bemuse legal professionals and jurors. This was, of course, the problem in R v Adams. In (Fenton et al., 2015) we show other examples where statisticians provide unnecessarily complex arguments).

The manual approach is also not scalable since it would otherwise mean having to explain and compute one of the BN inference algorithms, which even professional mathematicians find daunting.

5. The way forward

The scale of the challenge for Bayes and the law is well captured by the following statement made at a recent legal conference (to the first author of this paper²) by one of the UK’s most eminent judges:

“No matter how many times Bayesian statisticians try to explain to me what the prosecutors fallacy is I still do not understand it and nor do I understand why there is a fallacy.”

This is despite the fact that, in response to the cases described in Section 3.2, guidance to UK judges and lawyers specifies the need to be aware of expert witnesses making the prosecutor’s fallacy and to make such evidence inadmissible. Yet, based on informal evidence from cases we have been involved in, the prosecutor’s fallacy (and other related probabilistic fallacies) continues to be made regularly by both expert witnesses and lawyers. Indeed, one does not need an explicit statement of probability for the fallacy to be made. For example, a statement like:

“the chances of finding this evidence in an innocent man are so small that you can safely disregard the possibility that this man is innocent”

is a classic instance of the prosecutor’s fallacy that is frequently used by lawyers. Based on our own experiences as expert witnesses, we believe the reported instances are merely the tip of the iceberg.

That such probabilistic fallacies continue to be made in legal proceedings is a sad indictment of the lack of impact made by statisticians in general (and Bayesians in particular) on legal practitioners. This is despite the fact that the issue has been extensively documented by multiple authors including (Anderson et al., 2005; Balding and Donnelly, 1994; Edwards, 1991; Evett, 1995; Fenton and Neil, 2000; Freckelton and Selby, 2005; Jowett, 2001; Kaye, 2001; Koehler, 1993b; Murphy, 2003; Redmayne, 1995; Thompson and Schumann, 1987) and has even been dealt with in populist books such as (Gigerenzer, 2002; Haigh, 2003). There is almost unanimity among the authors of these works that a basic understanding of Bayesian probability is the key to avoiding probabilistic fallacies. Indeed, Bayesian reasoning is explicitly recommended in works such as (Evett 1995; Finkelstein & Levin 2001; Good 2001; Jackson et al. 2006; Redmayne 1995; Saks & Thompson 2003; Robertson & Vignaux 1995), although there is less of a consensus on whether or not experts are needed in court to present the results of all but the most basic Bayesian arguments (Robertson and Vignaux, 1998).

We argue that the way forward is to use BNs to present probabilistic legal arguments since this approach avoids much of the confusion surrounding both the over-simplistic LR and more complex models represented formulaically and computed manually. Unfortunately, it is precisely because BNs are assumed by legal professionals to be ‘part of those same problems’ that they have made little impact. The use of BNs for probabilistic analysis of forensic evidence and more general legal arguments is by no means new. As long ago as 1991 (Edwards, 1991) provided an outstanding argument for the use of BNs in which he said of this technology:

“I assert that we now have a technology that is ready for use, not just by the scholars of evidence, but by trial lawyers.”

He predicted such use would become routine within “two to three years”. Unfortunately, Edwards was grossly optimistic. In addition to the reasons already identified above there is the major challenge in getting legal professionals to accept the validity of subjective probabilities that are an inevitable part of Bayes. Yet, ultimately, any use of probability – even if it is based on frequentist statistics – relies on a range of subjective assumptions. The objection to using subjective priors may also be calmed by the fact that it may be sufficient to consider a range of probabilities, rather than a single value for a prior. BNs are especially suited to this since it is easy to change the priors and do sensitivity analysis (Fenton and Neil, 2012).

A basic strategy for presenting BNs to legal professionals is described in detail in (Fenton and Neil, 2011) and is based on the calculator analogy. This affirms that since we now have efficient and easy-to-use BN tools there should be no more need to explain the Bayesian calculations in a complex argument than there should be any need to explain the thousands of circuit level calculations used by a regular calculator to compute a long division.

Only the simplest Bayesian legal argument (a single hypothesis and a single piece of evidence) can be easily computed manually; inevitably we need to model much richer arguments involving multiple pieces of possibly linked evidence. While humans must be responsible for determining the prior probabilities (and the causal links) for such arguments, it is simply wrong to assume that humans must also be responsible for understanding and calculating the revised probabilities that result from observing evidence. The Bayesian calculations quickly become impossible to do manually, but any BN tool enables us to do these calculations instantly.

The results from a BN tool can be presented using a range of assumptions including different priors. What the legal professionals (and perhaps even jurors if presented in court) should never have to think about is how to perform the Bayesian inference calculations. They do, of course, have to consider the prior assumptions needed for any BN model. Specifically, they have to consider:

• whether the correct nodes and causal links have been modelled

• what are the suitable values (or range of values) required for the priors and conditional priors

• whether the hidden value K for ‘context’ has been considered and communicated throughout the model

But these are precisely what have to be considered in weighing up any legal argument. The BN simply makes this all explicit rather than hidden, which is another clear benefit of the approach.

We recognise that there are significant technical challenges to overcome to make the construction of BNs for legal reasoning easier. Recent work addresses the lack of a systematic, repeatable method for modelling legal arguments as BNs by using common idioms and an approach for building complex arguments from these (Fenton et al., 2013b; Hepler et al., 2007). We also have to overcome various technical constraints of existing BN algorithms and tools such as forcing modellers to specify unnecessary prior probabilities (this is being addressed in work such as (European Research Council, 2015). However, the greater challenges are cultural and presentational and these issues are being addressed in projects like (European Research Council, 2015; Isaac Newton Institute Cambridge, 2015; Royal Statistical Society, 2015) which involve close interaction with legal professionals and empirical studies on how best to present arguments.

One of the greatest opportunities offered by BNs is to provide a much more rigorous and accurate method to determine the combined impact of multiple types of evidence in a case (including, where relevant, absence of evidence). In particular, this applies urgently to any case in which DNA evidence with match probabilities is presented (hence avoiding the kind of errors highlighted in (Langley, 2012)). As was argued (and accepted) in R v Adams, if probability is to be used for one piece of evidence, it is unfair to exclude its use for other types of evidence.

BNs can also expose other features of DNA evidence (such as those relating to homogeneity of population samples) that clearly demonstrate the illogical and irrational decision in RvT to elevate DNA evidence to its privileged position of being the only class of evidence suitable for statistical analysis. Match probabilities for all types of trait evidence – including DNA – involve uncertainties and inaccuracies related to sampling and subjective judgment and inaccuracies in testing. Moreover, the situation with respect to low-template DNA evidence (Balding, 2004; Evett et al., 2002) is especially critical since a ‘DNA match’ in such cases may have low probative value (especially if the potential for secondary and tertiary transfer is considered) but still has a powerful impact on lawyers and jurors; we are currently involved in appeal cases where some low-template DNA evidence was assumed to ‘trump’ all the opposing evidence in the case. BN models demonstrate that the impact of the DNA evidence has been exaggerated (examples are provided in (Fenton et al., 2015)).

6. Conclusions

Proper use of Bayesian reasoning has the potential to improve the efficiency, transparency and fairness of criminal and civil justice systems. It can help experts formulate accurate and informative opinions; help courts determine admissibility of evidence; help identify which cases should be pursued; and help lawyers to explain, and jurors to evaluate, the weight of evidence during a trial. It can also help identify errors and unjustified assumptions entailed in expert opinions.

Yet, despite the impeccable theoretical credentials of Bayes in presenting legal arguments, and despite the enormous number of academic papers making the case for it, our review of the impact in practice of Bayes in the Law is rather depressing. It confirms that its impact on legal practice has been minimal outside of paternity cases. While it has been used in some well-known cases to expose instances of the prosecutor’s fallacy, that very fallacy continues to afflict many cases. And while the LR has been quite widely used to present the impact of forensic evidence, we have explained the multiple problems with it and the danger of allowing it to be seen as synonymous with Bayes and the law. The fact that these problems were not the reason for the RvT judgment in 2010 which effectively banned the use of the LR (outside of DNA evidence) makes the judgment even more of a travesty than many assume it to be.

In addition to the RvT judgment, we have seen the devastating appeal judgments in R v Adams (effectively banning the use of Bayes for combining ‘non statistical evidence’) and in (Nulty & Ors v Milton Keynes Borough Council, 2013) which went as far as banning the use of probability completely when discussing events that had happened but whose outcome was unknown. Even when an appeal judgment was favourable to Bayes ((R. v. George, EWCA Crim 2722, 2007)) subsequent research has discovered weaknesses in the LR reasoning (Fenton et al., 2013a). Similar weaknesses have been recently exposed in other ‘successful’ Bayesian arguments such as those used in the successful Sally Clark appeal (Fenton, 2014).

The good news is that the difficulties encountered in presenting Bayesian arguments can be avoided once it is accepted that over-simplistic LR models and inference calculations from first principles are generally unsuitable. We have explained that BNs are the appropriate vehicle for overcoming these problems since they enable us to model the correct relevant hypotheses and the full causal context of the evidence. Unfortunately, too many people in the community are unaware of (or reluctant to use) the tools available for easily building and running BN models.

We differ from some of the orthodoxy of the statistical community in that we believe there should never be any need for statisticians or anybody else to attempt to provide complex Bayesian arguments from first principles in court. The Adams case demonstrated that statistical experts are not necessarily qualified to present their results to lawyers or juries in a way that is easily understandable. Moreover, although our view is consistent with that of (Robertson and Vignaux, 1998) in that we agree that Bayesians should not be presenting their arguments in court, we do not agree that their solution (to train lawyers and juries to do the calculations themselves) is feasible. Our approach, rather, draws on the analogy of the electronic calculator.

There is still widespread disagreement about the kind of evidence to which Bayesian reasoning should be applied and the manner in which it should be presented. We have suggested methods to overcome these technical barriers, but there are still massive cultural barriers between the fields of science and law that that will only be broken down by achieving a critical mass of relevant experts and stakeholders, united in their objectives. We are building toward this critical mass of experts in projects such as (European Research Council, 2015; Isaac Newton Institute Cambridge, 2015; Royal Statistical Society, 2015).

Finally, our review has exposed the irrational elevation of DNA, by the legal community – and some members of the mathematical community – to a type of evidence (over and above that of other types) which has almost unique probabilistic qualities. In fact BNs offer a tremendous opportunity to radically improve justice in all cases that involve DNA evidence (especially low-template DNA), by properly capturing its impact in relation to all other evidence.

Figure 6. Posterior odds in correct model.