Increased Proportion of Variance Explained and Prediction Accuracy of Survival of Breast Cancer Patients with Use of Whole-Genome Multiomic Profiles

Abstract

Whole-genome multiomic profiles hold valuable information for the analysis and prediction of disease risk and progression. However, integrating high-dimensional multilayer omic data into risk-assessment models is statistically and computationally challenging. We describe a statistical framework, the Bayesian generalized additive model ((BGAM), and present software for integrating multilayer high-dimensional inputs into risk-assessment models. We used BGAM and data from The Cancer Genome Atlas for the analysis and prediction of survival after diagnosis of breast cancer. We developed a sequence of studies to (1) compare predictions based on single omics with those based on clinical covariates commonly used for the assessment of breast cancer patients (COV), (2) evaluate the benefits of combining COV and omics, (3) compare models based on (a) COV and gene expression profiles from oncogenes with (b) COV and whole-genome gene expression (WGGE) profiles, and (4) evaluate the impacts of combining multiple omics and their interactions. We report that (1) WGGE profiles and whole-genome methylation (METH) profiles offer more predictive power than any of the COV commonly used in clinical practice (e.g., subtype and stage), (2) adding WGGE or METH profiles to COV increases prediction accuracy, (3) the predictive power of WGGE profiles is considerably higher than that based on expression from large-effect oncogenes, and (4) the gain in prediction accuracy when combining multiple omics is consistent. Our results show the feasibility of omic integration and highlight the importance of WGGE and METH profiles in breast cancer, achieving gains of up to 7 points area under the curve (AUC) over the COV in some cases.

THE continued development of high-throughput genomic technologies has fundamentally changed the genetic analyses of complex traits and diseases. These technologies provide large volumes of data from multiple “omic” layers, including the genome (e.g., SNPs, copy-number variants, and mutations), the epigenome (e.g., methylation), the transcriptome (e.g., RNA-seq), the proteome, and so on. This information can be used to develop models for understanding and predicting disease risk and disease prognosis. Recently, several studies have uncovered unprecedented numbers of omic factors associated with disease risk and progression. For instance, in the last decade, genome-wide association studies (GWAS) have reported large numbers of SNPs (e.g., http://www.genome.gov/gwastudies/) and structural variants [e.g., copy-number variants (Beroukhim et al. 2010; Morrow 2010)] associated with disease risk. Likewise, several studies have reported methylation sites (Dedeurwaerder et al. 2011; Fackler et al. 2011; Fang et al. 2011) and genes with expression profiles associated with prognosis (Perou et al. 2000; Sørlie et al. 2001; Van’t Veer et al. 2002; Sotiriou and Pusztai 2009; Gyorffy et al. 2016). However, despite the tremendous progress achieved, use of this information in clinical practice remains limited in part because the proportion of variance in disease risk or prognosis explained by the individual factors identified still remains limited.

Data integration can be an avenue for improving our understanding and our ability to predict disease risk and prognosis. Integration can take place by combining information from multiple sites across the genome as well as by integrating inputs from different omics. In prediction of complex traits and disease risk, several studies (e.g., Purcell et al. 2009; de los Campos et al. 2010c; Yang et al. 2010; Makowsky et al. 2011; Vazquez et al. 2012) have demonstrated that the proportion of variance explained by use of whole-DNA profiles is considerably higher than that achieved by models that use a limited number of GWAS-significant variants. Likewise, several studies have demonstrated benefits of integrating data from multiple omics. For example, Chen et al. (2012) demonstrated how integrated omic profiles can provide insights into the development of type 2 diabetes. However, our ability to integrate whole-genome multilayer omic data into risk assessments still lags behind.

Wheeler et al. (2014) and Vazquez et al. (2014) proposed using what Wheeler called “Omic Kriging” for prediction of complex traits and disease risk using multiomic profiles. Kriging is a kernel-smoothing technique commonly used in spatial statistics (e.g., Cressie 2015). From a statistical perspective, kriging is the best linear unbiased predictor (BLUP) method commonly used in quantitative genetics (Henderson 1950; Robinson 1991) using pedigree (Henderson 1950, 1975) or DNA information (G-BLUP) (VanRaden 2008)]. OmicKriging is a multikernel method (de los Campos et al. 2010a, b) in which the resulting kernel is a weighted average of similarity matrices derived from different omics.

Although OmicKriging represents a promising method for integrating multiomic data, the method has potentially important limitations. First, the approach assumes that the architecture of effects is homogeneous across omic layers. This assumption may not hold if some omics have a sparse architecture of effect (i.e., a few factors have sizable effects, and the rest have no effect) and other omics have non-sparse-effects architecture (i.e., all inputs have small effects). Second, OmicKriging assumes implicitly that omics act in an additive manner (i.e., there are no interactions between omics). This may fail, for instance, if the effects of one layer (e.g., SNP) are modulated by a second layer (e.g., methylation).

In this study, we describe a modeling framework that (1) allows integration of high-dimension inputs from multiple omic layers, (2) contemplates different effect architectures across layers, and (3) incorporates interactions between omics. The approach is a Bayesian generalized additive model (BGAM) that integrates in a unified setting ideas from generalized additive models (Hastie and Tibshirani 1986) with Bayesian methods that allow for different architectures of effects (including estimation with or without shrinkage and variable selection methods) and recently developed techniques for modeling interactions between high-dimensional inputs (Jarquín et al. 2014). Importantly, the BGAM can be used with traditional quantitative traits and time-event (subject to censoring), ordinal, and binary (e.g., disease) outcomes.

We use BGAM and data from The Cancer Genome Atlas (TCGA) to develop models for analysis and prediction of breast cancer (BC) outcomes. Breast cancer is considered one of the most lethal types of cancer (Boyle and Levin 2008). In the United States alone, there are ∼180,000 new cases of BC each year (Eifel et al. 2000), and it has been estimated that about 12% of women will develop BC over their lifetime (Eifel et al. 2000; Smigal et al. 2006). Advances in early detection and in adjuvant therapy have reduced mortality due to BC. However, adjuvant therapy has important undesirable side effects on treated patients. Some of the most serious ones include permanent infertility, heart damage, cognitive impairment, and increased probability of developing other types of cancers (Eifel et al. 2000). Cancers in approximately 40% of BC patients are estimated to recur or metastasize (Weigelt et al. 2005). However, because current models cannot accurately predict BC progression, approximately 80% of BC patients are treated with adjuvant therapy. Thus, a substantial number of BC patients are being treated unnecessarily with adjuvant therapy. An accurate assessment of disease progression could be used to implement a more precise approach to the treatment of BC patients and reduce the impact of undesirable outcomes due to therapy. Here we apply a BGAM modeling framework to data from TCGA to develop models for prediction of the probability of survival after a diagnosis of BC. In our application, we compare multiomic models with risk assessments based on clinical covariates and the expression profiles of large-effect genes included in the Oncotype DX platform (Genomic Health) (Paik et al. 2004, 2006), which is a Food and Drug Administration (FDA)–approved platform used in clinical practice to predict BC progression. Our analysis demonstrates that the integration of whole-omic profiles can increase the proportion of interindividual differences in survival and enhance prediction accuracy of BC outcomes above and beyond that which can be achieved using clinical covariates (i.e., race, age, cancer subtype, and stage) and expression-based diagnostic tools (e.g., Oncotype DX).

In this article, we outline the main elements of the BGAM modeling framework and present a series of case studies in which we apply the methods to BC cases from TCGA. The Discussion section highlights the main findings of our study and offers a brief perspective on the strengths and limitations of the BGAM framework. Our results show how the integration of omics in a clinical model improves prediction accuracy for most omics, but the improvements are higher by combining clinical information with whole-genome methylation and gene expression profiles.

Modeling Framework

Assume that the multilayer omic data consist of a phenotype or disease outcome $y_{\mathrm{i}} (i=1,\dots ,n)$ and sets of predictors coming from L input layers; these layers may include demographics, clinical covariates, and data from several omics. We denote the data from these layers as $X=\left\{X_1,\dots ,X_{\mathrm{L}}\right\}$. Here $X_{\mathrm{l}}=\left\{x_{\mathrm{lij}}\right\}$ denotes a set of predictors from the lth data layer, and l = 1, …, L, i = 1, …, n, and j = 1, …,$p_{\mathrm{l}}$ index input layers l, individuals i, and predictors within an input layer j, respectively.

Generalized additive model (GAM)

Multilayer inputs can be incorporated into a regression model using the so-called generalized additive model (GAM) framework (Hastie and Tibshirani 1986). In a GAM, a regression function is expressed as the sum of L smooth functions

$${\eta }_{\mathrm{i}}=f_1\left(X_{1\mathrm{i}},{\mathrm{\alpha }}_1\right)+f_2\left(X_{2\mathrm{i}},{\mathrm{\alpha }}_2\right)+\cdots +f_{\mathrm{L}}\left(X_{\mathrm{Li}},{\mathrm{\alpha }}_1\right)$$ (1)

Each of these functions can be linear or nonlinear for the inputs and can be specified parametrically or using semiparametric methods (e.g., splines). Typically, these functions are indexed by a set of parameters ${\alpha }_{\mathrm{l}}$ estimated from data. When these parameters are high dimensional (i.e., $p_{\mathrm{l}}$ is large), estimation is typically carried out using L2-penalized (i.e., ridge-regression) estimators (Hastie and Tibshirani 1986); this approach renders smooth functions with shrunken parameter estimates. The extent of shrinkage of estimates is controlled by regularization parameters. When there is only smooth function, an optimal value for the regularization parameter can be chosen using cross-validation methods (e.g., Golub et al. 1979). However, when there are multiple regularization parameters (e.g., one per term of the linear predictor), the cross-validation approach becomes infeasible, and other approaches (e.g., mixed-effects models or Bayesian methods) are needed.

For some high-dimensional inputs (e.g., DNA markers and transcriptomes), variable selection, as opposed to shrinkage, may be desirable. This can be achieved in penalized regressions by using penalties other than those based on the L2 norm, e.g., with the L1 norm, as in the LASSO method (Tibshirani 1996). Alternatively, variable selection and/or shrinkage can be obtained in a Bayesian setting by choosing particular types of prior distributions. The Bayesian approach has several attractive features. First, within a Bayesian framework, multiple regularization parameters can be estimated from data without the need to conduct extensive cross-validations. Second, Bayesian models can accommodate both shrinkage and variable selection in a unified framework. Finally, using methods described later, within the Bayesian framework, one can accommodate interactions between inputs in high-dimensional sets. Therefore, in this study, we adopted a Bayesian generalized additive model (BGAM) framework for integrating multiomic inputs.

Bayesian generalized additive model (BGAM)

For ease of presentation, we introduce the model for the case of a Gaussian outcome and assume that each of the functions entering in (1) are linear on their inputs. Cases involving non-Gaussian outcomes or functions that are nonlinear on inputs are considered later. For the purpose of illustration, we consider only three input layers, including a set of nongenetic covariates $X_{1\mathrm{i}}={\left\{x_{1\mathrm{ij}}\right\}}_{\mathrm{j}=1}^{\mathrm{j}=p_1}$ and two omics $X_{2\mathrm{i}}={\left\{x_{2\mathrm{ij}}\right\}}_{\mathrm{j}=1}^{\mathrm{j}={\text{p}}_2}$ and $X_{\mathrm{3i}}={\left\{x_{3\mathrm{ij}}\right\}}_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_3}$. Extensions to more than three layers are straightforward. With this setting, the linear predictor becomes

$${\mathrm{\eta }}_{\mathrm{i}}=\mathrm{\mu }+{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_1}{x}_{1\mathrm{ij}}{\mathrm{\alpha }}_{1\mathrm{j}}+{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_2}{x}_{2\mathrm{ij}}{\mathrm{\alpha }}_{2\mathrm{j}}+{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_3}{x}_{3\mathrm{ij}}{\mathrm{\alpha }}_{3\mathrm{j}}$$ (2)

where ${\mathrm{\alpha }}_1={\left\{{\mathrm{\alpha }}_{1\mathrm{j}}\right\}}_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_1}$, ${\mathrm{\alpha }}_2={\left\{{\mathrm{\alpha }}_{2\mathrm{j}}\right\}}_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_2}$, and ${\mathrm{\alpha }}_3={\left\{{\mathrm{\alpha }}_{3\mathrm{j}}\right\}}_{\mathrm{j}=1}^{\mathrm{j}={\mathrm{p}}_3}$ are regression coefficients.

Bayesian likelihood

Under Gaussian assumptions, the conditional distribution of the outcome given the parameters of the linear predictors is

$$p\left(y|X_1,X_2,X_3,\theta \right)={\displaystyle \prod }_{\mathrm{i}=1 }^{\mathrm{i}=\mathrm{n}}\frac{\text{Exp}\left[-\frac{{\left(y_{\mathrm{i}}-{\mathrm{\eta }}_{\mathrm{i}}\right)}^2}{2{\sigma }_{\mathrm{\epsilon }}^2}\right]}{\sqrt{2\pi {\sigma }_{\mathrm{\epsilon }}^2}}$$ (3)

where $\theta =\left\{{\sigma }_{\epsilon }^2,\mathrm{\mu }, {\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2,{\mathrm{\alpha }}_3\right\}$ is a vector of model unknowns.

Prior distribution

In a Bayesian setting, layer-specific architectures of effects can be accommodated using layer-specific priors. Therefore, we structure the joint prior distribution of effects as follows:

$$p\left({\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2,{\mathrm{\alpha }}_3,{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2,{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2,{\mathrm{\Omega }}_3\right)\propto p\left({\sigma }_{\mathrm{\epsilon }}^2\right){\displaystyle \prod }_{\mathrm{l}=1 }^3\left[{\displaystyle \prod }_{\mathrm{j}=1 }^{\mathrm{j}={\mathrm{p}}_{\mathrm{l}}}p\left({\mathrm{\alpha }}_{\mathrm{lj}}|{\mathrm{\Omega }}_{\mathrm{l}}\right)\right]p({\mathrm{\Omega }}_{\mathrm{l}})$$

where $p\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\right)$ is a prior for the error variance (e.g., a scaled inverse chi-square), $p\left({\mathrm{\alpha }}_{\mathrm{lj}}\text{|}{\mathrm{\Omega }}_{\mathrm{l}} \right)$ are IID priors assigned to the effect of the 1st input layer, ${\mathrm{\Omega }}_{\mathrm{l}}$ is a set of layer-specific regularization hyperparameters, and $p({\mathrm{\Omega }}_{\mathrm{l}})$ is a prior distribution assigned to these hyperparameters.

Special cases

Estimation without shrinkage can be obtained by setting $p\left({\mathrm{\alpha }}_{\mathrm{lj}}\text{|}{\mathrm{\Omega }}_{\mathrm{l}} \right)$ to be a flat prior (e.g., a normal prior centered at zero and with a very large variance). Shrunken estimates can be obtained by setting $p\left({\mathrm{\alpha }}_{\mathrm{lj}}\text{|}{\mathrm{\Omega }}_{\mathrm{l}} \right)$ to be a normal prior centered at zero and with variance parameter (${\mathrm{\Omega }}_{\mathrm{l}}={\mathrm{\sigma }}_{{\mathrm{\alpha }}_{\mathrm{l}}}^2$) treated as unknown. This approach renders estimates comparable to those of ridge regression (Meuwissen et al. 2001) with an extent of shrinkage that is similar across effects. Differential shrinkage of estimates of effects can be obtained using priors from the thick-tailed family, such as the double-exponential or scaled-t distributions; these priors are used in the Bayesian LASSO (Park and Casella 2008) and in BayesA (Meuwissen et al. 2001). Finally, variable selection can be achieved by setting $p\left({\mathrm{\alpha }}_{\mathrm{lj}}\text{|}{\mathrm{\Omega }}_{\mathrm{l}} \right)$ to be a finite mixture with a point of mass (or a very sharp spike) at zero and a relatively flat slab (George and McCulloch 1993; Ishwaran and Rao 2005).

Functions that are nonlinear inputs

These can be accommodated by first mapping the original inputs (e.g., $X_{\mathrm{l}}$) into a set of basis functions ${\mathrm{\Phi }}_{\mathrm{l}}=\left\{{\mathrm{\phi }}_{\mathrm{l}1}\left(X_{\mathrm{l}}\right),{\mathrm{\phi }}_{\mathrm{l}2}\left(X_{\mathrm{l}}\right),\dots \right\}$ and then using the transformed inputs ${\phi }_{\mathrm{lj}}\left(X_{\mathrm{l}}\right)$ as covariates in the regression. This can be done either in parametric settings (e.g., with polynomials) or with semiparametric specifications (e.g., using splines or kernels).

Gaussian processes

When the coefficients entering a linear term are assigned IID normal priors, the resulting function can be viewed as a draw from a Gaussian process. For instance, if ${\alpha }_{\mathrm{lj}}\sim N\left(0,{\sigma }_{{\alpha }_{\mathrm{l}}}^2\right)$, then the function $f_{\mathrm{l}}={\mathrm{\Phi }}_{\mathrm{l}}{\alpha }_{\mathrm{l}}$ follows a normal distribution with null mean and covariance matrix given by $K_{\mathrm{l}}{\sigma }_{{\alpha }_{\mathrm{l}}}^2$, where $K_{\mathrm{l}}={\mathrm{\Phi }}_{\mathrm{l}}{{\mathrm{\Phi }}^{\prime }}_{\mathrm{l}}^{}$ is a covariance structure computed using cross-products of the basis functions. This treatment fully connects the BGAM with reproducing kernel Hilbert spaces (RKHS) regression methods (Wahba 1990; Shawe-Taylor and Cristianini 2004), a framework that can be used to implement various types of parametric and semiparametric regressions. Importantly, this framework can be implemented with almost any input sets, including text data, images, special data, graphs, and so on (Wahba 1990; de los Campos et al. 2009, 2010a).

Interactions between input layers

Model of expressions (1) and (2) assume that layers act additively. However, many applications may require modeling interactions between layers. Accommodating interactions can be particularly challenging when the number of inputs in the interacting layers is large. For instance, with 10,000 expression profiles and 10,000 SNPs, modeling all possible first-order interactions requires using 100 million contrasts. Dealing with interactions explicitly is not feasible. Therefore, we propose to deal with interactions implicitly using Gaussian processes with covariance structures based on the patterns induced by the so-called reaction-norm model. This approach has been used for modeling interactions between genetic factors and environmental covariates in plants and animals (Gregorius and Namkoong 1986; Calus et al. 2002; Su et al. 2006; Jarquín et al. 2014). Recently, Jarquín et al. (2014) developed methods for reaction norms involving high-dimensional genetic (e.g., SNP) and high-dimensional environmental inputs. The authors show that the covariance patterns induced by a reaction-norm model can be expressed as the Schur (or Hadamard) product of kernels that evaluate input similarity at each of the interacting layers. An example of the use of this method is provided in the fourth case study of the next section.

Non-Gaussian outcomes

Non-Gaussian outcomes (e.g., binary or ordered categorical outcomes) can be accommodated using the probit or logit link; in a Bayesian Markov chain Monte Carlo (MCMC) setting, the probit link can be implemented easily using data augmentation (Albert and Chib 1993).

Software

All the models described in this section can be implemented using the Bayesian generalized linear regression (BGLR) R package (Pérez and de los Campos 2014). This software implements BGAM for continuous, binary, and ordinal outcomes and offers users the possibility of specifying at each of the layers parametric and semiparametric methods for shrinkage and variable selection. Further details about the software can be found in Pérez and de los Campos (2014) and at the following website: https://github.com/gdlc/BGLR-R/.

Case Studies

In this section, we investigate the association between patient survival and several predictors that can be assessed at diagnosis, including information commonly used by clinicians to assess BC patients (hereafter we refer to these predictors as “clinical covariates”), gene expression profiles (RNA-seq), methylation, copy-number variant, and micro-RNA. All these omics were assessed at the primary tumor. We consider several research questions, and for each of these questions, we designed a case study that involves the comparison of several models, each of which is a special case of the BGAM framework described in the preceding section. All the case studies are based on data from BC patients from TCGA. The motivation for each of the case studies is briefly presented next.

Case study I

Clinical information such as tumor subtype or cancer stage is used to assess risk of possible cancer outcomes; precise prediction of outcomes improves the decision as to which treatment options should be used for each patient. Although the clinical covariates are predictive of the likelihood of disease progression, after accounting for differences attributable to these clinical predictors, important interindividual differences in the BC outcome remain. Gene expression has been demonstrated to be associated with BC progression (Sørlie et al. 2001, 2003). Therefore, in our first case study (CS-I), we assessed the relative contribution to variance and prediction accuracy of whole-genome gene expression (WGGE) profiles. We compare models based on WGGE profiles with others based on clinical covariates commonly used in clinical practice (BC subtype, stage, age at cancer diagnosis, histologic subtype, and race). In this study, we assessed the contribution to variance and prediction accuracy of WGGE profiles alone and in combination with clinical covariates. Sørlie et al. (2001) demonstrated that clusters derived from the gene expression profiles are associated with breast cancer subtypes. Our COV (M7) model and all other models that incorporate all clinical covariates already accounts for BC subtypes as dummy variables and therefore incorporates clustering. Several studies have demonstrated the association of gene expression patterns and BC outcome. However, these studies are based on data that have been conditioned by some dimension-reduction method (e.g., clustering or principal components). We argue that consideration of WGGE profiles is essential in capturing the diverse information on this trait of complex biology.

Case study II

Our first case study accounted for the main effects of commonly used clinical covariates and those of WGGE profiles. However, the patterns of gene expression and the prognosis of the cancer present substantial variation in both the different cancer subtypes and the different stages of development of the disease. Therefore, in our second case study (CS-II), we focused on a particular cancer subtype: luminal types at early stage—this is the most prevalent subtype. For early-stage luminal patients, there is a well-established commercial gene expression platform (Oncotype DX; Genomic Health, Inc, Redwood City, CA) (Paik et al. 2004, 2006) that has been approved by the FDA for use as a diagnostic tool. Oncotype DX analysis is based on the profile of a genetic signature consisting of only a few genes. We argue that the use of whole-genome gene expression profiles can lead to a larger proportion of variance explained and higher prediction accuracy than can be achieved using the expression profiles of a few genes. Therefore, in CS-II, we compared models based on (1) clinical covariates, (2) clinical covariates plus the expression profile of genes included in the Oncotype DX, and (3) clinical covariates and WGGE profiles. The models were fitted and compared based on data from patients with luminal types at early stage only, lymph node negative, and all lymph nodes.

Case study III

Information from omics other than the transcriptome, such as DNA information (e.g., copy-number variants), or data from the epigenome also can contribute to interindividual differences in survival. Therefore, in our third case study (CS-III), we considered the use of omics other than WGGE profiles, including micro-RNA (miRNA), methylation, and copy-number variant (CNV). For each omic, we assessed the proportion of variance explained and prediction accuracy of the omic alone and in conjunction with clinical covariates; in all cases, we considered one omic at a time and conducted separate analyses for each of the omics.

Case study IV

In our previous case studies, we assessed omics separately or in combination with COV. In our fourth case study (CS-IV), we evaluated the benefits of integrating two omics, WGGE and METH profiles and COV simultaneously; we explored this both with an additive model and with a specification that contemplates interactions between omics.

Data

The Cancer Genome Atlas (TCGA) offers data on BC patients with demographic, clinical, omic, and follow-up information from which survival information can be derived. Because data are still being collected, follow-up time is short for most patients. Therefore, our response variable was defined as subjects that either died (1) or were alive (0) and had at least three years of follow-up. All male records and females with incomplete follow-up or inconsistent clinical records (e.g., death shortly after the diagnosis of BC in an early stage without any record of progression) were removed. Also, women with distant metastases at the time of diagnosis or patients with history of a previous cancer were removed. After editing, these samples were reduced from over 1000 to 797 samples, from which only 285 met the minimum follow-up criteria. Thus, the baseline data set consisted of 285 patients; these included subjects with concordant data that were either dead (n = 60) or alive (n = 225) and had a minimum follow-up time of 3 years. Not all these patients had complete data for all the omics. Therefore, in some of the case studies, we further narrowed the set of patients to those who had complete data for the inputs relevant to the specific analysis. The original data set offered by TCGA was reduced to patients with at least three years of follow-up because follow-up is still too short [in the original TCGA data, the follow-up time averages (±SD) 2.05 (±1.14) years of last contact time for those still alive.]

In CS-I, CS-III, and CA-IV, models were obtained by regressing alive status (0/1) on the inputs that follow. These inputs were selected based on their association with survival in preliminary analyses. CS-II is a more homogeneous population, and fewer covariables were used (see Case study II section).

Demographics:

Demographics included age at diagnosis [55.6 ± 12.6 years (mean ± SD)] and race/ethnicity (Caucasian/African American).

Clinical information from the tumor:

Tumor clinical information included histologic type [whether the invasive tumor arose from lobular tissue (n = 35) or from ductal breast tissue (n = 251)], subtype classification based on the membrane receptors present in the tumor cell (luminal A, 179; luminal B, 24; Her2-Neu, 69; and triple negative, 13), and stage, as defined by the American Joint Committee on Cancer (Edge et al. 2010) (from I–IV; the number of patients per stage were 58, 159, and 68 in stages I, II, and higher, respectively).

Omics data:

Omics data included gene expression profiles from RNA-seq, whole-genome methylation, miRNA, and CNVs. Gene expression profiles were assessed using RNA-seq technology sequenced on an Illumina HiSeq 2000 platform. Normalized expression counts per gene were used. Workflows for the creation of level 3 RNA data were detailed previously (Li et al. 2010; Wang et al. 2010). CNV data were derived from Affymetrix Genome-Wide SNP Array 6.0. Mean log₂ ratios were used as a measure of per-segment CNVs. Full processing details are documented in a Broad Institute GenePattern pipeline (“GenePattern”). Source data for methylation were generated with the Illumina Infinium HumanMethylation450 Beadchip and were processed by the Johns Hopkins GSC to derive beta values for CpG sites and their association with gene regions using methylumi (Pidsley et al. 2013). miRNA values are quantified as reads per million (RPM) from the Illumina HiSeq miRNA 2500 platform. Short-sequence reads were aligned to the RCh37-lite reference genome using the Burrows-Wheeler Alignment (BWA) tool (Li and Durbin 2009) and normalized as RPMs (Network 2012). In TCGA, samples were randomly assigned to plates; therefore, there should be no association between batch and survival outcomes. However, to confirm this, we conducted analyses of dispersion due to batch (see Supplemental Material, File S1, Table S1.1).

Data analysis

Each of the case studies includes a baseline model plus extensions obtained by including different combinations of omics. In all cases, the response (survival, Yes/No) was regressed on predictors using a threshold model (Gianola and Foulley 1983; Agresti 2012) as implemented in the BGLR R package (Pérez and de los Campos 2014). In each study, models were first fitted to all the individuals that had complete data for the set of predictors used in the case study. From this analysis, we reported parameter estimates (e.g., variance components) and the posterior means of the log likelihoods.

Model specification:

The effects of clinical covariates were regarded as fixed, while the effects of different omics were regarded as random. For simplicity, all random effects were assumed to be IID Gaussian, with omic-specific variance parameters. We also conducted analyses using priors that induce variable selection. In other studies, these models did not show strong differences in risk for disease (Vazquez et al. 2015). Results of these analyses are given in the File S1, Table S1.2. Variance parameters were assigned scaled inverse-chi-square priors with five degrees of freedom (this gives a weakly informative prior) and scale parameters computed according to the rules described in Perez and de los Campos (2014); this is the default treatment of variances implemented in BGLR. For each model, we ran 500,000 iterations of a Gibbs sampler; the first 20,000 samples were discarded as burn-in, and the remaining samples were thinned at a thinning interval of five (see File S1, Figure S1.1 and Figure S1.2 and Table S1.3). For all case studies, we report the log likelihood, effective number of parameters in the model, and the deviance information criteria (DIC).

Prediction accuracy:

Prediction accuracy was assessed using cross-validations (CVs). We implemented a total of 200 independently generated 10-fold CVs. Prediction accuracy was assessed using the CV–area under the receiver operating characteristic curve (CV-AUC) (e.g., Fawcett 2006). Therefore, for each study and model, we had a total of 200 estimates of CV-AUC. Models were compared based on the average CV-AUC and also by counting the proportion of CVs (of 200) for which a given model had a higher CV-AUC than another. For CV analyses, models were fitted using 80,000 iterations collected after discarding the first 15,000 samples; furthermore, samples were thinned at an interval of five. For all case studies, we report the average and SD (across 200 CVs) of the CV-AUC and the proportion of times that a model had a CV-AUC greater than other models, also computed using results from 200 CVs. Code to implement the models described herein is provided in File S2 and on the following website: https://github.com/anainesvs/VAZQUEZ_etal_GENETICS_2016.

Data availability

The data used in this study is publically available, collected and distributed by TCGA, National Institutes of Health/National Cancer Institute project. Data can be obtained at https://tcga-data.nci.nih.gov/tcga. Additionally, to ensure reproducibility of this analysis, the lines of code used to execute this study are provided in File S2 and at the above- mentioned github repository.

Results

Case study I: integrating clinical covariates and whole-genome gene expression

The first case study (CS-I) was designed to assess the marginal association between survival and individual risk factors composed of clinical covariates (e.g., age, race, etc.) and to quantify the gains in prediction accuracy that can be achieved by adding gene expression data on a model that accounts for the clinical information. Six sets of risk factors were considered; these included two demographics (age and race), three clinical features of the cancer (whether it is a lobular carcinoma, cancer subtype, and pathologic stage), and gene expression profiles (RNA-seq) from the primary tumor.

Sequence of models:

A total of eight models were fitted, including six single-risk-factor models (labeled as M1–M6), a model based on all predictors except gene expression (M7, also labeled as COV), and a model that included all the available predictors (M8, labeled as COV + WGGE).

Results:

Table 1 provides goodness-of-fit statistics, measures of model complexity, and estimates of prediction accuracy for each of the eight models fitted in CS-I. Among the single-factor models, the one that fitted the data best and had the highest CV-AUC was the model using whole-genome gene expression (WGGE, M6); clearly, WGGE profiles were the most informative input.

Table 1. Parameter estimates, model goodness of fit, model complexity, and predictive accuracy (case study I).

Whole data analysis										200 CVs
Model	Predictors						Log likelihoodb	Effective number of parameters (pD)	Deviance information criteria (DIC)	Average CV-AUCc	Proportion of times (of 200 CVs) model in column had AUC > model in row
	Age at diagnosis	Racea	Lobular (Y/N)	Tumor subtype	Pathological stage	Gene expression					M2	M3	M4	M5	M6	M7 (COV)	M8 (COV + WGGE)
M1	X						−146.1	2.1	294.3	0.557d (0.007)	0.14	<0.01	>0.99	>0.99	>0.99	>0.99	>0.99
M2		X					−147.5	2.0	296.9	0.525d,e (0.023)		0.59	>0.99	>0.99	>0.99	>0.99	>0.99
M3			X				−144.3	2.0	290.6	0.526e (0.020)			>0.99	>0.99	>0.99	>0.99	>0.99
M4				X			−138.6	4.1	281.3	0.618f (0.013)				0.14	>0.99	>0.99	>0.99
M5					X		−142.4	2.0	286.9	0.596f (0.012)					>0.99	>0.99	>0.99
M6						X	−132.4	15.5	280.3	0.659g (0.011)						>0.99	>0.99
M7: COV	X	X	X	X	X		−146.3	3.2	295.8	0.704h (0.007)							>0.99
M8: COV + WGGE	X	X	X	X	X	X	−131.3	17.6	280.3	0.721i (0.010)

^aAfrican American, Y/N.

^bEstimated posterior mean of the log likelihood.

^cAverage over 200 tenfold CVs.

^d,e,f,g,h,iThe same letter indicates that the models are no different (empirical P < 0.05).

Comparison of the results obtained with models COV and COV + WGGE indicate that information from WGGE profiles can improve the assessment of survival, even after accounting for the predictors commonly considered in clinical practice. The increase in CV-AUC obtained when WGGE profiles were added to a model that includes all COVs was, on average, 1.7 points (COV + WGGE) higher than that for a model based on COV, and the comparison across 200 CVs shows that the model COV + WGGE outperformed the model based on clinical covariates (COV) 99% of the time. In other words, the increase in prediction accuracy was consistent.

Case study II: genetic signatures vs. whole-genome gene expression profiles within cancer subtypes

CS-I showed that the assessment of BC survival could be improved by using WGGE profiles from the tumor tissue. CS-I is an analysis that is not specific to a cancer subtype, although subtypes are considered in the model. The clinical value of WGGE profiles for BC has been demonstrated previously (Sørlie et al. 2001), and gene expression profiles from oncogenes are often used to assess BC patients; an example of this is the Oncotype DX platform (Paik et al. 2004, 2006), which is based on the expression profiles of 21 genes. Oncotype DX has been validated for assessing BC outcome among patients affected by tumors of the luminal (estrogen receptor–positive [ER+]) cancer subtype that are in an early stage of disease and do not have distant or nodal metastases. Therefore, in this case study, we focused only on luminal cancers and compared the relative contribution to variance and to prediction accuracy of the expression profile of the Oncotype DX with that of WGGE profiles.

Data:

Data consist of a subset of the patients (n = 186) used in CS-I who qualify for the Onctoype DX test; these are patients who had ER+ tumors at stage I or stage II. Results are presented for all early-stage luminal patients [ER⁺ or progesterone receptor positive (PR+)] and only for early-stage luminal patients with negative lymph nodes (the target population of the Oncotype DX). The platform includes 21 genes, 16 “risk” genes, and 5 reference (“housekeeping”) genes for the purpose of normalizing the data (Paik et al. 2004). From RNA-seq WGGE profiles, we retrieve the expression profiles from all the risk genes, except RPLP0.

Sequence of models:

The baseline model (COV) included age at diagnosis, race, and ethnicity. Tumor subtype and stage were not included as covariates of the baseline model because all patients had luminal tumors in early stage. The baseline model was first extended by adding the random effects of the expression of the genes included in the Oncotype DX panel (COV + ONCO). Subsequently, we extended the COV + ONCO model by adding the random effects of 17,899 genes not included in the Oncotype DX panel (we labeled this model COV + WGGE, standing for covariates plus whole-genome gene expression). The effects of race and age were treated as fixed, and those of the gene expression profiles of the genes included in either COV + ONCO or COV + WGGE were assigned IID normal priors with null mean and unknown variance (variances were assigned scaled inverse-chi-square priors).

Results:

The results from CS-II are given in Table 2. In this study, we report CV-AUC based on luminal types, all luminals, and only the ones with lymph node negatives. Estimates of variance components revealed that the contribution to variance of the expression of the gene in the Oncotype DX was low (0.027). However, the use of WGGE profiles lead to a sizable fraction of variance explained. Indeed, the estimated variance component associated with WGGE profiles (0.439) amounts to 30% of the variance in risk that is not explained by COV (computed as 0.439/1.439). However, owing to the small sample size, the posterior credibility region for the estimated variance component associated with WGGE profiles was wide. The DIC (“smaller is better”) also suggests that the best model was the one including COV and WGGE profiles. And the CVs based on all luminal cases revealed that adding information from the genes included in the Oncotype DX (COV + ONCO) improved CV-AUC relative to the baseline model by 2.7 points and that adding WGGE profiles increased CV-AUCs (also relative to COV) by 6.5 points. The analyses based on patients with lymph node–negative tumors also revealed a sizable increase in prediction CV-AUC when using WGGE profiles (compared to the baseline model, the model using COV and WGGE had 6.6 points in CV-AUC, and COV + WGGE outperformed COV in 99% of the 200 CVs). However, the prediction CV-AUC of the COV + ONCO model was similar to that obtained with the COV model only. Therefore, we conclude that using WGGE profiles leads to a higher proportion of variance of risk explained and a higher prediction accuracy than can be achieved using the expression profiles of a few genes.

Table 2. Parameter estimates, model goodness of fit, model complexity, and prediction accuracy (case study II).

Whole data analysis									200 CVs
Model	Covariatesa	Oncotype DX	Whole-genome gene expression (WGGE)	Estimated variance (90% posterior confidence region)		Log likelihoodb	Effective number of parameters (pD)	Deviance information criteria (DIC)	Average CV-AUC,c all luminals	AUC model in column > AUC model in row,d all luminals		Average CV-AUC,c lymph node negative	AUC model in column > AUC model in row,d lymph node negative
				Oncotype DX	Whole-genome gene expression					M10	M11		M10	M11
M9 (COV)	X			—	—	−59.7	4.4	123.7	0.703e (0.026)	0.96	>0.99	0.689e (0.052)	0.43	0.99
M10 (COV + ONCO)	X	X		0.027 (0.003; 0.056)	—	−45.3	4.2	94.9	0.725f (0.033)	—	0.99	0.685e (0.055)	—	>0.99
M11 (COV + WGGE)	X		X	—	0.439 (0.083; 0.931)	−37.7	9.2	84.6	0.774g (0.031)	—	—	0.755f (0.039)	—	—

^aAge and race (African American, Y/N).

^bEstimated posterior mean of the log likelihood.

^cAverage over 200 tenfold CVs.

^dProportion of times that the model in column had AUC > the model in row (in 200 tenfold CVs).

^e,f,gThe same letter indicates that the models are no different (empirical P < 0.05).

Case study III: comparison between omics

In the two preceding studies, we assessed the performance of models based on clinical covariates and gene expression information from the tumor cells. In this study, we compared the relative performance of models based on the other omics available: (1) CNVs, (2) methylation (METH), and (3) miRNA.

Data:

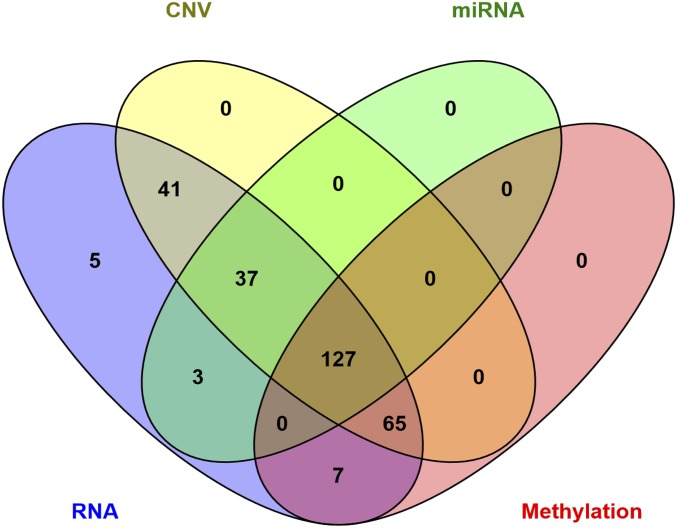
This study includes data from patients who had information for at least one of the omics considered. Figure 1 shows a Venn diagram (Oliveros 2007) representing the number of patients with omic data by layer. The number of individuals with complete omic data are relatively small (n = 127). Therefore, when fitting models for a given omic, we used all the individuals who had information for that omic. This leads to three different sets of patients (we labeled them as sets 1–3, corresponding to individuals with CNV, METH, and miRNA, respectively) to which models were fitted.

Figure 1.

Venn diagram with the number of patients who had information by omic layer (CNV, copy number variant; miRNA, micro-RNA; RNA, RNA abundance measured with RNA-seq).

Sequence of models:

For each set of patients, we compared the performance of a model based on covariates only (COV) with that of a model based on covariates plus data from the corresponding omic (COV + CNV, COV + METH, and COV + miRNA). As before, models were fitted using the BGLR R package with COV as fixed effects and omics as random effects, where the effects of the omics were treated as IID drawn from a normal distribution with null mean and unknown variance.

Results:

Table 3 shows estimates of goodness of fit, model complexity, variance components, and prediction accuracy (AUC in CV) by model. The comparison of models based on COV only with those based on one omic (either METH, CNV, or miRNA) suggests that a model using METH profiles fits the data better than and predicts survival equally well (actually slightly more accurate) as a model based on COV. This suggests that METH profiles information is capturing differences due to tumor subtype and stage. This was not observed for models based on CNV or miRNA; in these two cases, the model based on COV outperformed the prediction accuracy of the models based on either CNV or miRNA only.

Table 3. Parameter estimates, model goodness of fit, model complexity, and prediction accuracy (case study III).

Whole data analysis										200 CVs
Set	Model	Factors Included				Variance (90% posterior confidence region)	Log likelihoode	Effective number of parameters (pD)	Deviance information criteria (DIC)	Average CV-AUCf (SD)	Proportion of times model in column had AUC > model in the row
		Covariatesa	CNVb	METHc	miRNAd						M13, M16, M19: omic only	M14, M17, M20: COV + omic
Set 1 (n = 270)	M12: COV	X				—	−125.5	8.1	259.0	0.699g (0.009)	<0.01	>0.99
	M13: CNV		X			0.637 (0.155; 1.124)	−112.1	26.8	250.9	0.653h (0.012)	—	>0.99
	M14: COV + CNV	X	X			0.398 (0.070; 0.736)	−110.5	24.5	245.6	0.714i (0.009)	—	—
Set 2 (n = 199)	M15: COV	X				—	−88.7	8.4	185.7	0.667g (0.013)	0.60	>0.99
	M16: METH			X		0.652 (0.086; 1.261)	−76.6	18.7	171.8	0.672g,h (0.017)	—	0.76
	M17: COV + METH	X		X		0.402 (0.032; 0.739)	−78.9	18.5	176.3	0.684h (0.013)	—	—
Set 3 (n = 167)	M18: COV	X				—	−71.2	8.2	150.6	0.747g (0.011)	<0.01	0.29
	M19: miRNA				X	0.338 (0.072; 0.615)	−75.2	13.5	163.8	0.623h (0.018)	—	>0.99
	M20: COV + miRNA	X			X	0.179 (0.029; 0.324)	−67.3	13.8	148.5	0.744g (0.011)	—	—

^aAge: African American, Y/N; lobular (Y/N); cancer subtype and stage.

^bCopy-number variants.

^cMethylation.

^dWhole-genome RNA-seq.

^eEstimated posterior mean of the log likelihood.

^fAverage over 200 tenfold CVs.

^g,h,iThe same letter indicates that the models are no different (empirical P < 0.05).

The estimates of variance components derived from models using COV plus one omic (COV + CNV, COV + METH, COV + miRNA) show that METH profiles and CNVs explained a large fraction of interindividual differences in risk that cannot be explained by COV; however, the 95% posterior credibility regions are all wide. According to DIC, the models using COV plus one omic were all better than the model using COV only; however, the differences in DIC were, relative to the model based on COV, large for the case of COV + METH and COV + CNV and very small for the model COV + miRNA (only about 2 points). Finally, the evaluation of prediction accuracy suggests that adding either METH profiles or CNVs to a model based on COV increased prediction accuracy significantly (99% of the time in 200 CVs) but by 1.5 to 1.7 points of AUC. Considering all the results from these case studies, it appears that among the three omics evaluated, METH was the one that explained a large proportion of variance in risk and contributed most to prediction power, both when considered alone or in combination with COV.

Case study IV: integrating multiple omics

Among the four omics considered in the preceding studies, the METH and WGGE models appeared to be the ones that explain a large proportion of variance and achieved the highest levels of prediction accuracy both when considered alone and in combination with COV. Therefore, in this case study, we considered integrating these two omics together with COV into a risk-assessment model. Furthermore, we evaluated the impacts of including interactions between the two omics using a reaction-norm model.

Data:

Data include the individuals (n = 218) who had complete information for COV, METH, and WGGE.

Sequence of models:

The baseline model (COV) is the same as the one described in CS-I. This model was first expanded by adding METH and WGGE additively (COV + METH + WGGE) and subsequently further expanded by adding interactions between omics (COV + METH × WGGE) using a reaction-norm model. As before, COV was included as fixed effects and omics as random effects. In all cases, the random effects were assumed to be Gaussian, with omic-specific variance. The additive model COV + METH + WGGE had two variance parameters linked to the main effects of each of the omics included, and COV + METH × WGGE had three variance parameters, two for main effects and one for interactions.

Results:

Table 4 shows the results obtained in CS-IV. In the additive model (COV + METH + WGGE), the two omics explained about 27% of the variance in risk that was not accounted for by COV (this is estimated as the sum of the two variance components divide by the sum of the two variance components plus the error variance, which in the probit model is 1). When interactions were added, the estimated variance components of the main effects of each omic went down (this relative to the additive model), and the total proportion of variance in risk explained by omics (including main effects and interactions) stays roughly the same. The posterior mean of the log likelihood of the model COV + METH + WGGE was 15.8 points higher than that of the COV model; this indicates that adding the two omics increased goodness of fit markedly. When interactions were added, the change in the log-likelihood relative to COV + METH + WGGE was more modest. DIC (“smaller is better”) indicates a clear superiority of the additive model with two omics relative to COV and almost no difference between COV + METH + WGGE and COV + METH × WGGE. Finally, the evaluation of prediction accuracy from CVs showed that (1) the baseline model had a reasonably good AUC (0.724), (2) the additive model improved the performance by 3 points in AUC (importantly, this increase happened in 99% of the 200 CV), and (3) adding interactions did not clearly improved prediction accuracy (in 60% of the CV the additive model was better than the model having interactions, and in the other 40%, the opposite happened).

Table 4. Parameter estimates, model goodness of fit, model complexity, and prediction accuracy (case study IV).

Whole data analysis											200 CVs
Models	Models components				Estimated variance (90% posterior confidence region)			Log likelihoode	Effective number of parameters (pD)	Deviance information criteria (DIC)	Average CV-AUCf	Proportion of times model in column had AUC > model in row
	COVa	METHb	WGGEc	METH × WGGEd	METH	WGGE	METH × WGGE					COV + METH + WGGE	COV + METH × WGGE
COV	X				—	—	—	−85.7	6.4	177.9	0.724g (0.001)	>0.99	>0.99
COV + METH + WGGE	X	X	X		0.162 (0.075; 0.440)	0.220 (0.090; 0.690)	—	−73.9	17.6	165.4	0.754h (0.004)	—	0.40
COV + METH × WGGE	X	X	X	X	0.101 (0.046; 0.272)	0.138 (0.055; 0.474)	0.101 (0.044; 0.329)	−69.9	20.2	159.9	0.753h (0.005)	—	—

^aAge: African American Y/N; lobular (Y/N); and tumor subtype.

^bMethylation.

^cWhole-genome RNA-seq.

^dMethylation-by-WGGE.

^eEstimated posterior mean of the log likelihood.

^fAverage over 200 tenfold CVs.

^g,hThe same letter indicates that the models are no different (empirical P < 0.05).

Discussion

The availability of multiomic data sets has increased recently, and this trend is expected to continue. Modern omic data sets can be big (large n), high dimensional (each subject can have information on hundreds of thousands of variables), and have a multilayer structure (e.g., data may involve clinical information, demographics, lifestyle, and multiple omics). While recent advances in computational power and methodology have enhanced our ability to analyze these data sets, the availability of methods and data-analysis tools for integrating high-dimensional multilayer inputs for the prediction of disease risk is lacking.

Statistical models for the analysis of multilayer omic data should (1) be able to integrate data from multiple omics, (2) cope with high-dimensional inputs, (3) allow for different architectures of effects across layers, and (4) accommodate interactions between risk factors, including interactions between two or more high-dimensional sets. In this study, we described a Bayesian generalized additive model (BGAM) framework that fulfills those requirements. BGAMs integrate ideas from different sources, including (1) generalized additive models (GAMs) (Hastie 2008), (2) Bayesian regularized regressions (George and McCulloch 1993; Ishwaran and Rao 2005), and (3) modern approaches for modeling interactions between high-dimensional inputs primarily developed for the study of genetic-by-environment interactions (Jarquín et al. 2014). OmicKriging, a multiomic risk-assessment method (Vazquez et al. 2014; Wheeler et al. 2014), can be seen as a special case of the BGAM that assumes additive action across omics and a homogeneous architecture of effects (with Gaussian assumptions) across layers. Within the BGAM framework, some of these assumptions can be relaxed by specifying different prior distributions of effects across layers, by using layer-specific regularization parameters (e.g., layer-specific variances), and by incorporating interactions within or between layers using either parametric or semiparametric procedures. The BGLR R package (Pérez and de los Campos 2014) allows me to incorporate all these features for quantitative (censored or not), ordinal, and binary traits. In our application we used the BGLR with data from TCGA to build risk-assessment models for prediction of survival of BC patients using clinical covariates and multiple omics.

Omic information (e.g., gene expression patterns) can reveal important processes taking place at the cellular level. Previous studies (Wheeler et al. 2014) have shown successful integration of multilayer omics for prediction of cell phenotypes. In these studies, the phenotype was measured in the same cells where omics were assessed. Prediction of whole-organism phenotypes is considerably more challenging due to intercell variations in omics and traits and because the link between the cellular processes at the tissues where omics were assessed and target phenotype/disease may be weak owing to multiple intervening factors. Perhaps for this reason, the integration of multiple omics for prediction of whole-organism phenotypes has been much more limited. For instance, using OmicKriging Wheeler et al. (2014) did not observe benefits of integrating DNA and gene expression information for prediction of a pharmacogenetic trait (change in low-density lipoprotein cholesterol after simvastatin treatment) relative to models based on DNA information only.

Recently, Yuan et al. (2014) considered integrating omics with clinical covariates for prediction of survival in four different types of cancers (i.e., ovarian, renal, glioblastoma multiforme, and lung squamous cell carcinoma). In most cases, the authors did not find a significance gain in prediction accuracy by combining omics with clinical covariates relative to the covariate-only model. In a few combinations of cancers and omics, the authors reported a statistically significant gain in prediction accuracy, but the magnitude of the gain was very low. In our study, we found significant gains in prediction accuracy when integrating either WGGE or METH, with gains in AUC ranging from 2 to 7 points. An important difference between the study by Yuan et al. (2014) and this study is that the modeling approach used here (BGAM) assigned different regularization parameters for different sets of inputs. This allowed the model to weight differentially information from clinical covariates and from different omics. To illustrate the importance of assigning different priors/regularization parameters for different omics, we conducted a sensitivity analysis in which we fitted the model incorporating COV, WGGE, and METH of CS-IV without assigning different priors/regularization parameters for each of the three inputs sets. The results are presented in File S1, Table S1.4. Assigning the same prior/regularization parameters to all the effects resulted in a substantial loss in AUC: from 0.754 (model COV + WGGE + METH, CS-IV) to levels of AUC on the order of 0.56 when the same inputs were assigned the same prior/regularization parameters and 0.64 when the same inputs were assigned the same prior in a variable selection model (BayesB).

BC becomes lethal after migrating from the breast with the development of distant metastases on organs (e.g., brain or liver). An important strength of our application is that all the omics used for prediction of survival of BC patients were assessed at the primary tumor: the tissue where the disease is unfolding. An additional strength of this application is that the overwhelming majority of cancer samples are primary tumor only. Our response variable considered alive status (0/1), but one could also regress survival time as a censored outcome on covariates and omics using parametric (e.g., Weibull, log-normal) or semiparametric regression (e.g., Cox proportional hazard regression) (Cox 1972).

Several risk factors are associated with the likelihood of developing distant metastases and, ultimately, survival. The risk factors commonly considered when assessing cancer patients, including tumor type, subtype, and stage, were found to be significantly associated with survival in TCGA. Other factors commonly considered when assessing BC patients, including lymph node invasion, marginal status (whether cancerous cells are present in the remaining margins at the site of surgery), increased size of the primary tumor, and level of loss of histopathology differentiation in the tumor cells themselves were not significantly associated with survival when a full set of COV was included. Consequently, our baseline COV model included demographics (race and age at diagnosis) and the three clinical covariates that had significant association with survival (lobular/ductal, tumor subtype, and stage).

Cancer subtype and stage are the most important predictors considered by a clinician when assessing BC patients. Our study showed that these two predictors are indeed the clinical COV that offers highest prediction accuracy. Our CS-I also shows that WGGE profile had more predictive power than any of the predictors commonly used in clinical practice, including cancer subtype and state, which are well established in the literature (Koscielny et al. 1984; Carter et al. 1989; Rosen et al. 1989; Elston and Ellis 1991; Sørlie et al. 2001; Weigelt et al. 2005) as clinical predictors of BC progression and survival.

Gene expression is informative of cancer subtype and stage; indeed, gene expression patterns are predictive of intrinsic subtypes, which are then confirmed by receptor subtype (Sørlie et al. 2001). However, our results suggest that even after accounting for all the variables commonly used to assess cancer patients, including stage and cancer subtype, the addition of WGGE profiles can further improve prediction accuracy. The gains in prediction accuracy obtained when adding WGGE profiles were moderate in magnitude (2.0–2.5 points in AUC) when we considered all the cancer subtypes together to be very relevant (7 points in AUC) when models were fitted to a particular subtype, as was the case in CS-II. Because the COV model includes cancer stage and subtype, which are correlated with gene expression–derived clusters (Sørlie et al. 2001), the gains in predictive accuracy obtained with the addition of WGGE profiles cannot be attributed to clustering. To demonstrate this, we derived the leading five principal components (PCs) of gene expression and tested the significance of adding these PCs as predictors in the COV model using a likelihood-ratio test. The results (see File S1, Table S1.5) indicated that after accounting for COV, the leading five PCs did not have a significant effect on survival. Therefore, we conclude that the gains in predictive accuracy observed are largely owing to patterns other than the clustering obtainable with the first PC from gene expression.

The predictive power of gene expression profiles was established in the literature more than a decade ago. However, risk assessment is typically based on the expression profiles of a few large-effect genes (Paik et al. 2004; Glas et al. 2006). Results from SNP data in other contexts suggest that the information from large numbers of markers may increase the phenotypic variance explained better than preselecting small numbers of SNPs (Allen et al. 2010; Vazquez et al. 2010). While the expression profiles of preselected genes are certainly predictive of BC outcomes, valuable information may be lost when the nonselected genes are ignored. The results from CS-II confirmed this hypothesis. Indeed, our results indicate that the use of WGGE profiles leads to a larger proportion of variance in risk explained and provides higher predictive accuracy of BC patient survival than what can be obtained using the expression profiles of a few oncogenes. With modern sequencing technologies, assessing WGGE profiles has become feasible, and it should be economically viable. We argue that the use of WGGE profiles for assessment of BC patients should receive more attention.

In addition to WGGE profiles, the CNV and METH models offer some promising results. Methylation has been shown to be an interesting set to predict plant traits (Hu et al. 2015). In our study, methylation considered alone offered higher predictive accuracy than a model based on clinical predictors, including both cancer stage and subtype. Further studies are needed to assess whether the association between methylation and survival is due to common factors (e.g., carcinogenic factors that affect methylation pattern and BC progression at the same time) or to mediation (e.g., that the effects of carcinogenic factors may be mediated by methylation). However, our results did not show a large variance associated with miRNA in the survival of BC patients. Further studies with larger sample sizes will be needed to determine whether our model results involving miRNA are due to lack of power or to weak association between miRNA profiles and survival.

Methylation additively integrated to WGGE explains about 30% of the variance in risk that was not explained by COV, and the AUC of the model was 3 points greater than that achieved with COV. This gain in AUC is slightly greater (∼1 point greater) than what we achieved in CS-I and CS-III when we added one omic at a time. This suggests that even though METH and WGGE profiles provide, to some extent, redundant information, such redundancy is not complete, and there may be some benefits to including both omics in a model. When we added interactions, we did not observe performance improvement relative to the additive model. Neither the proportion of variance explained by omics nor predictive accuracy increased relative to the additive model. Further studies with higher sample sizes and perhaps with analyses within cancer subtype are needed to fully explore the potential benefits of including multiple omics with omic-by-omic interaction.

In this study, we demonstrate how clinical information can be integrated with whole-genome omic data derived from several omic layers, including the genome (e.g., CNV), epigenome (METH), and transcriptome (miRNA and WGGE profiles). With some of the omics, we found statistically significant and, in some cases, substantial gains in predictive accuracy relative to models based on clinical COV. However, our ability to detect improvements may have been limited by three main factors. The first is small sample size. Most of the models we considered involved large numbers of effects. Although Bayesian methods allow handling high-dimensional predictors even in settings where the number of effects exceeds sample size, the accuracy of estimates of individual effects is low when the number of effects is large relative to sample size. Therefore, considerably larger numbers of samples will be needed to realize the potential contribution to predictive accuracy. The second limiting factor is that in three of our four case studies, we treated BC as a single disease and included the cancer subtype in the model. When BC is treated as a homogeneous disease, a large fraction of interindividual difference in survival can be attributed to cancer subtype. We decided to carry out CS-I, CS-III, and CS-IV based on all BC cases because carrying out analyses within cancer subtype would have reduced the sample size. In the only case where we considered a within-subtype analysis (CS-II), we detected gains in prediction accuracy that were considerably larger than when all subtypes were considered jointly. This suggests that omics may contribute significantly to prediction of interindividual differences in progression and survival within subtypes, thus paving the way to a more precise approach to the treatment of BC patients. Finally, the third limiting factor is that TCGA is a relatively new repository for BC, and hence, follow-up time is short for many patients, and limited follow-up time reduces the information content of each case. In the near future, the availability of large data sets comprising clinical information and multilayer omic data will increase, and such data sets will allow researchers to explore the limits of what multilayer omic data can contribute to prediction of BC progression and patient survival.