Lasso adjustments of treatment effect estimates in randomized experiments

Abstract

We provide a principled way for investigators to analyze randomized experiments when the number of covariates is large. Investigators often use linear multivariate regression to analyze randomized experiments instead of simply reporting the difference of means between treatment and control groups. Their aim is to reduce the variance of the estimated treatment effect by adjusting for covariates. If there are a large number of covariates relative to the number of observations, regression may perform poorly because of overfitting. In such cases, the least absolute shrinkage and selection operator (Lasso) may be helpful. We study the resulting Lasso-based treatment effect estimator under the Neyman–Rubin model of randomized experiments. We present theoretical conditions that guarantee that the estimator is more efficient than the simple difference-of-means estimator, and we provide a conservative estimator of the asymptotic variance, which can yield tighter confidence intervals than the difference-of-means estimator. Simulation and data examples show that Lasso-based adjustment can be advantageous even when the number of covariates is less than the number of observations. Specifically, a variant using Lasso for selection and ordinary least squares (OLS) for estimation performs particularly well, and it chooses a smoothing parameter based on combined performance of Lasso and OLS.

Randomized experiments are widely used to measure the efficacy of treatments. Randomization ensures that treatment assignment is not influenced by any potential confounding factors, both observed and unobserved. Experiments are particularly useful when there is no rigorous theory of a system’s dynamics, and full identification of confounders would be impossible. This advantage was cast elegantly in mathematical terms in the early 20th century by Jerzy Neyman, who introduced a simple model for randomized experiments, which showed that the difference of average outcomes in the treatment and control groups is statistically unbiased for the average treatment effect (ATE) over the experimental sample (1).

However, no experiment occurs in a vacuum of scientific knowledge. Often, baseline covariate information is collected about individuals in an experiment. Even when treatment assignment is not related to these covariates, analyses of experimental outcomes often take them into account with the goal of improving the accuracy of treatment effect estimates. In modern randomized experiments, the number of covariates can be very large—sometimes even larger than the number of individuals in the study. In clinical trials overseen by regulatory bodies like the Food and Drug Administration and the Medicines and Healthcare products Regulatory Agency, demographic and genetic information may be recorded about each patient. In applications in the tech industry, where randomization is often called A/B testing, there is often a huge amount of behavioral data collected on each user. However, in this “big data” setting, much of these data may be irrelevant to the outcome being studied or there may be more potential covariates than observations, especially once interactions are taken into account. In these cases, selection of important covariates or some form of regularization is necessary for effective regression adjustment.

To ground our discussion, we examine a randomized trial of the pulmonary artery catheter (PAC) that was carried out in 65 intensive care units in the United Kingdom between 2001 and 2004, called PAC-man (2). The PAC is a monitoring device commonly inserted into critically ill patients after admission to intensive care, and it provides a continuous measurement of several indicators of cardiac activity. However, insertion of PAC is an invasive procedure that carries some risk of complications (including death), and it involves significant expenditure both in equipment costs and personnel (3). Controversy over its use came to a head when an observational study found that PAC had an adverse effect on patient survival and led to increased cost of care (4). This led to several large-scale randomized trials, including PAC-man.

In the PAC-man trial, randomization of treatment was largely successful, and a number of covariates were measured about each patient in the study. If covariate interactions are included, the number of covariates exceeds the number of individuals in the study; however, few of them are predictive of the patient’s outcome. As it turned out, the (pretreatment) estimated probability of death was imbalanced between the treatment and control groups (P = 0.005, Wilcoxon rank sum test). Because the control group had, on average, a slightly higher risk of death, the unadjusted difference-in-means estimator may overestimate the benefits of receiving a PAC. Adjustment for this imbalance seems advantageous in this case, because the pretreatment probability of death is clearly predictive of health outcomes posttreatment.

In this paper, we study regression-based adjustment, using the least absolute shrinkage and selection operator (Lasso) to select relevant covariates. Standard linear regression based on ordinary least squares (OLS) suffers from overfitting if a large number of covariates and interaction terms are included in the model. In such cases, researchers sometimes perform model selection based on observing which covariates are unbalanced given the realized randomization. This generally leads to misleading inferences because of incorrect test levels (5). The Lasso (6) provides researchers with an alternative that can mitigate these problems and still perform model selection. We define an estimator, ${\widehat{ATE}}_{\text{Lasso}}$, which is based on running an $l_1$-penalized linear regression of the outcome on treatment, covariates, and, following the method introduced in ref. 7, treatment by covariate interactions. Because of the geometry of the $l_1$ penalty, the Lasso will usually set many regression coefficients to 0, and is well defined even if the number of covariates is larger than the number of observations. The Lasso’s theoretical properties under the standard linear model have been widely studied in the last decade; consistency properties for coefficient estimation, model selection, and out-of-sample prediction are well understood (see ref. 8 for an overview).

In the theoretical analysis in this paper, instead of assuming that the standard linear model is the true data-generating mechanism, we work under the aforementioned nonparametric model of randomization introduced by Neyman (1) and popularized by Donald Rubin (9). In this model, the outcomes and covariates are fixed quantities, and the treatment group is assumed to be sampled without replacement from a finite population. The treatment indicator, rather than an error term, is the source of randomness, and it determines which of two potential outcomes is revealed to the experimenter. Unlike the standard linear model, the Neyman–Rubin model makes few assumptions not guaranteed by the randomization itself. The setup of the model does rely on the stable unit treatment value assumption, which states that there is only one version of treatment, and that the potential outcome of one unit should be unaffected by the particular assignment of treatments to the other units; however, it makes no assumptions of linearity or exogeneity of error terms. OLS (7, 10, 11), logistic regression (12), and poststratification (13) are among the adjustment methods that have been studied under this model.

To be useful to practitioners, the Lasso-based treatment effect estimator must be consistent and yield a method to construct valid confidence intervals. We outline conditions on the covariates and potential outcomes that will guarantee these properties. We show that an upper bound for the asymptotic variance can be estimated from the model residuals, yielding asymptotically conservative confidence intervals for the ATE, which can be substantially narrower than the unadjusted confidence intervals. Simulation studies are provided to show the advantage of the Lasso-adjusted estimator and to show situations where it breaks down. We apply the estimator to the PAC-man data, and compare the estimates and confidence intervals derived from the unadjusted, OLS-adjusted, and Lasso-adjusted methods. We also compare different methods of selecting the Lasso tuning parameter on these data.

Framework and Definitions

We give a brief outline of the Neyman–Rubin model for a randomized experiment; the reader is urged to consult refs. 1, 9, and 14 for more details. We follow the notation introduced in refs. 7 and 10. For concreteness, we illustrate the model in the context of the PAC-man trial.

For each individual in the study, the model assumes that there exists a pair of quantities representing his/her health outcomes under the possibilities of receiving and not receiving the catheter. These are called the potential outcomes under treatment and control, and are denoted as $a_i$ and $b_i$, respectively. In the course of the study, the experimenter observes only one of these quantities for each individual, because the catheter is either inserted or not. The causal effect of the treatment on individual i is defined, in theory, to be $a_i\mathrm{-}{b}_i$, but this is unobservable. Instead of trying to infer individual-level effects, we will assume that the intention is to estimate the average causal effect over the whole population, as outlined in the next section.

In the mathematical specification of this model, we consider the potential outcomes to be fixed, nonrandom quantities, even though they are not all observable. The only randomness in the model comes from the assignment of treatment, which is controlled by the experimenter. We define random treatment indicators $T_i$, which take on a value 1 for a treated individual, or 0 for an untreated individual. We will assume that the set of treated individuals is sampled without replacement from the full population, where the size of the treatment group is fixed beforehand; thus, the $T_i$ are identically distributed but not independent. The model for the observed outcome for individual i, defined as $Y_i$, is thus as follows:

$$Y_i=T_i{a}_i+\left(1-T_i\right)b_i.$$

This equation simply formalizes the idea that the experimenter observes the potential outcome under treatment for those who receive the treatment, and the potential outcome under control for those who do not.

Note that the model does not incorporate any covariate information about the individuals in the study, such as physiological characteristics or health history. However, we will assume we have measured a vector of baseline, preexperimental covariates for each individual i. These might include, for example, age, gender, and genetic makeup. We denote the covariates for individual i as the column vector ${\mathbf{x}}_i={\left(x_{i1},\dots ,x_{ip}\right)}^T\mathrm{\in }{\mathrm{ℝ}}^p$ and the full design matrix of the experiment as $X={\left({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\right)}^T$. In Theoretical Results, we will assume that there is a correlational relationship between an individual’s potential outcomes and covariates, but we will not assume a generative statistical model.

Define the set of treated individuals as $A=\left\{i\in \left\{1,\dots ,n\right\}:T_i=1\right\}$, and similarly define the set of control individuals as B. Define the number of treated and control individuals as $n_A=\left|A\right|$ and $n_B=\left|B\right|$, respectively, so that $n_A+n_B=n$. We add a line on top of a quantity to indicate its average and a subscript A or B to label the treatment or control group. Thus, for example, the average values of the potential outcomes and the covariates in the treatment group are as follows:

$${\overline{a}}_A=n_A^{-1}{\displaystyle {\sum }_{i\in A}{a}_i,}{\overline{\mathbf{x}}}_A=n_A^{-1}{\displaystyle {\sum }_{i\in A}{\mathbf{x}}_i},$$

respectively. Note that these are random quantities in this model, because the set A is determined by the random treatment assignment. Averages over the whole population are denoted as

$$\overline{a}=n^{-1}{\displaystyle {\sum }_{i=1}^n{a}_i},\hspace{0.17em}\overline{b}=n^{-1}{\displaystyle {\sum }_{i=1}^n{b}_i},\hspace{0.17em}\overline{\mathbf{x}}=n^{-1}{\displaystyle {\sum }_{i=1}^n{\mathbf{x}}_i}.$$

Note that the averages of potential outcomes over the whole population are not considered random, but are unobservable.

Treatment Effect Estimation

Our main inferential goal will be average effect of the treatment over the whole population in the study. In a trial such as PAC-man, this represents the difference between the average outcome if everyone had received the catheter, and the average outcome if no one had received it. This is defined as follows:

$$ATE=\overline{a}-\overline{b}.$$

The most natural estimator arises by replacing the population averages with the sample averages:

$${\widehat{ATE}}_{\text{unadj}}={\overline{a}}_A-{\overline{b}}_B,$$

The subscript “unadj” indicates an estimator without regression adjustment. The foundational work in ref. 1 points out that, under a randomized assignment of treatment, ${\widehat{ATE}}_{\text{unadj}}$ is unbiased for $ATE$, and derives a conservative procedure for estimating its variance.

Although ${\widehat{ATE}}_{\text{unadj}}$ is an attractive estimator, covariate information can be used to make adjustments in the hope of reducing variance. A commonly used estimator is as follows:

$${\widehat{ATE}}_{\text{adj}}\mathrm{=}\left[{\overline{a}}_A-{\left({\overline{\mathbf{x}}}_A-\overline{\mathbf{x}}\right)}^T{\widehat{\mathit{\beta }}}^{\left(a\right)}\right]-\left[{\overline{b}}_B-{\left({\overline{\mathbf{x}}}_B-\overline{\mathbf{x}}\right)}^T{\widehat{\mathit{\beta }}}^{\left(b\right)}\right],$$

where ${\widehat{\mathit{\beta }}}^{\left(a\right)},{\widehat{\mathit{\beta }}}^{\left(b\right)}\in {\mathrm{ℝ}}^p$ are adjustment vectors for the treatment and control groups, respectively, as indicated by the superscripts. The terms ${\overline{\mathbf{x}}}_A-\overline{\mathbf{x}}$ and ${\overline{\mathbf{x}}}_B-\overline{\mathbf{x}}$ represent the fluctuation of the covariates in the subsample relative to the full sample, and the adjustment vectors fit the linear relationships between the covariates and potential outcomes under treatment and control. For example, in the PAC-man trial, this would help alleviate the imbalance in the pretreatment estimated probability of death: the corresponding element of ${\overline{\mathbf{x}}}_B-\overline{\mathbf{x}}$ would be positive (due to the higher average probability of death in the control group), the corresponding element of ${\widehat{\mathit{\beta }}}^{\left(b\right)}$ would be negative (a higher probability of death correlates with worse health outcomes), so the overall treatment effect estimate would be adjusted downward. This procedure is equivalent to imputing the unobserved potential outcomes; if we define

$${\widehat{\overline{a}}}_B={\overline{a}}_A\mathrm{+}{\left({\overline{\mathbf{x}}}_B-{\overline{\mathbf{x}}}_A\right)}^T{\widehat{\mathit{\beta }}}^{\left(a\right)},\hspace{0.17em}{\widehat{\overline{b}}}_A={\overline{b}}_B+{\left({\overline{\mathbf{x}}}_A-{\overline{\mathbf{x}}}_B\right)}^T{\widehat{\mathit{\beta }}}^{\left(b\right)},$$

we can form the equivalent estimator:

$${\widehat{ATE}}_{\text{adj}}=n^{-1}\left(n_A{\overline{a}}_A+n_B{\widehat{\overline{a}}}_B\right)-n^{-1}\left(n_B{\overline{b}}_B+n_A{\widehat{\overline{b}}}_A\right).$$

If we consider these adjustment vectors to be fixed (nonrandom), or if they are derived from an independent data source, then this estimator is still unbiased, and may have substantially smaller asymptotic and finite-sample variance than the unadjusted estimator. This allows for construction of tighter confidence intervals for the true treatment effect.

In practice, the “ideal” linear adjustment vectors, leading to a minimum-variance estimator of the form of ${\widehat{ATE}}_{\text{adj}}$, cannot be computed from the observed data. However, they can be estimated, possibly at the expense of introducing modest finite-sample bias into the treatment effect estimate. In the classical setup, when the number of covariates is relatively small, OLS regression can be used. The asymptotic properties of this kind of estimator are explored under the Neyman–Rubin model in refs. 7, 11, and 12. We will follow a particular scheme that is studied in ref. 7 and shown to have favorable properties: we regress the outcome on treatment indicators, covariates, and treatment by covariate interactions. This is equivalent to running separate regressions in the treatment and control groups of outcome against an intercept and covariates. If we define ${\widehat{\mathit{\beta }}}_{\text{OLS}}^{\left(a\right)}$ and ${\widehat{\mathit{\beta }}}_{\text{OLS}}^{\left(b\right)}$ as the coefficients from the separate regressions, then the estimator is as follows:

$${\widehat{ATE}}_{\text{OLS}}=\left[{\overline{a}}_A-{\left({\overline{\mathbf{x}}}_A-\overline{\mathbf{x}}\right)}^T{\widehat{\mathit{\beta }}}_{\text{OLS}}^{\left(a\right)}\right]-\left[{\overline{b}}_B-{\left({\overline{\mathbf{x}}}_B-\overline{\mathbf{x}}\right)}^T{\widehat{\mathit{\beta }}}_{\text{OLS}}^{\left(b\right)}\right].$$

This has some finite-sample bias, but ref. 7 shows that it vanishes quickly at the rate of $1/n$ under moment conditions on the potential outcomes and covariates. Moreover, for a fixed p, under regularity conditions, the inclusion of interaction terms guarantees that it never has higher asymptotic variance than the unadjusted estimator, and asymptotically conservative confidence intervals for the true parameter can be constructed.

In modern randomized trials, where a large number of covariates are recorded for each individual, p may be comparable to or even larger than n. In this case, OLS regression can overfit the data badly, or may even be ill posed, leading to estimators with large finite-sample variance. To remedy this, we propose estimating the adjustment vectors using the Lasso (6). The adjustment vectors would take the following form:

$${\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(a\right)}=\underset{\mathit{\beta }}{\text{arg}\hspace{0.17em}\text{min}}\hspace{0.17em}\left[\frac{1}{2n_A}{\displaystyle \sum _{i\in A}{\left(a_i-{\overline{a}}_A-{\left({\mathbf{x}}_i-{\overline{\mathbf{x}}}_A\right)}^T\mathit{\beta }\right)}^2}+{\lambda }_a{\displaystyle \sum _{j=1}^p\left|{\beta }_j\right|}\right],$$ [1]

$${\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(b\right)}=\underset{\mathit{\beta }}{\text{arg}\hspace{0.17em}\text{min}}\hspace{0.17em}\left[\frac{1}{2n_B}{\displaystyle \sum _{i\in B}{\left(b_i-{\overline{b}}_B-{\left({\mathbf{x}}_i-{\overline{\mathbf{x}}}_B\right)}^T\mathit{\beta }\right)}^2}+{\lambda }_b{\displaystyle \sum _{j=1}^p\left|{\beta }_j\right|}\right],$$ [2]

and the proposed Lasso-adjusted ATE estimator is as follows:

$${\widehat{ATE}}_{\text{Lasso}}=\left[{\overline{a}}_A-{\left({\overline{\mathbf{x}}}_A-\overline{\mathbf{x}}\right)}^T{\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(a\right)}\right]-\left[{\overline{b}}_B-{\left({\overline{\mathbf{x}}}_B-\overline{\mathbf{x}}\right)}^T{\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(b\right)}\right].$$

[To simplify the notation, we omit the dependence of ${\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(a\right)}$, ${\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(b\right)}$, ${\lambda }_a$, and ${\lambda }_b$ on the population size n.] Here, ${\lambda }_a$ and ${\lambda }_b$ are regularization parameters for the Lasso, which must be chosen by the experimenter; simulations show that cross-validation (CV) works well. In the next section, we study this estimator under the Neyman–Rubin model and provide conditions on the potential outcomes, the covariates, and the regularization parameters under which ${\widehat{ATE}}_{\text{Lasso}}$ enjoys similar asymptotic and finite-sample advantages as ${\widehat{ATE}}_{\text{OLS}}$.

It is worth noting that, when two different adjustments are made for the treatment and control groups as in ref. 7 and here, the covariates do not have to be the same for the two groups. However, when they are not the same, the Lasso- or OLS-adjusted estimators are no longer guaranteed to have smaller or equal asymptotic variance than the unadjusted one, even in the case of fixed p. In practice, one may still choose between the adjusted and unadjusted estimators based on the widths of the corresponding confidence intervals.

Theoretical Results

Notation.

For a vector $\mathit{\beta }\mathrm{\in }{R}^p$ and a subset $S\subset \left\{1,\dots ,p\right\}$, let ${\beta }_j$ be the jth component of $\mathit{\beta }$, ${\mathit{\beta }}_S={\left({\beta }_j:j\in S\right)}^T$, $S^c$ be the complement of S, and $\left|S\right|$ the cardinality of the set S. For any column vector $\mathbf{u}={\left(u_1,\dots ,u_m\right)}^T$, let ${\Vert \mathbf{u}\Vert }_2^2={\displaystyle {\sum }_{i=1}^m{u}_i^2}$, ${\Vert \mathbf{u}\Vert }_1={\displaystyle {\sum }_{i=1}^m\left|u_i\right|}$, ${\Vert \mathbf{u}\Vert }_{\infty }={\text{max}}_{i=1,\dots ,m}\left|u_i\right|$, and ${\Vert \mathbf{u}\Vert }_0=\left|\left\{j:u_j\ne 0\right\}\right|$. For a given $m\times m$ matrix D, let ${\lambda }_{\text{min}}\left(D\right)$ and ${\lambda }_{\text{max}}\left(D\right)$ be the smallest and largest eigenvalues of D, respectively, and $D^{-1}$, the inverse of the matrix D. Let $\stackrel{d}{\to }$ and $\stackrel{p}{\to }$ denote convergence in distribution and in probability, respectively.

Decomposition of the Potential Outcomes.

The Neyman–Rubin model does not assume a linear relationship between the potential outcomes and the covariates. To study the properties of adjustment under this model, we decompose the potential outcomes into a term linear in the covariates and an error term. Given vectors of coefficients ${\mathit{\beta }}^{\left(a\right)},{\mathit{\beta }}^{\left(b\right)}\in {\mathrm{ℝ}}^p$, we write for $i=1,\dots ,n$,

$$a_i=\overline{a}+{\left({\mathbf{x}}_i-\overline{\mathbf{x}}\right)}^T{\mathit{\beta }}^{\left(a\right)}+e_i^{\left(a\right)},$$ [3]

$$b_i=\overline{b}+{\left({\mathbf{x}}_i-\overline{\mathbf{x}}\right)}^T{\mathit{\beta }}^{\left(b\right)}+e_i^{\left(b\right)}.$$ [4]

[Again, we omit the dependence of ${\mathit{\beta }}^{\left(a\right)}$, ${\mathit{\beta }}^{\left(b\right)}$, ${\lambda }_a$, ${\lambda }_b$, $e^{\left(a\right)}$, and $e^{\left(b\right)}$ on n.]

Note that we have not added any assumptions to the model; we have simply defined unit-level residuals, $e_i^{\left(a\right)}$ and $e_i^{\left(b\right)}$, given the vectors ${\mathit{\beta }}^{\left(a\right)},{\mathit{\beta }}^{\left(b\right)}$. All of the quantities in [3] and [4] are fixed, deterministic numbers. It is easy to verify that ${\overline{e}}^{\left(a\right)}={\overline{e}}^{\left(b\right)}=0$. To pursue a theory for the Lasso, we will add assumptions on the populations of $a_i$’s, $b_i$’s, and ${\mathbf{x}}_i$’s, and we will assume the existence of ${\mathit{\beta }}^{\left(a\right)},{\mathit{\beta }}^{\left(b\right)}$ such that the error terms satisfy certain assumptions.

Conditions.

We will need the following to hold for both the treatment and control potential outcomes. The first set of assumptions (1–3) are similar to those found in ref. 7.

Condition 1:

Stability of treatment assignment probability.

$$n_A/n\to p_A,\hspace{0.17em}\text{as}\hspace{0.17em}n\to \mathrm{\infty },$$ [5]

for some $p_A\in \left(\mathrm{0,1}\right)$.

Condition 2:

The centered moment conditions. There exists a fixed constant $L>0$ such that, for all $n=\mathrm{1,2},\dots$ and $j=1,\dots ,p$,

$$n^{-1}{\displaystyle {\sum }_{i=1}^n{\left(x_{ij}-{\left(\overline{\mathbf{x}}\right)}_j\right)}^4}\mathrm{\le }L;$$ [6]

$$n^{-1}{\displaystyle {\sum }_{i=1}^n{\left(e_i^{\left(a\right)}\right)}^4}\le L;\hspace{0.5em}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{\left(e_i^{\left(b\right)}\right)}^4}\le L.$$ [7]

Condition 3:

The means $n^{-1}{\displaystyle {\sum }_{i=1}^n{\left(e_i^{\left(a\right)}\right)}^2}$, $n^{-1}{\displaystyle {\sum }_{i=1}^n{\left(e_i^{\left(b\right)}\right)}^2}$, and $n^{-1}{\displaystyle {\sum }_{i=1}^n{e}_i^{\left(a\right)}{e}_i^{\left(b\right)}}$ converge to finite limits.

Because we consider the high-dimensional setting where p is allowed to be much larger than n, we need additional assumptions to ensure that the Lasso is consistent for estimating ${\mathit{\beta }}^{\left(a\right)}$ and ${\mathit{\beta }}^{\left(b\right)}$. Before stating them, we define several quantities.

Definition 1:

Given ${\mathit{\beta }}^{\left(a\right)}$ and ${\mathit{\beta }}^{\left(b\right)}$, the sparsity measures for treatment and control groups, $s^{\left(a\right)}$ and $s^{\left(b\right)}$, are defined as the number of nonzero elements of ${\mathit{\beta }}^{\left(a\right)}$ and ${\mathit{\beta }}^{\left(b\right)}$, i.e.,

$$s^{\left(a\right)}=\left|\left\{j:{\beta }_j^{\left(a\right)}\ne 0\right\}\right|,\hspace{0.17em}{s}^{\left(b\right)}=\left|\left\{j:{\beta }_j^{\left(b\right)}\ne 0\right\}\right|,$$ [8]

respectively. We will allow $s^{\left(a\right)}$ and $s^{\left(b\right)}$ to grow with n, although the notation does not explicitly show this.

Definition 2:

Define ${\delta }_n$ to be the maximum covariance between the error terms and the covariates.

$${\delta }_n=\underset{\omega =a,b}{\text{max}}\left\{\underset{j}{\text{max}}\left|\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(x_{ij}-{\left(\overline{\mathbf{x}}\right)}_j\right)\left(e_i^{\left(\omega \right)}-{\overline{e}}^{\left(\omega \right)}\right)}\right|\right\}.$$ [9]

The following conditions will guarantee that the Lasso consistently estimates the adjustment vectors ${\mathit{\beta }}^{\left(a\right)},{\mathit{\beta }}^{\left(b\right)}$ at a fast enough rate to ensure asymptotic normality of ${\widehat{ATE}}_{\text{Lasso}}$. It is an open question whether a weaker form of consistency would be sufficient for our results to hold.

Condition 4:

Decay and scaling. Let $s=\text{max}\left\{s^{\left(a\right)},s^{\left(b\right)}\right\}$.

$${\delta }_n=o\left(\frac{1}{s\sqrt{\log \hspace{0.17em}p}}\right).$$ [10]

$$\left(s\hspace{0.17em}\log \hspace{0.17em}p\right)/\sqrt{n}=o\left(1\right).$$ [11]

Condition 5:

Cone invertibility factor. Define the Gram matrix as $\mathrm{\Sigma }=n^{-1}{\displaystyle {\sum }_{i=1}^n\left({\mathbf{x}}_i-\overline{\mathbf{x}}\right){\left({\mathbf{x}}_i-\overline{\mathbf{x}}\right)}^T}$: There exist constants $C>0$ and $\mathit{\xi }>1$ not depending on n, such that

$${\Vert {\mathbf{h}}_S\Vert }_1\le Cs{\Vert {\displaystyle \Sigma \mathbf{h}}\Vert }_{\infty },\hspace{0.17em}\forall \mathbf{h}\in \mathcal{C},$$ [12]

with $\mathcal{C}=\left\{\mathbf{h}:{\Vert {\mathbf{h}}_{S^c}\Vert }_1\le \xi {\Vert {\mathbf{h}}_S\Vert }_1\right\}$, and

$$S=\left\{j:{\beta }_j^{\left(a\right)}\ne 0\hspace{0.17em}\text{or}\hspace{0.17em}{\beta }_j^{\left(b\right)}\ne 0\right\}.$$ [13]

Condition 6:

Let $\tau =\text{min}\left\{1/70,{\left(3p_A\right)}^2/70,{\left(3-3p_A\right)}^2/70\right\}$. For constants $0<\eta <\left(\xi -1\right)/\left(\xi +1\right)$ and $1/\eta <M<\infty$, assume the regularization parameters of the Lasso belong to the following sets:

$${\lambda }_a\in \left(\frac{1}{\eta },M\right]\times \left(\frac{2\left(1+\tau \right)L^{1/2}}{p_A}\sqrt{\frac{2\hspace{0.17em}\log \hspace{0.17em}p}{n}}+{\delta }_n\right),$$ [14]

$${\lambda }_b\in \left(\frac{1}{\eta },M\right]\times \left(\frac{2\left(1+\tau \right)L^{1/2}}{p_B}\sqrt{\frac{2\log p}{n}}+{\delta }_n\right).$$ [15]

Denote, respectively, the population variances of $e^{\left(a\right)}$ and $e^{\left(b\right)}$ and the population covariance between them by the following:

$$\begin{array}{c}{\sigma }_{e^{\left(a\right)}}^2=n^{-1}{\displaystyle {\sum }_{i=1}^n{\left(e_i^{\left(a\right)}\right)}^2},{\sigma }_{e^{\left(b\right)}}^2=n^{-1}{\displaystyle {\sum }_{i=1}^n{\left(e_i^{\left(b\right)}\right)}^2},\\ {\sigma }_{e^{\left(a\right)}{e}^{\left(b\right)}}=n^{-1}{\displaystyle {\sum }_{i=1}^n{e}_i^{\left(a\right)}{e}_i^{\left(b\right)}}.\end{array}$$

Theorem 1.

Assume Conditions 1–6 hold for some ${\mathit{\beta }}^{\left(a\right)}$ and ${\mathit{\beta }}^{\left(b\right)}$. Then,

$$\sqrt{n}\left({\widehat{ATE}}_{\text{Lasso}}-ATE\right)\stackrel{d}{\to }\mathcal{N}\left(0,{\sigma }^2\right),$$ [16]

where

$${\sigma }^2=\underset{n\to \infty }{\text{lim}}\hspace{0.17em}\hspace{0.17em}\left[\frac{1-p_A}{p_A}{\sigma }_{e^{\left(a\right)}}^2+\frac{p_A}{1-p_A}{\sigma }_{e^{\left(b\right)}}^2+2{\sigma }_{e^{\left(a\right)}{e}^{\left(b\right)}}\right].$$ [17]

The proof of Theorem 1 is given in SI Appendix. It is easy to show, as in the following corollary of Theorem 1, that the asymptotic variance of ${\widehat{ATE}}_{\text{Lasso}}$ is no worse than ${\widehat{ATE}}_{\text{unadj}}$ when ${\mathit{\beta }}^{\left(a\right)}$ and ${\mathit{\beta }}^{\left(b\right)}$ are defined as coefficients of regressing potential outcomes on a subset of covariates. More specifically, suppose there exists a subset $J\subset \left\{1,\dots ,p\right\}$, such that

$${\mathit{\beta }}^{\left(a\right)}={\left({\left({\mathit{\beta }}_J^{\left(a\right)}\right)}^T,\mathbf{0}\right)}^T,\hspace{0.17em}{\mathit{\beta }}^{\left(b\right)}={\left({\left({\mathit{\beta }}_J^{\left(b\right)}\right)}^T,\mathbf{0}\right)}^T,$$ [18]

where ${\mathit{\beta }}_J^{\left(a\right)}$ and ${\mathit{\beta }}_J^{\left(b\right)}$ are the population-level OLS coefficients for regressing the potential outcomes a and b on the covariates in the subset J with intercept, respectively.

Corollary 1.

For ${\mathit{\beta }}^{\left(a\right)}$ and ${\mathit{\beta }}^{\left(b\right)}$ defined in [18] and some ${\mathit{\lambda }}_a$ and ${\lambda }_b$, assume Conditions 1–6 hold. Then the asymptotic variance of $\sqrt{n}\hspace{0.17em}{\widehat{ATE}}_{\text{Lasso}}$ is no greater than that of the $\sqrt{n}\hspace{0.17em}{\widehat{ATE}}_{\text{unadj}}$. The difference is $\left(1/\left(p_A\left(1-p_A\right)\right)\right)\mathrm{\Delta }$, where

$$\mathrm{\Delta }=-\underset{n\to \infty }{\text{lim}}{\Vert X{\mathit{\beta }}_E\Vert }_2^2\le 0,\hspace{0.5em}{\mathit{\beta }}_E=\left(1-p_A\right){\mathit{\beta }}^{\left(a\right)}+p_A{\mathit{\beta }}^{\left(b\right)}.$$ [19]

Remark 1:

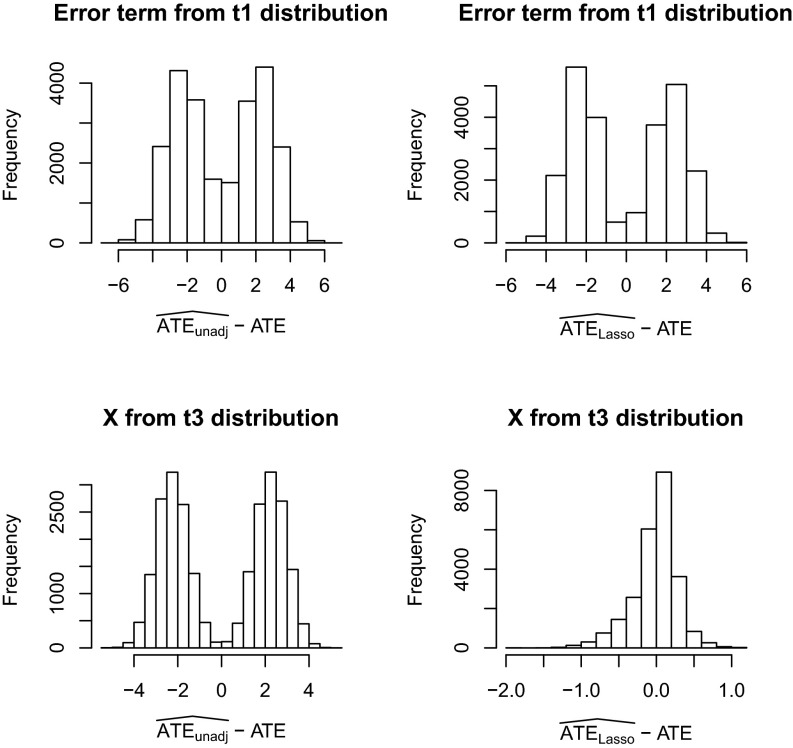
If, instead of Condition 6, we assume that the covariates are uniformly bounded, i.e., ${\text{max}}_{i,j}\left|x_{ij}\right|\le L$, then the fourth moment condition on the error terms, given in [7], can be weakened to a second moment condition. Although we do not prove the necessity of any of our conditions, our simulation studies show that the distributions of the unadjusted and the Lasso-adjusted estimator may be nonnormal when (i) the covariates are generated from Gaussian distributions and the error terms do not satisfy second moment condition, e.g., being generated from a t distribution with one degree of freedom; or (ii) the covariates do not have bounded fourth moments, e.g., being generated from a t distribution with three degrees of freedom. See the histograms in Fig. 1, where the corresponding p values of Kolmogorov–Smirnov testing for normality are less than $2.2e-16$. These findings indicate that our moment conditions cannot be dramatically weakened for asymptotic normality. However, we also find that the Lasso-adjusted estimator still has smaller variance and mean squared error than the unadjusted estimator, even when these moment conditions do not hold. In practice, when the covariates do not have bounded fourth moments, one may perform some transformation—e.g., a logarithm transformation—to ensure that the transformed covariates have bounded fourth moments while having a sufficiently large variance so as to retain useful information. We leave it as future work to explore the properties of different transformations.

Fig. 1.

Histograms of the unadjusted estimator and the Lasso-adjusted estimator when the moment conditions do not hold. We select the tuning parameters for Lasso using 10-fold CV. The potential outcomes are simulated from linear regression model and then kept fixed (see more details in SI Appendix). For the upper two subplots, the error terms are generated from t distribution with one degree of freedom and therefore do not satisfy second moment condition; whereas for the lower two subplots, the covariates are generated from t distribution with three degrees of freedom and thus violate fourth moment condition.

Remark 2:

Statement [11], typically required in debiasing the Lasso (15), is stronger by a factor of $\sqrt{\log \hspace{0.17em}p}$ than the usual requirement for $l_1$ consistency of the Lasso.

Remark 3:

Condition 5 is slightly weaker than the typical restricted eigenvalue condition for analyzing the Lasso.

Remark 4:

If we assume ${\delta }_n=O\left(\sqrt{\log \hspace{0.17em}p/n}\right)$, which satisfies [10], then Condition 6 requires that the tuning parameters are proportional to $\sqrt{\log \hspace{0.17em}p/n}$, which is typically assumed for the Lasso in the high-dimensional linear regression model.

Remark 5:

For fixed p, ${\delta }_n=0$ in [9], Condition 4 holds automatically, and Condition 5 holds when the smallest eigenvalue of $\mathrm{\Sigma }$ is uniformly bounded away from 0. In this case, Corollary 1 reverts to corollary 1.1. in ref. 7. When these conditions are not satisfied, we should set ${\lambda }_a$ and ${\lambda }_b$ to be large enough to cause the Lasso-adjusted estimator to revert to the unadjusted one.

Neyman-Type Conservative Variance Estimate.

We note that the asymptotic variance in Theorem 1 involves the cross-product term ${\sigma }_{e^{\left(a\right)}{e}^{\left(b\right)}}$, which is not consistently estimable in the Neyman–Rubin model as $a_i$ and $b_i$ are never simultaneously observed. However, we can give a Neyman-type conservative estimate of the variance. Let

$${\widehat{\sigma }}_{e^{\left(a\right)}}^2=\frac{1}{n_A-d{f}^{\left(a\right)}}{\displaystyle \sum _{i\in A}{\left(a_i-{\overline{a}}_A-{\left({\mathbf{x}}_i-{\overline{\mathbf{x}}}_A\right)}^T{\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(a\right)}\right)}^2},$$

$${\widehat{\sigma }}_{e^{\left(b\right)}}^2=\frac{1}{n_B-d{f}^{\left(b\right)}}{\displaystyle \sum _{i\in B}{\left(b_i-{\overline{b}}_B-{\left({\mathbf{x}}_i-{\overline{\mathbf{x}}}_B\right)}^T{\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(b\right)}\right)}^2},$$

where $d{f}^{\left(a\right)}$ and $d{f}^{\left(b\right)}$ are degrees of freedom defined by the following:

$$d{f}^{\left(a\right)}={\widehat{s}}^{\left(a\right)}+1={\Vert {\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(a\right)}\Vert }_0+1;\hspace{0.17em}d{f}^{\left(b\right)}={\widehat{s}}^{\left(b\right)}+1={\Vert {\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\left(b\right)}\Vert }_0+1.$$

Define the variance estimate of $\sqrt{n}\left({\widehat{ATE}}_{\text{Lasso}}-ATE\right)$ as follows:

$${\widehat{\sigma }}_{\text{Lasso}}^2=\frac{n}{n_A}{\widehat{\sigma }}_{e^{\left(a\right)}}^2+\frac{n}{n_B}{\widehat{\sigma }}_{e^{\left(b\right)}}^2.$$ [20]

We will show in SI Appendix, Theorem S1, that the limit of ${\widehat{\sigma }}_{\text{Lasso}}^2$ is greater than or equal to the asymptotic variance of $\sqrt{n}\left({\widehat{ATE}}_{\text{Lasso}}-ATE\right)$, and therefore can be used to construct a conservative confidence interval for the ATE.

Related Work.

The Lasso has already made several appearances in the literature on treatment effect estimation. In the context of observational studies, ref. 15 constructs confidence intervals for preconceived effects or their contrasts by debiasing the Lasso-adjusted regression, ref. 16 employs the Lasso as a formal method for selecting adjustment variables via a two-stage procedure that concatenates features from models for treatment and outcome, and similarly, ref. 17 gives very general results for estimating a wide range of treatment effect parameters, including the case of instrumental variables estimation. In addition to the Lasso, ref. 18 considers nonparametric adjustments in the estimation of ATE. In works such as these, which deal with observational studies, confounding is the major issue. With confounding, the naive difference-in-means estimator is biased for the true treatment effect, and adjustment is used to form an unbiased estimator. However, in our work, which focuses on a randomized trial, the difference-in-means estimator is already unbiased; adjustment reduces the variance while, in fact, introducing a small amount of finite-sample bias. Another major difference between this prior work and ours is the sampling framework: we operate within the Neyman–Rubin model with fixed potential outcomes for a finite population, where the treatment group is sampled without replacement, whereas these papers assume independent sampling from a probability distribution with random error terms.

Our work is related to the estimation of heterogeneous or subgroup-specific treatment effects, including interaction terms to allow the imputed individual-level treatment effects to vary according to some linear combination of covariates. This is pursued in the high-dimensional setting in ref. 19; this work advocates solving the Lasso on a reduced set of modified covariates, rather than the full set of covariate by treatment interactions, and includes extensions to binary outcomes and survival data. The recent work in ref. 20 considers the problem of designing multiple-testing procedures for detecting subgroup-specific treatment effects; they pose this as an optimization over testing procedures where constraints are added to enforce guarantees on type I error rate and power to detect effects. Again, the sampling framework in these works is distinct from ours; they do not use the Neyman–Rubin model as a basis for designing the methods or investigating their properties.

PAC Data Illustration and Simulations.

We now return to the PAC-man study introduced earlier. We examine the data in more detail and explore the results of several adjustment procedures. There were 1,013 patients in the PAC-man study: 506 treated (managed with PAC) and 507 control (managed without PAC, but retaining the option of using alternative devices). The outcome variable is quality-adjusted life years (QALYs). One QALY represents 1 year of life in full health; in-hospital death corresponds to a QALY of zero. We have 59 covariates about each individual in the study; we include all main effects as well as 1,113 two-way interactions, and form a design matrix $\mathbf{X}$ with 1,172 columns and 1,013 rows. See SI Appendix for more details on the design matrix.

The assumptions that underpin the theoretical guarantees of the ${\widehat{ATE}}_{\text{Lasso}}$ estimator are, in practice, not explicitly checkable, but we attempt to inspect the quantities that are involved in the conditions to help readers make their own judgement. The uniform bounds on the fourth moments refer to a hypothetical sequence of populations; these cannot be verified given that the investigator has a single dataset. However, as an approximation, the fourth moments of the data can be inspected to ensure that they are not too large. In this dataset, the maximum fourth moment of the covariates is 37.3, which is indicative of a heavy-tailed and potentially destabilizing covariate; however, it occurs in an interaction term not selected by the Lasso, and thus does not influence the estimate. [The fourth moments of the covariates are shown in SI Appendix, Fig. S9. The covariates with the largest two fourth moments (37.3 and 34.9, respectively) are quadratic term $interactne{w}^2$ and interaction term $IMscorerct:systemnew$. Neither of them is selected by the Lasso to do the adjustment.] Checking the conditions for high-dimensional consistency of the Lasso would require knowledge of the unknown active set S, and moreover, even if it were known, calculating the cone invertibility factor would involve an infeasible optimization. This is a general issue in the theory of sparse linear high-dimensional estimation. To approximate these conditions, we use the bootstrap to estimate the active set of covariates S and the error terms $e^{\left(a\right)}$ and $e^{\left(b\right)}$. See SI Appendix for more details. Our estimated S contains 16 covariates and the estimated second moments of $e^{\left(a\right)}$ and $e^{\left(b\right)}$ are 11.8 and 12.0, respectively. The estimated maximal covariance ${\delta }_n$ equals 0.34 and the scaling $\left(s\hspace{0.17em}\log \hspace{0.17em}p\right)/\sqrt{n}$ is 3.55. Although this is not close to zero, we should mention that the estimation of ${\delta }_n$ and $\left(s\hspace{0.17em}\log \hspace{0.17em}p\right)/\sqrt{n}$ can be unstable and less accurate because it is based on a subsample of the population. As an approximation to Condition 5, we examine the largest and smallest eigenvalues of the sub-Gram matrix $\left(1/n\right){\mathbf{X}}_S^T{\mathbf{X}}_S$, which are 2.09 and 0.18, respectively. Thus, the quantity in Condition 5 seems reasonably bounded away from zero.

We now estimate the ATE using the unadjusted estimator, the Lasso-adjusted estimator, and the OLS-adjusted estimator, which is computed based on a subdesign matrix containing only the 59 main effects. We also present results for the two-step estimator ${\widehat{ATE}}_{\text{Lasso}\mathrm{+}\text{OLS}}$, which adopts the Lasso to select covariates and then uses OLS to refit the regression coefficients. In the next paragraph and in SI Appendix, Algorithm 1, we show how we adapt the CV procedure to select the tuning parameter for ${\widehat{ATE}}_{\text{Lasso}+\text{OLS}}$ based on a combined performance of Lasso and OLS, or cv(Lasso+OLS).

We use the R package “glmnet” to compute the Lasso solution path and select the tuning parameters ${\lambda }_a$ and ${\lambda }_b$ by 10-fold CV. To indicate the method of selecting tuning parameters, we denote the corresponding estimators as cv(Lasso) and cv(Lasso+OLS), respectively. We should mention that for the cv(Lasso+OLS)-adjusted estimator, we compute the CV error for a given value of ${\lambda }_a$ (or ${\lambda }_b$) based on the whole Lasso+OLS procedure instead of just the Lasso estimator (SI Appendix, Algorithm 1). Therefore, the cv(Lasso+OLS) and the cv(Lasso) may select different covariates to do the adjustment. This type of CV requires more computation than the CV based on just the Lasso estimator because it needs to compute the OLS estimator for each fold and each given ${\lambda }_a$ (or ${\lambda }_b$), but it can give better prediction and model selection performance.

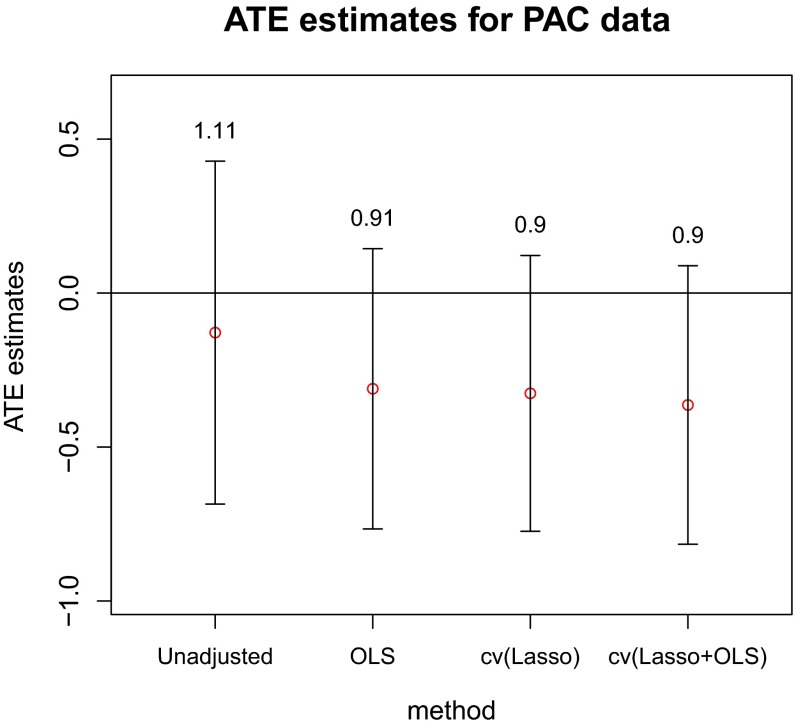
Fig. 2 presents the ATE estimates along with $95\mathrm{\%}$ confidence intervals. The interval lengths are shown on top of each interval bar. All of the methods give confidence intervals containing 0; hence, this experiment failed to provide sufficient evidence to reject the hypothesis that PAC did not have an effect on patient QALYs (either positive or negative). Because the caretakers of patients managed without PAC retained the option of using less invasive cardiac output monitoring devices, such an effect may have been particularly hard to detect in this experiment.

Fig. 2.

ATE estimates (red circles) and $95\mathrm{\%}$ confidence intervals (bars) for the PAC data. The numbers above each bar are the corresponding interval lengths.

However, it is interesting to note that, compared with the unadjusted estimator, the OLS-adjusted estimator causes the ATE estimate to decrease (from −0.13 to −0.31), and shortens the confidence interval by about $20\mathrm{\%}$. This is due mainly to the imbalance in the pretreatment probability of death, which was highly predictive of the posttreatment QALYs. The cv(Lasso)-adjusted estimator yields a comparable ATE estimate and confidence interval, but the fitted model is more interpretable and parsimonious than the OLS model: it selects 24 and 8 covariates for treated and control, respectively. The cv(Lasso+OLS) estimator selects even fewer covariates: 4 and 5 for treated and control, respectively, but performs a similar adjustment as the cv(Lasso) (see the comparison of fitted values in SI Appendix, Fig. S8). We also note that these adjustments agree with the one performed in ref. 13, where the treatment effect was adjusted downward to $-0.27$ after stratifying into four groups based on predicted probability of death.

The covariates selected by Lasso for adjustment are shown in Table 1, where “A$\cdot$ A” denotes quadratic term of the covariate A, and “A:B” denotes two-way interaction between two covariates A and B. Among them, patient’s age and estimated probability of death (p_death), together with the quadratic term “age$\cdot$ age” and interactions “age:p_death” and “p_death:mech_vent” (mechanical ventilation at admission), are the most important covariates for the adjustment. The patients in control group are slightly older and have slightly higher risk of death. These covariates are important predictors of the outcome. Therefore, the unadjusted estimator may overestimate the benefits of receiving PAC.

Table 1.

Selected covariates for adjustment

Method	Treatment	Covariates
cv(Lasso+OLS)	Treated	Age, p_death, age$\cdot$ age, age:p_death
cv(Lasso+OLS)	Control	Age, p_death, age$\mathrm{\cdot }$ age, age:p_death, p_death:mech_vent
cv(Lasso)	Treated	Pac_rate, age, p_death, age$\cdot$ age, p_death$\cdot$ p_death, region:im_score, region:systemnew,
		pac_rate:age, pac_rate:p_death, pac_rate:systemnew, im_score:interactnew, age:p_death,
		age:glasgow, age:systemnew, interactnew:systemnew, pac_rate:creatinine, age:mech_vent,
		age:respiratory, age:creatinine, interactnew:mech_vent, interactnew:male,
		glasgow:organ_failure, p_death:mech_vent, systemnew:male
cv(Lasso)	Control	Age, p_death, age$\mathrm{\cdot }$ age, unitsize:p_death, pac_rate:systemnew, age:p_death,
		interactnew:mech_vent, p_death:mech_vent*

^*Covariate definitions: age, patient’s age; p_death, baseline probability of death; mech_vent, mechanical ventilation at admission; region, geographic region; pac_rate, PAC rate in unit; creatinine, respiratory, glasgow, interactnew, organ_failure, systemnew, and im_score, various physiological indicators.

Because not all of the potential outcomes are observed, we cannot know the true gains of adjustment methods. However, we can estimate the gains via building a simulated set of potential outcomes by matching treated units to control units on observed covariates. We use the matching method described in ref. 21, which gives 1,013 observations with all potential outcomes imputed. We match on the 59 main effects only. The ATE is $-0.29$. We then use this synthetic dataset to calculate the biases, SDs, and root-mean-square errors ($\sqrt{\text{MSE}}$) of different ATE estimators based on 25,000 replicates of a completely randomized experiment, which assigns 506 subjects to the treated group and the remainders to the control group.

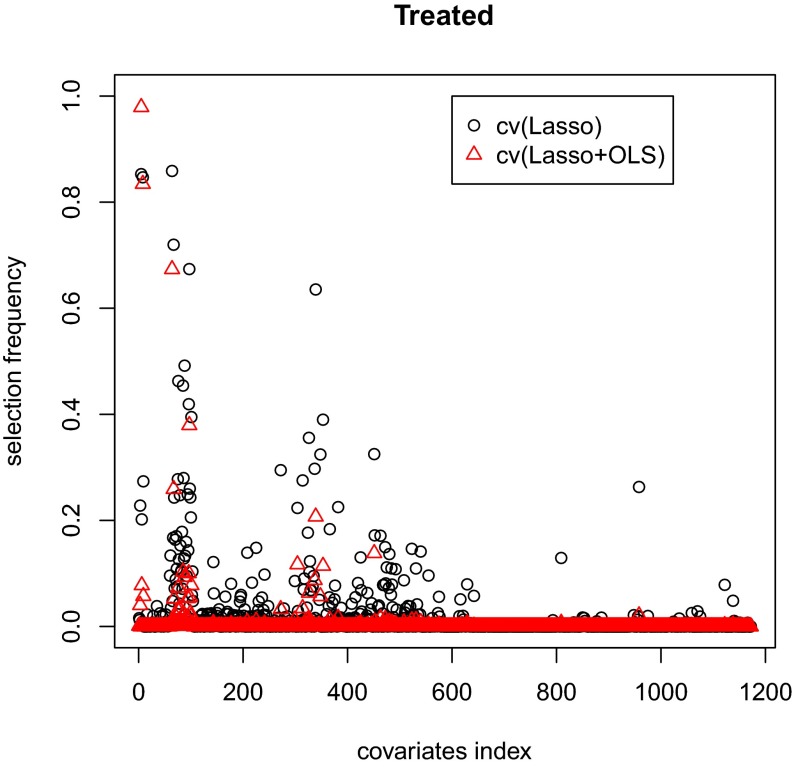
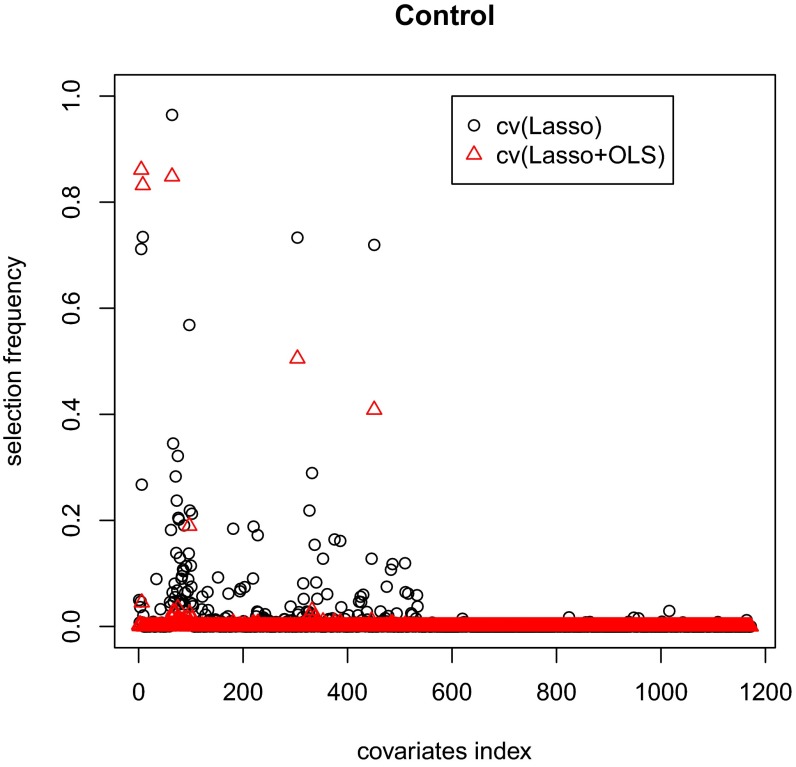
SI Appendix, Table S5, shows the results. For all of the methods, the bias is substantially smaller (by a factor of 100) than the SD. The SD and $\sqrt{\text{MSE}}$ of the OLS-adjusted estimator are both $10.2\mathrm{\%}$ smaller than those of the unadjusted estimator, whereas the cv(Lasso)- and cv(Lasso+OLS)-adjusted estimators further improve the SD and $\sqrt{\text{MSE}}$ of the OLS-adjusted estimator by ∼4.7%. Moreover, all these methods provide conservative confidence intervals with coverage probabilities higher than $99\mathrm{\%}$. However, the interval lengths of the OLS-, cv(Lasso)-, and cv(Lasso+OLS)-adjusted estimator are comparable and are ∼10% shorter than that of the unadjusted estimator. The cv(Lasso+OLS)-adjusted estimator is similar to the cv(Lasso)-adjusted estimator in terms of mean squared error, confidence interval length, and coverage probability, but outperforms the latter with much fewer and more stable covariates in the adjustment (see Figs. 3 and 4 for the selection frequency of each covariate for treatment group and control group, respectively). We also show in SI Appendix, Fig. S10, that the sampling distribution of the estimates is very close to Normal.

Fig. 3.

Selection stability comparison of cv(Lasso) and cv(Lasso+OLS) for treatment group.

Fig. 4.

Selection stability comparison of cv(Lasso) and cv(Lasso+OLS) for control group.

We conduct additional simulation studies to evaluate the finite sample performance of ${\widehat{ATE}}_{\text{Lasso}}$ and compare it with that of the OLS-adjusted estimator and the unadjusted estimator. A qualitative analysis of these simulations yields the same conclusions as presented above; however, for the sake of brevity, we defer the simulation details in SI Appendix.

Discussion

We study the Lasso-adjusted ATE estimate under the Neyman–Rubin model for randomization. Our purpose in using the Neyman–Rubin model is to investigate the performance of the Lasso under a realistic sampling framework that does not impose strong assumptions on the data. We provide conditions that ensure asymptotic normality, and provide a Neyman-type estimate of the asymptotic variance that can be used to construct a conservative confidence interval for the ATE. Although we do not require an explicit generative linear model to hold, our theoretical analysis requires the existence of latent “adjustment vectors” such that moment conditions of the error terms are satisfied, and that the cone invertibility condition of the sample covariance matrix is satisfied in addition to moment conditions for OLS adjustment as in ref. 7. Both assumptions are difficult to check in practice. In our theory, we do not address whether these assumptions are necessary for our results to hold, although simulations indicate that the moment conditions cannot be substantially weakened. As a by-product of our analysis, we extend Massart’s concentration inequality for sampling without replacement, which is useful for theoretical analysis under the Neyman–Rubin model. Simulation studies and the real-data illustration show the advantage of the Lasso-adjusted estimator in terms of estimation accuracy and model interpretation. In practice, we recommend a variant of Lasso, cv(Lasso+OLS), to select covariates and perform the adjustment, because it gives similar coverage probability and confidence interval length compared with cv(Lasso), but with far fewer covariates selected. In future work, we plan to extend our analysis to other popular methods in high-dimensional statistics such as Elastic-Net and ridge regression, which may be more appropriate for estimating adjusted ATE under different assumptions.

The main goal of using Lasso in this paper is to reduce the variance (and overall mean squared error) of ATE estimation. Another important task is to estimate heterogenous treatment effects and provide conditional treatment effect estimates for subpopulations. When the Lasso models of treatment and control outcomes are different, both in variables selected and coefficient values, this could be interpreted as modeling treatment effect heterogeneity in terms of covariates. However, reducing variance of the ATE estimate and estimating heterogenous treatment effects have completely different targets. Targeting heterogenous treatment effects may result in more variable ATE estimates. Moreover, our simulations show that the set of covariates selected by the Lasso is unstable, and this may cause problems when interpreting them as evidence of heterogenous treatment effects. How best to estimate such effects is an open question that we would like to study in future research.

Materials and Methods

We did not conduct the PAC-man experiment, and we are analyzing secondary data without any personal identifying information. As such, this study is exempt from human subjects review. The original experiments underwent human subjects review in the United Kingdom (2).