Allele Surfing Promotes Microbial Adaptation from Standing Variation

Abstract

The coupling of ecology and evolution during range expansions enables mutations to establish at expanding range margins and reach high frequencies. This phenomenon, called allele surfing, is thought to have caused revolutions in the gene pool of many species, most evidently in microbial communities. It has remained unclear, however, under which conditions allele surfing promotes or hinders adaptation. Here, using microbial experiments and simulations, we show that, starting with standing adaptive variation, range expansions generate a larger increase in mean fitness than spatially uniform population expansions. The adaptation gain results from ‘soft’ selective sweeps emerging from surfing beneficial mutations. The rate of these surfing events is shown to sensitively depend on the strength of genetic drift, which varies among strains and environmental conditions. More generally, allele surfing promotes the rate of adaptation per biomass produced, which could help developing biofilms and other resource-limited populations to cope with environmental challenges.

Introduction

The dynamics of adaptation has been intensely studied both theoretically and experimentally in situations where the time scales for demographic and adaptive change are vastly separated. Populations can then be treated as either stable or as having an effective population size summarizing the effect of demographic variations on time scales much faster than the adaptive dynamics considered (Muller 1932; Crow and Kimura 1965; Crow and Kimura 1970).

However, demographic equilibrium is frequently disrupted by, for instance, environmental changes, population growth, competition among species and local adaptation (Excoffier et al. 2009). The fate of a genetic variant then both depends on and influences the demography of a dynamically changing population. Consequently, demographic and evolutionary changes can become tightly coupled (Ferriere and Legendre 2012).

Such coupling between ecology and evolution is a particularly salient feature of range expansions (Excoffier and Ray 2008). Many mutations occur in the bulk of a population where they have to compete for resources with their neighboring conspecifics. Mutations that, by chance, arise in a region of growing population densities have a two-fold advantage: They enjoy a growth rate advantage compared to their conspecifics in the slow-growing bulk regions, and their offspring will have a good chance to benefit from future net-growth if parent-offspring locations are correlated. These correlated founder effects, summarized by the term “allele surfing”, lead to complex spatio-temporal patterns of neutral mutations and can rapidly drive mutations to high frequency by chance alone (Edmonds et al. 2004; Klopfstein et al. 2006; Travis et al. 2007; Hallatschek and Nelson 2008).

The importance of allele surfing has been increasingly recognized over the last 10 years (Excoffier et al. 2008; Excoffier et al. 2009; Waters et al. 2013). Allele surfing is believed to be a ubiquitous process in populations that constantly turn over, for instance, by range expansions and contractions, local extinction or expulsion and re-colonization (Hanski 1998; Freckleton and Watkinson 2002; Haag et al. 2005; Taylor and Keller 2007; Arenas et al. 2011). While these features are shared by many populations, they are most evident in microbial communities that frequently expand to colonize new surface regions in the environment or during infections (Cho and Blaser 2012; Costello et al. 2012).

Microbial experiments have shown that in the absence of selection allele surfing creates large mutant clones that are extremely unlikely to arise via neutral evolution of well-mixed populations. Characteristically, these clones take the shape of sectors with boundaries that exhibit characteristic fractal properties (Hallatschek et al. 2007). The random wandering of sector boundaries is a manifestation of genetic drift, as has been demonstrated experimentally in various micro-organisms, including bacteria, single-celled fungi and social slime molds, and under various demographic scenarios (Hallatschek et al. 2007; Korolev et al. 2011; Drescher et al. 2013; Freese et al. 2014; van Gestel et al. 2014).

While allele surfing is well understood in the neutral case, we do not have a comprehensive picture of its adaptive potential. In particular, it is unclear how efficiently pre-existing adaptive variation (Barrett and Schluter 2008) is selected for during range-expansions: Since allele surfing relies on enhanced genetic drift, it reduces the efficacy of selection per generation (Hallatschek and Nelson 2010; Peischl et al. 2013; Peischl and Excoffier 2015). On the other hand, for populations of the same final size, selection has more time to act at the front of a range expansion than in a comparable well-mixed expansion, which could promote adaptation (Hallatschek and Nelson 2010; Zhang et al. 2011; Greulich et al. 2012; Hermsen et al. 2012).

Here, we test whether allele surfing helps or hinders adaptation using microbial competition experiments to measure the efficiency of selection during growth processes. To get a sense of the range of possible evolutionary outcomes, we focus on two extreme cases: spatial range expansions and pure demographic growth of panmictic populations. We find increased adaptation during range expansions and rationalize our quantitative results using theory and simulations.

Materials and Methods

Strains and Conditions

Each experiment was performed using a pair of microbial strains that are distinguished by fluorescence and a selectable marker. The fluorescent color difference allows measuring the relative abundance of each strain in competition experiments by fluorescence microscopy as well as flow cytometry. The selectable marker was used to tune the selective difference between the strains in the following way: One strain of the pair, the sensitive strain (called ‘wild type’), grows slower in the presence of a drug, while the other strain, the resistant strain (called ‘mutant’), is largely unaffected. Tuning the concentration of the drug in the medium thus allowed us to adjust the selective difference between both strains. Selective advantages on plates and in liquid culture were measured separately for a range of drug concentrations using the colliding colony assay (Korolev et al. 2012) and flow cytometry (for S. cerevisiae), respectively (see Appendix C in Supporting Information), which give consistent results (see supplementary Fig. B1a). Selective differences reported throughout were obtained from linear fits.

Strains

We used S. cerevisiae strains with W303 backgrounds, where selective advantages were adjusted using cycloheximide. For experiments with E. coli, we used both DH5α and MG1655 strains, tuning fitness differences using tetracycline and chloramphenicol, respectively. Additionally, pairs of strains differing only in the fluorescent marker allowed us to perform truly neutral competition experiments (S. cerevisiae, S. pombe, E. coli). S. cerevisiae and E. coli strains with constitutively expressed fluorescent proteins were used to study the dynamics of cells at the front.

A detailed description of all strains and growth conditions is found in Appendix C.

Main Experiment

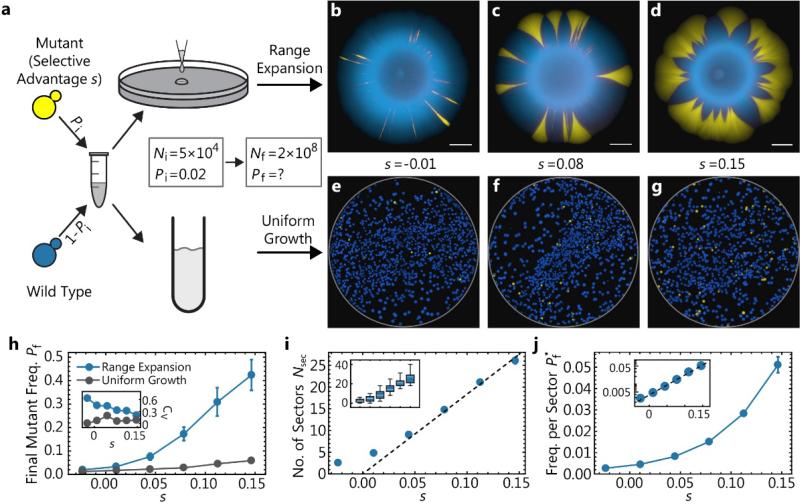
Adaptation from standing variation during two types of population expansions (see Fig. 1a): For each pair of mutant and wild type, a mixed starting population of size N_i was prepared that contained an initial frequency P_i of mutants having a selective advantage s, defined as the relative difference between mutant and wild-type growth rate (Korolev et al. 2012). The population was then grown to final size N_f in two ways, through a range expansion and, for comparison, through uniform growth, and the final mutant frequency P_f was determined. The associated increase in mean fitness W̄ follows as ΔW̄ = (P_f – P_i)s.

Fig. 1. Adaptation from standing variation during a population size increase.

Adaptation during the growth of a budding yeast population from an initial size N_i to N_f is studied for two demographic scenarios, Range Expansion and Uniform Growth. (a) Schematic of the experimental assay: Cultures of and wild-type and a faster-growing mutant strain are mixed at an initial mutant frequency P_i=0.02. Subsequently, a mixed population of initially N_i = 5 × 10⁴ cells is grown to a final population size of N_f = 2 × 10⁸. The growth process occurred either on agar plates (“Range Expansion”) over the course of 5 days, or overnight under uniform growth conditions (“Uniform Growth”). The selective advantage of the mutants is controlled by the concentration of cycloheximide, which inhibits the growth of the wild-type cells. The fluorescent microscopy images (b-d) show the distribution of both mutant (yellow) and wild-type (blue) cells at the end of range expansion experiments with selective advantage of s = −0.01, 0.08, and 0.15, respectively. Scale bars are 2mm. (e-g) After plating the final populations of the uniform growth experiments, one obtains a distribution of single colonies with a color ratio representing the ratio of mutants to wild type. (h) Final mutant frequency and corresponding coefficient of variation (inset) as a function of selective advantage determined in range expansions (blue, 35 replicates) and under uniform growth (gray, 2 replicates). Notice that the final mutant frequency is larger for range expansions and increasingly so for larger selective differences. (i) Number of sectors N_sec at the end of range expansions as a function of selective advantage. The inset illustrates the spread of data points as a box plot. (j) Final frequency $P_{\mathrm{f}}^{\ast }$ per sector, defined as the area of a single sector normalized by the area of the entire colony, as a function of selective advantage s. The inset displays the same data using a logarithmic axis for the frequency per sector. Only sectors without contact to other sectors were selected for analysis. Error bars are standard error of the mean throughout. The measurements for (h, i, j) were all done on the same 35 replicates per data point.

Uniform Growth

Mixtures of cells were grown in well-shaken liquid medium to the desired final population size and the final fraction of mutant cells was determined using flow cytometry.

Range Expansion

Colony growth was initiated by placing 2μl of the mixtures onto plates (2% w/v agar) and incubated until the desired final population size was reached. The number N_sec of sectors was determined by eye; the final fraction P_f was measured using image analysis (see Appendix C for details).

Cell-Tracking Experiments

To investigate the dynamics of cells at advancing colony fronts, we continually imaged the first few layers of most advanced cells in growing S. cerevisiae and E. coli colonies between a coverslip and an agar pad for about four hours using a Zeiss LSM700 confocal microscope. The resulting stack of images were segmented and cells were tracked as described in Appendix C.

Meta-Population Model

To simulate evolutionary change during the different modes of growth, we adapted a classic meta-population model for growing microbial colonies, the Eden model (Eden 1960) (Fig. 2a, Appendix A).

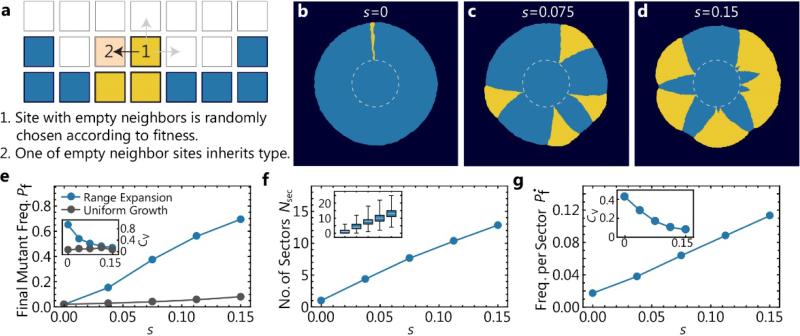
Fig. 2. Adaptation from standing variation emerging in a meta-population model of population growth.

(a) Illustration of the algorithm underlying our coarse-grained simulations (Methods). A lattice site at the population frontier is chosen and copied into an empty neighboring lattice site. The newly occupied site inherits the state of the parent site. (b-d) State of the lattice at the end of three simulations.

To mimic our experiments in Fig. 1, we initiated the expanding population as an occupied disk (dashed line) of radius R_i ≈ 550 such that a random fraction P_i = 0.02 of lattice sites is of the mutant type, and simulated until the final radius R_f ≈ 3R_i was reached. (e) Final mutant frequency P_f and corresponding coefficient of variation C_v (inset) as a function of selective advantage s determined in range expansions (blue, 500 simulations per condition) and corresponding simulations of uniform growth (gray, 3 simulations per condition, see Methods for algorithm) for the same parameters. Both final frequency and variation are larger for range expansions. (f) Number and standard error of mean of sectors at the end of range expansions as a function of selective advantage for the same simulations. Inset illustrates the spread of data points as a box plot. (g) Frequency per sector $P_{\mathrm{f}}^{\ast }$, calculated from colonies with only a single sector, which were simulated using a low initial mutant fraction P_i = 0.005.

Range Expansion

The population spreads on a lattice and each lattice point is in one of three states: empty, wild type or mutant. Growth of the populations occurs by randomly selecting an occupied “source” site with empty neighbors and copying it into a randomly chosen empty neighbor site. A mutant is more likely to be picked than a wild-type site by a factor of 1 + s. This process is repeated until the colony has reached the final average radius R_f and the final mutant fraction P_f is determined.

Uniform Growth

The range expansion simulation was modified such that a target site was an empty site randomly drawn from the entire lattice, rather than from the sites neighboring a given source site.

Individual-Based Simulations

To study the relevance of microscopic details on the adaptation process, we simulated a growing colony as a two-dimensional collection of sphero-cylinders (rods with hemispherical caps) of various lengths interacting mechanically (see (Farrell et al. 2013) and Appendix A for details). The cells continuously grew (and divided) by consuming nutrients, whose concentration was explicitly computed.

Results

The Adaptive Potential of Range Expansions

Our competition experiments in yeast show that when a population grows from a mixture of wild-type cells and faster growing mutant cells by a range expansion (Fig. 1a), it exhibits on average a larger final mutant frequency P_f than a well-mixed population grown to the same final population size N_f ≈ 2 × 10⁸ (Fig. 1h). The difference in final mutant frequency between range expansion and uniform growth increases strongly with increasing selective advantage s of the mutants. For instance, for s = 0.15, mutants make up nearly 50% of the final population (Fig. 1d), in contrast to less than 10% mutant frequency in the well-mixed population. The discrepancy between both growth modes is even more pronounced when we plot the change ΔW̄ = (P_f–P_i)s in mean fitness (Fig. B2). Hence, adaptation from pre-existing mutations leads to a much stronger increase in mean fitness in our experiments when a given population increase occurs via the expansion of range margins rather than by a homogeneous density increase.

The spatial distribution of the mutant alleles visible in Fig. 1b-d indicates that the observed adaptation gain of range expansions hinges on the formation and growth of “sectors”. These clonal regions are the footprints of surfing mutants that have locally established at the edge of the range expansion (Hallatschek et al. 2007; Hallatschek and Nelson 2010; Korolev et al. 2012). Sectors contain the vast majority of mutants in the population: If one removes the mutants that reside in sectors from the analysis, or chooses initial frequencies so low that sectors do not occur, the adaptation gain is essentially absent.

Selection has a strong impact on the shape and size of sectors: While a single mutant sector in yeast is stripe-like in the neutral case, it has a trumpet-like shape and can represent a substantial fraction of the total population when the mutants have a selective advantage (compare Figs. 1b-d). The rapid increase of sector size with selective advantage of the mutant strain is quantified in Fig. 1j. For instance, a single mutant sector with selective advantage s = 0.15 contains roughly 5% of the total population in our experiments. Under these conditions, a single clonal sector is like an adaptive “jackpot” event that can cause a substantial increase in the mean fitness of the population.

However, the early stages of surfing are a highly stochastic process, and therefore these jackpot events are rare. This is reflected in the rather small number of sectors (proportional to the initial frequency of mutants, see Fig. B3) detected in our experiments. The colonies shown in Fig. 1b-d, for instance, were started with about 10³ founder mutants in the inoculum, but only exhibit a handful of sectors (Fig. 1i). The number of sectors varies strongly between replicates (Fig. 1i, inset) and, if the mutants are very infrequent initially, there is a substantial chance that no sectors form (Fig. B4). Importantly, while the number of sectors is generally small, it increases with selective advantage, further contributing to the adaptation gain in range expansions.

Towards a Minimal Model for Adaptation by Gene Surfing

The population dynamics of our colonies differs from uniform growth in numerous aspects: Cells are delivered to the plate in a droplet, which forms a ring of cells after evaporation (Deegan et al. 1997). The cells start to grow and push each other across the surface of the agar. The population grows at first exponentially, until the growth of the core of the colony slows down due to nutrient depletion behind the front. The further advancement of the front is driven by a layer of proliferating cells (the “growth layer” (Hallatschek et al. 2007; Mitri et al. 2015)) at the edge of the colony (Fig. B5).

While some of these complexities are specific to microbial colonies and biofilms (Nadell et al. 2010), elevated growth rates at range margins combined with local dispersal are the characteristic features of range expansions. To see whether these features alone could reproduce the observed pattern of adaptation, we created a simple meta-population model (Methods), in which the frontier advances by random draws from the demes within the range margins. This simple model has been shown to exhibit universal fractal properties of advancing interfaces (Kardar et al. 1986), which have also been measured in bacterial range expansions (Hallatschek et al. 2007).

As can be seen in Fig. 2, a simulation analog of Fig. 1, the model mirrors our experimental findings: Beneficial mutations have a higher frequency in populations that have undergone a range expansion than uniform expansion. The simulations also reproduce the stochastic formation of sectors and the qualitative dependence of sector number and size on the selective advantage. Thus, the patterns of adaptation seen in our colony experiments seem to originate from the few general features of range expansions that are incorporated in our minimal simulations.

Indeed, we now provide mathematical arguments and individual-based simulations to show how the key features of range expansions conspire to generate the observed adaptation gain; detailed mathematical derivations are provided in Appendix A.

Qualitative Explanation for Adaptation Gain

We shall begin with a simple, qualitative argument that demonstrates an important difference between range expansions and uniform growth. In a well-mixed population, the mutant frequency grows exponentially with time, P_f ∝ e^sT. The number T of generations, however, increases only logarithmically with the final population size, T ∝ lnN_f, such that the mutant frequency changes by P_f/P_i = (N_f/N_i)^s. In our experiments, this leads to a modest relative change in mutant frequency, e.g., by a factor of 2 for a 6% beneficial mutation over the course of the growth process, which corresponds to about 12 generations. Importantly, the absolute frequency remains well below 1 when the initial frequency is small. Moreover, the final mutant frequency varies relatively little among different replicates, as quantified by the coefficient of variation (Fig. 1h inset). This is because nearly all initially present cells give rise to clones, with similar clone sizes, each corresponding to only a minute fraction of the total population.

In contrast to uniform growth, more generations need to pass to reach the same final population size N_f in a radially expanding population ($T\propto N_{\mathrm{f}}^{1∕2}$ in a radially expanding population, in contrast to T ∝ log(N_f) in the well-mixed case). This implies that selection has more time to act during a range expansion, so that one might expect an increased final mutant frequency.

Adaptation Gain Depends on Sector Shape and Number

The above run-time argument captures the main reason for the adaptation gain, but it ignores two important counterforces: (i) The efficacy of selection is reduced during a range expansion, because the frequency of a selected mutation increases only algebraically with time, in contrast to exponential sweeps in uniformly growing populations. (ii) Only few of the initially present cells give rise to expanding clones. Therefore, to fully understand the adaptive potential of range expansion we must examine the mechanism of sector expansion and formation, the latter being an inherently stochastic process caused by enhanced genetic drift at the front (Hallatschek et al. 2007). Ignoring any interaction between sectors and the small fraction of mutants in non-surfing clones, we can estimate the final frequency P_f of mutants by multiplying the number N_sec of sectors with their relative frequency $P_{\mathrm{f}}^{\ast }$ in the population,

$$P_{\mathrm{f}}=P_{\mathrm{f}}^{\ast }\times N_{\sec }.$$

While simple deterministic arguments exist to predict the frequency $P_{\mathrm{f}}^{\ast }$ of individual clones, new population genetic theory is required to predict the number N_sec of sectors. Remarkably, we shall see that the number of sectors is sensitive to microscopic details of the population growth process.

Final Frequency $P_{\mathrm{f}}^{\ast }$ of Expanding Clones

The two boundaries of sectors in radial range expansions are logarithmic spirals (Korolev et al. 2012). These spirals emerge from the origin of the sector at a characteristic opening angle $\phi \left(s\right)\approx 2\sqrt{2s}$ that is set by the selective advantage s of the mutant (Hallatschek and Nelson 2010). Up to logarithmic corrections, one therefore expects a final frequency of mutant cells from a single sector to be $P_{\mathrm{f}}^{\ast }\approx \phi \left(s\right)∕2\pi \sim \sqrt{s}$ in large colonies (see Eq. (A11) for the full result). This means that a single initial mutant can give rise to a macroscopically large clone of order $\sqrt{s}$. The fractional size of mutant sectors grows even faster in range expansions with straight rather than curved fronts.

Sector Number N_sec

The establishment of beneficial mutations is generally a result of the competition between random genetic drift and the deterministic force of selection. At the coarse-grained description of clones in terms of sectors, genetic drift manifests itself in the random wandering of sector boundaries, ultimately a result of randomness in the reproduction process (Hallatschek et al. 2007). Balancing the random sector boundary motion with the deterministic sector expansion due to selection, we show in Appendix A (see Eq. (A15)) that the number of sectors is proportional to s in two dimensions. Note that although the s-dependence of the number of sectors in two-dimensions is identical to Haldane's classical result “2s” for the establishment probability of beneficial mutations (Maruyama 1970; Patwa and Wahl 2008), the proportionality changes in the three-dimensional case to a predicted s^3.45 (Appendix A), which may be relevant to the evolution of solid tumors.

Modeling the Onset of Surfing

While our minimal model reproduces aspects of the experimental data reasonably well (see Fig. A2), it cannot predict how microscopic details influence the adaptation dynamics. Microscopic details are summarized by a fit parameter, the effective deme size, which enters our expression for the number of sectors N_sec (Eq. (A19)).

To study directly how these microscopic factors influence the number of sectors, we developed an individual-based off-lattice simulation framework for microbial range expansions, where each cell is modeled explicitly as a growing elastic body of variable aspect ratio (see Methods and Appendix A). These computer simulations reveal that surfing events result from a complex competition between selection and genetic drift: The probability for an individual cell to form a sector (the surfing probability) increases with selective advantage s but the increase is much faster for colonies with a smooth front line than for colonies with strongly undulating fronts (Fig. 3i). The observed difference between the rough and smooth fronts can be explained intuitively as follows: If a mutant resides in a front region that is lagging behind neighboring wild-type regions, it will likely be overtaken and enclosed by the neighboring wild-type regions, despite its higher growth rate (Fig. 3g). Such “occlusion” events are more likely for rougher fronts, thus increasing the probability that beneficial mutations are lost by chance. In line with this explanation, we find that colonies with rougher fronts also exhibit higher levels of genetic drift, as quantified (Hallatschek et al. 2007) by the lateral (perpendicular to the expansion direction) displacement of lineages from their origin (Fig. 3j). Importantly, we find that front roughness can be strongly influenced by several parameters that can vary among strains and conditions (Fig. A11, Tables A1, A2).

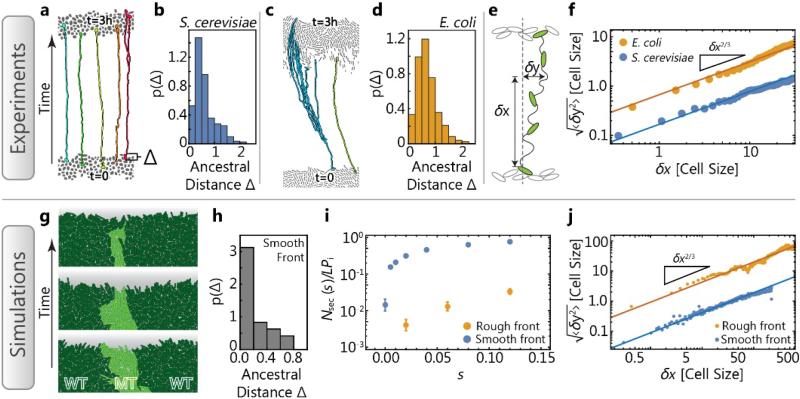
Fig. 3. Surfing depends sensitively on location and the strength of genetic drift.

Time-lapse microscopy (top row) and individual-based simulations (bottom row) reveal cell-scale dynamics at the front of expanding colonies. (a, c) Segmented micrographs of the initial front (bottom cells) and the front after three hours of growth (top cells) in S. cerevisiae (a) and E. coli (c) colonies, respectively. Colored lines track lineages backward in time (see also Figs. B8-B10). The histograms in (b, d, h) quantify how surfing success depends on position: The probability density p(Δ) that the lineages tracked for 3 hours back in time lead to an ancestor that had a distance Δ (in unit of cell diameters) to the front. Note the pronounced peak in both experiments (b, c) and simulations (h). (e) Illustration and measurement of the random meandering of tracked lineages. We measure the lateral displacement δy (in units of cell diameters) a lineage has undergone while moving a distance δx along the direction of the front propagation, and average 〈δy²〉 over all lineages. (f) Average (root mean square) lateral displacement of lineages in expanding colonies, showing that E. coli lineages are fluctuating substantially more strongly than S. cerevisiae lineages (absolute value at a given δx). The lateral displacement in both cases follows a characteristic scaling (slope), as expected for a spatially unbiased growth process with a rough front (Appendix A). These experimental observations can be reproduced in simulations (j) of expanding rough and smooth fronts, respectively. (g) In simulations with rough fronts, surfing beneficial mutations (light green) are frequently occluded by neighboring wild-type domains (dark green). (i) As a consequence, the number of sectors are much lower for rough than smooth fronts, for identical initial mutant frequency P_i and front length L.

Moreover, we find that only mutations that occur very close to the front line have any chance of long-term surfing (Fig. 3h). For our experiments, this implies that only those ancestral mutants have a chance to surf that, by chance, are in the first few cell layers of the dried inoculated droplet. The narrowness of the layer from which surfers are recruited, moreover, makes an important prediction about surfing of de novo mutations: Since the width λ of the growth layer where mutations occur can be much wider than the average width d of the cells in the front line, the effective mutation rate μ_eff of mutations occurring in the growth layer is the bare mutation rate μ reduced by a factor of d/λ, which is on the order of a few percent in most microbial colonies. Hence, the vast majority of beneficial mutations are effectively wasted in expanding populations because they occur behind the front line. Therefore, during range expansions with de novo mutations, a lot fewer surfing events should be observed than expected for a given mutation rate (as measured by, e.g., fluctuation analysis) and surfing probability (as measured by, e.g., the number of sectors), especially for a thick growth layer. This may contribute to the accumulation of deleterious mutations during range expansions.

Experimentally Probing the Onset of Surfing

Our individual-based model made two crucial predictions about the early stages of surfing, which we tested in a series of experiments described below.

(i) Surfing occurs only directly at the front

Control measurements show that the number of surfing events is proportional to the initial frequency (Fig. B3) and not significantly sensitive to the total number of cells, as long as they form a contiguous perimeter around the initial droplet (Fig. B6). These observations are consistent with the hypothesis that surfing events originate in the front region of the colony. To test whether surfers arise in the very first cell layer only, we took time-lapse movies (SI movies 1 and 2) of an advancing front at a resolution that allows us to track lineages backward in time. The resulting genealogies show that only cells at the very front remain as ancestor of future populations. We can extract histograms of ancestor distances from the front (Fig. 3b, d; see also Fig. B10), showing that cells have to be within about one cell diameter to have any chance of giving rise to a successful lineage.

(ii) The strength of genetic drift influences surfing rates, and is highly variable

We repeated our competition experiments using pairs of E. coli (Methods) strains and found up to an order of magnitude differences in surfing probability, i.e., proportion of surfing mutants N_sec/N_mut, for a given selective advantage (Fig. 4). This underscores that the selective advantage of a mutation alone has little predictive power over the probability of surfing. The reason is that allele surfing also depends on the strength of genetic drift, which can be estimated from the number of sectors emerging in neutral competition experiments (Fig. 4a, c, e). Fig. 4g shows a clear correlation between the number of surfing beneficial mutations and the number of surfing neutral mutations, for four conditions and different fitness effects. This suggests that measuring the strength of random genetic drift is necessary to predict the efficacy of adaptation.

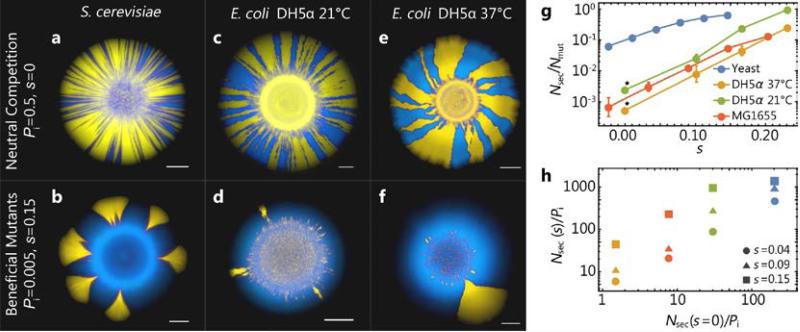
Fig. 4. Adaptation during range expansions for different strains and conditions.

(a-f) Top row: Images of colonies after neutral range expansions (Methods) with an initial mutation frequency of P_i = 0.5. The number of sectors formed (panel g) and their shape (see Fig. B7) varies between S. cerevisiae and E. coli and temperature at which colonies are grown. The bottom row shows corresponding range expansions when mutants have a selective advantage of s ≈ 0.15, at low initial mutation fraction of P_i = 0.005. Scale bars are 2mm in each image. (g) The number N_sec of sectors normalized by the number N_mut of mutant cells in the outside rim of the inoculum as a function of the selective advantage of the mutants for different species, strains, and growth conditions (about 35 replicates per data point). The asterisk (*) denotes the use of the neutral strain pairing as opposed to the mutant-wild-type pair. (h) The number of sectors N_sec normalized by the initial fraction P_i against the normalized number of sectors in the neutral case shows a clear correlation between neutral dynamics and the surfing probability of advantageous mutant clones: weaker genetic drift (more sectors in neutral competitions) is indicative of a higher surfing probability. Panel (h) is obtained by interpolating data from panel (g) for the selected values of s.

The difference between strains can partly be understood from time-lapse movies of the colony growth at single-cell resolution (SI movies 1 and 2). While cell motion perpendicular to the front direction is limited in yeast colonies, there is strong dynamics within the E. coli front. Tracking the cells through 3 hours of growth elucidates the difference in cellular dynamics, as shown in Fig. 3a and c. We quantify this observation by measuring the cells’ lateral displacement (Fig. 3e-f, Appendix C), which is about an order of magnitude stronger in E. coli compared to budding yeast, explaining (at least part) of the difference in genetic drift. The same effect can be observed in computer simulations of the individual-based model (Fig. 3i, j).

While it may not seem surprising that genetic drift varies somewhat (though not an order of magnitude) between taxa due to differences in the reproductive process, we also found that the level of genetic drift varies among different growth conditions for the same species. Fig. 4c-f show the results of competition experiments between two differently labeled but otherwise identical E. coli strains (DH5α background) at two different incubation temperatures. Notice that the neutral sectoring pattern undergoes a striking change: While only few sectors can be observed at 37°C, many spoke-like sectors arise at 21°C. Importantly, surfing probabilities varied, as predicted, with observed variations in the strength of genetic drift: repeating the establishment experiments at lower temperatures shows that the number of established clones indeed increased for smaller amounts of genetic drift (Fig. 4g, h).

Discussion

Laboratory evolution experiments usually investigate the rate of adaptation per unit time. This is the relevant quantity when resources are abundant or replenish faster than they are consumed, as for example in a chemostat (Kawecki et al. 2012).

By contrast, in our experiments we have compared the adaptive outcome of two types of population expansions, range expansion and uniform growth, under the condition that both types lead to the same final population size, no matter how long it may take. Thus, we have effectively measured the rate of adaptation per cell division or, equivalently, per biomass produced. We believe this is the crucial comparison when population growth is resource-limited, which may arguably apply not only to microbial biofilms (Stewart and Franklin 2008; Mitri et al. 2015), but also to various other types of natural populations, including tumors, and spreading pathogens (Lee 2002; Ling et al. 2015).

Our experiments show that, starting from standing adaptive variation, range expansions generate a larger, often much larger, mean fitness increase in microbial communities than equivalent uniform population expansions. In essence, this results from the effective serial dilution of the pioneer population, generated by the fact that the offspring of pioneers tend to be the pioneers of the next generation. As a consequence of these spatio-temporal correlations, selection can act over more generations at the front of a range expansion than in a uniform expansion.

However, because the relevant pioneer population is small, sampling effects (genetic drift) are important: The gain in adaptation comes in partial sweeps, visible in our experiments as large “sectors”, which represent successfully surfing alleles. The total adaptation gain during a range expansion depends on both the number of sectors and the size of sectors. While the shape of sectors simply reflects the selective advantage of the mutants, the stochastic number of sectors is a result of the competition between selection and (strong) genetic drift in the pioneer population.

Thus, predicting the number of sectors, and ultimately the rate of adaptation in population expansions, requires a measurement of both the strength of selection and genetic drift. In microbial experiments, the strength of genetic drift, which is related to the front roughness, can be measured by neutral mixing experiments with fluorescently labeled strains. Such measurements show that the strength of genetic drift varies by orders of magnitude among strains and conditions like growth medium or temperature, affecting surface roughness, growth layer width, or cell shape, as illustrated in Fig. 5. Thus, changes in the microbial growth processes can strongly influence the adaptive potential of range expansions via their impact on the strength of genetic drift. This may be important, for instance, for adaptation in developing biofilms with their complex surface properties (Xavier and Foster 2007; Drescher et al. 2013), and could be tested in flow chamber experiments.

Fig. 5. Variability of genetic drift across species, strains, and environmental conditions.

Each image shows a colony of two neutral strains grown with a starting frequency P_i = 0.5. Colored frames indicate the main differences between images. E. coli colonies (a-e) exhibit fewer sectors and are less regular than yeast colonies (f-g), which produce many sectors. Environmental factors, in particular temperature (a-b) or composition of media (c-d) also influence the strength of genetic drift. Even for identical conditions, different E. coli strains exhibit varying morphologies and sector numbers: For example, mutations influencing cell shape (e) may leads to straighter sectors boundaries and more sectors, although cell shape alone does not accurately predict the strength of genetic drift (compare E. coli (a-d) and S. pombe (g), which are both rod-shaped). All scale bars are 2mm.

Our results underscore the adaptive potential of allele surfing: Although, as was found previously in the neutral case, allele surfing is a rare event that depends on enhanced genetic drift at the frontier (Hallatschek et al. 2007), it becomes more likely as the selective advantage of the mutation increases. Nevertheless, out of the pre-existing mutant population only few mutants manage to establish and surf at the frontier. The ones that do, however, leave a strong mark on the population as a whole; driven by selection, their descendants sweep to high frequencies in the population.

In other words, allele surfing turns a population expansion into a high-paying evolutionary slot machine (Luria and Delbrück 1943): The expected gain in fitness is high on average but it relies on rare surfing events controlled by the competition of genetic drift and selection. Range expansions can thus lead to large evolutionary change if these jackpots events do occur. By contrast, well-mixed populations lead to a homogeneous growth of all cells, resulting in less overall change in frequencies.

As our experiments have focused on standing genetic variation, they have ignored the impact of spontaneous mutations occurring during the population expansion. Enhanced genetic drift at expanding frontiers is expected to promote the genetic load due to new deleterious mutations (Travis et al. 2007; Hallatschek and Nelson 2010; Peischl et al. 2013; Lavrentovich et al. 2015), which may lead in extreme cases to a slowdown of the population expansion, for instance when “mutator” strains are involved. Thus, enjoying an adaptation increase from a range expansion may require a sufficiently low rate of deleterious mutations.

Strikingly, our expanding colonies shifted from a predominantly wild-type to a largely resistant population under quite weak selective pressures. We hypothesize that adaptation by allele surfing could be a general mechanism for efficiently shifting the balance between pre-existing types after an environmental change. Moreover, a proposed connection (Lambert et al. 2011) between drug resistance in bacterial communities and malignant tissues suggests that similar effects could be at play in solid tumors that harbor standing variation prior to drug treatment.

Allele surfing may also help explain the efficient adaptation seen in some cases of species invasions, such as in cane toads, which developed longer legs in the course of the invasion of Australia (Phillips et al. 2006). Although we do expect our results to carry over to more complex scenarios, sex, death, recombination, dominance, and heterogeneities in resources and selection pressures may significantly complicate the dynamics. Key differences could arise, for instance, if mutants do not have an expansion velocity advantage, but are instead merely outcompeting the wild-type individuals within already occupied regions. In this case, we expect sectors to reach substantially lower frequencies than in our experiments.

Adaptation by gene surfing matches the pattern of a “soft” selective sweep (Hermisson and Pennings 2005; Barrett and Schluter 2008), in which multiple adaptive alleles sweep through the population at the same time, however with a unique spatial structure. Although these sweeps can be strong, as seen in our experiments, they may be hard to identify in population genomic studies when they carry along different genomic backgrounds. However, as sequencing costs drop further and spatial sampling resolution increases, the genomic signal of these localized soft sweeps may become directly discernable.