Abstract
Unlike dilute experimental conditions under which biological molecules are typically characterized, the cell interior is crowded by macromolecules, which affects both the thermodynamics and kinetics of in vivo processes. Although the excluded-volume effects of macromolecular crowding are expected to cause compaction of unfolded and disordered proteins, the extent of this effect is uncertain. We use a coarse-grained model to represent proteins with varying sequence content and directly observe changes in chain dimensions in the presence of purely repulsive spherical crowders. We find that the extent of crowding-induced compaction is dependent not only on crowder size and concentration, but also on the properties of the protein itself. In fact, we observe a nonmonotonic trend between the dimensions of the polypeptide chain in bulk and the degree of compaction: the most extended chains experience up to 24% compaction, the most compact chains show virtually no change, and intermediate chains compress by up to 40% in size at a 40% crowder volume fraction. Free-volume theory combined with an impenetrable ellipsoidal representation of the chains predicts the crowding effects only for collapsed protein chains. An additional scaling factor, which can be easily computed from protein-crowder potential of mean force, corrects for the penetrability of extended chains and is sufficient to capture the observed nonmonotonic trend in compaction.
Introduction
Our knowledge of the structural and functional properties of proteins and other biological molecules continues to expand rapidly, with thousands of structures added to the Protein Data Bank (1) annually. However, these molecules exist in the cell in a densely crowded environment, in contrast to the dilute conditions in which most in vitro observations are typically made. In fact, estimates of the crowded volume fraction in the cell reach as high as 40% (2). The presence of crowding macromolecules has been shown to affect various protein processes, including protein-protein interactions, protein aggregation, and protein folding (3, 4, 5, 6). In protein folding, although crowding-induced changes in the folded state have been reported (7), the observed stabilization of the folded state under crowded conditions is commonly attributed to destabilization of the unfolded state of the protein (8, 9, 10). The primary effect of crowding is the reduction of the volume available to proteins, which results in excluded volume effects (11). In the case of an unfolded protein, this may limit the accessibility of extended conformations of the protein, resulting in stabilization of a more compact folded state (12, 13, 14). In addition to affecting protein structure in the context of folding, crowding may also drive aggregation of disordered proteins (15, 16, 17, 18).
It is expected that the expanded states of intrinsically disordered proteins (IDPs), a functional class of proteins that do not have a stable tertiary structure, can be similarly disfavored by crowding. However, the effect of macromolecular crowding on the properties of IDPs is yet unclear (13, 19, 20). Although crowding-induced structure of an IDP has been observed (21), it appears that this is not a common effect across IDPs (22, 23, 24, 25, 26), and characterization of the dimensions of IDPs in a crowded environment reveals varying degrees of compaction (27, 28). Similarly, studies of crowding effects on model polymers, such as PEG, have yielded varied results (29, 30). For example, small-angle neutron scattering characterization of one IDP, λN, in crowded solutions of up to 0.22 volume fraction showed changes in the protein dimensions of only 3–6%, at most, without any observed dependence of protein radius of gyration (Rg) on crowder concentration (27). On the other hand, in a study of four different proteins across the charge/hydropathy space, a common metric to distinguish between foldable and disordered protein sequences, Soranno et al. found profoundly different effects of crowding on the four sequences, with the one foldable protein exhibiting the least collapse and the remaining three IDPs experiencing greater collapse with increases in charge and hydrophilicity (28).
Simulations have also been carried out in an effort to understand the excluded-volume effects of crowding, apart from intermolecular attraction and other factors that are difficult to control experimentally (27, 31, 32). From representations of proteins with all nonhydrogen atoms to a simplified self-avoiding walk (SAW), these previous studies typically find modest to moderate compaction of the protein chain of up to 35% for crowder volume fractions of up to 0.4, with both smaller crowders and higher packing fractions yielding greater effects. In fact, Kang et al. found that the effect of crowding at a given crowder concentration may be determined solely by the ratio between the polymer and crowder dimensions using an excluded-volume polymer model (32).
Although a SAW model may represent some intrinsically disordered or unfolded proteins, variations in sequence length and content give rise to varying degrees of disorder. In the innumerable sequence combinations that can be constructed, efforts have been made to identify simple factors that can be used to predict disorder among proteins. Uversky et al. found that IDPs may be separated from folded proteins by their position in a simplified two-dimensional space defined by mean hydrophobicity and mean net charge (33). This picture has expanded to include more complex factors, such as proline content or patterning of charged residues, to capture variation among IDPs (34, 35, 36). Unfolded proteins and IDPs have likewise been described by polymer theories and exist over a range of polymer scaling exponents (37, 38, 39, 40).
It is reasonable to expect, therefore, that the differences in the polymeric properties or sequences of different proteins may contribute to their varied responses to macromolecular crowding. Here, we use a simplified polymer IDP model proposed by Ashbaugh et al. to explore the effect of crowding on proteins that span a range of polymer scaling regimes (41, 42). In a bath of spherical, repulsive crowders, the proteins show varied degrees of compaction. In fact, there is a nonmonotonic trend between the extent of compaction due to crowding that an IDP experiences and the expansion of the protein chain in bulk. Although the most collapsed chains show virtually no change between crowded and bulk conditions (as expected), the most extended chains do not conversely experience the greatest effect. Predictions of existing theoretical models are compared to the simulation data. We find that free-volume theory of an ellipsoid in a bath of hard spheres, with a simple correction factor for penetrability of expanded chains, is sufficient to nearly quantitatively reproduce our simulation results.
Materials and Methods
Computational model
A simplified coarse-grained model developed by Ashbaugh and co-workers was used to model IDPs (41). This model has been shown to capture the charge-hydropathy separation of disordered from folded proteins as a coil-to-globule transition with changes in sequence content. Though all-atom models provide the most accurate representation of systems of this scale, the computational cost associated with such simulations is still challenging (43). Coarse-grained representations, on the other hand, can greatly increase the time- and lengthscales that can be reached by simulations. Here, we use a two-amino-acid alphabet consisting of only hydrophobic and hydrophilic beads to capture a range of protein chain characteristics. This representation allows us to capture the behavior of both extended and compact proteins across varying solvent conditions, as is later discussed. Nonbonded interactions are described by a modified Lennard-Jones potential (41):
| (1) |
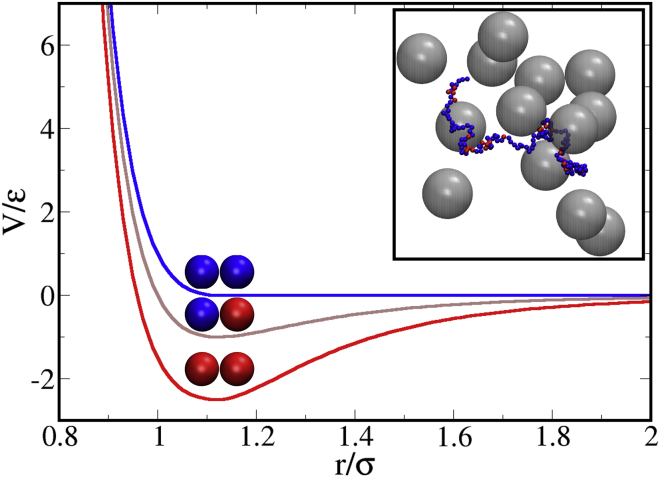
where is the usual Lennard-Jones potential and λ = 0, 1, and 2.5 for hydrophilic-hydrophilic, hydrophilic-hydrophobic, and hydrophobic-hydrophobic pair interactions, respectively (Fig. 1). For all intraprotein interactions, we set σ = 5 Å and ε = 0.3 kcal/mol. The potential cutoff is set equal to for all repulsive (λ = 0) interactions and for attractive interactions.
Figure 1.
Pair potential between protein beads, including hydrophilic-hydrophilic (blue), hydrophilic-hydrophobic (brown) and hydrophobic-hydrophobic (red) interactions. (Inset) Representative snapshot of an IDP chain in a bath of crowders. To see this figure in color, go online.
Proteins of 150 monomer units long were simulated with varying sequences. At each fraction of hydrophobic residues, <h>, four random sequences of hydrophobic and hydrophilic beads were generated. An example of the four <h> = 0.2 sequences used in the simulations is shown in Fig. S1 in the Supporting Material. For each <h>, different random number seeds were also used to generate initial velocities for four different runs. Molecular dynamics simulations were conducted using the LAMMPS package (44). Temperature was maintained at 300 K using a Langevin thermostat with a 1 ps damping coefficient, and dynamics were propagated using the velocity Verlet algorithm. A time step of 10 fs was used, and simulations were carried out for 10 μs, discarding the first 0.1–0.2 μs as equilibration time.
A Weeks-Chandler-Andersen potential (45) is used to model repulsive crowder-crowder and crowder-protein interactions (λ = 0 in Eq. 1), with kcal/mol and crowder radii equal to 13, 25, and 40 Å. This allows us to capture the excluded-volume effects of crowding. Although bulk simulations were carried out within a 400 Å cubic box, crowding simulations were carried out at box sizes of ∼150, 200, and 300 Å for crowders of 13, 25, and 40 Å, respectively. Exact box dimensions were adjusted to simulate crowder volume fractions of 0.1, 0.2, 0.3, and 0.4.
Average values presented below, including the average Rg, are first calculated from each trajectory independently, using block averaging with 10 blocks to determine the statistical uncertainty of each average. Simple averaging and propagation of error give the average values and errors across multiple sequences. Results from up to 12 randomly generated sequences are compared in Fig. S2, showing that the average protein properties are not significantly affected by the inclusion of additional sequences. As a result, we restrict our simulations to four sequences at each <h>.
Theoretical model
The simulation results are compared to the predictions of a theoretical model based on the free-volume theory of an ellipsoid—representing a protein—in a bath of hard spheres (46). In this approach, the structures of protein chains at a given <h> value from bulk simulations are clustered using a Euclidean distance in the space where are the eigenvalues of the gyration tensor defined by
| (2) |
Here, is the position of the ith bead of a protein with N segments from the center of mass of the protein. The quality threshold (QT) clustering algorithm with a threshold of 1 Å was adopted to cluster the structures. Specifically, in the QT algorithm, from each structure, we first find all neighboring structures that are within the cutoff distance of 1 Å in the space. The group with the largest number of neighboring structures is chosen as the first cluster. The structures that belong to this cluster are removed, and the same procedure is repeated with the reduced data set until all the structures are clustered. Fig. S3 (top) shows the resulting number of clusters out of 4 × 105 structures for each <h> and the populations of the top 10 clusters (Fig. S3, bottom).
Each cluster represented by the three eigenvalues of the gyration tensor is then mapped onto an ellipsoid whose principal radii, , are given by
| (3) |
where i denotes a cluster number. The factor is the ratio between the principal radii and the square root of the eigenvalues of the gyration tensor for a uniform ellipsoid. The free energy required to insert an ellipsoid in a bath of spherical crowders can be obtained using the fundamental measure theory (47, 48), a generalized form of the scaled particle theory, and is given by
| (4) |
where p, γ, and κ are the bulk pressure, surface tension at a planar wall, and bending rigidity of the crowders, and , , and are the volume, surface area, and integrated mean curvature of an ellipsoid representing the ith cluster. Here, is the crowder volume fraction where and are the crowder radius and number of crowders and is the volume of the simulation box. A general ellipsoid with principal radii , , and has volume , and and are numerically evaluated from the radii. The thermodynamic properties of the crowder bath are approximated by the Carnahan-Starling expressions for hard spheres (49):
| (5) |
| (6) |
| (7) |
The probability of finding a cluster i in a bath of crowders is approximated by
| (8) |
where is the probability for a cluster i in bulk with the eigenvalues of the gyration tensor, . The squared average of the radius of gyration, , is then calculated by
| (9) |
Results and Discussion
Model protein spans a range of polymer scaling regimes
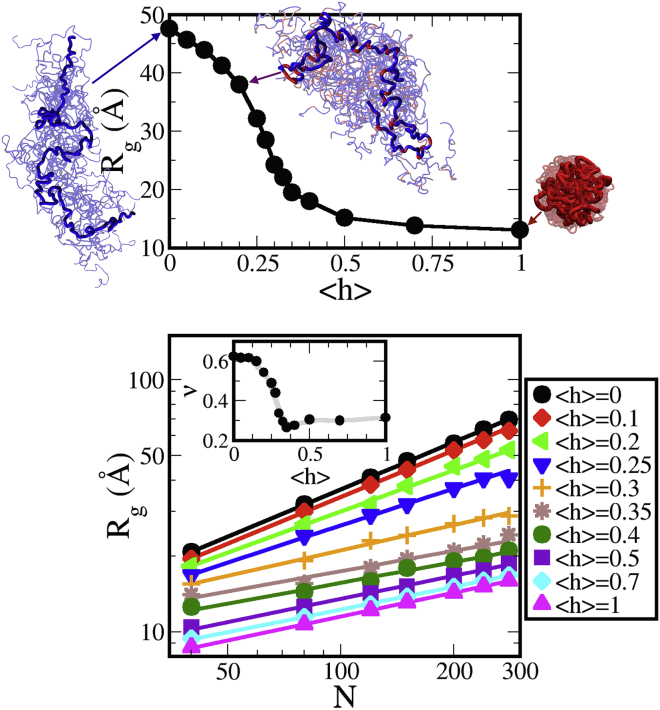
Using the protein model described above, one can capture the diversity in sequence content among protein chains by varying the fraction of hydrophobic residues, <h>, of the simulated sequence. As <h> increases, the protein chains begin to favor more compact conformations. The average radius of gyration, , of proteins with a given <h> therefore decreases with increasing hydrophobic content. In bulk, increasing <h> values from 0 to 1 results in average values ranging from ∼48 Å to 13 Å, respectively, for IDPs of 150 monomer units. Note that a Gaussian chain ( in Eq. 1) with the same number of beads yields Å. Fig. S4 shows the changes in distribution for <h> values of 0, 0.2, and 1. As the IDP becomes increasingly hydrophobic and compact, the distribution also narrows considerably. This is likewise reflected in the greater number of clusters at lower <h>, shown in Fig. S3. The model proteins can be further characterized by how their size scales with chain length, N, allowing comparison to proteins and other polymers which may behave similarly. Therefore, bulk simulations for protein lengths of , 80, 120, 180, 240, and 280 were performed in addition to the 150-bead simulations. The resulting values were fitted to to determine the polymer scaling exponent, ν, of the IDPs at each <h>. In good solvent, polymers expand with scaling as , whereas in poor solvent, collapse of polymers leads to a scaling exponent of 1/3 (50, 51). The ν values resulting from varying <h> in our simulations range from 0.30 at high <h> ( 0.6) to 0.62 at <h> = 0 (Fig. 2 lower, inset). Furthermore, this range of polymer chain characteristics is representative of proteins from compact globules to very extended chains that populate the proteome (35, 39). The model used herein therefore provides the versatility required to explore the effects of crowding on both extended and collapsed chains, or on proteins in varied solvent conditions, by varying the hydrophobic content, <h>, of a protein sequence. Although such a model obviously cannot capture the complexity of protein structure that arises from the 20 amino acids and additional posttranslational modifications that occur in nature (52), it is sufficient to give us significant insight into how general protein properties (i.e., polymer scaling) can dictate the extent of that protein’s response to crowding.
Figure 2.
Rg of the IDP chains in bulk. (Top) The Rg shows a coil-to-globule transition with increasing <h> (shown for 150-mer). (Bottom) Rg as a function of sequence length and (inset) the resulting scaling exponent, ν, vs. <h> from a best fit of . In this figure and hereafter, error bars are smaller than the symbol size. To see this figure in color, go online.
Crowding induces varying degrees of IDP compaction
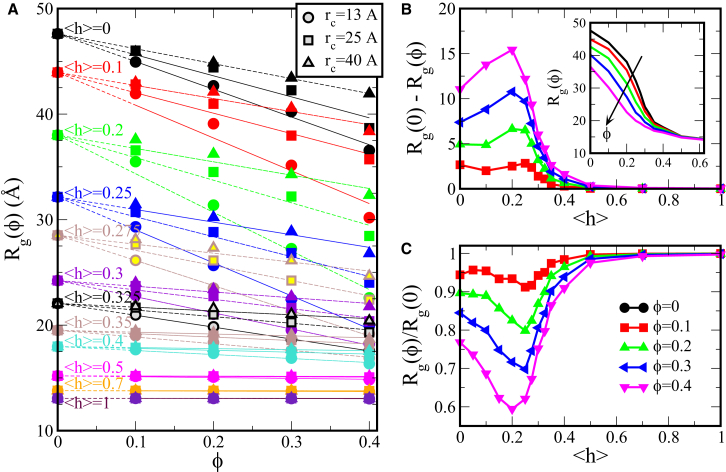
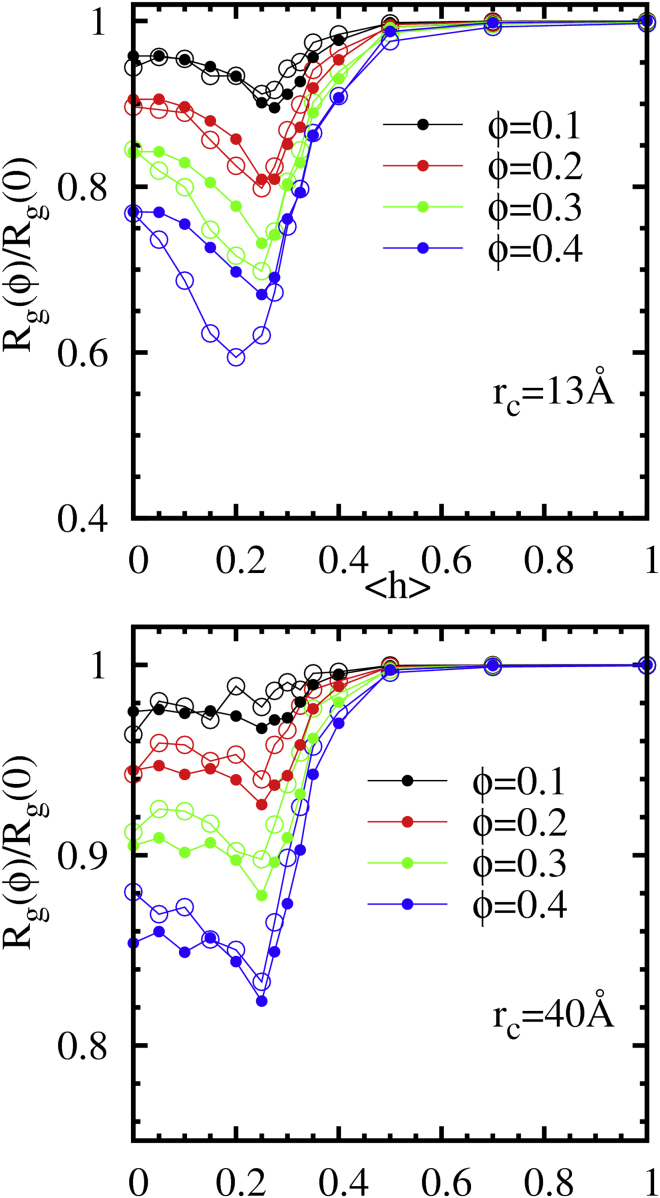
To determine the effect of crowding on proteins of varying sequence content, the 150-mer protein chains of different <h> values were simulated in a bath of repulsive, spherical crowders. We change both the volume fraction, ϕ, and the radius, , of the crowders to understand the effects of these variables on the protein chain over biologically relevant ranges. We use crowder radii, of 13, 25, and 40 Å, which are comparable to the dimensions of the most collapsed, intermediate, and extended IDP chains, respectively. The proteins of varying <h> show distinctly different responses to their crowded environment. In Fig. 3 A, we plot the of the chains as a function of crowder volume fraction, ϕ, showing a compaction due to crowding for many of the proteins. This compacting effect increases with both increasing crowder concentration and decreasing crowder size. Both these trends are expected, as both greater ϕ and smaller for a given ϕ result in less volume accessible to a protein chain. However, the degree of compaction under the same crowding conditions varies greatly between different IDP chains. In fact, the most hydrophobic chains (<h> 0.5) show virtually no compaction, even in a bath of the smallest (rc = 13 Å) crowders up to 40% crowder volume fraction, whereas the less hydrophobic, more extended chains show a significant decrease in under the same conditions.
Figure 3.
Average Rg of the IDP chains within crowders. (A) Average Rg of the IDP chains versus the crowder packing fraction, ϕ, for <h> ranging from 0 to 1, with crowder radii of 13, 25, and 40 Å. Symbol color is representative of the protein hydrophobicity, whereas shape signifies the crowder radius, shown in the legend. Dashed lines show linear fits and are provided as a visual guide. (B and C) The absolute magnitude of compaction, (B), and the scaled radius of gyration, (C) of the IDP chain within crowders are shown as a function of the fraction of hydrophobic residues in the chain (<h>) at various packing fractions. The inset in (B) shows unscaled Rg data as a function of <h> in bulk (, black curve) and within crowders (see color key in figure). To see this figure in color, go online.
To understand how the degree of compaction by crowders depends on the protein sequence content, we show Fig. 3, B and C, the absolute magnitude of compaction, , and the scaled radius of gyration, , respectively. The unscaled are also shown in the inset of Fig. 3 B, which show that Rg decreases monotonically with increasing protein hydrophobicity for a given environment, as expected. To understand the crowding-induced changes in protein size, it is more instructive to focus on the relative change in protein dimensions represented by or (32), because the bulk reference systems are different. We find that both these measures show a nonmonotonic trend as a function of <h>. Comparing the collapse due to crowding that the IDP shows across varying <h>, the greatest compaction is seen for chains composed of 20–25% hydrophobic residues. These chains correspond to scaling exponents of 0.54 to 0.49, respectively. With increasing hydrophobicity beyond this range, the chains are intrinsically more collapsed and undergo less compaction upon crowding, as may be expected. It may come as a surprise, however, that the most extended chains (<h> = 0) do not conversely exhibit the greatest compaction. This trend persists across the range of crowder sizes and packing fractions studied, although the effect is most striking with greater packing fractions and smaller crowders. Under these most crowded conditions, compaction of up to 40% is observed for the proteins composed of 20% hydrophobic residues. This effect diminishes to only 24% for the most hydrophilic, extended chains and to <1% for the most hydrophobic chains.
This effect on the protein dimensions is furthermore accompanied by a complementary change in the shape of the IDP chain. Fig. S5 shows the average asphericity of the IDPs both in bulk and in the presence of crowders. As is the case for the , the asphericity of the protein in bulk shows a monotonic decrease, becoming increasingly spherical () with increasing <h>. Increasing the crowder concentration for an IDP with a given hydrophobicity likewise results in a decrease in asphericity, and scaling asphericity values by those in bulk results in a nonmonotonic collapse, similar to that seen in .
Considering the distributions of the protein in addition to the average value gives further insight into the effect of crowding on these proteins. In bulk, the distributions become increasingly narrow (i.e., the variance decreases) with increasing <h> (Fig. S4). In the crowded environment, not only do the average values change, but the shapes of the distribution also display different behavior, as shown in Fig. S6. At <h> = 1, the distributions show essentially no change, as expected based on the average . At the opposite end, <h> = 0, although the protein chains show up to 23% reduction in in 13 Å crowders, the shape of the distribution is again largely unchanged. At <h> = 0.2, however, where the chains are compacted by up to 40%, the protein distribution narrows considerably. In a previous simulation work, Qin and Zhou observed similar changes in distributions for IDP chains of varying intramolecular interaction strength (31). There, too, a maximum compaction was observed at intermediate values of the intraprotein interaction parameter. The maximum in compaction observed by Qin and Zhou was explained by the greater width in the bulk distribution of that polymer. In other words, the degree of compaction was correlated with the variance of the polymer distribution; this is not the case in our simulations. However, we do find that the third moment, or skewness, of the distributions is greatest at intermediate <h> (Fig. S7). The greater-valued positive skewness of these distributions indicates that the distribution is more asymmetrical and spreads more at greater values. Because the expanded states are more affected by crowding than more compact states, this results in a greater change in in the presence of crowders.
Theoretical model development to account for IDP compaction
These results clearly demonstrate the differing effects crowding can have on IDPs of different sequence content. It is expected that purely repulsive crowders cause compaction of protein chains. This is due to the known entropic effects associated with loss of available volume. As the available volume is reduced, many more expanded conformations are disallowed, favoring a more compact ensemble. That is, the free energy of insertion of a more expanded chain (represented as a larger volume) in a bath of crowders is greater than that of its more compact (smaller volume) conformations. The effect of crowding is dependent not only on the size and density of the crowders, which directly affect the available volume, but also on the bulk properties of the protein itself. It is easy to rationalize why the most compact chains see the least effect due to crowding: at this extreme, the effect of crowding is limited by steric effects between residues, which are already very closely packed. However, this does not explain the reduced effect also seen for more extended chains in the <h> < 0.25 range. Although the crowders are purely repulsive, the polymer chain itself includes both repulsive and varying degrees of attractive interactions. Whereas crowders induce a modest degree of compaction in the most extended chain, which includes only repulsive interactions, the addition of hydrophobic residues adds an additional driving force for compaction. Going further, we compare prominent theoretical predictions to determine whether the nonmonotonic collapse with <h> can be theoretically resolved.
In an insightful simulation study of excluded-volume polymers, Kang et al. found that the effects of crowding on biopolymers could be described in a phase space of crowder concentration and the ratio between polymer and crowder size (32). The scaling argument therein is based on the expectation that when this ratio is on the order of 1, the polymer will be minimally impacted, whereas a much greater ratio will cause collapse of the polymer. The authors further note that this model may not be applied to highly charged polymers. Indeed, these observations have value in predicting the behavior of excluded volume polymers (those that scale with ) in crowded environments. Our excluded volume (<h> = 0) IDP chain shows similar compaction for varying chain lengths at a given ratio of 3.66 (Fig. S8). However, the effects of crowding on IDPs with varying <h> are not predicted by this argument. Holding constant, the <h> = 0.2 and 0.25 proteins show twice as much compaction (47–48% at ) as is seen in the <h> = 0 case (Fig. S8). This suggests that additional parameters, which take into account the much different conformational ensembles associated with varying chain hydrophobicity or solvent conditions (polymer scaling), may be needed to describe biopolymer collapse due to crowding.
In developing a theoretical model, it is therefore necessary to consider not only the ratio between protein and crowder sizes, but also details of protein shapes for different <h> values. Here, we adopt free-volume theory of an ellipsoid representing an IDP chain (see Materials and Methods) (46) and compare our simulation data to the predictions of this theory. First, when the representative ellipsoid is assumed to be impenetrable to crowders (as in Eq. 3), the free-volume theory predicts the extent of compaction quantitatively only for the most compact protein chains (see Fig. S9). The theory consistently overestimates the degree of compaction for small <h> (<0.3). Furthermore, the standard free-volume theory does not capture the nonmonotonic trend in compaction as a function of <h>.
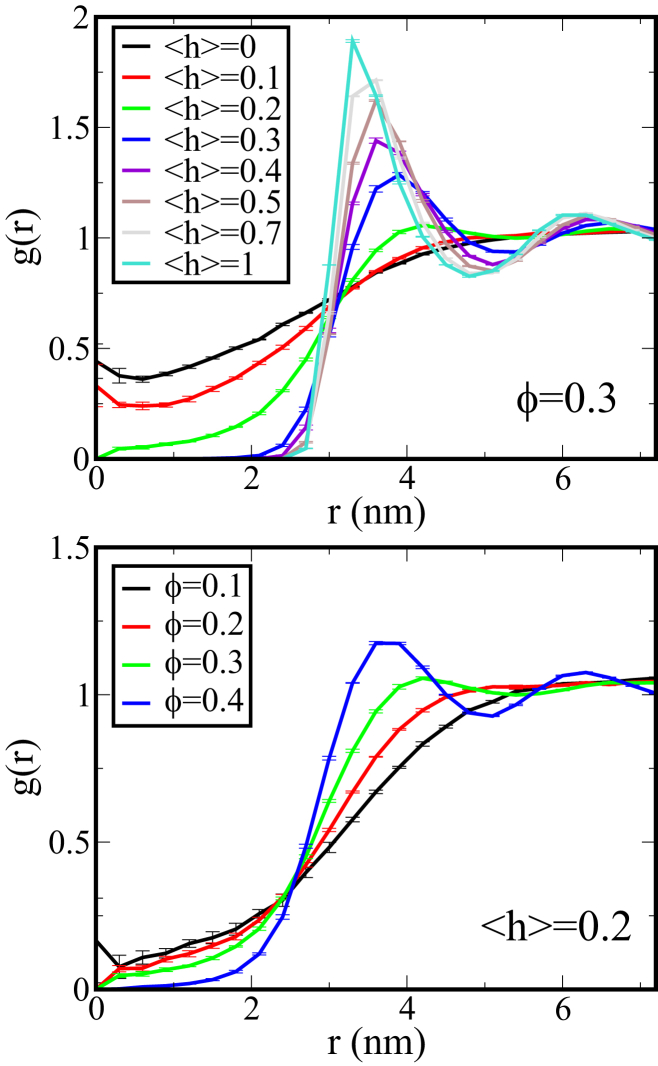
To help understand the breakdown of the free-volume theory, we also calculate the spatial distribution of the crowders relative to the protein chain. At high <h>, the collapse of the protein chain precludes crowders from occupying space within a distance of of the protein center of mass. For <h> = 0.2 and below, however, extended conformations are able to occupy regions between crowders, making the likelihood of finding a crowder near the center of mass of the protein not only finite, but also considerable (Fig. 4). This implies that at low <h>, the volume traced out by the of the protein is no longer impenetrable to crowders. As discussed below, this observation is crucial in developing a theoretical model that describes the nonmonotonic trend in the crowding-induced extent of compaction for IDPs of varying hydrophobicity.
Figure 4.
Average radial distribution function, g(r), of the crowders relative to the center of mass of the protein for rc = 13 Å. (Top) g(r) as a function of <h> shows penetration of the IDP volume by crowders for ϕ = 0.3, which decreases quickly as <h> increases. (Bottom) g(r) as a function of crowder concentration at <h> = 0.2 shows the finite probability of finding crowders at short distances at low crowder concentration. This probability diminishes quickly with increasing crowder concentration as the IDP collapses. To see this figure in color, go online.
Modified free-volume theory based on the penetrable ellipsoid model
Approximating protein chains as hard (impenetrable) ellipsoids whose principal radii are determined by the eigenvalues of the gyration tensor may work well for globular states, which occur at higher <h> values. However, for extended chain conformations predominant at small <h> values, such an approximation fails to describe the simulation data, as shown above. This is also apparent in the potential of mean force (PMF) between a protein chain and a spherical crowder (see Fig. S10). As shown in Fig. S10 (bottom), the PMF remains finite for small and <h>, even as the distance between the centers of mass of a protein chain and a crowder approaches zero. This results from the fact that at small <h>, the protein chains are highly extended, such that a small crowder particle can penetrate to the protein center of mass. Under such conditions, an impenetrable ellipsoid representation is not sufficient to describe the crowding effects on such a protein chain. A more realistic model for an extended chain must account for voids not represented by an ellipsoid of any shape. Unfortunately, an analytically tractable expression for estimating the insertion free energy of such a model in a bath of spherical crowders is not available in the current literature. Tran and Pappu have shown that the average shape of a highly denatured protein, which corresponds to <h> = 0 in this study, is represented by a prolate ellipsoid independent of protein sequence in the excluded-volume limit (53). However, the fluctuations in the Rg and asphericity values are large, suggesting that the chains in this limit are soft penetrable ellipsoids, which is also consistent with our simulation data.
Hence, we propose a penetrable ellipsoid model to represent extended protein chains for small <h> by introducing a scaling factor in the principal radii to capture the correct PMF behavior. Explicitly, the principal radii for a cluster i are now given by
| (10) |
where the scaling factor, s, depends on <h> and the crowder size, . Note that the cluster is still represented as a hard ellipsoid, but with principal radii now renormalized from the original values determined by the eigenvalues of the gyration tensor. To obtain the scaling factor, we first calculate the “effective” hard diameter from the crowder-protein PMF as
| (11) |
where is the orientation-averaged PMF between the crowder and the protein chain (Fig. S10). This approach has been applied to Lennard-Jones fluids via perturbation of hard-sphere fluids (54). The scaling factor for a given <h> is then defined by equating the average mean curvature of ellipsoids to that of a hard sphere of radius as
| (12) |
where is the mean curvature of the ellipsoid representing cluster i. The dependence of the scaling factor on <h> and is shown in Fig. S11. As anticipated, the scaling factor is small at small <h> but approaches a value close to unity as <h>.
The introduction of this scaling factor captures the nonmonotonic collapse observed in our simulations as shown in Fig. 5. In fact, it quantitatively captures the simulated results for most conditions, failing only by underestimating compaction of the intermediate protein chains (<h> between 0 and 0.3) at high packing fractions of small crowders (Å).
Figure 5.
/ for our 150-mer IDP chains (open circles) and the corresponding predictions by the ellipsoid model with free-volume theory (solid circles) at crowding volume fractions of ϕ = 0.1–0.4. The simulation results are compared with theoretical predictions for rc = 13 Å (top) and 40 Å (bottom). To see this figure in color, go online.
A simple homopolymer model is sufficient to recapitulate the observed trends in chain compaction
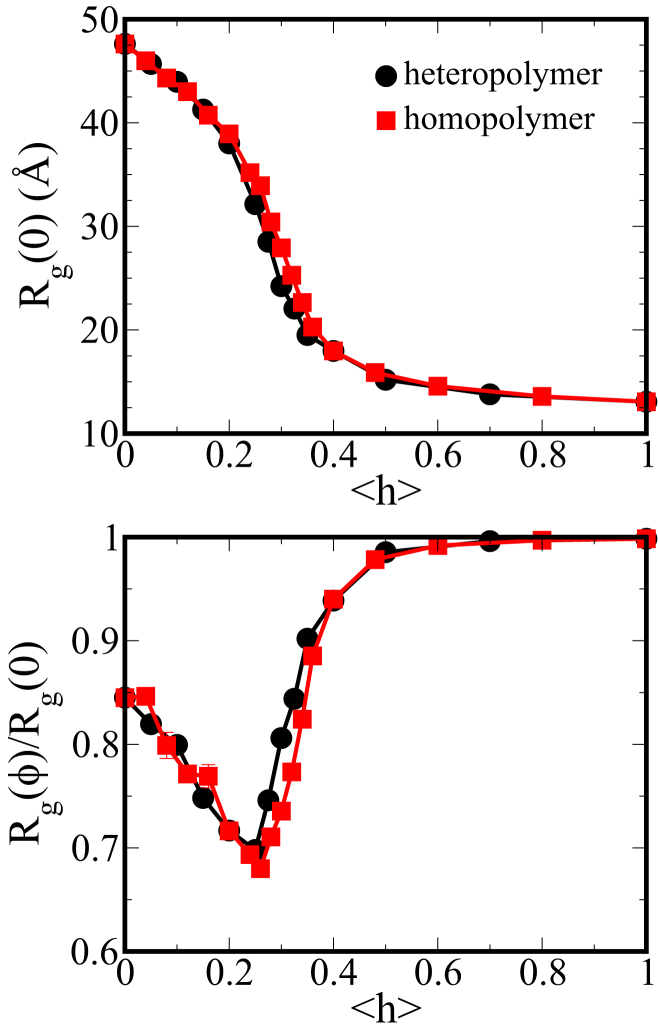
The results of Qin and Zhou (31) imply that the nonmonotonic trend in crowding-induced collapse we observe may be captured by a simple homopolymer model. We have therefore compared the results of our heteropolymer simulations with those of a similar homopolymer, allowing us to ensure that our observed results are not unique to the heteropolymer model used in this study. The homopolymer model for the IDP chain consists of 150 beads of the same kind in which the hydrophobicity is tuned by varying λ (Eq. 1) between all protein beads. To compare the two models across the same span of hydrophobicity, λ was varied between 0 and 2.5, which are taken to be the fully hydrophilic (<h> = 0) and fully hydrophobic (<h> = 1) cases, respectively, for the homopolymer. Such a model can also be used to more closely represent biological homopolymers, where changing λ tunes the solvent quality. Fig. 6 shows the results of this comparison. In bulk, the two models show a remarkably similar relationship between and hydrophobicity. Additionally, in a crowded environment, the nonmonotonic compaction of the protein chain with respect to <h> is preserved by the homopolymer representation. This result confirms that the nonmonotonic response to crowding exhibited by our model is not unique to the individual sequences simulated and the structures particular to those sequences (e.g., internal loops formed by hydrophobic contacts). Rather, the effect may be related to more general chain properties, such as mean hydrophobicity or, more generally, polymer scaling.
Figure 6.
Comparison of the heteropolymer model used above with a similar homopolymer model. <h> of the homopolymer is equal to λ/2.5, so that the <h> = 0 and <h> = 1 points are the same for both sets. (Top) Rg versus hydrophobicity for the two models in bulk. (Bottom) Rg scaled by that in bulk for rc = 13 Å and ϕ = 0.3. To see this figure in color, go online.
Degree and variation of observed compaction is comparable to experimental observations
Our results are also consistent with experimental findings on the effects of crowding on protein properties. Previous experimental studies have shown a great range in the responsiveness of the size of an IDP to a crowded environment, from virtually no effect to >30% reduction in (27, 28). In an NMR study, Cino et al. showed that although disorder is largely maintained by three IDPs in the presence of crowders, crowding may induce local stabilization of structured regions. Yet the structure of ubiquitin, a globular protein, was unaffected by crowding (26). Work by Goldenberg and Argyle found very little observed effect of crowding on , an IDP. Based on our results, the excluded-volume effects of crowding alone should cause moderate compaction of this extended protein. This difference can be accounted for by weak attractive crowder-protein interactions (27), as such attractive interactions can counter the excluded-volume effects of crowding (55). Soranno et al. explored the effects of crowding on four different IDPs of varying hydrophobicity and charge fractions (28). They observed that the most hydrophobic sequences, which are also the least charged, exhibit the least compaction. Although they found that increases, rather than decreases, in crowder size lead to increased compaction of their proteins, changes in crowder size are realized by increasing polymerization index. The crowder, polyethylene glycol (PEG), has a scaling exponent of 0.62, and the crowding effects of PEG of increasing weight therefore cannot necessarily be mapped to those of spherical crowders of increasing radius. Furthermore, the addition of ethylene glycol appears to have no effect on the proteins, indicating that some attractive interactions that are diminished by the effect of polymerization of the crowder may be at play. Inclusion of polymeric crowders in future work can provide additional insight into the effect of crowder configuration on protein chains.
A study of the effect of crowding by Ficoll on PEG, which is representative of a random-coil polymer, found a relatively high effect due to crowding of up to 50% compaction; however, experimental uncertainty is significant beyond ∼30% compaction (29). Additionally, polymeric effects of the crowder, which does not behave as a sphere, may contribute to additional compaction as in the work by Soranno et al. (28).
Conclusions
Here, we use a simplified model to represent proteins of varied characteristics, from expanded chains to compact globules, to sample across the space of naturally occurring proteins of varied intrinsic characteristics or in different solvent quality. This model is able to capture the wide variations in crowding effects on biological polymers that are observed experimentally. We find that crowding effects are greatest for our protein chains of intermediate hydrophobicity. Here, the intrachain attraction between hydrophobic residues may help to stabilize more compact conformations that are entropically disfavored. For both the purely repulsive excluded-volume chain, which does not experience intrachain attraction, and the more hydrophobic chains, whose compact bulk configurations are already closely packed, the effect of crowding is less. For naturally occurring proteins in vivo, this may lead not only to a varied response among different proteins, but also to local differences in crowding effects within the same IDP, as previously observed experimentally (26). As a result, areas of local structure may be stabilized, whereas more flexible regions remain relatively expanded. In vitro behavior and functionality may thereby be maintained, as long disordered coils as well as shorter, transiently structured target-binding regions are both associated with the functional roles of IDPs (56).
Predictions of the free-volume theory with an IDP chain represented as an ellipsoid are in good agreement with the simulation results for the more compact protein chains. However, this simple theory fails to predict the nonmonotonic behavior of the relative compaction of the average as a function of hydrophobicity. It is shown that introducing an additional scaling factor to account for the penetrability of the expanded chains yields predictions that capture the nonmonotonic compaction under crowding, in near agreement with the simulation results for the hydrophilic proteins in the most crowded (high ϕ and small crowder radius) conditions and in close quantitative agreement under all other conditions. However, future work is necessary to determine whether additional factors, such as charge content, may have a significant effect in different regions of the charge/hydropathy space. The coarse-grained model used here provides an extremely flexible framework in which to include added complexity, such as charged interactions, attractive protein-crowder interactions, and polymeric crowders, the characterization of which can lead to robust understanding and prediction of the effects of crowding on biomolecules in vivo.
Author Contributions
C.M.M., Y.C.K., and J.M. designed the project; C.M.M. performed research; Y.C.K. contributed analytic tools; C.M.M. and Y.C.K. analyzed data; C.M.M., Y.C.K., and J.M. wrote the manuscript; and J.M. supervised all aspects of the work.
Acknowledgments
We acknowledge support from the Alfred P. Sloan Foundation. Use of the high-performance computing capabilities of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (NSF) grant no. TG-MCB-120014, is gratefully acknowledged.
Editor: Rohit Pappu.
Footnotes
Eleven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30358-7.
Supporting Material
References
- 1.Berman H.M., Westbrook J., Bourne P.E. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ellis R.J., Minton A.P. Cell biology: join the crowd. Nature. 2003;425:27–28. doi: 10.1038/425027a. [DOI] [PubMed] [Google Scholar]
- 3.Minton A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- 4.Zhou H.X., Rivas G., Minton A.P. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bhattacharya A., Kim Y.C., Mittal J. Protein-protein interactions in a crowded environment. Biophys. Rev. 2013;5:99–108. doi: 10.1007/s12551-013-0111-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Theillet F.-X., Binolfi A., Selenko P. Physicochemical properties of cells and their effects on intrinsically disordered proteins (IDPs) Chem. Rev. 2014;114:6661–6714. doi: 10.1021/cr400695p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Biswas S., Chowdhury P.K. Unusual domain movement in a multidomain protein in the presence of macromolecular crowders. Phys. Chem. Chem. Phys. 2015;17:19820–19833. doi: 10.1039/c5cp02674a. [DOI] [PubMed] [Google Scholar]
- 8.Cheung M.S., Klimov D., Thirumalai D. Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc. Natl. Acad. Sci. USA. 2005;102:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Christiansen A., Wittung-Stafshede P. Quantification of excluded volume effects on the folding landscape of Pseudomonas aeruginosa apoazurin in vitro. Biophys. J. 2013;105:1689–1699. doi: 10.1016/j.bpj.2013.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mittal S., Singh L.R. Denatured state structural property determines protein stabilization by macromolecular crowding: a thermodynamic and structural approach. PLoS One. 2013;8:e78936. doi: 10.1371/journal.pone.0078936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Minton A.P. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol. Cell. Biochem. 1983;55:119–140. doi: 10.1007/BF00673707. [DOI] [PubMed] [Google Scholar]
- 12.Mittal J., Best R.B. Dependence of protein folding stability and dynamics on the density and composition of macromolecular crowders. Biophys. J. 2010;98:315–320. doi: 10.1016/j.bpj.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhou H.-X. Polymer crowders and protein crowders act similarly on protein folding stability. FEBS Lett. 2013;587:394–397. doi: 10.1016/j.febslet.2013.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dhar A., Samiotakis A., Cheung M.S. Structure, function, and folding of phosphoglycerate kinase are strongly perturbed by macromolecular crowding. Proc. Natl. Acad. Sci. USA. 2010;107:17586–17591. doi: 10.1073/pnas.1006760107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hatters D.M., Minton A.P., Howlett G.J. Macromolecular crowding accelerates amyloid formation by human apolipoprotein C-II. J. Biol. Chem. 2002;277:7824–7830. doi: 10.1074/jbc.M110429200. [DOI] [PubMed] [Google Scholar]
- 16.Munishkina L.A., Ahmad A., Uversky V.N. Guiding protein aggregation with macromolecular crowding. Biochemistry. 2008;47:8993–9006. doi: 10.1021/bi8008399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.O’Brien E.P., Straub J.E., Thirumalai D. Influence of nanoparticle size and shape on oligomer formation of an amyloidogenic peptide. J. Phys. Chem. Lett. 2011;2:1171–1177. doi: 10.1021/jz200330k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Latshaw D.C., Cheon M., Hall C.K. Effects of macromolecular crowding on amyloid β (16–22) aggregation using coarse-grained simulations. J. Phys. Chem. B. 2014;118:13513–13526. doi: 10.1021/jp508970q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Uversky V.N. Intrinsically disordered proteins and their environment: effects of strong denaturants, temperature, pH, counter ions, membranes, binding partners, osmolytes, and macromolecular crowding. Protein J. 2009;28:305–325. doi: 10.1007/s10930-009-9201-4. [DOI] [PubMed] [Google Scholar]
- 20.Elcock A.H. Models of macromolecular crowding effects and the need for quantitative comparisons with experiment. Curr. Opin. Struct. Biol. 2010;20:196–206. doi: 10.1016/j.sbi.2010.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Smith A.E., Zhou L.Z., Pielak G.J. Hydrogen exchange of disordered proteins in Escherichia coli. Protein Sci. 2015;24:706–713. doi: 10.1002/pro.2643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Flaugh S.L., Lumb K.J. Effects of macromolecular crowding on the intrinsically disordered proteins c-Fos and p27(Kip1) Biomacromolecules. 2001;2:538–540. doi: 10.1021/bm015502z. [DOI] [PubMed] [Google Scholar]
- 23.McNulty B.C., Young G.B., Pielak G.J. Macromolecular crowding in the Escherichia coli periplasm maintains α-synuclein disorder. J. Mol. Biol. 2006;355:893–897. doi: 10.1016/j.jmb.2005.11.033. [DOI] [PubMed] [Google Scholar]
- 24.Mouillon J.-M., Eriksson S.K., Harryson P. Mimicking the plant cell interior under water stress by macromolecular crowding: disordered dehydrin proteins are highly resistant to structural collapse. Plant Physiol. 2008;148:1925–1937. doi: 10.1104/pp.108.124099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Szasz C.S., Alexa A., Tompa P. Protein disorder prevails under crowded conditions. Biochemistry. 2011;50:5834–5844. doi: 10.1021/bi200365j. [DOI] [PubMed] [Google Scholar]
- 26.Cino E.A., Karttunen M., Choy W.-Y. Effects of molecular crowding on the dynamics of intrinsically disordered proteins. PLoS One. 2012;7:e49876. doi: 10.1371/journal.pone.0049876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Goldenberg D.P., Argyle B. Minimal effects of macromolecular crowding on an intrinsically disordered protein: a small-angle neutron scattering study. Biophys. J. 2014;106:905–914. doi: 10.1016/j.bpj.2013.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Soranno A., Koenig I., Schuler B. Single-molecule spectroscopy reveals polymer effects of disordered proteins in crowded environments. Proc. Natl. Acad. Sci. USA. 2014;111:4874–4879. doi: 10.1073/pnas.1322611111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Le Coeur C., Demé B., Longeville S. Compression of random coils due to macromolecular crowding. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:031910. doi: 10.1103/PhysRevE.79.031910. [DOI] [PubMed] [Google Scholar]
- 30.Gnutt D., Gao M., Ebbinghaus S. Excluded-volume effects in living cells. Angew. Chem. Int. Ed. Engl. 2015;54:2548–2551. doi: 10.1002/anie.201409847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Qin S., Zhou H.-X. Effects of macromolecular crowding on the conformational ensembles of disordered proteins. J. Phys. Chem. Lett. 2013;4:3429–3434. doi: 10.1021/jz401817x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kang H., Pincus P.A., Thirumalai D. Effects of macromolecular crowding on the collapse of biopolymers. Phys. Rev. Lett. 2015;114:068303. doi: 10.1103/PhysRevLett.114.068303. [DOI] [PubMed] [Google Scholar]
- 33.Uversky V.N., Gillespie J.R., Fink A.L. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 34.Müller-Späth S., Soranno A., Schuler B. From the Cover: Charge interactions can dominate the dimensions of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA. 2010;107:14609–14614. doi: 10.1073/pnas.1001743107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Das R.K., Pappu R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA. 2013;110:13392–13397. doi: 10.1073/pnas.1304749110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Marsh J.A., Forman-Kay J.D. Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J. 2010;98:2383–2390. doi: 10.1016/j.bpj.2010.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Goldenberg D.P. Computational simulation of the statistical properties of unfolded proteins. J. Mol. Biol. 2003;326:1615–1633. doi: 10.1016/s0022-2836(03)00033-0. [DOI] [PubMed] [Google Scholar]
- 38.Sherman E., Haran G. Coil-globule transition in the denatured state of a small protein. Proc. Natl. Acad. Sci. USA. 2006;103:11539–11543. doi: 10.1073/pnas.0601395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hofmann H., Soranno A., Schuler B. Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. Proc. Natl. Acad. Sci. USA. 2012;109:16155–16160. doi: 10.1073/pnas.1207719109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zerze G.H., Best R.B., Mittal J. Sequence- and temperature-dependent properties of unfolded and disordered proteins from atomistic simulations. J. Phys. Chem. B. 2015;119:14622–14630. doi: 10.1021/acs.jpcb.5b08619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ashbaugh H.S., Hatch H.W. Natively unfolded protein stability as a coil-to-globule transition in charge/hydropathy space. J. Am. Chem. Soc. 2008;130:9536–9542. doi: 10.1021/ja802124e. [DOI] [PubMed] [Google Scholar]
- 42.Ashbaugh H.S. Tuning the globular assembly of hydrophobic/hydrophilic heteropolymer sequences. J. Phys. Chem. B. 2009;113:14043–14046. doi: 10.1021/jp907398r. [DOI] [PubMed] [Google Scholar]
- 43.Zerze G.H., Miller C.M., Mittal J. Free energy surface of an intrinsically disordered protein: comparison between temperature replica exchange molecular dynamics and bias-exchange metadynamics. J. Chem. Theory Comput. 2015;11:2776–2782. doi: 10.1021/acs.jctc.5b00047. [DOI] [PubMed] [Google Scholar]
- 44.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 45.Weeks J.D., Chandler D., Andersen H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971;54:5237–5246. [Google Scholar]
- 46.Lim W.K., Denton A.R. Polymer crowding and shape distributions in polymer-nanoparticle mixtures. J. Chem. Phys. 2014;141:114909. doi: 10.1063/1.4895612. [DOI] [PubMed] [Google Scholar]
- 47.Oversteegen S.M., Roth R. General methods for free-volume theory. J. Chem. Phys. 2005;122:214502. doi: 10.1063/1.1908765. [DOI] [PubMed] [Google Scholar]
- 48.Roth R., Harano Y., Kinoshita M. Morphometric approach to the solvation free energy of complex molecules. Phys. Rev. Lett. 2006;97:078101. doi: 10.1103/PhysRevLett.97.078101. [DOI] [PubMed] [Google Scholar]
- 49.Carnahan N.F., Starling K.E. Equation of state for nonattracting rigid spheres. J. Chem. Phys. 1969;51:635–636. [Google Scholar]
- 50.Flory P.J. The configuration of real polymer chains. J. Chem. Phys. 1949;17:303–309. [Google Scholar]
- 51.De Gennes P.-G. Cornell University Press; Ithaca, NY: 1979. Scaling Concepts in Polymer Physics. [Google Scholar]
- 52.Zerze G.H., Mittal J. Effect of O-linked glycosylation on the equilibrium structural ensemble of intrinsically disordered polypeptides. J. Phys. Chem. B. 2015;119:15583–15592. doi: 10.1021/acs.jpcb.5b10022. [DOI] [PubMed] [Google Scholar]
- 53.Tran H.T., Pappu R.V. Toward an accurate theoretical framework for describing ensembles for proteins under strongly denaturing conditions. Biophys. J. 2006;91:1868–1886. doi: 10.1529/biophysj.106.086264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Barker J.A., Henderson D. Perturbation theory and equation of state for fluids. II. A successful theory of liquids. J. Chem. Phys. 1967;47:4714–4720. [Google Scholar]
- 55.Rosen J., Kim Y.C., Mittal J. Modest protein-crowder attractive interactions can counteract enhancement of protein association by intermolecular excluded volume interactions. J. Phys. Chem. B. 2011;115:2683–2689. doi: 10.1021/jp200625k. [DOI] [PubMed] [Google Scholar]
- 56.Tompa P. Intrinsically disordered proteins: a 10-year recap. Trends Biochem. Sci. 2012;37:509–516. doi: 10.1016/j.tibs.2012.08.004. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.