Shear-Induced Nitric Oxide Production by Endothelial Cells

Abstract

We present a biochemical model of the wall shear stress-induced activation of endothelial nitric oxide synthase (eNOS) in an endothelial cell. The model includes three key mechanotransducers: mechanosensing ion channels, integrins, and G protein-coupled receptors. The reaction cascade consists of two interconnected parts. The first is rapid activation of calcium, which results in formation of calcium-calmodulin complexes, followed by recruitment of eNOS from caveolae. The second is phosphorylation of eNOS by protein kinases PKC and AKT. The model also includes a negative feedback loop due to inhibition of calcium influx into the cell by cyclic guanosine monophosphate (cGMP). In this feedback, increased nitric oxide (NO) levels cause an increase in cGMP levels, so that cGMP inhibition of calcium influx can limit NO production. The model was used to predict the dynamics of NO production by an endothelial cell subjected to a step increase of wall shear stress from zero to a finite physiologically relevant value. Among several experimentally observed features, the model predicts a highly nonlinear, biphasic transient behavior of eNOS activation and NO production: a rapid initial activation due to the very rapid influx of calcium into the cytosol (occurring within 1–5 min) is followed by a sustained period of activation due to protein kinases.

Introduction

Nitric oxide (NO) plays a crucial biological role in the vasculature by stimulating the relaxation of vascular smooth muscle (1) and, therefore, regulating vascular resistance and blood pressure. It also has various secondary roles in the vasculature, e.g., the elimination of free radicals (2), and the prevention of plaque buildup (3). NO is produced by endothelial cells (ECs) upon exposure to mechanical forces, such as hemodynamic shear stress and intraluminal pressure (4). The mechanical stimulation of ECs triggers a complex cascade of biochemical reactions, which involves multiple cellular mechanosensors and enzymes. The ultimate target of this cascade is the activation of the endothelial nitric oxide synthase (eNOS) enzyme, which catalyzes the oxidation of the L-form of the α-amino acid arginine (L-Arg) (1, 4, 5), resulting in the production of NO.

Several mechanosensors are responsible for the initiation of the signal transduction cascade in an EC after mechanical stimulation (6, 7, 8, 9, 10, 11, 12), three of which are experimentally studied and incorporated into our model. First, the opening of mechanosensing ion channels (MSICs) mediates the influx of calcium from extracellular fluid into the cytosol (6). Second, the deformation of an EC activates G-protein-coupled receptors (GPCRs), which leads to the release of calcium ions inside the EC (7, 10, 13). Third, shear stress applied to an EC stimulates integrins—transmembrane receptors anchoring an EC to the extracellular matrix—which activates phosphatidylinositide 3-kinases (PI3K) enzymes (14, 15, 16), leading to the release of calcium inside the EC. Our model does not account for other potential mechanosensors (e.g., sodium and potassium ion channels; lipid rafts and vesicles; cytoskeletal remodeling; signaling via cadherins and other transmembrane proteins) because experimental evidence of their importance and functionality is relatively scarce.

The majority of previous modeling studies have focused on the influx of calcium ions into ECs exposed to external shear stress (17, 18, 19, 20, 21, 22). Consequently, these and other similar models treat MSICs as the sole mechanosensor responsible for shear-induced endothelial production of NO. On the biochemical side, these models have ignored the details of eNOS phosphorylation and activation of protein kinases responsible for this phosphorylation. A recent computational model (23) ameliorates these deficiencies by incorporating a more detailed description of the kinetics of eNOS activation by calcium-calmodulin complexes and protein kinase B (AKT), after exposure to shear stress. This model also incorporates two additional mechanosensors—GPCRs and integrins. However, it does not account for the inhibitory role of protein kinase C (PKC) or the role of cyclic guanosine monophosphate (cGMP) in providing negative feedback to the eNOS activation cascade. In addition, an analysis for how NO production (and eNOS activation) changes for different values of shear stress was lacking.

We build upon these and other previous efforts to develop a comprehensive model of NO production in ECs, which describes the biochemical reaction cascade induced by the three types of mechanosensors (MSICs, GPCRs, and integrins). Specifically, it relies on the experimental and modeling studies (7, 13, 14, 15, 17, 19, 20, 24) to represent both the calcium influx via MSICs and the activation of GPCRs and PI3K as functions of the applied shear stress. Our model accounts for the formation of calcium-CaM complexes, which leads to the recruitment of eNOS into an eNOS-CaM complex; the latter is subsequently phosphorylated by AKT (4), the details of which have been ignored in previous studies (17, 18, 19, 20, 21, 22). It also includes a negative feedback mediated by cGMP.

We use this model to elucidate the impact of the kinases AKT and PKC on shear-induced NO production by ECs. The model elucidates the role of calcium in the endothelium NO production, which remains an open question (4, 25, 26). Our analysis suggests that calcium affects both the early and later stages of NO production, albeit to different degrees.

Materials and Methods

Mathematical model of endothelial NO production

We assume that a layer of ECs is continuously supplied with metabolic substrates sufficient for maintaining endothelial NO production. Blood flow over the endothelial layer exerts shear stress τ on the surface of the outer cell wall, which triggers a cascade of biochemical reactions resulting in endothelial NO production. The reactions are assumed to occur in the cytosol, which is treated as a well-mixed continuum, i.e., concentration gradients are ignored. In what follows, the concentration of any reactant A is denoted by (A), with units of micromoles (μM).

Activation of G proteins

Deformation of a cell membrane by wall shear stress (WSS) activates GPCRs, which are mechanically coupled to the cell membrane and serve as force transducers that activate G proteins (10, 27, 28). The rate of G-protein activation is given by (13, 24)

$$\frac{\text{d}\left[G\right]}{\text{d}t}=k_a\left[R^{\ast }\right]\left(\left[G_t\right]-\left[G\right]\right)-k_d\left[G\right],$$ (1)

where $\left[G\right]$ is the concentration of activated G-proteins; $k_a$ and $k_d$ are, respectively, the forward and backward rate constants for G-protein activation (numerical values of these and all the other reaction rate constants and model parameters are reported in Table 1); $\left[R^{\ast }\right]$ is a fraction of the GPCRs activated by shear stress; and $\left[G_t\right]$ is the total concentration of G-proteins present in the cell. We assume the instantaneous activation of GPCRs in response to WSS τ and fit the experimental $\left[R^{\ast }\right]$ versus τ data from Fig. 4d in Chachisvilis et al. (7) with a curve

$$\left[R^{\ast }\right]=\text{tanh}\left(\frac{\pi \tau }{\Lambda }\right),$$ (2)

where τ is in dynes/cm². The data reported in Chachisvilis et al. (7) justify the assumption of instantaneous GPCR activation/inactivation: activation (or inactivation) of GPCRs in response to applied (or removed) WSS occurs on a timescale of 1 ns.

Table 1.

Reaction Rate Constants and Other Model Parameters

Parameter	Value	Reference	Parameter	Value	Reference
ka	0.017 s−1	(13)	kd	0.15 s−1	(13)
μ1	0.2 s−1	(17)	α	8.37 s−1	Supporting Material
Λ	15 dynes/cm2	Supporting Material	KdCaM	1 μM	Supporting Material
rr	10 s−1	Supporting Material	$k_{{\text{PIP}}_2}^{-}$	0.7024 s−1	(29)
Vr	3.5	(19)	qmax	17.6 μM s−1	(17)
krel	6.64 s−1	(19)	kres	5 μMs−1	(19)
kout	24.7 μM s−1	(19)	kCCE	8 × 10−7	(17)
k2	0.2 μM	(19)	k3	0.15 μM	(19)
k5	0.32 μM	(19)	koff	300 s−1	(17)
kon	100 μM−1 s−1	(17)	kleak	10−7μM−1 s−1	(17)
χ	28.6 dynes/cm	(17, 19)	aP13K	2.5	Supporting Material
η	0.003 s−1	Supporting Material	δ	24 dynes/cm2	Supporting Material
k1p	0.021 s−1	(29)	$k_{2p}$	0.022 s−1	(29)
$k_{\text{AKT}}^{-}$	0.1155 s−1	(29)	$k_{\text{PKC}}^{-}$	0.1155 s−1	(29)
$k_{\text{Thr}}^{+}$	0.002 s−1	(46)	$k_{\text{Thr}}^{-}$	2.22 ± 10−4 s−1	(46)
$k_{{\text{Ca}}_4-\text{CaM}}$	100 s−1	Supporting Material	β	2.7	Supporting Material
θ	0.0045	Supporting Material	$K_{\text{CaM}}^{+}$	7.5 s−1	Supporting Material
K0.5CaM	3 μM	(44)	$K_{\text{CaM}}^{-}$	0.01 s−1	(38)
$k_{\text{eAKT}}^{\text{max}}$	0.004 s−1	Supporting Material	$k_{\text{eAKT}}^{-}$	2.22 × 10−4 s−1	Supporting Material
λNO	382 s−1	(49)	$\Upsilon$	300 s−1	Supporting Material
ϕ	9	(41)	$R_{\text{NO}}^{\text{max}}$	0.022 s−1	(32)
$b_1$	15.15 nM	(32)	N	2	(17)
$a_0$	1200.16 nM2	(32)	a1	37.33 nM	(32)
$g_0$	4.8 nM2	(32)	g1	35.33 nM	(32)
X	0.0695 s−1	(33)	KcGMP	2 μM	(33)
$V_{\text{cGMP}}^{\text{max}}$	1.26 μM s−1	(33)	$\left[{\text{CaM}}_{\text{tot}}\right]$	30 μM	(34)
${\left[{\text{Ca}}^{2+}\right]}_{\text{e}}$	1500 μM	(17)	$\left[G_t\right]$	0.33 μM	(13, 24) and Supporting Material
$\left[{\text{PIP}}_{2_{\text{t}}}\right]$	10 μM	(75)	$\left[{\text{eNOS}}_{\text{tot}}\right]$	0.04 μM	Supporting Material
Kcp	0.002 μM−1	Supporting Material	SGC0	0.1 μM	Supporting Material
MATP	0.7937	Supporting Material	${\left[{\text{Ca}}^{2+}\right]}_{s,0}$	2828 μM	Supporting Material
ξ	0.0075 μM−1	Supporting Material	Btot	120 μM	(34)

An estimation procedure for the parameter values not found in the literature is discussed in Section S1 of the Supporting Material.

Activation of G proteins triggers the hydrolysis of PIP₂ (phosphatidylinositol 4,5-bisphosphate) and formation of IP₃ (inositol triphosphate) in accordance with a rate equation (13, 17)

$$\begin{array}{l}\frac{\text{d}\left[{\text{IP}}_3\right]}{\text{d}t}=r_f\left[{\text{PIP}}_2\right]-{\mu }_1\left[{\text{IP}}_3\right],\\ r_f=\alpha K_{cp}{M}_{\text{ATP}}\left[G\right],\end{array}$$ (3)

where ${\mu }_1$ is the rate of IP₃ degradation, and $r_f$ is the $\left[G\right]$-dependent rate of IP₃ formation from PIP₂ whose parameterization with coefficients α, $K_{cp}$, and $M_{\text{ATP}}$ is discussed in Section S1 of the Supporting Material. Equation 3 represents an IP₃-PIP₂ cycle (see Lemon et al. (13) for details), in which the produced IP₃ degrades to an intermediate phospholipid that is then converted back to PIP₂. The rate of change of $\left[{\text{PIP}}_2\right]$ is described by a rate equation (13, 29)

$$\frac{\text{d}\left[{\text{PIP}}_2\right]}{\text{d}t}=-\left(r_f+r_r\right)\left[{\text{PIP}}_2\right]-r_r\left[{\text{IP}}_3\right]+r_r\left[{\text{PIP}}_{2_{\text{t}}}\right]-k_{{\text{PIP}}_2}^{+}\left[{\text{PIP}}_2\right]+k_{{\text{PIP}}_2}^{-}\left[{\text{PIP}}_3\right],$$ (4)

in which the first three terms on the right-hand side represent the cycling of PIP₂ to IP₃ and back to PIP₂, and the remaining two terms account for the phosphorylation of PIP₂ to PIP₃ (phosphatidylinositol (3,4,5)-triphosphate). Here $r_r$ is the rate constant of replenishment of PIP₂, and $k_{{\text{PIP}}_2}^{+}$ and $k_{{\text{PIP}}_2}^{-}$ are the forward and backward rate constants of PIP₃ formation from PIP₂. Phosphorylation of PIP₂ forms PIP₃, a reaction that is catalyzed by activated PI3K in accordance with (29)

$$\frac{\text{d}\left[{\text{PIP}}_3\right]}{\text{d}t}=k_{{\text{PIP}}_2}^{+}\left[{\text{PIP}}_2\right]-k_{{\text{PIP}}_2}^{-}\left[{\text{PIP}}_3\right].$$ (5)

The catalytic role of PI3K is sensitive to the level of shear stress and is elaborated upon in Activation of Protein Kinases.

Calcium signaling

The shear stress τ causes the opening of MSICs, resulting in a sharp increase in ${\left[{\text{Ca}}^{2+}\right]}_{\text{c}}$ due to the influx of calcium ions from the extracellular fluid. This and other processes affecting the calcium balance in an endothelial cell (e.g., capacitative calcium entry or CCE) are modeled by mass balance equations (17, 19, 20)

$$\begin{array}{c}\frac{\text{d}\left({\left[{\text{Ca}}^{2+}\right]}_{\text{c}}+{\left[{\text{Ca}}^{2+}\right]}_{\text{b}}\right)}{\text{d}t}=q_{\text{rel}}-q_{\text{res}}-q_{\text{out}}+q_{\text{in}}+k_{\text{leak}}{\left[{\text{Ca}}^{2+}\right]}_{\text{s}}^2,\\ \frac{\text{d}{\left[{\text{Ca}}^{2+}\right]}_{\text{s}}}{\text{d}t}=-V_r\left(q_{\text{rel}}-q_{\text{res}}-k_{\text{leak}}{\left[{\text{Ca}}^{2+}\right]}_{\text{s}}^2\right),\end{array}$$ (6)

where ${\left[{\text{Ca}}^{2+}\right]}_{\text{s}}$ and ${\left[{\text{Ca}}^{2+}\right]}_{\text{b}}$ are the calcium concentrations in the EC internal stores (i.e., within the smooth endoplasmic reticulum) and buffered in dissolved cytosolic proteins, respectively. The fluxes $q_{\text{rel}}$, $q_{\text{res}}$, and $q_{\text{out}}$ represent calcium release from internal stores, calcium resequestration into these internal stores, and calcium efflux via the sodium-calcium exchanger (20), respectively. These concentration-dependent fluxes are given by

$$\begin{array}{c}{q}_{\text{rel}}=k_{\text{rel}}{\left(\frac{\left[{\text{IP}}_3\right]}{k_2+\left[{\text{IP}}_3\right]}\right)}^3{\left[{\text{Ca}}^{2+}\right]}_{\text{s}},\\ q_{\text{res}}=k_{\text{res}}{\left(\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}}{k_3+{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}}\right)}^2,\\ q_{\text{out}}=k_{\text{out}}\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}}{k_5+{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}},\end{array}$$ (7)

where $k_{\text{rel}}$, $k_{\text{res}}$, $k_{\text{out}}$, $k_1$, $k_3$, and $k_5$ are rate constants. Influx of calcium ions from the extracellular fluid into the cytosol occurs through both MSICs (17, 19) and CCE (30). The corresponding calcium fluxes are related by

$$q_{\text{in}}=q_{\text{MSIC}}+q_{\text{CCE}}.$$ (8)

Following Plank et al. (17), Comerford et al. (19), and Wiesner et al. (20), we assume that the rate of calcium influx via MSICs, $q_{\text{MSIC}}$, is linearly proportional to the fraction $f_0$ of ion channels open at a given WSS τ,

$$\begin{array}{c}{q}_{\text{MSIC}}=f_0\left(\tau \right)q_{\text{max}}=\frac{q_{\text{max}}}{1+N\text{exp}\left(-W\right)},\\ W\left(\tau \right)=W_0\frac{{\left(\tau +\sqrt{16{\chi }^2+{\tau }^2}-4\chi \right)}^2}{\tau +\sqrt{16{\chi }^2+{\tau }^2}},\end{array}$$ (9)

where $q_{\text{max}}$ is the maximal rate of influx, $W\left(\tau \right)$ quantifies the extent to which the applied mechanical force is converted to gating energy for MSICs, and the constant χ = 28.6 dynes/cm² represents the membrane shear modulus. The flux due to CCE, $q_{\text{CCE}}$, is caused by the depletion of internal calcium stores, which induces influx of calcium from the extracellular fluid (30). The magnitude of $q_{\text{CCE}}$ is affected by cGMP (18, 31), such that (17, 18, 19)

$$q_{\text{CCE}}=k_{\text{CCE}}\psi \left(\left[\text{cGMP}\right]\right)\left({\left[{\text{Ca}}^{2+}\right]}_{\text{s},0}-{\left[{\text{Ca}}^{2+}\right]}_{\text{s}}\right)\left({\left[{\text{Ca}}^{2+}\right]}_{\text{e}}-{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}\right),$$ (10)

where ${\left[{\text{Ca}}^{2+}\right]}_{\text{e}}$ is the calcium concentration in extracellular fluid (external, assumed to remain constant), and ${\left[{\text{Ca}}^{2+}\right]}_{\text{s},0}$ is the stored calcium concentration under basal conditions. The decreasing function $\psi \left(\left[\text{cGMP}\right]\right)$ accounts for the inhibition of CCE observed in Kwan et al. (31), where it is suggested that $\psi \left(\left[\text{cGMP}\right]\right)$ is a linear function of the cGMP concentrations,

$$\psi =1.00-\xi \left[\text{cGMP}\right],$$ (11)

over the range of $\left[\text{cGMP}\right]$ relevant to our model, i.e., on the order of 10 μM typical of ECs and smooth muscle (32, 33). Here ξ is a constant of proportionality, whose value is estimated in Section S1 and reported in Table 1. In addition to inhibition of CCE, increase in $\left[\text{cGMP}\right]$ also results in inhibition of calcium transport via MSICs (31). However, the relevant data suggest that at $\left[\text{cGMP}\right]$ on the order of 10 μM and below, the MSICs inhibition is negligible (31). We therefore ignore the role of cGMP inhibition on MSIC function.

Equation 6 includes calcium concentration in the buffer, ${\left[{\text{Ca}}^{2+}\right]}_{\text{b}}$. As the cytosolic-calcium concentration ${\left[{\text{Ca}}^{2+}\right]}_{\text{c}}$ increases, it forms calcium complexes with cytosolic proteins in accordance with a rate law (17, 34)

$$\frac{\text{d}{\left[{\text{Ca}}^{2+}\right]}_{\text{b}}}{\text{d}t}=k_{\text{on}}{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}\left(B_{\text{tot}}-{\left[{\text{Ca}}^{2+}\right]}_{\text{b}}\right)-k_{\text{off}}{\left[{\text{Ca}}^{2+}\right]}_{\text{b}}.$$ (12)

where $B_{\text{tot}}$ is the total concentration of calcium binding sites in cytosolic buffer proteins; and $k_{\text{on}}$ and $k_{\text{off}}$ are forward and backward buffering rate constants, respectively.

Activation of protein kinases

Integrins, which anchor an EC to the extracellular matrix, are connected to focal adhesion sites within the EC and act as mechanotransducers. Application of mechanical forces results in the tyrosine phosphorylation of focal adhesion kinases (FAKs), ultimately triggering the stimulation of PI3K. In ECs, this process has been studied in vitro, where the activation of integrins, FAKs, and PI3K are all measured as functions of mechanical stimulation (14, 15, 16).

Upon exposure to shear stress, PI3K is phosphorylated rapidly, reaching maximal activation on the order of 10 s (15, 35). This process is caused by activation of the FAK/Src complex through integrins (36) that serve as force transducers that mediate the mechanical signal. Because this timescale is an order-of-magnitude smaller than that of the other chemical reactions in our model (which generally occur at timescales of ∼1–100 min), we neglect the time lag between the application of mechanical force and PI3K activation; application of force thus results in immediate activation of PI3K. The active PI3K species, PI3K^∗, then gradually returns to its basal levels of activity, ${\left[\text{PI}3{\text{K}}^{\ast }\right]}_{\text{bas}}$. This process is modeled as

$$\frac{\left[\text{PI}3{\text{K}}^{\ast }\right]}{{\left[\text{PI}3{\text{K}}^{\ast }\right]}_{\text{bas}}}=1+a_{\text{PI}3\text{K}}\text{tanh}\left(\frac{\pi \tau }{\delta }\right){\text{e}}^{-\eta t},$$ (13)

where the constants $a_{\text{PI}3\text{K}}$, δ and η were fitted to the experimental data from Katsumi et al. (14) and Go et al. (15). The data reported in Go et al. (15) suggest that the decay of $\left[\text{PI}3{\text{K}}^{\ast }\right]$ to its basal level occurs on a relatively fast timescale of ∼5 min, while the corresponding data in Katsumi et al. (14) support a larger timescale of ∼30 min. In Eq. 13, this timescale is controlled by the parameter η. To account for the timescale variability observed in Katsumi et al. (14) and Go et al. (15), we consider a range of η-values. Fig. S1 in the Supporting Material reveals that the model predictions are relatively insensitive to variations in the value of δ; this suggests that the transient effects of PI3K activation on NO production are negligible. Finally, activation of PI3K increases the rate of PIP₂ phosphorylation to PIP₃ (29),

$$k_{\text{PIP}2}^{+}=k_{1p}\frac{\left[\text{PI}3{\text{K}}^{\ast }\right]}{{\left[\text{PI}3{\text{K}}^{\ast }\right]}_{\text{max}}}+k_{2p}=\frac{k_{1p}}{1+a_{\text{PI}3\text{K}}}\left[1+a_{\text{PI}3\text{K}}{\text{e}}^{-\eta t}\text{tanh}\left(\frac{\pi \tau }{\delta }\right)\right]+k_{2p},$$ (14)

thus playing a catalytic role in Eq. 5. The values of reaction rate constants $k_{1p}$ and $k_{2p}$ are given in Sedaghat et al. (29), and it follows from Eq. 13 that the maximum concentration of active PI3K is ${\left[\text{PI}3{\text{K}}^{\ast }\right]}_{\text{max}}={\left[\text{PI}3{\text{K}}^{\ast }\right]}_{\text{bas}}\left(1+a_{\text{PI}3\text{K}}\right)$.

PIP₃ meditates phosphorylation and subsequent activation of protein kinases AKT and PKC, which in turn phosphorylate eNOS (29). This activation is modeled by rate laws (29)

$$\begin{array}{l}\frac{\text{d}\left[{\text{AKT}}^{\ast }\right]}{\text{d}t}=k_{\text{AKT}}^{+}\left[\text{AKT}\right]-k_{\text{AKT}}^{-}\left[{\text{AKT}}^{\ast }\right],\\ \frac{\text{d}\left[{\text{PKC}}^{\ast }\right]}{\text{d}t}{k}_{\text{PKC}}^{+}\left[\text{PKC}\right]-k_{\text{PKC}}^{-}\left[{\text{PKC}}^{\ast }\right],\end{array}$$ (15)

where $\left[{\text{AKT}}^{\ast }\right]$, $\left[\text{AKT}\right]$, $\left[{\text{PKC}}^{\ast }\right]$, and $\left[\text{PKC}\right]$ are concentrations of the activated (phosphorylated) AKT, unactivated AKT, activated (phosphorylated) PKC, and unactivated PKC, respectively. The total concentrations of AKT and PKC are conserved, $\left[\text{AKT}\right]+\left[{\text{AKT}}^{\ast }\right]={\left[\text{AKT}\right]}_{\text{tot}}$ and $\left[\text{PKC}\right]+\left[{\text{PKC}}^{\ast }\right]={\left[\text{PKC}\right]}_{\text{tot}}$. The rate constants in Eq. 15 increase with $\left[{\text{PIP}}_3\right]$ in accordance with (29)

$$\begin{array}{l}{k}_{\text{AKT}}^{+}=0.1k_{\text{AKT}}^{-}\frac{\left[{\text{PIP}}_3\right]-{\left[{\text{PIP}}_3\right]}_{\text{min}}}{{\left[{\text{PIP}}_3\right]}_{\text{max}}-{\left[{\text{PIP}}_3\right]}_{\text{min}}},\\ k_{\text{PKC}}^{+}=0.1k_{\text{PKC}}^{-}\frac{\left[{\text{PIP}}_3\right]-{\left[{\text{PIP}}_3\right]}_{\text{min}}}{{\left[{\text{PIP}}_3\right]}_{\text{max}}-{\left[{\text{PIP}}_3\right]}_{\text{min}}},\end{array}$$ (16)

where $k_{\text{AKT}}^{-}$ and $k_{\text{PKC}}^{-}$ are rate constants, ${\left[{\text{PIP}}_3\right]}_{\text{min}}=0.0031{\left[{\text{PIP}}_2\right]}_{\text{tot}}$, and ${\left[{\text{PIP}}_3\right]}_{\text{max}}=0.031{\left[{\text{PIP}}_2\right]}_{\text{tot}}$. The significant transient behavior of $\left[{\text{PIP}}_3\right]$ (Fig. S8) renders the rate constants $k_{\text{AKT}}^{+}$ and $k_{\text{PKC}}^{+}$ time-dependent. This necessitates a numerical solution of the expressions in Eq. 15.

Phosphorylation and formation of eNOS complexes

Calcium forms several complexes with calmodulin (CaM), which then recruit eNOS into an eNOS-CaM complex; the presence of heat shock protein 90 (Hsp90) enhances the recruitment rate. Of the various Ca²⁺/CaM complexes only Ca₃-CaM and Ca₄-CaM appear to actively recruit eNOS. Among the two, Ca₄-CaM is the dominant species both in terms of cytosolic concentration (37) and affinity for eNOS (38). Hence only the role of Ca₄-CaM in the recruitment of eNOS is accounted for in our model. We use the Hill function to relate the concentration of free Ca₄-CaM in the cytosol to the cytosolic calcium concentration (39, 40),

$$\frac{\text{d}\left[{\text{Ca}}_4-\text{CaM}\right]}{\text{d}t}=k_{{\text{Ca}}_4-\text{CaM}}\left(\theta \frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}^{\beta }}{K_{\text{dCaM}}+{\left[{\text{Ca}}^{2+}\right]}_{\text{c}}^{\beta }}{\left[\text{CaM}\right]}_{\text{tot}}-\left[{\text{Ca}}_4-\text{CaM}\right]\right).$$ (17)

Here β is the Hill coefficient, $K_{\text{dCaM}}$ is the apparent Ca₄-CaM dissociation constant, $k_{{\text{Ca}}_4-\text{CaM}}$ is the reaction rate constant, and ${\left[\text{CaM}\right]}_{\text{tot}}$ is the total concentration of CaM in the cytosol. The coefficient θ determines the limiting amount of free Ca₄-CaM in the cytosol at steady state, at large cytosolic calcium concentrations ${\left[{\text{Ca}}^{2+}\right]}_{\text{c}}$.

We model activation of eNOS from its basal (inactive) state to its fully active (Ser-1197 phosphorylated) state as a three-step process (4, 9, 41, 42, 43).

Step 1. Caveolin-bound eNOS (eNOS_cav) forms a complex with Ca₄-CaM, which we denote by eNOS-CaM. The rate of its formation is modeled using Michaelis-Menten kinetics,

$$\frac{\text{d}\left[\text{eNOS}-\text{CaM}\right]}{\text{d}t}=\frac{k_{\text{CaM}}^{+}\left[{\text{Ca}}_4\text{CaM}\right]}{k_{0.5\text{CaM}}+\left[{\text{Ca}}_4\text{CaM}\right]}\left[{\text{eNOS}}_{\text{cav}}\right]-k_{\text{CaM}}^{-}\left[\text{eNOS}-\text{CaM}\right]-\frac{\text{d}\left[\text{eNOS}-{\text{CaM}}^{\ast }\right]}{\text{d}t},$$ (18)

where the forward $\left(k_{\text{CaM}}^{+}\right)$ and backward $\left(k_{\text{CaM}}^{-}\right)$ rate constants, and the Michaelis-Menten constant, $k_{0.5\text{CaM}}$, are obtained from the data presented in Michel et al. (44), McMurry et al. (38), and Ju et al. (45); and eNOS-CaM^∗ denotes the eNOS-CaM complex stabilized by phosphorylation due to AKT at Ser-1197.

Step 2. The latter process is assumed to follow first-order kinetics,

$$\frac{\text{d}\left[\text{eNOS}-{\text{CaM}}^{\ast }\right]}{\text{d}t}=k_{\text{eAKT}}^{+}\left[\text{eNOS}-\text{CaM}\right]-k_{\text{eAKT}}^{-}\left[\text{eNOS}-{\text{CaM}}^{\ast }\right],$$ (19)

where $k_{\text{eAKT}}^{+}=k_{\text{AKT}}^{\text{max}}\left[{\text{AKT}}^{\ast }\right]/{\left[\text{AKT}\right]}_{\text{tot}}$. The values of rate constants $k_{\text{eAKT}}^{-}$ and $k_{\text{AKT}}^{\text{max}}$ are estimated in Section S1 from the data presented in Takahashi and Mendelsohn (41). The stabilized complex eNOS-CaM^∗ complex is significantly more active than eNOS-CaM in stimulating NO production due to the catalysis of the L-Arg oxidation reaction (4, 9, 41, 42, 43).

Step 3. Phosphorylation of eNOS_cav by PKC (at Thr-495) inhibits this activation process by blocking the formation of eNOS-CaM (4); caveolin-bound eNOS in this inactivated state is denoted by ${\text{eNOS}}_{\text{cav}}^0$ (eNOS₀ is caveolin-bound eNOS phosphorylated at Thr-495). We assume that eNOS phosphorylation by PKC follows first-order kinetics,

$$\frac{\text{d}\left[{\text{eNOS}}_{\text{cav}}^0\right]}{\text{d}t}=k_{\text{Thr}}^{+}\frac{\left[{\text{PKC}}^{\ast }\right]}{{\left[\text{PKC}\right]}_{\text{tot}}}\left[{\text{eNOS}}_{\text{cav}}\right]-k_{\text{Thr}}^{-}\left[{\text{eNOS}}_{\text{cav}}^0\right],$$ (20)

where the forward $\left(k_{\text{Thr}}^{+}\right)$ and backward $\left(k_{\text{Thr}}^{-}\right)$ rate constants are estimated from the data in Bredt et al. (46).

The total amount of eNOS in different complexes is conserved, so that the total concentration of eNOS, ${\left[\text{eNOS}\right]}_{\text{tot}}$, remains constant throughout these transformations. This yields a constraint on the concentrations of eNOS in different complexes (23),

$$\left[{\text{eNOS}}_{\text{cav}}\right]+\left[{\text{eNOS}}_{\text{cav}}^0\right]+\left[\text{eNOS}-\text{CaM}\right]+\left[\text{eNOS}-{\text{CaM}}^{\ast }\right]=\left[{\text{eNOS}}_{\text{tot}}\right].$$ (21)

Two simplifications underpin our model of eNOS activation. First, the rate of dephosphorylation is assumed constant, even though dephosphorylation is mediated by various phosphatases (4, 47). We adopted this assumption because of the paucity of data on whether and how changes in shear stress affect the activation of phosphatases, such as PP2A and calcineurin. Second, the kinetics of eNOS activation is assumed insensitive to fluctuations in Hsp90 activity even though formation of eNOS-CaM is mediated by Hsp90 (4, 41). This assumption is reasonable because Hsp90 is usually present in large excesses, on the order of 100 μM (48), over the concentrations of other reactants, such as eNOS and CaM.

NO production

Once formed, the eNOS-CaM and eNOS-CaM^∗ complexes catalyze the oxidation of L-Arg, resulting in production of NO. The latter process is modeled with the rate law,

$$\frac{\text{d}\left[\text{NO}\right]}{\text{d}t}=Q_{\text{NO}}-Q_{\text{sGC}}-{\lambda }_{\text{NO}}\left[\text{NO}\right],$$ (22)

which represents a balance between NO production (with rate $Q_{\text{NO}}$) and consumption. The latter is due to both NO scavenging by soluble guanylate cyclase at rate $Q_{\text{sGC}}$ (32) and NO metabolism by red blood cells adjacent to the endothelial cells at rate ${\lambda }_{\text{NO}}$ (49). Following Buerk (50), we use Michaelis-Menten kinetics with constant O₂ supply to model NO production due to oxidation of L-Arg,

$$Q_{\text{NO}}=R_{\text{NO}}\frac{\left[{\text{O}}_2\right]}{k_{\text{mNO}}+\left[{\text{O}}_2\right]}.$$ (23)

Here $k_{\text{mNO}}$ is the Michaelis-Menten constant and $R_{\text{NO}}$ is the rate of NO production, which depends on the concentrations of both phosphorylated and unphosphorylated eNOS-CaM such that

$$R_{\text{NO}}=k_{\text{eNO}}\left(\left[\text{eNOS}-\text{CaM}\right]+\varphi \left[\text{eNOS}-{\text{CaM}}^{\ast }\right]\right),$$ (24)

where ϕ indicates the extent to which AKT phosphorylation increases eNOS activity in the presence of Hsp90. Assuming a constant supply of L-Arg and other substrates such as BH4 and NADH, the rate $k_{\text{eNO}}$ remains constant. For a constant oxygen supply,

$$k_{\text{eNO}}\frac{\left[{\text{O}}_2\right]}{k_{\text{mNO}}+\left[{\text{O}}_2\right]}=\Upsilon =\text{constant}.$$ (25)

The experimental evidence reported in Dimmeler et al. (25), Schmidt et al. (51), and Ahluwalia et al. (52) suggests functional presence of sGC in endothelial cells. We adopt the model of Ahluwalia et al. (32), developed for smooth muscle cells, to account for the possibility of NO being scavenged by soluble guanylate cyclase (sGC) to produce sGC-NO, which catalyzes production of cGMP from guanosine triphosphate (GTP),

$$Q_{\text{sGC}}=R_{\text{NO}}^{\text{max}}\frac{{\left[\text{NO}\right]}^2+b_1\left[\text{NO}\right]}{a_0+a_1\left[\text{NO}\right]+{\left[\text{NO}\right]}^2}\left[\text{sGC}\right],$$ (26)

where $b_1$, $a_0$, $a_1$, and $R_{\text{NO}}^{\text{max}}$ are constants whose values are obtained in Condorelli and George (32) by fitting NO-cGMP kinetics to experimental data. sGC is activated upon consuming NO, thereby stimulating the conversion of GTP into cGMP. The rate of cGMP production is expressed as a function of NO concentration (32),

$$\frac{\text{d}\left[\text{cGMP}\right]}{\text{d}t}=V_{\text{cGMP}}^{\text{max}}\frac{g_0+g_1\left[\text{NO}\right]+{\left[\text{NO}\right]}^2}{a_0+a_1\left[\text{NO}\right]+{\left[\text{NO}\right]}^2}-\frac{X{\left[\text{cGMP}\right]}^2}{k_{\text{cGMP}}+\left[\text{cGMP}\right]},$$ (27)

where $V_{\text{cGMP}}^{\text{max}}$, $g_0$, $g_1$, X, and $k_{\text{cGMP}}$ are constants whose values are obtained in Condorelli and George (32) by fitting NO-cGMP kinetics to experimental data. Increase in the cGMP concentration, $\left[\text{cGMP}\right]$, provides a negative feedback by reducing the capacitative calcium entry (CCE) into the cell in accordance with Eq. 10.

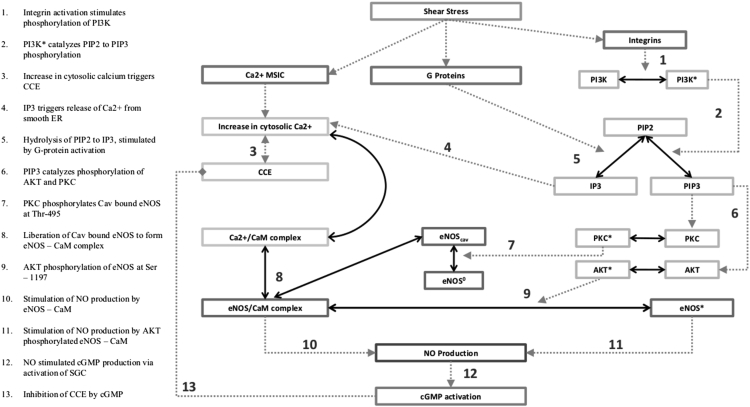
The system of coupled expressions found in Eqs. 1–27 constitutes a model of eNOS activation and NO production in response to mechanical stimulation of an endothelial cell by wall shear stress. The reaction network formed by these equations is shown in Fig. 1. The numerical solution of these equations is detailed in Section S3.

Figure 1.

Reaction network for shear-induced NO production.

Results

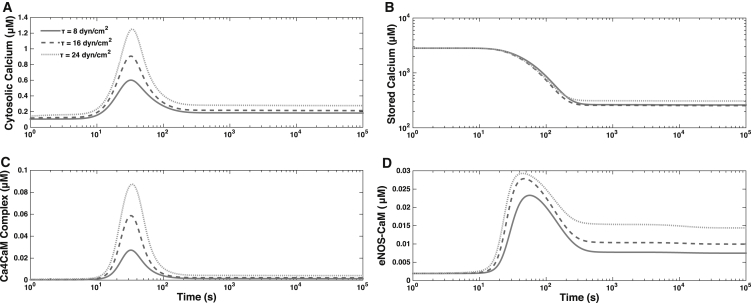
Fig. 2 shows the dynamics of concentrations of cytosolic calcium $\left({\left[{\text{Ca}}^{2+}\right]}_{\text{c}}\right)$, stored calcium $\left({\left[{\text{Ca}}^{2+}\right]}_{\text{s}}\right)$, calcium calmodulin complex $\left(\left[{\text{Ca}}_4\text{CaM}\right]\right)$, and the eNOS-CaM complex $\left(\left[\text{eNOS}-\text{CaM}\right]\right)$ for different levels of the applied WSS. The step increase in WSS τ, at time t = 0, induces a quick discharge of internal calcium stores within the cell as calcium enters the cytosolic volume. This results in a rapid spike in calcium levels, followed by a more gradual decline to a steady-state value of ${\left[{\text{Ca}}^{2+}\right]}_{\text{c}}$, which exceeds its basal-state counterpart. This predicted behavior is consistent with the observations in the literature (8, 19, 20, 53). The spike in ${\left[{\text{Ca}}^{2+}\right]}_{\text{c}}$ causes a corresponding increase in $\left[{\text{Ca}}_4\text{CaM}\right]$, leading to the formation of the eNOS-CaM complex. Unphosphorylated eNOS-CaM can lead to NO production, which is traditionally viewed as a calcium-independent part of the cascade. Furthermore, eNOS-CaM undergoes phosphorylation by AKT, which leads to further NO production at the longer timescale, and is also thought to be calcium-independent. The transients for the initial calcium-dependent stage of the reaction cascade occur very fast (on the order of 100 s); the subsequent, kinase-dependent portion of the eNOS activation cascade proceeds at a more gradual pace. This kinase-dependent eNOS activation phase is also calcium-dependent through the eNOS-CaM complex. Throughout their time course the concentrations of all forms of calcium increase with WSS τ due to the role of the MSICs and G proteins.

Figure 2.

Temporal variability of the concentrations of (A) cytosolic calcium, ${\left[{\text{Ca}}^{2+}\right]}_{\text{c}}$ and (B) stored calcium, ${\left[{\text{Ca}}^{2+}\right]}_{\text{s}}$, and the complexes (C) Ca₄CaM, $\left[{\text{Ca}}_4\text{CaM}\right]$ and (D) eNOS-CaM, $\left[\text{eNOS}-\text{CaM}\right]$ for WSS τ = 8, 16, and 24 dynes/cm².

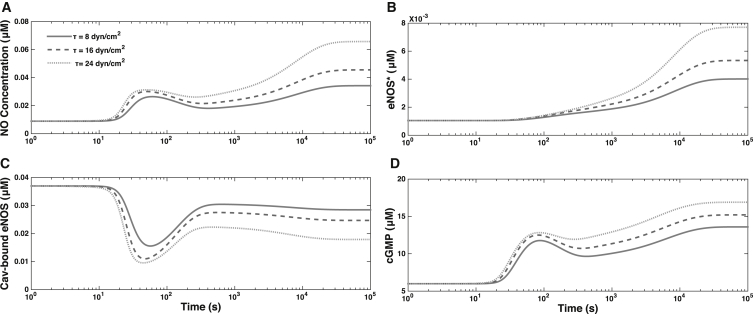
Fig. 3 shows the dynamics of AKT phosphorylation of eNOS-CaM, forming eNOS^∗. The increased concentrations of eNOS^∗ form gradually, over longer timescales than the initial calcium transients. The eNOS bound to caveolin (and hence inactivated) rapidly decreases after the initial calcium influx, before reaching a steady state. The extent of depletion of the eNOS-Cav complex increases with τ, as do the increased concentrations of eNOS^∗. This shear-induced NO production causes $\left[\text{NO}\right]$ to display bimodality over time: an initial peak corresponding to activation by calcium is followed by a second, prolonged peak reflecting the role of protein kinases in eNOS activation. This predicted behavior is in agreement with the observations in Balligand et al. (4), Shyy and Chien (9), and Mount et al. (43) of the dual nature of eNOS enzyme’s activation, which is partly calcium-dependent and partly AKT-dependent. Fig. 3 also shows that $\left[\text{cGMP}\right]$ increases with $\left[\text{NO}\right]$, thereby facilitating the vasodilatory role of NO.

Figure 3.

Temporal variability of (A) $\left[\text{NO}\right]$, (B) AKT-phosphorylated eNOS concentration, $\left[{\text{eNOS}}^{\ast }\right]$, (C) caveolin-bound eNOS concentration, $\left[{\text{eNOS}}_{\text{cav}}\right]$, and (D) $\left[\text{cGMP}\right]$ for three levels of WSS, τ = 8, 16, and 24 dynes/cm².

Model validation

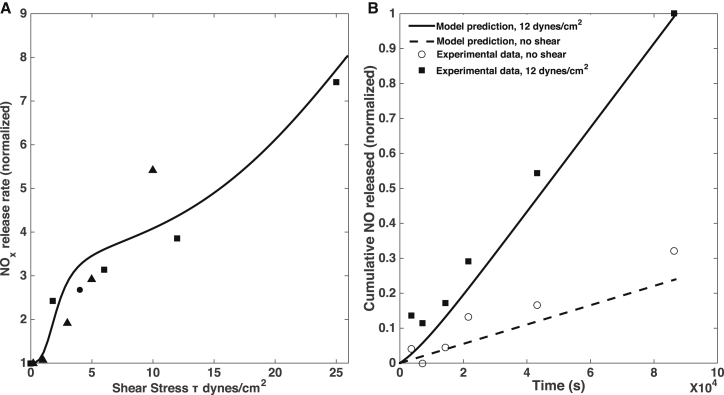
To verify that our model reproduces both realistic values of NO production and realistic transient behavior, we compare the model predictions with experimental observations. Because NO is unstable, many experiments report the accumulation of nitrites and nitrates concentration as NO_x. We compare the NO production rates estimated experimentally (typically inferred from measurements of NO_x accumulation rates) and predicted rates with our model (Eq. 22, where the Q_NO term gives NO production rate). Because the amount of NO metabolized by the ECs themselves (Q_sG) is found to be small, the NO production rate is equivalent to the amount of NO that is released and scavenged by surrounding blood/media into NO metabolites. This fact justifies the use of NO_x accumulation rates as a proxy for NO production rates in experimental studies; we, therefore, compare these values with our model simulations. The predicted and observed dependences of the rate of NO production at steady state after exposure to a range of WSS values are in general agreement with the experimental data (Fig. 4 A). Likewise, the cumulative amount of NO released by the endothelial cells (calculated using the first two terms in Eq. 22, which gives the amount of NO produced by the endothelial cell, minus the amount metabolized by the cell itself, and integrated over time) reproduces the observed accumulation of NO (and its metabolites) in conditioned media after application of WSS (54), and when compared versus NO release/accumulation in the absence of WSS (Fig. 4 B). Despite considerable scatter in the experimental data, our model predictions are broadly compatible with the observations.

Figure 4.

(A) Predicted (line) and observed (symbols) dependence of NO production rate on WSS. Predicted NO production rates are given by the $Q_{\text{NO}}$ term in Eq. 22, which at steady state is equal to the rate of release of NO by ECs and formation of NO metabolites in the surrounding blood/media (because NO consumption by the ECs themselves was found to be negligible). Experimental data are from the following sources: squares are from column C of Table 1 in Kuchan and Frangos (26), where NO production rates were estimated using measurements of NO_x accumulation rates; circles are from Fig. 4C in Kaur et al. (64), where NO production rates were estimated from nitrite accumulation rates; and triangles are from Fig. 8 in Kanai et al. (76), where NO production rates were estimated from direct measurements of moles of NO released per unit time. Each experimental data set was normalized to the rate at τ = 0, except for Kanai et al. (76), where the values were normalized to the lowest nonzero measurement, at τ = 0.2 dynes/cm²; the simulation results were normalized with the predicted rate at τ = 0. (B) The predicted (lines) and observed (symbols) cumulative release of NO to the media/bloodstream as a function of time. The experimental data are from the top panel of Fig. 1 in Tsao et al. (54), showing normalized increase (above baseline measurement) of NO_x accumulation in conditioned media. Both experimental and model data are normalized against cumulative NO/NO_x release at 12 dynes/cm² after 24 h.

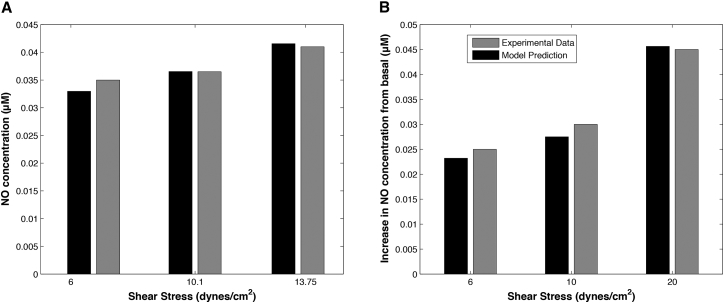
Fig. 5, A and B, demonstrates the model’s ability to predict steady-state NO concentrations at three levels of WSS τ. The predicted values of $\left[\text{NO}\right]$ are within 5% of the experimental observations reported in Mashour and Boock (55). This figure provides a quantitative justification for the assumption of a linear relationship between $\left[\text{NO}\right]$ and τ, which is routinely used in microcirculation models (see, e.g., Sriram et al. (56) and the references therein). While this relationship is clearly nonlinear, it can be treated as linear over the physiologically relevant range of WSS shown in Fig. 5. As a final exercise in model validation, Fig. 5 B shows that the predicted and observed (57) changes in $\left[\text{NO}\right]$ from its baseline value are within ∼10% of each other.

Figure 5.

(A) The predicted and observed NO concentration at three levels of WSS τ (in dynes/cm²). The experimental data are from Mashour and Boock (55). (B) The predicted and observed changes in NO concentration from its basal levels for three values of WSS (in dynes/cm²). The experimental data are from Andrews et al. (57).

Model predictions

Impact of inhibition of protein kinases on NO production

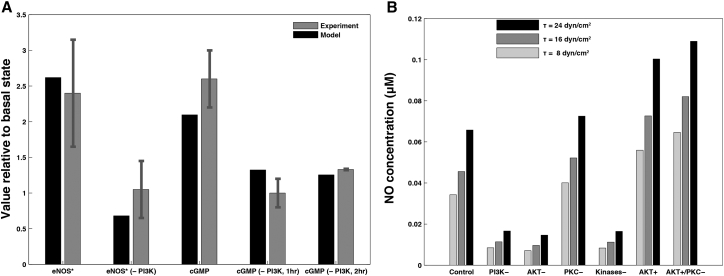
The role of protein kinases in eNOS activation is typically studied by inhibiting either the kinases individually (58, 59) or PI3K, which results in the subsequent inhibition of both AKT and PKC (25, 60). Fig. 6 A compares the model predictions with the experimental data from Dimmeler et al. (25) for AKT-phosphorylated eNOS ($\left[{\text{eNOS}}^{\ast }\right]$, normalized with the concentration at τ = 0) in response to a shear stress of τ = 12 dynes/cm² applied for 1 h (as stated in the methods in Dimmeler et al. (25); they also indicate that experiments were done at 15 dynes/cm² in the relevant figure legend. In either case, our results are in general agreement with their findings). Also shown are data from model versus experiment for the same, but with PI3K inhibited by wortmannin. Both model and experiment indicate that PI3K inhibition drastically reduces eNOS activation due to shear stress. Further, this inhibition of PI3K also impacts cGMP concentration; Fig. 6 B shows the predicted increase in cGMP concentrations over basal levels, after 1-h exposure to a shear stress of 15 dynes/cm², is similar in both model and experiment. Further, the inhibition of PI3K by wortmannin induces reduction in cGMP concentrations to a similar degree in model and experiment.

Figure 6.

Impact of modulation of protein kinase activity on NO production. (A) The predicted and observed eNOS phosphorylation by AKT, $\left[{\text{eNOS}}^{\ast }\right]$, at normal and completely inhibited kinase activity (PI3K and PI3K⁻). Also shown is the corresponding effect on cGMP, with and without PI3K inhibition after 1 and 2 h. The experimental data are from Dimmeler et al. (25). (B) The predicted changes in steady state $\left[\text{NO}\right]$, at three values of WSS, in response to elimination of PI3K activation (PI3K⁻) and elimination of phosphorylation of eNOS by either AKT (AKT⁻) or PKC (PKC⁻). Also shown is the impact on steady-state $\left[\text{NO}\right]$ of the simultaneous elimination of eNOS phosphorylation by both AKT and PKC, as well as of the increase in AKT activity with (AKT⁺) or without (AKT⁺/PKC⁻) PKC.

Fig. 6 B shows the impact of the complete inhibition of PI3K (PI3K-), AKT, and PKC phosphorylation of eNOS (AKT- and PKC-), and both AKT/AKT- and PKC/PKC- phosphorylation of eNOS occurring simultaneously (Kinases-), on predictions of steady-state NO concentration at WSS τ = 8, 16, and 24 dynes/cm². Inhibition of PI3K yields a significant (∼70–75%) reduction in $\left[\text{NO}\right]$ over a range of τ, while the inhibition of PKC alone results in a smaller but still significant (∼10–15%) increase in $\left[\text{NO}\right]$. The predicted magnitude of reduction in [NO] due to PI3K inhibition is in the vicinity of the data in Gallis et al. (61) for reductions in NO synthesis: ∼70–75% predicted versus 68% reported. This finding is in agreement with other experimental studies, which found that PI3K inhibition leads to decreased eNOS activity (25, 61) and that PKC inhibition elevates eNOS activity (59). Blocking eNOS activation by AKT has a nearly identical effect as inhibiting PI3K; blocking PKC phosphorylation (and inactivation) of eNOS does little to retrieve this loss of NO production. These results indicate that AKT phosphorylation (and activation) of eNOS has a significantly larger net effect on endothelial NO production than does phosphorylation (and inactivation) by PKC. Finally, Fig. 6 B indicates that increasing (doubling) AKT activity (by doubling the rate at which AKT phosphorylates eNOS, analogous to an AKT overexpressor model) significantly increases NO concentrations, an effect that is further enhanced by blocking PKC phosphorylation of eNOS.

Calcium-calmodulin dependence of eNOS activation and endothelial NO production

Various stages of eNOS activation and NO production in endothelial cells are thought to be “calcium-dependent” or “calcium-independent” (4, 25, 26). The sensitivity analysis reported below elucidates the dependency of NO production on calcium/CaM and AKT phosphorylation, i.e., the calcium-dependent and calcium-independent elements of the reaction cascade, respectively. In these simulations, the model was initialized using the default parameters specified in Table 1. Then, the concentrations of extracellular calcium and CaM were varied, while maintaining the WSS levels. This facilitates comparison of the model predictions and observational data from experiments, which consisted of simultaneous application of WSS and pharmacological modulation of the different pathways, such as calcium or AKT signaling.

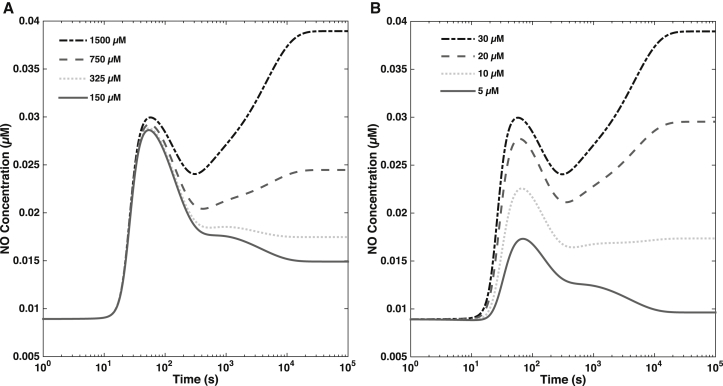
Fig. 7 A shows $\left[\text{NO}\right]$ and cytosolic calcium concentrations at WSS τ = 12 dynes/cm², for different concentrations of extracellular calcium. The decrease in the extracellular calcium concentration leads to the corresponding depletion of intracellular calcium, resulting in the reduction of endothelial NO production. The release of stored calcium causes an initial spike in NO production, which diminishes drastically at large times (at the timescale on which phosphorylation by AKT becomes an important driver of NO production), because Ca-CaM and thus eNOS-CaM concentrations fall as calcium is being depleted. Thus, while AKT activation/phosphorylation is itself independent of calcium (25, 62), there is less substrate (eNOS bound to CaM) for phosphorylated AKT to act upon. Hence, phases of NO production that are apparently calcium-independent and driven mainly by AKT are in fact calcium-dependent. The reduction of NO production with depletion of extracellular calcium is in agreement with results in Dimmeler et al. (25), where chelation of extracellular calcium was shown to substantially reduce endothelial NO production, regardless of AKT activation. Similarly, when CaM concentration is decreased, both the first and second phases of NO production are affected but for very low CaM concentration (∼5 μM), the second phase of NO production is completely abolished. These results indicate that both early and later stages of NO production are calcium-dependent in different ways.

Figure 7.

(A) Effect of external calcium concentration on NO production. At high external calcium concentration, we observe a biphasic dynamics of NO. When external calcium is depleted, the first phase of NO is unchanged (as this is largely driven by rapid release of calcium from internal stores) but the second phase of NO production is lost. (B) Effect of calmodulin concentration on NO production. When sufficient CaM is present, NO production displays biphasic kinetics. When CaM is depleted, a smaller first phase of NO is observed, but the second phase is abolished.

Discussion

We developed a biochemical model of the WSS-induced activation of eNOS in an EC. The model includes three key mechanotransducers: MSICs, integrins, and GPCRs. The reaction cascade consists of two interconnected parts. The first is rapid activation of calcium, which results in formation of calcium-calmodulin complexes, followed by recruitment of eNOS from caveolae. The second is phosphorylation of eNOS by PKC and AKT (both of which are activated by PI3K), which leads to further activation of eNOS. Our model also includes a negative feedback loop due to inhibition of calcium influx into the cell by cGMP. In this feedback, increased NO levels cause a rise in cGMP levels, so that cGMP inhibition of calcium influx can limit NO production.

The model was used to predict the dynamics of NO production by an EC subjected to a step increase of WSS from zero to a finite physiologically relevant value. To determine basal conditions, we ran the model at the steady-state regime with zero shear stimulation. At the basal conditions, $\left[{\text{IP}}_3\right]\approx 0$ and concentration of calcium stored in the smooth endoplasmic reticulum is at its maximal levels. Our model predicts that under these basal conditions there is a finite, nonzero level of NO production and finite, nonzero concentrations of AKT and PKC phosphorylated eNOS. These findings are in agreement with the observations (62).

The model predicts a highly nonlinear, biphasic transient behavior of eNOS activation and NO production: a rapid initial activation due to the very rapid influx of calcium into the cytosol (occurring within 1–5 min) is followed by a sustained period of activation due to protein kinases, which are in turn activated by PI3K (Figs. 2 and 3). The predicted calcium- and kinase-dependent phases of eNOS activation are in agreement with the existing paradigm of the sequential steps of eNOS activation (4, 9, 43). Over large time periods, the enhanced activation of PI3K and subsequent activation (above basal levels) of AKT and PKC due to WSS are not major factors in eNOS activation. This is due to the apparent rapid decay of PI3K (and hence phospho-AKT and PKC) activity back to their basal levels. More experimental data are needed to clarify the behavior of PI3K after a cell’s exposure to WSS and to fine-tune our model.

To validate the model, we compared its predictions with both quantitative and qualitative experimental observations. The model reproduces the observed dependence of NO production rate (Fig. 4) and NO concentrations (Fig. 5) on WSS, especially taking into account the significant amount of scatter in the available experimental data. The model reproduces the observed transient behavior of NO production rate after a cell’s exposure to shear stress (Fig. 4 B). The model predictions of both the increased levels of AKT phosphorylated eNOS and cGMP concentrations are within ∼10–15% of their measured counterparts (Fig. 6 A).

Our model predicts that the inhibition of PI3K, which results in downregulation of both AKT and PKC, leads to a drastic reduction (>70%) in NO concentrations (see Fig. 6); this is consistent with the observed behavior (25, 61). This suggests that the stimulatory effect of AKT phosphorylation dominates the inhibitory role of PKC, supporting the perspective that AKT is by far the most important protein kinase in eNOS activation. This hypothesis is further supported by the model’s prediction that inhibiting PKC alone results in a small but significant (∼15%) increase in NO production; hence, PKC has a smaller net effect on eNOS activation than AKT. We are not aware of quantitative measurements of the extent of kinase inhibition as a function of eNOS activity, at different levels of shear stress. Yet our model does agree with the empirical evidence for strong up-regulation of eNOS activity by AKT and weaker, but still significant, down-regulation of eNOS by PKC.

To summarize, our model captures the following observed features of eNOS activation by WSS:

• 1)eNOS activation and NO production are always dependent on calcium concentrations and the binding of eNOS with CaM. In other words, concentrations of calcium and CaM remain dependent variables for NO production/concentration and the depleting or inhibiting of either induces a precipitous decline in NO production.
• 2)Certain elements of the reaction cascade that results in eNOS activation and NO production are reported to be calcium-independent, as observed in Dimmeler et al. (25) and Ozeki et al. (62). In our model, the coupling of AKT phosphorylation to calcium signaling is weak and, practically, calcium-independent. As a result, eNOS activation and NO production can be altered even if calcium signaling is unchanged. For example, inhibiting AKT phosphorylation while leaving calcium stimulation unchanged results in a sharp decrease in $\left[\text{NO}\right]$ (see Figs. 6 and 7), in agreement with the experiment (25).
• 3)Upon exposure to shear stress, once calcium reaches its steady state, NO production/concentration continues to change. Hence, there is a lag between calcium and NO dynamics; this is due to the relatively slow rate at which eNOS binds with CaM and is then phosphorylated by AKT. That does not imply independence of NO production from calcium; if calcium levels are changed during this slower phase of activation, NO production/concentrations will also change, albeit more gradually.
• 4)Inactivation of AKT drastically reduces eNOS activity, whereas inhibition of PKC has a smaller, stimulatory effect on eNOS activation. While the elevation (above basal levels) of AKT activation due to WSS is not important over large timescales, the finite, basal activation of AKT is essential for maximal eNOS activation and NO production.
• 5)Concentrations of both NO and cGMP increase with WSS. Over a broad range of WSS, this increase is highly nonlinear, but within the physiologically relevant ranges of WSS (∼20 dynes/cm²), one can use a linear relation between (NO) and WSS (55, 56, 63).
• 6)The predicted steady-state and transient variations of NO production rates at different WSS levels are in general agreement with the observations, although the scatter in the reported data is large (26, 55, 57, 63, 64).
• 7)The predicted increase of $\left[\text{cGMP}\right]$ with $\left[\text{NO}\right]$ (Fig. 6 A) is consistent with the experimental data (25). Hence the model supports a role of shear stress as a stimulator of vasodilation by quantifying the shear-induced NO production that, in turn, elevates a cGMP level, ultimately leading to vasodilation.
• 8)Removal of WSS leads to an ultimate return to basal levels for all reactants, with the calcium transients occurring rapidly and the kinase-dependent transients following more slowly. The timescales over which the system returns to basal levels of (NO) are in a general agreement with the experiments (55).

Thus, sustained shear-induced endothelial NO production requires both calcium signaling and AKT phosphorylation; the system can, however, be manipulated/modulated by inhibiting or promoting one pathway without changing the other.

The presented model enhances the current understanding of the mechanistic and biochemical processes involved in the activation of eNOS and subsequent NO production in ECs. The model’s predictions might be used to facilitate the design of experiments, which focus on inhibition of the reactants and mechanosensors involved in the NO production reaction cascade. This is relevant to several fields of biomedical research, e.g., cancer (65), diabetes (66), and heart disease (3), where the regulation of endothelial NO production has significant clinical applications.

Model limitations

While our model captures many of the observed features of NO production in ECs, it has several limitations. It does not contain a mechanistic description of ECs. Instead, WSS acts as an input that triggers the reaction cascade resulting in eNOS activation. The lack of a mechanical model precludes the analysis of such factors as the role of viscoelasticity in determining the system’s transient behavior. Consequently, our model cannot be used to reproduce experimental studies, which show that viscoelastic properties of the cytoskeleton have a profound effect on the mechanical behavior of an EC exposed to oscillatory or pulsatile shear. Future extensions of our model will combine it with a mechanical model of ECs.

Our model accounts for three mechanosensors: MSICs, GPCRs, and integrins. As experimental data for other mechanosensors (sodium and potassium ion channels, lipid rafts and vesicles, cytoskeletal remodeling, signaling via cadherins and other transmembrane proteins, etc.) become available, their effects can be incorporated into our model. Such enhancements of our model are facilitated by its modular structure.

Author Contributions

K.S. performed research and wrote the article; J.G.L. led the revisions effort and edited the article; P.R. helped with analysis and wrote the article; D.M.T. designed research and wrote the article; and all authors agreed on the content of the article.

Editor: Jeffrey Fredberg.

Supporting Citations

References (67, 68, 69, 70, 71, 72, 73, 74) appear in the Supporting Material.