Clathrin Assembly Regulated by Adaptor Proteins in Coarse-Grained Models

Abstract

The assembly of clathrin triskelia into polyhedral cages during endocytosis is regulated by adaptor proteins (APs). We explore how APs achieve this by developing coarse-grained models for clathrin and AP2, employing a Monte Carlo click interaction, to simulate their collective aggregation behavior. The phase diagrams indicate that a crucial role is played by the mechanical properties of the disordered linker segment of AP. We also present a statistical-mechanical theory for the assembly behavior of clathrin, yielding good agreement with our simulations and experimental data from the literature. Adaptor proteins are found to regulate the formation of clathrin coats under certain conditions, but can also suppress the formation of cages.

Introduction

In eukaryotic cells, clathrin-mediated endocytosis is a major pathway for the internalization of cargo molecules such as hormones, receptors, transferrin, membrane lipids, and the occasional virus (1, 2, 3, 4, 5, 6, 7, 8, 9). The cargo molecules are collected and sorted in a clathrin-coated pit, which subsequently evolves into an encapsulating clathrin-coated vesicle. These coats arise through a self-assembly or polymerization process of clathrin proteins against the cytoplasmic face of cellular membranes. The clathrin protein has a peculiar shape with three long curved legs (see Fig. 1), which allows it to bind with many partners into a wide range of polyhedral cages, as well as to bind accessory proteins that assist at various stages of the endocytosis process (10, 11, 12, 13, 14, 15). Although clathrin is a major component and the namesake of clathrin-coated pits and clathrin-coated vesicles, it does not bind directly to either the membrane or the cargo. These are the tasks of so-called adaptor proteins, which often are active only at specific membranes in the cell (16, 17, 18, 19, 20). The members of the adaptor protein (AP) family, AP1–AP5, are tetrameric complexes consisting of two large and two small subunits. A second family of adaptor proteins is formed by the clathrin-associated sorting proteins (CLASP), a collection of monomeric proteins including AP180, epsin, and Eps15 (20, 21). The global structure of the members of both families is very similar: they consist of a neatly folded section that binds to the membrane and a long disordered segment with clathrin binding motifs. Members of the AP-family possess a second long disordered segment, to attract assisting proteins. Of all adaptor proteins (henceforth abbreviated as “AP”, irrespective of family), probably the most studied adaptor protein is the AP2 complex regulating endocytosis, which will also be the reference point in this study (11, 22, 23, 24).

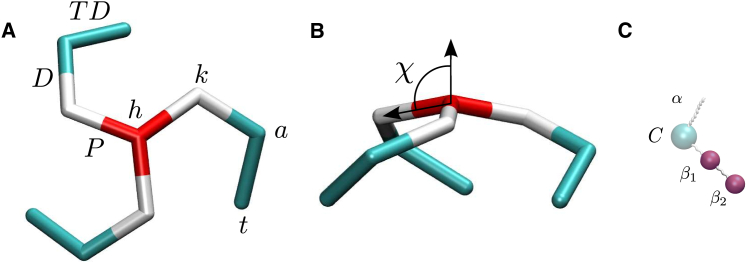
Figure 1.

The highly coarse-grained simulation models of (A and B) clathrin and (C) AP2 on the same scale. In the rigid clathrin model, three proximal leg segments (P) radiate from a central hip (h) to the knees (k), at a pucker angle χ relative to the symmetry axis, followed by distal leg segments (D) running to ankles (a) and terminal domains (TD) ending at the toes (t). The AP model features two binding sites for clathrin, β₁ and β₂, connected by a flexible linker. In the full AP2 protein, the β-linker connects to a folded core (c) and a flexible α-linker; these are omitted in the simulations because they do not play a role in the in vitro assembly process. To see this figure in color, go online.

In addition to linking clathrin to membrane and cargo, a main function of APs is to regulate the assembly of clathrin cages by binding to multiple triskelia simultaneously. A series of in vitro experiments established that clathrin proteins in solution can be induced to self-assemble by adding APs (10, 16). Recent structural studies revealed that AP2 can adopt two configurations, i.e., a closed state with part of the linker blocked from interacting with clathrin, and an open state where AP2 can bind two triskelia (25, 26). With AP2 adapting the open state only when bound to a membrane, the formation of clathrin cages in a cell is effectively limited to the membrane. This mechanism may also explain why the in vitro assembly behavior of clathrin varies with the preparation state of the adaptor proteins, with well-cleaned adaptors inducing less activity (27). Our objective in this study is this little-explored question: Beyond the ability to bind two triskelia simultaneously, what else is required of APs to induce the formation of clathrin cages in solution?

The presence of an AP binding site at the end of each clathrin leg, a location henceforth informally referred to as the “toes” by following the common analogy of the clathrin leg with the human leg (see Fig. 1), is well established. Experiments with recombinant clathrin fragments indicate that this binding site is crucial to the inducement by AP2 of cage formation (28). At least one additional binding site, also required for cage formation, resides higher up each leg. Experiments with clipped triskelia point at a location on the trimer hub (29), i.e., in the region extending from the “hip” to just beyond the “knee” (see Fig. 1). Pull-down experiments identified a binding site near the “ankle” (30). Both options will be explored here.

Besides in vivo and in vitro experiments, the assembly behavior of clathrin has also been explored by in silico studies. In earlier work, two of us developed a highly coarse-grained patchy particle model of clathrin as a rigid triskelion with either straight or bend legs, and showed that anisotropic leg-leg interactions are the key to self-assembly (31, 32). Simulations with this model that predicted a binding energy of ∼23 k_BT per clathrin in a cage, suggested a novel scenario, to our knowledge, for the transition from flat plaque to curved coat and yielded an assembly timescale in reasonable agreement with experiments (33, 34). Matthews and Likos (35) modeled clathrin as a collection of 13-bead patchy particles, endowed with anisotropic interactions, and showed how these triskelia deformed a lipid membrane into a bud. Cordella et al. (36) and VanDersarl et al. (37) modeled clathrin as a spherical particle with anisotropic interactions accounting for three straight legs, and studied, among other properties, how a membrane influences an adjacent clathrin lattice. Adaptor proteins, which are crucial in bringing triskelia together under in vivo conditions, have been omitted in all clathrin simulations to date.

To address our research question, we apply coarse-grained simulations and statistical-mechanical theory to explore the ability of APs to induce the assembly of triskelia cages in solution. Because the AP model is based on the aforementioned key features, it is to be expected that other adaptor proteins can be modeled in a similar way. This article is organized as follows. In Materials and Methods, the clathrin simulation model is briefly discussed, the matching AP simulation model is introduced, and the implementation of click-interactions in Monte Carlo simulations is described. The findings on simulations of mixtures of triskelia and APs are presented and interpreted in Results and Discussion. The deduced qualitative understanding is then translated into a fairly simple quantitative theory, obtaining remarkably good agreement with simulations and experiments. We end with Conclusions.

Materials and Methods

In several preceding studies (31, 32, 33, 34), we modeled clathrin as rigid patchy particles with three identical curved legs (see Fig. 1). The three legs are connected at a central hub, at a pucker angle χ relative to the threefold rotational symmetry axis of the particle, reflecting clathrin’s intrinsic nonzero curvature. We here select a pucker angle, χ = 101°, typical of soccer-ball cages containing 60 triskelia, which is the most common cage size for in vitro experiments in the presence of AP (38). Each leg consists of two segments (i.e., the proximal and distal sections; the terminal domains were not included because of their expected small contribution to the clathrin-clathrin binding interaction) connected at the knee under a fixed angle and ending at the ankle. All leg segments are straight and of identical length, σ = 17 nm. The orientation of the distal segments relative to the proximal segments was chosen to allow maximum overlap between a particle and a secondary particle whose hub is situated at a knee of the primary particle. In a completed cage, a hub is located at every vertex—on top of three knees and three ankles of neighboring and next-nearest triskelia, respectively. A lattice edge is thus composed of two proximal and two distal segments, where the amino-acid sequences in both pairs of like segments run in opposite directions (i.e., anti-parallel). The attractive interaction between any pair of segments, which for clathrin is believed to result from a multitude of weak interaction sites along the legs (39, 40, 41), is modeled by a four-site potential based on the distances between the end-points of the two segments, with a minimum value of $-ϵ$ for two perfectly aligned segments, as described in detail in the Supporting Material. The interaction is anisotropic under rotations around the long axes of the segments, to reflect that the binding sites are most likely concentrated on one side of the segment, to wit, the side that in a cage edge faces the three adjacent segments. Simulations revealed that this anisotropy of the attractive potential is crucial for the spontaneous self-assembly of triskelia into polyhedral cages (31, 32). Excluded volume interactions between triskelia were omitted for computational reasons: this requires a more complex particle shape with nonlinear proximal and distal segments, as well as demands some flexibility of the legs, for the particles to pack together into cages with four legs interweaving along each edge, while the simulation step has to be reduced to prevent the relatively thin legs from crossing each other. Excluded volume interactions are important to prevent triskelia from binding to a cage edge in a slot that is already occupied by another triskelion; this property is incorporated into the simulation model by a repulsive potential between parallel segments of the same type. The moderate flexibility of the clathrin protein extends its interaction range beyond that of a rigidified protein; this effect is to some extent accounted for by the enlarged range of the intersegmental potential. The terminal domains (TDs) at the ends of the legs (see Fig. 1) were not included in our previous simulations, but they are required in this study as binding sites for APs. The length and orientation of the TDs with respect to the proximal and distal segments were estimated using the structural information file PDB: 1XI4 for a clathrin cage (39), available at the Protein Data Bank (http://www.rcsb.org/pdb/home/home.do). Because the TDs are approximately equally as long as the proximal and distal segments, they are all assigned the same length σ in the model. The TDs are attached to the ankle at an angle of 114° relative to the distal domain, with the three segments of a leg forming a dihedral angle of 28°. The clathrin-clathrin interactions are kept identical to those in the previous model; the TDs do not contribute to these interactions.

Continuing in this reductionist approach, we here introduce a matching simulation model of an AP (see Fig. 1). The model comprises the part of the AP2 protein that is involved in clathrin binding, i.e., the C-terminal region of the β-linker comprising the clathrin-box LLNLD of residues 631–635, the clathrin-binding appendage domain formed by residues 705–937, and the flexible linker connecting these two interaction sites (22). Our coarse-grained representation of this AP2 fragment consists of two point particles, embodying the two binding sites, connected by a tether. Because the remainder of the AP2 tetramer does not partake in clathrin binding and assuming that AP2s do not bind to each other, the omission of the majority of the protein is of no further consequence to the cage assembly process studied here. Excluded volume interactions are again omitted for reasons of computational efficiency; we note that the interior volume of a cage is far larger than the collective volume of the APs bound to a cage. The short range of the clathrin-AP binding interaction is inconvenient from a numerical point of view (see below). Instead, we developed a potential in which the αth binding site on the ith triskelion and the βth particle of the jth AP dimer are bound with a fixed energy −ζ and are limited to a maximum separation ρ in the clicked state $\left(b_{i\alpha ,j\beta }=1\right)$, while there are no interactions between these sites in the unclicked state $\left(b_{i\alpha ,j\beta }=0\right)$. As a function of the distance $r_{i\alpha ,j\beta }$, the interaction potential then reads as

$${\varphi }_{\text{click}}\left(r_{i\alpha ,j\beta },b_{i\alpha ,j\beta }\right)=\{\begin{array}{cc}0& \text{for}{b}_{i\alpha ,j\beta }=0\\ \{\begin{array}{cc}-\zeta \text{for}& r_{i\alpha ,j\beta }<\rho \\ \infty \text{for}& r_{i\alpha ,j\beta }\ge \rho \end{array}& \text{for}{b}_{i\alpha ,j\beta }=1,\end{array}$$ (1)

where ζ > 0, as illustrated in Fig. S4 in the Supporting Material. Because excluded volume interactions between AP2 tetramers ensure that a binding site on a clathrin can host at most one AP site, the clicks in the simulation model are constructed to be mutually exclusive: a site can partake in one click only. The clicks are also specific: the β₁ AP bead solely binds to the end of the TDs, i.e., at the toes, while the β₂ bead clicks only to a site higher up a triskelion’s leg.

The two clathrin binding sites of AP2 are connected by an essentially structureless sequence of ∼70 residues (22). According to polymer theory, this flexible linker will effectively act as an entropic spring with a spring constant k and a maximum length L (42, 43). This behavior is modeled here by the finite extensible nonlinear elastic potential (44),

$${\varphi }_{\text{linker}}\left(l_j\right)=\{\begin{array}{cc}-\frac{1}{2}k{L}^2\text{ln}\left[1-{\left(l_j/L\right)}^2\right]& \text{for}{l}_j<L\\ \infty & \text{for}{l}_j\ge L,\end{array}$$ (2)

where $l_j$ denotes the length of the jth AP dimer. The spring constant of an entropic spring is given by (43)

$$k=\frac{3k_{\text{B}}T}{2L{l}_p},$$ (3)

where $l_p$ is the persistence length. Given an average residue length of 0.37 nm, the linker of 70 residues connecting the two clathrin binding sites has a contour length of L ≈ 26 nm ≈ 1.5σ. Combination with the experimental value $l_p\approx 0.6\text{nm}$ for disordered proteins then yields $k\approx 30k_{\text{B}}T/{\sigma }^2$ for the linker.

The assembly characteristics of the combined models were simulated by the Monte Carlo (MC) method, i.e., by the weighted acceptance of randomly generated changes of the system configuration (45, 46, 47). Suppose that, by a sequence of steps, the system arrives in state m. In the MC technique, the transition probability from this state m to a new state n is expressed as

$$P_{m\to n}=P_{m\to n}^{\text{trial}}{P}_{m\to n}^{\text{acc}},$$ (4)

where $P_{m\to n}^{\text{trial}}$ denotes the probability of generating the trial configuration n from state m, and $P_{m\to n}^{\text{acc}}$ is the probability of accepting n as the next state in the sequence of states; if the move is rejected, the system remains in the old state and m is added (again) to the sequence of sampled states. For a symmetric trial move generator, $P_{m\to n}^{\text{trial}}=P_{n\to m}^{\text{trial}}$, the acceptance probability,

$$P_{m\to n}^{\text{acc}}=\text{min}\left(1,\text{exp}\left\{-\beta \left[\Phi \left(m\right)-\Phi \left(n\right)\right]\right\}\right),$$ (5)

where $\Phi \left(m\right)$ denotes the potential energy of state m and $\beta =1/\left(k_{\mathrm{B}}T\right)$, will produce a sequence of states in agreement with the equilibrium Boltzmann distribution.

The algorithm employed in this study applies two different types of trial moves, namely trial moves that alter the positions and orientations of particles, and trial moves that alter the connectivity between particles. The type of move is selected at random in every MC step, with positional moves selected f times as often as connectivity moves. Positional trial moves start by randomly selecting a protein. If a clathrin is selected, its center of mass is displaced along all three Cartesian directions by random values in the range $\left[-\left(1/4\right)\sigma ,\left(1/4\right)\sigma \right]$, and the particle is rotated around a random axis through the center of mass over a random angle in the range $\left[-\left(1/2\right),\left(1/2\right)\right]$ rad. A known complication in MC simulations is the drastic reduction of the mobility of particles interacting with neighbors, relative to the mobility of noninteracting particles, as can be seen clearly in movies of MC simulations (32). This is a minor issue in the assembly of cages from a solution containing clathrin only, as the free triskelia readily diffuse to a nearly immobile cage fragment. In simulations of mixtures of clathrin and AP, however, the binding of APs to triskelia will slow down their combined diffusion and hence significantly delay their attachment to cage fragments, especially if the AP-clathrin bond is strong and short-ranged. The solution adopted here is to apply cluster moves (45, 48), i.e., the AP beads clicked to the selected triskelion move together with this clathrin, maintaining the statuses $b_{i\alpha ,j\beta }$ and distances $r_{i\alpha ,j\beta }$ of all clicks. Consider an AP with a bead clicked to the selected triskelion. If its other bead is unclicked or clicked to the same triskelion, the entire AP is moved with the clathrin as if they formed a rigid unit. If the AP’s other bead is clicked to another clathrin, then this second bead is excluded from the trial move and, consequently, the length of the AP changes in the trial move. Next, the move is accepted or rejected following Eq. 5. If in a positional trial move an AP is selected, its two beads will be displaced independently. An unclicked bead is displaced in all three Cartesian directions by random values in the range $\left[-\left(1/4\right)\sigma ,\left(1/4\right)\sigma \right]$, while a clicked bead is moved to a random position within a sphere of radius ρ centered around the clathrin’s matching clicking site. Next, the move is accepted or rejected following Eq. 5. Again, the statuses $b_{i\alpha ,j\beta }$ of all clicks are conserved by these trial moves. In a clicking trial move, an AP bead is selected at random. The neighborhood of radius ρ around this particle is scanned for matching clicking sites on triskelia; for a bead that is already clicked, its current partner will be among the K detected sites. The unclicked state is included as the zeroth option. Instead of the above selection and acceptance steps, we directly accept one of the K + 1 trial states as the next state. The probability of selecting the kth option is given by

$$P_k=\frac{\text{exp}\left(-\Delta {\varphi }_k^{\text{click}}\right)}{{\sum }_{k\prime =0}^K\text{exp}\left(-\beta \Delta {\varphi }_{k\prime }^{\text{click}}\right)},$$ (6)

where the energy change $\Delta {\varphi }_k^{\text{click}}$ between the old state and the kth trial state can only yield the values $\Delta {\varphi }_k^{\text{click}}=\zeta$ for an unclicking trial move; $\Delta {\varphi }_k^{\text{click}}=-\zeta$ for a clicking trial move; and $\Delta {\varphi }_k^{\text{click}}=0$ if the connection remains (un)clicked.

A number of simulations were run to verify that the unconventional click-potential and click-dependent MC cluster-moves sample the correct equilibrium distribution. Simulations with 1000 clathrins and 3000 APs in a cubic box of volume 10⁶σ³ were used to determine the equilibrium constants of the reactions between triskelia and AP, defined as

$$K_{n,m}^{\text{tri}}=\frac{{\left[C{A}_n^{\prime }{A}_m^{″}\right]}_0}{{\left[C\right]}_0{\left[A\right]}_0^{n+m}},$$ (7)

where ${\left[C\right]}_0$, ${\left[A\right]}_0$, and ${\left[C{A}_n^{\prime }{A}_m^{″}\right]}_0$ denote, respectively, the concentrations of unbound triskelia, unbound APs, and triskelia complexes with n single-bound and m double-bound adaptor proteins, in molars (see Appendix I). To improve the sampling efficiency, we reduced the number of distinct reaction products to three by reducing the number of clicking sites per triskelion from six to two—at the toes and ankle of the same leg—and reducing the entropic spring constant to $k=1k_{\text{B}}T/{\sigma }^2$, while retaining the maximum extensibility of 1.5σ. Furthermore, to enable comparison with exact analytical solutions, the adaptor proteins were not allowed to click to two clathrin particles simultaneously and the interactions between triskelia were turned off. Fig. S5 shows the equilibrium constants for triskelia that click once with an AP, $K_{\mathrm{1,0}}^{\text{tri}}$, and for triskelia that bind two APs, $K_{\mathrm{2,0}}^{\text{tri}}$, as functions of the clicking energy. Excellent quantitative agreement is observed with the statistical mechanical reaction equilibrium theory presented in Appendix I, which is shown in the graph as straight lines. Additional simulations confirm that equilibrium constants scale with the clicking radius ρ conform to the power-law dependence derived in Appendix I (data not shown). The graph also shows the equilibrium constants for APs that double-click to a clathrin leg, $K_{\mathrm{0,1}}^{\text{tri}}$, i.e., both sites of the AP are bound to the same triskelion leg. This occurs because the estimated maximum extensibility of the AP linker, L ≈ 26 nm, well exceeds the length of the TD, σ ≈ 17 nm, although the considerable elongation of the AP linker makes this double-click unfavorable. Again, the equilibrium constant is in good agreement with the theory. Several simulations were run with smaller systems to verify that the translation-versus-click-attempt ratio does not affect the results presented in this article; we settled on a value of f = 10 for reasons of computational efficiency.

The production simulations were all run with 1000 triskelia confined to a cubic box of volume 10⁶σ³ with periodic boundary conditions. The number density of one triskelion per 10³σ³ corresponds to an in vitro condition of ∼0.2 mg/mL. Self-assembly in the absence of APs is observed in vitro for a slightly acidic solution (pH 6.2, 20 mM MgCl₂), with a critical assembly concentration (CAC) of ∼0.1 mg/mL (49), i.e., the overall concentration where the fractions of bound and unbound triskelia are equal. In an earlier simulation study, we established that this concentration is the CAC of coarse-grained triskelia that gain $E_{\text{c}}\approx 23k_{\text{B}}T$ upon binding to a cage, which is realized for a segment-segment interaction parameter $ϵ\approx 6k_{\text{B}}T$ (33). There we also showed that concepts borrowed from the thermodynamics of micelles allow a theoretic derivation of the binding energy from the measured CAC. Muthukumar and Nossal (50) extended these ideas with energetic contributions reflecting the curvature of the clathrin coat and applied them to analyze cages grown in the presence of AP2, even though the adaptor molecules themselves were not included in the theoretical model. A novel, to our knowledge, statistical mechanical derivation linking the binding energy to the CAC, by considering a cage as a collection of p rigid triskelia with highly restricted translational and rotational freedom, is presented in Appendix II. For the assembly reaction $p\text{C}\rightleftharpoons {\text{C}}_p$, we obtain a standard state free difference of

$$\Delta G_p^0={\mu }_{C_p}^0-p{\mu }_C^0\approx p\Delta {\mu }_C^0,$$ (8)

with ${\mu }_X^0$ as the standard reference chemical potential of component X and $\Delta {\mu }_C^0\approx -16.4k_{\text{B}}T$ deduced from the CAC. Applied to the simulation model, this translates into a binding energy $E_c\approx 27k_{\text{B}}T$, in good agreement with the simulations. Recent experiments on the mechanical properties of clathrin coats adjacent to membranes confirm the binding (free) energies predicted by simulations and theory (51).

Results and Discussion

Simulations

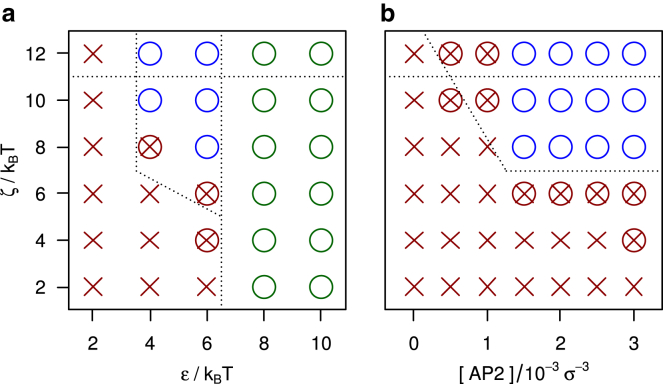
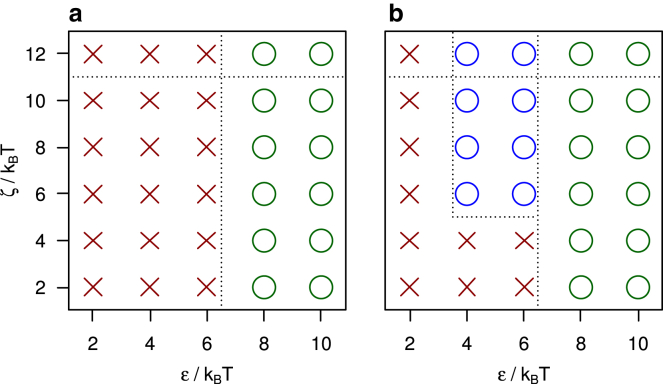
The effect of model APs on the self-assembly behavior of model triskelia is studied by systematically varying the clathrin-clathrin interaction ε, the AP-clathrin clicking strength ζ, and the AP/clathrin ratio. Fig. 2 shows the assembly behavior on two cross sections of this three-dimensional parameter space, for the AP model clicking to the ankles and toes of clathrin. Every marker represents five independent simulations of 10¹⁰ MC steps, requiring approximately a week each on a desktop computer. Red crosses mark conditions where no spontaneous self-assembly of sizable cage fragments is observed. Green and blue circles indicate the self-assembly of at least one complete cage across the five simulations. For the green circles, $ϵ>6k_{\text{B}}T$, cages already self-assemble in the absence of APs. The blue circles highlight conditions where triskelia do not self-assemble in the absence of APs but do form cages in their presence—this is the region of parameter space where APs induce and control the formation of clathrin cages. The assembly of cages in the green and blue regions proceeds by a nucleation and growth process, just like in clathrin-only simulations (31, 34). Small clusters of a few triskelia and APs (see Figs. 3 A and 4 A) are formed and destroyed continuously. Occasionally, one of these small aggregates crosses the nucleation barrier and grows into a cage, as illustrated by the snapshots in Fig. 3. Because of the rigidity of the clathrin model, these cages are all of approximately the same size, containing ∼60 triskelia in near-spherical polyhedra with 12 pentagonal and ∼20 hexagonal faces. The average cage diameter of ∼4.5σ (∼75 nm) agrees with that for cages grown in vitro in the presence of APs (38), which motivated our choice of a 101° pucker angle. Cages grown in simulations with and without AP particles are of the same size. For in vitro experiments, however, a size difference is observed between cages grown with AP and cages grown without AP (38). It is unclear whether this difference is caused by the presence of APs, or by the pH reduction to induce cage formation in the absence of APs. We note that the cage size is very sensitive to the pucker; a decrease from 101° to 100° increases the average cage size by ∼10 particles (31). Almost all self-assembled cages are complete, i.e., triskelion hubs reside at every vertex. Only rarely do one or two vertices of a nearly complete cage remain unoccupied, presumably because the remaining vacancies are less favorable binding sites than the occupied slots. The high prevalence of completed cages indicates that all vertices in these cages are of approximately equal binding affinity, which appears to confirm the “probable roads” hypothesis by Schein and Sands-Kidner (52). For low attachment rates at the edge of a growing fragment, particles binding in an unfavorable way have a high probability of being released again before the defect becomes permanently incorporated in the lattice through the attachment of subsequent particles. Aggregation becomes frustrated when the binding energies are too strong. For intersegmental interactions exceeding ∼10 k_BT, the triskelia easily stick together and thereby quickly form a multitude of small aggregates, which only very slowly merge into larger clusters. This evolution is reminiscent of that observed in vitro below pH 5.8 (53). A clicking energy exceeding ∼11 k_BT makes the APs eager to click to triskelia, thereby rapidly forming disordered clusters like that in Fig. 4 B, which only very slowly develop into cage fragments and ultimately, cages.

Figure 2.

Cage assembly diagrams for clathrin, for 1000 triskelia at a concentration of 10⁻³σ⁻³, combined with model APs clicking to the ends of the TDs and the ankles of clathrin, (a) as a function of the clathrin-clathrin binding strength ε and the clathrin-AP clicking strength ζ, at an AP/clathrin ratio of 3, and (b) as a function of the AP concentration (for AP/clathrin ratios from 0 to 3) and the clathrin-AP clicking strength, at a clathrin-clathrin binding strength of $ϵ=6k_{\text{B}}T$. The markers denote parameter combinations that result in the self-assembly of cages (a green circle if cages are also formed in the absence of APs; a blue circle if assembly only proceeds in the presence of APs), combinations that do not yield cages (red crosses), and conditions where cages do not assemble spontaneously but preassembled cages appear stable (red cross in red circle). The dashed lines indicate the approximate locations of phase boundaries, as discussed in more detail in the main text. To see this figure in color, go online.

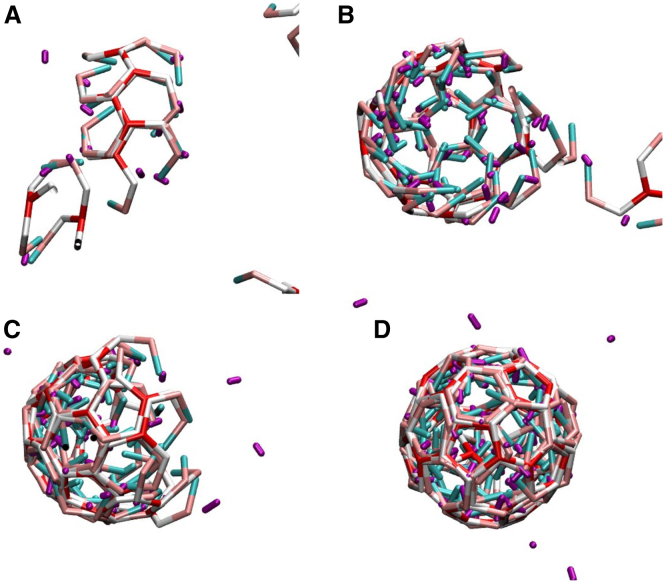
Figure 3.

(A–D) A sequence of snapshots of triskelia assembling into a cage in the presence of APs, for $ϵ=6k_{\text{B}}T$, $\zeta =8k_{\text{B}}T$, and an AP/clathrin ratio of 3, at intervals of 10⁹ MC steps. The coloring of the particles is the same as in Fig. 1. To see this figure in color, go online.

Figure 4.

Adaptor proteins will bring triskelia together without regard for the relative positioning and orientation of these triskelia. A common aggregate (A) comprising two clathrins bonded by six APs (purple), saturating all clicking sites of the cluster. When the cluster is small and the interactions are weak, there are many opportunities to break the AP bonds and reshuffle the triskelia into a more favorable configuration. At high AP-clathrin clicking strengths, large disordered clusters develop rapidly (B); these will only very slowly acquire more order. To see this figure in color, go online.

The rarity of nucleation necessitates excessively long simulations to accurately locate phase boundaries or to determine equilibrium cage concentrations (these will be obtained below by other means). The expedient used in the simulation phase diagrams of this section is the binary detection of self-assembled cages: green or blue circles if cages are formed, and red crosses otherwise. For phase points close to a phase boundary, additional simulations were initiated with configurations containing several half-spherical coats, to explore whether these aggregates grow into complete cages or disintegrate into monomers. In this context we note that the disassembly of an unstable coat fragment typically proceeds much faster than the completion of a stable fragment. The results of these simulations are included as green or blue circles or as red crosses in all simulation phase diagrams. For Fig. 2 only, a further refinement of the phase boundaries was obtained by running an additional set of simulations initiated with fully assembled cages stabilized by nearly three APs per clathrin (obtained from simulations at another phase point). The surviving cages are marked in Fig. 2 by red circles, superposed on the red cross indicating “no spontaneous assembly”. If two simulations with the same parameter settings but opposite starting configurations converge to the same final state, it is very likely that this final state is the equilibrium state. If their final states differ, then either the stability difference between these states is small or (at least) one of the simulations is trapped in a local minimum of the free energy landscape.

The dashed lines in Fig. 2 indicate the estimated phase boundaries, where the boundary slightly to the right of $ϵ=6k_{\text{B}}T$ was established previously and with greater accuracy (33) than the other boundaries. One sees in Fig. 2 a that, at the prevailing concentrations, the APs are able to regulate the emergence of cages for $4k_{\text{B}}T\mathrm{\lesssim }ϵ\mathrm{\lesssim }6k_{\text{B}}T$ and $\zeta \mathrm{\gtrsim }7k_{\text{B}}T$ (i.e., the blue region). A cross section of this region, by varying the AP concentration at fixed $ϵ=6k_{\text{B}}T$, is presented in Fig. 2 b. This plot shows that AP-induced cage assembly requires a clicking energy $\zeta \mathrm{\gtrsim }7k_{\text{B}}T$ as well as an AP concentration equal to or exceeding the clathrin concentration.

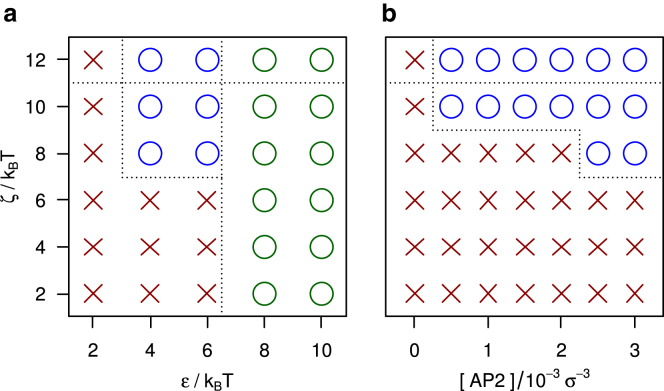
Besides the AP model discussed above, simulations were run with a number of alternative models to explore the conditions conducive to adaptor-induced cage formation. APs clicking at the knees and toes yield the assembly diagrams presented in Fig. 5. The graph on the left is similar to its counterpart in Fig. 2, and shows that APs binding at the knees are equally capable of regulating the assembly of cages as APs binding at the ankles. The graph on the right shows an interesting difference between the two cases: self-assembly continuous down to much smaller AP concentrations. Lowering the effective spring constant of the linker between the AP beads to $k=10k_{\text{B}}T/{\sigma }^2$ has little impact on the assembly diagrams of either adaptor model (data not shown). Upon a further reduction to $k=1k_{\text{B}}T/{\sigma }^2$ (see Fig. 6), the AP clicking to the knees and toes remains operational (with a slight shift in the smallest ζ inducing cage formation), while the AP clicking to the ankles and toes ceases to function.

Figure 5.

Assembly diagrams for model APs clicking to the ends of the TDs and the knees of clathrin, with all other conditions and markers in (a) and (b) identical to those in Fig. 2a and b, respectively. The blue circles again highlight the parameter space where cage formation is controlled by APs. To see this figure in color, go online.

Figure 6.

Assembly diagrams for model APs with a reduced (entropic) spring constant, $k=1ϵ/{\sigma }^2$; all other parameters are identical to those in Fig. 2a and 5a. APs clicking to the ankles and TDs of clathrin (a) are no longer able to regulate the formation of cages, while APs clicking to the knees and TDs of clathrin (b) are still operational. To see this figure in color, go online.

To understand the results reported above, we now turn to unraveling the mechanism by which APs induce the aggregation of triskelia. The discussion presented here is qualitative in nature; a quantitative analysis of the insights gained is presented in the next section. Consider first the AP model that binds to the toes and the knees. It is clearly energetically favorable for an AP to click to triskelia. The largest gain in energy is obtained when the adaptor clicks twice, which is only achieved—note that the toe-knee distance in a clathrin is longer than the maximum extensibility of the linker—if the AP binds to two distinct triskelia. Bringing two triskelia together strongly enhances their chances of adopting the correct relative positions and orientations, and hence promotes successful binding. Adaptor proteins may thus contribute to both the stability of clathrin aggregates and the rate at which they are formed. Note that this line of thought assumes that the energetic gain upon binding outweighs the accompanying entropic loss in translational freedom (and in rotational freedom for clathrin-clathrin binding) and thereby lowers the overall Helmholtz free energy of the system. Hence, whether the AP plays a supporting role in cage formation depends on the clicking strength as well as on the AP and clathrin concentrations.

For the adaptor clicking at the toes and ankle, the energetic gain upon double-clicking to one clathrin is identical to that of clicking to two triskelia. This partially invalidates the mechanism proposed above, by providing the APs with an alternative binding option that does not contribute toward cage assembly. Yet, the simulations of Fig. 2 indicate that these adaptors are able to induce cage formation. Inspection of the length distribution of the linkers (data not shown) reveals that 1) most APs bound to a cage are bridging between pairs of triskelia, and 2) the nearest toe-ankle distance in a cage is shorter than the toe-ankle distance of 1σ along a clathrin leg. This suggests that the shorter linker length in a cage, and between triskelia in the process of coming together, results in a lower elastic energy and hence a higher Boltzmann factor, and thereby favors APs connecting between sites on distinct triskelia over APs connecting to two sites on the same clathrin. The reader might note that the distribution of end-to-end distances of the real linker is determined by entropic effects, while this distribution is modeled here as an energetic effect (see Eq. 2), but this does not present any conceptual problem as both yield the same dependence of the free-energy on the interbead distance.

In support of the above considerations, we recall the impact on the assembly behavior of reducing the linker spring constant at constant maximum extensibility (see Fig. 6). For the model AP clicking at toes and knees, the reduction of the spring constant was of little consequence, in agreement with the mechanism where an adaptor clicking twice always establishes a link between two distinct triskelia. For the model AP clicking to toes and ankles, however, lowering the spring constant reduces the difference in internal energy between AP double-clicked to one clathrin (with the linker stretched to 1σ) and AP clicked to two triskelia (with a shorter linker length). With this reduction, the preference for interclathrin over intraclathrin bonds diminishes and, at $k=1k_{\text{B}}T/{\sigma }^2$, the number of APs links holding triskelia together becomes too low to stabilize a cage.

Theory

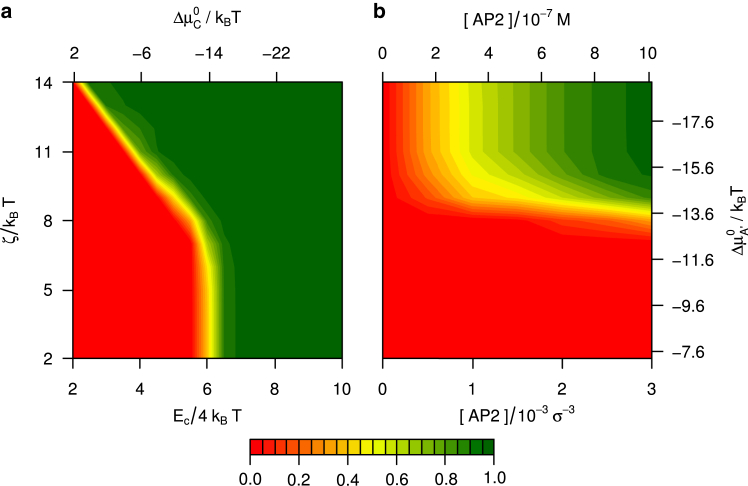
A statistical mechanical theory of AP-induced cage assembly, built on the concepts deduced above, is derived in Appendix III. The theory predicts the equilibrium constant $K_{p,n,m}^{\text{cage}}$ relating the concentrations of unbound triskelia and unbound APs to the concentration of cages of p triskelia decorated with n single-clicked APs and m intertriskelion double-clicked APs. Suppose one knows the average binding energy of a triskelion in a cage devoid of APs, E_c; the clathrin-AP interaction strength ζ; and the total concentrations of clathrin and AP in a system, ${\left[C\right]}_t$ and ${\left[A\right]}_t$, respectively. It is now possible to compute the equilibrium concentrations of all decorated cages in that system, $\left[C_p{A}_n^{\prime }{A}_m^{″}\right]$, by the iterative procedure outlined in Appendix III; the overall cage concentration then follows by a summation over all decorated cages, i.e., all values of p, n, and m. Because the simulations predominantly produced cages of 60 triskelia, we restrict the theoretical calculations to one cage size, p = 60. The phase diagrams calculated for the ankle-binding AP model are shown in Fig. 7. To facilitate the comparison with the simulation results in Fig. 2, the plots are based on the same total clathrin concentration, ${\left[C\right]}_t={10}^{-3}{\sigma }^{-3}$, and similar interclathrin binding energies. In theory, the maximum binding energy due to interclathrin interactions amounts to $E_c=6ϵ$ per triskelion in a cage. In practice, due to thermal vibrations and the inevitable alignment mismatches in cages formed by rigid identical particles, the average potential energy in the simulations is given by $E_c\approx 4ϵ$ (33). The latter relation has been used to rescale the horizontal axes of several phase diagrams in this section for ease of comparison with simulation results. For increasing binding strengths at constant AP concentration, Fig. 7 a shows a narrow transition region (yellow) between virtually no cage formation (dark red) and almost all triskelia absorbed in cages (dark green). A more gradual transition with increasing AP concentration is observed in Fig. 7 b. Considering the relative simplicity of the theory, the good agreement between Figs. 2 and 7 is very satisfactory. The theory does not reproduce two properties observed in the simulations: there are no disordered aggregates at high clicking energy, because this transient intermediate state is not included in the theory, and the self-assembly for $\zeta \gtrsim 10k_{\text{B}}T$ continues down to low AP concentrations. The latter confirms our earlier suspicions that the self-assembly simulations have not reached equilibrium, and agrees with the observation that preassembled cages appear stable under these conditions (see the red crossed circles in the top-left of Fig. 2 b).

Figure 7.

Assembly diagrams calculated using the theory derived in Appendix III, showing the fraction of clathrin bound in cages, for APs clicking to the ends of the TDs and the ankles of triskelia: (a) as a function of the binding energy per clathrin in an AP-free cage, E_c, and the clathrin-AP clicking strength, ζ, at an AP/clathrin ratio of 3; and (b) as a function of the AP concentration (for AP/clathrin ratios from 0 to 3) and the clathrin-AP clicking strength, at $E_{\text{c}}=22k_{\text{B}}T$. The two graphs refer to the same total clathrin concentration, ${\left[C\right]}_t={10}^{-3}{\sigma }^{-3}\approx 3.4\times {10}^{-7}\text{M}$, and similar interaction energies, as their counterparts in Fig. 2. For comparison purposes, the horizontal axis of the left plot is scaled by the simulation-based ratio $E_c/ϵ\approx 4$ (see main text). The alternative axes to the graphs are labeled with the standard chemical free energy differences of AP single-clicking to clathrin (see Eq. 23), and of clathrin assembling into AP-free cages (see Eq. 33), and with total AP concentrations in molars. To see this figure in color, go online.

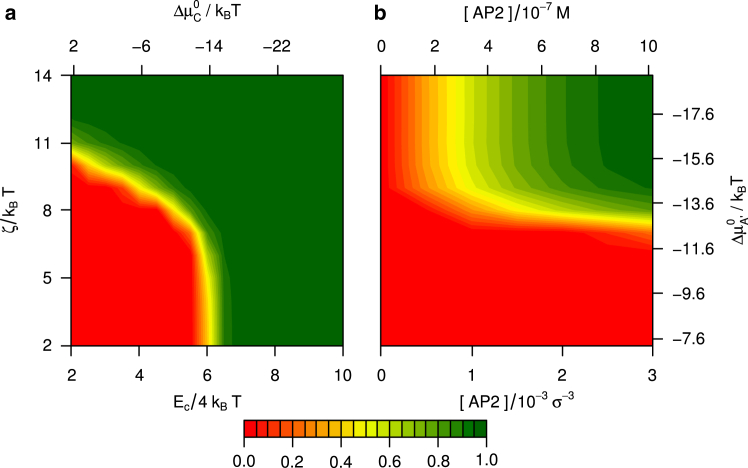
Calculated phase diagrams for the AP model binding to knee and toes are presented in Fig. 8, and compare well with the diagram deduced from the simulations (see Fig. 5). The striking resemblance between the calculated phase diagrams (compare Figs. 7 and 8) suggests that the sole difference between the two calculations, i.e., an AP model that can double-click to a single clathrin versus an AP model that cannot, is of little consequence to the equilibrium behavior. The main difference, the slope of the yellow phase boundary in the plots on the left, results from APs double-clicking to triskelia. For APs binding to the knee, intraclathrin double-clicks are impossible. Double-clicks are unlikely at moderate click strengths for APs binding to the ankle, because of the free energy penalty in stretching the AP linker, but they become important at high click strengths. The phase diagrams calculated for a reduced linker spring constant of $k=1ϵ/{\sigma }^2$ also agree well with the simulations: the model APs binding to the ankle do not induce cage assembly, while the model APs binding to the knee continue to function (data not shown). Collectively, these results provide strong support for the theory and the underlying concepts on the mechanism of cage stabilization by APs.

Figure 8.

Calculated fraction of clathrin bound in cages, for APs clicking to the ends of the TDs and the knees of triskelia, with all other conditions in (a) and (b) equal to those in Fig. 7a and b, respectively. These graphs are the theoretical counterparts to the simulation results in Fig. 5a and b, respectively. To see this figure in color, go online.

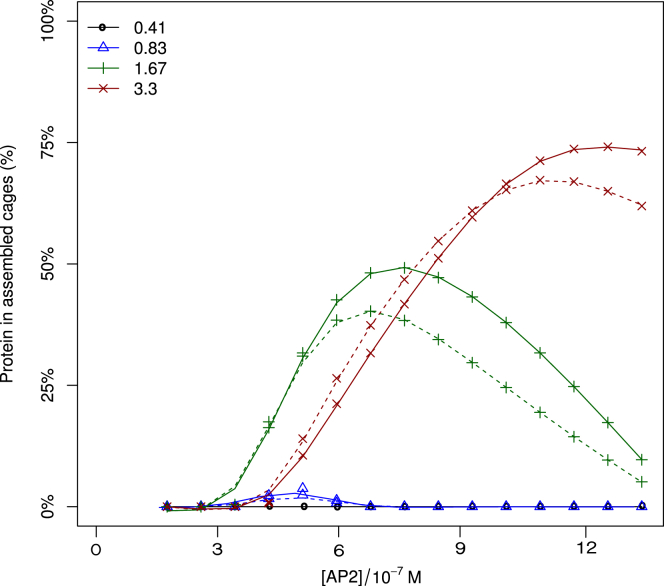
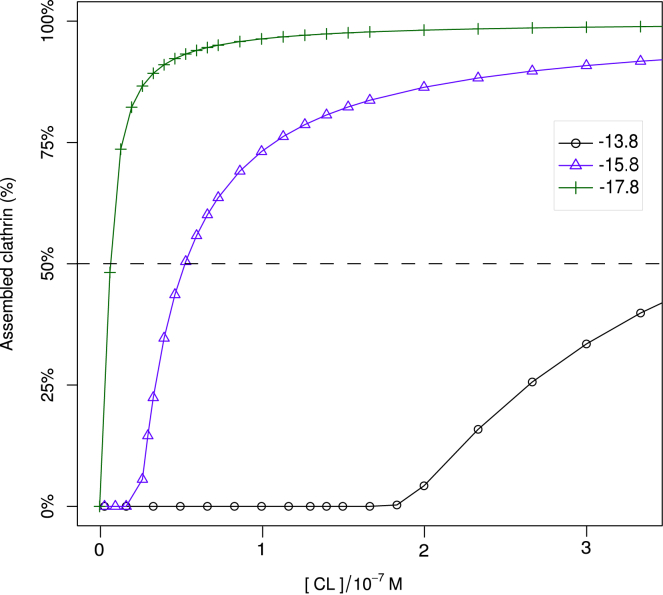
Under experimental conditions, the binding strengths E_c and ζ are typically unknown constants, whose values are codetermined by the acidity and salt conditions of the solvent, while the concentrations are readily varied. Four assembly phase diagrams pertaining to various binding strengths are presented in Fig. S6. To facilitate comparison with experiments, the data are presented in terms of the standard chemical potential difference of AP single-clicking to clathrin, $\Delta {\mu }_{A^{\prime }}^0$, as defined in Eq. 23, and the standard chemical potential difference of the formation of AP-free cages, $\Delta {\mu }_C^0$, as defined in Eq. 33. At $\Delta {\mu }_C^0=-13.8k_{\text{B}}T$ (see Fig. S6 a), the triskelia readily aggregate in the absence of APs at the higher end of the clathrin concentration range; adding APs with $\Delta {\mu }_{A^{\prime }}^0=-15.3k_{\text{B}}T$ enhances the cage concentration, but the effect quickly saturates. For the slightly weaker binding triskelia at $\Delta {\mu }_C^0=-11.8k_{\text{B}}T$, the assistance of APs is crucial to cage formation, with APs binding at $\Delta {\mu }_{A^{\prime }}^0=-14.3k_{\text{B}}T$ yielding significantly more cages than APs clicking at $\Delta {\mu }_{A^{\prime }}^0=-13.3k_{\text{B}}T$ (compare Fig. S6 b and c). An interesting feature is observed at even weaker clathrin bounding, $\Delta {\mu }_C^0=-7.8k_{\text{B}}T$, in combination with $\Delta {\mu }_{A^{\prime }}^0=-15.3k_{\text{B}}T$ (see Fig. S6 d), where for a constant overall clathrin concentration, of say, 1.7 × 10⁻⁷ M, the concentration of cages at first increases with the overall AP concentration, passes through a maximum, and then decreases with increasing AP concentration. This cross section is highlighted in Fig. 9, along with three profiles at lower and higher clathrin concentrations. A similarly shaped profile was obtained by the in vitro assembly experiments of Zaremba and Keen (38), but there the assembled protein mass fraction is plotted; curves of this type are also included in Fig. 9. These authors explain the local maximum as a saturation effect, with clathrin becoming the limiting component upon increasing the AP concentration. This effect is visible in the curves for ${\left[C\right]}_t=3.3\times {10}^{-7}\text{M}$, which saturates in the fraction of bound clathrin but decays in the fraction of bound protein. Our calculations provide an additional explanation for a maximum in the assembled fraction: the number of cages decreases beyond an optimum AP concentration. The underlying mechanism is the replacement of double-clicked APs with two single-clicked APs each, thereby weakening the integrity of cages. Hence increasing the AP concentration beyond its optimum results in a reduction of the cage concentration, as can be clearly seen for ${\left[C\right]}_t=1.7\times {10}^{-7}\text{M}$.

Figure 9.

Calculated number fraction of clathrin (solid lines) and weight fraction of protein (dashed lines) in self-assembled cages, as a function of the total AP concentration. The total clathrin concentration is indicated in the legend, in units of 10⁻⁷ molar; the APs bind to the ankle and TD of clathrin, $\Delta {\mu }_C^0=-7.8k_{\text{B}}T$ and $\Delta {\mu }_{A^{\prime }}^0=-15.3k_{\text{B}}T$. Note that the fractions bound in cages do not increase monotonically but pass through a maximum, for reasons explained in the main text. To see this figure in color, go online.

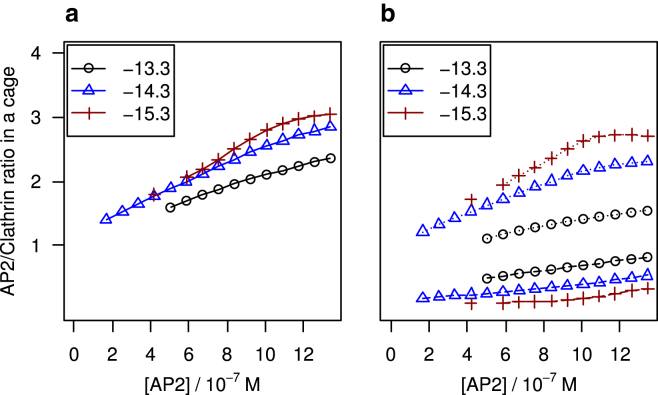
Plots of the number of APs bound to cages, normalized by the number of triskelia in a cage, are presented in Fig. 10. Because the cages are nearly saturated with double-clicked APs for the phase point explored in Fig. 9, we opted to present results for the chemical potential difference combinations in Fig. S6, b and c. Markers are plotted for cage concentrations exceeding 3 × 10⁻¹⁰ M, which corresponds to one cage in the simulated system. At this threshold, the average number of double-clicked APs per encaged clathrin equals approximately one, i.e., a clathrin is clicked to two cross-linking APs on average, while the average number of single-clicked APs is substantially lower. With increasing AP concentration, the number of double-clicked APs rises with approximately the same slope as the number of single-clicked APs for $\Delta {\mu }_{A^{\prime }}^0=-13.3k_{\text{B}}T$, while for higher click strengths the number of double-clicked increases more than the number of single-clicked. In addition to the growing number of APs per cage, the number of cages also rises over the range of AP concentrations. For $\Delta {\mu }_{A^{\prime }}^0=-15.3k_{\text{B}}T$, the number of single-clicked only starts to deviate from zero when the number of double-clicked APs levels off, at ∼2.7 AP per triskelion. These turning points coincide with the number of cages leveling off to a broad maximum, akin to those in Fig. 9.

Figure 10.

Calculated average AP/clathrin ratio for cages (a) and subdivision (b) into single-clicked (dashed lines) and double-clicked (solid lines), as functions of the total AP concentration. The clicking standard chemical free energy difference is indicated in the legend, in units of k_BT, the APs bind to the ankle and TD of clathrin, $\Delta {\mu }_C^0=-11.8k_{\text{B}}T$ and ${\left[C\right]}_t={10}^{-3}{\sigma }^{-3}$. To see this figure in color, go online.

Conclusions

A coarse-grained simulation model and a theory were developed to study the AP-induced self-assembly of triskelia into cages. The results of both approaches are in line with the experimental data, and provide a better understanding of how APs regulate the assembly of cages. This study reveals a number of restrictions on functional APs. Clearly, APs must bind clathrin in a manner sufficiently strong to bring two triskelia together, but cage formation is frustrated when APs bind too strongly. The flexible linker between the two binding sites of an AP must be long enough for intertriskelion connections in cages, but the linker should not be too long to avoid intratriskelion bonding. On a related note, the effective spring constant of the linker must be weak enough to allow intertriskelion connections in cages, but not too weak to suppress intratriskelion bonding. And the AP/clathrin ratio must be high enough, although not too high. While the numerical values used in the model and theory are based on AP2, we expect the results to apply to all types of APs. For the advancement of simulation models and theories, as well as for an improved understanding of the thermodynamics of coat and vesicle formation during endocytosis, it would be useful to obtain experimental values of all binding constants involved, as well as of the mechanical properties of the AP linker. One way of measuring these parameters is proposed in Appendix III.

Author Contributions

M.G., W.K.d.O., and W.J.B. designed the simulation model; M.G. implemented the simulation software, performed the simulations, and analyzed the data; W.K.d.O. developed the theoretical model; M.G. and W.K.d.O. wrote the article; and W.K.d.O. and W.J.B. supervised the study.

Editor: Markus Deserno.

Appendix I

Clathrin-AP complexes

In these Appendices, expressions are derived for the reaction equilibrium constants of AP binding to a triskelion, clathrin self-assembly into cages, and AP-induced cage assembly, respectively. We start by considering a mixture of clathrin (C) and adaptor (A) proteins in equilibrium with their supramolecular aggregates by reactions of the type

$$C+\left(n+m\right)A\rightleftharpoons C{A}_n^{\prime }{A}_m^{″},$$ (9)

where the primes represent the number of clicks binding an AP to the clathrin, in this case n single-clicked and m double-clicked APs. Because clathrin has six binding spots for AP, each capable of binding at most one AP, it follows that n ≥ 0, m ≥ 0, and n + 2m ≤ 6. For simplicity, we assume these six sites to have identical binding properties. Likewise, the two clicking sites of AP are assumed to have identical properties, except for their specificity to either the TD or the ankle/knee binding site of clathrin. The equilibrium constant of the above reaction can be defined as (54)

$$K_{n,m}^{\text{tri}}=\frac{\left(\left[C{A}_n^{\prime }{A}_m^{″}\right]/c_0\right)}{\left(\left[C\right]/c_0\right){\left(\left[A\right]/c_0\right)}^{n+m}},$$ (10)

with the square brackets denoting concentrations, i.e., particles per unit of volume; and $c_0$ is a reference concentration typically taken to be 1 molar. From the statistical mechanics of reaction equilibria in ideal mixtures (54, 55, 56), it follows that

$$K_{n,m}^{\text{tri}}=\frac{\left(q_{n,m}/V\right)}{\left(q_{\text{C}}/V\right){\left(q_{\text{A}}/V\right)}^{n+m}}{c}_0^{n+m}=e^{-\beta \Delta G_{n,m}^0},$$ (11)

where $q_{\text{C}}$, $q_{\text{A}}$, and $q_{n,m}$ denote the molecular partition functions of unbound clathrin, unbound AP, and the $C{A}_n^{\prime }{A}_m^{″}$ supramolecule, respectively; and $\Delta G_{n,m}^0$ is the standard state free-energy change of the reaction.

The semiclassical partition function of a rigid clathrin particle in an infinitely dilute solution, i.e., in the limit that nonbonded interactions can be ignored, is given by

$$q_C=\frac{1}{{\Delta }_C}\iint e^{-\beta \Phi }d\mathbf{r}d\mathit{\phi }\approx \frac{8{\pi }^{2}V}{{\Delta }_C}{e}^{-\beta {\Phi }_C},$$ (12)

with $\Phi$ as the interaction potential and ${\Phi }_C$ as the average solvation free energy of a clathrin. The position integrals run over the volume V of the system and the three-dimensional orientation angles run over their entire range, e.g., for the Euler angles ${\phi }_1\in \left[\mathrm{0,2}\pi \right)$, ${\phi }_2\in [0,\pi )$, ${\phi }_3\in \left[\mathrm{0,2}\pi \right)$, and $d\mathit{\phi }=\text{sin}{\phi }_{2}d{\phi }_{1}d{\phi }_{2}d{\phi }_3$. The elementary volume element ${\Delta }_C$ follows from

$${\Delta }_C^{-1}={\left(\frac{2\pi k_{\text{B}}T}{h^2}\right)}^3{m}_C^{3/2}{\left|{\mathbf{I}}_C\right|}^{1/2}\frac{1}{{\sigma }_C},$$ (13)

with h denoting Planck’s constant; $m_C$ and ${\mathbf{I}}_C$ are the mass and inertia tensor of a triskelion, respectively; the brackets $|\dots |$ denote a determinant; and where the symmetry number ${\sigma }_C$ has the value 3 for a particle with a threefold rotational axis. Note that h, $m_C$, and ${\mathbf{I}}_C$ do not enter the MC simulations, hence the theoretical and simulated equilibrium constants will only agree if these factors can be made to cancel out in the final expression. Treating an AP protein as two point particles of type a, one obtains at infinite dilution

$$q_A=\frac{1}{{\Delta }_a^2}\iint e^{-\beta \Phi }d{\mathbf{r}}_{1}d{\mathbf{r}}_2\approx \frac{1}{{\Delta }_a^2}V{q}_s{e}^{-\beta {\Phi }_A},$$ (14)

where ${\Delta }_a=h^3/{\left(2\pi m_a{k}_{\text{B}}T\right)}^{3/2}$ is the elementary volume element per particle; ${\Phi }_A$ is the average solvation free energy of an AP; and

$$q_s=4\pi {\int }_0^{\infty }{e}^{-\beta \psi \left(r_{12}\right)}{r}_{12}^{2}d{r}_{12},$$ (15)

is the contribution of the internal spring, with potential energy $\psi \left(r_{12}\right)$ at elongation $r_{12}$, to the partition function. The integral is readily solved for a Hookean spring with spring constant k, yielding $q_{\text{s}}={\left(2\pi k_{\text{B}}T/k\right)}^{3/2}$. Next, the partition function of a clathrin adorned with one single-clicked AP takes the form

$$\begin{array}{c}{q}_{\mathrm{1,0}}=\frac{1}{{\Delta }_C{\Delta }_a^2}\int \int \int \int e^{-\beta \Phi }d\mathbf{r}d\mathit{\phi }d{\mathbf{r}}_{1}d{\mathbf{r}}_2\\ \approx g_{\mathrm{1,0}}\frac{8{\pi }^{2}V}{{\Delta }_C}\frac{4\pi {\rho }^3{q}_s}{3{\Delta }_a^2}{e}^{-\beta \left({\Phi }_C+{\Phi }_A-\zeta \right)},\end{array}$$ (16)

where, in the last step, it has been used that either site of the AP dimer must be within a sphere of radius ρ centered around a clicking site on the triskelion, and ζ denotes the strength of the click. The number of clicking combinations will be denoted by $g_{n,m}$, and in this case has the value $g_{\mathrm{1,0}}=6$ because a triskelion offers six binding spots. Note that the AP-clathrin complex is not treated as a single molecule, but as a combination of two molecules with reduced rotational and translational freedom (57, 58). By combining the above equations, one arrives at the equilibrium constant

$$K_{\mathrm{1,0}}^{\text{tri}}=g_{\mathrm{1,0}}\frac{4}{3}\pi {\rho }^3{e}^{\beta \zeta }{c}_0,$$ (17)

where the elementary volumes have indeed canceled out. The approach is readily extended to several single-clicked APs per triskelion, with at most one AP per triskelion binding site, under the assumption that other interactions between these APs may be ignored. Fig. S5 shows that the theory is in good agreement with the simulations.

The partition function of a triskelion adorned with one double-clicked AP is given by an integral similar to that in Eq. 16, with the restriction that now both sites of the AP must be clicked to their counterpart sites on the triskelion. In view of the estimated maximum extensibility of the AP linker, L ≈ 1.5σ, a double-clicked AP will bind to two triskelion sites on the same leg and hence their interstitial distance is fixed, d_t = lσ. We then arrive at

$$q_{\mathrm{0,1}}\approx g_{\mathrm{0,1}}\frac{8{\pi }^{2}V}{{\Delta }_C}\frac{q_s^{″}\left(d_t\right)}{{\Delta }_a^2}{e}^{-\beta \left({\Phi }_C+{\Phi }_A-2\zeta \right)},$$ (18)

where $g_{\mathrm{0,1}}=3$ and the contribution of AP’s internal spring reads as

$$q_s^{″}\left(d\right)={\int }_{v_1}{\int }_{v_2}{e}^{-\beta \psi \left(|{\mathbf{r}}_1-{\mathbf{r}}_2|\right)}d{\mathbf{r}}_{1}d{\mathbf{r}}_2,$$ (19)

with $v_1$ and $v_2$ denoting the spherical volumes of radius ρ of two clicking sites at center-to-center distance d. For the actual proteins, the range of the click interaction is short compared to the distance between clicking sites, $\rho \ll d$, and the integral may be approximated as

$$q_{\text{s}}^{″}\left(d\right)\approx {\left(\frac{4}{3}\pi {\rho }^3\right)}^2{e}^{-\beta \psi \left(d\right)}$$ (20)

in the limit of $\beta kd\rho \ll 1$. Fig. S5 shows that the resulting equilibrium constant, $K_{\mathrm{0,1}}^{\text{tri}}$, is in good agreement with the simulations, for the low $k=1k_{\text{B}}T/{\sigma }^2$ value used in that plot. The combination of spring constant $k=30k_{\text{B}}T/{\sigma }^2$ and click radius $\rho =0.25\sigma$ used in the production simulations exceeds this limit and it proved necessary to evaluate the integral of Eq. 19 numerically, yielding a value $q_s^{″}\left(\sigma \right)\approx 9.6\times {10}^{-8}{\sigma }^6$ approximately two orders larger than the estimate $1.0\times {10}^{-11}{\sigma }^6$ by Eq. 20, to obtain a good agreement between theoretical and simulation phase diagrams.

The above results can be combined to obtain the equilibrium constants for all reactions of the type expressed in Eq. 9, in the dilute limit. Upon neglecting interactions between APs bound to the same triskelion, except for the mutual exclusivity of the clathrin-AP clicks, we arrive at

$$K_{n,m}^{\text{tri}}=g_{n,m}{\left(\frac{4}{3}\pi {\rho }^3\right)}^n{\left(\frac{q_s^{″}\left(d_t\right)}{q_s}\right)}^m{e}^{\beta \left(n+2m\right)\zeta }{c}_0^{n+m}.$$ (21)

The multiplicity $g_{n,m}$ is readily established by counting the number of ways of attaching n single-clicked and m double-clicked APs to a single triskelion, but in practice this number proves of little consequence because the other factors in the above equation are much larger. Upon neglecting this factor, the standard state free energy differences (54, 56) for the 15 possible $\left(n,m\right)$ combinations with $n+m>0$ reduce to

$$\Delta G_{n,m}^0={\mu }_{n,m}^0-{\mu }_C^0-\left(n+m\right){\mu }_A^0$$ (22)

$$\approx n\Delta {\mu }_{A^{\prime }}^0+m\Delta {\mu }_{A^{″}}^0\left(d_t\right),$$ (23)

with ${\mu }_i^0$ as the reference chemical potential of compound i at the reference concentration $c_0$, and where the reference chemical potential differences follow from Eq. 21 as

$$\Delta {\mu }_{A^{\prime }}^0=-k_{\text{B}}T\text{ln}\left(\frac{4}{3}\pi {\rho }^3{e}^{\beta \zeta }{c}_0\right),$$ (24)

$$\Delta {\mu }_{A^{″}}^0\left(d\right)=-k_{\text{B}}T\text{ln}\left(\frac{q_s^{″}\left(d\right)}{q_s}{e}^{\beta 2\zeta }{c}_0\right).$$ (25)

Inserting the parameters of the simulation model into the former difference yields

$$\Delta {\mu }_{A^{\prime }}^0\approx -5.3k_{\text{B}}T-\zeta ,$$ (26)

while in combination with the approximation in Eq. 20, the latter difference can be rewritten as

$$\Delta {\mu }_{A^{″}}^0\left(d\right)=2\Delta {\mu }_{A^{\prime }}^0+\psi \left(d\right)+k_{\text{B}}T\text{ln}\left[c_0{\left(2\pi k_{\text{B}}T/k\right)}^{3/2}\right],$$ (27)

and with the numerical evaluation of $q_{\text{s}}^{″}\left(d_{\text{t}}\right)$ we find for the simulation model

$$\Delta {\mu }_{A^{″}}^0\left(d_{\text{t}}\right)=2\Delta {\mu }_{A^{\prime }}^0+16.4k_{\text{B}}T.$$ (28)

These expressions are readily extended to include site-dependent clicking strengths, i.e., ${\zeta }_1$ for binding to the feet and ${\zeta }_2$ for binding to the ankle or knee.

Appendix II

Clathrin cages

The partition function of a clathrin cage of p triskelia is obtained by integrating over the positions r and orientations φ of all p triskelia, subject to the condition that the particles remain sufficiently close and properly oriented—relative to each other—to qualify as a cage. The overall translational and rotational freedom of a triskelion—amounting to V and $8{\pi }^2$, respectively, for a particle in solution (see Eq. 12)—are effectively reduced by these binding restrictions to $v_{\text{t}}$ and ${\omega }_{\text{r}}$, respectively, for a triskelion wobbling around a fixed location in a cage. The partition function of a cage of p triskelia can therefore be approximated as

$$q_p=\frac{1}{p!{\Delta }_C^p}\iint \cdots \iint e^{-\beta \Phi }d{\mathbf{r}}_{1}d{\mathit{\phi }}_1\cdots d{\mathbf{r}}_{p}d{\mathit{\phi }}_p$$ (29)

$$\approx g_p\frac{8{\pi }^{2}V}{{\Delta }_{\text{C}}^p}{\left(v_t{\omega }_r\right)}^{p-1}{e}^{-\beta p\left({\Phi }_C-E_c\right)},$$ (30)

where $E_c$ denotes the average binding energy of a clathrin in a cage, and $p!$ corrects for the indistinguishability of the p triskelions forming the cage. In evaluating the integral, one particle has retained the full factor $8{\pi }^{2}V$ to account for the translational and rotational freedom that a rigid coat will sample, while the remaining $\left(p-1\right)$ particles each contribute a factor $v_{\text{t}}{\omega }_{\text{r}}$ reflecting thermal fluctuations around this rigid shape. The multiplicity $g_p$ denotes the degeneracy of the ground state. Cages with pentagonal and hexagonal facets require an even p; there exists one cage structure for p = 20, none for p = 22, and multiple cage structures for p ≥ 24. Schein and Sands-Kidner (52) and Schein et al. (59) argued that, for $20\le p\le 60$, there typically exists just one preferred cage structure for every even value of p, because all other cages incorporate one or more edges with an unfavorably high torsional energy. This theory is confirmed by the cages spontaneously grown in our simulations. We note that the “exclusion of head-to-tail dihedral angle discrepancies” rule proposed by Schein and Sands-Kidner (52) and Schein et al. (59) can be expressed much more concisely as the “excluded 5566” rule: an unfavorable torsion arises when a facet has among its neighboring facets a sequence of two pentagons followed by two hexagons, regardless of clockwise or counterclockwise order. The “isolated pentagon rule” applies for p > 60, and there typically exist multiple favorable cages for p ≥ 70 (52, 59). Because the multiplicity is a small integer for the p ≈ 60 cages grown in the simulations, the exact value of $g_p$ proves to be of little consequence to the results of the calculations.

Combining the above results, the equilibrium constant for the cage formation reaction

$$p\text{C}\rightleftharpoons {\text{C}}_p$$ (31)

is found to be given by

$$K_p^{\text{cage}}=g_p{\left(\frac{v_t{\omega }_r}{8{\pi }^2}\right)}^{p-1}{e}^{\beta p{E}_c}{c}_0^{p-1}.$$ (32)

The corresponding standard free energy difference can be expressed as

$$\Delta G_p^0=-k_{\text{B}}T\text{ln}{K}_p^{\text{cage}}\approx p\Delta {\mu }_C^0,$$ (33)

$$\Delta {\mu }_C^0\approx -k_{B}T\text{ln}\left(\frac{v_t{\omega }_r}{8{\pi }^2}{e}^{\beta E_c}{c}_0\right),$$ (34)

for $p\gg 1$. Assuming that the simulated triskelia bound in a cage experience an estimated translational freedom of 0.1σ along every Cartesian direction and an estimated rotational freedom of 0.1 rad (∼6°) around every Cartesian axis,

$$\Delta {\mu }_C^0\approx 10.2k_{\text{B}}T-E_c.$$ (35)

The resulting fraction of clathrin bound in cages, $f=p\left[C_p\right]/{\left[C\right]}_t$, is plotted in Fig. 11 as a function of the total clathrin concentration, ${\left[C\right]}_t=\left[C\right]+p\left[C_p\right]$. This fraction reaches a value of 50%, i.e., the number of bound triskelia equals the number of unbound triskelia, when the total concentration equals the CAC; the first cages appear at approximately one-half this overall concentration. The above equilibrium constant can be related to the CAC, and thence to experimental data on clathrin. At the CAC, the number density of free triskelia reads as $\left[C\right]=c_{\text{CAC}}/2$ and that of cages as $\left[C_p\right]=c_{\text{CAC}}/\left(2p\right)$, hence

$$K_p^{\text{cage}}=\frac{1}{p}{\left(\frac{c_{\text{CAC}}}{2c_0}\right)}^{1-p},$$ (36)

$$\Delta {\mu }_{\text{C}}^0\approx k_{\text{B}}T\text{ln}\frac{c_{\text{CAC}}}{2c_0}$$ (37)

for $p\gg 1$. The experimental CAC of 100 μg/mL (49) then translates into $\Delta {\mu }_C^0\approx -16.4k_{\text{B}}T$, and this value is reproduced by the simulation model for $E_c\approx 27k_{\text{B}}T$. In simulations with an overall triskelion density close to the experimental CAC, the numbers of bound and unbound particles were approximately equal when using a leg-leg interaction strength $ϵ\approx 6k_{\text{B}}T$; the resulting average potential energy of ∼23 k_BT per clathrin (33) is in good agreement with the above theoretical estimate. We note that the elementary volume elements ${\Delta }_C$ have again cancelled out in the statistical mechanical expression for the equilibrium constant. This was not the case in our earlier derivation, which consequently overestimated the binding energy (33). Muthukumar and Nossal (50) presented a derivation based on mole fractions, following the common practice in micelle theory (60), to arrive at an enthalpic energy $E_c\approx k_{\text{B}}T\text{ln}{c}_s/c_{\text{CAC}}\approx 21k_{\text{B}}T$, with the subscript s referring to the solvent. There is no compelling physical reason to use mole fractions, and one now sees that the method works because the volume per solvent molecule, $v_s=1/c_s$, provides a reasonable order of magnitude estimate for the libration volume of a clathrin bound in a cage, $v_t{\omega }_r$.

Figure 11.

Theoretical concentration dependence of the fraction of particles bound in cages, for several values of the standard chemical potential difference $\Delta {\mu }_C^0$, indicated in units of k_BT in the legend, in the absence of APs. At the CAC, which varies with the interaction strength, the concentrations of free and bound clathrin are equal (dashed line). In this calculation, all cages are assumed of identical size, p = 60. Note the strong resemblance to the experimental data on in vitro assembly of clathrin cages (see Fig. 9 in Ungewickell and Ungewickell (62)). To see this figure in color, go online.

Appendix III

Decorated clathrin cages

Finally, we consider the formation of a cage decorated with n single-clicked APs and m double-clicked APs,

$$pC+\left(n+m\right)A\rightleftharpoons C_p{A}_n^{\prime }{A}_m^{″}.$$ (38)

To keep the derivation manageable, it is assumed that for every clicking site on a clathrin in a cage there is one nearest clicking site on an adjacent clathrin in that cage, such that the two sites—and hence the two triskelia—can be linked by an AP. Distance measurement reveal that the separation between two nearest sites on differing triskelia in a cage, d_c, is shorter than the distance d_t between two nearest sites on the same triskelion. Because of the functional forms of $q_s^{″}$ and ψ, a small reduction of the elongation of the entropic spring results in a pronounced increase of $q_s^{″}$—we may therefore ignore intraclathrin double-clicked APs. Combining the results from the two preceding Appendices, we then arrive at the equilibrium constant

$$K_{p,n,m}^{\text{cage}}=g_{p,n,m}{\left(\frac{v_t{\omega }_r}{8{\pi }^2}\right)}^{p-1}{\left(\frac{4}{3}\pi {\rho }^3\right)}^n{\left(\frac{q_s^{″}\left(d_c\right)}{q_s}\right)}^m{e}^{\beta \left[p{E}_c+\left(n+2m\right)\zeta \right]}{c}_0^{p+n+m-1},$$ (39)

where $n\ge 0$, $m\ge 0$, and $n+2m\le 6p$. Again, the elementary volume elements have cancelled out. The multiplicity is estimated as

$$g_{p,n,m}\approx g_p\frac{\left(3p\right)!}{m!\left(3p-m\right)!}\frac{\left(6p-2m\right)!}{n!\left(6p-2m-n\right)!},$$ (40)

where the first factor, accounting for the cage structure, has been discussed before, $g_p\approx 1$; the second factor counts the permitted distributions of m double-clicked APs over $3p$ pairs of nearest unlike click sites in a cage; and the third factor represents the permitted distributions of n single-clicked APs over the remaining $6p-2m$ free clicking sites of the cage. The standard free energy difference of the reaction can be expressed as

$$\Delta G_{p,n,m}^0\approx p\Delta {\mu }_C^0+n\Delta {\mu }_{A^{\prime }}^0+m\Delta {\mu }_{A^{″}}^0\left(d_c\right)-k_{\text{B}}T\text{ln}{g}_{p,n,m},$$ (41)

where the multiplicity is no longer negligibly small. The extension to site-dependent clicking strengths is again straightforward.

To obtain the number of cages at every point in the assembly diagrams of Figure 7, Figure 8, Figure 9, Figure 10, we consider a closed system of volume V with given total clathrin concentration ${\left[C\right]}_t$ and AP concentration ${\left[A\right]}_t$. For simplicity, we again consider only one cage size, p = 60. We denote the estimated concentrations of free, i.e., unbound, triskelia and APs as ${\left[C\right]}_f$ and ${\left[A\right]}_f$, respectively. The concentrations of decorated triskelia and decorated cages then follow by using the equilibrium constants derived above. A weighted sum over all species yields the sum concentrations of triskelia and APs present in the box,

$${\left[C\right]}_s={\left[C\right]}_f+\sum _{n,m}{K}_{n,m}^{\text{tri}}{\left[C\right]}_f{\left[A\right]}_f^{n+m}+p\sum _{n,m}{K}_{p,n,m}^{\text{cage}}{\left[C\right]}_f^p{\left[A\right]}_f^{n+m},$$ (42)

$${\left[A\right]}_s={\left[A\right]}_f+\sum _{n,m}\left(n+m\right)K_{n,m}^{\text{tri}}{\left[C\right]}_f{\left[A\right]}_f^{n+m}+\sum _{n,m}\left(n+m\right)K_{p,n,m}^{\text{cage}}{\left[C\right]}_f^p{\left[A\right]}_f^{n+m}.$$ (43)

We now solve the equations ${\left[C\right]}_s={\left[C\right]}_t$ and ${\left[A\right]}_s={\left[C\right]}_t$ by varying ${\left[C\right]}_f$ and ${\left[A\right]}_f$. This is achieved by minimizing the sum-squared differences between the imposed and calculated overall concentrations, followed by a Newton-Raphson zero-point solver (61). The second summation on the right-hand side of Eq. 42 then yields the concentration of cages in the system. The presented calculations assume $d_c=0.6\sigma$; because the limit underlying Eq. 20 does not hold true for the simulation model, the integral in Eq. 19 is solved numerically to yield $q_s^{″}\left(d_c\right)\approx 7.8\times {10}^{-5}{\sigma }^6$. The standard chemical potential differences of single- and double-clicked APs are then related by

$$\Delta {\mu }_{A^{″}}^0\left(d_c\right)=2\Delta {\mu }_{A^{\prime }}^0+9.7k_{\text{B}}T,$$ (44)

while Eq. 27 predicts a slightly higher offset of 11.5 k_BT.

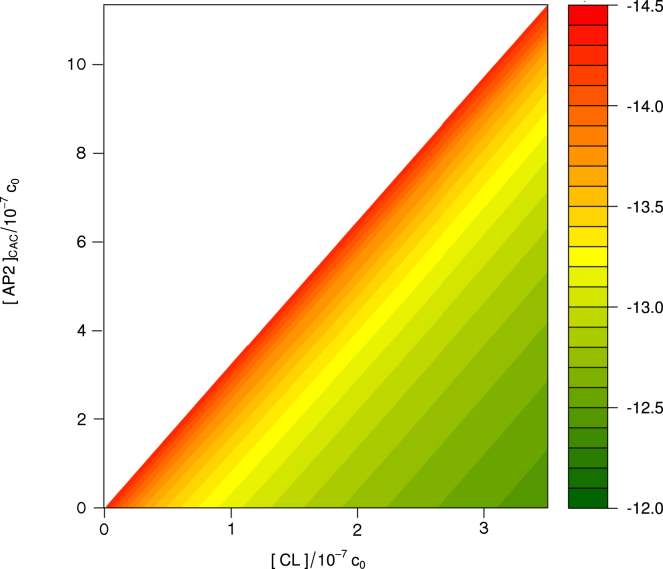
Measuring the hundreds of reaction equilibrium constants condensed into Eqs. 39 and 41 offers a daunting challenge, the more so as this requires identifying the numbers of triskelia, and single-clicked and double-clicked APs of every cage in the reaction mixture. To facilitate comparison of theory with experiment, we revert to a CAC. The condition where half the APs in a solution are bound to triskelia (both free triskelia and those in cages) is a complex function of all equilibrium constants of the mixture, as well as of the overall clathrin concentration, but it can be measured without detailed resolution of the compositions of aggregates. By measuring this CAC at a number of clathrin concentrations, it is in principle possible to extract all relevant standard chemical potential differences. An illustration hereof is provided in Fig. 12, where it is assumed that $\Delta {\mu }_C^0$ and the relation between $\Delta {\mu }_{A^{″}}^0\left(d\right)$ and $\Delta {\mu }_{A^{\prime }}^0$ are known in advance; by measuring AP’s CAC at a given overall clathrin concentration, one can read the corresponding $\Delta {\mu }_{A^{\prime }}^0$ from the graph.

Figure 12.

For any given total clathrin concentration (horizontal axis), there exists a total AP concentration (vertical axis) for which the fraction of bound AP equals the fraction of unbound AP. The plot relates both concentrations to the corresponding standard chemical potential difference for single-clicked APs, $\Delta {\mu }_{A^{\prime }}^0$, in units of k_BT. The underlying calculation is based on $\Delta {\mu }_C^0=-11.8k_{\text{B}}T$ and assumes $\Delta {\mu }_{A^{″}}^0$ and $\Delta {\mu }_{A^{\prime }}^0$ to be related by Eqs. 28 and 44. The diagonal represents the maximum attainable AP CAC for a given clathrin concentration. To see this figure in color, go online.