Role of turnover in active stress generation in a filament network

Abstract

We study the effect of turnover of cross-linkers, motors, and filaments on the generation of a contractile stress in a network of filaments connected by passive cross-linkers and subjected to the forces exerted by molecular motors. We perform numerical simulations where filaments are treated as rigid rods and molecular motors move fast compared to the time scale of an exchange of cross-linkers. We show that molecular motors create a contractile stress above a critical number of cross-linkers. When passive cross-linkers are allowed to turn over, the stress exerted by the network vanishes due to the formation of clusters. When both filaments and passive cross-linkers turn over, clustering is prevented and the network reaches a dynamic contractile steady state. A maximum stress is reached for an optimum ratio of the filament and cross-linker turnover rates. Taken together, our work reveals conditions for stress generation by molecular motors in a fluid isotropic network of rearranging filaments.

The cell cortical cytoskeleton is essential in processes involving cell shape changes [1, 2].In the cortex, myosin molecular motors are assembled in a bipolar filamentous structure which binds to actin filaments and generates forces by consuming the chemical energy of the hydrolysis of adenosine triphosphate. The action of myosin motors result in the generation of an active, contractile stress whose spatial distribution in the cortex plays a key role in cellular morphogenetic processes [3–5].

In living cells, passive and active cross-linkers and actin filaments are continuously exchanged between the cortex and the cytosol [1]. As a result, cytoskeletal networks can release elastic stresses stored in the network and undergo large-scale flows. Significant progress has been achieved to understand stress generation in networks with permanent filaments and fixed or unbinding cross-linkers, through in vitro studies and a theoretical analysis of actomyosin network [6–15]. It is unclear, however, what is the role of turnover in stress generation and how filament networks can simultaneously rearrange and exert a permanent internal active stress. In vivo experiments suggest that the rate of turnover is a major determinant of force generation by actomyosin networks [16, 17].

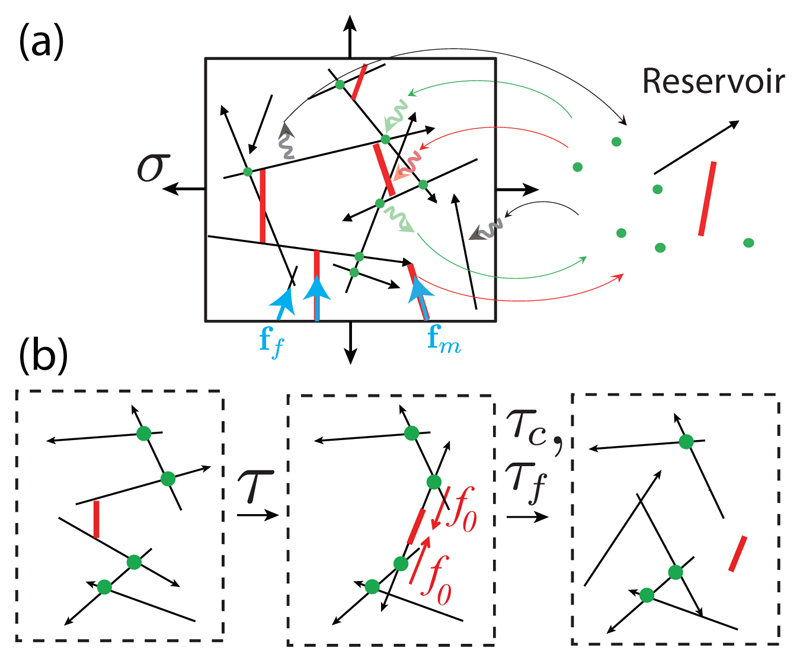
We ask here how the rate of turnover of passive cross-linkers and actin filaments influence the active stress generated by motors in the network. We study a simplified mechanical model for a cytoskeletal network in two dimensions whose constituents are turning over [Fig. 1(a)]. Filaments and motors are treated as rigid rods. Filaments have a polarity represented by arrows in Fig. 1. Passive cross-linkers are assumed to be pointlike and constrain the position of the filaments on which they are attached. Filaments are able to rotate freely around the cross-linker position and around motor heads. Motor heads exert an active force f_m with a constant magnitude |f_m| = f₀ on filaments, oriented toward the reverse direction of the arrow (the minus end of actin filaments).

Fig. 1.

(a) Schematic illustration of a 2D cytoskeletal network (left). Filaments are represented by black arrows, motors by red bars, and cross-linkers by green dots. The network exerts a stress σ on the boundaries of the box, arising from tensions acting within the filaments (f_f) and within the motors (f_m). Motors move towards the arrowhead of filaments (for actin, the arrowhead corresponds to the barbed end). Network components stochastically exchange with a reservoir (right). (b) Motors move on filaments and rearrange the network on a time scale τ. Cross-linkers and actin filaments turn over on longer time scales τ_c > τ and τ_f > τ.

To obtain forces acting on filaments, we introduce the effective mechanical potential, U = W + λ · g(x_f,i, n_f,i, x_m,k, n_m,k), where $W=-f_0{\displaystyle {\sum }_{\langle k,i\rangle }{s}_{ki}}$ is the work due to motor active forces, with S_ki i being the position of the kth motor head on the ith filament relative to the filament center of mass, and the sum ${\displaystyle {\sum }_{\langle k,i\rangle }}$ is performed for all of the pairs of filaments (i) and motors (k) connected with each other. In addition, geometrical constraints arise from the conditions that cross-linkers and motor heads are firmly attached to filaments, and that motor filaments have a fixed length. Lagrange multipliers λ impose these constraints, g(x_f,i, n_f,i, x_m,k, n_m,k) = 0, where x_f,i and n_f,i (x_m,k and n_m,k) indicate the center of mass position and orientation unit vector of the ith filament (kth motor). The motion of motors is taken into account by writing that the position of attachment of the kth motor S_ki relative to the center of mass of the filament i follows the dynamic equation

$$\mu \frac{d{s}_{ki}}{dt}=-\frac{\partial U}{\partial s_{ki}}$$ (1)

with μ being a scalar friction coefficient arising from translational friction between the motor heads and the filament [18–20]. Motors have a typical velocity υ_m = f₀/μ, and we introduce a reference time scale τ = l_fμ/2f₀. We neglect viscous forces arising from the fluid around the network compared to motor-filament friction, and the position and orientation of filaments x_f,i, n_f,i and motors x_m,k, n_m,k are relaxed instantaneously.

To fix ideas, cortical actomyosin networks in a cell have a mesh size ξ ∼ 20 – 250 nm [21, 22] and the typical cell diameter is several tens of micrometers. We therefore expect actin filaments to have a length l_f of the order 0.1 −1 μm, smaller than their persistence length l_p = 16 μm [23]. Myosins move on actin filaments with velocity υ_m ∼ 0.1 − 3 μm/s [24, 25]. The characteristic time for myosins to move on a filament is τ ∼ l_f/υ_m ∼ 0.03 − 10 s. To compare this time scale to the effect of viscous stresses arising in the solvent of viscosity η, we note that the velocity of a filament in the network subjected to a force f₀ is ∼ f₀ ln (ξ/r_f)/(ηl_f) from slender-body theory [26] taking into account the hydrodynamic screening effect [27], giving a time scale ${\tau }_{\upsilon }\sim l_f^2\eta /\left[f_0\ln \left(\xi /r_f\right)\right]$, with r_f ≃ 5 nm being the radius of a filament. Taking the force exerted by a myosin f₀ ∼ 6 − 12 pN, η ≃ 10⁻³ Pa·s for water, τ_υ ∼ 10⁻⁴ s ≪ τ. Finally, we expect the characteristic times τ_c and τ_f of the cross-linker and actin filament turnover to be of the order of 10 s- 1 min [28, 29], slow compared to these timescales, such that τ_c > τ and τ_f > τ.

Configuration with one motor and two filaments

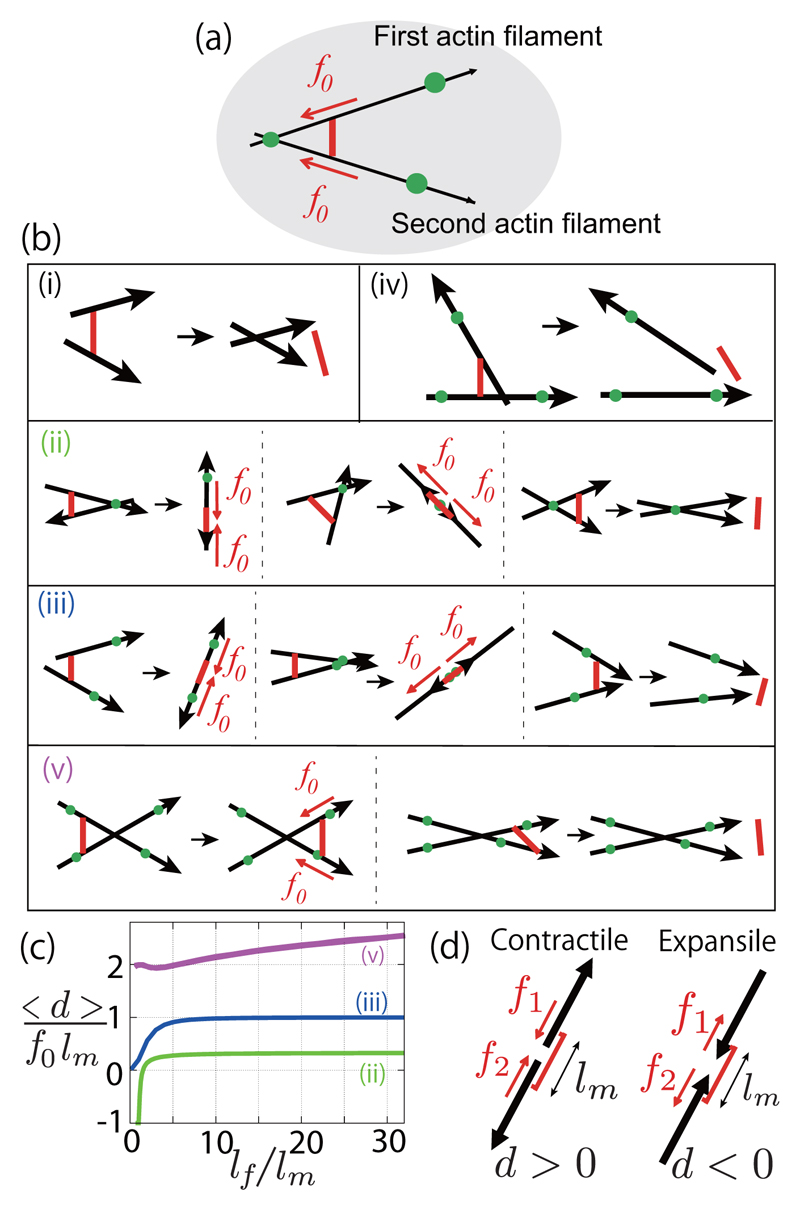
We start by discussing the dynamics of configurations involving one motor attached to two filaments [Fig. 2(a)]. The two filaments can be connected to a cross-linker, itself connected to the external network, here considered to be fixed in space. Depending on the positions of the cross-linkers, the two filaments can be completely free [Fig. 2(b)(i)], cross-linked to each other [Fig. 2(b)(ii)], or to the external network [Fig. 2(b)(iii)-(v)]. By averaging over possible initial configurations [30], we evaluate whether motors form on average positive or negative force dipoles at steady state [Fig. 2(c)]. The motor force dipole is d = (l_m/2)n₁₂·(f₁ − f₂),with l_m being the length of the motor, n₁₂ the unit vector giving the motor orientation, and f₁ and f₂ are the forces exerted by the motor ends on the filaments [see Fig. 2(d) and Supplemental Material [30]].

Fig. 2.

Contractile and expansile configurations for one motor and two filaments. (a) Two filaments are attached by fixed cross-linkers to the external network. (b) Possible initial configurations for one motor, two filaments, and one or several cross-linkers, and final configurations. (c) Average strength of the contractile force dipole generated by the molecular motor 〈d〉 in the final configurations (ii), (iii), (v) where the motor does not detach, as a function of the filament length l_f. (d) Contractile (force dipole d > 0) and expansile (d < 0) configurations.

In cases shown in Figs. 2(b)(i) and 2(b)(iv), filaments are moved relative to each other until the motor detaches, so that a motor-induced force dipole acts on a transient time τ, which can be neglected in the quasistatic limit τ ≪ τ_c [Fig. 2(b)]. In the cases shown in Figs. 2(b)(ii), 2(b)(iii), and 2(b)(v), filaments relax to a steady configuration where the motor exerts a constant force dipole, always positive on average in the cases shown in Figs. 2(c)(iii) and 2(c)(v). In the case shown in Fig. 2(c)(v), f₁ and f₂ include the forces exerted by the motor themselves and by geometrical constraints [30]. As shown in Ref. [9], the bias towards contractile states arises from instabilities of expansile configurations [30]. The average force dipole 〈d〉 vanishes for pointlike motors, l_m → 0 [14].

Numerical simulations of networks with turnover

We next numerically simulated a network of N_f filaments, N_m motor rods, and N_c passive cross-linkers in a square box of width W with periodic boundaries (Fig. 1). The frame of the box is not allowed to deform. The geometrical constraints g are enforced by stiff linear springs. Initial conditions are obtained by randomly positioning filaments. Turnover is introduced by stochastically removing cross-linkers, motors, and filaments from the network with rates 1/τ_c, 1/τ_m and 1/τ_f. For simplicity, turnover rates of cross-linkers are taken here independent of the forces they sustain. Note that the load dependency of cross-linking has been shown to influence network clustering [13]. Filaments, motors, and passive cross-linkers are added in random positions in the network with on rates $k_{on}^f$, $k_{on}^m$, and $k_{on}^c$.

We evaluate the components of the stress tensor σ_ij (i, j = x or y) acting on the boundary of the box [Fig. 1(a)]. The total stress is given by ${\sigma }_{ij}={\sigma }_{ij}^f+{\sigma }_{ij}^m$, with ${\sigma }_{ij}^f$ obtained by summing forces acting within the filaments and ${\sigma }_{ij}^m$ from forces acting within motor rods crossing the boundary of the box (Fig. 1). In a linear elastic or viscous material, $\langle {\sigma }_{ij}^f\rangle =0$ in the absence of large-scale deformation and where 〈·〉 denotes averaging over positions in the box [30]. In a nonlinearly elastic material however, $\langle {\sigma }_{ij}^f\rangle \ne 0$ [30]. At steady state, the average stress acting within the motors is given by (see Ref. [31] and the Supplemental Material [30])

$$\langle {\sigma }_{ij}^m\rangle =c\langle d{n}_i{n}_j\rangle ,$$ (2)

where n, d and c denote the orientation, the motor-induced force dipole strength, and the concentration of bound motors. When the dipoles are isotropically oriented, $\langle {\sigma }_{ij}^m\rangle ={\sigma }^m{\delta }_{ij}$, with σ^m = c〈d〉/2.

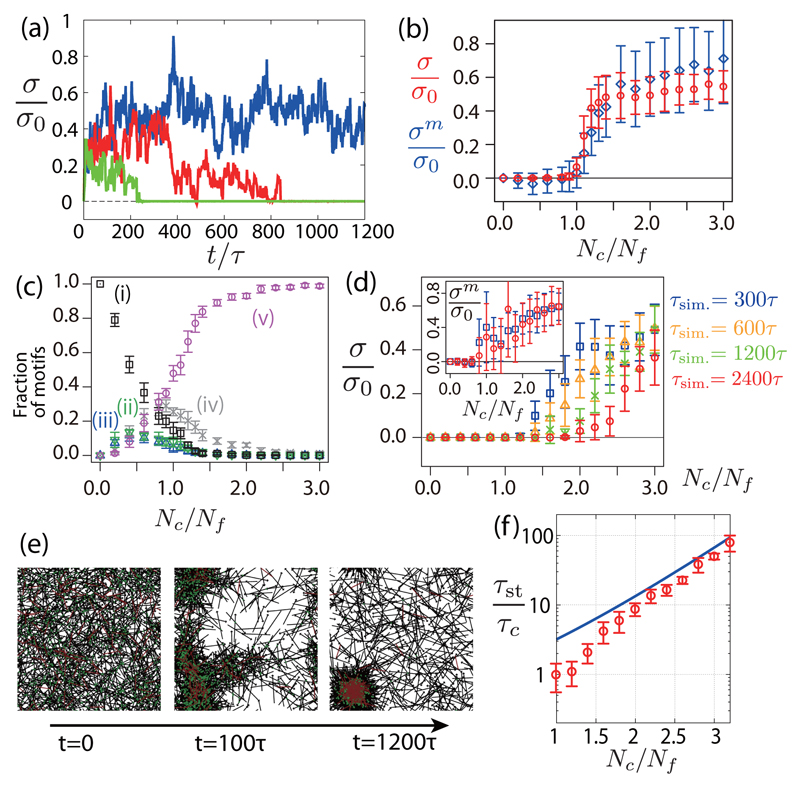
We first performed simulations without a turnover of filaments. We focus on the isotropic component of the stress σ ≡ (σ_xx + σ_yy)/2. Without cross-linker turnover, the system reaches a stationary state where the stress σ fluctuates around a finite positive value [Fig. 3(a)]. For a small number of cross-linkers (N_c → 0), no stress is generated, σ = 0, as motors are taken here to be identical. For nonidentical motors, a small isotropic stress can also be generated in the absence of cross-linkers [30]. Above a critical value of the number of cross-linkers $N_c>N_c^{*}\simeq N_f$, a transition occurs and a positive contractile stress appears in the system [Fig. 3(b)]. When $0.6N_f\underset{˜}{<}{N}_c<N_c^{*}$, filaments aggregate in clusters and hence σ ∼ 0, suggesting that the transition is associated with the network connectivity (see movies M1 and M2 in the Supplemental Material [30]). Such a transition to contractility as a function of the number of cross-linkers has been reported in in vitro reconstituted networks [10, 34], as well as network clustering [35]. The average stress within the motors σ^m is plotted in Fig. 3(b). The stress σ^m is larger than the total stress for a large number of cross-linker N_c > N_f, implying that the filament network is under compression (σ^f < 0). For large N_c, the configurations shown in Fig. 3(c)(v) dominate in the network. The saturating value of σ^m/σ₀ ∼ 0.6 is, nevertheless, smaller than the average force dipole obtained by averaging all possible filament orientations 〈d〉/(2f₀l_m) ∼ 1.0 [Fig. 2(c)]; this is because some configurations do not relax to equilibrium on the time scale of myosin turnover.

Fig. 3.

Stress in a network of motors and filaments, with and without cross-linker turnover. (a) Time evolution of the normalized stress σ/σ₀ for τ_c⁻¹ = 0, N_c = 1.2N_f (blue), τ_c = 100τ, N_c = 1.6 N_f (red) and τ_c = 100τ, N_c = 1.2N_f (green) (σ₀ = f₀l_mN_m/W²). (b) Steady-state isotropic stress σ (circles) and motor stress σ^m (diamonds) as a function of the cross-linkers number N_c for τ_c⁻¹ = 0. (c) Fraction of different configurations in Figs. 2(i)-2(v) at steady state as a function of the cross-linker number N_c for τ_c⁻¹ = 0. (d) Isotropic stress σ as a function of the cross-linker number N_c, for a finite cross-linker lifetime τ_c = 100τ, and for several simulation times (τ_sim. = 300, 600, 1200 and 2400τ). Stress within the motors σ^m is shown in the inset for τ_sim. = 300 and 2400τ. (e) Snapshots of a simulated network with cross-linker turnover (N_c = 1.2N_f, τ_c = 100τ). (f) Stress decay time τ_st as a function of the cross-linker number N_c with cross-linker turnover (τ_c = 100τ). Solid line, theoretical prediction (see the main text). Other parameters are N_f = 1000, N_m = 100, τ_f⁻¹ = 0, $k_{on}^c{\tau }_c=20$, l_f = 2l_m, W = 10l_m,τ_m = 100τ, and $k_{on}^m\tau =20$.

When cross-linkers are allowed to turn over, the average stress first reaches a positive value before decaying to zero [Fig. 3(a), red and green curves], even though the stress within the motors σ^m is still nonzero [Fig. 3(d)]. The decay of the stress correlates with the collapse of the network in an isolated cluster, where filaments accumulate [see Fig. 3(e) and movie M3 in the Supplemental Material [30]]. To evaluate the decay time scale τ_st, we fitted an exponentially decreasing function σ(t) = A exp(−t/τ_st) to the simulation results. τ_st increases exponentially with N_c for large N_c [Fig. 3(f)]. The time scale τ_st t corresponds to the relaxation Maxwell time on which the network becomes fluid due to turnover of passive cross-linkers enabling network rearrangements. With this picture, we estimate

$${\tau }_{st}\simeq \frac{{\tau }_c}{n_c^{*}}\left(e^{n_c^{*}}-1\right)$$ (3)

With $n_c^{*}=2N_c/N_f$, which accounts for τ_st for large values of N_c/N_f [Fig. 3(f)]. To obtain Eq. (3), we assume that filaments with at least one cross-linker are fixed, and only filaments with no cross-linker attachment can rearrange. We then compute the first passage time at which a filament is free from cross-linkers, starting from a configuration where the filament is attached with only one cross-linker [30]. Thus, networks with cross-linker turnover can sustain only a transient stress, on a time scale that increases with cross-linker concentration [36].

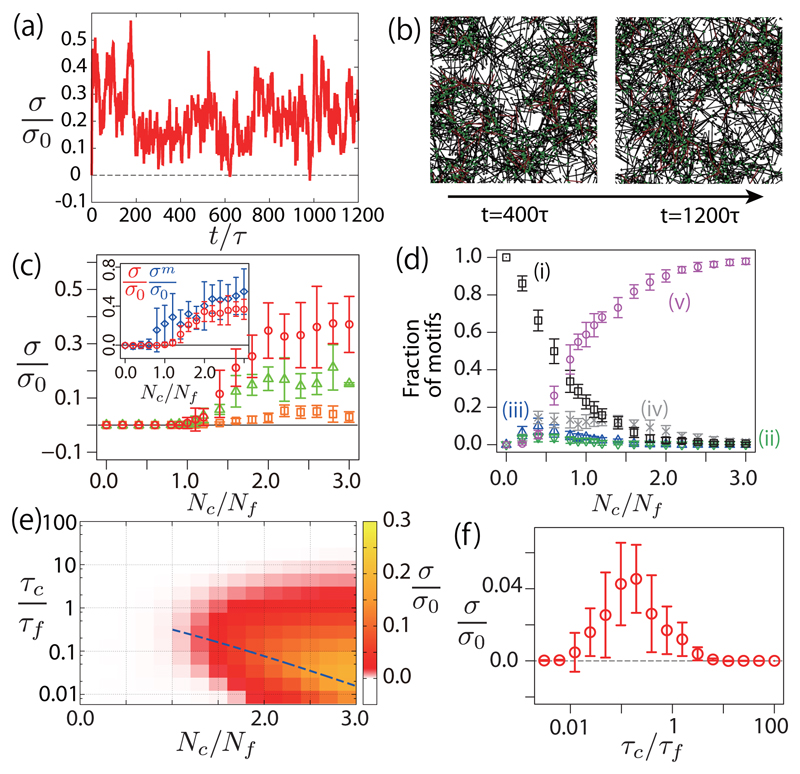
We now turn to simulations where both filaments and cross-linkers turn over. Remarkably, the network then evolves towards a steady state with a nonzero positive stress [Figs. 4a and 4b]. Introducing filament turnover prevents the clustering mechanism observed with cross-linker turnover (see movies M4 and M5 in the Supplemental Material [30]). As in the previous case, a transition from a noncontractile to a contractile network appears when the number of cross-linkers N_c is increased [Fig. 4(c)]. The stress σ deviates again from the average stress within the motors σ^m [Fig. 4(c), inset]. The dependency of the fraction of configurations as a function of N_c is qualitatively similar to the case without filament turnover [Fig. 4(d)].

Fig. 4.

Stress in a network with filament turnover. (a) Time evolution of the stress in a network with cross-linkers and filament turnover for τ_f = 100τ, τ_c = 100τ and N_c/N_f = 1.6. (b) Snapshots of the network evolution corresponding to (a). (c) Steady-state stress σ as a function of the number of cross-linkers for τ_c = τ_f = 100τ (circles), τ_c = τ_f = 10τ (triangles) and τ_c = τ_f = τ (squares). (Inset) Steady-state stress σ (circles) and motor stress σ^m (diamonds) for τ_c = τ_f = 100τ. (d) Fraction of different configurations (i)–(v) at steady state, as a function of N_c (τ_c = 100τ, τ_f = 100τ). (e) Heat map for contractile stress σ as a function of N_c and τ_c/τ_f (τ_c = τ). The broken line indicates τ_f = τ_st. (f) Stress as a function of the ratio of filament and cross-linker turnover rate (τ_c = τ, N_c = 1.6N_f). Other parameters are as in Fig. 3, except that ${\tau }_m^{-1}=0$ and $k_{on}^f{\tau }_f=20$.

We then varied the cross-linker number N_c and filament turnover time scale τ_f to obtain a phase diagram of stress generation [Fig. 4(e)]. The stress reaches a maximum for intermediate values of the filament turnover time scale τ_f ∼ τ_st [broken line in Fig. 4(e), and Fig. 4(f)]: for slow filament turnover τ_f ≫ τ_st, the network collapses in clusters due to cross-linker turnover, while for fast filament turnover τ_f ≪ τ_st, filaments are removed before motors reach a configuration where they can exert a force dipole in the network.

An optimal ratio of filament and cross-linker turnover times is therefore needed for contractile stress generation. Interestingly, experimentally measured values of turnover of actin and cross-linker times in the cell cortex, τ_f ∼ 15–45 s and τ_c ∼ 7–14 s [1] yield a ratio of turnover time scale τ_c/τ_f ∼ 0.15–1, which lies in the region of optimum stress generation near the transition cross-linker density in Fig. 4(f). It will be interesting to investigate stress generation in in vitro experiments where cross-linkers and filaments are allowed to turn over [37]. Future work will also have to investigate the role of motor multivalency, and cross-linker and motor angular elasticity in stress generation.