Automatic recognition of subject-specific cerebrovascular trees

Abstract

Purpose

An image filter designed for reconstructing cerebrovascular trees from MR images is described. Current imaging techniques capture major cerebral vessels reliably, but often fail to detect small vessels, whose contrast is suppressed due to limited resolution, slow blood flow rate, and distortions around bifurcations or non-vascular structures. An incomplete view of angioarchitecture limits the information available to physicians.

Methods

A novel Hessian-based filter for contrast-enhancement in MR angiography and venography for blood vessel reconstruction without introducing dangling segments is presented. We quantify filter performance with receiver-operating-characteristic and dice-similarity-coefficient analysis. Total extracted vascular length, number-of-segments, volume, surface-to-distance, and positional error are calculated for validation.

Results

Reconstruction of cerebrovascular trees from MR images of six volunteers show that the new filter renders more complete representations of subject-specific cerebrovascular networks. Validation with phantom models shows the filter correctly detects blood vessels across all length scales without failing at bifurcations or distorting diameters.

Conclusion

The novel filter can potentially improve the diagnosis of cerebrovascular diseases by delivering metrics and anatomy of the vasculature. It also facilitates the automated analysis of large datasets by computing biometrics free of operator subjectivity. The high quality reconstruction enables computational mesh generation for subject-specific hemodynamic simulations.

Introduction

Medical imaging is a common technique for non-invasive diagnosis of cerebrovascular diseases (CVD), which constitute the fourth leading cause of death in the United States (1). Magnetic resonance imaging (MRI) enables physicians to diagnose CVDs which often have no apparent symptoms. Crisp images also provide data for treatment planning (2). In raw magnetic resonance angiography (MRA) and venography (MRV), anatomical structures including gray and white matter overlap with the patient's cerebral vasculature hindering blood vessel detection. Small vessels like communicating arteries in the Circle of Willis are often invisible in raw MRA images due to their relatively weak contrast compared to stronger signals from larger arteries, such as the middle cerebral artery (MCA). Therefore, a method of separating different components of the MR signal without missing portions of the vessel network is needed. A vesselness filter is a digital image processing procedure for vessel contrast enhancement that aims at accentuating blood vessel contrast while eliminating other structures from the image.

In addition to vessel filtering for diagnosis, there is also a growing need for patient-specific vasculature reconstructions for computational fluid dynamics (CFD) studies. Researchers and physicians are beginning to demonstrate the benefits of cerebral hemodynamic simulations to acquire a more profound understanding of why CVDs occur, better plan endovascular interventions such as bypass surgery (3,4), or assess aneurysm (5) and arteriovenous malformation rupture risk (6). All CFD studies require subject-specific computational meshes delineating local features such as the carotid bifurcation (7–10), or extending to larger portions of the arterial tree, such as the Circle of Willis (11–13).

Numerous prior studies presented excellent Hessian-based filters for vessel segmentation (14-20). Eigenvalues of the Hessian matrices of the image intensity map can guide automatic algorithms to track network centerlines. Sato (14) proposed an algorithm based on experimental analysis of ideal tubes. The Frangi filter (15,16) has three adjustable parameters to select the best tradeoff between noise elimination and shape sensitivity. Erdt (17,18) developed a purely analytical function for fully automatic reconstruction.

All Hessian-based filters discussed so far amplify the contrast between tubular objects and their surroundings, thus enhancing elongated blood vessels while suppressing other anatomical features and noise. However, the eigenvalues of the Hessian experience sign changes in addition to wide variations in magnitude at bifurcations. This situation often causes existing filters to erroneously eliminate bifurcations, introducing dangling segments in the reconstructed network. The Shikata filter (19,20) is able to preserve network connectivity by also enhancing the contrast from plate or blob-like shapes, which favors bifurcations. Unfortunately, Shikata's improvement for bifurcations has the unwanted side effect of suppressing neighboring segments in the vicinity as pointed out by Drechsler (21). This filter behavior is undesirable because closeness of bifurcations to other branches frequently occurs in the pial network of the cerebral cortex. It would be ideal to design a novel filter, which accentuates tubular shapes, while maintaining network connectivity in bifurcations without losing neighboring segments. Accordingly, our proposed algorithm aims to achieve the following three objectives:

• Enhance the contrast of blood vessels across the entire spectrum of length scales from the internal carotid artery or superior sagittal sinus down to the pial network.

• Suppress the intensity of non-vascular tissues and reduce noise in the image.

• Preserve the connectivity of the reconstructed cerebrovascular network especially at bifurcations without creating dangling segments or suppressing neighboring branches.

This paper is organized as follows. First, MRA/MRV image acquisition parameters for vessel detection are presented. We then introduce a novel multi-scale composite filter (MCF) algorithm and its implementation. We compare its performance against previous algorithms in two phantom studies as well as in six human subject data sets. Finally, we discuss findings and indicate future research directions.

Methods

MR images were acquired from healthy volunteers to demonstrate the ability to create subject-specific reconstructions of their cerebral vasculature automatically. Although the methodology can be applied to any number of images, data and results for only six volunteers are presented to discuss performance metrics in detail. Moreover, filter performance was analyzed statistically in two additional phantom studies.

Image Acquisition

Six healthy human subjects with no known cerebral vascular disease were recruited and underwent MR imaging on a General Electric 3T MR750 scanner using a 32 channel phased array coil (Nova Medical, Inc., Wilmington, MA). MR angiograms and venograms were acquired under Institutional Review Board approval at our institution. Before the scan, stability pads were provided to reduce motion artifacts. No motion artifacts affecting the scan were observed in all six cases. For MR angiography, a 3D TOF pulse sequence was used with the following parameters: TR=26ms, TE=3.4ms, NEX=1, Flip Angle=18°, acceleration factor=2, number of slab=4, magnetization transfer=on, matrix size=512×512×408, voxel size=0.39×0.39×0.3mm³, scan time=30min.

MR venography was performed using a 2D INHANCE pulse sequence with the following imaging parameters: TR=18.5ms, TE=5.65ms, NEX=1, Flip Angle=8°, matrix size=512×248×512, voxel size=0.47×0.8×0.47mm³, scan time=15min. Automatic rigid coregistration with a one-plus-one evolutionary optimizer of the MRA and MRV was performed with the final voxel size of 0.39×0.39×0.3mm³. The MRA and MRV captured major branches of the cerebral arterial and venous systems, respectively.

Vesselness Filters

We first processed all angiograms and venograms with our MATLAB implementation of existing Hessian-based filters including Sato (14), Frangi (15,16), Erdt (17,18), and Shikata (19, 20). The mathematical background for each filter is given in Supporting Material. All filter functions use the raw 3D image intensity map I(x, y, z) as input, where x,y,z represent the spatial coordinates. The Hessian matrix, H̃(x, y, z, σ) of the image measures the curvature of the intensity at each voxel. Construction of Hessian matrices involved computations of gradients and second order derivatives, which are functions of voxel spacing in each direction, ∂x, ∂y, ∂z. To reduce noise in derivatives, Gaussian filtering was performed on the raw image as given in Eq. 1. Noise in directional derivatives around arteries shown in Supporting Fig. S1 is best suppressed by Gaussian filtering with its variance (σ-parameter) equal or close to the vessel diameter. Therefore, vesselness filters sensitive to different diameter ranges should use corresponding σ-values. The human cerebral vasculature covers multiple length scales from the 5mm range in the carotid to about 200μm in pial arteries. To address the need for multi-scale smoothing, multiple runs of Gaussian filtering with different σ-values was performed. Different Gaussian σ-settings produced distinct intensity maps, Ĩ(x, y, z, σ). Hessian matrices, H̃(x, y, z, σ), for each scale were computed as in Eq. 2. Furthermore, the three eigenvalues λ̃₁, λ̃₂, λ̃₃, of each Hessian matrix H̰(x, y, z, σ), were calculated for each voxel. Supporting table S1 shows the range of eigenvalues characterizing different geometrical shapes. For example, an ideal cylinder has λ̃₁ = 0, λ̃₂ < 0, λ̃₃ < 0. The eigenvalues permit the calculation of the image enhancement response f(x, y, z, σ, λ̃) for each of the five Hessian based filter algorithms. Each image filtered with a different σ-value leads to a different f-map. The final enhanced image intensity I_f(x, y, z) is assembled by selecting the highest voxel values among the different f-maps in Eq. 3. By electing locally the scale σ which achieves the maximum f-value, the filtered image benefits from the optimal contrast enhancement in each voxel. For example, a map of the corresponding σ-values that optimally maximized intensity in an axial image projection is shown in Supporting Fig. S2.

$$\begin{array}{c}{G}_{\sigma }(x,y,z)=\frac{1}{{(\sigma \sqrt{2\pi })}^3}{e}^{\frac{-(x^2+y^2+z^2)}{2{\sigma }^2}}\\ \stackrel{\sim }{I}(x,y,z,\sigma )=G_{\sigma }(x,y,z)\otimes I(x,y,z)\end{array}$$ Eq.1

$$\stackrel{\sim }{H}(x,y,z,\sigma )=\left[\begin{array}{ccc}\frac{{\partial }^2\stackrel{\sim }{I}}{\partial x^2}& \frac{{\partial }^2\stackrel{\sim }{I}}{\partial x\partial y}& \frac{{\partial }^2\stackrel{\sim }{I}}{\partial x\partial z}\\ \frac{{\partial }^2\stackrel{\sim }{I}}{\partial y\partial x}& \frac{{\partial }^2\stackrel{\sim }{I}}{\partial y^2}& \frac{{\partial }^2\stackrel{\sim }{I}}{\partial y\partial z}\\ \frac{{\partial }^2\stackrel{\sim }{I}}{\partial z\partial x}& \frac{{\partial }^2\stackrel{\sim }{I}}{\partial z\partial y}& \frac{{\partial }^2\stackrel{\sim }{I}}{\partial z^2}\end{array}\right]$$ Eq.2

$$\begin{array}{c}{\stackrel{\sim }{\lambda }}_1,{\stackrel{\sim }{\lambda }}_2,{\stackrel{\sim }{\lambda }}_3\leftarrow \mathit{\text{eig}}\{\stackrel{\sim }{H}(x,y,z,\sigma )\}\\ I_f(x,y,z)=\underset{\sigma }{max}f(x,y,z,\sigma ,\stackrel{\sim }{\lambda })\end{array}$$ Eq.3

Specifically, for MRA we chose fixed parameter settings, σ = {1, 2, 3, 4, 5mm}. This range spans the relevant length scale of the human arterial tree. It is worth noting that Gaussian σ-settings are not adjustable parameters, because physiological diameter ranges do not vary significantly between subjects. The recommended range gives optimal results in all human MRA we performed. In MRV, a fixed range of σ = {1, 2, 3, 4, 5, 6, 7, 8mm} was used. A wider range than for arteries was needed to cover the larger dimensions of veins.

The final scalar field I_f(x, y, z) reflects the intensity map of the enhanced image with multi-scale Gaussian filtering for each of the five filter algorithms. Some filters also have adjustable parameters as summarized in Supporting table S2. The mathematical background of a novel multi-scale composite filter (MCF) is presented next.

Multi-scale Composite Filter Function (MCF)

We discovered that gap creation in vesselness filters can be avoided by suitable combination of contrast enhancement of the Frangi algorithm with the bifurcation treatment of the Shikata algorithm. The novel multi-scale composite filter (MCF) has two stages as given in Eqs. 4 and Eqs. 5. Hessian matrices for each length scale, H̃(x, y, z, σ) are generated from smoothed intensity maps Ĩ(x, y, z, σ). For each voxel, its three eigenvalues are calculated and ordered by magnitude |λ̃₁| ≤ |λ̃₂| ≤ |λ̃₃|.

Step 1 uses the auxiliary scalar function, C₁, which is computed from the eigenvalues of the Hessian H̃(x, y, z, σ) according to a modification of the Frangi algorithm (15,16). For each scale, the C₁ value at each voxel is normalized with respect to the maximum intensity in the entire image as given by the maximum norm in Eqs. 4. Again, the maximum intensity among the different length scales is selected for each voxel. Thus, C₁ filtering produces a new normalized intensity map I_C1 (x, y, z).

To preserve bifurcations without cutting off segments, step 2 applies a modified Shikata procedure onto the normalized intensity map I_C1 (x, y, z). After a second pass of multiscale smoothing identical to step 1, the second largest eigenvalue exhibits consistent magnitude along a connected network, while the smallest eigenvalue often experiences sign changes as discussed in Shikata et al (19,20). Accordingly, the auxiliary scalar function, C₂, uses only the second largest eigenvalue λ͌₂ of Hessians, H͌(x, y, z, σ), derived from the C₁-filtered normalized intensity map I͌_C1 (x, y, z, σ). Moreover, positive second eigenvalues, λ͌₂ > 0, mark dark objects which cannot be blood vessels in MRA. Therefore, we set the final intensity to zero whenever λ͌₂ > 0 as indicated in Eqs. 5. Furthermore, we add an additional inequality λ͌₁/λ͌ < 0.25. If the inequality holds, the filter response is set to zero to suppress plate-like structures. We found in all case studies that the two inequality constraints do not induce speckle artifacts.

Step 1:

$$\begin{array}{c}{C}_1(\stackrel{\sim }{H})=\frac{(1-e^{\frac{r_a^2}{2a^2}})\cdot e^{\frac{r_b^2}{2b^2}}\cdot (1-e^{\frac{r_S^2}{2c^2}})}{{\Vert (1-e^{\frac{r_a^2}{2a^2}})\cdot e^{\frac{r_b^2}{2b^2}}\cdot (1-e^{\frac{r_S^2}{2c^2}})\Vert }_{\infty }}\\ r_A=\frac{|{\lambda }_2|}{|{\lambda }_3|};r_B=\frac{|{\lambda }_1|}{\sqrt{|{\lambda }_2{\lambda }_3|}};r_S=\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}\\ I_{C1}(x,y,z)\leftarrow \underset{\sigma }{max}{C}_1(\stackrel{\sim }{H}(x,y,z,\sigma ))\end{array}$$ Eq.4

Step 2:

$$\begin{array}{c}{\stackrel{\sim }{\stackrel{\sim }{I}}}_{C1}(x,y,z,\sigma )=G_{\sigma }(x,y,z)\otimes I_{C1}(x,y,z)\\ {\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_1,{\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_2,{\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_3,\leftarrow \mathit{\text{eig}}\{\stackrel{\sim }{\stackrel{\sim }{H}}(x,y,z,\sigma )\}\\ C_2(\stackrel{\sim }{\stackrel{\sim }{H}}(x,y,z,\sigma ))=\{\begin{array}{cc}0& {\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_2>0\\ 0& {\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_1/{\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_2<0.25\\ \frac{-{\sigma }^2{\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_2}{{\Vert -{\sigma }^2{\stackrel{\sim }{\stackrel{\sim }{\lambda }}}_2\Vert }_{\infty }}& \mathit{\text{else}}\end{array};I_{\mathit{\text{MCF}}}=\underset{\sigma }{max}{C}_2(\stackrel{\sim }{\stackrel{\sim }{H}}(x,y,z,\sigma ))\end{array}$$ Eq.5

For each length scale, the sequential application of C₁ and C₂ filter components produces a final scalar value at each voxel. The length scale leading to the highest intensity is selected for the final intensity I_MCF for each voxel. The three dimensional matrix of maxima, obtained perhaps with different σ for each voxel, gives the vessel enhanced intensity image. The novel filter also has three adjustable parameters (a, b, c) to allow for filter tuning.

Note that both the local C₁ and C₂ functions are normalized with highest intensity found in the entire image. Normalization also ensures that the relative contributions from the two auxiliary functions are commensurate.

The value of the scalar I_MCF at each voxel signifies the probability that it belongs to the vascular network. At vessel centerlines, the I_MCF values assume a local maximum. The centerline of the vascular network is the locus of extrema in the I_MCF map. The centerline trajectories form three dimensional space curves that trace the subject's vascular trees.

Computational Mesh Generation and Validation

Filtered images were processed to create logically connected networks for vectorized display or computational purposes. We applied the filters and the segmentation process to the human data for reconstructing computational meshes representing subject-specific cerebral vascular trees. Subject-specific computational meshes are needed for individualized high quality visualization of the angioarchitecture (27), solid mechanic injury simulations (28) or hemodynamic CFD simulations (29,30). The workflow for subject-specific automatic mesh generation is depicted in Fig. 1.

Figure 1.

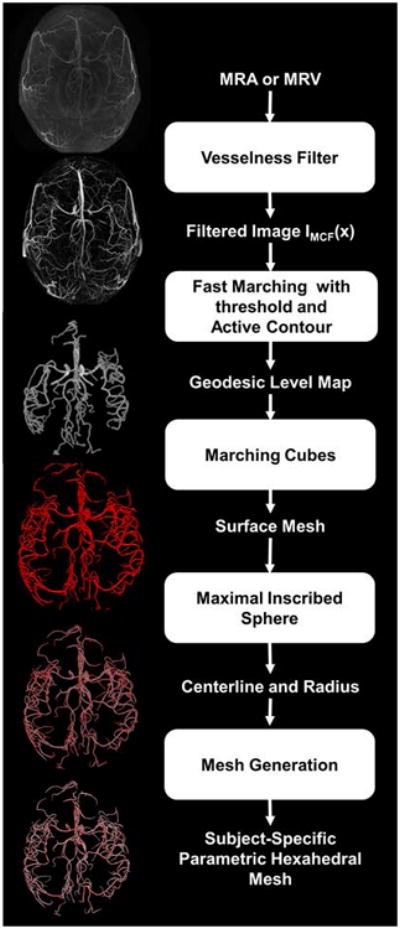
Workflow for automatic computational mesh generation of subject-specific vascular trees. First, raw MRA/MRV images are processed with vesselness filters for contrast enhancement of the cerebral vessel network. The filtered image crisply outlines the vasculature and is used as input for mesh generation. The fast marching algorithm with a cutoff threshold creates a connected domain in which geodesic levels are computed for each voxel with the zero level at the edges. The geodesic level map is then scanned by the marching cubes algorithm to extract physical coordinates of the zero level. This information is used to build a connected surface mesh enclosing the cerebral vasculature. We apply the maximal inscribed sphere algorithm onto the surface mesh to retrieve diameter and centerline information. Parametric hexahedral meshes can then be generated using the diameter and centerline for computational fluid dynamics studies.

First, we create a distance map between the vessel centerlines and the vessel surface, where a zero level set corresponds to the vessel walls. The fast marching algorithm with cutoff threshold (intensity threshold=0.01) was used to create a binary mask of the connected vascular tree (22). The binary mask delineates a connected domain. An active contour procedure is used to calculate the geodesic level of each interior point, in which the computed levels measure the distances of a point to the vessel wall, whose outer edges are assigned a zero level (23). With the entire image domain now parameterized in terms of wall distance, the marching cubes algorithm retrieves smooth physical coordinates of the vessel walls (40). Note that physical coordinates for the surface obtained by marching cubes is not limited to the original discrete voxel grid spacing. Optionally, isolated dangling surfaces that are not connected to the main arterial tree can be discarded. This situation typically affects external surface arteries. Because of the special attention to preserving connectivity with the C₂ filter, dangling segments do not occur in the territory of the main cerebral arteries.

The surface enclosing the arterial tree serves as input for unstructured mesh generation (25). Alternatively, parametric volumetric meshes (26) can be created with the help of centerline and diameter information. Coordinates of the centerline trajectory as well as corresponding vessel radii were tracked with the maximal inscribed spheres method (24). By using the fast marching algorithm with cutoff threshold, our method could eliminate the tendency to overestimate diameters in the maximal inscribed sphere method (39). With precise centerlines and radii, body-fitted smooth hexahedral computational meshes of the entire arterial trees were generated (33). Venous trees were created similarly from MRV data.

Validation

Volume, number of segments, as well as total length of the reconstructed arterial and venous trees are used as metrics for quantitative comparison of the filter performance. A segment is defined as a cylindrical connection between two adjacent centerline points. For further validation, we created two phantoms and rigorously tested filter performance in detecting blood vessel, connectivity at bifurcations, and diameter reconstruction against a ground truth reference.

Results

Image enhancement of MRA and MRV data from healthy volunteers

All filters were custom-coded in MATLAB on an Intel Xeon CPU E5645(x00040)2.40 GHz computer. The CPU time for existing filters is approximately 60s. The sequential implementation of the MCF consumes less than twice the CPU time. The top row of Fig. 2 shows an axial, sagittal, and coronal view of the original MRA image acquired from the first of the six volunteers. Each view is a maximum intensity projection displayed with its maximum and minimum filter response as the contrast window. The middle cerebral arteries (MCA) and external cerebral arteries appear the brightest. The sagittal view also depicts the major branches of the anterior (ACA) and posterior cerebral artery (PCA) territories. The Circle of Willis (COW) can only be seen partially in the coronal view. The thin anterior communicating (ACOM) and posterior communicating arteries (PCOM) are barely visible in the original MRA as highlighted in the magnified view in Fig. 2 with arrows indicating their usual anatomical position. In general, smaller arteries, particularly in the ACA and PCA territory, are hard to discern in the raw image.

Figure 2.

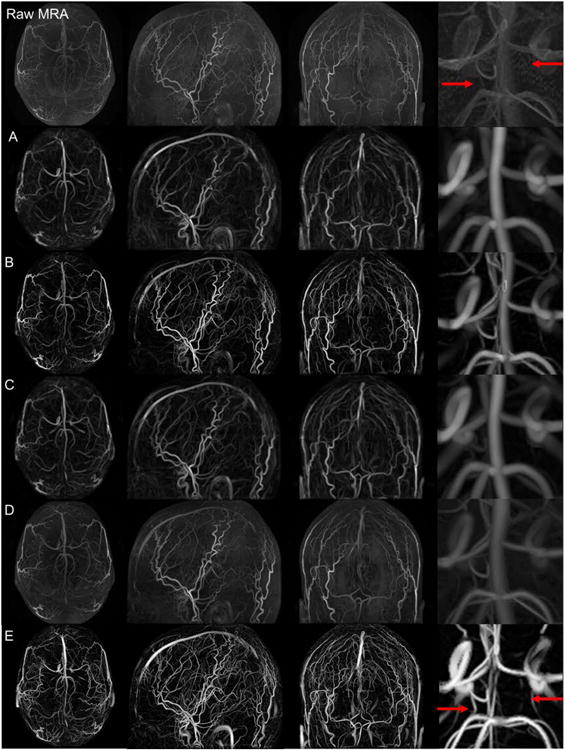
Maximum intensity projections of the raw MRA and five filter responses (A-E) in axial, sagittal, and coronal views as well as zoomed in detail around the circle of Willis. Top row. Raw MRA images. Filtered images from: A. Sato, B. Frangi, C. Shikata, D. Erdt, and E. Multi-scale composite filter (MCF). The MCF (frame E) crisply delineates the arterial tress down to the pial network and successfully suppresses non-vascular tissue signals and background noise. The magnified views in the right column show that the PCOMs are not detectable in the raw images (red arrows in top row). The MCF clearly depicts both PCOMs (red arrows in row E).

The images in Fig. 2A to 2D display axial, sagittal and coronal views produced by Sato, Frangi, Shikata and Erdt filters, respectively. The Sato filter in Fig. 2A suppresses noise and soft tissues, while enhancing blood vessels as seen most clearly in the coronal view. The Frangi algorithm offers tunable control. Its application with parameters, a=0.5, b=0.5, c=0.05, in Fig. 2B sharpens vessels better than the Sato filtered image. Structures not belonging to the cerebrovascular network such as gray and white matter are successfully suppressed in the Shikata filter as shown in Fig. 2C. The Erdt filter, which has previously been successful in computed tomography images, did not improve the vascular network contrast substantially as depicted in Fig. 2D.

Results for the novel MCF with parameters, a=0.5, b=0.5, c=0.05, are shown in Fig. 2E. These parameters can easily be set in the MATLAB implementation and gave the best results in all six case studies. The MCF clearly produces the brightest outline of arterial trees. The magnified view of the COW also clearly depicts the PCOMs, which are entirely missed in the raw images, and are hardly discernable in prior vesselness filters. This result demonstrates that MCF not merely sharpens vessel contrast, but more importantly crisply delineates small vessels whose signals are too faint to be seen with prior filtered or raw images. MCF is also able to reconstruct a good portion of the cortical surface network, which consists of small bifurcating pial arteries that are entirely missed in all existing filter techniques. The bright and crisp delineation of arterial trees show that the vessel intensity is enhanced for all diameters ranging from the large carotid arteries down to small pial vessels of about 400μm in diameter. The novel MCF also preserves the contrast around bifurcations, which is an essential feature for maintaining network connectivity without introducing dangling segments.

Statistical analysis of filter performance

To systematically evaluate the performance of the filters and to quantify the advantage of the novel MCF, we conducted receiver operating characteristic (ROC) analysis, dice similarity coefficient analysis, surface distance errors, and positional offsets with two artificially generated image phantoms. For the ROC analysis, thresholds, I_threshold, covering the entire range between zero and unity were chosen, and the number of correctly detected voxel belonging to vessels were counted. We also counted false positives, which is equal to voxels erroneously assigned to vessels. High threshold levels decreased the number of false positives, but miss many vessels. In general, there is a trade-off between specificity (avoidance of false positives) and recognition rate (fraction of detected vessels). The phantoms offer exact vessel coordinates and diameters as ground truth reference for objectively evaluating filter performance.

3D artificial tube network (lattice phantom)

The first phantom consists of a rectangular lattice of tubular objects embedded in a spherical domain to emulate a configuration of blood vessels embedded inside a brain image. Fig. 3 depicts the original phantom lattice, the filter responses and the ROC curves obtained for each filter. Fig. 3A shows that the Sato response loses signals in bifurcations and that it was unable to suppress the surrounding sphere. The Frangi filter in Fig. 3B suffers from artifacts at the intersection of the sphere with tubes. The quality of intensity enhancement achieved by the Shikata procedure is poor as shown in Fig. 3C. The lattice structure detected by the Erdt filter in Fig. 3D is severely distorted by the surrounding sphere. The image filtered by MCF in Fig. 3E renders the lattice with bright intensity. There is slight blurring where tubes and background intersect. The ROC curve confirms that the MCF filter has the best statistical performance with the analysis of area under the curve of 0.94. Moreover, for every threshold, the MCF curve is pareto-optimal, meaning that it has higher or equal true positives, for a given false positive level. The MCF also has the highest dice coefficient of 0.89 among all filters, including Frangi with 0.85, Sato with 0.82, Shikata with 0.75 and Erdt with 0.63.

Figure 3.

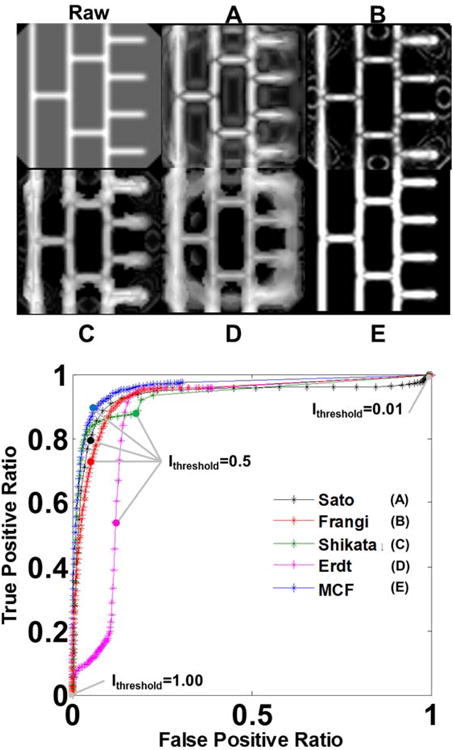
Statistical analysis of filter performance in a 3D lattice phantom. Top left, raw phantom image representing a tubular network inside a spherical background. A. Sato filter response. B. Frangi filter response. C. Shikata filter response. D. Erdt filter response. E. Multi-scale composite filter (MCF) response. The presence of the backdrop introduces noise in all filters. Visual inspection shows that the MCF produces the sharpest delineation of the vessel lattice. The ROC analysis, summarized at the bottom, quantifies the performance of the five filters (A-E) by computing the ratio between true positives (voxels categorized as vessels in both raw and filtered images) and false positives (voxels not categorized as vessels in the raw image but identified as vessels in the filtered image). Continuous ROC curves track computed true positive and false positive ratio for every threshold level between zero and unity (0<I_threshold<1). The MCF ROC curve (E) is pareto-optimal with respect to all prior filters at all threshold levels (A-D).

We further analyzed the performance of all filters with respect to connectivity in this case study with ten bifurcations. The Sato and Frangi filters give faint signals for all bifurcations as seen in Fig. 3A and 3B. Moreover, the two filter algorithms introduce dark stripe artifacts close to bifurcations. The Shikata, Erdt and MCF filters have no stripe artifacts. We counted the number of correctly detected bifurcations as well as false positives with respect to different intensity thresholds that mark a cutoff above which a voxel is considered to belong to a blood vessel. We count a bifurcation as connected when all six neighboring voxels are categorized as members of blood vessels. This analysis summarized in Table 1 demonstrates that the MCF correctly labeled all ten bifurcations without any false positives for the selected intensity thresholds.

Table 1.

Number of bifurcations detected from filter responses in phantom studies. Intensity thresholds mark the cutoff point in intensity above which a voxel is considered to belong to a blood vessel.

	Intensity Threshold	Sato	Frangi	Shikata	Erdt	MCF
Lattice Phantom (with 10 bifurcation)	0.1	10	10	10	10	10
	0.3	10	0	10	10	10
	0.5	0	0	10	10	10
	0.7	0	0	0	10	10
	0.9	0	0	0	0	10
Network Phantom (with 114 bifurcation)	0.1	21	58	13	65	110
	0.3	18	55	11	53	98
	0.5	15	47	9	47	86
	0.7	12	43	6	45	78
	0.9	10	40	3	44	75

We further used the ground truth diameter information to measure the fidelity of diameter reconstruction. All tubes in the artificial tube network had a diameter of 5 voxels. Diameter reconstruction with the Sato filter results in average of 5.2 with standard deviation of 0.3, the Frangi filter with 5.1±0.2, the Shikata filter with 5.3±0.5, and the Erdt filter with 5.4±0.2. The MCF with 5.1±0.1 was closest to the correct value.

3D microcirculation (network phantom)

The second phantom establishes a more physiologically realistic ground truth scenario against which filter performances were evaluated. It consists of a 3D microcirculatory network overlapped with an oval shaped backdrop to resemble arterioles within a cerebral sulcus. Bifurcating trees and branches were generated by a constructive growth algorithm to emulate the topology of the cerebral microcirculation (34, 41). The MCF filter eliminates the background as shown in Fig. 4a. The other filters erroneously characterize the sulcus as blood vessels. This artifact is especially severe in the Shikata filter. The Frangi filter suppresses the background, but fails to amplify vessel intensity. The MCF filter correctly identifies all arterioles, and eliminates the backdrop as desired. The ROC curve in Fig. 4b also indicates that the MCF has the best statistical performance with an area under the curve of 0.81. The MCF excels over all other filter by detecting more or equal vessels at any false positive level, making the MCF pareto-optimal. The dice coefficient similarity analysis of the MCF gives 0.73, Frangi with 0.68, Erdt with 0.64, Shikata with 0.62 and Sato with 0.56.

Figure 4.

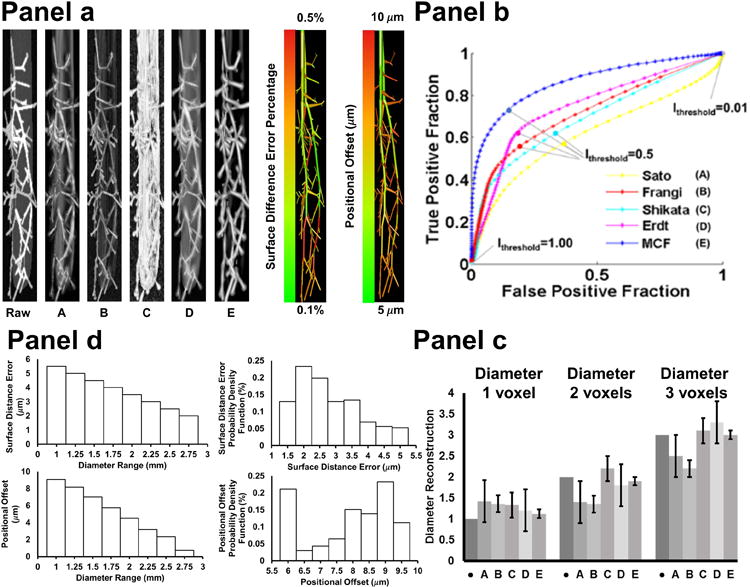
Visual and quantitative comparison of filter performance in a 3D network phantom study. (Panel a. top-left). The phantom consists of a microvascular tree embedded in an oval object mimicking a cerebral sulcus. A. Sato filter response. B. Frangi filter response. C. Shikata filter response. D. Erdt filter response. E. Multi-scale composite filter (MCF) response. The sulcus raises the noise level and introduces false vessel positives in all filters. Surface distance error and positional offset were analyzed as ground truth comparison with further details given in Panel c. (Panel b). The entire range of possible thresholds, (0<I_threshold<1), was evaluated to plot the ROC curve for each filter. The ROC curves show that the MCF has the best trade-off for true positives at any level of false positives for vessel characterization, hence the MCF is pareto-optimal.

(Panel c). Bar graph summarizes the quality of diameter reconstruction of filter (A-E). Dark gray bar with dot marks the true diameter (1, 2, and 3 voxels respectively). The MCF response (E) is closest to the ground truth diameters.

(Panel d). Top bar graphs show the surface difference error between ground truth and segmentation and the probability density functions of the surface distance error. The largest surface difference error is 5μm. Bottom right bar graphs show the positional offset between the ground truth and segmentation. The maximum positional offset is 10μm from the ground truth. This shows that imaging and segmentation do not introduce significant errors in vessel diameters and position.

We further measured how many of the 114 bifurcations in the microcirculatory phantom were correctly detected by each filter. Using the same criteria introduced above, the number of correctly detected bifurcation connections are given in Table 1 for each filter. All filters lose some bifurcations in the smallest diameter range (d∼1 voxel). However, the MCF always surpasses other algorithms for all threshold levels without creating false positives.

The microcirculatory network phantom also featured branches with thin diameters between one to three voxels, a dimension close to the theoretical image feature threshold. Results of the statistical analysis for three diameter ranges (1-3 voxels) are summarized in Fig. 4c. It demonstrates that all filters tend to overestimate the size of the thinnest branches (d=1 voxel). For three voxels thick vessels (d=3 voxels), reconstruction with Sato filter gives a mean value of 2.5 voxels with standard deviation of 0.5 voxels, the Frangi filter 2.2±0.2, Shikata 3.1±0.3, and Erdt 3.3±0.5. The MCF gave 3.0±0.1, which is again the closest estimate. The bar graph in Fig. 4c also indicates that diameter reconstructions with Sato and Erdt filters have very large variance. The Frangi underestimates vessel diameters in the two and three voxel range. The diameter reconstruction of the Shikata response was limited to vessels outside the sulcus, since the filter wrongly recognizes the sulcus as a blood vessel, preventing diameter reconstruction of vessels in the interior of the domain. We also found that MCF overestimates vessels of one voxel in diameter by 10%, which is inevitable when using Gaussian smoothing.

Surface distance error and positional offset

Surface distance errors and positional offset were further analyzed in the 3D microcirculation phantom. The phantom serves as an ideal reference, because the true diameter and coordinates of the original object were exactly known and could be compared objectively to filtered artifacts. We rigorously computed for each vascular segment the surface distance error (SDE) between the original network coordinates and the coordinates of the MCF segmented model. Fig. 4a also shows a color coded SDE map, according to which, surface distance error with MCF is less than 0.5% everywhere, which is an acceptable deviation. Fig. 4d provides the statistical analysis of the SDE, indicating that relative surface distance errors are largest in smallest vessels. Since one voxel thick vessels are equal to the imaging threshold, this error cannot be eliminated entirely. We also computed the probability density function as depicted in Fig. 4d.

Moreover, results of the analysis of positional offset due to imaging, filtering and segmentation are summarized in a color coded map in Fig. 4a. Here, the exact position of the centerlines in the ground truth network was subtracted from the locations of the segmented network. The norm of the difference was plotted for all segments, indicating that the largest offset occurs also at smaller vessels as expected. The positional error is always less than 10μm as shown in Fig. 4d.

These two results demonstrate that the MCF and segmentation do not induce significant position or diameter errors. Deviations from the ground truth at the resolution level are minor and unavoidable.

Subject-Specific Computational Meshes from MRA and MRV

We also quantified filter performance using subject-specific image data in a sample group of six subjects. The workflow of Fig. 1 illustrates steps for generating three dimensional computational meshes from filtered images of six volunteers. The networks reconstructed with prior filters encompass only the COW and the initial segments of the ACA, MCA, and PCA (data not shown). The ACA territory is poorly reconstructed in all previous filters. By contrast, the MCF recognizes the arterial tree including a large portion of the pial network while maintaining physiological network connectivity without dangling segments. Fig. 5 shows the raw image data and the vessel enhanced intensity map, as well as reconstructed arterial and venous trees for six subjects. The reconstructed trees clearly delineate the subject-specific vascular topology. The cortical surfaces shown in Fig. 5 were reconstructed using the method introduced by Dale et al (32).

Figure 5.

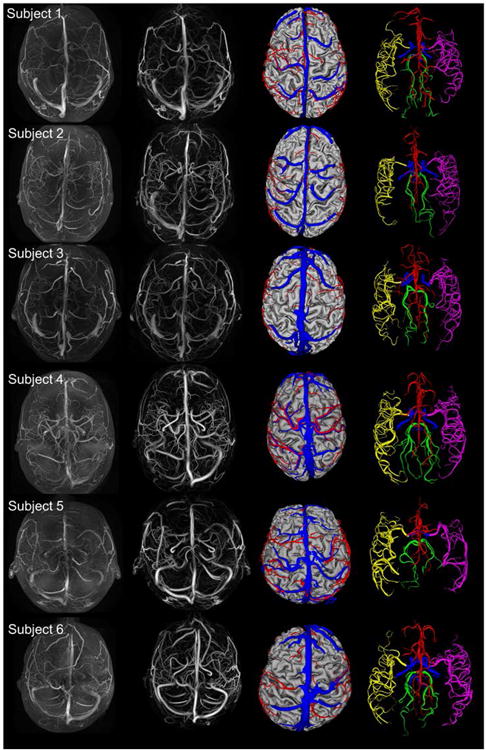
Reconstruction of the arterial and venous angioarchitecture from six subjects. First column. Superposition of raw MRA and MRV images. Second column. Superposition of filtered MRA and MRV images showing both the arterial and venous signal enhancement. Third column. Axial display of subject-specific arterial (red), venous (blue) and cortical surface meshes (grey). Fourth column. Arterial surface meshes labeled according to main territories, ACA (red), RMCA (purple), LMCA (yellow), PCA (green), and ICA (blue).

Quantification of filter performance with in vivo image data

Number of segments, length, and volume of the segmented vascular trees were used as metrics to assess filter performance. The size of the reconstructed vasculature was estimated by computing the number of segments, total length of segments and the volume enclosed by the surface mesh. Larger and longer trees indicate that a larger portion of the subjects' vascular network was reconstructed by the filter. All statistics are listed in Table 2, including total number of segments, arterial length, venous length, arterial volume, and venous volume.

Table 2.

Total segment numbers, length and volume of the segmented arterial and venous tree.

Number of Arterial Segments
	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6	Average
Sato	1213	1486	1534	1653	1518	1547	1487
Frangi	3254	2814	2943	3136	3194	3206	3087
Shikata	2859	2253	2456	2641	2363	2414	2493
Erdt	837	782	868	562	756	751	755
MCF	6471	5204	5894	6183	5518	5712	5827
Number of Venous Segments
	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6	Average
Sato	535	516	485	526	494	505	505.0
Frangi	657	611	626	635	666	711	646.7
Shikata	333	322	358	344	414	281	338.3
Erdt	236	214	259	243	226	212	226.7
MCF	1211	1426	1194	1543	1697	1460	1421.8
Arterial Length (m)
	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6	Average
Sato	1.2	1.5	1.5	1.7	1.5	1.5	1.21
Frangi	3.3	2.8	2.9	3.1	3.2	3.2	3.25
Shikata	2.8	2.3	2.5	2.6	2.4	2.4	2.85
Erdt	0.8	0.8	0.9	0.6	0.8	0.8	0.83
MCF	6.5	5.2	5.9	6.2	5.5	5.7	6.47
Venous Length (m)
	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6	Average
Sato	0.5	0.5	0.5	0.5	0.5	0.5	0.51
Frangi	0.7	0.6	0.6	0.6	0.7	0.7	0.65
Shikata	0.3	0.3	0.4	0.3	0.4	0.3	0.34
Erdt	0.2	0.2	0.3	0.2	0.2	0.2	0.23
MCF	1.2	1.4	1.2	1.5	1.7	1.5	1.42
Arterial Volumes (mL)
	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6	Average
Sato	1.29	1.01	1.34	1.23	1.13	1.18	1.20
Frangi	1.76	1.44	1.58	1.73	1.38	1.62	1.59
Shikata	1.43	1.18	1.35	1.39	1.23	1.31	1.32
Erdt	0.59	0.51	0.83	0.48	0.55	0.73	0.62
MCF	6.13	5.84	5.91	5.74	8.32	4.57	6.09
Venous Volumes (mL)
	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6	Average
Sato	4.05	4.4	8.28	5.34	5.28	6.79	5.69
Frangi	4.83	4.31	8.32	4.79	4.23	7.21	5.62
Shikata	3.52	3.34	3.49	3.58	3.46	3.49	3.48
Erdt	3.57	3.62	3.96	3.67	3.58	3.24	3.61
MCF	20.28	23.02	24.65	22.96	23.75	29.09	23.96

On average, the MCF detects arterial trees with more than 6000 segments and a total length exceeding five meters. Statistics for each of the six individuals are summarized in the bar charts of Fig. 6 and the tabulation of Table 2. The number of segments and length of the arterial networks identified with MCF are at least three times more complete than the best of the prior filters. A similar advantage of three times the number of segments and three times of length is achieved in the venous trees. Moreover, the novel MCF successfully segmented on average three times larger arterial volumes with 6.09 mL. By comparison, Frangi filter only recovered a tree with 1.59 mL, Shikata filter with 1.32 mL, Sato filter with 1.20 mL, and Erdt filter with 0.62 mL. We also measured the volumes of the venous trees. The MRV captured major branches of the cerebral venous system, including the superficial and deep structures. The novel MCF detects 20.28 mL of the venous volume for subject 1. The Frangi filter gives a venous tree with only 4.83 mL, Erdt filter with 3.57 mL, Sato filter with 4.05 mL, and Shikata filter with 3.52 mL. The MCF typically achieved three times higher volume recognition rate compared to other filters.

Figure 6.

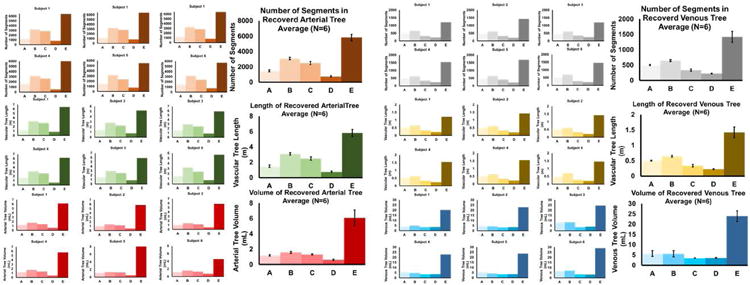
Quantification of recognition rate of arterial and venous trees in numbers of segments, length, and total volume for six human subjects. The top bar graphs show the number of segments in the arterial and venous trees. MCF gives on average 6000 segments which is roughly three times the number found by the second best filter. The middle bar graphs show that the length of segmented arterial tree is about 5 meters, the venous trees measured 1.4 meters. The MCF trees are 3-5 times longer than the existing filters. The bottom bar graphs show the volumes of the arterial and venous trees reconstructed for each subject with each filter (A-E). The volume segmentation gives 6.4 ml arterial tree and 21 ml in the venous tree. These volumes are three to five times higher in the MCF compared to previous filters. The MCF excels above other filters in all metrics including number of segments, length and volume.

These metrics show that MCF surpasses all prior vesselness filters. The MCF also preserves network connectivity which greatly simplifies the labeling of vascular territories. Color coded ACA, MCA, and PCA territories for the six subjects are depicted in Fig. 5. The labeling shown here was done manually, but can readily be automated. The statistics of volume, surface area, mean diameter and segment number for each territory are summarized in Table 3. The data also show that the MCF diameter reconstruction of main arteries and pial vessels agree with values reported in the literature (35-37). The agreement supports the notion that the MCF segmentation procedure does not induce diameter artifacts.

Table 3.

Statistics of vascular territories for model construction of six subjects.

	Subject 1	Subject 2	Subject 3	Subject 4	Subject 5	Subject 6
Surface Area (mm2)
ACA	5229.6	3483.7	4341.5	3951.9	2830.1	3655.6
MCA	11663.6	10115.9	11476.7	13160.6	11342.8	10620.3
PCA	2813.9	2227.8	2505.0	3294.9	1720.5	2670.3
Total Length (mm)
ACA	1512.9	1000.6	1331.9	996.3	741.4	1040.5
MCA	3490.2	2904.7	3343.2	3560.9	2682.2	3197.5
PCA	866.6	646.2	591.6	919.1	474.4	761.6
Total Volume (mm3)
ACA	1483.3	912.0	1374.7	1544.8	1409.6	1573.2
MCA	3360.3	3147.8	3047.9	3195.6	4082.8	4081.8
PCA	992.0	636.1	1222.6	1999.1	878.2	1220.1
Number of Segments
ACA	4286	2848	4323	2435	1878	4210
MCA	7034	8325	9862	9239	6293	13489
PCA	2568	1886	1680	2385	1294	3225
Mean Diameter (mm)*
ACA	2.2±0.1	2.1±0.2	2.3±0.1	2.2±0.3	2.3±0.3	2.2±0.2
MCA	2.8±0.3	3.1±0.3	3.2±0.3	2.9±0.2	3.2±0.1	2.9±0.3
PCA	2.1±0.2	2.2±0.2	2.3±0.1	2.1±0.1	2.3±0.1	2.1±0.2
Pial	0.42±0.01	0.41±0.02	0.39±0.03	0.41±0.01	0.40±0.02	0.41±0.01

^*Reported values in (35-37) in 100 cadaver studies and imaging studies show the average diameter for ACA 2.2mm, MCA 2.7mm, PCA 2.1mm, 1000μm > pial >200μm. The reconstructed diameters for ACA, MCA, and PCA compares well with reported values. For pial vessels, our reconstructed diameters fall in the range of reported values. Vessels smaller than 0.4mm cannot be visualized due to image resolution.

Discussion

Automatic vessel segmentation aims at reconstructing the entire cerebral vascular tree from MR images by enhancing blood vessel contrast across multiple length scales. Prior vesselness filters often fail to detect small tortuous vessels close to bifurcations resulting in incomplete segmentation of vascular trees. The novel MCF preserves the connectivity by combining the advantages of two separate contrast enhancement functions C₁ and C₂. C₁ identifies tubular objects, while C₂ magnifies vessel contrast without creating dangling segments. The multi-scale composite filter optimizes the contrast of the cerebral angioarchitecture across all length scales. Normalization along with thresholded levelsets in the fast marching achieved reasonably accurate diameter reconstructions.

The computational time for the MCF is roughly twice than that of the previous filters with total CPU time under 99s. The computational time could be further accelerated with parallel processing and GPU computation (31). Filter performance in terms of contrast enhancement, connectivity, surface distance error and positional offset was quantified in phantom studies. In all cases, MCF achieved the best score outperforming all prior algorithms.

We also performed expert manual delineation of the Circle of Willis. The ground truth was established by a neurosurgeon with more than 20 years of experience. The manually traced trajectory of major arteries in the raw image was compared to automatically reconstructed centerlines of the MCF image. No significant positional offset could be detected between manual and automatic segmentation (data not shown). However, the surgeon failed to identify significant structures such as the left and right posterior communicating arteries (PCOM) due to extensive blur in the raw image. This can be seen in Fig. 2. On the other hand, the MCF image clearly depicted both PCOMs as shown with arrows in Fig 2E. A similar limitation of the expert manual delineation was observed when trying to trace pial arteries (data not shown). Weak contrast impeded manual delineation of pial vessels, which only came to light in the MCF enhanced image. Given the inability even to trace prominent arteries in the COW by hand, we chose not to proceed with further manual delineation as a test for filter performance. Moreover, the large number of more than 6000 segments in each subject poses a practical limit on manual segmentation by expert surgeons or radiologists.

We successfully segmented subject-specific arterial and venous trees from in vivo data acquired in healthy human volunteers. The novel filter segmented a three times larger portion of the arterial and venous trees than any previous filter. The MCF enables the fully automatic reconstruction of the cerebrovascular angioarchitecture without requiring user supervision or input. The reconstructed subject-specific computational meshes can be used for CFD simulations of blood flow in the entire arterial or venous tree (39).

Limitations

The quality of the reconstructed vessel networks depend on the resolution of the acquired images. In the imaging study, the cerebral microcirculation could not be visualized since it is well below the image resolution of current MR scanners. The reconstruction of the venous network also suffers from the limited image quality because of slower venous flow. Because a 2D INHANCE sequence was used to acquire MRV, inter-slice discontinuity may diminish the reformatted 3D image quality. This limitation could be eliminated by using partially overlapping slices (i.e., negative slice gap) at the expense of increased number of slices to cover the brain, or by a 3D pulse sequence at the cost of longer acquisition time. The original MRA image contained some signals coming from the veins; these were eliminated by subtracting segments from the arterial image that are also registered in the MRV.

Conclusion

A novel multi-scale composite filter utilizes the eigenvalues of the Hessian matrix to achieve blood vessel enhancement over all relevant length scales. Our results confirm the feasibility of generating subject-specific computational meshes, with sufficient detail to track the ACA, MCA, and PCA territories in individual subjects almost down to the level of the pial network. Enhanced images provide more complete information about the pial blood supply for physicians to assess the status of the patient's cerebrovascular angioarchitecture.

Moreover, our filtering process enhances both large and small vessels without compromising network connectivity. The MCF allows the fully automatic reconstruction of major portions of the cerebrovascular network for the generation of high quality subject-specific computational meshes. The proposed automatic image segmentation could also be useful for computer-aided reconstruction of vascular trees to extract biometrics associated with pathological conditions in large data sets without variations caused by operator subjectivity (38). The novel filter will enable future studies on hemodynamic simulations of blood flow through the subject-specific angioarchitecture. This technology will be useful in predicting the outcome of planned intervention such as bypass surgery, stenting, or coiling of aneurysms.