Modeling and Simulation of the Effects of Cyclic Loading on Articular Cartilage Lesion Formation

Abstract

We present a model of articular cartilage lesion formation to simulate the effects of cyclic loading. This model extends and modifies the reaction-diffusion-delay model by Graham et al. [20] for the spread of a lesion formed though a single traumatic event. Our model represents “implicitly” the effects of loading, meaning through a cyclic sink term in the equations for live cells.

Our model forms the basis for in silico studies of cartilage damage relevant to questions in osteoarthritis, for example, that may not be easily answered through in vivo or in vitro studies.

Computational results are presented that indicate the impact of differing levels of EPO on articular cartilage lesion abatement.

1 Introduction

Cartilage is a tissue that thrives in a mechanically-active environment and has been well established to be biologically responsive to physical stimuli. The effect of dynamic loads on articular cartilage is partly of interest because periodic changes in loading profiles are physiological (e.g., walking, running, etc.) and pertinent to cartilage health and disease progression.

Articular cartilage that lines the surfaces of lower extremity joints in humans is routinely exposed to dynamic contact stresses in the 1–5 megapascal range [16]. At frequencies and rates commonly encountered in activities of daily life, stress levels in this range are not only tolerated by cartilage, but are necessary for long-term stability [1]. On the other hand, stresses much above 5 MPa, or stresses delivered outside physiologic norms of frequency or rate, can lead to progressive cartilage degeneration, a hallmark of osteoarthritis (OA) [25]. These observations have focused OA research on the cellular and molecular basis of cartilage mechano-responses. Although a great deal of progress has been made in understanding short-term responses at the tissue level, it is still unclear how these processes unfold to cause the slowly developing, organ-wide breakdown that occurs in osteoarthritic joints. As a result, though mechanical stresses probably play a decisive role in many cases of OA, there are currently no therapies targeting biologic mechanoresponses.

While the chronic effects of over- or under-loading can be studied in in vivo models, the actual stresses on cartilage in most experimental animals are a matter of conjecture and difficult to precisely control. In contrast, stresses can be closely monitored and controlled in in vitro systems, but only short-term responses can be studied due to culture-related instability. These limitations leave a knowledge gap that is unlikely to be bridged by further experimental work. However, it may still be possible to extrapolate from short term in vitro data to OA-relevant time frames using in silico models [20, 31]. Here we describe advanced biomathematical models that draw on the wealth of knowledge of chondrocyte mechanotransduction to portray realistic cartilage stress responses.

Articular cartilage response to mechanical loading is viscoelastic, largely due to the interaction between the solid and fluid phases of its composition. To this end, cartilage is described as a biphasic material and is generally studied as a mixture of an elastic solid and interstitial fluid. The diffusive momentum exchange between the two phases regulates matrix deformation (via fluid exudation) when mechanical stimulus is imposed.

In this investigation, we attempt to extend and modify a reaction-diffusion-delay model of cartilage lesion formation [20] by adding features of the linear biphasic theory to simulate cyclic compressive loading. The governing equations of this model would be able to predict displacement of the solid matrix of the tissue (referred to as tissue strain) when a cyclic loading waveform is applied. As opposed to a single blunt impact injury (as was the case in [20] and explored more fully in [19]), the objective of this study is to simulate cartilage response to injurious cyclic compressive loading.

Physiological cyclic loading generally produces tissue deformations of less than 20%, which are not considered to cause any meaningful destruction. The underlying criterion in this model is that chondrocytes die when consolidated tissue strains of large magnitudes (greater than 40% of original tissue thickness) are induced.

We make the following implicit modeling assumptions in our loading term about the material properties of articular cartilage: it is a composite structure with an intrinsically incompressible, porous and elastic solid phase (chondrocytes, collagen and proteoglycans); and the fluid phase is assumed to be intrinsically incompressible and inviscid. Moreover, we assume cyclic loading of cartilage is imposed on a known region of cartilage surrounded by unloaded tissue. The loaded region is simplified to be a radially symmetric one-dimensional case of cyclic compression via a porous filter in a confined configuration.

2 One-dimensional model with implicit mechanical loading

In articular cartilage, dynamic mechanical loads can stimulate biosynthetic activity. Studying the environment of chondrocytes under dynamic loading conditions can help explain this mechanical-biological phenomenon. In the model in this section, we modify a reaction-diffusion-delay model by Graham et al. [20]. In [20], the lesion was formed by an initial, severe traumatic event with no further loading. In the model in this section, we assume instead that there is no initial damage, but rather cyclic compressive loading on a small part of the cartilage. The loading is expressed through a deformation term in the system of partial differential equations, rather than through explicit mechanical terms.

We assume circular symmetry so that the system components depend only on radius (r), time (t) and time delays (τ₁, τ₂). We simulate an oscillating load on a small region near the origin (0 ≤ r ≤ 0.5 cm).

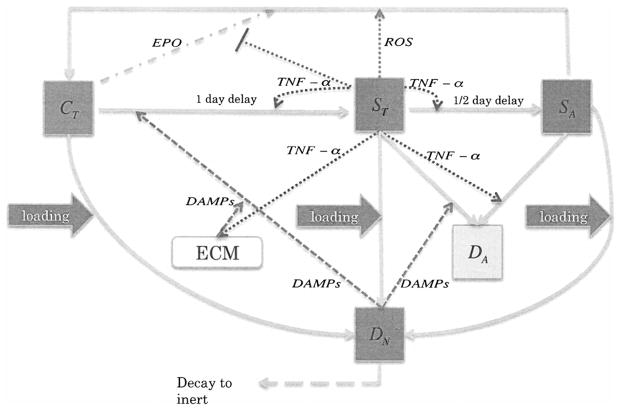
The components of our system fall into two main categories, cells and chemicals. We also track extracellular matrix density. A schematic of the system is presented in Figure 1. The cellular components of our system are

Figure 1.

Schmatic of the articular cartiage lesion formation process under cyclic loading.

• C(r, t) = population density (cells per unit area) of healthy chondrocytes.

• S_T(r, t) = population density of “catabolic” chondrocytes. Catabolic chondrocytes have been signaled by alarmins and are capable of synthesizing TNF-α and other cytokines associated with inflammation. Healthy cells signaled by DAMPs or TNF-α enter into the catabolic state and begin to synthesize TNF-α and produce reactive oxygen species (ROS).

• S_A(r, t) = population density of EPOR-active chondrocytes. EPOR-active chondrocytes are cells that have been signaled by TNF-α and express a receptor (EPOR) for EPO. It should be noted that there is a time delay of 8–12 hours before a cell expresses the EPO receptor after being signaled to become EPOR-active [14].

• D_N(r, t) = population density of necrotic chondrocytes. Necrotic (lysing) cells release DAMPs.

• D_A(r, t) = population density of apoptotic chondrocytes. Apoptotic cells no longer play a role in the system, and are tracked explicitly to verify the conservation of cell quantities.

Since EPOR-active cells express a receptor for EPO, they may switch back to the healthy state if signaled by EPO. However, as discussed in [14], TNF-α limits production of EPO. Thus there is a balance between EPO and TNF-α that determines the spreading behavior of cartilage lesions. The catabolic and EPOR-active “sick” classes form the penumbra, the boundary region between the lesion and healthy tissue. Because of the continuing role they play in the system, we explicitly track lysing necrotic cell densities (D_N). Cells that have become apoptotic (D_A) no longer play a relevant role in the system (by definition of apoptosis). Their densities are tracked explicitly in the mathematical model for bookkeeping purposes and as a placeholder for further models where cell volume fractions may be the quantities of interest. This differs from the model in [20] where apoptotic cells were not tracked explicitly, but were instead represented by sink terms in the equations for S_T and S_A.

We assume chondrocytes in all states have negligible motility, although we track them explicitly in space since their densities will differ as they respond to the biochemical components of the system.

The chemical and material components of our system are

• R(r, t) = concentration of reactive oxygen species (ROS). ROS affects the production of EPO by healthy cells.

• M(r, t) = concentration of alarmins (DAMPs). DAMPs signal healthy cells to enter the catabolic state, which in turn produce TNF-α.

• F(r, t) = concentration of tumor necrosis factor alpha (TNF-α). TNF-α, along with EPO, is the main driver of our system. TNF-α

  • causes healthy cells to become catabolic,

  • causes catabolic cells to enter the EPOR-active state [14],

  • influences apoptosis of catabolic and EPOR-active cells,

  • causes a chain of events that leads to the degradation of extracellular matrix, which in turn increases the concentration of DAMPs (for mathematical convenience we represent these as direct effects),

  • limits the production of EPO [14].

• P(r, t) = concentration of erythropoietin (EPO). EPO causes EPOR-active cells to return to the healthy state, and thus, in our model, is the check on the spread of the inflammation.

• U(r, t) = density of extracellular matrix (ECM). ECM is degraded by TNF-α, and in the process releases DAMPs.

The spatial dynamics of the system are governed by the diffusion of the four chemical components (R, M, F, P). The extracellular matrix, like the chondrocytes, is assumed to have negligible motility.

Our model equations are

$${\partial }_{t}C(r,t)=\alpha S_A\frac{P}{{\lambda }_P+P}-{\beta }_{1}C\frac{M}{{\lambda }_M+M}H(P_c-P)-{\beta }_{2}C\frac{F}{{\lambda }_F+F}H(P_c-P)-\mathrm{\Gamma }(\epsilon ,U,r)C,$$ (1a)

$${\partial }_t{S}_T(r,t)={\beta }_{1}C\frac{M}{{\lambda }_M+M}H(P_c-P)-{\beta }_{2}C\frac{F}{{\lambda }_F+F}H(P_c-P)-\gamma S_T(t-{\tau }_1)\frac{F(t-{\tau }_1)}{{\lambda }_F+F(t-{\tau }_1)}-\nu S_T\frac{F}{{\lambda }_F+F}\frac{M}{{\lambda }_M+M}-\mathrm{\Gamma }(\epsilon ,U,r)S_T,$$ (1b)

$${\partial }_t{S}_A(r,t)=\gamma S_T(t-{\tau }_1)\frac{F(t-{\tau }_1)}{{\lambda }_F+F(t-{\tau }_1)}-\alpha S_A\frac{P}{{\lambda }_P+P}-{\mu }_{S_A}{S}_A\frac{F}{{\lambda }_F+F}-\mathrm{\Gamma }(\epsilon ,U,r)S_A,$$ (1c)

$${\partial }_t{D}_N(r,t)=-{\mu }_{D_N}{D}_N+{\mu }_{S_T}{S}_T+\mathrm{\Gamma }(\epsilon ,U,r)(C+S_T+S_A),$$ (1d)

$${\partial }_t{D}_A(r,t)={\mu }_{S_A}{S}_A\frac{F}{{\lambda }_F+F}+\nu S_T\frac{F}{{\lambda }_F+F}\frac{M}{{\lambda }_M+M},$$ (1e)

$${\partial }_{t}U(r,t)=-{\delta }_{U}U\frac{F}{{\lambda }_F+F}H(P_c-P),$$ (1f)

$${\partial }_{t}R(r,t)=\frac{1}{r}{\partial }_r(r{D}_R{R}_r)-{\delta }_{R}R+{\sigma }_R{S}_T,$$ (1g)

$${\partial }_{t}M(r,t)=\frac{1}{r}{\partial }_r(r{D}_M{M}_r)-{\delta }_{M}M+{\sigma }_M{D}_N+{\sigma }_{U}U\frac{F}{{\lambda }_F+F},$$ (1h)

$${\partial }_{t}F(r,t)=\frac{1}{r}{\partial }_r(r{D}_F{F}_r)-{\delta }_{F}F+{\sigma }_F{S}_T,$$ (1i)

$${\partial }_{t}P(r,t)=\frac{1}{r}{\partial }_r(r{D}_P{P}_r)-{\delta }_{P}P+{\sigma }_{P}C\frac{R(t-{\tau }_2)}{{\lambda }_R+R(t-{\tau }_2)}\frac{\mathrm{\Lambda }}{\mathrm{\Lambda }+F},$$ (1j)

for t > 0 and 0 ≤ r ≤ r_m where r_m = 2.5 cm is the radius of our tissue sample.

The function H(θ) is the Heaviside function. From [14] we have P_c = 1 nanomolar.

For spatial densities, we assume uniformity in the top centimeter of the cartilage so that densities per cm³ are also densities per cm² on the surface.

Initial conditions are C(r, t) = 10⁵ cells/cm², U(r, t) = 30 mg/cm², and S_T(r, t) = S_A(r, t) = D_N(r, t) = D_A(r, t) = R(r, 0) = M(r, 0) = F(r, 0) = P(r, 0) = 0. We use homogeneous Neumann boundary conditions for the chemical concentrations:

$$\frac{\partial R}{\partial r}{\mid }_{r=0}=\frac{\partial M}{\partial r}{\mid }_{r=0}=\frac{\partial F}{\partial r}{\mid }_{r=0}=\frac{\partial P}{\partial r}{\mid }_{r=0}=0,$$

and

$$\frac{\partial R}{\partial r}{\mid }_{r=r_m}=\frac{\partial M}{\partial r}{\mid }_{r=r_m}=\frac{\partial F}{\partial r}{\mid }_{r=r_m}=\frac{\partial P}{\partial r}{\mid }_{r=r_m}=0.$$

2.1 The cyclic loading term

Central to our cyclic loading model is the function Γ(ε, U, r) that represents the damage caused by cyclic loading. Cyclic loading in our case is continuous and leads to a steady-state strain. The goal of the model described in system (1) is to give a simple, conceptual mathematical model and simulation of the effects of cyclic loading on articular cartilage lesion formation. The model in this section extends the model in [20] in a simple, yet still relevant way.

To represent the effects of loading we use the function

$$\mathrm{\Gamma }(\epsilon ,U,r)=-24ln(1-0.01p_0(e^{K_U\epsilon }-e^{20K_U}))\frac{{\lambda }_U}{{\lambda }_U+U},$$ (2)

for 0 ≤ r ≤ r_l, and Γ(ε, U, r) = 0 for r > r_l, where r_l = 0.25 cm is the radius of the region of tissue experiencing loading. We note that Γ is non-negative.

The form of Γ in (2) is based on recent results on cell death as a function of equilibrium strain [15]. There are some limitations to using this data, even though it is the best available. The death rate is measured one hour after loading; further results are needed to build a function with respect to both strain and time. Cells may not keep dying; death may stop at some point even if the same loading process continues.

In section 2.3 we present results for different values of the strain ε, which has unit of percent.

2.2 Parameterization

The dependence of Γ on ECM density U means that our equation for U is relevant to cell death. We assume that ECM is only degraded by the effects of TNF-α. The degradation of ECM is measured by the decrease in concentration of SO₄. The sulfite groups decorating the aggrecan proteins are the groups that matter – the aggrecan protein is just an elaborate means to keep sulfates in the solid phase and in place in the matrix (so-called “fixed charges”). In an “sGAG” assay [18] there is an average of 30 gSO₄/L cartilage. The molecular weight of SO₄ is 96 g/mol so that the molarity of SO₄ is

$$\frac{30\mathrm{g}/\mathrm{L}}{96\mathrm{g}/\text{mol}}=0.3125\text{mol}/\mathrm{L}=3125\text{micromolars}/{\text{cm}}^3.$$

To obtain the parameter δ_U for ECM decay we note that the decay rate of SO₄ under one nanomolar of TNF-α is about 16% per week under 25 ng/ml = 1.4706 nanomolar of TNF-α [24]. Then the decay modulus of SO₄ is

$$-{\delta }_U\frac{F}{{\lambda }_F+F}=ln(1-0.1/7)/\text{day}=-0.0144/\text{day}.$$

Using F = 1.4706 nM and λ_F = 0.5 nM we get δ_U = 0.0193/day.

For δ_F we have that the half life of TNF-α is around 100 hrs [30]. So ${\delta }_F=-\frac{24}{100}ln(\frac{1}{2})=0.1664\frac{1}{\text{day}}$. For The coefficient δ_P, the half life of EPO is around 30 hrs [17]. So ${\delta }_P=-\frac{24}{30}ln(\frac{1}{2})=0.5545\frac{1}{\text{day}}$. For δ_M, the half life of DAMPs is around 30 hrs [21]. So ${\delta }_M=-\frac{24}{30}ln(\frac{1}{2})=0.5545\frac{1}{\text{day}}$. To obtain decay rates from the experimental results in [21, 30], we used the “N-end rule” [29].

For the coefficient δ_R, the natural half life of ROS is around 14 hrs at 0.1 nanomolar concentration. So ${\delta }_R=-\frac{24}{14}ln(\frac{1}{2})=1.1883\frac{1}{\text{day}}$. However, under the superoxide dismute SOD, the decay of ROS is almost instantaneous. We don’t know when this reaction will happen, as it is hard to measure. So we assume the coefficient δ_R = 60 in our model, which means the half life of ROS is less than 20 mins.

To obtain the parameter σ_U for the release of DAMPs from ECM, we assume 30 mg/cm³ of ECM (i.e., SO₄) might release 10 ng/ml of DAMPs when exposed to 25 ng/ml of TNF-α. To estimate the molecular weight of DAMPs we consider the weight of one species, HMGB1, which has a molecular weight of 29 kDA. Recall the source term for DAMPs is ${\sigma }_{U}U\frac{F}{{\lambda }_F+F}$. Then

$$\begin{array}{l}{\sigma }_{U}U\frac{F}{{\lambda }_F+F}=\text{change}\text{rate}\text{of}\text{DAMPs}=10\text{ng}/({\text{cm}}^3·\text{day})\\ =\frac{10\times {10}^{-9}\mathrm{g}/{\text{cm}}^3·\text{day}}{29000\mathrm{g}/\text{mol}}=0.3448\times {10}^{-9}\text{mol}/(\mathrm{L}·\text{day}).\end{array}$$

Using U = 30 mg/cm³, F = 1.4706 nM and λ_F = 0.5 nM, we get

$$\begin{array}{l}{\sigma }_U=0.3448·0.7463/30\times {10}^{-9}\frac{\text{mol}/\mathrm{L}·\text{day}}{\text{mg}/{\text{cm}}^3}\\ =0.0154\frac{\text{nanomolar}·{\text{cm}}^3}{\text{mg}·\text{day}}.\end{array}$$

We need to reconcile the dimension to our model. The behavior of the cartilage is sufficiently homogeneous at the top 1 cm layer that we can use in the model the parameter ${\sigma }_U=0.0157\frac{\text{nanomolar}·{\text{cm}}^2}{\text{mg}·\text{day}}$.

To obtain the parameter σ_R for the release of ROS from catabolic cells, we assume 1–2% of oxygen consumed is converted to superoxides. Zhou et al. [32] estimate the maximum oxygen consumption rate to be 10 nMoles per million cells per hour in normal conditions (5%–21% oxygen). Then

$${\sigma }_R=\frac{0.01·10\text{nMoles}}{{10}^6\text{cells}·\mathrm{h}}=\frac{0.1·24·{10}^3}{{10}^6}\frac{\text{nMoles}}{\mathrm{L}}\frac{{\text{cm}}^3}{\text{day}·\text{cells}}.$$

Simplifying and assuming heterogeneity of the top layer, we get

$${\sigma }_R=0.0024\frac{\text{nanomolar}·{\text{cm}}^2}{\text{cells}·\text{day}}.$$

To obtain the parameter σ_F, we use that the release rate of TNF-α by catabolic cells is 100 pg/ml · per 12 hr by 5 × 10⁴ cells/ml [28]. Then

$${\sigma }_F=\frac{100\times {10}^{-12}\times {10}^3\mathrm{g}·({\text{cm}}^3/\mathrm{L})}{5\times {10}^4\times 0.5\times 17\times {10}^3(\mathrm{g}/\text{mol})·\text{cells}·\text{day}}.$$

Simplifying and assuming heterogeneity of the top layer, we get

$${\sigma }_F=2.35·{10}^{-7}\frac{\text{nanomolar}·{\text{cm}}^2}{\text{cells}·\text{day}}.$$

To obtain the parameter σ_M, we use that the release rate of HMGB1 is 3 ng/ml · per day by 2 × 10⁵ cells/ml [28]. Then

$${\sigma }_M=\frac{3\times {10}^{-9}\times {10}^3\mathrm{g}·({\text{cm}}^3/\mathrm{L})}{2\times {10}^5\times 29\times {10}^3(\mathrm{g}/\text{mol})·\text{cells}·\text{day}}.$$

Simplifying and assuming heterogeneity of the top layer, we get

$${\sigma }_M=5.17·{10}^{-7}\frac{\text{nanomolar}·{\text{cm}}^2}{\text{cells}·\text{day}}.$$

To obtain the parameter σ_P, we use that the release rate of EPO by healthy cells is 18 ng/ml · per 4 days by 10⁵ cells/cm² [14]. Then

$${\sigma }_P=\frac{18\times {10}^{-9}\times {10}^3\mathrm{g}·({\text{cm}}^3/\mathrm{L})}{{({10}^5)}^{\frac{3}{2}}\times 4\times 34\times {10}^3(\mathrm{g}/\text{mol})·\text{cells}·\text{day}}.$$

Simplifying and assuming heterogeneity of the top layer, we get

$${\sigma }_P=4.2·{10}^{-5}\frac{\text{nanomolar}·{\text{cm}}^2}{\text{cells}·\text{day}}.$$

For σ_P we also conduct runs with a higher value corresponding to treatment that increases EPO; this is not a “natural” production rate. We choose σ_P = 0.0033, which is high enough to trigger the Heaviside functions in the model so that P becomes larger than P_c and shuts off the inflammation response.

The parameters K_U and p₀ are experimental settings [15]. Diffusion coefficients were obtained from measurements presented in [23], delays from [14], and the remaining parameters were approximated. The parameters for system (1) are summarized in Table 1.

Table 1.

Parameter Values

Parameter	Value	Units	Reason
DR	0.1	$\frac{{\text{cm}}^2}{\text{day}}$	Determined from [23]
DM	0.05	$\frac{{\text{cm}}^2}{\text{day}}$	Determined from [23]
DP	0.005	$\frac{{\text{cm}}^2}{\text{day}}$	Determined from [23]
DF	0.05	$\frac{{\text{cm}}^2}{\text{day}}$	Determined from [23]
δR	60	$\frac{1}{\text{day}}$	Approximated
δM	0.5545	$\frac{1}{\text{day}}$	Determined from [21]
δF	0.1664	$\frac{1}{\text{day}}$	Determined from [30]
δP	3.326	$\frac{1}{\text{day}}$	Taken from [17]
δU	0.0193	$\frac{1}{\text{day}}$	Determined from [24]
σR	0.0024	$\frac{\text{nanomolar}·{\text{cm}}^2}{\text{day}·\text{cells}}$	Determined from [32]
σM	5.17 · 10−7	$\frac{\text{nanomolar}·{\text{cm}}^2}{\text{day}·\text{cells}}$	Determined from [28]
σF	2.35 · 10−7	$\frac{\text{nanomolar}·{\text{cm}}^2}{\text{day}·\text{cells}}$	Determined from [28]
σP	4.2 · 10−5 or 0.0033	$\frac{\text{nanomolar}·{\text{cm}}^2}{\text{day}·\text{cells}}$	Determined from [14]
σU	0.0154	$\frac{\text{nanomolar}·{\text{cm}}^2}{\text{day}·\text{mg}}$	Determined from [24]
Λ	0.5	nanomolar	Approximated
λR	10	nanomolar	Approximated
λM	0.5	nanomolar	Approximated
λF	0.5	nanomolar	Approximated
λP	0.5	nanomolar	Approximated
λU	1	mg/cm2	Approximated
KU	0.0545	proportion	Experimental setting [15]
α	1	$\frac{1}{\text{day}}$	Approximated
β1	10	$\frac{1}{\text{day}}$	Approximated
β2	5	$\frac{1}{\text{day}}$	Approximated
γ	1	$\frac{1}{\text{day}}$	Approximated
ν	0.05	$\frac{1}{\text{day}}$	Approximated
p0	1	$\frac{1}{\text{day}}$	Experimental setting [15]
μSA	0.1	$\frac{1}{\text{day}}$	Approximated
μDN	0.05	$\frac{1}{\text{day}}$	Approximated
Pc	1	nanomolar	Taken from [14]
τ1	0.5	day	Taken from [14]
τ2	1	day	Taken from [14]

2.3 Simulation results

We computed results of our system for four values of the strain, ε = 0.3, 0.4, 0.6, and 0.8, crossed with two values of the EPO production parameter: a “low” value of σ_P = 4.2 · 10⁻⁵ and a “high” value of σ_P = 3.3 · 10⁻³. The low value corresponds to the parameter obtained from [14] in Section 2.2, whereas the high value is set to trigger the Heaviside functions in our system and can correspond, for example, to the effects of treatment. Extremal values at t = 10 days of the system variables are presented in Tables 2 and 3 and provide an overview of the behavior of entire system. We focus on simulations results most relevant to understanding the inflammation process, namely the spatial and temporal dynamics of the healthy, catabolic and EPOR-active cell populations.

Table 2.

Table of variable ranges under low EPO production at t=10 days

variable	Strain=30%	Strain=40%	Strain=60%	Strain=80%
C min	1.374 × 104	2.58 × 103	71.02	0
ST max	7.254 × 104	8.627 × 104	8.909 × 104	9.07 × 104
SA max	2.79 × 103	5.524 × 103	1.105 × 104	1.533 × 104
DA max	22	64	180	302
DN max	1.213 × 104	2.888 × 104	6.35 × 104	8.616 × 104
U min	29.933	29.894	29.862	29.824
F max	0.0257	0.0332	0.0411	0.0476
M max	0.0253	0.0428	0.0663	0.0744
P max	0.3234	0.3159	0.3038	0.3006
R max	2.7323	3.3031	3.479	3.493

Table 3.

Table of variable ranges under high EPO production at t=10 days

variable	Strain=30%	Strain=40%	Strain=60%	Strain=80%
C min	8.029 × 104	5.74 × 104	1.01 × 104	0
ST max	4.778 × 103	7.527 × 103	2.78 × 104	9.022 × 104
SA max	21.29	38.28	118	355
DA max	0.099	0.39	1.648	7
DN max	1.213 × 104	2.887 × 104	6.35 × 104	8.616 × 104
U min	29.999	29.9988	29.9987	29.98
F max	0.0027	0.0037	0.005	0.0073
M max	0.0082	0.0168	0.0349	0.0411
P max	7.919	9.2917	13.718	21.28
R max	0.189	0.2967	0.5139	0.699

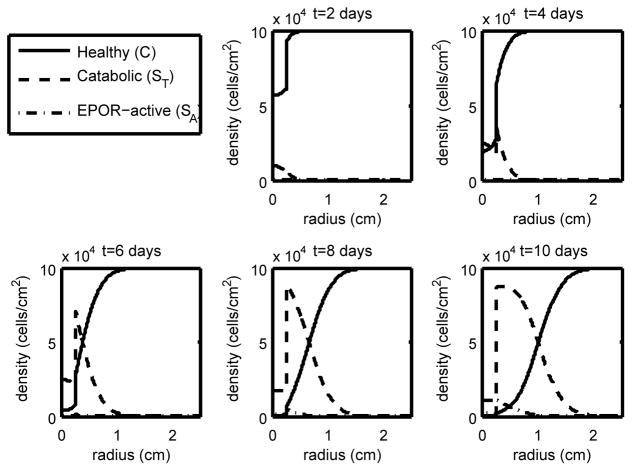
To more fully understand the changes in the system due to changes in the strain, we present computational results for ε = 0.4, 0.6, and 0.8 at low EPO production in Figures 2–4. To understand the effects of increasing EPO production, we present computational results for ε = 0.6 at high EPO production, noting that the responses at other strains are similar. Computational results for ε = 0.6 at high EPO production are shown in Figure 5.

Figure 2.

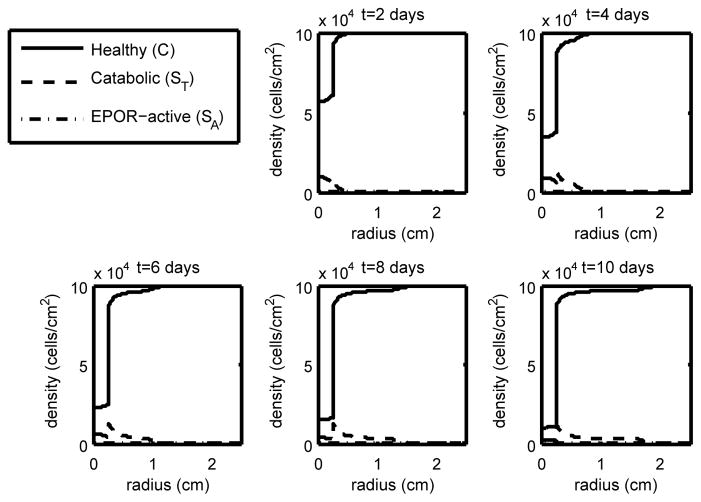
The density of the healthy, catabolic and EPOR-active chondrocytes (C(r, t), S_T(r, t), S_A(r, t)) at t = 2, 4, 6, 8, 10 days with ε = 0.4 and σ_P = 4.2 · 10⁻⁵ (light strain with low EPO production). We see that with relatively light strain we have a relatively narrow penumbra (the region dominated by S_T and S_A) compared to cases of higher strain with low EPO, constituting a relatively narrow lesion.

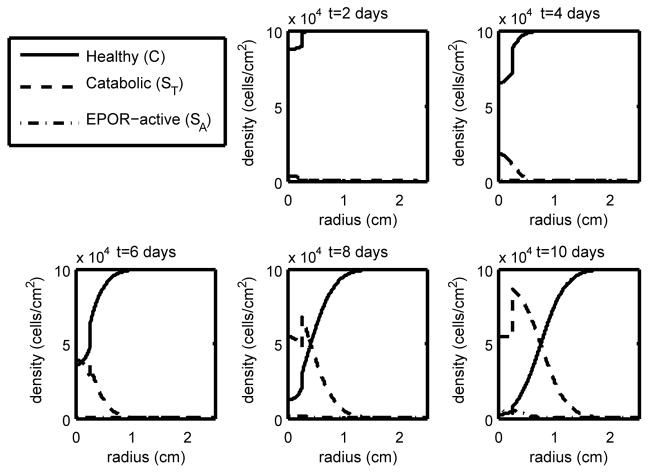
Figure 4.

The density of the healthy, catabolic and EPOR-active chondrocytes (C(r, t), S_T(r, t), S_A(r, t)) at t = 2, 4, 6, 8, 10 days with ε = 0.8 and σ_P = 4.2 · 10⁻⁵ (heavy strain with low EPO production). With high strain we have cell death further from the strike zone and our penumbra (the region dominated by S_T and S_A) has widened compared to the low and medium strain cases, resulting in a much larger lesion.

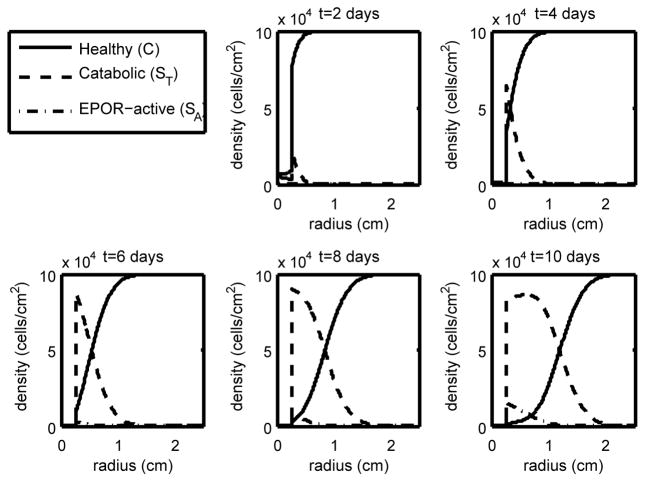
Figure 5.

The density of the healthy, catabolic and EPOR-active chondrocytes (C(r, t), S_T(r, t), S_A(r, t)) at t = 2, 4, 6, 8, 10 days with ε = 0.6 and σ_P = 3.3 · 10⁻³(medium loading with high EPO production). With high EPO production, we see abatement of the penumbra (the region dominated by S_T and S_A) and thus control of the lesion when compared to the low EPO production cases.

As expected, higher levels of strain result in lower levels of healthy cells and a larger area of inflammation (see the progression in Figures 2–4). Also as expected, elevated EPO levels result in a check on the inflammation process (Figure 5). The dynamics in the “penumbra”, the region of catabolic and EPOR-active cells, is perhaps the most insightful result, showing a preponderance of catabolic over EPOR-active cells (see Figures 2–4). The relative numbers of catabolic versus EPOR-active cells is currently difficult to measure.

The success of our model in incorporating a relatively large number of experimentally measured parameters and obtaining results matching observed inflammation response [15] under our “low” EPO case validates the mechanistic assumptions that went into our model (the match is semi-quantitative in that the cell numbers are not known exactly, but the lesion sizes are). As such, we find from our simulation results greater confidence that the model itself is a firm foundation for a truly predictive model. More importantly at this stage of theoretical development, the simulation results indicate that we have brought together disparate experiments and piecemeal understandings of system components and formed a more holistic understanding of articular cartilage lesion under cyclic loading.

For the “high” EPO case, much more work remains to be done, both in model refinement and validation. How one increases EPO or other chemicals that act like EPO in the cartilage environment affects both model refinement and model validation.

Although perhaps of less interest to a clinician, knowing the dynamics of live cell subtypes within the penubra is an important means of validating these results.

2.4 Parameter sensitivity

We studied the sensitivity of our estimated parameters (those not taken from experimental measurements in the literature). In particular, we considered α, β₁, β₂, γ, ν, λ_R, λ_M, λ_F, λ_P, λ_U, μ_DN, μ_SA, and Λ. The base values for these parameters are given in Table 1.

We conducted simulations with both high and low EPO production at strains of 0.3, 0.4, 0.6, and 0.8. We varied each parameter from the base values according to

$$\alpha \in \{0.1,0.5,1,1.5,2\},$$ (3a)

$${\beta }_1\in \{1,5,10,15,20\},$$ (3b)

$${\beta }_2\in \{1,2.5,5,7.5,10\},$$ (3c)

$$\gamma \in \{0.1,0.5,1,1.5,2\},$$ (3d)

$${\lambda }_F\in \{0.1,0.25,0.5,0.75,1\},$$ (3e)

$${\lambda }_M\in \{0.1,0.25,0.5,0.75,1\},$$ (3f)

$${\lambda }_P\in \{0.1,0.25,0.5,0.75,1\},$$ (3g)

$${\lambda }_R\in \{1,5,10,15,20\},$$ (3h)

$${\lambda }_U\in \{0.1,0.5,1,1.5,2\},$$ (3i)

$${\mu }_{D_N}\in \{0.01,0.025,0.05,0.075,0.1\},$$ (3j)

$${\mu }_{S_A}\in \{0.01,0.05,0.1,0.15,0.2\},$$ (3k)

$$\nu \in \{0.01,0.025,0.05,0.075,0.1\},$$ (3l)

$$\mathrm{\Lambda }\in \{0.1,0.25,0.5,0.75,1\}.$$ (3m)

For most parameters, we found only quantitative, rather than qualitative, differences in runs using the perturbed parameters. The exception was for the Michaelis-Menten constants λ_F, λ_M, and λ_R. For small values of these parameters (0.1, 0.1, and 1, respectively), the Michaelis-Menten functions behave closer to constant functions. The results are non-monotone behavior near the boundary of the strike zone and the rest of the tissue, in particular abiological spikes. This is a reminder that the Michaelis-Menten forms constitute switches. Values of the Michaelis-Menten constants that are too low result in a qualitatively different term in the equations, which render qualitatively different results.

2.5 Numerical methodology

We first did a semi-discretization in space, using the radially symmetric finite difference scheme presented in Appendix C of [2]. The semi-discrete system of delay-differential equations was then solved in MATLAB by using dde23 [26]. This approach is suitable for the models in this paper and was also used to solve the model equations in [20]. Computational convergence studies for each dependent variable in system (1) are shown in Tables 4–7.

Table 4.

∞-norm relative errors under low EPO production

variable	Strain=30%	Strain=40%	Strain=60%	Strain=80%
C	0.0242	0.0314	0.0244	0.0220
ST	0.0230	0.0225	0.0219	0.0212
SA	0.0383	0.0352	0.0304	0.0272
DA	0.0525	0.0460	0.0371	0.0318
DN	0.0000	0.0000	0.0000	0.0000
ECM	0.0000	0.0000	0.0000	0.0000
TNF-α	0.0224	0.0204	0.0204	0.0191
EPO	0.0240	0.0244	0.0319	0.0323
DAMPs	0.0219	0.0204	0.0184	0.0171
ROS	0.0230	0.0226	0.0838	0.1085

Table 7.

2-norm relative errors under high EPO production

variable	Strain=30%	Strain=40%	Strain=60%	Strain=80%
C	0.0002	0.0003	0.0008	0.0015
SA	0.0138	0.0134	0.0127	0.0116
ST	0.0164	0.0158	0.0143	0.0119
DA	0.0191	0.0192	0.0200	0.0167
DN	0.0000	0.0000	0.0000	0.0000
ECM	0.0000	0.0000	0.0000	0.0000
TNF-α	0.0128	0.0115	0.0204	0.0104
EPO	0.0130	0.0126	0.0135	0.0158
DAMPs	0.0124	0.0120	0.0115	0.0105
ROS	0.0135	0.0132	0.0148	0.0247

The relative errors found are well within experimental or real world measurement error, are primarily due to tracking a sharp front, and there is no indication that the computed solutions differ qualitatively from the true solutions. We include such detailed error results in keeping with the theme of the journal.

3 Conclusions

In this paper we presented biomathematical models based on observations of chondrocyte mechanotransduction. When run in concert with a finite element program to incorporate the physical effects of mechanical compression, our new model may prove to be useful for predicting the consequences of long-term exposure to the broad range stresses experienced by cartilage in human joints. As such the model may be useful for identifying critical stress thresholds that, over time, increase the risk for osteoarthritis.

We have demonstrated that using delay differential equations to model the delays in the cellular responses to cytokines in articular cartilage lesion formation is a reasonable approach for models with the complexity of those in this paper. However, as model complexity increases, the use of delay differential equations will lead to computational challenges down the line due to the need to keep in memory vast past history information. Adding somewhat to these challenges is that the commercial off-the-shelf (COTS) solution, dde23 in Matlab, uses an explicit time integration method for the differential equations. The stability constraints introduced by the semi-discretization in space force dde23 to take time steps much smaller than what truncation error alone would dictate. This, in turn, exasperates the memory issues caused by the need to store the past history of the system.

One solution may be to use a different time discretization. Ho we only have cell death near the strike zone, so that the lesion is abated despite low EPO. However, wever, even a “stiff” DDE solver for the programming environment R was found not to be appreciably faster [27]. Going further, we could write tailor-made compiled code for this problem, but the solver will still have the underlying challenge of needing to store the time histories of the system to compute the delay terms. These data sets can be quite large and create memory issues on all but the largest nodes in cluster, for example.

The limitations of using delay differential equations and the computational methods for them may be ameliorated by converting the delay into a physiological property of individual cells, namely time since exposure to the relevant cytokine. The partial differential equations for the cell populations that result from this approach include an additional independent variable and a derivative term for “age” structure. Essentially, one would be taking the equivalent of a non-Markov process and converting it into the equivalent of a Markov process. Although the addition of an extra dimension to the problem may seem like an unwanted complication, the reality is that the delays in a delay-differential equation require the retention of time histories of the system that can quickly become much larger to store in memory than the extra age dimension. This difference in cost is even more pronounced if we use highly efficient methods for age- and space-structured problems [3, 5, 9, 10]. These methods have a history of effective use in the modeling and simulation of biofilms [8, 11, 12, 22], avascular tumor invasion [13], and Proteus mirabilis swarm colony development [4, 6, 7]. Using age structure to represent the delays in cellular responses to cytokines is an approach suggested by our experiences with the simulations in this paper.

Despite the challenges the use of delay terms presents for computational studies with greater complexity, the use of delays in the first efforts in [20] and in this paper is warranted; we have the tautology that delay terms are more easily understood to represent delays. Moreover, some modelers may find the models with delays are better suited for inclusion in their own efforts. Other modelers may find that the greater flexibility inherent in using “age”, or some other physiologically structured variable, makes that approach preferable.

The value to the lab of our modeling and simulation effort is two-fold. First, the model serves as a “container” for a range of existing experimental data sets, and relates these data sets to one another in a manner that may not have been apparent beforehand. Second, the model validates and/or challenges assumptions about what mechanisms underlie what phenomena, and in doing so suggests what future experiments are most likely to lead to increased insight into articular cartilage lesion formation. A model fully parameterized by experiment is, in turn, a powerful predictive tool and thus serves to translate the work of the lab into products relevant to the clinic, such as the appropriate boosting of EPO concentrations at the lesion.

Figure 3.

The density of the healthy, catabolic and EPOR-active chondrocytes (C(r, t), S_T(r, t), S_A(r, t)) at t = 2, 4, 6, 8, 10 days with ε = 0.6 and σ_P = 4.2 · 10⁻⁵ (medium strain with low EPO production). We see that with medium strain our penumbra (the region dominated by S_T and S_A) has widened compared to the low strain case, constituting a potentially larger lesion.

Table 5.

2-norm relative errors under low EPO production

variable	Strain=30%	Strain=40%	Strain=60%	Strain=80%
C	0.0102	0.0132	0.0122	0.0110
SA	0.0140	0.0131	0.01237	0.0118
ST	0.0206	0.0186	0.0153	0.0134
DA	0.0261	0.0230	0.0180	0.0151
DN	0.0000	0.0000	0.0000	0.0000
ECM	0.0000	0.0000	0.0000	0.0000
TNF-α	0.0148	0.0122	0.0204	0.0114
EPO	0.0134	0.0144	0.0170	0.0175
DAMPs	0.0152	0.0137	0.0118	0.0107
ROS	0.0140	0.0133	0.0166	0.0235

Table 6.

∞-norm relative errors under high EPO production

variable	Strain=30%	Strain=40%	Strain=60%	Strain=80%
C	0.0006	0.0013	0.0045	0.0141
ST	0.0253	0.0305	0.0219	0.0420
SA	0.0375	0.0362	0.0304	0.0416
DA	0.0430	0.0588	0.0371	0.0559
DN	0.0000	0.0000	0.0000	0.0000
ECM	0.0000	0.0000	0.0000	0.0000
TNF-α	0.0213	0.0204	0.0203	0.0185
EPO	0.0249	0.0246	0.0306	0.0372
DAMPs	0.0188	0.0212	0.0220	0.0192
ROS	0.0253	0.0249	0.0743	0.1144